Российская академиянаук

Уральское отделение

Институт экономики

Л. А. Дедов, О. И.Боткин

ИНДЕКСНЫЙМакроструктурный

анализ экономическОЙдинамики

Основные понятия иприемы

макроструктурногоанализа

Монография

Екатеринбург 2013

УДК338(470)

ББК 65.012.2

Д86

Рецензенты:

доктор экономическихнаук, профессор А.Л.Кузнецов,

докторфизико-математических наук, профессорА.В. Летчиков

Ответственныйредактор

член-корреспондент РАН,доктор экономических наук,

профессор, Х.Н. Гизатуллин

Дедов, Л.А.

Д86 Индексныймакроструктурный анализ экономическойдинамики. Основные понятия и приемымакроструктурного анализа / Л.А. Дедов,О.И. Боткин. –Екатеринбург: Изд-во УРО РАН, 2013. – 107 с.

В монографии излагаютсяосновные приемы структурно-динамическогоанализа экономики. В том числе исследуютсябазовые структурные эффекты,разрабатывается теория сопряжения роста иструктурных сдвигов в экономике, даетсятеоретическая концепция структурногоцикла, подкрепленная статистическими расчетами.

Работа предназначенадля научных работников, преподавателейвузов, студентов и аспирантовэкономических специальностей.

ISBN978-5-9904608-1-2УДК 338 (470)

ББК 65.012.2

Dedov L.A., Botkin O.I. Index Macrostructural Analysis of Economic Dynamics.

The fundamental methods of structural-dynamicanalysis of economy are stated in monograph. Among others basic structuraleffects are investigated, the theory of growth and structural shiftsconjugating in economy is developed, the theoretical conception of structuralcycle, supported bystatistic calculations is given.

The monograph is intended for scientificworkers, teachers of high schools, students and post graduate students ofeconomic field.

© Л.А. Дедов, О.И. Боткин,2013

© УРО РАН, 2013

пРЕДИСЛОВИЕ

В основу предлагаемойработы положена ранее изданная монография:Л.А. Дедов, О.И. Боткин «Макроструктурныйдинамический анализ экономики. Часть 1.Основные понятия и приемымакроструктурного анализа» (Екатеринбург:УрО РАН, 2005). Причиной переиздания являетсязатянувшаяся работа над второй частьюмонографии, а также крепнущее убеждениеавторов, что уже изданный материал следуетуточнить и более четко отредактировать.Соответствующие изменения достаточнозначимы, и книга с их учетом можетрассматриваться как самостоятельнаяпубликация. Существенно приближена кобщепринятой используемая системаобозначений. Менее вольной стала такжетерминология. Ряд выводов сформулированыболее четко и более корректно.

С другой стороны, форматпереиздания имеет свои издержки. Так, неудалось в полной мере отреагировать на теновые результаты, которые получены запоследнее время специалистами в областианализа структурной динамикимакроэкономических систем.

Поэтому мы вынужденыограничиться общим перечислением авторов,как российских, так и зарубежных, которыевнесли наиболее заметный вклад запоследние 10 лет в теорию макроструктурногоанализа экономики. Из российскихспециалистов особо следует отметитьА.А. Акаева, В.А. Бессонова, П.А. Ватника,Д.В. Иванова, О.Ю. Кра-сильникова,Э.Н. Кузьбожева, Ю.В. Куренкова,Е.А. Назруллаеву, В.М. Пономарева,А.И. Сарыгулова, В.Н. Соколова,О.В. Спасскую, Н.В. Суворова, О.С. Сухарева,Е.В. Харченко, Ю.В. Яковца.

Наиболее интересныезарубежные авторы этого периода следующие:P. Dasgupta, D. Chakrobarty, J. Guo, M.A. Planting, M. Hirooka, Yi Kei-Mu,J. Zharg, J. Laitner, K. Natuhara, Pan Haoran, F. Kahrl, D.Rolang-Horst.

Интенсивно развиваютсяметоды структурно-динамического анализа. Вэтих условиях индексный макроструктурныйанализ является востребованным иактуальным направлением работы.

Авторы

Введение

Целью макроструктурногоанализа является:

–исследование влияния структурныхизменений в экономических агрегатах исистемах на их динамику;

–исследование влияния роста экономическихагрегатов на интенсивность и характерструктурных сдвигов.

Имеет смысл краткоостановиться на истории макроструктурногоанализа. Этот раздел экономическихисследований в основном сталразрабатываться начиная со второйполовины ХХ века. Основополагающиминеобходимо считать работы В. Леонтьева [21], А. Картер [17],Э. Денисона [15]. Наиболее глубокиерезультаты относительно взаимоувязкиструктуры и динамики выпускаэкономических систем получены в рамкахмагистральной теории. А именно доказано,что оптимальные траектории экономическойдинамики сходятся к состояниям с вполнеопределенной долевой структуройвыпуска [см. 20;22; 26; 36]. Параллельно с перечисленными вышенаправлениями в совместном анализединамики и структуры производстваразвивались экономико-статистическиеподходы их анализа, которые в ряде работбыли основными. Особо следует выделитьпопытки А.А. Нечаева и Ю.В. Яременко. А.А.Нечаев на большом фактическом материалепри помощи регрессионныхнелинейных зависимостейисследовал межстрановые различия вструктуре выпуска. Ю.В. Яременко вкомплексе изучил проблему влияниямежотраслевых связей на динамикународного хозяйства в рамках модели«затраты выпуск» [см. 25; 37]. Структурная проблематикав российской экономической наукеусилилась в трансформационный период1987–2002 гг.Выделяются основополагающие работы С.Ю.Глазьева и Д.С. Львова по теории технологических укладов[см. 10; 11; 12], важные исследованияосуществлены Х.Н. Гизатуллиным, егоучениками и последователями в областирасчета структурных траекторий развития,существен вклад Е.В. Балацкого, его коллег иучеников в теорию структурного цикла ианализа институциональных структурныхсдвигов в переходной экономике [см. 4; 5; 6; 7; 9;29]. Несмотря на сказанное, существует рядмалоизученных проблем индексногомакроструктурного анализа экономики. К нимможно отнести:

1) определение основныхструктурных эффектов в экономике ипринципов их расчета;

2) обоснованный выводпоказателя общего структурногосдвига;

3) выяснение свойствоценок сходства и различия экономическихструктур;

4) выявление зависимостимежду оценками структурных изменений ипоказателями роста экономическихагрегатов;

5) построениесинтетического показателя, позволяющегоквантифицировать структурно-динамическиепроцессы. Таким показателем в даннойработе является коэффициент структурнойэластичности выпуска;

6) разработкутеоретической концепции структурногоцикла в его основных вариантах:конъюнктурном, инновационном иинституциональном;

7) количественный анализфаз структурного цикла как стеоретических, так и с эмпирическихпозиций;

8) исследование явленияструктурно-динамическойнестабильности;

9) исследованиестационарных режимов макроструктурнойдинамики;

10) моделированиемакроструктурных динамических процессов,их проектирование и мониторинг;

11) исследованиерегиональных и отраслевых особенностейструктурной динамики;

12) исследованиемежстрановых различий в структурнойдинамике;

13) ретроспективныйанализ макроструктурных процессов вплановой экономике;

14) установление связеймежду макроструктурной динамикой иинновационными особенностямиэкономического развития, в том числевыявление прогрессивных и регрессивныхтенденций в динамике отраслевой структурыэкономики России и ее регионов;

15) формулировку основныхприемов экономического воздействия наструктурно-динамические процессы как спозиций макроуровня экономики, так и врегиональном аспекте.

Перечисленнаяпроблематика определяет содержание иструктуру данного исследования, котороеделится на две части. В части «Основныепонятия и приемы макроструктурногоанализа» изучается проблематика первых 8пунктов из приведенного выше их перечня. Вчасти «Специальные вопросымакроструктурного анализа» авторысосредотачивают внимание на исследованиипунктов с 9 по 15-й. Эта часть исследованиявыйдет отдельным выпуском.

1. Теориясопряжения роста

иструктурных сдвигов в экономике

Начать изложениецелесообразно с уточнения основныхприменяемых терминов и понятий.

В основном необходимоуточнить такие понятия, как структура,компонент структуры, структурный сдвиг ит.п. Кратко рассмотрим эти понятия.

Не вдаваясь детально вполемику по поводу термина «структура»,полемику, которая заняла целые десятилетияво время становления системной парадигмыисследования социально-экономическихявлений, будем понимать определяемыйтермин в смысле строения, устройстванекоторого объекта. Но и данное пониманиеявляется слишком широким для того, чтобыего операционально использовать. В этойсвязи следует заметить, что в такой отраслинаук о хозяйстве, как экономическаястатистика, уже устоялось вполнеопределенное толкование строенияэкономических агрегатов, разделяемоеведущими специалистами как в России, так иза рубежом.

Строение некоторогоэкономического агрегата или объектапонимается в данном случае как его долевойсостав, т.е. набор долей, каждая из которыххарактеризует некоторый внутреннеоднородный компонент. Чтобы не путатьтакое понимание структуры с другими, болееширокими версиями, будем в данной ситуацииговорить о долевой структуресоответствующего объекта или агрегата.Часто подобное узкое понимание структурыподвергается сомнению, особенно со стороныспециалистов по кибернетике ифилософии.

Так, утверждается, чтоструктура наряду с набором компонентовдолжна учитывать еще и связи междукомпонентами. Здесь надо отметить, чтодолевая структура в простейшем видеучитывает связи. А именно все долевыекомпоненты взаимосвязаны ивзаимообусловлены, ибо в сумме даютединицу. Таким образом, невозможноизменить один долевой компонент, не меняяпри этом некоторые другие, что и указываетна наличие связи.

Теперь надоопределиться стермином «структурный сдвиг», или«структурное изменение». Посколькупонятие долевой структуры уже разъяснено,то пояснить смысл структурного сдвига(изменения) несложно. Это не что иное, какпереход от одной долевой структурыисследуемого объекта или агрегата к другойего долевой структуре. Что касаетсяобъекта или агрегата, структура которогоисследуется, то здесь допустимы различныетолкования и уточнения. Мы прибегнем к нимв ходе дальнейшего анализа. Также далее втексте будут даны разъяснения еще рядаиспользуемых понятий.

1.1. Математическиеосновы анализа динамики

и структурыэкономики

1.1.1. Количества благ и ихдолевой состав

Теории экономическогороста и экономической структуры оперируютрядом сложных категорий и модельныхконструкций, в то время как некоторыебазовые понятия этих теорий, по сути дела,не определены, поэтому имеет смысл короткоих рассмотреть.

Прежде всего следуетвыяснить, что понимается под количеством вэкономике и товароведении. Естественносчитать, что экономические итовароведческие меры количеств заданы намножествах благ и услуг. Это означает, что вданном отношении можно использоватьконструкцию меры множества.

Предварительноопределим вспомогательные понятиясистемы, кольцаи полукольца множеств.

Системой множествназывается всякий объект, элементыкоторого представляют собой какие-либомножества. Дадим определение.

Непустая системамножеств Rназывается кольцом, если она обладает темсвойством, что из A  R иB  Rследует AB  R иA  B  R. Здесьзначок обозначает операциювзятия симметрической разности:

AB = (A \B) (B \ A).

Так как для любых А и В

А В = (АВ) (А В) иА \ В = А(А В),

то из А  R и В  R вытекает такжепринадлежность к R множеств А  В и А\ В. Таким образом, кольцо множеств естьсистема множеств, замкнутая по отношению квзятию суммы и пересечения, вычитанию иобразованию симметрической разности.Очевидно, что кольцо множеств замкнуто и поотношению к образованию любых конечныхсумм и пересечений вида

C =, D =.

Любое кольцо содержитпустое множество, так как всегда А \ А =.

Также введемопределение полукольца множеств.

Система множеств G называетсяполукольцом, если она содержит пустоемножество,замкнута по отношению к образованиюпересечений и обладает тем свойством, чтоиз принадлежности к G множеств А и вытекаетвозможность представления А в виде , где Аk – попарнонепересекающиеся множества из G, первое из которых есть заданноемножество А1.

Всякое кольцо множествR являетсяполукольцом, так как если А и А1 А входят в R, то имеет месторазложение

А = А1 А2,

где А2 =А \ А1.

Примером полукольца, неявляющегося кольцом множеств, можетслужить совокупность всех интервалов(a, b), отрезков [а,b]и полуинтервалов [а, b) и (а, b] на числовой прямой.При этом в число интервалов включается«пустой» интервал (а, а), а вчисло отрезков – отрезок, состоящий из однойточки [а, а].

Теперь можно перейти копределению меры.

Функция (А), где А – множество,называется мерой, если определена наполукольце множеств. Это требованиеявляется малоограничительным, так какэкономические и товароведческие объекты– блага иуслуги, как правило, допускают не толькоструктуру полукольца, но даже структурукольца множеств:

– – действительноечисло;

– (А) 0;

– (А В) = (А) + (В), если А В = [см. 18, с. 41, 42, 265].

Так как = и =, то () = ( ) = () + + (). Или () = 2(). Отсюда, () = 0, что имеет яснуюэкономическую интерпретацию для мер благ.Кроме того, считается, что имеет место и ещеодно более специфическое условие: (А) > 0, если А . Меру i-го блага, ресурса ит.п. будем также обозначать и другимибуквами, например Сi,Si, qi,xi, yi ит.п.

Кроме заданияаксиоматики меры блага, важно определитьправило перехода от меры к мере. Такойпереход происходит, например, когда благаоцениваются, и в других подобных случаях:метры переводятся в футы, килограммы– в фунты и т.п.Исходную меру обозначим через, а преобразованную– через , где –правило преобразования.

Выясним некоторыесвойства преобразования .

Итак, если А В =,А, то, во-первых, (А В) = (А) + (В), а во-вторых, , поскольку – мера.

Так как –преобразование, то ((А) + (В)).

Отсюда ((А) + (В)) = (А) + (В).

Следовательно, –аддитивный функционал. Известно, что если – рациональное число,а – аддитивныйфункционал, то ( ) = = ().

Наложим на следующее ограничение, естественновытекающее из смысла мер благ: если – рациональное число,то также обязано бытьрациональным. На экономическом языке этоозначает, например, что рациональноеколичество товара должно иметь цену,выраженную рациональным числом,рациональное число сантиметровпреобразуется в рациональное количестводюймов и т.п.

Для любогорационального и рационального(1) будет = (1),где –рациональное число. Кроме того, можнозаписать (1) =а (1).Отсюда

= ( (1)) = ((1)) = а (1) =а ( (1))=а.

Соотношение = (1) приразных рациональных и будет приводить к тому, что , т.е. число а –единственно для функционала 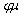на рациональных мерах. Кроме того,видно, что а– тожерациональное число.

В качестве мер (1)ограничимся теперь только рациональнымичислами. На самом деле, в явной формеэкономические измерения приводят только крациональным количествам благ и услуг. Вэтом имеется существенный смысл.Иррациональность, будь она явнозафиксирована, требовала бы приближения ипо избытку, и по недостатку. А подобнаянеопределенность вносит принципиальныезатруднения в установление правсобственности. Необходимость их четкойфиксации устраняет из экономической июридической практики иррациональные числакак выражения для мер благ и услуг, а такжеобъектов собственности любогохарактера.

Кроме того, допустивиррациональные числа для выраженияколичеств благ и услуг, мы бы сделалипроцедуру подсчета этих количествнеограниченной во времени, трансакциистали бы бесконечно дорогими и техническинереализуемыми. Следовательно, сделки вэтой ситуации в принципе невозможны.Реальное существование сделок говорит оналичии только рациональных экономическихмер.

В саму процедуруэкономических измерений заложена схемаприведения определяемых количеств какнацело кратных единичным количествам илиих целочисленным долям. Конечно, при этомфактические количества благ могут бытьиррациональными, но это игнорируют всесуществующие способы установленияэкономических и товароведческих мер. Так,количество копеек, следующих за 3копейками, будет равно 4 копейкам. Но никомуне придет в голову между 3 и 4 копейкамификсировать величину в копеек.

В силу сказанногоколичества благ и услуг естественнымобразом формируют линейноеквазипространство (квазипространство мы определяем какподмножество пространства, на которомреализуются не все свойства исходногопространства, в данном случае –. Обычно изопределений видно, какие свойствареализуемы, а какие – нет).

Рассмотрим свойства истроение . Его элементамиявляются наборы упорядоченныхрациональных неотрицательных чисел – количеств благ.х = (х1,х2, …, хn) – пример такогонабора (вектор). Аксиоматика, задающаяквазипространтво , такова:

– двумвекторам , где ,ставится в соответствие вектор z, называемый суммойx и y, т.е. z = x + y, и вычисляемый поправилу

;

– если  0 и – рациональное число,а , то .

Указанные два правилаобразования элементов из имеют следующие свойства, которыепроверяются непосредственно:

1) x + y =y + x,

2) (x + y) +z = x + (y + z),

3) x + 0 = x,где 0 = (0, 0,...,0),

4) 1 x =x,

5) (x) = ( ) x,

6) ( + )x = x + x,

7) (x +y) = x + y, причем и – рациональныечисла;

– если и , то при условии, что длявсех .

Таким образом, выше даныпредставления о мерах благ и об операциях сними.

Видно, что

где , причемединица стоит на i-й позиции в , аостальные позиции заполнены нулями.Направление , где 0 – любое рациональноечисло, называется i-й координатной осью в . Меры хi могут бытьименованными, т.е. указывать на конкретныеколичества конкретных благ или денежныесуммы, и могутне быть именованными, в этом случае по осямоткладываются относительные безразмерныевеличины.

Блага переводятся вденежное измерение посредствомформулы , гдеxi– количествоi-го блага,данное в именованных товароведческихединицах, pi – цена именованнойтовароведческой единицы, – стоимостьэтого количества .

Теперь следует датьпонятие о структуре набора благ. Для этогопространство понимается какнормированное, т.е. на нем определяетсяфункция векторного аргумента, называемая нормой иотвечающая следующим требованиям:

1) , причем только при x = 0;

2) для и;

3) , где – знак нормы.

Примеры норм: , .

Долевой структуройвектора хназывается вектор .

Другое названиеструктуры набора благ х = (х1,х2,..., хn) – долевой состав = (,,..., ),соответственно – доли.

Например, если хi– стоимостьнекоторого количества блага i (для всех i от 1 до n), то, применяя норму, имеем следующеевыражение для долей:

.

Здесь qi – количество i-го блага вестественных товароведческих мерах – литры, штуки,комплекты и т.п.; pi – цена единицы i-го блага.

1.1.2. Меры роста иструктурных изменений

Для измеренияколичественных изменений в выпускенекоторой экономической системыпредлагается следующая концепцияобобщенного индекса. Множество М назовем поглощающимотносительно точки y, если имеется такое число, что М y. Если при этом число единственное,то оно называется нами обобщенным индексомy относительноМ.Содержательно концепция обобщенногоиндекса вполне элементарна. показывает, насколько надо увеличить или уменьшитьМ, чтобы векторy = (y1,y2,..., yn) оказался в этомрасширенном (или суженном) множестве,например множестве производственныхвозможностей некоторой экономики. Дляпримера рассмотрим рис. 1.1.

Рисунок 1.1. Множествопроизводственных возможностей

На рисунке заштрихованомножество производственных возможностейN. N – это часть круга сцентром в точке О и с радиусом 40 мм. При 1,6N y. Такимобразом, Nявляется для упоглощающим множеством. Граница множестваN, обозначаемаячерез М, естьчасть окружности, являющаяся эффективнымподмножеством множества N, она будетудовлетворять условию: М у при единственном = 1,6, так какрадиус-вектор точки у равен в точности 64 мм.

Приведем другой, болеесодержательный пример. Пусть в экономикепроизведен состав благ q = (q1,q2,..., qn). Блага произведены впериод, который мы считаем базовым. Ценаединицы блага iсоставила величину pi. Общая стоимостьвыпуска равна V = q1p1 + q2p2 +... + qn pn. V – это некоторое число.Сопоставим значению V = const множество всех выпусковэкономики, при которых для данных ценp = (p1,p2,..., pn) выпуск составитвеличину V. Приэтом pi > 0 для всех i от единицы до n. Имеем уравнение

,

где – переменныевеличины.

Множество всех , удовлетворяющих написанному вышеуравнению, обозначим М. Это поглощающее множество в относительно любой точки y.Наборы благ, характерные дляМ, обеспечиваютзначение выпуска, равное V, и, таким образом,Мхарактеризует определенный,соответствующий величине V уровеньпроизводственных возможностей. Определиминдекс точки у =(у1, у2,..., уn) относительно М.

Уравнения луча,соединяющего ус началом координат, таковы:

.

Подставим эти выраженияв уравнение гиперплоскости, определяющейМ. Имеем , или

.

Искомый индекс = t –1. Приэтом .То есть .

Индексприспособлен для того, чтобы отображатьэкономический рост.

Теперь дадимпредставление об измерении структурныхсдвигов.

Естественной меройразличия между долевым составом = (, ,...,) и долевым составомW = (W1,W2,..., Wn), такими, что принекоторой норме ||||||||= 1 и || W || = 1,будет метрика, индуцированная этойнормой,

.

Или болееподробно:

Обычно вместо m1 берутвыражение .Будет 0 m 1.

Например, принорме имеемдля и W:

– принятыйв статистических расчетах коэффициентобщего структурного сдвига.Содержательная интерпретация функцииm1дается в пункте 1.2.1.

В магистральной теорииэкономической динамики чаще применяетсяевклидова норма:

.

Соответственно, вкачестве меры структурных сдвиговвводится так называемое угловоерасстояние, вычисляемое по формуле для.

При этом , , причем – фактический, а – базовый наборы благ,соответственно – базовая, а –фактическая долевые структуры этихнаборов благ.

Введя в рассмотрениемеры роста и структурных сдвигов вэкономике, мы в следующем пункте исследуемвзаимосвязь между явлениями роста иструктурными изменениями.

1.1.3. Основныеструктурные эффекты

Базовыми структурнымиэффектами являются:

– эффектзамещения роста со стороны структурныхсдвигов;

– эффектдополнения роста со стороны структурныхизменений;

– эффектвытеснения роста структурнымиизменениями. Важную роль играют такжеэффекты расширения и сжатияструктуры. Вданном разделе предлагается исследованиеперечисленных структурных эффектов.

В целях анализаструктурных эффектов рассмотрим одну избазовых абстракций теориипотребительского выбора – абстракциювыделения эффектов замены и дохода. Имеетместо рис. 1.2. На этом рисунке линия 1представляет бюджетное ограничениепотребителя или их группы (например, такойгруппой может быть семья, более широкоепонятие –домашнее хозяйство). Потребительприобретает два товара, количества которыхв их естественных мерах откладываются нарис. 1.2 по осям графика. Товары обозначеныкак Пр. 1 (продукт 1) и Пр. 2 (продукт 2). Кривыебезразличия обозначены римскими цифрами– I, II, III. Чемвыше и правее расположена криваябезразличия, тем более высокий уровеньудовлетворения потребностей в благах Пр. 1и Пр. 2 она представляет. На одной и той жекривой безразличия в ее разных точкахуровень удовлетворения потребностей одини тот же. Если по каким-либо причинам ценана продукт 2 уменьшается, то бюджетноеограничение из положения 1 сместится вположение 2, а точка оптимального выборапотребителя перейдет из позиции «а» в позицию «с». При этомнаблюдаются два основных эффекта теориипотребительского выбора. Обычно ихвыделяют следующим образом. Допустим, что при изменении ценыпотребитель решил остаться на прежнемуровне удовлетворения потребностей,т.е. впределах кривой I.

Рисунок 1.2. Структурныеэффекты

Тогда оптимальная точкапотребительского выборапереместится из позиции «a» в позицию «b», а бюджетная линия переместится вположение «3». Результатом станет экономияденежных средств, равная величине Э = Qp1– Q2p1, гдеQ – точка пересечениябюджетных прямых «1» и «2» с осью ординат, аQ2– точкапересечения бюджетной прямой «3» с той жеосью. p1 – ценапродукта Пр. 1.

Потребитель теперьможет расходовать дополнительноеколичество денег Э, и его потребительский выборвследствие этого переместится в позицию«с». Еслипотребитель по тем или иным причинам будетвынужден остаться в состоянии «а» (например,вследствие карточного распределения благ),то это будет эквивалентно потере средств вобъеме П =Q1 p1 – Q2 p1, ипосле этого точка «с» будет недостижимой. Чтобы такойпотери не произошло, необходимооптимизировать потребительский выбор прибюджетном ограничении «4» (точка d). Когда принимаетсярешение ограничиться прежним уровнемпотребления, то для недопущенияэкономических потерь следует перейти впозицию «b».Переход из «а»в «b» выражаеттак называемый эффект замены. В позиции«b» при том жеуровне удовлетворенияпотребностей субъект сталприобретать дополнительное количествотовара Пр. 2, на который понизилась цена, истал приобретать меньше по сравнению сначальной ситуацией товара Пр. 1. Иначеговоря, в потреблении субъекта произошлозамещение –дополнительное количество товара Пр. 2заменило некоторое, ставшее избыточнымколичество товара Пр. 1 без ущерба дляобщего уровня удовлетворенияпотребностей.

С точки зрения теориироста и структурных сдвигов эту ситуациюможно интерпретировать следующимобразом.

Поскольку перемещениевдоль кривой безразличия не означаетэкономического роста в рамках принятоймодели, т.е. роста потребления приреализации потребительского выбора, топереход из позиции «а» в позицию «b», являющийся структурным сдвигом,выполняет функцию замещения по отношению кросту. Такой замещающий структурный сдвигнеобходим для оптимизации составапотребляемых благ.

Другой вариантзамещающего структурного сдвига – переход в положение«d». При такомсдвиге сохраняется уровень расходуемыхсредств, и, следовательно, тоже нет роста– ростарасходуемого бюджета свыше величины,позволяющей приобретать набор благ«а» послеизменения цен.

Замещающие структурныесдвиги выполняют важную функцию вэкономике. Если нет возможностиосуществить рост ресурсного обеспечения,то замещающие по отношению к такому ростуструктурные сдвиги будутрационализировать состав выпускаемых благзатем, чтобы уровень удовлетворенияпотребностей возрастал при имеющихсяресурсных ограничениях (ситуация «а» «d» на рис. 1.2).

Если нет возможностиповысить уровень удовлетворенияпотребностей и осуществить рост в этомотношении, то замещающие структурныесдвиги так изменят состав выпуска, что приимеющемся уровне реализации потребностейбудет достигнута экономия ресурсов(ситуация «а»  «b»).

Эффект дохода в теориипотребительского выбора означает, чтосэкономленную сумму Э можно рассматривать как доход, засчет которого приобретаютсядополнительные количества как блага Пр. 1,так и блага Пр. 2, в результате чегопотребление перемещается в позицию«с».

С точки зренияструктурных эффектов здесь имеют место дваэффекта. Первый эффект – это рост кактаковой, переход с уровня удовлетворенияпотребностей I на уровень ихудовлетворения II. Или как альтернативапереход с линии бюджетного ограничения «4»на линию бюджетного ограничения «2». Эффектроста, однако, был бы не возможен безизменения пропорций в потреблении благ.Такое изменение выражается вспецифическом структурном эффекте – явлениидополнительности структурных изменений поотношению к росту. Этот эффект наблюдаетсякак при переходе «b» «с»,так и при переходе «d» «с»,и в первом случае выражен заменойнаправления L1на направлениеL2. Соответственно замена направленияL3на направление L2 выражает структурный компонентперехода «d» «с».

Итак, на элементарномпримере из теории потребительского выборабыли выявлены два структурных эффекта.Один из них –это эффект замещения роста структурнымиизменениями, другой – эффект дополнения структурныхсдвигов по отношению к росту.Соответственно этим эффектам структурныесдвиги надо рассматривать либо какзамещающие по отношению к росту вкаком-либо его проявлении, либо какдополнительные по отношению к росту.Предпримем попытку макроэкономическойиллюстрации эффектов замещения идополнения роста структурными сдвигами.Для этого рассмотрим рис. 1.3. На этомрисунке границей множествапроизводственных возможностей в исходнойситуации является линия АВ, или линия I.Реальный выпуск соответствуетобщественному выбору, и описываетсяситуацией «а».Иногда для характеристики общественноговыбора используют гипотетическуюмакроэкономическую функцию общественноговыбора. Точка «а» оказывается позицией касаниялинии безразличия функции выбора и границымножества производственных возможностей.Однако процедуру общественного выбораможно описать и без предположения оналичии агрегированной целевой функции. Мыможем считать, что в указанных целяхиспользуется любая достаточноправдоподобная схема.

На рис. 1.3 ситуация современем меняется. Ввиду того, что в экономике начинаетиспользоваться более совершеннаятехнология, граница производственныхвозможностей передвигается в положение III,а позицией общественного выборастановится точка «с». Однако субъекты, ответственные заэкономическую политику, могут принятьрешение ограничиться прежним уровнемпроизводства ради экономии редкихресурсов. Тогда линия производственныхвозможностей А1В1 будет проходитьчерез позицию «а». Но А1В1не совпадает полностью сАВ, посколькуновая технология не идентична прежней.Общественный выбор в общем случае приподобных обстоятельствах изменится – переместится впозицию «b».Структурный сдвиг «а» «b» является замещающим по отношению кросту, он оптимизирует выпуск присохраняющихся ресурсных ограничениях.Жесткость последних, таким образом,несколько ослабляется.

Структурный сдвиг,соответствующий переводу позицииобщественного выбора из положения «b» в положение «с», состоит в замененаправления L3 нанаправление L2. Этот сдвиг являетсядополняющим по отношению к росту. Каквидим, макроэкономическое обобщениеконцепции структурных сдвигов,дополняющих и замещающих рост, почти неусложняет их анализ.

Следует более подробноостановиться на аспектах обоснованиянеобходимости структурных сдвигов приизменении величины выпуска. Подобноеобоснование возможно как в рамках теориипотребления, так и в рамках теориипроизводства.

Рисунок 1.3.Макроэкономическая иллюстрацияэффектов

дополнения и замещенияроста структурными сдвигами

Известное условиеоптимальности потребительского выбораимеет вид

.()

Здесь pi – цена единицы i-го блага;

хi –количество приобретаемого потребителемi-гоблага;

ui (x) =ui(x1, x2,..., xn) – предельная полезность блага i.

Если соотношение() невыполняется, то потребитель будет изменятьсостав благ с целью его оптимизации, т.е.начнутся структурные изменения. Когдатакое явление станет массовым, структурныесдвиги совместно будут изменять структурувыпуска экономики.

В частности, еслиусловие ()сначала выполнялось, но затем изменилисьнекоторые из цен на продукты, то возникнутструктурные изменения, которые будутпродолжаться до восстановления условия(). И, наконец,увеличение количеств приобретаемых благпри сохранении условия () в общем случае неможет быть равномерным, посколькупотребности удовлетворяются с разнойнастоятельностью. Значит, снова начнетсяпроцесс изменения количественныхпропорций между величинами xi, ивозникнут замещающие и дополняющиеструктурные изменения, пока условие() невосстановится.

Рассмотрим аналогичнуюаргументацию с позиций теориипроизводства. Допустим, что при увеличениивыпуска его состав растет при постоянствепропорций между номенклатурнымипозициями. Однако ресурсы по-разномудефицитны, а технологии по-разномупроизводительны, следовательно,пропорциональное увеличение ихиспользования в конце концов приведет ксущественной неэкономии, преодолетькоторую можно, изменив пропорции выпуска впользу благ, производство которыхсопряжено с более высокойпроизводительностьюфакторов. После таких сдвигов сформируетсяновый состав выпуска, который отвечаетусловиям рационального функционированияпроизводства, и поэтому он определенноевремя будет оставаться без существенныхизменений. Затем снова выявятся разныепредельные производительности факторовпри выпуске ряда продуктов. Предельнаяпроизводительность факторов при этомрассматривается нами как взвешенная, т.е. вее отношении к цене по каждому ресурсу.Значит, необходимо варьировать составвыпускаемых благ, чтобы он был оптимальнымпо отношению к используемым ресурсам, недопускал их перерасхода. Начнутсязамещающие структурные изменения,являющиеся альтернативой наращиванияресурсного обеспечения. Вследствие этогоресурсные ограничения станут менеежесткими, и появится возможность роставыпуска на базе дополняющих структурныхсдвигов. И так до тех пор, пока система недостигнет ситуации нового экономическогоравновесия.

Из сказанного видно, чтоструктурные сдвиги представляют собойфеномен, отражающий сущностные свойстваэкономического развития. Структурныеизменения сопутствуют экономическомуразвитию, совершенствуя как составвыпуска, так и состав используемыхресурсов. Однако не всегда измененияструктуры носят позитивный характер поотношению к росту. В экономике частонаблюдается деструкция, затрудняющаяразвитие. Соответствующие деструкцииструктурные сдвиги можно назватьвытесняющими экономический рост, илиухудшающими. Эффект вытеснения ростаструктурными сдвигами состоит вформировании структуры хозяйства, менеепродуктивной, чем исходная.

Необходимо подробнеерассмотреть случай, когда наличествуютструктурные сдвиги, называемые нами вытесняющимиэкономический рост, деструктивными. Такиеизменения состава выпуска или (и) составаиспользуемых факторов обусловлены многимиобстоятельствами.

Так, может ухудшитьсяобщая экономическая конъюнктуравследствие самых разных причин. Например,внезапно могут стать более жесткимиресурсные ограничения на рост. Кроме того,неожиданно возникают шоки спроса ипредложения. Эти явления сводят на нетстремление компенсировать возрастающуюограниченность благ, совершенствуя ихсостав. Вектор структурных изменений ввыпуске в подобных условиях теряетвыраженную ориентацию, перестаетувязываться с тенденцией к оптимизациисостава выпуска. В целом возникаетпоследовательность ухудшенийэкономической структуры, подрывающаявозможность роста, так как стимулы кувеличению выпуска нерационального построению состава благ не могут бытьсущественными.

Большую роль вопределении структурных сдвигов какоптимизирующих или деструктивных имеютлаги экономических решений и ожиданияучастников хозяйственного процесса, ихоправданность. Ожидания и соответственнопервоначальные экономические решениямогут опираться на одни предположения овозможном будущем, а на практикереализуются совсем иные тенденции. Тогдате изменения структуры, которые в нее былипредварительно заложены, изоптимизирующих могут превратиться вглубоко разрушительные.

Тем не менее и вситуации ухудшившегося экономическогоположения мотивация экономическихсубъектов сохраняется. По-прежнему онистремятся рационально использоватьимеющиеся (или остающиеся) у нихвозможности для реализации своих целей.Вот эта преобладающая тенденция и ведет ктому, что в долговременной перспективеравнодействующая структурных измененийформируется преимущественно под влияниемрационализирующих выпуск замещающих идополняющих структурных сдвигов.

С другой стороны,замещающие и дополняющие структурныесдвиги сами создают ситуации приостановкироста в экономике. Например, оптимизацияструктуры выпуска, вызываемая замещающимиизменениями, дает возможностьэкономить надополнительном выпуске ряда благ. Внешнеэто выглядит как замедление роста.

Дополняющиеструктурные сдвиги открывают нишу ростаперед более настоятельнымипотребностями. В силу этогоряд традиционных потребностей начинаютперемещаться на задний план, часто вообщеперестают быть актуальными. Это вызываетнеобходимость структурной перестройки вхозяйстве, а она порой происходит весьмаболезненно, через элементы кризисногосостояния. В частности, возникаютдепрессивные регионы, отрасли ипроизводства.

Таким образом, видно,что деструкция не отделима от развития,является его составным элементом, адеструктивные изменения в экономике могутбыть следствием изменений, позитивных приобщей тенденции к экономическому росту вдлительной перспективе.

Замещающие идополняющие изменения взаимосвязаны.Замещающие по отношению к росту сдвигинеобходимы для накопления потенциалароста, из-за накопления такого потенциалаосуществляются дополняющие изменения,обусловливающие сам рост, вследствие чегоснова начинается этап оптимизации состававыпуска посредством замещающих ростизменений.

Об эффективностидополняющих и замещающих структурныхизменений можно судить прежде всего подинамике индикаторов (показателей) роста.Так, если рост устойчив, выражаетсясущественным темпом (индексом), имеетинновационную направленность, то этоявляется свидетельством оптимальностиструктурных эффектов дополнения изамещения.

На простом примерепроиллюстрируем принципиальную схемувыделения эффектов замещения ростаструктурными сдвигами, дополнения ивытеснения роста со стороны структурныхсдвигов. Пусть в некоторой экономической(хозяйственной) системе ХС имеются два видаресурсов: К-ресурсы (качественные ресурсы) иМ-ресурсы(массовые ресурсы). К-ресурсы составляют 25 % всехресурсов в некотором сопоставимомисчислении, а массовые – 75 % всех ресурсов. Вто же время, по предположению, массовыересурсы в целом обеспечивают 25 % выпуска, акачественные –75 % выпуска системы.

Существует возможностьпреобразования М-ресурсов в К-ресурсы. Издержки преобразованиямассовых ресурсов в качественные требуютпостоянных затрат, равных 20 % от исходнойвеличины выпуска ХС. Стоит задача уравнятьдоли К-ресурсови М-ресурсов всистеме и тем самым добиться увеличения еевыпуска. Если доли К-ресурсов и М-ресурсов станут равными (по 50 %), топрирост выпуска можно рассчитатьследующим образом. Один процент К-ресурсов в среднемобеспечивает 3 % выпуска ХС: 75 % / 25 % = 3.Предполагается, что средняя отдачакачественных и массовых ресурсовпостоянна. Поскольку общая величина К-ресурсов и М-ресурсов остаетсяпостоянной и равной 100 %, то = 50 % –25 % = –.Прирост выпуска равен =3 –0,33– 20 % = 46,67 %. Приэтом учитываем, что отдача одного процентаМ-ресурсовравна 25 % / 75 % = 0,33.

Можно рассчитать эффектзамещения роста структурными изменениями.Для этого вычисляется прирост качественных ресурсов, необходимыйдля сохранения исходного уровня выпускапри структурных преобразованиях. Имеем3 % = 20 % + 0,33 % или = 7,5 %. Тогдапереход от структуры К : М = 25 %: 75 % кструктуре (К+) : (М –) = 32,5 % : 67,5 %соответствует эффекту замещения:структурный сдвиг компенсирует отвлечениересурсов на постоянные затраты.

Эффекту дополненияроста структурными изменениямисоответствует в условиях рассматриваемойзадачи переход от структуры 32,5 % : 67,5 % к структуре:  = 50 % : 50 %. Если же < 7,5 %,то, как легко видеть, будет иметь местоэффект вытеснения роста со стороныструктурных изменений. Разумеется,приведенный пример весьма прост, и уже вслучае не двухкомпонентной, амногокомпонентной структуры выпуска иресурсов задача становится значительносложнее, однако в данном пункте цельсостояла в выявлении принциповопределения структурных эффектов,введенных выше, а для этого лучшеиспользовать именно элементарныйпример.

Также следует выделитьважные для последующего анализа эффектырасширения и сжатия структурэкономических агрегатов.

Эффект расширениявыражается в увеличении доли определенныхпродуктовых групп в выпуске экономики– онивытесняют из выпуска другие продуктовыегруппы. Если вытесняющие продуктовыегруппы соответствуют инновационнойнаправленности в развитии хозяйства, томожно говорить об оптимизирующем влиянииэффекта расширения. Если вытесняющиепродуктовые группы снижаютпотребительские и технологическиехарактеристики выпуска, то эффектрасширения можно определить какдеструктивный.

Эффект сжатияпроявляется относительно техноменклатурных групп в выпуске экономики,доли которых со временем уменьшились. Еслитакую динамику имеют номенклатурныегруппы, соответствующие устаревшейпродукции (как в потребительскомотношении, так и с точки зрения технологииизготовления), то это свидетельствует обоптимизирующем характере эффекта сжатия.Когда уменьшаются доли прогрессивныхпродуктовых групп, то можно сделать вывод одеструктивном проявлении эффектасжатия.

Важно, чтобыоптимизирующие по своим характеристикампроцессы сжатия и расширения былиустойчивыми на среднесрочных идолгосрочных интервалах времени. В этомслучае можно уверенно говорить обоптимизирующем действии структурныхэффектов на экономический рост.

1.2.Методысопряжения роста

иструктурных сдвигов

Основная идеяпредлагаемых подходов к сопряжению роста иструктурных сдвигов состоит в увязкеиндекса изменения выпуска некоторойэкономической системы и индексаструктурного сдвига. Эта задача нижерешается последовательно – от простейшегослучая до возможных наиболее общихпостроений.

1.2.1. Простейший вариантсопряжения роста

и структурныхизменений

При выводе основныхсоотношений в данном пункте мы начнем срассмотрения структурных эффектов,которые можно явно определить иизмерить.

Прежде всего следуетвыделить эффект расширения. Суть его, какуже отмечалось, заключается в том, что современем совокупная доля некоторыхноменклатурных позиций в общем составевыпуска возрастает, они вытесняют прочиеучтенные позиции из состава выпуска.

Соответствующий прирост равенвеличине

,(1)

где J –множество индексов i, таких, что > Wi.

При этомWi – начальная доляотрасли (номенклатурной группы) в общемсоставе выпуска; – ее последующая(фактическая) доля. В общем случаебудет:

; (2)

где n – общееколичество учтенных позиций.

Применяются следующиеобозначения:

– начальноеколичество товара вида i, данное вестественных товароведческих единицах,как то: метры, метры квадратные икубические, литры, килограммы, центнеры,тонны, штуки, наборы и комплекты и томуподобное;

– фактическоеколичество этого товара;

– начальная ценатовара i;

– фактическая ценатовара i.

Затем выделим эффектсжатия. Он равен совокупному уменьшениюдолей тех позиций, по которым нетувеличения долей:

(3)

где в томслучае, если .

то

Изопределений величины mследует, что

(4)

Вэкономико-статистической литературекоэффициент mназывается коэффициентом общегоструктурного сдвига. Более позднееназвание для m– массаструктурного сдвига. Имеет смыслподчеркнуть, что коэффициент m удовлетворяетсвойствам метрики в пространстве :

где W0 – некоторый вектордолей единицы [см. 18, с. 50].

Проанализируемвеличину :

При этом

– номинальный темпроста попозиции i;

– доляi-го видапродукции в начальном составевыпуска;

– индекс цен;

–индекс изменения выпуска в ценах отчетногопериода.

Таким образом, имеетместо соотношение:

Если ввести условныецены отчетного периода поформуле

,

т.е. с учетом измененияуровня цен, то станет

(5)

где

Легкоустанавливается, что .

Действительно,

,

откуда следуеттребуемое.

Рассмотрим множествоG = {1, 2, …, n}. Его можно разбить натри непересекающихся подмножества G1,G2, G3, объединение которыхдает G. В первоеиз упомянутых подмножеств G1отнесем те индексы i, для которых Ii < I. Можно сказать, чтопозиции с номерами из G1 характеризуютсяотносительной инерционностью по динамике– рост по нимотстает от роста исследуемого агрегата вцелом. Инерционность будет выраженанаибольшим образом, если станет Ii = 0, т.е.когда i-йкомпонент полностью прекратит своюдинамику.

К множеству G2отнесем те индексы i, для которых Ii = I. Так как имеет местоформула (5), то при iG2 имеем. То естьструктурный сдвиг по позициям из G2отсутствует. Это явление можно определитькак инерцию в изменении структуры.

Множество индексовG3характеризуется свойством Ii >I, если i  G3. Можно записатьIi = I + ti, гдеti> 0.

Слагаемое I в последнемвыражении обеспечивает такой рост попозиции i,который воспроизводит начальную долевуюсоставляющую по этой позиции. Можносказать, что компонент I темпа Iiреализует инерционность в измененииструктуры.

Легко видеть, чтоструктурный сдвиг по позициям i  G3 обусловленкомпонентами ti и равенвеличине для каждого i  G3.Индекс I теперьможет быть записан в следующем общем виде:

.(6)

Сумму можно назватьструктурным опережением. Эта величинаполностью исчерпывает увеличение индексароста, обусловленное приростом долевыхпозиций в составе выпуска.

Сформируем сумму

Составляющие величиныМ1 порождаютинерционность или по динамике (когдаIi< I), или поструктуре (остальные случаи). В целомМ1 – это общаясоставляющая инерции при изменениивыпуска.

Имеем разложение

I = М1 + М2(7)

индекса роста покомпоненту инерции М1 и составляющей опережения М2. Для М2 будет

.

В свою очередь,

Коэффициент m* = 1 – m имеет специальноеназвание в экономико-статистическойлитературе. Он называется коэффициентомсходства начальной и фактической долевыхструктур [см. 38, р. 189]. Коэффициент сходстваm* показывает,насколько совпадают по своему строениюначальная и фактическая долевые структуры,насколько фактическая долевая структурапреемственна по отношению к начальной,воспроизводит ее свойства и насколько, вкакой мере начальная структураприсутствует, проявляет себя в структурефактической.

Термин «сходство» можнопонимать следующим образом: сходствоизучаемого объекта по отношению кобъекту-прототипу выражает сохранениеколичественных и качественных параметровобъекта-прототипа в изучаемом объекте приего эволюции.

В исследуемом здесьслучае объектом-прототипом являетсяисходная, базовая долевая структуравыпуска. А фактическая долевая структурапредставляет собой изучаемый объект.Сохраняемость в таком объекте свойств истроения прототипа как таковаяхарактеризует инерционную сторонуэволюции объекта – долевой структуры выпуска. Поэтомумера сходства может быть истолкована какколичественная оценка инерционности, мераинерционности.

Оценка же структурногосдвига выражает и оценивает уровеньимеющих место изменений объекта, т.е.представляет собой характеристикуреконструктивного компонента в эволюцииструктуры.

Поскольку мераструктурных изменений в связи со своимиконструктивными особенностями заключена вединичном интервале [0, 1], то этот интервалотображает полный потенциал структурныхизменений. Логично полагать, что изменениеимеет место ровно настолько, насколькоотсутствует инерционность, и, наоборот,инерционность ограничена величинойнереализованного потенциала изменений.Тогда мера инерционности задается какостаточный компонент потенциаластруктурного сдвига, поэтому она должнабыть определена также на интервале [0, 1]. Таккак полный потенциал возможных измененийопределен единичным интервалом, ареализованный уровень изменениявыражается оценкой m, то остаточный потенциал изменений,т.е. уровень нереализованного изменения и вэтом смысле –инерционности, как раз и надоколичественно определить величиной 1– m.

Разложение индексаполучено при общих предпосылках, когдацены начального и фактического периодов непредполагались одинаковыми. Неудобстводанного подхода состоит в том, что здесь виндексе роста соизмерителями являются, какправило, цены текущего периода. Обычно жедля этих целей применяются цены некоторогофиксированного – базового – периода. Разница заключается в том,что текущий период постоянно меняется, анекоторый базовый период неизменен, чтосоздает определенные методическиепреимущества. Поэтому ниже предлагаетсяподход с использованием базовых цен. Вслучае выбора единых цен pi, гдеi изменяется от1 до n, приходимк следующему выражению для индексафизического объема выпуска:

.(8)

Кроме того,будет выполняться

(9)

При этом становится.

Остальной выводразложения индекса аналогиченприведенному ранее.

Следует отметить однуособенность: если длянекоторого i,то

Тогда .

С другой стороны, , но.

Поэтому –неопределенность.

Однаконеопределенность раскрывается. Положим,что –бесконечно малая величина и .

Тогда

что и требовалосьпоказать.

Индекс I может охватыватьразличные агрегаты в выпуске. Так, подI иногдапонимают индекс физического объема валовой добавленной стоимости (ВДС)[см. 4, с. 199]. Но в случае, когда считаетсяцелесообразным исследовать всюноменклатуру произведенной за некоторыйпериод продукции, кроме ВДС надо учитыватьи промежуточный продукт. При этом встоимостных агрегатах появляетсяповторный счет. Однако исходя изнеобходимости анализа всей производимойноменклатуры, а также из того, чтоисследуется физический показатель, т.е.физический объем выпуска, а не показательпроизведенной стоимости, допустимыэлементы повторного счета. Действительно,повторного учета номенклатурных позицийздесь нет, а это главное при изучениидинамики и структуры полного состававыпуска.

Отметим, чторассмотренная терминология, использующаяопределения «реконструктивный» и«инерционный» по отношению к компонентаминдекса I, неявляется единственнойи устоявшейся. Можноиспользовать и другие термины, тем болеечто понятие «инерция» имеет физическое, ане экономическое происхождение.

Называя М2 структурнымопережением, к компоненту М1 можно применитьопределение «запаздывание».Действительно, долевые составляющиеМ1 неувеличиваются, т.е. как бы отстают,запаздывают в своем росте.

1.2.2. Энтропийные(теоретико-информационные)

оценки структурногосходства и различия

Важно подчеркнуть, чтосуществует большое число оценокструктурного сдвига. Остановимся, вчастности, на энтропийных(теоретико-информационных) мерахструктурных изменений и инерции в выпускехозяйственной системы (ХС).

Любая фактическисуществующая хозяйственная система хотябы частично является стохастическим(вероятностным) объектом. Рассматриваяидеализированную модель ХС, мы можемпредполагать, что это полностьювероятностный объект. Такое предположениеявляется допустимым приближением кдействительности.

Вероятностный характерхозяйственной системы заключается в том,что долевые показатели выпуска – величины Wi и понимаются ввероятностном смысле. Например, Wiпредставляется вероятностью того, чтоданная в стоимостном измерении единицавыпуска ХС будет на самом деле единицейi-го результата– продукта,услуги и т.п.

Естественно записатьSi= Wi S+, где Si – полное количествопродукции i-говида, измеренное в стоимостном выражении, аS+ –суммарный выпуск всех продуктов и услуг.Ясно, что Еслиопределить Si соотношением , то получим

Последнее выражениесогласуется с экономическим смысломпараметра Wi как долевойхарактеристики выпуска.

Величина выглядит теперь как математическоеожидание выпуска по i-й позиции, а величина

представляетсяматематическим ожиданием общего объемавыпуска всех продуктов и услуг.

Выпуск ХС флуктуирует. Ипри вероятностях Wi существуетвозможность реализации состава,отклоняющегося от наивероятнейшего, т.е. отS = (S1,S2, …, Sn), как по отдельнымкомпонентам, так и в целом.

Например, не исключенавозможность, что ХС на самом деле реализуетсостав

С = (С1,С2, …, Сn),

где Сi =pi.

Состав С характеризуетсядолевой структурой . Доли также можнотрактовать в вероятностном смысле.

Естественной оценкойинформационной неопределенности,связанной с тем событием, что при априорныхвероятностях W =(W1, W2, …, Wn) насамом деле будет реализованораспределение ,является энтропийная мера

.

Если распределение уже заменилодолевую структуру W = (W1, W2, …,Wn), то информационнаянеопределенность уменьшится до величины

.

Разница между L* иH* есть информация о событии,состоящем в том, что долевая структура заменила долевуюструктуру W. Тоесть это не что иное, как величина

.

T* как мера информации о заменедолевых структур может рассматриваться вкачестве косвенной информационной оценкиструктурного сдвига. По построению имеем и .Покажем, что . Для этоговоспользуемся неравенством . Имеем

что и требовалосьпоказать.

Чтобы в дальнейшемиспользовать нормированные оценкиструктурных изменений и инерционности,перейдем к выражениям

и .

Имеемm* + m = 1; ;

Информационные мерысходства и различия структурпостроены.

Желательно обобщитьразложение (7) для произвольных оценокструктурного сдвига и структурногосходства. Для этого необходимо установитьобщие свойства таких оценок. Последнееможно осуществить, определив свойстваоценок сходства и различия на основеаксиоматического подхода.

1.2.3. Аксиоматическоеопределение общих свойств

для оценок сходства иразличия структур

В литературе [см. 16, с. 31]приводится система аксиом для мер сходстваструктур. Ниже перечисляются этитребования, а также формируютсядополнительные и альтернативныеаксиоматические схемы.

Оценка сходствасоставов и W неотрицательна. Этосвойство формально задается в виде

А1.

Второе постулируемоесвойство –аксиома симметрии – заключается в требовании, чтобымера сходства составов иW совпадала смерой сходства составов W и ,что записывается следующим образом:

А2.

Естественное третьетребование для меры сходства такое:сходство идентичных долевых структур неменьше, чем сходство структур, которыенеидентичны:

А3. .

Оценка удовлетворяет всем перечисленнымтребованиям.

Аксиоматика для мерразличия по аналогии может бытьтакой:

аксиоманеотрицательности Б1.

аксиомасимметрии Б2.

Третья аксиома требует,чтобы мера различия между идентичнымидолевыми структурами была не больше, чеммежду структурами неидентичными:

Б3.

Этим требованиямудовлетворяет оценка

.

Стеоретико-информационной точки зрения,которая является более общей, аксиомысимметрии А.2 и Б.2 неоправданны.Действительно, замена распределенияW нараспределение и заменараспределения нараспределение Wесть события, о которых заранее нельзясказать, что они несут одинаковуюинформацию. Поэтомутеоретико-информационная версия мерсходства и различия требует иной, болееслабой аксиоматики. Так, для мер сходстваподобной аксиоматикой будет набортребований:

А1*.

А2*.

А3*. .

Набору постулатовА1*–А3* дляоценок сходства удовлетворяетформула:

.

Для мер различиявозможна следующая аксиоматика:

Б1*.

Б2*.

Б3*.

Этим требованиямсоответствует оценка .

Легко видеть, что наосновании троек аксиом А1*–А3*,Б1*–Б3* можнопостроить оценки, удовлетворяющиеаксиомам А1–А3 и Б1–Б3, как для мерсходства, так и для мер различия.

Например,пусть –мера сходства,удовлетворяющая требованиям А1*–А3*.Если ввести оценку , такую,что

,

то будут удовлетворятьсяаксиомы А1–А3, в частности аксиомаА2.

То же самое можносказать и об оценках различия, а именно,вводятся оценки

,

где и – меры различия,удовлетворяющие требованиям Б1*–Б3*. Оценка удовлетворяет аксиомам Б1Б3.

В общем случае мерысравнения долевых структур не обязательнооказываются заданными на интервале [0, 1],однако возможно приведение этих оценок кединичному интервалу.

Так, если оценкаразличия , где а и b – некоторыепостоянные, то следует воспользоватьсяпреобразованием

.

Будет: ссохранением свойств мер различия.

Парная для оценка сходства определяетсяформулой

Если , товозможно преобразование

При этом оценкаразличия . Интервал можно условно замкнутьсправа.

Когда то

Соответствующая мерасходства определяется как

Также можно сначалаотображать оценки сходства изнеединичного интервала в единичный ссохранением их свойств и на этой основеопределять парные меры различия долевыхструктур.

Поэтому в дальнейшем мысчитаем, что потенциал структурныхизменений исчерпывается интервалом [0,1].

1.2.4. Обоснование общегоподхода

к разложению индексароста

Из результатов,полученных выше, вытекает общая схемаразложения индекса роста. При этом можнопроизвольно выбрать форму индекса.

Если имеется некоторыйизмеритель структурных изменений m, такой, что , то ему соответствует парная оценкаинерционности: . Тогдапростые преобразования приводят кразложению индекса:

.

–компонент, оценивающий инерцию, а –составляющая, связанная со структурнымсдвигом.

Правило разложенияиндекса по формуле допускает следующее общееобоснование.

Пусть заданыкоэффициенты структурного сходства () и различия (m), такие, что тождественновыполняется:

.

Будем искатьреконструктивный компонент индекса ростав виде зависимости:

М2.

Аналогично дляинерционного компонента индекса имеем

М1.

На функцию налагается естественноеграничное условие: .Аналогично .Интерпретация этих условий проста. Если отсутствуют структурные сдвиги или,например, инерционность, тосоответствующий компонент в разложениииндекса тоже должен быть равен нулю – для него нетоснований.

Поскольку мы строимразложение индекса, то должно тождественновыполняться

.

Из последнего выраженияпри имеем

.

Но тогда.

То есть.

Значит, М1+М2.

Выражения М1 иМ2 в качестве решений исходной системыфункциональных уравнений имеют весьмапростую структуру – они линейны по каждому из входящих вних аргументов. Как таковые при принятыхграничных условиях эти решенияединственны.

В важнейшем частномслучае, когда

,

можно воспользоватьсяединственным граничным условием , справедливым, поскольку здесьреконструктивный компонент единичногоуровня роста в точности исчерпываетсяэффектом расширения, мерой которогоявляется величина m. Получаем:

.

Получаем соотношенияМ1 и М2.

Среди мер структурногоразличия следует выделить оценку

(10)

Можно отметитьследующие достоинства оценки F: она позволяетсуммировать сдвиги за несколько лет,выявлять возвратные колебанияструктуры.

1.2.5. Взаимные задачи

структурно-динамическогоанализа

При исследованииструктурной динамики возникают двевзаимоувязанные проблемы.

Во-первых, необходимоуметь учитывать динамический масштабисследуемого процесса при анализе егоструктуры.

Во-вторых, требуетсяучитывать влияние структурных измененийна динамику масштаба изучаемогопроцесса.

Первая задача решаетсяпосредством масштабирования оценокструктурного сдвига и инерции структуры.Например, оценка структурного различияm из интервала[0, 1] переводится в интервал [, ] отображениемm K(I) m + g(I) = N2, гдеN2 – это не что иное, какмасштабирование со сдвигом, K(I) –коэффициент масштабирования, g(I) –коэффициент сдвига [см. 4].

Аналогично для оценкисходства m*имеем

m* K*(I) m* + g*(I) = N1.

Что касается второйзадачи, то она сводится к поиску функцийM1 = 1(I, m*) и M2 = 2(I, m) со свойствами, ужезаданными выше.

Проведемдополнительное исследование выраженийМ1 и М2.

Поскольку 1(I, m*) + 2(I, m) = Iтождественно, то из

получаемI = I1(1, m*) + I2(1, m), или1(I,m*) = I1(1, m*) + (I, m, m*) и2(I, m) =I2(1, m) – (I, m, m*).

На 1 и2 налагаются граничные условия2(I, 0) =1(I, 0) =0.

Как уже было сказано,это означает, что нулевой сдвиг структурыпорождает нулевой вклад в разложениеиндекса; аналогично обстоит дело с оценкойинерции. Поэтому имеем (I, 0, m*) = (I, m, 0) =(1, m, m*) = 0.

Нетривиальным примеромфункции может служить выражение

= I (I 1) m m*.

В общем случае сказатьчто-либо большее о величинах М1 и М2, N1 и N2 не представляетсявозможным. Однако один принципиальноважный случай имеет особый интерес. Этоименно тот случай, когда оценка масштаба,скорректированная на структурный сдвиг,приравнивается оценке структурногосдвига, скорректированной на масштаб,– своего родатребование эквивалентности.

Имеем N1 = M1 и N2 = M2, т.е. K*(I) m* + g*(I) = I1(1, m*)+ и K(I) m + g(I) = I2(1,m) –.

При m = 0 имеем g(I) = 0; при m*= 0 будет g*(I) =0.

ТогдаK*(I) m* =1(I, m*) и K(I) m =2(I, m).

ИлиK*(I) m* +K(I) m = I.

ТогдаK*(1) m* + K(1)m = 1. Тоесть I K*(1) m* + I K(1) m =I.

Зафиксируем некоторое значение I, тогдаполучим

K*(I) m* + K(I) m= I = I K*(1) m* + I K(1) m

тождественно, т.е.K*(I) = IK*(1)и K(I) =IK (1) = I.

Отсюда K*(1) = 1 и K(1) = 1.

Окончательноимеем

1(I, m*) = M1 = K*(I) m* = I K*(1) m* = I m* = N1.

Соответственно, N2 = M2 = I m.

Мы получили условияразрешимости взаимных задачструктурно-динамического анализа в ихестественной содержательнойинтерпретации.

1.2.6.Переход к разложению нормыроста

Индекс роста можно записать следующимобразом:

.