Автоматизация проектирования плотных раскладок матричных элементов на пушно-меховых полуфабрикатах и натуральных кожевенных матери а лах 05. 19. 04 – технология швейных изделий
На правах рукописи
Косова Елена Вячеславовна
Автоматизация проектирования плотных раскладок
матричных элементов на пушно-меховых
полуфабрикатах и натуральных
кожевенных материалах
05.19.04 – Технология швейных изделий
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата технических наук
Омск – 2011
Работа выполнена в Государственном образовательном учреждении высшего профессионального образования «Омский государственный институт сервиса»
| Научный руководитель | кандидат технических наук, доцент |
| Андросова Галина Михайловна | |
| Официальные оппоненты: | доктор технических наук, профессор |
| Бекмурзаев Лема Абдулхажиевич | |
| кандидат технических наук, доцент | |
| Ларькина Лариса Викторовна | |
| Ведущая организация | Государственное образовательное учреждение высшего профессионального образования Южно-Уральский государственный университет, г. Челябинск |
Защита состоится 29 июня 2011 г. в 10-00 часов на заседании диссертационного совета Д 212.313.01 при Федеральном государственном бюджетном образовательном учреждении высшего профессионального образования «Южно-Российский государственный университет экономики и сервиса» (ЮРГУЭС) по адресу: 346500, г. Шахты, Ростовская область, ул. Шевченко, д. 147, корпус 2, ауд. 247.
С диссертацией можно ознакомиться в библиотеке при Федеральном государственном бюджетном образовательном учреждении высшего профессионального образования «Южно-Российский государственный университет экономики и сервиса» (ЮРГУЭС).
Текст автореферата размещен на сайте ЮРГУЭС: http: //www.sssu.ru
Отзывы на автореферат направлять по адресу: 346500, г. Шахты, Ростовская область, ул. Шевченко, д. 147.
Автореферат разослан «28» мая 2011 г.
Ученый секретарь
диссертационного совета С. В. Куренова
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность работы. В связи с высокой стоимостью натуральных меха и кожи особенно остро стоит задача их рационального использования. С этой целью разрабатываются различные мероприятия по сокращению отходов производства. Однако полностью ликвидировать краевые и межлекальные отходы традиционными способами переработки не удается. По данным И. Н. Каграмановой, около 30 – 40 % площади полуфабрикатов являются отходами. Одним из направлений рационального использования пушно-меховых и кожевенных полуфабрикатов является применение их отходов для получения полотен или изделий.
Большую практическую ценность имеет способ проектирования меховых полотен, состоящих из матричных элементов, разработанный на кафедре технологии швейных изделий Омского государственного института сервиса, который позволяет использовать отходы, различные по размерам и конфигурации. При этом возникает задача размещения матричных элементов, сложных по конфигурации, на полуфабрикатах и их отходах, также имеющих сложный криволинейный контур. Для получения раскладок матричных элементов необходимо найти такое их расположение, которое позволит получить максимальный процент использования площади полуфабриката.
Размещение геометрических плоских фигур рассмотрено в работах В. А. Залгаллера, Ф. В. Бабаева, Ю. Л. Мойжеса и др. Решение задач получения плотных раскладок на полубесконечной плоскости осуществлялось в работах В. А. Скатерного, Т. Я. Шишкиной, Б. А. Козлова, В. А. Волосатова, Ю. Г. Стояна. Решены задачи размещения геометрических фигур в простом (бесконечная и полубеконечная плоскости, прямоугольник) контуре.
Для пушно-меховых полуфабрикатов и натуральных кожевенных материалов, имеющих сложный криволинейный контур, рассматривается размещение одной детали в виде шаблона или ограниченного количества в виде упрощенных лекал деталей одежды. В связи с этим вопросы проектирования плотной раскладки сложных геометрических фигур, какими являются матричные элементы, на пушно-меховых полуфабрикатах и кожевенных материалах с криволинейным контуром являются актуальными.
В настоящее время в швейной промышленности используются различные системы автоматизированного проектирования изделий, такие как «Ассоль», «Грация», «Автокрой», «Реликт», «Investronika», «Gerber», «Lectra sistem», «САПР-мех» и др., в которых разработаны модули проектирования раскладок. Однако ни одна из существующих САПР не позволяют получать плотные раскладки матричных элементов на полуфабрикатах с контурами сложной конфигурации, поэтому разработка математического и информационного обеспечения процесса размещения матричных элементов на меховых полуфабрикатах и натуральных кожевенных материалах является актуальным.
Целью диссертационной работы является повышение эффективности использования пушно-меховых полуфабрикатов и натуральных кожевенных материалов, ограниченных произвольным замкнутым контуром, в результате проектирования плотных раскладок матричных элементов на основе компьютерных технологий.
Для достижения указанной цели были поставлены и решены следующие научные и практические задачи:
– исследование способов повышения эффективности использования пушно-меховых полуфабрикатов и натуральных кожевенных материалов при проектировании раскладок из матричных элементов;
– разработка алгоритма построения годографа функции плотного размещения матричных элементов;
– разработка математической модели плотной раскладки матричных элементов на неограниченной плоскости;
– разработка алгоритма рационального размещения матричных элементов на меховом полуфабрикате и натуральном кожевенном материале со сложным криволинейным контуром;
– разработка программного обеспечения, позволяющего в автоматизированном режиме размещать матричные элементы на меховых полуфабрикатах и натуральных кожевенных материалах.
Методы исследований. Решение поставленных задач осуществлялось на основе теории и практики проектирования раскладок, математического анализа, использования методов математического моделирования, аналитической геометрии, сплайн-функций, теоретических основ САПР, алгоритмизации и программирования.
Исследования осуществлялись с привлечением аналитических, экспериментальных и статистических методов получения и обработки информации, принципов классификации. При исследовании деформационных свойств полотен из матричных элементов применялась стандартная методика. В ходе выполнения работы использовались текстовые, статистические и графические программы Microsoft Word, Microsoft Excel, Corel Draw Х3 Graphis, AutoCAD 2007 для операционной системы Windows XP.
Научная новизна работы:
– Разработан алгоритм построения годографа функции плотного размещения матричных элементов, позволяющий выполнять наиболее плотное размещение матричных элементов на плоскости.
– Разработана математическая модель получения плотной раскладки матричных элементов на пушно-меховых полуфабрикатах и натуральных кожевенных материалах с контуром сложной конфигурации, позволяющая повысить коэффициент их использования.
– Разработан алгоритм рационального размещения матричных элементов на пушно-меховом полуфабрикате и натуральном кожевенном материале, который дает возможность автоматизировать процесс проектирования рациональной раскладки.
Практическая значимость результатов работы заключается
– во внедрении разработанных математических моделей и автоматизированного проектирования плотных раскладок матричных элементов, что позволяет повысить процент использования пушно-меховых полуфабрикатов и натуральных кожевенных материалов до 75–85 %;
– в применении правил адаптивного конструирования при проектировании матричных элементов и плотных раскладок из них, что дает возможность рационально использовать полуфабрикаты и их отходы в результате увеличения плотности раскладок до 85–100 %;
– в разработке программного обеспечения, позволяющего в автоматизированном режиме получать плотные раскладки матричных элементов на полуфабрикатах с контурами сложной конфигурации.
Внедрение результатов работы.
Результаты работы внедрены в производственный процесс мехового салона-ателье «Ренард» г. Омска, ОГАРТ Меховой дом «Аделина» г. Пятигорска, используются в учебном процессе на кафедре сервиса и технологий изделий легкой промышленности Омского государственного института сервиса в лекционном курсе и для практических работ по дисциплинам «Технология скорняжного производства», «Технология изделий из кожи и меха по индивидуальным заказам», а также при выполнении курсового и дипломного проектирования научно-исследовательского характера для студентов специальности 100101 Сервис.
Апробация работы.
Основные теоретические положения и результаты диссертационной работы докладывались и получили положительную оценку на международных научно-практических конференциях «Молодежь и наука: реальность и будущее» (Невинномысск 2009), «Современные тенденции и перспективы развития образования в высшей школе» (Омск 2007, 2008); IV, V, VI, VII Межвузовских научно-практических конференциях «Молодежь, наука, творчество…», (Омск 2007, 2008, 2009, 2010); межвузовской научно-технической конференции аспирантов и студентов «Молодые ученые – развитию текстильной и легкой промышленности» (Иваново, 2008); Межвузовской научно-практической конференции студентов, аспирантов и молодых исследователей «Теоретические знания в практические дела» (Омск, 2008).
Публикации. Основные результаты диссертации отражены в 20 печатных работах, из них 3 опубликованы в изданиях, рекомендованных ВАК.
Структура и объем диссертационной работы. Работа состоит из введения, основной части из четырех глав, заключения, списка используемой литературы, включающего 125 источников и 3 приложений. Диссертация изложена на 161 странице, содержит 31 таблицу, 56 рисунков.
СОДЕРЖАНИЕ РАБОТЫ
Во введении обоснована актуальность исследований, определены их цель и задачи, научная новизна и практическая значимость работы.
В первой главе диссертационной работы рассмотрены методы проектирования плотных раскладок.
Вопросам рационального использования пушно-меховых полуфабрикатов и натуральных кожевенных материалов уделяется большое внимание. Экономное расходование площади полуфабриката во многом зависит от правильного назначения шкурок, подготовки их к раскрою и выбора метода раскроя. На результаты раскроя влияет ряд факторов: форма и взаимоукладываемость лекал деталей изделий, системы их размещения; форма и площадь лекал и полуфабриката; неоднородность свойств отдельных участков полуфабриката и др. В большинстве случаев детали имеют сложные формы, поэтому даже при наилучшем их размещении появляются отходы, которые имеют разнообразные размеры и конфигурацию, что затрудняет их эффективное использование. Переработка отходов является одним из путей снижения материальных затрат в производстве одежды и способствует непосредственной экономии меха и кожи. Перспективным направлением использования отходов является раскрой их на матричные элементы, форма и размер которых могут варьироваться в зависимости от параметров раскраиваемых материалов. Матричными они называются потому, что их можно представить в виде матрицы, состоящей из следующих компонентов: основы (I), областей соединения (II), декоративных (III) и соединительных (IV) отверстий (рисунок 1а).
Одной из важных задач является рациональное размещение лекал деталей с целью экономного расходования материалов и снижения процента межлекальных отходов. Анализ существующих разработок показал, что наиболее полно решены вопросы получения плотных раскладок геометрических фигур на бесконечной, полубесконечной плоскости и в прямоугольнике, что неприменимо для пушно-меховых полуфабрикатов и кожевенных материалов, имеющих произвольный замкнутый контур сложной конфигурации.
В главе также дается обзор исследований и разработок в области автоматизации проектирования раскладок. Большинство САПР, используемые в настоящее время на швейных предприятиях, предназначены для работы с текстильными материалами, и не позволяют решать задачу размещения матричных элементов на пушно-меховых полуфабрикатах и кожевенных материалах.
Вторая глава посвящена получению плотного размещения матричных элементов, имеющих сложную геометрическую форму, на неограниченной плоскости.
Для нахождения плотных раскладок матричных элементов использовались правила адаптивного конструирования: тропизация (выбор оптимального размещения элементов) (рисунок 1), лабилизация (изменение конфигурации размещаемых элементов) (рисунок 2), мультипликация (изменение размеров элементов) и метод комбинированного раскроя (рисунок 3).
а б
Рисунок 1 – Применение правила тропизации для уплотнения раскладки
матричных элементов: а - матричный элемент; б - варианты раскладок
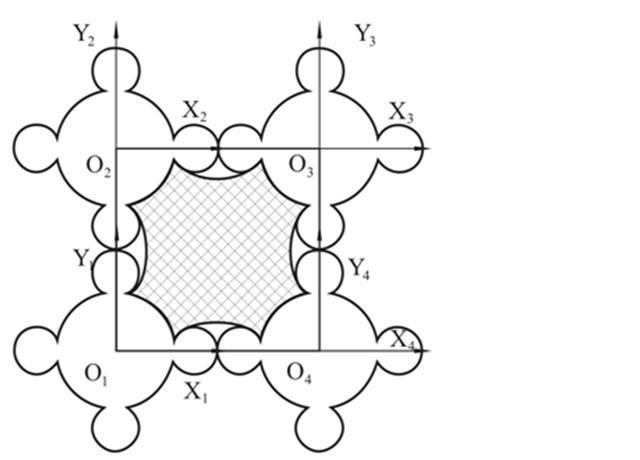
Таблица 1 – Результаты применения правил адаптивного конструирования
| SМЭ, мм2 | Тропизация | Лабилизация | Комбинированный раскрой | ||||
| Sпар, мм2 | p, % | Sпар, мм2 | p, % | SМЭ допол., мм2 | Sпар, мм2 | p, % | |
| 191,2 | 318,0 | 59,9 | 379,8 | 85,7 | 292,3 | 483,5 | 100 |
| 213,4 | 340,3 | 62,7 | 305,0 | 97,3 | 255,0 | 468,4 | 100 |
| 221,9 | 280,6 | 79,1 | 311,2 | 90,7 | 262,4 | 484,2 | 100 |
| 260,6 | 306,8 | 84,5 | 305,6 | 90,2 | 306,4 | 576,0 | 98,4 |
| 367,3 | 426,9 | 86,0 | 412,7 | 90,8 | 497,2 | 880,9 | 98,1 |
Однако следует отметить, что получаемые при этом раскладки, предполагают раскрой матричных элементов с отклонением от направления линии хребта шкурки. С целью изучения влияния угла наклона оси матричных элементов относительно линии хребта полуфабриката на свойства получаемых из них полотен проводились экспериментальные исследования релаксационных характеристик. В результате этих исследований была установлена величина допустимого отклонения ( 30°), при котором полотна характеризуются минимальными значениями абсолютной деформации, а также отсутствием остаточной и, соответственно, вызываемых ею дефектов внешнего вида.
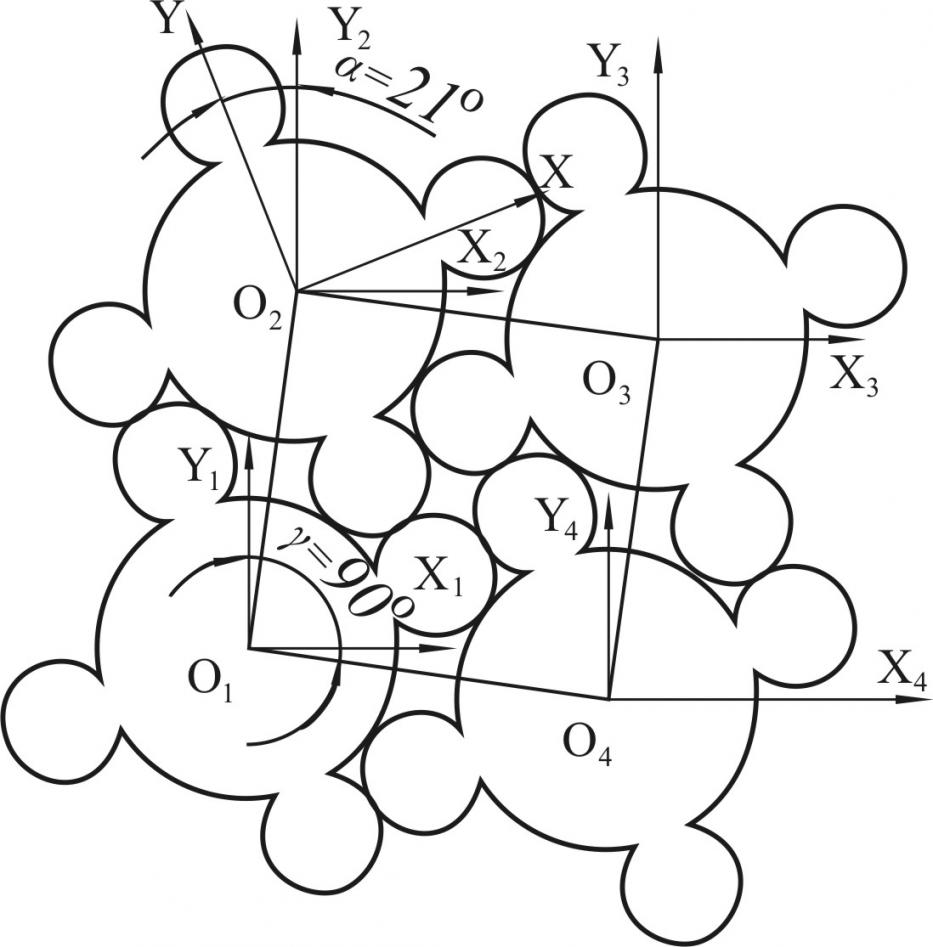
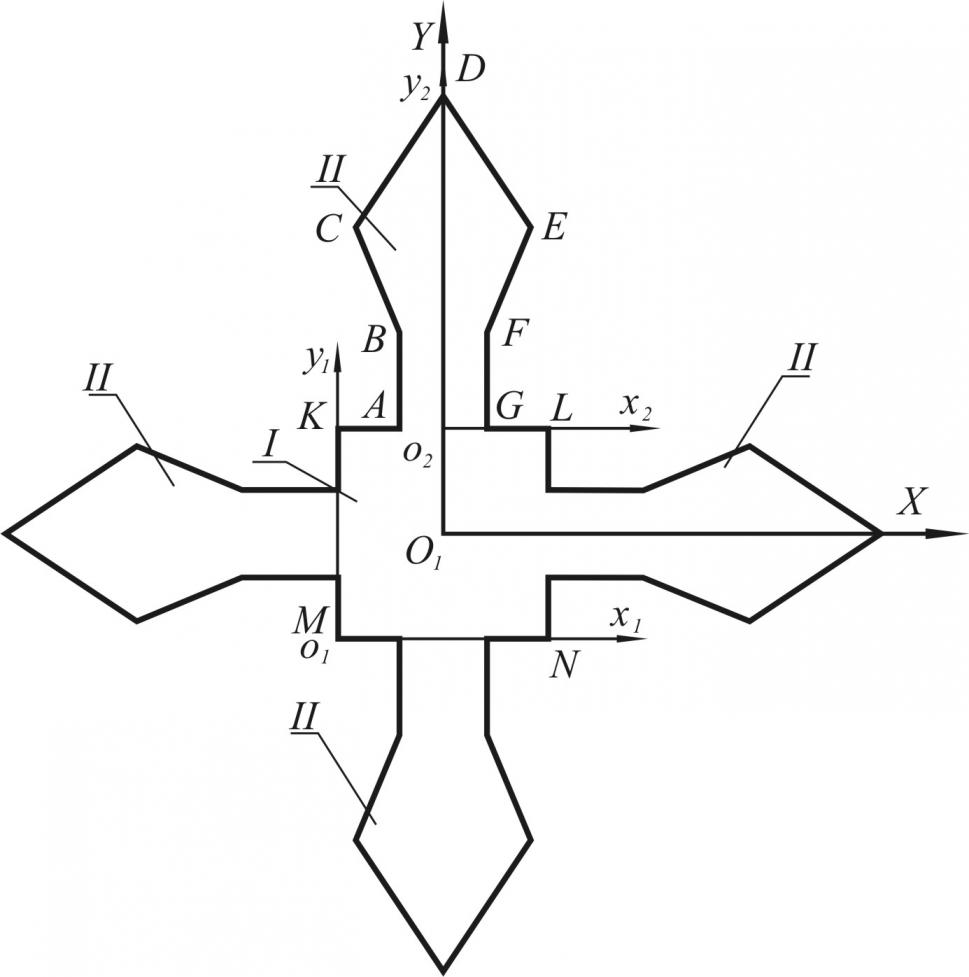
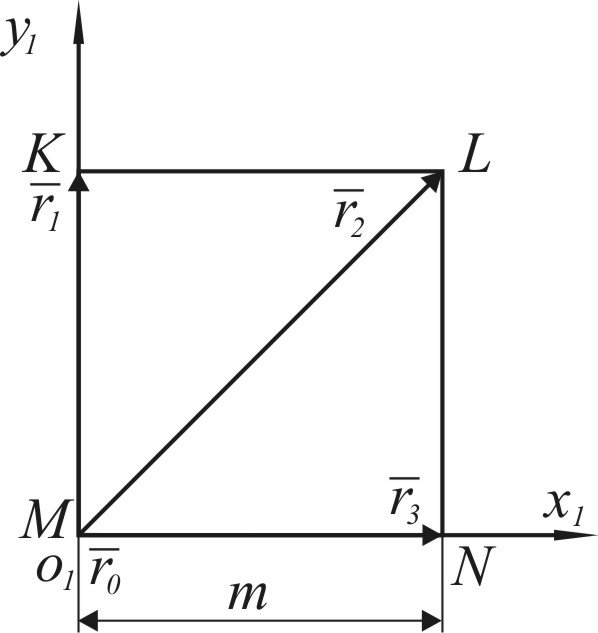
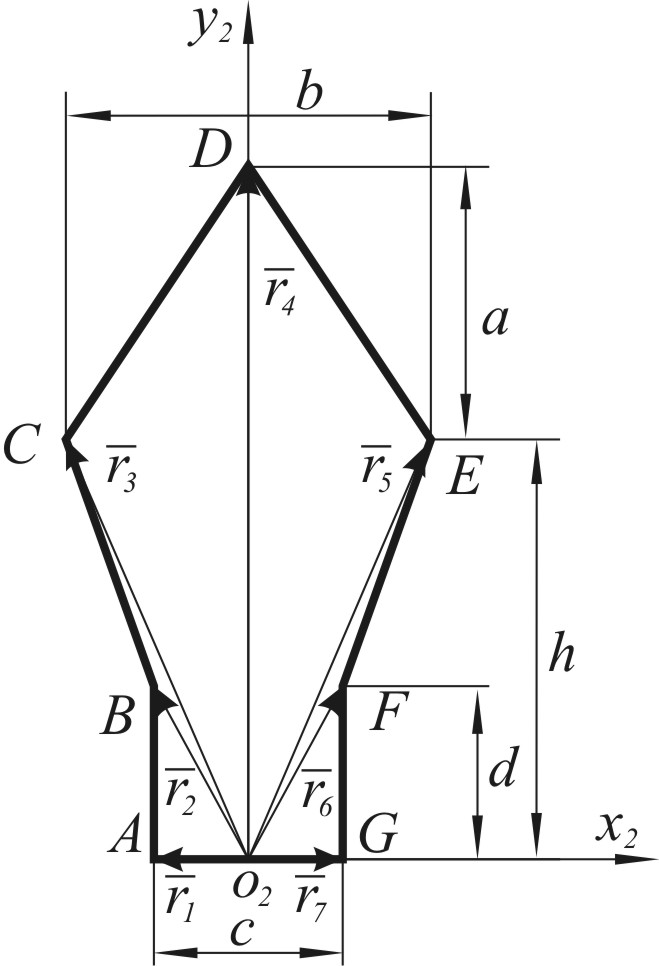
Для описания матричных элементов разработаны векторно-параметрические модели. Представленный в автореферате матричный элемент состоит из основы (I) и четырех областей соединения (II) (рисунок 4а). Основа описывается векторами 
в системе координат x1о1y1 (рисунок 4б), а область соединения – 
в системе координат x2о2y2 (рисунок 4в). Все структурные элементы приводятся к глобальной системе координат XOY. В качестве параметров выступают размеры a, b, c и т.д.
а б в
Рисунок 4 – Параметрическое описание матричного элемента:
а – матричный элемент; б – основа; в – область соединения
Плотное размещение матричных элементов определяется с помощью годографа функции плотного размещения (рисунок 5). Для его построения матричный элемент разбивается координатно-трапецеидальным способом, заключающимся в размещении на нем линий, параллельных оси OX.
Для нахождения массива точек пересечения секущих линий с контуром матричного элемента решается система уравнений, которая состоит из уравнений линий L1, L2,…,Ln, соединяющих точки матричного элемента (рисунок 6), и уравнений секущих линий:
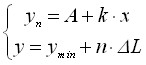. (1)
Оценкой плотного размещения матричных элементов является минимальное значение модуля вектора |
|. Для его нахождения используется годограф функции плотного размещения, представляющий собой совокупность точек конца вектора 
в процессе обхода одного матричного элемента относительно другого (рисунок 7). Результатом построения годографа является нахождение координат вектора 
при его минимальном модуле. Алгоритм построения годографа функции плотного размещения представлен на рисунке 8.
Для решения научной задачи, заключающейся в разработке математической модели плотной раскладки матричных элементов на плоскости, формируется полоса-сетка, которая образуется в виде семейств параллельных прямых {p} и {q}, проходящих через центры матричных элементов (рисунок 9). Параметры сетки (расстояние О1О2 и угол ) определяются в результате построении годографа функции плотного размещения.
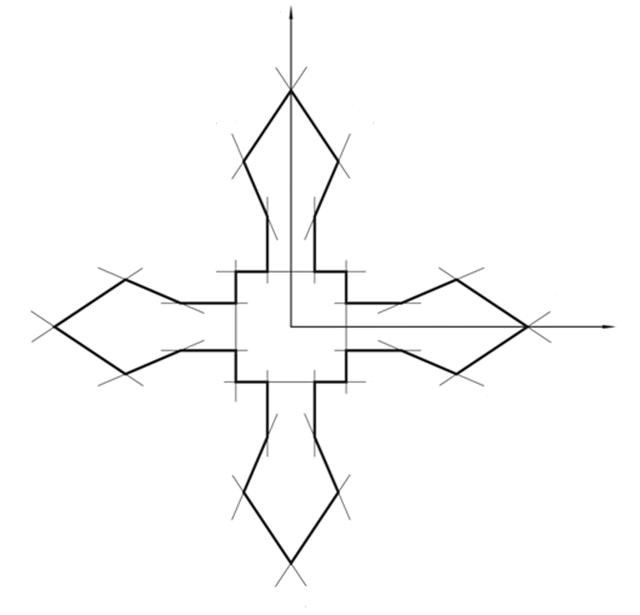
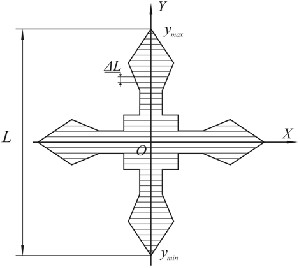
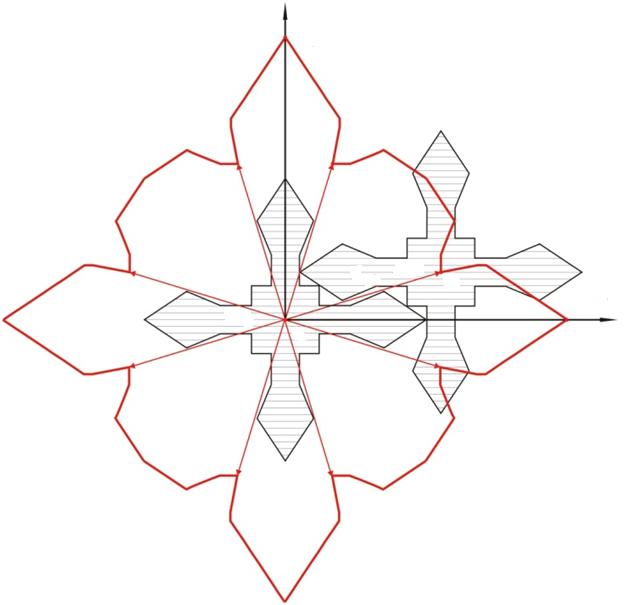
Рисунок 7 – Годограф функции плотного размещения матричных элементов
Для нахождения положения матричного элемента в раскладке определяются координаты центров Оi, которые являются точками пересечения прямых семейств {p} и {q}. Уравнения этих прямых записываются следующим образом:
(2)
Рисунок 8 – Алгоритм построения годографа функции
плотного размещения матричных элементов
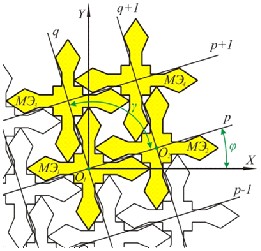
Рисунок 9 – Плотная раскладка матричных элементов в виде полосы сетки
Коэффициенты k1 и k2 определяются исходя из параметров и взаимного расположения матричных элементов в раскладке (рисунок 9):
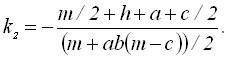(3)
Свободные коэффициенты Ap и Aq зависят от расстояния между центрами матричных элементов в раскладке (рисунок 9) и определяются по формулам:
(4)
где p – номер ряда в раскладке,
q – номер столбца в раскладке.
Для линий q и p, не проходящих через центр системы координат, свободные коэффициенты вычисляются следующим образом:
(5)
Для рассмотренного матричного элемента значения Ap и Aq находятся по формулам:
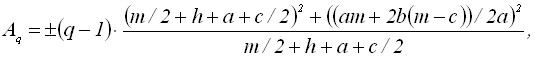
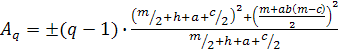
(6)
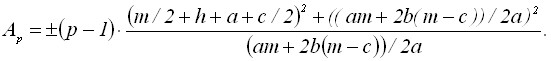
(7)
В результате совместного решения уравнений (2) с соответствующими коэффициентами Ap и Aq находятся координаты новых центров матричных элементов. Расположение матричных элементов, полученных таким образом, удовлетворяет условиям плотной раскладки.
В третьей главе рассматривается решение научной задачи, заключающейся в разработке алгоритма рационального размещения матричных элементов на меховых полуфабрикатах и кожевенных материалах. Для этого выполняется описание сложного контура полуфабриката с помощью сплайн-функции (рисунок 10). Параметрическое уравнение сегмента сплайна имеет вид:
, 
, (8)
где tk и tk+1 – значения параметров в начале и конце сегмента;
P(t) – вектор к любой точке сегмента.
Рисунок 10 –Наложение матричных элементов в виде сетки на контур полуфабриката
Постоянные коэффициенты Bi вычисляются из четырех граничных условий для сегмента сплайна. Значения параметров 
определяются по формуле
, (9)
где 
, 
, 
, 
– координаты точек кусочного сплайна.
Внутренние касательные векторы вычисляются из уравнения:
, (10)
где 
– квадратная матрица.
В координатной форме уравнение имеет вид:
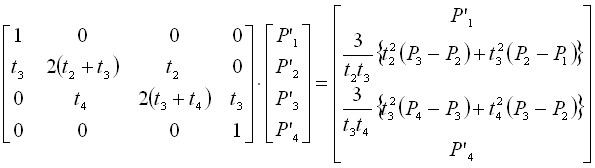. (11)
Для получения плотной раскладки матричных элементов на полуфабрикате раскладка в виде сетки накладывается на его контур. Система координат сетки X1O1Y1 совмещается с системой координат контура полуфабриката XOY и определяются матричные элементы, которые входят в контур. Для этого проверяется каждый матричный элемент в раскладке на непересечение с контуром полуфабриката. Подсчитывается количество матричных элементов, попавших в контур полуфабриката. После этого изменяется положение сетки, и цикл определения количества матричных элементов, попавших в контур, повторяется. Изменение координат сетки заканчивается, когда в контур полуфабриката попало наибольшее количество матричных элементов. Оценка выбранного варианта раскладки производится по проценту использования площади полуфабриката.
В четвертой главе решена практическая задача – разработано программное обеспечение для автоматизированного проектирования рациональных раскладок. Для этого разработан алгоритм рационального размещения матричных элементов на пушно-меховых полуфабрикатах и натуральных кожевенных материалах с контурами сложной конфигурации (рисунок 11), состоящий из подпрограмм, каждая из которых соответствует определенному этапу размещения матричных элементов.
Выбор матричных элементов осуществляется из базы данных структурных элементов (рисунок 12) или из базы данных матричных элементов. Для определения плотного размещения матричных элементов на плоскости строится годограф функции плотного размещения, с помощью которого формируется сетка из матричных элементов. Выбор полуфабриката для раскроя осуществляется из базы данных материалов или путем ввода его изображения. Для пушно-меховых полуфабрикатов производится выделение контура шкурки в автоматическом режиме. На полученный контур накладывается сетка из матричных элементов.
После определения наиболее рационального варианта размещения матричных элементов в контуре полуфабриката результаты раскладки выводятся на экран (рисунок 13). В окне «Результаты раскладки» приводится графическое изображение полученной раскладки, а также численные значения результатов, а именно, площадь полуфабриката и матричного элемента, количество вписанных элементов и коэффициент использования площади полуфабриката.
Рисунок 11 – Алгоритм размещения матричных элементов
на пушно-меховом полуфабрикате
Рисунок 12 – Окно базы данных структурных элементов
Рисунок 13 – Окно «Результаты раскладки»
Разработанный программный модуль позволяет в автоматизированном режиме осуществлять процесс рационального размещения матричных элементов на пушно-меховых полуфабрикатах и натуральных кожевенных материалах с контурами сложной конфигурации.
Основные выводы и результаты
1. На основании анализа литературных источников установлено, что до настоящего времени не решены вопросы эффективного использования пушно-меховых полуфабрикатов и натуральных кожевенных материалов.
Отходы, образующиеся при переработке этих материалов на швейные и меховые изделия, составляют (20–30 % – для кожи и 30–40 % – для меха).
2. В результате анализа отходов пушно-меховых полуфабрикатов установлено, что они имеют различный сложный контур, который затрудняет их применение. С целью рационального использования отходов предложено выкраивать из них матричные элементы, параметры которых могут изменяться в зависимости от параметров отходов.
3. Разработаны векторно-параметрические модели матричных элементов, позволяющие представлять их в ЭВМ, производить с ними модификации (изменение параметров) и аффинные преобразования, необходимые для размещения их на меховом полуфабрикате.
4. На основании экспериментальных исследований установлено, что условием повышения плотности раскладок матричных элементов является использование методов адаптивного конструирования. Их применение позволяет увеличить плотность раскладки до 85–100 %.
5. В результате аффинных преобразований векторно-параметрических моделей матричных элементов разработан алгоритм построения годографа функции плотного размещения, который основан на определении минимального расстояния между локальными системами координат матричных элементов в раскладке.
6. На основе векторно-параметрического задания матричных элементов и построения годографа функции плотного размещения разработана математическая модель построения годографа функции плотного размещения матричных элементов на неограниченной плоскости, которая позволяет определить узлы сетки для размещения в них локальных систем матричных элементов.
7. На основании получения координат узлов сетки, в которой располагаются центры матричных элементов, и аналитического описания контура полуфабриката разработан алгоритм их совместного наложения, позволяющий определить узлы, попавшие в контур полуфабриката, что приводит к сокращению операций по их перебору при определении матричных элементов, вписанных в контур.
8. На основе совместного решения уравнений прямых линий, проходящих через матричные элементы параллельно оси абсцисс, и сплайновых уравнений, описывающих контуры полуфабрикатов, определены точки их пересечения, что позволяет с помощью разработанного алгоритма определить матричные элементы, полностью размещенные в контуре.
9. На основе полученных математических моделей и алгоритмов сформированы состав и структура информационного обеспечения процесса автоматизированного проектирования, разработаны программный модуль, позволяющий проектировать раскладки матричных элементов на пушно-меховых полуфабрикатах и натуральных кожевенных материалах, и база данных структурных элементов, позволяющая проектировать матричные элементы с визуализацией их на экране ЭВМ.
10. Реализация предложенных разработок позволяет повысить процент использования пушно-меховых полуфабрикатов и натуральных кожевенных материалов на 10–25 % и сократить время на выполнение раскладок МЭ в 1,5–2,0 раза.
Основное содержание диссертации опубликовано
в следующих работах:
В изданиях, рекомендованных экспертным советом ВАК
1. Андросова, Г. М. Получение плотных раскладок матричных элементов сложной формы на безграничной плоскости [Текст] / Г.М. Андросова, И.Г. Браилов, Е.В. Бахтурина, С.В. Кубаева // Системы управления и информационные технологии. – 2009. – № 3 (37). – С. 47–50.
2. Андросова, Г. М. Применение кубических сплайнов при проектировании головного убора из матричных элементов [Текст] / Г. М. Андросова, И. Г. Браилов, С. В, Черепанова, Е. В. Бахтурина // Вестник Тамбовского государственного технического университета. – 2009. – Том 15. – № 4. – С. 777–789.
3. Андросова, Г. М. Решение задачи рационального использования пушно-меховых полуфабрикатов [Текст] / Г. М. Андросова, И. Г. Браилов, А. А. Старовойтова, Е. В. Бахтурина // Известия вузов. Технология легкой промышленности. – 2010. – № 3. – С. 51–55.
В других изданиях
4. Альтенгоф, Ю.В. К вопросу рационального использования отходов пушно-меховых полуфабрикатов [Текст] / Ю. В. Альтенгоф, Е. В. Бахтурина // V Межвузовская научно-практическая конференция студентов и аспирантов «Молодежь, наука, творчество» : сборник материалов. – Омск : ОГИС, 2007. – С. 262–263.
5. Андросова, Г. М. Определение факторов, влияющих на рациональное использование мехового и кожевенного полуфабриката, при изготовлении изделий из матричных элементов [Текст] / Г. М. Андросова, Е. В. Бахтурина // Формула успеха в подготовке специалистов : сборник научных статей. – Омск : Филиал ГОУ ВПО РосЗИТЛП в г. Омске, 2008. – С. 20–26
6. Андросова, Г. М. Применение правила тропизации для минимизации отходов мехового и кожевенного полуфабрикатов при раскрое матричных элементов [Текст] / Г. М. Андросова, Е. В. Бахтурина // VI Международная научно-практическая конференция «Научный потенциал высшей школы для инновационного развития общества» : сборник материалов. – Омск : ОГИС, 2008. – С. 30–32.
7. Андросова, Г. М. Разработка методики расчета полуфабриката на изделия из матричных элементов [Текст] / Г. М. Андросова, Е. В. Бахтурина // V Международная научно-практическая конференция «Современные тенденции и перспективы развития образования в высшей школе» : сборник материалов. – Омск : ОГИС, 2007. – С. 44–46.
8. Бахтурина, Е. В. Исследование свойств полотен из матричных элементов, раскроенных из меховых шкурок в различных направлениях [Текст] / Е. В. Бахтурина, Н. А. Шихова, М. А. Гептинг // VI Межвузовская научно-практическая конференция студентов и аспирантов «Молодежь, наука, творчество» : сборник материалов. – Омск : ОГИС, 2008. – С. 44–45.
9. Бахтурина, Е. В. Применение кубических сплайн-функций для описания контура матричного элемента [Текст] / Е. В. Бахтурина, С. В. Кубаева // Межвузовская научно-техническая конференция аспирантов и студентов «Молодые ученые – развитию текстильной и легкой промышленности» (ПОИСК – 2008) : сборник материалов. Часть 1. – Иваново : ИГТА, 2008. – С. 152–153.
10. Бахтурина, Е. В. Применение правила мультипликации с целью минимизации отходов пушно-меховых и кожевенных полуфабрикатов при раскрое матричных элементов [Текст] / Е. В. Бахтурина, Н. Н. Денисова // VIII Межвузовская научно-практическая конференция «Молодежь, наука, творчество» студентов и аспирантов: сборник материалов. В 2-х ч. Ч. 1. – Омск : ОГИС, 2010. – С. 70–72.
11. Бахтурина, Е. В. Разработка алгоритма рационального размещения матричных элементов на пушно-меховом полуфабрикате [Текст] / Е. В. Бахтурина, М. А. Гептинг // VIII Межвузовская научно-практическая конференция студентов и аспирантов «Молодежь, наука, творчество» : сборник материалов. В 2-х ч. Ч. 1. – Омск : ОГИС, 2010. – С. 77–79.
12. Бахтурина, Е. В. Разработка алгоритма рационального размещения матричных элементов на меховом и кожевенном полуфабрикатах [Текст] / Е. В. Бахтурина // Межвузовская научно-практическая конференция студентов, аспирантов и молодых исследователей «Теоретические знания в практические дела» : сборник материалов. – Омск : Филиал ГОУ ВПО РосЗИТЛП в г. Омске, 2007. – С. 26–27.
13. Бахтурина, Е. В. Разработка методики расчета количества матричных элементов [Текст] / Е. В. Бахтурина // Межвузовская научно-практическая конференция студентов, аспирантов и молодых исследователей «Теоретические знания в практические дела» : сборник материалов. – Омск : Филиал ГОУ ВПО РосЗИТЛП в г. Омске, 2008. – С. 21–24.
14. Бахтурина, Е. В. Разработка параметрической модели матричных элементов при проектировании плотной раскладки [Текст] / Е. В. Бахтурина, А. А. Кажигалимова // VI Межвузовская научно-практическая конференция студентов и аспирантов «Молодежь, наука, творчество» : сборник материалов. – Омск : ОГИС, 2009. – С. 116–118.
15. Бахтурина, Е. В. Формирование оптимальной раскладки матричных элементов на отходах мехового и кожевенного производства [Текст] / Е. В. Бахтурина, К. Б. Мальгельдинова // VII Межвузовская научно-практическая конференция студентов и аспирантов «Молодежь, наука, творчество» : сборник материалов. – Омск : ОГИС, 2008. – С. 50.
16. Бахтурина, Е. В. Методика вычисление площади краевых отходов пушно-мехового и кожевенного полуфабрикатов, получаемых при раскрое матричных элементов [Текст] / Е. В. Бахтурина // II Международная научно-практическая конференция «Молодежь и наука: реальность и будущее». – Невинномыск : НИУЭП, 2009. – С. 404-407.
17. Бахтурина, Е. В. Применение правила лабилизации с целью минимизации отходов пушно-меховых и кожевенных полуфабрикатов при раскрое матричных элементов [Текст] / Е. В. Бахтурина, Н. Н. Денисова // Межвузовская научно-практическая конференция студентов, аспирантов и молодых исследователей «Теоретические знания в практические дела» : сборник материалов. – Омск : Филиал ГОУ ВПО «РосЗИТЛП» в г. Омске, 2010. – С. 4–6.
18. Свириденко, О. В. Аналитическое описание проектирования структуры полотен из кожи и меха [Текст] / О. В. Свириденко, И. Г. Браилов, Г. М. Андросова, Е. В. Бахтурина // Теоретические и прикладные проблемы сервиса. – М. : МГУС, 2007. – № 3 (24). – С. 28–31.
19. Старовойтова, А. А. Определение коэффициента пропорциональности для создания оптимальной раскладки матричных элементов на меховом полуфабрикате [Текст] / А. А. Старовойтова, Е. В. Бахтурина // VI Международная научно-практическая конференция «Научный потенциал высшей школы для инновационного развития общества» : сборник материалов. – Омск : ОГИС, 2008. – С. 42–44.
20. Androsova, G. M. Enhancement of young people’s careers motivation in scientific areas [Text] / G. M. Androsova, I. G. Brailov, E.V. Bakhturina, S.V Kubaeva // International journal of experimental education. – 2008. – № 3. – p. 87.
Косова Елена Вячеславовна
Автоматизация проектирования плотных раскладок
матричных элементов на пушно-меховых полуфабрикатах
и натуральных кожевенных материалах
Автореферат диссертации на соискание ученой степени
кандидата технических наук
Подписано в печать 29.04.2011 г. Формат 60х84/16.
Бумага офсетная.. Усл.п.л. 1,0.
Тираж 100экз. Зак.
Отпечатано в типографии:.,
