Теоретические и прикладные аспекты прогнозирования распределения фасонных эффектов и пороков внешнего вида нитей и ткани

На правах рукописи

УДК 677.07.019:519.216.3

ЗЕМЛЯКОВА Ирина Владимировна

ТЕОРЕТИЧЕСКИЕ И ПРИКЛАДНЫЕ АСПЕКТЫ

ПРОГНОЗИРОВАНИЯ РАСПРЕДЕЛЕНИЯ ФАСОННЫХ ЭФФЕКТОВ

И ПОРОКОВ ВНЕШНЕГО ВИДА НИТЕЙ И ТКАНИ

Специальность 05.19.02 – Технология и первичная обработка текстильных

материалов и сырья

АВТОРЕФЕРАТ

диссертации на соискание ученой степени

доктора технических наук

Кострома

2006

Работа выполнена в Костромском государственном технологическом

университете (КГТУ)

Научный консультант: доктор технических наук,

профессор Лустгартен Нелли Владимировна

Официальные оппоненты: доктор технических наук,

профессор Оников Эдуард Аршакович

доктор технических наук,

профессор Мовшович Павел Михайлович

доктор технических наук,

профессор Маховер Валерий Львович

Ведущая организация: ОАО Костромской научно-исследовательский

институт льняной промышленности

(ОАО «КНИИЛП»), г.Кострома

Защита состоится 28 июня 2006 г. в 10 часов на заседания диссертационного совета Д 212.093.01 в Костромском государственном технологическом университет по адресу: 156005, г. Кострома, ул. Дзержинского, 17, ауд. Б-106.

С диссертацией можно ознакомиться в библиотеке Костромского государственного университета.

Автореферат разослан 27 мая 2006 г.

Ученый секретарь диссертационного совета,

доктор технических наук, профессор П. Н. Рудовский

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность темы

К тканям предъявляются требования двух типов – технические и эстетические. Эстетические требования – это требования к внешнему виду и оформлению ткани, которые играют решающую роль при формировании спроса. Текстильные предприятия страны производят большие объемы тканей на внешний рынок, где сталкиваются с проблемой разных требований к качеству тканей у зарубежных заказчиков по сравнению с требованиями ГОСТов, причем, прежде всего, по порокам внешнего вида тканей, которые связаны с пороками нитей. Кроме того, проблема заключается в том, что существуют ГОСТы, регламентирующие определение класса пряжи по внешнему виду и сорт ткани по порокам внешнего вида, а взаимосвязь между классами чистоты пряжи и оценкой ткани на наличие пороков внешнего вида отсутствует.

Задача определения взаимосвязи между распределением пороков внешнего вида на нити и ткани аналогична задаче проектирования распределения прерывистых фасонных эффектов по ткани. Это позволяет применить общие подходы к решению задачи прогнозирования распределения фасонных эффектов и пороков внешнего вида по поверхности ткани.

Фасонные нити разнообразны по своим свойствам и используются при производстве платьевых, костюмных, портьерных и других тканей. Одной из причин, ограничивающих масштабы применения фасонных нитей, является неравномерная группируемость эффектов по ткани. Неверно подобранный закон распределения расстояний между фасонными эффектами на нити приводит к появлению брака на ткани, так называемого «муара». В работах Д.И.Авербуха, А.М.Мурзиной, Ю.Б.Федорова и других авторов, затрагивался вопрос математического описания распределения фасонных эффектов по ткани. Большинство моделей распределения эффектов по поверхности ткани, предложенных исследователями, являются имитационными, а аналитические модели созданы лишь для частных случаев, что сужает возможность расширения ассортимента тканей за счет применения фасонных нитей.

Таким образом, проблема улучшения качества тканей на основе использования методов прогнозирования и проектирования распределения фасонных эффектов и пороков внешнего вида на ткани – актуальна, как в научном, так и прикладном значении.

Работа выполнялась в рамках НИР «Исследование взаимосвязи дефектности сырья, полуфабрикатов, суровой и готовой ткани, создания информационной базы для повышения качества выпускаемой продукции» по заказу ООО «БКЛМ – Актив».

Цель и задачи исследования

Целью работы является расширение ассортимента и улучшение качества тканей на базе автоматизированных процедур проектирования распределений фасонных эффектов и пороков внешнего вида на поверхности тканей.

В соответствие с данной целью в диссертационной работе поставлены и решены следующие основные задачи:

• создание детерминированных и стохастических моделей распределения фасонных эффектов уточной и основной нитей по ткани;
• формирование математических моделей распределения пороков внешнего вида на нити и ткани;
• создание программного обеспечения процесса проектирования распределений фасонных эффектов (ФЭ) и пороков внешнего вида по поверхности ткани;
• классификация рисунков расположения ФЭ уточной и основных нитей на ткани;
• создание методического, информационного и математического обеспечения АРМ дессинатора;
• разработка методического и математического обеспечения автоматизированной системы распознавания пороков внешнего вида и определения класса чистоты пряжи;
• создание методики оценки числа пороков внешнего вида на поверхности ткани.

Методы исследования

В диссертационной работе используются методы и аппарат теории чисел, теории множеств, функционального анализа, линейной алгебры, аналитической геометрии, теории вероятностей и математической статистики, теории случайных функций, теории массового обслуживания, методы оценки показателей качества текстильных материалов.

Реализация метода автоматизированного распознавания пороков внешнего вида и определения класса чистоты пряжи проводилась в интегрированной среде программирования Borland Delphi 7.0, а для автоматизированного проектирования распределения фасонных эффектов по ткани была выбрана среда Borland C++ Builder.

Научная новизна

В диссертационной работе впервые:

• расширены теоретические основы технологического проектирования текстильных изделий в части описания распределений фасонных эффектов и пороков внешнего вида на нитях и тканях, которое содержит:

- теоретико-множественный подход к описанию распределений эффектов и дефектов на ткани в зависимости от распределения их на нити и заправочных параметров ткани;

- описание процесса проектирования рисунков из фасонных эффектов на поверхности ткани на базе аппарата теории чисел;

- матричный метод определения расположения каждого эффекта на ткани.

• построена совокупность детерминированных и стохатисческих математических моделей распределения фасонных эффектов уточных и основных нитей по поверхности тканей в зависимости от:

- закона распределения расстояний между серединами эффектов на нити, закона распределения длин эффектов и диаметра эффекта;

- ширины ткани, ширины заправки по берду, ширины кромок, длины куска ткани, плотности ткани по основе и утку, уработки основы и утка, закона чередования числа фасонных и гладких нитей;

- обрывности в процессе получения нити и ткани.

• предложен формализованный метод теоретического исследования характера распределения фасонных эффектов по ткани, основанный на выборе базисных векторов распределения, что позволяет расширить диапазон применяемых вариантов оформления ткани фасонными эффектами.
• предложено методическое обеспечение для автоматизированного проектирования рисунков из фасонных эффектов уточной и основной нитей на поверхности ткани, позволяющее значительно расширить возможности использования фасонных нитей при производстве тканей;
• разработан метод прогнозирования качества тканей на основе анализа распределения пороков внешнего вида, позволяющий сформировать требования к качеству используемых нитей и существенно повышающий конкурентноспособность тканей.

Практическая ценность и реализация результатов работы

Настоящая работа дает возможность расширить ассортимент тканей за счет использования фасонных нитей в качестве утка и основы и улучшить их качество.

Результаты исследований оформлены в виде методики построения распределения фасонных эффектов по ткани и методики прогнозирования дефектности ткани из-за внешних пороков пряжи и рекомендаций по степени очистки пряжи.

На основе теоретических исследований были рассчитаны параметры нити и ткани и проведена наработка опытной партии фасонной нити и опытной партии ткани в условиях АО «Большая льняная мануфактура». Программный комплекс оценки ткани по наличию пороков внешнего вида принят к использованию в ООО «БКЛМ-Актив».

Апробация работы

Основные положения диссертационной работы докладывались и получили положительную оценку на семинарах и конференциях:

• заседаниях профессорского семинара Костромского государственного технологического университета в 2003, 2004, 2005 годах;
• международной научно-технической конференции «Проблемы развития текстильной и легкой промышленности в современных условиях (Иваново, 1992);
• международной научно-методической конференции «Математика в вузе – стандарты образования – базовая подготовка» (Кострома – С.-Петербург, 1996);
• международной научно-технической конференции «Актуальные проблемы переработки льна в современных условиях» (Кострома, 1992, 1998, 2004);
• международной научно-технической конференции «Математические методы в технике и технологиях» (Кострома, 2004; Казань, 2005).

Публикации

Основное содержание диссертации отражено в 24 публикациях, из них одна монография, пять – в журнале «Известия вузов. Технология текстильной промышленности», две – в журнале «Текстильная промышленность», три – в журнале «Вестник КГТУ», четыре – депонированных статей и девять – в трудах Международных научных конференций.

На защиту выносятся:

1. Теоретические положения, расширяющие представление об описании распределений фасонных эффектов на ткани.
2. Совокупность моделей и результаты моделирования распределений фасонных эффектов и пороков внешнего вида нитей и ткани.
3. Методическое обеспечение для автоматизированного проектирования рисунков из фасонных эффектов на ткани:
• матричный метод описания расположения эффектов по ткани, вырабатываемой с использованием фасонной нити в качестве утка;
• процедура количественной оценки характера расположения фасонных эффектов по ткани.
4. Методическое и математическое обеспечение автоматизированной системы распознавания пороков и определения класса чистоты пряжи.
5. Методика оценки числа внешних пороков на ткани и ее качества в зависимости от распределения пороков на нити.
6. Результаты практического исследования разработанных теоретических положений моделей, методик.

Структура и объем работы

Диссертационная работа состоит из введения, пяти глав, общих выводов, заключения, списка литературы и приложения. Работа изложена на 287 страницах, содержит 43 рисунка, 15 таблиц, список литературы включает 148 наименований.

СОДЕРЖАНИЕ РАБОТЫ

Во введении обоснованы актуальность темы диссертации, сформулированы цель, основные задачи и методы исследования, показаны научная новизна, практическая ценность и реализация результатов работы.

В первой главе рассмотрено современное состояние проблемы прогнозирования распределения фасонных эффектов и пороков внешнего вида нитей и ткани и общая схема решения задачи проектирования распределений.

Проанализированы основные способы оформления тканей и изложены основы композиции рисунка на тканях. В приведенном анализе особое внимание уделено оформлению тканей за счет применения фасонных нитей, как в качестве основы, так и в качестве утка. Использование фасонных нитей позволяет придать ткани интересное колористическое оформление, своеобразную рельефную поверхность. Как правило, оформление ткани достигается за счет наличия в структуре нити фасонного эффекта, а при выработке льняных тканей, в основном, применяются фасонные нити с ровничным эффектом.

Основным фактором, влияющим на расположение фасонных эффектов по ткани, является распределение эффектов на нити. Во многих работах, посвященных получению фасонных нитей и тканей с их использованием, затрагивался вопрос о выборе закона чередования расстояний между эффектами на нити и прогнозировании распределения фасонных эффектов по поверхности ткани. Ряд авторов (Д.И.Авербух, Ю.Б.Федоров, Л.В.Сухова, О.Р.Воронцова и др.) разработали математические модели распределения прерывистых фасонных эффектов по ткани в зависимости от некоторых заправочных параметров ткани и частных случаев распределений эффектов на нити. В этих работах были предложены программы, моделирующие распределение эффектов по ткани в зависимости от рассмотренных законов чередования их на нити. Была разработана система имитационных моделей для автоматизированного проектирования рисунков из фасонных эффектов на тканях, вырабатываемых с использованием уточной фасонной нити с различными законами распределения расстояний между эффектами и длин эффектов. Фасонные нити с ровничными эффектами применялись для получения на ткани теневых переходов. Были проанализированы работы, посвященные использованию фасонных нитей в трикотажных полотнах и изделиях, применению двухкомпонентных фасонных нитей с переменной круткой для создания полутоновых рисунков на текстильных полотнах.

В результате анализа математических описаний распределения фасонных эффектов по ткани сделаны следующие выводы:

- большинство моделей распределения прерывистых фасонных эффектов по ткани являются имитационными;

- аналитические модели распределения эффектов по ткани в зависимости от распределения их на нити и параметров ткани созданы лишь для частных случаев;

- необходимо создать комплекс новых, универсальных математических моделей, позволяющих в зависимости от параметров ткани и различных законов распределения расстояний между эффектами и их длин прогнозировать распределение фасонных эффектов по поверхности ткани.

В данной главе содержится описание пороков внешнего вида нитей и тканей и причины их возникновения, предложена классификация дефектов. Рассмотрены методы определения чистоты нитей и сорта тканей по стандартам, а также оценка сортности ткани по наличию пороков внешнего вида и требования, предъявляемые к экспортируемым тканям. Отмечено, что требования к экспортной ткани по количеству и размерам пороков внешнего вида существенно отличаются от требований стандартов. Для анализа распределений пороков внешнего вида нитей и тканей обычно предлагается единственная статистическая модель – распределение Пуассона, причем отдельно для нитей и тканей. Необходимо создать математическую модель прогнозирования распределения пороков внешнего вида по ткани.

Задачи прогнозирования распределения фасонных эффектов и пороков внешнего вида по ткани имеют много общего, а именно, важнейшим фактором, влияющим на расположение и эффектов, и дефектов по ткани является их распределение на нити. Кроме параметров нити, на распределение эффектов и пороков внешнего вида по поверхности ткани оказывают влияние параметры ткани и технологический режим получения нити и ткани. В связи со сказанным, предложена концептуальная модель прогнозирования распределений прерывистых фасонных эффектов и пороков внешнего вида (утолщений, утонений, шишек и т.п.) по ткани (рис.1) и общая схема решения задачи проектирования распределений по ткани, в которой фасонные эффекты и пороки внешнего вида объединены общим названием – прерывистые элементы (ПЭ).

Рис.1. Концептуальная модель распределения фасонных эффектов

и пороков внешнего вида нити по поверхности ткани

Решать задачу проектирования распределения ПЭ по ткани предлагается в метрическом пространстве (А, ), где А – упорядоченное множество ПЭ на нити, – расстояние (метрика) между элементами А. Расстояние между серединами ПЭ является функцией порядкового номера R(n), причем R(n) может быть числовой функцией или случайной последовательностью.

Входными параметрами и переменными являются:

1. технологические параметры: bз – ширина заправки по берду, см; bT – ширина ткани, см; bкр – ширина кромок, см; LT – длина куска ткани, см; Po, Py – плотность ткани по основе и по утку, н/10 см; Pо кр – число нитей в кромках на 10 см; ао, ау – уработка основы, утка, %;
2. управляемые переменные: R(n) – закон распределения расстояний между серединами ПЭ; l(n) – закон распределения длин ПЭ;

Nф / Nг – закон чередования числа фасонных и числа гладких нитей;

3. неуправляемые переменные: отклонение расстояний между ПЭ от расчетных; обрывность в процессе получения нити и ткани.

Выходными параметрами является количественная оценка распределения ПЭ на ткани: для пороков – мощность множества m(A), для фасонных эффектов – расстояние от x до множества A .

Во второй главе представлены детерминированные математические модели прогнозирования распределений фасонных эффектов уточной нити по поверхности ткани.

Дано описание расположения фасонных эффектов по ткани, вырабатываемой с использованием фасонной уточной нити, длина b которой кратна шагу a эффектов на нити, т.е. , где n – натуральное число. Эффекты на ткани располагаются вдоль вертикальных прямых. Изменяя n, закон чередования фасонных и гладких уточных нитей и длину эффекта lэ при неизменных ширине и плотности ткани по утку и основе, можно получать различные рисунки из фасонных эффектов на ткани: продольные и поперечные полосы, равномерное заполнение и близкое к нему, переходные распределения. Установлены зависимости характера распределения эффектов по ткани от шага эффектов на нити и параметров ткани, определены раппорты рисунков из фасонных эффектов по ширине и по высоте, приведена классификация рисунков. Теоретически для каждого натурального n = 1,2,…, при шаге на ткани можно получить рисунок из фасонных эффектов, середины которых расположены вдоль вертикальных прямых, но на практике это не всегда возможно. Число может быть либо целым, либо конечной десятичной дробью, либо бесконечной периодической дробью, а на практике при наработке фасонной нити шаг а, заданный в см, может быть либо целым, либо десятичной дробью с десятой долей единицы. При округлении значения шага эффекты на ткани будут располагаться вдоль наклонных прямых, тангенс угла наклона которых равен , где а* - округленное, приближенное значение шага.

Рассмотрено распределение эффектов по ткани в зависимости от ошибки округления значения шага. Выявлены условия, при которых происходят резкие изменения рисунка из фасонных эффектов. Для заданной длины уточной нити установлены значения шага и число фасонных и гладких нитей, при которых получаются рисунки из фасонных эффектов на поверхности ткани, наименее чувствительные к отклонениям значений шага от расчетных.

В общем случае шаг а эффектов нити и длина b уточной нити – действительные числа, но на практике утверждение, что две точки отстоят друг от друга на расстоянии, выражающемся иррациональным числом см (мм), не имеет смысла, поэтому отношение - рациональная дробь, либо может быть приведена к ней (от см перейти к мм). Рисунок расположения эффектов на ткани зависит, прежде всего, от отношения , поэтому модель распределения фасонных эффектов по ткани предлагается строить на базе теории чисел.

Дробь с помощью алгоритма Евклида представляем в виде конечной непрерывной дроби [m1, m2, m3,…, mk].. Составляем подходящие дроби , …, , где n1, n2 – натуральные числа, - несократимая дробь, эквивалентная дроби . При переводе в непрерывную дробь получаем набор остатков [r1, r2,…, rk-1, 0]. Как правило, шаг а эффектов нити меньше длины b уточной нити, поэтому m1 = 0, r1 = a. Тогда процесс заполнения эффектами поверхности ткани, вырабатываемой с использованием фасонной нити в качестве утка на станках типа СТБ при законе чередования фасонных и гладких нитей 1/Nг, может быть описан на базе теории чисел с помощью алгоритма Евклида (сформулированы и доказаны свойства, устанавливающие зависимость расположения эффектов на ткани от m1, …, mk, r1, …, rk). При равношаговом расположении фасонных эффектов на нити цикл распределения эффектов по ткани равен n1 фасонной уточной нити.

Середины фасонных эффектов на ткани образуют конечное множество, соединяя их различными способами, получим несколько семейств прямых, вдоль которых расположены эффекты. Для получения уравнений этих прямых необходимо ввести прямоугольную декартову систему координат, проведя ось абсцисс через ось первой фасонной уточной нити, а начало координат поместить в середину первого эффекта, зарабатываемого в правый конец первой уточной фасонной нити. На данном этапе приняты допущения: уточные нити в ткани располагаются по прямым линиям, а расстояние между осями соседних уточных нитей равны. Эти допущения оправданы, так как вследствие изгиба уточных нитей происходит пропорциональное сжатие рисунка, общий характер не искажается и это сжатие будет учтено в дальнейшем. Различия расстояний между осями уточных нитей несопоставимо малы по сравнению с другими размерами и практически не вносят изменений в рисунок. Векторы, имеющие вид , где n=1, 2, 3, …, k, (или , если размеры в мм) – расстояние между центрами двух соседних фасонных уточных нитей, назовем векторами распределения. Семейства прямых, проходящих через середины эффектов на ткани, направляющие векторы которых – векторы распределения , связаны с подходящими дробями следующим образом: число прямых в этих семействах, пересекающих первую уточную нить, равно , а разность номеров фасонных уточных нитей, где находятся соседние эффекты прямой семейства, равно . Если n – четно (n < k), то прямые имеют острый угол наклона n, т. е. . Если n – нечетно (n < k), то , а при n=k угол наклона равен . Тангенс угла наклона прямых вычисляется по формуле где

Все множества прямых, которые можно получить, соединяя середины эффектов разными способами, можно описать с помощью уравнений семейств прямых с направляющими векторами , n=1,2,…, k и , где n=3,4,…,k, i=1,2,…,mn-1.

Раппорт по ширине при выпрямленных уточных нитях равен , с учетом изгиба уточных нитей ; раппорт по высоте – (или , если размеры в мм).

Следующий шаг – выбор из множества семейств прямых того семейства, которое определяет характер распределения эффектов по ткани. В литературе принято описывать закон размещения элементов рисунка уравнением прямых, соединяющих точки при x=0 и x=1, причем единицей масштаба является одна клетка, включающая определенное число уточных прокидок и основных нитей. Может оказаться, что зрительно будет восприниматься рисунок в виде диагональных полос, уравнение которых получается при соединении других точек внутри раппорта, что объясняется разным расстоянием между элементами рисунка. Для количественной оценки распределения эффектов по ткани выделим отдельно множество – множество середин эффектов первой фасонной уточной нити и множество М фасонных эффектов на поверхности ткани, образованной фасонными уточными нитями с номерами 2, 3, …, (n1+1). Каждому фасонному эффекту соответствует точка Mij – середина фасонного эффекта. В качестве количественной оценки распределения эффектов на ткани при равношаговом распределении их на фасонной уточной нити предлагается расстояние от точки до множества М: . . Поскольку рисунок расположения эффектов по ткани повторяется, то точки Mij достаточно рассматривать в прямоугольной области P размером , содержащей точку . Вместо , где , можно рассматривать длины соответствующих векторов, тогда , а это означает, что минимальная длина вектора является количественной оценкой распределения эффектов по ткани. Выбрав вектор, имеющий наименьшую длину, получаем первый базисный вектор , где . Поскольку ткань рассматриваем как двумерное пространство, то второй базисный вектор следует выбирать из оставшегося множества векторов с длиной . Если номер первого базисного вектора нечетный, то на ткани получаем распределение вдоль наклонных прямых с углом наклона , если четный, то , если , то , а в случае и – идеальное равномерное заполнение ткани эффектами.

Базисные векторы определяют характер расположения фасонных эффектов по ткани, а для определения расположения каждого фасонного эффекта предлагается матричный метод. Координаты середин эффектов на ткани предлагается находить по формуле , где – вектор-строка, – целые неотрицательные числа, 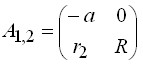– матрица, составленная из координат векторов и , – матрица подобия.

В работе указаны значения с1 и с2 для определения координат середин эффектов, расположенных на уточных фасонных нитях или вдоль диагоналей.

Координаты середин эффектов в случае распрямленных уточных нитей можно находить также по формуле , где – матрица, составленная из координат векторов распределения, – вектор-строка.

На основании математического описания распределения фасонных эффектов по ткани разработана методика проектирования рисунка расположения фасонных эффектов по ткани при равношаговом распределении их на уточной нити. В заключении приведена классификация рисунков из фасонных эффектов уточной нити по поверхности ткани.

В третьей главе представлены стохастические модели распределения эффектов на нити и ткани и анализ экспериментальных исследований.

Математические модели распределения фасонных эффектов по ткани, основанные на теории чисел, позволяют подобрать шаг эффектов на нити для получения на ткани желаемого рисунка из фасонных эффектов. Под влиянием ряда случайных факторов расстояния между серединами фасонных эффектов на нити будут несколько отличаться от расчетного значения шага, поэтому детерминированные математические модели дают приближенное, некоторое «среднее» описание распределения эффектов на ткани.

Для выявления влияния обрывности нити и отклонений длин интервалов между эффектами от номинальной длины на рисунок расположения фасонных эффектов по ткани, необходим аппарат теории случайных функций. Расстояние между серединами эффектов на нити фактически является случайной функцией, аргументом которой является номер интервала. Такие функции называются случайными последовательностями (случайными функциями целочисленного аргумента, случайным процессом с непрерывным состоянием и дискретным временем). Для получения на ткани желаемого рисунка расположения фасонных эффектов, необходимо удостовериться в том, что ни среднее расстояние между серединами эффектов, ни характер колебаний около средней длины интервала между эффектами не обнаруживают существенных изменений на всей паковке, то есть проверить случайную последовательность на стационарность.

Для определения основных характеристик случайной последовательности длин интервалов между серединами эффектов на нити необходимо иметь достаточно большое число реализаций при каждом значении аргумента. В случае, если случайная последовательность длин интервалов между серединами фасонных эффектов на нити является эргодической, то ее характеристики можно находить по одной реализации (нити с одной паковки) достаточно большой продолжительности.

Математическое ожидание и дисперсия случайной последовательности длин интервалов между серединами эффектов определяют полосу, заполняемую возможными реализациями случайной последовательности. В работе приведены способы определения основных характеристик случайной последовательности .

Следующий шаг – разработка стохастической модели распределения эффектов фасонной уточной нити по поверхности ткани. Кроме закона распределения расстояний между эффектами на нити на расположение эффектов по ткани влияют длина уточной нити, зарабатываемой в ткань, и расстояние R между центрами двух соседних уточных нитей, которые, вообще говоря, являются случайными величинами. Расстояние R значительно меньше расстояний между серединами эффектов, а отклонения от R тем более малы по сравнению с другими размерами, поэтому R можно считать постоянной величиной. Фактические длины уточных нитей, зарабатываемых в ткань, находятся в интервале , но на практике отклонения от номинального значения b оказывают незначительное влияние на рисунок расположения эффектов по ткани. В связи со сказанным, изменения рисунков из фасонных эффектов на ткани вызываются, как правило, отклонениями длин интервалов между серединами эффектов от расчетных и обрывностью нити. Указаны формулы для определения расчетного и фактического расстояний n-го эффекта от начала нити.

Положение фасонного эффекта на ткани определяется двумя координатами, а в связи с неизбежными отклонениями фактических расстояний от расчетных середина фасонного эффекта на ткани – это система двух случайных величин X и Y, которые рассматривают как случайную точку (X, Y) или случайный вектор. На практике чаще всего это двумерный нормальный закон распределения, плотность которого изображается поверхностью. Пересекая эту поверхность плоскостями, параллельными плоскости 0xy и проектируя на плоскость 0xy, получим семейство эллипсов с общим центром , которые называются эллипсами рассеивания, а полный эллипс рассеивания – тот, в который с практической достоверностью укладываются все рассеивания. Поскольку изменения рисунка расположения эффектов на ткани вызываются, как правило, отклонениями длин интервалов между серединами фасонных эффектов на нити, то середина фасонного эффекта на ткани будет располагаться в вырожденном эллипсе рассеивания с осью, параллельной оси 0x. Центр этого вырожденного эллипса (если нет систематических ошибок) находится в точке, координаты которой определяются по методике построения распределения эффектов на ткани. Длина оси рассеивания определяется средним квадратическим отклонением и вероятностью, которую мы принимаем за «практическую достоверность».

На рисунки из фасонных эффектов существенное влияние оказывает обрывность нити, причем в случае некорректируемого обрыва как и при получении нити, так и при выработке ткани рисунок расположения фасонных эффектов на ткани изменяется. При оценке и прогнозировании обрывности нитей в прядении и ткачестве используется распределение Пуассона. При ликвидации обрыва длину исключенного участка нити можно считать распределенной по нормальному закону с параметрами и . При прогнозировании распределения фасонных эффектов на ткани, безусловно, следует учитывать изменения рисунка, вызванные обрывностью, и из множества рисунков, образованных эффектами, выбирать те рисунки, которые существенно не изменяются при обрывности и колебаниях шага эффектов на нити.

Проведено исследование расположения ровничных эффектов льняной фасонной нити и их распределение на поверхности тканей, вырабатываемых с использованием фасонных уточных нитей с различными длинами интервалов между эффектами. Объектом исследования являлось распределение ровничных эффектов льняной фасонной нити, состоящей из стержневой нити – пряжи оческовой мокрого прядения 105 текс, 33% ПЭ; обкручивающей – пряжи линейной плотностью 29 текс, хлопчатобумажной; эффекта – ровницы цветной суровой, линейной плотностью 500 текс. На модернизированной машине ПК-100МФ было наработано 30 паковок и на каждой из паковок сделано по 40 замеров длин интервалов между серединами эффектов. Для проверки случайной последовательности длин интервалов между эффектами были применены два непараметрических критерия – метод превышений и метод последовательных разностей, гипотеза о стационарности случайной последовательности подтвердилась с вероятностью Pg = 0,98. На основании анализа вида корреляционной функции и из физических соображений был сделан вывод об эргодичности случайной последовательности. По критериям Бернштейна и Ястремского было установлено, что распределение длин интервалов подчинено нормальному закону распределения, математические ожидания длин интервалов между серединами фасонных эффектов на нити равны номинальным значениям шага.

На машине ПК-100МФ была наработана льняная фасонная нить с номинальными значениями шага эффектов 81,5 см и 82, 3 см, а также варианты нитей, среднее расстояние между серединами эффектов на которых имеют значения, близкие к 82,3 см. На станке СТБ4-220, с использованием фасонной нити в качестве утка, была получена ткань, ширина которой равна 180 см, плотность по утку – 80 н/10см, ширина проборки – 193 см, длина уточной нити – 196 см. Были построены математические модели распределения фасонных эффектов на ткани для названных выше входных параметров. Распределение эффектов на ткани, вырабатываемой с использованием фасонной нити со средним расстоянием 81,5 см между эффектами, характеризуется базисными векторами и , длина которых см, см. Первый базисный вектор имеет четный номер, его длина более чем в 2 раза меньше длины второго базисного вектора, значит на ткани получаем диагональное распределение эффектов вдоль прямых с острым углом наклона 17о, причем число прямых, пересекающих первую уточную нить, равно 12, между фасонными эффектами одной диагонали расположены 4 гладких нити.

Фактическое распределение эффектов на ткани соответствует теоретическому описанию, хотя наблюдаются отклонения расстояний между эффектами на диагонали и угла наклона диагоналей, вызванные отклонениями фактических расстояний между серединами фасонных эффектов на нити от номинального значения (Рис.2а).

Для ткани, вырабатываемой со средним значением расстояний между серединами эффектов 82,3 см, оба базисных вектора (а также минимальный по длине из оставшихся) мало отличаются друг о друга, на ткани получаем равномерное расположение эффектов (рис.2б). Обрыв уточной нити в этом случае не вносит существенных изменений в характер распределения эффектов по ткани.

В заключении представлены практические рекомендации по выбору шага фасонных эффектов на нити.

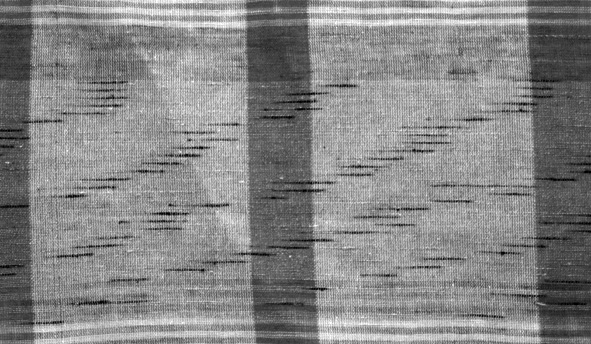
а) б)

Рис.2. Фотографии образцов ткани, выработанной с использованием

фасонной нити в качестве утка с номинальным значением

шага эффектов а на нити

а) а=81,5 см; б) а=82,3 см

Четвертая глава посвящена прогнозированию распределения эффектов основной фасонной нити по ткани.

Оригинальные варианты оформления ткани эффектами можно получать и за счет использования фасонной нити в качестве основы. Распределение эффектов основной фасонной нити по поверхности ткани зависит:

• от параметров нити: закона распределения расстояний между серединами фасонных эффектов на нити, закона распределения длин эффектов, диаметра эффекта;
• от параметров ткани: длины ткани, ширины ткани, плотности ткани по основе, закона чередования фасонных и гладких основных нитей;
• технологических режимов получения нити и ткани.

В отличие от распределения эффектов уточной фасонной нити расположение эффектов основной фасонной нити на поверхности ткани зависит от взаимного расположения эффектов на отдельных основных нитях в поперечном направлении, а именно, выравнены ли первые эффекты на всех основных нитях («общий старт») или их расположение случайно.

Для прогнозирования распределения эффектов основной фасонной нити разработаны детерминированные и стохастические модели этих распределений. Представлены математические описания распределения эффектов на ткани в случае, если расстояние между серединами основных фасонных эффектов и длина эффектов – постоянные величины, и в случае, если шаг эффектов и длина эффектов – числовые функции от номера основной нити. На основе этих описаний приведена классификация рисунков, образованных эффектами основной фасонной нити.

Разработана стохастическая имитационная модель расположения эффектов основной фасонной нити на поверхности ткани. Моделирование распределения эффектов производится с учетом возмущающих факторов: колебаний геометрических параметров фасонной нити (расстояний между эффектами и длин эффектов) и нестабильностью технологического режима получения нити и выработки ткани.

На поверхности ткани, вырабатываемой с использованием фасонной нити в качестве основы, можно получать равномерное распределение, теневые переходы, поперечные и продольные полосы из фасонных эффектов, геометрические орнаменты.

В данной главе представлены логическая схема метода компьютерного проектирования оформления ткани эффектами основной нити, основные алгоритмы имитационной модели распределения фасонных эффектов основной нити по ткани: алгоритм оформления фасонной нити, алгоритм моделирования отклонений от расчетных значений, алгоритм формирования рисунка из фасонных эффектов на ткани. Приведено описание программного комплекса, реализующего задачу автоматизированного проектирования рисунков, образованных фасонными эффектами основной нити на поверхности ткани.

На основе теоретических исследований были рассчитаны параметры нити и ткани и проведена наработка опытной партии фасонной нити на машине ПК-100МФ и наработка на станках СТБ2-180 опытной партии ткани с использованием основных фасонных нитей в условиях АО «Большая Костромская льняная мануфактура». Сопоставление расположения эффектов на ткани с моделируемым распределением, замер расстояний между фасонными эффектами на ткани и их сравнение с расчетными позволили сделать вывод об адекватности модели распределения эффектов фасонной нити по поверхности ткани.

В пятой главе представлено математическое моделирование распределения пороков внешнего вида на нити и ткани и система автоматизированного проектирования распределений прерывистых элементов на нити и ткани.

В начале главы представлен анализ взаимосвязей пороков ткани с пороками волокна и нитей и их влияние на качество продукции, выявлены наиболее часто встречающиеся пороки, оказывающие большое влияние на качество нитей и ткани.

Представлены математические модели распределения пороков внешнего вида на нити. Приведены формулы для расчета среднего числа утолщений, утонений, шишек и т. п., приходящихся на определенную длину нити. Указаны законы распределения длин между дефектами разных видов. Поток пороков внешнего вида получается в результате «сложения» потоков утолщений, утонений, шишек и т.п., а значит, близок к пуассоновскому. Разработаны математические модели распределения пороков внешнего вида на ткани размером , позволяющие прогнозировать качество ткани по наличию на ней пороков внешнего вида.

Разработаны методы и средства для автоматизированного распознавания пороков внешнего вида нити и определении класса чистоты, в том числе дано обоснование выбора программных средств, представлена структура автоматизированной системы распознавания пороков и определения класса чистоты пряжи. Разработаны алгоритмы распознавания пороков внешнего вида и определения класса пряжи, определения средней толщины нити. Представлены алгоритмы и программы проверки случайной последовательности длин интервалов между дефектами на стационарность и эргодичность. Дано описание программно-аппаратного комплекса, реализующего задачу распознавания пороков внешнего вида на ткани. Результатом является программный продукт, который обрабатывает изображение пряжи, а именно фильтрует и определяет количество пороков различных видов, дает заключение о качестве пряжи.

Разработана методика оценки числа пороков на ткани, включающая расчет длины нити, объема выборки, распознавание пороков, классификация, подсчет числа пороков, нахождение плотности потока утолщений, утонений, шишек, проверку на стационарность, расчет числа пороков на ткани. Далее следует проверка на соответствие требованиям заказчика и рекомендации, в случае необходимости, по очистке нити. Данная часть работы проводилась в рамках научно-исследовательской работы по заказу ООО «БКЛМ-Актив».

В заключении работы представлена система автоматизированного прогнозирования распределений прерывистых элементов (фасонных эффектов утка и основы; пороков внешнего вида) по поверхности ткани.

ОБЩИЕ ВЫВОДЫ

1. На основе анализа ранее проведенных исследований по прогнозированию распределения фасонных эффектов и пороков внешнего вида по ткани установлено, что:

• существующие аналитические модели проектирования распределений фасонных эффектов по ткани созданы лишь в зависимости от частных случаев распределения эффектов на нити, что сужает возможности применения фасонных нитей при производстве тканей;
• математические модели распределения пороков внешнего вида нитей и ткани и методы определения чистоты нитей, а также оценка сортности тканей по наличию пороков внешнего вида разработаны отдельно для нитей и ткани, не позволяют оценить качество ткани в зависимости от распределения пороков внешнего вида нити;
• к решению задач прогнозирования распределений фасонных эффектов и дефектов по ткани могут быть применены общие подходы, поскольку важнейшим фактором, влияющим на расположение эффектов и пороков внешнего вида по ткани, является их распределение на нити.

2. Разработана концептуальная модель прогнозирования распределения фасонных эффектов и пороков внешнего вида нити по поверхности ткани в зависимости от распределения их на нити, заправочных параметров ткани и технологического режима получения нити и ткани.
3. Впервые на теоретико-множественной основе предложена общая схема решения задачи математического описания распределений фасонных эффектов и пороков внешнего вида по ткани.
4. На основе аппарата теории чисел впервые создана детерминированная математическая модель распределения фасонных эффектов по ткани при равношаговом распределении их на нити, позволяющая для любого значения шага а эффектов нити проектировать рисунки из фасонных эффектов на ткани.
5. Впервые предложено описание матричным методом расположения фасонных эффектов по ткани, вырабатываемой с использованием фасонной нити в качестве утка.
6. Впервые предложена процедура количественной оценки характера расположения фасонных эффектов по ткани, что позволяет расширить диапазон применяемых вариантов оформления ткани фасонными эффектами.
7. Разработана методика построения рисунка расположения фасонных эффектов по ткани при равношаговом распределении их на уточной нити, ориентированная на автоматизированное проектирование.
8. Разработана обобщенная схема проектирования распределений фасонных эффектов на ткани, вырабатываемой с использованием фасонной нити в качестве утка и основы, что расширяет возможности применения фасонных нитей при производстве тканей.
9. Сформированы стохастические модели распределения фасонных эффектов по ткани, в которых учтены отклонения фактических расстояний между эффектами от расчетных и обрывность нити на расположение эффектов по ткани.
10. Выполнена расширенная классификация рисунков расположения фасонных эффектов на ткани, позволяющая увеличить ассортимент тканей, вырабатываемых с применением фасонных нитей.
11. Приведены практические рекомендации по выбору шага эффектов на нити и указаны рисунки из фасонных эффектов на ткани, наименее чувствительные к отклонениям фактических расстояний между эффектами на нити от расчетных, и к обрывности нитей.
12. Проведен анализ взаимосвязей пороков ткани с пороками волокна, пряжи и их влияния на качество продукции, в результате которого выявлены часто встречающиеся дефекты внешнего вида и пороки, оказывающие наибольшее негативное влияние на качество.
13. Предложены математические модели распределения пороков внешнего вида по нити и по поверхности ткани, позволяющие прогнозировать характер расположения пороков на ткани, количество утолщений, утонений, шишек и т.п. на ткани размером .
14. Разработано методическое и математическое обеспечение автоматизированной системы распознавания пороков, определения класса чистоты пряжи.
15. Разработана методика оценки числа пороков на ткани в зависимости от их распределения на нити и рекомендации по степени очистки нити, что позволяет улучшить качество тканей.

ОСНОВНЫЕ ПУБЛИКАЦИИ ПО ТЕМЕ ДИССЕРТАЦИИ

Монографии

1. Землякова И.В. Математические модели распределения эффектов фасонной нити по поверхности ткани. Монография. – Кострома : КГТУ, 2006. – 112 с.

Статьи в журналах, периодических изданиях, включенных в список ВАК

2. Федоров Ю.Б., Землякова И.В., Шереметьев А.Н. Метод оценки равномерности распределения по поверхности ткани элементов типа фасонных эффектов / / Изв. вузов : Технология текстильной промышленности. – 1989. – №2. – С. 21-22.
3. Федоров Ю.Б., Землякова И.В., Петрова О.Р. Моделирование распределения эффектов основной фасонной нити в ткани // Изв. вузов : Технология текстильной промышленности. – 1997. – №4. – С. 47-49.
4. Смирнова Н.А., И.В.Землякова, Е.А.Мальцева, Л.П.Юдина Определение комплексного показателя формировочной способности льняных тканей // Изв. вузов : Технология текстильной промышленности. – 1999. – №2. – С. 130-131.
5. Смирнова Н.А., Землякова И.В., Мальцева Е.А. Комплексная оценка технологичности льняных тканей для одежды // Изв. вузов : Технология текстильной промышленности. – 2001. - №4-5. – С.33-35.
6. Землякова И.В. Детерминированная математическая модель распределения эффектов уточной фасонной нити по поверхности ткани // Изв.вузов : Технология текстильной промышленности. – 2005. - №1. – С.144-146.
7. Землякова И. В., Воронцова О.Р. О создании имитационной системы процесса формирования рисунков расположения фасонных эффектов на ткани // Текстильная промышленность. – 2006. - №1-2. – С.21-22.
8. Землякова И.В. Количественная оценка и выбор базисных векторов распределения фасонных эффектов уточной нити по поверхности ткани // Изв. вузов : Технология текстильной промышленности. – 2006. – №1. – С.147-151.

Депонированные статьи

9. Землякова И.В. Математическое описание некоторых закономерностей распределения эффектов фасонной нити на поверхности ткани / Деп. в ЦНИИ ТЭИ, легпром. : М. №2958 –ЛП. – 1989. – 2с.
10. Землякова И.В. Сравнительный анализ распределения фасонных эффектов по ткани при применении одного или двух видов утка / Деп. в ЦНИИТЭИ, легпром : М. - №3485 – ЛП. – 1993. – 6с.
11. Воронцова О.Р., Землякова И.В. О моделировании приращения длины фасонных нитей и ровничных эффектов вследствие различного уровня натяжения нитей // Деп. в ООО «ЛЕГПРОМИНФОРМ» : М. - №4089 – ЛП. – 2003. – С.31.
12. Землякова И.В., Воронцова О.Р. Теоретико-множественный подход к математическому описанию распределения фасонных эффектов основной нити по ткани // Деп. в ВИНИТИ : М. – 2005. - №1525 – В2005. – 5с.

Вестник КГТУ и сборники научных трудов

13. Наумов А.К., Землякова И.В., Хомяков Е.С., Потапова Т.С. Вывод системы канонических уравнений Севостьянова в математической модели процесса скручивания двух нитей // Вестник КГТУ. – 2002. - №5. – С.17-19.
14. Воронцова О.Р., Землякова И.В. Математическое моделирование прерывистых эффектов // Сб. науч. тр. молодых ученых КГТУ. – 2004. - №5, ч.1. – С.39-42.
15. Землякова И.В., Краснов А.С. Моделирование распределений пороков внешнего вида на нити // Вестник КГТУ. – 2004. – №9. – С.19-20.

Статьи в сборниках трудов международных конференций

16. Землякова И.В., Петрова О.Р. Математическое моделирование распределения фасонных эффектов по ткани // Математика в вузе – стандарты образования – базовая подготовка : тр. межд. науч-методич. конф. / КГТУ – С.-Петребург. – 1996. – С.166.
17. Краснов А.С., Землякова И.В. Определение параметров распределения пороков внешнего вид на нити // Актуальные проблемы переработки льня в современных условиях : сб. трудов межд. науч-технич. конф. / КГТУ. – Кострома. – 2004. – С.40-41.
18. Землякова И.В., Левин М.Г., Лустгартен Н.В. Концептуальная модель распределения прерывистых элементов нити по поверхности ткани // Математические методы в технике и технологиях : сб. трудов XVII междр. науч. конф. / КГТУ. – Кострома. – 2004. т.5. – С.81-82.
19. Землякова И.В. Математическая модель распределения фасонных эффектов по ткани при равношаговом распределении их на уточной нити // Математические методы в технике и технологиях : сб. трудов XVII межд. науч. конф. / КГТУ. – Кострома. – 2004. – т.5. – С.82-84.
20. Землякова И.В., Куликова Н.Н. Расчет объема выборки для определения дефектов на ткани // Математические методы в технике и технологиях : сб. трудов XVIII межд. науч..конф. / Казанский государственный технолог. университет. – Казань. – 2005. – т.9. С.196-198.

Тезисы докладов международных и других конференций

21. Землякова И.В., Шереметьев А.Н. Применение вычислительной техники для получения равномерного распределения // Участие молодых ученых и специалистов в реализации научно-технич. проблем : тез. докладов обл. науч-техн. конф. / – Кострома. – 1998. – С.19-20.
22. Землякова И.В. Расчет шага эффектов уточной нити для получения равномерного распределения эффектов по ткани // Новые технические и технологические разработки и их внедрение в текст. и легк. пром-сти (Прогресс – 89). Тез. докладов обл. науч- техн. конф. / Иваново. – 1989. – С.96.
23. Землякова И.В. Распределение эффектов уточной фасонной нити на ткани, вырабатываемой на станке СТБ4-220 // Новое в технике и технологии в текст. производства (Прогресс – 90) : тез. докладов всесоюзной науч-техн. конф. / Иваново. – 1990. – С.107-108.
24. Землякова И.В. Оценка равномерности распределения и плотности заполнения ткани эффектами // Проблемы развития текстильной и легк. пром-сти в соврем. условиях (Прогресс – 92) : тез. докладов межд. науч-техн. конф. / Иваново. – 1992. – С.132-133.