Прочность и трещиностойкость эксплуатируемых железобетонных конструкций зданий и сооружений при статическом и кратковременном динамическом нагружении

На правах рукописи

Плевков Василий Сергеевич

ПРОЧНОСТЬ И ТРЕЩИНОСТОЙКОСТЬ

ЭКСПЛУАТИРУЕМЫХ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ

ЗДАНИЙ И СООРУЖЕНИЙ ПРИ СТАТИЧЕСКОМ И

КРАТКОВРЕМЕННОМ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ

05.23.01 - Строительные конструкции, здания и сооружения

Автореферат

диссертации на соискание учёной степени

доктора технических наук

Томск - 2003

Работа выполнена в Томском государственном

архитектурно-строительном университете

Официальные оппоненты:

Доктор технических наук, профессор Б.С. Расторгуев

Доктор технических наук, профессор В.М. Митасов

Доктор технических наук, профессор В.М. Картопольцев

Ведущая организация: 26 Центральный научно-исследовательский

институт МО РФ, г. Москва

Защита состоится 25 апреля 2003 г. в 14 часов на заседании диссертационного совета Д 212.265.01 при Томском государственном архитектурно-строительном университете по адресу: 634003, г.Томск, пл. Соляная 2, корп. 5, ауд. 307. Тел. (8-382-2) 65-42-61.

С диссертацией можно ознакомиться в библиотеке университета.

Автореферат разослан 14 марта 2003 г.

Ученый секретарь

диссертационного Совета Н.К.Скрипникова

Общая характеристика работы

Актуальность работы. В последние годы наблюдается тенденция к увеличению вероятности возникновения и воздействия на строительные конструкции зданий и сооружений кратковременных динамических нагрузок аварийного характера, вызванных развитием отраслей промышленности и жизнедеятельности человека, связанных с взрывоопасными материалами. По данным отечественной и зарубежной литературы, к настоящему времени более тысячи сырьевых материалов, их компонентов и продуктов производства относятся к числу взрывоопасных, вызывающих аварийные ситуации, которые приводят к значительным материальным потерям и гибели людей.

Учет пространственной работы зданий и сооружений - один из существенных источников повышения безопасности и экономии материалов. В железобетонных пологих оболочках и плитах эффект пространственной работы реализуется в наибольшей степени, что позволяет всё шире использовать данные конструкции в зданиях широкого профиля, сооружениях гражданской обороны и специального защитного назначения, для которых кратковременные динамические воздействия являются неотъемлемыми при проектировании и эксплуатации. Кроме того, последствия динамических воздействий аварийного характера в большинстве случаев требуют оценки технического состояния конструкций зданий и сооружений, их восстановления и усиления, с целью дальнейшей надежной эксплуатации с заданными начальными или меняющимися во времени параметрами.

В связи с этим задача совершенствования методов расчета эксплуатируемых стержневых железобетонных конструкций, пологих оболочек и плит при статическом и кратковременном динамическом нагружении, оценка их технического состояния, восстановления и усиления является научной проблемой, имеющей важное хозяйственное значение.

Работа выполнена в Томском государственном архитектурно-строительном университете в соответствии с межвузовской научно-технической программой Госкомвуза РФ «Архитектура и строительство» (приказ Минвуза РФ № 252 от 27.03.91, темы № 3.14 и № 11.1.2.3); грантом Минвуза РФ (№ 5.2.2.93 раздела 1.06); координационным планом научно-исследовательских работ Минвуза по строительной тематике (тема № 382 от 5.06.90); межотраслевой программой научно-инновационного сотрудничества между Министерством образования Российской Федерации и Федеральной службой специального строительства Российской Федерации «Наука, инновации, подготовка кадров в строительстве» (тема «Взрывобезопасность в строительстве на основе конструирования и расчета систем, допускающих большие деформации и разрушения конструкций», 2002 г.) и тематическим планом Томского государственного архитектурно-строительного университета за период с 1980 по 2002 г.

Цель работы состоит в развитии теоретических основ деформирования эксплуатируемых стержневых железобетонных конструкций, пологих оболочек и плит зданий и сооружений с учетом нелинейных диаграмм «напряжение -деформация» бетона и арматуры при кратковременном динамическом нагружении, разработке практических методов расчета и рекомендаций по оценке их технического состояния, восстановлению и усилению.

Научную новизну работы составляют:

- методы расчета прочности и трещиностойкости железобетонных конструкций при статическом и кратковременном динамическом нагружениях; выявленные основные закономерности изменения границ поверхностей и областей относительной прочности и трещиностойкости (сопротивления) железобетонных элементов в зависимости от нелинейных диаграмм деформирования бетона и арматуры, влияния скорости динамического нагружения на прочностные свойства материалов, особенностей армирования сечений, их формы, характера и величины предварительного напряжения и других параметров;

- установленные закономерности деформирования пологих оболочек при внутренних нагружениях; полученные параметры предельного состояния; разработанные расчетные предпосылки и модели деформирования пологих оболочек и плит при внутреннем кратковременном динамическом нагружении;

- сформулированные предельные состояния железобетонных конструкций, воспринимающих кратковременные динамические нагрузки, и способы их нормирования;

- аналитические и численные методы расчета железобетонных пологих оболочек и плит на действие кратковременных динамических нагрузок, учитывающие основные особенности их деформирования и работы материалов, выявленные в опытах.

На защиту выносятся:

- физические предпосылки и общий метод расчета прочности и трещиностойкости железобетонных конструкций при статическом и кратковременном динамическом нагружении;

- основные закономерности изменения поверхностей и областей относительной прочности и трещиностойкости (сопротивления) железобетонных конструкций на основе нелинейных динамических диаграмм деформирования бетона и арматуры с учетом влияния скорости и характера динамического нагружения на прочностные и деформативные свойства материалов, величины и характера предварительного напряжения арматуры, а также геометрических параметров и армирования конструкций;

- предельные состояния железобетонных оболочек и плит при внутреннем кратковременном динамическом нагружении и способы их нормирования;

- методики и результаты экспериментальных исследований железобетонных пологих оболочек;

- предпосылки и расчетные модели железобетонных конструкций при кратковременном динамическом нагружении; аналитический и численный методы расчета железобетонных пологих оболочек и плит на действие кратковременных динамических нагрузок, учитывающих основные особенности их деформирования;

- практические разработки и рекомендации по оценке технического состояния, восстановлению и усилению железобетонных пологих оболочек, плит и других конструкций зданий и сооружений, подверженных статическим и кратковременным динамическим нагрузкам.

Практическое значение работы. Разработаны методы динамического расчета и предложения по оценке технического состояния, восстановлению и усилению стержневых железобетонных конструкций, пологих оболочек и плит для практического применения в проектировании зданий и сооружений, подверженных кратковременным динамическим и статическим воздействиям.

Достоверность научных положений и выводов. Расчетные предпосылки основаны на обширных экспериментальных данных материалов и конструкций, которые имеют надежное метрологическое обеспечение. Расчетные модели учитывают основные особенности работы эксплуатируемых стержневых железобетонных конструкций, пологих оболочек и плит при кратковременном динамическом наружении. Расчетные зависимости получены в результате строгого решения задач в соответствии с принятыми предпосылками и моделями. Достаточная точность расчетных методик подтверждена удовлетворительным совпадением теоретических и экспериментальных результатов.

Реализация работы. Результаты исследований вошли в пособия и рекомендации по оценке технического состояния, восстановлению и усилению железобетонных конструкций (в том числе элементов пологих оболочек и плит) зданий и сооружений, пользователями которых к настоящему времени являются более 800 проектных, научно-исследовательских и учебных институтов, строительных и других предприятий и организаций России и стран СНГ; выпущено четыре монографии и пять пособий по методам расчета железобетонных конструкций, получено четыре авторских свидетельства и патента России.

Основные результаты работы докладывались и получили одобрение на: ХХ11 Международной конференции по бетону и железобетону (Иркутск, 1990 г.); 1-й, 2-й Всесоюзных конференциях по динамике сооружений (Харьков, 1978 г.; Тбилиси 1982 г.); Х Всесоюзной конференции по бетону и железобетону (Казань, 1988 г.); Всесоюзных совещаниях национального комитета СССР и России по участию в ИАСС (Душанбе, 1982 г.; Красноярск, 1983 г.; Белгород, 1986, 1995 и 1997 г.г.; Донецк, 1989, 1990 и 1991 г.г.); 1-м Всесоюзном координационном совещании по прочности железобетонных конструкций на действие однократных кратковременных динамических нагрузок (Москва); Всесоюзном координационном совещании «Железобетонные конструкции при интенсивных дина-

мических воздействиях» (Томск, 1986 г.); научно-технических конференциях МИСИ ( Москва, 1982 и 1991 гг.); 1-й, 3-й, 4-й, 5-й и 7-й Сибирских конференциях по бетону и железобетону (Новосибирск, 1991, 1994, 1995, 1996 и 1998 гг.; Омск, 1993 г.); международной научно-технической конференции «Надежность строительных элементов и систем» (Самара, 1997 г.); ХV111 Международной конференции по теории оболочек и пластин (Саратов, 29 сентября - 4 октября 1997 г.); международной научно-технической конференции «Архитектура и строительство» (Томск, 30 ноября - 1 декабря 2000 г., 11-12 сентября 2002 г.); Международном конгрессе МКПК-98 ( Москва, 22-26 июня 1998 г.). 1-й и 2-й Всероссийской конференциях по проблемам бетона и железобетона «Бетон на рубеже третьего тысячелетия» (Москва, 9-14 сентября 2001 г. ); межвузовских научно-практических конференциях и научных семинарах преподавателей и научных сотрудников (Томск, 1978, 1983 и 1986, 1989, 1994, 1997,1998, 2000 и 2002 гг.).

В полном объеме диссертационная работа докладывалась на научном семинаре кафедры «Железобетонные и каменные конструкции» Московского государственного строительного университета (Москва, 2002 г.), на объединенном научном семинаре кафедр Новосибирского государственного архитектурно-строительного университета (Новосибирск, 2003 г.), на объединенном научном семинаре кафедр Томского государственного архитектурно-строительного университета (Томск, 2002 г.).

Объем и структура работы. Диссертация состоит из введения, шести глав, общих выводов, списка литературы и приложений. Она включает 340 страниц основного машинописного текста, 121 иллюстрацию и 22 таблицы (на 133 с.), библиографию из 415 наименований и 63 страницы приложений.

Публикации. Основные результаты диссертации отражены в 98 работах, в том числе в четырех монографиях, десяти пособиях и рекомендациях, трех брошюрах, четырех авторских свидетельствах и патентах России. Монографии и пособия в разные годы рецензированы докторами технических наук, профессорами: Р.А. Бакировым, А.М. Болдышевым, А.В. Забегаевым, В.И. Колчуновым, О.Г. Кумпяком, В.М. Митасовым, Г.И. Поповым, Н.Н. Поповым, Б.С. Расторгуевым, Б.С. Соколовым, Г.К. Хайдуковым и Г.И. Швецовым, которым автор выражает глубокую признательность и благодарность.

В экспериментальных исследованиях под руководством автора принимали участие аспиранты и соискатели: И.В. Балдин, Е.А. Бояринцев, Е.А. Онащенко и П.В. Стуков.

СОДЕРЖАНИЕ РАБОТЫ

К настоящему времени методы расчета железобетонных конструкций на действие кратковременных динамических нагрузок определяют самостоятельный раздел динамики сооружений. Специфика данных нагрузок заключается в большой величине давления на конструкцию и малом времени их действия. Для рассматриваемых в настоящей работе железобетонных конструкций особая нагрузка вызывается воздействиями, источниками которых являются взрывы газопаровоздушных смесей (ГПВС), характеризуемые дефлаграционным или детонационным их горением. При этом действующие на конструкции кратковременные динамические нагрузки возникают в результате распространения волн от источника взрыва и взаимодействия их с конструкцией, подчиняющихся законам газовой динамики. Максимальные значения давлений, время нарастания и спада динамической нагрузки при дефлаграционном и детонационном горении ГПВС различно (поскольку скорость распространения фронта пламени может отличаться до двух порядков) и зависит от многих факторов: соотношения размеров здания, его объема, вида и концентрации ГПВС, источника воспламенения, наличия и расположения легкосбрасываемых или легковскрываемых конструкций, их площади и конструктивных решений, узлов их креплений, последовательности и времени вскрытия и многих других факторов. Вследствие сложности происходящих процессов в динамические расчеты железобетонных конструкций закладываются интегральные кусочно-линейные зависимости для динамической нагрузки с постепенным нарастанием давления (дефлаграционное горение ГПВС) и мгновенным нарастанием давления (детонационным горением ГПВС).

Разработка теоретических основ динамического рас­чета зданий и сооружений на действие динамических нагрузок взрывного типа интенсивно началась после Второй мировой войны в связи с необ­ходимостью проектирования надежных и экономичных спецсооружений, обеспечивающих защиту от ядерного взрыва, а также зданий и сооружений взрывоопасных производств.

В последующие годы динамические методы расчета железобетонных конструкций, основы которых заложены А.А. Гвоздевым и И.М. Рабиновичем, получили интенсивное развитие в России и за рубежом. Динамическому расчету широкого класса железобетонных конструкций на основе жесткопластических и упруго-пластических диаграмм деформирования посвящены работы P.O. Бакирова, И.А. Диковича, В.И. Жарницкого, Т.Ж. Жунусова, А.В. Забегаева, Б.Г. Коренева, В.А. Котляревского, О.В. Лужина, Г.И. Попова, Н.Н. Попова, Б.С. Расторгуева, А.Е. Саргсяна, А.П. Синицына, Г.Н. Ставрова, Б.И. Тетерина, М. Чарыева, Ю.Т. Чернова, И.В. Балдина, А.А. Беликова, И.К. Белоброва, Т.Н. Виноградовой, В.И. Ганушкина, С.А. Девятова, А.В. Дмитриева, О.Д. Егоровой, В.Н. Караваева, Д.Г. Копаницы, В.Ф. Кузнецова, К.В. Лингуряна, О.М. Лоскутова, А.И. Плотникова, Ю.И. Пузанкова, В.А. Рахманова, А.Г. Смолянина, М.А. Тамова, Н.Н. Трекина, А.У. Усманова, Х.Ш. Хамди, В.И. Щербины и др. При создании упругопластических методов расчета рассматривали комплекс вопросов, имеющих значение при проектировании: определение внутренних усилий и перемещений; установление предельных состояний и способов их нормирования; расчет сечений. Определение величин внутренних усилий и перемещений железобетонных конструкций от кратковременной динамической нагрузки производится методами динамики упругопластических сред. Наибольшее распространение получили методы, основанные на использовании рабочих диаграмм, или диаграмм сопротивления, которые интегрально характеризуют прочностные и деформативные свойства железобетонных конструкций и их сечений при внешних силовых воздействиях.

Развитие методов динамического расчета железобетонных конструкций тесно связано с изучением поведения арматуры и бетона при скоростных нагружениях. Методы расчета железобетонных конструкций на кратковременные динамические нагрузки на основе полных диаграмм деформирования бето­на и арматуры интенсивно развиваются в последние годы. Работы В.И. Жарницкого, В.А. Котляревского, Г.И. Попова, Н.Н. Попова, Б.С. Расторгуева, Г.Н. Ставрова, Ю.Т. Чернова и др. привели к созданию современных вариантов данных методов расчета. Совершенствование общих физических моделей деформирования железобетона с трещинами и развитие на их основе методов расчета железобетонных конструкций рассматривались В.М. Бондаренко, А.А. Гвоздевым, Г.А. Гениевым, А.С. Городецким, С.А. Дмитриевым, Н.И. Карпенко, С.М. Крыловым, О.Г. Кумпяком, В.М. Митасовым, В.И. Мурашевым, Т.А. Мухамедиевым, Я.М. Немировским и др. Эти методы динамического и статического расчетов применимы к анализу напряжен­но-деформированного состояния во всем диапазоне загружения широкого класса стержневых железобетонных конструкций, пологих оболочек и плит.

Развитие конструктивных решений пологих оболочек и плит в значительной степени определялось состоянием методов их расчета, основы которых заложили в своих трудах: Н.П. Абовский, А.В. Александров, В.Н. Байков, В.С. Бартенев, Д.В. Вайберг, П.М. Варвак, А.В. Вольмир, В.З. Власов, А.Л. Гольденвейзер, А.Н. Гузь, Ф. Дишингер, Н.В. Колкунов, Н.Н. Леонтьев, П.А. Лукаш, А.И. Лурье, И.Е. Милейковский, В.В. Новожилов, П.Л. Пастернак, Г.Н. Пшеничников, В.Д. Райзер, А.Р. Ржаницын, С.П. Тимошенко, М. Рюле, А.П. Филин, В. Флюге и др. При этом особую актуальность приобрела проблема совершенствования методов расчета железобетонных оболочек в нелинейной постановке с учетом реальных свойств материалов при статическом и кратковременном динамическом нагружении.

При внешнем динамическом нагружении исследования железобетонных оболочек с учетом пластической работы материалов рассматривались Н.В. Ахвледиани, А.С. Девятовым, М.И. Ерховым, Б.С. Жармагамбетовым, Я.Ш. Исхаковым, А.М. Кислером, А.Ш. Лурье, А.М. Медетбековым, Е.К. Нурмагамбетовым, Н.Н. Поповым, Б.С. Расторгуевым, М.И. Ройтманом, С.Р. Роззаковым, В.Н. Шаишмелашвили и др. При статическом нагружении прямоугольные в плане оболочки исследовали В.А. Архипов, А.М. Болдышев, А.С. Дехтярь, А.М. Дубинский, М.Ш. Варвак, Л.И. Кривелев, М.Б. Краковский, А.Ф. Кальмейер, Я.К. Кулгавий, И.Е. Милейковский, Е.Н. Митрофанов, В.Ю. Мирзабекян М.Ш. Микеладзе, К.П. Пятикрестовский, Л.М.Пухонто, А.О. Рассказов, А.И. Стрельбицкая, Г.К. Хайдуков, Я.Ф. Хлебной, Ю.В. Чиненков, В.В. Шугаев, Г.С. Шапиро и др. Значительная часть опубликованных исследований пологих железобетонных оболочек посвящена определению верхней границы несущей способности кинематическим методом и нижней границы статическим методом.

Анализ методов расчета железобетонных конструкций при статическом и кратковременном динамическом нагружении показывает, что наряду с развитием и применением численных методов расчета представляется необходимым дальнейшее развитие аналитических методов на экспериментально-теоретической основе, которые в пределах того или иного класса конструкций имеют высокую эффективность.

Для эксплуатируемых железобетонных конструкций, запроектированных из условия прочности нормальных сечений в плоскости несущих поперечных рам зданий и сооружений, учет пространственной работы зданий при динамических воздействиях, а также отступления при возведении и нарушения при эксплуатации приводят к возникновению в конструкциях дополнительных значительных по величине поперечных сил, изгибающих и крутящих моментов, существенно изменяющих работу железобетонных конструкций. В связи с этим отмечается необходимость совершенствования методов прогнозирования предельных состояний. Анализ существующих нормативных документов показывает, что к настоящему времени имеют место методологические разрывы в расчетах прочности нормальных и наклонных сечений, между расчетами по прочности и трещиностойкости. Совместное воздействие продольных сил, изгибающих и крутящих моментов, трудно реализуемое при статике, но имеющее место при динамике, не рассмотрено вообще. При этом континуальные (интегральные) модели, заложенные в нормативные документы, строятся на использовании понятия расчетного сечения. Для нормальных сечений железобетонных конструкций вычисленные из статического или кратковременного динамического нагружения внутренние усилия относительно центра тяжести, как правило, бетонного сечения, в дальнейшем сопоставляются относительно равнодействующей усилий арматуры растянутой зоны. При этом возникает от 35 до 56 расчетных случаев и зависимостей с учетом комбинаций продольных сил и изгибающих моментов, а также параметров расчетных сечений. Для внецентренного сжатия железобетонных конструкций не определены границы случаев малых и случайных эксцентриситетов.

В настоящее время возрастает значимость проблем оценки остаточной прочности и трещиностойкости эксплуатируемых и реконструируемых железобетонных конструкций, в том числе на вероятностной основе.

Современное развитие методов динамических расчетов железобетонных конструкций основано на общем принципе использования полных запасов их прочности, при этом допускается кратковременное деформирование сечений и элементов в стадии разрушения материалов. Физической основой развития методов расчета железобетонных конструкций при кратковременном динамическом нагружении являются действительные нелинейные диаграммы деформирования бетона и арматуры, аналитическое описание которых получено на основе обобщения имеющихся экспериментальных данных. Кратковременные динамические воздействия на бетон и арматуру приводят к изменению их прочностных и деформативных характеристик по сравнению со статическим нагружением. Для аналитического описания нелинейных диаграмм бетона и арматуры различными авторами предлагаются аппроксимации уравнениями полиномов второй, третьей и пятой степени; уравнением эллипса; диаграммой Прандтля; в виде экспоненты; тригонометрических рядов; дробно-рациональных функций; используется также аппарат сплайн-функций. На основе анализа опытных и теоретических исследований В.Н. Байкова, Ю.М. Баженова, П.П. Баландина, О.Я. Берга, В.М. Бондаренко, Г.А. Гениева, В Дилгера, Н.И. Карпенко, В.М. Круглова, Е.С. Лейтеса, В.Н. Макагонова, В.М. Митасова, А.Р. Нелепова, Г.И. Попова, С.В. Цветкова, А.В.Яшина и др. приняты нелинейные диаграммы деформирования бетона и арматуры, основные параметрические точки которых трансформируются вдоль временной координаты для аналитических методов и координаты скорости деформирования для численных методов расчета. Для аналитических методов расчета принята скорректированная логарифмическая зависимость Ю.М. Баженова для коэффициентов динамического упрочнения основных параметрических точек нелинейных диаграмм бетона и арматуры.

В диссертации условия относительной прочности и трещиностойкости нормальных сечений стержневых железобетонных элементов (во всем диапазоне их загружения от растяжения до сжатия) определены численно на основе деформационной модели и аналитически. Предельные изгибающие моменты, воспринимаемые железобетонным элементом, приняты относительно центра тяжести бетонного сечения. За единичные параметры назначены несущая способность бетонного сечения при сжатии и сжатии с изгибом относительно его центра тяжести. Анализ результатов численных и аналитических расчетов, в которых варьировались виды нелинейных диаграмм деформирования бетона и арматуры; величина их предельных деформаций; скорости деформирования; характер и величины армирования сечений, их форма; характер и величины предварительного напряжения и другие параметры, показывает, что при статическом нагружении зависимости предельного относительного изгибающего момента m = = Mu /(RbS) от относительного продольного усилия n = Nu /(RbA) соответствует область, ограниченная выпуклой кривой. При кратковременном динамическом нагружении данная область трансформируется вокруг временной координаты (в аналитических расчетах) и координаты скорости деформирования (в численных расчетах), описывая поверхность относительной динамической прочности нормальных сечений железобетонных стержневых элементов. При этом показано, что для бетонных сжатых элементов зависимости mb и nb [mb = = Mbu /(RbS) и nb = Nbu /(RbA)] существенно зависят от вида нелинейных диаграмм деформирования бетона сжатой зоны и формы поперечного сечения. Однако область относительной прочности mb nb слабо чувствительна к данным диаграммам. Для прямоугольных сечений

±mb = 4nb(1- nb). (1)

Для других сечений элементов кривые, ограничивающие область относительной прочности, отличаются от парабол. При этом для симметричных сечений (ромбовидных, двутавровых, крестообразных, кольцевых, многоугольных и др.) эти отличия незначительны (3-5%), поэтому для практических расчетов симметричных сечений можно использовать параболы (1). В общем случае кривая, ограничивающая область относительной прочности несимметричных бетонных сечений, может быть аппроксимирована восходящей и нисходящей ветвями двух парабол, основание которых соответственно равны 1 + b и 1 - b (здесь b = (А1 – А2) / А – коэффициент асимметрии бетонного сечения; А, А1, А2 – площади всего сечения и его частей, расположенных выше и ниже центра тяжести).

Для железобетонных стержневых элементов область относительной прочности аппроксимирована двумя кривыми области прочности бетонного сечения mb nb перемещающимися вертикально и горизонтально по наклонным направляющим, зависящим от расположения арматуры в сечении. При этом вертикальные смещения обусловлены увеличением арматуры в сечении, а горизонтальные - ее перераспределением из нижней зоны сечения в верхнюю и наоборот. Величины вертикальных смещений выпуклых кривых mb nb относительно оси n и горизонтальных относительно оси m, соответствующие заданному продольному армированию сечений, можно определить следующими выражениями:

; (2)

,

где k = Ah / S – безразмерный параметр (коэффициент формы нормального сечения железобетонного элемента); А и S - площадь сечения и статический момент сжатой зоны бетона относительно центра тяжести бетонного сечения при x = h – у или х = у (для прямоугольного сечения A = bh и S = bh2 / 8); sk = - s, , s = as / h, - относительные расстояния от равнодействующих усилий в арматуре растянутой и сжатой зон сечения до центра тяжести бетонного сечения, а также до нижней и верхней граней рассматриваемого сечения; = y / h - относительное расстояние от центра тяжести бетонного сечения до нижней грани сечения; - коэффициент асимметрии армирования сечения, который изменяется от +1 до –1; sdk = RsdkAsk / (RbdA) - относительное усилие в «k-м» арматурном стержне растянутой зоны (технический коэффициент армирования); - то же для «j-го» арматурного стержня сжатой зоны сечения.

Для предварительно напряженных железобетонных элементов, а также элементов со смешанным армированием, вертикальные смещения выпуклых кривых mb nb происходят несимметрично относительно оси n поскольку Rscd / Rsd 1. Перераспределение продольной арматуры из сжатой (верхней) зоны сечения в растянутую (при s,tot = const) соответствует горизонтальным смещениям выпуклых кривых: верхней – влево, нижней – вправо. Перераспределение продольной арматуры из нижней зоны сечения в верхнюю вызывает горизонтальное смещение выпуклых кривых в противоположную сторону. При этом горизонтальные смещения кривых несимметричны относительно оси m, если Rscd / Rsd 1.

Прямолинейные участки границы области относительной прочности зависят от геометрических параметров сечения, количества и расположения арматуры по высоте сечения, с углами наклона относительно оси n равными s = - arctg(ksk), . Они пересекаются в точках В и B’ с координатами:

точка В n = - s,tot,t, ;

точка B’ n = 1 + s,tot,c, ,

где s,tot,t и s,tot,c – относительные суммарные усилия, воспринимаемые продольной арматурой сечения при растяжении и сжатии; mst, , mst, - относительные положительные и отрицательные моменты, воспринимаемые продольной арматурой относительно центра тяжести бетонного сечения.

На рис. 1 показано изменение границ относительной прочности нормальных сечений бетонного и железобетонного элементов при последовательном увеличении в сечении продольной арматуры. Положение 1 ограничивает область относительной прочности нормального сечения бетонного элемента (As = = 0). Положение 2 соответствует армированию сжатой зоны элемента ( > 0, As = 0, s = -1). Положение 3 характеризует симметричное армирование элемента (As = , s = 0). При несимметричном армировании ( < As, s > 0) границы области занимают положение 4. Из рис. 1 видно, что при последовательной установке продольной арматуры (при Rscd = Rsd) в сечении, выпуклые кривые симметрично смещаются относительно осей n и m. При смешанном армировании сечений, а также при наличии предварительно напряженной арматуры эти смещения несимметричны относительно осей n и m. Однако все точки верхней и нижней границ области симметричны относительно точек, координаты которых можно определить зависимостями: ni = 0.5[1 – (s,tot,t - s,tot,c)], mi = 0.5(mot - moc)].

При этом линия нулевых значений моментов (линия BB’ на рис. 1) поворачивается относительно оси n на угол

= arctg [(mot + moc)/(1 + s,tot,t + s,tot,c)].

Изменение положения арматуры по высоте сечения, с одной стороны, приводит к уменьшению угла наклона прямолинейных участков границ области прочности относительно оси n, тангенс угла которого изменяется от четырех до нуля. С другой стороны, это вызывает разрыв выпуклых кривых границы прочности бетонного сечения в пропорциях , соответствующих и . При этом разорванные участки кривых смещаются по линии нулевых моментов соответственно к точкам В и , а точки их разрыва соединяются прямолинейными участками границы прочности, которые являются касательными в точках разрыва выпуклых кривых . Аналитическое описание областей относительной прочности нормальных сечений железобетонных элементов симметричных и несимметричных профилей с обычным и предварительно напрягаемым армированием детально рассмотрено в работе и заложено в программный комплекс «POISK».

В диссертации приведен сопоставительный анализ предлагаемой поверхности относительной прочности нормальных сечений стержневых железобетон

ных элементов с экспериментальными данными отечественных и зарубежых

ученых при статическом и кратковременном динамическом нагружении. Выполненные многочисленные расчеты показывают полное совпадение результатов по предлагаемому расчету с результатами по нормативным документам во всем диапазоне загружений нормальных сечений при расположении арматуры только в сжатой зоне железобетонного элемента. При наличии арматуры в растянутой зоне сечения отмечено расхождение результатов расчетов при малых эксцентриситетах. При этом с увеличением количества арматуры в растянутой зоне сечения расхождения в результатах расчетов возрастают. Заниженная оценка прочности железобетонных элементов в зоне малых эксцентриситетов по нормативным документам в сравнении с экспериментальными данными отмечалась многими авторами. В работе приведен анализ зависимости для динамически нагруженных стержневых железобетонных элементов. Использование высоты сжатой зоны в качестве основного параметра для определения напряжения в продольной арматуре сечения позволило получить зависимость , применимую как для внецентренно сжатых и растянутых, так и для изгибаемых элементов железобетонных элементов.

Результаты экспериментальных исследований И.К. Белоброва, Ю.П. Гущи, С.А. Дмитриева, А.П. Васильева, Ю.П. Вильдавского, Ю.А. Иванова, А.Т. Калинаускаса, В.Т. Королькова, Я.Д. Ливщица, Т.И. Мамедова, М. Нофаля, В.А. Рахманова, Е.А. Чистякова, Ш.А. Хакимова, В.А. Хрынова, А.М. Янкаускаса и др. показали, что в предельном состоянии связь между приращениями деформаций арматуры относительной высоты сжатой зоны при статическом и кратковременном динамическом нагружении определяется гиперболической зависимостью, соответствующей гипотезе плоских сечений. При статическом нагружении гиперболическая зависимость более пологая, чем при динамическом.

Анализ экспериментальных исследований бетонных призм и железобетонных балок при кратковременном динамическом нагружении, проведенных в НИИЖБе И.К. Белобровым и во ВНИИЖелезобетона В.А. Рахмановым, показали, что влияние скорости деформирования не сказывается на значениях характеристики сжатой зоны. Так, при динамических и статических испытаниях во ВНИИЖелезобетона 15 серий железобетонных балок, в которых варьировались: тип армирования (однородное и комбинированное); вид армирования (ненапрягаемое и напрягаемое); класс арматурной стали (А-I, А-III, А-IV, А-V и Вр-II); коэффициенты армирования сечения продольной арматурой (0,00440,0187); различное соотношение расчетного пролета и высоты сечения (Lp / h = 7,51,6), установлены изменения в пределах s = 0.5480.803 (при Rb = 47.554.3 МПа) и d = 0.5130.797 (при Rbd = 51.364.5 МПа), а среднее значение = 0.671 (при = 51,6 МПа) близко = 0.674 (при = 61,9 МПа). Отмеченные особенности динамического деформирования бетона сжатой зоны сечения, в частности, его деформативная способность, несколько видоизменяют характер динамической зависимости , что позволяет более эффективно использовать арматуру в сечении.

С развитием в продольной арматуре деформаций, выходящих за пределы ее упругой работы, связь между напряжениями и деформациями в арматуре существенно меняется и не может описываться гиперболической зависимостью s от. Поскольку в качестве продольной ненапрягаемой арматуры нормальных сечений стержневых железобетонных элементов, как правило, используют арматурные стали, имеющие физический предел текучести, то для таких сталей напряжения в арматуре не могут превышать при растяжении и сжатии значений Rsd и Rscd. При этом на гиперболические зависимости накладываются ограничения вида Rsd > sd 0 (при 0 d) и 0 > sd > Rscd (при d < < 1,0), пересечения которых с гиперболической зависимостью соответствуют на оси величинам Rd и R1d. Граничные значения Rd и R1d определяются выражениями:

. (3)

Здесь: Rd – значение, выше которого напряжение в растянутой арматуре становится меньшим, чем значения Rsd; R1d - значение, при котором напряжение в продольной арматуре сечения Аs достигает значений, равных Rsсd.

Значения Rd и R1d зависят от вида, класса бетона и арматуры, скорости нарастания нагрузки и формы поперечного сечения элементов. Минимальные значения R, R1 и, а также условные деформации упругой работы арматуры с физическим пределом текучести s = Rsi / Es для разных классов бетона и арматуры приведены в работе.

Введение дополнительного понятия граничной высоты сжатой зоны R1d определяет границы расчетов внецентренно сжатых стержневых железобетонных элементов при больших ( Rd), малых (Rd < < R1d) и случайных ( R1d) эксцентриситетах.

Для гиперболической зависимости в зоне малых эксцентриситетов изменение напряжений в продольной арматуре от Rsd до 0 происходит на участке Rd < d, а изменение от 0 до Rsсd на участке d < < R1d, длина проекций которых на ось отличается в 1,52 раза. Е.А. Чистяковым вместо гиперболической зависимости на участке > R при статическом нагружении предложена линейная зависимость, вошедшая в нормативные документы, которая имеет симметрию от Rs до Rsс и упрощает расчеты прочности нормальных сечений. Однако как и гиперболическая, так и линейная зависимости в зонах R и R1 имеют «скачкообразное» изменение значений si при малом, а углы касательных к данным зависимостям и прямым ограничений в точках = R и = R1 различны. Предложенная в работе зависимость с плавным переходом от одного участка к другому приближает результаты экспериментальных исследований к расчетным.

На основе теории ядровых моментов (А.А. Гвоздева, С.А. Дмитриева), деформационной модели с нелинейными диаграммами деформирования бетона и замкнутых аналитических зависимостей с учетом жесткопластической и упругопластической эпюры растянутой зоны сечения в диссертационной работе приведен сопоставительный анализ относительной трещиностойкости нормальных сечений стержневых железобетонных элементов при статическом и кратковременном динамическом нагружениях. Показано, что в области растяжения расхождения составляют не более 5-10%, а в области сжатия снижаются до 3-5%. При этом области и поверхности относительной трещиностойкости в области внецентренного сжатия по теории ядровых моментов становятся невыпуклыми. Выпуклость областей относительной трещиностойкости по постулату Д. Драккера и Р. Хилла достигается введением дополнительного коэффициента kN, учитывающего влияние нормальных сил на изменение момента трещинообразования за счет развития неупругих деформаций в сжатой зоне сечения.

На основе анализа полученных результатов условия трещинообразования в относительных величинах представлены в виде

, (4)

где ; ; ; ; и - изгибающие моменты и продольные силы от внешних воздействий и усилие предварительного обжатия;

и - относительные эксцентриситеты продольных сил до центра тяжести сечения; - относительное расстояние от центра тяжести сечения до ядровой точки, наиболее удаленной от растянутой зоны, трещиностойкость которой проверяется; и - коэффициенты формы сечения по прочности и трещиностойкости. Для прямоугольного сечения ( - для жесткопластической и = 1,54 -для упругопластической эпюры растянутой зоны сечения).

Из выражения (4) видно, что усилия предварительного обжатия приводят к смещению осей m и n относительно первоначального их положения на величину и np. Это дает наглядное представление о влиянии обжатия на трещиностойкость рассматриваемого сечения, позволяет эффективно регулировать влияние обжатия сечения в зависимости от решаемых задач.

Наложение областей или поверхностей относительной прочности и трещиностойкости наглядно показывает соотношения усилий, при которых рассматриваемые нормальные сечения, части или конструкция в целом работают с трещинами или без таковых. При этом в области между границами трещиностойкости и прочности ширина раскрытия нормальных трещин изменяется от минимального значения, соответствующего границе относительной трещиностойкости до максимальных величин, соответствующих,как показывают расчеты, = 0,20,22 - границам области или поверхности относительной прочности.

Область работы с трещинами, ограниченная границами областей относительной трещиностойкости и прочности может быть разделена на отдельные участки с различной шириной раскрытия нормальных трещин. Границы этих участков удовлетворительно аппроксимируются линейными зависимостями, рассмотренными в диссертационной работе.

Анализ результатов обследований зданий и сооружений показал, что большинство стержневых железобетонных конструкций эксплуатируются в условиях косого внецентренного нагружения, обусловленного смещением конструкций с проектного положения, неравномерными воздействиями, учетом пространственной работы зданий и т.п. Расчету прочности железобетонных конструкций, работающих на косой изгиб и косое внецентренное сжатие или растяжение при статическом нагружении, посвящены работы В.Н. Байкова, В.И. Бабича, М.А. Борисовой, П.Ф. Вахненко, С.Н. Глазера, И.И Гольденблата, К.Х. Доля, А.С. Залесова, Э.Н. Кодыша, А.А. Лемыша, Н.В. Никитина, И.К. Никитина, Н.А. Поповича, Э.Г. Рату, К.Н. Ратушинского, Н.И. Смолина, Л.И. Сердюка, О.Н. Тоцкого, М.С. Тарянина, Л.В. Фалеева, А.Е. Шавельского и др. При кратковременном динамическом нагружении подобные работы практически отсутствуют. Полученные выше расчетные зависимости, описывающие области относительной прочности и трещиностойкости (сопротивления) нормальных сечений железобетонных элементов, позволяют распространить их и на такое сложное загружение железобетонных конструкций с равносимметричными сечениями (круглые, восьмиугольные, шестиугольные). Действительно, в рассматриваемом случае на сечение железобетонного элемента действуют сжимающие или растягивающие продольные силы, а также изгибающие моменты Мх и Му в двух взаимно перпендикулярных плоскостях, которые могут быть заменены одним суммарным моментом в абсолютных или относительных величинах, действующим в плоскости, повернутой на угол относительно плоскости действия момента Мх.

Для неравносимметричных (прямоугольных, двутавровых, ромбовидных, крестовых, х-образных и др.) и несимметричных (тавровых и др.) сечений такой подход приводит к рассмотрению несимметричных сечений, на которые в некоторых случаях могут действовать дополнительные воздействия, обусловленные кручением.

Приведенные в работе аналитические зависимости описывают выпуклую замкнутую в пространстве координат n, mx, my поверхность относительной прочности (сопротивления) нормального сечения железобетонного элемента (рис. 2). При динамических расчетах поверхности сопротивления трансформируются вокруг временной координаты () или координаты скорости деформирования конструкции. В работе показано, что следы от рассечения поверхности прочности (сопротивления) плоскостями, проходящими через оси n, mx ( = 0) и n, my ( = /2), могут быть аппроксимированы двумя параболами и четырьмя отрезками прямых. Наличие продольной арматуры увеличивает размеры поверхности прочности. При этом , , , ; ().

Следы от пересечения поверхности прочности с плоскостями n = const зависят от формы поперечного сечения элемента и его армирования. Для круглого сечения эти кривые при ni = const будут окружностями. Для произвольного сечения и угла замкнутые кривые проходят через точки mbxi, ±mbyi, -mbxi (рис. 2).

Приведенные в нормативных документах графики несущей способности или кривые взаимодействия при косом внецентренном сжатии при различных величинах s,tot,c и ni, построенные на основе расчетных зависимостей общего случая прочности нормальных сечений, можно рассматривать как следы пересечения плоскости n = const с поверхностью прочности, но построенные в других относительных координатах (манипуляторах, по В.В.Михайлову). При этом некоторые из приведенных графиков не соответствуют реальной работе железобетонных элементов, поскольку при = const, они построены для точек, где mx = my = 0 (осевое сжатие), или для точек, которые выходят за пределы поверхности прочности при определенных соотношениях размеров сечения и его армирования.

Железобетонные стрежневые конструкции, элементы пологих оболочек и плит при статическом или кратковременном динамическом нагружениях могут

одновременно воспринимать изгибающие моменты Mi(t), продольные Ni(t) и поперечные времени по величине и знаку. Существу-

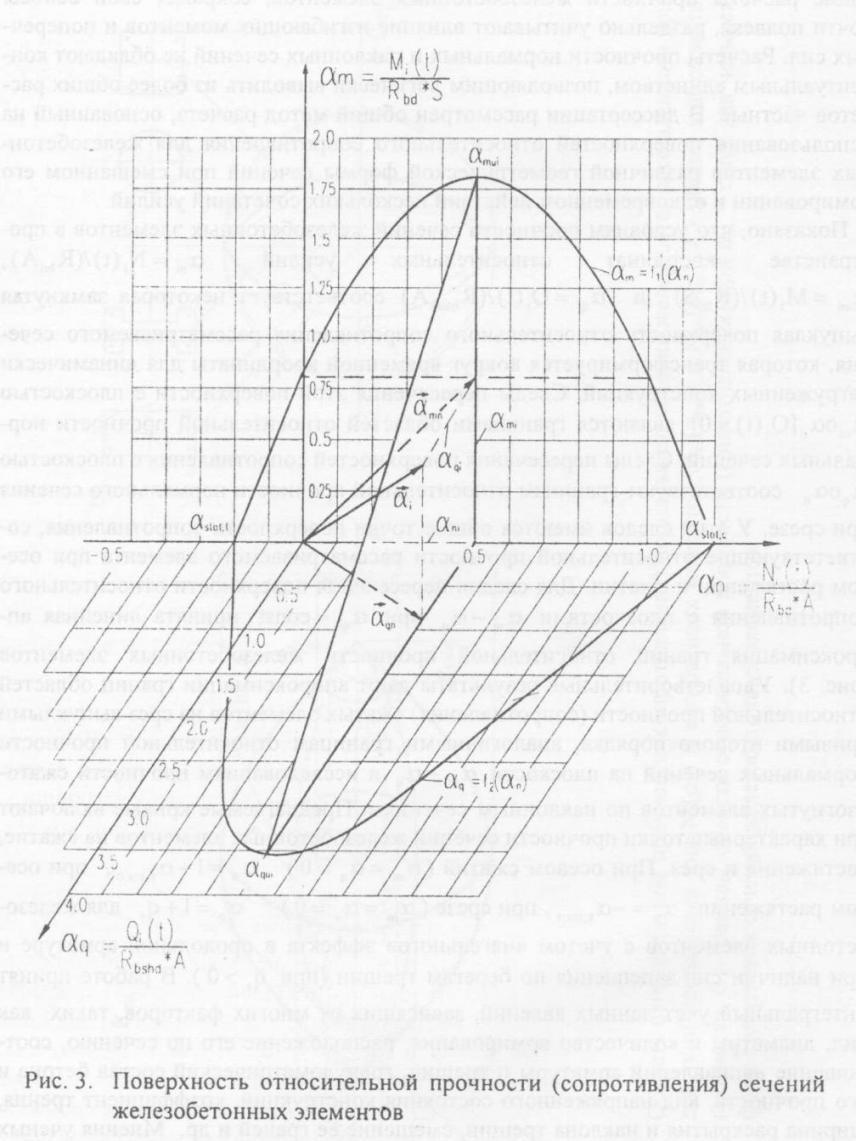
ющие расчеты прочности железобетонных элементов, сохраняя свои основы почти полвека, раздельно учитывают влияние изгибающих моментов и поперечных сил. Расчеты прочности нормальных и наклонных сечений не обладают концептуальным единством, позволяющим логически выводить из более общих расчетов частные. В диссертации рассмотрен общий метод расчета, основанный на использовании поверхностей относительного сопротивления для железобетонных элементов различной геометрической формы сечений при смешанном его армировании и одновременном действии нескольких сочетаний усилий.

Показано, что условиям прочности сечений железобетонных элементов в пространстве координат относительных усилий , и соответствует некоторая замкнутая выпуклая поверхность относительного сопротивления рассматриваемого сечения, которая трансформируется вокруг временной координаты для динамически нагруженных конструкций. Следы пересечения этой поверхности с плоскостью являются границами областей относительной прочности нормальных сечений. Следы пересечения поверхностей сопротивления с плоскостью соответствуют границам относительной прочности нормального сечения при срезе. У этих следов имеются общие точки поверхности сопротивления, соответствующие относительной прочности рассматриваемого элемента при осевом растяжении и сжатии. Для следов пересечения поверхности относительного сопротивления с плоскостями при принята линейная аппроксимация границ относительной прочности железобетонных элементов (рис. 3). Удовлетворительные результаты дают аппроксимации границ областей относительной прочности (сопротивления) сжатых элементов на срез выпуклыми кривыми второго порядка, аналогичными границам относительной прочности нормальных сечений на плоскости и исследованиям прочности сжато-изогнутых элементов по наклонным сечениям. Предлагаемые кривые включают три характерные точки прочности сечений железобетонных элементов на сжатие, растяжение и срез. При осевом сжатии () , при осевом растяжении , при срезе () для железобетонных элементов с учетом «нагельного» эффекта в продольной арматуре и при наличии сил зацепления по берегам трещин (при ). В работе принят интегральный учет данных явлений, зависящих от многих факторов, таких как вид, диаметры и количество армирования, расположение его по сечению, соотношение направлений арматуры и трещин, гранулометрический состав бетона и его прочность, вид напряженного состояния конструкций, коэффициент трения,

ширина раскрытия и наклона трещин, смещение ее граней и др. Мнения ученых по учету данных явлений в расчетах противоречивы: от полного отрицания до

необходимости их учета. В экспериментальных исследованиях величина параметра qs изменялась от до . При этом отмечается некоторое повышение параметра qs при динамических нагружениях, по сравнению со статическими испытаниями. В работе приведен анализ аналитических зависимостей, описывающих влияние «нагельного» эффекта в арматуре и наличие сил зацепления, удовлетворительно согласуемых с экспериментальными данными.

Для экспериментальной проверки предлагаемой аппроксимации границ областей относительной прочности сжатых железобетонных элементов на срез аспирантом Е.А. Бояринцевым под руководством и непосредственном участии автора были проведены в 1992-1995 годах испытания 32 серий (175 образцов) железобетонных элементов. В опытных образцах варьировались вид армирования (симметричное или одиночное), количество и диаметры арматуры, а также расположение арматуры в сечении. Испытывали сжатые элементы на срез в специальных стендах с созданием различных уровней относительного обжатия и относительного усилия среза . Выполненные экспериментальные исследования позволили выявить фактические разрушающие усилия при срезе нормальных сечений железобетонных элементов в зависимости от характера и количества продольного армирования, а также величины обжатия сечений продольной сжимающей силой. Анализ полученных данных показывает, что абсолютные значения разрушающих усилий имеют значительный разброс. Вместе с тем, отмечается общее повышение разрушающих поперечных сил с увеличением обжатия сечений от нуля до значений близких половине прочности сечения на центральное сжатие. Дальнейшее увеличение уровня обжатия нормальных сечений приводит к снижению абсолютных значений разрушающих поперечных сил , которые в зоне прочности сечений на центральное сжатие стремятся к нулю. Увеличение количества продольного армирования в сечении или величины защитного слоя бетона приводят к повышению разрушающих поперечных сил . При переходе от абсолютных значений к относительным величинам разброс экспериментальных точек сокращается, а отмеченные ранее закономерности изменения максимальной относительной поперечной разрушающей силы в зависимости от уровня продольного относительного обжатия сохраняются. Аналогичные закономерности влияния продольных сжимающих сил выявлены в обширных экспериментальных исследованиях А.С. Залесова, Р.Л. Маиляна, С.Г. Шениной при исследовании прочности наклонных сечений сжато-изогнутых железобетонных элементов.

Для принятой аппроксимации поверхности сопротивления железобетонных элементов получены аналитические расчетные зависимости, показывающие, что сопротивление железобетонных элементов по наклонным трещинам зависит от прочности на изгиб и срез по нормальным сечениям, аналогично известной в физике закономерности сопротивления электрической цепи с параллельным соединением сопротивлений. Разрушение железобетонных элементов по наклонной трещине возможно после обеспечения необходимой прочности нормальных сечений. В противном случае отказ конструкции будет происходить с разрушением нормальных сечений. Результаты расчетов по предлагаемому методу хорошо согласуются с опытными данными И.К. Белоброва, О.М. Лоскутова, С.Г. Шениной и др., полученными при исследовании железобетонных сжато-изогнутых балок при статическом и кратковременном динамическом нагружении.

Большая наглядность в расчетах прочности железобетонных элементов достигается при векторном представлении относительных усилий, возникающих в рассматриваемых сечениях, части или элементе в целом от внешних воздействий. При этом каждому воздействию или сумме воздействий будут соответствовать компоненты векторов действующих относительных усилий:,и. Концы данных векторов описывают поле или поверхность относительных усилий от внешних воздействий. В то же время отдельным точкам поверхности или областям относительной прочности железобетонных элементов соответствуют компоненты вектора сопротивления, равные

; ; ,

где , , – компоненты вектора сопротивления сечений железобетонных элементов; и – относительные изгибающие моменты, воспринимаемые бетоном и арматурой сечения относительно его центра тяжести; , , и – относительные усилия, воспринимаемые бетоном и арматурой сечения на сжатие, растяжение, а также срез.

Разность между компонентами векторов относительного сопротивления и действующих относительных усилий названа компонентами векторов запаса прочности сечений железобетонных элементов. При положительном их значении условия прочности рассматриваемого элемента выполняются, т.е.

; ; . (5)

В противном случае – не выполняются. Графически это означает, что если векторы относительных усилий от внешних воздействий располагаются внутри поверхности сопротивления, то условия прочности сечений выполняются, если выходят за пределы поверхности сопротивления, то прочность не обеспечивается (рис. 2 и рис. 3).

Использование выражений (5) в виде равенств в кинематическом методе предельного равновесия позволяет выявлять верхнюю оценку прочности железобетонных элементов с учетом взаимного влияния продольных и поперечных сил на предельные изгибающие моменты в пластических зонах железобетонных конструкций.

При построении поля векторов относительных усилий от внешних воздействий необходимо учитывать все возможные комбинации усилий M и N, возникающие на стадиях изготовления, транспортировки, складирования, монтажа и эксплуатации конструкции, а не ограничиваться только тремя комбинациями , ; , ; ,. Это связано с тем, что в рассматриваемом сечении могут возникать и другие более невыгодные сочетания усилий, не учитываемые, как правило, в расчетах. На стадии эксплуатации конструкции первым от начала координат , откладывается вектор относительных усилий ,, соответствующий постоянным нагрузкам. Векторы других загружений суммируются с вектором постоянных нагрузок в произвольном порядке, при этом суммарные векторы будут иметь различную длину и направление (рис. 4, а ). При суммировании векторов относительных усилий, соответствующих трем и более загружениям, учет коэффициентов сочетания приводит к уменьшению длины векторов относительных усилий от временных нагрузок. Учет гибкости внецентренно сжатых элементов производится умножением относительных суммарных моментов на коэффициент , определяемый согласно СНиП 2.03.01-84. Это приводит к увеличению длины суммарных векторов и изменению углов их наклона.

При динамическом нагружении железобетонных конструкций с учетом их совместной работы, а также податливости опорных устройств искомые величины усилий N и M достигают максимальных значений в разные промежутки времени t. При этом с уменьшением продолжительности действия динамической нагрузки и увеличением податливости конструкций эффект снижения перемещений и усилий возрастает, а процесс достижения их максимальных значений (перемещений и усилий) может носить колебательный характер. Переходя к относительным значениям усилий [ и ], после их проекцирования на плоскость и получим изменение следа относительных усилий во времени (рис. 4, б). Далее с помощью областей относительной прочности можно решать прямые и обратные задачи проектирования железобетонных элементов, воспринимающих динамические нагрузки.

При определении продольного армирования железобетонных элементов на поле векторов относительных усилий от внешних воздействий накладываются верхние и нижние границы области относительной прочности таким образом, чтобы все векторы относительных усилий оказались внутри области, а значения

и были бы минимальными. При таком положении границ области определяются значения вертикальных и горизонтальных смещений выпуклых кривых относительно осей и (;; ; ), а также координаты

точек пересечения прямолинейных участков границ области прочности (точки и ). В общем случае для железобетонного элемента с учетом найденных параметров можно записать две группы уравнений относительно искомых величин. В первую группу уравнений входят уравнения относительных усилий. Вторую группу уравнений составляют уравнения относительных моментов для вышеуказанных характерных параметров области прочности. Из данных уравнений можно определить относительные усилия в арматуре растянутой и сжатой зон сечения и армирование железобетонного элемента. Так, при обычном армировании железобетонного элемента арматурой класса A-I, А-II, А-III, приплощадь поперечного сечения продольной арматуры, согласно обозначениям выражения (2), определяется по формулам:

(6)

Полученное по выражению (6) армирование будет минимальным для рассматриваемого поля относительных усилий от внешних воздействий. Кроме минимального армирования, предлагаемая методика расчета позволяет анализировать без громоздких расчетов влияние прочностных характеристик материалов и геометрических параметров рассматриваемого сечения на его прочность при заданном поле относительных усилий от внешних воздействий.

Эффективность и наглядность расчетов достигается при оценке прочности нормальных сечений, части или конструкции в целом реконструируемых зданий или сооружений, когда в построенные области прочности (сопротивления) рассматриваемых сечений вписываются поля векторов усилий внешних воздействий до и после реконструкции. При этом области сопротивления сечений могут быть построены с учетом изменения прочностных характеристик материалов за период эксплуатации, влияния коррозии и т.п. На рис. 4,в показана область сопротивления отдельных сечений железобетонных колонн бункерного отделения главного корпуса Кемеровской ГРЭС до и после реконструкции покрытия котельного отделения, предусматривающей увеличение высоты помещений котельного отделения и установку дополнительного кранового оборудования. В некоторых случаях при реконструкции зданий требуется обнаружить весь спектр дополнительного возможного загружения конструкций без их усиления, что также может быть успешно выполнено по данному методу.

Расчеты по предлагаемому методу могут выполняться аналитически, графоаналитически или графически с помощью специальных номограмм, а также на ЭВМ. Предложенный метод расчета реализован в программах «POISK» и «PNS», написанных в разные годы на языках ФОРТРАН IV для ЭВМ типа СМ 1420/03 и Turbo Pascal для персональных компьютеров типа «Искра 1030», «СМ 1841» и IBM PC. Программы предназначены для решения прямых и обратных задач прочности сечений, части или конструкции в целом при статическом и кратковременном динамическом нагружениях, рассчитываемых в абсолютных или относительных величинах. Структурно данные пакеты программ состоят из головных программ и четырех - одиннадцати подпрограмм. В работе приведена структурная схема программы «POISK», иллюстрирующая связь между отдельными модулями. В разработанных программах ввод исходных данных производится в диалоговом режиме с терминалов ЭВМ, автоматизированы все этапы расчета. Кроме текстовой и цифровой информации о результатах расчетов предусмотрен графический вывод на экран мониторов областей прочности (сопротивления) рассматриваемого сечения, части или конструкции в целом с нанесенным в нее полей векторов усилий или их следов от внешних воздействий. Использование данных программ существенно упрощает расчеты, повышает их точность и во многих случаях позволяет получать более экономичные и наглядные решения.

Предложенные поверхности сопротивления железобетонных конструкций были использованы при расчетах пологих оболочек и плит на статические и кратковременные динамические воздействия. При этом характер деформирования железобетонных пологих оболочек и плит зависит от схем образующихся и развивающихся трещин, которые характеризуются последовательностью их возникновения и ориентации на внешней и внутренней поверхностях конструкции, а также прохождением трещин по толщине сечения элемента. Для элементов таких конструкций условия трещиностойкости сформулированы на основе теории ядровых моментов в пространстве компонентов относительных внутренних усилий по главным площадкам. При этом гипотеза трещинообразования по главным площадкам использована только для выявления схем образующихся трещин. В процессе динамического нагружения (вследствие перераспределения усилий) площадки трещин могут отклоняться от главных площадок. При выводе расчетных зависимостей трещиностойкости железобетонных оболочек учитывалась упругопластическая работа бетона растянутой зоны, а также изменение прочностных и деформативных характеристик бетона сжатой зоны железобетонных элементов, находящихся в условиях двухосного напряженного состояния.

Для экстремальных значений относительных ядровых моментов и относительных нормальных сил на главных площадках сформированы условия отсутствия трещин в железобетонных элементах динамически нагруженных оболочек и плит в виде

mr max,i  mcrc ,    mr min,i  mcrc,

nmax  ncrc, nmin  ncrc = Kp (btn ± np), (7)

где mcrc – относительные изгибающие моменты, воспринимаемые сечениями перед образованием трещин для нижней и верхней граней, которые определяются правой частью выражения (4) с введением дополнительного коэффициента Kp, учитывающего влияние двухосного напряженного состояния на относительный момент трещинообразования рассматриваемого сечения.

Если экстремальные значения относительных ядровых моментов и относительных мембранных сил меньше mcrc, ncrc, т.е. условия (7) выполняются, то железобетонные элементы, работающие без трещин, проходят две стадии: упругую и упругопластическую, связанную с развитием неупругих деформаций в бетоне. Неупругие деформации в бетоне могут развиваться в зонах с большими сжимающими или растягивающими напряжениями. При нарушении одного, двух и более неравенств условий (7) в железобетонном элементе появляются непересекающиеся и пересекающиеся трещины на верхней или нижней поверхности элемента, а также сквозные трещины, характеризуемые различными комбинациями. В работе рассмотрено восемнадцать комбинаций образующихся трещин, сгруппированных по шести базовым схемам работы железобетонных элементов, приводятся области возможного образования и развития возможных схем трещин в железобетонных элементах с различным их армированием во всем диапазоне загружения сечений относительными моментами и продольными силами.

Условия прочности железобетонных пологих оболочек и плит сформулированы в пространстве относительного запаса прочности, равного разности относительного сопротивления рассматриваемого сечения, части или конструкции в целом, и относительных усилий, возникающих в сечении, части или конструкции в целом от внешних кратковременных динамических или статистических воздействий. При назначении предельной поверхности или области относительного сопротивления сечения, части или конструкции в целом учтено влияние относительных продольных и поперечных сил на предельные относительные моменты.

Искомое условие динамической прочности для железобетонных оболочек можно получить при интегрировании условия прочности в напряжениях по толщине оболочки. Однако такой подход не приводит, ввиду сложностей при интегрировании, к удовлетворительным результатам. Другой подход заключается в допущении о мгновенной пластификации сечения тонкой оболочки в тот момент, когда на ее поверхности напряжения достигают предельных значений. Используя такое допущение и исследования А.С. Дехтяря, на основе общего условия прочности железобетона Г.А. Гениева, В.Н. Киссюка и Г.А. Тюпина, в работе сформулировано условие прочности динамически нагруженных оболочек с полным взаимодействием относительных усилий. В то же время данные подходы в определении условий прочности оболочек не учитывают особенностей деформирования железобетонных элементов с трещинами, ориентации трещин относительно направления армирования, величины и расположения арматуры в сечении и т.п. Избежать интегрирования по толщине и связанных с ним трудностей и недостатков можно, если выделить железобетонный элемент оболочки с трещинами и сформировать для него условие прочности непосредственно в усилиях. Такой подход на основе теории Н.И. Карпенко реализован в работе в относительных величинах внутренних усилий для различных схем образующихся трещин, с учетом предложенных поверхностей относительного сопротивления по прочности для динамически нагруженных оболочек. При этом условия прочности в компонентах запаса сопротивления элементов представлены в виде

kij  0,   k = m, n, g ,   i = x, y,   j = x, y,

которые дают оценку относительной несущей способности снизу. А условие относительной прочности

kij < 0 ,    k = m, n, g , i = x, y,   j = x, y   

использовано (при kji = 0) в кинематическом методе предельного равновесия для оценки несущей способности конструкции сверху.

Аналитический метод расчета железобетонных пологих оболочек и плит при внутреннем кратковременном динамическом нагружении базируется на обобщенных диаграммах деформирования конструкций, позволяющих рассчитывать широкий класс пологих оболочек и плит с учетом податливости опорных устройств и бортовых конструкций. Результаты экспериментальных исследований более ста семидесяти моделей пологих оболочек при внутреннем их нагружении показывают, что вначале в оболочке погашаются начальные сжимающие напряжения от внешних статических воздействий, далее, работая в основном на растяжение, оболочка проходит условно упругую и пластические стадии работы. Рассмотрены тонкие, пологие, прямоугольные в плане оболочки постоянной толщины, на которые действует кратковременная динамическая нагрузка P(t), приложенная как к внешней выпуклой, так и к внутренней вогнутой поверхности оболочки (рис. 5). Последний случай имеет место при расчете покрытий взрывоопасных цехов, взрывных камер и т.п. Рассматриваемые оболочки могут иметь центральные фонарные отверстия, которые наряду с выполнением свето-аэрационных функций, в период взрыва внутри сооружения будут частично уменьшать величины действующих динамических нагрузок. Расчет оболочек в упругой стадии выполняется вариационным методом с учетом основных допущений и гипотез, лежащих в основе теории тонких пологих оболочек. Аналитическое решение задачи о напряженно-деформированном состоянии оболочки с центральным отверстием осложняется трудностью выбора аппроксимирующих перемещения координатных функций, удовлетворяющих граничным условиям на краю отверстия. При наличии заполнения центрального отверстия оболочка рассматривалась как система со ступенчато переменной жесткостью. После вскры

тия заполнения центрального отверстия (при внутреннем динамическом нагружении) оболочка рассматривается как система с разрывными параметрами, которые обусловлены конечными разрывами жесткости и действующей нагрузки в области центрального отверстия. Жесткость оболочки с открытым центральным отверстием и действующая на оболочку кратковременная динамическая нагрузка описаны с помощью функции Хевисайда, которая позволила формально свести разрывную задачу к задаче с непрерывно меняющимися параметрами.

Перемещения точек срединной поверхности оболочки представлены в виде:

w(x, y, t) =  Wmn(x, y);

u(x, y, t) =  Umn(x, y); (8)
v(x, y, t) =  Wmn(x, y).

Здесь: Zmn(t), Zmn(t) и Zmn(t) – наибольшие значения вертикальных и мембранных перемещений точек оболочки, изменяющиеся во времени, обусловленные деформацией поля оболочки, ее контурных элементов и опорных устройств; Wmn(x, y), Umn(x, y) и Vmn(x, y) – аппроксимирующие функции, выбираются по методу Ритца таким образом, чтобы каждая из них удовлетворяла кинематическим граничным условиям опирания оболочки, и заданы комбинацией тригонометрических балочных функций. Представление перемещений конструкций с помощью комбинаций балочных функций, впервые примененное В.З. Власовым, широко используется в вариационных методах расчета. В выражении (8) неизвестными, подлежащими определению являются, Zmn(t), Zmn(t) и Zmn(t), которые можно рассматривать как обобщенные координаты. Они определяются из уравнений движения оболочки в условной упругой стадии.

Вывод уравнений движения пологой железобетонной оболочки (являющейся системой с N-степенями свободы в зависимости от,,, m и n) при кратковременном динамическом нагружении производили с использованием вариационного метода – принципа Гамильтона, который позволил непосредственно получить уравнение движения для любой заданной системы конструкций, в том числе для оболочек. Принцип Гамильтона обладает тем преимуществом, что он рассматривает только чисто скалярные величины энергий, которые могут складываться алгебраически, в то время как в других методах (принцип возможных перемещений и метод равновесия с использованием принципа Даламбера) силы и перемещения являются по своему характеру векторами, которые могут складываться по правилам векторного анализа. Принцип Гамильтона использован также для решения задач статически нагруженных оболочек. В этом случае значение кинетической энергии T не учитывается, а подынтегральные выражения в оставшихся членах принципа Гамильтона инвариантны во времени. При этом данное выражение принимает форму (Эд – Эн) = 0, хорошо известного принципа минимума потенциальной энергии, широко применяемого в статическом анализе.

После подстановки найденных значения энергий в выражение принципа Гамильтона и дифференцирования по каждой обобщенной координатной функции при фиксированных значениях m = i и n = j, с учетом фильтрующих особенностей единичных функций Хевисайда для оболочек с центральным отверстием получены системы, состоящие из трех групп уравнений. В первую группу входят дифференциальные неоднородные уравнения второго порядка, описывающие движение пологих оболочек при кратковременном нагружении. Вторая и третья группа уравнений получены из условий и . Состоят они из линейных алгебраических уравнений и определяют взаимосвязь коэффициентов разложений нормальной Zmn(t) и мембранных Zmn(t) и Zmn(t) обобщенных координатных функций. Полученная система уравнений в общем случае нераспадающаяся, т.е. имеет полную матрицу, размеры которой определяются количеством членов ряда функций, аппроксимирующих перемещения оболочек. Решение такой системы уравнений реализовано численно на ЭВМ. В общем случае пологая оболочка представляет собой систему с бесконечным числом степеней свободы. Поскольку в большинстве случаев в области поля оболочки принятые обобщенные координатные функции в виде двойных тригонометрических рядов обладают хорошей сходимостью, их первые и вторые производные являются взаимно ортогональными, то искомая система состоит из трех групп распадающихся уравнений, решение которых получено в замкнутом виде. Вычислив неизвестные коэффициенты разложений координатных функций, по линейной теории оболочек определены внутренние усилия и перемещения в любой точке срединной поверхности, а также скорость перемещений точек поверхности в конце условной упругой стадии работы оболочек.

Приведенные расчетные зависимости позволяют рассматривать напряженно-деформированное состояние других разновидностей пологих железобетонных оболочек, а также плит. Полагая переменными параметры, и, рассмотрена работа оболочек с учетом податливости диафрагм и опорных устройств, а также совместная работа рассматриваемой конструкции с поддерживающими ее железобетонными элементами (рис. 5). Расчетные зависимости для железобетонных пологих оболочек двоякой положительной гауссовой кривизны с центральным отверстием и без него, с учетом податливости опорных устройств детально рассмотрены в работе для квадратных и прямоугольных в плане оболочек при внутреннем кратковременном динамическом нагружении. Полагая в вышеприведенных зависимостях kx или ky, или обе кривизны равными нулю, при варьировании соотношениями геометрических параметров конструкций, а также параметров, и, получены расчетные зависимости, описывающие работу динамически нагруженных железобетонных цилиндрических оболочек и плит.

Динамический расчет железобетонных пологих оболочек и плит в пластической стадии работы поля или опорных устройств и конструкций выполнен с учетом положений, допущений, гипотез тонких пологих оболочек. При этом перемещения отдельных элементов поля оболочки, опорных устройств и конструкций выражаются через наибольшие углы поворота, как правило, недеформируемых звеньев, соединенных пластическими зонами, на которые разделяется поле оболочки в конце условной упругой стадии. Анализ экспериментальных исследований пологих оболочек показывает, что характер их разрушения при внутреннем нагружении определяется армированием зон центрального отверстия и поля оболочки в целом. При этом выявлено пять схем разрушения пологих оболочек при внутреннем нагружении. Для железобетонных плит с отверстиями в поле и проемами у внешнего контура принято двадцать девять базовых схем разрушения, зависящих от размеров и места расположения отверстия или проема, условий опирания плит на внешнем контуре, армирования плиты и других параметров. При «диагональной», «лепестковой» и «крестовых» схемах разрушения оболочек и большинства схем разрушения плит с отверстиями и проемами таким параметром является угол поворота элементов, сопряженных с контурными элементами. Для «девятиэлементной» и «восьмиэлементной» схем разрушения оболочек – это угол суммарного поворота внутренних элементов поля оболочек. При этом изменение наибольшего угла поворота отдельных элементов увязывается расчетными зависимостями с углами поворота всех элементов кинематического механизма и основными геометрическими параметрами рассматриваемой схемы разрушения на бесконечно малых перемещениях элементов. Для принятых схем разрушения получены расчетные зависимости динамического деформирования оболочек и плит в пластической стадии, которые заложены в программы «Плита» и «Shale».

Величины внутренних кратковременных динамических нагрузок, при которых оболочка, работая в пластической стадии, имеет конечные перемещения, не превышающие предельно допустимых значений, должны находиться в следующих пределах:

РI P PII,

где РI ограничивает работу оболочек в условной упругой стадии; PII - в пластической стадии.

Приведенные расчетные зависимости позволяют решать задачи прямого и обратного проектирования железобетонных пологих оболочек и плит, фиксируя при этом области возможных схем их разрушения в зависимости от вида воздействия, геометрии конструкции, ее армирования, условий опирания, формы и размеров отверстий в поле и проемов у внешнего контура и других параметров. Приводятся графики и номограммы такого проектирования, полученные в результате расчетов более пятисот вариантов конструктивного решения оболочек при внутреннем нагружении.

Выполненные расчеты показали, что податливость опорных устройств значительно влияет на деформативность, прочность и трещиностойкость конструкций. Влияние различных факторов на податливость узлов сопряжения железобетонных конструкций была выявлена в ходе экспериментальных исследований восемнадцати серий закладных деталей конструкций на заводе ЖБК-100 г. Томска под руководством и непосредственном участии автора, в которых варьировались: виды и геометрия металлических закладных деталей, расположение, количество, диаметры и длина арматурных анкерных стержней. Проведенные исследования позволили предложить расчетные обобщенные диаграммы деформирования узлов сопряжения железобетонных конструкций. Разрушение железобетонных плит покрытия от кратковременного динамического воздействия паровоздушной смеси на Асиновском ЛПК в г. Асино Томской области качественно подтвердило результаты выполненных ранее расчетов. При этом железобетонные плиты покрытия на неподатливых опорах разрушились с образованием пластических зон в середине пролета, в то время как плиты с податливыми опорами не имели подобных разрушений.

В работе рассмотрен численный метод расчета железобетонных пологих оболочек и плит при статическом и кратковременном динамическом нагружении. Определение напряженно-деформированного состояния динамически и статически нагруженных железобетонных пологих оболочек и плит осуществлено методом конечных элементов. Базовым элементом принят прямоугольный конечный элемент пологой оболочки двоякой кривизны, в каждом узле которого пять степеней свободы. Преимущества данного элемента заключаются в том, что он точно описывает геометрию оболочки, для него нет необходимости составлять матрицу перехода от локальной системы координат к глобальной, проще организуется ввод-вывод исходных данных и результатов расчета. На основе метода конечных элементов реализована в приращениях процедура итерационного расчета уравнений движения системы. При этом для повышения точности получаемых результатов использована экстраполяционная зависимость Ричардсона, с помощью которой даже на крупных сетках можно получать удовлетворительные для практических расчетов уточненные конечные результаты. Разработанный численный метод доведен до программы расчета железобетонных пологих оболочек и плит на персональных компьютерах. Использование разработанных программ «Томск» и «Поиск» позволяет решать задачи прямого и обратного проектирования железобетонных оболочек и плит при статическом и кратковременном динамическом нагружении. Проведенные расчеты показали возможность и целесообразность применения железобетонных пологих оболочек с проемами в сооружениях, воспринимающих кратковременные динамические нагрузки. При этом наибольший эффект имеет место при возможности работы элементов оболочек в пластической стадии и учете податливости бортовых элементов и опорных устройств.

Экспериментальные исследования железобетонных конструкций, результаты которых приведены в работе, выполнены с целью обоснования корректности разработанного теоретического аппарата, проверки основных принятых предпосылок, выявления особенностей процесса сопротивления и возникновения предельных состояний при статическом и кратковременном динамическом нагружении. Кроме вышеупомянутых экспериментальных исследований стержневых железобетонных конструкций и узлов их сопряжений, приводятся результаты экспериментальных исследований ста семидесяти двух моделей (пяти серий) пологих оболочек на квадратном и прямоугольном плане, а также двадцати трех железобетонных моделей (трех серий) составных оболочек вращения при статическом или кратковременном динамическом нагружении. В моделях составных оболочек вращения сохранилось подобие с применяемыми в практике энергетического строительства составными защитными оболочками по форме, размерам и характеру армирования. Модели были выполнены в масштабе 1:150 (пять моделей – первая серия), 1:100 (девять моделей – вторая серия) и 1:50 (девять моделей – третья серия). Принятые для испытания железобетонные модели оболочек представляли собой замкнутые цилиндры, которые внизу монолитно связаны с круглой плитой, имеющей центральное круглое отверстие. Сверху цилиндр прикрывался куполом с переменным радиусом. В месте сопряжения купола с цилиндром имелось железобетонное кольцо. В моделях (пяти серий) пологих оболочек покрытий зданий варьировались: геометрические размеры в плане и стрела подъема, их соотношения, конструкции и жесткость бортовых элементов, условия опирания поля оболочек по внешнему контуру, величина и форма центральных отверстий, армирование поля и контура центрального отверстия, вид загружения моделей (внутреннее или внешнее, статическое или кратковременное динамическое) и другие параметры (стенды, приборы и их количество и т.п.). Испытывались модели на специальных стендах и установках, конструкции которых позволяли создавать статические или кратковременные динамические нагрузки, приложенные по всей поверхности оболочки или части ее. Статические нагрузки создавались гидростатическим методом через систему резиновых шлангов и мешков. Одновременное использование в стендах горизонтальных и вертикальных шлангов позволило создавать произвольный закон распределения действующей нагрузки по высоте и окружности внешней поверхности испытываемой оболочки. В процессе испытания можно регулировать величины нагрузок и вести разрушение оболочки с любой скоростью, изменяя количество жидкости, поступающей в мешки, в вертикальные и горизонтальные шланги. При этом имелась возможность производить многократно нагрузку и разгрузку испытываемой конструкции. Данный способ испытания позволяет регистрировать изменение суммарных перемещений (объема) оболочки. Испытание оболочек при кратковременном динамическом нагружении выполнено на стендах копрового типа с рычажной системой и без, а также в пневмодинамической установке. Разработанные стенды, приборы и методики испытания железобетонных оболочек показали эффективность и способность определять искомые параметры оболочек в трудно доступных местах, повышая тем самым автоматизацию и безопасность проводимых экспериментальных исследований.

Комплексными экспериментальными исследованиями железобетонных пологих оболочек, охватывающими все стадии работы при статическом и кратковременном динамическом нагружении, подтверждены основные положения разрабатываемого расчетно-теоретического аппарата. Кроме общих закономерностей, в работе подробно анализируются полученные опытные данные для конкретных оболочек и условий нагружения. Получены новые опытные данные, характеризующие процесс сопротивления и особенности возникновения предельных состояний конструкций. Показано, что для железобетонных пологих оболочек пластические деформации локализуются в отдельных зонах поля оболочки, а характер их разрушения определяется армированием зон центрального отверстия и поля оболочки в целом. Выявлено девять схем разрушения пологих оболочек, шесть из которых получены впервые при внутреннем их нагружении.

В диссертации, для обоснования принятых предпосылок методов расчета, также использованы результаты экспериментальных исследований бетона, арматуры, стержневых железобетонных конструкций, пологих оболочек и плит при статическом и кратковременном динамическом нагружении, выполненные отечественными и зарубежными учеными.

После кратковременного динамического воздействия в большинстве случаев требуется оценка технического состояния с выявлением запасов несущей способности не только стержневых железобетонных конструкций, элементов пологих оболочек и плит, но поддерживающих их других строительных конструкций, включая железобетонные фундаменты. В последние годы в связи с реконструкцией зданий и сооружений требуется оценка технического состояния железобетонных конструкций и при статических воздействиях. При этом желателен единый подход в оценке прочности сечений и достаточности геометрических параметров конструкций. Полученные в диссертационной работе расчетные зависимости позволяют с единых позиций оценивать прочность бетонных и железобетонных, каменных и армокаменных с продольным, поперечным или смешанным армированием конструкций. Кроме прочности и трещиностойкости предложенный метод расчета позволяет определить достаточность геометрических параметров строительных конструкций заданному полю относительных усилий от внешних воздействий. При этом для железобетонных фундаментов разработан метод по определению оптимальных размеров фундаментов различной геометрической формы в плане, по оценке трещиностойкости плитной и стаканной частей фундаментов, а также по назначению минимального армирования железобетонных фундаментов, воспринимающих статические или кратковременные динамические нагружения.

Предлагаемый метод расчета основан на представлении в относительных величинах функциональной зависимости действующих усилий, конструктивных параметров фундамента, в предположении линейного или нелинейного распределения контактных давлений по подошве, учете деформирования фундамента, изменения прочностных характеристик материалов тела и основания, а также особенностей работы наложенных на фундамент связей. Выявлены основные закономерности изменения и построения областей относительного сопротивления основания и сечений тела железобетонного фундамента в зависимости от вышеуказанных параметров.

Наиболее эффективен предлагаемый метод расчета при проектировании фундаментов с наложенными связями для реконструируемых зданий и сооружений с учетом сложного нагружения конструкций, в том числе динамических воздействий. Использование данного метода расчета позволяет решать ряд задач, связанных с определением дополнительных нагрузок на фундамент, проверкой достаточности размеров подошвы и резервов прочности тела фундаментов реконструируемых зданий, выявлением максимально возможных значений эксцентриситетов приложения нагрузок, определением количества необходимых накладываемых на фундамент связей и их расположение по подошве и т.п. Задачи при этом могут решаться аналитически, графически или графоаналитически, в том числе на ЭВМ. Наглядность расчетов по предлагаемому методу достигается при графическом и графоаналитическом способах. При этом принимаются векторные представления действующих на фундамент относительных усилий от внешних воздействий, на которые накладываются области относительного условного сопротивления основания, а также области прочности и трещиностойкости сечений тела фундамента.

Подробно вывод рассмотренных зависимостей и конструктивных решений для фундаментов с наложенными связями при линейной и нелинейной эпюре контактных давлений по подошве, а также новые типы задач прямого и обратного проектирования рассмотрены в работе, некоторые решения защищены патентами России.

Осуществлен комплексный анализ научно-исследовательских работ, направленных на разработку конструктивных решений и методов усиления и восстановления строительных конструкций реконструируемых зданий и сооружений, в том числе при динамическом нагружении. Проведены теоретические и экспериментальные исследования, накоплен практический опыт по систематизации причин и способов усиления железобетонных конструкций, а также разработке проектно-конструкторских решений, используемых при реконструкции зданий и сооружений. Подготовлен ряд пособий и рекомендаций, получены авторские свидетельства и патенты. При подготовке пособий ставилась цель - наглядно, в доступной форме показать специалистам способы оценки технического состояния, расчета, восстановления и усиления строительных конструкций зданий и сооружений. При этом сделана попытка методологического единства в рассмотрении вопросов восстановления и усиления (бетонных и железобетонных, каменных и армокаменных, металлических и деревянных) строительных конструкций зданий и сооружений (от фундаментов до конструкций покрытий). Для элементов пологих оболочек применительно к взрывоопасным производствам такие решения предложены впервые. Отличительной особенностью пособий является то, что они содержат в основном графический материал в виде схем и чертежей с пояснительными текстами, что позволяет оперативно инженерам и исследователям принимать необходимые решения. Данные пособия и рекомендации получили положительные отзывы от специалистов проектных, строительных и других организаций, ведущих строительных вузов России и стран СНГ, широко используются в настоящее время, а также рекомендованы в качестве учебной литературы при подготовке инженеров-строителей специальности ПГС (Программа дисциплины «Обследование, испытание и реконструкция зданий и сооружений» для специальности 2903 «Промышленное и гражданское строительство». М.:Учебно-методическое объединение вузов РФ по строительному образованию, 1998. 8 с. ).

С целью автоматизации проектирования восстановления и усиления строительных конструкций зданий и сооружений разработан программный комплекс на базе «AutoCAD», позволяющий решать задачи, связанные с оценкой технического состояния, выбором и разработкой вариантов усиления и восстановления строительных конструкций, а также с их проектированием и расчетом при статическом и кратковременном динамическом нагружении. Использование программного комплекса позволяет сократить трудоемкость и затраты времени при выполнении проектных работ по разработке вариантов усиления и восстановления строительных конструкций.

Результаты исследований вошли в нормативный документ МО РФ, в пособия и рекомендации по оценке технического состояния, восстановлению и усилению железобетонных конструкций (в том числе элементов пологих оболочек и плит) зданий и сооружений, пользователями которых к настоящему времени являются более 800 проектных, научно-исследовательских и учебных институтов, строительных и других предприятий и организаций России и стран СНГ. Выписки из справок от 93 организаций, под­твердивших использование пособий и рекомендаций в своей практической деятельности приве­дены в приложении 3, которое показывает, что, наряду с конкретными экономическими эффектами, получено снижение трудозатрат, а также сроков выполнения проектных и ремонтно-восстановительных работ.

ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ

1. Рассмотрен комплекс вопросов, необходимых для решения проблемы расчета прочности и трещиностойкости эксплуатируемых стержневых железобетонных конструкций, пологих оболочек и плит при статическом и кратковременном динамическом нагружении, включающий экспериментальное обоснование расчетных предпосылок, разработку методов расчета и предложений по оценке технического состояния, восстановлению и усилению конструкций, имеющий важное хозяйственное значение.
2. Разработан общий метод расчета с использованием поверхностей относительного сопротивления по прочности и трещиностойкости железобетонных конструкций при статическом и кратковременном динамическом нагружении. На основе деформационной модели численно и аналитически сформулированы условия относительной прочности и трещиностойкости железобетонных конструкций, показывающие взаимосвязь предельных моментов, продольных и поперечных сил во всем диапазоне динамического или статического загружения конструкций (от центрального растяжения до центрального сжатия) с учетом нелинейных диаграмм деформирования бетона и арматуры, влияния скорости и характера динамического нагружения на прочностные свойства материалов, особенностей армирования сечений, их формы, характера и величины предварительного напряжения и других параметров. Выявлены основные закономерности изменения границ поверхностей и областей относительной прочности и трещиностойкости (сопротивления) железобетонных элементов в зависимости от вышеуказанных параметров. Установлено, что условиям относительной динамической прочности и трещиностойкости стержневых железобетонных конструкций соответствуют выпуклые поверхности, трансформированные вокруг временной координаты в аналитических расчетах или координаты скорости деформирования в численных расчетах.
3. Условия прочности и трещиностойкости железобетонных конструкций сформулированы в пространстве компонентов относительного запаса прочности, равного разности компонентов относительного сопротивления рассматриваемого сечения, части или конструкции в целом и компонентов относительных усилий, возникающих в сечении, части или конструкции в целом от внешних кратковременных динамических воздействий. Наглядность в расчетах железобетонных конструкций достигается при векторном представлении действующих относительных усилий, их следов или полей от внешних воздействий. Совмещение поверхностей или областей относительного сопротивления по прочности и трещиностойкости позволяет более обоснованно определять необходимое обычное или предварительно напряженное армирование для работы конструкций с трещинами или без таковых. Минимальное армирование достигается при нулевых значениях компонентов векторов запаса прочности (сопротивления) рассматриваемых сечений, частей или конструкций в целом.
4. Условия трещиностойкости железобетонных пологих оболочек и плит получены на основе теории ядровых моментов в пространстве компонентов относительных внутренних усилий по главным площадкам. Рассмотрено восемнадцать комбинаций образующихся трещин, сгруппированных по шести базовым схемам работы железобетонных элементов. При выборе расчетных зависимостей трещиностойкости железобетонных оболочек и плит необходимо учитывать упругопластическую диаграмму работы бетона растянутой зоны, а также изменение прочностных и деформативных характеристик бетона сжатой зоны железобетонных элементов, находящихся в условиях двухосного напряженного состояния. Для предельной относительной прочности бетона предложена сингулярная поверхность, трансформируемая вокруг временной координаты в аналитических расчетах и скорости деформирования в численных расчетах.
5. Предложены интегральные относительные прочностные и деформативные параметры критериев предельных состояний для железобетонных элементов пологих оболочек и плит. Для железобетонных оболочек, воспринимающих внутренние кратковременные динамические нагрузки, данные критерии предложены впервые.
6. Для стержневых железобетонных элементов предложены аналитические зависимости изменения расчетных напряжений в продольной арматуре во всем диапазоне приложения внешней динамической нагрузки. В зоне малых эксцентриситетов предложена тригонометрическая функция изменения расчетных напряжений sd от, которая более плавно описывает зоны около Rd и R1d. Кроме Rd, введено понятие R1d – значение относительной высоты сжатой зоны сечения, при котором напряжения в арматуре Аs достигают значений sd = Rscd. Анализ результатов расчета нормальных сечений железобетонных элементов с использованием тригонометрической функции дал более близкое совпадение с предложенными границами относительной прочности и экспериментальными данными. Величина отклонений снижается примерно в два раза по сравнению с гиперболической зависимостью. Введение дополнительного понятия граничной относительной высоты сжатой зоны сечения R1d позволяет установить границы применимости расчетных зависимостей для внецентренно сжатых стержневых железобетонных элементов при больших ( Rd), малых (Rd < < R1d) и случайных ( R1d) эксцентриситетах.
7. Разработаны аналитический, базирующийся на обобщенных диаграммах деформирования конструкций, и численный (на основе МКЭ) методы расчета железобетонных пологих оболочек и плит при внутреннем кратковременном динамическом нагружении, позволяющие рассчитывать широкий класс пологих оболочек и плит с учетом податливости опорных устройств и бортовых конструкций. При расчете прочности железобетонных элементов необходимо учитывать влияние продольных и поперечных сил на предельные величины изгибающих моментов в пластических зонах конструкций. Предложенные методы доведены до программ расчета пологих оболочек и плит на персональных компьютерах.
8. Комплексными экспериментальными исследованиями на моделях и натурных конструкциях железобетонных оболочек, охватывающими все стадии работы при статическом и кратковременном динамическом нагружении, подтверждены основные положения разрабатываемого расчетно-теоретического аппарата. Получены новые опытные данные, характеризующие процесс сопротивления и особенности возникновения предельных состояний конструкций. Показано, что для железобетонных пологих оболочек, пластические деформации локализуются в отдельных зонах поля оболочки, а характер их разрушения определяется армированием зон центрального отверстия и поля оболочки в целом. Выявлено девять схем разрушения пологих оболочек, шесть из которых получены впервые при внутреннем их нагружении.
9. Разработанные программы и рекомендации, реализующие предложенные методы расчета, позволяют значительно расширить задачи прямого и обратного проектирования железобетонных конструкций и дают возможность принимать более обоснованные решения. Практическая направленность исследований выражена также в разработке методов оценки технического состояния, восстановления и усиления эксплуатируемых стержневых конструкций, пологих оболочек и плит зданий и сооружений, включая переоборудование их под взрывоопасные производства. Разработанные пособия и рекомендации используются проектными, научными и строительными организациями, обеспечивающими безопасность строительной отрасли России и стран СНГ, результаты исследований вошли в нормативный документ МО России.

Основное содержание диссертации опубликовано в четырех монографиях, десяти пособиях и рекомендациях, четырех патентах России и восьмидесяти публикациях, основные из которых следующие:

Монографии:

1. Болдышев А.М., Плевков В.С. Прочность нормальных сечений железобетонных элементов. - Томск: Изд-во Том. ЦНТИ, 1989. - 236 с.
2. Попов Н.Н., Кумпяк О.Г., Плевков В.С. Вопросы динамического расчета железобетонных конструкций. - Томск: Изд-во Том. ун-та, 1990. - 288 с.
3. Мальганов А.И., Плевков В.С., Полищук А.И. Восстановление и усиление строительных конструкций аварийных и реконструируемых зданий. - Томск: Изд-во Том. ун-та, 1992. - 456 с.
4. Мальганов А.И., Плевков В.С. Восстановление и усиление строительных конструкций инженерных сооружений. -Томск: Изд-во Том. ЦНТИ, 1996. - 532 с.; Издание второе, дополненное и переработанное.- Томск: Изд-во Том. гос. арх-строит. ун-та, 1999. – 538 с.

Пособия и рекомендации:

5. Пособие по организации и проведению обследования технического состояния строительных конструкций зданий и сооружений Министерства обороны Российской Федерации.- М.: 26 ЦНИИ МО РФ, 1999. – 228 с.
6. Мальганов А.И., Плевков В.С. Восстановление и усиление ограждающих строительных конструкций зданий и сооружений. Рекомендовано Министерством общего и профессионального образования РФ в качестве учебного пособия для студентов, обучающихся по всем строительным специальностям.-Томск: Изд-во Том. гос. арх.-строит. ун-та, 2000. – 372 с. ( в том числе электронная версия); Томск: Печатная мануфактура, 2002. – 391 с.
7. Организация и проведение обследования технического состояния строительных конструкций зданий и сооружений. (Пособие – авторы: Морозов А.С., Ремнев В.В., Тонких Г.П., Кумпяк О.Г., Мальганов А.И., Плевков В.С., Полищук А.И. и др.). Москва, 2001. – 212 с.; Томск-Москва, Печатная мануфактура,2001. – 196 с.
8. Болдышев А.М., Плевков В.С. Рекомендации по расчету на ЭВМ прочности нормальных сечений железобетонных элементов с использованием программ «Поиск-1» ( «Поиск-2»). - Томск: Изд-во Том. ЦНТИ, 1990. - 36 с. (38 c.).
9. Мальганов А.И., Плевков В.С., Полищук А.И. Оценка технического состояния и усиление строительных конструкций реконструируемых зданий: Пособие. - Томск: Изд-во Том. ЦНТИ, 1991. - 309 с.
10. Попов Н.Н., Плевков В.С., Балдин И.В. Расчет железобетонных коротких цилиндрических оболочек покрытий зданий и сооружений на действие кратковременных динамический нагрузок: Учебное пособие. - Томск: Изд-во Том. политехн. ун-та,1992. - 96 с.
11. Плевков В.С., Мальганов А.И., Балдин И.В. Восстановление и усиление железобетонных цилиндрических оболочек покрытий зданий и сооружений. - Томск: Изд-во Том. ун-та,1993. - 84 с.
12. Мальганов А.И., Плевков В.С. Оценка технического состояния, восстановление и усиление строительных конструкций инженерных сооружений: Пособие. - Томск: Изд-во Том. ЦНТИ, 1994. - 284 с.
13. Болдышев А.М., Мальганов А.И., Плевков В.С. Расчет и проектирование железобетонных конструкций при статических и кратковременных динамических воздействиях. / Под. ред. В.С. Плевкова - Томск: Изд-во Том. ЦНТИ, 1994. - 164 с.
14. Плевков В.С., Мальганов А.И., Балдин И.В. Рекомендации по автоматизированному проектированию восстановления и усиления железобетонных плит (цилиндрических оболочек), (балок) покрытий и перекрытий зданий и сооружений на персональных компьютерах. - Томск: Изд-во Том. ЦНТИ, 1995. - 45 с. (1996. - 43 с.), (1997. - 75 с.).

Статьи в журналах и сборниках научных трудов:

15. Попов Н.Н., Плевков В.С., Исследование пологих оболочек положительной гауссовой кривизны на действие импульсных нагрузок большой интенсивности // Международная конференция по облегченным пространственным конструкциям покрытий для строительства в обычных и сейсмических районах. Алма - Ата 13-16 сентября 1977: Доклады - М.: Стройиздат, 1977. - С. 102-107.
16. Плевков В.С. Расчет пологой оболочки при действии внутренней кратковременной динамической нагрузки с учетом податливости опор // Теоретические исследования строительных конструкций. - М.: ЦНИИСК им. Кучеренко, 1977. - С. 34-39.
17. Болдышев А.М., Плевков В.С. Экспериментальное исследование железобетонных пологих оболочек с центральным отверстием при импульсном загружении // Исследования по расчету сооружений. - Томск: Изд-во Том. ун-та, 1978. - С. 3-8.
18. Плевков В.С. Работа пологих оболочек при действии внутренней кратковременной нагрузки // Исследования по строительным конструкциям и фундаментам. - Томск: Изд-во Том. ун-та, 1979. - С. 154-174.
19. Забегаев А.В., Плевков В.С., Усманов А.У. Расчет железобетонных плит перекрытий на действие внутренних динамических нагрузок // Технические науки, Т XI. - Томск: Изд-во Том. ун-та, 1980. - С. 30-34.
20. Плевков В.С. К расчету упругих пологих оболочек при внутреннем кратковременном динамическом нагружении // Исследование строительных конструкций и фундаментов. - Томск: Изд-во Том. ун-та,1980. - С. 84-95.
21. Попов Н.Н., Забегаев А.В., Плевков В.С., Усманов А.У. Проектирование железобетонных плит перекрытий и покрытий промышленных зданий на кратковременные динамические нагрузки большой интенсивности. – МИСИ им. В.А. Куйбышева; ТИСИ, 1981. - 28 с.
22. Кумпяк О.Г., Плевков В.С., Лоскутов О.М. Экспериментальные исследования железобетонных составных оболочек при внешнем локальном статическом и динамическом нагружениях // Деп. во ВНИИИС Госстроя СССР, 1983. №3929. - 21 с.
23. Плевков В.С., Подшивалов И.И. Экспериментальные исследования составных железобетонных оболочек вращения при внешнем неравномерном нагружении // Пространственные конструкции в Красноярском крае: Межвузовский сборник. - Красноярск: Кр. ПИ, 1987. - С. 74-82.
24. Плевков В.С. Разрушение железобетонных составных оболочек вращения при внешнем статическом и динамическом нагружении // Исследование по строительным конструкциям и строительной механике. - Томск: Изд-во Том. ун-та, 1987. - С. 123-131.
25. Плевков В.С., Подшивалов И.И. Железобетонные составные оболочки при внешнем неравномерном нагружении // Известия вузов. Строительство и архитектура. 1988. № 9. - С. 119-121.
26. Болдышев А.М., Плевков В.С. Расчет прочности нормальных сечений железобетонных элементов // Бетон и железобетон. – 1990. № 4. - С. 38-39; № 11 - С.25-27.
27. Плевков В.С., Коляскин С.Ю. Оценка прочности статически и динамически нагруженных железобетонных пологих оболочек и плит методом конечных элементов // Деп. во ВНИИТПИ Госстроя СССР, 1990. № 10836. - 95 с.
28. Плевков В.С., Болдышев А.М. Прочность нормальных сечений предварительно напряженных железобетонных элементов // Известия вузов. Строительство и архитектура. – 1991.- № 1. - С. 3-11.
29. Болдышев А.М., Плевков В.С. Оценка прочности нормальных сечений преднапряженных железобетонных элементов // Бетон и железобетон. – 1992.- № 7. - с. 19-20.
30. Плевков В.С. Условие прочности нормальных сечений динамически нагруженных железобетонных оболочек и плит // Динамика железобетонных конструкций и сооружений при интенсивных кратковременных воздействиях: Сб. науч. тр. - М.: МИСИ, 1992. - С. 87-100.
31. Плевков В.С., Балдин И.В. Расчет железобетонных пологих цилиндрических оболочек покрытий при статическом и кратковременном динамическом нагружении // Динамика железобетонных конструкций и сооружений при интенсивных кратковременных воздействиях: Сб. науч. тр. - М.: МИСИ, 1992. - С. 172-180.
32. Плевков В.С., Мальганов А.И., Балдин И.В. Усиление железобетонных оболочек покрытий при переоборудовании зданий и сооружений под взрывоопасные производства // Научные труды Общества железобетонщиков Сибири и Урала. Вып. 2. - Новосибирск: Изд-во СибГАПС, 1994. - С. 47-50.
33. Плевков В.С., Мальганов А.И., Болдышев А.М., Балдин И.В. Разработка эффективных приемов восстановления и усиления строительных конструкций и методов расчета для зданий и сооружений // Известия вузов. Строительство.- 1994.- № 12. - С. 13-15.
34. Плевков В.С., Бояринцев Е.А. Оценка прочности железобетонных элементов по нормальным и наклонным сечениям // Научные труды Общества железобетонщиков Сибири и Урала. Вып. 3. - Новосибирск: Изд-во Сиб.ГАПС, 1995. - С. 65-70.
35. Плевков В.С. Динамическая прочность бетона и арматуры железобетонных конструкций.- Томск: Изд-во Том. ЦНТИ, 1996. – 65 с.
36. Plevkov V.S., Malganov A.I., Baldin I.V. Restoration and strengthening of reinforced concrete shallow shells and slabs of buildings and structures // Spatial Structures in new and renovation projects of buildings and construction. Proceedings international congress ICSS-98, June 22-26, 1998. - Moscow, RUSSIA.- Volume II. - Р. 899-903.
37. Плевков В.С., Мальганов А.И., Болдышев А.М. Совершенствование методов расчета и эффективных приемов усиления строительных конструкций // Вестник Томского государственного архитектуроно-строительного университета. – 1999.- № 1.- С. 222-232.
38. Кумпяк О.Г., Плевков В.С., Копаница Д.Г., Балдин И.В. Некоторые вопросы динамики железобетона // Вестник Томского государственного архитектурно-строительного университета. – 2000.- № 1.- С. 124-136.
39. Плевков В.С., Балдин И.В. Оценка прочности и трещиностойкости железобетонных плит с проемами и опертых по контуру при действии статических и кратковременных динамических нагрузок // Бетон на рубеже третьего тысячелетия. Материалы 1-ой Всероссийской конференции по проблемам бетона и железобетона, 9-14 сентября 2001 г., Москва: В 3 кн. – М.: Ассоциация «Железобетон», 2001. – Кн. 2: Секционные доклады: Секции 1-11. – С. 635 – 639.
40. Плевков В.С. Прочность и трещиностойкость эксплуатируемых железобетонных конструкций при статическом и кратковременном динамическом нагружении//Архитектура и строительство. Наука, образование, технологии, рынок: Тезисы докладов научно-технической конференции. Секция «Проблемы развития теории сооружений и совершенствования строительных конструкций». 11-12 сентября 2002 г., г. Томск. – Томск: Изд-во Том. гос.арх.-строит. ун-та, 2002.- С. 6-7.

Патенты и авторское свидетельство:

41. Мальганов А.И., Плевков В.С., Полищук А.И. Способ реконструкции промышленного здания путем разрежения колонн. А.с. № 1717770 от 23.03.1990. Бюл. № 9,1992.
42. Мальганов А.И., Плевков В.С., Полищук А.И. Способ реконструкции промышленного здания. Патент № 2002014. Опубл. в БИ. 1993.- № 1.
43. Плевков В.С., Полищук А.И., Мальганов А.И. Способ усиления стаканной части фундамента под колонну. Патент № 1787185. Опубл. в БИ 1993.- № 1.
44. Плевков В.С., Полищук А.И., Мальганов А.И. Способ усиления фундамента от увеличения эксплуатационных моментных нагрузок одного знака. Патент № 2053329. Опубл. в БИ 1996.- № 3.

_____________________________________________________________________

Подписано к печати 12.03.2003. Ризограф.

Формат 60 х 90/16. Бумага офсет.

Отпечатано с оригинал-макета в ООП ТГАСУ

Тираж 100 экз. Заказ 109.

634003, г. Томск. ул. Партизанская,15.