Разработка расчетных моделей и оптимизация ядер жесткости уголкового профиля связевых железобетонных каркасов
На правах рукописи
ЧАПАЕВА СВЕТЛАНА ГЕННАДЬЕВНА
РАЗРАБОТКА РАСЧЕТНЫХ МОДЕЛЕЙ
И ОПТИМИЗАЦИЯ ЯДЕР ЖЕСТКОСТИ
УГОЛКОВОГО ПРОФИЛЯ
СВЯЗЕВЫХ ЖЕЛЕЗОБЕТОННЫХ КАРКАСОВ
05.23.17 – строительная механика;
05.23.01 – строительные конструкции, здания и сооружения
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата технических наук
Томск – 2008
Работа выполнена в государственном образовательном учреждении высшего профессионального образования «Новосибирский государственный архитектурно-строительный университет» (Сибстрин)
Научный руководитель доктор технических наук, профессор
Гребенюк Григорий Иванович
Научный консультант доктор технических наук, профессор
Пантелеев Николай Николаевич
Официальные оппоненты: доктор технических наук, профессор
Люкшин Борис Александрович
кандидат технических наук, доцент
Балдин Игорь Владимирович
Ведущая организация ГОУ ВПО «Сибирский государственный университет путей сообщения»
университет (СПбГУ)
Защита состоится 17 октября 2008 г. в 1400 часов на заседании диссертационного совета Д 212.265.01 в Томском государственном архитектурно-строительном университете по адресу: 634003, Томск, Соляная пл., 2, корп. 5, ауд. 307.
С диссертацией можно ознакомиться в библиотеке Томского
государственного архитектурно-строительного университета.
Автореферат разослан 16 сентября 2008 г.
Ученый секретарь
диссертационного совета Копаница Н.О.
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность работы. В последние годы в нашей стране и за рубежом возводится большое число многоэтажных зданий с железобетонным каркасом. При высоте зданий выше 30 метров для обеспечения их пространственной жесткости зачастую уже не достаточно перекрестной системы плоских диафрагм. Решением данной проблемы является объединение плоских диафрагм в пространственные ядра жесткости. Применение ядер жесткости для зданий со сложной в плане структурой затруднено недостаточной разработкой методик их расчета. Актуальными являются также не решенные пока вопросы оптимизации конфигурации, армирования и расстановки ядер в плане здания.
Работа выполнялась по программе научных исследований в области разработки новых конструктивных решений зданий и сооружений Сибирского регионального отделения РААСН и в рамках Всероссийской программы «Архитектура и строительство».
Объект исследования – связевые каркасы многоэтажных сложных в плане зданий.
Предмет исследования – ядра жесткости уголкового профиля высотных связевых сложных в плане железобетонных каркасов.
Целью работы является - развитие методики расчета и оптимизации ядер жесткости связевых железобетонных каркасов на случай многоэтажных каркасов со сложной в плане структурой; разработка и программная реализация алгоритма расчета и оптимизации уголковых ядер жесткости при произвольном направление ветра.
Для достижения поставленной цели были определены следующие задачи:
- разработать методики расчета и подбора необходимой арматуры монолитных ядер жесткости открытого уголкового профиля на регулярной сетке колонн при произвольном направлении ветра;
- выполнить постановку задачи оптимизации: выбрать критерии, метод оптимизации, сформировать целевые функции и основные ограничения;
- разработать принципы формирования начальной конфигурации и расстановки ядер жесткости в плане здания;
- разработать алгоритм и программный модуль оптимизации монолитных ядер жесткости;
- рассмотреть пример оптимизации ядер жесткости открытого уголкового профиля;
- выполнить анализ эффективности разработанных методик, алгоритмов и программ.
Научная новизна работы заключается в следующем:
1. Разработке методик расчета ядер жесткости уголкового профиля высотных сложных в плане связевых железобетонных каркасов при произвольном направлении ветра;
2. Оптимизации объемно-планировочного решения с выбором наиболее оптимального расположения ядер жесткости в плане здания;
3. Разработке приближенной и точной методик расчета ядер жесткости при их продольно-поперечном изгибе;
4. Разработке двухэтапного алгоритма оптимизации ядер жесткости, включая вопросы формирования целевых и ограничительных функций.
Личный вклад автора состоит:
- в разработке методики расчет ядер жесткости уголкового профиля при произвольном направлении ветра;
- в решении вопросов формирования целевых и ограничительных функций на этапах оптимизации ядер жесткости;
- в разработки программ расчета и оптимизации ядер жесткости на языке программирования FORTRAN;
- в проведении численных экспериментов;
- в анализе результатов оптимизации ядер жесткости с использованием различных методик расчета.
На защиту выносятся:
- методика расчета монолитных ядер жесткости уголкового профиля при произвольном направлении ветра;
- принципы формирования начальной конфигурации и расстановки ядер жесткости в плане здания;
- методика определения необходимого армирования ядер жесткости в процессе их оптимизации при произвольном направлении ветра;
- двухэтапный алгоритм и программный модуль оптимизации монолитных ядер жесткости;
- результаты расчета и оптимизации ядер жесткости открытого уголкового профиля 20 этажного здания.
Достоверность результатов и выводов по работе обеспечена корректной постановкой задачи исследования, использованием отработанных классических методов теоретических исследований, а также соответствием результатов, полученных как на основе разработанных методик расчета, так и с использованием известных расчетных программных комплексов (SCAD, Мономах).
Практическая значимость исследований состоит:
- разработаны методики определения перемещений и усилий в сечениях ядер жесткости;
- разработана методика расчета ядер жесткости по прочности при произвольном направлении ветрового напора;
- разработаны принципы формирования количества, начальной конфигурации и ориентации ядер жесткости в плане здания;
- разработан двухэтапный алгоритм оптимизации расположения и армирования ядер жесткости.
Реализация работы. Разработанные методики, алгоритм и расчетная программа приняты к использованию Федеральным государственным унитарным предприятием «Сибирский промстройпроект» г. Новокузнецк. Результаты исследований внедрены в учебный процесс по дисциплинам «Железобетонные конструкции», «Конструкции городских зданий и сооружений», а также используются в курсовом и дипломном проектировании при обучении студентов ГОУ ВПО «Сибирского государственного индустриального университета» по специальности 270102 – «Промышленное и гражданское строительство» и другим смежным специальностям.
Апробация работы:
Основные положения диссертационной работы и результаты исследований представлены на:
- 61-й научно-технической конференции НГАСУ (Сибстрин), г. Новосибирск, 2004 г.
- Всероссийской научной конференции студентов, аспирантов и молодых ученых «Наука и молодежь: проблемы, поиски, решения», СибГИУ, г. Новокузнецк, 2005 г.
- V Всероссийском семинаре «Проблемы оптимального проектирования сооружений», г. Новосибирск, 2005 г.
- 63-й научно-технической конференции НГАСУ (Сибстрин), г. Новосибирск, 2006 г.
- Всероссийской научно-технической конференции «Роль механики в создании эффективных материалов, конструкций и машин XXI века», СибАДИ, г. Омск, 2006 г.
- 64-й научно-технической конференции НГАСУ (Сибстрин), г. Новосибирск, 2007 г.
- I Всероссийской конференции «Проблемы оптимального проектирования сооружений», г. Новосибирск, 2008 г.
Публикации
Основное содержание диссертационной работы опубликовано в 8 работах, включая одну научную статью в журналах, входящих в перечень ВАК.
Структура и объем работы
Диссертация состоит из введения, четырех глав, выводов, списка литературы. Список литературы содержит 106 наименований.
Автор выражает благодарность руководителям и сотрудникам кафедр строительной механики и железобетонных конструкций Новосибирского государственного архитектурно-строительного университета; к.т.н. Е.В. Янькову; руководителю и сотрудникам кафедры инженерных конструкций Сибирского государственного индустриального университета; Федеральному государственному унитарному предприятию «Сибирский промстройпроект»; Сибирскому государственному университету путей сообщения за оказанное содействие при подготовке материалов данной диссертационной работы.
ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ
Во введении обосновывается актуальность темы диссертации, сформулированы цель и задачи исследования, научная новизна и практическая значимость полученных результатов, показана ее апробация, приведены сведения о публикациях, приведена структура диссертации и краткое содержание по главам.
В первой главе « Анализ существующих конструктивных решений, методов расчета и оптимизации каркасов железобетонных многоэтажных зданий» дана классификация конструктивных систем многоэтажных зданий, описаны существующие конструктивные схемы зданий, приведен их анализ, рассмотрены варианты конструктивных решений диафрагм и ядер жесткости, обоснован выбор направлений для дальнейших исследований высотных зданий связевой конструктивной системы с монолитными ядрами жесткости.
В работе рассмотрены труды ученых, связанные с разработкой методов расчета связевых железобетонных каркасов, с расчетами монолитных и сборных диафрагм и ядер жесткости. Существенный вклад в решение данной проблемы внесли Александров А.В., Гребенюк Г.И., Додонов М.И., Дроздов П.Ф., Дыховичный Ю.А., Кузьминер Н.Я., Лишак В.И., Лапушнер И.Л., Мануйлов Г.Ф, Мелешонков Е.И., Пантелеев Н.Н., Паньшин Л.Л., Петров В.П., Подольский Д.М., Поляков С.В., Рубаненко Б.Р., Саруханян Р.Л., Себекин И.М., Ханжи В.В., Холевицкий А., Яньков Е.В. и другие.
В результате анализа работ перечисленных авторов был сделан вывод о недостаточной на текущий момент разработке методик расчета ядер жесткости высотных сложных в плане железобетонных зданий.
Проведен также анализ работ по оптимизации топологических параметров диафрагм и ядер жесткости, выполненных: Ханжи В.В., Дыховичным Ю.А., Александровым А.В., Шапошниковым Н.Н., Мануйловым Г.А., Кузьминером Н.Я., Лапушнером И.Л. и другими.
В работах этих авторов есть ряд рекомендаций по оптимальному размещению систем диафрагм в плане здания, также даны рекомендации по минимально допустимым размерам диафрагм в плане здания. Разработкой методик и алгоритмов оптимизации армирования диафрагм и ядер жесткости никто из перечисленных авторов не занимался.
Приведен анализ работ ряда ученых по развитию методов и алгоритмов оптимального проектирования применительно к железобетонным конструкциям.
Во второй главе «Разработка методики расчета ядер жесткости уголкового профиля» приведены упрощающие положения, на которых базируются разработанные методики расчета. Изложены методики определения геометрических и жесткостных характеристики ядер жесткости уголкового профиля, методика определения ветровой нагрузки на ядра здания с учетом изгибно-крутильных жесткостей ядер, методика определения вертикальной нагрузки.
Приведена «приближенная» методика определения перемещений и усилий в сечениях уголковых ядер жесткости.
Приближенная методика основана на использовании приближенного решения задачи продольно-поперечного изгиба ядра жесткости. Для определения «эйлерового» критического значения параметра сжимающей нагрузки использован метод Рэлея-Ритца. Расчетная схема 
- того ядра при продольном изгибе и заданная однопараметрическая форма потери устойчивости приведены на рисунке 1.
Рисунок 1 - а) Расчетная схема 
- того ядра, б) Однопараметрическая форма отклонения
Для каждой из главных плоскостей ядра методика определения критического значения параметра нагрузки одинакова. В тексте диссертации приводится методика для плоскости 
.
Энергия упругой деформации ядра 
(без учета сдвигов):
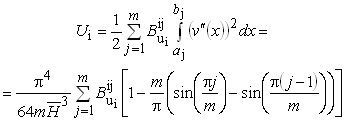, (1)
где 
, 
- координаты 
верха и низа 
- того этажа соответственно; 
- высота этажа; 
- количество этажей; 
- приведенная жесткость 
-того ядра на 
-том этаже относительно оси 
.
Работа внешних сил определяется согласно выражению:
, (2)
где 
- вертикальная нагрузка от мансардного этажа, 
- вертикальная нагрузка от типового этажа.
Приравнивая 
и 
получим выражение для критической силы:
(3)
Коэффициент увеличения эксцентриситета (общий для всех этажей ядра):
(4)
Эксцентриситет продольной силы 
на 
-том этаже 
-того ядра:
, (5)
где 
- изгибающий момент от ветровой нагрузки, действующий в нижнем сечении 
-того этажа 
-того ядра, при 
.
Полный эксцентриситет на 
-том этаже 
-того ядра:
, (6)
где 
- случайный эксцентриситет.
Изгибающие моменты, соответствующие главным осям ядра, действующие на i - тое ядро на этаже j, учитывающие добавку при расчете по деформированной схеме:
 ;  | (7) |
Далее приведена «точная» методика определения перемещений и нагрузок в сечениях ядер, которая основывается на решении дифференциального уравнения прогибов. Расчетная схема 
-того ядра представлена на рисунке 2.
Так же, как в случае рассмотрения «приближенной» методики, расчеты для двух главных плоскостей ядра 
и 
аналогичны.
Рисунок 2 - Расчетная схема ядра 
В тексте приведена методика расчета для плоскости 
.
На рисунке 2: 
, 
, 
, …, 
- приведенная к узловой ветровая нагрузка, приходящаяся на 
-тое ядро в направлении 
. Нумерация участков на рисунке 2 представлена в овалах.
На участке 
в связи с отсутствием распределенной поперечной нагрузки дифференциальное уравнение для
прогибов имеет вид:
  , | (8) |
где 
, 
.
Общее решение уравнения (8):
 | (9) |
где 
, 
, 
, 
- постоянные интегрирования на участке 
.
С учетом (9), получим выражения для углов поворота и усилий:
 | (10) |
Используя граничные условия, условия стыковки участков, выражения (10), а также, выполнив преобразование 
, получаем систему уравнений, которую можно записать в каноническом виде:
 . | (11) |
Далее в тексте диссертации приведена методика подбора необходимого армирования ядер жесткости на этажах. Для этого определяется полный изгибающий момент, действующий на сечение 
-того ядра на 
-том этаже по формулам «приближенного» или «точного» метода:
(12)
и угол наклона плоскости изгибающей пары к оси 
:
, (13)
где 
- угол наклона главной оси 
-того ядра 
к центральной оси ядра 
.
Согласно СНиП проверка армирования должна производиться из условия:
 | (14) |
где 
расстояние продольной силы 
до оси, параллельной прямой, ограничивающей сжатую зону, и проходящей через центр тяжести сечения растянутого стержня, наиболее удаленного от указанной прямой (Рисунок 3 - Линия 1); 
- расчетное сопротивление бетона сжатию, 
статический момент площади сечения сжатой зоны бетона относительно этой оси; 
- количество условных арматурных стержней в ядре жесткости, 
статический момент площади сечения 
– того стержня продольной арматуры относительно этой оси, 
- расчетное сопротивление арматуры (для сжатого стержня – сжатию, для растянутого – растяжению).
Высота сжатой зоны бетона 
(Рисунок 3) определяется из решения уравнения:
 | (15) |
где 
- площадь бетонной части сечения ядра жесткости; 
- площадь 
– того стержня продольной арматуры; 
; 
; 
- характеристика сжатой зоны бетона; 
относительная высота сжатой зоны бетона; 
расстояние от оси проходящей через центр тяжести сечения рассматриваемого 
- того стержня и параллельной прямой, ограничивающей сжатую зону, до наиболее удаленной точки сжатой зоны сечения.
Для определения положения границы сжатой зоны при косом внецентренном сжатии, кроме использования формул (14) и (15) требуется соблюдение дополнительного условия (третьего условия): точка приложения внешней продольной силы (Рисунок 3. Точка 1), точка, через которую проходит равнодействующая усилий в сжатом бетоне и арматуре (Рисунок 3. Точка 2) и точка, через которую проходит равнодействующая усилий в растянутой арматуре (Рисунок 3. Точка 3) должны лежать на одной прямой.
Рисунок 3 - К проверке сечения по прочности
Методика подбора необходимого армирования ядер жесткости на этажах реализуется в виде следующего алгоритма. Для ядра 
на этаже 
:
1. Определяются продольная сила 
, равная весу вышележащих этажей на грузовой площади ядра и изгибающие моменты в нижнем сечении ядра на этаже.
2. На шаге 
поискового метода задаемся начальным
значением армирования в колонне 
.
3. Определяются геометрические и жесткостные характеристики сечения ядра на этаже.
4. Для заданного армирования 
определяется положение нейтральной оси. Для этого сначала определяется угол наклона нейтральной оси без учета особенностей работы железобетона по методикам косого изгиба из сопротивления материалов 
относительно оси 
. Далее задается угол наклона условной нейтральной оси ядра к оси 
- 
. Величину 
изменяем в пределах от 
до 
с заданным малым шагом 
. Кроме того, задается величина 
, которая характеризует положение нейтральной оси и изменяется с заданным малым шагом 
.
Варьируя угол наклона 
и параметр положения нейтральной оси 
, определяем место положения условной нейтральной оси, которое удовлетворяет третьему условию с заданной допустимой погрешностью.
Если, варьируя угол наклона 
и параметр положения 
, не удалось найти такое положение нейтральной оси, которое с допустимой погрешностью удовлетворяет третьему условию, то принятого на шаге армирования 
недостаточно. 
изменяется на заданное малое число 
и производится возврат к пункту 3 данного алгоритма.
Если были найдены такие значения 
и 
, при которых третье условие удовлетворяется, то производится проверка условий (14) и (15). В случае, если хотя бы одно из условий не удовлетворяется, то принятого на шаге армирования 
недостаточно 
увеличивается на заданное малое число 
и производится возврат к пункту 3 данного алгоритма. Если же условия удовлетворяются, то принятой на шаге арматуры 
достаточно.
В третьей главе «Формирование и решение задачи оптимизации ядер жесткости» была выполнена постановка задачи оптимизации, выделены три группы варьируемых параметров. К первой группе отнесены не формализуемые параметры конфигурации ядер и дискретные параметры, определяющие топологию ядер: 
– количество ядер на здание; 
, 
, 
- количества простенков в ядрах (в направлении осей 
и 
соответственно). Во вторую группу объединены параметры, определяющие расположение ядер жесткости в плане здания. В третьей, наиболее многочисленной группе объединены параметры армирования ядер жесткости на этажах, которые приняты в виде коэффициентов армирования колонны ядра 
в пределах этажей: 
, параметр армирования 
увязан с площадью арматуры колонны ядра, т.е. 
, 
– площадь бетонного сечения колонны.
Топологические параметры 
, 
, 
являются целочисленными переменными верхнего уровня. Задачу определения их оптимальных значений можно ставить как комбинаторную, с полным перебором всех возможных комбинаций этих параметров на заданной сетке колонн. Однако такая постановка связана как с повышенной трудоемкостью решения, так и с определенным произволом при выборе конфигурации и расположения ядер, что может противоречить сложившимся общим архитектурно-планировочным решениям. Поэтому в основу выбора параметров верхних уровней положен сравнительный анализ геометрических характеристик плана здания и сечений ядер. В данном исследовании топологические параметры, а также параметры, определяющие размеры колонн и стенок, в число варьируемых параметров не входят.
При выборе количества подобластей, конфигурации и ориентации ядра в пределах подобласти использованы следующие положения:
- ядра жесткости должны располагаться равномерно в плане здания;
- конфигурация и ориентация ядер должны быть такими, чтобы оси ядер жесткости, относительно которых их жесткость максимальна примерно совпадали с осью здания, относительно которой жесткость здания минимальна
, 
.
Согласно принятой постановке задачи оптимизация ядер производится в два этапа. На первом этапе армирование ядер считается фиксированными. В качестве варьируемых параметров приняты координаты центров тяжести ядер в подобластях плана здания 
, 
. Вектор варьируемых параметров имеет вид:
(16)
где 
, 
,..., 
, 
.
На этом этапе определяется наилучшее расположение ядер жесткости в подобластях плана с позиции минимизации возможного эффекта закручивания здания. Целевая функция на первом этапе принята в виде:
 | (17) |
где 
, 
– координаты центра жесткости здания в условных главных осях здания:
 ,  , | (18) |
где 
, 
- усредненные по этажам изгибные жесткости 
- того ядра относительно осей 
, 
, параллельных главным осям здания и проходящим через центр 
- того ядра; 
, 
– координаты центра 
-той подобласти плана здания.
Пределы изменения переменных зависят от размера подобласти и направления условных главных осей здания.
Решение задачи оптимизации ядер жесткости на этапе 1 заключается в поиске минимума функции 
при учете параметрических ограничений.
На втором этапе в качестве варьируемых параметров принимаются коэффициенты армирования колонн ядер на этажах 
, где 
, 
- число этажей здания.
Вектор варьируемых параметров на данном этапе имеет вид:
, (19)
где: 
, 
; 
, (20)
где 
- площадь сечения арматуры колонны 
-того ядра на этаже 
.
В качестве целевой функции принят общий расход арматуры на ядра здания:
 | (21) |
где 
– коэффициент, увязывающий армирование колонн и стенок ядер на этажах; 
– высота 
- того этажа здания.
На данном этапе необходимо учитывать ограничения по прочности, которые учитываются косвенно в форме ограничений, относящихся к необходимому армированию 
:
 ,  ;  , | (22) |
а также ограничение по жесткости каркаса, которое накладывается на максимальное из перемещений верха ядер. В ограничениях (22) величины 
- функции составляющих вектора 
, которые могут быть аппроксимированы каким-либо образом, либо их значения могут находиться согласно выше изложенной методике на каждом шаге поиска. При определении перемещений в «приближенной» методике использовался метод Мора. Ограничение принимает вид:
 | (23) |
Ограничение по жесткости для «точного» решения имеет вид:
 | (24) |
где 
, 
- перемещения в главных осях ядра 
, определенные по формуле (9) для первого участка при 
с соответствующими значениями постоянных интегрирования.
Решение задачи оптимизации ядер жесткости на втором этапе заключается в поиске минимума функции 
при учете ограничений по прочности и жесткости. Задача на данном этапе сводится к безусловно-экстремальной и решается методом подвижного внешнего штрафа.
В четвертой главе « Решение прикладных задач оптимизации уголковых ядер жесткости» даны результаты численного эксперимента, полученные с использованием «приближенной» и «точной» методик расчета.
В качестве здания для расчета выбрано здание, изображенное на рисунке 4. Здание имеет связевую структуру. Размеры здания в плане 84 м 78 м. Высота этажей одинакова и составляет 3 м. Размер колонн принят согласно действующим строительным нормам 0.4 м 0.4 м, толщина стенки ядра принята одинаковой в двух координатных направлениях 0.2 м.
Рисунок 4 - Схема связевого каркаса 20-ти этажного здания
Вся область плана здания была разделена на 6 подобластей (Рисунок 5). Для обеспечения пространственной жесткости каркаса были выбраны шесть ядер (три симметричных трех колонных и три – несимметричных четырех колонных). Начальное положение ядер показано на рисунке 5. Начальный допустимый проект находился при заданном начальном положении ядер и в предположении равномерного армирования ядер в пределах этажей.
После оптимизации положения ядер жесткости в начальном проекте (Рисунок 5) ядра жесткости приняли положение, показанное на рисунке 6.
На рисунке 7 представлена сходимость процесса оптимизации на первом этапе оптимизации ядер жесткости.
На рисунке 8 представлена сходимость процесса оптимизации на втором этапе оптимизации ядер жесткости.
Рисунок 5 - Разбивка плана здания на подобласти. Начальное расположение ядер жесткости
Значения целевой функции после второго этапа оптимизации и наиболее опасные направления ветрового давления, полученные при начальной и при оптимальной ориентации ядер жесткости, найденные с использованием «приближенной» и «точной» методик расчета ядер представлены в таблице 1.
Оптимальная ориентация и положение ядер жесткости представлены на рисунке 9.
Рисунок 6 - Оптимальное положение ядер жесткости при их начальной ориентации
Рисунок 7 - Сходимость процесса оптимизации конструкций на первом этапе
Рисунок 8. Сходимость процесса оптимизации конструкций на втором этапе
Рисунок 9 - Оптимальное положение и ориентация ядер жесткости
Таблица 1.
Значения целевой функции
Значение целевой функции  ,  | ||||
| Начальный проект | «Приближенная» методика | «Точная» методика | ||
| Начальное положение ядер | Оптимальное положение ядер | Начальное положение ядер | Оптимальное положение ядер | |
| 13,824 | 8,0429 | 6,7582 | 7,4006 | 6,1310 |
Направление наиболее опасного ветрового давления (относительно оси  ), град | ||||
 ,  |  ,  |  |  ,  |  |
ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ
- Разработана приближенная методика расчета монолитных ядер жесткости уголкового профиля при произвольном направлении ветра с использованием метода Рэлея-Ритца для определения «эйлерового» критического параметра сжимающей нагрузки;
- Разработана точная методика расчета монолитных ядер жесткости уголкового профиля при произвольном направлении ветра на основе решения системы дифференциальных уравнений продольно-поперечного изгиба на участках;
- Разработанные методики расчета, при их достаточной точности существенно снижают трудоемкость расчетов ядер жесткости, по сравнению с расчетами на основе существующих программных комплексов, что особо важно при реализации алгоритмов оптимизации;
- Разработаны принципы формирования начальной конфигурации и расстановки ядер жесткости в плане здания;
- Разработана методика определения необходимого армирования ядер жесткости в процессе их оптимизации при произвольном направлении ветра;
- Разработан двухэтапный алгоритм оптимизации положения и армирования монолитных ядер жесткости;
- На основе алгоритма оптимизации монолитных ядер жесткости разработан программный модуль на языке программирования FORTRAN;
- На примере 20 этажного здания выполнен расчет и оптимизация ядер жесткости открытого уголкового профиля с использованием приближенной и точной методик расчета ядер жесткости. Получены оптимальные ориентация и положения ядер жесткости в плане здания, найдено оптимальное армирование ядер;
- Результаты расчетов свидетельствуют об эффективности разработанного двухэтапного алгоритма оптимизации. Экономия арматуры в оптимальном проекте по положению, ориентации и армированию ядер достигает 55% по сравнению с начальным допустимым проектом и 17,1% по сравнению с проектом, оптимальным по армированию, но не оптимальным по ориентации ядер.
Основные положения диссертации изложены в следующих публикациях:
- Гребенюк, Г.И. Расчет и оптимизация уголковых ядер жесткости связевых железобетонных каркасов высотных, нерегулярных в плане зданий при произвольном направлении ветра / Г.И. Гребенюк, Н.Н. Пантелеев, С.Г. Чапаева // Известия вузов. Строительство. – Новосибирск, - 2007 г. №12. - С. 4-10.
- Гребенюк, Г.И. Армирование ядер жесткости связевых железобетонных каркасов при произвольном направлении ветра / Г.И. Гребенюк, С.Г. Чапаева // Труды Всероссийской научно-технической конференции «Роль механики в создании эффективных материалов, конструкций и машин XXI века». –Омск: СибАДИ, 2006. - С.112-115.
- Гребенюк, Г.И. Расчет и оптимизация ядер жесткости связевых железобетонных каркасов зданий при наиболее опасном направлении ветра /Г.И. Гребенюк, Н.Н. Пантелеев, Е.В. Яньков, С.Г. Чапаева // Сборник докладов V-го Всероссийского семинара «Проблемы оптимального проектирования сооружений». - Новосибирск, 2005. - С.131-142.
- Гребенюк, Г.И. Оптимизация армирования и положения ядер жесткости железобетонных каркасов многоэтажных зданий/Г.И. Гребенюк, Н.Н. Пантелеев, Е.В. Яньков, С.Г. Чапаева // Тезисы докладов 61-й научно-технической конференции. - Новосибирск: НГАСУ, - 2004. - С.5-6.
- Гребенюк, Г.И. Разработка расчетной модели и оптимизация уголковых ядер жесткости связевых железобетонных каркасов при косом продольно-поперечном изгибе / Г.И. Гребенюк, Н.Н. Пантелеев, С.Г. Чапаева // Тезисы докладов 63-й научно-технической конференции. – Новосибирск: НГАСУ, - 2006. - С.7.
- Гребенюк, Г.И. Определение оптимальных параметров уголковых ядер жесткости связевого железобетонного каркаса при произвольном направлении ветра / Г.И. Гребенюк, Н.Н. Пантелеев, С.Г. Чапаева // Тезисы докладов 64-й научно технической конференции. – Новосибирск: НГАСУ, - 2007. - С. 5.
- Гребенюк, Г.И. Алгоритм подбора арматуры в уголковых ядрах жесткости железобетонных нерегулярных в плане зданий / Г.И. Гребенюк, С.Г. Чапаева // Труды всероссийской научной конференции студентов, аспирантов и молодых ученых «Наука и молодежь: проблемы, поиски, решения». – Новокузнецк: СибГИУ, - 2005. – С.179-182.
- Гребенюк, Г.И. Методика нелинейного расчета уголкового ядра жесткости при косом продольно-поперечном изгибе/ Г.И. Гребенюк, Н.Н. Пантелеев, С.Г. Чапаева // Доклады I Всероссийской конференции «Проблемы оптимального проектирования сооружений». – Новосибирск, - 2008. – С.136-146.
Чапаева Светлана Геннадьевна
РАЗРАБОТКА РАСЧЕТНЫХ МОДЕЛЕЙ
И ОПТИМИЗАЦИЯ ЯДЕР ЖЕСТКОСТИ
УГОЛКОВОГО ПРОФИЛЯ
СВЯЗЕВЫХ ЖЕЛЕЗОБЕТОННЫХ КАРКАСОВ
АВТОРЕФЕРАТ
Изд. Лиц. №021253 от 31.10.97 г.
Подписано в печать 10.09.08 г. Формат 6084 1/16
Бумага офсет. Гарнитура Таймс. Усл.-печ. л. 1,1. Уч.-изд. л. 1,0.
Тираж 100 экз. Заказ №___
Изд-во ГОУ ВПО «ТГАСУ», 634003, г. Томск, пл. Соляная, 2.
Отпечатано с оригинал-макета автора в ООП ГОУ ВПО «ТГАСУ».
634, г. Томск, ул. Партизанская, 15.
