Исследование силового воздействия оползневых массивов на удерживающие конструкции симплекс-методом
На правах рукописи
КАН ТХЭ САН
ИССЛЕДОВАНИЕ СИЛОВОГО ВОЗДЕЙСТВИЯ
ОПОЛЗНЕВЫХ МАССИВОВ НА УДЕРЖИВАЮЩИЕ
КОНСТРУКЦИИ СИМПЛЕКС-МЕТОДОМ
Специальность 05.23.02
«Основания и фундаменты, подземные сооружения»
Автореферат диссертации на соискание ученой степени
кандидата технических наук
Томск, 2005
Работа выполнена в Сибирском государственном университете путей сообщения
| Научный руководитель: кандидат технических наук, доцент | Караулов Александр Михайлович |
Официальные оппоненты:
| доктор технических наук, профессор | Полищук Анатолий Иванович |
| кандидат технических наук, доцент | Нуждин Леонид Викторович |
Ведущая организация:
ЗАО «Сибирский научно-исследовательский институт транспортного строительства» (СИБЦНИИТС), г. Новосибирск
Защита состоится 27 апреля 2005 года в 14 часов 00 мин на заседании диссертационного совета Д 212.265.02 при Томском государственном архитектурно-строительном университете по адресу: Российская Федерация, 634003, Томск, пл. Соляная, 2.
С диссертацией можно ознакомиться в библиотеке Томского государственного архитектурно-строительного университета
Автореферат разослан 26 марта 2005 г.
| Ученый секретарь диссертационного совета |  | Недавний О.И. |
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность работы. Оползни широко распространены как на территории РФ, так и на территории КНДР. Оползневые явления наносят большой вред народному хозяйству, препятствуя освоению естественных склонов и нормальной эксплуатации инженерных сооружений. Борьба с оползнями, предупреждение оползневых процессов представляют, таким образом, важную народно-хозяйственную проблему.
Одним из эффективных способов предупреждения обрушения откосов и склонов является возведение противооползневых удерживающих сооружений. Для проектирования надежных противооползневых конструкций необходимо, прежде всего, установить инженерно-геологические условия склона и причины развития оползневых деформаций. Располагая качественной базой исходных данных, следует решить другую, не менее важную проблему, а именно определить интенсивность силового воздействия сползающих масс грунта на проектируемую удерживающую конструкцию.
Вследствие сложности граничных условий решение задачи определения оползневого давления не удается найти строгими методами теории предельного равновесия грунтов. Широкие возможности для описания склоновых процессов открывает конечноэлементный анализ упругопластического деформирования грунтовых массивов. Это направление разрабатывается в научных организациях, имеющих необходимое оборудование и методики определения параметров упругопластических моделей грунта.
В практической работе проектных организаций для определения силового воздействия оползневых масс на подпорные сооружения, как правило, используются приближенные методы расчета, основанные на расчетной схеме «метода отсеков». Многовариантность «методов отсеков» обусловлена статической неопределимостью задачи и введением в расчет для ее раскрытия дополнительных гипотез различного характера относительно направления и положения сил взаимодействия отсеков с окружающим грунтом. При этом отсутствует метод теоретического анализа возможного диапазона изменения этих сил и, соответственно, диапазона изменения оползневого давления.
Совершенствование методов определения силового воздействия оползневых масс на удерживающие сооружения является важной и актуальной проблемой, решение которой позволит повысить надежность и эффективность противооползневых конструкций.
Цель работы заключалась в разработке методики определения максимально возможной по условиям статического равновесия и прочности грунта интенсивности силового воздействия оползневого массива на удерживающие конструкции и разработке на этой основе принципов их расчета.
Задачи исследований. Для достижения поставленной цели были сформулированы следующие задачи:
- Определить возможный по условиям статического равновесия и прочности грунтов диапазон изменения системы сил взаимодействия отсеков с окружающим грунтом в рамках расчетной схемы «метода отсеков».
- Разработать методику определения максимальных величин составляющих оползневого давления в рамках расчетной схемы «метода отсеков» на основе анализа всего диапазона изменения системы сил взаимодействия, допустимого по условиям статического равновесия и прочности грунтов.
- Исследовать влияние степени дискретизации расчетной схемы «метода отсеков», формы линии скольжения и положения сил взаимодействия отсеков с окружающим грунтом на расчетную величину оползневого давления.
- Разработать алгоритм и программу расчета составляющих силового воздействия оползневого массива на удерживающие сооружения симплекс-методом.
- Разработать принципы расчета противооползневых удерживающих конструкций на основе экстремального анализа параметров силового воздействия на них оползневых масс.
Научная новизна работы заключается:
- в постановке и решении задачи определения предельного давления грунта на подпорные стенки как задачи линейного программирования;
- в разработанных алгоритме и программе расчета силового воздействия оползневых массивов на удерживающие конструкции;
- в разработанных принципах расчета противооползневых удерживающих конструкций с помощью симплекс-метода.
Практическая ценность работы заключается в возможности использования полученных результатов при проектировании противооползневых удерживающих конструкций. Реализация такой возможности обеспечивается следующими разработками:
- Разработана методика составления исходной симплекс-таблицы, алгоритм и программа расчета симплекс-методом предельного давления на подпорную стенку в рамках расчетной схемы «метода отсеков». Даны рекомендации по использованию результатов решения. Вычислительная работа может выполняться как по разработанной программе, так и с помощью стандартных программ, реализующих симплекс-метод.
- Разработаны принципы расчета подпорной стенки по предельным состояниям в соответствии с требованиями нормативных документов и на основе экстремального анализа составляющих оползневого давления, выполняемого симплекс-методом.
- Разработаны принципы расчета противооползневых свайных рядов или промежуточных стенок на основе экстремального анализа составляющих оползневого давления, выполняемого симплекс-методом.
Методы исследований. Для решения поставленных задач использовалась расчетная схема «метода отсеков». Определение силового воздействия оползневого массива на удерживающие конструкции осуществлялось симплекс-методом линейного программирования. В разработанной методике расчета оползневого давления обеспечивалось выполнение условий статического равновесия и прочности грунтов. При этом находилось наиболее невыгодное распределение сил взаимодействия отсеков с окружающим грунтом, которому соответствовала максимальная интенсивность силового воздействия оползневого массива на подпорное сооружение.
Апробация работы. Основные результаты исследований докладывались на 61-й и 62-й научно-технических конференциях НГАСУ (г. Новосибирск, 2003, 2004), на научно-технических конференциях СГУПС (г. Новосибирск, 2004), на научно-техническом семинаре СГУПС (г. Новосибирск, 2005).
Публикации. По теме диссертации опубликовано 5 работ.
На защиту выносятся:
- Постановка и решение симплекс-методом задачи о предельном давлении грунта на подпорную стенку в рамках расчетной схемы «метода отсеков» как задачи линейного программирования.
- Результаты анализа составляющих оползневого давления в зависимости от формы линии скольжения и положения сил взаимодействия отсеков с окружающим грунтом, а также результаты сопоставительных расчетов.
- Алгоритм и программа расчета симплекс-методом составляющих оползневого давления.
- Принципы расчета противооползневых сооружений подпорных стенок и промежуточных удерживающих конструкций на основе экстремального анализа оползневого давления.
Объем и структура работы. Диссертация состоит из введения, пяти разделов, выводов, приложений и списка литературы, общий объем составляет 180 страниц, в т.ч. 64 рисунка и 80 таблиц. Список литературы содержит 144 источника.
КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ
В первой главе приводится анализ существующих методов определения оползневого давления на удерживающие конструкции. Оползни сложные геологические процессы, возникающие при нарушении равновесия земляных масс на откосах и склонах. Изучению оползневых процессов посвящены обобщающие труды А.П. Павлова, Ф.П. Саваренского, С.К. Абрамова, Е.П. Емельяновой, Г.С. Золотарева, А.М. Дранникова, Н.Н. Маслова, М.Н. Гольдштейна, Г.М. Шахунянца, Л.К. Гинзбурга, Г.Л. Фисенко, А.М. Демина, Г.И. Тер-Степаняна, В.Е. Ольховатенко, К. Терцаги, Л. Бьеррума, Л. Шукле, Р. Шустера, Р. Кризека, Хван Хо Рела, Вон Ха Ока и многих других. В диссертации рассматривается один тип оползней по характеру движения, а именно оползни скольжения. Этот тип оползней часто встречается как на естественных склонах, так и в приоткосных частях искусственных земляных сооружений. Важнейшим вопросом при проектировании противооползневых сооружений является определение оползневого давления. Эта проблема решалась в работах А.И. Билеуша, А.Я. Будина, Л.К. Гинзбурга, А.Г. Раздольского, В.Э. Даревского, А.М. Романова, М.П. Дубровского, В.П. Дыбы, А.М. Балашова, Ю.К. Зарецкого, Е.П. Смирнова, Н.К. Снитко, Л.Р. Ставницера, П.И. Яковлева, Ли Хен Су, Ро Мен Хо и многих других.
Основой для оценки устойчивости грунтовых массивов и определения предельного давления на подпорные сооружения является теория предельного равновесия, развитие которой отражено в трудах Ш. Кулона, Р. Ренкина, Ф. Кеттера, Л. Прандтля, В.В. Соколовского, С.С. Голушкевича, В.Г. Березанцева, М.В. Малышева, А.С. Строганова, Л.Р. Ставницера, Ю.И. Соловьева, В.Г. Федоровского, Р. Шилда и многих других. Следует отметить, что строгие решения получены только для ряда относительно простых по своим граничным условиям расчетных схем. Построение статических решений для неоднородных оползневых склонов произвольного очертания не представляется возможным.
Все большее применение для описания оползневых процессов находит конечноэлементный анализ упругопластического деформирования, развитию которого посвящены работы Ю.К. Зарецкого, А.К. Бугрова, В.Н. Николаевского, С.Б. Ухова, З.Г. Тер-Мартиросяна, А.Б. Фадеева, В.Г. Федоровского, А.Л. Гольдина, В.Н. Парамонова, М.М. Дубины, Ро Сол Се и многих других. В настоящее время существует целый ряд программных пакетов, например PLAXIS, COSMOS/M, NASTRAN, Геомеханика и других, на основе которых можно выполнять совместный расчет упругопластического деформирования грунтовых массивов и взаимодействующих с ними конструкций. В то же время, остается ряд вопросов, необходимость решения которых диктуется практикой геотехнического строительства. К таким вопросам относятся, например, выбор модели грунта и определение ее параметров, моделирование фазы локальных сдвигов, определение природного напряженного состояния оползневых массивов.
Для практических расчетов устойчивости оползневых склонов и, соответственно, для определения силового воздействия сползающих масс грунта на удерживающие противооползневые конструкции, применяются, как правило, приближенные методы расчета. Особое место среди них занимают решения с использованием расчетной схемы «методов отсеков». Развитию этих методов посвящены труды Н.Н. Маслова, Г.М. Шахунянца, Л.П. Ясюнас, Г. Крея, Р.Р. Чугаева, И.В. Федорова, Н. Янбу, А.Л. Можевитинова, В.Н. Бухарцева, Л.К. Гинзбурга, А. Бишопа, К. Терцаги, В. Феллениуса, Е. Нонвейе, В.И. Хорькова, В.И. Хазина, Я.Х. Хуана, И.М. Васильева, В.И. Грицыка и многие другие.
Построение любого варианта приближенного метода отсеков тем лучше отвечает действительному поведению оползня, чем качественнее решены два вопроса определение очертания поверхности скольжения и определение системы сил взаимодействия отсеков с окружающим грунтом. Теоретически обоснованное очертание линии скольжения находится методами вариационного исчисления. Это направление было развито в трудах Ю.И. Соловьева, М.Н. Гольдштейна, А.Г. Дорфмана, Ю.М. Почтмана, А.Л. Колесниченко, В.Г. Федоровского, И.Л. Дудинцевой, У.Х. Магдеева, М.И. Шевченко, А.Д. Гиргидова, В.Э. Даревского и других. Второй вопрос о системе сил взаимодействия в настоящее время решается введением в расчет ограничений-равенств относительно величины и положения части сил взаимодействия между отсеками для раскрытия статической неопределимости задачи.
Линейное программирование один из современных математических методов, на основе которого могут быть решены многие сложные математические и технические задачи. Применение методов линейного программирования для решения задач механики грунтов впервые было осуществлено Ю.М. Почтманом и А.Л. Колесниченко. Эти исследования были посвящены определению нормальных и касательных напряжений вдоль линии скольжения, которым соответствует минимальное отклонение касательных напряжений от их предельных значений. При этом распределение усилий в обрушаемой области не рассматривалось.
Во второй главе приводится обоснование выбранного направления исследований. В механике грунтов достаточно полно разработан вопрос определения активного и пассивного давления грунта на подпорные стенки. Указанные решения необходимы, но недостаточны для обеспечения проектирования противооползневых удерживающих конструкций. Оползневое давление может значительно превосходить по величине активное давление грунта, являющееся следствием предельного состояния области грунта, непосредственно примыкающей к подпорной стенке.
Существующие методы расчета оползневого давления базируются, как правило, на расчетной схеме «метода отсеков», преимущественно для условий плоской деформации. В этой расчетной схеме неизвестными являются силы взаимодействия отсеков с окружающим грунтом. В этой связи представляется необходимым оценить диапазон возможного изменения системы сил взаимодействия и разработать методику определения наиболее неблагоприятного сочетания сил, при котором силовое воздействие на удерживающее сооружение будет максимальным. Таким образом, задача определения силового воздействия оползневого массива на удерживающие конструкции рассматривается как экстремальная задача, в которой находится максимальная величина оползневого давления в зависимости от системы сил взаимодействия. Область определения этой величины ограничивается условиями статического равновесия отсеков и условием прочности грунта, которым должна удовлетворять система сил взаимодействия.
В третьей главе приводится постановка и решение задачи определения предельного давления грунта на подпорную стенку как задачи линейного программирования. Задача линейного программирования заключается в нахождении экстремума линейной функции, область определения которой дается конечным числом линейных ограничений-равенств и ограничений-неравенств. Система ограничений определяет многогранное множество, имеющее угловые точки, в одной из которых линейная функция цели достигает минимума или максимума. Для решения этой задачи Дж. Данцигом был предложен симплекс-метод, обеспечивающий направленный перебор угловых точек, при котором оптимальное решение находится по кратчайшему пути.
Рассматривается случай предельного давления грунта, когда его перемещения направлены в сторону стенки. Подпорная стенка препятствует общему обрушению склона, и при этом линия скольжения либо определяется геологическим строением склона, либо устанавливается из условия максимума предельного давления, называемого оползневым давлением. Математическая формулировка задачи оптимизации, решаемой симплекс-методом, имеет вид:
| (xi) max при gi(xi) 0 и hi(xi) = 0. | (1) |
В нашем случае ограничениями-неравенствами gi(xi) 0 будут служить условия прочности грунта и ограничения по положению равнодействующих давлений, а ограничениями-равенствами hi(xi) = 0 уравнения равновесия и условие предельного сопротивления сдвигу по линии скольжения. Неизвестными xi являются здесь силы и моменты, определяющие статическую работу области обрушения в рамках выбранной расчетной схемы. В качестве функции цели могут выступать различные выражения в соответствии с выполняемыми расчетами. Например, это может быть горизонтальная составляющая оползневого давления.
Далее приводятся выражения (1) для расчетной схемы «метода отсеков». На рис.1 показана общая схема склона, удерживаемого от обрушения подпорной стенкой. Предположим, что смещение грунта может произойти по некоторой линии скольжения ADB. Область обрушения разделена вертикальными прямыми на n отсеков. Схема действия сил и моментов на отдельный отсек показана на рис. 2. Для удобства записи выражений равнодействующие внешних нагрузок и массовых сил и равнодействующие силы, приложенные к боковой грани и подошве отсека, приведены к крайней правой точке m подошвы отсека.
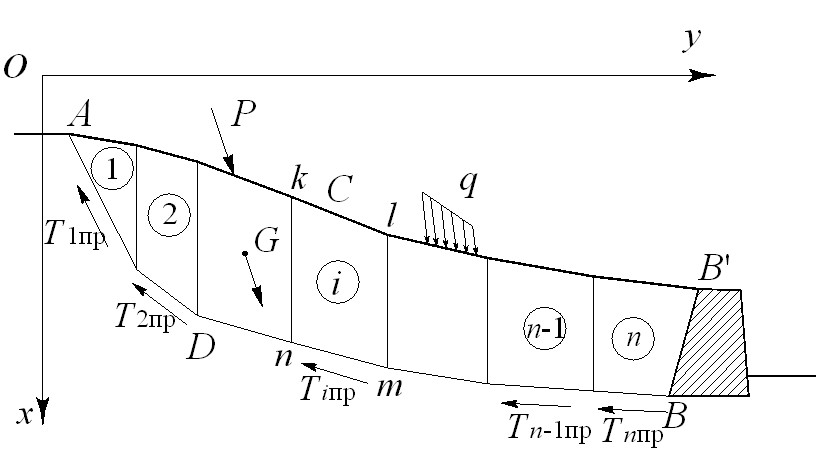
Рис. 1. Расчётная схема «метода отсеков» для определения предельного
давления грунта на подпорную стенку (P, q внешние нагрузки, G массовые силы, Тiпр силы сопротивления сдвигу по линии скольжения)
Таким образом, на отдельный отсек действуют следующие силы и моменты сил: Ui, Vi, Wi вертикальная, горизонтальная силы и момент, эквивалентные действию внешних нагрузок и массовых сил на i-ый отсек; Xi, Yi, Mi вертикальная, горизонтальная силы и момент, эквивалентные силовому воздействию на вертикальную грань i-го отсека; Ni, Ti, Ci нормальная, касательная к подошве i-го отсека силы и момент, эквивалентные силовому воздействию по подошве i-ого отсека.
Геометрические параметры отсека высота hi вертикальной грани, ширина bi и длина li подошвы и угол i ее наклона к горизонтали, обозначены на рис. 2. Показанные на этом рисунке направления сил, а также величины ai и i (ai = bi tg i) считаются положительными.
 |  |
| Рис. 2. Силовое воздействие на i-ый отсек | Рис. 3. Силовое воздействие на n-ый отсек |
Система ограничений-равенств и ограничений-неравенств, которым должны удовлетворять силы взаимодействия, для отдельного отсека при ![]() имеет вид:
имеет вид:
| 0 = Xi 1 + Ni cos i + Ti sin i + Xi Ui ; 0 = Yi 1 + Ni sin i Ti cos i Yi + Vi ; 0 = Xi 1 bi + Yi 1 ai + Mi 1 + Ci – Mi Wi ; 0 = Ni tg i + ci li – Ti ; 1i = Yi tg i* + ci* hi Xi 0; 2i = Yi tg i* + ci* hi + Xi 0; 3i = Ni li Ci 0; 4i = Yi hi Mi 0, | (2) |
где i, ci параметры прочности грунта на линии скольжения (угол внутреннего трения и удельное сцепление); i*, ci* средневзвешенные значения параметров прочности грунтов, которые пересекают боковые грани отсека.
В последнем отсеке «n» правая граница может быть в общем случае наклонена к вертикали на угол, если наклонной выполнена задняя грань подпорной стенки (рис. 3). Направление Xn примем параллельным задней грани подпорной стенки, а направление Yn – перпендикулярным к ней. Коэффициент трения грунта по задней грани подпорной стенки обозначим как tg. Соответственно для n-го отсека дается следующая система ограничений-равенств и ограничений-неравенств:
| 0 = – Xn 1 + Nn cos n + Tn sin n + Yn sin + Xn cos Un ; 0 = Yn 1 + Nn sin n Tn cos n Yn cos + Xn sin + Vn ; 0 = Xn 1 bn + Yn 1 an + Mn 1 + Cn – Mn Wn ; 0 = Nn tg n + cn ln – Tn ; 1n = Yn tg – Xn 0; 2n = Yn tg + Xn 0; 3n = Nn ln Cn 0; 4n = Yn | (3) |
Первые три равенства в системах (2) и (3) представляют собой уравнения равновесия. Четвертое равенство условие предельного сопротивления сдвигу грунта по линии скольжения. Пятое и шестое ограничения-неравенства обеспечивают выполнение условия прочности грунта на сдвиг по боковым граням отсека. Седьмое и восьмое неравенства ограничивают положение равнодействующих давления по граням отсека его размерами.
Функция цели в данной задаче формулируется в соответствии с выполняемым расчетом подпорной стенки. Например, для определения максимального значения горизонтальной составляющей силы оползневого давления функция цели записывается в виде:
| = Yn cos – Xn sin. | (4) |
Для установления максимального опрокидывающего момента, действующего на заднюю грань подпорной стенки функция цели дается равенством:
| = Mn. | (5) |
Неизвестными в данной постановке задачи являются силы и моменты Xi, Yi, Mi, Ni, Ti, Ci. Величины Yi, Ni, Mi, Ci, Ti являются положительными.
Заметим, что в рассматриваемой задаче ограничения-равенства, ограничения-неравенства и функции цели линейны относительно неизвестных сил взаимодействия отсеков с окружающим грунтом. Для поиска максимума функции цели применяется алгоритм симплекс-метода, включающий в себя следующие этапы: исключение лишних неизвестных и 0-строк, нахождение базисного решения, нахождение оптимального плана. Лишними неизвестными являются переменные Xi, принимающие как положительные, так и отрицательные значения. Система ограничений-равенств и ограничений-неравенств оформляется в виде исходной симплекс-таблицы, включающей также искомую функцию цели. Преобразования симплекс-таблицы в соответствие с указанными этапами решения осуществляется с помощью модифицированных Жордановых исключений (МЖИ).
В четвертой главе изложены результаты анализа составляющих оползневого давления, выполненного симплекс-методом.
Все расчеты выполнялись по специально разработанным программам «ISK» и «NCSIMP» в среде Visual Basic 6.0. В программе «ISK» реализован расчет составляющих оползневого давления симплекс-методом и поиск опасной линии скольжения заданной формы (круглоцилиндрической или в виде логарифмической спирали). Программа «NCSIMP» позволяет выполнять симплекс-анализ для линии скольжения произвольной формы. В обеих программах предусмотрен учет произвольного очертания и геологического строения склона, а также произвольных внешних нагрузок.
Итак, прежде всего, была исследована устойчивость решения задачи определения оползневого давления симплекс-методом в рамках расчетной схемы «методов отсеков». Установлено влияние числа отсеков на конечный результат, т.е. дана оценка точности решения с позиций степени дискретизации. Для однородных и неоднородных склонов показано, что при числе отсеков больше 30 результат практически не меняется. Расчеты выполнялись с использованием круглоцилиндрических поверхностей скольжения, а также для линий скольжения в виде логарифмических спиралей. Заметим, что при построении численного решения был принят определенный порядок исключения лишних неизвестных и 0-строк. При выборе разрешающих элементов, для шагов МЖИ использовались неизвестные, значения которых в результате решения ожидалось ненулевым. Такой порядок преобразования симплекс-таблицы существенно снижает возможность зацикливания в процессе работы алгоритма.
В общем случае определялось наиболее невыгодное в отношении искомой величины составляющей оползневого давления положение линии скольжения. Для этого выполнялась серия расчетов при различных ее положениях. Варьируемыми параметрами в таких расчетах являлись положение линии скольжения и система сил взаимодействия отсеков с окружающим грунтом.
Следует отметить, что положение линии скольжения, соответствующей максимуму горизонтальной составляющей оползневого давления, не совпадает по положению с линией скольжения, соответствующей максимуму момента опрокидывания. Поэтому в практике проектирования противооползневых удерживающих сооружений с использованием расчетов симплекс-методом нужно выполнять проверки устойчивости на сдвиг и на опрокидывание с учетом двух пар значений составляющих оползневого давления горизонтальной силы и момента.
Поскольку совместное решение задачи об установлении наиболее неблагоприятной системы сил и экстремальной формы линии скольжения пока не получено, то на данном этапе можно выполнять эти решения отдельно. Например, форму линии скольжения для общего случая неоднородного по геологическому строению склона можно устанавливать с использованием методики В.Г. Федоровского. Далее, используя полученную линию скольжения, можно провести анализ системы сил взаимодействия по предлагаемой методике с помощью симплекс-метода.
В системе ограничений-равенств и ограничений-неравенств, определяющих область возможных значений системы сил взаимодействия, диапазон приложения равнодействующих сил на отсек ограничен полными размерами соответствующих граней отсеков. Однако следует признать, что действительное положение равнодействующей грунтового давления на ту или иную грань отсека находится в пределах некоторой ее части. Маловероятно, чтобы точка приложения равнодействующей силы давления грунта находилась в крайних точках грани. Определяя диапазон приложения равнодействующих сил полными гранями отсеков при выполнении расчетов удерживающей конструкции, мы получаем наибольшую гарантию надежности результатов расчета, но в то же время конструктивное решение противооползневого сооружения будет содержать некоторые излишние запасы и может оказаться неэкономичным.
Поэтому было исследовано влияние положения равнодействующей силы давления между отсеками на результаты определения составляющих силового воздействия грунтового массива на подпорное сооружение. Для этого в системе (2) принят другой набор ограничений-неравенств, учитывающий уменьшенный диапазон приложения равнодействующих:
| 1i = Yi tg i* + ci* hi Xi 0 ; 2i = Yi tg i* + ci* hi + Xi 0 ; 3i = Ni li Ci 0 ; 4i = Yi hi1 Mi 0 ; 5i = Mi Yi hi2 0, | (6) |
где hi1, hi2 высоты, определяющие диапазон возможного положения равнодействующей давления по боковой грани отсека (0 hi1 hi2 h) (рис. 4).
Влияние диапазона приложения равнодействующих сил на величину предельного давления оказалось весьма существенным. В некоторых расчетах при уменьшении диапазона приложения равнодействующей от полных размеров граней до одной трети горизонтальная составляющая оползневого давления снижалась до 54%. В практических расчетах может быть принят уменьшенный диапазон, например, треть средней части боковых граней отсеков.
 | Для сравнения результатов определения оползневого давления симплекс-методом и различными существующими вариантами «методов отсеков» были выполнены сопоставительные расчеты для 17 реальных объектов. Для иллюстрации на рис. 5 и в табл. 1 приведены расчетная схема оползневого склона и характеристики грунтов выделенных инженерно-геологических элементов (ИГЭ), а на рис. 6 эпюры оползневого давления, рассчитанные методами Г.М. Шахунянца, Н.Н. Маслова и симплекс-методом. |
| Рис. 4. Расчетная схема i-ого отсека при сужении диапазона приложения равнодействующей силы давления R между отсеками. | |
Таблица 1. Характеристики грунтов выделенных ИГЭ
| № ИГЭ | 1 | 2 | 3 | 4 | 5 | 6 |
| Удельный вес, кН/м | 17 | 18,6 | 18,5 | 19,3 | 19,0 | 18,5 |
| Удельное сцепление с, кПа | 0 | 18 | 15 | 0 | 21 | 15 |
| Угол внутреннего трения, ° | 27 | 12 | 12 | 24 | 8,5 | 12 |
В данном случае по методу Н.Н. Маслова оползневое давление в расчетном сечении составляет 1146 кН, по методу Г.М. Шахунянца 858,16 кН, симплекс-анализ дает значение 1097 кН. Заметное расхождение в результатах требует их критической оценки. Обоснованность результатов, полученных симплекс-методом, усматривается в том, что в исходной системе уравнений наиболее полно отражены ограничения для системы сил взаимодействия, и обеспечивается выполнение уравнений равновесия для всех отсеков. В то же время, дается максимально возможная величина оползневого давления. В принципе, фактическое оползневое давление может оказаться меньше полученного в симплекс-анализе и оказаться ближе к результату, полученному в методе Г.М. Шахунянца. Значение, полученное, по методу Н.Н. Маслова оказывается в данном случае завышенным, поскольку не может отвечать общим ограничениям для системы сил взаимодействия и уравнениям равновесия.
В целом проведенный анализ показал возможность использования симплекс-метода для определения оползневого давления и достаточную надежность получаемых результатов.

Рис. 5. Расчетная схема оползневого склона

Рис. 6. Эпюры оползневого давления
В пятой главе изложены принципы расчета удерживающих конструкций с использованием симплекс-метода.
Согласно действующим нормативным документам по проектированию подпорных стенок их расчет выполняется в следующем порядке. На первом этапе определяется предельное давление в расчетном сечении. Затем, на втором этапе, выполняется серия расчетов по двум группам предельных состояний той или иной конструкции удерживающего сооружения. При этом все расчеты выполняются на одно и то же силовое воздействие, определенное на первом этапе, с соответствующими коэффициентами перегрузок, сочетаний нагрузок, условия работ и надежности. Имеется в виду, что метод определения силового воздействия на подпорную стенку не зависит от выполняемого расчета.
Как было показано в предыдущих разделах, применение методов линейного программирования позволяет определить возможный по условиям статического равновесия и прочности грунта диапазон изменения системы сил взаимодействия в расчетной схеме «метода отсеков». Соответственно, для каждого отдельного расчета подпорной стенки можно найти наиболее неблагоприятную систему сил.
Итак, принцип расчета подпорной стенки с помощью симплекс-метода заключается в выполнении серии проверок подпорной стенки по первой и второй группе предельных состояний с определением в каждом случае наиболее невыгодной системы сил взаимодействия, а также наиболее невыгодного положения линии скольжения, если ее очертание заранее не предопределено геологическим строением склона.
На рис. 7 приведена расчетная схема подпорной стенки для условий плоской деформации. Задняя грань стенки наклонена к вертикали на угол, ширина подошвы равна b, глубина заложения d. Коэффициент трения между материалом стенки и грунтом обозначим как tg. Оползневой массив, поддерживаемый подпорной стенкой, выделяется линией скольжения и разбивается вертикальными линиями на отсеки.
Заметим, что любой предполагаемой линии скольжения, проходящей ниже подошвы подпорной стенки, должен отвечать коэффициент устойчивости больше единицы. Другими словами, общая устойчивость подпорной стенки против глубокого сдвига должна быть безусловно обеспечена.
Для принятой расчетной схемы обрушения составляется система ограничений-равенств и ограничений-неравенств. Конкретный расчет подпорной стенки определяется функцией цели.
Расчеты, которые необходимо выполнять для подпорных стенок в реальном проектировании, т.е. согласно требованиям нормативных документов (Е.А. Сорочан, А.В. Вронский, А.С. Снарский и др.), с применением симплекс-метода могут быть представлены в следующем виде. Например, проверка устойчивости стенки против сдвига (расчет по первой группе предельных состояний) выполняется с помощью функции цели вида:
| = Fsa | (7) |
Здесь c коэффициент условий работы грунта основания; n коэффициент надежности по назначению сооружения.
Сдвигающая сила Fsa и удерживающая сила Fsr даются выражениями:
| Fsa = Yn cos Xn sin ; | Fsr = Fv tg ( ) + b с + Er, | (8) |
где Fv = GF + Xn cos + Yn sin +  вертикальная сила давления на линию сдвига, наклоненную к подошве на угол стенки ( удельный вес грунта, GF – вес стенки); Er пассивный отпор грунта, действующий на отрезке hr.
вертикальная сила давления на линию сдвига, наклоненную к подошве на угол стенки ( удельный вес грунта, GF – вес стенки); Er пассивный отпор грунта, действующий на отрезке hr.

Рис. 7. Расчетная схема к расчету подпорной стенки
Проверка (7) выполняется для значений угла = 0; /2; и считается выполненной, если функция цели 0.
Далее, ограничение давления по подошве стенки величиной расчетного сопротивления грунта основания (расчет по второй группе предельных состояний) представляется с помощью следующей функции цели:
| (9) |
где Fv0 = GF + Xn cos + Yn sin ; A, W площадь и момент сопротивления подошвы стенки; R – расчетное сопротивление грунта основания;  ; МСТ момент силы тяжести стенки относительно центра подошвы.
; МСТ момент силы тяжести стенки относительно центра подошвы.
Проверка (9) считается выполненной также при 0. В случае необходимости выполняется расчет осадки основания стенки. Здесь тоже можно применить расчет симплекс-методом для определения максимального среднего давления по подошве стенки с использованием функции цели = Fv0. Таким образом, традиционные выражения для проверок подпорной стенки записываются в виде функций цели (7) и (9). Сдвигающие и удерживающие силы, а также давление по подошве стенки зависят от неизвестных усилий Xn, Yn, Mn и определяются при оптимизации функции цели симплекс-методом. Аналогично могут быть построены и другие проверки для подпорной стенки.
Наряду с устройством массивных подпорных стенок в нижней части склона, все большее применение находят промежуточные удерживающие конструкции, располагаемые в средней части оползневого склона по его длине. Эти конструкции выполняют в виде свайных рядов, свайно-панельных рядов или удерживающих стенок на свайных фундаментах. Возможны, конечно, и другие конструктивные решения.
Определение силового воздействия от сползающих масс грунта на промежуточные удерживающие конструкции также можно осуществить с помощью симплекс-метода. Для изложения принципа расчета на рис. 8 приведена схема оползневого массива с фиксированной поверхностью скольжения AFEDC.

Рис. 8. Расчётная схема «метода отсеков» для определения предельного
давления грунта на промежуточную удерживающую конструкцию
Согласно расчетной схеме «метода отсеков» выделенная область обрушения разбивается вертикальными прямыми на блоки. Допустим, что в
 | сечении ВЕ будет расположена удерживающая стенка. Выполняя экстремальный анализ системы сил взаимодействия в области ABEF, устанавливается максимальная величина горизонтальной составляющей оползневого давления Ymax в расчетном сечении. Далее, для этого же сечения определяется минимальное значение горизонтальной силы давления Ymin, которое может вызвать смещение нижележащих пород в области BCDE. Разность между силами давления слева и справа от сечения |
| Рис. 9. Расчётная схема i-го отсека зоны BCDE | |
ВЕ можно использовать в качестве расчетной нагрузки на удерживающую стенку.
В левой от сечения ВЕ части области обрушения решение выполняется по изложенной выше методике. Расчётная схема i-го отсека зоны BCDE, находящейся справа от стенки, показана на рис. 9. В соответствии с расчетной схемой зоны BCDE запишем ограничения-равенства для i-го отсека в виде:
| 0 = Xi 1 + Ni cos i + Тi sin i + Xi Ui ; 0 = Yi 1 Ni sin i + Ti cos i + Yi Vi ; 0 = Xi 1 bi Yi 1 ai Mi 1 Ci + Mi + Wi ; 0 = Ni tg i + ci li Ti. | (10) |
Ограничения-неравенства отвечают выражениям (2). Для поиска минимальной величины Ymin использовалась функция цели:
| = Yn. | (11) |
Поиск Ymax осуществляется симплекс-методом при функции цели (4) при = 0, и ограничениях-равенствах и ограничениях-неравенствах (2), записанных для всех отсеков левой части ABEF. Для поиска Ymin принимается функция цели (11) при ограничениях-равенствах (10) и ограничениях-неравенствах из (2), записанных для отсеков правой части BCDE.
В качестве примера на рис. 9 приведена расчётная схема реального оползневого склона. На схеме выделено 5 инженерно-геологических элементов (ИГЭ). Значения характеристик грунтов, используемых в расчёте, приведены в таблице 2.
Таблица 2. Характеристики грунтов выделенных ИГЭ
| № ИГЭ | 1 | 2 | 3 | 4 |
| Удельный вес, кН/м | 17 | 19 | 17 | 18,3 |
| Удельное сцепление с, кПа | 0 | 21 | 0 | 18 |
| Угол внутреннего трения, ° | 27 | 8,5 | 24 | 12 |
В результате поиска, наиболее опасной круглоцилиндрической линией скольжения оказалась линия скольжения с координатами центра: x0=15,57 м, y0 = 32,31 м и радиусом R0 = 33,36 м (см. рис.10а). Далее, были рассчитаны эпюры Ymax и Ymin по длине склона. На основе сопоставления этих эпюр найдено расчетное сечение 11, в котором разность Ymax Ymin минимальна. В этом сечении и была расположена промежуточная противооползневая удерживающая конструкция. В расчётном сечении горизонтальная сила Ymax, действующая слева, и соответствующий ей опрокидывающий момент Mn в положительном направлении составили: Ymax = 198,4 кН; Mn = 241,8 кН·м (см. рис.10б). В решении для нижней части области обрушения, справа от стенки, были получены значения Ymin = 23,5 кН; Mn = 0 кНм (см. рис.10в).

Рис.10. Расчётная схема оползневого склона
Весь процесс решения сопровождался применением специально составленных программ. Как показано на рис.10г, в рассматриваемом сечении 11 (y = 30,8 м) имеет место экстремальная точка, и значение горизонтального давления составляет Е =198,4 23,5 = 174,9 175кН.
Таким образом, противооползневая удерживающая конструкция, расположенная в расчетном сечении должна воспринять усилия, представляющие разность между максимальным воздействием слева от сечения и минимальным сопротивлением правой части области обрушения: E=175кН; М = 241,8 кНм. Эти усилия были приняты для расчета противооползневой конструкции. В данном случае промежуточная удерживающая конструкция была выполнена в виде двух рядов буронабивных свай, объединенных плитой ростверка.
ОСНОВНЫЕ ВЫВОДЫ
- Показано, что область возможного по условиям статического равновесия и прочности грунтов изменения системы сил взаимодействия отсеков с окружающим грунтом в расчетной схеме «метода отсеков» для условий плоской деформации определяется системой линейных относительно сил взаимодействия ограничений-равенств и ограничений-неравенств. Указанная система ограничений получена для задачи определения силового воздействия оползневых массивов на удерживающие сооружения.
- Симплекс-методом решена задача о силовом воздействии оползневых массивов на удерживающие сооружения в рамках расчетной схемы «метода отсеков». Показано, что составляющие оползневого давления могут рассматриваться в качестве функции цели задачи линейного программирования. Получаемые значения составляющих оползневого давления являются максимально возможными по условиям статического равновесия и прочности грунтов.
- Разработан алгоритм и составлены программы расчета силового воздействия оползневого массива на удерживающие сооружения симплекс-методом. В программах предусмотрен учет произвольности контура и неоднородности геологического строения склона. Описание программы с использованием круглоцилиндрических поверхностей скольжения приведен в диссертации.
- Показано, что степень дискретизации области обрушения откоса в расчетной схеме «метода отсеков» должна составлять 25 … 30 отсеков для получения удовлетворительной точности расчета.
- Показано, что максимальным значениям составляющих оползневого давления горизонтальной силе и моменту в расчетном сечении, где будет расположено подпорное сооружение, отвечают различные экстремальные линии скольжения. В общем случае, при использовании расчетной схемы «метода отсеков» следует учитывать две пары экстремальных значений горизонтальной силы и момента, характеризующих оползневое давление.
- Установлено существенное влияние ограничения по положению равнодействующих сил взаимодействия между отсеками на величину составляющих оползневого давления. В практических расчетах диапазон возможного приложения равнодействующих давления между отсеками может приниматься в пределах трети размера соответствующих граней отсеков в их средней части.
- Сопоставление результатов расчета оползневого давления, полученных с помощью существующих приближенных методов расчета, основанных на расчетной схеме «метода отсеков» с расчетами симплекс-методом, показало, что существующие методы расчета приводят к значениям оползневого давления, существенно отличающимся от экстремальной величины, получаемой симплекс-методом, как в большую, так и в меньшую сторону.
- Если величина оползневого давления отличается от экстремального значения в большую сторону, то этот результат может не рассматриваться вследствие его несоответствия условиям статического равновесия и прочности грунтов. Если же оползневое давление получено меньше, чем его экстремальная оценка, то это значение может использоваться в расчете удерживающего сооружения при соответствующем обосновании гипотез, заложенных в примененном методе расчета. Экстремальная оценка оползневого давления при фиксированной поверхности обрушения может использоваться для расчета подпорного сооружения без дополнительного обоснования.
- Разработаны принципы расчета подпорной стенки на основе экстремального анализа составляющих оползневого давления симплекс-методом. В каждом отдельном расчете находится экстремальная линия скольжения и соответствующая система сил взаимодействия, создающие наиболее неблагоприятные условия работы удерживающей конструкции.
- Разработаны принципы расчета промежуточной удерживающей противооползневой конструкции на основе экстремального анализа составляющих оползневого давления и удерживающей способности части склона, расположенной ниже подпорного сооружения, выполняемого с помощью симплекс-метода.
Основные положения диссертации опубликованы в следующих работах:
- Кан Тхэ Сан. Численная реализация симплекс-метода для задачи определения оползневого давления // Сборник трудов 61-й научно-технической конференции профессорско-преподавательского состава НГАСУ / Новосибирск: Изд-во НГАСУ, 2004. С. 9698.
- Кан Тхэ Сан. Анализ факторов, определяющих величину оползневого давления в расчетной схеме «метода отсеков». // Материалы научно-технической конференции «Наука и молодежь XXI века» / Новосибирск: Изд-во СГУПС, 2005. С. 1518.
- Кан Тхэ Сан. Экстремальная оценка силового воздействия оползневых масс на подпорные стенки // Материалы научно-технической конференции «Наука и молодежь XXI века» / Новосибирск: Изд-во СГУПС, 2005. С. 1921.
- Караулов А.М., Кан Тхэ Сан. Применение линейного программирования для определения предельного давления на подпорную стенку // Сборник трудов 61-й научно-технической конференции профессорско-преподавательского состава НГАСУ / Новосибирск: Изд-во НГАСУ, 2004. С. 98100.
- Караулов А.М., Кан Тхэ Сан. Постановка и решение задачи о предельном давлении грунта на подпорную стенку как задачи линейного программирования // Известия вузов. Строительство и архитектура. 2005. №1. С. 102107.
__________________________________________________________
Подписано в печать 25.03.05
1.5 усл. печ. л. Заказ № 1384. Тираж 100 экз.
Формат 6084 1/16
Отпечатано с готового оригинал-макета на участке
оперативной полиграфии издательства СГУПС
630049, Новосибирск, ул. Д.Ковальчук, 191
Тел.: (383-2) 287-381. E-mail: press @ stu.ru

