Внутренняя геометрия поверхностей и распределений проективно-метрического простра н ства
КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
На правах рукописи
Абруков Денис Александрович
Внутренняя геометрия поверхностей
и распределений проективно-метрического пространства
01.01.04 – геометрия и топология
А В Т О Р Е Ф Е Р А Т
диссертации на соискание ученой степени
кандидата физико-математических наук
Казань – 2002
Работа выполнена в Чувашском государственном педагогическом
университете имени И.Я. Яковлева
Научный руководитель:
доктор физико-математических наук, профессор Столяров А.В.
Официальные оппоненты:
Ведущая организация:
Защита состоится «___» ___________ 2002 г. в ____ час. ____ мин. на заседании диссертационного совета Д. 212.081.10 при Казанском государственном университете по адресу: 420008, Казань, ул. Кремлёвская, 18, конференц-зал научной библиотеки КГУ.
С диссертацией можно ознакомится в научной библиотеке Казанского государственного университета.
Автореферат разослан «___» _____________ 2002 г.
Ученый секретарь
диссертационного совета
кандидат физико- М.А. Малахальцев
математических наук, доцент
- Общая характеристика диссертации
Актуальность темы. Теория различных дифференцируемых подмногообразий (в том числе и оснащенных) в однородных и обобщённых пространствах составляет одно из основных направлений исследований современной дифференциальной геометрии. Обзор большого числа работ по геометрии многомерной поверхности как в пространствах с фундаментальными группами, так и в обобщённых пространства приведен в работах Г.Ф. Лаптева[1] ) и Ю.Г. Лумисте[2] ).
Г.Ф. Лаптев[3] ), [4] ) при помощи разработанного им метода продолжений и охватов в инвариантной аналитической форме построил дифференциальную геометрию гиперповерхности в проективном пространстве и пространстве проективной связности.
Н.М. Остиану[5] ) изучала геометрию m-мерной поверхности n-мерного проективного пространства ![]() .
.
Существенные результаты по проективно-дифференциальной геометрии многомерной поверхности принадлежат А.П. Нордену[6] ) и его школе и получены методом нормализации.
М.А. Акивис[7] ) методом Г.Ф. Лаптева осуществил инвариантное построение геометрии поверхностей конформного пространства.
В 60-х-70-х годах прошлого века обобщённая теория распределений m-мерных линейных элементов в пространстве проективной связности ![]() (в частности, в проективном пространстве
(в частности, в проективном пространстве ![]() ) получила значительное развитие в инвариантной аналитической форме в работах Г.Ф. Лаптева[8] ), Н.М. Остиану[9] ), Ю.Г. Лумисте[10] ).
) получила значительное развитие в инвариантной аналитической форме в работах Г.Ф. Лаптева[8] ), Н.М. Остиану[9] ), Ю.Г. Лумисте[10] ).
В работах А.В. Столярова[11] ) и Ю.И. Попова[12] ) изучаются соответственно двух- и трехсоставные распределения проективного пространства ![]() . Распределениями гиперплоскостных элементов (m=n-1), погружёнными в проективное пространство
. Распределениями гиперплоскостных элементов (m=n-1), погружёнными в проективное пространство ![]() и пространство проективной связности
и пространство проективной связности ![]() занимались Н.М. Остиану[13] ), А.В. Столяров[14] ) и др.
занимались Н.М. Остиану[13] ), А.В. Столяров[14] ) и др.
Представляет интерес теория подмногообразий, погружённых в пространства, фундаментальная группа которых есть подгруппа проективной (евклидовой, аффинной) группы, преобразования которой оставляют неподвижным некоторое подмногообразие (абсолют), вложенное в данное пространство. Проблемой изучения пространств с абсолютом (а также подмногообразий, погруженных в эти пространства) в разное время занимались такие исследователи как А.П. Норден[15] ), А.Э. Хатипов[16] ), А.П. Широков[17] ) и другие отечественные и зарубежные геометры.
В настоящем диссертационном исследовании предметом изучения являются подмногообразия, погружённые в n-мерное проективно-метрическое пространство ![]() 6); под пространством
6); под пространством ![]() понимается n-мерное проективное пространство
понимается n-мерное проективное пространство ![]() , в котором задана неподвижная гиперквадрика
, в котором задана неподвижная гиперквадрика ![]() (абсолют); фундаментальной группой пространства
(абсолют); фундаментальной группой пространства ![]() является подгруппа группы проективных преобразований пространства
является подгруппа группы проективных преобразований пространства ![]() , а именно, стационарная подгруппа абсолюта
, а именно, стационарная подгруппа абсолюта ![]() .
.
А.В. Столяров[18] ) изучает внутреннюю геометрию нормализованного в смысле А.П. Нордена проективно-метрического пространства ![]() .
.
Задача изучения геометрии подмногообразий проективно-метрического пространства ![]() , а именно, m-мерной поверхности
, а именно, m-мерной поверхности ![]()
![]() была поставлена А.П. Норденом6).
была поставлена А.П. Норденом6).
Объектом изучения настоящей работы являются как голономные (поверхности ![]() ), так и неголономные (распределения m-мерных линейных элементов) подмногообразия пространства
), так и неголономные (распределения m-мерных линейных элементов) подмногообразия пространства ![]() . Эти исследования являются актуальными, представляют большой научный интерес, ибо:
. Эти исследования являются актуальными, представляют большой научный интерес, ибо:
1) геометрия поверхности ![]() в
в ![]() изучена далеко не полно;
изучена далеко не полно;
2) геометрия распределений m-мерных линейных элементов в ![]() (даже в случае m=n-1) до настоящего времени не изучалась;
(даже в случае m=n-1) до настоящего времени не изучалась;
3) изучение геометрии указанных подмногообразий (как голономных, так и неголономных) в диссертации осуществляется, как правило, с привлечением теории двойственности, что до настоящего времени исследователями не проводилось.
Цель работы. Целью настоящего диссертационного исследования является изучение геометрии многомерных поверхностей и распределений, погружённых в проективно-метрическое пространство ![]() ; решаются следующие ключевые задачи:
; решаются следующие ключевые задачи:
1) осуществить подход к изучению геометрии поверхности ![]() (m<n-1), не принадлежащей абсолюту
(m<n-1), не принадлежащей абсолюту ![]()
![]()
![]() , с общих позиций, а именно, от геометрии неголономной поверхности (распределения m-мерных линейных элементов) с использованием подобъектов её фундаментальных объектов порядка
, с общих позиций, а именно, от геометрии неголономной поверхности (распределения m-мерных линейных элементов) с использованием подобъектов её фундаментальных объектов порядка ![]() перейти к геометрии голономной поверхности
перейти к геометрии голономной поверхности ![]() ; доказать основную теорему теории поверхности
; доказать основную теорему теории поверхности ![]()
![]()
![]() , не принадлежащей абсолюту
, не принадлежащей абсолюту ![]() , то есть найти её полный внутренний фундаментальный объект (глава I);
, то есть найти её полный внутренний фундаментальный объект (глава I);
2) внутренним инвариантным образом изучить двойственную геометрию поверхности ![]() (m<n-1), принадлежащей абсолюту
(m<n-1), принадлежащей абсолюту ![]() проективно-метрического пространства
проективно-метрического пространства ![]() (глава I);
(глава I);
3) построить основы двойственной геометрии как неголономной, так и голономной гиперповерхности, погруженной в проективно-метрическое пространство ![]() (главы II и III);
(главы II и III);
Методика исследования. В диссертационной работе используются инвариантные методы дифференциально-геометрических исследований, а именно, метод внешних дифференциальных форм Э. Картана[19] ) и метод продолжений и охватов Г.Ф. Лаптева3). Использование указанных методов позволило:
1) исследование геометрии подмногообразий пространства ![]() провести инвариантным образом путём построения и изучения полей геометрических объектов, охваченных полями фундаментальных объектов;
провести инвариантным образом путём построения и изучения полей геометрических объектов, охваченных полями фундаментальных объектов;
2) изучить дифференциально-геометрические факты подмногообразий, связанные с дифференциальными окрестностями по возможности высоких (до четвертого) порядков.
Геометрия аффинных связностей, индуцируемых нормализацией различных подмногообразий проективно-метрического пространства ![]() , исследуется с привлечением теории связностей в расслоенных пространствах в форме, данной Г.Ф. Лаптевым.
, исследуется с привлечением теории связностей в расслоенных пространствах в форме, данной Г.Ф. Лаптевым.
Все рассмотрения в диссертации приводятся с локальной точки зрения; функции предполагаются достаточное число раз дифференцируемыми, то есть изучаемые подмногообразия достаточно гладкие.
Все результаты получены в минимально специализированных системах отнесения.
Научная новизна полученных результатов обусловлена тем, что, с одной стороны, изучение дифференциальной геометрии подмногообразий происходит посредством исследования дифференциально-геометрических структур, индуцируемых полями его фундаментальных объектов, а с другой стороны, с использованием аналитического метода продолжений и охватов Г.Ф. Лаптева, позволяющего получить результаты в инвариантной форме. Результаты, полученные в диссертационном исследовании, являются новыми.
В работе приведены доказательства всех основных предложений, которые сформулированы в виде теорем.
Теоретическая и практическая значимость. Исследование имеет теоретическое значение. Полученные результаты могут быть использованы при дальнейшем изучении различных подмногообразий, погружённых в проективно-метрическое пространство ![]() . Основными направлениями подобных исследований являются:
. Основными направлениями подобных исследований являются:
• изучение внутренней геометрии гиперполос, гиперполосного распределения и распределения m-мерных линейных элементов пространства ![]() ;
;
• исследование пространств с линейной связностью, индуцируемых внутренними инвариантными оснащениями данных подмногообразий.
Теория, разработанная в диссертации, может служить в качестве материала специальных лекционных курсов для студентов старших курсов и аспирантов математических факультетов, а именно:
а) по теории подмногообразий в пространствах с фундаментальными группами;
б) по теории двойственных линейных связностей на оснащённых подмногообразиях пространств с фундаментальными группами.
Апробация. Основные результаты диссертации докладывались и обсуждались на конференциях и семинарах по современным проблемам геометрии: на научных конференциях студентов, аспирантов и докторантов Чувашского государственного педагогического университета (Чебоксары, 2000-2002 г. г.), на итоговых научных конференциях преподавателей ЧГПУ (Чебоксары 2001-2002 г. г.), на заседаниях молодых исследователей по геометрии (ЧГПУ, Чебоксары, 2001-2002 г. г.), на IX Международной конференции «Математика. Образование. Экономика. Экология» (Чебоксары, 2001 г.), на Международной молодежной научной школе-конференции «Лобачевские чтения» (Казань, 2001), на X Международной конференции «Математика. Экономика. Образование» (Ростов-на-Дону, 2002), на заседаниях научно-исследовательского геометрического семинара Казанского госуниверситета (2002 г.).
Публикации. Основные научные результаты, включённые в диссертацию, опубликованы в десяти печатных работах [1]-[10] автора.
Вклад автора в разработку избранных проблем. Диссертация является самостоятельным исследованием автора. Все опубликованные работы по теме диссертации выполнены без соавторов.
Структура и объем работы. Диссертация состоит из введения (общая характеристика работы), краткого изложения её содержания, трех глав и списка использованной литературы, включающего 120 наименований. Полный объем работы составляет 130 страниц машинописного текста.
II. Краткое содержание диссертации
Глава I диссертации посвящена изучению внутренней геометрии поверхности ![]() (m<n-1) проективно-метрического пространства
(m<n-1) проективно-метрического пространства ![]() .
.
В § 1 приводится материал, носящий реферативный характер; он необходим в дальнейшем изложении.
Центральным результатом § 2 является теорема I.1: распределение m-мерных линейных элементов ![]() (m<n-1), центр которого не принадлежит абсолюту
(m<n-1), центр которого не принадлежит абсолюту ![]() проективно-метрического пространства
проективно-метрического пространства ![]() , в дифференциальной окрестности первого порядка порождает инвариантно присоединённое к нему гиперполосное распределение m-мерных линейных элементов
, в дифференциальной окрестности первого порядка порождает инвариантно присоединённое к нему гиперполосное распределение m-мерных линейных элементов ![]() , для которого данное распределение
, для которого данное распределение ![]() является базисным; найдено условие регулярности распределения
является базисным; найдено условие регулярности распределения ![]() .
.
В § 3, п. 1 с использованием подобъектов ![]() ,
, ![]() ,....,
,....,![]() соответственно фундаментальных объектов
соответственно фундаментальных объектов ![]() ,
, ![]() ,…,
,…,![]() распределения
распределения ![]() в
в ![]() доказана теорема I.2, которая является аналогом теоремы I.1 применительно к поверхности
доказана теорема I.2, которая является аналогом теоремы I.1 применительно к поверхности ![]() (m<n-1), не принадлежащей абсолюту
(m<n-1), не принадлежащей абсолюту ![]() пространства
пространства ![]() : поверхность
: поверхность ![]() (m<n-1), не принадлежащая абсолюту
(m<n-1), не принадлежащая абсолюту ![]() , в дифференциальной окрестности второго порядка внутренним образом порождает инвариантно присоединённую к ней гиперполосу
, в дифференциальной окрестности второго порядка внутренним образом порождает инвариантно присоединённую к ней гиперполосу ![]() , для которой данная поверхность является базисной; найдено условие регулярности гиперполосы
, для которой данная поверхность является базисной; найдено условие регулярности гиперполосы ![]() .
.
Теорема I.2 позволяет свести изучение геометрии поверхности ![]() (m<n-1), не принадлежащей абсолюту
(m<n-1), не принадлежащей абсолюту ![]() , к изучению геометрии ассоциированной с ней гиперполосы
, к изучению геометрии ассоциированной с ней гиперполосы ![]() ; последний факт заметно упрощает задачу изучения внутренней геометрии подмногообразия
; последний факт заметно упрощает задачу изучения внутренней геометрии подмногообразия ![]() . Сказанное подтверждается результатами, полученными в § 3, п. 2, 3, а именно, доказаны следующие центральные теоремы I.3 (п. 2), I.4 (п. 2), I.7 (п. 3) соответственно:
. Сказанное подтверждается результатами, полученными в § 3, п. 2, 3, а именно, доказаны следующие центральные теоремы I.3 (п. 2), I.4 (п. 2), I.7 (п. 3) соответственно:
- внутренним образом определённая инвариантная нормализация гиперполосы
 , а значит, и внутренняя инвариантная нормализация её базисной поверхности
, а значит, и внутренняя инвариантная нормализация её базисной поверхности 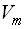
 (m<n-1), не принадлежащей абсолюту
(m<n-1), не принадлежащей абсолюту  , возможна лишь в третьей дифференциальной окрестности текущей точки
, возможна лишь в третьей дифференциальной окрестности текущей точки  поверхности
поверхности  и определяется полями квазитензоров
и определяется полями квазитензоров  третьего порядка;
третьего порядка; - внутреннее инвариантное оснащение в смысле Э. Картана гиперполосы
 в
в  , а значит, и её базисной поверхности
, а значит, и её базисной поверхности 
 (m<n-1), не принадлежащей абсолюту
(m<n-1), не принадлежащей абсолюту  , возможно лишь в четвертой дифференциальной окрестности текущей точки
, возможно лишь в четвертой дифференциальной окрестности текущей точки  поверхности
поверхности  и определяется полями квазитензоров соответственно второго и четвертого порядков
и определяется полями квазитензоров соответственно второго и четвертого порядков  ,
,  и полем геометрического объекта четвертого порядка
и полем геометрического объекта четвертого порядка  ;
; - порядок полного внутреннего фундаментального объекта поверхности
 , не принадлежащей абсолюту проективно-метрического пространства
, не принадлежащей абсолюту проективно-метрического пространства  (m<n-1), равен пяти, то есть при задании этого объекта поверхность
(m<n-1), равен пяти, то есть при задании этого объекта поверхность  определяется с точностью до преобразования фундаментальной группы пространства
определяется с точностью до преобразования фундаментальной группы пространства  .
.
Последний результат (теорема I.7) является фундаментальным в теории поверхности ![]()
![]() (m<n-1), ибо он представляет собой аналог теоремы Петерсона-Кодацци для поверхности
(m<n-1), ибо он представляет собой аналог теоремы Петерсона-Кодацци для поверхности ![]() трехмерного евклидова пространства
трехмерного евклидова пространства ![]() .
.
В § 4 исследуется геометрия m-мерной поверхности, принадлежащей абсолюту ![]() проективно-метрического пространства
проективно-метрического пространства ![]() .
.
Центральным результатом § 4, п. 1 является теорема I.8: m-мерная поверхность ![]() , текущая точка которой принадлежит абсолюту
, текущая точка которой принадлежит абсолюту ![]() пространства
пространства ![]() (m<n-1), порождает инвариантно присоединённую к ней гиперполосу
(m<n-1), порождает инвариантно присоединённую к ней гиперполосу ![]() , для которой данная поверхность
, для которой данная поверхность ![]() будет базисной и касательная гиперплоскость
будет базисной и касательная гиперплоскость ![]() к абсолюту в текущей точке
к абсолюту в текущей точке ![]() является главной касательной гиперплоскостью гиперполосы
является главной касательной гиперплоскостью гиперполосы ![]() ; в случае невырожденности абсолюта гиперполоса
; в случае невырожденности абсолюта гиперполоса ![]() является регулярной.
является регулярной.
Таким образом, изучение геометрии поверхности, принадлежащей невырожденному абсолюту ![]() пространства
пространства ![]() , сводится к изучению геометрии регулярной квадратичной гиперполосы
, сводится к изучению геометрии регулярной квадратичной гиперполосы ![]() , ассоциированной с этой поверхностью; эта гиперполоса в дальнейшем обозначается
, ассоциированной с этой поверхностью; эта гиперполоса в дальнейшем обозначается ![]() (
(![]() ).
).
Доказано (теорема I.9), что в случае невырожденности абсолюта ![]() пространства
пространства ![]() квадратичная гиперполоса
квадратичная гиперполоса ![]() (
(![]() ) является конической[20] ) тогда и только тогда, когда она плоская20). Ниже предполагается, что гиперполоса
) является конической[20] ) тогда и только тогда, когда она плоская20). Ниже предполагается, что гиперполоса ![]() (
(![]() ) не является конической (а, следовательно, плоской).
) не является конической (а, следовательно, плоской).
Два пространства с линейной связностью называются двойственными14), если структурные формы этих пространств преобразуются друг в друга по иволютивному закону.
Основным результатом § 4, п. 2 является теорема I.10: m-мерная поверхность ![]() , лежащая на абсолюте
, лежащая на абсолюте ![]() пространства
пространства ![]() , индуцирует:
, индуцирует:
- тангенциальное проективно-метрическое пространство
 (
( ) с абсолютом
) с абсолютом  – тангенциальной гиперквадрикой, двойственное пространству
– тангенциальной гиперквадрикой, двойственное пространству (
( ); образующими элементами этой гиперквадрики являются касательные гиперплоскости
); образующими элементами этой гиперквадрики являются касательные гиперплоскости  абсолюта
абсолюта  пространства
пространства  .
. - во второй дифференциальной окрестности подмногообразие
 (
( ), двойственное гиперполосе
), двойственное гиперполосе  (
( ).
).
В § 4, п. 3 найдены внутренние инвариантные оснащения в смысле Нордена-Чакмазяна гиперполосы ![]() (
(![]() ). Приводятся примеры построения в третьей дифференциальной окрестности внутренних инвариантных двойственных и полярных6) (относительно абсолюта
). Приводятся примеры построения в третьей дифференциальной окрестности внутренних инвариантных двойственных и полярных6) (относительно абсолюта ![]() ) нормализаций регулярной квадратичной гиперполосы
) нормализаций регулярной квадратичной гиперполосы ![]() (
(![]() ), а следовательно, её базисной поверхности
), а следовательно, её базисной поверхности ![]() .
.
В § 4, п. 4 показано, что нормализация в смысле Нордена-Чакмазаяна гиперполосы ![]() (
(![]() ) в
) в ![]() индуцирует две двойственные аффинные связности
индуцирует две двойственные аффинные связности ![]() и
и ![]() без кручения; приведены геометрические характеристики аналитических условий параллельного перенесения допустимых направлений в связностях
без кручения; приведены геометрические характеристики аналитических условий параллельного перенесения допустимых направлений в связностях ![]() и
и ![]() вдоль кривой l, принадлежащей базисной поверхности
вдоль кривой l, принадлежащей базисной поверхности ![]() гиперполосы
гиперполосы ![]() (
(![]() ).
).
Изучается внутренняя геометрия двойственных аффинных связностей ![]() и
и ![]() . Доказана справедливость утверждений (теоремы I.11-I.14):
. Доказана справедливость утверждений (теоремы I.11-I.14):
1) Связность ![]() (
(![]() ), индуцируемая некоторой нормализацией регулярной квадратичной гиперполосы
), индуцируемая некоторой нормализацией регулярной квадратичной гиперполосы ![]() (
(![]() ), будет вейлевой с полем метрического тензора
), будет вейлевой с полем метрического тензора ![]() тогда и только тогда, когда данная нормализация полярна (относительно абсолюта
тогда и только тогда, когда данная нормализация полярна (относительно абсолюта ![]() ).
).
2) Внутренняя геометрия любой из двойственных аффинных связностей ![]() и
и ![]() , индуцируемых полярной нормализацией
, индуцируемых полярной нормализацией ![]() гиперполосы
гиперполосы ![]() (
(![]() ) пространства
) пространства ![]() (m<n-1), является римановой тогда и только тогда, когда нормализация вполне гармонична6) подмногообразию
(m<n-1), является римановой тогда и только тогда, когда нормализация вполне гармонична6) подмногообразию ![]() .
.
3) Полярная нормализация ![]() гиперполосы
гиперполосы ![]() (
(![]() ) пространства
) пространства ![]() вполне гармонична подмногообразию
вполне гармонична подмногообразию ![]() тогда и только тогда, когда поле нормалей первого (второго) рода сопряжено6), то есть
тогда и только тогда, когда поле нормалей первого (второго) рода сопряжено6), то есть ![]() =0 (гармонично6), то есть
=0 (гармонично6), то есть ![]() =0) гиперполосе
=0) гиперполосе ![]() .
.
4) Двойственные аффинные связности ![]() и
и ![]() , индуцируемые нормализацией гиперполосы
, индуцируемые нормализацией гиперполосы ![]() (
(![]() ) проективно-метрического пространства
) проективно-метрического пространства ![]() , совпадают тогда и только тогда, когда нормализация гиперполосы
, совпадают тогда и только тогда, когда нормализация гиперполосы ![]() (
(![]() ) полярна относительно абсолюта
) полярна относительно абсолюта ![]() ; при этом связность
; при этом связность ![]() риманова с полем метрического тензора
риманова с полем метрического тензора ![]() .
.
В § 4, п. 5 найдена связь между геометриями поверхности ![]()
![]() пространства
пространства ![]() и m-мерной поверхности конформного пространства
и m-мерной поверхности конформного пространства ![]() . Справедлива теорема I.15: геометрия m-мерной поверхности
. Справедлива теорема I.15: геометрия m-мерной поверхности ![]() , принадлежащей абсолюту
, принадлежащей абсолюту ![]() овального типа n-мерного пространства
овального типа n-мерного пространства ![]() (m<n-1), изоморфна геометрии m-мерной поверхности
(m<n-1), изоморфна геометрии m-мерной поверхности ![]() собственно конформного пространства
собственно конформного пространства ![]() ; при этом метрическим тензором
; при этом метрическим тензором ![]() пространства
пространства ![]() является тензор
является тензор ![]() .
.
В главе II диссертации изучается двойственная геометрия распределения первого рода ![]() гиперплоскостных элементов, центр которого – точка
гиперплоскостных элементов, центр которого – точка ![]() – не принадлежит абсолюту
– не принадлежит абсолюту ![]() пространства
пространства ![]() .
.
Центральным результатом § 1, п. 2 является теорема II.1: регулярное распределение гиперплоскостных элементов, погружённое в пространство ![]() , индуцирует:
, индуцирует:
- в третьей дифференциальной окрестности тангенциальное проективно-метрическое пространство
 с абсолютом
с абсолютом  – тангенциальной гиперквадрикой, двойственное
– тангенциальной гиперквадрикой, двойственное  .
. - в первой дифференциальной окрестности – многообразие
 , двойственное исходному распределению
, двойственное исходному распределению  .
.
Следует заметить, что тангенциальный абсолют ![]() , вообще говоря, не совпадает с тангенциальным абсолютом
, вообще говоря, не совпадает с тангенциальным абсолютом ![]() , образующими элементами которого являются касательные гиперплоскости к абсолюту
, образующими элементами которого являются касательные гиперплоскости к абсолюту ![]()
![]()
![]() .
.
В § 2, п. 1 в третьей дифференциальной окрестности текущего элемента распределения получены определяемые внутренним инвариантным образом поля инвариантных соприкасающихся гиперквадрик ![]() и
и ![]() распределения в
распределения в ![]() и двойственного подмногообразия
и двойственного подмногообразия ![]() в
в ![]() соответственно.
соответственно.
В случае голономного распределения обращение в нуль тензора Дарбу ![]() есть условие касания третьего порядка соприкасающихся гиперквадрик поля
есть условие касания третьего порядка соприкасающихся гиперквадрик поля ![]() (
(![]() ) с распределением
) с распределением ![]() (подмногообразием
(подмногообразием ![]() в
в ![]() ).
).
В § 2, п. 2 приведены примеры построения двойственных внутренним образом определяемых инвариантных оснащений в смысле А.П. Нордена регулярного распределения ![]() в
в ![]() .
.
В § 2, п. 3 показано, что нормализация в смысле А.П. Нордена регулярного распределения гиперплоскостных элементов ![]() в
в ![]() индуцирует две двойственные аффинные связности
индуцирует две двойственные аффинные связности ![]() и
и ![]() без кручения. Доказано, что двойственные аффинные связности
без кручения. Доказано, что двойственные аффинные связности ![]() и
и ![]() обобщённо сопряжены6) относительно поля тензора
обобщённо сопряжены6) относительно поля тензора ![]() вдоль любой кривой l, принадлежащей распределению
вдоль любой кривой l, принадлежащей распределению ![]() в
в ![]() . В случае голономности распределения
. В случае голономности распределения ![]() найдено условие совпадения связностей
найдено условие совпадения связностей ![]() и
и ![]() (теорема II.2): на нормализованном голономном распределении гиперплоскостных элементов
(теорема II.2): на нормализованном голономном распределении гиперплоскостных элементов ![]() в
в ![]() двойственные аффинные связности
двойственные аффинные связности ![]() и
и ![]() совпадают тогда и только тогда, когда нормализация подмногообразия
совпадают тогда и только тогда, когда нормализация подмногообразия ![]() есть нормализация Михэйлеску и соприкасающиеся гиперквадрики
есть нормализация Михэйлеску и соприкасающиеся гиперквадрики ![]() с распределением
с распределением ![]() имеют касание третьего порядка.
имеют касание третьего порядка.
В § 3 найдена квадратичная форма, определяющая метрику тангенциального проективно-метрического пространства ![]() . Доказано, что данная метрика является невырожденной тогда и только тогда, когда абсолют
. Доказано, что данная метрика является невырожденной тогда и только тогда, когда абсолют ![]() пространства
пространства ![]() невырожден:
невырожден: ![]() .
.
В § 4 исследуется внутренняя геометрия нормализованного тангенциального проективно-метрического пространства ![]() . Суть нормализации пространства
. Суть нормализации пространства ![]() состоит в задании некоторого однозначного, непрерывного и дифференцируемого соответствия «гиперплоскость
состоит в задании некоторого однозначного, непрерывного и дифференцируемого соответствия «гиперплоскость ![]() связка гиперплоскостей с центром в точке
связка гиперплоскостей с центром в точке ![]() »,
», ![]() . Нормализация пространства
. Нормализация пространства ![]() будет полярной относительно тангенциального абсолюта
будет полярной относительно тангенциального абсолюта ![]() , если центр
, если центр ![]() нормализующей связки гиперплоскостей является полюсом нормализуемой гиперплоскости
нормализующей связки гиперплоскостей является полюсом нормализуемой гиперплоскости ![]() относительно абсолюта
относительно абсолюта ![]() .
.
Доказано, что нормализация пространства ![]() индуцирует пространство аффинной связности
индуцирует пространство аффинной связности ![]() без кручения. Имеют место следующие предложения (теоремы II.3-II.5):
без кручения. Имеют место следующие предложения (теоремы II.3-II.5):
1) внутренняя геометрия симметрического пространства аффинной связности ![]() , индуцируемого полярной нормализацией тангенциального проективно-метрического пространства
, индуцируемого полярной нормализацией тангенциального проективно-метрического пространства ![]() , является метрической с полем метрического тензора
, является метрической с полем метрического тензора ![]() и эквиаффинной;
и эквиаффинной;
2) для того, чтобы связность пространства ![]() , индуцируемого некоторой нормализацией тангенциального проективно-метрического пространства
, индуцируемого некоторой нормализацией тангенциального проективно-метрического пространства ![]() с невырожденной метрикой, являлась вейлевой, необходимо и достаточно, чтобы данная нормализация была полярной;
с невырожденной метрикой, являлась вейлевой, необходимо и достаточно, чтобы данная нормализация была полярной;
3) пространство аффинной связности, индуцируемое полярной нормализацией тангенциального пространства ![]() с невырожденной метрикой, является римановым
с невырожденной метрикой, является римановым ![]() постоянной кривизны
постоянной кривизны ![]() ; при этом если пространство
; при этом если пространство ![]() является собственно римановым, то при
является собственно римановым, то при ![]() > 0 абсолют пространства
> 0 абсолют пространства ![]() есть тангенциальная гиперквадрика овального типа, а при
есть тангенциальная гиперквадрика овального типа, а при ![]() < 0 – тангенциальная мнимая гиперквадрика.
< 0 – тангенциальная мнимая гиперквадрика.
Справедлива теорема II.6: регулярное распределение гиперплоскостных элементов ![]() , погружённое в пространство
, погружённое в пространство ![]() , при полярной нормализации точечного и тангенциального пространств
, при полярной нормализации точечного и тангенциального пространств ![]() и
и ![]() соответственно в случае невырожденности их абсолютов
соответственно в случае невырожденности их абсолютов ![]() и
и ![]() индуцирует два римановых пространства
индуцирует два римановых пространства ![]() и
и ![]() одинаковой постоянной кривизны
одинаковой постоянной кривизны ![]() , причем эти пространства являются изоморфными относительно инволютивного преобразования структурных форм пространств
, причем эти пространства являются изоморфными относительно инволютивного преобразования структурных форм пространств ![]() и
и ![]() .
.
В главе III работы изучается геометрия регулярной гиперповерхности ![]() , текущая точка которой не принадлежит абсолюту
, текущая точка которой не принадлежит абсолюту ![]() пространства
пространства ![]() .
.
В § 1 доказана теорема III.1: регулярная гиперповерхность ![]() в проективно-метрическом пространстве
в проективно-метрическом пространстве ![]() индуцирует:
индуцирует:
а) в третьей дифференциальной окрестности проективное пространство ![]() , двойственное пространству
, двойственное пространству ![]() ;
;
б) во второй дифференциальной окрестности – многообразие ![]() , двойственное исходной гиперповерхности
, двойственное исходной гиперповерхности ![]() .
.
В § 2 изучается гиперповерхность ![]() , полярная по отношению к исходной гиперповерхности
, полярная по отношению к исходной гиперповерхности ![]() пространства
пространства ![]() .
.
В § 2, п. 1 показано, что регулярная гиперповерхность ![]() в
в ![]() внутренним образом индуцирует регулярную гиперповерхность
внутренним образом индуцирует регулярную гиперповерхность ![]() , полярную данной
, полярную данной ![]() относительно абсолюта
относительно абсолюта ![]() с невырожденным тензором
с невырожденным тензором ![]() ; при этом касательной гиперплоскостью
; при этом касательной гиперплоскостью ![]() (
(![]() ) в текущей точке
) в текущей точке ![]()
![]() (
(![]()
![]() ) будет поляра точки
) будет поляра точки ![]() (
(![]() ).
).
Справедлива теорема III.3: регулярная гиперповерхность ![]() в
в ![]() вырождается в гиперквадрику
вырождается в гиперквадрику ![]() тогда и только тогда, когда полярная ей (относительно абсолюта
тогда и только тогда, когда полярная ей (относительно абсолюта ![]() ) гиперповерхность
) гиперповерхность ![]() вырождается в гиперквадрику
вырождается в гиперквадрику ![]() .
.
В § 2, п. 2 доказана теорема III.4: полярная гиперповерхность ![]() , погружённая в пространство
, погружённая в пространство ![]() , индуцирует:
, индуцирует:
а) в третьей дифференциальной окрестности проективное пространство ![]() , двойственное
, двойственное ![]() (
(![]() );
);
б) во второй дифференциальной окрестности – подмногообразие ![]() , двойственное исходному
, двойственное исходному ![]() .
.
В § 3 в четвертой дифференциальной окрестности текущей точки гиперповерхности ![]()
![]()
![]() построено поле канонического пучка нормалей первого рода
построено поле канонического пучка нормалей первого рода ![]() , определяемое полями квазитензоров
, определяемое полями квазитензоров ![]() (поле нормалей Фубини) и
(поле нормалей Фубини) и ![]() (поле директрис Вильчинского), а также поле однопараметрического пучка нормалей второго рода
(поле директрис Вильчинского), а также поле однопараметрического пучка нормалей второго рода ![]() с
с ![]() -мерной вершиной в касательной плоскости
-мерной вершиной в касательной плоскости ![]() гиперповерхности
гиперповерхности ![]() . Гиперповерхность, в каждой точке
. Гиперповерхность, в каждой точке ![]() (
(![]()
![]() ) которой канонический пучок нормалей первого рода
) которой канонический пучок нормалей первого рода ![]() (
(![]() ) вырождается в одну нормаль, по аналогии с поверхностью
) вырождается в одну нормаль, по аналогии с поверхностью ![]() назовём коинцидентной[21] ).
назовём коинцидентной[21] ).
Центральным результатом § 3 является теорема III.6: нормализация в смысле А.П. Нордена одной из регулярных гиперповерхностей ![]() или
или ![]() в
в ![]() равносильна нормализации другой; при этом нормаль первого (второго) рода
равносильна нормализации другой; при этом нормаль первого (второго) рода ![]() гиперповерхности
гиперповерхности ![]() полярна (относительно абсолюта
полярна (относительно абсолюта ![]() ) нормали второго (первого) рода
) нормали второго (первого) рода ![]() гиперповерхности
гиперповерхности ![]() , причем оснащающие объекты
, причем оснащающие объекты ![]() и связаны соотношениями
и связаны соотношениями
![]() ,
, ![]() (*)
(*)
Определение. Нормализации полярных гиперповерхностей ![]() и
и ![]() в
в ![]() полями объектов
полями объектов ![]() и
и ![]() соответственно, связанных между собой соотношениями (*), назовем полярными по отношению друг к другу.
соответственно, связанных между собой соотношениями (*), назовем полярными по отношению друг к другу.
Доказаны следующие основные утверждения, касающиеся канонических пучков нормалей первого и второго родов гиперповерхностей ![]() и
и ![]() в
в ![]() :
:
- В каждой точке




 (
(



 ) пучок нормалей первого рода
) пучок нормалей первого рода  (
( ) гиперповерхности
) гиперповерхности  (
( ) вырождается в одну нормаль тогда и только тогда, когда в этой точке пучок нормалей второго рода
) вырождается в одну нормаль тогда и только тогда, когда в этой точке пучок нормалей второго рода  (
( ) вырождается в одну нормаль (теоремы III.5, III.10).
) вырождается в одну нормаль (теоремы III.5, III.10). - В точке




 пучок нормалей первого рода
пучок нормалей первого рода  (второго рода
(второго рода  ) вырождается в одну нормаль тогда и только тогда, когда в соответствующей точке
) вырождается в одну нормаль тогда и только тогда, когда в соответствующей точке 
 полярный пучок нормалей второго рода
полярный пучок нормалей второго рода  (первого рода
(первого рода  ) полярной гиперповерхности
) полярной гиперповерхности 

 вырождается в одну нормаль; следовательно, полярные гиперповерхности
вырождается в одну нормаль; следовательно, полярные гиперповерхности  и
и  в
в  могут быть коинцидентными лишь одновременно (теорема III.11).
могут быть коинцидентными лишь одновременно (теорема III.11).
В § 4 изучается внутренняя геометрия двойственных аффинных связностей, индуцируемых полярными нормализациями гиперповерхностей ![]() и
и ![]() пространства
пространства ![]() .
.
Нормализация в смысле А.П. Нордена регулярной гиперповерхности ![]() (
(![]() ) в
) в ![]() индуцирует две двойственные аффинные связности
индуцирует две двойственные аффинные связности ![]() и
и ![]() (
(![]() и
и ![]() ) без кручения. Аффинные связности
) без кручения. Аффинные связности ![]() и
и ![]() (
(![]() и
и ![]() ) сопряжены относительно поля тензора
) сопряжены относительно поля тензора ![]() (
(![]() ). Аффинная связность
). Аффинная связность ![]() (
(![]() ), средняя по отношению к
), средняя по отношению к ![]() и
и ![]() (
(![]() и
и ![]() ), является вейлевой с полем невырожденного метрического тензора
), является вейлевой с полем невырожденного метрического тензора ![]() (
(![]() ). Заметим, что
). Заметим, что  .
.
Найдены аналитические условия эквиаффинности связностей ![]() и
и ![]() (
(![]() и
и ![]() ), а также условие римановости средней связности
), а также условие римановости средней связности ![]() (
(![]() ); в частности, геометрии двойственных пространств аффинной связности
); в частности, геометрии двойственных пространств аффинной связности ![]() и
и ![]() (
(![]() и
и ![]() ), индуцируемых нормализацией Фубини гиперповерхности
), индуцируемых нормализацией Фубини гиперповерхности ![]() (
(![]() ) в
) в ![]() , являются эквиаффинными, а их средняя связность – риманова.
, являются эквиаффинными, а их средняя связность – риманова.
Справедливо следующее условие совпадения связностей ![]() и
и ![]() (
(![]() и
и ![]() ) (теоремы III.12, III.13): двойственные аффинные связности
) (теоремы III.12, III.13): двойственные аффинные связности ![]() и
и ![]() (
(![]() и
и ![]() ), индуцируемые на нормализованной гиперповерхности
), индуцируемые на нормализованной гиперповерхности ![]() (
(![]() ) проективно-метрического пространства
) проективно-метрического пространства ![]() , совпадают тогда и только тогда, когда рассматриваемая гиперповерхность есть гиперквадрика и её нормализация является автополярной; при этом связность
, совпадают тогда и только тогда, когда рассматриваемая гиперповерхность есть гиперквадрика и её нормализация является автополярной; при этом связность ![]() (
(![]() ) риманова с метрическим тензором
) риманова с метрическим тензором ![]() (
(![]() ).
).
III. Основные результаты диссертации,
выносимые на защиту
1) Доказано, что распределение m-мерных линейных элементов пространства ![]() (m<n-1) порождает присоединённое к нему внутренним инвариантным образом гиперполосное распределение m-мерных линейных элементов.
(m<n-1) порождает присоединённое к нему внутренним инвариантным образом гиперполосное распределение m-мерных линейных элементов.
2) Доказано основное предложение теории m-мерной поверхности ![]() (m<n-1), не принадлежащей абсолюту
(m<n-1), не принадлежащей абсолюту ![]() пространства
пространства ![]() : порядок полного внутреннего фундаментального объекта поверхности
: порядок полного внутреннего фундаментального объекта поверхности ![]() равен пяти; при задании этого объекта поверхность
равен пяти; при задании этого объекта поверхность ![]() определяется с точностью до преобразования фундаментальной группы пространства
определяется с точностью до преобразования фундаментальной группы пространства ![]() (заметим, что для общей m-мерной поверхности
(заметим, что для общей m-мерной поверхности ![]() , m<n-1 проективного пространства
, m<n-1 проективного пространства ![]() вопрос о порядке полного внутреннего фундаментального объекта, вообще говоря, остается открытым).
вопрос о порядке полного внутреннего фундаментального объекта, вообще говоря, остается открытым).
3) Показано, что с m-мерной поверхностью ![]() , m<n-1, принадлежащей абсолюту
, m<n-1, принадлежащей абсолюту ![]() пространства
пространства ![]() , внутренним инвариантным образом ассоциируется квадратичная гиперполоса
, внутренним инвариантным образом ассоциируется квадратичная гиперполоса ![]() (
(![]() ), что позволило построить двойственную геометрию данной поверхности.
), что позволило построить двойственную геометрию данной поверхности.
4) Показано, что регулярное распределение гиперплоскостных элементов ![]() (неголономная гиперповерхность) с центром, не принадлежащим абсолюту
(неголономная гиперповерхность) с центром, не принадлежащим абсолюту ![]() пространства
пространства ![]() , внутренним инвариантным образом в третьей дифференциальной окрестности элемента подмногообразия
, внутренним инвариантным образом в третьей дифференциальной окрестности элемента подмногообразия ![]() индуцирует тангенциальное проективно-метрическое пространство
индуцирует тангенциальное проективно-метрическое пространство ![]() с абсолютом
с абсолютом ![]() – тангенциальной гиперквадрикой; изучаются некоторые вопросы метрики тангенциального пространства
– тангенциальной гиперквадрикой; изучаются некоторые вопросы метрики тангенциального пространства ![]() и внутренней геометрии нормализованного пространства
и внутренней геометрии нормализованного пространства ![]() . В разных дифференциальных окрестностях получен ряд результатов, определяющих двойственную геометрию нормализованного подмногообразия
. В разных дифференциальных окрестностях получен ряд результатов, определяющих двойственную геометрию нормализованного подмногообразия ![]() .
.
5) Исследуется двойственная геометрия гиперповерхности ![]() , текущая точка которой не принадлежит абсолюту
, текущая точка которой не принадлежит абсолюту ![]() пространства
пространства ![]() : построена полярная (относительно абсолюта
: построена полярная (относительно абсолюта ![]() ) гиперповерхность
) гиперповерхность ![]() , найдены двойственные образы
, найдены двойственные образы ![]() и
и ![]() гиперповерхностей
гиперповерхностей ![]() и
и ![]() соответственно, рассмотрены примеры построения внутренним образом двойственных и полярных нормализаций гиперповерхностей
соответственно, рассмотрены примеры построения внутренним образом двойственных и полярных нормализаций гиперповерхностей ![]() и
и ![]() , найдена связь между ними; исследуется внутренняя геометрия двойственных аффинных связностей, индуцируемых этими нормализациями.
, найдена связь между ними; исследуется внутренняя геометрия двойственных аффинных связностей, индуцируемых этими нормализациями.
IV. Работы автора, опубликованные по теме диссертации
- Абруков Д.А. Распределения гиперплоскостных элементов в проективно-метрическом пространстве // ВИНИТИ РАН. – 2001. – 21 с. – № 872-В2001 Деп.
- Абруков Д.А. Геометрия гиперповерхности проективно-метрического пространства // ВИНИТИ РАН. – 2001. – 34 с. – № 2420-В2001 Деп.
- Абруков Д.А. Распределения гиперплоскостных элементов в проективно-метрическом пространстве // Тезисы докл. IX международной конференции «Математика. Образование. Экономика. Экология», Чебоксары. – 2001. – С. 29.
- Абруков Д.А. О взаимном распределении гиперплоскостных элементов в проективно-метрическом пространстве // Сб. науч. тр. студентов, аспирантов и докторантов. – Чебоксары: ЧГПУ, 2001. – В. 9. – С. 9-15.
- Абруков Д.А. Внутренняя геометрия тангенциального проективно-метрического пространства // Вестник ЧГПУ. Физико-математические науки. – Чебоксары: ЧГПУ, 2001. – № 2(21). – С. 9-15.
- Абруков Д.А. Гиперповерхность в проективно-метрическом пространстве // Материалы межд. науч. молодежной школы-конференции. Казань: Изд-во ДАС, 2001. – С. 73.
- Абруков Д.А. Взаимная гиперповерхность проективно-метрического пространства // Сб. науч. тр. студентов, аспирантов и докторантов. – Чебоксары: ЧГПУ, 2001. – В. 10. – С. 173-179.
- Абруков Д.А. Геометрия поверхности, принадлежащей абсолюту проективно-метрического пространства // ВИНИТИ РАН. – 2002. – 24 с. – № 493-В2002 Деп.
- Абруков Д.А. О геометрии поверхности, не принадлежащей абсолюту проективно-метрического пространства // ВИНИТИ РАН. – 2002. – 14 с. – № 1009-В2002 Деп.
- Абруков Д.А. m-мерная поверхность, принадлежащая абсолюту проективно-метрического пространства // Тезисы докл. X международной конференции «Математика. Экономика. Образование», Ростов-на-Дону. – 2002. – С. 54.
Подписано в печать 15.10.02 Формат 60х84/16. Усл. печ. л. 1.
Тираж 100 экз. Заказ № _________. Бесплатно
Отпечатано на участке оперативной полиграфии
Чувашского государственного педагогического университета им. И.Я. Яковлева
428000, Чебоксары, К. Маркса, 38
[1]. Лаптев Г.Ф. Дифференциальная геометрия многомерных поверхностей // Геометрия (1963) / Итоги науки и техники ВИНИТИ АН СССР. – 1965. – С. 5-64.
[2]. Лумисте Ю.Г. Дифференциальная геометрия подмногообразий // Итоги науки. Алгебра. Топология. Геометрия. –Т. 13. – ВИНИТИ АН СССР – М., 1977. – С. 273-380.
[3]. Лаптев Г.Ф. Дифференциальная геометрия погружённых многообразий. Теоретико-групповой метод дифференциально-геометрических исследований // Тр. Моск. мат. об-ва, 1953. – Т. 2. – С. 275-382.
[4]. Лаптев Г.Ф. Гиперповерхность в пространстве проективной связности // ДАН СССР. – 1958. – Т. 121. – № 1. – С. 41-44.
[5]. Остиану Н.М. О геометрии многомерной поверхности проективного пространства // Тр. Геом. семинара / Ин-т. научн. информ. АН СССР. – 1966. – Т. 1. – С. 239-263.
[6]. Норден А.П. Пространства аффинной связности. – М.: Наука, 1976. – 432 с.
[7]. Акивис М.А. К конформно-дифференциальной геометрии многомерных поверхностей // Матем. сб. – 1961. – Т. 53. – №1. – С. 53-72.
[8]. Лаптев Г.Ф., Остиану Н.М. Распределения m-мерных линейных элементов в пространстве проективной связности. I // Тр. Геом. семинара / Ин-т. научн. информ. АН СССР. – 1971. – Т.3. – С. 49-94.
[9]. Остиану Н.М. Распределения m-мерных линейных элементов в пространстве проективной связности. II // Тр. Геом. семинара / Ин-т. научн. информ. АН СССР. – 1971. – Т. 3. – С. 95-114.
[10]. Лумисте Ю.Г. Распределения на однородных пространствах // Проблемы геометрии / Итоги науки техники ВИНИТИ АН СССР. – 1977. – Т. 8. – С. 5-24.
[11]. Столяров А.В. Проективно-дифференциальная геометрия регулярного гиперполосного распределения m-мерных линейных элементов // Проблемы геометрии / Итоги науки техники ВИНИТИ АН СССР. – 1975. – Т. 7. – С. 117-151.
[12]. Попов Ю.И. Основы теории трехсоставных распределений проективного пространства. – С.-Петребург: С.-Петребургский ун-т, 1992. – 172 с.
[13]. Остиану Н.М. Распределение гиперплоскостных элементов в проективном пространстве // Тр. Геом. семинара / Ин-т. научн. инф. АН СССР. – 1973. – Т. 4. – С. 71-120.
[14]. Столяров А.В. Двойственная теория оснащённых многообразий: Монография. – Чебоксары, 1994. – 290 с.
[15]. Норден А.П. О полярной нормализации в пространстве с вырожденным абсолютом // Тр. сем. по вект. и тенз. анализу / МГУ. М., 1952. – Вып. 9. – С. 198-212
[16]. Хатипов А.Э. Теория поверхностей в пространстве с абсолютом, распавшимся на пару комплексно-сопряжённых плоскостей // Тр. Узбек. ун-та. – 1955. – 59. – С. 105-132.
[17]. Широков А.П. Геометрия обобщённых биаксиальных пространств // Уч. зап. Казанского гос. ун-та, 1954. – Т. 114. – кн. 2. – С. 123-166.
[18]. Столяров А.В. Внутренняя геометрия проективно-метрического пространства // Диф. геометрия многообразий фигур. – Калининград: Калининградский ун-т, 2001. – Вып. 32. – С. 94-101.
[19]. Фиников С.П. Метод внешних форм Картана в дифференциальной геометрии. – М. – Л.: ГИТТЛ, 1948. – 432 с.
[20]. Василян М.А. Проективная теория многомерных гиперполос // Изв. АН Арм. ССР. Матем. – 1971. – Т. 6. – №6. – С. 477-481.
[21]. Mihailescu T. Geometrie differentiala projectiva. – Bucureti Acad. RPR. – 1958. – 494 p.

