Фарадж изучение спектральных характеристик одной несамосопряженной задачи с негладкими коэффициентами
На правах рукописи
Жвамер Карван Хама Фарадж
Изучение спектральных характеристик одной несамосопряженной задачи с негладкими коэффициентами
01.01.02 – Дифференциальные уравнения, динамические системы и оптимальное управление
Автореферат
диссертации на соискание ученой степени
кандидата физико-математических наук
Ростов-на-Дону
2010
Работа выполнена на кафедре математического анализа ГОУ ВПО «Дагестанский государственный университет»
Научный руководитель: доктор физико-математических наук,
профессор Айгунов Гасан Абдуллаевич
Официальные оппоненты: заслуженный деятель науки РФ, доктор физико-математических наук, профессор Латышев Анатолий Васильевич
кандидат физико-математических наук,
доцент Сазонов Леонид Иванович
Ведущая организация: Московский государственный университет
им. М.В. Ломоносова
Защита состоится «15» июня 2010 г. в 14 часов на заседании диссертационного совета Д. 212.208.29 по физико-математическим наукам в Южном Федеральном университете по адресу: 344090,Ростов-на-Дону, ул. Мильчакова,8А,факультет математики,механики и компьютерных наук ЮФУ,ауд.211.
С диссертацией можно ознакомиться в библиотеке Южного Федерального университета по адресу: г. Ростов-на-Дону, ул.Пушкинская, 148.
Автореферат разослан ____ мая 2010 г.
Ученый секретарь
диссертационного совета Д212.208.29 В.Д. Кряквин
Общая характеристика работы
Актуальность темы. В современных приложениях часто возникают задачи с негладкими данными, что затрудняет их рассмотрение, так как классические результаты получены при жестких ограничениях на гладкость функций, входящих в них. Возникла практическая и теоретическая необходимость в изучении задач с негладкими коэффициентами и рассмотрении их решений в обобщенном смысле.
Цель работы. Диссертация посвящена изучению асимптотического поведения собственных значений и собственных функций одной несамосопряженной краевой задачи с негладкими коэффициентами, получению верхних оценок нормированных собственных функций в случае суммируемой весовой функции и установлению максимально возможной скорости роста собственных функций рассматриваемой задачи в случае различных весовых функций. Доказано, что в случае весовой функции, удовлетворяющей условию Липшица (в регулярном случае) нормированные собственные функции задачи равномерно ограничены.
Научная новизна. 1. Доказано, что множество собственных значений рассматриваемой несамосопряженной краевой задачи в случае суммируемой весовой функции образует счетное множество и расположено в нижней полуплоскости (
).
2. Получены верхние оценки нормированных собственных функций рассматриваемой спектральной задачи в случае суммируемых весовых функций, как в регулярном, так и в нерегулярном случае.
3. В регулярном случае (
) доказана достижимость верхних оценок данной задачи в случае суммируемой весовой функции.
4. Изучено асимптотическое поведение нормированных собственных функций задачи в случае непрерывной весовой функции
5. Установлена возможная скорость роста нормированных собственных функций рассматриваемой задачи в случае весовых функций близких к функциям из класса Гельдера.
6. Доказана равномерная ограниченность нормированных собственных функций рассматриваемой задачи в случае весовой функции, удовлетворяющей условию Липшица.
7. Установлено также, что в случае непрерывных весовых функций и весовых функций из класса 
порядок роста нормированных собственных функций такой же, как и в объемлющем классе 
.
Практическая значимость. Результаты работы могут быть использованы при решении различных задач механики, теории упругости, математической физики, оптимального управления, ибо, как известно, спектральные краевые задачи моделируют многие прикладные задачи. Результаты работы могут найти применение и в самой математике при обосновании метода Фурье, при изучении сходимости различных разложений и т.д.
Личный вклад соискателя. Диссертация является самостоятельным научным исследованием. Доказательства всех основных положений получены соискателем. В совместной работе научному руководителю принадлежат постановка задач и намеченная методика их решения.
Внедрение результатов работы. Результаты работы внедрены в учебный процесс в виде разделов в спецкурсах: а) спектральные краевые задачи, б) обобщенная проблема оценок собственных функций несамосопряженных краевых задач, используются при чтении курсов дифференциальных уравнений и уравнений математической физики, а также при разработке тем дипломных и курсовых работ.
Апробация работы. Полученные результаты докладывались и обсуждались на кафедре дифференциальных и интегральных уравнений ЮФУ и на научном семинаре, руководимом профессорами А.Г. Костюченко, А.А. Шкаликовым при механико-математческом факултета МГУ им. М.В. Ломоносова.
Основные результаты диссертационной работы докладывались на Третьей и Четвертой международных конференциях, г. Махачкала 2007-2009, на научно-теоретических конференциях, проводимых в Дагестанском государственном университете (2005-2009г.), на межвузовских конференциях «Функционально-дифференциальные уравнения и их приложения» (2005-2009г.), на заседаниях семинара по спектральной теории кафедр дифференциальных уравнений и математического анализа (2005-2009г.) Дагестанского государственного университета.
Публикации. Основные результаты диссертации опубликованы в работах [1]-[8].
Структура и объем работы. Диссертация состоит из введения, трех глав и списка литературы из 57 наименований. Полный объем диссертации составляет 145 страниц машинописного текста.
КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ
Многочисленные проблемы теории колебаний пространственно-распределенных систем приводят к необходимости изучения собственных значений и соответствующих им собственных функций дифференциальных операторов, а также к вопросам, связанным с изучением различных функционалов от собственных чисел и собственных функций.
Как известно, многие задачи математической физики, механики, теории упругости, оптимального управления приводят к задаче изучения спектра дифференциальных операторов и разложения произвольной функции в ряд по собственным функциям такого оператора. Классические результаты в этом направлении принадлежат Ж. Лиувиллю, Ж. Штурму, В.А. Стеклову, Г.Д. Биркгофу, Я.Д. Тамаркину, М.Г. Крейну.
Не меньшее значение имеет изучение и общих эллиптических операторов и спектральных краевых задач для таких операторов при различных краевых условиях.
Хотя к настоящему времени многие спектральные задачи изучены довольно хорошо и общую теорию их можно считать завершенной, однако непосредственное применение этой теории к конкретным задачам в ряде случаев затруднительно. Поэтому изучение таких задач представляет интерес. Кроме того, многие классические результаты получены при очень жестких ограничениях на гладкость коэффициентов, в то время как коэффициенты задач, возникающих в современных приложениях, в большинстве своем не удовлетворяют требуемым условиям гладкости. К тому же некоторые классические результаты в общем случае неверны. В связи с этим возникла практическая и теоретическая необходимость в изучении задач с негладкими коэффициентами и рассмотрении их решений в обобщенном смысле.
Отметим, что для гладких весовых функций, а именно, при 
оценки собственных функций задачи 
получены в работах, где доказано, что нормированные собственные функции данной задачи равномерно ограничены, если 
(регулярный случай) и растут как 
в случае 
(нерегулярный случай).
Заметим, что для задачи Штурма – Лиувилля в случае гладких весовых функций собственные функции равномерно ограничены.
Настоящая диссертация примыкает к рассматриваемому кругу вопросов, к подробному изложению которых мы и переходим.
Пусть 
– фиксированные числа. Обозначим через 
множество всех суммируемых функций 
на сегменте 
, удовлетворяющих условию 
.
В дальнейшем такие функции будем называть весовыми функциями.
На множестве 
рассмотрим обычную 
– метрику. Пусть 
. Рассмотрим спектральную задачу 
:
, 
(1)
, 
, (2)
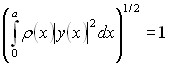, (3)
где 
– спектральный параметр.
Обозначим через 
– решение задачи 
. Будем также пользоваться обозначениями 
и 
, если непосредственно ясно, о какой весовой функции или параметре идет речь.
Эта задача впервые была рассмотрена для случая 
итальянским физиком Т. Редже, который показал, что система собственных функций задачи (1) – (2) полна и изучил асимптотику собственных чисел этой задачи.
А.О. Кравицкий указал класс функций, которые допускают разложение в равномерно сходящиеся ряды по собственным и присоединенным функциям задачи Т. Редже (когда 
).
В работах М.М. Гехтмана, И.В. Станкевича задача Т. Редже была обобщена на случай уравнения четвертого порядка.
Чтобы получить краевые условия, обобщающие условия излучения (2), вначале рассматривается некоторый самосопряженный в 
оператор с непрерывным спектром, а затем изучается аналитическое продолжение резольвенты этого самосопряженного оператора на риманову поверхность («нефизические листы»).
М.М. Гехтман рассмотрел обобщение задачи Т. Редже в случае дифференциального оператора четного порядка. Более общий случай уравнения n-го порядка, когда все коэффициенты 
зависят от спектрального порядка 
, рассмотрен в работах Шкаликова А.А.
Укажем еще работы Г.А. Айгунова и Т.Ю. Гаджиевой, которые рассмотрели случай 
задачи типа Т. Редже для уравнения 2n-го порядка.
В отличие от перечисленных работ настоящая работа посвящена не вопросу разложения определенных классов функций в ряды по собственным и присоединенным функциям, а вопросам оценки нормированных собственных функций задачи 
и достижимости верхних оценок в случае определенных «негладких» весовых функций 
.
Результаты, установленные в диссертации, примыкают к кругу вопросов, относящихся к известной проблеме В.А. Стеклова об условиях ограниченности (в терминах весовой функции 
) ортонормированной системы многочленов 
на всем интервале ортогональности или ее части, где 
. В последнее время значительно возрос интерес к этой проблеме. Сравнив результаты работ Геронимуса Я.Л, Рахманова Е.А и Амброладзе М.У., можно заметить аналогию в асимптотическом поведении общих ортонормированных многочленов 
и нормированных собственных функций спектральных задач на конечном отрезке. Поэтому было бы интересно выяснить, справедливы ли утверждения теорем в случае общих ортонормированных полиномов. Заметим, что и ортонормированные полиномы, и собственные функции спектральных задач обладают свойством ортогональности. В диссертации доказывается, что асимптотические свойства собственных функций не связаны непосредственно с ортогональностью, а обусловлены специальным характером колеблемости решений дифференциального уравнения, величина же максимально возможного роста последовательности нормированных собственных функций определяется только нормировочным условием (3).
Прежде чем перейти к изложению результатов диссертации, предварительно отметим, что получению аналогичных оценок собственных функций для задачи Штурма – Лиувилля посвящены работы В.А Ильина, И. Йо, И.А Шишмарева, В.В Жикова, В.Я. Якубова, М.М. Гехтмана, Г.А. Айгунова.
Перейдем к изложению содержания диссертации.
В первой главе диссертации доказаны следующие теоремы:
Теорема 1.2.1. Собственные числа 
непрерывно зависят от весовой функции 
в том смысле, что для любого 
существует 
такое, что для любого 
из неравенства 
следует 
.
Теорема 1.2.2. Собственная функция 
непрерывно зависит от весовой функции 
в том смысле, что для любого 
, существует 
такое, что для любого 
из неравенства 
следует
.
Из этих двух теорем вытекает
Следствие 1.2.1. Для любого 
и 
существует 
такое, что для всех 
, удовлетворяющих неравенству 
, справедливо неравенство
.
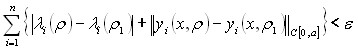Для доказательства теорем 1.2.1 и 1.2.2 предварительно доказывается теорема о непрерывной зависимости решения задачи Коши от весовой функции и начальных условий.
Пусть 
– произвольная точка из сегмента 
, 
и 
– произвольные комплексные числа. Рассмотрим задачу Коши:
(4)
, 
(5)
и пусть 
– решение этой задачи. Имеет место следующая.
Теорема 1.2.3. Для любого 
существует 
такое, что для любых 
и 
справедливо неравенство
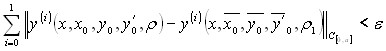, если
.
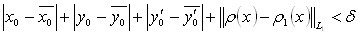Доказательство данной теоремы опирается на следующую лемму.
Лемма 1.2.1. Решение задачи Коши (4) – (5) может быть представлено в виде
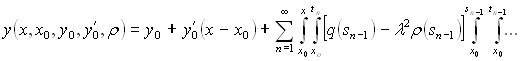
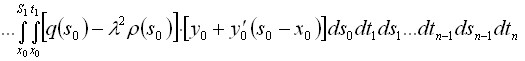
Далее в I главе доказывается теорема 1.4.1, дающая возможность изучения поведения собственных значений задачи 
в случае негладких коэффициентов.
Теорема 1.4.1. Пусть 
, 
, тогда для задачи 
справедливы следующие утверждения:
1) Задача 
имеет счетное множество собственных значений.
2) Для собственных значений задачи 
справедливо неравенство 
, причем если 
- собственное число и собственная функция задачи и 
, то 
.
Из утверждения 1.2.2, теоремы 1.4.1,учитывая, что 
, вытекает важное следствие 1.4.1.
Следствие 1.4.1. Собственные функции задачи 
удовлетворяют соотношению 
, где 
- собственное число, соответствующее собственной функции 
.
Доказательство теоремы 1.4.1 основывается на лемме 1.3.1 и утверждении 1.4.1.
Лемма 1.3.1. Задача 
имеет счетное множество собственных значений.
Утверждение 1.4.1. Если 
- собственное число и соответствующая собственная функция задачи 
и 
то справедливы соотношения 
и
Асимптотика собственных значений и их распределение в комплексной плоскости задачи (1) – (2) в случае (
) изучена в работах Т. Редже, А.О. Кравицкого; а для уравнения 2n-го порядка - Гехтманом М.М., в случае 
- в работах Айгунова Г.А. и Гаджиевой Т.Ю. Во всех ранее известных работах коэффициенты дифференциальных уравнений являются достаточно гладкими функциями, а в рассматриваемой диссертации они являются всего лишь суммируемыми и отделенными от нуля функциями.
Вторая глава посвящена получению верхних оценок для нормированных собственных функций задачи типа Т. Редже 
(теорема 2.1.1) и доказательству леммы 2.2.1, которая является основной леммой данной работы.
Теорема 2.1.1. Пусть 
, 
.Тогда существует константа С, не зависящая от 
и 
, что для любого собственного числа 
и соответствующей собственной функции 
задачи 
.
.
Для 
задача 
в случае гладких коэффициентов изучена в работе [16], где установлено, что при 
(регулярный случай), то мнимые части собственных чисел 
и собственные функции 
равномерно по 
ограничены (
,
), если же 
( нерегулярный случай) мнимые части 
собственных чисел задачи 
не ограничены равномерно (
), не ограничены также и собственные функции 
(
).
В дальнейшем мы будем рассматривать случай, когда 
который назовём регулярным, а соответствующую этому случаю функцию 
регулярной весовой функцией задачи 
.
Пусть 
, 
. Тогда функцию 
назовем кусочно-гладкой на 
, если 
имеет ограниченные производные любого порядка на 
.
Лемма 2.2.1. Пусть даны 
,
кусочно-гладкая
, 
и достаточно малое 
, удовлетворяющие условиям 
,
и 
.
Тогда существует константа 
и номер 
такие, что для любого 
существует кусочно-гладкая весовая функция 
такая, что
, 
если 
и справедливо неравенство
.
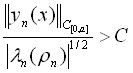При этом постоянная 
не зависит от 
и 
, а 
не зависит от 
и 
(
и 
собственные числа и собственные функции задачи 
, соответствующие коэффициентам 
и 
).
Из данной леммы вытекает следствие
Следствие 2.2.1. Если функция 
непрерывна, то существуют непрерывные весовые функции 
, удовлетворяющие условиям леммы и равенству 
.
Введем обозначения: 
, 
,
и 
-действительные числа, 
, 
.
Если записать задачу 
, используя введенные обозначения, то после несложных преобразований, мы придем к задаче вида:
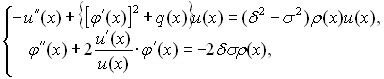(6)
, 
, 
, (7)
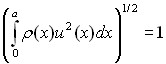. (8)
Третья глава является основной и посвящена изучению асимптотического поведения нормированных собственных функций задачи 
для весовых функций различных промежуточных классов.
Заметим, что в III главе рассматривается регулярный случай.
В §1 III главы, используя лемму 2.2.1, доказывается достижимость верхних оценок нормированными собственными функциями задачи 
в случае суммируемой весовой функции. Имеет место
Теорема 3.1.1. Для любой 
существует 
такая, что
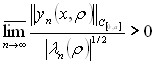
Эта теорема доказывает не только достижимость верхних оценок собственными функциями задачи 
в случае суммируемой весовой функции, но и то, что их порядок роста – 
.
В §2 III главы рассматривается асимптотическое поведение собственных функций задачи 
в случае непрерывной весовой функции. Справедлива
Теорема 3.2.1 . Для любой последовательности
существует непрерывная весовая функция 
такая, что
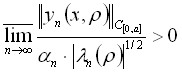
Доказательство этой теоремы основывается на следствии 1.4.1 из леммы 2.2.1.
В §3 III главы изучается возможная скорость роста нормированных собственных функций задачи 
для классов весовых функций, близких к весовым функциям из класса Гельдера.
Рассмотрим класс функций 
, удовлетворяющих условиям:
1) 
имеет не более счетного множества точек разрыва 
, причем все эти точки разрыва первого рода и множество 
может иметь только одну точку сгущения 
;
2) на любом участке 
не содержащем точек разрыва, 
удовлетворяет условию Гельдера 
, где 
, 
, 
;
3) скачки 
удовлетворяют неравенством 
, при этом, если число точек разрыва конечно и равно 
, то 
.
Очевидно, в окрестности любой функции из класса 
существуют функции, удовлетворяющие условиям 1) – 3). Обозначим рассматриваемый класс функций через 
. Класс функций 
является расширением класса 
.
Справедлива следующая
Теорема 3.3.1. Пусть 
- весовая функция, 
и 
. Тогда существует весовая функция 
, удовлетворяющая условиям 
, 
при 
такая, что если 
собственные значения и собственные функции нашей задачи с весом 
, то
.
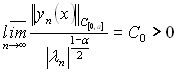Таким образом, доказывается, что на весовых функциях, которые являются некоторыми промежуточными классами весовых функций между гладкими и суммируемыми, также возможен рост нормированных собственных функций задачи 
как 
, где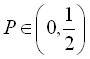 
.
В §4 III главы получены равномерные оценки для нормированных собственных функций задачи 
в случае весовой функции, удовлетворяющих условию Липшица. Доказана следующая лемма 3.4.1.
Рассмотрим класс весовых функций 
удовлетворяющих условию Липшица.
Лемма 3.4.1. Для любого 
и 
существует функция 
такая, что
,
,
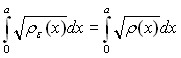и 
, где с- константа,не зависящая от 
и 
.
Пользуясь этой леммой, доказывается следующая
Теорема 3.4.1. Существует константа 
(единая для всего класса 
) такая, что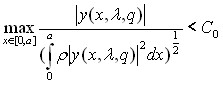 
для всех достаточно больших по модулю значений 
, где 
- класс непрерывных на 
функций 
, удовлетворяющих неравенству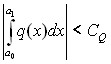 
, 
, 
.
Из теоремы 3.4.1 и леммы 3.4.1 вытекает следствие 3.4.1
Следствие 3.4.1. Пусть 
- непрерывная функция, а 
. Тогда решение задачи Коши
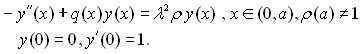
удовлетворяет соотношению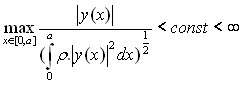 
для всех достаточно больших значений 
из полосы 
.
Утверждение следствия 3.4.1 верно и для собственных функций задачи 
так, как если 
, а 
, то функция 
является решением рассматриваемой задачи Коши.
Таким образом, доказывается, что нормированные собственные функции задачи 
в случае весовых функций, удовлетворяющих условию Липшица, равномерно ограничены.
По материалам диссертации были сделаны сообщения на научно-теоретических конференциях, проводимых в Дагестанском государственном университете (2005–2009 г.г.), на межвузовских конференциях «Функционально-дифференциальные уравнения и их приложения» (2007 – 2009 гг.), на заседаниях семинара по спектральной теории кафедры дифференциальных уравнений и математического анализа (2005 – 2009 гг.) при ДГУ, на семинаре проф. Шкаликова А.А., проф. Костюченко А.Г. при механико-математическом факультете МГУ в 2009.
Основные результаты диссертации отражены в работах [1] – [8].
Пользуясь, случаем, приношу искреннюю благодарность своему научному руководителю профессору Г.А. Айгунову за постоянное внимание и руководство работой.
СПИСОК РАБОТ ПО ТЕМЕ ДИССЕРТАЦИИ
- Издания, рекомендованные ВАК МО РФ для публикаций
материалов кандидатских диссертаций по математике:
[1] Жвамер Карван Х. Асимптотическое поведение ортонормированных собственных функций задачи типа Т. Редже с суммируемой положительной весовой функцией / Г.А. Айгунов, К. Х. Жвамер // УМН. Москва, 2009. Т. 64. Вып. 6(390). С.169-170.
[2] Жвамер Карван Х. Изучение поведения собственных значений и оценка собственных функций задачи типа Т. Редже в случае суммируемой весовой функции на конечном отрезке 
/ Г.А. Айгунов, К. Х. Жвамер // Изв. вузов. Сев.-Кавк. регион. Естест. науки, г. Ростов-на-Дону. 2009. № 6(154).-С. 5-7.
[3] Жвамер Карван Х. О возможной скорости роста нормированных собственных функций задачи Т. Редже в случае суммируемой и непрерывной весовых функций / Г.А. Айгунов, К. Х. Жвамер // Изв. вузов. Сев.-Кавк. регион. Естест. науки, г. Ростов-на-Дону. 2010. № 2(156). С. 8-12.
II. Остальные публикации:
[4] Жвамер Карван Х. Асимптотика собственных значений одной нерегулярной краевой задачи на отрезке 
/ Г.А. Айгунов, К. Х. Жвамер // Матем. сборник, г. Махачкала, 2007 ( Toм III). С. 49-54.
[5] Жвамер Карван Х. Получение верхних оценок собственных функций спектральной задачи Т. Редже с суммируемой весовой функцией на конечном промежутке / К. Х. Жвамер // Матем. сборник, г. Махачкала, 2008 ( Toм IV).-С. 45-50.
[6] Жвамер Карван Х. Асимптотическое поведение собственных функций задачи Т. Редже в случае непрерывной весовой функции / К. Х. Жвамер // Сб.: Функц. - диф. уравнения и их приложения, г. Махачкала. 2009. Вып. № 5. С. 84-87.
[7] Жвамер Карван Х. К вопросу о непрерывной зависимости собственных чисел и собственных функций задачи типа Т. Редже от суммируемой весовой функции / Г.А. Айгунов, К. Х. Жвамер // Вестник ДГУ, Естеств. науки, г. Махачкала. 2009. Вып. 1. С.36-43.
[8] Жвамер Карван Х. К вопросу о достижимости верхних оценок собственными функциями задачи типа Т. Редже / Г.А. Айгунов, К. Х. Жвамер // Вестник ДГУ, Естеств. науки. г. Махачкала, 2009. Вып. 6. С. 11-20.
Формат 60x84/16. Бумага офсетная.
Печать офсетная. Гарнитура «Times New Roman»
Тираж 120. Заказ № 47/10.
Издательско-полиграфический отдел ООО «ДИНЭМ»
367030, Республика Дагестан, г. Махачкала, ул. М. Гаджиева, 94.
Тел./факс: +7 (722) 68-16-59
Тел.: +7 (928) 874-57-53
E-mail: [email protected]
