Нелинейная краевая задача на собственные значения для системы дифференциальных уравнений распространяющихся электромагнитных тм-волн в круглом нелинейном волноводе

На правах рукописи

ХОРОШЕВА Эльвира Александровна

НЕЛИНЕЙНАЯ КРАЕВАЯ ЗАДАЧА
НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ РАСПРОСТРАНЯЮЩИХСЯ ЭЛЕКТРОМАГНИТНЫХ ТМ-ВОЛН
В КРУГЛОМ НЕЛИНЕЙНОМ ВОЛНОВОДЕ

01.01.02 – дифференциальные уравнения, динамические системы и оптимальное управление

Автореферат

диссертации на соискание ученой степени

кандидата физико-математических наук

КАЗАНЬ 2010

Работа выполнена на кафедре «Математика и супер­компь­ютерное моделирование» Пензенского государ­ствен­ного университета.

Научный руководитель – доктор физико-матема­ти­че­ских наук,  профессор
 Смирнов Юрий Геннадьевич.

Официальные оппоненты: доктор физико-математи­ческих наук, профессор

                                            Ильинский Анатолий Серафимович;

                                                 доктор физико-математических наук, доцент

                                                  Карчевский Евгений Михайлович.

Ведущая организация – Московский государственный институт радиотехники, электроники и автоматики (технический университет), г. Москва.

Защита диссертации состоится 18 ноября 2010 г., в 14 часов 30 ми­нут, на заседании диссертационного совета Д 212.081.10 при Казанском (При­волжском) федеральном университете по адресу: Российская Фе­де­рация, 420008, г. Казань, ул. Профессора Нужина, 1/37, НИИММ,
ауд. 324.

С диссертацией можно ознакомиться в научной библиотеке Ка­зан­­ского (Приволжского) федерального университета. Автореферат ра­зослан и размещен на сайте Казанского (При­волж­ского) феде­раль­ного университета www.ksu.ru

Ученый секретарь

диссертационного совета

кандидат физико-математических наук,

доцент Липачев Е. К.

Общая характеристика работы

Диссертация посвящена решению нелинейной краевой задачи на собственные значения распространяющихся ТМ-поляризованных элект­ромагнитных волн в круглом диэлектрическом волноводе с не­ли­нейностью, выраженной законом Керра.

Актуальность темы.

Изучение задач распространения электро­маг­нитных волн в нели­ней­ных средах является актуальным в связи с тем, что эти явления находят широкое применение в физике плазмы, в совре­мен­ной микро­элект­ро­ни­ке, оптике и лазерной технике. Кроме того, они пред­став­ляют и само­сто­я­тельный математический интерес, поскольку такие задачи являются не­линейными краевыми задачами на собственные значения, общие методы решения которых недостаточно разработаны. Таким образом, про­гресс в аналитическом исследовании подобных задач важен и с те­о­ретической, и с практической точек зрения. Разработка численных мето­дов для реше­ния задач этого класса также является актуальной. Результаты анали­ти­ческого исследования могут существенно помочь при разработке числен­ных методов. Данное направление было и явля­ется предметом иссле­дования многих авторов (В. П. Силин, П. Н. Еле­он­ский, К. М. Leung,
Н. W. Shurmann, В. С. Серов, Ю. В. Шестопалов, Ю. Г. Смирнов).

Цель работы:

– Строгая постановка задачи о распространении ТМ-по­ля­ри­зо­ван­ных (собственных) волн в цилиндрических диэлект­ри­ческих вол­но­водах круглого сечения с нелинейным заполнением сре­ды по за­ко­ну Керра как краевой задачи на собственные значения для системы уравнений Максвелла.

– Разработка математического аппарата для исследования задачи о собственных волнах; доказательство базовых теоретических ре­зуль­татов о существовании решений дисперсионных уравнений и ин­тег­ральных уравнений, отвечающих краевой задаче.

– Построение, обоснование и реализация эффективных чис­лен­ных методов для расчета собственных значений и соответствующих им собственных функций для поставленной задачи.

Научная новизна:

– впервые получено дисперсионное уравнение для задачи рас­пространения электромагнитных ТМ-волн в нелинейном круглом вол­новоде с нелинейностью, выраженной законом Керра;

– предложен метод сведения нелинейной краевой задачи на соб­ственные значения к решению дисперсионного уравнения и доказана теорема о спектральной эквивалентности краевой задачи и дис­пер­сионного уравнения;

– доказаны базовые теоретические результаты о существовании и единственности решений дисперсионных уравнений (относительно спектрального параметра) и интегральных уравнений, отвечающих краевой задаче (относительно собственных функций);

– с помощью дисперсионного уравнения приближенно вычислены собственные значения и собственные функции краевой задачи.

Практическая значимость.

Большое практическое значение в представленной работе имеет по­лученное дисперсионное уравнение, анализ которого позволяет не толь­ко доказать существование решений краевой задачи (а значит, и ис­ходной задачи о распространении волн), но и исследовать свойства рас­про­стра­няющихся ТМ-волн в зависимости от различных пара­метров. Кроме того, полученное дисперсионное уравнение может быть решено численно на компьютере. Систему дифференциальных урав­нений задачи также мож­но записать в виде, удобном для чис­ленных расчетов. Таким образом, име­ется возможность вычислять не только собственные зна­че­ния краевой задачи, но и собственные функ­­ции, отвечающие этим собст­вен­ным зна­че­ниям, а, следо­ва­тель­но, изучать структуру поля электромаг­нитной волны.

Реализация и внедрение полученных результатов.

Результаты, полученные в диссертационной работе, включены в от­четы НИР и гранта, выполненных на кафедре «Математика и су­пер­­компь­­ютерное моделирование»; грант Минобрнауки «Иссле­дова­ние трех­­­мер­ных векторных задач электродинамики в нелинейных сре­дах ме­то­­дом ма­тематического моделирования на многопро­цессор­ных си­сте­мах».

Апробация работы.

Основные результаты работы докладывались на научных кон­фе­ренциях и семинарах:

– XXVIII конференции молодых ученых механико-мате­мати­че­ского факультета МГУ (Москва, 2006);

– X Международной научно-методической конференции «Универ­ситетское образование» (Пенза, 2006);

– научном семинаре кафедры «Математика и суперкомпьютерное моделирование» Пензенского государственного университета;

– научном семинаре кафедры «Прикладная математика» Казан­ско­го федерального (Приволжского) университета.

Публикации.

По материалам диссертации опубликовано шесть печатных работ, спи­сок которых приведен в конце автореферата, две работы – в жур­на­лах, рекомендованных ВАК РФ.

Объем и структура диссертации.

Работа состоит из введения, четырех глав, приложения и списка литературы, содержащего 90 наименований. Работа изложена на
98 страницах машинописного текста, содержит 6 графиков.

содержание работы

Во введении приводится обзор работ по теме диссертации и во­просам, примыкающим к ней; обосновывается актуальность темы, фор­мулируется цель работы; излагаются краткое содержание и ос­нов­­ные результаты работы.

Первая глава посвящена постановке задачи для рас­прост­раняю­щихся поляризованных электромагнитных ТМ-волн в круглом не­ли­нейном волноводе с нелинейностью, выраженной законом Керра. Из си­стемы уравнений Максвелла выводится система дифферен­ци­альных урав­нений, для которой в дальнейшем ставится краевая за­дача.

Рассмотрим задачу о собственных волнах цилиндрического ди­элект­рического волновода. Пусть все трехмерное пространство заполнено изотропной средой без источников с диэлектрической проницаемостью , где – диэлектрическая про­ни­ца­емость вакуума, а – относительная диэлектрическая про­ницаемость среды. В эту среду помещен цилиндрический диэлект­рический волновод радиуса одно­род­но­­го заполнения с образующей, параллельной оси , и поперечным круговым сечением.

Пусть диэлектрическая проницаемость внутри волновода определяется по закону Керра:

,

где и – вещественные положительные константы; – коэф­фи­циент не­ли­ней­ности; – постоянная составляющая проницае­мо­сти .

Среда предполагается изотропной и немагнитной, , где – магнитная проницаемость вакуума.

Требуется отыскать поверхностные волны, распространяющиеся вдоль образующей волновода, т.е. собственные волны структуры. Электромагнитное поле собственной волны Е, Н удовлетворяет системе уравнений Максвелла:

(1)

условиям непрерывности касательных составляющих поля и при переходе через границу волновода и условиям экспонен­циаль­ного затухания поля на бесконечности.

Перейдем к цилиндрической системе координат . В случае ТМ-поляризации . Из уравнений Макс­велла следует, что и не зависят от .

Решение задачи будем искать в форме осесимметричных волн:

(2)

(3)

(4)

где – вещественная постоянная распространения волны.

Предполагаем, что внутри и вне волновода , , где – относительная диэлектрическая проницаемость. Обозначим также , где – волновое число вакуума.

Из уравнений Максвелла получим нелинейную систему дифференциальных уравнений:

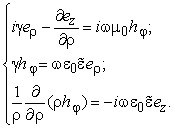(5)

Обозначим

(6)

. (7)

Будем предполагать, что – вещественные функции.

Обозначая , получим систему дифференциальных уравнений внутри волновода:

(8)

где производная означает дифференцирование по и

, (9)

, . (10)

Вне волновода , , тогда

,

, (11)

где – произвольная постоянная; – функ­ция Макдональда.

С учетом условий сопряжения на границе волновода

, (12)

получим:

. (13)

Сформулируем краевую задачу на собственные значения (задача Р): требуется отыскать не равные одновременно тождественно нулю на полубесконечном интервале функции класса

и соответствующие собственные значения такие, что удов­летворяют системе уравнений (8) на интервале , уравнени-
ям (11) на интервале , условиям сопряжения (12) и условиям экспоненциального убывания функций на бесконечности при . Спектральным параметром задачи является вещественное число .

Определение 1. Вещественное число называется собственным значением, отвечающим собственному вектору (собственным фун­к­циям) , если при этом существует нетри­виаль­ное ре­шение краевой задачи P.

Во второй главе из системы нелинейных уравнений (8) получаем дифференциальное уравнение второго порядка

, (14)

с линейной частью , дифференциальный опера­тор которой определяется формулой .

Уравнение (14) перепишем в виде

, (15)

где

. (16)

Построим функцию Грина для краевой задачи:

(17)

Получим

Из условий сопряжения следует дисперсионное уравнение:

. (19)

Внутри волновода при решения имеют представление

(20)

где

.

Для представления системы (20) в виде матричного оператора введем матрицу ядер:

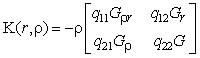(21)

и матрицу коэффициентов

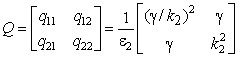, (22)

а также матричный линейный интегральный оператор с операторами , связанный с системой (24),

, (23)

где .

Тогда система интегральных уравнений (20) может быть записана в операторном виде

, (24)

где , а оператор определяется формулой

. (25)

Операторы являются линейными. Введем также линейные опе­раторы и .

Будем рассматривать уравнение (24) в пространстве непре­рыв­ных функций с нормой , где .

Пусть ,

.

Под непрерывностью функции в (в ) понимается, что для любой точки ( )

().

Под непрерывностью функции в понимается, что функция непрерывна во всех точках (в вышеуказанном смысле), за исключением точки . При этом функция , непре­рыв­ная в и в , не будет, вообще говоря, непрерывна в .

Утверждение 1. Функции и непрерывны в квад­рате . Функция ограничена в и непрерывна в и в , функция ограничена в и непрерывна в и в .

Утверждение 2. Пусть интегральный оператор задан формулой с кусочно-непрерывным в квад­ра­те ядром . Тогда он ограничен и верна оценка для его нормы

, (26)

где

. (27)

Утверждение 3. Пусть интегральный оператор задан формулой с ограниченными в квадрате ядрами, заданными формулами (21) и (22). Тогда он ограничен и верна оценка для его нормы

, (28)

где

                           . (29)

Приближенные решения , си­сте­мы интегральных уравнений (20) могут быть определены с помощью итерационного процесса метода сжимающих отображений

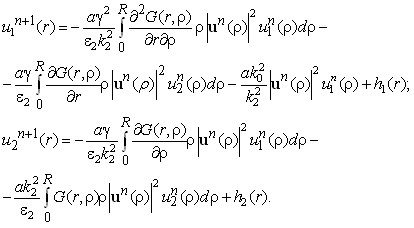(30)

Теорема 1. Пусть – шар радиуса с центром в нуле и выполнены два условия

(31)

и

. (32)

Тогда существует и единственное решение уравнения (24) [или системы (20)], и последовательность приближенных решений уравнения (24) [или системы (20)], определяемых посред­ст­вом итерационного алгоритма

(33)

сходится в норме пространства к (единственному) точному решению уравнения (24) [или системы (20)] при любом начальном приближении со скоростью геометрической прогрессии с показателем .

Рассмотрим вспомогательное числовое кубическое уравнение

, (34)

где норма оператора .

Лемма 1. Если выполняется неравенство

, (35)

то уравнение (34) имеет два неотрицательных решения r и r, r < r.

Теорема 2. Если ,

где (36)

и

,

то уравнение (24) имеет единственное решение в шаре , являющееся непрерывной функцией

.

В третьей главе доказано утверждение о существовании соб­ст­вен­ных значений для нелинейной задачи на собственные значения, т. е. су­ще­ствование решений дисперсионного уравнения (19) при некоторых достаточных условиях, наложенных на параметры задачи. Основным методом при доказательстве будет метод малого пара­метра.

Теорема 3. Пусть ядра матричного оператора и правая часть уравнения (24) непрерывно зависят от параметра , , на некотором отрезке ве­щественной числовой оси. Пусть также

. (37)

Тогда решения уравнения (24) при существуют, единственны и непрерывно зависят от параметра , .

Теорема 4. Пусть числа удовлетворяют условиям и ,

где , (38)

(39)

и выполняется условие

(40)

для определенного . Тогда существует, по крайней мере, соб­ст­венных значений , краевой задачи .

В четвертой главе рассмотрен численный метод для отыскания при­бли­женных решений нелинейной краевой задачи на собственные зна­чения P.

Приближенные решения системы интег­раль­ных уравнений (20) могут быть определены с помощью ите­ра­ционного процесса

. (41)

Утверждение 4. Пусть . Последовательность при­бли­женных решений системы уравнений (20), опре­де­ляе­мых посредством итерационного алгоритма (41), существует и схо­дит­ся в норме пространства к (единственному) точному решению системы уравнений (24), и верна оценка скорости схо­ди­мости:

, (42)

где – коэффициент сжатия отображения.

Теорема 5. Пусть существуют , удовлетворяющие ус­ло­виям , где определяется соотношением (38), и выпол­няется условие (40) для определенного . Тогда для каждого , существует, по крайней мере, значений , , удовлет­во­р­я­ю­­­щих неравенствам и являющихся корнями урав­не­ния

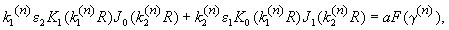(43)

где , а определяется соотношением (41).

Теорема 6. Пусть существуют , удовлетворяющие усл­о­виям , где определяется соотношением (38), и выпол­н­я­ет­ся условие (40) для определенного . Пусть и со­от­вет­ст­венно точное и приближенное собственные зна­че­ния проблемы на отрезке ( и – корни точного и прибли­женного ди­спер­сион­ных урав­нений, соответственно ). Тогда при .

На рисунке представлен график зависимости спектрального параметра от радиуса волновода для дисперсионного уравнения (19). Сплошными линиями на графике показана зависимость , пунктирными – ре­ше­ния уравнения (полюса функции Грина).

Выбор параметров: диэлектрическая проницаемость среды вне вол­новода ; диэлектрическая проницаемость среды внутри вол­но­вода ; радиус волновода ; волновое число сво­бод­но­го пространства ; коэффициент нелинейности .

В заключении сформулированы основные результаты работы.

В приложении содержатся постановка и решение соот­вет­ствую­щей линейной задачи о распространении ТМ-волн в волноводе, а так­­же вы­вод дисперсионного уравнения для этого случая.

ОСНОВНЫЕ РЕЗУЛЬТАТЫ ДИССЕРТАЦИИ

1. Нелинейная краевая задача на собственные значения, отве­чающая процессу распространения поверхностных ТМ-поляризо­ван­ных электро­магнитных волн в круглом диэлектрическом волноводе, заполненном не­линейной средой, описываемой по закону Керра, све­де­на к эквивалент­ной задаче на собственные значения для систе­мы интегральных уравне­ний.

2. Доказано существование единственного решения системы ин­тегральных уравнений при фиксированных значениях спектраль­ного параметра при выполнении определенных достаточных условий.

3. Получено дисперсионное уравнение, спектрально эквива­лент­ное исходной краевой задаче на собственные значения; доказаны тео­ремы о существовании и локализации собственных значений нели­ней­ной краевой задачи.

4. Предложен итерационный численный алгоритм для нахождения приближенных собственных значений и приближенных собственных функ­ций нелинейной краевой задачи; доказана сходимость прибли­жен­ных собственных значений и приближенных собственных функ­ций к точ­ным собственным значениям и собственным функциям за­дачи; выпол­нены численные расчеты приближенных собственных значений и при­бли­женных собственных функций для различных зна­чений параметров.

ПУБЛИКАЦИИ ПО ТЕМЕ ДИССЕРТАЦИИ

1. Хорошева, Э. А. Задача о распространении электромагнитных ТМ-волн в цилиндрических диэлектрических волноводах, заполнен­ных нелинейной средой / Э. А. Хорошева // Тр. XXVIII конф. молодых ученых механико-математического факультета МГУ. –
   М. : МГУ, 2006. – С. 218–223.
2. Хорошева, Э. А. Распространение электромагнитных ТМ-волн в цилиндрических диэлектрических волноводах с нелинейной сре­дой, выраженной законом Керра / Э. А. Хорошева // Надежность и ка­че­ство : тр. Междунар. симп. В 2 томах. Том 1 / под ред. Н. К. Юр­кова. – Пенза : Изд-во Пенз. гос. ун-та, 2006. – 410 с.
3. Хорошева, Э. А. О распространении электромагнитных
   ТМ-волн в цилиндрических диэлектрических волноводах, заполнен­ных нелинейной средой / Э. А. Хорошева // Надежность и качество : тр. Меж­дунар. симп. В 2 томах. Том 1 / под ред. Н. К. Юркова. –
   Пенза : Изд-во Пенз. гос. ун-та, 2006. – 410 с.
4. Хорошева, Э. А. Применение функций Грина к решению си­стем нелинейных дифференциальных уравнений / Э. А. Хорошева //
   Уни­верситетское образование : сб. ст. X Междунар. науч.-метод. конф. – Пенза, 2006. – С. 58–60.
5. Хорошева, Э. А. Распространение электромагнитных ТМ-волн в круглых диэлектрических волноводах, заполненных нелинейной сре­дой / Э. А. Хорошева, Ю. Г. Смирнов // Известия высших учеб­ных заведений. Поволжский регион. Естественные науки. – 2006. –
   № 5. – С. 106–114.
6. Хорошева, Э. А. Численное решение задачи о распространении электромагнитных ТМ-волн в круглых диэлектрических волново­дах, заполненных нелинейной средой / Э. А. Хорошева, М. Ю. Медведик, Ю. Г. Смирнов // Известия высших учебных заведений. Поволжский регион. Физико-математические науки. – 2010. – № 1. – С. 2–13.

Научное издание

Хорошева Эльвира Александровна

НЕЛИНЕЙНАЯ КРАЕВАЯ ЗАДАЧА
НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ СИСТЕМЫ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
РАСПРОСТРАНЯЮЩИХСЯ ЭЛЕКТРОМАГНИТНЫХ ТМ-ВОЛН
В КРУГЛОМ НЕЛИНЕЙНОМ ВОЛНОВОДЕ

01.01.02 – дифференциальные уравнения,
динамические системы и оптимальное управление

Редактор Т. В. Веденеева

Корректор Н. А. Сидельникова

Компьютерная верстка С. В. Денисовой

Подписано в печать 08. 10.10. Формат 60x841/16.

Усл. печ. л. 1,05. Тираж 100. Заказ № 615.

_______________________________________________________

Издательство ПГУ

440026, Пенза, Красная, 40.