Итеративный алгоритм для класса оптимизационных задач транспортного типа
На правах рукописи
Кузовлёв Дмитрий Игоревич
Итеративный алгоритм для класса оптимизационных задач транспортного типа
01.01.09 - Дискретная математика и математическая кибернетика
Автореферат диссертации на соискание ученой степени
кандидата физико-математических наук
Москва
2013
Работа выполнена в Федеральном государственном бюджетном учреждении науки Вычислительный центр им. А.А. Дородницына Российской академии наук
| Научный руководитель: | доктор физико-математических наук, профессор ЦУРКОВ Владимир Иванович |
| Официальные оппоненты: | ДИКУСАР Василий Васильевич, доктор физико-математических наук, главный научный сотрудник, Федеральное государственное бюджетное учреждение науки Вычислительный центр им. А.А. Дородницына Российской академии наук; МОКРЯКОВ Алексей Викторович, кандидат физико-математических наук, доцент, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «МАТИ – Российский государственный технологический университет имени К.Э.Циолковского» |
| Ведущая организация: | Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Тверской государственный университет» |
Защита состоится 26 декабря 2013 года на заседании диссертационного совета Д002.017.02 при Федеральном государственном бюджетном учреждении науки «Вычислительном центре им. А.А. Дородницына Российской академии наук» по адресу: 119333, г. Москва, ул. Вавилова, дом 40, конференц-зал в 15:00.
С диссертацией можно ознакомиться в библиотеке ВЦ РАН.
Автореферат разослан ______________ 20___ года.
Ученый секретарь
диссертационного совета Д 002.017.02,
д.ф.-м.н., профессор В.В. Рязанов
Общая характеристика работы
Уже прошло более 70 лет, как появились первые работы, где была поставлена и формализована транспортная задача. Центральным подходом в решении является метод улучшения плана (симплекс-метод линейного программирования). Специфика транспортной задачи предполагает рассмотрение таблицы, где в клетках записываются коэффициенты целевой функции и неизвестные количества перевозимой продукции из пунктов производства в пункты потребления. Переход от одного допустимого (базисного) решения к другому осуществляется с помощью построения цикла, в котором перемещается продукт, так что одна из клеток обнуляется. В результате осуществляется переход к базисному решению с меньшим значением функционала. Весьма распространённым в этом направлении является так называемый метод потенциалов, где переход к новому опорному решению осуществляется с помощью двойственных соотношений, которые для транспортной задачи имеют специфический вид. Широкое применение в транспортных постановках получил так называемый венгерский метод. В его основе лежит построение максимальных потоков через транспортную сеть с частично разрешёнными коммуникациями и последующее сокращение невязок. Известны также другие специальные методы. Например, предлагается применить двухуровневую технику метода декомпозиции Данцига-Вулфа для классической транспортной задачи. При этом исходная матрица условий разбивается по горизонтали таким образом, что верхний уровень решает независимые задачи с одним ограничением.
В данной работе предлагается метод решения задач транспортного типа, где последовательно решаются двумерные задачи с одной связывающей переменной. В результате задаются коэффициенты целевой функции для связывающей переменной, затем формулируются одномерные задачи. Их решения могут дать исходный оптимум или определить систему ограничений на переменные. Допустимые решения этой системы дают оптимальное решение исходной задачи. В другом случае упомянутая система не имеет допустимых решений. Здесь ставятся задачи о максимальном потоке, находится множество так называемых взаимно удовлетворённых пар. Затем формируется множество обобщённых производителей и потребителей и путём суммирования строится новая задача с меньшим числом ограничений. После этого процесс последовательного решения двумерных задач повторяется. Алгоритм строит последовательность так называемых псевдорешений с монотонным возрастанием функционала. Метод напрямую распространяется на широкий класс транспортных и распределительных задач.
Актуальность темы. Развитие железнодорожных и других перевозок приводит к постановкам всё более сложных и важных задач. Развиваемый в диссертации метод решения транспортных задач напрямую распространяется на достаточно широкий класс, например, указывается на применение к модификациям, когда каждому пункту потребления и производства сопоставляется собственные пункты производства и потребления, соответственно, куда направляется и вывозится соответствующее количество товаров. Стоимости за указанные перевозки могут нелинейно зависеть от количества товаров. Конструкции алгоритмов для этой модели совершенно не меняются. Таким образом, метод может использоваться в конкретных приложениях.
Цели и задачи исследования. Распространение метода улучшения плана для модификаций транспортных задач представляется нелёгким делом. Уже появление дополнительных переменных и функционалов на них вызывает усложнение конструкций традиционной схемы симплекс-метода. Ещё сложнее обстоит дело, когда, например, функционал на дополнительных переменных является нелинейным. Такая постановка рассматривается в диссертации. При этом алгоритм без каких-либо дополнительных процедур применяется так же как и к задаче о назначении с дополнительными работами и исполнителями, а также в случае запретов.
Научная новизна. Отправной точкой данной работы является анализ развития сетей связи с минимизацией капиталовложений при получении заданных потоков продукта. В соответствующих моделях рассматриваются, в частности, вопросы о построении тех или иных каналов. В соответствующих задачах большой размерности появляются булевы переменные, которые характеризуют тот факт, надо или не надо прокладывать каналы связи. Для смешанных частично-целочисленных задач применяются методы декомпозиции Бендерса, разделения переменных и т.д. Промежуточные задачи в алгоритмах понижающих размерность содержат большое количество булевых переменных – это так называемые многомерные задачи о ранце. Решение этих задач для практических размерностей вызывает большие трудности. Лишь в частных случаях удаётся построить эффективные алгоритмы. Один из таких случаев – это наличие лестничной структуры ограничений. Предлагаемый ранее в этом случае алгоритм последовательно решает двумерные задачи о ранце с зацеплениями. Возникает идея использовать эту технику для других классов задач с унимодулярными матрицами. Таким классом является задача транспортного типа. Предлагаемый алгоритм последовательно решает двумерные задачи с единственным зацеплением. В случае несовместности финальных систем уравнений в двумерных задачах зацепление может быть более сложным.
Методы исследования. В работе используются стандартные методы теории оптимизации. Алгоритм строит последовательность решений промежуточных одномерных задач. Из них строятся псевдорешения, которые не являются допустимыми для исходной задачи. Имеет место монотонный рост по функционалу. Выписываются формулы решений промежуточных двумерных задач с зацепляющими переменными. Последовательно пересчитываются коэффициенты функционалов. В финале ищется допустимое решение в системе равенств. Если его нет, решается задача о максимальном потоке. По некоторому правилу формируются корреспондирующие пары. Все этапы работы алгоритма, а также распространение для разных классов задач иллюстрируются примерами.
Теоретическая и практическая ценность. Алгоритм распространяется на широкий класс транспортных задач и задач о назначении. Одним из примеров может быть стохастическая постановка, когда правые части подчиняются экспоненциальному закону. В детерминированном эквиваленте фигурируют квадратичные по дополнительным переменным члены в функционале. Обоснование метода в этом случае подробно описано в диссертации.
Апробация. Результаты, представленные в работе докладывались на семинарах в ВЦ РАН и МАТИ, а также на конференциях:
Технические науки: теория и практика (г. Чита, апрель 2012 г.);
Всероссийская научная конференция, посвященная 60-летию ТТИ ЮФУ (ТРТИ, ТРТУ) "Современные проблемы математического моделирования, супервычислений и информационных технологий (СПМиИТ-2012)", Таганрог: 25-29 июня 2012 г.;
Технические науки в России и за рубежом (II) (г. Москва, ноябрь 2012 г.).
Публикации. По материалам диссертации опубликованы шесть работ, из них четыре находятся в изданиях из перечня ВАК (вторая и последние три из цитированных).
Структура работы. Работа состоит из настоящего введения, трёх глав, заключения, списка литературы. Объём диссертации 112 страниц.
Результаты, выносимые на защиту.
1. Представлены конструкции итеративного декомпозиционного метода на основе последовательного решения двумерных задач, а также пересчёта коэффициентов целевой функции, для постановки одномерных целочисленных задач.
2. Исследован случай, когда финальная система транспортных условий несовместна. Сформулировано правило введения обобщённых потребителей и поставщиков для нового цикла.
3. Даётся распространение подхода для широкого класса задач транспортного типа. Вводится постановка с собственными потребителями и поставщиками с линейными и квадратичными стоимостями перевозки в эти пункты. Представлены конструкции алгоритма для указанных моделей.
4. Итеративный метод распространяется для задач о назначении различных типов. Даётся конкретизация для классической задачи о назначении, а также для случая дополнительных работ и исполнителей, равно как и при наличии запретов. Представлено применение метода для задач распределения целей при эффективной стрельбе.
Содержание работы
Во вводных параграфах первой главы рассматривается проблема эффективного вложения капиталов на развитие сети - это задача минимизации капиталовложений при обеспечении заданных объемов потоков каждого продукта, или задача максимизации прибыли или нормы прибыли, или задача о выделении средств на развитие сети. Окончательно приходим к целочисленной задаче с булевыми переменными, которая в литературе известна как многомерная задача о ранце. При значительных размерностях её решение становится весьма трудоёмким. В специальном случае лестничной структуры ограничений удаётся построить эффективный алгоритм. Он основан на последовательном решении задач с двумя ограничениями и зацеплениями. Эта техника используется в дальнейшем для построения итеративного алгоритма для задач транспортного типа.
Далее в содержательной части первой главы представлены конструкции итеративного алгоритма на примере классической транспортной задачи. Подробно изложены его три этапа. Это – решение промежуточных двумерных задач с одной общей переменной, формирование одномерных целочисленных задач, отыскание допустимых решений финальных систем уравнений. Детально исследован случай, когда окончательная система линейных ограничений несовместна. Здесь решается задача о максимальном потоке через соответствующую транспортную сеть и по некоторому правилу строится система обобщённых поставщиков и потребителей. Затем итеративный процесс запускается вновь уже с новыми редуцированными ограничениями. Представлены примеры, которые детально иллюстрируют все шаги итеративного алгоритма. Численный тест рассматривает случай, когда невозможно провести вычисления аналитически.
Рассмотрим классическую транспортную задачу:
, (1)
, (2)
, (3)
. (4)
Предположим, что 
- целые положительные числа, а 
- чётные неотрицательные числа при всех 
.
Первый этап решения выглядит так. Вычислим 
и составим 
оптимизационных задач с ограничениями (1):
, 
(5)
-целые, 
(6)
Составим также ещё 
оптимизационных задач с ограничениями (2) и (6):
(7)
Задачи вида (1), (5), (6), и (2), (6), (7) решаются простым выбором нескольких наименьших коэффициентов целевой функции, а именно: пусть в задаче вида (1), (5), (6)
, тогда 
,
далее, если
, тогда 
и т. д.
Точно так же решаются и задачи (2), (6), (7).
Предположим, что все 
задач (1), (5), (6) и (2), (6), (7) решены. Объединение оптимальных решений всех 
одномерных задач назовём псевдорешением исходной транспортной задачи, а соответствующую сумму значений целевых функций - значением целевой функции псевдорешения. Значение целевой функции псевдорешения не превосходит значения целевой функции оптимального решения исходной транспортной задачи (1) –(4). Если объединение оптимальных решений всех 
задач (1), (5), (6) и (2), (6), (7) (псевдорешение исходной транспортной задачи) является допустимым решением исходной задачи (1)–(4), то оно является её оптимальным решением.
Рассмотрим второй этап решения. Пусть объединение оптимальных решений 
задач (1), (5), (6) и (2), (6), (7) не является допустимым решением исходной задачи (1)–(4). В этом случае строим итеративный процесс решения следующих двумерных оптимизационных задач. На первом шаге выпишем первое ограничение из (1), (
), и первое ограничение из (2), (
):
, (8)
. (9)
Составим целевую функцию:
(10)
и рассмотрим задачу (6), (8)–(10).
Выпишем первую из задач вида (1), (5), (6) и первую из задач (2), (6), (7) с новыми величинами 
и 
. Эти величины удовлетворяют условиям: их сумма равна 
, имеет место равенство сумм оптимальных значений одномерных задач оптимальному значению двумерной задачи. В результате сумма оптимальных значений одномерных задач будет увеличиваться.
Решение задачи (6), (8)–(10) является первым шагом итеративного процесса. На втором шаге этого процесса решается двумерная задача, формируемая из первого ограничения вида (1), т.е. 
, и второго ограничения вида (2), т.е. 
. Далее, на третьем шаге, снова 
, 
и т.д. до 
. На 
-м шаге полагаем 
,
и т.д. до 
,
.
После 
-го шага итерационного процесса получаем псевдорешения, сумма функционалов которых увеличивается по сравнению с нулевой итерацией, но не превосходит оптимального значения целевой функции исходной задачи.
Затем начинаем новый цикл до тех пор пока целевая функция на псевдорешениях не перестаёт увеличиваться. В результате имеют место следующие возможности. Одномерные задачи, которые формируют псевдорешения, имеют единственное оптимальное решение. Тогда они задают оптимум исходной задачи, и процесс заканчивается. Множества ограничений оптимальных решений одномерных задач, полученных по итогам цикла, имеют допустимые решения. Тогда они определяют оптимум исходной задачи. Наконец, упомянутые системы из ограничений для оптимальных решений одномерных задач являются несовместными. В этом случае предлагаются дополнительные конструкции. Рассмотрим максимальный поток через данную транспортную сеть, используя лишь линии, входящие в полученную систему ограничений транспортной задачи. Очевидно, что производители, вывезшие не весь свой продукт, вывозили его лишь в пункты потребления, которые полностью удовлетворили свои потребности. И, наоборот, потребители, не удовлетворившие свои потребности, получили свои поставки только из пунктов производства, вывезшие весь свой продукт. Пусть из пункта 
производства в построенном максимальном потоке вывезен не весь продукт. Обозначим через 
,
, … перечень пунктов потребления, куда вывозился продукт из пункта 
. Очевидно, что пункты потребления 
,
, … удовлетворены поставщиками полностью, иначе можно было бы увеличить общий поток вопреки его максимальности. Продолженная таким образом цепочка «производители – потребители» однозначно задаст некоторое подмножество полностью удовлетворённых потребителей и второе подмножество – это подмножество их производителей. Так заданные подмножества производителей и потребителей назовём обобщёнными производителями и потребителями соответственно. К имеющимся ограничениям исходной задачи добавим соответствующие суммы ограничений обобщённых производителей и потребителей и начнём новый цикл итеративного процесса, решая последовательность двумерных задач.
Все конструкции алгоритма иллюстрируются аналитическими примерами. Кроме того, метод демонстрируется для транспортной задачи размерности 7х7. Здесь не представляется возможным осуществить последовательные расчеты, как это делается для иллюстрирующих примеров, поэтому задача решается численно. Результаты расчёта совпадают с аналогом, полученным по классическому методу потенциалов.
Во второй главе итеративный метод распространяется для различных модификаций транспортной задачи. Сначала рассматривается известная модель с ограниченными пропускными способностями. Алгоритм переносится без каких-либо изменений. Только несколько меняются формулы решения промежуточных двумерных задач, где учитываются двусторонние ограничения на переменные. Затем ставится задача, где каждый потребитель и поставщик имеют помимо общих также собственных производителей и потребителей соответственно. На дополнительные переменные формулируются линейные и квадратичные зависимости стоимостей перевозок. Формулы решения промежуточных двумерных задач существенно изменяются, особенно в квадратичном случае, однако все шаги итеративного алгоритма остаются такими же. Наконец, рассматривается транспортная задача с запретами, когда по некоторым парам индексов перевозки невозможны. В приведённом примере на некотором шаге алгоритм указывает на недопустимость решений в исходной задаче.
Остановимся на задаче с дополнительными пунктами производства и потребления. Пусть 
-ый производитель товара 
может поставлять товар не только каждому 
-му потребителю 
, но и своему индивидуальному 
-му потребителю. Объём поставок товара 
-му потребителю 
, в отличие от 
-х потребителей, не фиксирован. Он неотрицателен, разумеется, ограничен объёмом производства в 
-ом пункте производства 
. Пусть также каждый 
-ый потребитель 
имеет возможность удовлетворить свои потребности за счёт поставки товара от своего индивидуального 
-го поставщика 
. Объём поставки 
-му потребителю от индивидуального поставщика не фиксирован и ограничен объёмом потребности 
-го потребителя 
. Пусть заданы стоимости поставки единицы товара от 
-го поставщика 
-му потребителю 
, а также заданы стоимости поставки единицы товара каждому индивидуальному потребителю 
и стоимость поставки товара от индивидуального поставщика 
. В заданных условиях необходимо минимизировать общие расходы на перевозку товара при фиксированных объёмах производства у обычных поставщиков и фиксированных объёмах потребления у обычных потребителей.
Формальная запись задачи имеет вид
, (11)
, (12)
, (13)
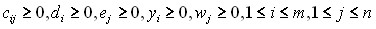. (14)
Первый этап строится по аналогии со стр. 8.
Вторым этапом алгоритма будет итерационный процесс решения двумерных оптимизационных задач. Приведём формулы их решения. На первом шаге решается следующая задача
, (15)
, (16)
(в ограничениях вида (11) полагается 
, а в ограничениях вида (12) 
)
. (17)
Здесь могут иметь место три случая. Первый случай:
. (18)
Тогда полагаем 
, одно из двух ограничений выходит при этом на равенство далее задача (15)-(17) по существу превращается в одномерную задачу. После решения задачи (15)-(17) найдём новые 
и 
сначала из системы уравнений
Затем, при необходимости, округлим 
до ближайшего целого в меньшую сторону, а 
- в большую сторону. Второй случай:
. (19)
Пусть для определённости, 
и двойные минимумы в (19) достигаются при 
и 
соответственно. В этом случае вместо решения выписываем уравнения 
. Далее, как и в предыдущем случае, задача (15)-(17) решается как одномерная. Выписываем новые значения 
и 
.
Если двойные минимумы в (19) равны 
и 
, уравнения вместо решения имеют вид 
. Выписываем новые значения коэффициентов при 
в одномерных задачах 
. Если первый двойной минимум в (19) равен 
, а второй достигается на некотором 
, то соответствующие уравнения имеют вид 
и, соответственно, 
и 
. Третий случай:
.
Временно исключим из рассмотрения 
, полагая равным нулю, и решим две получившиеся одномерные задачи. Если имеет место неравенство
, то тем самым двумерная задача решена. Далее, найдём новые 
и 
сначала из системы уравнений
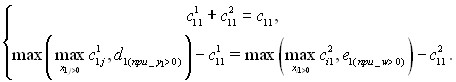
Округлим до целого так же, как и во втором случае. Если имеет место равенство
,
то, очевидно, что у решаемой задачи оптимальное решение не единственно и 
может принимать целочисленные значения от 
до 
в сумме с 
(может быть 
) или 
(может быть 
) соответственно. Здесь 
и 
- остатки от 
и 
перед назначением последних положительных значений переменных в соответствующих одномерных задачах. Этот факт мы запишем в виде ограничений 
(возможно, 
) и 
(возможно, 
). Коэффициенты 
и 
в этом случае принимают значения 
(или 
) и 
(или 
). Если 
, то, очевидно, в оптимальной решении двумерной задачи должно иметь место неравенство 
. Предположим, что 
. Обнуляя 
и 
, полагаем 
. Одно из ограничений при этом выйдет на равенство и далее задача становится одномерной. Теперь пусть, для определённости, 
. В этом случае обнуляем 
, увеличиваем 
на 
, 
уменьшаем на 
и переходим в сравнению 
и суммы 
, где 
- номер следующей ненулевой переменной в оптимальном решении соответствующей одномерной задачи. Если имеет место равенство 
, то выписываем ограничения. Если имеет место неравенство 
, то процесс нахождения значения 
окончен. Учитывая, что 
, новые значения 
и 
определим следующим образом: 
.
Теорема 1. Объединение оптимальных решений двух одномерных задач, сформированных по итогам решения задачи (15)-(17) будет совпадать с оптимальных решением задачи (15)-(17).
Заметим, что сумма значений целевых функций в оптимальных решениях одномерных задач, сформированных после решения двумерной задачи (15)-(17), будет не меньше чем сумма значений целевых функций этих же одномерных задач до объединения их в двумерную задачу.
На втором шаге снова полагаем 
, но 
. Далее, на третьем шаге 
, и так далее до 
. На 
шаге полагаем 
и т.д. до 
. После 
-го шага итерационного процесса снова полагаем 
, то есть ограничения будут такими же, как и на первом шаге, изменится лишь целевая функция.
Итерационный процесс окончен, когда сумма значений целевых функций во всех 
одномерных задачах перестает возрастать.
Предположим, что в итоге все 
одномерные задачи имеют единственное решение. Тогда, очевидно, имеет место утверждение.
Теорема 2. Объединение оптимальных решений одномерных задач является оптимальным решением исходной задачи (11)-(14).
В следующем параграфе берутся квадратичные зависимости по перевозкам продукта из пунктов потребления в пункты производства. Все конструкции метода остаются теми же самыми, хотя решение промежуточных двумерных задач усложняется.
Наконец, в последнем параграфе данной главы алгоритм применяется к так называемым транспортным задачам с запретами. Эти задачи, вообще говоря, могут не иметь допустимого решения. Поэтому алгоритм может либо построить оптимальное решение, либо установить недопустимость.
В третьей главе метод распространяется на распределительные задачи.
Сначала берётся классическая постановка о распределении работ по исполнителям с минимизацией общей суммы рабочего времени. Здесь промежуточные формулы двумерных и одномерных задач упрощаются, однако возможность отсутствия допустимого решения финальной системы остаётся, и приведённые примеры это показывают. Далее рассматривается задача о назначении с дополнительными работами и исполнителями. Она обобщает постановку второй главы с собственными поставщиками и потребителями. Здесь имеет смысл только линейный штраф ввиду булевых переменных. Приводятся конструкции алгоритма для этого случая. Затем демонстрируется нахождение оптимального решения задачи о назначении в случае запретов, при этом алгоритм одновременно показывает наличие допустимых решений в этой постановке.
Итак, имеем задачу о назначении:
, (20)
, (21)
, (22)
- целые, 
, 
. (23)
Здесь используется известная интерпретация. Имеются 
работ и 
исполнителей. 
- количество рабочих часов, которые затрачивает 
-й исполнитель на 
-ю работу. Целью является минимизация суммы рабочего времени на выполнение всех 
работ.
Первый этап аналогичен стр. 8.
На втором этапе строим итеративный процесс решения следующих двумерных оптимизационных задач. На первом шаге выпишем первые ограничения из (20) и из (21), (
), и первое ограничение из (21):
, (24)
. (25)
Составим целевую функцию:
(26)
и рассмотрим задачу (24)-(26).
При решении задачи (24)-(26) могут иметь место три случая.
Первый случай:
(27)
Тогда полагаем 
и задача (24)-(26) решена. После решения задачи (24)-(26) найдём новые 
и 
сначала из системы уравнений
Затем, при необходимости, округлим 
до ближайшего целого в меньшую сторону, а 
- в большую сторону.
Второй случай:
Пусть
(28)
Тогда обозначим 
и 
, вместо решения выписываем ограничения
, 
. Вычисляем новые значения 
и 
.
Третий случай:
(29)
Тогда, очевидно, что 
, 
и задача (24)-(26) решена. Далее, найдём новые 
и 
из системы уравнений
Округлим до целого так же, как и во втором случае. Сформируем с новыми значениями 
и 
две одномерные задачи. Первая задача
(30)
при ограничениях (1.6), (2.1) и вторая задача
(31)
при ограничениях (25).
Имеет место следующее утверждение.
Теорема 3. Во всех вышеперечисленных случаях (выполняется соотношение (27), (28) или (29) ) объединение оптимальных решений одномерных задач (24), (30) и (25), (31) с новыми значениями 
и 
является оптимальным решением двумерной задачи (24)-(26).
Решение задачи (24)-(26) является первым шагом итеративного процесса. На втором шаге решается двумерная задача, формируемая из первого ограничения вида (20), т.е. 
, и второго ограничения вида (21), т.е. 
. Далее, на третьем шаге, снова 
, 
и т.д., до 
. На 
-ом шаге полагаем 
,
и т.д. до 
,
. После 
-го шага итерационного процесса снова полагаем 
в ограничениях вида (20) и 
в ограничениях вида (21), то есть, ограничения будут такими же как и на первом шаге пошагового процесса. Целевая функция будет той, которая получится к этому 
-му шагу. Как уже отмечалось, в результате итерационного процесса сумма значений целевых функций 
одномерных задач возрастает.
Пусть цикл окончен. Предположим, что в итоге все 
одномерные задачи имеют единственное решение. Тогда справедлив критерий оптимальности.
Теорема 4. Объединение решений одномерных задач является оптимальным решением исходной задачи о назначении (20)-(23).
Рассмотрим далее другую возможность – во всех одномерных задачах по итогам цикла получены ограничения на переменные, т.е. любое допустимое решение каждой одномерной задачи является её оптимальным решением. Пусть множество ограничений одномерных задач, полученных по итогам цикла является множеством ограничений новой задачи о назначении с меньшим, в общем случае, числом переменных, чем исходная. Тогда имеет место следующий критерий оптимальности.
Теорема 5. Любое допустимое решение редуцированной задачи о назначении, полученной в результате пошагового процесса есть её оптимальное решение.
Возможна ситуация, когда система итоговых ограничений формирует ограничения задачи, которая может не иметь допустимых решений. Здесь верны дополнительные конструкции, связанные с построением обобщённых работ и исполнителей.
Далее в третьей главе ставится задача с дополнительными работами и исполнителями, которая в идейном смысле близка к постановке второго параграфа. Конструкции итеративного алгоритма представлены и для этого случая. Наконец, в третьем параграфе данной главы рассматривается пример, который иллюстрирует работу алгоритма для задачи о назначении с запретами. Наконец, в последнем параграфе алгоритм применяется к задаче о целераспределении при эффективной стрельбе.
Заключение
Итак, предлагаемый итеративный метод строит не одно, а множество оптимальных решений исходной задачи и применим для широкого класса задач транспортного типа. Постановки второго и третьего параграфа второй главы непосредственно могут использоваться в стохастическом программировании. В первом случае имеем непосредственное отношение в двухэтапной задаче, когда правые части задаются конечным набором величин с заданными вероятностями, и детерминированная эквивалентная задача близка к рассматриваемой в диссертации модели. Во втором случае квадратичные по дополнительным переменным слагаемые в функционале типичны для одноэтапной стохастической постановки при экспоненциальном распределении случайной правой части исходных ограничений. Следующим шагом исследований в распространении алгоритма могли бы быть так называемые распределительные задачи, где часть транспортных ограничений для данного набора индексов включает некоторые матрицы. Самым близким классом в этом направлении являются задачи об эффективной стрельбе, которые формализуются в виде унимодулярных матриц ограничений. Наконец, могли бы быть рассмотрены несколько пунктов потребления, соответствующих одному пункту производства, а также несколько пунктов производства, соответствующих одному пункту потребления, в задаче с дополнительными пунктами как в транспортной постановке, так и в аналоге для распределительной модели. В задаче об эффективной стрельбе могли бы быть рассмотрены собственные цели и огневые точки. Изучение этой задачи приводит к предположениям о замене трудоемкой процедуры максимизации потока на более простые конструкции. Однако, эти обобщения остаются за рамками данного исследования и только прогнозируются.
Список публикаций по теме диссертации
1. Кузовлев Д.И., Тизик А.П., Тресков Ю.П. Метод последовательных изменений параметров функционала при решении задачи о назначении // Известия Российской академии наук. Теория и системы управления. 2011. №6. С.67–78.
2. Кузовлев Д.И., Тизик А.П., Тресков Ю.П. Декомпозиционный алгоритм для решения транспортной задачи с ограниченными пропускными способностями // Мехатроника, автоматизация, управление. 2012. № 1. С.45–48.
3. Тизик А.П., Кузовлев Д.И., Соколов А.А. Метод последовательной модификации функционала для транспортной задачи с дополнительными пунктами производства и потребления // Вестник ТвГУ. Серия прикладная математика. 2012. №4. С.91-98.
4. Кузовлев Д.И., Тизик А.П., Тресков Ю.П. Итеративный алгоритм для задачи о назначении // Технические науки: теория и практика: материалы междунар. заоч. науч. конф. (г. Чита, апрель 2012 г.). – Чита: Издательство Молодой ученый, 2012., С.41-43.
5. Кузовлев Д.И., Тизик А.П., Тресков Ю.П. Итеративный метод решения транспортной задачи с ограниченными пропускными способностями // Труды Всероссийской научной конференции, посвященной 60-летию ТТИ ЮФУ (ТРТИ, ТРТУ) "Современные проблемы математического моделирования, супервычислений и информационных технологий (СПМиИТ-2012)", Таганрог: 25-29 июня 2012 г., Известия ЮФУ. Технические науки, № 6 (131). 2012 г., С.252-255.
6. Кузовлев Д.И., Тизик А.П., Тресков Ю.П. Задача о назначении с дополнительными работами и исполнителями // Технические науки в России и за рубежом (II): материалы междунар. заоч. науч. конф. (г. Москва, ноябрь 2012 г.). – Москва: Буки-Веди, 2012., С.16-18.
