Равномерная сходимость приближенных решений сингулярного интегрального уравнения первого рода с ядром коши
На правах рукописи
Хайруллина лилия ЭМИТОВНА
РАВНОМЕРНАЯ СХОДИМОСТЬ ПРИБЛИЖЕННЫХ
РЕШЕНИЙ СИНГУЛЯРНОГО ИНТЕГРАЛЬНОГО
УРАВНЕНИЯ ПЕРВОГО РОДА С ЯДРОМ КОШИ
Специальность 01.01.01 – вещественный, комплексный и
функциональный анализ
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата физико-математических наук
Казань-2011
Работа выполнена на кафедре теории функций и приближений ФГАОУВПО “Казанский (Приволжский) федеральный университет”
| Научный руководитель: | кандидат физико-математических наук, доцент Ожегова Алла Вячеславовна |
| Официальные оппоненты: | доктор физико-математических наук, профессор Плещинский Николай Борисович |
| кандидат физико-математических наук, доцент Апайчева Любовь Алексеевна | |
| Ведущая организация: | Национальный исследовательский Саратовский государственный университет имени Н.Г. Чернышевского |
Защита состоится "24" ноября 2011 г. в 14.30 часов на заседании диссертационного совета Д212.081.10 при ФГАОУВПО “Казанский (Приволжский) федеральный университет” по адресу: 420008, г.Казань, ул. Профессора Нужина, 1/37, ауд.337.
С диссертацией можно ознакомиться в Научной библиотеке им. Н.И.Лобачевского ФГАОУВПО “Казанский (Приволжский) федеральный университет” по адресу: 420008, г. Казань, ул. Кремлевская, 18.
Автореферат разослан "19" октября 2011 г. и размещен на официальном сайте ФГАОУВПО “Казанский (Приволжский) федеральный университет”.
| Ученый секретарь совета Д 212.081.10 к.ф.-м.н., доцент |  | Е.К. Липачев |
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы. Диссертация посвящена систематическому исследованию равномерной сходимости приближенных методов решения сингулярного интегрального уравнения (кратко с.и.у.) с ядром Коши на отрезке вещественной оси, а также его двумерного аналога с сингулярными интегралами, понимаемыми в смысле главного значения по Коши.
Рассматриваемые в работе сингулярные интегральные уравнения находят широкое применение в задачах теории упругости, аэродинамики, электродинамики, теории автоматического управления, квантовой механики и других областях математической физики и техники.
Теория таких уравнений достаточно хорошо разработана. Она изложена, прежде всего, в известных монографиях Н. И. Мусхелишвили[1], ФД. Гахова[2], И.Ц. Гохберга и И.Я. Крупника[3]. Из теории таких уравнений следует, что найти точное решение с.и.у. в замкнутой форме удается лишь в отдельных случаях, причем для получения числового результата приходится вычислять регулярные и сингулярные интегралы со сложными плотностями. Поэтому разработка и теоретическое обоснование аппроксимативных методов их решения является актуальной задачей. При этом как для теории, так и для практики наиболее интересны равномерные оценки погрешности приближенных решений. Установление таких оценок представляет определенную трудность, которая связана, прежде всего, с тем, что в пространстве непрерывных функций задача решения исследуемых уравнений является некорректно поставленной.
Один из подходов к решению указанной задачи, разработанный А.Н. Тихоновым, М.М. Лаврентьевым, В.К. Ивановым, их учениками и последователями[4], основан на некорректной постановке задачи и решении ее соответствующими методами. С.М. Белоцерковским[5] был создан метод дискретных вихрей численного решения с.и.у. В дальнейшем он был развит в работах И.К. Лифанова[6] и его учеников. Доказано, что метод дискретных вихрей является методом регуляризации численного решения некорректного в равномерной метрике с.и.у. первого рода.
В данной работе используется другой подход, основанный на отыскании корректной постановки задачи решения с.и.у. путем подбора пространств искомых элементов и правых частей с последующим применением аппроксимативных методов решения и их теоретическим обоснованием в этих пространствах. К настоящему времени корректность задачи решения рассматриваемых с.и.у. установлена в пространствах гельдеровых функций и в весовых пространствах Лебега, в них проведено обоснование ряда приближенных методов решения изучаемых уравнений. При этом в работах зарубежных математиков основное внимание уделено численной реализации. Определенные итоги и библиографию по результатам таких исследований можно найти в обзорных работах В.В.Иванова[7], Б.Г.Габдулхаева[8], в монографиях и работах В.В.Иванова[9], Б.Г.Габдулхаева[10], З. Прёсдорфа[11], М.А. Шешко[12], И.В. Бойкова[13], их учеников и последователей. Однако систематически сходимость приближенных решений указанных уравнений в равномерной метрике до сих пор не изучалась. Это определяет актуальность темы исследований.
Цель работы. Целью работы является получение равномерных оценок погрешности приближенных решений исследуемых уравнений путем установления корректной постановки задачи на парах специально подобранных пространств непрерывных функций и проведение в них теоретического обоснования различных аппроксимативных методов.
В диссертации под теоретическим обоснованием понимается следующий круг вопросов:
а) доказательство теорем существования и единственности решения, аппроксимирующего уравнения;
б) доказательство сходимости приближенных решений к точному решению и определение скорости сходимости;
в) установление эффективных оценок погрешности приближенного решения, учитывающих структурные свойства исходных данных;
г) исследование устойчивости и обусловленности аппроксимативных методов.
Методы исследования. При выводе и обосновании результатов диссертации используется аппарат полиномиального приближения из конструктивной теории функций, методики из общей теории приближенных методов, функционального анализа и теории сингулярных интегральных уравнений.
Научная новизна. Все результаты, полученные в диссертации, являются новыми. В работе для различных классов решений введены новые пары пространств искомых элементов и правых частей, являющихся сужением пространства непрерывных функций, в которых задачи решения исследуемых сингулярных интегральных уравнений поставлены корректно. Во введенных пространствах разработаны элементы конструктивной теории функций. На базе полученных результатов дано теоретическое обоснование вычислительных схем ряда известных приближенных методов и получены равномерные оценки сходимости приближенного решения к точному.
Теоретическая и практическая значимость. Диссертация носит теоретический характер. Полученные в диссертационной работе результаты могут быть использованы в теории приближенных методов решения сингулярных интегральных уравнений, а также применены при решении конкретных прикладных задач физики, механики и математической физики, сводящихся к указанным уравнениям.
Апробация работы. Основные результаты диссертации докладывались и обсуждались на Итоговых научных конференциях Казанского государственного университета (2003 - 2009) и Татарского государственного гуманитарно-педагогического университета (2010), на Казанских международных летних научных школах-конференциях (г. Казань, 27 июня - 4 июля 2003 г., 26 сентября - 1 октября 2004 г., 27 июня - 4 июля 2007 г., 1 - 7 июля 2009 г., 1 - 5 июля 2011 г.), а также представлялись на международных научно-практических конференциях "Научный потенциал мира - 2004" (Днепропетровск, 2004), "Дни науки" (Днепропетровск, 2005, 2006).
Публикации. Основные результаты диссертации опубликованы в работах [1] – [7], работа [4] – из списка ВАК. В совместных работах научному руководителю принадлежат постановка задач и идея методики исследования, соответствующие результаты получены лично диссертантом.
Структура и объем работы. Диссертационная работа изложена на 103 страницах и состоит из введения, двух глав, включающих параграфы, и библиографического списка использованной литературы, содержащего 92 наименования.
ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ
Во введении дается обзор используемой литературы по теме диссертации, излагается краткое содержание работы, формулируются основные результаты, выносящиеся на защиту.
Первая глава (§§1 - 3) посвящена исследованию равномерной сходимости приближенных методов решения с.и.у. первого рода с ядром Коши на отрезке вещественной оси вида
где h(t, t), f(t) – известные непрерывные функции в своих областях определения, j(t) – искомая функция, а сингулярный интеграл (с.и.)
понимается в смысле главного значения по Коши.
В параграфе 1 рассмотрен класс решений, неограниченных на обоих концах отрезка [-1, 1]. Согласно общей теории с.и.у., решение уравнения (1) может быть представлено в виде 
, где 
- новая искомая функция, а 
. Параграф состоит из нескольких пунктов.
В пункте 1.1 вводятся линейные нормированные весовые пространства Xr[-1, 1] и Yq[-1, 1], 
.
Xr = Xr[-1, 1] - пространство непрерывных на [-1,1] функций x(t), удовлетворяющих условию
,
для которых с.и. 
является также непрерывной функцией на (-1, 1) и допускающей непрерывное продолжение на концы отрезка интегрирования.
Yq = Yq[-1, 1] - пространство непрерывных на [-1,1] функций f(t) таких, что с.и. I(qf; t) является непрерывной функцией.
В этих пространствах определены следующие нормы
;
,
где 
.
В лемме 1.1 доказано, что сингулярный оператор 
, где
непрерывно обратим и справедливы равенства
, 
.
Пространства Х и Yq являются полными.
Установлены достаточные условия корректности задачи решения уравнения (1).
В пункте 1.2 получены оценки норм известных полиномиальных операторов и установлены их аппроксимативные свойства в пространстве Yq.
Пусть 
- оператор Фурье, ставящий в соответствие любой функции L[-1; 1] ее отрезок ряда Фурье
по полиномам Чебышева II рода 
, где 
- коэффициенты Фурье-Чебышева.
Доказана
Лемма 1.2. Для любой функции j О С[-1; 1] справедлива оценка
.
Если Yq, то
,
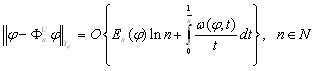где En(j) - наилучшее равномерное приближение функции j(t) алгебраическими полиномами порядка не выше n, w(j, d) - модуль непрерывности функции j(t) с шагом d О (0; 2].
Через 
обозначим множество функций, имеющих непрерывную производную r-го порядка, удовлетворяющую условию Гельдера с показателем a, 0 < a Ј 1, r і 0.
Через 
обозначим множество функций, имеющих непрерывную производную r-го порядка, удовлетворяющую неравенству 
, где M = const, а r > 0 - произвольно фиксированное действительное число.
Через 
обозначим множество функций, имеющих непрерывную r-ую производную, модуль непрерывности которой не превосходит заданного модуля непрерывности = (), 
.
Установлена
Лемма 1.4. Если 
, то справедливо соотношение
, 0 < a Ј 1, r і 0.
Если 
, то справедливо соотношение
, r > 0.
Если 
, то
, r і 0.
Пусть Ln() = Ln(j; t) – интерполяционный полином Лагранжа функции j О С[-1; 1] по системе узлов
.
Доказана
Лемма 1.5. Для любой функции j О С[-1; 1] справедлива оценка
.
Если j О Yq, то
.
Пусть Пn - оператор подобластей, ставящий в соответствие любой функции j О С[-1; 1] алгебраический полином Пn(j, s), однозначно определяющийся из условий
, 
.
Лемма 1.6. Для любой функции j О С[-1; 1] справедлива оценка
.
Если 
, то справедливо соотношение
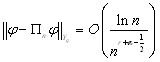, 0 < a Ј 1, r і 0, r + a > 
.
Полученные в леммах 1.2 – 1.6 результаты позволили теоретически обосновать известные аппроксимативные методы рассматриваемого с.и.у. (1) и установить равномерные оценки погрешности. Кроме того, эти результаты в дальнейшем могут быть использованы для исследования других классов интегральных уравнений.
В пункте 1.3 с.и.у. (1) решается с помощью общего проекционного метода, согласно которому приближенное решение исходного уравнения определяется как точное решение приближенного функционального уравнения
Knxn PnKxn = Sxn + PnVxn = Pnf,
(xn Hn X, Pnf Hn-1 Yq),
где 
, Hn – множество алгебраических многочленов степени не выше n, Pn – некоторый линейный оператор, отображающий пространство Yq в подпространство Hn-1. Имеет место
Теорема 1.3. Пусть выполнены условия:
а) с.и.у. (1) однозначно разрешимо в пространстве Хr при любой правой части f(t) из Yq;
б) ядро h(t, t) таково, что оператор V: Хr Yq вполне непрерывен;
в) оператор 
и Pn E сильно в Yq, где Е – единичный оператор.
Тогда, начиная с некоторого n О N, аппроксимирующие уравнения также однозначно разрешимы и приближенные решения 
сходятся к точному 
со скоростью
,
где 
означает, что оператор Рn применен к h(t, ) по переменной t.
В теореме 1.4 установлена скорость сходимости общего проекционного метода в терминах наилучшего приближения функций алгебраическими полиномами в пространстве Yq.
В пунктах 1.4 - 1.6 рассмотрены и теоретически обоснованы известные вычислительные схемы методов ортогональных многочленов, коллокации и подобластей решения уравнения (1), являющихся конкретными реализациями общего проекционного метода.
В методе ортогональных многочленов приближенное решение ищется в виде
,
где Тk(t) – полиномы Чебышева I рода k-го порядка, а неизвестные коэффициенты k, 
, определяются из СЛАУ
,
,
.
Справедлива
Теорема 1.5. Пусть выполнены условия:
а) с.и.у. (1) однозначно разрешимо в пространстве Хr при любой правой части f(t) из Yq;
б) функция f(t) О WrHa, ядро h(t, t) О WrHa по переменной t равномерно относительно t, 0 < a Ј 1, r і 0.
Тогда, начиная с некоторого n О N, система линейных алгебраических уравнений (СЛАУ) метода ортогональных многочленов имеет единственное решение {ak*}, 
. Приближенные решения 
сходятся к точному х*(t) равномерно со скоростью
, 0 < a Ј 1, r і 0.
Для этого метода в теореме 1.6 доказана сходимость невязок приближенных решений.
В пункте 1.7 установлена равномерная сходимость метода механических квадратур решения уравнения (1).
В пункте 1.8 рассмотрен проекционно-итеративный метод решения уравнения (1). Доказана теорема о его сходимости, получены равномерные оценки погрешности.
Пункт 1.9 посвящен исследованию устойчивости и обусловленности рассмотренных выше приближенных методов.
Теорема 1.11. В условиях теорем 1.5, 1.7, 1.8, 1.9 справедливы утверждения:
а) методы ортогональных многочленов, коллокации, подобластей и механических квадратур устойчивы относительно малых возмущений элементов соответствующих аппроксимирующих систем линейных алгебраических уравнений;
б) из хорошей обусловленности точного с.и.у. (1) следует хорошая обусловленность соответствующих аппроксимирующих уравнений исследованных методов.
В параграфе 2 исследуется случай решения, ограниченного на обоих концах отрезка. Здесь 
, где 
. Параграф состоит из 5 пунктов.
Пункт 2.1 посвящен установлению корректной постановке задачи на паре пространств искомых элементов 
и правых частей 
, 
.
- пространство непрерывных на [-1, 1] функций x(t), для которых сингулярный интеграл 
также является непрерывной функцией.
- пространство непрерывных на [-1, 1] функций f(t) таких, что 
является непрерывной функцией на (-1, 1), допускающей непрерывное продолжение на концы отрезка интегрирования, и выполняется условие
Нормы в этих пространствах определены соответственно следующим образом:
;
В лемме 2.1 устанавливается непрерывная обратимость сингулярного интегрального оператора на введенной паре пространств.
В пункте 2.2 получены оценки, характеризующие аппроксимативные свойства операторов Фурье по полиномам Чебышева первого рода, операторов Лагранжа и подобластей в пространстве Yq.
Установленные в пункте 2.2 оценки, имеющие и самостоятельный интерес, позволили теоретически обосновать в пункте 2.3 известные вычислительные схемы методов ортогональных многочленов, коллокаций, подобластей, механических квадратур и установить равномерные оценки погрешности приближенных решений.
В пункте 2.4 исследован аппроксимативно-итеративный метод, позволяющий уточнять приближенное решение, найденное прямым методом.
Пункт 2.5 посвящен установлению скорости сходимости к нулю невязки метода ортогональных многочленов.
В параграфе 3 рассматривается случай решения, ограниченного на одном конце отрезка [-1, 1] и неограниченного на другом. В этом случае 
, 
.
Пункт 3.1 посвящен выбору пространств, в которых задача решения уравнения (1) будет корректно поставлена. Показано, что в качестве таких пространств могут быть выбраны следующие.
Пусть Х - пространство непрерывных на [-1,1] функций x(t), для которых сингулярный интеграл 
является непрерывной функцией на [-1, 1), допускающей непрерывное продолжение в точку t = 1. Здесь 
.
В качестве Yq выбрано пространство непрерывных на [-1, 1] функций f(t) таких, что 
является непрерывной функцией на (-1, 1], допускающей непрерывное продолжение в точку t = -1, 
.
Нормы в этих пространствах определены следующим образом:
В пункте 3.2 в пространстве Yq установлены оценки приближения функций отрезками рядов Фурье по полиномам, ортогональным с весом q(t) на [-1, 1], и интерполяционными полиномами Лагранжа. Эти оценки позволили в пункте 3.3 доказать равномерную сходимость методов ортогональных многочленов и коллокаций.
Вторая глава (§§1 - 3) посвящена приближенному решению двумерного с.и.у. первого рода вида
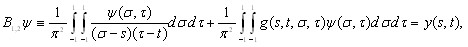
|s| < 1, |t| < 1,
где g(s, t, s, t), y(s, t) – известные непрерывные функции в своих областях определения, y(s, t) – искомая функция, а сингулярный интеграл
понимается в смысле главного значения по Коши.
Как и в одномерном случае, задача решения уравнения (2) является некорректно поставленной в пространстве непрерывных функций. Однако и здесь возможно отыскание корректной постановки на паре пространств, являющихся сужением пространства непрерывных функций, что дает возможность применения аппроксимативных методов решения с последующим теоретическим обоснованием и получением равномерных оценок погрешности. В диссертационной работе рассмотрены три класса решений. Результаты для других классов решений могут быть получены аналогично.
В параграфе 1 рассмотрен класс решений, ограниченных на двух смежных сторонах квадрата [-1, 1]2 и неограниченных на двух других его сторонах. Решение уравнения ищется в виде 
, где x(s, t) - новая искомая функция, а 
.
Пусть 
- пространство непрерывных в квадрате [-1, 1]2 функций x(s, t), для которых с.и. 
является непрерывной функцией в области [-1,1)[-1,1), допускающей непрерывное продолжение на стороны s = 1, t = 1.
- пространство непрерывных в квадрате [-1, 1]2 функций y(s, t) таких, что с.и. 
является непрерывной функцией в области (-1,1](-1,1], допускающей непрерывное продолжение на стороны s = -1, t = -1, 
.
Нормы в этих пространствах определяются следующим образом:
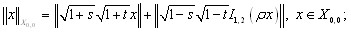
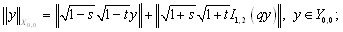
здесь и далее 
.
Теорема 1.1. Характеристическое уравнение
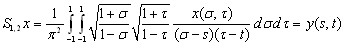
имеет единственное решение 
при любой правой части 
, причем
-1 < s, t < 1,
где
,
а Rk() и Qj() - полиномы, ортогональные на отрезке [-1, 1] с весами соответственно 
и 
.
В пространстве Y00 установлены оценки нормы двумерного оператора Фурье 
, ставящего в соответствие любой функции 
ее отрезок ряда Фурье
Доказаны
Лемма 1.1. Для любой функции 
справедлива оценка
.
Лемма 1.2. Если 
, то справедливо соотношение
,
0 < a, b Ј 1, r, l і 0.
Здесь через 
обозначено множество функций, имеющих непрерывную производную r-го порядка по первой переменной, удовлетворяющую по этой переменной условию Гельдера с показателем, и имеющих непрерывную производную l-го порядка по второй переменной, удовлетворяющую по этой переменной условию Гельдера с показателем b (0 < a, b Ј 1, r, l і 0).
Полученные оценки позволили теоретически обосновать метод ортогональных многочленов:
Теорема 1.4. Пусть выполнены условия:
а) с.и.у. (2) однозначно разрешимо в пространстве Х0,0 при любой правой части y(s, t) из Y0,0;
б) функция 
, ядро 
по переменным s, t равномерно относительно s, t.
Тогда, начиная с некоторых n, т О N таких, что
, n, m ® Ґ,
система линейных алгебраических уравнений метода ортогональных многочленов имеет единственное решение и для погрешности приближенного решения справедливо соотношение
, 
.
В §§2 и 3 исследованы соответственно класс решений, ограниченных на одной стороне квадрата [-1, 1]2 и неограниченных на других его сторонах и класс решений, неограниченных на одной стороне квадрата [-1, 1]2 и ограниченных на трех других.
Заключение. В работе получены и выносятся на защиту следующие основные результаты:
1) Введены новые пары пространств искомых элементов и правых частей, являющиеся сужениями пространства непрерывных функций, в которых задача решения сингулярного интегрального уравнения с ядром Коши на отрезке является корректно поставленной. В введенных пространствах установлены оценки норм сингулярного и обратного к нему операторов.
2) Разработаны элементы конструктивной теории функций в введенных пространствах. Получены оценки, характеризующие сходимость интерполяционного процесса, рядов Фурье по ортогональным многочленам и полиномов, получающихся с помощью операторов подобластей, учитывающие структурные свойства исходных данных.
3) Проведено теоретическое обоснование общего проекционного метода и известных полиномиальных методов решения сингулярного интегрального уравнения в предложенных пространствах и получены равномерные оценки погрешностей приближенных решений.
4) Установлена корректность постановки задачи решения двумерного с.и.у. с ядром Коши на [-1, 1]2 на новой паре пространств искомых элементов и правых частей, являющихся сужениями пространства непрерывных на [-1,1]2 функций. В терминах рядов Фурье установлена структура двумерного обратного сингулярного оператора и теоретически обоснован метод ортогональных многочленов.
Основные положения диссертации отражены в следующих публикациях автора:
1. Валиуллова Л.Э. О равномерной сходимости метода ортогональных многочленов решения сингулярного интегрального уравнения первого рода/ Л.Э. Валиуллова // Труда Матем. центра им. Н.И. Лобачевского / Казанское математическое общество. Актуальные проблемы математики и механики // Материалы международной научной конференции «Актуальные проблемы математики и механики». – Казань: Изд-во Казанского математического общества, Изд-во КГУ, 2004. Т.25 — С. 59-61.
2. Валиуллова Л.Э. О равномерной аппроксимации решения сингулярного интегрального уравнения I рода проекционными методами/ Л.Э. Валиуллова, А.В. Ожегова // Материалы первой междунар. научно-практической конф. "Научный потенциал мира - 2004". - Днепропетровск, 2004. - Т. 31. - С. 9- 17.
3. Валиуллова Л.Э. Равномерная сходимость метода ортогональных многочленов решения сингулярного интегрального уравнения первого рода с ядром Коши на отрезке/ Л.Э. Валиуллова, А.В. Ожегова // Матерiали Мiжнар. науково-практ. конф. "Днi науки - 2005". - Днiпропетровськ, 2005. - Т.18. - С. 13-16.
4. Валиуллова Л.Э. Равномерные приближения решений сингулярного интегрального уравнения первого рода с ядром Коши на отрезке/ Л.Э. Валиуллова, А.В. Ожегова // Изв. вузов. Математика. - 2006. №9. - С. 17-22.
5. Хайруллина Л.Э. О равномерной сходимости приближенных решений двумерного сингулярного интегрального уравнения первого рода/ Л.Э. Хайруллина //Матерiали II Мiжнар. науково-практ. конф. "Днi науки - 2006". - Днiпропетровськ, 2006. - Т.35. - С. 18-21.
6. Хайруллина Л.Э. Решение сингулярного интегрального уравнения методом осциллирующих функций/ Л.Э. Хайруллина. // Труда Матем. центра им. Н.И. Лобачевского / Казанское математическое общество. Теория функций, ее приложения и смежные вопросы // Материалы Восьмой международной Казанской летней научной школы-конференции «Теория функций, ее приложения и смежные вопросы». – Казань: Изд-во Казанского математического общества, Изд-во КГУ, 2007. Т. 35. - С. 259- 260.
7. Хайруллина Л.Э. О корректной постановке задачи решения двумерного сингулярного интегрального уравнения первого рода / Л.Э. Хайруллина // Труда Матем. центра им. Н.И. Лобачевского / Казанское математическое общество. Теория функций, ее приложения и смежные вопросы // Материалы Девятой международной Казанской летней научной школы-конференции «Теория функций, ее приложения и смежные вопросы». – Казань: Изд-во Казанского математического общества, Изд-во КГУ, 2009. Т.38 - С. 291 – 292.
Отпечатано в типографии
«Деловая полиграфия»
420111, г. Казань, ул. М. Межлаука, 6
т/ф (843) 292-08-43
е-mail: [email protected]
Подписано в печать 18.10.2011 г.
Бумага офсетная Тираж 100 экз.
Заказ № 163/2011
[1] Мусхелишвили Н.И. Сингулярные интегральные уравнения. – М.: Наука, 1968. – 512 с.
[2] Гахов Ф.Д. Краевые задачи. – М.: Наука, 1977. – 638 с.
[3] Гохберг И.Ц., Крупник Н.Я. Введение в теорию одномерных сингулярных операторов. – Кишинев: Штиинца, 1973. – 428 с.
[4] Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. – М.: Наука, 1979. – 288 с.
[5] Белоцерковский С.М. Тонкая несущая поверхность в дозвуковом потоке газа. – М.: Наука, 1965. – 244 с.
[6] Лифанов И.К. Метод сингулярных интегральных уравнений и численный эксперимент. – М.: ТОО «Янус», 1995. – 520 с.
[7] Иванов В.В. Методы приближенного решения сингулярных интегральных уравнений // Итоги науки и техники. Матем.анализ. – М.: Изд-во ВИНИТИ АН СССР, 1965. -С. 125 - 177.
[8] Габдулхаев Б.Г. Конечномерные аппроксимации сингулярных интегралов и прямые методы решения особых интегральных и интегро-дифференциальных уравнений // Итоги науки и техники. Матем.анализ, Вып. 18. – М.: Изд-во ВИНИТИ АН СССР, 1980. -С. 251 – 307.
[9] Иванов В.В. Теория приближенных методов и ее применение к численному решению сингулярных интегральных уравнений. – Киев: Наукова Думка, 1968. – 287 с.
[10] Габдулхаев Б.Г. Прямые методы решения сингулярных интегральных уравнений I рода. – Казань: Изд-во Казан. ун-та, 1994. – 285 с.
[11] Prossdorf S. Approximation methods for solving singular integral equations // Berlin, 1981. – Preprint. – P.-Math. – 12/81. – 31 p.
[12] Шешко М.А. Интегральные уравнения, содержащие кратные интегралы с ядрами Коши // Дифференц. уравенния. – 1986. – Т.22, №3. – С. 523 – 538.
[13] Бойков И.В. Приближенные методы решения сингулярных интегральных уравнений. – Пенза: Изд-во Пенз.ун-та, 2004. – 297 с.
