Полигоны и мультиполигоны над полугруппами
На правах рукописи
Максимовский Михаил Юрьевич
Полигоны и мультиполигоны над полугруппами
Специальность 01.01.06 – математическая логика,
алгебра и теория чисел
Автореферат
диссертации на соискание ученой степени
кандидата физико-математических наук
Казань – 2010 г.
Работа выполнена на кафедре высшей математики № 1 Московского государственного института электронной техники (национального исследовательского университета)
Научный руководитель: доктор физико-математических наук,
профессор
Кожухов Игорь Борисович
Официальные оппоненты: доктор физико-математических наук,
профессор
Тищенко Александр Владимирович,
кандидат физико-математических наук, доцент
Ильин Сергей Николаевич
Ведущая организация: Московский педагогический государственный университет
Защита диссертации состоится «25» ноября 2010 года в 16 часов на заседании диссертационного совета Д 212.081.24 при ФГАОУВПО «Казанский (Приволжский) федеральный университет» по адресу: 420008, г. Казань, ул. Кремлевская, д. 35, конференц-зал библиотеки им. Н. И. Лобачевского КФУ.
С диссертацией можно ознакомиться в библиотеке им. Н. И. Лобачевского по адресу: 420008, г. Казань, ул. Кремлевская, д. 35. Автореферат диссертации опубликован на сайте ФГАОУВПО «КФУ» (www.ksu.ru).
Автореферат разослан «___» ____________ 2010 г.
Ученый секретарь
диссертационного совета
к. ф.-м. н., доцент А. И. Еникеев
Общая характеристика работы
Актуальность темы исследования. Полигоны над полугруппой, т.е. множества, на которых действует полугруппа, возникают в разных разделах алгебры и ее приложений. Понятие полигона является алгебраическим выражением понятия автомата[1],[2] (точнее, автомата Мура, т.е. автомата без выхода). Это означает, что все работы по алгебраической теории автоматов можно рассматривать как относящиеся к теории полигонов. Если обычный полигон над полугруппой является алгебраической интерпретацией автомата, то мультиполигоны можно интерпретировать как автоматы с несколькими входными алфавитами. Теория полигонов является довольно молодым разделом общей алгебры, имеющим гораздо менее богатую историю, чем многие другие разделы, а теория мультиполигонов вообще находится на начальной стадии развития. Поэтому разработка этих теорий представляется актуальной математической задачей.
Понятие полигона над полугруппой аналогично понятию модуля над кольцом, ввиду чего теория полигонов развивалась под большим влиянием теории колец и модулей. Гомологическая классификация колец, т.е. исследование свойств кольца по свойствам категории модулей над этим кольцом, вызвала аналогичные вопросы в теории полигонов. По аналогии с модулями рассматривались артиновы и нетеровы, инъективные и проективные, плоские и свободные полигоны и т.д. Этими вопросами занимались многие математики России и зарубежья: М. Кильп[3],5, В. Фляйшер[4], П. Нормак[5] (Эстония), Л. А. Скорняков[6],
А. В. Михалев[7], И. Б. Кожухов[8] (Россия), У. Кнауэр[9], С. Буллман-Флеминг[10], М. Петрич[11] и др. И. Б. Кожухов исследовал подпрямо неразложимые полигоны, т.е. полигоны, не разложимые в нетривиальное подпрямое произведение. Он доказал, что если порядки всех подпрямо неразложимых полигонов над полугруппой ограничены в совокупности, то полугруппа периодическая. Все подпрямо неразложимые полигоны состоят не более чем из двух элементов тогда и только тогда, когда полугруппа является полурешеткой[12].
В теории групп широко известной и развитой является теория представлений групп, причем рассматривались как линейные представления (т.е. представления линейными отображениями векторных пространств), так и представления подстановками (взаимно однозначными отображениями множества в себя). Аналогично этому рассматриваются представления полугрупп: как линейные представления, так и представления преобразованиями (не обязательно взаимно однозначными) множества. Теория представлений полугрупп тесно связана с теорией полигонов.
В работе В. И. Кима[13] полугруппа изотонных отображений ![]() конечной цепи
конечной цепи ![]() в конечную цепь
в конечную цепь ![]() рассматривалась как биполигон над полугруппами
рассматривалась как биполигон над полугруппами ![]() слева и
слева и ![]() справа. Было доказано, что биполигон
справа. Было доказано, что биполигон ![]() порожден одним элементом.
порожден одним элементом.
Если полугруппа или семейство полугрупп имеют простое строение, то полигоны или мультиполигоны над ними могут быть описаны. В работе А. Ю. Авдеева и И. Б. Кожухова[14] было получено в теоретико-множественных терминах полное описание полигонов над прямоугольной связкой. В качестве следствий из этой теоремы получались описания полигонов над полугруппами левых и правых нулей. В другой работе этих же авторов[15] было приведено полное описание полигонов над прямоугольной группой. Позже авторам удалось получить описание полигонов над вполне простыми и вполне 0-простыми полугруппами[16]
, что обобщало предыдущие результаты.
В настоящей работе некоторые из этих результатов переносятся на случай биполигонов и мультиполигонов над полугруппами левых и правых нулей: доказана теорема о строении биполигонов над двумя рисовскими матричными полугруппами с нулями, получено полное описание ![]()
![]()
![]()
![]() -биполигонов, где
-биполигонов, где ![]() полугруппы левых нулей,
полугруппы левых нулей, ![]() полугруппы правых нулей. Получено полное описание мультиполигонов над семействами полугрупп, каждая из которых является полугруппой левых или правых нулей.
полугруппы правых нулей. Получено полное описание мультиполигонов над семействами полугрупп, каждая из которых является полугруппой левых или правых нулей.
Цели и задачи исследования данной работы заключаются в исследовании алгебраического строения полигонов над полурешетками и мультиполигонов над семействами полугруппам специального вида (полугруппами левых и правых нулей и т.д.).
Методы исследования. В работе используются методы алгебраической теории полугрупп и теории частично упорядоченных множеств. Для проверки некоторых гипотез и получения информации о строении полигонов был использован компьютер.
Личный вклад автора. В диссертации изложены результаты, полученные как лично автором, так и совместно с научным руководителем проф. Кожуховым И. Б. Постановки задач выполнены совместно с научным руководителем.
Достоверность результатов, полученных в данной работе, определяется обоснованными теоретическими выкладками и строгими доказательствами, опирающимися на методы алгебраической теории полугрупп и теории частично упорядоченных множеств.
Научная новизна. В диссертации получен ряд результатов о строении полигонов над цепями, биполигонов и мультиполигонов над полугруппами специального вида. Полученные результаты являются новыми.
Научные положения, выносимые на защиту
- Установление свойств частично упорядоченных множеств, являющихся полигонами над полурешетками.
- Описание полигонов над конечной цепью и связных частично упорядоченных множеств, являющихся полигонами над какой-либо цепью.
- Выяснение строения мультиполигона над семейством моноидов.
- Описание мультиполигонов над семействами полугрупп левых и правых нулей.
Практическая и теоретическая значимость. Работа носит теоретический характер. Полученные в ней результаты могут быть использованы в структурной теории полугрупп и (мульти)полигонов.
Апробация работы. Результаты диссертации неоднократно докладывались на научно-исследовательском семинаре “Кольца и модули” кафедры высшей алгебры МГУ, а также на следующих конференциях: 14-й и 15-й Международных конференциях “Проблемы теоретической кибернетики” (Пенза, 2005, Казань, 2008); 14-х и 15-х математических чтениях РГСУ (Москва, 2005, 2006); Международной алгебраической конференции, посвященной 100-летию И. Г. Конторовича и 70-летию Л. Н. Шеврина (Екатеринбург, 2005); 12-й и 13-й Всероссийских межвузовских конференциях “Микроэлектроника и информатика” (Москва, МИЭТ, 2005, 2006); Международном семинаре по компьютерной алгебре и информатике (Москва, МГУ, 2005); 6-й и 7-й Международных алгебраических конференциях на Украине (Каменец-Подольский, 2007; Харьков, 2008); Международной алгебраической конференции, посвященной 100-летию А. Г. Куроша (Москва, МГУ, 2008); 1-м международном семинаре “Дискретная математика и ее приложения” (Москва, МГУ, 2010); 7-й Международной конференции “Алгебра и теория чисел” ( Тула, 2010).
Публикации. По теме диссертации опубликовано 17 работ, в том числе 2 в рецензируемых научных журналах, рекомендованных ВАК.
Структура диссертации. Диссертация состоит из введения, трех глав, разбитых на параграфы, списка литературы и списка публикации автора по теме диссертации. Общий объем работы составляет 88 страниц. Список литературы включает 49 наименований.
Содержание работы
Во введении обосновывается актуальность темы диссертации, формулируются общие проблемы, цели и задачи исследования, научное и практическое значение полученных результатов.
Первая глава посвящена изучению полигонов над полурешетками.
Правым полигоном над полугруппой ![]() (или правым
(или правым ![]() полигоном) называется множество
полигоном) называется множество ![]() на котором действует полугруппа
на котором действует полугруппа ![]() причем
причем ![]() при
при ![]()
![]() Левый полигон определяется двойственным образом. Нижним конусом элемента
Левый полигон определяется двойственным образом. Нижним конусом элемента ![]() частично упорядоченного множества
частично упорядоченного множества ![]() называется множество
называется множество ![]()
Установлен ряд свойств полигонов над полурешетками. А именно, доказано, что всякий полигон ![]() над полурешеткой
над полурешеткой ![]() является частично упорядоченным множеством относительно порядка
является частично упорядоченным множеством относительно порядка
![]()
![]()
![]()
(предложение 1.2). Доказано, что нижний конус любого элемента является полурешеткой (предложение 1.3).
Естественным образом возникают 2 вопроса:
- как устроен полигон над данной полурешеткой
 ?
? - каким условиям должно удовлетворять частично упорядоченное множество, чтобы оно являлось полигоном над какой-нибудь полурешеткой?
Необходимые условия (т.е. частичный ответ на 1-й вопрос) дают уже упомянутые предложения 1.2, 1.3. Однако, эти условия не являются достаточными: в работе приведен пример 7-элементного частично упорядоченного множества, которое удовлетворяет вышеприведенным условиям, но не является полигоном ни над какой полурешеткой. Важным частным случаем полурешетки является линейно упорядоченное множество, т.е. цепь. Для полигонов над цепями можно поставить такие же вопросы 1 и 2, какие были сформулированы для полурешетки. Доказано, что если частично упорядоченное множество ![]() является полигоном над цепью, то нижний конус любого его элемента является деревом (предложение 1.6). Доказана теорема о строении полигонов над конечной цепью:
является полигоном над цепью, то нижний конус любого его элемента является деревом (предложение 1.6). Доказана теорема о строении полигонов над конечной цепью:
Теорема 1.7. Пусть ![]() натуральное число и
натуральное число и ![]() частично упорядоченное множество, обладающее свойствами:
частично упорядоченное множество, обладающее свойствами:
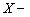 дерево;
дерево;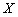 представимо в виде объединения попарно не пересекающихся подмножеств
представимо в виде объединения попарно не пересекающихся подмножеств 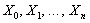 ;
; состоит из одного элемента (будем считать, что
состоит из одного элемента (будем считать, что  ;
;- если
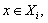
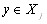 и
и  то
то 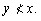
Пусть ![]() цепь
цепь ![]() Для элементов
Для элементов ![]() и
и ![]() положим
положим
![]()
Тогда ![]() является полигоном над цепью
является полигоном над цепью ![]() Наоборот, всякий связный полигон над конечной цепью устроен таким образом.
Наоборот, всякий связный полигон над конечной цепью устроен таким образом.
В случае произвольных цепей (не обязательно конечных) полный ответ на вопрос №2 получен для связных частично упорядоченных множеств. При помощи леммы Цорна получено необходимое и достаточное условие того, что связное частично упорядоченное множество является полигоном над некоторой цепью:
Теорема 1.13. Связное частично упорядоченное множество ![]() является полигоном над некоторой цепью в том и только том случае, если
является полигоном над некоторой цепью в том и только том случае, если ![]() дерево.
дерево.
Для несвязных частично упорядоченных множеств получены некоторые достаточные условия того, что данное множество является полигоном над цепью (предложения 1.14, 1.15, 1.16, 1.17).
Обозначим категорию левых полигонов над полугруппой ![]() через
через ![]() а категорию правых
а категорию правых ![]() -полигонов через
-полигонов через ![]() Автором отмечено, что категории левых полигонов над полугруппой изоморфна категории правых полигонов над дуальной полугруппой:
Автором отмечено, что категории левых полигонов над полугруппой изоморфна категории правых полигонов над дуальной полугруппой: ![]() (предложение 1.19). Охарактеризованы полигоны над свободными комутативными полугруппами (теорема 1.21).
(предложение 1.19). Охарактеризованы полигоны над свободными комутативными полугруппами (теорема 1.21).
Вторая глава посвящена изучению биполигонов над полугруппами специального вида.
Биполигон ![]() (или
(или ![]() -биполигон) – это множество, на котором действуют полугруппа
-биполигон) – это множество, на котором действуют полугруппа ![]() слева и полугруппа
слева и полугруппа ![]() справа, причем действия этих полугрупп перестановочны, т.е.
справа, причем действия этих полугрупп перестановочны, т.е. ![]() при
при ![]()
![]()
![]() . Унитарный биполигон над моноидами
. Унитарный биполигон над моноидами ![]() и
и ![]() – это такой
– это такой ![]() -биполигон, в котором единицы моноидов действуют тождественно. Категорию
-биполигон, в котором единицы моноидов действуют тождественно. Категорию ![]() -биполигонов будем обозначать через
-биполигонов будем обозначать через ![]() а категорию унитарных
а категорию унитарных ![]() -биполигонов через
-биполигонов через ![]()
Из упомянутого ранее изоморфизма категорий полигонов легко получается следующий результат:
Теорема 2.1. Для произвольных моноидов ![]() имеет место следующий изоморфизм категорий
имеет место следующий изоморфизм категорий
![]()
В теоретико-множественных терминах описано строение произвольных биполигонов над двумя моноидами:
Теорема 2.4. Пусть выполнены условия:
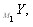
 унитарные полигоны над моноидами
унитарные полигоны над моноидами 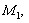
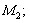
 – биполигон, являющийся подполигоном полигонов
– биполигон, являющийся подполигоном полигонов  и
и 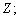
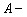 множество такое, что
множество такое, что 

 и
и  такие отображения, что
такие отображения, что  и
и  тождественные отображения множеств
тождественные отображения множеств 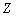 и
и 
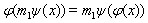 и
и 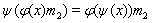 при
при 

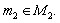
Доопределим действия ![]() и
и ![]() до умножения других элементов из
до умножения других элементов из ![]() на элементы моноидов
на элементы моноидов ![]() слева и элементы из
слева и элементы из ![]() справа, полагая
справа, полагая
![]()
при ![]()
![]() и
и
![]()
при ![]()
![]() Тогда
Тогда ![]() станет
станет ![]() -биполигоном. Наоборот, каждый биполигон над моноидами
-биполигоном. Наоборот, каждый биполигон над моноидами ![]() изоморфен биполигону, полученному таким образом.
изоморфен биполигону, полученному таким образом.
Понятие подбиполигона может быть определено двумя не эквивалентными друг другу способами, причем оба определения естественны. А именно, непустое подмножество ![]()
![]() -биполигона
-биполигона ![]() называется подбиполигоном биполигона
называется подбиполигоном биполигона ![]() в узком смысле, если
в узком смысле, если ![]() и
и ![]()
![]() – подбиполигон в широком смысле, если
– подбиполигон в широком смысле, если ![]()
При помощи теоремы 2.4 описаны все подбиполигоны (в узком и широком смыслах) биполигона над моноидами (теоремы 2.9 и 2.10).
Теорема 2.9. Пусть ![]()
![]() -биполигон, где
-биполигон, где ![]()
![]() моноиды. Подмножество
моноиды. Подмножество ![]() будет подбиполигоном в узком смысле в том и только том случае, если
будет подбиполигоном в узком смысле в том и только том случае, если ![]() можно представить в виде
можно представить в виде ![]() где
где ![]()
![]() подполигон унитарного полигона
подполигон унитарного полигона ![]()
![]() подполигон унитарного полигона
подполигон унитарного полигона ![]()
![]() унитарный подбиполигон биполигона
унитарный подбиполигон биполигона ![]() (см. теорему 2.4) и выполнены условия:
(см. теорему 2.4) и выполнены условия: ![]()
![]()
Теорема 2.10. Пусть ![]()
![]() -биполигон, где
-биполигон, где ![]()
![]() моноиды. Подмножество
моноиды. Подмножество ![]() будет подбиполигоном в широком смысле в том и только том случае, если
будет подбиполигоном в широком смысле в том и только том случае, если ![]() можно представить в виде
можно представить в виде ![]() где
где ![]()
![]()
![]() подмножества такие, что
подмножества такие, что ![]() унитарный подбиполигон биполигона
унитарный подбиполигон биполигона ![]() (см. теорему 2.4) и выполнено условие
(см. теорему 2.4) и выполнено условие ![]()
Используя результаты, полученные И. Б. Кожуховым и А. Ю. Авдеевым15, автор доказывает теорему о строении биполигонов над двумя рисовскими матричными полугруппами с нулем.
Теорема 2.12. Пусть ![]() и
и ![]() рисовские матричные полугруппы и
рисовские матричные полугруппы и ![]() множество с некоторым элементом
множество с некоторым элементом ![]() (который назовем нулем). Далее, пусть
(который назовем нулем). Далее, пусть ![]() и
и ![]() семейства подгрупп групп
семейства подгрупп групп ![]() и
и ![]() соответственно,
соответственно,![]()
![]() –копроизведения унитарных левых
–копроизведения унитарных левых ![]() - и правых
- и правых ![]() - полигонов соответственно. Наконец, пусть для любых
- полигонов соответственно. Наконец, пусть для любых ![]() ,
, ![]() ,
, ![]() ,
, ![]() , существуют отображения
, существуют отображения ![]()
![]()
![]()
![]() удовлетворяющие условиям:
удовлетворяющие условиям:
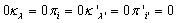 ;
;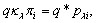
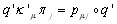 для любых
для любых 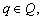
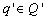 ;
;  для всех
для всех 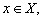
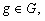
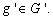
Положим для ![]() ,
, ![]() ,
, ![]()
![]()
![]()
![]()
где ![]() нули
нули ![]() и
и ![]() соответственно. Тогда
соответственно. Тогда ![]()
![]() - биполигон. Кроме того, любой биполигон над рисовскими матричными полугруппами с нулем устроен таким образом.
- биполигон. Кроме того, любой биполигон над рисовскими матричными полугруппами с нулем устроен таким образом.
Получено полное описание ![]()
![]()
![]()
![]() -биполигонов, где
-биполигонов, где ![]() полугруппы левых нулей,
полугруппы левых нулей, ![]() полугруппы правых нулей (теоремы 2.16, 2.20, 2.14), а также их подбиполигонов в широком и узком смыслах (теоремы 2.18, 2.19, 2.22, 2.23, 2.26, 2.27). В частности, доказаны следующие теоремы.
полугруппы правых нулей (теоремы 2.16, 2.20, 2.14), а также их подбиполигонов в широком и узком смыслах (теоремы 2.18, 2.19, 2.22, 2.23, 2.26, 2.27). В частности, доказаны следующие теоремы.
Теорема 2.16. Пусть ![]() - множества,
- множества, ![]()
![]() отношения эквивалентности на множестве
отношения эквивалентности на множестве ![]() и
и ![]() Для любых
Для любых ![]()
![]() пусть
пусть ![]()
![]() подмножества множества
подмножества множества ![]() являющиеся множествами представителей классов отношений
являющиеся множествами представителей классов отношений ![]()
![]() соответственно, т.е. для любых
соответственно, т.е. для любых ![]() ,
, ![]() ,
, ![]()
![]()
![]()
Пусть при этом для любого ![]() -класса
-класса ![]() существует
существует ![]() такое, что при любых
такое, что при любых ![]()
![]() выполняются условия:
выполняются условия:
![]()
![]()
и
![]()
![]()
Определим на множествах ![]() и
и ![]() операции, полагая
операции, полагая ![]() при
при ![]() и
и ![]() при
при ![]() Тогда
Тогда ![]() и
и ![]() будут являться полугруппами правых нулей. Определим действия этих полугрупп на множестве
будут являться полугруппами правых нулей. Определим действия этих полугрупп на множестве ![]() полагая
полагая
![]()
![]()
и
![]()
![]()
Тогда ![]() будет являться
будет являться ![]() -биполигоном (где
-биполигоном (где ![]() . Наоборот, любой
. Наоборот, любой ![]() -биполигон, где
-биполигон, где ![]() полугруппа левых нулей, а
полугруппа левых нулей, а ![]() полугруппа правых нулей, изоморфен биполигону, построенному таким способом.
полугруппа правых нулей, изоморфен биполигону, построенному таким способом.
Теорема 2.18. Пусть ![]()
![]() -биполигон, где
-биполигон, где ![]() и
и ![]() полугруппы правых нулей. Подмножество
полугруппы правых нулей. Подмножество ![]() будет подбиполигоном
будет подбиполигоном ![]() в узком смысле тогда и только тогда, когда
в узком смысле тогда и только тогда, когда ![]() и
и ![]() для всех
для всех ![]()
Теорема 2.19. Пусть ![]()
![]() -биполигон, где
-биполигон, где ![]() и
и ![]() полугруппы правых нулей. Подмножество
полугруппы правых нулей. Подмножество ![]() будет подбиполигоном
будет подбиполигоном ![]() в узком смысле тогда и только тогда, когда
в узком смысле тогда и только тогда, когда ![]() для всех
для всех ![]() .
.
В третьей главе изучаются мультиполигоны. Мультиполигон над семейством ![]() полугрупп – это множество
полугрупп – это множество ![]() на котором действуют полугруппы
на котором действуют полугруппы ![]() , причем действия этих полугрупп перестановочны (т.е.
, причем действия этих полугрупп перестановочны (т.е. ![]() при
при ![]()
![]()
![]()
![]() ). Ясно, что понятие мультиполигона обобщает понятия полигона и биполигона.
). Ясно, что понятие мультиполигона обобщает понятия полигона и биполигона.
На основании результатов, полученных в предыдущей главе, доказывается ряд теорем о строении мультиполигонов над семействами полугрупп специального вида.
Вначале отмечено, что в унитарном случае мультиполигон над моноидами может быть сведен к обычному полигону:
Теорема 3.1. Категория унитарных ![]() мульти-полигонов изоморфна категории унитарных правых полигонов над дискретным прямым произведением
мульти-полигонов изоморфна категории унитарных правых полигонов над дискретным прямым произведением ![]() моноидов
моноидов ![]()
В неунитарном случае также можно сводить мультполигоны к обычным полигонам, но здесь формулировка выглядит сложнее.
Теорема 3.2. Пусть выполнены условия:
(a) ![]() семейство унитарных полигонов над моноидами
семейство унитарных полигонов над моноидами ![]()
(b) ![]() подмножества множества
подмножества множества ![]() для всех
для всех ![]()
(c) для любых ![]()
![]() унитарный биполигон, являющийся подполигоном полигонов
унитарный биполигон, являющийся подполигоном полигонов ![]() и
и ![]()
(d) ![]() отображения
отображения ![]() такие, что
такие, что ![]() тождественные отображения множеств
тождественные отображения множеств ![]()
(e) ![]() для всех
для всех ![]()
![]()
Доопределим действия ![]() до умножения других элементов из
до умножения других элементов из ![]() на элементы моноидов
на элементы моноидов ![]() полагая
полагая
![]()
при ![]()
![]() Тогда
Тогда ![]() станет
станет ![]() -мультиполигоном. Наоборот, всякий мультиполигон над семейством моноидов устроен таким образом.
-мультиполигоном. Наоборот, всякий мультиполигон над семейством моноидов устроен таким образом.
На основе теорем главы 2 доказываются теоремы о строении мультиполигонов над семействами полугрупп левых и правых нулей (теоремы 3.3, 3.4, 3.5). В частности, доказана следующая теорема.
Теорема 3.3. Пусть ![]() ,
, ![]() произвольные непустые множества,
произвольные непустые множества, ![]() отношение эквивалентности на
отношение эквивалентности на ![]() для каждого
для каждого ![]() и
и ![]() для всех
для всех ![]() ,
, ![]() . Для каждого
. Для каждого ![]() положим
положим ![]() множества представителей каждого
множества представителей каждого ![]() соответственно, т.е. для всех
соответственно, т.е. для всех ![]() ,
, ![]() ,
, ![]()
![]()
Пусть для каждого ![]() , для всех
, для всех ![]()
![]() существует элемент
существует элемент ![]() (где
(где ![]()
![]() -класс элемента
-класс элемента ![]() ) такой, что выполняются условия
) такой, что выполняются условия
![]()
![]()
Для ![]() положим
положим ![]() . Тогда
. Тогда ![]() будут полугруппами правых нулей для всех
будут полугруппами правых нулей для всех ![]() . Положим
. Положим
![]()
(![]() ,
, ![]() ). Тогда
). Тогда ![]() будет мультиполигоном над семейством полугрупп правых нулей
будет мультиполигоном над семейством полугрупп правых нулей ![]() . Наоборот, всякий мультиполигон над семейством полугрупп правых нулей будет изоморфен мультиполигону, полученному таким способом.
. Наоборот, всякий мультиполигон над семейством полугрупп правых нулей будет изоморфен мультиполигону, полученному таким способом.
Автор выражает глубокую благодарность своему научному руководителю – доктору физико-математических наук, профессору Игорю Борисовичу Кожухову за постановку задач и постоянному вниманию к работе.
РЕЗУЛЬТАТЫ ДИССЕРТАЦИИ ОПУБЛИКОВАНЫ В СЛЕДУЮЩИХ РАБОТАХ:
В журналах из списка ВАК:
- М. Ю. Максимовский, О полигонах над полурешётками. Фундаментальная и прикл. матем., 14:7 (2008), 151–156.
- М. Ю. Максимовский, О биполигонах и мультиполигонах над полугруппами. Матем. заметки, 87:6 (2010), 855–866.
В прочих изданиях:
(в работах в соавторстве соискателю принадлежит 50% результатов)
- И. Б. Кожухов, М. Ю. Максимовский, Об автоматах над полурешетками. “Системный анализ и управление”, сборник научных трудов под ред. В. А. Бархоткина, Москва, 2006 г., 19-34.
- М. Ю. Максимовский, Биавтоматы над рисовскими матричными полугруппами. Сборник научных трудов “Моделирование, алгоритмизация и программирование при проектировании информационно-управляющих систем”, под ред. В. А. Бархоткина, Москва, 2008 г., 104-109.
- И. Б. Кожухов, М. Ю. Максимовский, Биполигоны и мультиполигоны над некоторыми классами полугрупп. Материалы 14-й Международной конференции “Проблемы теоретической кибернетики”, Пенза, 2005, 64.
- И. Б. Кожухов, М. Ю. Максимовский, О биполигонах и мультиполигонах над полугруппами. Материалы 14-х математических чтений РГСУ, Москва, 2005, 39-43.
- И. Б. Кожухов, М. Ю. Максимовский, О мультиполигонах над полугруппами. Материалы Международной алгебраической конференции, Екатеринбург, 2005, 12-13.
- М. Ю. Максимовский, Биполигоны и мультиполигоны над полугруппами определенного вида. Материалы докладов 12-й Всероссийской межвузовской конференции “Микроэлектроника и информатика”, Москва, МИЭТ, 2005, 180.
- И. Б. Кожухов, М. Ю. Максимовский, О полигонах над цепями. Материалы 15-х математических чтений РГСУ, Москва, 2006, 67-71.
- И. Б. Кожухов, М. Ю. Максимовский, О строении счетных полигонов над цепями. Материалы 13-й Всероссийской межвузовской конференции “Микроэлектроника и информатика”, Москва, МИЭТ, 2006, 155.
- M. Yu. Maksimovskiy, Biacts over Rees matrix semigroups. Материалы 6-th International Algebraic Conference in Ukraine, 2007, 133-134.
- И. Б. Кожухов, М. Ю. Максимовский, О полигонах над полурешетками. Материалы международной алгебраической конференции, посвященной 100-летию А. Г. Куроша, Москва, МГУ, 2008, 125-126.
- И. Б. Кожухов, М. Ю. Максимовский, Автоматы над свободными коммутативными полугруппами. Материалы 15-й международной алгебраической конференции “Проблемы теоретической кибернетики”, Казань, 2008, 50.
- M. Yu. Maksimovski, On multiacts over right zero semigroups. Материалы 7-th International Algebraic Conference in Ukraine, 2009, 94-95.
- М. Ю. Максимовский. О подбиполигонах биполигонов. Материалы 10-го международного семинара “Дискретная математика и ее приложения”, Москва, МГУ, 2010г., с 189-190.
- М. Ю. Максимовский, О мультиполигонах над полугруппами. Материалы 7-й Международной алгебраической конференции “Алгебра и теория чисел”, Тула, 2010, 126-127.
- И. Б. Кожухов, М. Ю. Максимовский, Действия коммутативных полугрупп идемпотентов на множествах. Вестник МГАДА, 2010, вып. 5.
Подписано в печать:
Заказ № Тираж 100 экз. Уч.-изд.л. 0,8. Формат 60х84 1/16
Отпечатано в типографии МИЭТ (НИУ).
124498, Москва, МИЭТ (НИУ).
[1] В. Б. Кудрявцев, С. В. Алешин, А. С. Подколзин, Введение в теорию автоматов. М.:Наука, 1985.
[2] Ж. Лаллеман, Полугруппы и комбинаторные приложения. М.:Мир, 1985.
[3] М. Кильп, Гомологическая классификация моноидов. Сиб. мат. журн., 13:578-586, 1972.
[4] В. Г. Фляйшер, Об эндоморфизмах свободных полигонов. Уч. записки Тартус. ун-та, 1974, вып. 336, 189-105.
[5] П. Нормак, О нетеровых и конечно представимых полигонах. Уч. записки Тартус. ун-та, 1977, вып. 431, 37-46
[6] Л. А. Скорняков, О гомологической классификации моноидов. Сиб. мат. журн., 10:5 (1969), 1139–1143.
[7] M. Kilp, U. Knauer, A. V. Mikhalev, Monoids, Acts and Cathegories. De Gruyter Exp. Math., 29, Walter de Gruyter, Berlin, 2000.
[8] И. Б. Кожухов, Условия конечности для подпрямо неразложимых полигонов и модулей. Фундамент. и прикл. матем., 4:2 (1998), 763–767.
[9] U. Knauer, P. Normak, Hereditary endomorphism monoids of projective acts. Manuscripta math., 70:133-143, 1991.
[10] S. Bulman-Fleming, Pullback-flat acts are strongly flat. Canad. Math. Bull., 34:456-461, 1991.
[11] U. Knauer, M. Petrich, Characterization of monoids by torsion-free, flat, projective, and free acts. Arch. Math., 36:289-294, 1981.
[12] I. B. Kozhuhov, One characteristical property of semilattices. Commutations In Algebra, 25(8), 2569-2577, 1997.
[13] V. I. Kim, On isotone mappings of partially ordered set. 6-th International Algebraic Conference in Ukraine, 2007, 99-100.
[14] А. Ю. Авдеев, И. Б. Кожухов, Полигоны над полугруппами простого строения. Труды шестых математических чтений РГСУ, Москва, 1999, 103-107.
[15] А. Ю. Авдеев, И. Б. Кожухов, Полигоны над прямоугольными группами. 12-я международная конференция “Проблемы теоретической кибернетики”, Нижний Новгород, 1999, стр. 5.
[16] A. Yu. Avdeev, I. B. Kozhuhov, Acts over completely 0-simple semigroups. Acta Cybernetica, 14:4 (2000), 523-531.

