Двухточечная краевая периодическая задача для дифференциальных уравнений с максимумами
На правах рукописи
КИРЮШКИН ВАСИЛИЙ ВЛАДИМИРОВИЧ
ДВУХТОЧЕЧНАЯ КРАЕВАЯ ПЕРИОДИЧЕСКАЯ ЗАДАЧА
ДЛЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
С МАКСИМУМАМИ
01.01.02 – Дифференциальные уравнения
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата физико-математических наук
ПЕРМЬ 2007
Работа выполнена в Рязанском государственном университете им. С.А. Есенина
Научный руководитель: доктор физико-математических наук,
профессор Терехин Михаил Тихонович
Официальные оппоненты: доктор физико-математических наук,
профессор Симонов Петр Михайлович
кандидат физико-математических наук,
профессор Ермолаев Михаил Борисович
Ведущая организация Мордовский государственный университет
Защита состоится 10 октября 2007 г. в 15 часов на заседании диссертационного совета К 212.188.02 в Пермском государственном техническом университете по адресу: 614990, Пермь, Комсомольский проспект, 29, ауд. 423б, гл. корпус
С диссертацией можно ознакомиться в библиотеке Пермского государственного технического университета.
Автореферат разослан ’’ __ ’’ ______ ______ г.
Ученый секретарь
диссертационного совета,
канд. физ.-мат. наук, доцент В.А. Соколов
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы. В качественной теории дифференциальных уравнений с отклоняющимся аргументом одними из основных является вопрос нахождения условий существования периодических решений (решений двухточечных краевых периодических задач) в окрестности известного решения. Периодическим решениям в практических задачах соответствуют различные циклические процессы, значение которых в многообразии сфер деятельности человечества трудно переоценить.
Особый интерес вызывают уравнения с отклонением, значение которого априори неизвестно. К таким уравнениям относятся дифференциальные уравнения с максимумами, в которых отклонение аргумента зависит от искомой функции.
В последнее время уравнения с максимумами все чаще возникают при решении различных прикладных задач. Наиболее широкое применение подобные уравнения нашли в теории автоматического регулирования и экономике.
Результаты исследований, посвященных дифференциальным уравнениям с обычным отклонением нельзя автоматически перенести на уравнения с максимумами, поскольку правые части подобных уравнений являются функционалами или операторами, не обладающими свойствами линейности, даже в случае линейных уравнений.
Существенный вклад в становление и развитие теоретических аспектов дифференциальных уравнений с максимумами внесли Н.В. Азбелев, Л.Ф. Рахматуллина, П.М. Симонов, В.П. Максимов, М.Б. Ермолаев, А.Р. Магомедов, Ю.А. Рябов, В.Р. Петухов, С.А. Вавилов, Д.Д. Байнов, П. Гонсалес, М. Пинто.
Одной из проблем, имеющей важнейшее значение как для теории дифференциальных уравнений с максимумами, так и для ее приложений, является проблема определения условий существования решений двухточечной краевой периодической задачи. Исследованию этой проблемы и посвящена диссертационная работа.
В теории дифференциальных уравнений с отклонением исследуются проблемы существования решений в различных классах функций, в том числе в классах кусочно-непрерывных и абсолютно непрерывных функций. В диссертационной работе вследствие того, что правая часть уравнения с максимумами непрерывна по совокупности переменных, и необходимости решения задач прикладного характера, исследуется проблема существования решения двухточечной периодической задачи уравнения с максимумами в классе непрерывно дифференцируемых функций.
В настоящее время достаточно глубоко разработана теория устойчивости уравнений с максимумами, но слабо изученным остается вопрос, касающийся нахождения периодических решений (решений двухточечных краевых периодических задач) для таких уравнений. Используемые для исследования данной проблемы методы имеют ограниченное применение и не позволяют решать широкий спектр задач.
Таким образом, как для теории дифференциальных уравнений с максимумами, так и для решения задач прикладного характера актуальной является проблема определения условий существования на заранее заданном промежутке решений двухточечных краевых периодических задач.
Цель работы. Определить условия существования ненулевого решения двухточечной краевой периодической задачи для дифференциального уравнения с максимумами
(0.1)
если 
,
где 
– искомая непрерывно дифференцируемая функция, 
– начальное значение, 
– параметр, 
и 
– непрерывные матрицы, 
– непрерывная скалярная функция, влияющая на отклонение аргумента, 
.
Методика исследования. С помощью методов общей теории дифференциальных уравнений проблема определения условий существования ненулевого решения двухточечной краевой периодической задачи сводится к проблеме разрешимости системы уравнений относительно начального значения и параметра.
Доказательство существования решения системы уравнений проводится методом неподвижной точки с использованием предложенного в диссертационной работе способе линеаризации по параметру главной части системы уравнений, линейной по начальному значению, разложения в степенной ряд нелинейной как по начальному значению, так и по параметру главной части системы уравнений.
Научная новизна. В работе доказана нелокальная теорема о существовании непрерывно дифференцируемого решения, получена структура решения и найдены условия отсутствия и существования ненулевых решений двухточечной краевой периодической задачи дифференциальных уравнений с максимумами в достаточно малой окрестности нулевого решения. Предложена методика исследования операторных уравнений, основанная на линеаризации главной части оператора, методика построения множества, содержащего неподвижную точку оператора с положительными координатами.
Теоретическая и практическая ценность работы. Работа носит теоретический характер. Полученные результаты представляют собой развитие методов качественной теории дифференциальных уравнений с отклоняющимся аргументом, расширен класс уравнений с максимумами для которых найдены условия существования решения двухточечных краевых периодических задач, предложены методы исследования проблемы разрешимости различных типов операторных уравнений. Результаты исследований могут быть использованы для решения задач прикладного характера.
На защиту выносятся следующие положения:
1) нелокальная теорема существования, единственности и непрерывной зависимости решения дифференциального уравнения с максимумами от начальных данных и параметра;
2) структура решений нелинейного дифференциального уравнения с максимумами (0.1);
3) схема исследования операторных уравнений, основанная на линеаризации главной части оператора;
4) признаки существования ненулевых решений двухточечной краевой периодической задачи для уравнения (0.1) в достаточно малой окрестности нулевого решения, сводящиеся к использованию свойств линейной составляющей правой части уравнения (0.1).
5) условия существования ненулевых решений двухточечной краевой периодической задачи для уравнения (0.1) в достаточно малой окрестности нулевого решения, полученные с привлечением нелинейных членов правой части уравнения (0.1).
Апробация диссертации. Основные результаты докладывались на заседаниях научно-исследовательского семинара по качественной теории дифференциальных уравнений в Рязанском государственном педагогическом университете им. С.А. Есенина, на Всероссийской научной конференции молодых ученых, аспирантов и студентов “Проблемы и перспективы российских реформ” в Рязанском государственном педагогическом университете им. С.А. Есенина, на международных научных конференциях “Современные проблемы математики, механики, информатики” в г. Тула, на Х Всероссийской научно-технической конференции студентов, молодых ученых и специалистов “Новые информационные технологии в научных исследованиях и в образовании” в Рязанской государственной радиотехнической академии, на научной конференции “Герценовские чтения – 2005” в г. Санкт–Петербург.
Публикации. Основные результаты работы отражены в одиннадцати публикациях, список которых приведен в автореферате.
Структура и объем диссертации. Диссертация состоит из введения, трех глав, заключения и списка литературы, включающего 97 наименований. Общий объем диссертации – 111 страниц машинописного текста.
КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ
Во введении дается обоснование актуальности темы диссертации, содержится краткий обзор работ по ее тематике, краткое описание методики исследования и содержания работы.
Первая глава посвящена изучению свойств решений нелинейного дифференциального уравнения с максимумами, содержащего параметр. Центральным направлением исследований является получение структуры решений данного уравнения.
В § 1.1 вводятся основные определения и обозначения и формулируется задача исследования.
В работе использованы следующие обозначения: 
, 
, 
, 
, 
, 
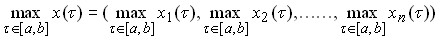– множество непрерывных на 
–мерных вектор-функций, 
– 
–мерный вектор, 
– 
–матрица 
, 
; 
, 
, 
, 
, 
, 
, где 
, 
, 
.
Рассматривается дифференциальное уравнение с максимумами
, (1.1)
, если 
,
где 
, 
– параметр, функция 
непрерывна на сегменте 
и удовлетворяет условию 
при любом 
, 
, вектор-функция 
непрерывна и удовлетворяет условию Липшица с постоянной 
по 
и 
переменной на множестве 
, 
, 
.
Определение 1.1. Решением уравнения (1.1) будем называть непрерывно дифференцируемую на сегменте 
–мерную вектор-функцию 
, удовлетворяющую уравнению (1.1) при некотором 
всюду на сегменте 
.
Вектор-функцию 
будем называть начальной вектор-функцией. В случае, если в уравнении (1.1) 
при 
, то будем говорить, что задано начальное значение 
.
Двухточечная краевая периодическая задача для дифференциального уравнения (1.1) заключается в нахождении начального значения 
и параметра 
таких, что уравнение (1.1) при 
, 
и 
имеет решение 
, удовлетворяющее краевым условиям
.
Ставится задача – найти условия существования ненулевых решений двухточечной краевой периодической задачи для уравнения (1.1) в достаточно малой окрестности нулевого решения.
В § 1.2 приводятся вспомогательные утверждения, необходимые для дальнейшего исследования: рассматривается неравенство, касающееся максимумов, доказывается лемма о непрерывности максимума функции, зависящей от параметра.
В § 1.3 доказывается нелокальная теорема о существовании, единственности и непрерывной зависимости от начальных данных и параметра решения уравнения (1.1).
Теорема 1.1. Если при 
уравнение (1.1) имеет решение 
c начальной вектор-функцией 
и 
, то существует 
, такое, что для любой начальной вектор-функции 
, удовлетворяющей условию 
и параметра 
, уравнение (1.1) имеет единственное решение 
, непрерывно зависимое от начальной вектор-функции и параметра и 
.
Доказательство теоремы производится методом последовательных приближений.
В теореме 1.2 получена оценка разности двух решений уравнения (1.1).
Теорема 1.2. Для любых двух решений уравнения (1.1) 
и 
с начальными вектор-функциями 
и 
при любом 
справедливо неравенство 
.
В § 1.4 изучается структура решений дифференциального уравнения с максимумами вида
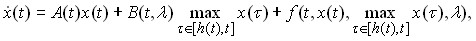(1.3)
если 
,
где 
, 
– параметр, функция 
непрерывна на сегменте 
и удовлетворяет условию 
при любом 
, 
, матрицы 
и 
– непрерывны на множествах 
и 
соответственно, 
при 
, вектор-функция 
непрерывна и удовлетворяет условию Липшица с постоянной 
по 
и 
переменной на множестве 
, 
при 
и 
, 
равномерно относительно 
, 
.
Установлено, что решение уравнения (1.3) выражается формулой
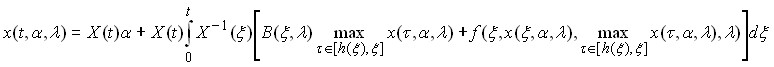(1.5)
Свойства второго слагаемого правой части (1.5) рассмотрены в теореме 1.3.
Теорема 1.3. Решение 
уравнения (1.3) представимо в виде 
, где 
,
равномерно относительно 
, 
и 
равномерно относительно 
, 
.
Использование вида решения, полученного в теореме 1.3, совместно с формулой (1.5), позволяет свести проблему определения условий существования ненулевых решений двухточечной краевой периодической задачи для уравнения (1.3) к проблеме разрешимости относительно 
операторного уравнения
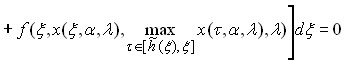, (1.6)
в котором 
, 
, 
равномерно относительно 
, 
, 
равномерно относительно 
, 
, 
.
Во второй главе диссертации изучается проблема существования ненулевого решения двухточечной краевой периодической задачи для дифференциального уравнения с максимумами (1.3) в достаточно малой окрестности нулевого решения. Рассматриваются условия отсутствия и существования ненулевого решения двухточечной краевой периодической задачи для уравнения (1.3). Устанавливаются признаки существования решений двухточечной краевой периодической задачи с положительными компонентами параметра 
. Условия разрешимости двухточечной краевой периодической задачи для уравнения (1.3), полученные в рамках данной главы, определяются только линейными членами правой части уравнения (1.3) и не зависят от поведения нелинейной составляющей.
В § 2.1 рассматривается условие отсутствия ненулевых решений двухточечной краевой периодической задачи для уравнения (1.3) и приводится пример уравнения с максимумами, обладающего этим свойством.
Теорема 2.1. Если 
, то существует 
такое, что уравнение (1.3) при любом 
и 
не имеет ненулевых решений двухточечной краевой периодической задачи.
Дальнейшие исследования в работе проводятся в предположении выполнения условия 
.
В § 2.2 изучается особый класс систем алгебраических уравнений, исследование которых тесно связано с вопросом разрешимости двухточечной краевой периодической задачи.
Рассматриваются системы вида
(2.1)
, 
, 
, 
, 
, 
.
Уравнения системы (2.1), приводятся логарифмированием к линейным относительно 
, 
. По аналогии с матрицей линейной системы для систем (2.1) вводится в рассмотрение понятие «степенной» матрицы.
Определение 2.1. Степенной матрицей системы (2.1) назовем 
матрицу 
, элементы которой определяются равенством: 
.
Устанавливается, что условие разрешимости системы (2.1) определяется соотношением 
.
Основным результатом параграфа является теорема о непрерывной зависимости решения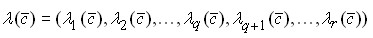 
от столбца свободных членов 
.
В § 2.3 доказываются теоремы об условиях существования ненулевых решений двухточечной краевой периодической задачи для уравнения (1.3).
Согласно результатам первой главы, решаемая задача сводится к определению условий существовании вектора 
, 
являющегося решением уравнения (1.6).
Для изучения вопроса, связанного с разрешимостью уравнения (1.6) в рассмотрение вводится понятие определяющего вектора матрицы, являющегося вектор-функцией 
.
Определение 2.3. Пусть 
– 
матрица, каждый элемент которой представлен в виде 
, где 
– непрерывные функции от 
, 
, 
для любого 
и 
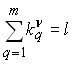. Определяющим вектором матрицы 
будем называть вектор 
, построенный следующим образом:
1) выпишем все различные 
(повторяющиеся 
следует учесть один раз) и расположим их в порядке убывания степеней сначала 
, затем 
, 
и так далее, до 
;
2) из получившейся последовательности составим вектор 
так, что 
-тая компонента вектора 
является 
-тым элементом построенной последовательности.
Определяющий вектор 
матрицы позволяет осуществить ее линеаризацию относительно 
.
Для матрицы 
, дифференцируемой по компонентам вектора 
, справедливо представление 
, где компоненты матрицы 
– формы порядка 
по 
, 
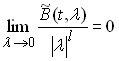равномерно относительно 
.
Предполагается, что 
, вектор 
размерности 
– определяющий вектор матрицы 
, 
равномерно относительно 
. В частности 
в следующих случаях: 1) 
; 2) 
; 3) 
.
С помощью равносильных преобразований уравнение (1.6) приводится к виду
, (2.6)
где 
, 
.
Последовательность замен:
1) 
, 
– 
–матрица, столбцами которой являются линейно независимые решения уравнения 
,
2) 
, 
, 
,
приводит уравнение (2.6) к виду
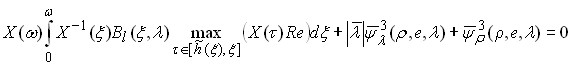, (2.8)
где 
, 
.
Использование свойств определяющего вектора 
матрицы 
позволяет представить первое слагаемого левой части уравнения (2.8) в виде 
, где 
матрица.
Уравнение (2.8) примет вид
. (2.9)
Предположив существование вектора 
: 
такого, что 
, получим уравнение
, (2.10)
где 
, 
, 
- 
матрица, составленная из 
линейно-независимых столбцов матрицы 
, 
матрица, составленная из оставшихся столбцов матрицы 
, 
и 
вектора, являющиеся частями вектора 
, соответствующие матрицам 
и 
, составляющие в совокупности всех своих компонент вектор 
, 
,
.
Таким образом, задача определения условий существования ненулевых решений двухточечной краевой периодической задачи свелась к проблеме разрешимости уравнения (2.10).
Теорема 2.4. Если 
, 
– нечетное число и существует вектор 
:
такой, что 
, то для любого 
существуют 
, 
и 
такие, что уравнение (1.3) имеет ненулевое решение двухточечной краевой периодической задачи при 
и 
.
В частности справедливо утверждение
Следствие 2.2. Если существует вектор 
: 
такой, что 
, 
(компоненты матрицы 
– формы первого порядка по 
), то для любого 
существуют 
, 
и 
такие, что уравнение (1.3) имеет ненулевое решение двухточечной краевой периодической задачи при 
и 
.
Доказательство теоремы проведено методом неподвижной точки оператора.
Условия теоремы 2.4 обеспечивают однозначное непрерывное соответствие 
в окрестности нуля, что позволяет с помощью принципа Брауэра установить существование неподвижной точки из этого множества для оператора, построенного по правой части (2.10). Если в окрестности нуля указанная зависимость отсутствует (например, при 
, 
четное число, данное соответствие справедливо только для полуокрестности нуля), то использование принципа Брауэра на множестве содержащем нуль становится невозможным.
Дальнейшие исследования главы посвящены ситуации, когда в окрестности нуля вектора 
и 
не связаны однозначной непрерывной зависимостью.
От оператора 
потребуется наличие дополнительных свойств.
Определение 2.4. Будем говорить, что оператор 
, 
матрица, сохраняет знак в точке 
, если 
, 
и 
, 
, 
.
Согласно определению вектора 
, каждое 
, 
представляется в виде 
, где 
, 
и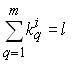 
, 
.
Введем в рассмотрение систему уравнений
(2.11)
где 
, 
, 
, 
, 
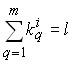, а левые части уравнений системы представляют собой компоненты вектора 
.
Пусть 
степенная матрица системы (2.11).
Теорема 2.5. Если существуют вектор 
: 
и точка 
такие, что 
, 
и оператор 
сохраняет знак в точке 
, то для любого 
существуют 
, 
и 
, такие что уравнение (1.3) имеет ненулевое решение двухточечной краевой периодической задачи при 
и 
.
Доказательство теоремы использует принцип Брауэра, применяемый к оператору 
, построенному по правой части (2.10). Сохранение знака оператора 
в точке 
позволяет выбрать отделенное от нуля, замкнутое, выпуклое множество 
, расположенное в первом квадранте, такое что оператор 
отображает это множество в себя. Условие 
определяет существование непрерывного отображения 
на множестве 
, что обеспечивает непрерывность оператора 
на 
.
Теорема 2.5 устанавливает условия существования ненулевых решений двухточечной краевой периодической задачи с положительными значениями компонент параметра 
.
В конце главы рассмотрены три примера уравнений с максимумами, для которых устанавливается существования ненулевых решений двухточечной краевой периодической задачи.
В третьей главе диссертации рассматривается другой способ решения поставленной задачи. В отличие от подхода второй главы, здесь для определения условий существования ненулевых решений двухточечной краевой периодической задачи привлекаются нелинейные члены правой части уравнения (1.3).
В § 3.1 доказаны теоремы об условиях отсутствия и теорема существования
ненулевых решений двухточечной краевой периодической задачи уравнения (1.3).
Уравнение (1.6) рассматривается в предположении, что матрица 
и вектор 
представлены следующим образом: 
, компоненты матрицы 
– формы порядка 
, 
по 
, 
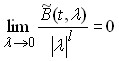равномерно относительно 
, 
, компоненты вектора 
– формы порядка 
, 
по 
, 
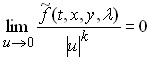. Указанные представления всегда можно осуществить, если 
имеет частные производные 
го порядка по компонентам вектора 
, а 
частные производные 
го порядка по компонентам вектора 
.
С помощью цепочки преобразований уравнение (1.3) приводится к виду:
, (3.4)
где 
, 
, 
, а вектор-функция обладает свойством: 
для любого 
.
Последовательность замен:
1) 
, 
– 
–матрица, столбцами которой являются линейно независимые решения уравнения 
,
2) 
, 
, 
,
, 
, 
.
приводит уравнение (3.4) к виду
, (3.6)
где 
, 
.
Таким образом, задача определения условий существования ненулевых решений двухточечной краевой периодической задачи свелась к проблеме разрешимости уравнения (3.6).
Рассмотрены две теоремы, позволяющие установить существование множеств начального значения и параметра, определяющих отсутствие ненулевых решений двухточечной краевой периодической задачи для уравнения (1.3).
Теорема 3.1. Если существует вектор 
, 
такой, что 
, то для любого 
существуют множества 
и 
такие, что уравнение (1.3) при любых 
не имеет ненулевых решений двухточечной краевой периодической задачи.
Теорема 3.2. Если 
для любого вектора 
: 
, то существует 
такое, что уравнение (1.3) при любых 
, 
, 
не имеет ненулевых решений двухточечной краевой периодической задачи.
Условия существования ненулевых решений двухточечной краевой периодической задачи для уравнения (1.3) сформулированы в теореме 3.3.
Теорема 3.3. Если существуют вектор 
, 
, 
и число 
такие, что 
, функция 
дифференцируема на множестве 
и 
, где 
матрица Якоби, то для любого 
существуют 
, 
и 
такие, что уравнение (1.3) имеет ненулевое решение двухточечной краевой периодической задачи при 
и 
.
Доказательство теоремы основано на применении формулы Тейлора к вектор-функции 
в окрестности точки 
и последующем использовании метода неподвижной точки оператора.
Значимым требованием теоремы является дифференцируемость вектор-функции 
в окрестности некоторой точки 
. Существование частных производных вектор-функции 
зависит от дифференцируемости вектор-функции 
: 
по параметру 
в окрестности точки 
.
В § 3.2 доказываются теоремы о достаточных условиях дифференцируемости по параметру функции 
и изучаются случаи, когда такое дифференцирование невозможно.
Результаты главы применены для исследования численных примеров.
В заключении сформулированы основные результаты работы, получен-
ные в ходе диссертационного исследования.
ОСНОВНЫЕ РЕЗУЛЬТАТЫ
1) доказана нелокальная теорема существования, единственности и непрерывной зависимости решения дифференциального уравнения с максимумами от начальных данных и параметра;
2) получена структура решений нелинейного дифференциального уравнения с максимумами (0.1);
3) предложена новая схема исследования операторных уравнений, основанная на линеаризации главной части оператора;
4) на основе разработанного подхода получены эффективные признаки существования ненулевых решений двухточечной краевой периодической задачи для уравнения (0.1) в достаточно малой окрестности нулевого решения, сводящиеся к анализу величин, определяемых линейной составляющей правой части уравнения (0.1).
5) установлены новые условия существования ненулевых решений двухточечной краевой периодической задачи для уравнения (0.1) в достаточно малой окрестности нулевого решения, полученные с привлечением нелинейных членов правой части уравнения (0.1).
В работе рассмотрено 7 различных численных примеров.
В заключении подводятся общие итоги проведенной работы.
СОДЕРЖАНИЕ ДИССЕРТАЦИИ ДОСТАТОЧНО ПОЛНО ОТРАЖЕНО В СЛЕДУЮЩИХ ПУБЛИКАЦИЯХ:
- Кирюшкин В.В. Теорема существования и единственности решений систем дифференциальных уравнений с максимумами // Современные проблемы математики, механики, информатики: Тезисы докладов Международной научной конференции. – Тула: Изд-во ТулГУ, 2004. – С. 22–24.
- Кирюшкин В.В. Структура решений дифференциальных уравнений с максимумами // Некоторые актуальные проблемы современной математики и математического образования: Материалы научной конференции «Герценовские чтения – 2005». – С.-Петербург: Изд-во Библиотека Академии наук, 2005. – С. 55–59.
- Кирюшкин В.В. Свойства решений системы дифференциальных уравнений с максимумами // Новые информационные технологии в научных исследованиях и в образовании НИТ-2005: Тезисы докладов Х Всероссийской научно-технической конференции студентов, молодых ученых и специалистов. – Рязань: Изд-во РГРТА, 2005. – С. 20–21.
- Кирюшкин В.В. Теорема существования и единственности решения системы дифференциальных уравнений с максимумами // Известия РАЕН. Дифференциальные уравнения, 2005. – №9. – С. 11–18.
- Кирюшкин В.В. О представлении решения системы дифференциальных уравнений с максимумами // Известия РАЕН. Дифференциальные уравнения, 2005. – №9. – С. 19–23.
- Кирюшкин В.В. Системы алгебраических уравнений специального вида // Информатика и прикладная математика: Межвуз. Сб. науч. Тр., Ряз. гос. пед. ун-т. – Рязань: Изд-во РГПУ. – 2005. – С. 135–139.
- Кирюшкин В.В. Условия существования решения двухточечной краевой задачи системы дифференциальных уравнений с максимумами // Современные проблемы математики, механики, информатики: Тезисы докладов Международной научной конференции. – Тула: Изд-во ТулГУ, 2005. – С. 105–106.
- Кирюшкин В.В. О непрерывной дифференцируемости функции
по параметру // Известия Тульского Государственного Университета. Серия: Дифференциальные уравнения и прикладные задачи – Тула: Изд-во ТулГУ, 2005. – С. 40–45. - Кирюшкин В.В. Решение двухточечной краевой задачи по виду линейной части для систем дифференциальных уравнений с максимумами // Математика. Компьютер. Образование: Тезисы докладов XIII Международной конференции. – М. – Ижевск: Изд-во «Регулярная и хаотическая динамика», 2006. – Вып. 13 – С. 30.
- Кирюшкин В.В. Двухточечная краевая задача системы дифференциальных уравнений с максимумами // Новые информационные технологии в научных исследованиях и в образовании НИТ-2005: Тезисы докладов ХI Всероссийской научно-технической конференции студентов, молодых ученых и специалистов. – Рязань: Изд-во РГРТА, 2006. – С. 8–9.
- Кирюшкин В.В. Проблема решения двухточечных краевых задач систем дифференциальных уравнений с максимумами // Новые информационные технологии в научных исследованиях и в образовании НИТ-2005: Тезисы докладов ХI Всероссийской научно-технической конференции студентов, молодых ученых и специалистов. – Рязань: Изд-во РГРТА, 2006. – С. 9–10.
