Вырождающиеся эллиптические уравнения и связанные с ними весовые пространства
На правах рукописи
ВИХРЕВА Ольга Анатольевна
Вырождающиеся
эллиптические уравнения и
связанные с ними весовые пространства
01.01.02 - дифференциальные уравнения
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата физико-математических наук
Якутск – 2009
Работа выполнена на кафедре дифференциальных уравнений
ГОУ ВПО «Якутский государственный университет имени М.К. Аммосова»
Научный руководитель: доктор физико-математических наук,
профессор Егоров Иван Егорович
Официальные оппоненты: доктор физико-математических наук,
профессор Хлуднев Александр Михайлович,
Институт гидродинамики
имени М.А. Лаврентьева СО РАН,
г. Новосибирск
доктор физико-математических наук,
доцент Подгаев Александр Григорьевич,
Тихоокеанский государственный
университет, г. Хабаровск
Ведущая организация: Институт математики имени С.Л. Соболева
СО РАН, г. Новосибирск
Защита состоится «30» апреля 2009 года в 16 часов на заседании диссертационного совета К 212.306.05 при Якутском государственном университете имени М.К. Аммосова по адресу: 677000, г. Якутск, ул. Белинского, 58.
С диссертацией можно ознакомиться в библиотеке Якутского государственного университета имени М.К. Аммосова.
Автореферат разослан « » марта 2009 г.
Ученый секретарь
диссертационного совета,
кандидат физ.-мат. наук, доцент В.Е. Федоров
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы исследования. В работах Лаврентьева М.А., Келдыша М.В., Векуа И.Н., Христиановича С.А., Чаплыгина С.А., Гудерлея Л.Г. и др. была отмечена важность проблемы неклассических уравнений математической физики при решении задач, возникающих в трансзвуковой газовой динамике, в магнитогидродинамических течениях с переходом через скорость звука и скорость Альфена, в течениях жидкости в открытом канале, в теории бесконечно малых изгибаний поверхностей, а также в безмоментной теории оболочек с кривизной переменного знака и во многих прикладных задачах механики. Поэтому краевые задачи для вырождающихся эллиптических уравнений привлекают внимание многих авторов.
Интерес к изучению граничных задач для вырождающихся дифференциальных уравнений вновь заметно возрос после появления работ Г. Фикера и О.А. Олейник. Фундаментальные результаты в этом направлении, как известно, принадлежат М.В. Келдышу. Полученные им результаты затем развивались и обобщались в работах О.А. Олейник, Н.Д. Введенской, А.М. Ильина и др.
Изучение обобщенных решений вырождающихся эллиптических уравнений второго порядка началось с работ С.Г. Михлина и М.И. Вишика. Вслед за этим появился ряд работ, в которых методами, близкими к методу М.И. Вишика, изучались вырождающиеся уравнения второго и более высокого порядка.
Довольно много работ и монографий посвящено разрешимости краевых задач для вырождающихся эллиптических уравнений, но не достаточно изучено поведение весов на различных частях границы области. Поэтому отметим последние исследования.
В работах Егорова И.Е. и Тихонова Н.А в области 
, ограниченной в 
границей 
, часть 
которой лежит в гиперплоскости 
, а остальная часть 
- в полупространстве 
, рассматривается эллиптическое уравнение
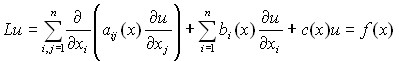, (1)
где 
- непрерывные функции в 
. Предполагается, что в уравнении (1) коэффициенты 
непрерывно дифференцируемы в 
, где 
- любое положительное число, а функция 
непрерывна в 
. Считается выполненным условие
и 
.
Также выполняются неравенства
где 
- непрерывная положительная функция при 
, 
.
При таких предположениях эллиптическое уравнение (1) вырождается на 
, поэтому краевые условия на 
ставятся в зависимости от сходимости интеграла 
и младшего коэффициента 
. Рассматриваются первая и третья краевые задачи для данного уравнения с произвольным вырождением. Доказаны теоремы существования и единственности обобщенных решений краевых задач, и изучены спектральные свойства оператора первой краевой задачи, которые обобщают известные результаты для вырождения степенного характера.
Цель работы. Исследовать краевые задачи для эллиптических уравнений второго порядка, вырождающихся с различной скоростью на разных частях границы области. Доказать существование и единственность обобщенных решений поставленных задач.
Методы исследования. Основными методами исследования являются: метод, основанный на теории вложения весовых функциональных пространств, и модифицированный метод Вишика. А также используются теорема о сжимающих отображениях и вариационный метод.
Научная новизна. В диссертации получены следующие основные результаты:
- Вводится определение одного класса весовых пространств С.Л. Соболева. Доказана теорема о плотности финитных функций в весовом пространстве в кубе. Дается приложение этого весового пространства при изучении задачи Дирихле и задачи Е для одного вырождающегося эллиптического уравнения второго порядка.
- Доказана обобщенная разрешимость первой краевой задачи для двух классов эллиптических уравнений, вырождающихся на различных частях границы с разными «скоростями» вырождения. При этом в первом случае доказана теорема вложения соответствующего весового пространства в
. Кроме того, доказана однозначная обобщенная разрешимость третьей краевой задачи для второго из указанных классов уравнений. - Доказана обобщенная и фредгольмова разрешимость смешанной краевой задачи для вырождающегося эллиптического уравнения. При этом доказана теорема о компактности вложения соответствующего весового пространства в
. - С помощью теоремы о сжимающих отображениях и вариационного метода доказана однозначная обобщенная разрешимость задачи Дирихле для нелинейного вырождающегося эллиптического уравнения.
Теоретическая и практическая значимость. Работа носит теоретический характер, заполняя определенный пробел в теории дифференциальных уравнений с частными производными. Ее результаты могут быть использованы для дальнейшей разработки теории краевых задач для вырождающихся эллиптических уравнений и найти приложение в теории краевых задач для уравнений смешанного типа, возникающих при решении многих важных вопросов прикладного характера (теории малых изгибаний поверхностей вращения, безмоментной теории оболочек и т.д.). Особо значительную роль такие уравнения играют в газовой динамике.
Апробация работы. Результаты, изложенные в диссертации, докладывались и обсуждались на семинаре профессора И.Е. Егорова «Дифференциальные уравнения с частными производными» (НИИ математики при ЯГУ, г. Якутск), на семинаре профессора А.И. Кожанова «Неклассические уравнения математической физики» (ИМ СО РАН, г. Новосибирск), а также доложены на различных конференциях: Всероссийская школа-семинар студентов, аспирантов, молодых ученых и специалистов «Математическое моделирование развития северных территорий в условиях рынка» (2004, 2005, 2006); Лаврентьевские чтения Республики Саха (Якутия) (2002, 2005); IV и V Международные конференции по математическому моделированию (2004, 2007); Республиканская научно - практическая конференция «Информационные технологии в науке, образовании и экономике» (2003); Всероссийская конференция «Космо - и геофизические явления и их математические модели» (2002). Работа поддержана грантом №8425 Ведомственной научной программы Федерального агентства по образованию «Развитие научного потенциала высшей школы» на 2005 год и грантом 2006-РИ-19.0/001/711 научной программы «Проведение научных исследований молодыми учеными» Федерального агентства по науке и инновациям Министерства образования и науки РФ.
Публикации. Основные результаты диссертации опубликованы в 9 печатных работах, список которых приведен в конце автореферата.
Структура и объем диссертации. Работа состоит из введения, трех глав и списка литературы. Общий объем работы составляет 65 страниц. Список литературы содержит 52 наименования.
СОДЕРЖАНИЕ РАБОТЫ
Во введении даны краткие исторические сведения по теме диссертации, обосновывается актуальность темы, сформулированы цели исследования, приводится содержание работы, а также дан краткий обзор использованной литературы.
Первая глава носит вспомогательный характер.
В этой главе дается определение одного класса весовых пространств С.Л. Соболева. Приведены теоремы вложения и компактности весовых пространств, ранее доказанные И.Е. Егоровым. А также доказана теорема о плотности финитных функций в весовом пространстве Соболева в кубе 
. Дается приложение этого весового пространства при изучении задачи Дирихле и задачи Е для одного вырождающегося эллиптического уравнения второго порядка.
Пусть 
- куб со стороной 
: 
. Обозначим через 
замыкание множества 
по норме
,
а через 
- приграничную полосу ширины 
. Здесь 
, а весовые функции 
удовлетворяют условию
(2)
В качестве 
примем замыкание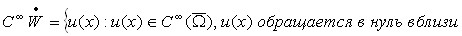 
по норме 
, где 
, 
.
Теорема 1. Если 
- куб со стороной 
: 
, и выполняется условие (2), то для равенства 
необходимо и достаточно выполнения условия 
, где 
- любой шар с центром в точках 
.
Пусть выполняются условия
, (3)
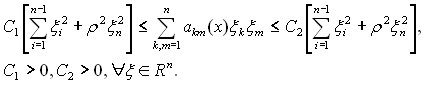(4)
Рассмотрим квадратичную форму
,
которая определяет норму, эквивалентную норме 
при 
. Через 
и 
обозначим положительные самосопряженные операторы, порожденные формой 
на гильбертовых пространствах 
и 
соответственно.
Теорема 2. Пусть выполняются условие (2), (3), (4) и 
в 
. Тогда равенство 
справедливо, если и только если
для любого шара 
с центром на 
.
Основной вопрос, который мы исследуем во второй главе - это однозначная обобщенная разрешимость первой краевой задачи для вырождающегося эллиптического уравнения
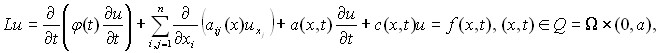(5)
где функция 
удовлетворяет условиям:
- непрерывная функция при 
, 
; 
- вещественные измеримые в 
функции 
, удовлетворяющие условию симметричности: 
, а 
непрерывна в 
, и 
непрерывна в 
для 
.
Предполагается, что выполнено неравенство
,
где 
.
Положим
.
Введем вспомогательную функцию
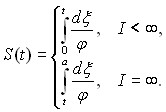
При 
будем считать, что выполнено условие
вблизи 
. (6)
Пусть 
- замыкание класса 
по норме
.
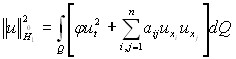Для 
и 
рассмотрим билинейную форму
.
Определение 1. Функция 
называется обобщенным решением первой краевой задачи для уравнения (5), если выполнено тождество
для любой функции 
.
Теорема 3. Пусть коэффициент 
при 
удовлетворяет неравенству (6), а при 
вблизи 
и 
,
для любого шара 
с центром на 
. Если
,
вблизи 
,
то первая краевая задача для уравнения (5) имеет единственное обобщенное решение для любой функции 
, где весовая функция 
положительна в 
и 
вблизи 
.
Также доказана теорема о существовании и единственности обобщенного решения первой краевой задачи для вырождающегося эллиптического уравнения
(7)
где функции 
удовлетворяют условиям:
- непрерывные функции при 
, 
; 
- вещественные измеримые в 
функции 
, удовлетворяющие условию симметричности: 
. При этом область 
совпадает с областью, в которой рассматривается уравнение (1).
Предположим, что выполнены неравенства
(8)
Для доказательства существования обобщенных решений используется модифицированный метод Вишика, а для доказательства единственности обобщенного решения также используется схема М.И. Вишика.
Положим
.
Введем вспомогательные функции
При 
будем считать, что вблизи 
выполнено условие
. (9)
При 
будем считать, что вблизи 
выполнено условие
. (10)
Пусть 
- замыкание класса 
по норме
.
Для 
и 
рассмотрим билинейную форму
.
Определение 2. Функция 
называется обобщенным решением первой краевой задачи для уравнения (7), если выполнено тождество
для любой функции 
обращается в нуль вблизи 
и 
}.
Теорема 4. Пусть коэффициенты 
при 
и 
удовлетворяют неравенствам (9), (10), а при 
в некоторой окрестности 
,
и при 
вблизи 
.
Если
,
то первая краевая задача для уравнения (7) имеет единственное обобщенное решение для любой функции 
, где весовая функция 
положительна в 
и
В третьей главе сначала изучается третья краевая задача для эллиптического уравнения (7). Доказывается существование и единственность её обобщенного решения.
При выполнении условий (8) эллиптическое уравнение (7) вырождается на части боковой поверхности и на основаниях цилиндрической области (вырождается по двум направлениям).
Краевая задача. Найти решение уравнения (7) в области 
, такое, что
, 
, (11)
где 
при 
, 
при 
, 
при 
, 
при 
, а 
- единичный вектор внешней нормали к 
,
,
- непрерывная функция на замыкании 
.
Пусть 
- замыкание класса функций из 
, равных нулю вблизи 
, по норме
,
где 
- непрерывная функция, отличная от нуля в некоторой окрестности внутренней точки 
.
Для 
и 
рассмотрим билинейную форму
где 
.
Определение 3. Функция 
называется обобщенным решением краевой задачи (7), (11), если выполнено тождество
для любой функции 
.
Теорема 5. Пусть выполнены неравенства (8), (9), (10) и 
при 
, 
при 
,
где 
для 
, 
для 
и 
Тогда краевая задача (7), (11) может иметь не более одного обобщенного решения.
Теорема 6. Пусть выполнены условия теоремы 5. Тогда краевая задача (7), (11) имеет обобщенное решение при любых 
и 
, где 
в 
где 
Также в третьей главе доказана обобщенная и фредгольмова разрешимость смешанной краевой задачи для вырождающегося эллиптического уравнения (5).
Предположим, что выполнено неравенство
. (12)
При 
будем считать, что выполнено условие
вблизи 
. (13)
Пусть 
- замыкание множества комплекснозначных функций из класса 
, равное нулю вблизи 
и Г, по норме
.
Краевая задача. Найти решение уравнения (5) в области 
такое, что
, (14)
где 
и 
.
Теорема 7. Пусть выполнены условия (12) и 
. Тогда ограниченное в 
множество компактно в 
.
Теорема 8. Пусть выполнены условия теоремы 4 и 
. Тогда задача (5), (14) не может иметь более одного обобщенного решения из 
, и она действительно разрешима в 
при любом 
, где 
при 
и 
вблизи 
.
Теорема 9. Пусть выполнены неравенства (12), (13) и 
. Тогда для смешанной краевой задачи (5), (14) имеет место альтернатива Фредгольма, а задача на собственные значения
приводит к дискретному и конечномерному спектру.
В конце данной главы исследована задача Дирихле для нелинейного вырождающегося эллиптического уравнения
(15)
где функция 
удовлетворяет условиям: 
- непрерывная функция при 
, 
; 
- вещественные непрерывные в 
функции 
, удовлетворяющие условию симметричности: 
для 
, а 
непрерывна в 
, и 
непрерывна в 
для 
.
Пусть 
- замыкание класса 
по норме
,
где 
.
Предполагается, что выполнены неравенства
,
,
, где 
– положительное число, не зависящее от 
.
При определенных условиях на коэффициенты уравнения с помощью теоремы о сжимающих отображениях и вариационного метода доказывается существование единственного обобщенного решения задачи Дирихле для уравнения (15).
Определение 4. Функция 
называется обобщенным решением задачи Дирихле для уравнения (15), если выполнено интегральное тождество
.
Теорема 10. Пусть 
и пусть коэффициент 
при 
в некоторой окрестности 
удовлетворяет условию
и 
,
для любого шара 
с центром на 
. Если
,
то для любой функции 
существует единственное обобщенное решение задачи Дирихле для уравнения (15).
Работы автора по теме диссертации
[1] Вихрева О.А. Обобщенная и фредгольмова разрешимость смешанной краевой задачи для вырождающегося эллиптического уравнения / О.А. Вихрева // Вестник СамГУ, 2007. Т. 56, №6. - С.194-202.
[2] Вихрева О.А. О весовом пространстве Соболева в кубе 
// Сборник трудов аспирантов ЯГУ им. М.К. Аммосова / О.А. Вихрева // Под ред. В.Ю. Фридовского и др. - Якутск: Изд-во Якутского университета, 2004. - С. 29-34.
[3] Вихрева О.А. Краевая задача для вырождающегося эллиптического уравнения / О.А. Вихрева // Сборник трудов II Республиканской научно-практической конференции «Информационные технологии в науке, образовании и экономике». - Якутск: ЯГУ, 2003. - С. 113-118.
[4] Вихрева О.А. Обобщенная и фредгольмова разрешимость смешанной краевой задачи для вырождающегося эллиптического уравнения / О.А. Вихрева // Тезисы докладов V Международной конференции по математическому моделированию. - Якутск, 2007. - С. 16-17.
[5] Вихрева О.А. Об одной краевой задаче для вырождающегося эллиптического уравнения / О.А. Вихрева // Математические заметки ЯГУ, 2006. Т. 13, выпуск 1. - C. 58-67.
[6] Вихрева О.А., Егоров И.Е. Обобщенная разрешимость первой краевой задачи для вырождающегося эллиптического уравнения / О.А. Вихрева // Сборник статей IX Лаврентьевских чтений, посвященных Международному году физики. Т.1. – Якутск: ГУ РОНПО, 2005. - С. 34-41.
[7] Вихрева О.А. О смешанной краевой задаче для вырождающегося эллиптического уравнения / О.А. Вихрева // Тезисы докладов IV Всероссийской школы-семинара «Математическое моделирование развития северных территорий в условиях рынка». - Якутск, 2006. - С. 36-37.
[8] Вихрева О.А. Об обобщенной разрешимости первой краевой задачи для вырождающегося эллиптического уравнения / О.А. Вихрева // Тезисы докладов IV Международной конференции по математическому моделированию. - Якутск, 2004. - С.11-13.
[9] Вихрева О.А. Задача Дирихле для нелинейного вырождающегося эллиптического уравнения / О.А. Вихрева // Математические заметки ЯГУ, 2008. Т. 15, выпуск 1. - C. 39-44.
ВЫРОЖДАЮЩИЕСЯ ЭЛЛИПТИЧЕСКИЕ УРАВНЕНИЯ
И СВЯЗАННЫЕ С НИМИ ВЕСОВЫЕ ПРОСТРАНСТВА
автореферат
ВИХРЕВА Ольга Анатольевна
Подписано в печать 18.03.2009 г. Формат 60
84/16
Печ. л. 1,0. Уч.-изд. л. 1,25. Тираж 100 экз. Заказ 3
Отпечатано в филиале издательства ЯГУ,
Институт математики и информатики ЯГУ.
Адрес: г. Якутск, ул. Кулаковского, 48. Тел.: (4112)496833
