Математические задачи нелинейной теории переноса. газокинетическое уравнение
На правах рукописи
МАКИН Руслан Сергеевич
МатематическИЕ ЗАДАЧИ НЕЛИНЕЙНОЙ ТЕОРИИ ПЕРЕНОСА.
газокинетическое уравнение
Специальность: 01.01.03– математическая физика
Автореферат
диссертации на соискание учёной степени
доктора физико-математических наук
Москва 2009
Работа выполнена в ОАО «Государственный научный центр Научно – исследовательский институт атомных реакторов» ( ОАО «ГНЦ НИИАР» )
Официальные оппоненты:
доктор физико-математических наук, профессор
Малинецкий Георгий Геннадьевич
доктор физико-математических наук, профессор
Кащенко Сергей Александрович
доктор технических наук
Селезнев Евгений Федорович
Ведущая организация: Научно-исследовательский ядерный университет – Московский инженерно-физический институт (НИЯУ – МИФИ)
Защита состоится «06» октября 2009 г. в 11 часов на заседании диссертационного совета Д 002.024.02 при Институте прикладной математики им. М.В. Келдыша РАН по адресу: 125047, Москва, Миусская пл., д.4
С диссертацией можно ознакомиться в научно-технической библиотеке.
Отзывы на автореферат диссертации отправлять по адресу: 125047, Москва,
Миусская пл., д.4
Автореферат разослан «__» ________ 2009 г.
Учёный секретарь диссертационного
совета к.ф.-м.н. О.В.ЩЕРИЦА
1. Общая характеристика РАБОТЫ
Актуальность темы. Безопасность эксплуатации ядерных энергетических реакторов и других радиационно-опасных установок различного назначения является одной из важнейших проблем современной энергетики и нелинейной динамики. Большое значение в решении этой проблемы имеет знание и исследование их динамических характеристик. Целью исследования динамики в конечном итоге является доказательство устойчивости стационарных режимов нелинейной системы или отыскание условий, при которых обеспечивается указанная устойчивость. Обычно a priory такой информации либо нет, либо ее чрезвычайно мало. В этих условиях практически единственной возможностью является создание адекватных математических моделей и их последующий анализ. При этом резко возрастает роль различных эффектов, связанных с распределенностью, неоднородностью систем и нелинейностью происходящих сложных процессов. В то же время используемые для анализа подобных нелинейных систем весьма упрощенные математические модели либо вообще не учитывают указанных эффектов, либо учитывают их очень приближенно, например, в рамках линеаризованных моделей. Это связано в первую очередь с тем, что сложные распределенные системы в неоднородных нелинейных средах обычно описываются системой уравнений в частных производных или системой интегро-дифференциальных уравнений и должны рассматриваться в весьма общих банаховых пространствах. Заметим, что сама процедура линеаризации для сложных нелинейных систем, как правило, требует строгого обоснования.
Таким образом, разработка адекватных распределенных нелинейных моделей сложных объектов, процессов и исследование возникающих режимов, вопросов устойчивости и нелинейных явлений, включая асимптотическое и нерегулярное (хаотическое) поведение, является весьма актуальной задачей. Кроме того, решение вопросов существования, единственности, свойств спектра, полноты корневых векторов, положительности решений и некоторых других представляет значительный интерес. Данное обстоятельство связано с решением нового класса задач, описывающих гораздо более сложные процессы, чем, например, краевая задача для эллиптического уравнения второго порядка, которая, как известно, является достаточно грубым диффузионным приближением для рассматриваемых процессов переноса.
Начиная с первых работ по теории переноса излучения (нейтронов) в размножающих и замедляющих средах, выполненных Э.Ферми, И.В.Курчатовым с сотрудниками, исследования по теории реакторов тесно связаны с именами А. Вейнберга, Ю. Вигнера[1] в США, академиков РАН В.С.Владимирова[2], Г.И. Марчука, заложивших основы математической теории взаимодействия излучения с веществом, в том числе переноса нейтронов. Существенный вклад в развитие математической теории реакторов внесли профессора С.М. Фейнберг, С.Б. Шихов[3], А.Д. Галанин, В.В. Орлов, Л.Н. Усачев, Г.А. Бать и научные коллективы РНЦ «Курчатовский институт», ГНЦ ФЭИ, ИТЭФ, ОКБМ, МИФИ, ИПМ, ИПЭ НАН Беларуси и др. Работы отечественных ученых Т.А. Гермогеновой, М.В. Масленникова, Б.Б. Кадомцева, С.Б. Шихова, Ю.И. Ершова[4], В.В. Смелова, В.И. Лебедева, В.И. Агошкова, В.Я. Гольдина, В.В. Учайкина, А.В. Крянева, Ю.А. Кузнецова и их учеников, а также зарубежных ученых Б. Дэвисона, Р. Маршака, С. Чандрасекара, Е. Хопфа, К. Кейза[5], Дж. Ленера, Г. Винга и др., отражающие основные положения этой теории, хорошо известны.
Одним из важнейших открытий второй половины прошлого века явилось установление нового факта, говорящего о том, что нелинейная детерминированная динамическая система при отсутствии в ней каких-либо случайных внешних возмущений может генерировать стохастические колебания, т.е. порождать динамический или детерминированный хаос. Такой хаос может возникать в ситуации, когда в фазовом пространстве динамической системы имеется ограниченная область, из которой траектории не уходят, и при этом они неустойчивы по Ляпунову. В силу неустойчивости сколь угодно близкие вначале траектории расходятся за конечный промежуток времени. Поэтому практически невозможно предсказать длительное поведение детерминированной нелинейной динамической системы, поскольку реально начальные условия задаются лишь с конечной степенью точности.
Сегодня, несмотря на значительные успехи, теория нелинейных динамических систем[6] далека от завершения даже для конечномерных пространств. Известно, например, что хаос в нелинейных системах возникает при наличии в их фазовом пространстве гомоклинических (в общем случае – гиперболических) структур. Существующие критерии возникновения хаоса труднопроверяемы, поскольку требуют, например, определения условий взаимного пересечения устойчивых и неустойчивых инвариантных многообразий, и в общем случае отсутствуют. Поэтому актуальной остается задача разработки конструктивных критериев хаоса, которые были бы применимы для широкого класса нелинейных динамических систем.
В настоящее время, после открытия в 1964 г. первой модельной системы (системы Лоренца) с хаотическим поведением, известны многочисленные примеры систем с подобным поведением в различных областях физики, механики, гидродинамики, биологии (список можно продолжить)[7], в том числе в реакторных системах. Возникающий здесь круг вопросов в основном связан с устойчивостью поведения решений и возникновением динамического хаоса. Традиционно в теории устойчивости изучается асимптотическое поведение траекторий, лежащих вблизи уже известной (стационарной) траектории, или, как в теории ветвления, обнаружение и исследование решений, ответвляющихся от известного по мере изменения параметров задачи. Несмотря на обширные исследования, существующие трудности далеки от преодоления. Обычно исследуются на устойчивость решения, появляющиеся при первой бифуркации, если их удается получить. Очевидно, такой путь исследования задач гидродинамики имел в виду Л.Д. Ландау, высказавший гипотезу, что при возрастании параметра – числа Рейнольдса, усложнение (турбулизация) течения объясняется появлением все большего числа несоизмеримых периодов у решения. Можно принять и «физическую» точку зрения, восходящую к Э. Хопфу, О.А. Ладыженской и др. – решения диссипативных систем «забывают» свои начальные данные и формируются под действием постоянно и стационарно действующих факторов. В строгом математическом смысле это не так, потому что в детерминированной системе решение (глобальное или локальное) полностью определяется своими начальными и дополнительными данными, а также внешним воздействием (например, системой управления). Однако с течением времени решение может «далеко» уйти от этих данных и в этом смысле «забыть» их. В связи с этим возникает вопрос о той части фазового пространства, к которой притягиваются все решения, и динамике рассматриваемой системы на ней. Структура этого (компактного) притягивающего инвариантного множества (аттрактора) может быть весьма сложной, как и динамика на нем; другими словами, такое множество должно являться объектом исследования. Сложность изучения таких притягивающих множеств (аттракторов, квазиаттракторов) нелинейных динамических систем заключается в отсутствии законченной теории таких множеств (гиперболических множеств) не только для бесконечномерных, но даже для конечномерных динамических систем[8]. Кроме того, не исключено (строго не установленный факт) появление так называемых «диких гиперболических множеств» (Ньюхаус) в составе притягивающих многообразий. Этот вопрос является дискуссионным и затрагивает другой, более важный: правильно ли мы определяем притягивающие множества и достаточно ли для описания динамики на них концепции грубости (типичности) Андронова-Понтрягина. Постановка и решение этих вопросов представляют несомненный, в том числе и самостоятельный интерес.
Для ряда нелинейных динамических систем наблюдается последовательность бифуркаций удвоения периода при изменении параметра от значений, при которых оно имеет лишь неподвижные точки, к значениям, при которых существует бесконечное множество периодических орбит. Эти каскады бифуркаций удвоения периода обладают богатой структурой (универсальность Фейгенбаума). Существуют свойства, ассоциированные с этими каскадами, которые универсальны в том смысле, что не зависят от выбора конкретной динамической системы. При этом весьма актуальной является задача установления механизма перехода к «хаосу» через бифуркации удвоения периода для конкретной распределенной модельной задачи переноса, который наблюдался экспериментально. Важно отметить, что для нелинейных распределенных динамических систем возможен пространственно-временнй хаос, характеризующийся тем, что в процессе колебаний случайными оказываются не только временные реализации процесса, но и пространственные распределения поля (излучения, температуры). Такой режим пространственно-временнго хаоса в теории нелинейных динамических систем имеет специальное название – диссипативные структуры. Этому режиму присуще соответствующее притягивающее множество (квазиаттрактор). В последние годы в исследовании структуры и свойств таких множеств на базе новых идей и понятий (инерциальные многообразия и инерциальные формы, параметры порядка, фрактальные множества и т.п.), а также основных положений (парадигм) синергетики достигнуты определенные успехи[9],[10],[11]. Существенные достижения в разработке соответствующих методов и подходов для широкого класса нелинейных систем получили коллективы исследователей ИПМ им. М.В. Келдыша, РНЦ КИ, МГУ, МИФИ, ННГУ, СГУ и др., а также зарубежные исследователи П. Константин, К. Фойяш, Б. Николаенко, Р. Темам, Дж. Хейл со своими сотрудниками. Однако результаты исследований нелинейных распределенных моделей переноса и их различных приближений немногочисленны, а в части изучения инвариантных многообразий, структуры притягивающих множеств и сопутствующих вопросов публикаций еще меньше.
Анализ современного состояния теории нелинейного переноса на основе газокинетического уравнения с распределенными параметрами позволяет сформулировать как одну из важнейших проблем нелинейной динамики проблему разработки и создания теоретических методов анализа динамики и свойств решений модельных задач переноса. При решении этой проблемы на первый план выступают модельные задачи переноса в распределенных неоднородных средах, в основе которых лежат газокинетическое уравнение или многогрупповое диффузионное (Р1-) приближение.
Цель работы. Развитие и обоснование строгой математической теории нелинейных уравнений переноса, включающее следующие этапы исследования:
- Выбор математической модели (моделей) исследования, адекватно описывающей реальные физические процессы (на примере переноса излучения (нейтронов)) в распределенных нелинейных неоднородных и ограниченных средах.
- Формулировка и доказательство теорем существования и единственности решений исходной нелинейной задачи, где перенос описывается газокинетическим уравнением, в некотором бесконечномерном функциональном пространстве.
- Установление условий существования и свойств решений стационарной нелинейной задачи, отвечающей исходной системе, включая вопросы полноты собственных (корневых) векторов, устойчивости решений и существования точек бифуркации.
- Обоснование метода линеаризации (первого метода Ляпунова) в задаче устойчивости стационарных и периодических решений исходной нелинейной задачи.
- Анализ спектральных свойств линеаризованной задачи, нелинейным образом зависящей от спектрального параметра; исследование структуры спектра, его асимптотики и других важных спектральных свойств.
- Доказательство обобщенной теоремы Смейла – Биркгофа (условий существования гомоклинической точки трансверсального пересечения инвариантных (локальных) многообразий (метод Мельникова)). Установление существования инвариантного гиперболического множества, топологически эквивалентного подсдвигу конечного типа (подкове Смейла) для исходной нелинейной задачи.
- Установление условий существования инвариантных конечномерных множеств – инерциальных многообразий, исследование их свойств. Проверка спектрального условия (условия конуса) и доказательство существования конечномерных инерциальных многообразий для исходной нелинейной задачи.
- Применение изложенных методов для более общих нелинейных динамических систем. Демонстрация вышеуказанного подхода на примере одной практической модельной задачи, в которой перенос описывается в многогрупповом диффузионном (Р1-) приближении.
Методы исследования. Для исследования использовался аппарат функционального анализа (теория полугрупп операторов, теория операторов, инвариантных относительно положительных конусов в банаховых пространствах, теория знакорегулярных (квазизнакорегулярных) операторов, спектральная теория самосопряженных и несамосопряженных операторов), топологические методы, аппарат теории нелинейных динамических систем (гиперболические множества, инвариантные притягивающие множества (аттракторы, квазиаттракторы) и инвариантные инерциальные многообразия), теория устойчивости и теория бифуркаций; использованы также результаты линейной теории переноса. В основе развитого подхода лежат принципы линеаризации и локализации, а также основные положения синергетики.
Научная новизна и практическая ценность работы:
- сформулированы условия существования глобального (сильного) решения и условия существования локального решения для исходной нелинейной распределенной системы уравнений в ограниченных средах, где перенос описывается многоскоростным газокинетическим (интегродифференциальным) уравнением или его многогрупповым диффузионным (Р1-) приближением; доказаны соответствующие теоремы существования (несуществования) глобальных решений в выбранном функциональном (фазовом) пространстве;
- исследованы свойства операторов и решений исходной нелинейной задачи, включая свойство положительности решений в некоторых банаховых пространствах с положительными конусами;
- сформулированы и доказаны теоремы существования и свойства решений нелинейной стационарной задачи, отвечающей исходной нелинейной задаче, включая свойства положительности и условия существования ведущего собственного значения;
- доказаны теоремы полноты собственных (корневых) векторов в общем случае; указаны условия существования базиса Рисса;
- установлено существование счетного множества простых вещественных собственных значений и отвечающих им собственных элементов из некоторых множеств конечномерных положительных конусов (конусов конечного ранга) в однородной среде;
- указана оценка спектрального зазора (расстояния между ведущим собственным значением и остальным спектром) и установлено, в каких случаях базисные функции являются чебышевскими (Т-системами), что позволяет применять чебышевские методы ускорения сходимости;
- показано существование счетного множества точек бифуркации в случае однородной среды; рассмотрены вопросы о количестве, характере и устойчивости решений на некотором инвариантном множестве;
- проведен анализ спектральных свойств линеаризованной задачи и установлен принцип линеаризации и спектр линеаризации (по В.И. Юдовичу) для исходной нелинейной задачи; установлены свойства гладкости нелинейной диссипативной полугруппы, разрешающей исходную задачу;
- сформулированы и доказаны теоремы о структуре спектра (точечного, непрерывного, существенного) операторного пучка (обобщенного пучка типа М.В. Келдыша), отвечающего линеаризованной задаче, где спектральный параметр нелинейным (дробно-рациональным и/или полиномиальным) образом входит в пучок; найдена асимптотика спектра задачи;
- доказана полнота корневых векторов (кратная полнота по М.В. Келдышу) и условия сходимости по ним в некотором функциональном пространстве; установлены условия существования (u0-положительность) ведущего собственного значения и отвечающего ему (единственного)элемента из положительного конуса;
- существенно уточнены спектральные свойства и асимптотические оценки в одномерной геометрии:
- Минимальность, полнота и базисность системы корневых векторов;
- Принадлежность операторного пучка классу вполне положительных операторов;
- Существование счетного подмножества простых вещественных собственных значений и отвечающего ему множества собственных элементов, обладающих осцилляционными свойствами (ряды Маркова);
- установлены условия существования (обобщенный метод Мельникова) гомоклинической (гетероклинической) точки трансверсального пересечения (локальных) устойчивого и неустойчивого инвариантных многообразий для некоторого семейства абстрактных эволюционных уравнений (обобщенная теорема Биркгофа - Смейла); эти условия проверены для исходной нелинейной задачи; сформулировано утверждение: трансверсальная гомоклиническая (гетероклиническая) траектория порождает хаос («динамический реакторный хаос») в бесконечномерном фазовом пространстве;
- доказано существование инвариантного гиперболического множества, топологически эквивалентного подсдвигу конечного типа (канторова множества, топологически эквивалентного подкове Смейла);
- проведен анализ экспериментально наблюдавшегося перехода к «реакторному хаосу» через последовательность бифуркаций удвоения периода (универсальность Фейгенбаума) как общего свойства (модельных) нелинейных систем, приближающихся к гомоклиническому касанию устойчивого и неустойчивого многообразий некоторой периодической орбиты (неподвижной точки);
- установлены условия существования инвариантных экспоненциально притягивающих конечномерных многообразий – инерциальных многообразий для исходной нелинейной задачи с компактной (квазикомпактной) полугруппой и нормальным гиперболическим множеством;
- проведен анализ основных свойств инерциальных многообразий; сформулирован принцип сведения, проверено спектральное условие (условие конуса) и установлено существование k-мерного инерциального многообразия для исходной нелинейной задачи (гипотеза Э. Хопфа); сформулирован нелинейный динамический метод Галеркина;
- развитый подход распространен на семейства модельных задач, где перенос описывается в многогрупповом диффузионном (Р1-) приближении; соответствующие результаты получены для вышеуказанного семейства моделей; рассмотрены возможности применения вышеизложенного подхода для более сложных нелинейных модельных задач.
Проведенные в диссертационной работе исследования, предложенные подходы и полученные результаты позволили развить и обосновать строгую математическую теорию нелинейных уравнений переноса. Тем самым осуществлен важный этап в развитии нового направления теории переноса – нелинейной теории переноса. Кроме того, изложенные в работе методы и подходы представляют самостоятельный интерес для общей теории нелинейных динамических систем и вносят определенный вклад в общие представления синергетики. Материал диссертационной работы, будучи в первую очередь теоретическим исследованием, является основой для формулировки конкретных вычислительных алгоритмов и решения актуальных практических задач в соответствующих областях физики и техники. С другой стороны, полученные в работе результаты и поставленные вопросы могут являться основой для последующих исследований.
На защиту выносятся:
- Качественный анализ свойств решений исходной нелинейной задачи, включая положительность решений в пространствах с положительными конусами и условия продолжимости (непродолжимости) решений. Доказательство условий существования по крайней мере одного стационарного положительного нетривиального решения нелинейной стационарной задачи, отвечающей исходной нелинейной задаче.
- Анализ полноты корневых векторов стационарной (условно-критической) задачи; базисность системы корневых векторов и условия сходимости разложений; некоторые тонкие свойства спектра в случае одномерной геометрии – знакорегулярность, существование счетного множества простых вещественных собственных значений; конструктивная оценка спектрального зазора, обоснование чебышевских методов ускорения сходимости вычислительных алгоритмов.
- Обоснование метода линеаризации применительно к задаче устойчивости стационарных (периодических) решений исходной нелинейной задачи. Исследование структуры спектра линеаризованной задачи; метод исследования операторного пучка с нелинейным вхождением спектрального параметра; теоремы полноты (кратной полноты по М.В. Келдышу) корневых векторов и условий сходимости; условия существования в спектре ведущего (крайне правого) собственного значения и оценка спектрального зазора. Спектральные свойства и асимптотические оценки для собственных значений и элементов в случае однородной среды.
- Условия существования гомоклинической точки трансверсального пересечения (локальных) устойчивого и неустойчивого инвариантных многообразий (обобщенная теорема Смейла – Биркгофа); существование инвариантного гиперболического множества, топологически эквивалентного подсдвигу конечного типа для исходной нелинейной задачи. Доказательство существования инвариантных экспоненциально притягивающих конечномерных многообразий – инерциальных многообразий; свойства инерциальных многообразий: липшицева непрерывность, экспоненциальная дихотомия, устойчивость и неустойчивость компактных инвариантных множеств.
- Результаты по п.п. (1-4) для модельной нелинейной задачи, где перенос описывается в многогрупповом диффузионном (Р1-) приближении.
Апробация работы. Основные результаты диссертационной работы отражены в 42 публикациях.
Результаты исследований, изложенные в диссертации, по мере их получения докладывались на семинарах в следующих организациях: «ГНЦ РФ – Научно-исследовательский институт атомных реакторов»; ГНЦ РФ – Физико-энергетический институт им. академика А.И. Лейпунского; Московском инженерно-физическом институте (кафедра прикладной математики, кафедра «Ядерные реакторы и энергетические установки»); Всероссийском научно-исследовательском институте по эксплуатации атомных электростанций; Научно-исследовательском и конструкторском институте энерготехники им. академика Н.А.Доллежаля; Научно-исследовательском технологическом институте им. академика А.П.Александрова; Институте прикладной математики им. академика М.В. Келдыша; Санкт-Петербургском техническом университете; Математическом институте им. В.А. Стеклова РАН; Ульяновском государственном университете; Ульяновском государственном техническом университете; Новосибирском государственном университете; Институте математики СО РАН; Факультете вычислительной математики и кибернетики МГУ им. М.В. Ломоносова.
Основные результаты диссертации докладывались на следующих научных форумах:
- XXXIV ежегодная научно-техническая конференция МИФИ. Москва, 1988 г.
- Третья Международная научная конференция Ядерного Общества России. С.-Петербург, Россия, 1992 г.
- 7-ой Европейский Симпозиум по моделированию (ESS’95), Эрланген – Нюрнберг, Германия, 1995 г.
- 12-ая Международная конференция по моделированию (SI’95), Феникс, Аризона, США, 1995 г.
- Международный семинар «Days on Diffraction», С.-Петербург, 2005 -2008 г.г.
- 10-е Харитоновские чтения.г. Саров, 2008 г.
Структура и объем диссертации. Диссертация состоит из введения, 8 глав, 29 параграфов, заключения и 3 приложений, а также содержит 12 рисунков и 498 библиографических ссылок. Общий объем диссертации 372 страницы.
2. основное содержание работы
Введение содержит обзор работ по методам нелинейной динамики и нелинейной теории переноса излучения и вещества, выделены возникающие здесь узловые вопросы. Во введении обоснована актуальность диссертации, определен предмет и цели исследований, приведено краткое описание содержания диссертации по главам.
В главе 1 «Нелинейная нестационарная система уравнений переноса» дана постановка задачи для общей нелинейной модели переноса излучения в размножающих распределенных средах. В рамках рассматриваемой модели определены основные операторы и установлены их свойства, для чего приведены необходимые сведения из теории операторов в банаховых пространствах (параграф 1 и Приложение 1).
В параграфе 2 представлена математическая модель (семейство моделей), в рамках которой функция распределения излучения (нейтронов) удовлетворяет газокинетическому уравнению переноса, ядерно-физические характеристики которого функционально зависят от температуры среды; температура среды в свою очередь подчиняется уравнению, записанному в общем виде, так что все встречающиеся на практике варианты являются его частным случаем[12] :
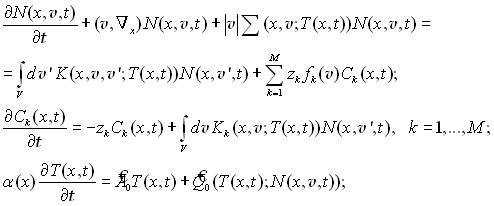(1)
начальные и граничные условия:
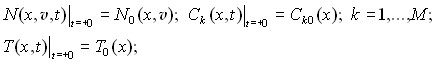(2)
(3)
Здесь коэффициенты и ядра даются выражениями:
(4)
Функции 
, характеризуются макроскопическими нейтронными сечениями; р – тип взаимодействия излучения (нейтронов) с ядрами l-го нуклида, входящего в состав среды.
Система (1) – (3) описывает эволюцию во времени пространственно – энергетического (скоростного) распределения плотности излучения (нейтронов) 
, пространственного распределения М групп запаздывающего излучения (нейтронов) 
, и температуры среды 
в некотором (мультиплицирующем) объеме G с границей 
. Температура 
отсчитывается от температуры окружающей среды; по физическому смыслу задачи 
. Далее предполагается, что 
соответствует состоянию системы с 
.
Заметим, что операторное уравнение для температуры в системе (1) записано в достаточно общем виде, позволяющем охватить практически все случаи переноса тепла в размножающих и замедляющих средах. Конкретизация линейного, вообще говоря, неограниченного оператора 
соответствует конкретизации способа и характера переноса тепла в различных частях объема G; конкретизация нелинейного оператора 
соответствует конкретизации характера выделения тепла (энерговыделения) в процессе деления ядер делящихся материалов и (или) других актов выделения тепла.
В качестве примера конкретизации нелинейного оператора 
можно принять, что (см. (4))
(5)
Простым, но важным примером конкретизации линейного неограниченного оператора 
можно считать оператор теплопроводности (типа диффузионного)
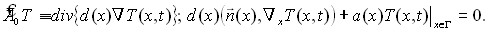(6)
Более сложный пример конкретизации оператора 
доставляет распределенная активная среда, состоящая из технологических каналов, в которых тепло выделяется в результате процесса деления ядерного топлива. В то же время система технологических каналов охлаждается с помощью жидкого теплоносителя, который прокачивается через активную среду в пространстве между тепловыделяющими элементами12. Отметим, что в определение линейного оператора 
с областью определения D(
) входят краевые условия на Г типа (6); они могут быть более сложными.
Система (1) – (3) представляет собой наиболее общее семейство моделей описания переноса излучения (нейтронов) и температурных распределений в неоднородных размножающих средах.
Далее предполагаются выполненными следующие условия относительно областей G, V, а также коэффициентов и ядер системы (1) – (3), которые не носят ограничительного характера.
Условие 1. Пусть 
– ограниченная выпуклая область в трехмерном евклидовом пространстве Е3 с границей 
– внешняя нормаль к Г в точке 
– ограниченная область, причем для всех 
. Область G может быть разбита на (N+1) подобластей Gi поверхностями Гi, i=1,…,N, являющимися поверхностями Ляпунова, гомеоморфными сфере и не пересекающимися между собой и Г.
Условие 2. Функции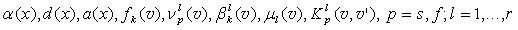 
; 
, представляют из себя неотрицательные измеримые в соответствующих областях определения функции, удовлетворяющие следующим условиям ограниченности и суммируемости:
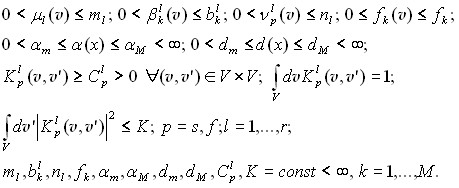
При 
функции 
, где 
. Функция 
.
Пусть Е1, Е2 – банаховы пространства с нормами 
, соответственно; 
– оператор, действующий из Е1 в Е2. Множества линейных замкнутых, ограниченных и вполне непрерывных операторов 
обозначим через 
и 
, соответственно.
Относительно операторов 
, входящих в выражения (4), далее используется одно из следующих предположений.
Условие А. Нелинейные операторы 
, 
, имеют производные Фреше 
, липшицево непрерывные по Т, так что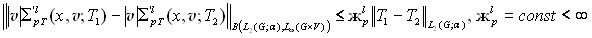 
для всех 
. При любых фиксированных значениях 
являются ограниченными измеримыми в 
функциями и справедлива равномерная по 
оценка
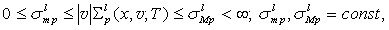(7)
причем хотя бы для одного 
.
Условие В. Операторы 
, представимы в виде:
(8)
где функции 
удовлетворяют неравенству (7); 
– зависящие от 
линейные над 
функционалы, такие, что
(9)
– измеримые в области 
функции с оценкой 
почти всюду в 
, и неотрицательные почти всюду на множестве 
, p=s,f.
В параграфе 3 определено пространство 
как прямая сумма соболевских пространств 
функций f(x), определенных на Gi и имеющих две производные на 
, суммируемых с квадратом. Норма в 
определяется как 
; здесь производные понимаются в смысле обобщенных функций. Пространство 
очевидным образом гильбертово, а из теорем вложения следует, что 
; здесь 
– пространство непрерывных вместе с k-ой производной функций в G; 
.
Пусть 
, Ei – банаховы пространства с конусами 
. Оператор 
называется положительным, если 
. Замкнутое множество 
называется конусом, если 
, и по крайней мере один из элементов х или –х 
не принадлежит 
. Конус 
является нормальным и воспроизводящим[13].
Пусть оператор 
, порождает С0-полугруппу 
. Для положительности полугруппы 
, т.е. 
, достаточно, чтобы резольвента 
для достаточно больших.
Лемма 1. Замкнутый линейный неограниченный оператор 
системы (1) обладает следующими свойствами: (1) 
; (2) 
уравнение 
однозначно разрешимо в 
; (3) существует положительный обратный оператор 
; (4) оператор 
положительно определен, т.е. 
, 
; 
– скалярное произведение в гильбертовом пространстве 
.
Далее для определенности воспользуемся реализацией (6) оператора 
. Введем оператор диффузии 
с областью определения 
, состоящей из множества функций 
, для которых выполнено граничное условие из (6) и условия сопряжения на поверхностях Гi, i=1,…,N:
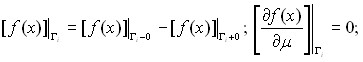(10)
здесь 
– производная по конормали к поверхности Гi в точке х; 
– внешняя по отношению к Gi нормаль к Гi, i=1,…,N.
Введем в гильбертовом пространстве 
функций f(x), квадратично суммируемых на G с весом (х), линейный оператор 
с областью определения 
, состоящей из множества функций 
, удовлетворяющих граничному условию из (6) и условиям сопряжения (10). Установлена
Лемма 2. Линейный оператор 
обладает следующими свойствами: (1) 
; (2) 
уравнение 
однозначно разрешимо в 
; (3) спектр 
оператора 
состоит из счетного множества изолированных точек 
, точечного спектра 
, расположенного на вещественной оси. В спектре 
существует ведущее собственное значение 
, которому отвечает единственная (с точностью до нормы) собственная функция 
, такая, что 
; (4) 
существует 
, для которой справедлива оценка 
. При этом оператор 
положителен 
; (5) оператор 
является производящим оператором С0-полугруппы положительных сжимающих операторов 
, для которых справедлива оценка
(11)
Введем в 
операторы
(12)
здесь Т(х) – некоторая фиксированная функция из 
. Свойства оператора 
хорошо изучены2,3. С помощью оценки (7) установлено, что для любой фиксированной функции 
оператор 
из (12) обладает аналогичными свойствами.
Лемма 3. Пусть выполнены Условия 1,2,А. Тогда для любой фиксированной функции 
справедливы следующие утверждения: (1) 
; (2) 
уравнение 
однозначно разрешимо в 
; (3) существует оператор 
, положительный относительно конуса 
; (4) спектр 
пуст; справедлива равномерная по 
оценка
(5) оператор 
является производящим оператором положительной 
-полугруппы 
.
Введем операторы:
(13)
Лемма 4. Пусть выполнены Условия 1,2,А и 
- фиксированная функция. Тогда: (i) 
; 
(ii) 
; 
; 
; (iii) 
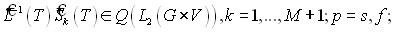(iv) если 
для какого-нибудь 
, то операторы 
-положительны, 
; (v) 
и совпадает с ведущим собственным значением 
оператора 
(здесь 
- спектральный радиус оператора 
). При этом можно считать, что равномерно по 
справедлива оценка 
. Оператор 
- любая фиксированная функция, обладает следующими свойствами: (а) 
; (в) 
.
Введем в рассмотрение следующие линейные операторы:
(14)
Из свойств коэффициентов и ядер системы (1)-(3) установлена
Лемма 5. Пусть выполнены Условия 1,2,А. Тогда 
фиксированных, операторы 
p=s,f;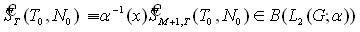 
.
С помощью Условия А найдено, что линейные операторы (14) являются производными Фреше в точке 
от нелинейных операторов 
, соответственно.
Аналогичные утверждения справедливы при выполнении Условия В.
В главе 2 «Теоремы о существовании решений» установлены соответствующие теоремы о существовании сильных решений исходной задачи (1) – (3) при выполнении Условия 1,2,А и Условия 1,2,В, соответственно. Установлены условия продолжимости и непродолжимости решений задачи (1) – (3) на всей временнй оси.
Для этого введено в рассмотрение гильбертово пространство 
вектор-функций 
с обычным определением нормы и скалярного произведения:
;
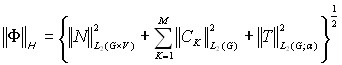Конус неотрицательных в 
вектор-функций обозначен через 
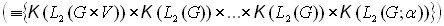; он является воспроизводящим и нормальным13.
Тогда исходную систему (1)-(3) запишем в виде абстрактной задачи Коши (АЗК)
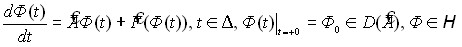. (15)
Здесь 
- линейный оператор с 
; 
; 
– нелинейный оператор вида:
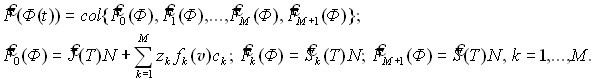(16)
В случае конкретизации (6) оператора 
в (15) он заменяется на оператор 
.
Под решением АЗК (15) на отрезке 
понимается вектор-функция 
, удовлетворяющая уравнению (15) на 
.
В параграфе 2 установлены важные свойства операторов 
и 
в Условиях 1,2,А и 1,2,В. В частности, в Условиях 1,2,А установлено: (i) оператор 
является производящим оператором С0-полугруппы сжимающих положительных операторов 
; (ii) нелинейный оператор 
ограничен и имеет сильно непрерывную производную Фреше по Ф 
с оценками Липшица в каждом шаре 
:
(17)
С помощью этих свойств и теоремы о продолжении АЗК в банаховом пространстве доказана теорема о существовании сильного глобального решения задачи (1) – (3) (АЗК (15)) 
. Более того, в Условиях 1,2,А установлена устойчивость решения задачи (1) – (3) по возмущению коэффициентов и начальных условий системы, т.е. смешанная задача для системы (1) – (3) поставлена корректно.
В параграфе 3 АЗК (15) исследована в Условиях 1, 2, В и установлено, что в отличие от предыдущего глобальное решение уже может не существовать. Такое решение называется непродолжимым в отличие от локального, которое существует на компакте [0,h] и может быть продолжено на более широкий интервал. Не исключается возможность того, что уход на бесконечность решения задачи (1) – (3) по норме может происходить за счет ухудшения дифференциальных свойств (по пространственным переменным), и норма решения может оставаться конечной. Показано, что для задачи (1)-(3) такой сценарий невозможен.
Содержание параграфа 1 главы 2 составляют необходимые общие сведения о продолжимости решений АЗК типа (15) в банаховом пространстве.
В главе 3 «Качественные свойства решения нелинейной задачи» при некоторых дополнительных предположениях о характере ядерно-физических и начальных данных установлены интересные и полезные свойства задачи (1) – (3).
Содержание параграфа 1 составляют результаты о положительности АЗК (15), полученные на основе обобщения известных теорем сравнения[14]. В параграфе 2 данной главы рассмотрен важный вопрос о положительности решений задачи (1) – (3). В частности, указаны требования на коэффициенты и начальные данные задачи (1) – (3), при которых наблюдается положительность решений исходной задачи (АЗК (15)) для случая справедливости Условия А. Аналогичные результаты о положительности получены при выполнении Условия В, в частности, когда операторы 
, линейны по температуре. Отметим, что указанные результаты не требуют монотонности операторов сдвига по траекториям системы и поэтому легко проверяемы на практике.
Содержание параграфа 3 составляет рассмотрение вопроса о несуществовании глобального решения задачи (1) – (3) при выполнении Условия В. В частности, опираясь на свойство положительности решения Ф(t) АЗК (15) установлено, что решение уходит на бесконечность по норме пространства Н за конечное время (имеет «взрывной» характер) в условиях положительной обратной связи; дана оценка времени ухода через параметры задачи (1) – (3).
Заметим, что предлагаемый подход является достаточно общим и применим для широкого класса нелинейных (диссипативных) систем эволюционного типа с распределенными параметрами.
Глава 4 «Стационарная нелинейная задача» посвящена рассмотрению свойств нелинейной стационарной задачи, отвечающей системе (1) – (3):
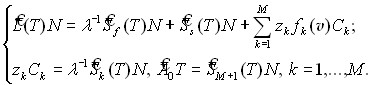(18)
Параметр в системе (18) соответствует «эффективному коэффициенту размножения kэф», который используется в практических расчетах размножающих систем1,3. Отметим, что указанный способ введения спектрального параметра является типичным, но не единственным. Все определяется удобством исследования возникающей при этом спектральной задачи.
С помощью установленных в леммах 1-4 свойств входящих в систему (18) операторов удобно записать ее в следующем виде:
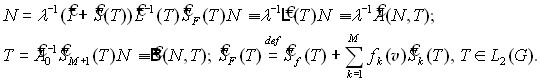(19)
В параграфе 1 главы 4 для задачи (19), рассматриваемой в пространстве 
вектор-функций 
, установлено, что эта задача при выполнении Условий 1,2,А имеет малые по норме в Н положительные (в соответствующем конусном пространстве 
) решения при 
, если функционал 
, или при 
, если 
. В соответствии с леммой 5 знак функционала 
определяется характером температурной связи по сечениям процессов,
Здесь 
, 
определяются из решения линейной в 
задачи
(20)
и им отвечает простое собственное значение 
; 
– собственная функция линейной краевой задачи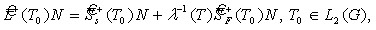 
отвечающая 
при 
; здесь 
– скалярное произведение. Аналогичные результаты получены при выполнении Условия В. Случай 
требует отдельного рассмотрения.
В параграфе 2 главы 4 продолжено рассмотрение нелинейной системы (18) и эквивалентного ей нелинейного операторного уравнения
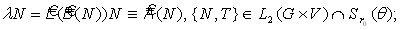(21)
здесь 
– ограниченный, положительный, вполне (квазивполне) непрерывный оператор, дифференцируемый по Фреше, причем 
. Очевидно, что уравнение (21) имеет тривиальное решение 
при всех, поскольку 
. Поэтому при исследовании вопроса о существовании ненулевых решений уравнения (21) полезно ввести понятие точки бифуркации13.
Число 
называется точкой бифуркации уравнения (21) (оператора 
), если любому >0 соответствует такое, 
, при котором уравнение (21) имеет по крайней мере одно ненулевое решение 
, причем 
. Отсюда и из результатов М.А. Красносельского следует, что каждое нечетнократное (в частности, простое) собственное значение оператора 
является точкой бифуркации оператора 
(21). В частности, 
– точка бифуркации операторного уравнения (21).
Параграф 3 главы 4 посвящен установлению существования у задачи (19) (системы (18)) условно-непрерывной ветви полусобственных векторов.
Решение 
задачи (19) называется полусобственным вектором оператора 
, если 
. Соответствующее этому решению значение 
называется полусобственным. Говорят, что полусобственные векторы 
оператора 
образуют условно-непрерывную ветвь 
длины 
, если для границы 
любого открытого в 
множества 
из шара 
, существует такой полусобственный вектор 
оператора 
, что 
. Если R – любое число, то говорят, что ветвь имеет бесконечную длину.
Установлено, что при выполнении Условий 1,2,А относительно коэффициентов и ядер задачи (1) – (3) отвечающая ей нелинейная стационарная система (18) имеет условно непрерывную ветвь полусобственных векторов бесконечной длины.
Содержание параграфа 4 главы 4 посвящено существованию стационарных решений исходной задачи (1) – (3). Вопрос о существовании нетривиальных стационарных решений задачи (1) – (3) сводится к вопросу о существовании неподвижных точек оператора 
в конусе 
. При выполнении Условий 1,2,А задача (1) – (3) имеет по крайней мере одно положительное стационарное решение 
; при этом отсутствуют требования монотонности макроскопических сечений процессов. Полученные здесь результаты говорят о том, что если задача (1) – (3) удовлетворяет Условиям 1,2,В, то система, охваченная положительной температурной обратной связью, может работать на любом стационарном уровне мощности.
Затронутые в §4 вопросы тесно связаны с вопросами устойчивости стационарного решения задачи (1) – (3) 
, чему посвящен параграф 5 главы 4. Из многочисленных определений устойчивости в общей теории устойчивости систем с распределенными параметрами рассмотрена устойчивость по норме, более удобная для нашей задачи. Стационарное решение 
задачи (1) – (3) (АЗК (15)) называется устойчивым (по Ляпунову), если по любому наперед заданному >0 можно указать >0 такое, что для любых 
решение Ф(t) задачи (1) - (3) (АЗК (15)) остается в шаре 
, если в начальный момент 
. Если, кроме того,
для любых 
, (22)
то стационарное решение задачи (1)-(3) 
называется асимптотически устойчивым. Стационарное решение 
задачи (1)-(3) (АЗК (15)) называется устойчивым в большом (в области 
), если оно устойчиво и условие (22) выполняется для всех начальных возмущений 
, таких, что 
. Область 
в этом случае называется областью притяжения (аттрактором) стационарного решения 
.
Установлено, что если выполнены Условия 1,2,А и полугруппа 
, отрицательного типа, 
, то область притяжения к 
непуста и содержит некоторый шар в Н, а стационарное решение 
задачи (1) – (3) существует и устойчиво асимптотически; здесь 
– линеаризованный в окрестности стационарного решения 
АЗК (15) оператор.
Свойство оператора 
порождать С0-полугруппу тесно связано со структурой и свойствами спектра 
оператора 
; этому важному вопросу посвящена глава 6.
В главе 5 «Свойства оператора нелинейной стационарной задачи» продолжено исследование свойств оператора стационарной задачи (18) для ряда практически важных моделей теории переноса. В частности, для несамосопряженной условно-критической задачи второго рода (20) получен важный результат о полноте корневых векторов. Другая серия результатов позволяет уточнить и обобщить результаты главы 4. Оказывается, можно выделить новый класс линейных положительных операторов, который естественным образом возникает при спектральном анализе некоторых задач теории переноса. С его помощью установлен ряд важных свойств решений задачи (20), например, принадлежность к системам типа чебышевской (Т-системам), свойство не повышения числа перемен знака, что весьма важно с точки зрения построения эффективных вычислительных алгоритмов, методов ускорения сходимости и других прикладных вопросов.
Параграф 1 главы 5 посвящен установлению полноты корневых векторов условно-критической задачи второго рода, т.е. для оператора 
. А именно, с помощью классической теоремы М.В. Келдыша[15] при выполнении Условий 1,2,А (1,2,В) доказана полнота системы корневых векторов оператора 
(линейной в Н0 операторной задачи (20)) в области 
; спектр оператора 
(задачи (20)) в области 
является счетным, точечным, с предельными точками на прямой 
. Более того, при выполнении Условия 1,2,А в точечном спектре оператора 
существует положительный собственный элемент 
и отвечающее ему простое собственное значение 
i=1,2,…, такие, что 
. Других собственных элементов, принадлежащих собственным значениям из 
, оператор 
не имеет.
Если же выполнен принцип детального равновесия для ядра 
и условие четности для него, то система корневых векторов оператора 
(задачи (20)) в области 
будет составлять некоторый базис Рисса в 
.
Интересно отметить, что в рассматриваемой постановке задачи оператор 
трактуется как возмущение (в смысле М.В. Келдыша) самосопряженного оператора 
вполне непрерывным оператором 
. С этой точки зрения физической причиной, порождающей существование положительного решения задачи (20), следует признать особые свойства мультиплицирующей среды 
.
Установленные результаты позволяют строить и реализовывать эффективные численные алгоритмы решения рассматриваемых задач. Прежде всего это относится к нахождению ведущего собственного значения 
– центральной задаче математической теории переноса, и связанной с ней задачей оценки спектрального зазора 
. Установленная базисность (по Риссу) системы корневых векторов задачи позволяет успешно применять эффективные методы ускорения сходимости, в частности, чебышевские методы ускорения сходимости.
Оказывается, что в ряде частных случаев, например, в однородной среде, спектральные результаты §1 можно существенно уточнить, чему посвящен параграф 2 главы 5. Поскольку постановка задачи носит общий характер, рассмотрена абстрактная задача на собственные значения в банаховом пространстве Е с конусом 
(23)
причем 
и 
. Здесь 
– производная по конусу 
оператора 
, 
, где 
– некоторый абстрактный аналог условно-критической задачи (18).
В главе 4 установлено, что если 
и u0 – положителен (это так, например, в Условиях 1,2,А), то задача (23) имеет единственное простое позитивное полусобственное значение 
, которому отвечает единственный положительный полусобственный элемент 
. Очевидно, что в общем случае возможны другие полусобственные значения в спектре оператора 
, которые также могут являться точками бифуркации задачи 
. Для исследования этого случая при малых по норме в 
считаем справедливым представление13
; (24)
здесь 
- однородный оператор порядка 
, т.е. 
; 
- оператор более высокого порядка по сравнению с 
, т.е. 
при 
.
Хорошо известно[16], что в ряде случаев в точечном спектре 
оператора 
можно установить существование счетного (конечного) множества простых вещественных собственных значений с соответствующими собственными функциями, которые в общем случае не являются положительными, т.е. 
. Известны классы линейных положительных операторов, для которых устанавливается наличие не одного, а целой группы ведущих собственных значений. Один из таких классов образуют знакорегулярные (осцилляционные, квазизнакорегулярные) операторы16, для анализа которых применяется теория конусов.
В параграфе 2 главы 5 установлены тонкие результаты о детальном поведении решений задачи 
, 
{классу вполне положительных (ВП), осцилляционных операторов} в окрестности точек бифуркации и в условиях (24) в зависимости от знака функционала 
, 
; 
-собственный элемент, которому отвечает собственное значение 
оператора 
. Основным результатом здесь является появление нового класса решений – инвариантного множества 
, такого, что 
;впервые для задач теории переноса оно было введено автором, близкие результаты для задач эллиптического типа получены Matano.
Если 
при каких-то 
, то вопрос о количестве и характере решений задачи 
на множествах 
, зависит от вида оператора более высокого порядка малости, нежели чем 
в представлении (24), и проводится по той же схеме с введением функционала катастрофы первого порядка. Тем самым, продолжая процесс, решаем проблему существования и количества стационарных решений эволюционного уравнения с оператором 
.
В параграфе 3 главы 5 изложены общие результаты о точках бифуркации для бифуркационного уравнения общего вида
, 
, (25)
полезные для нас далее, которые имеют также самостоятельный интерес. Здесь: 
– линейный замкнутый неограниченный оператор; 
– линейный оператор Фредгольма, 
– изолированное собственное значение оператора 
; 
– нелинейное отображение, – окрестность нуля в Е; – спектральный параметр; 
– множество всех непрерывно дифференцируемых по Фреше (по u и ) отображений. Нас интересуют нетривиальные решения бифуркационного уравнения (25). Сводка основных результатов о спектре замкнутого оператора представлена в Приложении 1.
Известны две основные серии результатов, относящихся к проблеме бифуркации (не обязательно для уравнения вида (25))13: (1) при соответствующих условиях всегда возникает бифуркация, если кратность собственного значения 
оператора 
нечетна (такой подход реализован выше в параграфе 2 главы 5); (2) ничего не предполагается относительно кратности 
, но предполагается, что оператор 
есть градиентный (потенциальный) оператор. При установлении этих двух серий результатов не подчеркивалась связь между ними.
В параграфе 3 главы 5 установлено, что обе серии результатов являются специальными случаями более общего геометрического принципа, а именно: если определенное касательное векторное поле, зависящее от 
, на единичной сфере в 
, имеет нуль, то возникает бифуркация; здесь 
– обобщенное нуль-пространство оператора 
. Интересно, что эта связь исчезает явно при 
.
Изложенные в §3 результаты применены для рассмотрения нелинейной стационарной задачи (18), отвечающей исходной системе (1) – (3). Введение спектрального параметра можно осуществлять технически различными способами (но разумными в рамках физического содержания рассматриваемой задачи). Выбор того или иного подхода определяется возникающими сложностями технического характера, иногда трудно преодолимыми. Предлагаемый подход продемонстрирован на двух достаточно простых примерах в §4; показано, что один из них приводит к более простому техническому анализу нелинейной (по ) задачи. При рассмотрении более сложных спектральных задач, например, с полиномиальным и (или) дробно-рациональным вхождением параметра, отличие в различных подходах может быть весьма существенным и в результате может приводить к успешному анализу, что продемонстрировано в главе 6.
Глава 6 «Свойства линеаризованной задачи» посвящена исследованию свойств линеаризованной задачи, отвечающей исходной системе (1) – (3). Основанием для такого анализа являются теоремы существования, установленные в главе 2, и общий принцип линеаризации, примененный для абстрактной задачи Коши (15), который, в свою очередь, опирается на результаты исследований решений стационарной задачи, отвечающей исходной системе (1) – (3), установленные в главах 4,5. Такая постановка задачи естественным образом приводит к изучению спектральной задачи для операторного пучка с нелинейным, полиномиальным и(или) дробно-рациональным, вхождением спектрального параметра и непустым существенным спектром достаточно общего вида
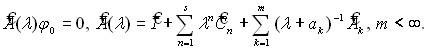(26)
Здесь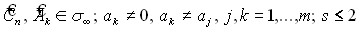 
; определение пространств 
, дано в §1 главы 6. Поскольку теория спектральных задач с произвольным вхождением параметра далека от завершения, исследование возникающих в теории переноса модельных задач, приводящих к операторным пучкам вида (26), представляет самостоятельный интерес и задача сформулирована в абстрактной форме. Исследование существенно усложняется, поскольку входящие в (26) операторы в общем случае являются несамосопряженными и имеют сложную структуру спектра.
В параграфе 1 главы 6 введены необходимые основные понятия и определения теории операторных пучков; сводка основных результатов для полиномиальных операторных пучков, которые носят законченный характер, представлена в Приложении 2.
Для семейства операторных пучков вида (26) воспользуемся определением цепочки собственных и присоединенных к ним векторов и соответствующих собственных значений (по М.В. Келдышу) и введем пространство 
и вектор-функцию 
, 
; 
; 
; 
.
В параграфе 2 главы 6 изложен метод сведения операторного пучка (26) к операторному уравнению с линейным вхождением спектрального параметра вида
(27)
Здесь 
– линейный в 
оператор из класса операторов Радона-Никольского; 
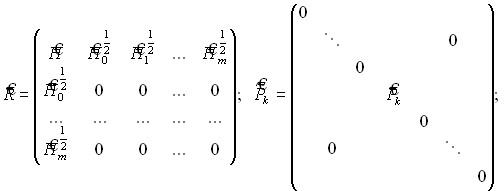
– оператор проектирования на подпространство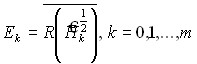 
; 
; 
.
Результаты анализа операторного уравнения (27), а значит, операторного пучка (26), содержатся в следующей теореме.
Теорема 1. В условиях формулировки операторного пучка (26) (значит, уравнения (27)) справедливы следующие утверждения: (а) спектр оператора 
состоит из точек 
, и только из них. Кратность собственного числа 
совпадает с размерностью подпространства 
;
(b) существенный (предельный) спектр операторов 
и 
совпадает; (с) существенный (предельный) спектр оператора 
состоит из нуля и тех точек 
, которым соответствуют бесконечномерные подпространства 
, 
; (d) спектр оператора 
является точечным, счетным с предельными точками (точками накопления) в 
. Точечный спектр 
оператора 
определяется оператором 
. Собственные подпространства, отвечающие точкам точечного спектра, конечномерны и, если 
нормален, ортогональны.
Параграф 3 главы 6 посвящен исследованию свойств линеаризованной задачи, отвечающей исходной системе (1) – (3). В главе 4 для нелинейного эволюционного уравнения достаточно общего вида (15) определена достаточно гладкая нелинейная (частичная) полугруппа 
, которую порождает оператор 
при Условии А (соответственно, при Условии В). В соответствии с общим принципом линеаризации АЗК (15) поставим в соответствие линеаризованную в некоторой окрестности 
стационарного решения задачи (15) (далее рассматриваем Условие А) задачу
(28)
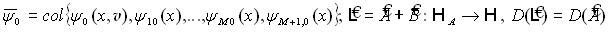. Здесь 
– банахово пространство, состоящее из элементов 
с нормой 
; 
;
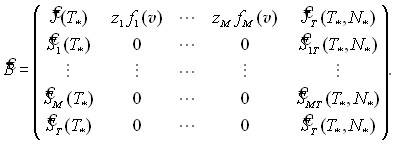
Математическая корректность процедуры линеаризации АЗК (15) и постановки задачи (28) обеспечена существованием неподвижных точек оператора стационарной задачи (15), а также существованием у оператора 
сильно непрерывной производной Фреше 
по Ф, липшицевой в некотором шаре 
. Установлено, что в Условиях 1,2,А полугруппа 
, имеет неподвижную точку 
, т.е. 
, и 
– сильно непрерывная линейная на Н полугруппа класса С0 (теорема Хилле – Иосида - Филипса). Соответствующие результаты получены также в Условиях 1,2,В.
АЗК (28) поставлена в соответствие задача на собственные значения
(29)
в области 
; 
. Для последующего анализа рассмотрена вспомогательная задача следующего вида
(30)
с оператором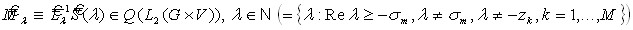 
; 
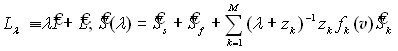. Задача (30) имеет самостоятельный интерес, поскольку соответствует линейной задаче переноса излучения (нейтронов) с учетом запаздывающего излучения. Результатом анализа с помощью лемм (1-4) операторного пучка 
(30) является важная теорема о кратной полноте корневых векторов.
Теорема 2. Пусть выполнены Условия 1,2,А. Тогда в области 
система корневых векторов операторного пучка (30) (задачи (29)) (М+1)-кратно полна в пространстве 
с некоторым новым скалярным произведением (Нs), топологически эквивалентным исходному. Спектр задачи является точечным, счетным, с предельными точками 
и (-). Собственные подпространства, отвечающие точкам из 
, конечномерны.
Более того, обращая дифференциальную часть оператора 
, задачу (30) удается свести к виду (26) с оператором 
при m=M, s=1, что позволяет применить теорему 1 и установить:
(i) характер и структуру спектра спектральной задачи (29); (ii) условия существования ведущего собственного значения задачи (29) и сопряженной к ней, которому отвечает единственный собственный вектор из конуса 
.
Вышеуказанные результаты в соответствующей формулировке установлены в Условиях 1,2,В.
В параграфе 4 главы 6 в частном, но важном случае однородной среды результаты теоремы 2 существенно уточнены.
Теорема 3. В условиях теоремы 2 система корневых векторов задачи (30) (пучка 
), минимальна и полна в Нs. Более того, для всех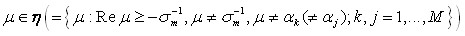 
справедливы утверждения. (1°) В случае однородной среды система корневых векторов пучка 
образует ортогональный в Нs базис. Для любых векторов 
, безусловно сходятся (М+1)-кратные разложения со скобками по набору последовательностей 
, где 
– набор собственных и присоединенных функций задачи (30). (2°) Операторный пучок 
, 
, принадлежит классу 
операторов и обладает (квази) осцилляционными свойствами; все собственные значения являются простыми, вещественными и образуют счетное множество; система отвечающих им векторов образует ряд Маркова.
Опираясь на результаты, полученные для вспомогательной задачи (30), установлен важный результат для спектральной задачи (29).
Теорема 4. Пусть выполнены Условия 1,2,А. Тогда спектр задачи (29) состоит из собственных значений конечной кратности, симметричен относительно вещественной оси и имеет предельные точки 
, и, возможно, на прямой 
. Для достаточно больших все собственные значения, за исключением, быть может, конечного числа, попадают в область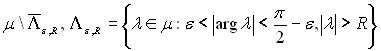 
, где >0 – произвольное достаточно малое число. Система корневых векторов задачи (29) полна в 
.
В рамках теоремы 3 установлен также важный результат об асимптотике спектра оператора 
спектральной задачи (30), из которого вытекает существование счетного подмножества 
, состоящего из простых вещественных чисел 
. При этом не исключается, что часть множества 
может находиться в области 
, но они не участвуют в формулировке теорем 2,3. Более того, в случае однородной среды получены двусторонние оценки асимптотического спектра.
В заключение главы 6 приведено несколько полезных замечаний и выводов. Прежде всего, несомненный интерес представляет рассмотрение операторного пучка 
(30) в случае М=1 (одной группы запаздывающего излучения (нейтронов)); тогда его можно записать в следующем виде
этот абстрактный пучок известен и достаточно хорошо изучен. Для пучка 
возможен детальный и полный анализ, основным нетривиальным фактом здесь является принадлежность пучка 
(задачи (30)) к типу так называемых сильно демпфированных систем (в теории колебаний механических систем изучаются квадратичные пучки такого типа).
Остановимся на физической трактовке полученных результатов для задачи (30) (пучка 
), 
. Рассматривая нашу задачу в случае М=1 по аналогии с демпфированными колебаниями механических систем, сделан вывод, что роль внутреннего сопротивления играет запаздывающее излучение. Существует счетное множество нормальных колебаний, которые представляют собой апериодические движения; периодических колебаний нет. Нормальные колебания образуют двухкратно полную систему. Не существует сколь угодно быстро затухающих апериодических движений (0). Особо отмечается, что при наличии запаздывающего излучения множество N всегда не пусто.
Другой вывод касается принципа линеаризации – теорема 4 определяет структуру и спектр устойчивости (по В.И. Юдовичу) стационарных решений исходной системы (1) – (3). Если спектр устойчивости расположен внутри левой полуплоскости комплексной плоскости, то стационарное решение устойчиво (асимптотически устойчиво). Если хотя бы одна точка спектра устойчивости находится внутри правой полуплоскости, то стационарное решение неустойчиво. Если в правой полуплоскости нет точек спектра устойчивости, но они имеются на мнимой оси (критический случай), то нельзя сделать заключение об устойчивости, ограничиваясь линейным приближением (см. Гл.5). В конечномерном случае эти утверждения составляют содержание известных теорем А.М. Ляпунова. В главе 6 эти теоремы установлены для одного класса бесконечномерных уравнений, включающих интегродифференциальный оператор переноса и параболический оператор, т.е. для несамосопряженной системы уравнений в частных производных смешанного типа. В этой связи необходимо отметить, что оператор переноса, вообще говоря, не относится к классу классических уравнений математической физики (например, уравнения параболического типа, волновые уравнения, уравнения Навье – Стокса и т.д.).
Глава 7 «Инвариантные многообразия и нелинейные свойства решений» посвящена рассмотрению нелинейных явлений и свойств решений исходной задачи (1) – (3). Анализ нелинейной диссипативной системы уравнений (1) – (3) проведен на основе результатов, полученных в предыдущих главах, с использованием данных о характере и структуре спектра линеаризованной задачи (28), а также с привлечением понятий теории гиперболических множеств, теории бифуркаций и притягивающих инвариантных множеств.
В параграфе 1 главы 7 даны необходимые понятия и определения, в частности, устойчивые и неустойчивые инвариантные (локальные) многообразия, притягивающие множества (аттракторы, квазиаттракторы), гомоклинические и гетероклинические траектории, а также некоторые другие необходимые результаты теории бесконечномерных диссипативных динамических систем.
Параграф 2 главы 7 посвящен рассмотрению в вещественном банаховом пространстве Е абстрактного эволюционного уравнения
(31)
неавтономное слагаемое 
периодично по t с периодом Т(>0). Класс исследуемых задач определен с помощью системы условий (А1) – (А5). В качестве частного случая он включает в себя системы квазилинейных уравнений в частных производных с линейной главной частью и, возможно, непустым существенным спектром.
(А1) (i) 
– неограниченный линейный оператор со всюду плотной областью определения 
; 
– неограниченный нелинейный оператор 
, порождающий однопараметрическую непрерывную полугруппу (группу);
(ii) нелинейные отображения 
, имеют класс гладкости 
. При этом, возможно, 
– производная Фреше в точке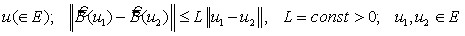 
;
(iii) уравнение (31) порождает в 
локальный по времени полупоток (поток) диффеоморфизмов 
определен для всех 
и достаточно малых >0.
(А2) (i) Неавтономное слагаемое в (31) имеет вид 
, где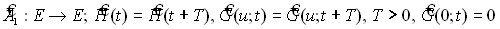 
;
(ii) линеаризованное уравнение
(32)
имеет Т-периодическое решение 
, причем 
.
(А3) Для семейства операторов 
(i)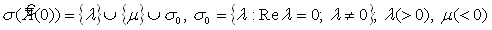 
– простые вещественные собственные значения оператора 
;
(ii) 
– простые вещественные собственные значения для достаточно малых >0 и 
. Множество 
состоит из точек спектра с отрицательной действительной частью и 
, где S – единичная окружность на комплексной плоскости; 
– образ 
относительно отображения 
.
(А4) Состояние равновесия невозмущенного (=0) семейства операторов 
имеет гомоклиническую траекторию 
, т.е. 
для всех 
. Предполагается, что при 
гомоклиническая траектория стремится к нулю, касаясь собственного подпространства 
оператора 
, отвечающего собственному значению. В свою очередь, при 
, касаясь собственного подпространства 
, отвечающего собственному значению.
(А5) Предполагается, что существует кососимметрическая, непрерывная, слабо невырожденная, билинейная (симплектическая)форма 
и гладкая функция 
такие, что 
для всех 
.
Если у автономной динамической системы имеется гомоклиническая траектория состояния равновесия, то при малых по времени периодических возмущениях она может расщепиться с образованием в ее окрестности «грубой» гомоклинической траектории гиперболической периодической орбиты. В свою очередь это означает существование у возмущенной динамической системы нетривиального гиперболического множества, гомеоморфного канторову совершенному множеству[17].
В §2 главы 7 показано, что в Условиях (А1) – (А5) для достаточно малых >0 гомоклиническая (гетероклиническая) траектория может расщепиться таким образом, что устойчивое 
и неустойчивое 
многообразия периодической гиперболической орбиты 
, рождающейся из состояния равновесия невозмущенного (=0) уравнения, будут иметь точку трансверсального пересечения. Для этого введены полупоток (поток) 
, порожденный уравнением (31), и 
– каноническая проекция. Определено также отображение Пуанкаре для полупотока (потока) 
на сечении 
, причем 
, Т – периодическим орбитам 
отвечают неподвижные точки 
. Пусть 
– периодическая траектория полупотока 
и 
– устойчивое, сильно устойчивое и неустойчивое локальные инвариантные многообразия траектории 
. С помощью модифицированного метода Мельникова установлено поведение и характер пересечения 
и 
при достаточно малых >0. Для этого рассмотрена функция 
; здесь 
– точка трансверсального пересечения 
с некоторой гиперплоскостью 
коразмерности единица, проходящей через точку 
. Аналогично определяется точка 
. Для функции 
установлена справедливость представления
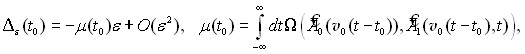(33)
позволяющая вычислить первый член разложения 
по ; 
– известная функция Мельникова. Суть данного подхода составляет обобщенный метод Мельникова.
Если L – линейное подпространство в Е, то 
, где 
– касательное подпространство к многообразию в точке v. Гомоклиническая траектория 
симметрична, если 
для всех 
. Основным результатом §2 является
Теорема 5 (обобщенная теорема Биркхофа - Смейла). Пусть выполнены Условия (А1) – (А5) и форма невырождена на подпространстве 
. Если гомоклиническая (гетероклиническая) траектория 
симметрична, функция 
имеет невырожденный нуль, то при достаточно малых >0 многообразия 
и 
неподвижной точки 
отображения 
имеют точку трансверсального пересечения.
В силу общности предположений установленное существование трансверсальной гомоклинической (гетероклинической) точки пересечения влечет за собой существование бесконечного, по крайней мере, счетного множества гомоклинических (гетероклинических) точек пересечения с различными траекториями.
Более того, сделан важный вывод: трансверсальные пересечения порождают хаос (в наших условиях); близкие результаты получены в работах[18],[19]. Указано также, что установление условий теоремы связано с исследованием конкретной модели динамической системы в соответствующих функциональных пространствах.
В параграфе 3 главы 7 рассмотрены примеры динамических систем, для которых установлены некоторые аналоги теоремы 5. Для этого исходная система (1) – (3) записана в следующем виде
(34)
; T>0 – некоторый период; 0 – малый параметр. Операторы 
и 
определены следующим образом:
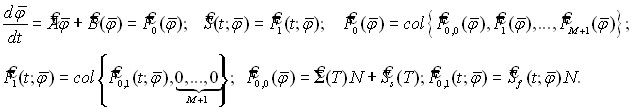
Задача (34) порождает в 
локальный по времени диффеоморфизм 
, который определен для всех 
и всех 
, достаточно малых.
Класс задач вида (34) включает в себя системы уравнений смешанного типа: например, интегродифференциальные и параболические уравнения в частных производных с линейной главной частью и непустым существенным спектром, включая, возможно, континуум непрерывного спектра. Системы подобного типа трудны для анализа, поскольку в общем случае сложно установить структуру и характер спектра; дополнительные трудности возникают вследствие несамосопряженности задачи.
Опираясь на результаты предыдущего анализа, в частности, результаты спектрального анализа главы 5, в §3 главы 7 установлена справедливость системы Условий (А1) – (А5) для задачи (34) при некоторых уточняющих условиях гладкости. Основным результатом такого анализа является
Теорема 6. Пусть выполнены Условия 1,2,А и форма невырождена на подпространстве 
, т.е. функция Мельникова (33) имеет простые нули и не зависит от >0. Если гомоклиническая траектория 
симметрична, то устойчивое 
и неустойчивое 
инвариантные многообразия неподвижной точки 
отображения 
имеют точку трансверсального пересечения, т.е. 
при достаточно малых >0.
Значение данного результата обусловлено возможностью конструктивной проверки существования трансверсальных гомоклинических (гетероклинических – в общем случае) орбит для конкретных динамических систем. Из факта существования таких орбит, в силу теоремы Смейла – Биркхофа, следует, что некоторая итерация 
отображения Пуанкаре имеет инвариантное гиперболическое множество – подкову Смейла. Это множество содержит счетное множество (неустойчивых) периодических орбит, несчетное множество ограниченных непериодических орбит и плотную орбиту. Представляет большой практический интерес чувствительность к выбору начальных данных, которую придает подкова полупотоку для данной динамической системы.
Фактически анализ хаотического поведения для конкретных динамических систем включает в себя идентификацию гиперболических инвариантных множеств, что должно являться предметом отдельного исследования. В §3 главы 7 с помощью теоремы 6 и на основании гомоклинической теоремы Смейла получен важный результат.
Теорема 7. Пусть выполнены Условия теоремы 6 и 
-диффеоморфизм, порождаемый задачей (31) (системой (1) – (3)), для которого существует гиперболическая неподвижная точка р. Тогда существует 
, такое, что 
и 
обладает гиперболическим инвариантным множеством, на котором 
топологически эквивалентен подсдвигу конечного типа.
Поскольку нуль-мерные гиперболические множества топологически сопряжены подсдвигам конечного типа, то из теоремы 7 вытекает существование нуль-мерного множества, т.е. канторова совершенного нигде не плотного множества, топологически эквивалентного инвариантному множеству подковы Смейла.
В качестве одного из следствий теоремы 7 сделан вывод о возможности введения марковских разбиений для описания динамики инвариантного гиперболического множества. Более того, опираясь на результаты главы 4, на марковских разбиениях предлагается ввести топологические марковские цепи, которые являются удобным инструментом для структурного анализа притягивающих множеств (аттракторов, квазиаттракторов) диффеоморфизма 
8.
В параграфе 3 главы 7 указан также практический пример хаотического нерегулярного поведения реальной динамической системы, описываемой задачей (1) – (3).
В результате анализа экспериментальных данных была построена модель и дана теоретическая трактовка последовательностям бифуркаций удвоения периода в некотором однопараметрическом семействе при изменении параметра (мощность, давление). Эти последовательности обладают структурой универсальных последовательностей Фейгенбаума, в том числе, масштабной инвариантностью. Установлено, что переход к «хаосу» через последовательности бифуркаций удвоения периода является общим свойством рассматриваемых нелинейных диссипативных систем, приближающихся к гомоклиническому касанию устойчивого и неустойчивого многообразий некоторой периодической орбиты (неподвижной точки).
В качестве более простого примера динамической системы в заключение §3 рассмотрено известное уравнение типа синус-Гордон с нулевыми граничными условиями Дирихле на отрезке [0,1], которое возмущено внешней периодической силой и силой вязкого трения. В форме системы уравнений первого порядка оно имеет вид
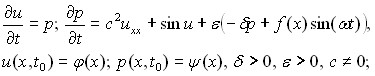(35)
f(x) – заданная гладкая функция. Проверка условий теоремы 5 для системы (35) говорит о том, что при достаточно малых >0 она будет иметь грубую гомоклиническую траекторию гиперболической периодической орбиты, если у функции Мельникова 
существует невырожденный нуль. В случае
невырожденный нуль существует при условии
Параграф 4 главы 7 посвящен исследованию условий существования и анализу свойств инвариантных экспоненциально притягивающих конечномерных многообразий – инерциальных многообразий для исходной задачи (1) – (3). В последнее время интенсивно обсуждается эффект «конечного» поведения решений диссипативных эволюционных уравнений при 
[20]. В ряде случаев такое поведение решений определяется динамикой на некотором инвариантном (
) конечномерном (гомеоморфном 
) многообразии 
. В известном смысле это обстоятельство позволяет свести уравнение (31) к системе обыкновенных дифференциальных уравнений (ОДУ) в 
(гипотеза Е. Хопфа)[21].
В §4 установлено, что в условиях (А1) – (А5) уравнение (31) обладает (универсальным) минимальным глобальным аттрактором (более точно – В-аттрактором) 
для нелинейной полугруппы 
, который является основным объектом исследований[22]. Ввиду конечной размерности А его исследование заключается во вложении в гладкое конечномерное многообразие М, и если М инвариантно, то сужение векторного поля исходной системы на многообразие М означает:
(i) инерциальное многообразие содержит все компактные инвариантные множества уравнения (31), что позволяет свести описание таких множеств к соответствующей задаче ОДУ в 
; (ii) множество М обладает свойством нормальной гиперболичности на А, что возникает при рассмотрении уравнения в вариациях (32).
Инерциальное многообразие М является нормально гиперболическим на А, если существует разложение 
на подпространства, непрерывно зависящие от 
. Здесь 
– касательное подпространство множества М в точке 
; 
– некоторое дополнительное (ко)подпространство в точке 
. Касательные и нормальные пучки 
с необходимостью положительно инвариантны с потоком, равномерно удовлетворяющим экспоненциальным оценкам для решений 
:
для всех 
для всех 
Таким образом, в условиях (А1) – (А5) уравнение в вариациях (32) допускает экспоненциальную дихотомию. Идея данного понятия состоит в том, что множество М испытывает сжатие в нормальном направлении сильнее (>), чем в касательном. Как следствие нормальной гиперболичности в условиях (А1) – (А5) установлен принцип сведения: компактные инвариантные множества М уравнения (31) и множества М соответствующей системы ОДУ устойчивы или неустойчивы одновременно. Поэтому существование инерциального многообразия М можно рассматривать как динамическую версию метода Галеркина.
В параграфе 4 главы 7 указаны достаточные условия того, что уравнение (31) обладает инерциальным многообразием. Эти условия фактически сводятся к оценке спектрального зазора (в литературе употребляется термин «условие конуса») для оператора линеаризованной задачи (1).
Теорема 8. Пусть выполнены Условия (А1) – (А5) и к+1 –к<2L;{ к} - изолированные вещественные собственные значения конечной кратности оператора 
, т.е. принадлежащие дискретному спектру 
; L – постоянная Липшица из оценки (А1) (ii). Тогда в Е существует k-мерное инерциальное многообразие с асимптотической фазой.
Условия теоремы накладывают достаточно жесткие ограничения на возможность существования инерциальных многообразий; известны контрпримеры20. Это происходит не по причине отсутствия гладкости у оператора 
, и не по причине того, что аттрактор А слишком большой. Требование нормальной гиперболичности вместе с возможным появлением собственных (и присоединенных) значений высокой кратности для линеаризованной задачи накладывает очень жесткие ограничения на возможную размерность инерциального многообразия М. Вышеуказанный контрпример говорит о том, что возникновение нормального гиперболического инерциального многообразия является весьма тонким и деликатным явлением; оно возникает только в подпространстве достаточно низкой размерности. Требование нормальной гиперболичности инерциальных многообразий не является, очевидно, необходимым условием. Однако без этого свойства нельзя ожидать, что инерциальные многообразия будут грубыми (типичными) и устойчивыми при малых возмущениях.
В §4 указано на возникающее определенное противоречие. Если мы работаем с устойчивыми (в классическом смысле определения Андронова - Понтрягина) инвариантными многообразиями (экспоненциальными аттракторами), тогда действительно нужно принимать во внимание только устойчивые (в определенном смысле) инерциальные многообразия. С другой стороны, известно о существовании квазиаттракторов (странных аттракторов), которые не являются устойчивыми, но мы уверены, что такие системы являются реалистичными моделями хаотического поведения[23]. Укажем также на существование «диких» гиперболических множеств, которые по определению являются неустойчивыми. Таким образом, регулярные (по Андронову – Понтрягину) инвариантные множества могут представлять собой весьма малую часть всех возможных инерциальных многообразий.
В заключение §4 главы 7 установлены условия существования инерциальных многообразий для исходной задачи (1)-(3) в Условиях 1,2,А. Для применения теоремы 8 необходимо провести оценку спектрального зазора (проверить условие конуса), которая проведена на основании результатов в случае однородной среды (см. комментарии к теореме 3).В общем случае такие оценки неизвестны. Проверка других условий теоремы 8 не вызывает затруднений.
Глава 8 «Задачи нелинейной теории переноса в многогрупповом диффузионном (Р1-) приближении» посвящена общей постановке задачи (1) – (3), где перенос излучения и вещества описывается в многогрупповом диффузионном (Р1-) приближении, и кратком обзоре полученных здесь результатов. Эти результаты важны с практической точки зрения, поскольку почти все проектные и инженерные расчеты, комплексы вычислительных программ основаны на много (мало) групповом диффузионном (Р1-) приближении. Для функционирования этих вычислительных комплексов разработана соответствующая система обеспечения многогрупповыми ядерно-физическими константами.
В параграфе 1 главы 8 дана общая постановка модельной задачи (семейства моделей) переноса в многогрупповом диффузионном (Р1)-приближении, которая описывается следующей, наиболее распространенной в практике, системой уравнений:
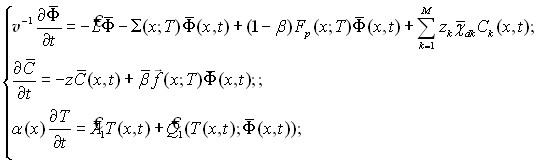(36)
, с начальными и граничными условиями
(37)
(38)
Здесь 
– производная по конормали к поверхности Г, j=1,…,m; 
– внешняя нормаль к границе Г выпуклой ограниченной области G в точке 
. За точку отсчета температуры T(x,t) принята температура окружающей среды. В системе (36) – (38)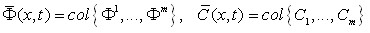 
; 
; 
; 
; 
; 
; 
; 
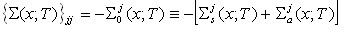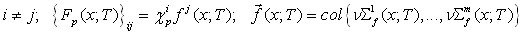– плотность и скорость излучения (нейтронов) в группе j; 
– концентрация источников запаздывающего излучения в группе k; 
– действительные неотрицательные постоянные; k=1,…,M(<); i,j=1,…,m.
Операторное уравнение для температуры в системе (36) записано в достаточно общем виде, позволяющем охватить практически все случаи переноса тепла в размножающих и замедляющих средах. Конкретизация нелинейного оператора 
соответствует конкретизации характера выделения тепла (энерговыделения) в процессе деления ядер делящихся материалов и (или) других актов выделения тепла.
В качестве примера конкретизации нелинейного оператора 
можно принять, что
. (39)
Конкретизация линейного, вообще говоря, неограниченного оператора 
соответствует конкретизации способа и характера переноса тепла в различных частях объема 
; в качестве простого примера для оператора 
можно указать выражение (6). Более сложный пример конкретизации оператора 
доставляет распределенная активная среда, состоящая из технологических каналов, в которых тепло выделяется в результате процесса деления ядерного топлива. В то же время система технологических каналов охлаждается с помощью жидкого теплоносителя, который прокачивается через активную среду в пространстве между тепловыделяющими элементами.
Система (36) – (38) является наиболее общим семейством моделей переноса излучения (нейтронов) в многогрупповом диффузионном (Р1-) приближении с учетом температурной обратной связи. Условия на область G совпадают с Условием 1. Следующее условие является аналогом Условия 2.
Условие 2D. Функции 
представляют из себя неотрицательные измеримые в соответствующих областях определения функции, удовлетворяющие следующим условиям ограниченности:
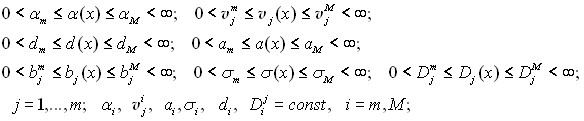
при 
, 
, 
; 
. На Гi функции 
могут терпеть разрывы первого рода, при этом выполнены условия согласования на поверхностях раздела зон Гi, i=1,…,N.
В общей формулировке задачи (1) – (3) нет аналога следующим двум условиям.
Условие 3D. Будем считать, что существуют 
, такие, что
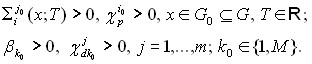
Условие 4D. Будем считать, что функции 
при любой фиксированной 
являются ограниченными измеримыми на G функциями, причем равномерно по 
справедливы оценки:
здесь 
– постоянные; t=m,M; i=a,s,f; l,j=1,…,m. Отметим, что возможны случаи, когда 
для всех 
, где 
, 
, 
. Кроме того, функции 
, рассматриваемые как отображения из 
в 
, обладают липшицево непрерывной производной Фреше 
.
Параграф 2 главы 8 посвящен постановке модельной задачи (семейству моделей) об устойчивости пространственного нейтронно-температурного распределения в размножающих средах с учетом поведения предшественников запаздывающего излучения в многогрупповом диффузионном (Р1-) приближении (так называемая ксеноновая неустойчивость). Наиболее общая система уравнений имеет вид:
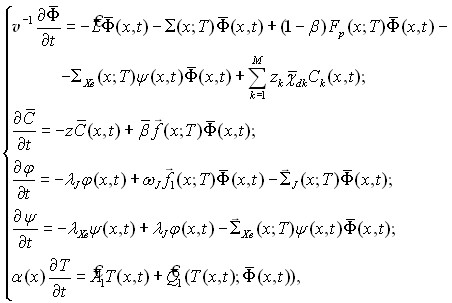(40)
с начальными и граничными условиями (37), (38). Здесь 
; 
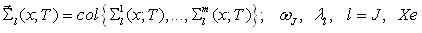– действительные положительные постоянные; 
– концентрация ядер предшественников (йода и ксенона) запаздывающего излучения (нейтронов).
Задача об устойчивости системы (39), (37), (38) имеет значительный практический интерес и актуальность вследствие экспериментального обнаружения явления ксеноновой неустойчивости. Данная задача рассматривалась при выполнении Условий 1, 2D - 4D; для функций 
справедливы все положения Условия 4D, l=J, Xe. Анализ задачи (39), (37), (38) проведен на основе результатов исследования задачи (36) - (38) с помощью методов и подходов, примененных к задаче (1) – (3). Это позволило установить ряд важных результатов по п.п. (1 – 5), в частности, о структуре и характере спектра линеаризованной задачи, условиях существования ведущего собственного значения, полноте корневых векторов и ряд других.
Параграф 3 главы 8 посвящен сравнительному анализу результатов, полученных для нелинейных задач (1) – (3) и (36) – (38), где перенос излучения и вещества описывается, соответственно, газокинетическим уравнением и его многогрупповым диффузионным (Р1-) приближением. Указано на качественные отличия в структуре и характере спектра этих двух задач, что, в свою очередь, приводит к различному характеру асимптотического поведения решений. С другой стороны, отмечено, что при определенных условиях может существовать ведущее собственное значение задачи, которому отвечает единственное решение; эти условия существенно различные для задачи (1)-(3) и задачи (36)-(38). Выполненный анализ позволил сформулировать некоторые качественные выводы относительно изменений в спектральной картине модельных задач.
Заключение
В диссертационной работе дано развитие и обоснование строгой математической теории нелинейных уравнений переноса и на этой основе решен ряд проблем теоретического и прикладного характера, относящихся к вопросам устойчивости и нелинейным явлениям для диссипативных динамических (реакторных) систем.
1. Сформулированы условия существования глобального решения и условия существования локального решения для нелинейной системы (семейства) уравнений, описывающей нестационарные нейтронно-температурные распределения в ограниченных (мультиплицирующих) средах. Исследованы свойства операторов нелинейной задачи, включая свойство положительности решений в банаховых пространствах с положительными конусами. Эти результаты обобщают теоремы о продолжимых и непродолжимых решений в теории нелинейных динамических систем с распределенными параметрами.
2. Построена теория нелинейной стационарной задачи, отвечающей исходной; установлены теоремы существования и свойства решений; указаны условия существования ведущего собственного значения; доказаны теоремы полноты собственных (корневых) векторов и условия существования базиса Рисса. Исследованы тонкие свойства спектра в некоторых важных частных случаях, а именно: установлено существование счетного множества простых вещественных собственных значений над некоторым множеством положительных конусов конечного ранга; найдена оценка спектрального зазора; показано существование счетного множества точек бифуркации; обоснованы чебышевские методы ускорения сходимости вычислительных алгоритмов; наконец, проведен качественный анализ количества, характера и устойчивости решений на некотором инвариантном множестве.
3. Построена спектральная теория для линеаризованной задачи, которая базируется на результатах теории нелинейной стационарной задачи и результатах анализа ее спектральных свойств. В частности, установлены принцип линеаризации и спектр линеаризации (по В.И. Юдовичу); исследованы свойства гладкости нелинейной диссипативной полугруппы, разрешающей исходную задачу; доказаны теоремы о структуре спектра операторного пучка (обобщенного в смысле М.В. Келдыша), где спектральный параметр нелинейным образом входит в пучок, найдена асимптотика спектра; установлена полнота корневых векторов (кратная полнота по М.В. Келдышу) и условия сходимости; найдены условия существования ведущего собственного значения и отвечающего ему (единственного) элемента из положительного конуса. В случае однородной среды результаты существенно уточнены: установлена минимальность, полнота и базисность системы корневых векторов; показана принадлежность операторного пучка классу вполне положительных операторов; обнаружено существование собственных элементов, обладающих (квази)осцилляционными свойствами.
4. Для абстрактного эволюционного уравнения достаточно общего вида сформулирована обобщенная теорема Биркхофа – Смейла. Тем самым найдены условия существования (обобщенный метод Мельникова) гомоклинической (гетероклинической) точки пересечения (локальных) устойчивого и неустойчивого инвариантных многообразий для некоторого семейства абстрактных эволюционных уравнений. Установлены условия существования инвариантного гиперболического множества, топологически эквивалентного подсдвигу конечного типа (канторова, топологически эквивалентного подкове Смейла). В качестве примера рассмотрена исходная нелинейная задача и уравнение типа sin-Гордон; сформулировано утверждение: трансверсальная гомоклиническая (гетероклиническая) траектория порождает хаос («динамический реакторный хаос»).
5. Дана трактовка экспериментально наблюдавшегося перехода к «реакторному хаосу» через последовательность бифуркаций удвоения периода в некотором однопараметрическом семействе при изменении параметра от значений, при которых оно имеет лишь неподвижные точки, к значениям, при которых существует бесконечное (по крайней мере, счетное) множество периодических орбит. Каскады бифуркаций удвоения периода обладают структурой универсальных последовательностей Фейгенбаума и свойством масштабной инвариантности. Установлено, что переход к «хаосу» через последовательность бифуркаций удвоения является общим свойством рассмотренных модельных систем, приближающихся к гомоклиническому касанию устойчивого и неустойчивого многообразий некоторой периодической орбиты (неподвижной точки).
6. Развит конструктивный подход в теории нелинейных динамических систем, основанный на существовании инвариантных экспоненциально притягивающих конечномерных многообразий – инерциальных многообразий и на его основе впервые установлены условия их существования для абстрактных эволюционных уравнений с компактной (квазикомпактной) полугруппой и нормальным гиперболическим множеством. Проведен качественный анализ инерциальных многообразий для исходной нелинейной задачи и установлена экспоненциальная дихотомия, асимптотическая k-мерность, свойство притяжения с асимптотической фазой; сформулирован принцип сведения. Для исходной задачи установлено существование конечномерного инерциального многообразия и тем самым сформулирован нелинейный динамический метод Галеркина.
7. Изложенные подходы и методы распространены на семейство модельных задач, где перенос описывается в многогрупповом диффузионном (Р1-) приближении; соответствующие результаты получены для этой задачи. В качестве примера более сложной нелинейной задачи сформулирована достаточно общая модельная задача, которая описывает ксеноновую неустойчивость реакторных систем и представляет практический интерес.
Рассматривая работу, в целом можно сделать вывод, что в ней решена важная научно-техническая проблема, связанная с дальнейшим развитием и обоснованием математической теории нелинейных уравнений переноса излучения (нейтронов), включая семейство модельных задач в многогрупповом диффузионном (Р1 -) приближении, а также с исследованием сложных нелинейных нерегулярных режимов и динамических характеристик с целью обеспечения безопасности эксплуатации ядерных реакторов.
список основных публикаций по теме диссертации
- Макин Р.С. О существовании ведущего собственного значения для одной задачи Р1-приближения. // Функц. анализ и его приложения. 1984. Т.18. Вып.4. с.88-89.
- Макин Р.С. О спектре стационарного односкоростного уравнения переноса с изотропным рассеянием. // Докл. АН СССР. 1984. Т.274. №3. с.536-540.
- Макин Р.С. О спектре стационарного односкоростного уравнения переноса с линейной зависимостью индикатрисы рассеяния от углов. // Дифференц. уравнения. 1985. Т.21. №.6. с.1032-1036.
- Макин Р.С. Метод собственных функций решения некоторых задач термализации нейтронов. // Вопросы атомной науки и техники. Серия: Физика и техника ядерных реакторов. 1984. Вып.6(43). С.18-22.
- Makin R.S. On the spectrum of the steady-state single-speed transport equation with isotropic scattering. \\ Soviet Math. Dokl. 1984. V.29. №1. p.59-63.
- Макин Р.С. О спектре многогруппового диффузионного приближения уравнения переноса нейтронов. // Дифференц. уравнения. 1986. Т.22. №9. с.1623-1626.
- Либенсон М.Н., Макин В.С., Макин Р.С. Дисперсия поверхностных поляритонов в среде с пространственно неоднородной диэлектрический проницаемостью. // Оптика и спектроскопия. 1985. Т.59. Вып.4. с.916-919.
- Макин Р.С. О существовании ведущего собственного значения для одной линеаризованной задачи динамики реакторов. // Функц. анализ и его приложения. 1987. Т.20. №1. с.80-81.
- Макин Р.С., Шихов С.Б. О полноте системы собственных функций многогруппового диффузионного приближения условно-критической задачи с однородной активной зоной и произвольным отражателем. // Дифференц. уравнения. 1987. Т.23. №10. с.1812-1815.
- Макин Р.С. О спектре стационарного многоскоростного спектра переноса с линейной зависимостью индикатрисы рассеяния от углов. // Ред. журнала «Дифференциальные уравнения». 1987. Деп. статья. №4816-887. с.1-19.
- Макин Р.С. Об одном классе линейных положительных операторов. // Математические заметки. 1988. Т.43. №1. с.71-81.
- Макин Р.С. О полноте корневых векторов системы интегродифференциальных уравнений кинетики реактора. // Дифференц. уравнения. 1988. Т.24. №3. с.508-516.
- Макин Р.С. О полноте корневых векторов одной задачи кинетики реактора в диффузионном приближении. // Дифференц. уравнения. 1988. Т.24. №6. с.1053-1056.
- Макин Р.С. О свойствах решений и полноте собственных функций одной интегродифференциальной системы уравнений динамики реактора. // Дифференц. уравнения. 1988. Т.24. №10. с.1811-1818.
- Макин Р.С. О спектре стационарного односкоростного уравнения переноса с краевыми условиями типа отражения. // Функц. анализ и его приложения. 1990. Т.24. Вып.2. с.99-100.
- Макин Р.С. О полноте корневых векторов одной линеаризованной задачи динамики реакторов. // Дифференц. уравнения. 1990. Т26. №10. с.1800-1805.
- Макин Р.С. Об ограниченности области притяжения стационарного решения нелинейной диффузионной системы уравнений динамики регулируемого реактора. // Дифференц. уравнения. 1991. Т.27. №3. с.511-520.
- Макин Р.С. О полноте корневых векторов одной линеаризованной задачи динамики реактора в многогрупповом диффузионном приближении. // Вопросы атомной науки и техники. Серия: Ядерная техника и технология. 1991. Вып.6. с.29-36.
- Макин Р.С. О существовании глобального решения одной нелинейной диффузионной системы уравнений. // Вопросы атомной науки и техники. Серия: Ядерная техника и технология. 1991. Вып.6. с.22-29.
- Макин Р.С. Об асимптотике решений некоторых задач динамики реакторов. // Вопросы атомной науки и техники. Серия: Ядерная техника и технология. 1992. Вып.6. с.59-67.
- Макин Р.С. Об устойчивости кипящего реактора как нелинейной динамической системы. // Вопросы атомной науки и техники. Серия: Ядерная техника и технология. 1992. Вып.6. с.24-28.
- Макин Р.С. Свойства решений некоторых интегродифференциальных задач динамики реакторов. // Вопросы атомной науки и техники. Серия: Ядерная техника и технология. 1992. Вып.6. с.29-38.
- Макин Р.С. О спектре стационарного односкоростного оператора переноса с анизотропным рассеянием. // Вопросы атомной науки и техники. Серия: Физика и техника ядерных реакторов. 1993. Вып.1. с.13-19.
- Makin R.S. Some Regularity in Simulating of Sophisticated Dynamical Systems. // Proceedings of 7-th European Simulation Symposium ESS’95. Erlangen – Nuremberg, Germany. 1995. p.798-801.
- Макин Р.С. О свойствах решений одной задачи динамики реакторов с учетом ксеноновых колебаний. // Дифференц. уравнения. 2004. Т.40. №4. с.80-89.
- Макин Р.С. О гомоклинических траекториях для одной задачи динамики реакторов. // Вестник УлГТУ. 2005. Вып.1(29). с.21-31.
- Макин Р.С. О гомоклинических траекториях эволюционных уравнений. // Дифференц. уравнения. 2005. Т.41. №4. с.479-489.
- Makin R.S. On homoclinic trajectories of evolution equations. \\ Differ. Eqts. 2005. V.41. №4. p.506-517.
- Макин Р.С. О стационарных решениях нелинейной динамики реакторов. // Вестник УлГТУ. 2006. Вып.1(30). с.23-33.
- Макин Р.С. О свойствах решений одной нелинейной интегродифференциальной системы уравнений переноса. // Сб. статей: Матем. методы теорет. физики. Ульяновск: УлГУ. 2007. с.3-59.
- Макин Р.С. О гомоклинических траекториях эволюционных уравнений. // Сб. статей: Матем. методы. теорет. физики. Ульяновск: УлГУ. 2007. с.81-100
- Makin R.S. On one the nonlinear spectrum problem. // Proceedings of the International Seminar “Days on Diffraction – 2006”, 2006. St.-Petersburg. p.161-166.
- Макин Р.С. Математические задачи нелинейной теории переноса.Газокинетическая теория. Ульяновск-Димитровград. Изд-во УлГТУ,2006. 256 с.
- Макин Р.С. Введение в теорию инвариантных притягивающих множеств (аттракторов). Учебное пособие. Ульяновск-Димитровград. Изд-во УлГТУ, 2006. 100 С.
- Макин Р.С. Введение в теорию нелинейных диссипативных динамических систем. Учебное пособие. Ульяновск-Димитровград: Изд-во УлГТУ,2006.
- Makin V.S., Makin R.S., Vorobyev A.Yu., Guo Ch. Universality of Feigenbaum and dissipative microstructures for highly nonequilibrium nonlinear systems. \\ Proc. of Inter. Seminar “Days on Diffraction-2007”. St.-Petersburg, 2007. p.60-66.
- Makin V.S., Makin R.S. Feigenbaum universality and Sharkovsky order for dissipative structures of highly nonequilibrium nonlinear systems.\\ Proc. of Intern. Conference “Fundamentals of Laser Assisted Micro- and Nano-technologies ( FLAMN-07)”. St.-Petersburg. 2007. p.56-57.
- Макин В.C., Макин Р.С., Воробьев А.Ю., Гуо Ч. Диссипативные наноструктуры и универсальность Фейгенбаума в неравновесной нелинейной динамической системе металл-мощное поляризованное короткоимпульсное излучение. // Письма в ЖТФ. 2008. Т.34. Вып.9. с. 55-64.
- Макин Р.С. Введение в динамическую теорию бифуркаций. Ульяновск-Димитровград: Изд-во УлГТУ, 2008. 59 с.
- Makin V.S., Makin R.S. Fundumental universality and dissipative microstructures for highly nonequilibrium nonlinear systems. \\ Proc. of Intern. Conference-10-th Charitonov scientific colloquium “ Power laser and investigations of the highly densities energy physics ”. Sarow. 2008. p. 21-23.
- Makin V.S., Makin R.S., Vorobyev A.Yu.,Guo Ch. Dissipative nanostructures and Feigenbaum’s universality in the “Metall-High-Power Ultrashot-Pulsed Polarized Radiation” nonequilibrium nonlinear dynamic system. \\ Techn. Phys. Letters. 2008. V.34. №5. p.387-390.
- Макин Р.С. Нелинейные задачи теории реакторов. Газокинетическое уравнение. Учебное пособие. Ульяновск – Димитровград: Изд-во УлГТУ,2008.
- Makin V.S., Makin R.S. Fundamental universality and dissipative micro- and nanostructures for highly nonlinear systems. // Proc. of Conf. “ Applied Optics – 2008 ”. St.-Petersburg, 2008. V.2. p. 187-191.
- Макин В.С., Макин Р.С., Воробьев Ф.Я., Гуо Ч. Универсальность Фейгенбаума и порядок Шарковского в лазерно-индуцированных периодических структурах на поверхностях и в объеме конденсированных сред. // В сб. статей: Нелинейность в современном естествознании. М.: Изд-во УРСС, 2008. с.319-341.
- Макин Р.С. О собственных значениях для некоторых классов положительных операторов. // Матем. заметки. 2009. Т.85. №2. с.214-226.
[1] Вейнберг А., Вигнер Е. Физическая теория ядерных реакторов. М.: ИЛ, 1961.
[2] Владимиров В.С. Математические задачи односкоростной теории переноса частиц. // Тр. Матем. ин-та им. В.А. Стеклова т.61. Изд-во АН СССР. 1961.
[3] Шихов С.Б. Вопросы математической теории реакторов. М.: Атомиздат, 1973.
[4] Шихов С.Б., Ершов Ю.И. Математические основы теории переноса. Т.1; Т.2. М.: Энергоатомиздат, 1985.
[5] Кейз К., Цвайфель П. Линейная теория переноса. М.: Мир, 1972.
[6] Малинецкий Г.Г., Потапов А.Б. Современные проблемы нелинейной динамики. М.: УРСС, 2002.
[7] Лихтенберг А., Либерман Г. Регулярная и стохастическая динамика. М.: Мир, 1984.
[8] Песин Я.Б. Общая теория гладких гиперболических динамических систем. // Итоги науки и техники. Современные проблемы математики. Фундаментальные направления. М.: ВИНИТИ. 1985. с.123-173.
[9] Ахромеева Т.С., Курдюмов С.П., Малинецкий Г.Г., Самарский А.А. Нестационарные структуры и диффузионный хаос. М.: Наука, 1992.
[10] Шустер Г. Детерминированный хаос: Введение. М.: Мир, 1988.
[11] Малинецкий Г.Г. Математические основы синергетики. Хаос, структуры, вычислительный эксперимент. Изд. 4-ое. Москва, УРСС. 2005.
[12] Крянев А.В., Шихов С.Б. Вопросы математической теории реакторов: Нелинейный анализ. М.: Энергоатомиздат, 1983.
[13] Красносельский М.А. Положительные решения операторных уравнений. М.: Физматгиз, 1962.
[14] Сабаев Е.Ф. Системы сравнения для нелинейных дифференциальных уравнений и их приложения в динамике реакторов. М.: Атомиздат, 1980.
[15] Гохберг И.Ц., Крейн М.Г. Введение в теорию линейных несамосопряженных операторов. М.: Наука, 1965.
[16] Гантмахер Ф.Р., Крейн М.Г. Осцилляционные матрицы и ядра и малые колебания механических систем. М.-Л.: Гостехиздат, 1950.
[17] Смейл С. // УМН, 1970. Т.25. №1. с.113-185.
[18] Лерман Л.М., Шильников Л.П. // Сиб. матем. ж., 1988. Т.29. №3. с.92-103.
[19] Hale J.K., Xiao – Biao Lin // Ann. Math. Pura Appl., 1986. V.144. №4. p.229-259.
[20] Constantin P., Foias C., Nicolaenco B., Temam R. Integral manifolds and inertial manifolds for dissipative partial differential equations. N.-Y. etc.: Springer, 1989.
[21] Hopf E. // Comm. Pure Appl. Math., 1948. V.1. p.303-322.
[22] Ладыженская О.А. // Теорет. и мат. физика: Сб. обзорных статей. 3. Труды МИАН СССР. Т.175. М.: Наука, 1986.
[23] Гукенхеймер Д., Холмс Ф. Нелинейные колебания, динамические системы и бифуркации векторных полей. М.-Ижевск: РХД. 2002.
