Характеристические граничные задачи для л и нейных уравнений высокого порядка со ста р шими частными производными
На правах рукописи
Уткина Елена Анатольевна
Характеристические граничные задачи для линейных уравнений высокого порядка со старшими частными производными
01.01.02 – дифференциальные уравнения, динамические системы и оптимальное управление
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
доктора физико-математических наук
Казань 2011
Работа выполнена на кафедре дифференциальных уравнений ФГАОУВПО “Казанский (Приволжский) федеральный университет”
Научный консультант: доктор физико-математических наук,
профессор
Жегалов Валентин Иванович
Официальные оппоненты: доктор физико-математических наук,
профессор
Кожанов Александр Иванович
доктор физико-математических наук,
профессор
Логинов Борис Владимирович
доктор физико-математических наук,
профессор
Пулькина Людмила Степановна
Ведущая организация: ГОУ ВПО “Московский государственный
университет им.М.В.Ломоносова”
Защита состоится «22» сентября 2011 г. в 14 часов 30 минут на заседании диссертационного совета Д 212.081.10 при ФГАОУВПО “Казанский (Приволжский) федеральный университет” по адресу: 420008, г.Казань, ул. Профессора Нужина, 1/37, ауд.337.
С диссертацией можно ознакомиться в Научной библиотеке им. Н.И.Лобачевского ФГАОУВПО “Казанский (Приволжский) федеральный университет” по адресу: 420008, г.Казань, ул. Кремлевская, 18.
Автореферат разослан «___» __________2011 г. и размещен на официальном сайте ФГАОУВПО “Казанский (Приволжский) федеральный университет”: www.ksu.ru
Ученый секретарь совета Д 212.081.10
к.ф.-м.н., доцент Липачев Е.К.
Общая характеристика работы
Актуальность темы. Объектом исследования в предлагаемой диссертации являются уравнения вида
 , (1)
, (1)
где ![]() - декартовы координаты точки x,
- декартовы координаты точки x, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - целые неотрицательные числа,
- целые неотрицательные числа, ![]() ,
, ![]() - искомая, а
- искомая, а ![]() ,
, ![]() - известные функции.
- известные функции.
При ![]() ,
, ![]() данное уравнение вошло в математическую литературу под именем Л.Бианки, который одновременно с О.Никколетти еще в 1895г. рассматривал его как многомерный аналог хорошо известного в математической физике уравнения
данное уравнение вошло в математическую литературу под именем Л.Бианки, который одновременно с О.Никколетти еще в 1895г. рассматривал его как многомерный аналог хорошо известного в математической физике уравнения
![]() . (2)
. (2)
Исследование более сложных уравнений (1) в случаях кратного дифференцирования искомой функции по независимым переменным представляет собой естественный дальнейший этап на пути теоретических обобщений. Ценность получаемых при этом теоретических результатов существенно возрастает в связи с тем, что подобные уравнения встречаются в приложениях. А именно, частные случаи (1) возникают при моделировании процессов вибрации и играют существенную роль в теории аппроксимации, теории отображений, к ним сводится задача интегрального представления преобразований одних обыкновенных линейных дифференциальных операторов в другие. Такие уравнения встречаются в теории упругости, при изучении фильтрации жидкости в трещиноватых породах, влагопереноса в почвогрунтах, передачи тепла в гетерогенных средах, моделировании различных биологических процессов и явлений, при изучении распространения волн в диспергирующих средах, а также в теории оптимальных процессов и обратных задачах (см. библиографические ссылки в конце статьи[1]
).
Среди этих уравнений наиболее известными являются указанное И.Н.Векуа уравнение изгиба тонкой сферической оболочки
 , (3)
, (3)
а также уравнения Аллера и Буссинеска – Лява
![]() ,
, ![]() .
.
Первое из них описывает процесс переноса почвенной влаги в зоне аэрации, а второе встречается при изучении продольных волн в тонком упругом стержне с учетом эффектов поперечной инерции и еще описывает волновой процесс в периодических слоистых средах. К виду (1) относятся и поливибрационные уравнения Д.Манжерона.
Таким образом, актуальность построения общей теории уравнений вида (1) обусловлена как логикой развития теоретических исследований, так и востребованностью обсуждаемых уравнений в приложениях.
Степень разработанности проблемы.
После L.Bianci и O.Niccoletti различные вопросы, связанные с уравнениями вида (1) изучали за рубежом H.Bateman, E.Lahaye, H.Hornich, D.Mangeron, M.Ogustoreli, D.Colton, S.Easwaran, V.Radochova, A.Corduneany, W.Rundell, M.Stecher и др. В нашей стране интерес к общему уравнению вида (1) при n=2 возник в связи с задачами теории упругости. Статьи Н.И.Мусхелишвили (1919г.) и И.Н.Векуа (1937г.) положили начало целому направлению исследований в данной области, развивавшемуся в течение ряда десятилетий до работ А.П.Солдатова, М.Х.Шханукова, О.М.Джохадзе и др.(1987 - 1996). При n>2 публикаций на русском языке, посвященных уравнениям вида (1) было сравнительно немного: М.К.Фаге (с 1956г.), В.И.Жегалов с учениками (с 1990г.), В.Ф.Волкодавов с учениками (с 1993г.).
Практически все вышеуказанные авторы, начиная с Л.Бианки развивали в своих исследованиях метод, предложенный в свое время Б.Риманом для уравнения (2), отправляясь от его классического варианта и внося в него те или иные изменения и дополнения. Так, М.К.Фаге[2], отмечая, что «…Бианки и Никколетти разработали лишь формальную часть теории, не вдаваясь в аналитические детали…» представил вариант метода Римана, более соответствующий современному уровню развития математики. Здесь же обращает на себя внимание некоторая самооценка автора: «… изучение сопровождается довольно сложными выкладками» (с.281). В названии же работы, вслед за Г.Бейтменом (1933г.) он использует термин «уравнение Бианки». В некоторых работах уравнения (1) назывались псевдопараболическими (первым такое название использовал Д.Колтон (1972г.)).
Еще одно видоизменение метода Римана было предложено И.Н.Векуа и А.В.Бицадзе: при решении основной характеристической задачи (Гурса) еще для уравнения (2) они вместо основного дифференциального тождества Римана использовали соотношение
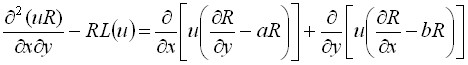 . (4)
. (4)
В варианте метода Римана, предложенном для уравнения Бианки В.И.Жегаловым при n=3 (1990г.) и распространенном им совместно с В.А.Севастьяновым (1996,1997) на случай любого числа измерений n, были построены аналоги тождества (4). При этом было введено еще одно изменение: функция Римана определялась не как решение сопряженного уравнения, удовлетворяющее граничным условиям, число которых очень быстро увеличивается с ростом n, а как решение некоторого интегрального уравнения. Все это позволило получить существенно более прозрачную и лаконичную схему решения задач Гурса и Коши для уравнения Бианки, чем в работах предшественников. К тому же появились дополнительные возможности построения функций Римана в явном виде путем непосредственного решения интегральных уравнений.
Наконец, В.И.Жегаловым и А.Н.Мироновым для уравнения Бианки были исследованы кроме задачи Гурса и другие характеристические задачи, получаемые заменой граничных значений искомой функции значениями нормальной производной от этой функции. Первым автором в 1992г. было выяснено, что для уравнения (2) такие задачи являются содержательными только в случаях, когда хотя бы один из коэффициентов a, b, c не равен тождественно нулю, а их разрешимость приобретает в этих случаях вариантный характер. Вместе со вторым автором эти результаты в 2000г. были распространены на трехмерный аналог уравнения (2). Затем А.Н.Миронов обобщил их на случай уравнений с ![]() .
.
В связи с вышеизложенным естественно возникла идея обобщения указанных результатов В.И.Жегалова, В.А.Севастьянова и А.Н.Миронова на уравнения (1) с кратным дифференцированием по независимым переменным при ![]() . Далее, так как (1) есть обобщение (2), целесообразным представлялось развитие других аспектов исследования (2) с целью применения соответствующих результатов к уравнению (1): изучение нелокальных задач, задачи типа Дирихле, разработка каскадного метода.
. Далее, так как (1) есть обобщение (2), целесообразным представлялось развитие других аспектов исследования (2) с целью применения соответствующих результатов к уравнению (1): изучение нелокальных задач, задачи типа Дирихле, разработка каскадного метода.
Цели диссертационной работы:
1. Вывод основного дифференциального тождества и отыскание решения задачи Гурса для общего случая уравнения (1).
2. Изучение задач для уравнения (1), получаемых из задачи Гурса путем повышения порядка нормальных производных в граничных условиях.
3. Отыскание вариантов корректно поставленных задач типа Дирихле для уравнений вида (1).
4. Постановка и исследование новых многомерных задач с нелокальными граничными условиями.
5. Выделение из класса уравнений вида (1) аналогов уравнения Эйлера-Пуассона-Дарбу, разрешимых в явном виде с последующим решением для них граничных задач.
Методика исследования. Основным моментом является развитие метода Римана с целью его применения к общему уравнению (1), при этом пришлось комбинировать аналитический подход с компьютерным. Используются и другие методы из теории уравнений с частными производными: каскадного интегрирования и априорных оценок. Применяются результаты из теории интегральных уравнений Вольтерра и Фредгольма.
Научная новизна. Все результаты диссертации являются новыми. Стержневую роль играет вывод формулы решения задачи Гурса для общего уравнения (1): эта формула используется в качестве общего представления решений, позволяя при определенных (получаемых в диссертации) условиях редуцировать все задачи из второй и третьей глав к задаче Гурса. Новизна содержится и в развиваемых здесь методах Римана и Лапласа: область их применения существенно расширяется. Новой является качественная картина разрешимости рассматриваемых задач, а также выделяемые в работе случаи разрешимости в квадратурах.
Теоретическое и практическое значение. Работа носит теоретический характер, заполняя определенный пробел в теории дифференциальных уравнений с частными производными. Автору представляется, что имеются возможности использования полученных результатов в качестве основы для дальнейших исследований. Не исключена возможность практических приложений.
Апробация работы. Результаты работы, по мере их получения, докладывались на семинарах кафедры дифференциальных уравнений Казанского государственного университета, часть была доложена на итоговых ежегодных научных конференциях КГУ за период с 1997 по 2010. Также был сделан доклад в МГУ на семинаре акад. Е.И.Моисеева, 2002г.
Обзорные доклады по диссертации были сделаны:
в Институте математики им.С.Л.Соболева РАН в Новосибирске на семинарах по неклассическим уравнениям математической физики (руководитель проф. А.И.Кожанов) и по качественной теории дифференциальных уравнений (руководитель проф.В.С.Белоносов), 2004г.;
на семинаре кафедры математического анализа Белгородского государственного университета (руководитель проф.А.П.Солдатов), 2005г.;
в МГУ на семинаре акад. Е.И.Моисеева, 2011г.;
в РУДН на семинаре по дифференциальным и функционально-дифференциальным уравнениям (руководитель проф.А.Л.Скубачевский), 2011г.
Результаты работы докладывались также на различных научных конференциях, в том числе, международных. Например:
Третьем сибирском конгрессе по прикладной и индустриальной математике (biprim –98), посвященном памяти С.Л. Соболева (Новосибирск, 1998);
Международной научной конференции, посвященной 70-летию акад. В.А. Ильина (Стерлитамак,1998);
Международной научной конференции «Актуальные проблемы математики и механики» (Казань, 2000);
Международной конференции AMADE (Минск, Беларусь, 2003);
III международной конференции «Нелокальные краевые задачи и родственные проблемы математической биологии, информатики и физики»(Нальчик, 2006);
Международной конференции "Современные проблемы математики, механики и их приложений", посвященной 70-летию акад. В.А.Садовничего (Москва, 2009).
Названия других конференций указаны в списке литературы [25]-[29], [31], [33], [38]-[42], [44]- [46], [48]- [49], [51]- [54], [56]-[57], [59]- [61].
Публикации. По теме диссертации опубликовано 62 работы, в том числе 24 статьи - в журналах, определенных Высшей аттестационной комиссией (ВАК) Министерства образования и науки Российской Федерации для публикации результатов научных исследований. Из общего числа 9 выполнены в соавторстве с научным руководителем кандидатской диссертации, которому здесь принадлежат постановки задач и общие идеи о возможных путях их решения.
Структура и объем работы. Диссертационная работа состоит из введения, четырех глав, разбитых на параграфы, списка литературы из 206 наименований и занимает 263 страниц машинописного текста.
Нумерация параграфов производится одним символом, а нумерация пунктов и подпунктов – двумя и тремя соответственно. Нумерация параграфов, пунктов и подпунктов, а также формул в каждой главе своя.
Краткое содержание работы
Во введении проведено обоснование темы диссертации и дан обзор работ, имеющих отношение к этой теме, а также кратко охарактеризованы результаты автора, изложенные в последующих главах.
В первой главе «Задача Гурса» наибольших усилий потребовал вывод тождества, играющего роль (4).
Проблема состояла в том, что закономерность построения упомянутого тождества, обнаруженная В.И.Жегаловым и В.А.Севастьяновым в процессе их работы с уравнением Бианки, здесь не действовала. Для установления нужной закономерности рассматривались сначала частные случаи при малых значениях ![]() . Наиболее изученным предшественниками было обобщение уравнения Аллера
. Наиболее изученным предшественниками было обобщение уравнения Аллера
![]() , (5)
, (5)
для которого функция Римана ![]() определялась как решение задачи Гурса с помощью некоторой задачи Коши. Такой способ обеспечивает существование функции R, но вопрос о ее явном построении остается открытым. Наша работа тоже началась с уравнения (5). Функция Римана при этом вводилась как решение интегрального уравнения
определялась как решение задачи Гурса с помощью некоторой задачи Коши. Такой способ обеспечивает существование функции R, но вопрос о ее явном построении остается открытым. Наша работа тоже началась с уравнения (5). Функция Римана при этом вводилась как решение интегрального уравнения
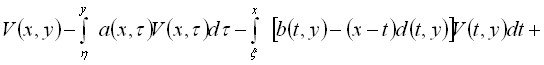 (6)
(6)

а искомое тождество было получено в форме
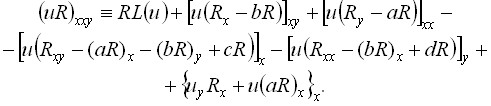 (7)
(7)
Затем рассматривались более сложные, чем (5), уравнения со старшими частными производными ![]() ,
, ![]() ,
, ![]() ,
, ![]() и т.д. При этом была выделена некая «главная» часть (которая строилась по тому же принципу, что и в случае уравнения Бианки, и присутствовала при каждом построении) и «остаток», который вычислялся каждый раз путем вычитания левой и «главной» части тождества. Долгое время не удавалось спрогнозировать общий вид этого «остатка». Излагать подробно всю историю вопроса в диссертации представлялось нецелесообразным, поэтому был избран способ изложения, являющийся по мнению автора более простым для восприятия: сначала берется случай, когда в уравнение входит производная лишь по одной из переменных, а потом уже производятся усложнения, которые более или менее естественным образом приводят к общему случаю.
и т.д. При этом была выделена некая «главная» часть (которая строилась по тому же принципу, что и в случае уравнения Бианки, и присутствовала при каждом построении) и «остаток», который вычислялся каждый раз путем вычитания левой и «главной» части тождества. Долгое время не удавалось спрогнозировать общий вид этого «остатка». Излагать подробно всю историю вопроса в диссертации представлялось нецелесообразным, поэтому был избран способ изложения, являющийся по мнению автора более простым для восприятия: сначала берется случай, когда в уравнение входит производная лишь по одной из переменных, а потом уже производятся усложнения, которые более или менее естественным образом приводят к общему случаю.
Задача Гурса (общая постановка): найти в D![]()
![]() решение уравнения (1) из класса
решение уравнения (1) из класса
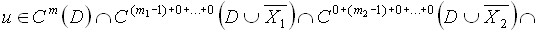
![]() , удовлетворяющее условиям
, удовлетворяющее условиям
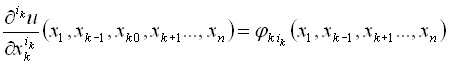 , (8)
, (8)
![]() ,
, 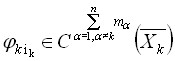 ,
,
причем граничные значения из (8) на ребрах D согласуются, а сами согласованные значения непрерывно дифференцируемы.
Здесь ![]() - класс непрерывных в
- класс непрерывных в ![]() вместе с их производными
вместе с их производными ![]() (
(![]() ,
, ![]() ,…
,…![]() ), функций.
), функций.
В §1 главы 1 рассматривается уравнение (1) с дифференцированием лишь по первой переменной. Задача Гурса в данном случае переходит в задачу Коши, формулируемую следующим образом.
Найти решение уравнения
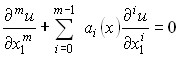
при выполнении условий
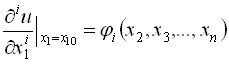
![]()
![]() ,
, ![]() .
.
Аналог тождества (7) в данном случае имеет вид
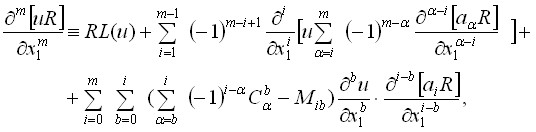
![]() , если
, если ![]() и
и ![]() в остальных случаях;
в остальных случаях; ![]() - биномиальные коэффициенты. Решение задачи Гурса строится путем интегрирования указанного тождества, но для этого последнее слагаемое в нем требует преобразования в другую форму, причем установление этой формы представляло главную трудность. При малых m удалось прийти к ней аналитическим путем и спрогнозировать ее вид в общем случае. Затем к доказательству указанной гипотетической формулы был применен компьютерный метод. К сожалению, компьютерная составляющая ведет к накоплению погрешности при вычислениях, поэтому окончательную формулу решения задачи Гурса можно считать доказанной с точностью до
- биномиальные коэффициенты. Решение задачи Гурса строится путем интегрирования указанного тождества, но для этого последнее слагаемое в нем требует преобразования в другую форму, причем установление этой формы представляло главную трудность. При малых m удалось прийти к ней аналитическим путем и спрогнозировать ее вид в общем случае. Затем к доказательству указанной гипотетической формулы был применен компьютерный метод. К сожалению, компьютерная составляющая ведет к накоплению погрешности при вычислениях, поэтому окончательную формулу решения задачи Гурса можно считать доказанной с точностью до ![]() при m=40.
при m=40.
§2 и 3 посвящены изучению уравнения (1) при ![]() ,
, ![]() соответственно.
соответственно.
В §4 упомянутая схема рассуждений реализована уже для общего случая рассматриваемого уравнения (1). Для компактности записи применяются мультииндексы.
Вывод указанной формулы может быть истолкован как доказательство существования решения. Но мы приводим и независимое доказательство существования и единственности решения. В процессе этого доказательства выведена вспомогательная формула, которую можно считать интегральным аналогом формулы Лейбница, связанной с дифференцированием произведения. Таково содержание первой главы.
Полученная формула решения задачи Гурса служит основой для глав II-III, где она применяется в качестве общего представления решений уравнения (1).
Если в задаче Гурса заменить хотя бы одно из граничных значений ![]()
![]() ,
, ![]() на
на ![]() для некоторого
для некоторого ![]() , то получится новая задача. Такие задачи с повышением порядка нормальных производных являются предметом изучения во второй главе «Повышение порядка нормальных производных в граничных условиях».
, то получится новая задача. Такие задачи с повышением порядка нормальных производных являются предметом изучения во второй главе «Повышение порядка нормальных производных в граничных условиях».
В случае, когда наивысший порядок нормальной производной на границе увеличивается на единицу, такие задачи для уравнения (1) мы обозначаем как ![]() .
.
В §1 этой главы рассматриваются задачи типа ![]() для уравнения (1) (при
для уравнения (1) (при ![]() ,
, ![]() и общий случай). Изучение начинается со случаев, когда заменяется одно условие только на одной характеристике. Выяснено, что тогда соответствующие значения Гурса определяются единственным образом. Приведем одну из постановок указанных задач.
и общий случай). Изучение начинается со случаев, когда заменяется одно условие только на одной характеристике. Выяснено, что тогда соответствующие значения Гурса определяются единственным образом. Приведем одну из постановок указанных задач.
Задача 2.1.1. Найти функцию ![]()
![]()
![]()
![]() , являющуюся в D решением уравнения (1) (при
, являющуюся в D решением уравнения (1) (при ![]() ), удовлетворяющую условиям
), удовлетворяющую условиям
![]()
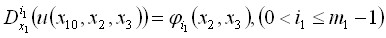 ,
,
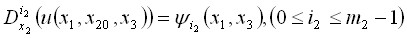 ,
,
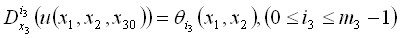 .
.
Редукция задачи 2.1.1 к задаче Гурса состоит в отыскании функции ![]() . Для ее определения было выведено интегральное уравнение Вольтерра. Выяснено, что характер его разрешимости зависит от групп условий:
. Для ее определения было выведено интегральное уравнение Вольтерра. Выяснено, что характер его разрешимости зависит от групп условий:
1) ![]() . Функция
. Функция ![]() записывается через резольвенту уравнения. Запись
записывается через резольвенту уравнения. Запись ![]() в явном виде обеспечивается любым из наборов условий:
в явном виде обеспечивается любым из наборов условий:
1) ![]() и
и

![]() ,
, ![]() ;
;
2)![]() ,
, 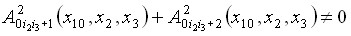
![]() ,
, ![]() ;
;
3)![]() и
и
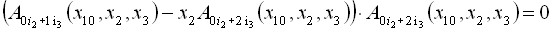
![]() ,
, ![]() ;
;
4)![]() ,
,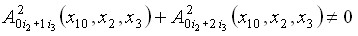
![]() ,
, ![]() ,
,
причем остальные коэффициенты ![]() в каждом случае считаем нулевыми.
в каждом случае считаем нулевыми.
Здесь
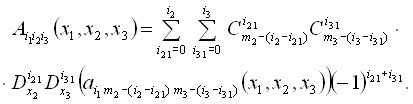
Подобные задачи (2.1.1, 2.1.4, 2.1.5) рассматриваются в п.п.1.1,1.2.
В п.1.3 рассматриваются задачи, когда условия Гурса заменены на парах характеристик. Здесь приходится исследовать на разрешимость уже два интегральных уравнения, а сама картина разрешимости приобретает более разветвленный характер. Например, если ![]() , то функции
, то функции ![]() ,
, ![]() зависят от одной произвольной функции
зависят от одной произвольной функции ![]() . Если же коэффициент
. Если же коэффициент ![]() , то
, то ![]() и
и ![]() определяются однозначно. В каждой из задач 2.1.6 и 2.1.7 выделено по 25 вариантов. Поэтому для компактной записи результата в рассмотрение были введены специальные матрицы-строки, элементами которых являются блоки из условий на коэффициенты, обеспечивающие тот или иной характер разрешимости соответствующих задач.
определяются однозначно. В каждой из задач 2.1.6 и 2.1.7 выделено по 25 вариантов. Поэтому для компактной записи результата в рассмотрение были введены специальные матрицы-строки, элементами которых являются блоки из условий на коэффициенты, обеспечивающие тот или иной характер разрешимости соответствующих задач.
В п.1.4 рассмотрена одна из задач, когда заменены данные Гурса уже на всех трех характеристиках.
В п.1.5 рассуждения распространены на (1) в четырехмерном пространстве.
В п.1.6 рассматриваются задачи ![]() для общего уравнения (1).
для общего уравнения (1).
Дальнейшим этапом развития задач Гурса после ![]() являются задачи
являются задачи ![]() , когда граничные условия заменяются на нормальные производные, порядок которых повышается уже на
, когда граничные условия заменяются на нормальные производные, порядок которых повышается уже на ![]() по сравнению с максимальным порядком производной в задаче Гурса на заданной характеристике (он равен порядку уравнения по соответствующей переменной, уменьшенному на единицу).
по сравнению с максимальным порядком производной в задаче Гурса на заданной характеристике (он равен порядку уравнения по соответствующей переменной, уменьшенному на единицу).
В §2 той же главы с помощью обсуждаемого подхода рассматриваются задачи ![]() . Считаем порядок производной N превышающим наивысший порядок граничного условия из задачи Гурса на данной характеристике больше чем на единицу. Рассуждения ведутся сразу для общего уравнения (1). Доказан следующий результат о достаточных условиях редукции к задаче Гурса.
. Считаем порядок производной N превышающим наивысший порядок граничного условия из задачи Гурса на данной характеристике больше чем на единицу. Рассуждения ведутся сразу для общего уравнения (1). Доказан следующий результат о достаточных условиях редукции к задаче Гурса.
Теорема 2.2.1. Если коэффициенты уравнения (1) принадлежат классу 
![]() и, кроме того, коэффициент при
и, кроме того, коэффициент при ![]() в левой части
в левой части
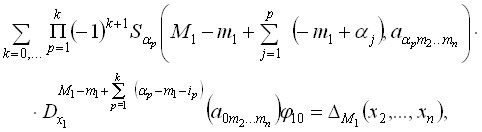
отличен от нуля, то задача 2.2.1 редуцируется к задаче Гурса.
Здесь ![]() может принимать значения 0,…,
может принимать значения 0,…,![]() . Если
. Если ![]() , то
, то ![]() ,
,
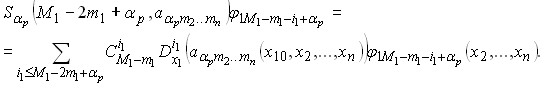
Только что изложенные результаты вывели теорию общего уравнения (1) примерно на тот же уровень, на котором находилась теория уравнения Бианки.
С другой стороны, как уже отмечалось выше, и для уравнения Бианки, и, тем более, для общего уравнения (1) оставались неисследованными многие вопросы. Например, задачи типа Дирихле, задачи со смещением в граничных условиях и др. Указанным вопросам посвящены последующие главы данной диссертации. Их, вместе с результатами главы II, можно рассматривать как области приложения результатов главы I.
В третьей главе «Задача Дирихле и нелокальные задачи» сначала рассматривается первая из указанных задач для уравнений
 (9)
(9)
и
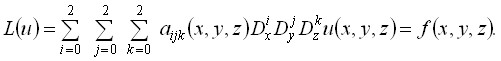
В обоих случаях применяется одинаковый подход, поэтому поясним подробнее идею этого подхода только на примере уравнения (9).
Задача 3.1. В области ![]() ,
, ![]() ,
, ![]() , найти функцию
, найти функцию 
![]() , являющуюся в D решением уравнения (9) и удовлетворяющую условиям
, являющуюся в D решением уравнения (9) и удовлетворяющую условиям
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Для нахождения решения были получены уравнения Фредгольма, которым удовлетворяют недостающие данные Гурса ![]() ,
, ![]() . После этого методом априорных оценок выведены условия на коэффициенты (9), которые обеспечивают однозначную разрешимость этих уравнений. Результатом проведенных рассуждений является
. После этого методом априорных оценок выведены условия на коэффициенты (9), которые обеспечивают однозначную разрешимость этих уравнений. Результатом проведенных рассуждений является
Теорема 3.1. Если коэффициенты уравнения (9) удовлетворяют неравенствам
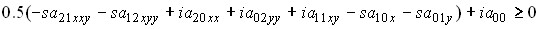 ,
, ![]() ,
,![]() ,
,![]() ,
,
то задача Дирихле имеет единственное решение.
Здесь ![]() ,
, ![]() .
.
Из нелокальных задач мы рассматриваем варианты, связанные с отысканием решений по соотношениям, связывающим значения искомой функции в различных переменных точках, лежащих на границе и внутри рассматриваемой области (задачи со смещениями). Второй параграф третьей главы посвящен изучению таких задач для уравнений с некратным и кратным дифференцированием. А именно, первоначально рассматриваются задачи для двух плоских уравнений с кратным дифференцированием – (5) и (9). Затем – задачи для уравнения Бианки в пространствах ![]() . Результат исследования каждой задачи сформулирован в виде теоремы. Остановимся сначала на одной из упомянутых задач для n=2, сделав предварительно пояснения.
. Результат исследования каждой задачи сформулирован в виде теоремы. Остановимся сначала на одной из упомянутых задач для n=2, сделав предварительно пояснения.
Обозначим точки, лежащие на границе и внутри области ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Точки, получаемые из
. Точки, получаемые из ![]() заменой
заменой ![]() на
на ![]() обозначим соответственно через
обозначим соответственно через ![]() .
.
Задача 3.3. Требуется найти функцию ![]() , являющуюся в D решением уравнения (5) и удовлетворяющую следующим трем условиям
, являющуюся в D решением уравнения (5) и удовлетворяющую следующим трем условиям

![]()

![]()

При этом на отрезках своего определения![]() .
.
Доказана
Теорема 3.3. Задача 3.3 при выполнении условий
 ,
, ![]()
однозначно разрешима.
Задача для уравнения Бианки в случае ![]() формулируется как
формулируется как
Задача 3.5. Найти функцию ![]() , являющуюся в области
, являющуюся в области ![]() решением упомянутого уравнения и удовлетворяющую условиям
решением упомянутого уравнения и удовлетворяющую условиям
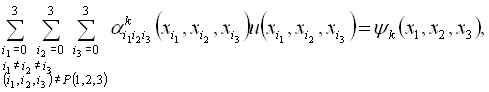 (
(![]() )
)
![]() - перестановка чисел 1, 2, 3,
- перестановка чисел 1, 2, 3, ![]() ,
,![]() на соответствующих гранях
на соответствующих гранях ![]() .
.
Результатом проведенных рассуждений является
Теорема 3.5. Задача 3.5 при заданных условиях и неравенстве нулю определителя соответствующей матрицы имеет единственное решение.
Все предыдущие задачи рассматривались в характеристическом параллелепипеде, а коэффициенты уравнения были достаточно гладкими, чтобы обеспечить существование функции Римана, в терминах которой в конечном счете записывались решения задач. Однако для (2) известен еще каскадный метод Лапласа, иногда позволяющий записывать в квадратурах представления решений уравнений, коэффициенты которых имеют особенности. Примером здесь может служить хорошо известное в математической физике уравнение Эйлера-Пуассона-Дарбу (ЭПД)
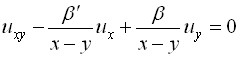 .
.
В связи с этим возникла идея: попытаться выделить из (1) с сингулярными коэффициентами такие случаи, которые с точки зрения метода Лапласа можно было бы рассматривать как аналоги уравнения ЭПД. Реализации этой идеи посвящена четвертая глава «Уравнения с сингулярными коэффициентами». Были построены следующие аналоги уравнения ЭПД.
1)В случае уравнения типа Аллера (со старшей производной ![]() ):
):
 . (10)
. (10)
2) Для общего уравнения (1) на плоскости:

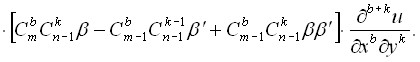
3) В n – мерном пространстве
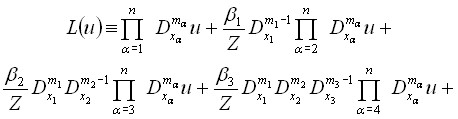

где
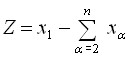 ,
,
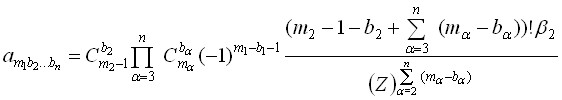 ,
, ![]() ,
, ![]() (
(![]() ),
),
 ,
, ![]() ,
, ![]() , (
, (![]() ),
),

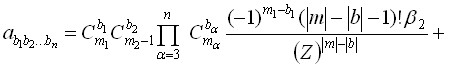


Для некоторых построенных уравнений были поставлены задачи Гурса, а также ![]() . Они несколько отличаются от уже изложенных в главе I. А именно, меняются как область (она выбирается так, чтобы внутри нее коэффициенты оставались гладкими), так и интегральное уравнение функции Римана, сопряженное уравнение и основное тождество. В п.1.1 упомянутый метод был применен сначала к уравнению (5), для которого были получены пары групп условий на коэффициенты (5), позволяющие понизить порядок уравнения на единицу. Одной из указанных групп является набор
. Они несколько отличаются от уже изложенных в главе I. А именно, меняются как область (она выбирается так, чтобы внутри нее коэффициенты оставались гладкими), так и интегральное уравнение функции Римана, сопряженное уравнение и основное тождество. В п.1.1 упомянутый метод был применен сначала к уравнению (5), для которого были получены пары групп условий на коэффициенты (5), позволяющие понизить порядок уравнения на единицу. Одной из указанных групп является набор
![]() ,
, ![]() ,
, ![]() .
.
В п.1.2 были построены аналоги уравнений ЭПД. Одним из таких уравнений можно считать (10). При этом было показано, что построение каскада удалось осуществить при некоторых дополнительных ограничениях на коэффициенты. Для этих уравнений в п.1.3 были рассмотрены характеристические задачи Гурса и ![]() .
.
Задача Гурса. Пусть D- треугольная область, ограниченная характеристиками ![]() ,
, ![]() и прямой
и прямой ![]() . Найдем решение(10)
. Найдем решение(10) ![]() , удовлетворяющее условиям
, удовлетворяющее условиям
![]() ,
, ![]() ,
, ![]() , (11)
, (11)
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Доказана
Теорема.Задача Гурса (10), (11) однозначно разрешима.
В п.1.4 подобные рассуждения были проведены для уравнения (9), а затем - для общего уравнения на плоскости.
Второй параграф посвящен распространению результатов на случай трехмерного пространства.
При этом в п.2.1 рассматривается уравнение Бианки, а затем (в п.2.2)- уравнение (1) в трехмерном пространстве.
Третий параграф посвящен общему уравнению ЭПД в n-мерном пространстве.
§4 посвящен граничным задачам типа Г1, которые в п.4.1 рассматриваются для уравнения четвертого порядка.
В заключение сформулируем основные положения, выносимые на защиту:
-Построена формула решения задачи Гурса для общего уравнения (1).
-Исследованы вопросы разрешимости новых характеристических задач с нормальными производными в граничных условиях.
-Выведены достаточные условия существования и единственности решения задачи Дирихле для уравнений четвертого и шестого порядка в двух- и трехмерном пространствах.
-Исследованы новые задачи со смещениями в граничных условиях для уравнений с кратным дифференцированием и уравнений Бианки трех и четырех измерений.
-Для уравнения (1) с сингулярными коэффициентами построены аналоги уравнения Эйлера-Пуассона-Дарбу и для них решены задачи типа Гурса.
Публикации автора по теме диссертации.
Статьи в ведущих рецензируемых научных журналах, включенных в Перечень ВАК РФ
1.Жегалов, В.И.Об одном псевдопараболическом уравнении третьего порядка/В.И.Жегалов, Е.А.Уткина//Изв. вузов. Математика.1999.№10. С.7376.0,25 п.л.
2.Жегалов, В.И.Задача Гурса для одного трехмерного уравнения со старшей частной производной/В.И.Жегалов, Е.А.Уткина// Изв. вузов.Матема-тика.2001.№11.С.7781.0,313 п.л.
3.Жегалов, В.И.Об одном уравнении в частных производных четвертого порядка с тремя независимыми переменными/ В.И.Жегалов, Е.А.Уткина// Дифференц. уравнения.2002.Т.38.№1.С.9397.0,313 п.л.
4.Уткина, Е.А. О задачах Гурса с дополнительными нормальными про-изводными в краевых условиях/Е.А.Уткина// Изв. вузов. Математика.2004. №3.С.6165.0,313 п.л.
5.Уткина, Е.А. Об одном дифференциальном уравнении со старшей частной производной в трехмерном пространстве/Е.А.Уткина//Дифференц. уравнения.Т.41.№5.2005.С.697701.0,313 п.л.
6.Уткина, Е.А. К общему случаю задачи Гурса/ Е.А.Уткина// Изв. вузов. Математика.2005.№8.С.5762.0,375 п.л.
7.Уткина, Е.А.Об одном уравнении в частных производных с син-гулярными коэффициентами/Е.А.Уткина//Изв.вузов.Математика.2006.№9 С. 6770.0,25 п.л.
8.Уткина, Е.А.Об одном применении метода каскадного интегри-рования/ Е.А.Уткина// Дифференц. уравнения.2007.Т. 43.№ 4.C.566569. 0,25 п.л.
9.Уткина, Е.А. Повышение порядка нормальных производных в граничных условиях задачи Гурса/Е.А.Уткина// Изв. вузов. Математика.– 2007.– №3.– С. 79–83.0,313 п.л.
10.Уткина, Е.А.Об одной краевой задаче со смещениями в четырехмерном пространстве/Е.А.Уткина//Изв.вузов.Математика.2009. №3.С. 50–55. 0,375 п.л.
11.Уткина, Е.А.Задача со смещениями для трехмерного уравнения Бианки/ Е.А.Уткина//Дифференц. уравнения.2010.Т. 46.№ 4.С. 535–539. 0,313 п.л.
12.Уткина, Е.А. Задача Дирихле для одного уравнения четвертого по-рядка/ Е.А.Уткина //Дифференц. уравнения.–2011.–Т.47.–№4.–С.400–404. 0,313 п.л.
13.Уткина, Е.А. Теорема единственности решения одной задачи Дирих-ле/ Е.А.Уткина// Изв. вузов. Математика.–2011.– №5.– С. 62–67.0,375 п.л.
14.Уткина, Е.А.Об одной трехмерной задаче Гурса/ Е.А.Уткина//Вест-ник Самарского государственного технического университета. Серия физ.-мат.науки.2001.Вып. 12.С.3035.0,375 п.л.
15.Уткина, Е.А.К задачам с условиями на характеристиках для общего псевдопараболического уравнения/Е.А.Уткина//Вестник Самарского госу-дарственного технического университета. Серия «Математическая».2003. №2.С.217223.0,438 п.л.
16.Уткина, Е.А. Вариант метода Римана в четырехмерном евклидовом пространстве/Е.А.Уткина//Вестник Самарского государственного техни-ческого университета. Серия «Математическая».2004.№3.С.6380.1,5 п.л.
17.Уткина, Е.А. Задача Гурса для одного n-мерного уравнения/ Е.А.Уткина//Вестник Самарского государственного университета. Спец. выпуск.2004.С.6467.0,25 п.л.
18.Уткина, Е.А. О задачах со смещениями в граничных условиях для двух уравнений с частными производными/ Е.А.Уткина// Уч.записки Казанского университета. Серия физ.-мат.науки.– 2006.–Т.148,книга 3.– С.76–82. 0,438 п.л.
19.Уткина, Е.А. Об одном обобщении интегральных уравнений Вольтера/Е.А.Уткина//Вестник Татарского государственного гуманитарно-педа-гогического университета.–2006.–№7.– С. 90–93.0,25 п.л.
20.Уткина, Е.А. К задачам со смещениями для четырехмерного уравнения Бианки/Е.А.Уткина//Вестник Самарского государственного университета. Естественнонауч.серия.2008.№8/2.С.212221.0,625 п.л.
21. Уткина, Е.А. Задача Неймана для одного уравнения четвертого порядка/Е.А.Уткина//Вестник Самарского государственного технического университета. Серия физ.-мат. науки.– 2009. – № 2 (19).–С. 1–9.0,563 п.л.
22.Уткина, Е.А. Задача Дирихле для одного трехмерного уравнения/ Е.А.Уткина//Вестник Самарского государственного университета. Естествен-нонауч. серия.–2010.–№2(76).–С.84–95.0,75 п.л.
23.Уткина, Е.А. О единственности решения полуинтегральной задачи для одного уравнения четвертого порядка/ Е.А.Уткина // Вестник Самарского государственного университета. Естественнонауч.серия.–2010.–№4(78).–С.98 – 102.0,313 п.л.
24.Utkina, Е.А. On a partial differential equation in 4-dimensional Euclidean space/ Е.А.Utkina//Lobachevskii Journal of Mathematics.–2005.–Vol.18. – P. 151–175.1,5 п.л.
Публикации в других изданиях
25.Жегалов, В.И.Вариант метода Римана для одного уравнения третьего порядка/ В.И.Жегалов, Е.А.Уткина// Труды седьмой межвузовской конференции «Математическое моделирование и краевые задачи».– Самара, 1997.– Ч.3. – С.32–33.0,125 п.л.
26.Жегалов, В.И.Случаи явного решения задачи Гурса для одного псевдопараболического уравнения третьего порядка/ В.И.Жегалов, Е.А.Уткина// Труды третьей международной конференции «Дифференциальные уравнения и их приложения».–Саранск,1998.–С.27.0,063 п.л.
27.Жегалов, В.И.Один пространственный вариант задачи Гурса/ В.И.Жегалов, Е.А.Уткина// Труды X межвуз. конф. «Математическое моделирование и краевые задачи».– Самара,2000.– Ч.З.–С. 65–67.0,188 п.л.
28.Жегалов, В.И.Задача Гурса для одного уравнения в трехмерном пространстве/ В.И.Жегалов, Е.А.Уткина// Материалы международной научной конф. «Актуальные проблемы математики и механики».– Казань, 2000.–С.270–271.0,125 п.л.
29.Жегалов, В.И. Краевая задача со смещениями в ![]() / В.И.Жегалов, Е.А.Уткина//Материалы докладов III международной конференции «Нело-кальные краевые задачи и родственные проблемы матем.биологии, инфор-матики и физики».–Нальчик: Изд-во «Эльбрус», 2006.–С.118–120.0,188 п.л.
/ В.И.Жегалов, Е.А.Уткина//Материалы докладов III международной конференции «Нело-кальные краевые задачи и родственные проблемы матем.биологии, инфор-матики и физики».–Нальчик: Изд-во «Эльбрус», 2006.–С.118–120.0,188 п.л.
30.Жегалов, В.И.Трехмерная нелокальная задача с нормальными производными в граничных условиях/ В.И.Жегалов, Е.А.Уткина// Известия РАЕН. Дифференц. уравнения.–Рязань: Рязанский государственный универ-ситет, 2006.– № 11.– С. 86–87.0,125 п.л.
31.Уткина, Е.А. Некоторые видоизменения граничных условии одной задачи Гурса/ Е.А.Уткина//Материалы конференции «Алгебра и анализ», посвященной 100-летию Б.М. Гагаева.– Казань,1997.– С.221–222.0,125 п.л.
32.Уткина, Е.А.Об одном псевдопараболическом уравнении четвертого порядка/ Е.А.Уткина// Тезисы докладов Третьего сибирского конгресса по прикладной и индустриальной математике, посвященного памяти С.Л.Собо-лева.– Новосибирск,1998.– С.42.0,063 п.л.
33.Уткина, Е.А. Некоторые видоизменения граничных условий одной задачи Гурса/ Е.А.Уткина// Сб. трудов международной научной конференции «Спектральная теория дифференциальных операторов и смежные вопросы», посвященной 70-летию акад. В.А. Ильина, г. Стерлитамак.– Уфа: Изд-во Гилем, 1998.– Ч.1.– С.59–60.0,125 п.л.
34.Уткина, Е.А. К характеристическим задачам для псевдопараболи-ческих уравнений третьего и четвертого порядка/ Е.А.Уткина/ Казанский ун-т.– Казань, 1999.– 31с. Деп. в ВИНИТИ 29.01.99, №277–В99.1,938 п.л.
35.Уткина, Е.А. К решению одной задачи Гурса/ Е.А.Уткина/ Казанский ун-т.– Казань, 1999.– 35с. Деп. в ВИНИТИ 26.02.99, №578–899.2,188 п.л.
36.Уткина, Е.А. О явной редукции характеристических задач с нор-мальными производными высокого порядка к задаче Гурса/ Е.А.Уткина/ Казанский ун-т.– Казань, 1999.– 27с. Деп. в ВИНИТИ 17.03.99, №818–899. 1,688 п.л.
37.Уткина, Е.А. Об одном уравнении в частных производных четвер-того порядка/ Е.А.Уткина/ Ред. ж. "Дифференц. уравнения".– Минск, 1999.–13с. Деп. В ВИНИТИ 28.06.99, №2059–В99.0,813 п.л.
38.Уткина, Е.А. Граничные свойства решений задачи Гурса для одного уравнения четвертого порядка/ Е.А.Уткина// Труды IX межвуз. конф. «Математическое моделирование и краевые задачи».– Самара, 1999.–Ч. З.–С. 134–139.0,375 п.л.
39.Уткина, Е.А. Об одной характеристической задаче/ Е.А.Уткина// Материалы научной конференции, посвященной 125-летию Казанского государственного педагогического университета «Проблемы современной математики». Труды математического центра им.Лобачевского.– Казань: Казанское математическое общество, 2001.–Т.11.–С.261–263.0,188 п.л.
40.Уткина, Е.А. О некоторых трехмерных характеристических задачах/ Е.А.Уткина// Труды международной научной конференции «Дифференциальные уравнения и их приложения».–Самара,2002.–С.353–355.0,188 п.л.
41.Уткина, Е.А.Об одной плоской характеристической задаче/ Е.А.Уткина// Труды международной конференции «Спектральная теория дифференциальных операторов и родственные проблемы», г. Стерлитамак.– Уфа: Изд-во Гилем, 2003.–Т.1.–С.239–240.0,125 п.л.
42.Уткина, Е.А. Вариант каскадного метода для обобщенного уравнения Буссинеска-Лява/Е.А.Уткина// Материалы 6-й Казанской международной школы-конференции «Теория функций и ее приложения». Труды математического центра им.Лобачевского.–Казань, 2003.–Т.19.–С.219–220. 0,125 п.л.
43.Уткина, Е.А. Об одной трехмерной характеристической задаче/ Е.А.Уткина// Аналитические методы анализа и дифференциальных уравнений. Сб. тезисов международной конференции AMADE. Минск. Ин-т матем.НАН Беларуси, 2003.– С.175. 0,063 п.л.
44.Уткина, Е.А. К граничным задачам для псевдопараболического уравнения высокого порядка/Е.А.Уткина// Материалы международного российско- узбекского симпозиума «Уравнения смешанного типа и родственные проблемы анализа и информатики».– Нальчик: Изд-во «Эльбрус», 2003.–С.90–91.0,125 п.л.
45.Уткина, Е.А. Одновременное обобщение интегральных уравнений Вольтерра и Фредгольма/ Е.А.Уткина// Материалы третьей всероссийской молодежной научной школы-конференции. Труды Математического центра им. Н.И.Лобачевского.–Казань, 2003.– Т.21. –С.221–223.0,188 п.л.
46.Уткина, Е.А. К краевым задачам для одного трехмерного уравнения высокого порядка/ Е.А.Уткина// Материалы XL всероссийской конференции по проблемам математики, информатики, физики и химии.–Москва: Издательство РУДН, 2004.– С.28–31.0,25 п.л.
47.Уткина, Е.А. О повышении порядка нормальных производных в граничных условиях одной пространственной задачи Гурса/Е.А.Уткина// Известия РАЕН. Дифференц. уравнения.– Рязань: Рязанский государственный университет, 2004.–№ 8.– С. 92 – 97.0,375 п.л.
48.Уткина, Е.А. Об одном пространственном уравнении в частных производных шестого порядка/ Е.А.Уткина// Труды Всероссийской конференции «Современные проблемы физики и математики», г. Стерлитамак.– Уфа: Изд-во Гилем, 2004. – Т.1. – С.108–112.0,417 п.л.
49.Уткина, Е.А. Об одном аналоге уравнения Эйлера-Пуассона-Дарбу/ Е.А.Уткина//Материалы международной научной конференции «Актуальные проблемы математики и механики». Труды Математического центра им. Н.И.Лобачевского.–Казань, 2004.– Т.25.–С.267–269.0,188 п.л.
50.Уткина, Е.А. Об одной неклассической задаче для псевдопараболического уравнения/Е.А.Уткина// Вестник Казанского государственного педагогического университета.–2004.–№2.– С.25–31.0,438 п.л.
51.Уткина, Е.А. Об одном уравнении в частных производных высокого порядка с сингулярными коэффициентами/ Е.А.Уткина// Труды второй всероссийской научной конференции «Математическое моделирование и краевые задачи».– Самара, 2005.– Ч. 3. – С.236–239.0,25 п.л.
52.Уткина, Е.А. К развитию метода Лапласа для одного общего трехмерного уравнения/ Е.А.Уткина// Труды международной научной конференции «Современные методы физико-математических наук».– Орел, 2006.– С.126–129.0,25 п.л.
53.Уткина, Е.А. Краевая задача со смещениями в ![]() / Е.А.Уткина// Материалы III международной конференции «Нелокальные краевые задачи и родственные проблемы математической биологии, информатики и физики».–Нальчик: Изд-во «Эльбрус», 2006. –С.118–120.0,188 п.л.
/ Е.А.Уткина// Материалы III международной конференции «Нелокальные краевые задачи и родственные проблемы математической биологии, информатики и физики».–Нальчик: Изд-во «Эльбрус», 2006. –С.118–120.0,188 п.л.
54.Уткина, Е.А. Нелокальная краевая задача для уравнения Бианки в ![]() / Е.А.Уткина// Труды международной конференции «Дифференциальные уравнения и их приложения».– Самара, 2007.–С.45–48.0,25 п.л.
/ Е.А.Уткина// Труды международной конференции «Дифференциальные уравнения и их приложения».– Самара, 2007.–С.45–48.0,25 п.л.
55.Уткина, Е.А. Об одном уравнении в частных производных третьего порядка с сингулярными коэффициентами/ Е.А.Уткина // Вестник Самарского государственного технического университета.–2007.–№5.–С.110–113. 0,25 п.л.
56.Уткина, Е.А. Задача со смещениями в граничных условиях для общего уравнения с оператором Аллера/ Е.А.Уткина// Материалы Восьмой международной Казанской летней научной школы-конференции. Труды Математического центра им. Н.И.Лобачевского.–Казань, 2007.–Т.35.–С.251–253. 0,188 п.л.
57.Уткина, Е.А. Задача со смещениями в граничных условиях для общего псевдопараболического уравнения на плоскости/ Е.А.Уткина// Материалы Шестой молодежной научной школы-конференции «Лобачевские чтения 2007». Труды Математического центра им. Н.И.Лобачевского.–Казань, 2007.– Т.36.– С.229–232.0,25 п.л.
58.Уткина, Е.А.Об одной трехмерной нелокальной задаче для уравнения четвертого порядка/ Е.А.Уткина// Вестник Самарского государственного технического университета. Серия «Математическая».–2007.–№6.– С. 110–115.0,375 п.л.
59.Уткина, Е.А. Задача со смещениями для уравнения пятого порядка в ![]() / Е.А.Уткина// Материалы Международного Российско-Азербайджанского симпозиума «Уравнения смешанного типа и родственные проблемы анализа и информатики».–Нальчик: Изд-во «Эльбрус»,2008.– С.164–166.0,188 п.л.
/ Е.А.Уткина// Материалы Международного Российско-Азербайджанского симпозиума «Уравнения смешанного типа и родственные проблемы анализа и информатики».–Нальчик: Изд-во «Эльбрус»,2008.– С.164–166.0,188 п.л.
60.Уткина, Е.А. Краевая задача со смещениями для четырехмерного уравнения Бианки/ Е.А.Уткина// Труды участников Международной школы-семинара по геометрии и анализу памяти Н.В.Ефимова.–Ростов-на-Дону, 2008.–Секция 3.–С.249–251.0,188 п.л.
61.Уткина, Е.А. Об одном обобщении задачи Гурса/ Е.А.Уткина// Труды международной научной конференции «Дифференциальные уравнения и смежные проблемы», г.Стерлитамак. – Уфа: Изд-во Гилем, 2008. – Т.1. – С.209–215.0,438 п.л.
62.Уткина Е.А. Об одной задаче с интегральным граничным условием для уравнения Бианки в ![]() / Е.А.Уткина// Материалы международной конференции "Современные проблемы математики, механики и их приложений", посвященной 70-летию ректора МГУ академика В.А.Садовничего.–Москва, 2009.– С. 223.0,063 п.л.
/ Е.А.Уткина// Материалы международной конференции "Современные проблемы математики, механики и их приложений", посвященной 70-летию ректора МГУ академика В.А.Садовничего.–Москва, 2009.– С. 223.0,063 п.л.
Публикации [1], [25]–[27], [33]–[38] относятся к периоду работы над кандидатской диссертацией, однако я сочла возможным включить их и в представленный список, поскольку данная диссертация является ее непосредственным развитием. А именно, в ней изучались характеристические задачи (Гурса, ![]() ,
, ![]() ) для обобщений уравнений Аллера и Буссинеска-Лява, а также задача Гурса для (1) при
) для обобщений уравнений Аллера и Буссинеска-Лява, а также задача Гурса для (1) при ![]() .
.
В заключение пользуюсь случаем, чтобы выразить признательность руководителям и участникам семинаров, на которых докладывались результаты диссертации: их вопросы и замечания существенно учитывались затем в моей работе. Я искренне благодарна научному консультанту профессору Валентину Ивановичу Жегалову за постоянное внимание к работе.
[1] Джохадзе О.М.// Дифференциальные уравнения, 2004.-Т.10,№1.-С.58-68.
[2] Матем.сборник, 1958.-Т.451(87), №3.-С.281-322.

