WWW.DISUS.RU

БЕСПЛАТНАЯ НАУЧНАЯ ЭЛЕКТРОННАЯ БИБЛИОТЕКА
 
<< ГЛАВНАЯ [ АГРОИНЖЕНЕРИЯ ] [ АСТРОНОМИЯ ] [ БЕЗОПАСНОСТЬ ] [ БИОЛОГИЯ ] [ ЗЕМЛЯ ] [ ИНФОРМАТИКА ] [ ИСКУССТВОВЕДЕНИЕ ] [ ИСТОРИЯ ] [ КУЛЬТУРОЛОГИЯ ] [ МАШИНОСТРОЕНИЕ ] [ МЕДИЦИНА ] [ МЕТАЛЛУРГИЯ ] [ МЕХАНИКА ] [ ПЕДАГОГИКА ] [ ПОЛИТИКА ] [ ПРИБОРОСТРОЕНИЕ ] [ ПРОДОВОЛЬСТВИЕ ] [ ПСИХОЛОГИЯ ] [ РАДИОТЕХНИКА ] [ СЕЛЬСКОЕ ХОЗЯЙСТВО ] [ СОЦИОЛОГИЯ ] [ СТРОИТЕЛЬСТВО ] [ ТЕХНИЧЕСКИЕ НАУКИ ] [ ТРАНСПОРТ ] [ ФАРМАЦЕВТИКА ] [ ФИЗИКА ] [ ФИЗИОЛОГИЯ ] [ ФИЛОЛОГИЯ ] [ ФИЛОСОФИЯ ] [ ХИМИЯ ] [ ЭКОНОМИКА ] [ ЭЛЕКТРОТЕХНИКА ] [ ЭНЕРГЕТИКА ] [ ЮРИСПРУДЕНЦИЯ ] [ ЯЗЫКОЗНАНИЕ ] [ РАЗНОЕ ] КОНТАКТЫ
Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.

Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.

Авторефераты диссертаций  >>  Авторефераты - Разное

Двойственная геометрия регулярной гиперповерхности в пространстве аффинной связности

На правах рукописи

Христофорова Анастасия Владимировна

ДВОЙСТВЕННАЯ ГЕОМЕТРИЯ

РЕГУЛЯРНОЙ ГИПЕРПОВЕРХНОСТИ

В ПРОСТРАНСТВЕ АФФИННОЙ СВЯЗНОСТИ

01.01.04 – геометрия и топология

Автореферат

диссертации на соискание ученой степени

кандидата физико-математических наук

Казань – 2010

Работа выполнена на кафедре геометрии ГОУ ВПО «Чувашский государственный педагогический университет им. И. Я. Яковлева»

Научный руководитель: доктор физико-математических наук,

профессор

Столяров Алексей Васильевич

Официальные оппоненты: доктор физико-математических наук,

профессор

Малаховский Владислав Степанович

доктор физико-математических наук,

доцент

Толстихина Галина Аркадьевна

Ведущая организация: Нижегородский государственный университет

имени Н. И. Лобачевского

Защита состоится 7 октября 2010 года в ХХ часов ХХ минут на заседании диссертационного совета Д. 212.081.10 при Казанском государственном университете им. В. И. Ульянова-Ленина по адресу: 420008, г. Казань, ул. Профессора Нужина, 1/37, НИИММ, ауд. XXX.

С диссертацией можно ознакомиться в Научной библиотеке имени Н. И. Лобачевского Казанского государственного университета им. В. И. Ульянова-Ленина (г. Казань, ул. Кремлевская, 18).

Автореферат разослан «__» хххххх 2010 г.

Ученый секретарь

диссертационного совета

канд. физ.-мат. наук, доцент Липачев Е. К.

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Постановка вопроса и актуальность темы. Аффинная и в особенности проективная дифференциальная геометрия подмногообразий (поверхностей, распределений) является областью исследований многих геометров с начала XX столетия. Существенные результаты в геометрии гиперповерхности принадлежат Нордену А.П. [15] и его школе; Лаптев Г.Ф. разработал в инвариантной форме дифференциальную геометрию гиперповерхности в многомерном пространстве проективной связности с кривизной и кручением [9]; основные факты аффинной геометрии поверхности были распространены на гиперповерхность (в центроаффинном пространстве) в работах Фернандеса [30] и Лаугвитца [31]; задачи инвариантного оснащения подмногообразия в многомерных пространствах рассматривали А.Е. Либер [13], П.И. Швейкин [26], Г.Ф. Лаптев [12], Н.М. Остиану [16] и другие.

В дифференциальной геометрии подмногообразий важнейшее место занимает теория связностей, берущая начало от работ Т. Леви-Чивита [32] о параллельном перенесении вектора в римановой геометрии. Г. Вейль [33] для построения единой теории поля ввел понятие пространства аффинной связности. В середине ХХ века В. В. Вагнер [5] и Ш. Эресман [29] независимо друг от друга ввели общее понятие связности в расслоенном пространстве. Первые применения связности к геометрии подмногообразий в проективном пространстве дал Э. Картан [28]; дальнейшее развитие теория связностей получает в методе нормализации Нордена А.П. [15], позволяющем в касательных расслоениях подмногообразий проективного пространства индуцировать аффинные связности без кручения. Лаптев Г.Ф., следуя идеям Э. Картана, дал строгое определение пространства аффинной связности [10], [11]. Широков П.А. и Широков А.П. исследовали локальные строения подмногообразия в аффинном пространстве с помощью аффинной связности в касательном расслоении [27]. В работе Рыбникова А.К. [18] рассмотрены некоторые вопросы реализации аффинных связностей на оснащенных гиперповерхностях аффинного пространства.

В настоящее время теория связностей представляет собой обширную область исследования расслоенных пространств благодаря работам Чакмазяна А.В. [25], Лумисте Ю.Г. [14], Евтушика Л.Е. [7], [8], Рашевского П.К. [17], Васильева А.М. [6], Близникаса В.И. [4], Столярова А.В. [21], [22] и других геометров. Теория подмногообразий, погруженных в аффинное пространство и пространство аффинной связности, получила значительное развитие в работах Акивиса М.А. [1], Алшибая Э.Д. [2], [3], Степанова С.Е. [20], Симона У. [19]; вопросами геометрии оснащенной гиперповерхности занимались Столяров А.В. [21], [23] (в пространствах проективном, проективно-метрическом, проективной связности) и его ученики: Долгов С.В. (в проективном пространстве), Глухова Т.Н. (в конформном пространстве).

Предметом исследования диссертационной работы являются подмногообразия, погруженные в пространство аффинной связности, а также связности, индуцируемые оснащением рассматриваемых подмногообразий и поиск приложения связностей к изучению геометрии сетей. Задача сводится к изучению двойственной геометрии указанных оснащенных подмногообразий посредством исследования дифференциально-геометрических структур, индуцированных полями их фундаментальных и оснащающих объектов.

Актуальность диссертационного исследования обусловлена тем, что в нем изучается двойственная геометрия оснащенных подмногообразий в пространстве аффинной связности путем расширения его до пространства проективной связности ; заметим, что такой подход к изучению геометрии подмногообразий в до настоящего времени в математической литературе отсутствовал.



Цель работы. Цель настоящего диссертационного исследования заключается в решении следующих ключевых задач:

  1. построение основ двойственной геометрии гиперповерхности (как голономной, так и неголономной) в пространстве аффинной связности;
  2. построение двойственной теории линейных связностей (аффинных, проективных, нормальных), индуцируемых при различных классических оснащениях (в смысле А.П. Нордена, Э. Картана, Э. Бортолотти) гиперповерхности в пространстве аффинной связности;
  3. приложение двойственной теории линейных связностей к исследованию геометрии сетей на рассматриваемых подмногообразиях (а именно, на гиперповерхности и на распределении гиперплоскостных элементов), вложенных в пространство аффинной связности.

Методы исследования. В диссертационной работе используются инвариантные методы дифференциально-геометрических исследований, а именно, теоретико-групповой метод продолжений и охватов Г.Ф. Лаптева [10], метод внешних дифференциальных форм Э. Картана [24], метод нормализации А.П. Нордена [15]. Применение указанных методов позволило получить дифференциально-геометрические факты, связанные с дифференциальными окрестностями высокого (до четвертого) порядков. Отметим, что результаты по теории линейных связностей получены с применением теории связностей в расслоенных пространствах в форме, данной Г.Ф. Лаптевым [10].

Все результаты получены в минимально специализированной системе отнесения, что позволило получить их в инвариантной форме. Рассмотрения в диссертации проводятся с локальной точки зрения. Все встречающиеся функции предполагаются достаточное число раз дифференцируемыми (то есть изучаемые подмногообразия достаточно гладкие).

Научная новизна. До настоящего времени вопросы двойственной геометрии оснащенных подмногообразий в аффинном пространстве и пространстве аффинной связности математиками не рассматривались. Все результаты, полученные в диссертационном исследовании в ходе решения поставленных задач, являются новыми. В работе приведены доказательства сформулированных в виде теорем всех основных выводов.

Теоретическая и практическая значимость. Диссертационная работа имеет теоретическое значение. Полученные в ней результаты могут быть использованы при исследовании многообразий, погруженных в однородные и обобщенные пространства, а также при изучении пространств с линейной связностью, индуцируемых оснащением рассматриваемых многообразий.

Теория, разработанная в диссертационной работе, может быть использована в качестве специальных лекционных курсов для студентов старших курсов и аспирантов математических факультетов, а также при выполнении ими курсовых, дипломных и научных работ.

Апробация. Основные результаты диссертации докладывались и обсуждались на конференциях и семинарах по современным проблемам геометрии: на конференциях студентов, аспирантов и докторантов Чувашского государственного педагогического университета (Чебоксары, 2006-2009 гг.), на заседаниях научно-исследовательского семинара молодых исследователей по дифференциальной геометрии (Чувашский госпедуниверситет, Чебоксары, 2006-2009 гг.), на региональной конференции «Современные вопросы геометрии и механики деформируемого твердого тела» (Чебоксары, 2006 г.); на заседаниях Молодежной научной школы-конференции «Лобачевские чтения» (Казань, 2008-2009 гг.), XXIV Всероссийского конкурса-конференции научно-исследовательских, творческих и изобретательских работ обучающихся «Национальное достояние России» (работа отмечена серебряным знаком отличия и дипломом I-ой степени победителя конкурса) (Москва, 2009 г.), Международной научной студенческой конференции «Студент и научно-технический прогресс» (Новосибирск, 2009 г.), Международной научной конференции «Лаптевские чтения – 2009» (Москва – Тверь, 2009 г.), на заседании Казанского городского научно-исследовательского геометрического семинара (Казань, КГУ, 2009).

Публикации. Основные результаты диссертации опубликованы в 17 печатных работах автора (см. [1] – [17]).

Вклад автора в разработку избранных проблем. Диссертационная работа является самостоятельным исследованием автора. Все опубликованные научные работы по теме исследования выполнены без соавторов.

Структура и объем работы. Диссертация состоит из введения (исторический обзор, общая характеристика диссертации, содержание диссертации), трех глав и списка литературы, включающего 96 наименований. Полный объем диссертации составляет 110 страниц машинописного текста.

КРАТКОЕ СОДЕРЖАНИЕ ДИССЕРТАЦИИ

Глава I диссертации посвящена построению двойственной геометрии гиперповерхности в пространстве аффинной связности .

В § 1 приводятся основные факты, связанные с геометрией регулярной гиперповерхности в пространстве . Вводится понятие расширенного пространства аффинной связности . Выводится дифференциальное уравнение гиперповерхности , строятся поля фундаментальных и некоторых охваченных геометрических объектов до четвертого порядка включительно. С помощью этих полей в четвертой дифференциальной окрестности точки гиперповерхности в найдено поле соприкасающихся гиперквадрик.

В § 2 доказано, что с регулярной гиперповерхностью в ассоциируются два двойственных пространства проективной связности и (базой служит «тангенциальная гиперповерхность» ).

В § 3 строятся инвариантные классические оснащения регулярной гиперповерхности в пространстве : оснащение в смысле А.П. Нордена, оснащения в смысле Э. Катрана и Э. Бортолотти. Доказано, что

– нормализация одной из регулярных гиперповерхностей или равносильна нормализации другой; при этом найдены соотношения, связывающие компоненты полей оснащающих объектов;

– функции и , определяющие соответственно нормализацию Фубини и Вильчинского регулярной гиперповерхности, задают на ней двойственные поля нормалей первого и второго родов;

– оснащение в смысле Э. Картана регулярной гиперповерхности в пространстве аффинной связности равносильно оснащению ее двойственного образа в смысле Э. Бортолотти, и наоборот; определены зависимости, связывающие оснащающие объекты.





Глава II диссертации посвящена построению основ теории двойственных линейных связностей, индуцируемых на оснащенной регулярной гиперповерхности в пространстве аффинной связности .

В § 1 второй главы изучаются аффинные связности на нормализованной регулярной гиперповерхности в пространстве . Заметим, что в случае вырождения пространства аффинной связности в аффинное пространство изучаемые связности являются двойственными аффинными связностями (без кручения) первого и второго родов, рассмотренными А.П. Норденом [15]. Центральными результатами § 1 являются (теоремы II.1 – II.5):

1) на нормализованной регулярной гиперповерхности в индуцируются две двойственные аффинные связности и , обобщенно сопряженные относительно поля тензора гиперповерхности ; при этом в случае симметрии тензора их средняя связность является вейлевой (вообще говоря, с кручением) с полем метрического тензора ;

2) найдена геометрическая интерпретация условия совпадения связностей и при некоторых предположениях, а именно: если на нормализованной регулярной гиперповерхности в с полем симметричного тензора индуцируются двойственные аффинные связности и без кручения, то эти связности совпадают тогда и только тогда, когда нормализация взаимна относительно поля соприкасающихся гиперквадрик и гиперквадрики этого поля имеют соприкосновение третьего порядка с гиперповерхностью;

3) если нормализация регулярной гиперповерхности в аффинном пространстве взаимна относительно поля соприкасающихся гиперквадрик, то аффинные связности и могут быть эквиаффинными лишь одновременно; в случае их эквиаффинности средняя связность является римановой с полем метрического тензора ;

4) геометрии двойственных аффинных связностей и , индуцируемых нормализацией Фубини регулярной гиперповерхности в аффинном пространстве , являются эквиаффинными, а их средняя геометрия – риманова;

5) если для некоторой взаимной нормализации регулярной гиперповерхности в аффинном пространстве тензоры Риччи связностей и совпадают, то данная нормализация является нормализацией Вильчинского.

В случае аффинной нормализации гиперповерхности показано (теоремы II.6, II.7), что:

1) геометрия связности второго рода является проективно-евклидовой;

2) если полем нормалей первого рода служит поле аффинных нормалей, то связности и одновременно являются эквиаффинными, а их средняя связность – риманова с полем метрического тензора .

В § 2 главы II получены приложения двойственных аффинных связностей и , индуцируемых оснащением в смысле А. П. Нордена регулярной гиперповерхности в пространстве , к геометрии сетей, заданных на . Найдены аналитические условия, при которых сопряженная сеть, заданная на нормализованной гиперповерхности с полем симметричного тензора , является геодезической или чебышевской первого или второго рода. Доказана справедливость следующих утверждений (теоремы II.9, II.9*):

1) если сеть, заданная на регулярной нормализованной гиперповерхности с полем симметричного тензора , вложенной в пространство аффинной связности , является геодезической первого (второго) рода, то поле нормали первого (второго) рода есть поле гармонических прямых (гиперпрямых) сети;

2) сопряженная сеть на регулярной нормализованной гиперповерхности с полем симметричного тензора , вложенной в , является сетью с совпавшими псевдофокусами (псевдофокальными гиперплоскостями) тогда и только тогда, когда относительно поля гармонических гиперпрямых (гармонических прямых ) данная сеть есть геодезическая второго (первого) рода.

В случае аффинного пространства доказано (теоремы II.10, II.11), что:

1) двойственные аффинные связности и , индуцируемые взаимной нормализацией регулярной гиперповерхности , когда полем нормалей второго (первого) рода служит поле гармонических гиперпрямых (прямых) сопряженной чебышевской сети первого (второго) рода, являются эквиаффинными, а их средняя геометрия – риманова;

2) если гиперповерхность , несущая голономную сопряженную сеть с совпавшими псевдофокусами и псевдофокальными гиперплоскостями, нормализована полями гармонических прямых и гиперпрямых сети, то индуцируемые аффинные связности и являются эквиаффинными, а их средняя геометрия – риманова.

В § 3 главы II диссертации изучаются двойственные проективные связности на оснащенной в смысле Э. Картана и Э. Бортолотти регулярной гиперповерхности в пространстве аффинной связности .

Доказано (теорема II.13, II.15), что оснащение в смысле Э. Картана (Э. Бортолотти) регулярной гиперповерхности в индуцирует две двойственные проективные связности (вторая проективная связность определяется в случае симметрии тензора ); соответствующие пространства проективной связности обозначены и ( и ). Справедливы утверждения (теоремы II.12, II.14, II.15):

1) оснащающая точка гиперповерхности в аффинном пространстве неподвижна тогда и только тогда, когда является плоским;

2) необходимым и достаточным условием совпадения связностей двойственных пространств и ( и ) является вырождение гиперповерхности в гиперквадрику.

3) в случае пространство является проективным тогда и только тогда, когда оснащающая плоскость неподвижна.

В § 4 установлена связь между двойственными аффинными и проективными связностями на оснащенной регулярной гиперповерхности в с полем симметричного тензора . Показано, что:

1) на оснащенной в смысле Э. Картана гиперповерхности в кроме пространства индуцируется еще четыре пространства проективной связности ; найдены строения компонентов их тензоров кривизны-кручения;

2) на нормализованной гиперповерхности в индуцируется пять пространств аффинной связности , причем связностью пространства является аффинная связность . Найдены строения компонентов тензоров кривизны и кручения указанных пространств.

Основным результатом параграфа является теорема II.17: на оснащенной в смысле Нордена-Картана регулярной гиперповерхности каждое пространство аффинной связности при фиксированном является сужением соответствующего пространства проективной связности ; причем в случае сужением пространства является пространство аффинной связности , определяемое системой форм:

.

В § 5 рассматриваются двойственные нормальные связности на оснащенной регулярной гиперповерхности .

В п. 1 § 5 доказано, что на нормализованной гиперповерхности в расслоении нормалей первого и второго родов индуцируются соответственно нормальные связности и , двойственные по отношению друг к другу (при этом нормализация предполагается отличной от аффинной). Справедливы следующие предложения (теоремы II.19–II.22, II.24, II.25):

1) связности и могут быть полуплоскими, а в случае – плоскими лишь одновременно;

2) связности и совпадают тогда и только тогда, когда нормальная связность (а следовательно, и ) полуплоская;

3) для того, чтобы нормальная связность (), индуцируемая на нормализованной гиперповерхности , была плоской, необходимо и достаточно, чтобы конгруэнция (псевдоконгруэнция) нормалей первого (второго) рода и псевдоконгруэнция (конгруэнция) нормалей второго (первого) рода составляли пару, односторонне расслояемую в сторону от нормалей первого (второго) рода к нормали второго (первого) рода;

4) на нормализованной гиперповерхности поле нормалей первого рода является параллельным в нормальной связности , а поле нормалей второго рода является параллельным в нормальной связности .

В п. 2 § 5 рассматриваются нормальные связности на оснащенной в смысле Нордена-Картана и Нордена-Бортолотти гиперповерхности с полем симметричного тензора в пространстве аффинной связности .

Одним из основных результатов являются теоремы II.26 и II.31: на оснащенной в смысле Нордена-Картана (Нордена-Бортолотти) регулярной гиперповерхности с полем симметричного тензора в расслоении нормалей первого (второго) рода, кроме (), индуцируются еще четыре нормальные связности .

Найдены условия попарного совпадения рассматриваемых нормальных связностей и условия вырождения любой тройки нормальных связностей в одну; например (теоремы II.28, II.29):

1) нормальные связности и , и , индуцируемые в расслоении нормалей первого рода на оснащенной в смысле Нордена-Картана гиперповерхности , совпадают тогда и только тогда, когда нормализация гиперповерхности является взаимной;

2) на оснащенной в смысле Нордена-Картана гиперповерхности совпадение любой тройки нормальных связностей из совокупности равносильно одному из следующих предложений:

а) нормализация гиперповерхности есть нормализация Фубини,

б) рассматриваемая четверка нормальных связностей вырождается в одну.

Справедливы двойственные предложения (теоремы II.33, II.34).

Доказаны следующие утверждения:

1) связность (), индуцируемая нормализацией Фубини гиперповерхности , является полуплоской.

2) если на оснащенной в смысле Нордена-Картана гиперповерхности , несущей голономную сеть с совпавшими псевдофокусами и псевдофокальными гиперплоскостями, полями нормализующих объектов являются поля гармонических прямых и гиперпрямых сети, то нормальные связности являются полуплоскими.

3) если на оснащенной в смысле Нордена-Бортолотти гиперповерхности все нормали второго рода лежат в одной гиперплоскости, то индуцируемые нормальные связности , являются плоскими тогда и только тогда, когда они полуплоские;

4) если нормальные связности и ( и ), индуцируемые в расслоении нормалей первого (второго) рода на оснащенной в смысле Нордена-Картана (Нордена-Бортолотти) гиперповерхности , совпадают, то средняя аффинная связность является римановой.

Глава III диссертации посвящена изучению двойственной геометрии оснащенного регулярного распределения гиперплоскостных элементов в пространстве аффинной связности .

В § 1 вводится понятие распределения гиперплоскостных элементов, погруженного в пространство аффинной связности. В репере нулевого порядка выводятся дифференциальные уравнения распределения , а также строятся поля фундаментальных геометрических объектов до третьего порядка включительно. Доказано (теорема III.1), что регулярное распределение гиперплоскостных элементов в индуцирует:

– во второй дифференциальной окрестности пространство проективной связности , двойственное относительно инволютивного преобразования их форм связности, причем пространства и могут быть плоскими лишь одновременно;

– в первой дифференциальной окрестности многообразие в , двойственное исходному распределению .

В п. 3 § 1 рассматривается оснащенное в смысле А. П. Нордена распределение гиперплоскостных элементов в . Доказано, что нормализация одного из регулярных распределений гиперплоскостных элементов в или в равносильна нормализации другого.

Основной результат § 2 главы III содержится в теореме III.3: для того чтобы при задании регулярного распределения гиперплоскостных элементов в индуцировалось пространство аффинной связности , двойственное исходному , необходимо и достаточно, чтобы слоевые формы пространства обращались в нуль; при этом пространства и могут быть плоскими лишь одновременно.

Геометрическое истолкование условия существования пространства , двойственного , заключается в теореме III.4: для того чтобы при задании регулярного распределения гиперплоскостных элементов в индуцировалось пространство аффинной связности , двойственное исходному, достаточно, чтобы направление A0An в связности пространства переносилось параллельно вдоль любой кривой пространства .

Найдено аналитическое условие, в случае выполнения которого при задании регулярного распределения гиперплоскостных элементов в двойственные аффинные связности (подсвязности), определяемые соответственно системами структурных форм и двойственных пространств и , являются обобщенно сопряженными относительно поля тензора вдоль любой кривой пространства аффинной связности .

Основные результаты § 3 главы III отражены в следующих предложениях (теоремы III.6 – III.10):

1) на нормализованном регулярном распределении в индуцируются две двойственные аффинные связности и , обобщенно сопряженные относительно поля тензора вдоль любой кривой, принадлежащей распределению в ; при некоторых предположения найдено условие их совпадения (теорема III.7).

2) нормализация регулярного распределения в индуцирует двойственные пространства аффинной связности и , определяемые соответственно системами форм и 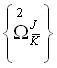(теорема III.8);

3) аффинная связность и связность 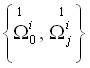совпадают тогда и только тогда, когда направление нормали первого рода в связности пространства переносится параллельно вдоль любой кривой, принадлежащей распределению в ; при этом нормальная точка нормали совпадает с ее точкой Кенигса;

4) направление нормали первого рода распределения гиперплоскостных элементов в () обладает свойством абсолютного параллелизма относительно связности пространства тогда и только тогда, когда точка Кенигса этой нормали неподвижна.

ОСНОВНЫЕ РЕЗУЛЬТАТЫ ДИССЕРТАЦИИ,

ВЫНОСИМЫЕ НА ЗАЩИТУ

1. Для данного пространства аффинной связности введено понятие расширенного пространства . В разных дифференциальных окрестностях построены инвариантные внутренним образом определяемые оснащения регулярной гиперповерхности и распределения гиперплоскостных элементов в пространстве аффинной связности .

2. Построены основы теории двойственных линейных связностей (аффинных, проективных и нормальных), индуцируемых различными оснащениями гиперповерхности в (оснащениями в смысле А.П. Нордена, Э. Картана, Э. Бортолотти).

3. Найдено приложение двойственных аффинных связностей и к изучению внутренней геометрии некоторых классов сопряженных сетей на гиперповерхности в (чебышевских и геодезических сетей первого и второго родов, сетей с совпавшими псевдофокусами и псевдофокальными гиперплоскостями).

4. При задании регулярного распределения гиперплоскостных элементов в пространстве найдено условие существования пространства аффинной связности , двойственного исходному пространству ,

5. Исследована геометрия двойственных аффинных связностей, индуцированных нормализацией регулярного распределения гиперплоскостных элементов в .

Список литературы

  1. Акивис М. А. К аффинной теории соответствия Петерсона между гиперповерхностями / М. А. Акивис // Известия вузов. Математика. – Казань, 1994. – № 4. – С. 3-9.
  2. Алшибая Э. Д. К геометрии распределений гиперплоскостных элементов в аффинном пространстве / Э. Д. Алшибая // Тр. Геометр. семинара. Ин-т научн. информ. АН СССР. – 1974. – Т. 5. – С. 169-193.
  3. Алшибая Э. Д. Об аффинных связностях на распределении гиперплоскостных элементов в / Э. Д. Алшибая // Известия вузов. Математика. – Казань, 2002. – № 8. – С. 72-74.
  4. Близникас В. И. Некоторые внутренние геометрии гиперповерхности пространства аффинной связности / В. И. Близникас // Liet. mat. rinkinys, Лит. мат. сб. – 1964. – Т. 4. – № 2. – С. 165-182.
  5. .Вагнер В. В. Теория составного многообразия / В. В. Вагнер // Тр. семинара по векторн. и тензорн. анализу. – 1950. – В. 8. – С. 11-72.
  6. Васильев А. М. Инвариантные аффинные связности в пространстве линейных элементов / А.М. Васильев // Матем. сб. – 1963. – Т. 6. – № 4. – С. 411-424.
  7. .Евтушик Л. Е. Дифференциально-геометрические структуры на многообразиях / Л. Е. Евтушик, Ю. Г. Лумисте, Н. М. Остиану, А. П. Широков // Проблемы геометрии. Итоги науки и техники. ВИНИТИ АН СССР. – 1979. – Т. 9. – 246 с.
  8. Евтушик Л. Е. Дифференциальные связности и инфинитезимальные преобразования продолженной псевдогруппы / Л. Е. Евтушик // Тр. Геометр. семинара. Ин-т научн. информ. АН СССР. – 1969. – Т. 2. – С. 119-150.
  9. .Лаптев Г. Ф. Гиперповерхность в пространстве проективной связности / Г. Ф. Лаптев // Докл. АН СССР. – 1958. – Т. 121. – № 1. – С. 41-44.
  10. Лаптев Г. Ф. Дифференциальная геометрия погруженных многообразий / Г. Ф. Лаптев // Труды Моск. матем. общества. – 1953. – Т. 2. – С. 275-382.
  11. Лаптев Г. Ф. О выделении одного класса внутренних геометрий, индуцированных на поверхности пространства аффинной связности / Г. Ф. Лаптев // ДАН СССР. – 1943. – Т. 41. – № 8. – С. 329-331.
  12. Лаптев Г. Ф. Об инвариантном оснащении поверхности в пространстве аффинной связности / Г. Ф. Лаптев // Докл. АН СССР. – 1959. – № 3. – С. 490-493.
  13. Либер А. Е. О геометрии поверхностей в аффинных пространствах // А. Е. Либер // Научн. ежегодник. – Саратовск. гос. ун-т, 1955. – С. 669-671.
  14. Лумисте Ю. Г. Индуцированные связности в погруженных проективных и аффинных расслоениях / Ю. Г. Лумисте // Уч. зап. Тартуск. ун-та. – 1965. – В. 177. – С. 6-42.
  15. Норден А. П. Пространства аффинной связности / А. П. Норден. – М.: Наука, 1976. – 432 с.
  16. Остиану Н. М. Об инвариантном оснащении многомерной поверхности в проективном пространстве / Н. М. Остиану // Тезисы докл. Второй Всес. геом. конф. – Харьков, 1964. – С. 203.
  17. Рашевский П. К. Симметрические пространства аффинной связности с кручением. I. / П. К. Рашевский // Тр. сем. по векторн. и тензорн. анализу. – 1950. – В. 8. – С. 82-92.
  18. Рыбников А. К. Аффинные связности, индуцируемые на многомерных поверхностях аффинного пространства / А. К. Рыбников // Тр. Геометр. семинара. Ин-т научн. информ. АН СССР. – 1974. – Т. 6. – С. 135-155.
  19. Симон У. К аффинной теории гиперповерхностей: калибровочно-инвариантные структуры / У. Симон // Известия вузов. Математика. – Казань, 2004. – № 11. – С. 53-81.
  20. Степанов С. Е. Реализация чебышевской связности на гиперповерхности аффинного пространства / С. Е. Степанов // Соврем. геометрия : Вопросы дифференц. геометрии. – Л. – 1980. – С. 73-76.
  21. Столяров А. В. Двойственная теория оснащенных многообразий / А. В. Столяров. – Чебоксары, 1994. – 290 с.
  22. Столяров А. В. Двойственная геометрия нормализованного пространства аффинной связности / А. В. Столяров // Вестник Чувашск. гос. пед. ун-та. – 2005. – № 4. – С. 21 – 27.
  23. Столяров А. В. О сетях и полярно сопряженных конфигурациях на гиперповерхностях проективного пространства / А. В. Столяров // Изв. вузов. Матем. – 1970. – № 7 – С. 96-101.
  24. Фиников С. П. Метод внешних форм Картана / С. П. Фиников. – М.: ГИТТЛ, 1948. – 432 с.
  25. Чакмазян А. В. Нормальная связность в геометрии подмногообразий / А. В. Чакмазян. – Ереван: Армянск. пед. ин-т, 1990. – 116 с.
  26. Швейкин П. И. Инвариантные построения на m-мерной поверхности в n-мерном аффинном пространстве / П. И. Швейкин // Докл. АН СССР. – 1958. – № 5. – С. 811-814.
  27. Широков П. А. Аффинная дифференциальная геометрия / П. А. Широков, А. П. Широков. – М.: Физ-матем. изд., 1959.
  28. Cartan E. Les spaces a connexion projective – Труды семинара по векторному и тензорному анализу / E. Cartan. – МГУ, 1937. – № 4. – С. 147-159.
  29. Ehresmann C. Les connections infinitesimales dans un espace fibre differentiable / C. Ehresmann // Collque de Topologie. – Bruxelles, 1950. –P. 29-55.
  30. Fernndez G. Geometria differencial afin hipersperficies / G. Fernndez // Rev. Unin mat. argent. y Asoc. fis. argent. 1955. 17. 29-38.
  31. Laugwitz D. Zur Differential geometrie der Hyperflchen in Vektorrumen und zur affingeometrischen Deutung der Theorie der Finsler-Rume. Math. Z. 1957. 67. V. 1. 63-74.
  32. Levi-Civita T. Nozioni di parallelismo in una varieta qualunque e conseguente specificazione geometrica della curvature Riemannianna / Levi-Civita T. // Rend. circ. vatem. – Palermo, 1917. – V. 42. – P. 173-205.
  33. Weyl H. Raum, Zeit, Materie / H. Weyl. – Berlin, 1918.

РАБОТЫ АВТОРА, ОПУБЛИКОВАННЫЕ ПО ТЕМЕ ДИССЕРТАЦИИ

  1. Христофорова А. В. Двойственная геометрия гиперповерхности в пространстве аффинной связности / А. В. Христофорова // Вестник Чувашск. гос. пед. ун-та. – 2006. – № 3(50). – С.35 – 42.
  2. Христофорова А. В. Двойственная геометрия сетей на гиперповерхности в пространстве аффинной связности / А. В. Христофорова // Дифференциальная геометрия многообразий фигур. Вып.39 : Межвуз. темат. сб. науч. тр. – Калининград, 2008. – С. 140-147.
  3. Христофорова А. В. Двойственность геометрии гиперповерхности в пространстве аффинной связности / А. В. Христофорова // Материалы Шестой молодежной науч. школы-конф. – Казань : Изд-во Казанского мат. об-ва, 2007. – Т. 36. – С. 238–241.
  4. Христофорова А. В. Двойственность геометрии распределения гиперплоскостных элементов в пространстве аффинной связности / А. В. Христофорова // ВИНИТИ РАН. – 2009. – № 28-В2009 Деп. – 20 с.
  5. Христофорова А. В. Двойственные аффинные связности на нормализованной гиперповерхности в пространстве аффинной связности / А. В. Христофорова // ВИНИТИ РАН. – 2008. – № 237-В2008 Деп. – 13 с.
  6. Христофорова А. В. Двойственные аффинные связности на распределении гиперплоскостных элементов в пространстве аффинной связности / А. В. Христофорова // Материалы Седьмой молодежной науч. школы-конф. – Казань : Изд-во Казанского мат. об-ва, 2008. – Т. 37. – С. 186-189.
  7. Христофорова А. В. Двойственные линейные связности на оснащенной гиперповерхности пространства аффинной связности / А. В. Христофорова // Известия вузов. Математика. – Казань, 2009. – № 11. – С. 72-79.
  8. Христофорова А. В. Двойственные проективные связности на гиперповерхности в пространстве аффинной связности / А. В. Христофорова // Вестник докторантов, аспирантов, студентов Чув. гос. пед. ун-та. – Чебоксары, 2008. – № 1(11). – С. 30-35
  9. Христофорова А. В. Двойственные пространства аффинной связности на распределении гиперплоскостных элементов в пространстве аффинной связности / А. В. Христофорова // Дифференциальная геометрия многообразий фигур. Вып.40 : Межвуз. темат. сб. науч. тр. – Калининград, 2009. – С. 137-144.
  10. Христофорова А. В. Двойственные пространства аффинной связности, определяемые неголономной гиперповерхностью / А. В. Христофорова // Вестник Чувашск. гос. пед. ун-та. – 2009. – № 1(61). – С.36 – 43.
  11. Христофорова А. В. Двойственные связности на гиперповерхности / А. В. Христофорова // Труды XLVII Межд. науч. студ. конф. «Студент и НТП»: Математика. – Новосибирск, 2009. – С. 104-105.
  12. Христофорова А. В. Исследование гиперповерхности в пространстве аффинной связности / А. В. Христофорова // Вестник Чувашск. гос. пед. ун-та. – 2008. – № 2(58). – С.46 – 52.
  13. Христофорова А. В. Линейные связности, индуцируемые оснащением гиперповерхности пространства аффинной связности / А. В. Христофорова // Сб. тезисов докладов участников XXIV Всерос. конф. обуч-ся «Национальное Достояние России». – Минобрнауки РФ, Рособразование, РОСКОСМОС, РАО, НС «Интеграция», 2009. – С. 725-726
  14. Христофорова А. В. О двойственной геометрии гиперповерхности в пространстве аффинной связности / А. В. Христофорова // ВИНИТИ РАН. – 2006. – № 713-В2006 Деп. – 10 с.
  15. Христофорова А. В. О двойственной геометрии распределения гиперплоскостных элементов в пространстве аффинной связности / А. В. Христофорова // Труды Межд. науч. конф. «Лаптевские чтения-2009». – М., 2009. – С.37.
  16. Христофорова А. В. Проективные и аффинные связности на гиперповерхности пространства аффинной связности / А. В. Христофорова // ВИНИТИ РАН. – 2009. – № 412-В2009 Деп. – 17 с.
  17. Христофорова А. В. Фундаментально-групповые линейные связности на гиперповерхности в пространстве аффинной связности / А. В. Христофорова // ВИНИТИ РАН. – 2008. – № 910-В2008 Деп. – 31 с.

Подписано к печати ______________. Формат 6084 / 16.

Бумага ксероксная. Печать трафаретная.

Усл. печ. л. 1. Тираж 100 экз. Заказ ____.

Отдел оперативной полиграфии

Чувашского государственного педагогического университета

428000, г. Чебоксары, ул. К. Маркса, 38.



 
Авторефераты диссертаций  >>  Авторефераты - Разное




наверх

<
 
<<  ГЛАВНАЯ   |    КОНТАКТЫ
2013 www.disus.ru - «Бесплатная научная электронная библиотека»

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.