Структурно алгоритмическая обработка сигналов хроматографа с сигма дельта аналого цифровым преобразованием
На правах рукописи
ДОАН ВАН ХОА
СТРУКТУРНОАЛГОРИТМИЧЕСКАЯ ОБРАБОТКА СИГНАЛОВ
ХРОМАТОГРАФА С СИГМАДЕЛЬТА АНАЛОГОЦИФРОВЫМ
ПРЕОБРАЗОВАНИЕМ
05.11.13 – Приборы и методы контроля природной среды,
веществ, материалов и изделий
АВТОРЕФЕРАТ
диссертации на соискание учёной степени
кандидата технических наук
МОСКВА 2010
Работа выполнена в Московском государственном университете инженерной экологии, на кафедре мониторинга и автоматизированных систем контроля.
Научный руководитель – доктор технических наук, профессор
Латышенко Константин Павлович.
Научный консультант – доктор технических наук
Гайтова Тамара Борисовна.
Официальные оппоненты: доктор технических наук, профессор
Пушкин Игорь Александрович;
кандидат технических наук
Чернякин Владимир Николаевич.
Ведущая организация – НПО «Химавтоматика», г. Москва.
Защита диссертации состоится 28 октября 2010 года в 15.30 в аудитории В-23 на заседании диссертационного совета Д 212.145.02 в Московском государственном университете инженерной экологии по адресу: 105066, Москва, ул. Старая Басманная, 21/4.
С диссертацией можно ознакомиться в библиотеке университета.
Отзывы в двух экземплярах, заверенные печатью, просим направлять по адресу: 105066 г. Москва, ул. Старая Басманная, 21/4.
Автореферат разослан 27 сентября 2010 года.
Учёный секретарь
диссертационного совета
кандидат технических наук, доцент Н.В. Мокрова
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы. Хроматографический анализ природной среды, веществ и материалов в настоящее время стал одним из основных методов при анализе сложных смесей, вытеснив во многих случаях другие методы.
В последнее время особое внимание уделяется вопросам совершенствования процесса измерения и обработки данных хроматографического анализа, в том числе улучшению метрологических характеристик химико-аналитических комплексов (ХАК).
Метрологические параметры ХАК зависят от собственно хроматографа и цифровой части, в которой аналого-цифровой преобразователь (АЦП) играет важную роль. Во-первых, из-за сложности конструктивного исполнения хроматографа для повышения точности измерения требуется использовать дорогостоящие приборы в хроматографе. Во-вторых, точность разделения пиков и определения их площади, коррекция базисной линии, фильтрация, вычисление погрешностей и т.п. в значительной степени зависит от точности АЦП. Из-за особенностей сигналов хроматографического анализа правильность выбора АЦП и режима его работы является нетривиальной задачей.
В настоящее время многие разработчики в области хроматографии используют сигма-дельта АЦП (СДАЦП) для регистрации и обработки сигналов хроматографического анализа. Однако, научное обоснование применения такого типа преобразования для их регистрации и обработки остается недостаточным.
Каждый год исследования принципа работы сигма-дельта модулятора (СДМ) и СДАЦП освещаются и представляются на международных конференциях IEEЕ, «Информационные средства и технологии», «Радиоэлектроника, электроника и энергетика» и др. Большой вклад в решение этих проблем внесли российские Шахов Э.К., Диденко В.И., Солодов Ю.С. и зарубежные учёные Benabes, Alderebt, Kielbasa, Gomes Cama, Bota, Montana, Smitier и др.
СДМ, СДАЦП предоставляют интерес для современной измерительной техники. При этом погрешность квантования информативного сигнала является неотъемлемой частью СДАЦП, она непосредственно влияет на его точность и, следовательно, на точность хроматографического анализа.
Примерами современных хроматографических ХАК служат: комплекс JSC «Lcad», содержащий АЦП с линейным динамическим диапазоном преобразования аналогового сигнала в цифровой – не менее 106 (разрядность преобразования – не менее 22 бит) при частоте выдачи данных 5 Гц, комплекс программно-аппаратный хроматографический «ZXPOM» содержащий СДАЦП, у которого эффективное число разрядов равно 20 при частоте выдачи данных 10 Гц и динамический диапазон около 106, отечественные ИНЛАН-ИХ, ИНЛАН-ГХ и др. Приведённые диапазоны не покрывают диапазона сигналов на выходе современных хроматографов. Следовательно, проблема улучшения динамического диапазона АЦП является актуальной для хроматографического анализа.
Целью диссертационной работы является решение актуальной научно-технической задачи структурно-алгоритмической обработки сигналов хроматографов с сигма-дельта аналого-цифровым преобразованием, заключающейся в исследование сигма-дельта аналого-цифрового преобразования, разработке на этой основе и внедрения устройства сопряжения между хроматографом и компьютером для регистрации и обработки хроматографических сигналов с улучшенными метрологическими и эксплуатационными характеристиками.
Основные задачи диссертационной работы. Для достижения поставленной цели в работе решались следующие задачи:
- разработка математической модели СДМ и СДАЦП;
- исследование и сравнение СДМ первого и второго порядков с целью получения более высокой точности СДАЦП;
- анализ параметров хроматографических сигналов (ХС) и их погрешностей;
- разработка и создание на основе проведённых исследований устройства сопряжения ПФИ-24;
- анализ погрешностей устройства сопряжения ПФИ-24.
Методы исследования. Для решения поставленных задач использованы методы системного анализа, математического моделирования, математические методы обработки результатов (метод скользящего усреднения, наименьших квадратов, полиномиальной фильтрации и т.п.). Для моделирования по разработанным программам, реализующим предложенные методы, использованы пакеты программ MATLAB и Delphi.
Основные результаты и положения, выносимые на защиту:
- структурные схемы СДМ и СДАЦП, обеспечивающие высокую точность преобразования;
- математические модели СДМ и цифрового фильтра (ЦФ), анализ погрешностей при формировании ХС;
- математические модели сигналов ХС с использованием СДАЦП;
- способ улучшения метрологических характеристик СДАЦП в процессе регистрации и обработки ХС.
Научная новизна работы заключается в следующем:
- исследована зависимость точности регистрации сигналов хроматографической информации от свойств и режима работы СДАЦП. Доказано, что режим работы СДАЦП с устройством выборки-хранения (УВХ) даёт меньшую погрешность при измерении параметров ХС, но слабее подавляет высокочастотные помехи;
- показано, что повышенная точность СДАЦП определяется эффектом отрицательной корреляции между элементами кодов на выходе СДМ;
- установлено, что СДМ второго порядка обеспечивает более высокую точность СДАЦП при применении трёхзвенного ЦФ скользящего усреднения вместо однозвенного. Использование ЦФ первого порядка для СДМ первого порядка даёт не намного большую точность, чем для СДМ второго порядка;
- предложен способ увеличения динамического диапазона измерений СДАЦП при обработке сигналов хроматографа
Достоверность. Результаты аналитических исследований подтверждаются результатами компьютерного моделирования и физического эксперимента. Эксперименты были проведены на физической установке сигма-дельта АЦП модели ADS1242.
Практическая ценность работы. Практическая ценность работы состоит в разработке математических моделей СДМ и ЦФ, которые могут быть применены для моделирования любого этапа работы АЦП.
Разработано устройство сопряжения ПФИ-24 с улучшенными метрологическими и эксплуатационными характеристиками.
Реализация результатов. Результаты данной работы реализованы ООО «ИНФОРХРОМ» и использованы другими предприятиями и организациями, разрабатывающими приборы для газовой и жидкостной хроматографии (НПО «Химавтоматика», ВНИИХром и т.д.).
Апробация работы. Основные положения и результаты диссертации доложены и обсуждены на междунароной нучно-технической конференции «Информационные средства и технологии» (2008 г.), «Радиотехника, радиоэлектроника и энергетика» (2006, 2008, 2009 г.) МЭИ (ТУ), МГУИЭ (2010 г.).
Публикации. По теме диссертационной работы опубликовано 6 работ, в том числе две статьи в журналах, рекомендованных ВАК.
Структура и объём диссертации. Диссертационная работа состоит из введения, четырёх глав, выводов, списка литературы и приложений. Общий объём работы составляет 156 страниц, в том числе 39 рисунков и 9 таблиц. Список литературы включает в себя 93 наименования.
ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ
Во введении показана актуальность темы и практическая значимость работы, приведены её цель и задачи, сформулированы научная новизна и практическая ценность, а также результаты их реализации и апробации.
В первой главе проведён анализ работ и состояние современной хроматографии, показана значимость хроматографического метода для различных отраслей промышленности, научных исследований и охраны окружающей среды. Рассмотрено математическое описание выходного сигнала хроматографа, его модели и параметры, источники погрешностей в аналитической части и модели хроматографических пиков. Проанализирована фильтрация ХС, отмечены особенности и недостатки каждого вида фильтрации, технические требования к АЦП для автоматического анализа ХС.
Во второй главе построены структурные схемы СДМ и ЦФ для компьютерного моделирования (рис. 1). Проведён ряд компьютерных исследований СДМ и СДАЦП разных порядков.
Рис. 1. Структурная схема модели СДМ с переносом зарядов
первого (а) и второго (б) порядков: M умножитель, обеспечивающий
устойчивость работы СДМ 2-го порядка; Z1 – элемент задержки
Пусть X нормированный цифровой сигнал (последовательность чисел) на входе СДМ. Причём, 
, где UX напряжение на входе СДМ, U0 – опорное напряжение, |X| < 1. Выходной сигнал СДМ W равен 1 при отрицательном сигнале на входе компаратора и –1 при положительном, т.е. код на его выходе 1 и –1.
Информативным параметром выходного сигнала СДМ является вероятность возникновения +1 в последовательности чисел (импульсов) на его выходе. В любой момент времени W = 1 с вероятностью P или W= 1 с вероятностью (1 P). При этом:
X = M[W] = 2P 1. (1)
При начальных условиях, когда Y = X = 0, информация не снимается.
Математическая модель СДМ первого (2) и второго порядков (3) имеет вид:
X = Xi; Yi = Yi1 + Xi Wi1 Wi= 1 при Yi>0, иначе Wi= 1, (2)
Zi = M Yi1; Ui = Ui1 + Zi Wi1; Wi = 1
при Ui > 0, иначе Wi = 1, где i такт. (3)
При i = L на выходе СДМ образуется последовательность положительных или отрицательных единиц длиной L, несущая закодированную информацию о входном сигнале. Для декодирования этой информации на выходе преобразователя находится ЦФ скользящего усреднения (рис. 2), который выделяет сигнал X из кодовой последовательности длиной N на выходе СДМ, сумма чисел в регистре.
| 1 | 2 | 3 | N |
| 1 | 2 | 3 | N |
| 1 | 2 | 3 | N |
Выход ЦФ
Рис. 2. Структурная схема трёхзвенного ЦФ скользящего усреднения
Амплитудно-частотная характеристика ЦФ:
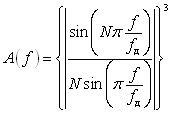, (4)
где fд частота дискретизации, f – частота сигнала.
Чем больше порядок ЦФ, тем лучше он подавляет помехи, но тем дольше время его установления. Например, подавление помех трёхзвенного ЦФ при отклонении частоты режекции ±1 % составляет 120 дБ, а не 40 дБ, как подавление однозвенного ЦФ (рис. 3). При этом полоса пропускания на уровне 3 дБ уменьшается всего лишь в 1,5 раза.
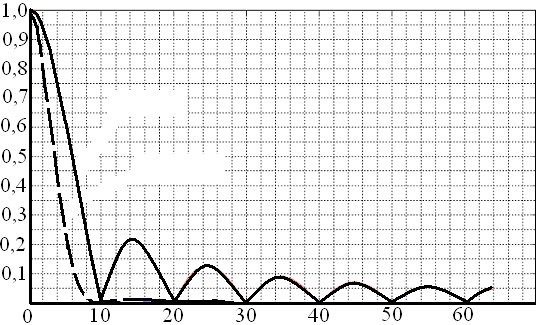
Рис. 3. АЧХ одно- и трёхзвенного ЦФ скользящего усреднения
Проведены исследования последовательности данных, выдаваемых СДМ при подаче на вход случайного постоянного сигнала, откуда следует, что СКО шума уменьшается при увеличении длины отрезка усреднения. Теоретически доказано, что если случайная величина статически независимая, то при удвоении длины усреднения, СКО уменьшается в 
раз. Уменьшение СКО шума в 2 раза означает, что последовательные коды на выходе СДМ статически зависимы, причём корреляционный момент отрицателен. Это говорит о том, что если на выходе СДМ +1, то вероятность возникновения следующей 1 на выходе больше, чем возникновения +1 и наоборот. СКО зависит не только от длины отрезка усреднения, но и от значений входного сигнала. Для модуляторов первого и второго порядка они практически одинаковы при одинаковой длине отрезка усреднения. Можно сделать вывод, что характер поведения данных на выходе СДМ одинаков для обоих модуляторов. Полученные результаты шума квантования в СДМ первого и второго порядка показывают, что использование вероятностного информативного параметра не даёт предполагаемого преимущества СДМ 2-го порядка перед СДМ 1-го порядка.
Формула для приближённого расчёта СКО шума квантования в СДМ:
, (5)
где n – порядок СДМ; K – коэффициент децимации.
Для СДМ первого порядка при n = 1, K = 128 (параметры взяты для СДМ AD7714 фирмы Analog Devices) получаем кв = 2,56·10–4. Для СДМ второго порядка при n = 2, K = 128, кв = 3,76·10–6. Реальные значения СКО шума квантования получены следующим путём: биты с выхода модулятора поступают на вход ЦФ скользящего усреднения с некоторой частотой, а на его выходе данные регистрируются с частотой в 128 раз реже. Проведён эксперимент на моделях СДМ с двух- и трёхзвенным ЦФ скользящего усреднения и получены значения СКО шума квантования (рис. 4).
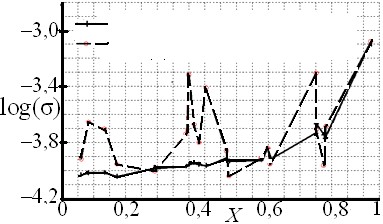
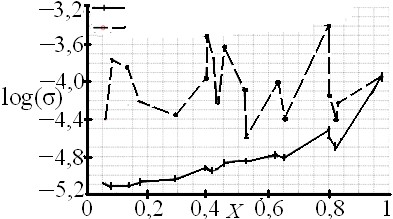
Рис. 4. СКО шума при усреднении выходного сигнала СДМ двухзвенным (а) и трёхзвенным (б) ЦФ скользящего усреднения для 20 случайных входных значений от 0 до 1
Расчётные значения СКО шума квантования для СДМ с однозвенным ЦФ и K = 128, совпадает с результатами, рассчитанными по формуле (5). Расхождение для СДМ второго порядка получилось больше, чем для первого. Это объясняется тем, что формула (5) даёт приблизительный результат, в котором не учтены особенности схемы СДМ, корреляции на его выходе и т.д. Использование СДМ высшего порядка лучше только при применении ЦФ, порядок которого выше порядка СДМ. Здесь проявляется общая особенность СКО шума квантования для модулятора второго порядка оно растёт при увеличении входного сигнала. Модулятор второго порядка обладает большей разрешающей способностью при условии его периодического обнуления. СДМ производит неравномерное квантование.
Проведено исследование СКО на модели СДМ при входном линейно изменяющемся сигнале (рис. 5).
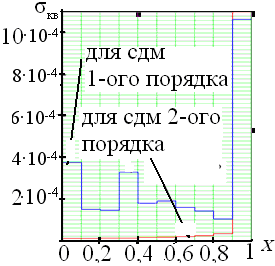
Рис. 5. Зависимость СКО шума СДМ от входного сигнала
На графике показано, что для СДМ и первого и второго порядка наибольшие значения погрешностей, математического ожидания и СКО шума лежат в конце диапазона измерений. Погрешность СДМ второго порядка меньше, чем первого в несколько раз (за исключением последнего поддиапазона). Отсюда можно заключить, что СДМ второго порядка работает для линейно изменяющихся сигналов точнее, чем СДМ первого порядка.
В третьей главе исследованы регистрация и обработка ХС с применением СДАЦП. При регистрации и обработке ХС с помощью СДАЦП необходимо ставить перед АЦП фильтр низкой частоты. Можно представить хроматографический пик в виде
, (6)
где h высота пика; µ = 3 ширина пика; t0 время удерживания.
При прохождении ХС через ФНЧ сигнал искажается и образует хвост на его выходе. График сигнала на выходе ФНЧ показан на рис. 6.
Была исследована точность измерения параметров ХС в зависимости от режима работы СДАЦП.
Рис. 6. Искажение гауссова пика при его
прохождении через ФНЧ первого порядка
Пусть сигнал на выходе хроматографа имеет форму гауссова пика шириной 1 с и высоты 0,5 В. Тогда моделирование проводим при следующих условиях: СДМ выдаёт данные с частотой fд = 19,5 кГц (частота дискретизации), длина одного звена ЦФ скользящего усреднения L = 390 и частота выдачи на его выходе fвыдачи = fд/L = fд/390 = 50 Гц. Если СДАЦП работает с УВХ (рис. 7), то частота выборки УВХ fв = 50 Гц.
Рис. 7. Структурная схема СДАЦП с УВХ
Режим работы без УВХ: погрешность измерения площади S 0,04 %, погрешность измерения высоты пика h = 1,59 %
Режим с УВХ: S 0,04 %, h = 1,3510–5 %.
Отсюда следует, что в случае использования СДМ с УВХ погрешность измерения высоты уменьшается, а погрешность определения площади остаётся почти неизменной и форма пика искажается. При этом скользящее усреднение устраняет высокочастотные помехи.
Была исследована зависимость точности регистрации гауссовых сигналов, зависящая от числа звеньев ЦФ скользящего усреднения. Рассмотрена степень сглаживания ЦФ (длина одного звена ЦФ L = 390 и параметры хроматографического пика (6) t0 = 6, h = 0,9, = 0,5). Найдено, что чем больше порядок ЦФ, тем больше искажение входного сигнала и степень сглаживания. При выбранных выше параметрах ЦФ скользящего усреднения третьего порядка он не сильно влияет на погрешность измерения параметров пиков.
Рассмотрена реакция СДАЦП при подаче на его вход хроматографических пиков с добавлением помех. Параметры эксперимента:
ХС включает последовательность двух пиков и случайный белый шум;
параметры пиков: t01 = 3; h1 = 0,03; 1 = 0,25; t02 = 6; h2 = 0,6; 2 = 1;
величина белого шума: hш = 0,015; 0,15; 0,6;
ЦФ скользящего усреднения третьего порядка, длина одного звена которого равна 256; частота дискретизации fд = 19,5 кГц, fвыдачи = fд = 19,5 кГц.
График ХС и этот же сигнал на выходе СДАЦП показан на рис. 8.
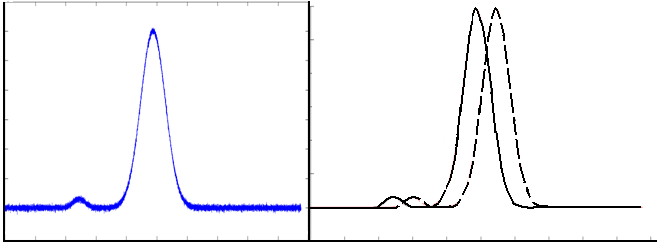
а б
а б
Рис. 8. Вид ХС на входе (а) и выходе СДАЦП (б)
Относительная погрешность от высоты: h1 = 1,21 %; h2 = 1,39 %. В результате исследований выяснео, что при увеличении значения шума в 10 раз на выходе возникают неинформативные пики на базисной линии. В случае, когда шум равен половине высоты пика, на выходе СДАЦП получаем множество пиков с малой амплитудой, а главный пик при этом искажает форму. Относительная погрешность высоты главного пика h = 3,23 %.
Исследования показали, что СДМ выполняет роль не только преобразователя аналогового сигнала в цифровой код, но и фильтра, подавляющего высокочастотные помехи.
Выходной сигнал хроматографа представляет собой суперпозицию информативных si(t) и неинформативных siн(t) пиков, с наложением шума n(t) и базисного сигнала yб.с.(t):
(7)
где m, p количество пиков.
Тогда математическая модель абсолютной y и относительной y погрешности ХС, а также его СКО имеет вид
y = 
= 
, (8)
y = 
, (9)
. (10)
В главе четыре разработано устройство сопряжения между хроматографом и компьютером ПФИ-24 и предложен способ улучшения динамического диапазона для регистрации ХС.
В данной работе был выбран АЦП типа ADS1242 фирмы Burr-Brown со встроенным усилителем с коэффициентами усиления от 1 до 128 и разрядностью до 24 бит, который также обладает высокой помехоустойчивостью.
Предусмотрена возможность ввода полученных данных в компьютер. Управляет СДАЦП, считывает и хранит данные микроконтроллер, в нашем случае МК-51, и по запросу компьютера он пересылает ему данные.
Сопряжение между микроконтроллером и компьютером осуществляется с гальваническим разделением, при этом устраняется несоответствие их уровней напряжения, уменьшается влияние возможной помехи общего вида, а также компьютер и микроконтроллер защищаются от высокого напряжения.
Устройство сопряжения ПФИ-24 (рис. 9) содержит четыре независимых одинаковых канала АЦП. Это позволит ему измерять напряжение в четырёх точках объекта одновременно или в разные моменты времени.
а б
Рис. 9. Структурная схема устройства сопряжения ПФИ-24 (а) и его внешний вид (б)
Входные сигналы поступают по четырём каналам СДАЦП, который преобразует аналоговые напряжения в цифровой двоичный код. Чтобы управлять действиями СДАЦП, временно хранить данные и в дальнейшем передавать на компьютер, использован микроконтроллер МК-51 типа АТ89С51 фирмы ATMEL. В качестве устройства сброса используется супервизор типа ADM810.
Алгоритм работы основной программы устройства приведён на рис. 10. В начальный момент времени микроконтроллер должен настроить микросхему ADS1242 на необходимый режим работы путём записи необходимых значений в её регистры. Каждый регистр содержит по 8 бит и играет свою роль. Особенно можно выделить: регистр калибровки смещения нуля и полной шкалы. Установлением необходимых значений битов в этих регистрах уменьшается погрешность смешения нуля и полной шкалы.
Рис. 10. Блоксхема алгоритма основной программы
Основным источником погрешностей в предложенном устройстве является СДАЦП ADS1242. Использование СДМ в микросхеме обеспечивает высокую точность преобразования. В данной микросхеме предусмотрены несколько режимов калибровки микросхемы: системная калибровка нуля, конца шкалы, смещения, фоновая автокалибровка и автокалибровка, во время выполнения которых устраняются такие погрешности СДАЦП, как смещение нуля, смещение конца шкалы и погрешности от дрейфа коэффициента усиления и смещения.
Суммарная погрешность ПФИ-24 равна:
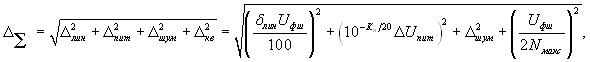
где лин. погрешность линейности; Uфш. значение напряжения полной шкалы; Uмакс максимальное напряжение на входе АЦП; Nмакс максимальный выходной код АЦП.
В табл. 1 приведены значения шума при различных коэффициентах усиления Kу при работе без буферирования входного сигнала и частоте обновления данных на выходе 15 Гц.
Таблица 1
СКО уровня шума ADS1242
| Kу | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | ||
| СКО, мкВ | 2,74 | 1,04 | 0,52 | 0,37 | 0,23 | 0,13 | 0,11 | 0,11 | ||
Изменение коэффициентов усиления происходит программным путём в два этапа: осуществление в одном цикле модулятора нескольких отсчётов входного сигнала и изменение значения отношения опорной ёмкости к входной. Для повышения отношения сигнал/шум необходимо устанавливать больший коэффициент усиления, при этом диапазон измерений не должен превышать диапазон АЦП (5 В).
На рис. 11 показана зависимость выходного сигнала СДАЦП при подаче на его вход единичного скачка. Погрешность преобразования численно равна площади S, она является систематической и может быть исключена в процессе градуировки. Расчёт показывает, что при изменении коэффициента усиления погрешность в установившемся режиме составляет S 6 %. Алгоритм установления Ку в процессе обработки хроматограммы показан на рис. 12.
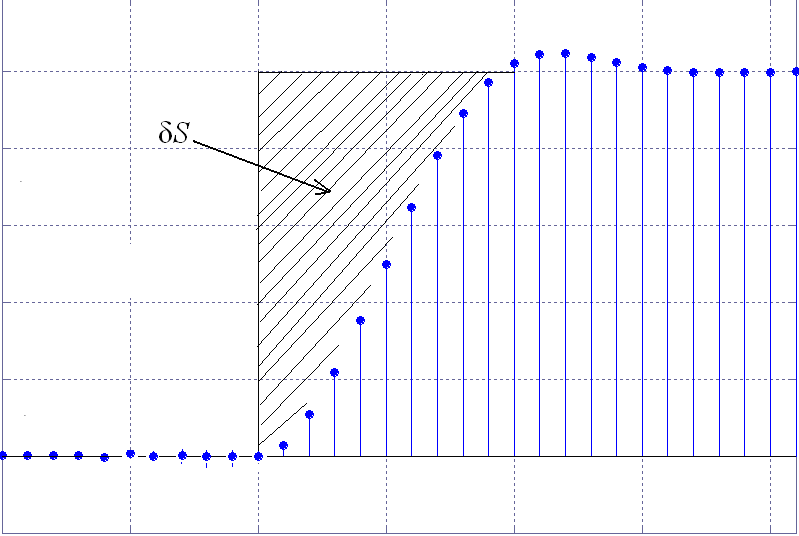
Рис. 11. Выходной сигнал цифрового фильтра
при подаче на его вход единичного скачка
Таким образом, предложен способ увеличения динамического диапазона измерений СДАЦП при обработке сигналов хроматографа. В результате изменения коэффициента усиления динамический диапазон измерений СДАЦП увеличивается в несколько раз по сравнению с работой в режиме с постоянным коэффициентом усиления, что существенно улучшает результаты обработки хроматограммы. Без регулирования Kу число эквивалентных битов 21, а с регулированием 22,5.
Рис. 12. Алгоритм изменения Ку в процессе измерения
Разработанное устройство сопряжения ПФИ-24 имеет следующие характеристики: диапазон входного напряжения –2,5 – 2,5 В, частота преобразования от 10 до 25 Гц, разрешая способность большее 21 бит, скорость изменения напряжения входного сгнала не более 1 В/с. Он применяется в жидкостной и газовой хроматографиях.
ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ
Общим результатом работы является решение актуальной научно-технической задачи структурно-алгоритмической обработки сигналов хроматографов с сигма-дельта аналого-цифровым преобразованием, заключающейся в исследовании СДАЦП, разработке на этой основе и внедрении устройства сопряжения между хроматографом и компьютером ПФИ-24 с улучшенными метрологическими и эксплуатационными характеристиками.
- Предложен способ увеличения динамического диапазона измерений СДАЦП, заключающийся в программном изменении коэффициента усиления, что позволяет повысить динамический диапазон измерений сигналов хроматографического анализа больше 107.
- В результате структурной оптимизации в качестве АЦП выбрал СДМ 2-го порядка с ЦФ 3-его порядка.
- Разработаны математические модели и алгоритмы работы СДМ первого и второго порядка, а также модель ЦФ скользящего усреднения.
- Показано, что СДМ второго порядка имеет лучшую разрешающую способность по сравнению с модулятором первого порядка.
- Установлено, что точность результата измерения существенно повышается из-за эффекта отрицательной корреляции между элементами выходных кодов СДМ. При определении погрешности результата измерения входного напряжения как среднего арифметического результатов N наблюдений принципиально необходимо учитывать корреляционные связи между результатами наблюдений.
- Доказано, что СКО шума СДМ второго порядка увеличивается с увеличением значения входного сигнала. Его величина для линейно изменяющихся входных сигналов зависит не только от диапазона изменения входного сигнала, но и от скорости его возрастания. Он увеличивается с увеличением скорости возрастания сигнала. При одной и той же скорости возрастания его величина для СДМ второго порядка всегда меньше, чем первого.
- Предложено использовать СДМ второго порядка с ЦФ скользящего усреднения для регистрации и обработки ХС. При этом точность обработки сигналов обусловлена ещё и тем, что СДМ играет роль ФНЧ. Показано, что в случае использования СДАЦП без УВХ погрешность измерения амплитуды возрастает, а погрешность определения площади остается неизменной, так же искажается форма пика, но в этом случае преобразователь подавляет высокочастотные помехи.
- Разработано и исследовано четырёхканальное устройство сопряжения ПФИ-24, которое отвечает современным требованиям.
Основное содержание диссертационной работы опубликовано в следующих работах:
- Латышенко К.П., Доан Ван Хоа, Свирюкова О.В., Федина П.А. Обработка хроматографических сигналов с применением сигма-дельта аналого-цифрового преобразования. Экологические системы и приборы, 2010, № 5. – С. 16 – 18.
- Доан Ван Хоа, Солодов Ю.С. Исследование эффекта отрицательной корреляции между элементами выходного сигнала сигма-дельта модуляторов. Вестник MЭИ (ТУ), 2003, № 3. – С. 72 – 76.
- Доан Ван Хоа. Способ улучшения динамического диапазона СДАЦП при преобразовании хроматографических сигналов. Тез. докл. н.-тех. конф. – М.: МГУИЭ, 2010. – С. 26.
- Доан Ван Хоа, Солодов Ю.С. Измерительная установка для хроматографического анализа. Тез. докл. XII межд. н.-тех. конф. «Радиоэлектроника, электроника и энергетика». – М.: 2006, т. 1. – С. 518 – 519.
- Доан Ван Хоа, Солодов Ю.С. Исследование межкодовых переходов для сигма-дельта модуляторов. Там же. – М.: 2009, т.1. – С. 357 – 359.
- Доан Ван Хоа, Солодов Ю.С. Исследование эффекта отрицательной корреляции элементов выходного сигнала сигма–дельта модуляторов. Труды XVI н.-тех. конф. «Информационные средства и технологии». – М.: 2008, т. 3. – С. 125 – 128.
Подписано в печать 23.09.2010. Зак. 38/д. Тир. 100. 2,0 печ. л.
Издательский центр МГУИЭ
105066, Москва, Старая Бассманная ул., 21/4
