Разработка методов расчета и обработки рефракционных картин в лазерной системе визуализации тепловых полей
На правах рукописи
Лапицкий Константин Михайлович
Разработка методов расчета и обработки рефракционных картин в лазерной системе визуализации тепловых полей
Специальность 05.11.07 – Оптические и оптико-электронные приборы и комплексы
Автореферат
диссертации на соискание ученой степени
кандидата технических наук
Москва – 2009
Работа выполнена в
ГОУВПО Московском энергетическом институте (техническом университете)
на кафедре физики им. В.А.Фабриканта
Научный руководитель доктор физико-математических наук,
профессор Ринкевичюс Бронюс Симович
Официальные оппоненты: доктор технических наук,
доцент Лубенченко Александр Владимирович,
кандидат технических наук, заведующий
лабораторией Ивочкин Юрий Петрович
Ведущая организация: ФГУП Научно-исследовательский институт
прецизионного приборостроения
Защита состоится «_19_» ___июня___ 2009 г. в _14_ часов _00_ минут в аудитории __Е-603__ на заседании диссертационного совета Д 212.157.12 при Московском энергетическом институте (техническом университете) по адресу: 111250, Москва, Красноказарменная ул., д. 13.
Отзывы на автореферат в двух экземплярах, заверенные печатью учреждения, просим направлять по адресу: 111250, Москва, Красноказарменная ул., д. 14, Ученый совет МЭИ (ТУ).
С диссертацией можно ознакомиться в библиотеке Московского энергетического института (технического университета).
Автореферат разослан «_____» __________________ 2009 г.
Ученый секретарь диссертационного совета
Д 212.157.12, к.т.н., доцент И.Г. Буре
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность работы. Лазерная диагностика потоков жидкости и газа – область физики, которая имеет важное научно-практическое значение и в настоящее время интенсивно развивается. Одним из методов диагностики потоков жидкости и газа является их визуализация, основанная на неоднородности показателя преломления среды. На данном принципе основано действие компьютерно-лазерного рефракционного (КОЛАР) метода, в котором исследуемая среда зондируется лазерным излучением различной формы. В процессе распространения излучения в оптически неоднородной среде происходит изменение его траектории, что приводит к смещению пучка в плоскости регистрации. Цифровая регистрация изображений при помощи видеокамеры пучка позволяет оперативно передавать данные в компьютер для дальнейшей обработки.
В силу своей практической безынерционности такие измерения могут использоваться для диагностики нестационарных быстропротекающих процессов в оптически прозрачных средах. Использование маломощного лазерного излучения позволяет избежать внесения искажений в исследуемую среду и обеспечивает также бесконтактность и дистанционность измерений.
Наибольшее распространение получили схемы КОЛАР метода с использованием в качестве зондирующего излучения астигматического лазерного пучка эллиптического сечения, размер которого по одной из осей существенно больше, чем по другой. Такой пучок называют также «лазерной плоскостью» (ЛП). Благодаря возможности получения ЛП малого поперечного размера возможно исследовать пограничные слои размером менее одного миллимера и указать на наличие краевых эффектов.
Одним из широко распространенных видов потоков является естественная конвекция в жидкости около нагретых тел. Основная сложность исследования таких потоков заключается в их трехмерности, существенной нерегулярности и нестационарности. Численное моделирование на основе современных математических моделей конвективных течений требует значительных вычислительных ресурсов.
Аналитическое решение как прямой задачи расчета траектории распространения геометрооптических лучей в оптически неоднородной среде, так и обратной задачи восстановления закона распределения показателя преломления среды возможно только в случае осесимметричных тел (например, сфера, эллипсоид вращения, цилиндр), или тел плоской формы без учета краевых эффектов. Во всех других случаях расчет должен проводиться только численными методами. К тому же, использование для подобных вычислений широко распространенных универсальных программ расчета оптических систем (например, CodeV, Zemax) связано со многими затруднениями, заключающихся в неопределенности методов расчета, и, как следствие, области применимости и погрешности, а также не адаптированности для расчета траекторий лучей в оптически прозрачных средах с градиентом температуры.
Таким образом, актуальность приобретает решение задачи распространения оптического излучения в неоднородной среде с учетом краевых эффектов, разработка методов определения параметров температурного поля по экспериментальным рефракционным картинам, а также создание специализированного программного обеспечения в компьютерно-лазерной рефракционной системе.
Цель работы. Основной целью данной работы является разработка методов расчета теоретических и обработки экспериментальных рефракционных картин для визуализации тепловых полей и получения количественных характеристик процессов естественной конвекции в лазерной системе визуализации тепловых полей. Для достижения данной цели необходимо было решить следующие задачи:
- разработать метод моделирования траектории распространения геометрооптических лучей в оптически неоднородной среде с известным законом распределения показателя преломления;
- разработать и исследовать метод расчета рефракции плоского лазерного пучка в геометрооптическом приближении в трехмерном температурном поле в жидкости вокруг нагретого тела с учетом краевых эффектов;
- разработать метод обработки экспериментальных рефракционных картин для определения толщины пограничного слоя около нагретого тела с радиальной симметрией, помещенного в жидкость;
- разработать методику сравнения расчетных и экспериментальных рефракционных картин для восстановления температурного профиля около нагретого тела с радиальной симметрией, помещенных в жидкость.
Научная новизна работы:
Разработан численный метод расчета траектории лучей в геометрооптической модели астигматического лазерного пучка, распространяющегося в трехмерной оптически прозрачной среде.
С помощью разработанного метода решена задача рефракции астигматического лазерного пучка в тепловом поле нагретых тел, в том числе с учетом краевых эффектов для тел с кромками. Создана специализированная программная реализация, адаптированная для использования в компьютерно-лазерной рефракционной системе.
Разработана методика проведения эксперимента по исследованию теплового пограничного слоя вокруг нагретого тела в жидкости и обработки рефракционных картин с цель восстановления параметров неоднородной среды.
Разработан метод обработки экспериментальных рефракционных картин пограничного слоя около нагретого тела с радиальной симметрией, помещенного в жидкость, позволяющий определить толщину теплового пограничного слоя, а также температурный профиль в пограничном слое.
Основные положения, выносимые на защиту:
- Разработанный численный метод расчета траектории лучей в геометрооптической модели астигматического лазерного пучка в оптически прозрачной неоднородной среде позволяет учесть краевые эффекты и изменение конфигурации неоднородной среды.
- Разработанный метод расчета распространения плоского лазерного пучка в трехмерном температурном поле позволяет проводить моделирование рефракционных картин вблизи поверхности нагретого тела в геометрооптическом приближении с учетом краевых эффектов.
- Разработанный метод получения и обработки экспериментальных рефракционных картин позволяет определить толщину пограничного слоя около неподвижного и движущегося нагретого тела с радиальной симметрией, помещенного в жидкость.
- Разработанный метод обработки экспериментальных рефракционных картин позволяет провести восстановление температурного профиля около нагретого тела с радиальной симметрией, помещенного в жидкость.
Практическая ценность работы. Разработанные методы и алгоритмы расчета и обработки рефракционных картин применимы для совершенствования компьютерно-лазерных рефракционных систем диагностики тепловых полей в оптически прозрачных жидкостях, что существенно расширяет область применения и возможности этих систем. Данные методы позволяют проводить исследование процессов естественной конвекции в жидкости при наличии краевых эффектов на кромках тел и получать количественную информацию о температурном распределении в пограничном слое в аппаратах, использующих технологии нагрева и охлаждения.
Разработанное специализированное программное средство расчета рефракционных картин геометрооптической модели астигматического лазерного пучка в оптически прозрачной неоднородной среде может быть использовано при моделировании процессов теплообмена с целью верификации получаемых результатов и оценки погрешности расчета.
Внедрение. Материалы исследования включены в научно-технические отчеты по грантам Минобрнауки (проект 1109, проект РНП.2.1.2.686) и РФФИ (проект 07-07-13529-офи_ц). Результаты работы были использованы при создании макета экспериментальной установки и при подготовке описания лабораторной работы «Исследование распространения лазерного пучка в оптически неоднородной среде» по курсу «Лазерная интерферометрия» для студентов, обучающихся по специальности «Квантовая и оптическая электроника».
Достоверность полученных результатов.
- Тестирование программной реализации разработанного метода расчета распространения геометрооптической модели лазерного пучка в оптически неоднородной среде на основе сравнения результатов расчета с известными аналитическими решениями показало совпадение результатов в пределах допустимой погрешности машинных вычислений.
- Сравнение результатов расчета рефракционных картин с краевыми эффектами по созданному специализированному программному средству с результатами, получаемыми с помощью программы оптического конструирования CodeV, показало совпадение результатов в пределах допустимой погрешности машинных вычислений.
- Полученные по предложенному методу обработки величины толщины пограничного слоя и формы температурного профиля в пограничном слое сравнивались с результатами моделирования при помощи пакета прикладных программ на основе теплофизического расчета, при этом наблюдается непротиворечивость результатов сравнения в пределах методической погрешности эксперимента.
Апробация работы. Основные материалы работы докладывались на следующих конференциях и семинарах в период с 2004 по 2009 гг.:
- XV Школа-семинар молодых ученых и специалистов под рук. академика РАН А.И. Леонтьева «Проблемы газодинамики и тепломассообмена в энергетических установках»; Калуга, 2005 г.;
- VIII, IX Международные научно-технические конференции «Оптические методы исследования потоков»; Москва, 2005, 2007 гг.;
- 12th International Symposium on Flow Visualization; Gttingen, 2006;
- 4 Российская национальная конференция по теплообмену; Москва, 2006;
- 15 Международная конференция «Высокие технологии в биологии, медицине и геоэкологии»; 16 Международная конференция «Лазерно-информационные технологии в медицине, биологии и геоэкологии»; Новороссийск, 2007, 2008 гг.;
- 16-я Всероссийская межвузовская научно-техническая конференция студентов и аспирантов «Микроэлектроника и информатика»; Москва, 2009;
- 10,11,12,13,14 Международные научно-технические конференции студентов и аспирантов “Радиоэлектроника, электротехника и энергетика”, МЭИ (ТУ), 2004-2008 гг.
- 3rd International conference on Laser Optics for Young Scientists; St. Petersburg, 2006.
Публикации. Основные материалы диссертации опубликованы в 12 печатных работах, из них 2 статьи – в реферируемых журналах, без соавторов – 3 работы, а также в 6 тезисах докладов.
Структура и объем работы. Диссертация состоит из введения, четырех глав, заключения, списка литературы и приложений. Работа содержит 161 страницу машинописного текста, включая 95 рисунков, 2 таблицы, 52 наименования списка литературы, 1 приложение.
СОДЕРЖАНИЕ РАБОТЫ
Во введении обосновывается выбор научного направления и актуальность работы. Приведены цель и основные задачи диссертации. Кратко рассмотрены оптические методы и возможность их применения для решения задач процессов тепломассообмена. Сформулированы научная новизна работы и основные положения, выносимые на защиту.
В первой главе проведен краткий обзор научно-технической литературы по существующим оптическим методам диагностики потоков жидкости и газа. Рассмотрены основные соотношения, связывающие теплофизические и оптические свойства сред. Приведены оптические схемы и описания основных классических теневых методов. Показано, что ограничение возможности применения классических теневых методов связано с дороговизной оптических установок и требований точной настройки и юстировки. Их высокая чувствительность делает их практически непригодными для диагностики оптически прозрачных тепловых полей в жидкостях со значительным градиентом температуры.
Рассмотрены принципы и экспериментальная установка компьютерно-лазерного рефракционного (КОЛАР) метода для исследования нестационарной естественной конвекции в жидкости вблизи нагретых тел, разработанные на кафедре физики им. В.А. Фабриканта. Принцип действия КОЛАР метода основан на зондировании потока плоским лазерным пучком – астигматическим пучком с эллиптическим сечением, размер которого по одной из осей существенно больше, чем по другой (такой пучок называют также «лазерной плоскостью» – ЛП).
Установка (рис. 1) состоит из лазера 1, оптической системы формирования лазерной плоскости 2, кюветы с жидкостью 3, нагретого тела 4, диффузно-рассеивающего экрана 5, цифровой видеокамеры 6, персонального компьютера 7 и специального программного обеспечения. ЛП направляется под нагреваемым объектом, находящемся в кювете с жидкостью. При распространении ЛП через оптически неоднородный поток из-за рефракции происходит отклонение отдельных её участков от плоской поверхности, т.е. получается сложная криволинейная поверхность, изменяющаяся как в пространстве, так и во времени. Проекции лазерной плоскости на выходе из оптической неоднородности (рефракционные картины, или рефрактограммы) наблюдаются на экране, регистрируются цифровой видеокамерой и вводятся в компьютер для дальнейшей обработки.

Рис. 1. Схема экспериментальной установки КОЛАР метода
Описано состояние исследований по разработке КОЛАР метода к началу работы над диссертацией. В статьях, посвященных разработке и применению КОЛАР метода, описывается его применение к исследованию естественной конвекции в жидкости около нагретых тел плоской и сферической формы и получению количественной информации о градиенте температуры в нестационарном режиме.
Во второй главе рассмотрен алгоритм моделирования траектории геометрооптических лучей в оптически неоднородной среде. Приведены основные соотношения для расчета траектории геометрооптических лучей в оптически неоднородной среде. Приведены примеры рассчитанных траекторий для плоскослоистой и сферически-слоистой среды. Показано, что на практике плоскослоистые неоднородности, возникающие около тел плоской формы, всегда сопровождаются краевыми эффектами, сильно влияющими на результат рефракции лучей, учесть которые удается только численными методами.
Разработан алгоритм расчета в двумерной оптической неоднородности. При известной зависимости показателя преломления от координат n(x, z) траектория луча находится пошагово путем определения единичного вектора l (x, z), касательного к лучу в каждой точке его траектории, на основе решения лучевого уравнения. Расчетная область разбивается на ячейки с шагом zk (рис. 2) так, чтобы n(x, z) const в каждой ячейке. Минимальное значение zk выбирается на основе результатов аналитических расчетов для тестовых задач.

Рис. 2. Дискретизация расчетной области
При известных координатах точки входа луча в среду (x0, z0) и угле 0 вычисляется функция l (x, z), после чего определяется траектория луча. Участок траектории в пределах каждой ячейки считаем прямой линией, поэтому Sk = zk / cos k. Изменение направления вектора lk на угол k при переходе в следующую ячейку определяется как
 ,
,
где угол k – угол между направлениями градиента и луча в k-й ячейке:
 .
.
Направление луча в следующей ячейке будет задаваться углом: k+1 = k + k, где k = – k = – (k+1 – k), а точка входа луча в следующую ячейку: xk+1 = xk + zk tg k.
Проведен расчет траектории луча по численному алгоритму для температурного поля плоскослоистой неоднородности с учетом и без учета краевых эффектов. Результаты расчета приведены на рис. 3.


Рис. 3. Траектории лучей под дном цилиндра с плоским дном; 0 = 0,01°,
z0 = –20 мм; 1 – x0 = 0,1 мм; 2 – x0 = 0,3 мм; 3 – x0 = 0,5 мм.
— без учета краевых эффектов, --- с учетом краевых эффектов
Сделан вывод о необходимости их учета при моделировании и обработке экспериментальных результатов.
Также проводилась оценка степени влияния конфигурации неоднородного поля на траекторию луча на примере модели двумерного сферически-слоистого температурного поля и эллиптически-слоистого поля. На рис. 4 приведены результаты моделирования траекторий геометрооптических лучей в температурных полях различной конфигурации. Кривые 1,2,3 представляют собой изотермы температурного поля, соответствующие одинаковой температуре: 1 – сферически-слоистая модель, 2 – эллиптически-слоистая модель с соотношением осей эллипса по осям Z и X, равным 9:10, 3 – эллиптически-слоистая модель с соотношением осей эллипса по осям Z и X, равным 11:10. Кривые 4,5,6 – примеры расчета траекторий геометрооптических лучей по методике, указанной в п.1 (соответствие изотерм и траекторий: 1–4, 2–5, 3–6). Зависимость относительной погрешности вычислений конечного угла отклонения луча от количества разбиений по оси Z в сферически-слоистом неоднородном поле приведена на рис. 5.
Как показали расчеты, растяжение или сжатие сферически-симметричного поля на величину 10% по одной из осей приводит к изменению угла отклонения примерно на такую же величину. Это показывает необходимость уточненного знания структуры температурного поля для более уверенной верификации данных расчета и эксперимента и снижения методической погрешности при решении обратной задачи восстановления температурного поля.

Рис. 4. Моделирование траектории луча в сферически-слоистой и эллиптически-слоистой неоднородной среде; 0 = 0, z0 = –10 мм; x0 = 12,1 мм
Для достижения относительной погрешности вычисления конечного угла отклонения величины 0,5% необходимо разбить расчетную область на сетку с шагом примерно a/160 a/80, где a – толщина пограничного слоя по уровню спада температуры в e раз.

Рис. 5. Зависимость относительной погрешности вычислений конечного угла отклонения луча от количества разбиений по оси Z в сферически-слоистом неоднородном поле, форма ячейки квадратная; 0 = 0, z0 = –10 мм; x0 = 12,1 мм; кривые 1 и 2 соответствуют разным моделям температурного поля
В третьей главе проводится описание метода численного расчета рефракционных картин в трехмерной неоднородности. Приведена схема расчета и основные соотношения. Приведено описание программы RELAS (REfraction of LAser Sheet) для решения задачи распространения лазерной плоскости в трехмерной оптически неоднородной среде. В качестве примера на рис. 6 приведено окно результатов расчета рефрактограммы для распространения лазерной плоскости около дна нагретого цилиндра, помещенного в холодную воду, с учетом краевых эффектов.
Оценка достоверности результатов проводилась на основе сравнения с аналитическим решением для сферически-слоистой среды (рис. 7) для различного числа узлов расчетной сетки NZ и при помощи программы расчета оптических систем для цилиндрической неоднородности (рис. 8). На основании сравнения графиков сделан вывод о достоверности расчетов по приведенному алгоритму.
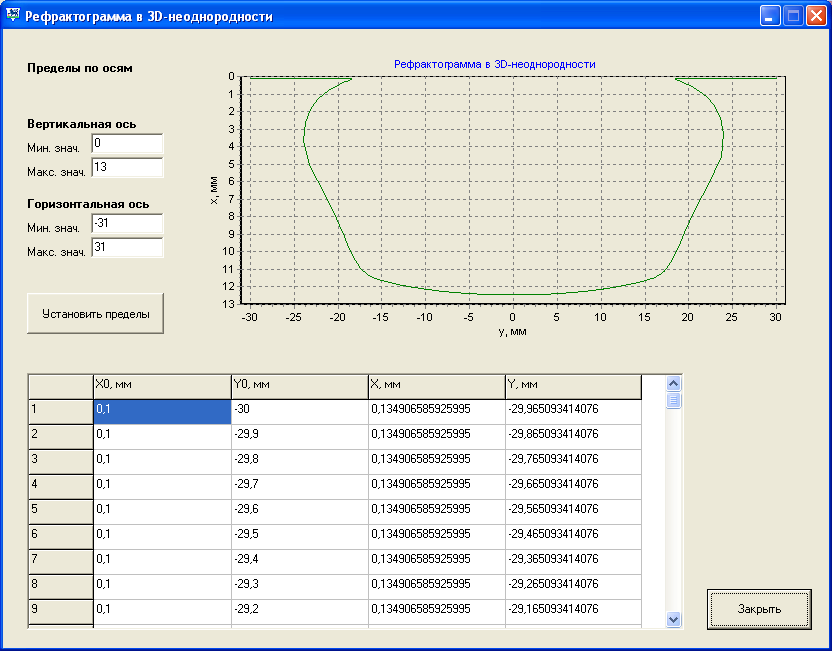
Рис. 6. Окно вывода результатов расчета рефрактограмм для цилиндрической неоднородности
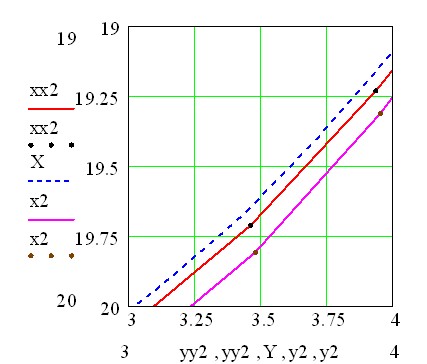

Рис. 7. Расчет рефрактограмм при прохождении
под нагретым цилиндром с полусферическим дном в воде: 1 – NZ = 100,
2 – NZ = 1000, 3 – NZ = 10000 и аналитический расчет

Рис. 8. Сравнение расчетных рефрактограмм, полученных по приведенному численному алгоритму и при помощи программы расчета оптических систем
В четвертой главе приведено описание экспериментальной установки для реализации компьютерно-лазерного рефракционного метода исследования тепловых пограничных слоев в жидкости вокруг нагретых тел. Рассмотрены принципы визуализации пограничного слоя при помощи лазерной плоскости, приведены примеры экспериментальных рефрактограмм для тел различной формы (рис. 9).
Рассмотрена методика определения толщины пограничного слоя для тел со сферической поверхностью, а также алгоритм восстановления температурного поля около тел со сферической и цилиндрической симметрией (рис. 10).
Пусть изначально ЛП проходит на расстоянии h от тела. Рассмотрим алгоритм обработки рефрактограмм в соответствии со схемой, показанной на рис. 10. Предварительно проводится обработка всех рефрактограмм для построения зависимости величины максимального отклонения элемента ЛП от первоначального по оси Y (точка G) от времени и температуры тела. Это будет точка B с координатами xp = (R + h)xt/yt, yp = R + h, которые получаются из рассмотрения треугольника OAF.
  а) а) |   в) в) |   г) г) |
  б) б) |   д) д) | |
Рис. 9. Примеры рефрактограмм при прохождении ЛП в воде: а – под цилиндром с полусферическим дном; б – под цилиндром с плоским дном; в – параллельно боковой поверхности цилиндра с плоским дном; г – под углом к боковой поверхности цилиндра (штриховкой обозначено положение цилиндра);
д – под параллелепипедом
  Рис. 10. Алгоритм обработки рефрактограмм для восстановления профиля температуры Рис. 10. Алгоритм обработки рефрактограмм для восстановления профиля температуры |
Величина отклонения элемента ЛП вдоль выбранного направления равна длине отрезка AB = r = [(xt – xp)2 + (yt – yp)2]1/2. По величине r определяется температура среды в заданном направлении на расстоянии OB = r от поверхности тела, строится зависимость T(r). Следует отметить, что в эксперименте фиксируется температура поверхности тела, а не температура среды на расстоянии h от тела. Поэтому для уменьшения погрешности получаемого распределения температуры жидкости в пограничном слое рекомендуется выбирать значение h наименьшим из возможных, которое, как правило, определяется размером ЛП в перетяжке, которая располагается под нижней точкой полусферы.
На рис. 11 приведены графики зависимости температуры воды от координаты в пограничном слое на основании обработки экспериментальных рефрактограмм по приведенному алгоритму.
 Рис. 11. Зависимость температуры воды от координаты в пограничном слое цилиндра при температуре дна: Рис. 11. Зависимость температуры воды от координаты в пограничном слое цилиндра при температуре дна:1 – 75 °С, 2 – 66 °С, 3 – 56 °С, 4 – 46 °С |
Сравнение данных проводилось путем решения прямой задачи распространения лазерной плоскости в сферически-слоистой среде и сравнения полученной расчетной рефрактограммы с экспериментальной (рис. 12). Наблюдается, в основном, совпадение участков экспериментальной и рассчитанной на основе полученных данных рефрактограмм. Наличие небольшого расхождения между ними может быть обусловлено методической погрешностью обработки, а также возможной неравномерностью прогрева цилиндра.
Проанализированы погрешности юстировки элементов установки, влияющие на точность метода. На рис. 13 приведена зависимость относительной погрешности измерения смещения пучка от угла входа в оптическую неоднородность, которая иллюстрирует необходимость выставления оптической оси излучения.
В приложении приведен текст основного расчетного блока программы RELAS.
 Рис. 12. Расчетная (1) и экспериментальная (2) рефрактограммы, Tц = 75°С Рис. 12. Расчетная (1) и экспериментальная (2) рефрактограммы, Tц = 75°С |   Рис. 13. Зависимость относительной погрешности измерения смещения пучка от угла входа в оптическую неоднородность Рис. 13. Зависимость относительной погрешности измерения смещения пучка от угла входа в оптическую неоднородность |
В заключении кратко сформулированы основные результаты, полученные в диссертации.
ОСНОВНЫЕ РЕЗУЛЬТАТЫ РАБОТЫ
- Предложенный алгоритм расчета траектории геометрооптического луча в произвольной двумерной оптически неоднородной среде позволяет учесть краевые эффекты и изменение конфигурации неоднородной среды.
- Разработанный метод расчета распространения плоского лазерного пучка в трехмерном температурном поле позволяет проводить моделирование рефракционных картин вблизи поверхности нагретого тела в геометрооптическом приближении с учетом краевых эффектов.
- На основе разработанных алгоритмов расчета создано и протестировано программное средство расчета рефракционных картин в трехмерных температурных неоднородностях с учетом краевых эффектов около кромок тел.
- Разработанный метод получения и обработки экспериментальных рефракционных картин позволяет определить толщину пограничного слоя около нагретого тела с радиальной симметрией, помещенного в жидкость.
- По разработанной методике обработки экспериментальных рефракционных картин проведено восстановление температурного профиля около нагретого тела с радиальной симметрией, помещенного в жидкость. Достоверность полученных результатов определена на основе сравнения расчетной и экспериментальной рефракционной картины.
Список основных публикаций по теме диссертации
- Лапицкий К.М., Расковская И.Л., Ринкевичюс Б.С. Моделирование влияния краевых эффектов на рефракцию лазерного пучка в температурной неоднородности // Измерительная техника. – 2008, №7. С. 28 – 33.
- Лапицкий К.М. Моделирование влияния конфигурации температурного поля в жидкости на рефракцию лазерного излучения // Метрология. – 2008, №7. С. 33 – 41.
- Лапицкий К.М., Толкачев А.В. Лазерная установка для исследования теплового пограничного слоя в жидкости // Оптические методы исследования потоков: Тр. 8-й Международной научно-технической конференции./ Под ред. Ю.Н. Дубнищева, Б.С. Ринкевичюса. – М.: Знак, 2005. С. 116 – 119.
- Лапицкий К.М., Толкачев А.В. Визуализация естественной конвекции в жидкости около нагретого цилиндра с помощью лазерной плоскости // Проблемы газодинамики и тепломассообмена в энергетических установках: 15-я Школа-семинар молодых ученых и специалистов под рук. акад. РАН А.И. Леонтьева. – М.: Издательство МЭИ, 2005. Т.1. С. 347 – 350.
- Артемов В.И., Евтихиева О.А., Лапицкий К.М., Ринкевичюс Б.С., Толкачев А.В., Яньков Г.Г. Исследование нестационарного температурного поля при естественной конвекции КОЛАР методом // Оптические методы исследования потоков: Тр. 8-й Международной научно-технической конференции./ Под ред. Ю.Н. Дубнищева, Б.С. Ринкевичюса. – М.: Знак, 2005. С. 478 – 481.
- Евтихиева О.А., Лапицкий К.М., Расковская И.Л. Распространение лазерной плоскости в тепловом поле нагретого шара в воде // Оптические методы исследования потоков: Тр. 8-й Международной научно-технической конференции./ Под ред. Ю.Н. Дубнищева, Б.С. Ринкевичюса. – М.: Знак, 2005. С. 332 – 335.
- Lapitsky K.M., Raskovskaya I.L., Rinkevichyus B.S. Quantitative visualization of transparent spherical temperature layer // CD-ROM Proceedings of the 12th International Symposium on Flow Visualization./ Ed. J. Kompenhans, A. Schroeder, I. Grant. – Goettingen, Germany: German Aerospace Center (DLR), 2006. Paper No. 55. (Лапицкий К.М., Расковская И.Л., Ринкевичюс Б.С. Количественная визуализация прозрачного сферического температурного слоя // Труды 12-го международного симпозиума по визуализации потоков, CD-ROM./ Под ред. Ю. Компенханса, А. Шредера. – Геттинген, Германия: Немецкое аэрокосмическое агентство, 2006. Доклад №55.)
- Артемов В.И., Яньков Г.Г., Евтихиева О.А., Лапицкий К.М., Расковская И.Л., Ринкевичюс Б.С., Толкачев А.В. Численное и экспериментальное исследование естественной конвекции в жидкости около нагретого цилиндра // Труды Четвертой Российской национальной конференции по теплообмену. – М.: Издательский дом МЭИ, 2006. Т.3. С. 42 – 46.
- Лапицкий К.М., Расковская И.Л. Численный расчет рефракции геометрооптических лучей в двумерном температурном поле // Оптические методы исследования потоков: Тр. 9-й Международной научно-технической конференции./ Под ред. Ю.Н. Дубнищева, Б.С. Ринкевичюса. – М.: Издательский дом МЭИ, 2007. С. 490 – 493.
- Лапицкий К.М. Определение времени остывания нагретого тела лазерным рефракционным методом // Труды 15-й Международной конференции «Высокие технологии в биологии, медицине и геоэкологии»./ Под ред. В.Е. Привалова. – Абрау-Дюрсо, 2007. С. 47 – 49.
- Лапицкий К.М. Методика анализа краевых эффектов в температурном поле лазерным рефракционным методом // Труды 16-й Международной конференции «Лазерно-информационные технологии в медицине, биологии и геоэкологии»./ Под ред. Привалова В.Е. – Новороссийск, 2008. С.25–27.
- Лапицкий К.М., Расковская И.Л., Ринкевичюс Б.С. Алгоритм количественной визуализации трехмерных оптических неоднородностей // Труды 16-й Всероссийской межвузовской научно-технической конференции студентов и аспирантов «Микроэлектроника и информатика – 2009». – М.: МИЭТ, 2009. С. 132.

