Интегрирующие аналого-цифровые преобразователи, использующие методы однобитной сигма-дельта-модуляции
На правах рукописи
ТЕР-АРАКЕЛЯН Руслан Геворкович
ИНТЕГРИРУЮЩИЕ АНАЛОГО-ЦИФРОВЫЕ
ПРЕОБРАЗОВАТЕЛИ, ИСПОЛЬЗУЮЩИЕ МЕТОДЫ
ОДНОБИТНОЙ СИГМА-ДЕЛЬТА-МОДУЛЯЦИИ
Специальность 05.11.01 Приборы и методы измерения
(электрические и магнитные величины)
А в т о р е ф е р а т
диссертации на соискание ученой степени
кандидата технических наук
ПЕНЗА 2012
Работа выполнена в федеральном государственном бюджетном образовательном учреждении высшего профессионального образования «Пензенский государственный университет» на кафедре «Информационно-вычислительные системы».
| Научный руководитель – | доктор технических наук, профессор Чувыкин Борис Викторович. |
| Официальные оппоненты: | доктор технических наук, профессор Васильев Валерий Анатольевич; |
| кандидат технических наук, доцент Сёмочкина Ирина Юрьевна. | |
| Ведущая организация – | ОАО «Научно-исследовательский институт физических измерений», г. Пенза |
Защита диссертации состоится 1 марта 2012 г., в 12 часов, на
заседании диссертационного совета Д 212.186.02 в федеральном государственном бюджетном образовательном учреждении высшего профессионального образования «Пензенский государственный университет» по адресу: 440026, г. Пенза, ул. Красная, 40.
С диссертацией и авторефератом можно ознакомиться в библиотеке федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Пензенский государственный университет». Автореферат размещен на сайте университета www.pnzgu.ru и на сайте Минобрнауки РФ.
Автореферат разослан «__» ________ 2012 г.
Ученый секретарь
диссертационного совета
доктор технических наук,
профессор Светлов А. В.
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность работы. Повышение эффективности, совершенствование методов цифровой обработки измерительной информации являются актуальными задачами, поэтому в области высокоточных АЦП произошла смена поколений. Интегрирующие АЦП (ИАЦП)
с промежуточным преобразователем в широтно-импульсные, фазо-импульсные и частотно-имульсные сигналы были вытеснены ИАЦП, использующими методы сигма-дельта-модуляции, которые являются развитием известных методов импульсно-разностной модуляции.
Преимущества ИАЦП, использующих методы сигма-дельта-модуляции, заключаются в высокой точности и линейности функции преобразования, что достигается применением однобитных сигма-дельта-модуляторов. Другими преимуществами являются малое энергопотребление и возможность изготовления по технологии цифровых интегральных микросхем («система на кристалле»), чем обусловлена их сравнительно низкая стоимость.
Значительный вклад в теорию и практику ИАЦП внесли научные коллективы, руководимые Л. И. Волгиным, Ю. И. Гитисом, В. С. Гутниковым, В. И. Диденко, К. Б. Карандеевым, В. Ю. Кнеллером, Л. Ф. Куликовским, Е. А. Ломтевым, П. В. Новицким, П. П. Орнадским, Ю. С. Солодовым, Ю. М. Тузом, Э. К. Шаховым, В. М. Шляндиным и зарубежными учеными Benabes, Alderebt, Kielbasa, Gomes Cama, Bota, Montana, Smitier и др.
В настоящее время область применения ИАЦП, использующих методы сигма-дельта-модуляции, непрерывно расширяется: беспроводная связь, обработка видеосигналов, хроматография, медицина, геология, что достигается благодаря новым структурно-алгоритмическим решениям и совершенствованию технологии производства микросхем. Вопросы совершенствования ИАЦП, использующих методы сигма-дельта-модуляции, постоянно обсуждаются на международных конференциях IEEЕ, «Информационные средства и технологии», «Радиоэлектроника, электроника и энергетика» и др.
В последнее время в измерительной технике появилась тенденция перехода на беспроводные технологии передачи данных и построения датчиков в виде автономных измерительных систем. Для беспроводных датчиков требуются, как правило, 16–24-битные АЦП, работающие в режиме однократного преобразования и обладающие наилучшим энергетическим показателем количества энергии, которое тратится на получение единицы измерительной информации. Этим требованиям удовлетворяют в первую очередь ИАЦП, использующие методы однобитной сигма-дельта-модуляции. Однако теоретические вопросы проектирования таких ИАЦП проработаны недостаточно полно, что связано с трудностями их математического описания и большим разнообразием возможных вариантов структурно-алгоритмических решений.
Целью работы является совершенствование интегрирующих аналого-цифровых преобразователей, использующих однобитные сигма-дельта-модуляторы и цифровые фильтры в режиме однократного преобразования.
Задачи исследования:
1) анализ тенденции развития и систематизация ИАЦП, использующих методы однобитной сигма-дельта-модуляции. Выявление путей снижения энергопотребления, повышения быстродействия и уменьшения погрешности квантования ИАЦП в режимах однократного и циклического преобразований;
2) определение минимального значения погрешности квантования, которое может быть достигнуто ИАЦП с однобитным сигма-дельта-модулятором высокого порядка в режиме однократного преобразования;
3) разработка математических моделей однобитных сигма-дельта- модуляторов высокого порядка на базе аналоговых интеграторов, алгоритмов численного расчета погрешности квантования и времени окончания переходных процессов ИАЦП в режиме однократного преобразования;
4) разработка методики расчета значений коэффициентов обратной связи (ОС) однобитных сигма-дельта-модуляторов высоких порядков по критерию их устойчивой работы для режима аналого-цифрового преобразования входных сигналов малого и большого уровня.
5) исследование путей уменьшения погрешности квантования ИАЦП в режиме однократного преобразования за счет введения нелинейных вычислительных процедур в алгоритм работы цифрового фильтра-дециматора;
6) разработка комплекса программ численного расчета и анализа для исследования погрешности квантования, времени окончания нелинейных переходных процессов ИАЦП, условий обеспечения устойчивой работы однобитных сигма-дельта-модуляторов, оптимизации коэффициентов передаточной функции цифрового фильтра-дециматора по критерию минимума среднеквадратического отклонения (СКО) шума квантования;
7) разработка методики расчета и рекомендаций по проектированию микромощных ИАЦП в составе многоузловой беспроводной сенсорной сети для решения инженерных задач по обеспечению режимов микропотребления.
Объектом исследования являются интегрирующие аналого-цифровые преобразователи, использующие методы однобитной сигма-дельта-модуляции и цифровой фильтрации-децимации.
Предмет исследований:
– структуры и алгоритмы ИАЦП. Методы однобитной сигма-дельта-модуляции и цифровой фильтрации-децимации измерительных однобитных сигналов;
– математические и имитационные модели однобитных сигма-дельта-модуляторов высоких порядков; аналоговых и аналого-дискретных интеграторов, цифровых фильтров.
Методы исследований включают в себя элементы теории дискретизации и квантования аналоговых сигналов, теории линейных импульсных систем, аналоговой и цифровой фильтрации, операторные методы, системы визуального программирования Matlab & Simulink, математические пакеты-Maple и программы объектно ориентированного программирования – Delphi.
Научная новизна работы:
1. Получена математическая оценка минимального значения погрешности квантования, которое может быть достигнуто ИАЦП с однобитным сигма-дельта-модулятором высокого порядка в режиме однократного преобразования.
2. Разработана уточненная математическая модель однобитных сигма-дельта-модуляторов высокого порядка, в которой учитывается эффект сквозного прохождения входного сигнала по цепи аналоговых интеграторов в составе сигма-дельта-модуляторов.
3. Определены условия устойчивой работы однобитных сигма-дельта-модуляторов k-го порядка в режиме преобразования сигналов малого уровня в виде систем неравенств, ограничивающих область допустимых значений коэффициентов ОС.
4. Для синтеза алгоритма нелинейного цифрового фильтра-дециматора, оптимального по минимаксному критерию амплитуды шума квантования ИАЦП, предложено использовать математическое условие эквивалентности импульсных характеристик цифрового фильтра (ЦФ) по отношению к импульсным характеристикам аналогового фильтра (АФ), которые выделены из структуры однобитного сигма-дельта-модулятора методом декомпозиции.
5. Выявлено свойство подобия нелинейных переходных процессов для однобитных и многобитных сигма-дельта-модуляторов, на основе которого разработан алгоритм расчета и минимизации времени преобразования ИАЦП.
Практическое значение результатов работы:
1) оценка согласно концепции информационной энтропии по Шеннону и Хартли максимального объема измерительной информации, который может быть получен в режиме однократного преобразования ИАЦП с алгоритмом прямого декодирования однобитных измерительных сигналов и использован на этапе формирования технического решения в качестве критерия выбора и оптимизации структуры однобитного сигма-дельта-модулятора при проектировании ИАЦП;
2) алгоритм нелинейной цифровой фильтрации однобитных сигналов сигма-дельта-модуляторов высокого порядка, позволяющий по сравнению с линейными алгоритмами класса SINC в высокоточных ИАЦП широкого применения уменьшить максимальную погрешность квантования ИАЦП в режиме однократного преобразования в 5–10 раз или время преобразования – в 2–4 раза;
3) комплекс программ для инженерных расчетов, который на этапе синтеза структуры и алгоритма ИАЦП позволяет осуществлять:
– выбор порядка и вариант структуры однобитного сигма-дельта модулятора по критерию максимальной информативности;
– расчет области значений коэффициентов ОС по критерию устойчивости в режиме преобразования входных сигналов «малого» и «большого» уровня и выбор их оптимальных значений по критерию минимума СКО шума квантования;
– расчет минимального времени однократного преобразования ИАЦП для заданных вариантов однобитного сигма-дельта-модулятора и алгоритма ЦФ;
4) рекомендации по проектированию микромощных ИАЦП, использующих методы однобитной сигма-дельта-модуляции и алгоритмы линейной и нелинейной цифровой фильтрации в режиме однократного преобразования для многоузловой беспроводной сенсорной сети,
работающей в режиме микропотребления.
На защиту выносятся:
1) математическая оценка минимальной погрешности квантования ИАЦП в режиме однократного преобразования и алгоритм прямого декодирования измерительных сигналов однобитных сигма-дельта-модуляторов для ее реализации;
2) математическая модель в виде графоаналитического описания однобитных сигма-дельта-модуляторов высокого порядка, в которой учитывается эффект сквозного прохождения входного сигнала по цепи аналоговых интеграторов;
3) закономерность периодических колебаний однобитных выходных сигналов сигма-дельта-модуляторов k-го порядка в режиме аналого-цифрового преобразования сигналов малого уровня и полученные на ее основе математические условия их устойчивой работы;
4) формулы для расчета коэффициентов передаточной функции нелинейного цифрового фильтра-дециматора, оптимального по минимаксному критерию амплитуды шума квантования ИАЦП для режима однократного преобразования;
5) алгоритм расчета переходных процессов и минимального времени однократного преобразования ИАЦП, в котором учитывается нелинейность вида sign аналого-цифрового преобразования в однобитных сигма-дельта-модуляторах.
Внедрение результатов исследования. Теоретические и практические результаты работы использованы:
1) при выполнении НИР, осуществленных на кафедре «Информационно-вычислительные системы» в Пензенском государственном университете:
– «Разработка путей реализации режимов микропотребления многоузловой беспроводной сенсорной сети» (составная часть научно-
исследовательской работы «Датчик-ПГУ», Федеральное государственное унитарное предприятие «Научно-исследовательский институт физических измерений», госконтракт от 05.02.2009 г. № 783-0623/09);
– «Исследование непрерывно-дискретных систем со структурами неканонического вида» (по заданию Министерства образования и науки РФ на проведение НИР, регистрационный номер: 0120.0 52703 от 01.01.05 г.);
– «Исследование нелинейных непрерывно-дискретных структур динамического хаоса» (2010 г., по заданию Министерства образования и науки РФ на проведение НИР, регистрационный номер: 1.4.10 01201052991);
– «Проведение фундаментальных научных исследований свойств тонкопленочных нано- и микроэлектромеханических систем при воздействии стационарных и нестационарных температур» (в рамках выполнения аналитической ведомственной целевой программы Министерства образования и науки РФ «Развитие научного потенциала высшей школы (2009–2011)» (2011 г., регистрационный номер: 2.1.2/10274));
2) в учебном процессе кафедры «Информационно-вычислительные системы» Пензенского государственного университета.
Апробация работы. Основные положения диссертационной работы докладывались и обсуждались на НТС Пензенского государственного университета, Пензенской государственной технологической академии и ОАО «НИИ физических измерений» (Пенза), а также на ряде конференций и симпозиумов: Международная научно-практическая конференция «Актуальные научные исследования» (Киев, 2011); Международная научная конференция «Перспективные информационные технологии для авиации и космоса (ПИТ-2010)» (Самара, 2010); XI Международная научно-практическая конференция «Наука и современность – 2011» (Новосибирск, 2011); Международная научно-техническая конференция «Математическое и компьютерное моделирование естественнонаучных и социальных проблем» (Пенза, 2011); VII Всероссийская научно-техническая конференция «Современные методы и средства обработки пространственно-временных сигналов» (Пенза, 2009); Всероссийская научно-методическая конференция «Информатизация образования – Поволжье – 2010» (Пенза, 2010).
Публикации. По теме диссертации опубликовано 19 печатных работ, в том числе 3 статьи в изданиях, рекомендованных ВАК. Получены 3 свидетельства РФ о государственной регистрации программ для ЭВМ.
Структура и объем диссертации. Диссертация состоит из введения, четырех глав, заключения и приложений. Основной текст изложен на 135 страницах; библиография – 110 наименований, приложения – на 56 страницах – содержат описание комплекса программ, справочные данные и документы, подтверждающие внедрение результатов работы.
СОДЕРЖАНИЕ ДИССЕРТАЦИИ
Во введении обоснована актуальность темы исследования, кратко охарактеризовано состояние проблемы, сформулированы научная новизна, основные защищаемые положения, цели и задачи исследования.
В первой главе проведен анализ производства микросхем АЦП общего назначения на примере компаний Texas Instruments и Analog Devices (на них приходится около 70 % мирового рынка ЦАП и АЦП), который показал, что доля ИАЦП, использующих методы сигма-дельта-модуляции, составляет примерно 30 %.
Приведены обзор, анализ и классификация известных методов построения ИАЦП, использующих методы сигма-дельта-модуляции, определены тенденции их развития как базового элемента измерительных каналов и потенциальные возможности для совершенствования средств измерения. Было выявлено, что наибольшее распространение получили ИАЦП, использующие методы однобитной сигма-дельта- модуляции и алгоритмы линейной цифровой фильтрации. Показано, что для беспроводных датчиков, имеющих автономное электропитание, требуются 16–24-битные АЦП с наилучшим показателем «энергия/бит», т.е. количеством энергии, которая тратится на получение единицы объема измерительной информации в режиме однократного преобразования.
Для количественного сопоставления с характеристиками существующих ИАЦП была проведена оценка максимального объема измерителей информации, который теоретически может быть получен ИАЦП при использовании однобитных сигма-дельта-модуляторов в режиме однократного преобразования за M частных циклов работы модулятора. Разработан метод расчета, основанный на концепции информационной энтропии по Шеннону и Хартли, содержащий два этапа.
На первом этапе расчета для M частных циклов преобразования сигма-дельта-модулятора определяется количество K однобитных выходных уникальных кодов Nj(j = 1, 2, …, K) при равномерном законе распределения вероятности амплитуд входного сигнала в диапазоне 0–Xmax.
Максимальный объем измерительной информации IХ можно оценить по формуле Хартли:
(1)
Равенство в формуле (1) выполняется при условии одинаковой вероятности появления выходных кодов Nj, что имеет место только для однобитных сигма-дельта-модуляторов первого порядка.
На втором этапе для однобитных сигма-дельта-модуляторов высоких порядков рассчитывается вероятность Pj появления j-го кода:
, (2)
где Xj, Xj + 1 – нижняя и верхняя границы интервала значений амплитуды входного сигнала, которому соответствует уникальный выходной код Nj.
С учетом вероятности (2) появления выходных кодов Nj максимальный объем измерительной информации IШ, который может быть получен в режиме однократного преобразования ИАЦП с алгоритмом прямого декодирования однобитных измерительных сигналов сигма-дельта-модуляторов, можно оценить по формуле Шеннона:
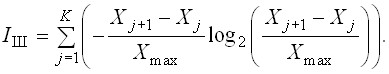(3)
Согласно алгоритму прямого декодирования каждому уникальному коду Nj ставится в соответствие амплитуда входного сигнала
Х*j = (Xj+1 + Xj) / 2 с интервалом неопределенности j = (Xj+1 – Xj) / 2, который можно рассматривать как погрешность квантования ИАЦП.
Разность IX – IШ дает количественную оценку неравномерности шкалы квантования при использовании алгоритма прямого декодирования.
В табл. 1 приведен результат расчета максимального объема измерительной информации для ИАЦП с однобитным сигма-дельта-модулятором 3-го порядка и алгоритмом прямого декодирования для различного числа частных циклов преобразования M.
Таблица 1
Результат расчета максимального объема измерительной информации
для ИАЦП
| M, кол. циклов | K, кол. кодов | IX, бит | IШ, бит | IX – IШ, бит |
| 24 | 401 | 8,65 | 8,20 | 0,45 |
| 32 | 1255 | 10,29 | 9,82 | 0,47 |
| 48 | 6294 | 12,62 | 12,13 | 0,49 |
| 64 | 19 883 | 14,28 | 13,75 | 0,53 |
| 96 | 99 780 | 16,61 | 16,06 | 0,55 |
| 128 | 31 347 | 18,26 | 17,69 | 0,57 |
На рис. 1 приведен пример расчета гистограммы распределения интервалов неопределенности j для варианта количества частных циклов M = 64.
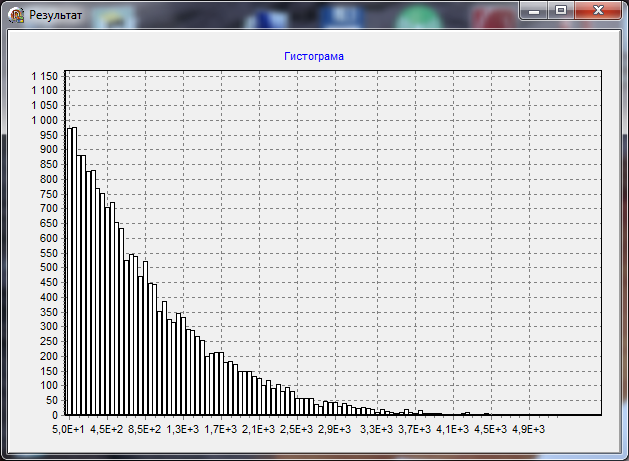
Рис. 1. Гистограмма распределения интервалов неопределенности j для однобитного сигма-дельта-модулятора 3-го порядка:
ось Х, масштаб по оси Х равен 220; количество частных
циклов M = 64; количество кодов K = 19 883
Сопоставление результатов расчета максимального объема измерительной информации, приведенных в табл. 1, с аналогичными характеристиками известных ИАЦП с однобитными сигма-дельта-модуляторами 3–4-го порядка показало, что существует потенциальная возможность увеличения разрядности выходного кода на 3–4 бита без увеличения времени преобразования за счет перехода к нелинейным алгоритмам цифровой фильтрации.
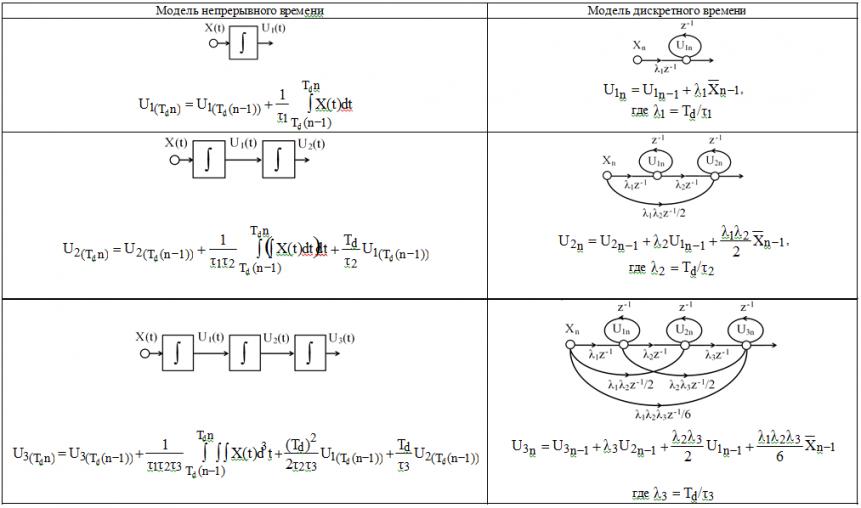
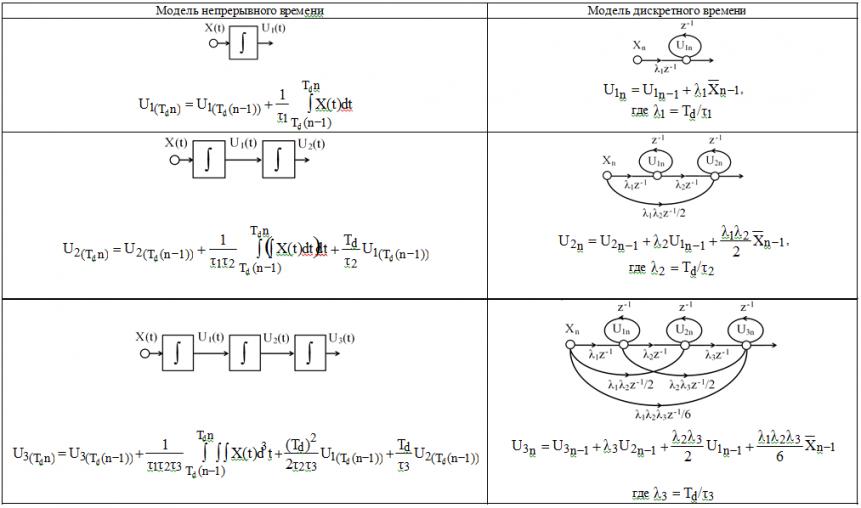
Во второй главе разработаны математические модели в виде систем нелинейных разностных уравнений, описывающих состояние интеграторов однобитных сигма-дельта-модуляторов с однопетлевой и многопетлевой структурой в дискретном пространстве времени. Для получения систем нелинейных разностных уравнений был использован графоаналитический метод описания сигма-дельта-модуляторов, в котором учитывался эффект сквозного прохождения входного сигнала по цепи аналоговых интеграторов в составе сигма-дельта-модуляторов. Математическая связь моделей непрерывного и дискретного времени, описывающих переходные процессы в цепочке аналоговых интеграторов, иллюстрируется в табл. 2. Данный переход корректен при выполнении условия постоянства амплитуды входного сигнала для цепи ОС в течение частного цикла преобразования.
Таблица 2
Эквивалентные преобразования непрерывной модели в дискретную
| Модель непрерывного времени | Модель дискретного времени |
 |  |
 |  |
 |  |
В качестве примера ниже приводится последовательность перехода согласно разработанному методу от структурной схемы однобитного сигма-дельта-модулятора 3-го порядка с многопетлевой структурой (рис. 2) к соответствующему графу (рис. 3) и системе нелинейных уравнений (4), которые описывают состояние интеграторов (для нулевых начальных условий) в дискретные моменты времени
t = Tdn, где Td – шаг дискретизации модулятора; n – номер частного цикла преобразования.
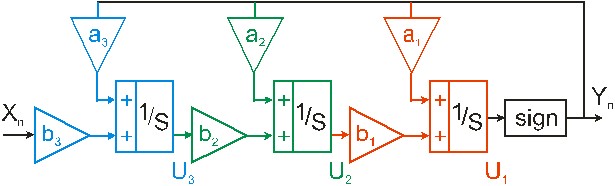
Рис. 2. Структура однобитного сигма-дельта-модулятора 3-го порядка
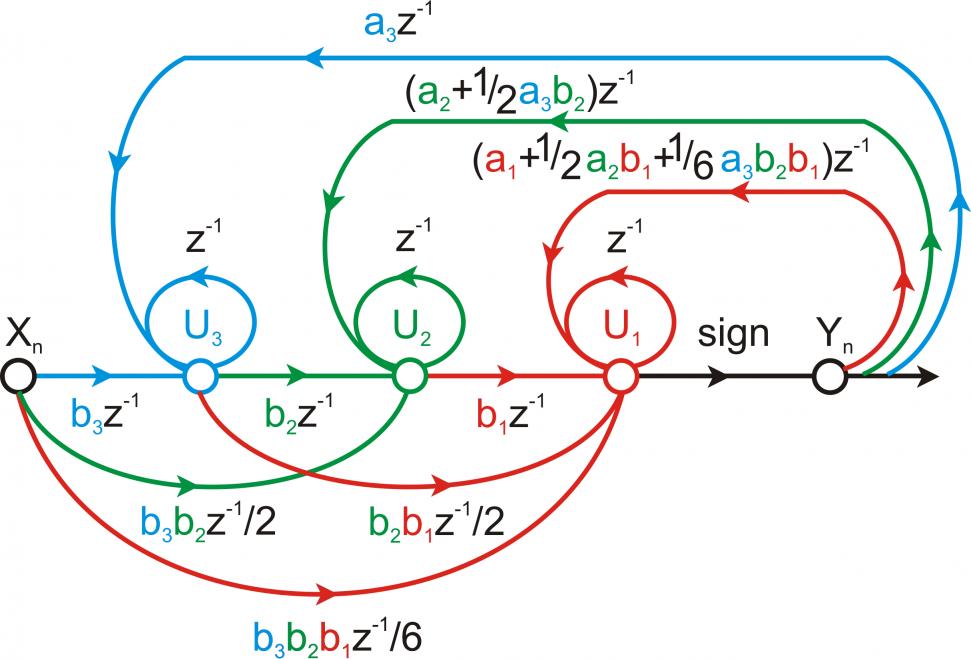
Рис. 3. Граф однобитного сигма-дельта-модулятора 3-го порядка
При проектировании ИАЦП, использующих методы сигма-дельта-модуляции, одной из сложных является задача нахождения условий обеспечения устойчивой работы модулятора при заданных входных сигналах за счет выбора значений коэффициентов ОС и ограничения максимальной амплитуды входного сигнала. Поскольку эта задача не имеет аналитического решения, выбор значений коэффициентов ОС осуществляется численными методами, что представляет значительные вычислительные трудности.
Для уменьшения объема численных расчетов значений коэффициентов ОС, обеспечивающих устойчивую работу однобитного сигма-дельта-модулятора и минимум СКО шума квантования, был предложен метод аналитического решения задачи нахождения условий обеспечения устойчивой работы однобитного сигма-дельта-модулятора в режиме преобразования сигнала малого уровня. Было установлено, что при входном сигнале малого уровня на выходе однобитного сигма-дельта-модулятора k-го порядка наблюдается знакочередующийся периодический сигнал Y[n] = ak[n] с периодом 2k, который не зависит от коэффициентов ОС. В табл. 3 приведены значения знаковой функции ak[n] для k = 1, 2, 3, 4.
Таблица 3
Значения знаковой функции ak[n]
| k\n | n = 0 | n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 |
| 1 | + | – | + | – | + | – | + | – |
| 2 | + | – | – | + | + | – | + | – |
| 3 | + | – | – | + | – | + | + | – |
| 4 | + | – | – | + | – | + | + | – |
| k\n | n = 8 | n = 9 | n = 10 | n = 11 | n = 12 | n = 13 | n = 14 | n = 15 |
| 1 | + | – | + | – | + | – | + | – |
| 2 | + | – | + | – | + | – | + | – |
| 3 | + | – | – | + | – | + | + | – |
| 4 | – | + | + | – | + | – | – | + |
Знаковая функция ak[n] может быть описана в общем виде полиномом
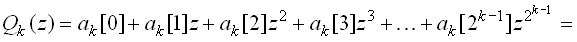
(5)
Выходной сигнал Yk[n] формируется как сумма реакций по каждой цепи ОС и в общем виде может быть рассчитан как
(6)
где
, 
, …,
–
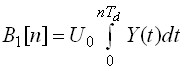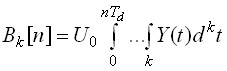это реакции интеграторов по k-й цепи ОС; 
– шаг дискретизации; 
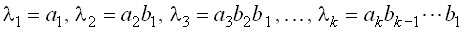– произведение постоянных времени интеграторов по каждой петле ОС; 
– амплитуда импульсов ОС.
Из условия Y[n] = ak[n], которое наблюдается при устойчивой работе однобитного сигма-дельта-модулятора k-го порядка в режиме преобразования сигнала малого уровня и с учетом (6), следует, что
. (7)
В табл. 4 приведены значения Bk[n] для k = 1, 2, 3 (U0 = 1).
Таблица 4
Значения Bk[n]
| Bk[n] | n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 |
| B1[n] | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| B2[n] | 1/2 | 1 | 1/2 | 0 | 1/2 | 1 | 1/2 | 0 |
| B3[n] | 1/6 | 1 | 11/6 | 2 | 11/6 | 1 | 1/6 | 0 |
Из уравнения (7) для n = 1, 2, 3, …, 2k можно составить систему неравенств из 2k уравнений, решением которой будут неравенства, ограничивающие область значений коэффициентов 
, соответствующих устойчивой работе однобитного сигма-дельта-модулятора в режиме преобразования сигнала малого уровня. Примеры решений для первых трех порядков приведены в табл. 5, где C – входной сигнал малого уровня (С 0).
Таблица 5
Примеры решений для первых трех порядков
| Порядок k = 1 | Порядок k = 2 | Порядок k = 3 |
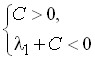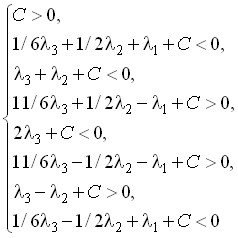 Решение: |  Решение:  |  Решение:  |
Область значений коэффициентов ОС устойчивой работы сигма-дельта-модулятора для режима малого сигнала уменьшается по мере увеличения амплитуды входного сигнала, и для уточнения их новых границ необходимо проведение дополнительных численных расчетов.
На рис. 4 приведен пример расчета области значений коэффициентов ОС 
(при условии 
) для модулятора 3-го порядка с многопетлевой структурой (см. рис. 2). Линиями ограничена область устойчивой работы модулятора (серое поле) для сигнала малого уровня согласно условию 
(см. табл. 5, k = 3), область устойчивой работы модулятора для сигналов большого уровня с амплитудой меньше 
отмечена белым полем и получена методом численного расчета по формуле (4).
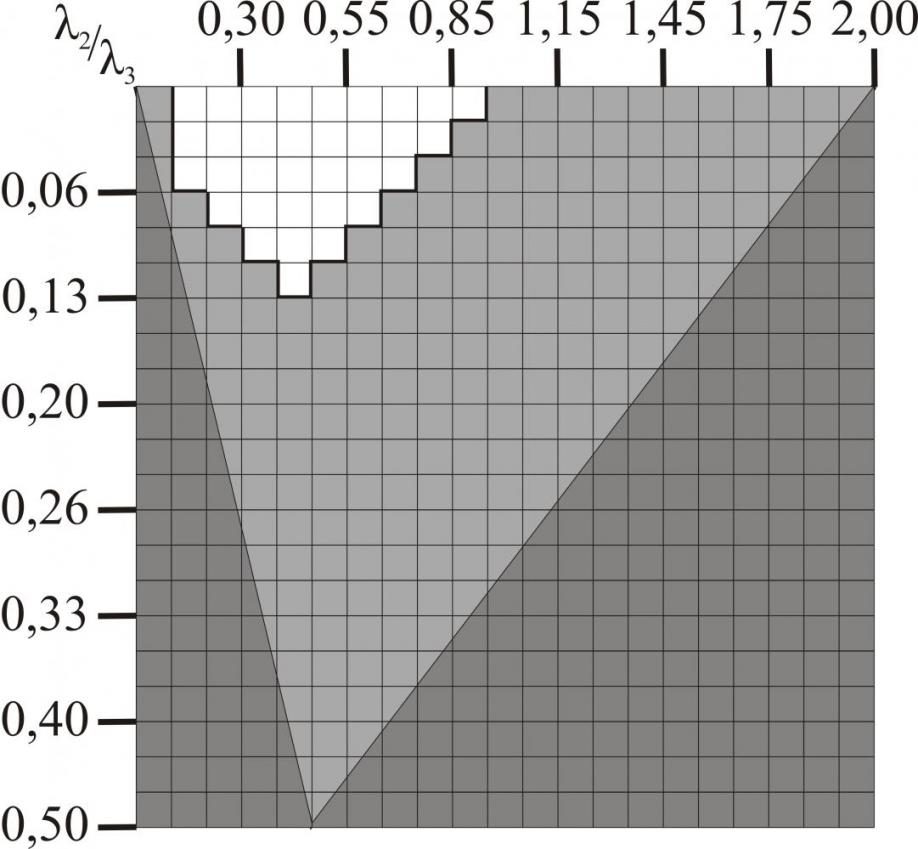
Рис. 4. Область устойчивой работы модулятора
Аналитическое решение задачи расчета значений коэффициентов ОС по критерию устойчивости работы однобитных сигма-дельта-модуляторов высоких порядков в режиме преобразования сигналов малого уровня позволяет существенно (на 1–2 десятичных порядка) уменьшить объем численных расчетов компьютерного моделирования на этапе проектирования ИАЦП.
В третьей главе рассмотрены вопросы синтеза алгоритмов нелинейной цифровой фильтрации однобитных сигналов сигма-дельта модуляторов по минимаксному критерию амплитуды шума квантования ИАЦП в режиме однократного преобразования. Предложено для синтеза алгоритмов нелинейной цифровой фильтрации использовать метод декомпозиции структур однобитных сигма-дельта модуляторов и принцип эквивалентности импульсных характеристик АФ и ЦФ.
Метод предполагает такую последовательность операций.
1. Используя метод декомпозиции, преобразуем структуру модулятора с выделением каналов прямого преобразования и канала ОС. Это иллюстрируется на примере однобитного сигма-дельта-модулятора 3-го порядка с многопетлевой структурой (рис. 5 и 6).
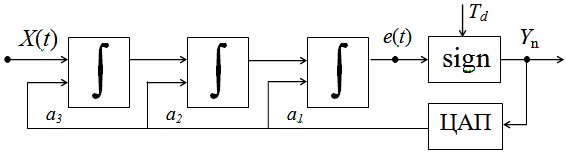
Рис. 5. Структура однобитного сигма-дельта-модулятора 3-го порядка
с многопетлевой структурой
Рис. 6. Эквивалентная структура однобитного сигма-дельта-модулятора, полученная методом декомпозиции
2. Для ИАЦП в режиме однократного преобразования начальные состояния интеграторов равны нулю. Это дает возможность аналитически рассчитать сигнал рассогласования e(t):
= 
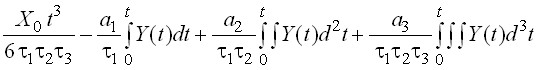, (8)
где A(t) – реакция интеграторов на входной сигнал X(t) = X0; B(t) – реакция интеграторов на сигнал ОС Y(t), а сигнал ОС Y(t) на каждом n-м цикле преобразования задается функцией sign:
Из формулы (8) следует, что амплитуду входного сигнала X0 можно выразить через амплитуду B(t) и погрешность квантования 
:
, (9)
где
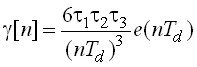. (10)
3. Для получения цифрового эквивалента входного сигнала X0 согласно формуле (9) небходимо синтезировать алгоритм ЦФ, реакция которого на однобитный выходной сигнал Y[n] будет с точностью до масштабного коэффициента совпадать с сигналом ОС B(nTd). Для синтеза алгоритма ЦФ воспользуемся принципом эквивалентности импульсных характеристик АФ и ЦФ, согласно которому передаточная функция H(z) линейной части алгоритма ЦФ находится путем перехода от передаточной функции АФ H(p) к эквивалентной передаточной функции ЦФ H(z). Критерий эквивалентности – это совпадение импульсной характеристики ЦФ с импульсной характеристикой АФ в моменты времени дискретизации. С учетом передаточной функции однобитного ЦАП в цепи ОС однобитного сигма-дельта-модулятора эквивалентную передаточную функцию ЦФ Hk(z) для цепочки из k интеграторов согласно принципу эквивалентности можно записать следующим образом:
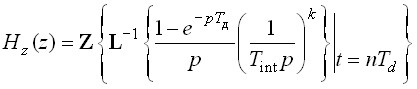, (11)
где L1{*} – оператор обратного преобразования Лапласа; Z{*} – оператор прямого z-преобразования.
4. Для получения алгоритма вычисления выходного кода X*[n] ИАЦП согласно формуле (10) введем элемент нелинейного функционального преобразования в линейную часть алгоритма ЦФ и перейдем от операторной формы записи алгоритма к временной.
В данном примере получим алгоритм нелинейного ЦФ 3-го порядка в виде системы рекурсивных уравнений:
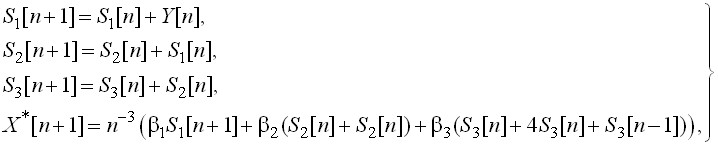(12)
где 
; 
; 
.
Для сравнения приведем алгоритм аналогичного линейного ЦФ типа SINС 3-го порядка:
(13)
где M – число циклов усреднения для каждого сумматора, общее число циклов ЦФ равно 3M.
Поскольку амплитуда сигнала рассогласования e(nTd) ограничена (
), то согласно (10) можно оценить максимальное значение погрешности квантования 
ИАЦП с модулятором 3-го порядка и алгоритмом нелинейного ЦФ в режиме однократного преобразования:
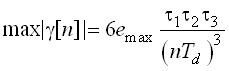, (14)
а с модулятором k-го порядка:
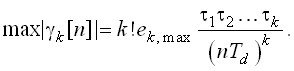(15)
На рис. 7,а,б приведены примеры расчета погрешности ИАЦП
с однобитным сигма-дельта-модулятором многопетлевой структуры
3-го порядка для нелинейного и линейного ЦФ 3-го порядка класса SINC с временем преобразования 96 тактов (M = 32). Постоянные времени интеграторов заданы 1 = 2 = 3 = 2Тd, для этих значений максимальный сигнал рассогласования составил 
. Согласно (14) получаем формулу для оценки погрешности 
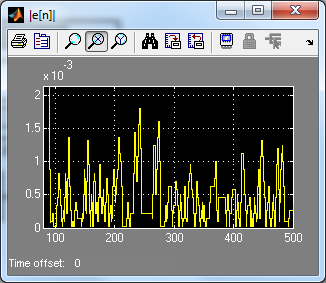
а) б)
Рис. 7. Погрешность квантования 
ИАЦП с нелинейным ЦФ (а)
и линейным ЦФ класса SINC (б)
Из рисунка видно, что использование алгоритма нелинейной цифровой фильтрации позволяет в режиме однократного преобразования (при нулевых начальных состояниях интеграторов) непрерывно получать на выходе ИАЦП цифровой код, пропорциональный входному сигналу. При этом погрешность квантования уменьшается обратно пропорционально n3 и для фиксированного времени преобразования
(n = 96) на десятичный порядок меньше, чем погрешность для варианта алгоритма линейного ЦФ.
В четвертой главе рассмотрены вопросы проектирования ИАЦП для беспроводных датчиков и построения на их основе автономных измерительных систем различного назначения: интеллектуальных измерительных систем экологического мониторинга и экологической безопасности; сетей интеллектуальных датчиков группового мониторинга параметров, автономных систем анализа электрокардиосигналов и многоузловой беспроводной сенсорной сети датчиков для контрольно-измерительной аппаратуры.
Было установлено, что для беспроводных датчиков оптимальными по критерию «энергия/точность» являются 1624-битные АЦП, использующие методы однобитной сигма-дельта-модуляции, работающие в режиме однократного преобразования. В том случае, когда нет ограничений на массогабаритные характеристики, преимуществом обладают однобитные сигма-дельта-модуляторы, выполненные на базе аналоговых интеграторов.
На основе полученных математических моделей однобитных сигма-дельта-модуляторов был разработан в среде Delphi 2009 комплекс программ численного расчета и анализа ИАЦП:
– оптимизации сигма-дельта-модуляторов n-го порядка;
– моделирования сигма-дельта-модуляторов высоких порядков;
– моделирования и визуализации динамики переходных процессов сигма-дельта-модуляторов ИАЦП.
Предложена методика проектирования ИАЦП, которая состоит из следующих этапов:
1) анализ задания, выбор структуры модулятора и ЦФ;
2) расчет области значений коэффициентов ОС сигма-дельта-модулятора по критерию устойчивости и минимума СКО шума квантования с учетом заданных допусков;
3) расчет времени переходного процесса ИАЦП;
4) синтез функциональной схемы сигма-дельта-модулятора и расчет постоянных времени интеграторов путем денормализации значений полученных коэффициентов ОС модели сигма-дельта-модулятора;
5) проверка полученного схемотехнического решения методом компьютерного моделирования с учетом влияния неидеальности элементов реальной электрической схемы.
Расчет времени переходных процессов необходим из-за сложности анализа динамики сигма-дельта-модуляторов. Особенностью предложенного метода является параллельный расчет СКО динамической погрешности и СКО шума квантования. Критерием остановки вычислений является их соразмерность.
В заключении даны рекомендации по проектированию ИАЦП, использующих методы однобитной сигма-дельта-модуляции для режима однократного преобразования, в части выбора порядка и варианта структуры однобитного сигма-дельта-модулятора, оценки его информативной способности, расчета области значений коэффициентов ОС по критерию устойчивости, рекомендации по синтезу алгоритмов нелинейной цифровой фильтрации.
Предложенная методика расчета используется при проектировании микромощных ИАЦП в составе многоузловой беспроводной сенсорной сети для решения инженерных задач по обеспечению режима микропотребления.
ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ
1. Установлено, что для построения беспроводных сенсорных сетей наиболее перспективными являются ИАЦП, использующие методы однобитной сигма-дельта-модуляции и алгоритмы нелинейной цифровой фильтрации, с применением аналоговых интеграторов, выполненных по технологии «система на кристалле» и требующих наименьших энергетических затрат на получение заданного объема измерительной информации.
2. Получена математическая оценка минимального значения погрешности квантования, которая может быть достигнута ИАЦП с однобитным сигма-дельта-модулятором высокого порядка в режиме однократного преобразования, что позволяет дать количественную оценку потенциальной возможности улучшения их метрологических характеристик.
3. Разработан комплекс программ численного расчета и анализа ИАЦП, работающих в режиме однократного преобразования. Комплекс программ разработан в среде Delphi 2009 и позволяет осуществлять:
– выбор порядка и вариант структуры однобитного сигма-дельта- модулятора по критерию максимальной информативности;
– расчет области значений коэффициентов ОС однобитного сигма-дельта-модулятора по критерию устойчивости в режиме преобразования входных сигналов «малого» и «большого» уровня;
– оптимизацию структурно-алгоритмических решений ИАЦП по критерию минимума СКО погрешности квантования;
– расчет минимального времени однократного преобразования ИАЦП для заданных вариантов однобитного сигма-дельта-модулятора и алгоритма ЦФ.
4. Найдено аналитическое решение задачи расчёта значений коэффициентов ОС по критерию устойчивости работы однобитных сигма-дельта-модуляторов высоких порядков в режиме преобразования сигналов малого уровня, которое позволяет существенно (на 1–2 десятичных порядка) уменьшить объем численных расчетов компьютерного моделирования на этапе проектирования ИАЦП.
5. Разработан нелинейный алгоритм работы ЦФ сигналов однобитных сигма-дельта-модуляторов, работающих в режиме однократного преобразования, применение которого по сравнению с аналогичным линейным алгоритмом ЦФ класса SINC позволяет в 5–10 раз уменьшить погрешность квантования или в 2–4 раза – время преобразования существующих ИАЦП.
6. Разработаны графоаналитические модели расчета и анализа сигма-дельта-модуляторов с однопетлевой и многопетлевой структурой.
7. Разработаны рекомендации по проектированию микромощных ИАЦП, использующих методы однобитной сигма-дельта-модуляции и алгоритмы линейной и нелинейной цифровой фильтрации в режиме однократного преобразования для многоузловой беспроводной сенсорной сети, работающей в режиме микропотребления.
ОСНОВНЫЕ ПУБЛИКАЦИИ ПО ТЕМЕ ДИССЕРТАЦИИ
Статьи в журналах, рекомендованных ВАК
1. Тер-Аракелян, Р. Г. Метод определения длительности переходного процесса в -АЦП с однобитным -модулятором высокого порядка / Б. В. Чувыкин, В. Н. Ашанин, Р. Г. Тер-Аракелян // Известия высших учебных заведений. Поволжский регион. Технические науки. – 2010. – № 3(15). С. 7081.
2. Тер-Аракелян, Р. Г Оценка максимальной погрешности сигма-дельта-модуляторов с использованием метода декомпозиции / Б. В. Чувыкин, Р. Г. Тер-Аракелян // Научно-технический вестник Поволжья. – 2011. – № 5. С. 264267.
3. Тер-Аракелян, Р. Г Проектирование сигма-дельта-модуляторов по критерию устойчивости / Б. В. Чувыкин, В. Н. Ашанин, Р. Г. Тер-Аракелян // Известия высших учебных заведений. Поволжский регион. Технические науки. 2011. –
№ 4 (20). С. 5162.
Публикации в других изданиях
4. Тер-Аракелян, Р. Г. Модель -АЦП с модулятором 3-го порядка /
Б. В. Чувыкин, И. А. Долгова, Р. Г. Тер-Аракелян // Вычислительные системы и технологии обработки информации : межвуз. сб. науч. тр. – Пенза : Изд-во ПГУ, 2010. – Вып. 9(32). С. 150153.
5. Тер-Аракелян, Р. Г. Графоаналитический метод моделирования сигма-дельта-преобразователей информации замкнутой структуры / Б. В. Чувыкин,
А. В. Селезнев, Р. Г. Тер-Аракелян // Перспективные информационные технологии для авиации и космоса (ПИТ-2010) : тр. междунар. конф. с элементами научной школы для молодежи. Самара : М-во образования и науки РФ : СГАУ, 2010. С. 6063.
6. Тер-Аракелян, Р. Г. Математическое моделирование детерминированного хаоса в первичных преобразователях информации / Б. В. Чувыкин,
И. А. Долгова, Р. Г. Тер-Аракелян // Математическое и компьютерное моделирование естественнонаучных и социальных проблем : сб. ст. III Междунар. науч.-техн. конф. молодых специалистов, аспирантов и студентов. – Пенза : Приволж. Дом знаний, 2009. – С. 105106.
7. Тер-Аракелян, Р. Г. Корреляционный анализ сигналов сейсмических датчиков волн Релея с использованием -АЦП / Р. Г. Тер-Аракелян // Современные методы и средства обработки пространственно-временных сигналов : сб. ст.
VII Всерос. науч.-техн. конф. – Пенза : Приволж. Дом знаний, 2009. – С. 3335.
8. Тер-Аракелян, Р. Г. Континуально-дискретный алгоритм Хаара для обработки пространственно-временных сигналов на базе интегрирующего АЦП /
Р. Г. Тер-Аракелян // Современные методы и средства обработки пространственно-временных сигналов : сб. ст. VII Всерос. науч.-техн. конф. – Пенза : Приволж. Дом знаний, 2009. – С. 3537.
9. Тер-Аракелян, Р. Г. Энтропийная оценка информативности измерительных преобразователей с нелинейной шкалой квантования / Б. В. Чувыкин,
Р. Г. Тер-Аракелян, И. А. Сидорова // Математическое и компьютерное моделирование естественнонаучных и социальных проблем : сб. ст. V Междунар. науч.-техн. конф. молодых специалистов, аспирантов и студентов. – Пенза : Приволж. Дом знаний, 2011. – С. 192197.
10. Тер-Аракелян, Р. Г. Анализ флуктуационных шумов квантования
-АЦП / И. А. Долгова, И. А. Сидорова, Р. Г. Тер-Аракелян // Наука и современность – 2011 : сб. материалов XI Междунар. науч.-практ. конф. – Новосибирск, 2011. – С. 274279
11. Ter-Arakelyan, R. G. Estimation method of transient process duration in
-ADC with one-bit -modulator of high order / B. V. Chuvykin, R. G. Ter-Arakelyan, I. A. Sidorova // Актуальные научные исследования : материалы Междунар. науч.-практ. конф. – Киев, 2011. – С. 1828.
12. Программа оптимизации сигма-дельта-модуляторов n-го порядка : свидетельство о государственной регистрации программы для ЭВМ № 2011612981 / Р. Г. Тер-Аракелян. – Опубл. 17.06.2011.
13. Программа моделирования и визуализации динамики переходных процессов сигма-дельта-модуляторов интегрирующих АЦП : свидетельство о государственной регистрации программы для ЭВМ № 2011616089 / Р. Г. Тер-Аракелян. – Опубл. 04.08.2011.
14. Программа моделирования сигма-дельта модуляторов высоких порядков : свидетельство о государственной регистрации программы для ЭВМ
№ 2011613923 / Р. Г. Тер-Аракелян. – Опубл. 04.10.2011.
Научное издание
ТЕР-АРАКЕЛЯН Руслан Геворкович
ИНТЕГРИРУЮЩИЕ АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ,
ИСПОЛЬЗУЮЩИЕ МЕТОДЫ ОДНОБИТНОЙ
СИГМА-ДЕЛЬТА-МОДУЛЯЦИИ
Специальность 05.11.01 – Приборы и методы измерения
(электрические и магнитные величины)
Редактор Е. П. Мухина
Технический редактор Р. Б. Бердникова
Компьютерная верстка Р. Б. Бердниковой
Распоряжение № 5/2012 от 25.01.2012.
Подписано в печать 17.01.12.
Формат 60841/16. Усл. печ. л. 1,16.
Тираж 100. Заказ № 10.
Издательство ПГУ.
440026, Пенза, Красная, 40.
Тел./факс: (8412) 56-47-33; e-mail: [email protected]
