Методы и средства неразрушающего тепло в ого контроля температурно-временных характеристик структурных превращений в полимерных материалах

На правах рукописи

Майникова Нина Филипповна

МЕТОДЫ И СРЕДСТВА
НЕРАЗРУШАЮЩЕГО ТепловОГО КОНТРОЛЯ
ТЕМПЕРАТУРНО-ВРЕМЕННЫХ ХАРАКТЕРИСТИК СТРУКТУРНЫХ ПРЕВРАЩЕНИЙ
В ПОЛИМЕРНЫХ МАТЕРИАЛАХ

05.11.13 – Приборы и методы контроля природной среды,

веществ, материалов и изделий

А В Т О Р Е Ф Е Р А Т

диссертации на соискание ученой степени

доктора технических наук

Тамбов 2007

Работа выполнена в Государственном образовательном учреждении высшего профессионального образования «Тамбовский государственный технический университет» (ТГТУ).

Научный консультант: Заслуженный деятель науки и техники РФ, доктор технических наук, профессор Мищенко Сергей Владимирович

Официальные оппоненты: Заслуженный деятель науки РФ, доктор физико-математических наук, профессор Карташов Эдуард Михайлович

Заслуженный деятель науки РФ,
доктор технических наук, профессор
Шатерников Виктор Егорович

Доктор технических наук, профессор Герасимов Борис Иванович

Ведущая организация: ЗАО НИИИН МНПО «Спектр», г. Москва

Защита диссертации состоится 23 ноября 2007 г. в 14:00 на заседании диссертационного совета Д 212.260.01 Тамбовского государственного технического университета по адресу: г. Тамбов, ул. Советская, 106, ТГТУ, Большой зал.

Отзывы в 2-х экземплярах, скрепленные гербовой печатью, просим направлять по адресу: 392000, г. Тамбов, ул. Советская, 106, ТГТУ, ученому секретарю.

С диссертацией можно ознакомиться в библиотеке университета.

Автореферат разослан « » 2007 г.

Ученый секретарь

диссертационного совета,

д.т.н., профессор А.А. Чуриков

общая характеристика работы

Актуальность темы исследования. Все усложняющиеся задачи по повышению качества промышленной продукции, надежности объектов требуют дальнейшего совершенствования методов и средств контроля и диагностики состояний изделий из полимерных материалов (ПМ). Широкое применение ПМ обусловлено разнообразием их свойств, которые можно изменять, используя новые технологии. Гибкость молекул полимеров обеспечивает наличие ряда агрегатных и фазовых состояний, богатство морфологических структур кристаллических образований, различные физические и релаксационные состояния аморфного полимера. Введение пластификаторов, наполнителей в ПМ влияет на все типы состояний и переходов в готовых изделиях при эксплуатации. Изучение суперпозиций состояний и переходов ПМ необходимо для назначения технологических режимов их переработки в изделия и последующей эксплуатации.

Применяющиеся для изучения ПМ рентгеновские методы, дифференциальный термический анализ, дифференциальная сканирующая калориметрия и др. требуют изготовления специальных образцов, длительного времени испытания, использования дорогостоящего оборудования. Среди существующих методов термичес­кого анализа (ТА) не имеется неразрушающих тепловых методов для регистрации температурно-временных характеристик структурных превращений в ПМ.

Учитывая, что методы неразрушающего контроля (НК) базируются на моделях
полупространств (плоского, сферического), получение точного решения задачи нестационарного теплопереноса в системе: изделие-зонд при наличии структурного превращения в ПМ, затруднительно, так как не известны теплофизические свойства (ТФС) полимерного материала в температурном интервале структурного превращения, не известен закон движения границы структурного перехода. Известные решения краевых задач, описывающие процесс распространения тепла в теле при наличии структурного превращения, сложны и не пригодны для использования в методе НК.

А.В. Лыковым доказано, что регулярные тепловые режимы первого и второго рода имеют общее свойство, характеризующееся независимостью от времени отношения теплового потока в любой точке тела к потоку тепла на его поверхности. Математичес­кая модель, описывающая термограмму, в данном случае чаще всего является линейной по параметрам или легко линеаризуется. Однако основная часть этих методов базируется на моделях для тел конечных размеров (пластина, шар). Применительно же к методам НК следует говорить не о регулярном тепловом режиме для всего тела (так как оно принимается неогра­ниченным), а о регуляризации теплового процесса только для определенной области тела. Следовательно, если проводить ТА, основываясь только на участках термограммы, соответствующих регуляризации теплового режима в области нагревателей и термоприемников, то расчетные соотношения будут более простыми и во многих случаях линейными по параметрам. Причем, чем больше таких характерных участков будет найдено и описано аналитически, тем больше появляется возможностей определить температурно-временные характеристики структурных превращений в исследуемом объекте по аномальным значениям ТФС при изменении температуры, используя различные математические модели, адекватно отражающие процессы теплопереноса в определенные интервалы времени.

Таким образом, проблема разработки методов НК и реализующих их мобильных приборов и информационно-измерительных систем (ИИС), обеспечивающих точность и оперативность определения температурно-временных характеристик структурных превращений в полимерах и композитах на их основе как на стадии технологического контроля в процессе их производства, так и в процессе эксплуатации изделий из них, является важной и актуальной.

Диссертация выполнялась в соответствии со следующими планами научно-исследовательских работ (НИР): межвузовской программой «Диагностика и контроль» на 1993–1995 гг. (тема «Разработка микропроцессорных приборов и ИИС НК качественных показателей изделий»); планом НИР Госкомитета РФ по высшему образованию на 1991–2000 гг. (тема «Разработка интегрированных автоматизированных систем для организации технологических процессов теплопереноса»); межвузовской программой «Неразрушающий контроль и диагностика» на 1996–2000 гг.; планами НИР Тамбовс­кого государственного технического университета на 1996–2007 гг.

Целью работы является разработка методов и средств, обеспечивающих оперативный неразрушающий тепловой контроль температурно-временных характеристик структурных превращений (переходов) в полимерах и композиционных материалах на их основе.

Для достижения указанной цели были поставлены и решены следующие задачи:

–обоснована актуальность и определены основные направления разработки
методов и средств НК температурно-временных характеристик структурных превра­щений в ПМ;

–применен многомодельный подход к анализу и аналити­ческому описанию
нестационарного процесса теплопереноса с учетом множества состояний функциони­рования тепловой системы;

теоретически исследованы возможности использования контактного зондового метода неразрушающего ТА и возникающих процессов нестационарной теплопровод­ности в ПМ для определения законов движения границ фазовых переходов (ФП);

–определены оптимальные условия НК температурно-временных характеристик структурных превращений в ПМ, обеспечивающие адекватность разработанных математических моделей распространения тепла в полуограни­ченных телах от действия плоского круглого источника тепла при регуляризации тепловых потоков в локальных областях, реальным процессам;

–разработаны методы и средства НК, обеспечивающие достаточную точность и оперативность определения температурно-временных характеристик структурных превращений в ПМ по аномальным изменениям ТФС, а также по ряду информативных параметров разработанных математических моделей за счет использования характерных участков экспериментальных термограмм;

–проведен анализ источников погрешности измерений температурных характе­ристик структурных переходов в ПМ предлагаемыми методами НК;

–разработаны математическое, алгоритмическое, программное и аппаратное
обеспечения мобильных приборов и ИИС, реализующих разработанные методы НК
в промышленных и лабораторных условиях;

–проведены экспериментальные исследования, производственные испытания и внедрение результатов работы.

Научная новизна

1.  Впервые разработаны основы многомодельного подхода к анализу и аналитическому описанию нестационарного процесса тепло­переноса с учетом множества состояний функционирования тепловой системы при НК температурно-временных характеристик структурных превращений в ПМ. Данный подход позволил использовать в качестве основы математического и алгоритмического обеспечений многоканальной ИИС полученные автором решения краевых задач нестационарной теплопроводности в системе двух тел, нагреваемых через бесконечный плоский и поверхностный сферический нагреватели тепловыми потоками постоянной мощности. В конечном итоге существенно расширился температурный диапазон, в котором возможно определение температурно-временных характеристик структурных превращений (фазовых и релаксационных) в ПМ в одном краткосрочном опыте без разрушения объекта исследования. Информация о фазовых переходах позволяет назначать оптимальные технологические режимы переработки ПМ в изделия, а информация о релаксационных переходах в ПМ необходима для назначения условий последующей эксплуатации изделий из них.

2.  Разработаны и исследованы математические модели, позволяющие определять
неразрушающим способом законы движения границ ФП по температурным откликам на воздействие от круглого источника тепла постоянной мощности, действующего на поверхности полуограниченного тела из ПМ. Знание закона движения границы ФП существенно упрощает определение температурного поля и величины теплового эффекта в исследуемом полимерном объекте.

3.  Получены решения краевых задач нестационарной теплопроводности в системе двух тел, имеющих равномерное начальное температурное распределение и нагреваемых через бесконечный плоский и поверхностный сферический нагреватели тепловыми потоками постоянной мощности, в формах, пригодных для использования в качестве основы математического и алгоритмического обеспечений многомодельных методов и ИИС НК температурно-временных характеристик структурных превращений в ПМ.

4.  Разработаны новые контактные методы НК структурных превращений в ПМ, основанные на нестационарном распространении тепла от тонкого плоского круглого источника постоянной мощности при регуляризации тепловых потоков на моделях плоского и сферического полупространств. Методы позволяют регистрировать и различать твердофазные полиморфные и релаксационные переходы в ПМ при одной реализации эксперимента, обеспечивают осуществление самоконтроля.

Первый метод основан на регистрации аномальных изменений ТФС в областях структурных переходов при нагреве и остывании изделий из ПМ и предусматривает предварительную градуировку ИИС по образцовым мерам. Данный метод НК структурных превращений в ПМ обеспечивает повышенную точность и достоверность результатов измерений при работе ИИС. Во втором методе НК структурных превращений в ПМ, основанном на регистрации изменений ряда информативных параметров математических моделей, адекватно описывающих рабочие участки экспериментальных термограмм, и величин дисперсии этих параметров без дополнительных градуировочных экспериментов, значительно упрощена и ускорена обработка результатов, что существенно удешевляет метод. Данный метод позволяет проводить экспресс-контроль структурных превращений в ПМ, а также экспресс-анализ экспериментальных данных при выборе режимных параметров работы ИИС. Одновременно с двумя перечисленными методами ИИС реализует регистрацию изменений скоростей нагрева или остывания, определяемых с экспериментальных термограмм, зафиксированных на объектах исследования при НК.

Практическая ценность работы. Созданы мобильные приборы и ИИС, реализу­ющие разработанные методы, обеспечивающие достаточную точность и оперативность определения температурно-временных характеристик структурных превращений в ПМ.

Созданные методы и программные продукты защищены свидетельствами об
официальной регистрации программ и патентами на изобретения Российской Федерации.

Работоспособность созданных методов и средств НК, оперативность и достоверность полу­чаемой с их помощью информации подтверждены при исследованиях структурных превращений (фазовых и релаксационных) в политетрафторэтилене (ПТФЭ), коксонаполнен­ном фторопласте (Ф4К20), полиметилметакрилате (ПММА), полиэтилене низкой плотности (ПЭНП), полистироле (ПС) и в полиамидах – поликапроамиде и капролоне.

Реализация научно-технических результатов. Научные результаты, полученные в диссертационной работе, подтверждены актами об их использовании и внедрении, выданными: РХТУ им. Д.И. Менделеева (Москва, 1996, 2003 гг.); ОАО «Завод Комсомолец» (Тамбов, 1998 г.); ОАО «Завод технологического оборудования» (Тамбов, 1998 г.); ОАО «Бокинский силикатный завод» (Бокино, Тамбовская обл., 1998, 2005 гг.);
ОАО «НИИХИМПОЛИМЕР» (Тамбов, 2001 г.); ОАО «Алмаз» (Котовск, Тамбовская обл., 2001 г.); ФГУП «ТЗ Октябрь» (Тамбов, 2003 г.); ОАО «Электроприбор» (Тамбов, 2003 г.); Липецким государственным техническим университетом (Липецк, 2004 г.);
ЗАО «ТАМАК» (Тамбов, 2004 г.); ФГУП «Котовский завод пластмасс» (Котовск, Тамбовская обл., 2004 г.); ОАО «Ливныпластик» (Ливны, Орловская обл., 2005 г.). Результаты диссертационной работы используются в Тамбовском государственном техническом университете при подготовке инженеров.

Апробация работы. Результаты диссертационной работы докладывались и обсуждались на научно-технических конференциях (НТК), Международных школах, в том числе: VII Междунар. НТК «Оптические, радиоволновые, тепловые методы и средства контроля природной среды, материалов и промышленных изделий» (Череповец, 1997 г.); II – IV Российских национальных НТК по теплообмену (Москва, 1998, 2002, 2006 гг.); Междунар. НТК «Системные проблемы надежности, математического моделирования и информационных технологий» (Москва, 1998 г.); I Всероссийской НТК «Компьютерные технологии в науке, проектировании и производстве» (Н. Новгород, 1999 г.); IV Всероссийской НТК «Методы и средства измерений физических величин» (Н. Новгород, 1999 г.); Междунар. НТК «Информационные технологии в проектировании микропроцессорных систем» (Тамбов, 2000 г.); I, II Междунар. НТК «Теория, методы и средства измерений, контроля и диагностики» (Новочеркасск, 2000, 2001 гг.); IV, V Междунар. теплофизических школах (Тамбов, 2001, 2004 гг.); XV Междунар. НТК «Математические методы в технике и технологиях», (Тамбов, 2002 г.); V – IX Междунар. НТК «Фундаментальные и прикладные проблемы приборостроения» (Москва, 2002 – 2007 гг.);
XI Российская НТК по теплофизическим свойствам веществ (СПб, 2005 г.),
IV, V Междунар. НТК «Проблемы промышленной теплотехники» (Украина, Киев, 2005, 2007 г.).

На защиту выносятся

1.  Результаты применения к НК принципа моделируемости теории систем, включающего постулат многообразия моделей, согласно которому сложная система может быть представлена конечным множеством моделей, различающихся используемыми математическими зависимостями и физическими закономерностями.

2.  Метод НК температурно-временных характеристик структурных превращений в ПМ, основанный на регистрации аномальных изменений ТФС в областях структурных переходов при нагреве и остывании изделий из ПМ с предварительной градуировкой ИИС по образцовым мерам.

3.  Метод НК температурно-временных характеристик структурных превращений в ПМ, основанный на регистрации ряда информативных параметров математических моделей, адекватно описывающих рабочие участки экспериментальных термограмм, и по величинам дисперсии этих параметров без дополнительных градуировочных экспериментов.

4.  Математические модели, позволяющие определять неразрушающим способом законы движения границ ФП по температурным откликам на воздействие от круглого источника тепла постоянной мощности, действующего на поверхности полуограниченного тела из ПМ.

5.  Математическое, алгоритмическое, программное и аппаратное обеспечения
мобильных приборов и ИИС, реализующих разработанные методы НК в промышленных и лабораторных условиях.

Публикации. Материалы диссертационной работы опубликованы в 2 книгах, 1 препринте, в 90 научных статьях и докладах, 3 патентах на изобретения Российской Федерации, 5 свидетельствах об официальной регистрации программ.

Все результаты, составляющие основное содержание диссертации, получены автором самостоятельно. Во всех совместных опубликованных статьях, докладах и патентах автором сформулированы постановка задачи и метод ее решения.

Структура и объем работы. Диссертационная работа состоит из введения, семи глав, заключения, списка использованных источников и приложений. Основная часть диссертации изложена на 435 страницах машинописного текста, содержит 200 рисунков и 35 таблиц. Список использованных источников включает 433 наименования.
Приложения содержат 45 страниц.

Содержание работы

Во введении обоснована актуальность темы, определены цель и задачи работы, раскрыты научная новизна и практическая ценность, приведены результаты апробации и реализации работы. Сформулированы результаты, выносимые на защиту.

В первой главе приведены обзор и сравнительный анализ известных методов и средств контроля структурных превращений (фазовых и релаксационных) в ПМ. Отме­че­но, что среди существующих методов ТА не имеется неразрушающих методов для осу­ществления регистрации температурно-временных характеристик структурных превра­щений в полимерах и определения законов движения границ фазовых переходов в ПМ.

Известные решения краевых задач теплопроводности стефановского типа сложны для реализации в способах НК структурных превращений. Указанные обстоятельства требуют поиска новых моделей и их аналитических решений, разработки алгоритмического обеспечения, измерительных методик, пригодных к использованию в способах НК. На основе анализа современного состояния теории и практики теплофизических измерений определены наиболее перс­пек­тивные направления исследований.

Показано, что современные методы НК наиболее эффективно реализуются ИИС, позволяющими автоматизировать проведение измерений, адаптивно изменять режимные параметры, обеспечивать адекватность физической и математической моделей теплового процесса, обеспечивать оперативность и точность измерений при сохра­не­нии целостности и эксплуатационных характеристик объектов исследования. Определена область исследования, сформулированы задачи и намечены пути их решения.

Во второй главе изложен многомодельный подход к разработке методов НК структурных превращений в ПМ.

Согласно принципу моделируемости теории систем, включающему постулат
многообразия моделей, сложная система может быть представлена конечным множеством моделей, которые различаются используемыми математическими зависимостями и физическими закономерностями.

Динамика тепловой системы при НК характеризуется следующими переменными: вектором входа, характеризующим тепловое воздействие; вектором переменных состоя­ния, в качестве которого рассматриваются тепловые потоки, проходящие через точки контроля сис­темы; вектором выхода – значениями температур Т в точках контроля.
При смене условий тепловая система переходит из одного состояния функционирования hi в другое hi+1 (i = 1, 2, 3, …, n – 1). Все возможные состояния тепловой системы образуют множество состояний функционирования (МСФ).

Основу математической модели Mh в состоянии функционирования h составляют:
1) дифференциальное уравнение теплопроводности (ДУТ); 2) начальные условия (НУ);
3) граничные условия (ГУ). Множество таких моделей для всех образует модель на МСФ – MH.

На термограммах, зафиксированных при НК, можно выделить два вида участков: участки, на которых наблюдается хорошее совпадение экспериментальных и расчетных значений температур, и участки, для которых построение математических моделей вызывает большие трудности. Участки первого вида названы рабочими, а второго – переходными. За одну реализацию эксперимента появляется возможность определить ряд ТФС исследуемого объекта с использованием различных математических моделей, адекватно отражающих реальный процесс теплопереноса в определенные интервалы времени. При нагреве и остывании системы структурные превращения в ПМ, сопровождающиеся тепловыми эффектами, проявляются на экспериментальных термограммах и могут быть выявлены по отклонениям от аналитических моделей.

Пусть ИИС некоторое время находится в четком (однородном) состоянии функционирования h, тогда процесс измерения адекватно описывается одним оператором, соблюдаются необходимые ограничения и условия. Все четкие состояния h образуют подмножество четких состояний H0. Когда описание процесса измерения на определенном интервале времени одним (известным) оператором с соответствующими условиями и ограничениями можно признать лишь приближенным, ИИС переходит в нечеткое (переходное) состояние . В этом состоянии процесс может быть представлен супер­позицией различных операторов. Все нечеткие состоя­ния образуют подмножество нечетких состояний .

Модель процесса измерения MH на множестве состояний функционирования H образуется совокупностями моделей {Мh , } и {, }, т. е.

.

Исследования показали, что в отсутствии непредсказуемых изменений состояний функционирования модель процесса измерения на множестве H представляет собой кортеж моделей вида

. (1)

Структурное превращение в ПМ может быть зарегистрировано в рабочем
состоянии функционирования по аномальным изменениям ТФС.

Идентифицируемые состояния функционирования образуют подмножество
рабочих состояний . Модели используются при разработке математического обеспечения методов и средств НК структурных превращений в ПМ.

В состоянии процесс может быть представлен суперпозицией (взвешенной суммой) различных операторов, при этом "веса" этих операторов не остаются постоянными. Например, модель в нечетком состоянии в момент времени может быть записана в виде:

, (2)

где и – модели в четких состояниях и ; – весовой коэф­фици­ент, изменяющийся во времени; [", "'] – временной интервал действия модели .

С позиции теории нечетких множеств состояниям соответствуют функции принадлежности, характеризующие степень уверенности в том, что вместо модели можно использовать одну из моделей четкого состояния .

Процедура определения температурно-временных характеристик структурных превращений в ПМ в состояниях включает следующие операторы:

– на основе сопоставления экспериментальных данных и данных, полученных с использованием математических моделей , осуществляется поиск рабочих участков термограмм , где эти модели адекватно описывают тепловой процесс (к – номер рабочего участка);

– по рабочим участкам термограмм определяются параметры математических моделей;

– на основании параметров математических моделей определяется (массив ТФС и других существенных параметров, характеризующих свойства материала) на каждом рабочем участке термограмм;

– на основе анализа
оценок параметров (i – номер оценки по k точкам измерения
(k – нечетное число, более трех); Nn – число оценок для n-ой термограммы) и используемых статистических критериев (– задаваемый уровень доверия для критерия ) определяются температурно-временные характеристики структурных превращений на каждой из термограмм для рабочего участка с номером к;

– на основе анализа
характеристик и соответствующих скоростей изменения температуры определяется вид структурного превращения (фазовый или релаксационный).

ТФС исследуемых ПМ в температурно-временном интервале рабочего участка вне зоны структурного превращения изменяются несущественно по сравнению с аномалиями ТФС при структурном переходе. Модели, описывающие экспериментальные термограммы на рабочих участках вне зоны структурного превращения, находятся на основе решений соответствующих краевых задач теплопроводности.

Многомодельный подход к анализу и аналитическому описанию нестационарного процесса теплопереноса с учетом МСФ тепловой системы использован автором при разработке методов НК структурных превращений в ПМ.

В третьей главе даны теоретические обоснования тепловых методов НК структур­ных превращений в ПМ: первого – по аномалиям на температурных зависимостях ТФС в соответствии с аналитическими закономерностями регулярных тепловых режимов применительно к моделям плоского и сферического полупространств; второго – по ряду информативных параметров математических моделей, определяемых с экспериментальных термограмм.

Процесс нестационарного теплопереноса в полимерном теле в одномерном случае описывается уравнением вида:

, n = 0, 1, 2, (3)

в нецилиндрической области

; ; ,,

где все () – непрерывно дифференцируемые функции, подлежащие нахождению
в задачах типа Стефана для уравнения теплопроводности со свободной границей;
Qп– количество поглощаемого или выделяемого тепла в единицу времени в единице объема ПМ при структурном переходе. Определить распределение температуры в
иссле­дуемом теле в любой момент времени затруднительно, вследствие нелинейности задачи.

Измерительная и тепловая схемы разработанных методов представлены на рис. 1, 2. Тепловое воздействие на исследуемое тело осуществляется с помощью нагревателя, выполненного в виде тонкого диска радиусом Rпл, встроенного в подложку измерительного зонда (ИЗ). Температурное распределение контролируется несколькими (не менее трех) термоприемниками (ТП).

На рис. 3 представлены термограммы, полученные экспериментально на изделии из ПТФЭ при следующих условиях: начальная температура Тн = 23 °С; Т *  температура изделия, Т * = Тн + Т; радиус нагревателя Rпл = 4 мм; мощность нагревателя W = 0,6 Вт; временной интервал измерения температуры  = 0,25 с. В общем случае на каждой из трех термограмм можно выделить несколько участков, соответствующих различным состояниям температурного поля исследуемой системы. Так, для термограммы, зафиксированной центральным ТП на изделии из ПМ вне области структурных превращений, характерны восемь участков (рис. 4).

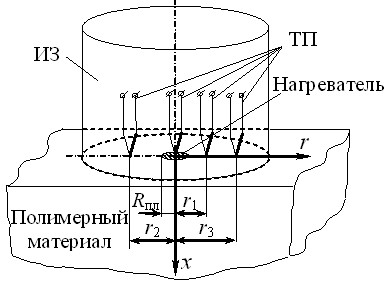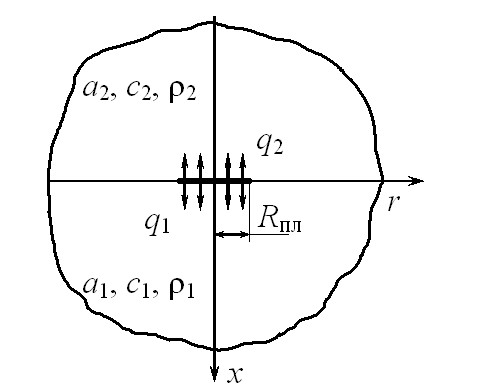Рис. 1 Измерительная схема		Рис. 2 Тепловая схема системы
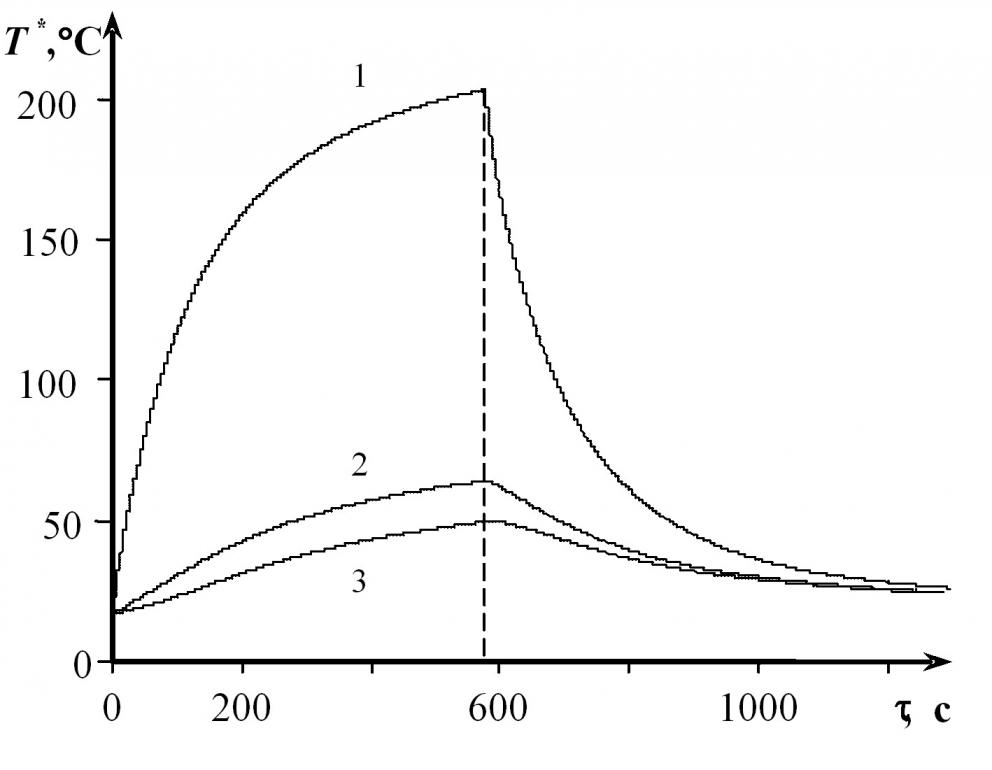Рис. 3 Термограммы для ПТФЭ: 1 – в центре зонда; 2, 3 – на расстояниях 7 и 9 мм от центра	Рис. 4 Термограмма 1 (рис. 3) с выделенными участками

Первому участку соответствует одномерное температурное поле в локальной области исследуемого тела (вблизи нагревателя). Тепловые потоки, поступающие в изделие (q1) и зонд (q2), изменяются во времени, так как между нагревателем и исследуемым телом имеется термическое сопротивление, нагреватель обладает инерционностью. Второму участку отвечает одномерное температурное поле, но процесс проходит стадию регуляризации в локальной области исследуемого тела, расположенной вблизи нагревателя и термоприемников. Третьему участку соответствует двухмерное температурное поле в образце, поскольку нельзя пренебречь распространением тепла в радиальном направлении. Четвертому участку соответствует тепловой процесс, вышедший на стадию регуляризации. В локальной области исследуемого ПМ формируется температурное поле, близкое к одномерному полусферическому. На пятом участке нарушаются условия полуограниченности исследуемого тела.

После отключения нагревателя ( > откл), на стадии остывания, можно выделить шестой участок, когда тепловые потоки q1 и q2 изменяются во времени, седьмой участок термограммы, тепловой процесс в котором проходит стадию регуляризации, и восьмой участок, где тепловой процесс изменяется.

Участки термограммы II, IV и VII – рабочие, так как вне области структурного превращения в ПМ возможно однозначно определить значения ТФС в зависимости от параметров аналитических моделей, описывающих термограмму на данных температурно-временных интервалах, используя регулярные тепловые режимы на моделях плоского и сферического полупространств.

Для разработки математических моделей определения ТФС материалов при НК использована следующая аналогия развития теплового процесса: на начальной стадии развития теплового процесса рассматривается задача о распространении тепла от бесконечного плоского нагревателя с удельной поверхностной мощностью q в плоском полупространстве (модель А); при больших значениях – в предположении, что плоский круглый нагре­ватель заменен эквивалентным ему поверхностным сферическим, рассматриваются задачи о распространении тепла в сферическом полупространстве (при нагреве и остывании – модели B и C).

Постановки краевых задач теплопроводности по моделям A, B и С представлены в диссертации. Решения задач, описывающие процесс распространения тепла в исследуемом объекте контроля (первое тело) по моделям А, В, С для поверхностного слоя (х = 0) в предположении отсутствия структурного перехода (рис.2), имеют следующий вид:

по модели А

, > 0; (4)

по модели В

; .

(5)

по модели С

, ; (6)

при r = R, , .

Выражения (4) – (6) описывают термограмму на температурно-временных интервалах, соответствующих моделям плоского и сферического полупространств на стадиях нагрева и остывания изделия из ПМ вне области структурного превращения.

При нагреве и остывании системы структурные переходы в ПМ, сопровождаю­щиеся тепловыми эффектами, проявляются на различных участках экспериментальных термограмм и могут быть выявлены по аномалиям на температурных зависимостях ТФС в соответствии с аналитическими закономерностями регулярных тепловых режимов применительно к моделям плоского (4) и сферического (5), (6) полупространств.

Рис. 5. Тепловая схема
системы с поверхностным
сферическим нагревателем

С целью разработки метода неразрушающего определения закона движения границы фазового перехода была рассмотрена задача о распространении тепла в сферическом пространстве (рис. 5).

Начальная температура тела из ПМ во всех точках одинакова и равна нулю. В момент времени  = 0 на сферической поверхности с координатами r = R начинает действовать источник тепла с поверхностной мощностью q. При температуре T = Tп ПМ имеет фазовый переход, теплота которого – Qп. ТФС тела в результате ФП меня­ются незначительно. Необходимо найти распределение температуры внутри тела в любой момент времени. До тех пор, пока температура в любой точке тела меньше Tп, задача будет описываться классическим уравнением теплопроводности в сферических координатах с граничными условиями второго рода на поверхности с координатами r = R.

Решение задачи известно:

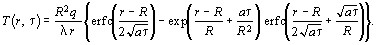(7)

Температурное поле на момент времени нп , соответствующий началу ФП, определяется выражением:

(8)

Выражения (7), (8) в безразмерной форме:

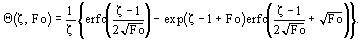	(9)
	(10)

где ; ; ; ; .

В момент образования новой (первой) фазы начальное распределение температуры определяется зависимостью

,

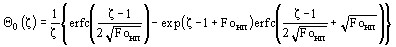(11)

а распределение температуры в теле находится из задачи стефановского типа:

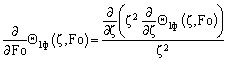, , ;	(12)
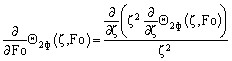, , ;	(13)
, ;	(14)
, ;	(15)
, ;	(16)
, ;	(17)
, .	(18)

Здесь: – свободная граница, которая не задана и подлежит определению вместе с безразмерными температурами и в новой (индекс «1ф») и старой (индекс «2ф») фазах; – теплота ФП в безразмерном виде.

При условии, что поверхность с координатой r = R достигает Тп при больших
значениях Fo, начальное условие (14) в безразмерной форме:

.

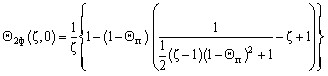(19)

Для определения закона движения границы ФП применены два варианта преобразований.

Вариант 1. Считаем, что закон движения границы ФП такой же, как закон движения изотермы с температурой Тп в случае отсутствия перехода. В результате получено выражение:, где . (20)

Решение уравнения (20) имеет вид:

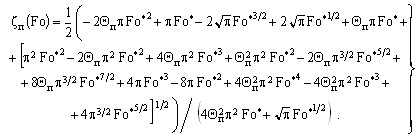(21)

Выражение (21) имеет достаточно сложный вид для применения его на практике. Введем дополнительные упрощения. Предполагаем, что .

Случай 1. Пренебрегаем в выражении (20) величинами и :

.

(22)

Случай 2. Пренебрегаем в выражении (20) величиной :

.

(23)

Вариант 2. Закон движения границы ФП должен удовлетворять следующим
условиям.

Условие 1. В момент времени Fo = 0, координата границы перехода должна
соответствовать .

Условие 2. При отсутствии ФП в теле возникает квазистационарное температурное поле, определяемое выражением . Очевидно, что подобное квазистационарное распределение температуры соответствует и случаю с ФП. При координата перехода должна принимать значение . Условие 2 применимо для ФП, сопровождающегося поглощением тепла.

Условие 3. Значения координат границы перехода будут отставать от координат изотермы с соответствующей температурой в случае отсутствия ФП, если переход идет с поглощением тепла, и опережать, если он идет с выделением тепла.

Для получения закона движения границы ФП в качестве искомых были подобраны функции, удовлетворяющие условиям 1 и 2.

По варианту 1 на основании выражений (22) и (23):

, к > 0, m > 0. (24)

, к > 0, m > 0. (25)

По варианту 2:

, к > 0, m > 0. (26)

Подбор параметров к и m найденных функций осуществляется таким образом, чтобы удовлетворялось условие 3 при наилучшем приближении к данным, полученным в результате численного решения задачи (12) – (18) с учетом эквивалентности радиусов реального круглого плоского и модельного сферического источников тепла.

В четвертой главе представлены расчетные зависимости, реализуемые ИИС при НК структурных превращений в ПМ.

Обозначим 1 =, 2 = и . Тогда уравнение (4) можно представить в виде:

. (27)

Здесь

(28)    и

.

(29)

,, – параметры ИИС, определяемые режимами опыта, ТФС материалов нагревателя и подложки зонда.

Для расчета текущих значений коэффициентов , d1i и d0i термограмму, полученную в центре нагревателя (рис. 3), разобьем на интервалы: 1… k; 2… k + 1; u – k + 1…u, где k – количество точек в интервале, целое положительное нечетное число (k 3);
u – количество точек в термограмме; i – номер интервала, целое число. Из уравнения (28) получено соотношение для вычисления текущего значения коэффициента
по каждому интервалу термограммы:

,		(30)
где	, ,	(31)
, (32);,		(33)

d1i – текущие значения параметра d1; d11, d12, 01, 02 – параметры d1 и тепловые актив­ности образцовых мер.

Текущие значения параметра d0i:

(34)    и

,

(35)

где Ts – средняя температура изделия из k измерений в каждом интервале; Tj – температура на j шаге измерения.

Преобразуем выражение (5) к виду:

,			(36)
где	, (37)	,	(38)
, , , , 2 = ', 1 =.

Параметры А, В, С, ', ' – параметры ИИС, учитывающие конструктивные особенности устройства и режимы опыта;, – теплопроводность и тепловая активность ПМ.

Параметры ИИС определяются из градуировочных экспериментов, значения коэффициентов и – по термограммам методом наименьших квадратов. Используя формулу (38), текущие значения теплопроводности для n-й термопары:

,	(39)
, ,

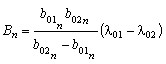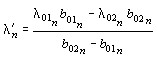здесь n – порядковый номер термопары, считая от центра зонда; Вn,  параметры ИИС для n-ой термопары; – текущие значения коэффициента; ,  – теплопроводности образцовых мер; ,  – коэффициенты, определенные по термограммам, зафиксированным на образцовых мерах.

Представим выражение (6) в виде:

,

(40)

где . Обозначим и , тогда .

Постоянную D находят из градуировочного эксперимента: ,
где h0 – коэффициент, определенный по термограмме, зафиксированной на образцовой мере; 0 – теплофизический комплекс образцовой меры.

Выражение для вычисления текущих значений * при r = R: ,
где hi – текущие значения коэффициента, которые определяются по термограмме методом наименьших квадратов.

Модели (4), (5) и (6) не учитывают возможного структурного перехода в исследуемом ПМ.

Первый многомодельный метод предполагает регистрацию структурных превращений по анома­лиям ТФС в узких температурном и временном интервалах с изменением интенсивного параметра (температуры или времени) и предусматривает проведение градуировки ИИС по двум образцовым мерам. Метод включает в себя следующие этапы.

1.  Градуировка ИИС: получение термограмм на двух образцах с известными ТФС; определение рабочих участков термограмм; расчет постоянных ИИС.

2.  Фиксирование термограмм на исследуемом ПМ. Определение рабочих участков каждой термограммы. Для расчета текущих значений коэффициентов d1i, d0i, b1i, b0i и hi экспериментальную термограмму разбивают на интервалы. Для каждого интервала вычис­ляют значения d1i, d0i, b1i, b0i, hi и Ts. Вычисление текущих значений ТФС (*, *, с*, a*, *) по каждому интервалу. Построение зависимостей * = f(Ts), * = f(Ts), с* = f(Ts), a* = f(Ts), * = f(Ts). Построение зависимостей * = f(), * = f(), с* = f(), a* = f(), * = f().

3.  Определение температурно-временных характеристик структурных превращений, которые сопровождаются аномальными изменениями ТФС на узких температурном и временном интервалах, путем анализа построенных зависимостей *, *, с*, a*, * от температуры и времени.

4.  Дифференцирование релаксационных и твердофазных превращений по данным (например, трех) термограмм, зафиксированных при различных скоростях изменения температуры (с ростом скорости изменения температуры релаксационные переходы перемещаются в сторону больших температур, чего не происходит с фазовыми).

Показано, что температурные поля в исследуемой системе, полученные численным моделированием методом конечных элементов, близки аналитическим моделям A, B, C в температурно-временных интервалах рабочих участков. Выполнена визуализация температурных полей и полей плотности тепловых потоков в системе зонд-изделие при различных режимных параметрах, которая свидетельствует о реализации одномерного температурного поля, соответствующего стадии регуляризации тепловых потоков на II участке термограммы, и сферических одномерных полей, соответствующих стадиям регуляризации тепловых потоков на IV и VII участках.

Показана адекватность разработанных моделей A, B, C на рабочих участках термограмм реальным тепловым процессам. На II участке термограммы относительная погрешность отклонения температуры Т, обусловленная различием математических моделей распространения тепла от плоского круглого и бесконечного плоского нагревателей, не превышает 2 %. На IV и VII участках относительная погрешность отклонения температуры Т, обусловленная различием математических моделей распространения тепла от плоского круглого и эквивалентного ему поверхностного сферического нагревателей, не превышает 1% (для полуограниченных тел с одинаковыми ТФС) и 2 % (для полуограниченных тел с различными ТФС). Продолжительность стадии нагрева подбирается таким образом, чтобы температурные поля на VII участке, полученные от сферического поверхностного и плоского круглого нагревателей, были близкими. Предложен критерий, с помощью которого определяется оптимальная температура отключения источника тепла (Тоткл).

Реализация второго многомодельного метода НК не требует проведения
градуировочных экспериментов. Он может быть использован для экспресс-контроля.

В области структурных превращений ПМ наблюдаются аномалии, выражающиеся в скачках и разрывах на зависимостях ТФС от температуры (или времени), которые могут быть зафиксированы по изменениям текущих параметров моделей A, B и C. Построив зависимости между каждым из параметров d1i, d0i, b1i, b0i, hi и температурой образца, по характерным пикам определяют температурно-временные характеристики структурных превращений.

Рассматривая модели A, B и C как случайные стационарные процессы (протека­ющие во времени однородно, частные реализации которых с постоянной амплитудой
колеблются вокруг средней функции), для которых дисперсии по сечениям – посто­янные, разработана следующая методика НК структурных превращений в ПМ. Если в исследуемом ПМ происходит, например, твердофазное превращение из одной кристаллографической модификации в другую, которое сопровождается тепловым эффектом, то величины дисперсий коэффициентов d1i, d0i, b1i, b0i, hi будут резко изменяться в достаточно узких временном и температурном интервалах.

Дисперсии , текущих параметров d1i, d0i, для каждого интервала
оценивают по формулам:

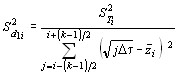	, (41) ,	(42)
где	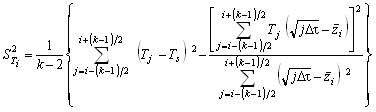,	(43)

– оценка дисперсии значений температуры.

Дисперсии , текущих параметров b0i, b1i (для модели B, соответствующей распространению тепла в сферическом полупространстве) по каждому интервалу:

, ,	(44)
,	(45)
, , ,

где Tj – температура на j шаге измерения, – промежуток времени, через который производятся измерения, i – номер интервала. Величины находятся аналогично .

Фиксирование аномалий на кривых зависимостей дисперсий коэффициентов d1i, d0i, b1i, b0i, hi (,,,,) от температуры и времени позволяет проводить экспресс-контроль структурных превращений в ПМ, а также экспресс-анализ экспериментальных данных при выборе режимных параметров работы ИИС.

Третий метод НК структурных переходов основан на регистрации первой производной по времени от основной величины – температуры в нескольких точках контроля исследуемого полимерного тела в динамических термических режимах при нагреве и остывании. Данный метод может быть реализован одновременно с двумя вышеупомянутыми методами.

Для расчета значений скорости V * изменения температуры термограмму разбивали на интервалы: 1… k; 2… k + 1; u – k + 1…u, где k – количество точек в интервале, целое положительное нечетное число (k 3); u – количество точек в термограмме; i – номер интервала. Определение линии регрессии для каждого интервала при нагреве и остывании проводили по методу наименьших квадратов.

Строили прямые по k точкам термограммы, определяли скорости изменения температуры, которые относили к температуре середины каждого интервала Ts. Таким образом удалось повысить чувствитель­ность измерений и получить запись в “спектральной форме”, т. е. в виде пиков в тех температурно-временных областях, где обнару­живаются различия в значениях “структурочувствительных” свойств (в областях, в которых возможны структурные переходы, сопровождающиеся тепловыми эффектами).

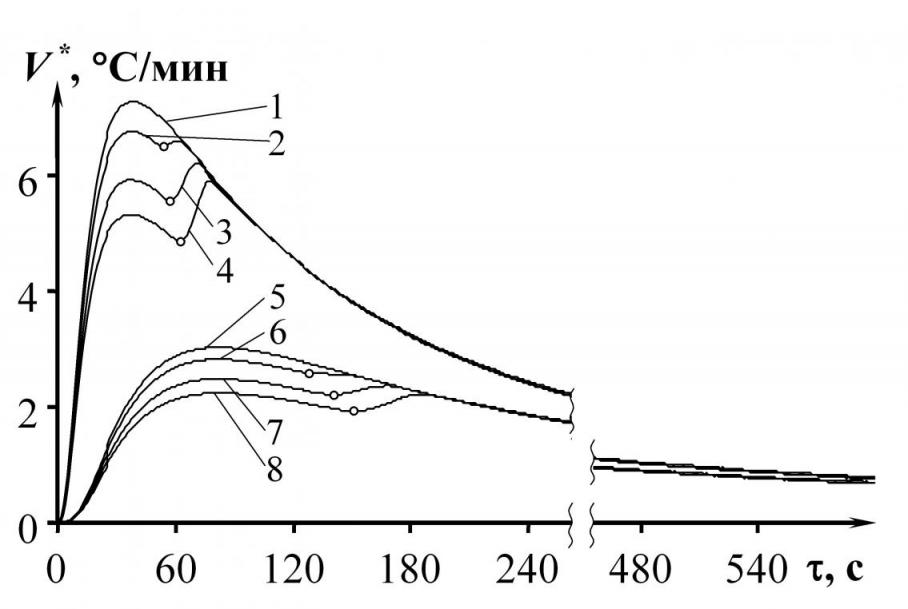
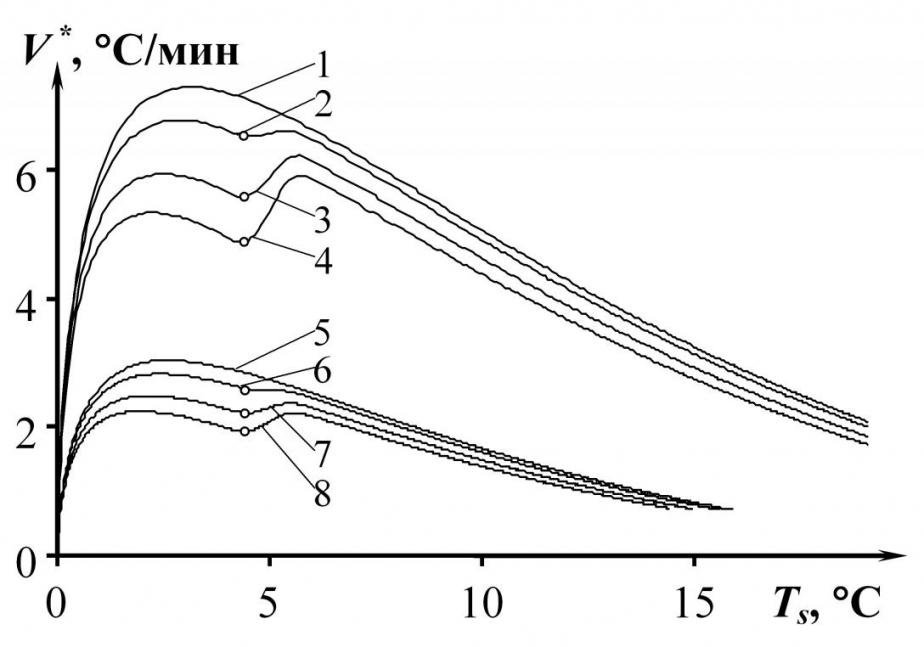
Рис. 6 Значения V *= f() (а) и V *= f(Ts) (б) изделия из ПТФЭ в точках,
расположенных на расстояниях 7 мм (1-4) и 9 мм (5-8) от центра нагревателя

Реализация метода может осуществляться одновременно с двумя вышеописанными методами.

Регистрация первой производной по времени от температуры, выражающей скорость (V *) изменения этой величины на кривой температурной зависимости, реализована ИИС с измерительными зондами, снабженными: а)  круглым плоским нагревателем постоянной мощности; б)  круглым плоским нагревателем, реализующим программным путем постоянную скорость нагрева в локальной области исследуемого изделия.

В пятой главе представлены результаты имитационного исследования, которое выполнялось с целью подтверждения основных идей, заложенных в разрабатываемые методы. Полученные данные позволяют определять диапазон температур, при которых возможна регистрация структурного перехода в ПМ, а также характер отклонений от аналитических моделей на графических зависимостях в случае проявления перехода.

По результатам ряда вычислительных экспериментов получены уравнения регрессии для определения значений температуры начала и середины рабочих участков в зависимости от ТФС ПМ и мощности нагревателя для ИЗ с различными подложками.

При переходе ИИС от нормального функционирования к неустойчивому применен экспресс-алгоритм, который позволяет максимально быстро определять к – время окончания измерения.

В качестве примера на рис. 6 представлены результаты численного моделирования по третьему методу НК, проведенного при следу­ющих условиях: исследуемый материал – ПТФЭ; подложка ИЗ – рипор; q = 10000 Вт/м2; Rпл = 4 мм;  = 0,5 с; k = 5. Структурный переход задан при Т = 4...6 °С скачками теплоемкости: с = 1005 (1, 5), 2000 (2, 6), 4000 (3, 7), 6000 (4, 8) Дж/(кг·К). Определен характер отклонений от аналитических моделей (кривые 1, 5) на графических зависимостях в случае проявления структурного перехода (кривые 2 – 4 и 6 – 8).

На рис. 7 представлены зависимости п=f (Foп), полученные при п = 5 и п = 0,7:
численным решением задачи (12) – (18) методом конечных элементов (точки);
1 – по (24); 2 – по (25); 3 – по (26). Значения Foп = Fo – Foнп соответствуют п =  – нп . Представленные данные свидетельствуют о хорошем совпадении теоретических зависимостей (24) – (26) с результатами численного решения.

На рис. 8 предс­тавлены зависимости п = f (Foп), полученные численным моделированием (точки) и по уравнению (26) (линии) при п = 5 и п = 0,45 (1); 0,5 (2); 0,55 (3); 0,6 (4); 0,65 (5); 0,7 (6); 0,75 (7); 0,8 (8); 0,85 (9); 0,9 (10).

Исследовано влияние теплового режима воздействия, теплоты ФП, ТФС на закон движения границы. Показано хорошее совпадение теоретических результатов с численными расчетами.

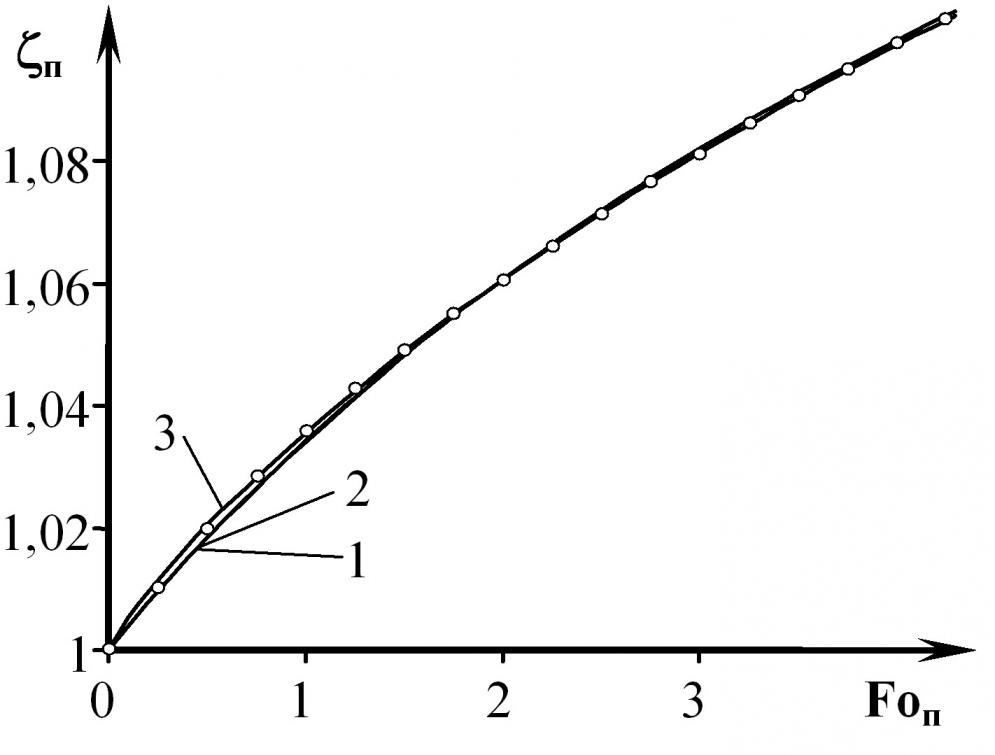
Рис. 7 Зависимости п= f (Fo) полученные:
численным моделированием (точки);
1 – по (24); 2 – по (25); 3 – по (26)

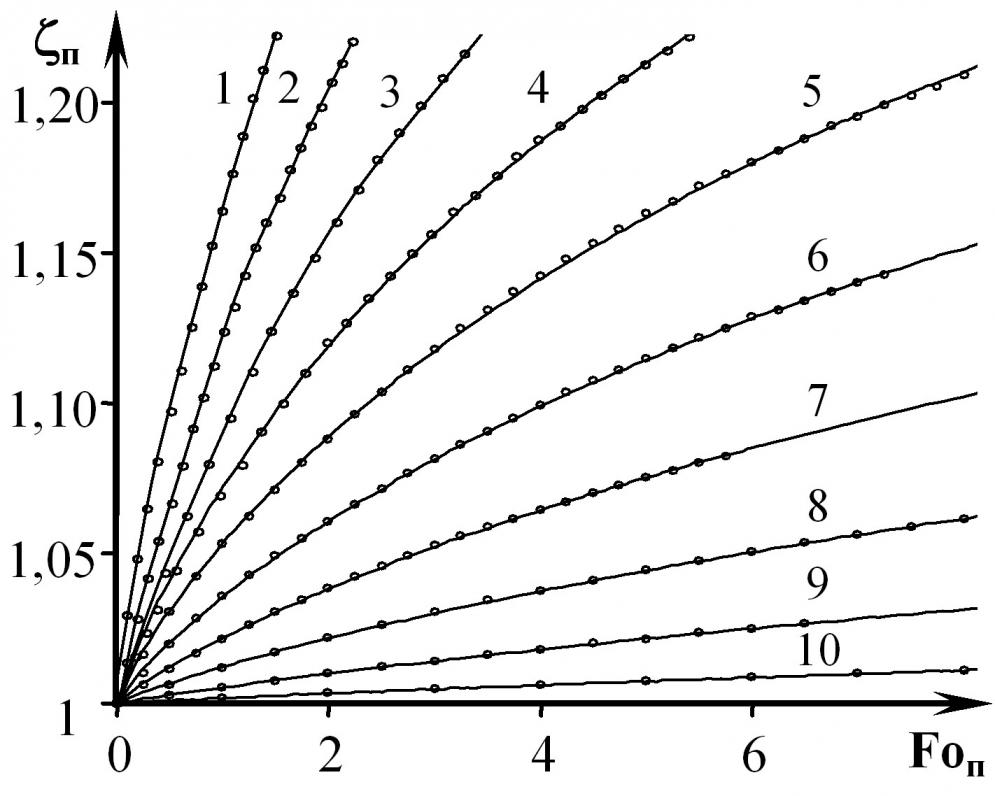
Рис. 8 Зависимости п= f (Fo):

численное моделирование (точки);
по (26) (линии)

В шестой главе представлены описания мобильных приборов и ИИС, реализующих разработанные методы, схемы используемых ИЗ, их конструктивные особенности.

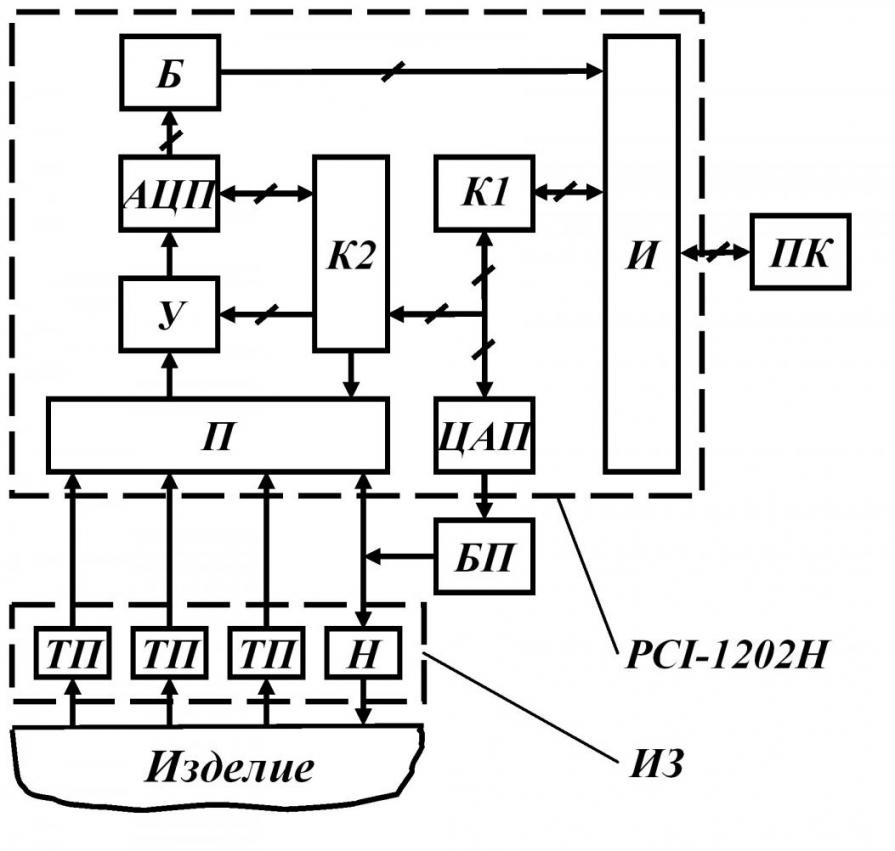
Рис. 9 Структурная схема ИИС
с платой PСI-1202H

ИИС (рис. 9) состоит из персонального компьютера (ПК), измерительно-управляющей платы PCI-1202H, сменных измерительных зондов (ИЗ), регулируемого блока питания (БП). Зонд обеспечивает создание теплового воздействия на исследуемое изделие, фиксирование температуры в заданных точках контроля термоэлектрическими преобразователями (ТП). При измере­ниях ИЗ устанавливают контактной сторо­ной на поверхность иссле­дуемого изделия. Тепловое воздействие осуществляется с помощью нагревателя (Н), выполненного в виде диска и встроенного в подложку ИЗ. Мощность и длительность теплового воздейст­вия БП задаются программно через интерфейс (И), контроллер К1, цифро-аналоговый преобразователь (ЦАП). Сигналы с ТП поступают через мультиплексор (П), усилитель (У), аналого-цифровой преобразователь (АЦП), буфер обмена (Б) и интерфейс (И) в ПК. Контроллер К2 обеспечивает необходимый порядок опроса каналов и различные диапазоны измерения на каждом из них. Сбор информации производится при нагреве и остывании исследуемого тела.

На рис. 10 представлена структурная схема ИИС, в состав которой помимо ПК и ИЗ входит микропроцессорное устройство (МПУ). Данную ИИС применяют в лабораторных и производствен­ных условиях (без ПК). В состав ИИС входят: измерительно-вы­числительное устройство (ИВУ), персональный компьютер (ПК), периферийные устройства (ПУ), программное обеспечение (ПО). ИВУ включает в себя: ИЗ, блок усилителей (БУ) и МПУ. МПУ реализовано на базе 8-битного микропроцессора (М) с тактовой частотой 11 МГц. В состав МПУ входит: АЦП, интерфейс (И), память, набор аналоговых, цифровых и релейных портов, блок питания и управления нагревом (БП).

В качестве ПК в ИИС используется IВМ-совместимый компьютер. ПО включает системное (СПО), прикладное (ППО) и вспомогательное (ВПО) обеспечения.

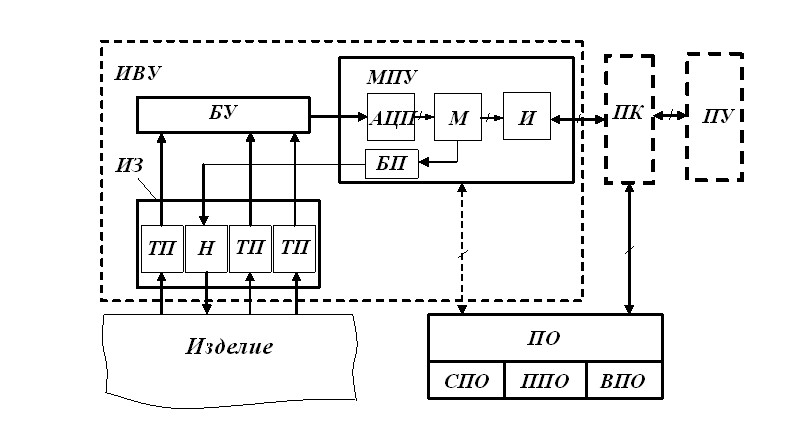
Рис. 10 Структурная схема ИИС
с микропроцессорным устройством

ИИС реализует алгоритмы определения ТФС, контролятемпе­ратурно-временных характе­ристик структурных превращений в ПМ, управления режимами эксперимента. Алгоритм контроля за ходом эксперимента и обработка экспе­ри­ментальных данных осуществляется согласно схеме, представленной на рис. 11. Основные операции выделены укрупненными блоками: A, B, C, D, E, F, G, H, K, L.

Блок А.  Осуществляется активная стадия проведения эксперимента, которая включает: термостатирование, тепловое воздействие постоянной мощности на исследуемое изделие, фиксирование температурных откликов, отключение нагревателя при оптимальной температуре, фиксирование температурных откликов на стадии остывания, контроль времени окончания измерения. Реализация алгоритма фиксирования неустановившегося режима работы ИИС.

Блок В.  Обработка экспериментальных данных при НК ТФС. Выделяются рабочие участки термограмм на основе статистического критерия Дарбина-Ватсона. По методу наименьших квадратов оцениваются параметры моделей, описывающих II, IV и VII рабочие участки термограмм. Рассчитываются значения,, по трем каналам. Определяются погрешности оценки параметров моделей. Рассчитываются оценки погрешностей определения ТФС. Осуществляется самоконтроль результатов.

Блок C.  Обработка данных при НК структурных переходов по модели плоского полупространства. Строятся термограммы, графики V *=f(Ts). Выделяются рабочие участки. Рассчитываются d1i , d0i , Ts . Строятся графики d1i=f(Ts), d0i=f(Ts), . Анализ построенных зависимостей.

Блок D.  Обработка данных при НК структурных переходов по модели плоского по­лу­пространства. Строятся термограммы, графики V *=f(Ts). Выделяются рабочие участки. Рассчитываются *. Строятся графики *=f(Ts). Анализ построенных зависимостей.

Блок E.  Обработка данных при НК структурных переходов по модели сферичес­кого полупространства. Строятся графики V *=f(Ts). Выделяются рабочие участки. Рассчитываются b1ni, b0ni, hni, Ts. Строятся графики b1ni=f(Ts), b0ni=f(Ts), hni=f(Ts), , , . Анализ построенных зависимостей.

Блок F. Обработка данных при НК структурных переходов по модели сферичес­кого полупространства. Строятся графики V *=f(Ts). Выделяются рабочие участки. Рассчитываются , а*. Строятся графики *=f(Ts), *=f(Ts), c*=f(Ts), а*=f(Ts). Анализ построенных зависимостей.

Блок G.  Обработка данных при НК структурных переходов. Строятся термо­граммы, графики V *=f(Ts), V *=f(). Анализ построенных зависимостей.

Блок H.  Осуществляется активная стадия эксперимента: термостатирование,
тепловое воздействие с постоянной скоростью нагрева, фиксирование температурных откликов, отключение нагревателя при заданной температуре, фиксирование темпера­туры на стадии остывания, контроль времени окончания измерения.

Блок K.  Обработка экспериментальных данных при НК структурных переходов. Строятся термограммы, графики V *=f(), V *=f(Ts), W=f(), W=f(Ts), dW/d=f(), dW/d=f(Ts). Анализ построенных зависимостей.

Блок L.  Определение вида перехода (фазовый или релаксационный). Определение Тп, п, коэффициентов к, m закона движения границы ФП.

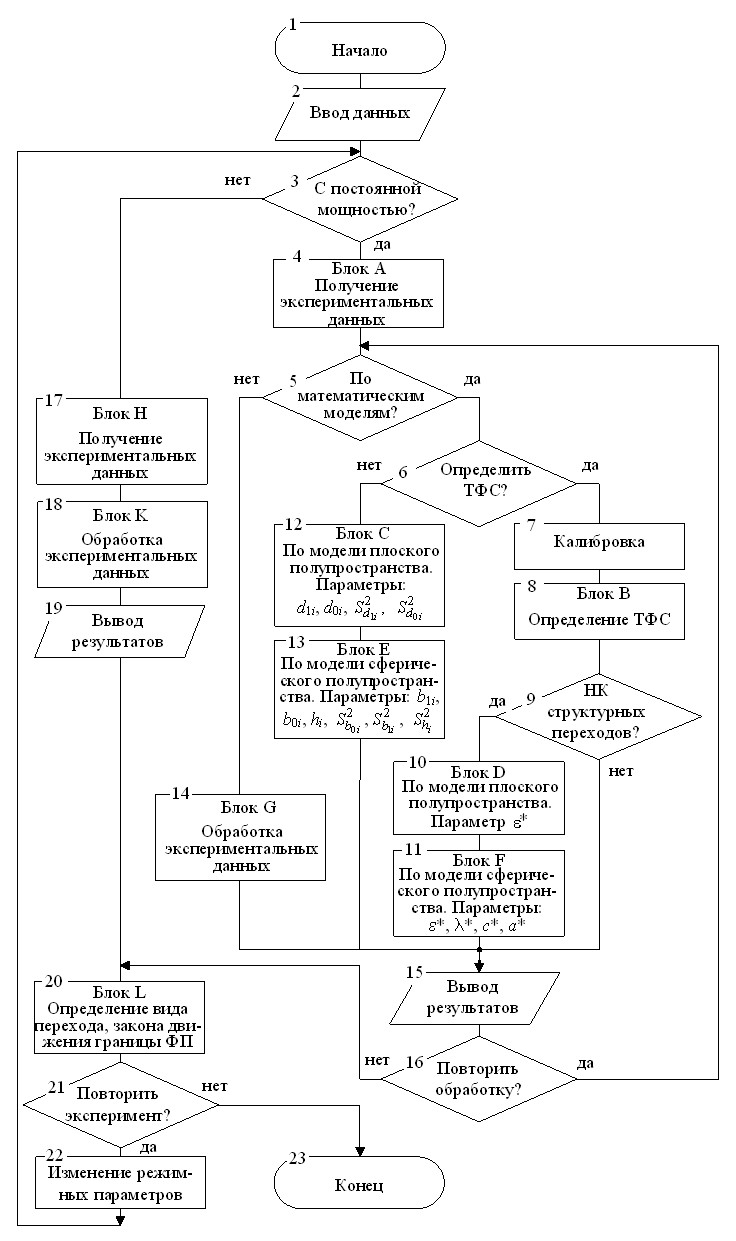
Рис. 11 Алгоритм контроля за ходом эксперимента
и обработка экспериментальных данных

В седьмой главе приведены результаты экспериментальной проверки разрабо­танных методов и ИИС, реализующих НК структурных превращений в ПМ.

На рис. 12 приведены зависимости текущих значений параметра d1 и тепловой актив­ности ПТФЭ от средней температуры из 5 (k = 5) текущих пошаговых измерений. Использована термограмма, зафиксированная центральным ТП после калибровки ИИС на материалах с известными ТФС. Условия опыта: Rпл = 4 мм; W = 0,7 Вт;  = 0,5 с; Tн = 21 °С. При температуре ниже 19,6 °С элементарная ячейка ПТФЭ имеет триклиническую структуру. В интервале от 19,6 °С до 30°С существует гексагональная элементарная ячейка, выше 30оС стабильной становится псевдогексагональная решетка. Удельные теплоты переходов составляют соответственно: 4,00,5 кДж/кг и 1,2±0,3 кДж/кг. Твердофазный переход в ПТФЭ, происходящий при Tп = 30 °С и сопровожда­ющийся эндотермическим эффектом, зарегистрирован при Tп = 29,8 °С (рис. 12).

На рис. 13 представлена зависимость , полученная по термограмме, зафик­си­рованной на изделии из капролона. Твердофазное превращение в капролоне, соответ­ствующее переходу при 25 °С гексагональной решетки в моноклинную, проявилось в интервале температур 24,7… 25,3 °С, что хорошо согласуется со справочными данными.

Рис. 14  Зависимость
для изделия из ПТФЭ

На рис. 14 представлена зависимость = f(Ts), построенная по термограмме, зафиксированной на изделии из ПТФЭ. Полиморфные твердофазные переходы в ПТФЭ проявились в виде дублетов в интервалах температур 19…22 °С и 28…32 °С.

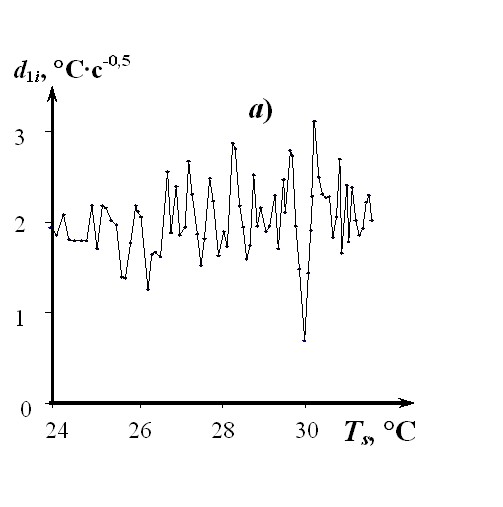
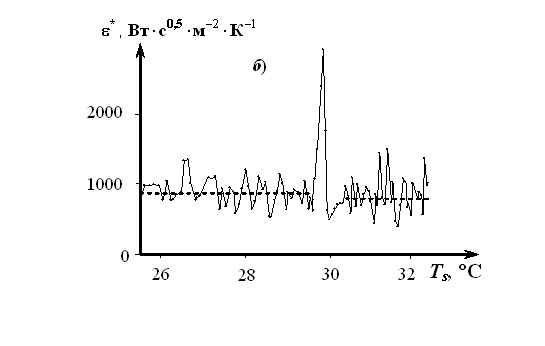
Рис. 12  Зависимости: а) ; б) для изделия из ПТФЭ

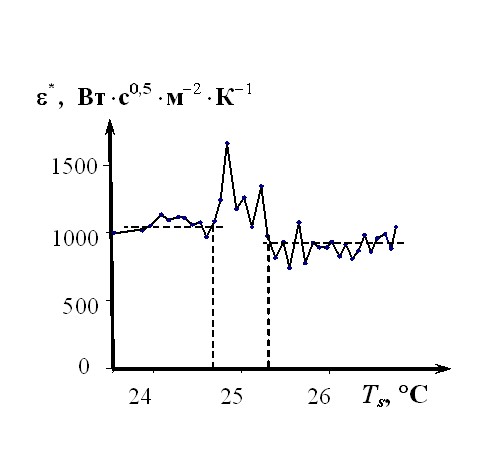
Рис. 13 Зависимость
для изделия из капролона

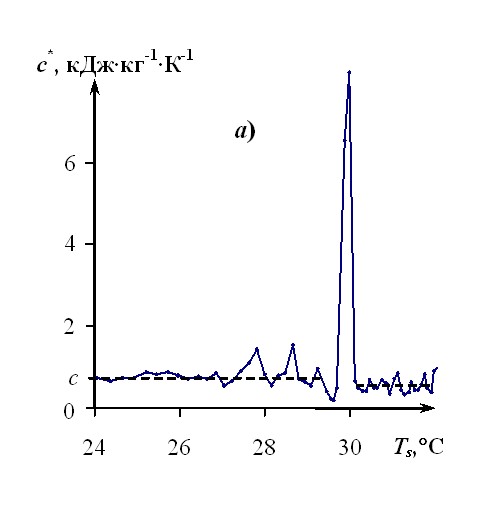Рис. 15 Иллюстрация аномалий с* и *на кривых с* = f(Ts) (а) и * = f(Ts) (б) для Ф4К20

На рис. 15 представлены зависимости с* = f(Ts) и * = f(Ts) для Ф4К20, построенные по термограмме, зарегистрированной в центре зонда на стадии нагрева при следующих условиях: Тн = 18,3 °С; Rпл = 2,5 мм; W = 1,6 Вт;  = 0,5 с; k = 5.

Зависимость * = f(Ts) для ПТФЭ (рис. 16, а) построена по термограмме, зафиксированной в центре зонда на стадии нагрева. Условия проведения опыта: Тн = 13,8 °С;
Rпл = 4 мм; W = 0,9 Вт; = 0,5 с. Полиморфные твердофазные переходы в Ф4К20 и в ПТФЭ (рис. 15, 16) при 30 °С явно зафиксированы. На рис. 16 (б, в) представлены зависимости b1i = f(Ts), b0i = f(Ts) для Ф4К20. Условия опыта такие же, как в опыте, результат которого представлен на рис. 15.

Анализируя зависимости b0i = f(Ts) и b1i = f(Ts) (рис. 16, б, в), можно сделать вывод о том, что параметры b0i и b1i реагируют на появление твердофазного полиморфного превращения.

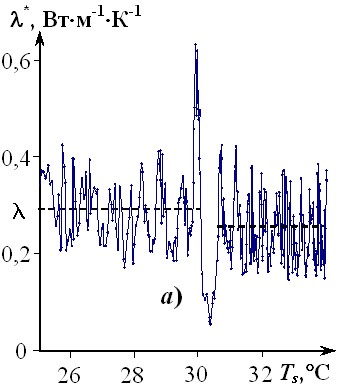
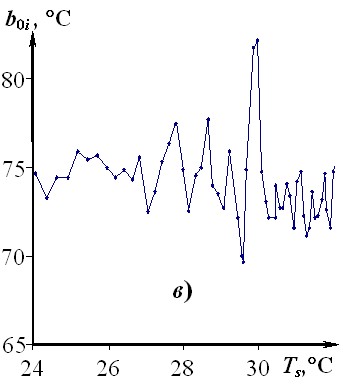
Рис. 16 Зависимости: * = f(Ts) для ПТФЭ (а); b1i = f(Ts) (б), b0i = f(Ts) (в) для Ф4К20

Выполнена статистическая обработка результатов экспериментов. С помощью кри­териев Пирсона и Колмогорова показано, что на рабочих участках термограмм вне области структурного превращения текущие значения ТФС подчиняются нормальному закону. Критерий «трех сигм» и -критерий использованы для доказательства неслучайности аномалий значений ТФС исследуемых ПМ на рабочих участках термограмм при проявлениях структурных переходов.

Таким образом, первый многомодельный метод позволяет осуществлять неразрушающий контроль температурно-временных характеристик структурных превращений в ПМ по аномалиям ТФС, наиболее информативной из которых является теплоемкость.
По второму многомодельному методу без калибровочных экспериментов фиксирование аномалий на кривых зависимостей d1i , d0i , b1i , b0i , hi , , , , и от температуры позволяет проводить контроль температурно-временных характеристик структурных превращений в ПМ и экспресс-анализ при выборе режимных параметров работы ИИС.

По третьему методу проведен эксперимент на изделии из ПЭНП, температура плавления которого Тпл=105 °С. Термо­граммы, зафиксированы при следующих условиях опыта: Rпл = 4 мм; W= 1,4 Вт; Тн = 19,5 °С; = 0,25 с; k = 41. На рис. 17 представлены значения скоростей остывания V * изделия из ПЭНП, зарегистрированные ТП, располо­женным в центре нагревателя, отнесенные к температуре точки контроля. Процесс кристаллизации ПЭНП из расплава явно зафиксирован при температуре около Т=100 °С, что соответствует справочным данным.

На рис. 18 представлены результаты обработки экспериментальных термо­грамм, снятых на изделии из ПТФЭ при следующих усло­виях: Тн = 11,5…13 °С;  = 0,2 с; k = 41; Rпл = 4 мм; r = 9 мм. Мощность нагревателя: W= 0,35 Вт (1); W= 0,5 Вт (2); W= 0,68 Вт (3); W= 0,89 Вт (4); W= 1,13 Вт (5); W= 1,68 Вт (6); W= 2 Вт (7). Твердофазное превра­щение в ПТФЭ зафиксировано при 19,6 °С. Переход проявился ступенькой на кривой V *= f(Ts). Это хорошо согласуется с результатами ДТА и имитационного моделирования, полученными автором на этом же материале.

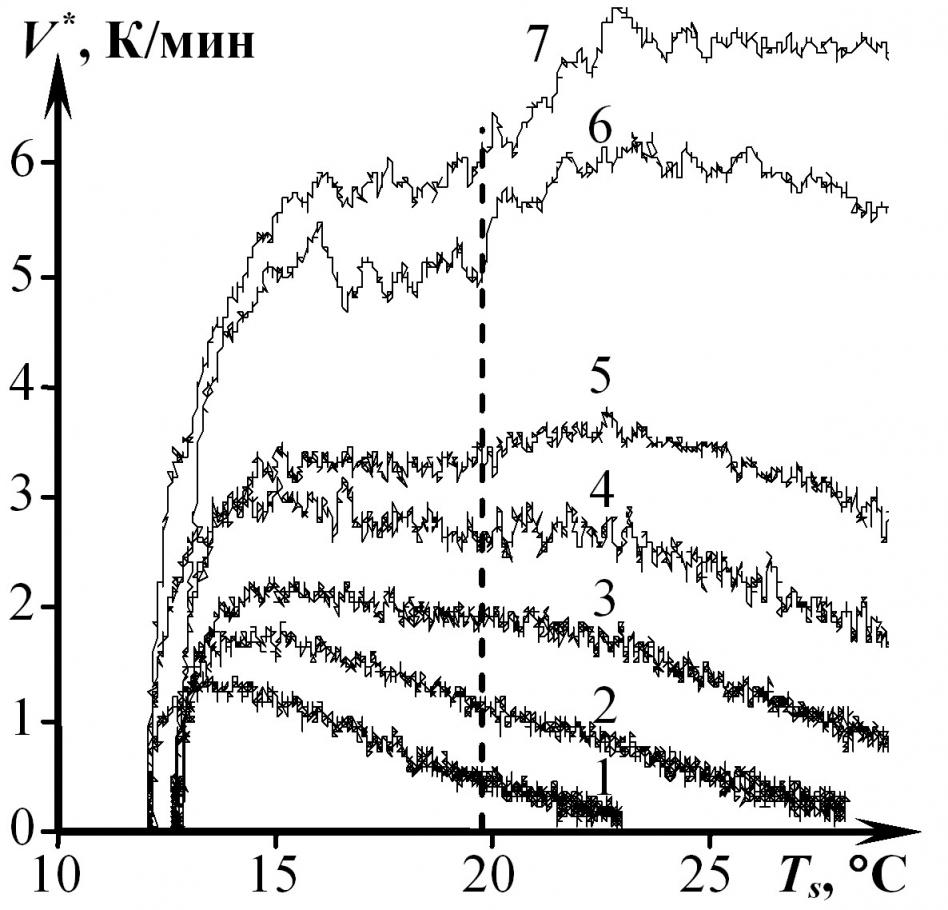
Рис. 18 Скорости нагрева изделия из ПТФЭ
в точке, расположенной на расстоянии r = 9 мм при различной мощности нагревателя

Рис. 17 Значения скорости остывания
изделия из ПЭНП,
отнесенные к температуре точки

В диссертационной работе автором также зафиксированы релаксационные переходы: в капролоне при Tп = 37 °С; в поликапроамиде при Tп = 27 °С; в ПММА при Tп = 32 °С, что хорошо согласуется с литературными данными.

Таким образом, разработанные многомодельные методы НК структурных превращений в ПМ с применением плоского круглого нагревателя постоянной мощности обеспечивают достаточную точность и оперативность измерений за счет использования рабочих участков нескольких термограмм, зафиксированных в одной реализации эксперимента. Разработанные методы и ИИС позволяют за непродолжительное время фиксировать структурные переходы в ПМ по аномалиям ТФС, наиболее информативной из которых является теплоемкость. Получение информации о структурном переходе по параметрам d1i , d0i , b1i , b0i , , , и не требует калибровки ИИС, что значительно упрощает и ускоряет обработку полученных результатов.

Регистрация первой производной по времени от температуры, выражающей скорость (V *) изменения этой величины на кривых температурных зависимостей от времени, реализуемая согласно методу, разработанному автором, позволяет осуществлять НК температур структурных переходов в ПМ без дополнительной калибровки измерительного средства. ИИС и мобильные приборы со сменными измерительными зондами, снабженными: а)  круглым плоским нагревателем постоянной мощности; б)  круглым плоским нагревателем, обеспечивающим программным путем постоянную скорость нагрева, позволили обнаружить различия в значениях “структурочувствительных” свойств (в областях, где возможны структурные превращения,
сопровождающиеся тепловыми эффектами) в узких температурно-временных областях.

Проведена метрологическая оценка погрешностей и их характеристик при НК структурных превращений в ПМ.

Оперативность, достаточную точность и достоверность НК температурно-временных характеристик структурных превращений разработанные методы обеспечивают за счет осуществления самоконтроля при работе ИИС в каждой реализации эксперимента. Методы позволяют регистрировать и различать твердофазные полиморфные и релаксационные переходы в ПМ при одной реализации эксперимента.

На рис. 19 представлены экспериментальные термограммы, снятые на изделии из ПТФЭ в центре нагревателя (1) и на расстояниях 7, 8, 9 мм от центра (2, 3, 4). Условия проведения опыта: Тн = 12 °С;  = 0,2 с; Rпл = 4 мм; W=1,13 Вт.

По уравнению (26) с учетом значений ТФС, геометрических и режимных параметров опыта, полученных значений i для термограмм 1–3 (рис. 19) найдены законы движения границ первого (Тп1=19,6 °С, п1= 0,0425) и второго (Тп2=30 °С, п2= 0,1005) переходов в ПТФЭ:

, (46)

. (47)

На рис. 20 представлены графики зависимостей (46) и (47), на которых точками показаны значения Fo, соответствующие экспериментальным значениям, полученным по термограмме 4 (рис. 19) для координаты r = 9 мм.

Таким образом, предложенная математическая модель позволяет реализовать на практике метод неразрушающего определения закона движения границы фазового перехода в ПМ.

В Приложениях приведены протоколы экспериментов, схемы алгоритмов, фрагменты программ, документы, подтверждающие использование и внедрение результатов работы.

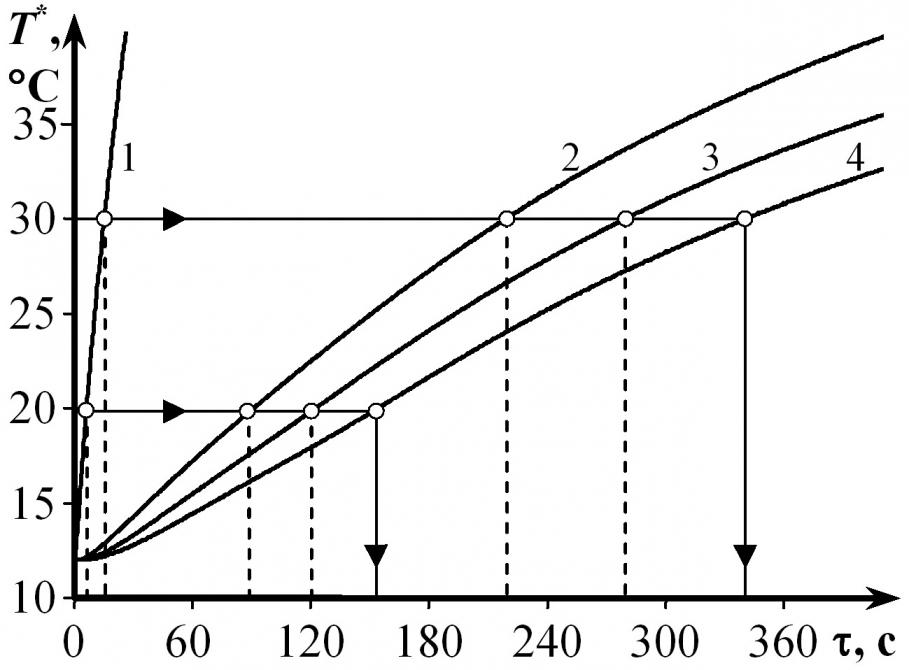
Рис. 19 Термограммы зафиксированные на изделии из ПТФЭ: 1 – в центре нагревателя; 2, 3, 4 – на расстояниях 7, 8, 9 мм

Рис. 20

Зависимости:
1 – п1 = f(Foп), 2 – п2 = f(Foп)

Основные выводы и результаты

Общим результатом работы является научно обоснованное решение проблемы создания многомодельных методов и средств НК температурно-временных характе­ристик структурных превращений в полимерах и композиционных материалах на их основе.

При решении данной проблемы получены следующие результаты.

1. Предложены основы многомодельного подхода к разработке методов и средств НК структурных переходов в ПМ на множестве состояний функционирования системы.

2. Впервые предложена расчетная модель, теоретически исследован и реализован на практике теплофизический метод неразрушающего определения законов движения границ ФП в полимерных материалах.

3. Разработаны математические модели распространения тепла в объектах контроля от действия бесконечного плоского и поверхностного сферического постоянной мощности источников тепла. Получены решения соответствующих краевых задач, пригодные для реализации в методах НК структурных превращений в ПМ.

4. Впервые созданы и исследованы новые многомодельные методы НК структурных превращений в ПМ, обеспечивающие оперативность, надежность и достаточную точность за счет использования рабочих участков нескольких термограмм, зафиксированных при нагреве и остывании объектов контроля. Реализован самоконтроль работы ИИС НК температурно-временных характеристик структурных превращений в ПМ при каждой реализации эксперимента.

5. Разработаны и исследованы два новых способа НК структурных превращений в ПМ, защищенные патентами на изобретения Российской Федерации и свидетельствами об официальной регистрации программ. Первый по аномальным изменениям ТФС
в областях структурных переходов при нагреве и остывании изделий из ПМ с предва­рительной градуировкой ИИС по образцовым мерам. Второй по ряду параметров
математических моделей, адекватно описывающих рабочие участки экспериментальных термограмм, и по величинам дисперсии этих параметров без дополнительных градуировочных экспериментов.

Третий способ может быть реализован одновременно с двумя вышеупомянутыми способами. Данный способ основан на регистрации первой производной по времени от основной величины – температуры в нескольких точках контроля исследуемого полимерного тела в динамических термических режимах при нагреве и остывании.

6. Выполнена оценка адекватности разработанных математических моделей реальным тепловым процессам эксперимента.

7. Разработаны математическое, алгоритмическое, программное и техническое обеспечения ИИС и мобильных приборов, реализующих многомодельные методы НК температурно-временных характеристик структурных превращений в полимерах и композиционных материалах на их основе.

8. Основные результаты теоретических и экспериментальных исследований приняты к использованию и внедрены в различных научно-исследовательских и промышленных предприятиях и организациях России в виде методик НК, программных продуктов, ИИС и мобильных приборов, а также используются в учебном процессе Тамбовского государственного технического университета.

Обозначения и аббревиатуры

а – температуропроводность; q1, q2  – плотности тепловых потоков, поступающих в объект контроля и материал подложки ИЗ, соответственно; Qп и п – теплота фазового перехода в размерном и безразмерном представлениях; R,Rпл – радиус сферического и плоского нагревателей, соответственно; r и – координата в размерном и безразмерном представлениях; T и – избыточная температура в размерном и безразмерном представлениях; Тн  – начальная температура; Т* – температура поверхности изделия; Тs – среднее значе­ние температуры из k измерений;  – теплопроводность; *, а*, с*, * – текущие значения теплопроводности, температуропроводности, удельной теплоемкости и тепловой активности, определенные из k измеренных значений; 01, 02, 01, 02 – тепловые активности и теплопроводности образцовых мер; и Fo – время в размерном и безразмерном представлениях; нп и Foнп – время возникновения фазового перехода в размерном и безразмерном представлениях, ; – временной интервал измерения температуры; V* – скорость изменения температуры; W – мощность на нагревателе; к, m, p0i, p1i, p2i, p3i – коэффициенты; ИИС – информационно-измерительная система; ИЗ – измерительный зонд; капролон – полиамид блочный;
НК – неразрушающий контроль; ПМ – полимерный материал; ПММА – полиметил­метакрилат; ПС – полистирол; ПТФЭ – политетрафтор­этилен; ПЭНП – полиэтилен низкой плотности; ТФС – теплофизические свойства; ТА – термический анализ;
ТП – термоприемник; Ф4К20 – коксонаполненный фторопласт.

Индексы: 1 – объект контроля (исследуемое изделие из ПМ); 2 – материал подложки зонда; 1ф, 2ф – новая и старая фазы; п – переход; пл – плоский; нп – начало перехода.

Основные результаты диссертации представлены в следующих публикациях
( – в журналах по перечню ВАК, в других изданиях, учитываемых ВАК):

Монографии, препринт

1.  Многомодельные методы в микропроцессорных системах неразрушающего
контроля теплофизических характеристик материалов / С.В. Мищенко, Н.Ф. Майникова, Ю.Л. Муромцев, Н.П. Жуков, И.В. Рогов. – Тамбов: Изд-во ТГТУ, 2001. – 112 с.

2. Майникова Н. Ф. Многомодельный метод неразрушающего теплофизического контроля структурных превращений в полимерных материалах / Н.Ф. Майникова, Ю.Л. Муромцев, А.С. Чех // Вестник Тамбовского государственного технического университета. – 2003. – Т.9, № 2. Рубрика 01. Препринт № 07. – 36 с.

3.  Жуков Н.П. Многомодельные методы и средства неразрушающего контроля теплофизических свойств твердых материалов и изделий / Н.П. Жуков, Н.Ф. Майникова //
Монография. – М.: Машиностроение – 1, 2004. – 288 с.

Публикации в журналах, трудах конференций
и других изданиях, патенты, свидетельства:

4. Майникова Н.Ф. Измерительная система и метод неразрушающего контроля структурных превращений в полимерных материалах / Н.Ф. Майникова // Приборы и системы. Управление, контроль, диагностика. – 2006. – № 1. – С. 56 – 61.

5. Жуков Н.П. Моделирование процесса теплопереноса от плоского источника
тепла постоянной мощности при теплофизических измерениях / Н.П. Жуков, Н.Ф. Майникова // Инженерно-физический журнал. – 2005. – Т. 78. № 6. – С. 56 – 63.

6. Майникова Н.Ф. Измерительно-вычислительная система неразрушающего
теплофизического контроля / Н.Ф. Майникова, Н.П. Жуков // Приборы и техника эксперимента. – 2005. – №2. – С. 153 – 154.

7. Жуков Н.П. Измерительно-вычислительная система неразрушающего контроля теплофизических свойств / Н.П. Жуков, Н.Ф. Майникова // Приборы и техника экспери­мента. – 2005. – №3. – С. 164 – 166.

8. Майникова Н.Ф. Об одном методе термического анализа для неразрушающего контроля теплофизических свойств полимеров / Н.Ф. Майникова, И.В. Рогов, А.А. Балашов // Пластические массы. 2001. № 2. С. 30 33.

9. Майникова Н.Ф. Об одном методе исследования твердофазных переходов
в полимерных материалах / Н.Ф. Майникова, Ю.Л. Муромцев // Пластические массы. – 2002. – № 6. – С. 23 – 26.

10.  Роботизированный контролер теплофизических характеристик твердых материалов / Н.Ф.Майникова, Ю.Л.Муромцев, Е.И. Глинкин, В.Н. Чернышов // Тезисы докл. III Всесоюзн. науч. конф. – Челябинск, 1983. – С. 22.

11.  Майникова Н.Ф. Экспериментальное исследование структурных изменений в композиционных материалах / Н.Ф. Майникова, А.П. Пудовкин // Математическое моделирование и оптимизация систем переменной структуры: межвуз. сб. науч. трудов – М.: Моск. ин-т хим. машиностр., 1989. – С. 151 – 155.

12.  Майникова Н.Ф. Метод неразрушающего контроля комплекса характеристик композитов / Н.Ф. Майникова, Ю.Л. Муромцев // Труды Всесоюзн. науч. конф.
“Полимерные композиты - 90”. – Ч. 2. – Л., 1990. – С. 79 – 82.

13.  Метод неразрушающего контроля теплофизических свойств композиционных полимерных материалов / Н.Ф. Майникова, Ю.Л. Муромцев, А.П. Пудовкин, И.В. Рогов // Труды VII Междунар. конф. “Оптические, радиоволновые, тепловые методы и средства контроля природной среды, материалов и промышленных изделий”. – Череповец, 1997. – С. 95 – 98.

14. Метод, устройство и автоматизированная система неразрушающего контроля теплофизических свойств композитов / Н.П. Жуков, Н.Ф. Майникова, И.В. Рогов,
А.П. Пудовкин // Вестник Тамбовского государственного технического университета. – 1997. – Т. 3, № 4. – С.406 – 415.

15.  Майникова Н.Ф. Теплофизические свойства композитов строительного наз­начения / Н.Ф. Майникова, А.А. Балашов // Труды II Рос. нац. конф. по теплообмену. – Т. 8. – М.: Изд-во МЭИ, 1998. – С.121 – 122.

16. Жуков Н.П. Моделирование процесса теплопереноса от плоского источника
тепла при теплофизических измерениях / Н.П. Жуков, Ю.Л. Муромцев, Н.Ф. Майникова // Вестник Тамбовского государственного технического университета. – 1999. – Т. 5, № 4. – С. 543 – 553.

17. Майникова Н.Ф. Исследование теплофизических свойств композитов строительного назначения / Н.Ф. Майникова, И.В. Рогов, З.М. Селиванова // Вестник Тамбовс­кого государственного технического университета. – 1999. – Т. 5, № 2. – С. 285 – 289.

18. Mainikova N.F. Multimodel Method of Non-Destructive Control of Thermophysical Characte­ristics of Solid Materials / N.F. Mainikova, N.P. Zukov, I.V. Rogov // Вестник Тамбовского государственного технического университета. – 2000. – Т. 6, № 2. –
С. 192 – 200.

19. Жуков Н.П. Анализ погрешностей метода измерения теплофизических
характеристик композитов. Оценка случайных погрешностей / Н.П. Жуков, Н.Ф. Майникова, И.В. Рогов // Вестник Тамбовского государственного технического университета. – 2000. – Т. 6, № 3. – С.416 – 424.

20. Жуков Н.П. Анализ погрешностей метода измерения теплофизических
характеристик композитов. Оценка систематической погрешности / Н.П. Жуков, Н.Ф. Майникова, И.В. Рогов // Вестник Тамбовского государственного технического университета. – 2000. – Т. 6, № 4. – С. 562 – 571.

21.  Микропроцессорная система неразрушающего контроля теплофизических свойств и оценки структурных переходов в полимерах / Н.Ф. Майникова, И.В. Рогов,
А.А Балашов, А.П. Пудовкин // Труды Междунар. конф. “Информационные технологии в проектировании микропроцессорных систем”. – Тамбов, 2000. – С. 86 – 89.

22.  Майникова Н.Ф. Измерительно-вычислительная система для контроля тепло­физических свойств и структурных превращений в полимерах / Н.Ф. Майникова, Н.П. Жуков, А.А. Бала­шов // Труды IV Междунар. теплофиз. шк. “Теплофизические измерения в XXI веке”. – Тамбов, 2001. – С. 44 – 45.

23. Измерительно-вычислительная система для исследования температурных зависимостей теплопроводности и теплоемкости материалов / Майникова Н.Ф., Н.П. Жуков, В.И. Ляшков, С.В. Балашов // Вестник Тамбовского государственного технического
университета. – 2001. – Т. 7, № 1. – С. 35 – 44.

24. Некорректно поставленные задачи при неразрушающем контроле теплофизи­ческих характеристик материалов / Н.П. Жуков, Ю.Л. Муромцев, Н.Ф. Майникова,
И.В. Рогов // Вестник Тамбовского государственного технического университета. – 2001. – Т. 7, № 4. – С. 524 – 533.

25.  Майникова Н.Ф. Неразрушающий теплофизический метод контроля структурных превращений в полимерных материалах / Н.Ф. Майникова, А.А. Балашов // Труды Междунар. конф. “Теория, методы и средства измерений, контроля и диагностики”. – Новочеркасск, 2001. – Ч. 1. – С. 49 – 51.

26. Измерительно-вычислительная система для регистрации температурных
зависимостей теплопроводности и теплоемкости материалов / Н.Ф. Майникова, Ю.Л. Муромцев, В.И. Ляшков, С.В. Балашов // Заводская лаборатория. – 2001. – Т. 67,
№ 8.– С. 35 – 37.

27. Mainikova N. F. Non – destructive control of physical and mechanical characteristics of composite materials / N.F. Mainikova, I.V.Rogov, A. A. Balashov // Вестник Тамбовского государственного технического университета. – 2001. – Т. 7, № 3. – С. 391 – 393.

28.  Майникова Н.Ф. Моделирование информационно-измерительной системы
конт­роля твердофазных превращений в полимерах / Н.Ф. Майникова, А.С. Чех //
Труды XV Междунар. конф. “Математические методы в технике и технологиях”. – Тамбов, 2002. –Т. 7. – С. 130 – 132.

29.  Теплофизический метод контроля структурных превращений в полимерах / С.В. Мищенко, Н.Ф. Майникова, Ю.Л. Муромцев, Н.П. Жуков // Труды III Рос. нац. конф. по теплообмену. – М., 2002. – Т. 7. – С. 196 – 199.

30. Определение теплофизических свойств материалов неразрушающим способом / Н.П. Жуков, Ю.Л. Муромцев, Н.Ф. Майникова, И.В. Рогов // Вестник Тамбовского государствен­ного технического университета. – 2002. – Т. 8, № 1. – С. 54 – 62.

31. Жуков Н.П. Моделирование процесса теплопереноса при теплофизических
измерениях / Н.П. Жуков, Н.Ф. Майникова // Вестник Тамбовского государственного технического университета. – 2002. – Т. 8, № 2. – С. 182 – 190.

32.  Измерительно-вычислительная система для исследования структурных превращений в полимерах / С.В. Мищенко, Ю.Л. Муромцев, Н.П. Жуков, Н.Ф. Майникова // Труды V Междунар. конф. “Фундаментальные и прикладные проблемы приборо­строения”. – М., 2002. – С. 136 – 140.

33.  Измерительно-вычислительный комплекс для исследования структурных превращений в полимерах / Н.Ф. Майникова, Ю.Л. Муромцев, П. Латцель, Р. Циммерманн // Труды XV Междунар. конф. “Математические методы в технике и технологиях”. –
Тамбов, 2002. – Т. 7. – С. 122 – 125.

34.  Майникова Н.Ф. Распределение температурного поля в полуограниченном теле от источника тепла постоянной мощности / Н.Ф. Майникова, С.С. Никулин, А.С. Чех // Труды III Рос. нац. конф. по теплообмену. – М., 2002. – Т. 7. – С. 181 – 183.

35. Многомодельный метод неразрушающего теплофизического контроля структурных превращений в полимерных материалах / Н.П. Жуков, Н.Ф. Майникова, Ю.Л. Муромцев, А.С. Чех // Вестник Тамбовского государственного технического университета. – 2003. – Т. 9, № 2. – С. 196 – 198.

36.  Жуков Н.П. Измерительно-вычислительная система для теплофизического
контроля / Н.П. Жуков, Н.Ф. Майникова // Труды VI Междунар. конф. “Фундаментальные и прикладные проблемы приборостроения”. – М., 2003. – С. 76 – 82.

37.  Майникова Н.Ф. Распределение температуры от действия источника тепла
постоянной мощности / Н.Ф. Майникова, А.С. Чех // Проблемы газодинамики и тепломассообмена в энергетических установках. – М.: Изд-во МЭИ, 2003. – С. 413 – 417.

38.  Майникова Н.Ф. Информационно-измерительная система теплофизического
неразрушающего контроля структурных превращений в полимерных материалах / Н.Ф. Майникова, А.С. Чех // Информационные системы и процессы. Сб. науч. тр. – Тамбов; Москва; Баку; Вена: Изд-во “Нобелистика”, 2004. – Вып. 1. С. 175 – 180.

39.  Майникова Н.Ф. Информационно-измерительная система теплофизического контроля полимерных материалов / Н.Ф. Майникова, А.А. Балашов, Ю.Л. Муромцев // Информационные системы и процессы. Сб. науч. тр. –М.: Изд-во “Нобелистика”, 2004. – Вып. 2. С. 150 – 153.

40.  Майникова Н.Ф. Об одном решении краевой задачи теплопроводности / Н.Ф. Майникова // Труды V Междунар. теплофиз. шк. “Теплофизические измерения при контроле и управлении качеством”. – Тамбов, 2004. – Ч. 1. – С. 216 – 220.

41. Майникова Н.Ф. О термических сопротивлениях при неразрушающем контроле теплофизических характеристик материалов / Н.Ф. Майникова, И.В. Рогов // Вестник Тамбовского государственного технического университета. – 2004. – Т. 10, № 1А. –
С. 43 – 46.

42.  Майникова Н.Ф. Программно-аппаратные средства информационно-измеритель­ной системы теплофизического контроля / Н.Ф. Майникова, А.А. Балашов // Труды V Междунар. теплофиз. шк. “Теплофизические измерения при контроле и управлении качеством”. – Тамбов, 2004. Ч. 2. С. 16 20.

43.  Майникова Н.Ф. О решении одной краевой задачи теплопроводности / Н.Ф. Майникова // Труды VII Междунар. конф. “Фундаментальные и прикладные проблемы приборостроения”. – М., 2004. – С. 138 – 141.

44.  Майникова Н.Ф. Моделирование процесса теплопереноса от плоского источника тепла постоянной мощности при неразрушающем теплофизическом контроле / Н.Ф. Майникова, Н.П. Жуков // №511-B2004, Б.У. ВИНИТИ “Депонированные работы”, 2004. – № 6. – 9 с.

45.  Майникова Н.Ф. Статистическая обработка результатов неразрушающего контроля теплофизических свойств полимеров / Н.Ф. Майникова, Н.П. Жуков //
№657-B2004, Б.У. ВИНИТИ “Депонированные работы”, 2004, – № 6. – 21 с.

46.  Майникова Н.Ф. Статистическая обработка результатов неразрушающего контроля температурно-временных характеристик структурных превращений в полимерах / Н.Ф. Майникова, Н.П. Жуков // №658-B2004, Б.У. ВИНИТИ “Депонированные работы”, 2004, – № 6. – 14 с.

47.  Майникова Н.Ф. Математическое моделирование процесса теплопереноса в методе теплофизического контроля / Н.Ф. Майникова, А.С. Чех, Н.П. Жуков // Проблемы газодинамики и тепломассообмена в энергетических установках. – М.: Изд-во МЭИ, 2005. – Т. 1. – С. 398 – 401.

48. Мищенко С.В. Метод неразрушающего контроля структурных превращений в полимерных материалах / С.В. Мищенко, Н.Ф. Майникова // Вестник Тамбовского государственного технического университета. – 2005. – Т. 11, № 1А. – С. 69 – 75.

49.  Майникова Н.Ф. Метод неразрушающего контроля структурных переходов в полимерных материалах / Н.Ф. Майникова, С.С. Никулин // Труды XI Росс. конф. по теплофизическим свойствам веществ. – СПб., 2005. – С. 64.

50.  Mischenko S.V. Measuring System Realizing Termalphysic Method of Nondestructive Check of Structural Transitions in Polymeric Materials / S.V. Mischenko, N.F. Mainikova // Abstracts IV-th international conference “Problems of industrial heat engineering”. – Kyiv, Ukraine, 2005. – P. 298 – 299.

51. Метод неразрушающего теплофизического контроля структурных превращений в полимерных материалах / Н.П. Жуков, Н.Ф. Майникова, С.С. Никулин // Труды IX Междунар. конф. “Фундаментальные и прикладные проблемы приборостроения”. –
М., 2006. – С. 67 – 71.

52. Майникова Н.Ф. Математическая модель нестационарного процесса теплопереноса в системе двух полуограниченных тел / Н.Ф. Майникова, С.С. Никулин, А.С. Чех // Труды IV Рос. нац. конф. по теплообмену. – М., 2006. – Т. 7. – С. 222 – 225.

53. Майникова Н.Ф. Информационно-измерительная система для неразрушающего теплофизического контроля материалов / Н.Ф. Майникова // Труды IX Междунар.
конф. “Фундаментальные и прикладные проблемы приборостроения”. – М., 2006. – С. 133 – 136.

54. Многомодельный подход к разработке метода неразрушающего контроля структурных превращений в полимерах / Н.Ф. Майникова, Ю.Л. Муромцев, С.С. Никулин // Труды IX Междунар. конф. “Фундаментальные и прикладные проблемы приборо­строения”. – М., 2006. – С. 137 – 141.

55. Майникова Н.Ф. Метод контроля температурных характеристик структурных переходов в полимерных материалах / Труды IV Рос. нац. конф. по теплообмену. –
М., 2006. – Т. 7. – С. 276 – 279.

56. Определение условий адекватности модели распределения тепла в плоском
полупространстве реальному процессу при теплофизическом контроле/ Н.П. Жуков, Н.Ф. Майникова, А.А. Балашов, С.С. Никулин // Вестник Тамбовского государственного технического университета. – 2006. – Т. 12, № 3А. – С. 610 – 616.

57. Майникова Н.Ф. Измерительная система неразрушающего контроля структурных превращений в полимерных материалах / Н.Ф. Майникова // Приборы и системы. Управление, контроль, диагностика. – 2006. – № 9. – С.45 – 48.

58.  Mainikova N.F. Information-Measurement System of Nondestructive Control
Termophysical Properties and Structural Conversion in Polymer Materials / N.F. Mainikova, S.V. Mischenko, N.P. Zhukov // Abstracts V-th international conference “Problems of industrial heat engineering”. – Kyiv, Ukraine, 2007. – P. 317 – 318.

59. Патент 2161301 РФ, G 01 N 25/18. Способ неразрушающего определения теплофизических свойств материалов/ Жуков Н.П., Муромцев Ю.Л., Майникова Н.Ф.,
Рогов И.В., Балашов А.А. № 99104568, заявл. 03.03.1999, опубл. 27.12.2000, Бюл № 36.

60. Патент 2167412 РФ, G 01 N 25/18. Способ комплексного определения теплофизических свойств материалов / Жуков Н.П., Майникова Н.Ф., Муромцев Ю.Л.,
Рогов И.В. № 99103718, заявл. 22.02. 1999, опубл. 20.05.2001, Бюл № 14.

61. Патент 2 287 152 РФ, G 01 N 25/18. Способ неразрушающего определения теплофизических свойств твердых материалов/ Жуков Н.П., Майникова Н.Ф., Чех А.С.,
Никулин С.С. № 2005114237, заявл. 11.05.2005, опубл. 10.11.2006, Бюл №31.

62. Свидетельство об официальной регистрации программы. – № 2003610580. Определение тепловой активности / Н.П. Жуков, Н.Ф. Майникова, А.С. Чех, А.А. Балашов.

63. Свидетельство об официальной регистрации программы. – № 2003610931.
Определение ТФХ / Н.П. Жуков, Н.Ф. Майникова, Ю.Л. Муромцев, А.С. Чех.

64. Свидетельство об официальной регистрации программы. – № 2003610932.
Регистрация аномалий тепловой активности материалов / Н.П. Жуков, Н.Ф. Майникова, А.С. Чех, А.А. Балашов.

65. Свидетельство об официальной регистрации программы. – № 2003611204.
Регистрация аномалий ТФХ / Н.П. Жуков, Н.Ф. Майникова, Ю.Л. Муромцев, А.С. Чех.

Гарнитура Тimes New Roman. Формат 60 84/16. Бумага офсетная.

Печать офсетная. Объем: 2,0 усл. печ. л.; 2,0 уч.-изд. л.

Тираж 100 экз.

Издательско-полиграфический центр ТГТУ

392000, Тамбов, Советская, 106, к. 14

66. Свидетельство об официальной регистрации программы. – № 2006612383.
Построение термограмм в методе неразрушающего теплофизического контроля/ Н.П. Жуков, Н.Ф. Майникова, И.В. Рогов, С.С. Никулин.