Параметрическая оптимизация информационно-измерительной системы определения параметров движения изображения подстилающей поверхности

На правах рукописи

ЧЕКОТИЛО Елена Юрьевна

ПАРАМЕТРИЧЕСКАЯ ОПТИМИЗАЦИЯ ИНФОРМАЦИОННО-ИЗМЕРИТЕЛЬНОЙ СИСТЕМЫ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ ИЗОБРАЖЕНИЯ ПОДСТИЛАЮЩЕЙ ПОВЕРХНОСТИ

Специальность 05.11.16 – Информационно - измерительные и

управляющие системы (промышленность)

Автореферат

диссертации на соискание ученой степени

кандидата технических наук

Самара - 2008

Работа выполнена на кафедре «Электропривод и промышленная автоматика» Государственного образовательного учреждения высшего профессионального образования «Самарский государственный технический университет».

Научный руководитель: Доктор технических наук, профессор

КУЗНЕЦОВ Павел Константинович

Официальные оппоненты: Доктор технических наук, профессор

ГРЕЧИШНИКОВ Владимир Михайлович

Кандидат технических наук, доцент

СВИРИДОВ Вячеслав Павлович

Ведущая организация: ФГУП ГНП РКЦ "ЦСКБ – Прогресс"

(г. Самара)

Защита диссертации состоится 3 июля 2008 г. в 10 часов 00 мин. на заседании диссертационного совета Д 212.217.03 ГОУ ВПО Самарский государственный технический университет по адресу: г. Самара, ул. Галактионовская, 141, корпус 6, аудитория 28.

Отзывы по данной работе в двух экземплярах, заверенные печатью, просим направлять по адресу: Россия, 443100, Самара, ул. Молодогвардейская 244, Главный корпус на имя ученого секретаря диссертационного совета Д 212.217.03; факс: (846) 278-44-00.

С диссертацией можно ознакомиться в библиотеке Самарского государственного технического университета (ул. Первомайская, 18)

Автореферат разослан 2 июня 2008 г.

Ученый секретарь

диссертационного совета Губанов Н. Г.

Д 212.217.03.

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность работы Важной задачей для многих отраслей промышленности является улучшение методов создания информационно-измерительных систем определения параметров движения (ИИС ОПД) изображений, способных определять текущее положение диагностируемого объекта и прогнозировать его новое положение (рассматриваемые в работе изображения – это объекты с собственным или отраженным электромагнитным излучением). Примером таких ИИС ОПД является задача определения параметров движения подстилающей поверхности, когда нежелателен или затруднен непосредственный контакт с контролируемым яркостным объектом. Задача бесконтактного определения параметров движения особенно актуальна в том случае, когда применение контактных методов в принципе невозможно или недопустимо. Например, при создании автономных средств навигации и ориентации космических и летательных аппаратов, систем наведения, слежения и обнаружения движущихся объектов с помощью оптико-электронных систем видимого и инфракрасного диапазонов, размещенных на борту летательных и космических аппаратов. Подобный случай имеет место также при измерении скорости движения автономных промышленных транспортных средств (транспортных роботов). Перечисленные задачи требуют определения параметров движения яркостных объектов по видеоинформации, получаемой на достаточно коротких интервалах времени, т.е. в реальном времени.

Существуют ИИС ОПД, решающие в той или иной мере перечисленные выше задачи. Фундаментальным научным проблемам в области обработки аэрокосмических изображений и созданию ИИС на их основе посвящены работы российских ученых: член-корр. РАН Сойфера В.А., Порфирьева Л.П., Сухопарова С.А., Сергеева В.В., Титова В.И., Злобина В.К., Еремеева В.В., Обуховой Н.А., Ташлинского А.Г. и их научных школ. Перспективным методом, обладающим высоким быстродействием и универсальностью является т.н. метод функционализации параметров изображения 1. Однако, этот метод апробирован только для случая плоско-параллельного движения носителя оптической системы (ОС) относительно плоской подстилающей поверхности. Метод функционализации является обобщением известного «градиентного» метода, используемого для вычисления оптического потока 2.

Практика использования ИИС ОПД, построенных на алгоритмах, реализующих этот метод, показала высокое быстродействие и хорошие метрологические характеристики ИИС ОПД, но только в условиях стабильности освещенности сцены. Оказалось, что при вариации освещенности сцены возникает методическая погрешность, пропорциональная производной по времени функции изменения освещенности.

Настоящая работа посвящена развитию и апробации метода функционализации в приложении к определению движения подстилающей поверхности с тремя степенями свободы (случай, когда носитель ОС совершает плоско-параллельное движение относительно подстилающей поверхности и вращение в плоскости движения) в условиях изменяющейся освещенности сцены и вариации типов изображений подстилающей поверхности.

Тема данной работы сформировалась при разработке пассивных высокоточных систем обнаружения и слежения за движущимися яркостными объектами по заказам Секции прикладных проблем при Президиуме РАН (СПП РАН), ГНП РКЦ "ЦСКБ – Прогресс", Минобрнауки - Госбюджетная фундаментальная НИР №522/08 «Создание основ теории и способов реализации алгоритмически точных методов определения алгоритмов оптимального управления объектами с распределенными параметрами».

Целью диссертационной работы является расширение функциональных возможностей и повышение быстродействия информационно-измерительной системы определения параметров движения изображения подстилающей поверхности на основе развития метода функциональных преобразований параметров изображения.

Для достижения поставленной цели в работе должны быть решены следующие задачи:

1. Развитие метода функциональных преобразований с целью обеспечения инвариантности к изменению освещенности подстилающей поверхности.
2. Развитие итерационных процедур определения параметров движения изображения подстилающей поверхности для трех степеней подвижности (плоско-параллельное движение и вращение в плоскости движения), реализующих метод функционализации.
3. Получение аналитических оценок сходимости и быстродействия итерационного метода измерения параметров движения изображения подстилающей поверхности.
4. Анализ влияния аддитивного шума и изменения интенсивности освещенности изображения на сходимость итерационного метода измерения параметров движения изображения подстилающей поверхности.
5. Получение с помощью компьютерных экспериментов оценок быстродействия и погрешности рассматриваемой ИИС ОПД.

Методы исследований основаны на использовании теории оптико-электронных систем, основных разделов математического анализа и математических методов обработки экспериментов.

Основные теоретические и практические выводы диссертации подтверждены результатами моделирования на ЭВМ и экспериментальными исследованиями макетных образцов.

Научная новизна и значимость работы заключается в следующем:

1. Получена математическая модель (уравнение функциональной связи), связывающая доступные измерению характеристики изображения с параметрами движения подстилающей поверхности и освещенностью сцены. Математическая модель представляет собой линейное алгебраическое уравнение, неизвестными которого являются составляющие вектора скорости и освещенность сцены. Это уравнение может быть параметризовано и решено известными методами.
2. Получены алгоритмы вычисления скорости движения подстилающей поверхности, инвариантные к изменению освещенности сцены.
3. Предложен итерационный алгоритм определения параметров движения изображения подстилающей поверхности обладающей тремя степенями подвижности (плоско-параллельное движение и вращение в плоскости движения).
4. Проведен аналитический и экспериментальный анализ влияния изменения параметров (коэффициент обратной связи, размер окон анализа) итерационного метода определения вектора скорости движения изображений на его сходимость и быстродействие.
5. Произведена параметрическая оптимизация ИИС ОПД изображения подстилающей поверхности, результатом которой стало расширение функциональных возможностей и быстродействия рассматриваемой системы.
6. Проведен экспериментальный анализ влияния аддитивного шума, изменения интенсивности освещенности наблюдаемой сцены на погрешность и быстродействие ИИС ОПД.

Практическая ценность

1. Предложена универсальная структура информационно-измерительной системы определения параметров движения (плоско-параллельное движение и вращения в плоскости движения) изображения подстилающей поверхности инвариантная к изменению интенсивности освещенности рассматриваемой сцены.
2. Получены оценки сходимости и быстродействия предложенных алгоритмов определения параметров движения изображения.
3. Создана программная модель ИИС ОПД, получены оценки быстродействие и погрешности рассматриваемой системы.

Внедрение результатов работы осуществлено при разработке по заказу ФГУП ГНП РКЦ "ЦСКБ – Прогресс" (г. Самара) информационно-измерительной системы компенсации смаза изображений, получаемых при дистанционном зондировании Земли из космоса. Результаты используются в учебном процессе кафедры «Электропривод и промышленная автоматика» ГОУ ВПО «СамГТУ» в курсе «Элементы систем автоматики».

Апробация работы. Результаты работы докладывались, обсуждались и были одобрены на международных, всероссийских и межвузовских научно-технических конференциях, в том числе на V Международной конференции молодых ученых «Актуальные проблемы современной науки» (Самара, 2004), Всероссийской научной конференции «Управление и информационные технологии» (Санкт - Петербург, 2005), III Всероссийской научной конференции «Математическое моделирование и краевые задачи» (Самара, 2006), XIII Международной научно-технической конференции студентов и аспирантов «Радиоэлектроника, электротехника и энергетика» (Москва, 2007), IV Всероссийской научной конференции «Математическое моделирование и краевые задачи» (Самара, 2007).

Публикации. По теме диссертационной работы опубликовано 7 печатных работ, в том числе 2 статьи в издании из перечня, рекомендуемого ВАК РФ.

Объем и структура работы. Диссертационная работа состоит из введения, четырех разделов, выводов и списка литературы из 233 наименований. Общий объем 120 страниц, 3 таблицы, 35 рисунков.

На защиту выносятся следующие положения:

1. Вариант метода функциональных преобразований параметров изображений инвариантный к изменению интенсивности освещенности подстилающей поверхности.
2. Итерационный метод определения параметров движения изображения подстилающей поверхности для трех степеней подвижности (плоско-параллельное движение и вращение в плоскости движения), реализующий метод функционализации.
3. Аналитические оценки сходимости и быстродействия итерационного метода определения параметров движения для случая плоско-параллельного движения и вращения в плоскости движения изображения подстилающей поверхности.
4. Методика, алгоритмы и результаты параметрической оптимизации ИИС ОПД подстилающей поверхности.
5. Модифицированная структура быстродействующей прецизионной ИИС ОПД, в которой реализованы алгоритмы оптимизации параметров измерения.
6. Оценки погрешностей и быстродействия предложенной информационно-измерительной системы определения параметров движения изображения подстилающей поверхности.
7. Результаты компьютерного экспериментального исследования ИИС ОПД.

СОДЕРЖАНИЕ РАБОТЫ

Во введении обосновывается актуальность темы исследования, кратко характеризуется состояние проблемы, формулируются цели и задачи исследования, характеризуется научная новизна и практическая ценность полученных результатов, приводятся основные положения, выносимые на защиту.

В первом разделе рассматривается состояние проблемы и обосновывается направление исследования.

В общем случае ИИС ОПД выполняет следующие основные функции: формирования изображения с помощью изобразительной системы; преобразования изображения в электрический сигнал; предварительной обработки видеосигнала (оцифровки, фильтрации, нормализации, выделения требуемых параметров); реализации основного целевого алгоритма; слежения за движущимися объектами; адаптации параметров ИИС ОПД к изменяющимся условиям наблюдения (изменение времени экспозиции, автоматическая фокусировка изображения, изменение освещенности сцены); представления выходных данных в требуемой форме. На рисунке 1 дана обобщенная структура ИИС ОПД в составе информационно- управляющей системы зондирования яркостных объектов, выполняющая перечисленные функции. Конкретизация алгоритмов и характеристики подсистем и самой ИИС ОПД определяется реализованным в ней методом определения параметров движения.

В приведенном обзоре выделены три большие группы методов определения параметров движения яркостных объектов – методы, основанные на анализе пространственных частот изображения, методы, основанные на измерении смещения изображения и градиентные методы.

Из всех перечисленных методов наиболее перспективен для создания быстродействующих универсальных ИИС ОПД метод функциональных преобразований, который является обобщением градиентных методов 3.

Метод функциональных преобразований отличается от известных существенно меньшей вычислительной сложностью и поэтому позволяет строить ИИС ОПД, работающие в реальном времени. Этот метод и реализующая его система рассматриваются в данной работе.

Во втором разделе метод функциональных преобразований распространен на случай определения параметров движения при трех степенях подвижности носителя оптической системы (платформы) относительно плоского недеформируемого изображения подстилающей поверхности с учетом изменяющихся условий освещенности сцены. В работе рассмотрена математическая модель движения изображения яркостного объекта в картинной плоскости оптической системы, на основе которой ранее было получено уравнение движения изображения точки, находящейся на изображении подстилающей поверхности, которое для рассматриваемого в данной работе случая имеет вид:

, (1)

где – вектор столбец, компоненты которого являются координатами изображения точки в картинной плоскости оптической системы; – фокусное расстояние оптической системы; – кососимметричная матрица, элементы которой являются проекциями вектора угловой скорости носителя оптической системы на оси связанной с носителем оптической системы координат; - вектор смещения главной точки оптической системы относительно центра масс оптической системы; – матрица косинусов углов между осями систем координат, связанных с яркостным объектом и носителем оптической системы; – вектор поступательной скорости движения носителя оптической системы; , где – матрица-строка, являющаяся третьей строкой матрицы ; – расстояние от центра масс носителя оптической системы до яркостного объекта.

Согласно методу функциональных преобразований в окне анализа задается функционал , например мультипликативного типа:

(2)

где D – односвязная регулярная область анализа с границей Г(D); - непрерывная и дифференцируемая почти всюду по всем своим аргументам функция веса; – равномерно ограниченная и дифференцируемая почти всюду по всем своим аргументам функция распределения освещенности изображения яркостного объекта.

Далее вычисляется полная производная по времени от функционала (2) в силу уравнения движения изображения (1) с учетом того, что освещенность сцены меняется во времени. Для того чтобы учесть изменение во времени освещенности сцены, функция распределения освещенности изображения представляется в виде:

,

где - функция распределения альбедо,- интенсивность внешнего источника, облучающего подстилающую поверхность.

В таком случае полная производная по времени от функционала (2) приобретает вид:

(3)

где - вспомогательная переменная, отражающая изменение функции освещенности во времени;

Г(D) – граница окна анализа D; = [sin, -cos, 0] - матрица строка (- локальное уравнение границы Г(D) окна анализа D); - матрица строка.

Полученное уравнение (3) является ФС - уравнением, которое связывает компоненты вектора угловой скорости и вектора поступательной скорости носителя оптической системы относительно яркостного объекта с временными и пространственными характеристиками изображения подстилающей поверхности в картинной плоскости оптической системы.

Значения интегралов должны вычисляться на границе окна анализа Г(D). Точное измерение значения этого интеграла не представляется возможным. Поэтому способы определения движения, вытекающие из ФС - уравнений, будут реализуемы лишь при условии, что функция веса непрерывна и равна нулю на границе окна анализа . Примем, что подстилающая поверхность плоская, недеформируемая и отсутствуют объекты, движущиеся на ее фоне, тогда компоненты вектора скорости могут быть вынесены за знак интеграла и уравнение (3) для движения с тремя степенями подвижности сводится к линейному алгебраическому уравнению следующего вида:

, (4)

где , , - составляющие вектора скорости плоско-параллельного и вращательного движения в плоскости подстилающей поверхности носителя оптической системы, q – введенная выше вспомогательная переменная характеризующая освещенность сцены;

b1 - b4 - коэффициенты уравнения, определяемые из выражений:

;

;

;

.

Составляющие вектора скорости движения носителя ОС определяются из системы ФС - уравнений, составленной из i уравнений типа (4), коэффициенты для каждого из которых получаются по информации из i –го окна анализа:

, (5)

где - вектор-столбец; B=[bi,j] – матрица коэффициентов; P=[pi]T – вектор-столбец; i=1…N (NМ), j=M (M =1…4).

Решение системы уравнений (5) может быть найдено методом квазиобращений:

. (6)

Как следует из вида коэффициентов ФС - уравнения (3), их вычисление значительно упрощается, если окно анализа имеет форму прямоугольника, границы которого параллельны осям координат в картинной плоскости ОС.

Критерием выбора функции веса являются простота реализации и корректность способа определения параметров движения яркостных объектов.

В третьем разделе рассматривается итерационный алгоритм определения параметров движения изображения подстилающей поверхности.

При исследованиях принято, что видеосигнал имеет вид:

,

где - видеосигнал; - случайный аддитивный шум, некоррелированный с ни по , ни по t.

Аналитически показано, что в рассматриваемом случае смещение математического ожидания оценки скорости движения при прямо пропорционально фактической скорости движения изображения подстилающей поверхности:

, (7)

где ;

;

;

;

i = 1…N – номер окна анализа.

Из соотношения (7) следует, что для того, чтобы смещение математического ожидания оценки скорости стремилось к нулю, измерение движения необходимо организовать так, чтобы измеряемая скорость стремилась к нулю. Это может быть реализовано в компенсационном варианте метода функциональных преобразований, с использованием физического или «электронного» (режим ВЗН ПЗС матриц) подслеживания движения изображения.

В компенсационном методе используется итерационная процедура совмещения изображений подстилающей поверхности в двух последовательных во времени кадрах изображений. При этом в ОЗУ ИИС ОПД хранятся два последовательных кадра и , - кадровый период.

Согласно методу функциональных преобразований на каждом шаге итерационной процедуры формируется система алгебраических уравнений, необходимая для определения оценок составляющих вектора смещения изображения . Для этого в каждом кадре выделяются идентичные системы N окон анализа Dij размером (i = 1, 2 – номер кадра; j = 1, 2, …, N – номер окна в кадре), образующих покрытие некоторой области кадра. Правильным называется покрытие, обладающее следующим свойством:

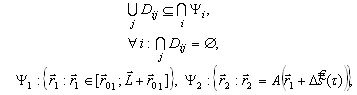(8)

где - размеры кадра, - начальное положение первого кадра.

Для каждой j - ой пары окон записывается уравнение функциональной связи (4) относительно компонент вектора смещения:

, (9)

где - разностное представление производной по времени от функционала (2).

Тогда решение системы ФС – уравнений (5):

,

где находится методом квазиобращений (6).

В итерационной процедуре на каждом шаге определяются оценки компонент вектора смещения изображения подстилающей поверхности:

, (10)

где = 0, 1, 2,…, n – номер итерации; ;

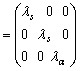- матрица коэффициентов обратной связи;

- априорно известная оценка смещения изображения.

На каждой итерации изображение второго кадра смещается на величину противоположную. В следующей итерации используется функция. Описанные процедуры повторяются до тех пор, пока компоненты вектора смещения на n - ом шаге не станут меньше заданных величин , и .

В итоге, оценка скорости постоянно корректируется и постепенно приближается к скорости движения изображения подстилающей поверхности.

Для простоты реализации итерационного метода удобно использовать «пирамидальную» функцию веса :

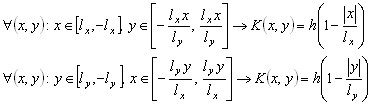. (11)

Таким образом, параметрами функции веса являются размеры окон анализа .

Задачей является оптимизация параметров вычислений (размеров, количества окон анализа и матрицы коэффициентов обратной связи) на основании критериев:

1. максимизации области сходимости (по начальным данным 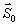) итерационной процедуры (10);
2. минимизации количества итераций.

Для решения задачи оптимизации получены аналитические оценки сходимости итерационного метода с «пирамидальной» функцией веса без учета аддитивного шума для тестового изображения, заданного функцией освещенности:

, (12)

где ; - первая и вторая строки матрицы .

В силу сложности получения аналитических оценок сходимости итерационного метода для общего случая (12), рассматривается отдельно плоско-параллельное движение и вращение в плоскости движения подстилающей поверхности.

Для случая плоско - параллельного движения () система уравнений (10) принимает вид:

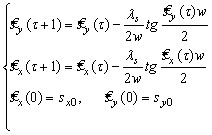, (13)

где - составляющие вектора смещения изображения подстилающей поверхности относительно окна анализа. Показано, что достаточным признаком, сходимости итерационной процедуры (13) является выполнение условий:

(14)

(15)

Например, при погрешности метод сходится на шаге .

Соотношение (14) дает оценку области сходимости в пространстве начальных данных, в случае, когда изображение является тестовым вида (12).

Для случая чистого вращения при в плоскости движения также получена аналогичная аналитическая оценка сходимости итерационного метода. Итерационная процедура совмещения изображения при анализе вращения имеет вид:

. (16)

Достаточным признаком сходимости итерационной процедуры (16) является следующее условие:

. (17)

Условие сходимости (17) будет выполняться для всех таких, что

(18)

где

- функция нескольких переменных: . Таким образом, сходимость итерационного процесса (16) зависит от размеров окон анализа и параметров тестового сигнала (12). Обозначим через максимальное значение, отвечающее достаточному признаку сходимости (18).

В таблице 1 приведены результаты анализа зависимости количества итераций итерационного процесса (16) от критического значения коэффициента обратной связи и параметров тестового сигнала. Условие (18) является лишь достаточным. Анализ показал, что значение может быть увеличено, при этом скорость сходимости увеличивается.

Таблица 1

Длина стороны окна анализа		Погрешность приближения
		Максимальное число итераций n
	0,193	14	20	31
	0,1763	31	45	72
	0,00277	128	234	341
	0,04616	20	29	46

Для определения наилучшего в смысле сходимости значения произведен численный эксперимент по исследованию влияния на процесс сходимости итерационной процедуры (16) для тестового изображения (12). Результаты моделирования приведены в таблице 2.

Таблица 2

Длина стороны окна анализа	Коэффициент обратной связи
	Максимальное число итераций n
	6	5	5
	27	15	7
	52	24	18
	28	10	7

При увеличении сначала увеличивается количество итераций, а затем процесс (16) теряет устойчивость. Таким образом, можно сделать вывод, что наилучшая сходимость с точки зрения максимального быстродействия итерационного процесса достигается при . В таблице 2 приведены результаты соответствующие допустимой погрешности . При других значениях значение остается в тех же пределах.

В общем случае изображение не является моночастотным. Оно представляется спектром пространственных частот (частотно-контрастным спектром), в котором путем фильтрации можно выделить гармоническую составляющую вида (12) с желаемой частотой . Очевидно, желаемыми являются такие спектральные составляющие, которые удовлетворяют соотношению (14) и отношение сигнал/шум на них находится в допустимых пределах. Требуемая фильтрация может быть обеспечена выбором параметров весовых функций и .

Элемент матрицы коэффициентов обратной связи вычисляется по частоте и должен удовлетворять (15).

Значение коэффициента обратной связи , где выбирается по частоте из таблицы 1.

Эти выводы положены в основу излагаемой в четвертом разделе процедуры оптимизации параметров измерения.

В четвертом разделе диссертации предложен алгоритм оптимизации параметров процесса измерения, реализованный в блоке СУППИ, блок-схема которого приведена на рисунке 2.

Разработан алгоритм оптимизации параметров процесса измерения.

Исходными данными являются:

• функция спектральной плотности исходного сигнала;
• размеры кадра ;
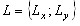• априорная оценка начального смещения второго кадра относительно первого ;
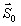• функция веса 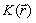имеет вид «пирамиды».

1. Блок ВСХ.

1. Для (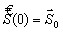) в соответствии с (13) вычисляется предельная частота спектральной плотности сигнала

.

2. Определяются доминирующие частоты 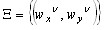, . Доминирующие частоты – это частоты, которые являются экстремумами функции спектральной плотности 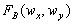и для которых выполняется условие:

сигнал/шум>0.

3. Формируется множество пар допустимых доминирующих частот , .

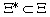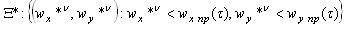2. Блок ОППИ.

1. Для каждой пары допустимых доминирующих частот 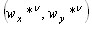выбирается типоразмер 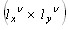окна анализа, максимизирующий амплитудно-частотную характеристику 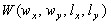фильтра с функцией веса на этих частотах. Каждый типоразмер окна анализа используется далее для образования правильного покрытия изображения. В результате получается несколько покрытий (система слоев покрытия) одних и тех же участков изображения окнами разного типоразмера. Слои покрытия образуются последовательно, начиная со слоя, соответствующего окну наиболее крупного размера. Для текущей системы покрытий определяются коэффициенты системы уравнений (9). Образование покрытия останавливается при выполнении следующего условия:

где или при нарушении правильности покрытия (8) во всех слоях.

2. Из таблицы 1 для каждого типоразмера окна анализа 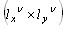выбирается критическое значение коэффициента обратной связи 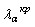. Значение коэффициента 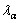назначается .

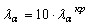3. Блок ВУ. С использованием итерационной процедуры вычисляется новое значение оценки . Повторяются пункты 1. – 2. Процесс останавливается при .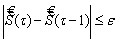

С целью систематизации результатов моделирования была произведена классификация изображений на основе исследования их вероятностных характеристик методами корреляционного анализа двумерных сигналов. От двумерной корреляционной функции осуществлялся переход к усредненным одномерным функциям и следующим образом: для каждого значения x производилось усреднение по переменной y, а для каждого значения y – по переменной x. Посредством аппроксимации усредненных автокорреляционных функций освещенности изображения подстилающей поверхности полиномом четвертой степени были получены следующие результаты:

1. Для изображений типа «Горы» оценка усредненных автокорреляционных функций имеет вид:

; (18)

2. Изображения типа «Река» описываются усредненными автокорреляционными функциями, имеющими следующие оценки:

; (19)

Существенно, что в общем случае коэффициенты разложения корреляционной функции могут отличаться от полученных для конкретных изображений, однако отношение коэффициентов при одинаковых степенях x и y разложений и для одного и того же типа изображений группируются в окрестности некоторого значения, характерного для данного типа изображения.

Для апробации предложенной итерационной процедуры вычисления оценок вектора скорости движения и определения погрешности получаемых оценок было применено компьютерное моделирование функционирования ИИС ОПД. В качестве изображений подстилающей поверхности использовались фрагменты поверхности Земли типа «Река», «Горы», корреляционные функции которых имели вид (18) – (19).

Первая серия компьютерных экспериментов проводилась без учета случайного шума в видеосигнале. Учитывалось только дискретное по пространству и времени представление сигналов. Эксперименты проводились для случаев:

• простого плоско – параллельного движения (без поворота);
• простого поворота в плоскости движения (без плоско – параллельного движения);
• сложного движения - движения с тремя степенями подвижности (сложение простого плоско – параллельного движения и простого вращения).

Были получены следующие результаты на множестве более тысячи реализаций:

1. Экспериментально показана инвариантность предложенного метода к изменению интенсивности освещенности сцены (рисунок 3).

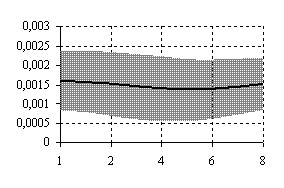
2. Проведен сравнительный анализ зависимости математического ожидания 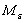относительной погрешности 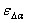оценки угла поворота и доверительного интервала D0,95 (при доверительной вероятности РД=0,95) от фактического угла поворота изображения подстилающей поверхности для изображений разных типов (рисунок 4).

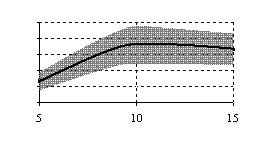
Сходимость зависит от типа изображения. При процесс сходится для изображений рассмотренных типов. При итерационная процедура для изображения типа «Река» сходится, а сходимость итерационного процесса для изображения типа «Горы» теряет устойчивость.

3. Для сложного движения подтверждены аналитически полученные выводы (таблица 2) о том, что при увеличении коэффициента обратной связи скорость сходимости увеличивается (рисунок 5); увеличение коэффициента 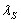не приводит к существенному изменению количества итераций и может быть принято равным единице .

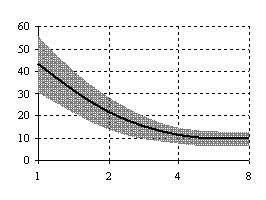
4. Экспериментально показано, что при сложном движении компоненты вектора смещения определяются с заданной погрешностью за 8 – 9 итераций, что хорошо соответствует аналитическим оценкам. Оценка угла поворота имеет постоянное смещение порядка 1% как при простом, так и при сложном движении. Это можно объяснить влиянием дискретного представления видеосигнала. Сходимость к этому значению также осуществляется за 8 - 9 итераций (рисунок 6).

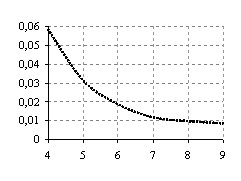
5. Проведены компьютерные эксперименты по оценке области сходимости итерационного метода по начальным данным и скорости сходимости. Результаты экспериментов сравнивались с результатами, полученными модифицированным методом наискорейшего спуска по критерию минимума квадрата попиксельной разности совмещаемых изображений (рисунки 7,8).

Во второй серии экспериментов дополнительно в видеосигнал аддитивно добавлялся шум с равномерной плотностью распределения. Этим моделировался шум тракта преобразования видеосигнала. Считалось, что шум не коррелирует с видеосигналом ни по x, y, ни по t. Целью моделирования являлось исследование влияния амплитуды плотности распределения шума Аш на точность и быстродействие ИИС ОПД (рисунок 9).

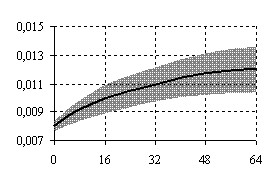
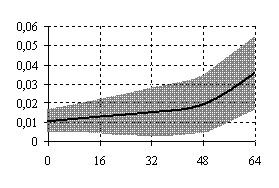
Эксперименты проводились при начальном смещении окон анализа, равным пяти пикселям для плоско-параллельного движения, десяти градусам для поворота при максимальном размахе видеосигнала 256 емр (емр – единица младшего разряда цифрового представления видеосигнала). При этом необходимое количество итераций не превышает 7 – 9 для плоско-параллельного и 10 – 12 для поворота изображения подстилающей поверхности.

Проведенные эксперименты показали работоспособность метода в случае сложного движения и его существенное преимущество по точностным характеристикам и диапазону измеряемых величин с другими известными методами.

На основе полученных данных была разработана бортовая ИИС ОПД, содержащая блок СУППИ со структурой, представленной на рисунке 2.

Получена оценка быстродействия бортовой ИИС ОПД. Быстродействие складывается из времени формирования двух кадров изображения (время запаздывания) и времени вычислений компонент вектора скорости. Время формирования кадров определяется топологией приемника изображений, типом используемых ПЗС - матриц и способом формирования изображения кадра.

В рассматриваемой системе для формирования двух кадров использованы две ПЗС - матрицы размером 102432 пикселя, работающие в режиме ВЗН. Расстояние между матрицами равно 288 пикселей. Время вычислений определяется сложностью алгоритма и быстродействием вычислителя. Это время при реализации вычислений на нейро - матричном процессоре типа 1879ВМ2 составляет не более 12 мс при минимальной скорости движения изображения (28 мм/с) и 3 мс при максимальной скорости движения изображения (132 мм/с).

Заключение

1. Проведенный анализ существующих методов определения параметров движения яркостных объектов со случайным распределением яркости показал, что методы, основанные на вычислении производных по времени и пространству от функции распределения яркости на изображении наиболее перспективны для построения быстродействующих систем определения параметров движения яркостных объектов при слабых ограничениях на количество степеней свободы движения наблюдаемого объекта.

2. Предложен вариант метода функциональных преобразований параметров инвариантный к изменению интенсивности освещенности подстилающей поверхности.

3. Реализован и опробован итерационный метод определения параметров движения изображения подстилающей поверхности обладающей тремя степенями подвижности, инвариантный к изменению интенсивности освещенности яркостного объекта.

4. С учетом результатов аналитического и экспериментального анализа сходимости итерационной процедуры определения движения проведена оптимизация параметров (размер окна анализа, матрица коэффициентов обратной связи) ИИС ОПД, которая позволила существенно (в 3-5 раз) расширить область сходимости по начальным данным и уменьшить (в 5 и более раз) количество итераций итерационного процесса.

5. Предложена модифицированная структура быстродействующей прецизионной системы определения параметров движения изображения подстилающей поверхности, отличающаяся возможностью расширения диапазона измеряемых скоростей, повышения быстродействия и инвариантностью к изменению освещенности наблюдаемой сцены.

Основное содержание диссертации опубликовано в работах:

1. Чекотило Е. Ю. Спектральный анализ вероятностных характеристик изображений [Текст] / Е. Ю. Чекотило, П. К. Кузнецов // Вестник Самарского Государственного, технического университета. Серия «Физико-математические науки». - Самара, 2006. - №42. - С. 212-215.
2. Чекотило Е. Ю. Влияние вида изображения и погрешности цифрового представления информации на точность изменения характеристик движения яркостных полей [Текст] / Е. Ю. Чекотило, П. К. Кузнецов // Вестник Самарского Государственного, технического университета. Серия «Физико-математические науки». - Самара, 2005. - №38. - С. 172-174.

3. Чекотило Е. Ю. (Шарапова Е.Ю.) Алгоритм фильтрации в задаче определения скорости движения яркостных полей [Текст] / Е. Ю. Чекотило (Е.Ю. Шарапова), П. К. Кузнецов // Труды пятой международной конференции молодых ученых. «Актуальные проблемы современной науки» Части 1, 2. Математика. Математическое моделирование. - Самара, 2004. - С. 117-119.
4. Чекотило Е. Ю. (Шарапова Е.Ю.) Исследование характеристик движения яркостных полей в задаче АКСИ [Текст] / Е. Ю. Чекотило (Е.Ю. Шарапова), П. К. Кузнецов // Всероссийская научная конференция. Управление и информационные технологии (УИТ-2005). Сборник докладов в двух томах. Том 2. - Санкт-Петербург: СПбГЭТУ «ЛЭТИ», 2005. - С. 172-174.
5. Чекотило Е. Ю. Восстановление статистических характеристик изображения по смазанному изображению [Текст] / Е. Ю. Чекотило, П. К. Кузнецов // Труды Третьей Всероссийской научной конференции. «Математическое моделирование и краевые задачи» Часть 4. Математические модели в информационных технологиях. - Самара, 2006. - С. 107-109.
6. Чекотило Е. Ю. Исследование статистических характеристик изображения методами спектрального анализа. [Текст] / Е. Ю. Чекотило, П. К. Кузнецов // Труды Четвертой Всероссийской научной конференции «Математическое моделирование и краевые задачи» Часть 4. Информационные технологии в математическом моделировании. – Самара, 2007. - С. 104-107.
7. Чекотило Е. Ю. Исследование характеристик изображения методами спектрального анализа [Тезисы] / Е. Ю. Чекотило, П. К. Кузнецов // Тринадцатая Международная научно-техническая конференция студентов и аспирантов «Радиоэлектроника, электротехника и энергетика». Тезисы докладов. - Москва: МЭИ, 2007. - С. 175.

Автореферат отпечатан с разрешения диссертационного совета Д212.217.03 ГОУ ВПО Самарский государственный технический университет

(протокол № 6 от 7 мая 2008 г.)

Заказ №145 Тираж 100 экз.

Отпечатано на ризографе.

ГОУВПО Самарский государственный технический университет

Отдел типографии и оперативной печати

443100 г. Самара ул. Молодогвардейская, 244