Информационные модели и методы решения задач ортогонального раскроя-упаковки на основе конструктивных и нейросетевых подходов
На правах рукописи
КОРЧЕВСКАЯ
Оксана Валериевна
ИНФОРМАЦИОННЫЕ МОДЕЛИ И
МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ОРТОГОНАЛЬНОГО РАСКРОЯ-УПАКОВКИ НА ОСНОВЕ КОНСТРУКТИВНЫХ И НЕЙРОСЕТЕВЫХ ПОДХОДОВ
05.13.17 – теоретические основы информатики
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата технических наук
Красноярск - 2009
Работа выполнена на кафедре информационных технологий ГОУ ВПО «Сибирский государственный технологический университет»
Научный руководитель кандидат технических наук, доцент
Жуков Леонид Александрович
Официальные оппоненты: доктор технических наук, профессор
Доррер Георгий Алексеевич
доктор технических наук, профессор
Миркес Евгений Моисеевич
Ведущая организация: Уфимский государственный авиационный технический университет
Защита диссертации состоится « 7 » апреля 2009 года в 14.00 часов на заседании диссертационного совета Д 212.099.11 при Сибирском федеральном университете по адресу: 660074, г. Красноярск, ул. Киренского, 26, корпус Ж, ауд. 1-15.
С диссертацией можно ознакомиться в научной библиотеке Сибирского федерального университета по адресу: ул. Киренского, 26, ауд. Г274.
Автореферат разослан « 6 » марта 2009 г.
Ученый секретарь
диссертационного совета
к.т.н., доцент Покидышева Л. И.
Общая характеристика работы
Актуальность темы. Среди проблем теоретической информатики важное место занимает создание информационных моделей сложных технологических процессов. Такие модели позволяют сформулировать в наиболее общем виде требования к технологическим процессам, описать ограничения и методы их оптимизации.
В один из классов задач комбинаторной оптимизации, достаточно часто встречающийся в реальных производственных условиях, выделены задачи раскроя и упаковки. Их объединяет необходимость установления определенного соответствия между двумя группами, как правило, больших и малых объектов.
Задачи раскроя-упаковки имеют различное прикладное толкование. Наиболее часто встречающимися задачами являются ортогональная упаковка и раскрой, где в качестве малых объектов выступают заготовки прямоугольной формы – прямоугольники или ящики различных размеров, а в качестве крупных – материал, поступающий в виде полос, рулонов, прямоугольных листов, стержней или контейнеров различной вместимости.
Эти задачи представляют собой проблему как теоретического, так и практического плана, которая в течение последних десятилетий привлекает внимание многих исследователей и производственников. Причина растущего интереса к задачам раскроя-упаковки состоит в их разнообразии и сложности.
Задачи раскроя-упаковки относят к классу NP-трудных задач комбинаторной оптимизации. Это означает, что не существует алгоритмов полиномиальной сложности для поиска оптимального решения, точный результат в общем случае может быть получен только за экспоненциальное время.
Точные и псевдоточные методы решения оптимизационных задач комбинаторной оптимизации, так или иначе, связаны с методом ветвей и границ. Для их применения необходимо знать нижние границы решения или иметь алгоритм их вычисления. Однако точную нижнюю границу пока найти не удалось. Это ограничивает применение как точных, так и приближенных методов, основанных на методе ветвей и границ.
Из-за значительных затрат вычислительного времени и необходимости учета технологических ограничений для решения подобного класса задач, как правило, используют приближенные методы и эвристики.
Фундаментальные научные разработки в области решения задач раскроя-упаковки принадлежат Л.В. Канторовичу и В.А. Залгаллеру (1950). Результаты дальнейших исследований в этой области отражены в работах Э.А. Мухачевой (1979), Е.П. Бороновского (1967), А.Ф. Валеевой (2000), И.П. Норенкова (1999), Ю.А. Кочетова (2000), И.В. Романовского (1977), А.С. Филипповой (1999), Житникова В.П. (2000), В.М. Картак (2004); за рубежом – P. Gilmore & R. Gomory (1965), G. Scheithauer & J. Terno (1970), H. Dyckhoff (1990), A. Bortfeldt (1998) и др.
В работах А.Ф. Валеевой выделена тенденция развития методов решения задач упаковки, которые развиваются в двух направлениях. Для первого характерно то, что поиск локально-оптимальных решений ведется в некоторой окрестности исходного решения с применением декодеров – алгоритмов, которые восстанавливают эскиз упаковки. Другим направлением является разработка конструктивных методов, имеющих дело с покомпонентным построением упаковки: к частично построенной упаковке добавляется новый компонент до тех пор, пока она не будет построена полностью.
В большинстве работ в области раскроя-упаковки рассмотрены вопросы решения задач прямоугольного раскроя. Для сравнения эффективности различных методов на однотипном классе задач определяют коэффициент раскроя. Для задачи двухмерной упаковки – это процентное отношение суммарной площади всех размещенных предметов к площади затраченного материала. Однако важным вопросом при выборе того или иного метода является время решения, которое в виду NP-полноты и большом количестве малых и больших предметов, может быть значительным.
Для решения задач трехмерной упаковки используют, в основном, эвристические подходы. Большинство из них базируется на декомпозиции исходной задачи и сведению ее к задачам меньшей размерности путем разбиения на слои и заполнением каждого слоя какой-либо эвристикой. Некоторые алгоритмы используют двухфазные процедуры. На первой фазе происходит упаковка коробок в слои, на второй – процесс обмена коробок внутри слоя для улучшения локального решения. Разбиение параллелепипеда на блоки (слои), с одной стороны, облегчает решение, однако это не гарантирует получение плотной упаковки.
При решении реальных трехмерных задач раскроя-упаковки и повышения грузовой стабильности необходимо учитывать объединение пустот, которые образуются как внутри слоя, так и между ними. Кроме того, время решения задач трехмерной упаковки, за счет улучшения локального решения внутри каждого выделенного слоя последовательными методами приводит к большим временным затратам.
Нейронные сети, в последнее время, рассматривают как один из эффективных инструментов, в том числе и для решения оптимизационных задач. Использование аппарата искусственных нейронных сетей позволяет получить приемлемые решения многих задач комбинаторной оптимизации. Нейросетевая модель, обученная на некоторой выборке, позволяет получить решение многих задач.
Применение нейронных сетей обеспечивает возможность достаточно быстрого перебора большого количества вариантов, что обеспечивает повышение эффективности получения решения.
Цель работы состоит в разработке информационных моделей и высокопроизводительных методов решения задач двух (прямоугольного) и трехмерного (параллелепипедного) ортогонального раскроя-упаковки с применением конструктивных и нейросетевых подходов.
В рамках цели решаются следующие задачи:
- Проанализировать известные постановки и методы решения задач раскроя-упаковки и наметить пути их совершенствования.
- Разработать алгоритмы для решения задач двух и трехмерного ортогонального раскроя и упаковки.
- Применить аппарат нейронных сетей для решения задач раскроя-упаковки.
- Провести серии экспериментов и проанализировать полученные результаты.
- Реализовать теоретические результаты в виде алгоритмов и прикладного программного обеспечения.
Методы исследования.
Результаты исследований, выполненных в работе, базируются на методах исследования операций, теории нейронных сетей, принципах модульного и структурного программирования. Для анализа эффективности предложенных методов проведены численные эксперименты.
На защиту выносятся:
- Информационные модели задач раскроя-упаковки.
- Конструктивный метод плоскостей, предполагающий непосредственное решение задач двух и трехмерного ортогонального раскроя-упаковки.
- Алгоритмы формирования безотходных двух и трехмерных упаковок, обеспечивающие получение приоритетных списков для заданного количества объектов.
- Подход к определению нижних границ решения задачи раскроя-упаковки с помощью сигмоидных нейронных сетей.
Научная новизна работы:
- Разработаны методы решения задач двух и трехмерного ортогонального раскроя-упаковки.
- Разработаны алгоритмы формирования двух и трехмерных безотходных упаковок.
- Разработан подход к определению нижних границ решения задач раскроя-упаковки с использованием сигмоидных нейронных сетей.
Практическая ценность работы:
- Приведены информационные модели задач n-мерной (n = 1, 2, 3) ортогональной упаковки-раскроя.
- Разработаны высокоэффективные алгоритмы решения задач двух и трехмерного раскроя-упаковки, позволяющие быстро строить карты раскроя с коэффициентом раскроя, в среднем, от 85%.
Достоверность полученных результатов диссертации подтверждается сравнительным анализом существующих подходов к решению поставленной задачи и результатами экспериментальных данных.
Реализация результатов работы. В настоящее время результаты исследования и разработок используются несколькими организациями, что подтверждается соответствующими актами о внедрении: ГОУ ВПО «Сибирский государственный технологический университет», логистической компанией «Транс-Бизнес».
Апробация работы и публикации.
Результаты работы, а также отдельные ее разделы были представлены на конференциях и семинарах, основными из которых являются: Всероссийская научно-практическая конференция «Лесной и химический комплексы – проблемы и решения (экологические аспекты)», Красноярск, 2004, 2007; Семинар «Новые информационные технологии», Москва, МГИЭМ, 2005; Всероссийская научно-техническая конференция «Нейроинформатика – 2005», Москва, МИФИ, 2005; IV, V Всесибирcкий конгресс женщин – математиков, Красноярск, 2006, 2008; IX Всероссийский семинар «Моделирование неравновесных систем», Красноярск, ИВМ СО РАН, 2006; IV Международная научно-техническая конференция «Искусственный интеллект в XXI веке. Решения в условиях неопределенности», Пенза, 2006; III Всероссийская научно-практическая конференция «Компьютерная интеграция производства и ИПИ технологии», Оренбург, 2007; X Всероссийская конференция «Проблемы информатизации региона», Красноярск, 2007; Всероссийская научная конференция «Модели и методы обработки изображений», Красноярск, 2007; VI Международная научно-техническая конференция «Материалы и технологии XXI века», Пенза, 2008.
Публикации. Основные результаты работы опубликованы в 12 печатных работах (из них 2 статьи в изданиях по списку ВАК), 1 свидетельство об официальной регистрации программ для ЭВМ.
Структура и объем диссертации.
Диссертация состоит из введения, 4 глав, заключения и списка использованных источников. Основное содержание работы изложено на 126 страницах текста, содержит 29 рисунков и 20 таблиц. Список используемых источников включает 183 наименования.
Основное содержание работы
Во введении обоснована актуальность темы исследования в области задач упаковки и раскроя. Сформулированы цель работы и решаемые в ней задачи, представлена научная новизна и практическая значимость вынесенных на защиту результатов.
В первой главе приведен обзор многообразия задач раскроя-упаковки и выделен класс задач, решаемых в рамках диссертационной работы. Приведены постановки и модели наиболее известных задач n-мерного ортогонального раскроя-упаковки (n = 1, 2, 3) и обзор методов их решения.
Описано применение нейронных сетей для решения прикладных задач. Приведены достоинства и недостатки использования нейросетевой технологии. Определен класс нейронных сетей для решения задач комбинаторной оптимизации. Выявлен круг нерешенных задач.
Во второй главе приведены информационные модели задач раскроя-упаковки. Представлены обобщенная схема решения задач раскроя-упаковки и математические модели задач ортогонального раскроя-упаковки для n = 1, 2, 3. Приведена модель обработки данных с помощью нейронных сетей в нотации IDEF0. Представлено формальное описание групп операций при нейросетевом исследовании с помощью нейронных сетей Хопфилда. Такой подход в общем случае позволяет формализовать технологию работы пользователя при нейросетевом исследовании.
Традиционно задачи раскроя-упаковки решают с использованием последовательных алгоритмов. Однако, в связи с NP-полнотой данного класса задач, целесообразно использовать и нейросетевые подходы при решении данного класса задач (см. рисунок 1).
Рисунок 1 – Подходы к решению задач раскроя-упаковки
В настоящее время существуют различные модели представления n-мерных задач (n = 1, 2, 3) раскроя-упаковки. В диссертационной работе, в качестве основных, представлены модели трехмерной (параллелепипедной) упаковки.
Входная информация для задач параллелепипедной упаковки в общем виде может быть задана в следующем виде:
<W, L, Н, k, u, М, w, l, h, m, b,,, g, V>,
где W= (W1, W2,…, Wk) – ширина, L= (L1, L2,…, Lk) – длина, H = (H1, H2,…, Hk) – высота параллелепипедов; k – количество типов параллелепипедов; u = (u1, u2,…, uk) – количество параллелепипедов определенного вида; М = (М1, М2, …, Мk) – предельно допустимая масса параллелепипедов; w = (w1, w2,…, wm) – ширина, l = (l1, l2,…, lm) – длина, h = (h1, h2,…, hm) – высота коробок; m – количество типов коробок; b = (b1, b2, …,bm) – количество коробок определенного типа; – признак направления: = 1, если объекты можно поворачивать, = 0 в противном случае; – признак гильотинности: = 1, если задачу решают с учетом признака гильотинности, и полагают равным 0 в противном случае; g = (g1, g2, …, gm) – масса объектов; V – набор технологических ограничений; ![]() – общее количество параллелепипедов;
– общее количество параллелепипедов; ![]() – общее количество коробок.
– общее количество коробок.
Выходной информацией (в общем виде) является карта раскроя, представленная в виде следующего набора:
<П, X, Y, Z, Р, E>,
где П – преобразованный список коробок; Х = (х1, х2, …, xn), Y = (y1, y2, …, yn), Z = (z1, z2, …, zn) – векторы минимальных координат коробок; Р – множество исходных параллелепипедов, в которые упакованы некоторые коробки; Е = (е1, е2,…, en) – признаки поворота, значение которых может принимать одно из 6 значений.
Зададим КРА – коэффициент раскроя (процентное отношение суммарного объема всех упакованных коробок к занятому объему параллелепипеда), а – время решения задачи.
Математическую модель для задач ортогональной упаковки коробок в параллелепипед с неограниченной длинной можно представить в следующем виде:
< П, X, Y, Z, E> = (<W, Н, М, w, l, h, m, b,,, g, V>).
L min
min
Необходимо найти такое отображение, которое преобразует входные данные в выходные, причем соблюдаются следующие условия:
- ортогональное размещение коробок в параллелепипеде;
- неперекрытие коробок между собой;
- неперекрытие коробками граней параллелепипедов.
Кроме того, требуется за минимальное время, учитывая ограничения по массе и технологические ограничения, минимизировать длину занятой части параллелепипеда.
Для задач с фиксированным сторонами параллелепипедов, необходимо найти их минимальное количество
< П, X, Y, Z, Р, E> = (<W, L, Н, k, u, М, w, l, h, m, b,,, g, V>),
![]()
КРА 100%
min
На данную систему оказывают влияние следующие факторы:
- способ (метод) решения задачи;
- приоритетный список (последовательность объектов);
- параметры оптимизации.
В третьей главе описаны алгоритмы формирования безотходных двух и трехмерных упаковок. В результате такого разбиения формируется последовательность заданного количества прямоугольников, отвечающего безотходной упаковке, с указанием их размеров при фиксированных значениях больших объектов. Представлено описание метода плоскостей для решения задач трехмерного (параллелепипедного) и двухмерного (прямоугольного) ортогонального раскроя-упаковки. Рассмотрены экспериментальные исследования эффективности применения метода плоскостей для решения задач трех и двухмерных упаковок. Приведены данные для сравнения с другими методами для однотипных классов задач, сгенерированных на основе методики Г. Вешера и безотходных примерах E. Hopper.
Шаги алгоритма для формирования безотходной трехмерной упаковки:
1) задать количество областей qх, qz и qхi ;
2) определить целое число коробок в каждой области параллелепипедной формы по формуле:
 .
.
3) для одной из отсеченных параллелепипедных областей задать случайным образом координаты правого верхнего угла p – 1 коробок: случайным образом генерируются координаты по Х в диапазоне от 1 до L/ qхi –, по оси У – от 1 до W/qy –, где – случайная величина, введенная для устранения попадания на края области; координата по оси Z фиксирована и определяется координатой z параллелепипедной области;
4) координаты последней коробки определяются остатком от незанятой части области;
5) достроить коробки, полностью заполнив текущую параллелепипедную область;
6) повторить шаги 3 – 5 для оставшихся отсеченных параллелепипедных областей.
Таким образом можно для заданных размеров параллелепипеда и требуемом количестве коробок определить размеры коробок для безотходной упаковки.
Метод плоскостей для решения трехмерных задач раскроя-упаковки.
Особенностями метода являются:
- непосредственное решение задач, а не сведение их к задачам меньшей размерности;
- использование как слойной, так и бесслойной стратегий;
- заполнение по, так называемым, приоритетным осям;
- анализ пустот и рассмотрение способов их объединения;
- допускается использование не одного, а нескольких параллелепипедов.
Слойная стратегия. Метод плоскостей, как и большинство методов, основан на понятии пустого места – области параллелепипеда без коробок, упакованных внутри. Первая коробка определяет слой. Поэтому, алгоритм оценивает все виды коробок и их ориентации, чтобы открыть новый слой. Допусти, что выбрано приоритетное заполнение по оси Z. Как только первая коробка помещена в параллелепипед, она автоматически формирует слой, который будет заполняться по высоте. В зависимости от размеров коробки и параллелепипеда все пространство разбивается на параллелепипедные области.
Для описания размеров пустых областей используются координаты: x1, y1, y2, z1, z2, а также флаг: 0 – область не заполнена; 1 – область полностью заполнена; -1 – игнорировать при заполнении данного слоя; -2 – игнорировать полностью. Запоминать значение координаты x2 не целесообразно, т.к. для случая слойной стратегии она определяется длиной слоя, для бесслойной – это длина самого параллелепипеда.

Рисунок 2 – Разбиения на области, определяемые первой коробкой
Существует восемь случаев размещения коробки в пустую область. В каждом случае вновь образованные области пустот будут разбиваться на одну, две, три, ни одной.
Кроме сохранения файла с координатами пустых областей, динамически создается файл коробок, в котором содержится следующая информация:
- координаты коробок x1, х2, y1, y2, z1, z2 относительно параллелепипеда;
- номер коробки из первоначального приоритетного списка;
- номер слоя, в котором размещена коробка.
Когда алгоритм отмечает новое место, как «временно отключено», подключается процедура, которая пробует увеличить размер этого места, соединяя его со смежными, которые также были «временно отключены», либо заполнены не полностью. Предусмотрено четырнадцать вариантов, когда пустота может быть объединена с одной или двумя соседними.
С целью сокращения полного перебора вариантов решений в режим оптимизации включены следующие параметры:
- метод сортировки: без сортировки; по невозрастанию объема; по невозрастанию ширины; по невозрастанию массы; по невозрастанию удельного веса;
- шесть способов поворота коробок;
- шесть вариантов заполнения по приоритетным направлениям;
- использование как слойной, так и бесслойной стратегий.
После завершения цикла оптимизации будет выведена карта раскроя с максимальным значением коэффициента раскроя.
Бесслойная стратегия. Процедура с использованием метода без формирования слоев отличается от рассмотренной выше тем, что толщина слоя принимается равной длине параллелепипеда, т.е. отсутствует блок, отвечающий за формирование слоев.
Приведенный выше метод плоскостей с некоторыми доработками реализован и для решения задач двухмерной упаковки.
Для оценки эффективности решения задач двух и трехмерного ортогонального раскроя-упаковки методом плоскостей проведена серия расчетов на основе методики Г. Вешера и безотходных примеров E. Hopper.
За основу разбиения на различные классы предметов для задачи трехмерной упаковки взято: нижнее ограничение длины предметов – v1, верхнее ограничение длины предметов v2 (![]() , i =1,…, n); нижнее ограничение ширины предметов w1, верхнее ограничение ширины предметов w2 (
, i =1,…, n); нижнее ограничение ширины предметов w1, верхнее ограничение ширины предметов w2 (![]() , i=1,…, n); нижнее ограничение высоты предметов 1, верхнее ограничение высоты предметов 2 (
, i=1,…, n); нижнее ограничение высоты предметов 1, верхнее ограничение высоты предметов 2 (![]() , i=1,…, n).
, i=1,…, n).
Серия №1. Целью данного эксперимента была проверка необходимости включения в оптимизацию разбиение на слои для разных групп предметов. Выполнены численные эксперименты, параметрами которых являлись: высота параллелепипеда H = 150, его ширина W = 100; количество предметов n = 50, 100, 200, 250, 500, 1000. Предметы были отсортированы по классам: «мелкие» (v1, = 0.1, v2= 0.2; w1 = 0.1, w2 = 0.2; 1 = 0.2, 2 = 0.25), «средние» (v1= 0.2, v2= 0.4; w1 = 0.2, w2 = 0.4; 1 = 0.2, 2 = 0.25) и «разнородные» (v1 = 0.1, v2= 0.3; w1 = 0.1, w2 = 0.2; 1 = 0.2, 2 = 0.25). Для каждого класса задач было сгенерированно по 10 тестовых примеров, усредненные значения коэффициентов раскроя приведены на рисунке 3.
Таким образом, при тестировании метода плоскостей для задач трехмерных упаковок на разной группе предметов было выявлена необходимость совместного использования как процедуры формирования слоя, так и бесслойной процедуры. Это позволяет формировать более плотную упаковку и, следовательно, повышает грузовую стабильность при решении реальных задач. Метод плоскостей показывает лучшие результаты при большом количестве и, в основном, «разнородных» предметов. Время решения задачи на ПК (Celeron (R) CPU 3.2 GHz, 1Гб ОЗУ) от нескольких секунд до двух минут (для n = 1000).

Рисунок 3 – Усредненные значения коэффициентов раскроя для задач трехмерной упаковки (на основе метода плоскостей)
Серия №2. Выполнены численные эксперименты для анализа различных методов решения задач трехмерной упаковки, параметрами которой являлись: длина параллелепипеда L = 150, его ширина W = 100; количество предметов n = 50, 100, 200, 250. Предметы были отсортированы по классам: «мелкие» (v1, = 0.1, v2= 0.2; w1 = 0.1, w2 = 0.2; 1 = 0.1, 2 = 0.25), «средние» (v1= 0.2, v2= 0.1; w1 = 0.2, w2 = 0.25; 1 = 0.2, 2 = 0.25) и «разнородные» (v1, = 0.1, v2= 0.25; w1 = 0.1, w2 = 0.2; 1 = 0.2, 2 = 0.25). Значения коэффициентов раскроя приведены в таблице 1.
Таблица 1 – Значения коэффициентов раскроя для задач параллелепипедной упаковки при решении различных классов задач
| Методы | Мелкие предметы, % | Средние предметы, % | Разнородные предметы, % |
| MBA - Метод на основе бесслойного алгоритма | 77 | 79 | 80 |
| EABD - «Наивный» эволюционный алгоритм | 74 | 78 | 76 |
| GABD - Классический генетический алгоритм | 76 | 77 | 75 |
| SABD - Метод случайных перестановок | 73 | 74 | 76 |
| Метод плоскостей | 76 | 82 | 83 |
Таким образом, метод плоскостей показывает лучшие результаты в классе «средних» и «разнородных» предметов.
Серия № 3. Метод плоскостей для решения задач двухмерной упаковки был протестированы с помощью безотходных примеров E. Hopper на определение признака реставрации – способности метода восстанавливать карту раскроя по приоритетному списку. В тестовых примерах в качестве входной информации, кроме размеров прямоугольников и ширины полосы, подавался оптимальный (Опт.) и измененный (Изм.) список (см. таблицу 2).
Таблица 2 – Результаты решения безотходных задач E. Hopper серии N и С
| Задачи | n | Среднее значение КРА, % | Задачи | n | Среднее значение КРА, % | ||
| Опт. | Изм. | Опт. | Изм. | ||||
| N1a – N1e | 17 | 100 | 92.6 | С1 | 16,17 | 100 | 96.0 |
| N2a – N2e | 25 | 100 | 92.7 | С2 | 25 | 100 | 95.4 |
| N3a – N3e | 29 | 100 | 94.1 | С3 | 28,29 | 100 | 93.8 |
| N4a – N4e | 49 | 100 | 94.0 | С4 | 49 | 100 | 95.2 |
| N5a – N5e | 73 | 100 | 94.9 | С5 | 73 | 100 | 97.1 |
| N6a – N6e | 97 | 100 | 96.7 | С6 | 97 | 100 | 96.8 |
| N7a – N7e | 197 | 100 | 97.0 | С7 | 196,197 | 100 | 96.6 |
Выявлено, что метод плоскостей обладает свойством «реставрации», с его помощью по известному оптимальному приоритетному списку формируется оптимальная безотходная упаковка. В реальных условиях, в связи с отсутствием в методе схем полного перебора, при подаче измененного оптимального списка, он позволяет получить упаковку с коэффициентом раскроя более 90%.
Серия № 4. Целью данного эксперимента было сравнение метода плоскостей с алгоритмом рандомизированного динамического перебора (DSR) для решения задач прямоугольной упаковки. Были сгенерированы следующие классы задач для W = 225: «малые» предметы (v1, = 0.05, v2= 0.1; w1 = 0.1, w2 = 0.15), «средние» предметы (v1, = 0.25, v2= 0.35; w1 = 0.35, w2 = 0.45) и «малые и большие» предметы (v1, = 0.05, v2= 0.25; w1 = 0.05, w2 = 0.95). Для каждого класса задач сгенерировано по 10 тестовых примеров. Критерием оценок также выступал коэффициент раскроя КРА, значения которого приведены на рисунке 4.
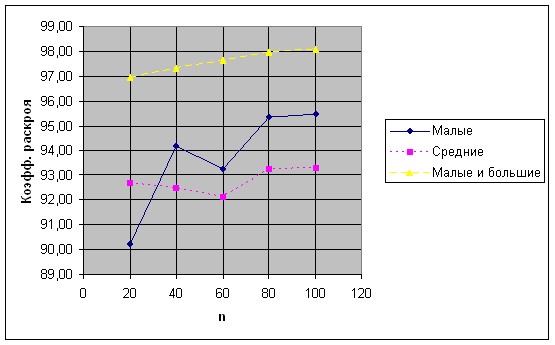
Рисунок 4 – Усредненные значения коэффициентов раскроя для задач двухмерной упаковки, полученные методом плоскостей
Согласно данным, приведенным А.Ф. Валеевой для такого же класса задач, значения коэффициентов раскроя, полученных методом DSR, для класса «малых» предметов составляет 92 – 96%; «средних» - 98 – 100%; «малых и больших» - 93 – 95%. Таким образом, метод плоскостей показывает сравнимые результаты для класса «малых» и более лучшие для класса«разнородных» («малых и больших») предметов.
В четвертой главе рассмотрено применение аппарата искусственных нейронных сетей к решению задач раскроя-упаковки.
Задача раскроя-упаковки представлена в нейросетевом описании в терминах энергетической функции Хопфилда. Приведен вариант совместного использования программы-декодера и нейроимитатора для решения задачи раскроя. На основе алгоритмов формирования безотходных упаковок обучены сигмоидные нейронные сети. Приведены тестовые данные определения нижних границ решения задач двух и трехмерных упаковок, которые позволяют сделать вывод о целесообразности использования такого подхода.
Использование сигмоидных нейронных сетей для определения нижних границ решения задач раскроя-упаковки. На основе тестовых данных, полученных с помощью безотходных двух и трехмерных алгоритмов, были проведены численные эксперименты по обучению сигмоидных нейронных сетей в нейроимитаторе NeuroPro 0.25. Структура нейросети: три слоя, каждый из которых содержал по десять нейронов.
Количество прямоугольников/коробок изменялось в диапазоне от 20 до 100, количество примеров для каждой обучающей выборки было сгенерировано в два раза больше количества объектов. Было произведено обучение нейронных сетей, при этом количество правильно решенных примеров составило 100%. В таблице 1 приведены результаты тестирования для задач двухмерной упаковки.
Была исследована зависимость разброса длины и ширины в обучающих примерах на значение ошибки. Выявлено, что при подборе обучающей выборки следует установить фиксированным значение одной из граней полосы на основе известной, например, W, а другое выбрать в диапазоне: Lmin = Si / W; Lmax = Lmin + Срзнач(li), где Si – суммарная площадь всех прямоугольников, Срзнач(li) – среднее значение длин прямоугольников.
Как обучающие, так и тестовые примеры были сгенерированы на основе безотходных упаковок. Однако известно, что изменение порядка следования прямоугольников приводит, как правило, к получению другой карты раскроя и, соответственно, длины занятой части полосы. В связи с этим для тестовой выборки случайным образом был изменен порядок следования прямоугольников. Было сгенерировано по 10 тестовых примеров для случая n = 20. Среднее значение ошибки составило 4.4 %.
Таблица 3 – Тестовые данные для задач двухмерной упаковки и полученные значения ошибок
| № | Кол-во прямоуголь-ников | Диапазон изменения L | Диапазон изменения W | Средняя ошибка, % | Средняя максимальная ошибка, % |
| 20 | 100-200 | 100-200 | 46.3 | 127.3 | |
| 20 | 100-300 | 100-300 | 50.5 | 127.9 | |
| 20 | 278-288 | 278-288 | 12.1 | 32.3 | |
| 10 | 100-120 | 100 | 6.3 | 16.1 | |
| 10 | 400-440 | 400 | 14.9 | 29.9 | |
| 40 | 400-440 | 400 | 14.0 | 32.8 | |
| 100 | 400-440 | 400 | 13.4 | 30.5 |
При обучении сигмоидных нейронных сетей на основе трехмерных безотходных примеров наблюдались такие же тенденции, что и для задач двухмерных упаковок.
Основные результаты и выводы
- Формализована постановка задач раскроя-упаковки и предложены информационные модели и методы их решения. Конструктивный метод плоскостей позволяет существенно повысить коэффициент раскроя и снизить время решения за счет использования эвристических подходов. Метод плоскостей обладает свойством реставрации и позволяет получить решение для задач большой размерности за приемлемое время. Алгоритмы формирования безотходных двух и трехмерных упаковок обеспечивают получение приоритетных списков для заданного количества объектов.
- Для определения нижних границ решения задач раскроя-упаковки впервые применен аппарат нейронных сетей. На основании разработанных безотходных алгоритмов обучены сигмоидные нейронные сети. Результаты тестовых выборок дают конечную оценку с хорошей точностью.
- Предложенные в работе эвристические подходы реализованы в виде прикладного программного обеспечения. Полученные в работе результаты используются в ГОУ ВПО «Сибирский государственный технологическом университете» и ГОУ СПО «Красноярский техникум информатики и вычислительной техники» в учебном процессе при выполнении практических, курсовых и дипломных работ, а также логистической компанией «Транс-Бизнес».
ПУБЛИКАЦИИ ПО ТЕМЕ ДИССЕРТАЦИИ
- Корчевская, О.В. О преимуществах комбинирования нейросетевого и традиционных подходов при решении дискретных и комбинаторных задач (на примере задачи раскроя) / О.В. Корчевская // Вестник КрасГАУ № 15, 2006. – С. 172-177.
- Жуков, Л.А. Метод плоскостей: численный эксперимент для задач двух и трехмерной ортогональной упаковки / Л.А.Жуков, О.В. Корчевская // Информационные технологии, 2008. – № 11. – С. 41-45.
- Корчевская О.В., Получение нижних границ для задач двух и трехмерной ортогональной упаковки с помощью нейронных сетей, используя алгоритм безотходной упаковки / О.В Корчевская, Л.А. Жуков // Электронный журнал "Исследовано в России", 62, 2008. – С. 685-694, http: // zhurnal. ape. relarn.ru / articles/ 2008/062.pdf
- Корчевская, О.В. Элементы формального описания технологии обработки данных с помощью нейронных сетей Хопфилда / О.В. Корчевская, Л.А. Жуков // Новые информационные технологии: сб. материалов восьмого семинара. – М.: МГИЭМ, 2005. – С.89-95.
- Жуков, Л.А. О формализации нейросетевой технологии решения прикладных задач на примере сетей с учителем и сетей Хопфилда / Л.А. Жуков, Н.В. Решетникова, О.В. Корчевская // Нейроинформатика – 2005: сб. научн. тр. VII Всероссийской научно-технической конференции.– М.: МИФИ, 2005. – Ч. 1. – С. 68-75.
- Жуков, Л. А. Особенности применения нейронных сетей Хопфилда для решения прикладных оптимизационных задач / Л. А. Жуков, О. В. Корчевская // Сибирский государственный технологический университет. – Красноярск, 2006. – 44 с. – Деп. в ВИНИТИ 04.12.2006, № 1486 – В2006.
- Корчевская, О.В. Однопроходный эвристический алгоритм для решения задачи двумерной ортогональной упаковки / О.В. Корчевская // Искусственный интеллект в XXI веке. Решения в условиях неопределенности: Сб.ст. IV Международной научно – технической конференции. – Пенза, 2006. – С. 71-73.
- Корчевская, О.В. Решение задачи двумерной упаковки в полубесконечную полосу с помощью метода профиля / О.В. Корчевская // Вестник КрасГАУ № 1. – Красноярский государственный аграрный университет, 2007. – С. 34-37.
- Корчевская, О.В., Конструирование функции энергии сети для задачи ортогональной упаковки / О.В. Корчевская, Л.А.Жуков, А. В. Больсявичус // Компьютерная интеграция производства и ИПИ технологии: Сб. материалов III Всероссийской научно – практической конференции. – Оренбург: ИПК ГОУ ОГУ, 2007. – С. 352-357.
- Корчевская, О.В. Решение задачи трехмерной упаковки методом профиля / О.В. Корчевская, Л.А. Жуков // V Всесибирский конгресс женщин – математиков: тез. докл. – Красноярск: Изд. РИО СибГТУ, 2007. – С. 58-60.
- Корчевская, О.В. Обобщенная модель обработки данных с помощью нейронных сетей на примере задачи раскроя / упаковки / О.В. Корчевская, Л.А. Жуков // Альманах современной науки и образования. – Тамбов: Грамота, 2008. – № 1(8): Математика, физика, строительство, архитектура, технические науки и методика их преподавания. – С. 100-103.
- Корчевская, О.В. Применение метода плоскостей для решения безотходных задач раскроя / упаковки Е. Hopper / О.В. Корчевская, Л.А. Жуков // Материалы и технологии XXI века: Сб.ст. VI Международной научно – технической конференции. – Пенза, 2008. – С. 147-149.
Корчевская Оксана Валериевна
ИНФОРМАЦИОННЫЕ МОДЕЛИ И МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ОРТОГОНАЛЬНОГО РАСКРОЯ-УПАКОВКИ НА ОСНОВЕ КОНСТРУКТИВНЫХ И НЕЙРОСЕТЕВЫХ ПОДХОДОВ
05.13.17 – теоретические основы информатики
Автореферат
Подписано в печать 3 марта 2009г.
Формат 60х84/16. Бумага писчая. Объем 1п.л.
Тираж 100 экз. Заказ № 843
Отпечатано в Экспресс-Офсет
660062, г. Красноярск, ул. Крупской, 42.

