Разработка методов и схемных решений для обеспечения криптографической защиты данных в полиномиальной системе классов вычетов
На правах рукописи
Чипига Александр Александрович
РАЗРАБОТКА Методов и схемных решений для обеспечения криптографической защиты
данных в ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ
КЛАССов ВЫЧЕТОВ
Специальность: 05.13.19 – Методы и системы защиты информации,
информационная безопасность
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата технических наук
Ставрополь 2010
Работа выполнена
в Северо-Кавказском государственном техническом университете
на кафедре «Защита информации»
| Научный руководитель: | доктор технических наук, профессор Калмыков Игорь Анатольевич |
| Официальные оппоненты: | Доктор технических наук, профессор Кравченко Павел Павлович |
| Кандидат технических наук Шапошников Алексей Вячеславович | |
| Ведущая организация: | Краснодарское высшее военное училище (военный институт) военной академии связи (г. Краснодар) |
Защита состоится « 30 » июня 2010г. в 12 часов на заседании диссертационного совета Д 212.208.25 в Таганрогском технологическом институте Южного федерального университета по адресу: Россия, 347928, Таганрог, Ростовская область, пер. Некрасовский, 44, корпус «И» аудитория И409.
С диссертацией можно ознакомиться в научно-технической библиотеке ТТИ ЮФУ.
Автореферат разослан « 28 » мая 2010 г.
| Ученый секретарь диссертационного совета |  | Брюхомицкий Ю.А. |
Общая характеристика работы
Актуальность темы. В последнее десятилетие задача обеспечения информационной безопасности стала особенно актуальной в связи увеличением объема конфиденциальной информации, развитием средств информационных атак, глобализацией информационного пространства. В информационном обществе, материальной базой которого является информационная экономика, акцент значимости смещается на информационный ресурс. В этом случае информационные ресурсы рассматриваются как стратегические ресурсы страны, которые требуют постоянной защиты от несанкционированного доступа (НСД) других пользователей. Высокая степень автоматизации, широкое внедрение компьютерных систем в различные сферы человеческой деятельности делают автоматизированные системы обработки данных чрезвычайно уязвимыми по отношению к деструктивным воздействиям, ставят общество в зависимость от степени безопасности используемых информационных технологий. Поэтому важнейшей характеристикой любой компьютерной системы становится безопасность циркулирующей по ней информации.
Однако задача защиты конфиденциальной информации от НСД является одной из самых древних и полностью нерешенных до настоящего времени проблем. Чтобы уменьшить последствия от НСД необходимо создавать систему безопасности, целью которой предупреждение последствий умышленных и случайных деструктивных воздействий, следствием которых могут быть разрушение, модификация или утечка информации. Следует отметить, что в зависимости от объекта защиты возможна различная расстановка приоритетов среди свойств такой системы безопасности. Проведенные исследования показали, что среди множества организационных и технических мер особое место занимают методы криптографической защиты информации.
В настоящее время существует целый ряд алгоритмов шифрования данных. Все множество криптографических средств защиты информации можно разбить на две большие группы. Основу первой группы составляют методы, построенные на основе симметричного шифрования, характерной чертой которого является использование одного и того же ключа для выполнения зашифрования и расшифрования. Ко второй группе относятся криптографические системы, использующие асимметричные алгоритмы шифрования. Данные системы криптографических преобразований характеризуются тем, что используют два различных ключа. Однако следует отметить, что алгоритмы асимметричных криптосистем настолько трудоемки по сравнению с обычными симметричными алгоритмами, что на практике рационально их использовать там, где объем шифрованной информации незначителен, но очень важен.
В тоже самое время современные инфотелекоммуникационные системы характеризуются высокой скоростью передачи. Это связано, в первую очередь, с появлением новых информационных технологий, таких как видео и речевая связь, голосовая почта, системы видеоконференций. Так как передача звуковой, графической и видеоинформации во многих случаях требует конфиденциальности, то возникает задача шифрования больших массивов информации в реальном масштабе времени.
Известно, что системы с побитовым шифрованием обеспечивают высокое быстродействие процесса зашифрования и расшифрования, соизмеримое со скоростью поступления данных. Однако данная система не обладает достаточной степенью стойкости. Несмотря на то, что шифр, основанный на сложении битов псевдослучайной последовательности (ПСП) с битами исходного текста по модулю два, в общем случае теоретически нераспознаваем, сама система шифрования не отличается стойкостью и может быть мгновенно раскрыта при наличии определенного количества символов исходного и шифрованного текста. Уязвимость системы к атакам на основе исходных и подобранных текстов обусловлено тем, что при битовом шифровании потока данных сложение символов по модулю два является единственным способом построения обратимой функции шифрования.
Таким образом, сложилось следующее противоречие. С одной стороны системы поточного шифрования, базирующиеся на использовании ПСП и обладающие быстродействием соизмеримым со скоростью поступления открытой информации, не обеспечивают требуемый уровень криптозащиты, а применение нелинейных систем шифрования в современных инфотелекоммуникационных системах сдерживается низкой скоростью реализации арифметических процедур выполненных по модулю.
Решить данное противоречие возможно за счет использования полиномиальной системы классов вычетов (ПСКВ) при выполнении криптографических преобразований. Поэтому разработка метода нелинейного шифрования высокоскоростного потока мультипликативных данных является актуальным
Таким образом, целью диссертационной работы является повышение скорости нелинейного шифрования больших объемов данных за счет применения полиномиальной системы классов вычетов и индексного представления элементов расширенных полей Галуа.
Объектом диссертационных исследований являются методы и алгоритмы криптографической защиты информации.
Предметом диссертационных исследований являются методы и алгоритмы нелинейного шифрования на основе операций возведения в степень по модулю, реализуемых в конечных и расширенных полях Галуа.
Научная задача, решение которой, содержится в диссертационной работе, состоит в разработке высокоскоростного метода нелинейной криптографической защиты потока данных на основе применения полиномиальных систем счисления и индексного представления элементов полей Галуа.
Для решения поставленной общей научной задачи была проведена ее декомпозиция на ряд частных задач:
1. Разработка метода нелинейного шифрования информации с использованием операции возведения в степень для полей Галуа, обеспечивающего более высокую степень криптографической защиты информации по сравнению с поточными системами шифрования за счет использования мультипликативных операций, реализуемых в GF(pv).
2. Обоснование возможности применения полиномиальной системы классов вычетов в разработанном методе нелинейного шифрования с целью повышения скорости выполнения мультипликативных процедур при зашифровании потока данных.
3. Разработка алгоритмов поиска и коррекции ошибок на основе использования модулярных полиномиальных кодов, применение которых позволит синтезировать устройства, осуществляющих обнаружение и исправление ошибок, возникающих при передаче зашифрованных данных.
4. Разработка метода нелинейного шифрования в полях Галуа с использованием операции возведения в степень по модулю и индексного представления данных, позволяющих повысить скорость процедур зашифрования и расшифрования потока данных.
5. Синтез структуры системы криптографической защиты на основе нелинейного шифрования потока данных с использованием операции возведения в степень по модулю.
Методы исследования базируются на использовании математического аппарата теории полей Галуа, теории чисел, теории криптографической защиты информации, теории кодирования.
Достоверность и обоснованность проведенных исследований подтверждается физической аргументированностью и математической корректностью исследуемых вопросов, строгостью принятия допущений и введенных ограничений, использованием апробированного математического аппарата, сходимостью результатов расчета с известными из литературных источников и полученными на основе эвристических соображений
Научная новизна диссертационной работы состоит в следующем:
- разработан и исследован метод нелинейного шифрования данных на основе операции возведения в степень по полиномиальному модулю в полях Галуа, позволяющий повысить степень криптографической защиты данных по сравнению с побитовым шифрованием за счет использования мультипликативных операций;
- разработан метод нелинейного шифрования на основе операции возведения в степень по модулю с использованием ПСКВ, характеризующийся более высокой скоростью выполнения процедур зашифрования за счет перехода к многомерной обработке малоразрядных данных;
- на основе анализа корректирующих способностей кодов полиномиальной системы классов вычетов были разработаны алгоритмы поиска и коррекции ошибок, возникающих при передачи зашифрованных данных по каналу связи, схемные реализации которых характеризуются меньшими аппаратурными и временными затратами;
- разработан метод нелинейного шифрования потока информации на основе операции возведения в степень по модулю с использованием индексного представления данных, который характеризуется минимальными временными затратами по сравнению с ранее известными методами и алгоритмами нелинейного шифрования.
Основные положения, выносимые на защиту:
- метод нелинейного шифрования данных на основе операции возведения в степень по полиномиальному модулю в расширенных полях Галуа, позволяющий повысить степень криптографической защиты данных по сравнению с побитовым шифрованием за счет использования мультипликативных операций;
- метод нелинейного шифрования на основе операции возведения в степень по модулю с использованием ПСКВ, характеризующийся более высокой скоростью за счет перехода к многомерной обработке малоразрядных данных;
- алгоритмы поиска и коррекции ошибок с использованием полиномиальной системы классов вычетов, схемные реализации которых характеризуются меньшими аппаратурными и временными затратами;
- метод нелинейного шифрования потока информации на основе операции возведения в степень по модулю с использованием индексного представления данных, который характеризуется минимальными временными затратами по сравнению с ранее известными алгоритмами нелинейного шифрования.
Практическая ценность работы:
- разработан метод нелинейного шифрования на основе мультипликативных операций с использованием ПСКВ, который позволяет реализовывать криптографические устройства, обладающие более высокой производительностью по сравнению с ранее известными;
- разработаны алгоритмы поиска и локализации ошибки, а так же их схемные реализации, применение которых позволит повысить отказоустойчивость систем шифрования, использующих ПСКВ;
- разработан метод нелинейного шифрования на основе операции возведения в степень по модулю с использованием индексного представления, применение которого позволяет повысить скорость работы устройств криптографической защиты информации.
Реализация результатов работы.
Основные результаты диссертационной работы использованы в Ставропольском краевом фонде обязательного медицинского страхования, в филиале ФГУП «Радиочастотный центр ЮФО» по Ставропольскому краю и в учебном процессе на кафедре защиты информации Северо-Кавказского государственного технического университета, что подтверждается актами реализации.
Апробация работы. Основные результаты работы обсуждались на международных конференциях III Санкт-Петербургская межрегиональная конференция «Информационная безопасность регионов России», Санкт-Петербург, 2003; VI Международная научно-практическая конференция «Информационная безопасность», Таганрог, 2004;III Международный Форум по проблемам науки, техники и образования, Москва, 2004; III Международная научно-техническая конференция «Инфокоммуникационные технологии в науке, производстве и образовании. Инфоком 3», Кисловодск, 2008; Электронная заочная конференция Российской Академии Естествознания «Прикладные исследования и разработки по приоритетным направлениям науки и техники». 15-20 ноября 2009.
Публикации. Основные результаты достаточно полно изложены в 13 научных трудах, в том числе 2 статьях, которые опубликованы в журналах «Информационные технологии», 2007, «Известия ЮФУ. Технические науки», 2009 (рекомендованы ВАК РФ для публикации основных результатов диссертаций); «Успехи современного естествознания», 2007, № 5; «Фундаментальные исследования», 2007, № 2. Получен 1 патент на изобретение.
Структура и объем диссертации. Диссертационная работа изложена на 172 страницах машинописного текста, иллюстрируется 18 рисунками и 19 таблицами, и состоит из введения, 4 разделов, списка используемых источников из 133 наименований, 3 приложений.
СОДЕРЖАНИЕ РАБОТЫ
Во введении обосновывается актуальность разработки метода нелинейного шифрования высокоскоростного потока мультимедийных данных с использованием полиномиальной системы классов вычетов, сформулирована цель работы, поставлена научная задача и ее декомпозиция на частные научные задачи, определены объект и предмет следования, представлены основные положения, выносимые на защиту, показана практическая ценность, апробация и реализация результатов работы.
В первой главе показана актуальность защиты информации от НСД. Проведен анализ основных видов угроз информационной безопасности, а также основных методов сдерживания, обнаружения и предотвращения возможных нарушений защиты информационных систем. Показано целесообразность применения криптографических методов защиты информации. Проведен анализ основных методов симметричного и асимметричного шифрования. На основе результатов системного анализа предметной области был сделан вывод о необходимости разработки метода нелинейного шифрования высокоскоростного потока мультимедийных данных с использованием полиномиальной системы классов вычетов и индексного представления элементов поля Галуа. В качестве показателя оценки эффективности разработанных методов выбрана функциональная производительность
![]() , (1)
, (1)
где П – производительность системы; ![]() - схемные затраты необходимые на данную реализацию; Аj - схемные затраты необходимые на реализацию j-го процессорного элемента; т – число элементов, входящих в состав системы.
- схемные затраты необходимые на данную реализацию; Аj - схемные затраты необходимые на реализацию j-го процессорного элемента; т – число элементов, входящих в состав системы.
Проведена постановка задачи исследования
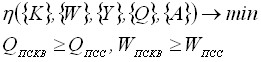 , (2)
, (2)
где ![]() и WПСКВ - размерность блоков открытых данных и криптографическая надежность разработанного метода нелинейного шифрования в расширенных полях Галуа;
и WПСКВ - размерность блоков открытых данных и криптографическая надежность разработанного метода нелинейного шифрования в расширенных полях Галуа; ![]() и WПСС – размерность блоков открытых данных и криптографическая надежность методов и алгоритмов зашифрования, реализованных в позиционной системе счисления.
и WПСС – размерность блоков открытых данных и криптографическая надежность методов и алгоритмов зашифрования, реализованных в позиционной системе счисления.
Для эффективного решения поставленной задачи произведена ее декомпозиция на ряд частных задач.
Вторая глава посвящена вопросам разработки методов нелинейного шифрования потока данных в расширенных полях Галуа. Проведенные результаты исследований криптографических характеристик показали, что генераторы ПСП, обладая при больших значениях n практически идеальными статистическими характеристиками, к сожалению, не являются криптостойкими. В свою очередь, системы шифрования, использующие конечные поля Галуа GF(pv), обладают более широкими возможностями по реализации различных криптографических функций обеспечения конфиденциальности и целостности информации. Применение в таких системах основных мультипликативных операций позволяет повысить уровень защиты информации.
Разработан метод шифрования потока данных с операцией возведения в степень символов расширенного поля Галуа GF(pv). В данной системе криптографической защиты информации выбирается неприводимый полином ![]() , порождающий все элементы мультипликативной группы данного поля. При этом степень порождающего полинома
, порождающий все элементы мультипликативной группы данного поля. При этом степень порождающего полинома ![]() . Входная последовательность, представляющая собой поток двоичных символов, разбивается на блоки
. Входная последовательность, представляющая собой поток двоичных символов, разбивается на блоки ![]() по
по ![]() символов в каждом. При этом блок в полиномиальной форме будет представляться
символов в каждом. При этом блок в полиномиальной форме будет представляться
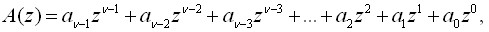 (3)
(3)
где ![]() двоичный код блока А,
двоичный код блока А, ![]()
Степень такого полинома A(z) ![]() В этом случае блок считается элементом расширенного поля Галуа.Для выполнения разработанного метода нелинейного шифрования ключ, а это показатель степени, будет сниматься одновременно с нескольких выходов линий задержки многотактового фильтра, используемого для генерации ПСП. Порядок считывания информации с выбранных линий задержки генератора ПСП может быть любой
В этом случае блок считается элементом расширенного поля Галуа.Для выполнения разработанного метода нелинейного шифрования ключ, а это показатель степени, будет сниматься одновременно с нескольких выходов линий задержки многотактового фильтра, используемого для генерации ПСП. Порядок считывания информации с выбранных линий задержки генератора ПСП может быть любой
![]() (4)
(4)
Тогда метод нелинейного шифрования потока данных в расширенных полях Галуа GF(pv) будет определяться решением уравнения вида
![]() (5)
(5)
где ![]() - j-й блок зашифрованного сообщения; j = 0, 1, ….
- j-й блок зашифрованного сообщения; j = 0, 1, ….
Для дешифрования сообщения на приемной стороне решается обратная задача выражению (5). В этом случае j-й блок открытого сообщения j = 0, 1, 2… вычисляется
![]() (6)
(6)
При применении криптографических функций должна использоваться мультипликативная группа расширенного поля Галуа GF(pv). Чтобы при выполнении криптографических преобразований не нарушалось выполнение бинарных операций нулевой символ ![]() должен быть заменен на другой элемент мультипликативной группы. Так в качестве такого элемента может выступить число
должен быть заменен на другой элемент мультипликативной группы. Так в качестве такого элемента может выступить число ![]() .
.
Если взять для выработки псевдослучайной последовательности многотактовый фильтр, в котором число линий задержек значительно превосходит степень порождающего полинома ![]() , т.е.
, т.е.![]() то при этом резко возрастает число возможных ПСП символов, которые можно использовать в качестве показателей степени по модулю
то при этом резко возрастает число возможных ПСП символов, которые можно использовать в качестве показателей степени по модулю ![]() . Это позволяет повысить уровень криптозащиты данных от НСД при использовании процедур нелинейного шифрования. В этом случае число различных псевдослучайных последовательностей будет определяться как
. Это позволяет повысить уровень криптозащиты данных от НСД при использовании процедур нелинейного шифрования. В этом случае число различных псевдослучайных последовательностей будет определяться как
![]() (7)
(7)
Проведенные исследования показали, что уже при n = 255 и восьмой степени полинома ![]() число возможных ПСП, снимаемых параллельно с выходов различных линий задержки, превысит число 1018, что свидетельствует о высокой степени криптографической защиты. Показано, что данный метод позволяет обеспечить требуемый уровень криптографической защиты информации от НСД за счет сложности определения значения дискретного логарифма.
число возможных ПСП, снимаемых параллельно с выходов различных линий задержки, превысит число 1018, что свидетельствует о высокой степени криптографической защиты. Показано, что данный метод позволяет обеспечить требуемый уровень криптографической защиты информации от НСД за счет сложности определения значения дискретного логарифма.
С целью сокращения временных затрат в работе был разработан метод нелинейного шифрования с использованием ПСКВ. В данной системе используется набор неприводимых полиномов pi(z), i=1,2,3…, которые определяют рабочий диапазон
![]() (8)
(8)
Пусть даны два полинома A(z) и B(z). Тогда в ПСКВ каждый полином может быть однозначно определен вектором остатков, т.е. в виде
 (9)
(9)
где ![]()
![]()
Следовательно, операции суммирования (10), вычитания (11) и умножения (12) можно свести к соответствующим операциям над остатками
 , (10)
, (10)
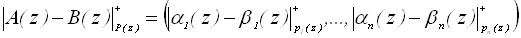 , (11)
, (11)
 . (12)
. (12)
Исходя из условия построения системы криптографической защиты информации в расширенных полях Галуа на основе полиномиальной системы класса вычетов, имеем, что каждый блок A(z), представленный в полиномиальной форме, однозначно представляется в виде набора остатков по выбранным основаниям ![]()
![]() (13)
(13)
где 
При этом к блоку остатков применяется нелинейное шифрование согласно выражения (5). Так как сравнения по одному и тому же модулю можно почленно умножать, то это выражение представляется в виде:
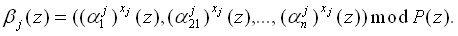 (14)
(14)
Таким образом, операция возведения в степень по модулю Р(z), являющаяся основой разработанного метода нелинейного шифрования, сводится к совокупности операций возведения в степень остатков ![]() по соответствующим основаниям
по соответствующим основаниям ![]() .
.
На приемной стороне осуществляется процедура расшифрования согласно выражения (6). Так как операции выполняются в кольце полинома Р(z), то справедливо
![]() (15)
(15)
где ![]()
Для вычисления корня степени хj из j необходимо свести данную немодульную операцию к совокупности модульных. Исходя из условия
![]() (16)
(16)
необходимо определить мультипликативную обратную величину ![]() относительно
относительно ![]() по модулю
по модулю ![]() Для этого необходимо на приемной стороне использовать блок, позволяющий вычислить данную величину по значению
Для этого необходимо на приемной стороне использовать блок, позволяющий вычислить данную величину по значению ![]() .
.
В ходе проведенных исследований было выявлено, что применение полиномиальной системы классов вычетов для реализации нелинейного шифрования позволило снизить временные затраты на 9,2 процентов по сравнению с выполнением метода шифрования с возведением в степень по модулю в расширенном поле Галуа GF(23).
Так процедуры шифрования производятся с непозиционными кодами, то конечная скорость шифрования будет также определяться временем выполнения немодульных операций. Одной из первых немодульных процедур, необходимой для функционирования процессоров ПСКВ, является реализация прямого преобразования позиционного кода в код ПСКВ. На основе анализа основных методов прямого преобразования ПСС-ПСКВ был выбран метод непосредственного суммирования
 , (17)
, (17)
где ![]() ,
, ![]() ,
,
а так же произведена его схемная реализация, которая характеризуется меньшими временными и схемными затратами по сравнению с ранее известными.
Наряду с прямым преобразованием из позиционного кода в модулярный существует и обратный перевод из непозиционного кода в код ПСС. В настоящее время известны два основных способа перевода:
- на основе китайской теоремы об остатках (КТО);
- на основе перевода в обобщенную полиадическую систему (ОПС).
Задача перевода n-мерного представления полинома A(z) к позиционному виду на основе КТО представляется следующим образом:
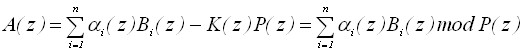 , (18)
, (18)
где ![]() - ортогональные базисы системы; K(z) – ранг полинома.
- ортогональные базисы системы; K(z) – ранг полинома.
В ходе выполнения диссертационной работы была разработана схемная реализация преобразователя ПСКВ-ПСС. Учет отсутствия межразрядных связей при выполнении преобразования позволил свести выражение (18) к виду
 , (19)
, (19)
где ![]() - разряд
- разряд ![]() -го остатка
-го остатка ![]() по модулю
по модулю ![]() .
.
При этом устройство преобразования из кода ПСКВ в ПСС, характеризуется отсутствием выходного сумматора по модулю ![]() , что в значительной степени приводит к повышению быстродействия и уменьшению схемных затратами по сравнению с раннее известными реализациями.
, что в значительной степени приводит к повышению быстродействия и уменьшению схемных затратами по сравнению с раннее известными реализациями.
Для повышения криптографической стойкости системы нелинейного шифрования в ПСКВ было предложено менять набор оснований. Для этого необходимо осуществлять пересчет ортогональных базисов при переводе из ПСКВ в ПСС. В работе представлен метод пересчета ортогональных базисов при деградации структуры процессоров ПСКВ, позволяющий решить данную задачу. В этом случае значения ортогональных базисов Bi(z), i=1,…,k+r, определяются
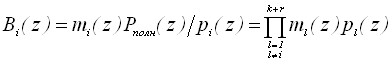 , (20)
, (20)
где ![]() – вес l-го основания ПСКВ.
– вес l-го основания ПСКВ.
Промежуточная система ОПС составляет основу второго способа перевода из ПСКВ в ПСС, при этом число А изображается в виде
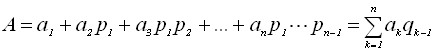 , (21)
, (21)
где ak - цифры в ОПС; ![]() – вес цифры в ОПС.
– вес цифры в ОПС.
На основе анализа в диссертационной работе был выбран алгоритм вычисления коэффициентов ОПС в расширенных полях Галуа, базирующийся на КТО
 ,
,![]() . (22)
. (22)
Для обеспечения более высокой криптостойкости системы шифрования в ПСКВ за счет изменения ансамбля оснований был предложен алгоритм пересчета значений коэффициентов ОПС, реализуемый согласно
 . (23)
. (23)
Анализ выражения (23) показывает, что данная процедура описывается формулой Горнера и может быть успешна реализована на основе применения параллельно-конвейерной организации вычислений.
В третьей главе рассмотрены вопросы применения корректирующих кодов ПСКВ в системах нелинейного шифрования. Если полином A(z), представленный в ПСКВ, принадлежит рабочему диапазону ![]() , где
, где ![]() , k - количество информационных оснований, то он считается разрешенным. В противном случае полином A(z) – содержит ошибку.
, k - количество информационных оснований, то он считается разрешенным. В противном случае полином A(z) – содержит ошибку.
Для обнаружения и исправления ошибок в кодах ПСКВ предлагается использовать позиционную характеристику интервальный номер, который определяется
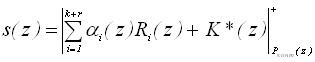 , (24)
, (24)
где ![]() ;
;![]() - ранг безизбыточной системы, задаваемый
- ранг безизбыточной системы, задаваемый
![]() . (25)
. (25)
В основу данного алгоритма положено свойство подобия ортогональных базисов полной, содержащей контрольные основания, и безизбыточной ПСКВ.
Если полином, представленный в ПСКВ, не содержит ошибки то интервальный равен нулю s(z)=0, в противном случае – код ПСКВ содержит ошибку. С целью повышения скорости вычисления характеристики был разработан алгоритм, базирующийся на КТО, согласно которому (24) сводится к параллельному вычислению
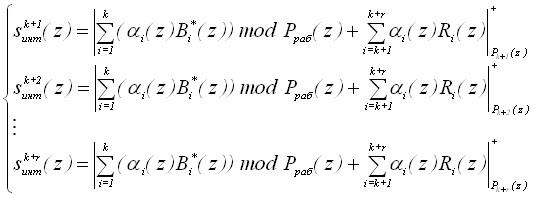 (26)
(26)
Так для поля GF(25) реализация алгоритма, определяемого выражением (26) позволило сократить схемные затраты на 5,6% по сравнению с классическим методом, определяемым согласно (24). Дальнейшее совершенствование корректирующих характеристик кодов ПСКВ возможно за счет использования потенциальных возможностей обнаружения и исправления ошибок в частотной области.
В работе был разработан алгоритм коррекции, позволяющий осуществлять обнаружение и исправление ошибок в спектральной области кода. Так как для разрешенной комбинации ПСКВ справедливо s(z)=0, то это означает, что s(z) должен делиться без остатка на контрольные основания. Другими словами, корни контрольных полиномов ![]() должны являться корнями интервального полинома. Если в качестве порождающих полиномов для GF(pv) использовать контрольные основания
должны являться корнями интервального полинома. Если в качестве порождающих полиномов для GF(pv) использовать контрольные основания ![]() , то исходный вектор s(z) преобразуется в вектор S(z), реализуемый в частотной области согласно выражения
, то исходный вектор s(z) преобразуется в вектор S(z), реализуемый в частотной области согласно выражения
![]() , (27)
, (27)
где - j-ая спектральная составляющая полинома ![]() ;
; ![]() - первообразный элемент расширенного поля GF(pv), порожденный основанием
- первообразный элемент расширенного поля GF(pv), порожденный основанием ![]() ;
; ![]() .
.
Если элемент ![]() является корнем полинома s(z) во временной области, то соответствующая ему спектральная составляющая должна быть Sj(z)=0. Таким образом, по величине соответствующих спектральных составляющих Sj(z) можно определить местоположение и глубину ошибки в коде ПСКВ. Характерной чертой разработанного алгоритма является то, что его применение позволяет контролировать работу устройства обнаружения и коррекции ошибок (УОКО). Использование двух спектральных составляющих позволяет однозначно обнаружить отказ в оборудовании блока УОКО. В ходе работы было разработано устройство, реализующее этот алгоритм, по которому получен патент.
является корнем полинома s(z) во временной области, то соответствующая ему спектральная составляющая должна быть Sj(z)=0. Таким образом, по величине соответствующих спектральных составляющих Sj(z) можно определить местоположение и глубину ошибки в коде ПСКВ. Характерной чертой разработанного алгоритма является то, что его применение позволяет контролировать работу устройства обнаружения и коррекции ошибок (УОКО). Использование двух спектральных составляющих позволяет однозначно обнаружить отказ в оборудовании блока УОКО. В ходе работы было разработано устройство, реализующее этот алгоритм, по которому получен патент.
В четвертой главе был разработан метод нелинейного шифрования потока информации на основе операции возведения в степень по модулю с использованием индексного представления данных. Известно, что индексное или степенное представления ненулевых элементов полей Галуа наиболее удобны для выполнения мультипликативных и им обратных операций (таблица 1).
Таблица 1 – Степенное выполнение мультипликативных операций
| Операция | Степенное представление |
| Умножение | 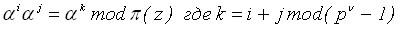 |
| Деление |  |
| Возведение в степень | 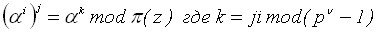 |
| Дискретный логарифм | 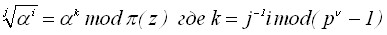 |
Исходный поток разбивается на блоки А = {А0, А1, А2, …}, каждый из которых содержит двоичных разрядов. Каждый блок считается элементом мультипликативной группы поля GF(pv).. Это блок в двоичном коде подается на входы устройства вычисления индекса, реализующего
![]() (28)
(28)
где l - индекс полинома A(z); - порождающий элемент мультипликативной группы поля Галуа GF(pv).
Вычисленный lj индекс в виде параллельного кода подается на первые входы умножителя по модулю р-1. На вторые входы этого умножителя поступает параллельный двоичный код ключа xj,снятого с выходов генератора ПСП. Умножитель по модулю р-1 реализует модульную операцию
![]() (29)
(29)
Полученный результат j представляет индекс элемента поля GF(pv), который является результатом зашифрованного блока Аj согласно выражения (5). Он в параллельном виде подается на вход преобразователя «индекс – элемент поля»
![]() (30)
(30)
В результате зашифрованный блок данных j, передается на приемную сторону.
На приемной стороне блок зашифрованных данных j поступает на входы устройства вычисления индекса, реализующего операцию обратную выражению (30). Полученный результат  виде параллельного кода подается на первые входы умножителя по модулю р-1. Для выполнения операции дешифрования согласно (6) необходимо определить значение элемента х-1, являющегося мультипликативно обратным элементу х. Для этого с выходов генератора ПСП значение х поступает на вход устройства, реализующего выражение (16). Полученное значение подается на вторые входы умножителя, который выполняет
виде параллельного кода подается на первые входы умножителя по модулю р-1. Для выполнения операции дешифрования согласно (6) необходимо определить значение элемента х-1, являющегося мультипликативно обратным элементу х. Для этого с выходов генератора ПСП значение х поступает на вход устройства, реализующего выражение (16). Полученное значение подается на вторые входы умножителя, который выполняет
![]() (31)
(31)
Вычисленное значение индекса lj поступает на блок, осуществляющего операцию
![]() (32)
(32)
Результатом такого преобразования является j-й блок открытого сообщения, который и поступает пользователю.
В ходе проведенных исследований были разработаны блок, реализующий вычисление индекса по значению элемента расширенного поля, а также блок, предназначенный для выполнения обратной операции «индекс-элемент». Проведен анализ их работы, оценены временные и схемные затраты.
На основе последовательности решения частных задач диссертации была осуществлена разработка структуры устройства, реализующего нелинейное шифрования в расширенных полях Галуа с использованием индексного представления для порождающего полинома![]() . В качестве характеристического полинома для определения структуры генератора ПСП был выбран
. В качестве характеристического полинома для определения структуры генератора ПСП был выбран ![]() . Проведена разработка блока, позволяющего вычислить значение индекса элемента расширенного поля Галуа, устройства для определения значения величины элемента поля по значению индекса. Кроме того, осуществлен синтез устройства для вычисления мультипликативно обратных элементов по модулю р-1. Проведены расчеты по необходимым временным и аппаратным затратам на реализацию операции преобразования.
. Проведена разработка блока, позволяющего вычислить значение индекса элемента расширенного поля Галуа, устройства для определения значения величины элемента поля по значению индекса. Кроме того, осуществлен синтез устройства для вычисления мультипликативно обратных элементов по модулю р-1. Проведены расчеты по необходимым временным и аппаратным затратам на реализацию операции преобразования.
Проведена сравнительная оценка разработанного нелинейного шифратора расширенного поля Галуа, использующего индексное представление с шифратором, обеспечивающим криптографическую защиту данных на основе операции возведения в степень по модулю. Результаты исследований показали, что при обработке 8 – разрядных операндов нелинейный шифратор, использующий индексное представление, характеризуется функциональной производительностью 7,54 Гц/вентиль, что в 1,55 раза выше по сравнению с техническим решением на основе операции возведения в степень по модулю. Другими словами, для увеличения скорости шифрования более чем в 2 раза потребовалось увеличить аппаратурные затраты, необходимые на реализацию преобразований «элемент-индекс» и обратно, всего лишь на 65 процентов. На рисунке 1 приведены в графическом виде обобщенные результаты сравнительного анализа по эффективности различных методов нелинейного шифрования.
 v v | Для удобного восприятия графические данные представлены в относительном масштабе | |
| Рисунок 1 – Сравнительная оценка эффективности разработанного метода | ||
В заключении обобщены итоги и результаты проведенных исследований.
основные результаты работы
В ходе исследований были получены следующие результаты:
- Разработан метод нелинейного шифрования с использованием операции возведения в степень по модулю в расширенных полях Галуа. Показано, что данный метод позволяет обеспечить требуемый уровень криптографической защиты информации от НСД за счет сложности определения значения дискретного логарифма.
- С целью сокращения временных затрат был разработан метод нелинейного шифрования с использованием ПСКВ. Вычисления, выполняемые в ПСКВ с малоразрядными остатками, без учета немодульных преобразований, позволили повысить скорость реализации процедур нелинейного шифрования в поле Галуа GF(23) на 9,2 процента по сравнению с обработкой данных в кольце полиномов P(z)=z7+1.
- Для сокращения временных затрат были проведены исследования основных методов и алгоритмов выполнения прямого преобразования ПСС-ПСКВ. На основе полученных результатов был выбран метод преобразования, который характеризуется минимальными временными задержками. В ходе работы были проведены исследования операций обратного перевода из модулярного кода ПСКВ в двоичный код как на основе КТО, так и с использованием коэффициентов ОПС. С целью повышения эффективности такого преобразования были представлены алгоритмы пересчета коэффициентов ОПС и значений ортогональных базисов, применение которых позволит реализовать системы шифрования в ПСКВ с изменяемым ансамблем оснований.
- Для борьбы с ошибками, возникающими при передаче зашифрованных данных, предлагается использовать корректирующие способности кодов ПСКВ. Разработан алгоритм вычисления позиционной характеристики интервальный номер полинома, который благодаря параллельным вычислениям позволяет понизить временные затраты на 3-5% в зависимости от размерности поля Галуа по сравнению с реализацией ранее известных алгоритмов.
- Показано, что наряду с определением ошибки, базирующимся на вычисление позиционной характеристики во временной области, существует возможность поиска и коррекции ошибок на основе спектрального представления кодов ПСКВ. Разработан алгоритм спектрального обнаружения и коррекции ошибок на базе которого синтезировано патентоспособное устройство. Проведен сравнительный анализ с устройством обнаружения и коррекции ошибок, использующим принцип дублирования. Полученные результаты позволили сделать вывод о том, спектральный метод, имея одинаковую информационную надежность обрабатываемых данных по сравнению с УОКО, позволяет снизить аппаратурные затраты на реализацию поиска и коррекции ошибок, что в конечном итоге положительно отразиться на надежности функционирования всего устройства
- Произведена разработка метода нелинейного шифрования на основе операции возведения в степень по модулю в полях Галуа с использованием индексного представления элементов. Переход к индексной обработке позволяет повысить скорость шифрования по сравнению с ранее известными операциями криптографической защиты данных связанных с операциями возведения в степень по модулю.
- Для организации индексного представления элементов расширенного поля Галуа были разработаны блоки, осуществляющие преобразование «элемент-индекс» и обратно для поля Галуа GF(23). Определены временные и схемные затраты необходимые на реализацию этих преобразований.
- На основе последовательности решений частных задач диссертации осуществлена разработка шифрующего устройства, предназначенного для обработки 8-разрядных данных Проведенная сравнительная оценка разработанного нелинейного шифратора, использующего индексное представление с шифратором, обеспечивающим криптографическую защиту данных на основе операции возведения в степень по модулю. Результаты исследований показали, что при обработке 8–разрядных операндов нелинейный шифратор, использующий индексное представление, характеризуется функциональной производительностью 7,54 Гц/вентиль, что в 1,55 раза выше по сравнению с техническим решением на основе операции возведения в степень по модулю.
- В ходе проведенных исследований было выявлено, что при увеличении разрядности обрабатываемых данных эффективность применения математической модели шифрования в расширенных полях Галуа с использованием индексного представления, увеличивается с 1,55 (для 8 разрядов) до 3,63 (для 64 разрядов) по сравнению с шифратором, использующим быстрый алгоритм возведения в степень по модулю.
Список основных работ по теме диссертации
- Чипига, А.А. Алгоритм обеспечения информационной скрытности для адаптивных средств передачи информации [Текст] / А.А. Чипига, И.А. Калмыков // Информационные технологии, № 3. – 2007. – С.159-162.
- Чипига, А.А. Применение расширенных полей Галуа для повышения информационной скрытности передачи данных [Текст] / А.А. Чипига, И.А. Калмыков, А.Б. Хайватов, Сагдеев А.К. // Успехи современного естествознания, № 5. - 2007. – С.103-105.
- Чипига, А.А. Разработка структуры дешифратора для системы криптографической защиты информации, функционирующей в расширенных полях Галуа [Текст] // Материалы электронной заочной конференции Российской Академии Естествознания «Прикладные исследования и разработки по приоритетным направлениям науки и техники». 15-20 ноября 2009. – www.congressinform.ru (www.rae.ru)
- Чипига, А.А. Реализация процедуры обратной нелинейному шифрованию с использованием индексного представления для поля Галуа GF(23)/ А.А. Чипига, И.А. Калмыков, А.В. Барильская, О.А. Кихтенко, В.Р. Гахов // Материалы электронной заочной конференции Российской Академии Естествознания «Прикладные исследования и разработки по приоритетным направлениям науки и техники». 15-20 ноября 2009. – www.congressinform.ru (www.rae.ru
- Чипига, А.А. Разработка метода нелинейного шифрования потока данных в расширенных полях Галуа [Текст] / А.А. Чипига, И.А. Калмыков, А.В. Барильская, О.А. Кихтенко // Материалы электронной заочной конференции Российской Академии Естествознания «Прикладные исследования и разработки по приоритетным направлениям науки и техники». 15-20 ноября 2009. – www.congressinform.ru (www.rae.ru)
- Чипига, А.А. Постановка задачи разработки обеспечения информационной скрытности для цифровых систем передачи информации [Текст] / А.А. Чипига, И.А. Калмыков // Материалы III Международной научно-технической конференции «Инфокоммуникационные технологии в науке, производстве и образовании. Инфоком 3», часть 2. Кисловодск, 2008. – С.154-155.
- Чипига, А.А. Нейроалгоритм для вычисления коэффициентов обобщенной полиадической системы в GF(pv) [Текст] / А.А. Чипига, И.А. Калмыков, Ю.О. Щелкунова, А.А. Шилов // Материалы III Санкт-Петербургской межрегиональной конференции «Информационная безопасность регионов России (ИБРР-2003)», Санкт-Петербург, 2003. С. 55.
- Чипига, А.А. Методика пересчета коэффициентов ОПС для живучих систем биометрической аутентификации пользователя [Текст] / А.А. Чипига,
И.А. Калмыков // Материалы VI Международной научно-практической конференции «Информационная безопасность». Таганрог, 2004. – С.144-146. - Чипига, А.А. Применение интервального номера для коррекции ошибок в кодах полиномиальной системы класса вычетов [Текст] / А.А. Чипига, И.А. Калмыков, И.А.Петлеваный, В.Р. Гахов // Научно-теоретический журнал «Фундаментальные исследования», № 2. - 2006. – С. 37-38.
- Чипига, А.А. Разработка нейронной сети для определения интервального номера числа [Текст] / А.А. Чипига, И.А. Калмыков, Ю.О. Щелкунова, А.А. Шилов // Материалы III Санкт-Петербургской межрегиональной конференции «Информационная безопасность регионов России (ИБРР-2003)», Санкт-Петербург, 2003. С. 54.
- Чипига, А.А. Разработка метода пересчета ортогональных базисов в полиномиальной системе класса вычетов и его нейросетевая реализация [Текст] / А.А. Чипига, И.А. Калмыков, А.А. Шилов // Материалы VI Международной научно-практической конференции «Информационная безопасность». Таганрог, 2004. – С.152-154.
- Чипига, А.А. Разработка нейронного преобразователя из позиционного кода в полиномиальную систему классов вычетов [Текст] / А.А. Чипига, И.А. Калмыков, А.В. Лисицын // Труды Международного Форума по проблемам науки, техники и образования. – М.: Академия наук, 2004. – С.135-136.
- Пат. 23014418 Российская Федерация, G06F 7/72. Устройство спектрального обнаружения и коррекции ошибок в кодах полиномиальной системы классов вычетов [Текст] / Чипига А.А., Калмыков И.А., Лободин М.В.; заявитель и патентообладатель Ставрополь, Северо-Кавказский государственный университет; публ. 20.06.2007, Бюл. № 17
- Чипига, А.А. Криптографическая защита данных в информационных технологиях на базе непозиционных полиномиальных систем [Текст] / А.А. Чипига, И.А. Калмыков, А.В. Барильская, О.А. Кихтенко // Известия ЮФУ. Технические науки. Таганрог, 2009. – С.210-220
Личный вклад автора в работах, выполненных в соавторстве: [1],[2],[4]-[6], [14] – метод нелинейного шифрования с использованием операции возведения в степень по модулю и индексным представлением в расширенных полях Галуа; [7],[8] - нейросетевая реализация алгоритма вычисления коэффициентов ОПС; [9],[10] – алгоритм параллельного вычисления интервального номера полинома; [11],[12] - нейросетевые алгоритмы выполнения немодульных операций; [13] – алгоритм обнаружения и коррекции ошибок в спектральной области.

