Теоретическое исследование анизотропии механических свойств белковых молекул
На правах рукописи
ФАЛЬКОВИЧ СТАНИСЛАВ ГРИГОРЬЕВИЧ
ТЕОРЕТИЧЕСКОЕ ИССЛЕДОВАНИЕ АНИЗОТРОПИИ
МЕХАНИЧЕСКИХ СВОЙСТВ БЕЛКОВЫХ МОЛЕКУЛ
Специальность 02.00.06 – высокомолекулярные соединения
Автореферат
диссертации на соискание ученой степени
кандидата физико-математических наук
Санкт-Петербург – 2011
Работа выполнена в Учреждении Российской академии наук
Институте высокомолекулярных соединений РАН
Научный руководитель: доктор физ.-мат. наук
Анатолий Анатольевич ДАРИНСКИЙ
Официальные оппоненты: доктор физ.-мат. наук, проф.
Александр Михайлович СКВОРЦОВ
доктор физ.-мат. наук
Михаил Геннадьевич ПЕТУХОВ
Ведущая организация: кафедра молекулярной биофизики физического факультета Санкт-Петербургского государственного университета, г. Санкт-Петербург
Защита диссертации состоится 26 мая 2011 г. в 10 часов на заседании диссертационного совета Д 002.229.01 при Учреждении Российской академии наук Институте высокомолекулярных соединений РАН по адресу: 199004, г. Санкт-Петербург, Большой пр., д. 31, конференц-зал.
С диссертацией можно ознакомиться в библиотеке Учреждения Российской академии наук Института высокомолекулярных соединений РАН.
Автореферат разослан: 19 апреля 2011 г.
Ученый секретарь
Диссертационного совета,
кандидат физ.-мат. наук Долотова Н. А.
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность. Белковые молекулы – один из важнейших видов макромолекул живой природы. Они выполняют множество функций: ферментативную (каталитическую), структурную, сократительную и др. В процессе функционирования белковые молекулы нередко подвергаются механической деформации. Это происходит при внешнем воздействии на клетку, при сокращении и растяжении мышечной ткани, при транспортировке белковых молекул через биологические мембраны. Изменения в структуре молекулы белка, вызванные механическим растяжением, могут влиять на способность этой молекулы выполнять свои функции. Знание механических свойств отдельных белковых молекул и факторов, определяющих эти свойства, важно для понимания их функционирования как внутри, так и вне организма. Именно поэтому механические свойства белковых молекул активно исследуются в последние десятилетия. Эти работы активизировались с появлением метода атомно-силовой микроскопии, позволившего изучать механические свойства отдельных белковых молекул.
Молекулы белка – гетерогенные полимерные структуры, и эта гетерогенность не может не отражаться на их механических свойствах. Белковые молекулы разделяются на две морфологически различные группы: глобулярные, существующие в форме компактной глобулы, и фибриллярные, существующие в виде суперспирали, состоящей из обвитых друг вокруг друга -спиралей. Из экспериментов по атомно-силовой микроскопии известно, что глобулярные белки по-разному реагируют на растяжение, когда механическая нагрузка приложена к различным парам точек на поверхности белковой глобулы, т.е. их механические свойства анизотропны. Однако происходящие при растяжении в различных направлениях структурные перестройки остаются недостаточно исследованными и, кроме того, мало изучен вопрос о связи механизмов спонтанного разворачивания белка и его разворачивания под действием внешней нагрузки. Анизотропия механических свойств фибриллярных белков обусловлена анизотропией их суперспиральной структуры. До сих пор не проводилось ни экспериментальных, ни теоретических исследований, где сравнивалась бы реакция одного и того же фибриллярного белка на растяжение вдоль и поперёк оси суперспирали, и не известны молекулярные механизмы деформации белковой суперспирали при её растяжении в различных направлениях.
Цель работы – установление механизмов анизотропной деформации белковых молекул методами компьютерного моделирования. Для достижения данной цели были поставлены следующие задачи:
- Изучить способность молекулы глобулярного белка сопротивляться растяжению, проводимому в различных направлениях с постоянной скоростью.
- Установить механизм разворачивания молекулы глобулярного белка при растяжении в различных направлениях.
- Сравнить механизм спонтанного разворачивания молекулы глобулярного белка с механизмом её разворачивания под действием механической нагрузки, приложенной в различных направлениях.
- Сравнить способность суперспиральной молекулы фибриллярного белка сопротивляться нагрузке, приложенной вдоль и поперёк оси суперспирали.
- Исследовать механизмы продольной и поперечной деформации суперспирали фибриллярного белка.
Объектами исследования являлись глобулярный регуляторный белок убиквитин и фибриллярный белок мышечной ткани миозин, как представители своих классов белковых молекул с наиболее полно изученными механическими свойствами. В качестве метода исследования использовано компьютерное моделирование, а именно метод молекулярной динамики с применением различных моделей, корректно описывающих поведение белковых молекул.
Научная новизна работы. Впервые проведено компьютерное моделирование механического растяжения макромолекулы глобулярного белка в 12 направлениях с постоянной скоростью. Установлено, что модель объединённых атомов и полноатомная модель позволяют получить согласующиеся друг с другом результаты. Показано, что разворачивание белковой глобулы начинается в окрестности точек приложения нагрузки, а наиболее стабильными элементами молекулярной структуры глобулярного белка являются -спираль и -шпилька. Найдены направления приложения нагрузки, растяжению в которых белковая глобула сопротивляется в наименьшей степени. Установлено, что эти направления могут не совпадать с «координатой реакции» её спонтанного разворачивания.
Впервые методом молекулярной динамики проведено моделирование растяжения фибриллярного белка с постоянной скоростью в продольном и поперечном направлениях. Установлено, что при его продольной деформации вначале происходит раскручивание суперспирали и разворачивание -спиральных витков на концах цепей, затем разворачивание -спиральных витков внутри обеих спиралей и в конце растягиваются развернутые участки цепей. Показано образование новых гидрофобных контактов и водородных связей между развёрнутыми участками цепей. Предложен механизм поперечной деформации белковой суперспирали, состоящий во взаимодействии одной из цепей с суперспиральной частью молекулы белка.
Положения, выносимые на защиту.
1. Для всех направлений растяжения разворачивание молекулы глобулярного белка убиквитина начинается в пространственной близости от точек приложения нагрузки. В процессе деформации молекулы -спираль и -шпильки разрушаются в последнюю очередь, если нагрузка не приложена непосредственно к ним.
2. У молекул глобулярного белка направление с наименьшей степенью сопротивления растяжению и «координата реакции» спонтанного разворачивания не обязательно совпадают.
3. Сила реакции при растяжении белковой суперспирали в продольном направлении превышает силу реакции при её поперечной деформации.
4. Продольная деформация белковой суперспирали проходит в три этапа: раскручивание суперспирали и разворачивание -спиральных витков на концах цепей; разворачивание витков внутри обеих -спиралей; растяжение уже развернутых участков цепей.
5. В зависимости от скорости растяжения возможны два механизма разворачивания белковой суперспирали: поэтапное разделение цепей без их взаимодействия с суперспиральной частью молекулы при больших скоростях растяжения и разделение при наличии такого взаимодействия при меньших скоростях растяжения.
Практическая значимость. Согласие между результатами моделирования, полученными с использованием обобщенной и полноатомной моделей, позволяет исследовать механические свойства глобулярных белков, используя только обобщенные модели, что значительно ускоряет расчеты. Полученные результаты могут быть использованы при разработке гибридных материалов для биомедицинских приложений, обладающих повышенной прочностью, а также для разработки «молекулярных машин» на основе суперспиральных белков.
Апробация работы и публикации. Основные результаты работы представлены на шестом симпозиуме «Порядок и подвижность в полимерных системах» (Санкт-Петербург, Россия, Июнь 2008), Европейском полимерном конгрессе (Граз, Австрия, Июль 2009), Международном симпозиуме «Достижения полимерной науки» (Майнц, Германия, Июнь 2009), Международной конференции «Новые направления в теории и компьютерном моделировании полимеров» (Россия, Москва, Июнь 2010), четвёртой и пятой петербургских конференциях молодых учёных «Современные проблемы науки о полимерах» (Россия, Санкт-Петербург, Апрель 2008 и Октябрь 2009), первой международной научной школе "Наноматериалы и нанотехнологии в живых системах" (Россия, Москва, июнь 2009).
По материалам диссертации опубликованы восемь работ (в том числе 2 статьи в рецензируемых журналах).
Структура и объём работы Диссертационная работа состоит из введения, трёх глав, выводов, списка цитируемой литературы (87 наименований). Работа изложена на 107 страницах, включает 34 рисунка, 9 таблиц и 3 приложения.
Личный вклад автора состоял в проведении компьютерного моделирования изученных систем, в обработке, анализе и интерпретации полученных результатов, а также в подготовке докладов и публикаций.
КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ
Во Введении обоснована актуальность темы диссертации, сформулированы цель и основные задачи исследования, обозначены научная новизна и практическая значимость работы, представлены положения, выносимые на защиту.
Глава 1. В первой главе диссертации дан обзор литературы, представлены сведения об экспериментальных и теоретических работах, посвященных исследованию механических свойств белков. Основное внимание уделено результатам исследований анизотропии механических свойств белковых молекул.
Главе 2 Исследование механических свойств убиквитина изложены результаты компьютерного моделирования растяжения глобулярного белка убиквитина с постоянной скоростью. Растяжение проводилось с использованием двух моделей: полноатомной (5 направлений растяжения) и модели объединённых атомов (12 направлений). В полноатомной модели учитывались все атомы белка и растворителя (воды). В модели объединённых атомов атомы каждого аминокислотного остатка объединялись в одну сферическую частицу. Использовался потенциал G: притяжение действовало только между теми остатками, атомы которых контактировали в нативной структуре, остальные остатки отталкивались.
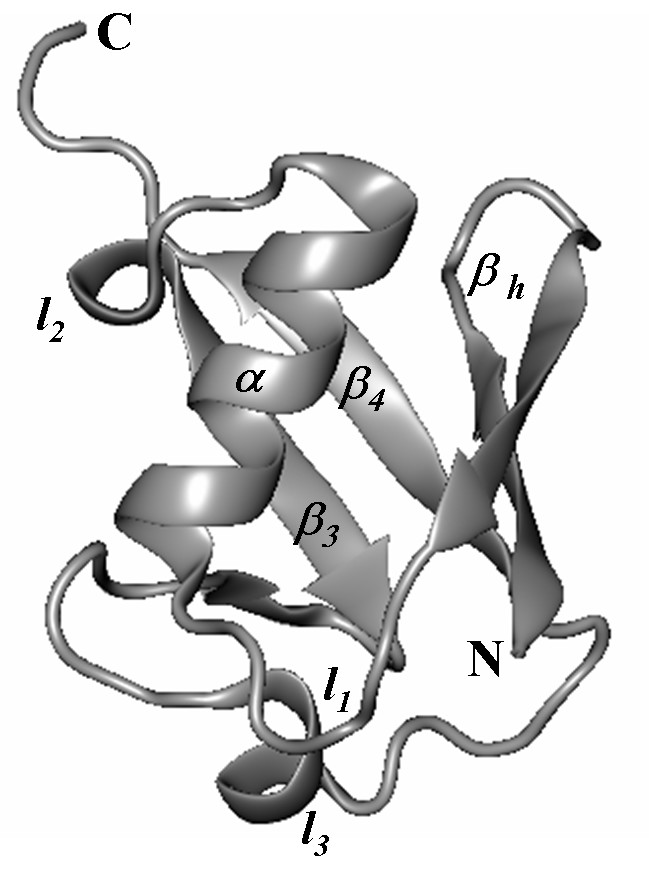
Рис. 1. Структура убиквитина.
Растворитель описывался неявно, через эффективные потенциалы взаимодействия между частицами. Направления растяжения выбирались так, чтобы нагрузка прикладывалась к парам аминокислотных остатков, принадлежащих различным элементам белковой структуры. Растяжение проводилось с постоянной скоростью 510-3 нм/пс, которая на 6-8 порядков выше скоростей, используемых в эксперименте.
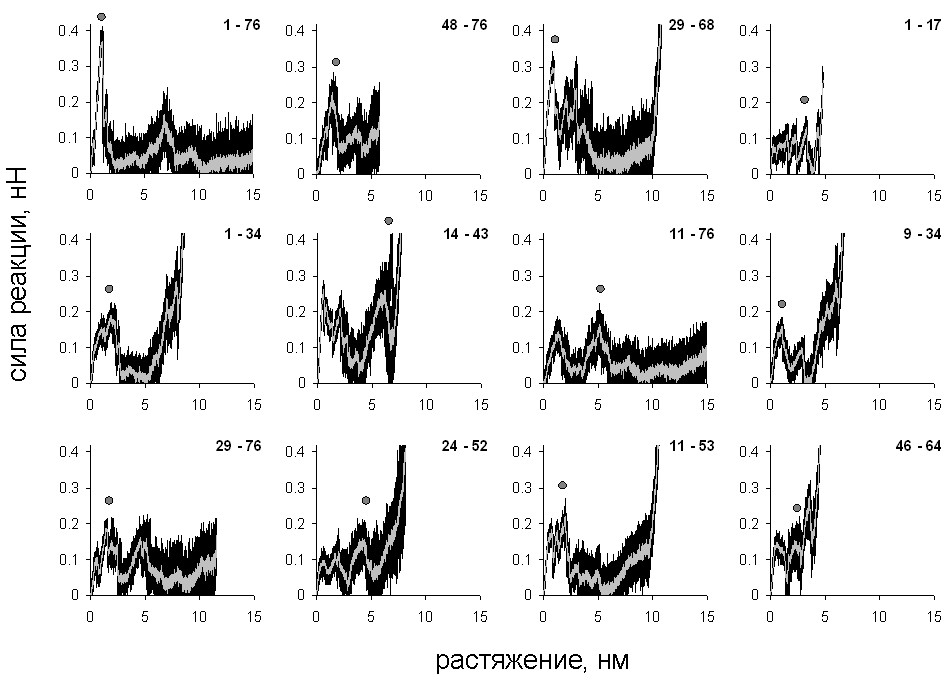
Рис. 2. Зависимость силы реакции от растяжения, модель объединённых атомов. Кривые, соответствующие каждой из 10 траекторий (чёрный) и усреднённые кривые (серый). Точки – наибольшие пики силы реакции. Около каждого рисунка показаны номера остатков, к которым приложена нагрузка.
Для каждого направления получено 10 молекулярно-динамических траекторий, по которым построены графики зависимости силы реакции от растяжения. Кривые для одного и того же направления растяжения близки, что говорит о единственности пути разворачивания при растяжении в каждом направлении. Для разных направлений зависимости (см. рис. 2, 3) различаются по форме, однако все они имеют несколько пиков. Финальный рост силы реакции возникает, когда участок между точками приложения нагрузки полностью растягивается. В качестве меры сопротивляемости молекулы растяжению в данном направлении использовалась высота наибольшего пика силы реакции.
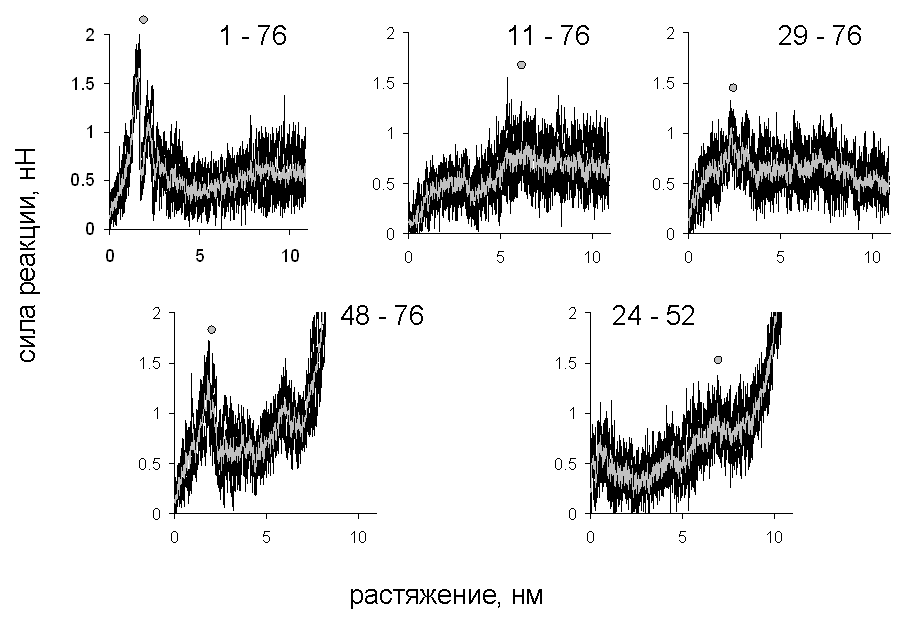
Рис. 3. Зависимость силы реакции от растяжения, полноатомная модель.
Табл. 1
Сопротивляемость убиквитина растяжению
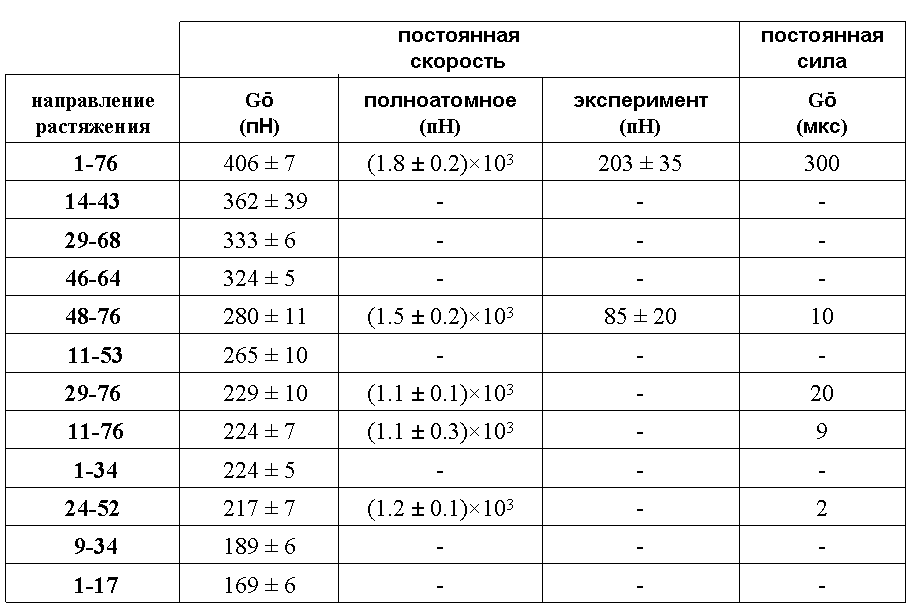
Эти значения ранжированы для модели объединённых атомов по величине (табл. 1). Там же представлены величины силы на максимуме для полноатомной модели, экспериментальные данные, а также данные, полученные в работе Best et al. (2008) по моделированию растяжения убиквитина под действием постоянной силы с использованием той же модели объединённых атомов, что и в настоящей работе (последний столбец). В этом случае характеристикой сопротивляемости является время, в течение которого белок не разворачивается при заданной внешней силе. В силу использования при моделировании более высоких значений скорости, чем в эксперименте, рассчитанные значения силы оказались выше экспериментальных.
Из полученных данных следуют два вывода:
1. Результаты, полученные с использованием модели объединённых атомов, согласуются с результатами, полученными при использовании полноатомной модели: направления растяжения одинаково ранжированы по сопротивляемости растяжению. Это даёт основания для использования обобщённой модели и для других направлений или других глобулярных белков.
2. Результаты находятся в качественном согласии с экспериментальными данными и с данными моделирования при приложении постоянной силы. Таким образом, моделирование глобулярного белка при постоянной скорости деформации позволяет корректно предсказывать наиболее сильные и наиболее слабые направления растяжения, хотя скорость деформирования на несколько порядков превышает экспериментальную.
Табл. 2
Последовательность, в которой разрываются нативные контакты между элементами структуры убиквитина (модель объединённых атомов)
| 1-76 | 29-68 | 46-64 | 14-43 | 48-76 | 11-53 |
| h и 4 | и 4 | 3 и 4 | h и 3 | 3 и 4 | h и l3 |
| h - l1 | h - | 3 - 4 | 3 - 4 | 3 - 4 | - l3 |
| h - 4 | 3 | 3 - l3 | 3 - l3 | 3 | 3 - l3 |
| h | - l3 | l3 | 3 | l2 - 4 | 3 |
| h - | l2 - 3 | - l3 | - l2 | l3 - 4 | l1 - l3 |
| l1 | - l2 | l3 - 4 | - l3 | h - 4 | |
| 3 - 4 | 3 - 4 | 3 | - l3 | 3 - l3 | h - |
| l1 - l3 | l3 - 4 | h - 4 | 3 | l3 | 3 |
| 3 | 3 - l3 | h - | h - | h - 4 | - l2 |
| - l2 | l3 | l1 - l3 | h - | l2 - 3 | |
| - l3 | 3 | h - 4 | l2 - 4 | ||
| l3 - 4 | |||||
| 3 - l3 | |||||
| l3 | |||||
| 3 | |||||
Анализ изменения количества нативных контактов внутри и между элементами структуры при разворачивании молекулы убиквитина позволил сделать выводы об общих характеристиках механизмов разворачивания. В структуре убиквитина можно выделить следующие элементы (рис. 1): N-концевая -шпилька (обозначаемая далее h); первая петля (l1); -спираль (); вторая петля (l2); третий -тяж, включающий в себя короткую -шпильку (3); третья петля (l3); С-концевой -тяж (4). В табл. 2 в первой строке приведены номера остатков, к которым приложена нагрузка, во второй – элементы структуры, которым принадлежат эти остатки, и далее показана последовательность разрыва контактов между элементами структуры для различных направлений растяжения. Если указан один элемент структуры, то разрыв контактов происходит внутри него.
Табл. 2
Продолжение
| 29-76 | 1-34 | 11-76 | 24-52 | 9-34 | 1-17 |
| и 4 | h и | h и 4 | и l3 | h и | h |
| l2 - 4 | h - | h - 4 | - l3 | h - | h - l1 |
| 3 - 4 | h - l1 | h - | l1 - l3 | h - 4 | h |
| h - | h - l3 | h - l3 | 3 - l3 | h - l3 | h - l3 |
| l1 - | h | l1 - l3 | 3 | l1 - l3 | l1 - l3 |
| l1 - l3 | h -4 | 3 - 4 | h - l3 | l1 | h - 4 |
| - l3 | l1 - l3 | l2 - 4 | h - 4 | l1 - | |
| 3 – l3 | - l3 | - l3 | l3 - 4 | 3 | |
| h - 4 | l3 - 4 | - l2 | |||
| 3 | - l2 | h | |||
| - l2 | 3 - l3 | ||||
| l2 - 3 | l3 | l2 - 3 | |||
| 3 | |||||
| l2 - 3 | |||||
При растяжении во всех направлениях в первую очередь разрываются нативные контакты, образованные обоими или (реже) одним элементом нативной структуры, к которым приложена нагрузка, а разрушение в других частях молекулы начинается позже. Также существует закономерность: -спираль и обе -шпильки не разрушаются до самого конца разворачивания либо разрушаются в последнюю очередь, кроме случаев, когда нагрузка прикладывалась непосредственно к ним или когда они находились вблизи одной из точек приложения нагрузки.
Моделирование с использованием полноатомной модели приводит к аналогичным выводам: разрушение контактов также начиналось вблизи точек приложения нагрузки, а -спираль и обе -шпильки не разрушались либо разрушались в последнюю очередь.
Для механических свойств белка важным представляется определение его «слабых мест», т.е. направлений растяжения, где сила реакции минимальна. До настоящей работы предполагалось (Best et al. (2008)), что самым «слабым» является направление 24-52, близкое к «координате реакции» спонтанного разворачивания без внешнего воздействия. Из табл. 1. следует, что направление растяжения 24-52 является только третьим по «слабости», причём ещё несколько направлений растяжения имеют такую же, в пределах погрешности, сопротивляемость. Таким образом, координата реакции спонтанного разворачивания не обязательно определяет направление самого лёгкого механического растяжения.
При растяжении в слабых направлениях нагрузка приложена не к концам цепи, и часть молекулы остаётся неразвёрнутой. Для ответа на вопрос о дальнейшей «судьбе» неразвёрнутой части молекулы данные о вовлечённости аминокислотных остатков в ядро сворачивания, полученные при изучении спонтанного разворачивания убиквитина экспериментально, были сопоставлены с результатами моделирования. Ядро сворачивания определяется как часть белка, имеющая преимущественно нативные контакты в переходном состоянии на вершине барьера свободной энергии (рис. 4). Для убиквитина определена степень вовлечённости в ядро сворачивания (Ф-величина) для 20 остатков, из них 9 имеют величину Ф > 0.5.
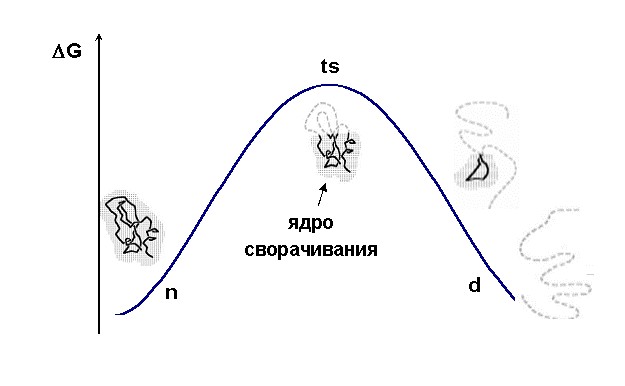
Рис. 4. Преодоление барьера свободной энергии (G) при спонтанном разворачивании белковой глобулы. Слева схематично показано нативное, глобулярное состояние белка (n), справа – денатурированное, клубковое состояние белка (d), на вершине барьера свободной энергии – переходное состояние (ts). Части рисунка адаптированы из книги О.Б. Птицына и А.В. Финкельштейна «Физика белка».
Для различных направлений растяжения из молекулярно-динамических траекторий для каждого из этих остатков была определена доля нативных контактов при максимальном растяжении. Среднее по 9 остаткам значение этой доли не превышает среднего значения <Фядроэкп> = 0.7 ± 0.2, полученного при усреднении по экспериментальным значениям Ф (табл. 3). Это означает, что при полном растяжении белок находится на вершине барьера свободной энергии либо преодолел его, и можно полагать, что оставшаяся неразрушенной часть белка спонтанно развернётся достаточно быстро.
Табл. 3
Доля нативных контактов в ядре сворачивания при полном растяжении

В Главе 3 Исследование механических свойств миозина представлены результаты компьютерного моделирования растяжения фибриллярного белка миозина с постоянной скоростью в различных направлениях методом молекулярной динамики.

Рис. 5. Схематичное изображение нерастянутой молекулы миозина.
Был исследован суперспиральный фрагмент миозина человека, состоящий из двух обвитых друг вокруг друга цепей (A и B) в -спиральной конформации. Каждая из цепей состоит из 126 аминокислотных остатков (35 витков -спирали), длина цепи в нерастянутой конформации 18 нм, в растянутой – 48 нм, см. рис. 5. Моделирование продольной (сдвиговая и продольная деформация одной из цепей, рис. 6а,б) и поперечной (рис. 6в,г) деформации молекулы миозина с постоянной скоростью было проведено с использованием полноатомного описания молекулы, неполярные атомы водорода были обобщены со связанными с ними атомами углерода. Растворитель описывался неявно. Моделировалось растяжение при двух значениях скорости растяжения: 10-1 нм/пс и 10-2 нм/пс.
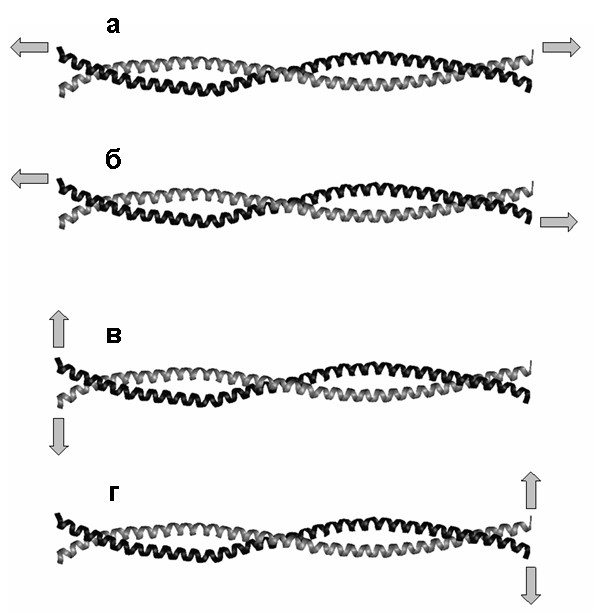
Рис. 6. Направления деформации суперспирали миозина, состоящей из двух полипептидных цепей: цепь A показана чёрным, цепь B - серым. Места приложения нагрузки показаны стрелками: (а) сдвиговая деформация, (б) продольная деформация цепи A, (в) поперечная деформация, нагрузка приложена к N-концам, (г) поперечная деформация, нагрузка приложена к C-концам.
Для двух способов деформации молекулы вдоль оси суперспирали: сдвиговой деформации и продольной деформации одной из цепей на рис. 7 показана зависимость силы реакции от растяжения. Зависимость для обоих типов деформации оказывается сходной при значениях растяжения, не превышающих 25 нм. На зависимости наблюдается начальный рост, затем - плато, и ещё один участок роста. В случае сдвиговой деформации при дальнейшем растяжении сила реакции падает. Величина силы реакции растет с ростом скорости растяжения.
Молекулярные механизмы сдвиговой деформации и продольной деформации одной из цепей (рис. 8) оказываются сходными, несмотря на то, что в первом случае нагрузка приложена к концам разных цепей, а во втором - к концам одной цепи (рис. 6). Вначале происходит расплетание суперспирали как целого и разворачивание витков -спиралей около концов цепей, к которым приложена нагрузка. Затем начинается разворачивание витков внутри -спиральных участков. После того, как все -спиральные витки (кроме витков на концах цепей, свободных от нагрузки) развёрнуты, удлинение молекулы происходит за счёт дополнительного растяжения участков цепей, уже потерявших -спиральную конформацию. Существенно, что в случае сдвиговой деформации цепи не смещаются друг относительно друга, пока полностью не растянутся. Только после этого начинается их проскальзывание.
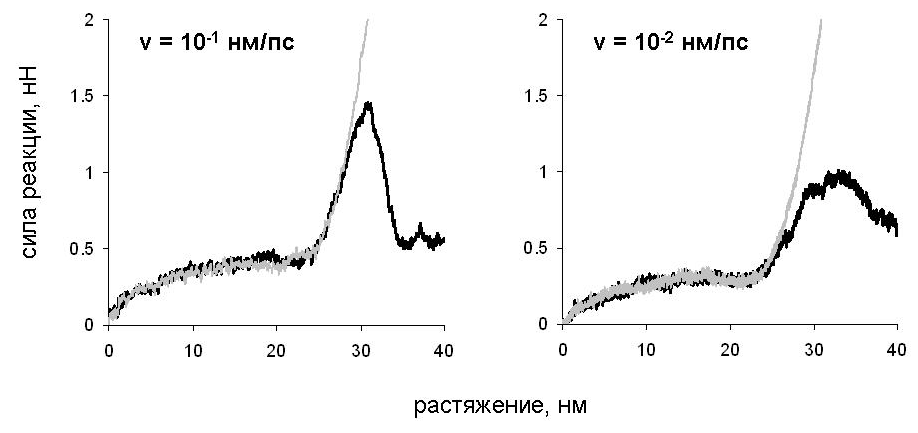
Рис. 7 Зависимость силы реакции от растяжения при сдвиговой деформации (чёрные кривые) и продольной деформации цепи А (серые кривые).
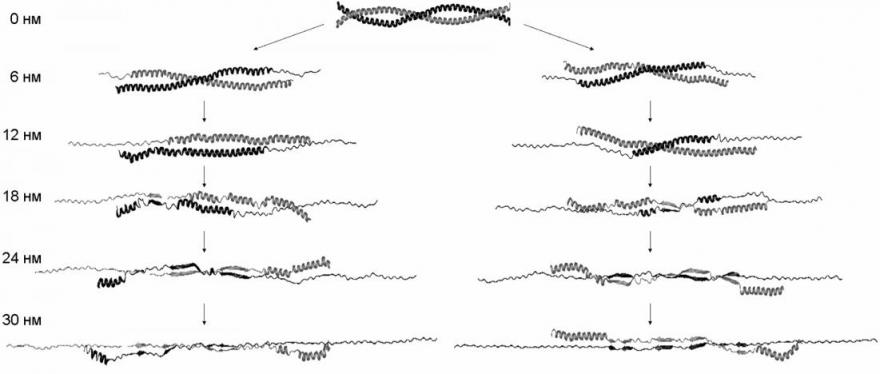
Рис. 8. Структуры молекулы миозина, наблюдаемые при различных степенях растяжения при сдвиговой деформации (слева) и продольной деформации цепи A (справа). -спирали показаны широкими изогнутыми кривыми, -структура – широкими прямыми, развёрнутые части цепей – тонкими прямыми.
Наблюдаемые структурные изменения в молекуле миозина и зависимость силы реакции от растяжения связаны с разрывом первоначальных и появлением новых внутри- и межцепных гидрофобных контактов и водородных связей (рис. 9). При расплетании суперспирали по всей длине молекулы разрываются гидрофобные контакты, которые в нативной структуре соединяли цепи. Поэтому сила реакции в начале деформации растёт (рис. 7). Затем, когда суперспираль расплетена и начинается разворачивание витков внутри -спиралей, происходит разрыв внутрицепных водородных связей. Поскольку для разворачивания каждого витка требуется примерно одинаковая работа, на зависимости силы реакции от растяжения наблюдается плато. Одновременно с этим в центральной области молекулы возникают новые межцепные гидрофобные контакты и водородные связи. Последние формируют элементы -структуры между развёрнутыми участками цепей, оказавшимися друг напротив друга (рис. 8). Отметим, что формирование -структуры при растяжении суперспирального белка наблюдалось экспериментально в работе Kreplak et al. (2004). В случае сдвиговой деформации межцепные контакты не позволяют цепям разделиться до тех пор, пока они не будут полностью растянуты, что приводит к росту силы реакции при растяжении цепей и к уменьшению силы реакции после начала проскальзывания цепей и уменьшения количества межцепных контактов.
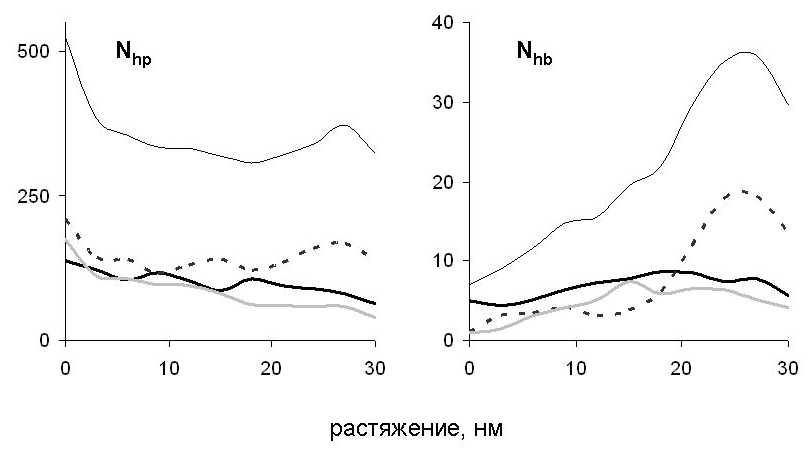
Рис. 9. Зависимость количества гидрофобных контактов Nhp и водородных связей Nhb между цепями от величины растяжения при сдвиговой деформации (для продольной деформации цепи А графики аналогичны). Тонкая чёрная кривая соответствует всей молекуле, толстая чёрная кривая остаткам с номерами 1-42, пунктир - остаткам 43-84, толстая серая кривая – остаткам с номерами 85-126.
Поперечная деформация миозина. Моделирование деформации суперспирали миозина в поперечном направлении проводилось при трех скоростях растяжения: 10-1, 10-2 и 10-3 нм/пс. Оказалось, что механизм поперечной деформации существенно зависит от скорости растяжения.
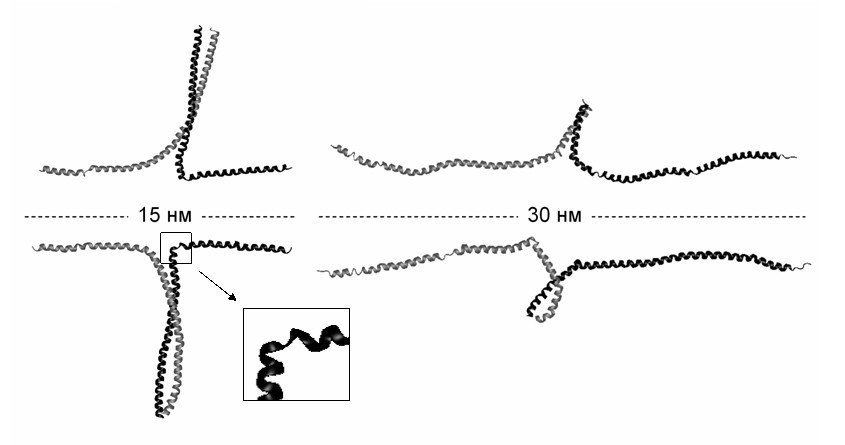
Рис. 10. Структуры молекулы миозина, наблюдаемые при поперечном растяжении со скоростью 10-1 нм/пс. Нагрузка приложена к N-концам (вверху), к C-концам (внизу).
При наибольшей из рассмотренных скоростей растяжения 10-1 нм/пс наблюдается последовательное разделение цепей без разворачивания -спиралей (рис. 10). В ходе деформации спирали изгибаются, и в них образуются участки, в которых несколько расположенных подряд спиральных витков разрушены. Эти участки играют роль «шарниров», вокруг которых спираль ломается. В ходе дальнейшей деформации такие изломы могут «залечиваться».
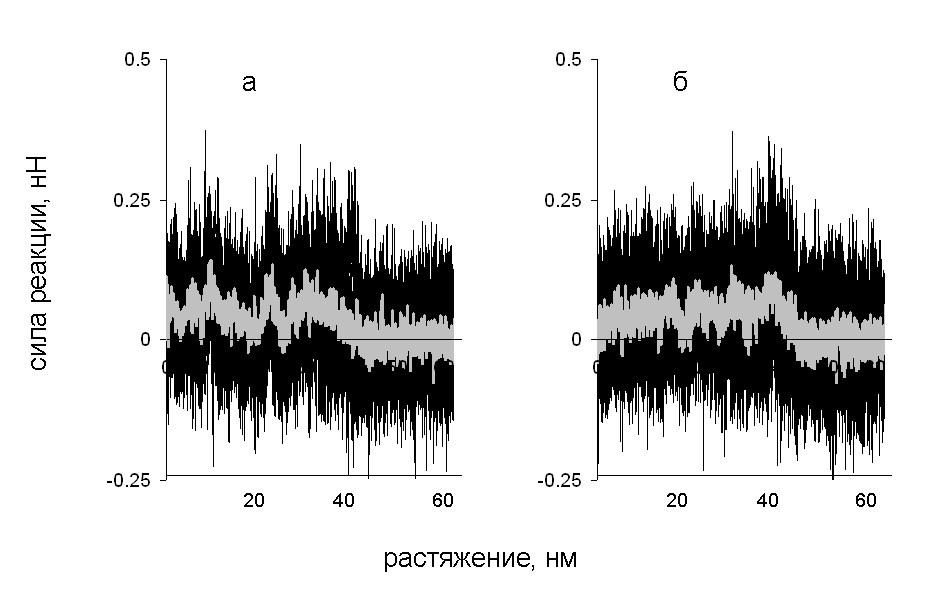
На зависимости силы реакции от растяжения, показанной (рис. 11) имеются два участка: плато при значениях растяжении меньших, чем 40 нм, и нулевое значение силы реакции при больших значениях растяжения. Поскольку при разделении каждой пары витков из соседних цепей совершается примерно одинаковая работа, на зависимости силы реакции от растяжения наблюдается плато. Полное разделение цепей происходит, когда расстояние между концами двух цепей, к которым приложена нагрузка, достигает 40 нм. При этом сила реакции уменьшается до нуля. Механизм деформации не зависит от того, к какой паре концов цепей приложена нагрузка.
Рис. 11. Зависимость силы реакции от растяжения при поперечной деформации со скоростью 10-1 нм/пс. Нагрузка приложена к N-концам (а) и к C-концам (б) цепей.
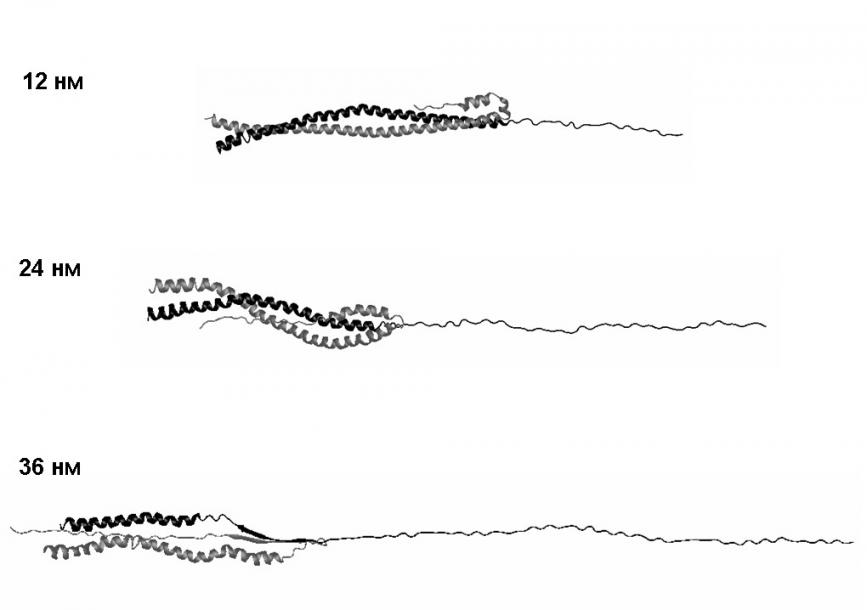
Рис. 12. Структуры молекулы миозина при поперечном растяжении со скоростью 10-3 нм/пс.
При наименьшей из рассмотренных скоростей растяжения 10-3 нм/пс наблюдается другой «сценарий» поперечной деформации (рис. 12). Сразу после начала разделения суперспирали на две -спирали одна из них растягивается, а вторая загибается, растягивается и вступает в контакт с частью молекулы, сохранившей суперспиральную структуру. При дальнейшем растяжении продолжается разделение цепей: одна из них проскальзывает вдоль постепенно уменьшающейся суперспиральной части макромолекулы, а другая растягивается в начальном направлении; одна цепь как бы «сдирается» с другой. В процессе растяжения между развёрнутым участком цепи и суперспиральной частью молекулы возникают гидрофобные контакты и водородные связи (рис. 13). При проскальзывании развёрнутой части молекулы относительно суперспиральной части эти контакты разрываются и снова возникают с другими партнёрами.
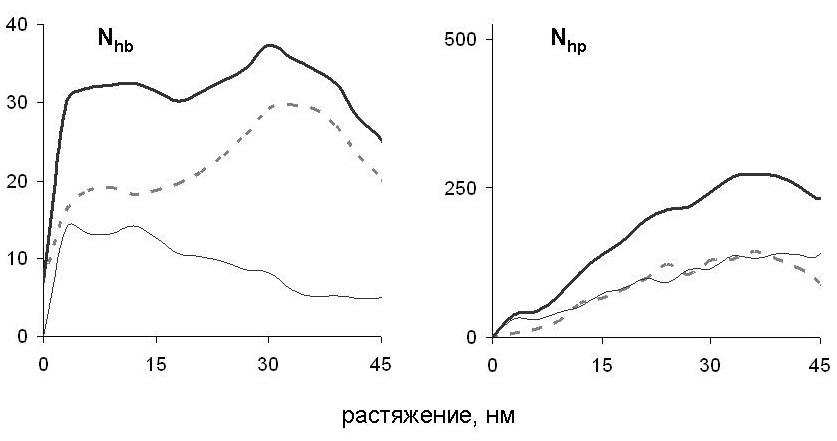
Рис. 13. Зависимость числа водородных связей Nhb и гидрофобных контактов Nhp между развёрнутым участком цепи и суперспиральной частью миозина от растяжения. Показано взаимодействие цепи с собой (тонкая линия), с другой цепью (пунктир) и общее число взаимодействий (широкая линия).
Зависимость силы реакции от растяжения при таком механизме показана рис. 14. Сначала сила реакции растет, а затем падает. Такое поведение связано с изменением числа межцепных контактов на разных стадиях растяжения. Сначала число контактов растет (рис. 13), поскольку удлиняется развернутая цепь, которая контактирует со все большим участком суперспирали (рис. 12).
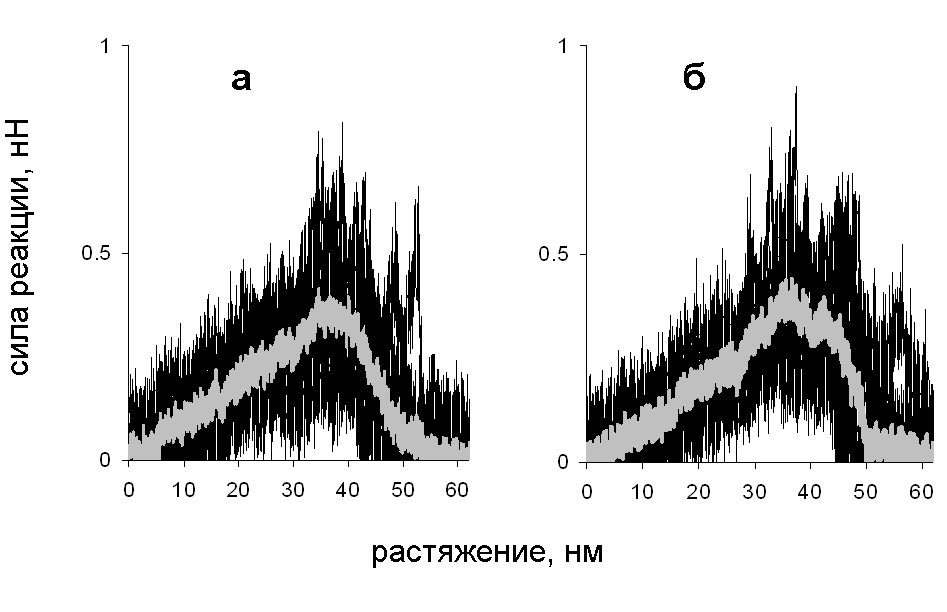
Рис. 14. Зависимость силы реакции от растяжения при поперечной деформации со скоростью растяжения 10-3 нм/пс: (а) нагрузка приложена к N-концам цепей, (б) нагрузка приложена к C-концам цепей.
При проскальзывании развёрнутого участка цепи вдоль суперспиральной части молекулы все контакты разрываются одновременно, поэтому сила реакции при проскальзывании растет с ростом длины области, на которой участки молекулы контактируют. На некотором этапе развёрнутый участок цепи становится длиннее, чем остаток суперспирали, и при дальнейшем проскальзывании цепи вдоль суперспирали число контактов между ними начинает уменьшаться, что приводит к уменьшению силы реакции. Аналогичные графики зависимости силы реакции от растяжения наблюдались в эксперименте по поперечному растяжению суперспиральных белков в работах Bornschlgl et al. (2006, 2009).
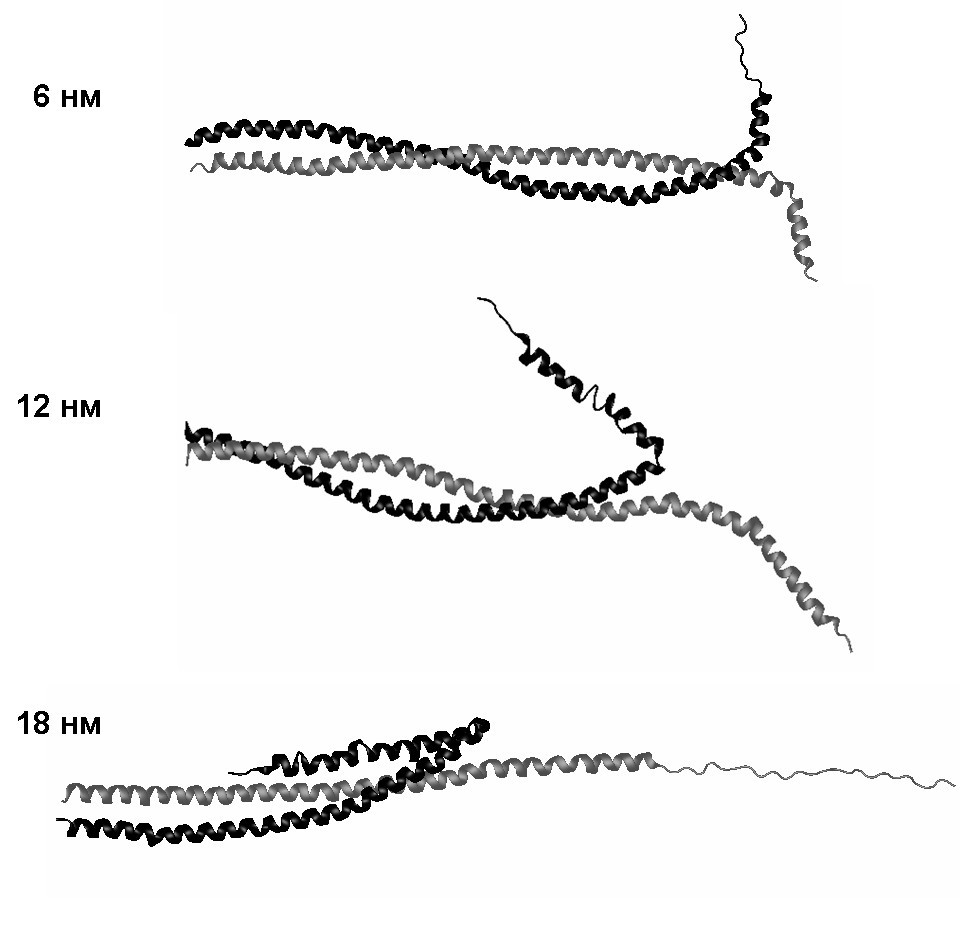
При растяжении со скоростью 10-2 нм/пс реализуется промежуточный механизм деформации (рис. 15). Cначала разделяются неразвёрнутые -спирали, как при растяжении со скоростью 10-1 нм/пс. Затем одна из этих -спиралей вступает в контакт с суперспиральной частью молекулы и далее протягивается вдоль неё, как при скорости растяжения 10-3 нм/пс.
Рис. 15. Структуры молекулы миозина, наблюдаемые при поперечном растяжении со скоростью 10-2 нм/пс.
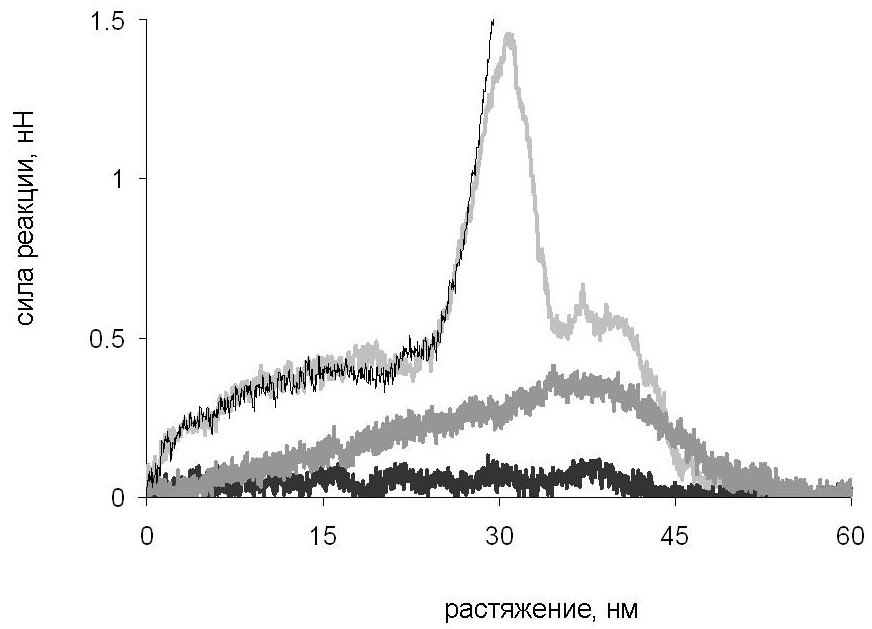
Сравнение сопротивляемости суперспирали растяжению в различных направлениях. Результаты такого сравнения представлены на рис. 16. Из него видно, что суперспираль сопротивляется сдвиговой деформации и продольному растяжению одной из цепей значительно сильнее, чем поперечному растяжению.
Рис. 16. Зависимость силы реакции от растяжения для сдвиговой деформации (тонкая серая кривая), продольной деформации цепи A (тонкая чёрная кривая), для поперечной деформации при последовательном разделении цепей (чёрная кривая) и при образовании контакта между развёрнутой и суперспиральной частями молекулы (серая кривая).
ВЫВОДЫ
1. Проведённое компьютерное моделирование процесса растяжения молекул глобулярного и фибриллярного белков позволило установить механизмы их деформации при растяжении в различных направлениях. Показано, что механические свойства белковых макромолекул обоих типов анизотропны: сопротивляемость молекулы глобулярного белка деформации в различных направлениях растяжения различается более чем в 2 раза, сопротивляемость молекулы фибриллярного белка растяжению вдоль оси суперспирали выше, чем сопротивляемость поперечному растяжению, более чем в 3 раза.
2. Показано, что для молекулы глобулярного белка результаты моделирования, полученные с помощью упрощенной модели объединённых атомов, согласуются с результатами, полученными на основе более детальной полноатомной модели, а также с экспериментальными результатами. С использованием обеих моделей показано, что разворачивание молекулы начинается в пространственной близости от точек приложения нагрузки, а наиболее стабильными элементами молекулярной структуры являются -спираль и -шпилька.
3. Установлено, что у молекул глобулярного белка направление с наименьшей степенью сопротивления растяжению и «координата реакции» спонтанного разворачивания не обязательно совпадают.
4. Показано, что молекулярный механизм продольной деформации белковой суперспирали включает три этапа. На первом этапе происходит расплетание суперспирали и разворачивание -спиральных витков на концах цепей, на втором - разворачивание витков внутри обеих спиралей; на третьем - растяжение уже развернутых участков цепей. Между развёрнутыми участками цепей образуются новые гидрофобные контакты и водородные связи, не позволяющие цепям разделиться до того, как они оказываются полностью растянуты.
5. Показано, что механизм поперечной деформации белковой суперспирали зависит от скорости растяжения. При скоростях, превышающих 10-2 нм/пс, разделение -спиралей происходит без их взаимодействия с суперспиральной частью молекулы. При меньших скоростях растяжения развёрнутый участок одной из цепей взаимодействует с неразрушенной частью суперспирали, что повышает сопротивляемость молекулы механической нагрузке, приложенной перпендикулярно оси суперспирали.
СПИСОК РАБОТ, ОПУБЛИКОВАННЫХ ПО ТЕМЕ ДИССЕРТАЦИИ
Статьи:
- Фалькович С.Г., Неелов И.М., Даринский А.А. Механизм продольной деформации суперспирали миозина. Компьютерное моделирование // Высокомолекулярные соединения. A. 2010. Т. 52. №6. С. 662–670.
- Falkovich S.G., Darinskii A.A., Balabaev N.K., Neelov I.M. Simulation of the Mechanical Unfolding of the Ubiquitin by Pulling in Different Directions with Constant Speed // Macromolecular Symposia. 2009. V. 278. №1. P. 105-113.
Тезисы докладов:
- Neelov I.M., Falkovich S.G., Darinskii A.A. Computer simulation of mechanical properties of macromolecules with different secondary structure in single molecule AFM experiments // EPF09, European Polymer Congress. Graz, Austria. July 2009. P. 54.
- Neelov I.M., Falkovich S.G., Darinskii A.A., Balabaev N.K. Mechanical anisotropy of coiled-coil polymer structure in single molecule AFM. Computer simulation // International Symposium "Frontier in Polymer Science". Mainz, Germany. June 2009. P. 169.
- Neelov I.M., Falkovich S.G., Neelov A.I., Balabaev N.K., Darinskii A.A. Computer simulation of viscoelastic properties of coarse-grained model of macromolecule in single molecule AFM experiments // International Symposium "Frontier in Polymer Science". Mainz, Germany. June 2009. P. 67.
- Falkovich S.G., Balabaev N.K., Neelov I.M., Darinskii A.A. Simulation of a mechanical unfolding of ubiquitin: comparison of models and approaches // 4th Saint-Petersburg Young Scientists Conference "Modern problems of polymer science". Book of abstracts. April 2008. P. 41.
- Falkovich S.G., Neelov I.M., Darinskii A.A. Longitudial deformation of protein superhelix // 5th Saint-Petersburg Young Scientists Conference "Modern problems of polymer science". October 2009. Book of abstracts. P. 73.
- Фалькович С.Г., Неелов И.М., Даринский А.А. Продольное растяжение суперспирализованного белка миозина. Компьютерное моделирование. // 1-ая международная научная школа "Наноматериалы и нанотехнологии в живых системах". Июнь 2009. С. 118.
Бесплатно
Автореферат отпечатан в ИВС РАН. Ризография
Тираж 100 экз.

