Разделение и глубокая очистка веществ кристаллизационными методами
На правах рукописи
МАЛЫШЕВ ВЛАДИМИР МИХАЙЛОВИЧ
РАЗДЕЛЕНИЕ И ГЛУБОКАЯ ОЧИСТКА ВЕЩЕСТВ
КРИСТАЛЛИЗАЦИОННЫМИ МЕТОДАМИ
Специальность 02.00.04 – Физическая химия
(химические науки)
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
доктора химических наук
Нижний Новгород – 2012
Работа выполнена на кафедре «Физика и технология материалов и компонентов электронной техники» Нижегородского государственного технического университета им. Р. Е. Алексеева.
Научный консультант: доктор химических наук, профессор.
Воротынцев Владимир Михайлович
Официальные оппоненты: Гринберг Евгений Ефимович
доктор химических наук, профессор
Государственный научно-исследовательский институт химических реактивов и особо
чистых веществ, заместитель директора.
Князев Александр Владимирович
доктор химических наук, доцент
Нижегородский государственный университет им. Н.И. Лобачевского, профессор.
Кутьин Александр Михайлович
доктор химических наук,
Институт химии высокочистых веществ им. Г.Г. Девятых РАН, ведущий научный сотрудник.
Ведущая организация: Учреждение Российской академии наук
Ордена Трудового Красного Знамени
Институт нефтехимического синтеза
им. А. В. Топчиева РАН
Защита состоится « 15 » марта 2013 г. в 1330 часов на заседании диссертационного совета Д 212.165.06 при Нижегородском государственном техническом университете им. Р. Е. Алексеева по адресу:
603950, г. Нижний Новгород, ул. Минина, д. 21.
С диссертацией можно ознакомиться в библиотеке Нижегородского государственного технического университета им. Р. Е. Алексеева.
Автореферат разослан « 29 » января 2013 г.
Ученый секретарь совета Соколова Т.Н.
Общая характеристика работы
Актуальность проблемы. Для разделения и очистки веществ, в различных отрослях промышленности широко применяются двухфазные дистилляционные и кристаллизационные методы. Кристаллизационные методы имеют ряд преимуществ перед дистилляционными методами. Они менее энергоемки, так как теплота плавления веществ, как правило, ниже теплоты испарения, проводятся при более низких температурах, а, следовательно, меньше загрязнение очищаемых веществ материалом аппаратуры.
Среди традиционных методов кристаллизации из расплава наиболее перспективным является метод противоточной кристаллизации. Однако, несмотря на большие потенциальные возможности этого метода, имеется ряд причин, которые сдерживают его использование для очистки веществ. К ним прежде всего следует отнести явление укрупнения кристаллов, движущихся в кристаллизационной колонне, снижающее эффективность процесса очистки. Существующие в настоящее время методы, предотвращающие укрупнение кристаллов – малоэффективны.
В очищаемых кристаллизационными методами веществах кроме примесей, растворенных в молекулярной форме, присутствуют субмикронные, в том числе и наноразмерные частицы, которые для ряда применений, особенно в оптике, лимитируют качество получаемых веществ. Источником наноразмерных частиц могут быть малорастворимые примесные компоненты, материал аппаратуры, попадающий в основное вещество в результате трения ее частей и самопроизвольного диспергирования твердых тел в жидкости.
Взвешенные наноразмерные частицы вносят существенный вклад в суммарное содержание примесей при получении высокочистых веществ с их содержанием на уровне 10-6 – 10-8 %. При очистке и разделении веществ кристаллизационными методами было изучено поведение только макро- и микрочастиц, поведение же примесей в виде наноразмерных взвешенных частиц практически не исследовалось. В связи с этим остался открытым и требующим ответа вопрос об эффективности кристаллизационных методов при очистке от взвешенных наноразмерных частиц.
Для расширения номенклатуры очищаемых веществ и возможности использования кристаллизационных методов для глубокой очистки веществ в газовой фазе представляет интерес использование кристаллизационного метода, основанного на перераспределении компонентов газовой смеси при образовании газовых гидратов.
Процесс газогидратной кристаллизации может протекать при температурах около 0°С и невысоких давлениях. Он обеспечивает высокую эффективность, безопасность и экологичность процесса разделения и очистки при сравнительно низких энергетических затратах по сравнению с традиционными методами. Однако реальное использование метода газогидратной кристаллизации в большинстве случаев затрудняется отсутствием данных о коэффициентах распределения в системе газ – газовый гидрат. Отсутствуют методы расчета, позволяющие заранее оценить эффективность разделения и очистки исследуемых веществ.
Таким образом, широкое использование кристаллизационных методов разделения и очистки веществ сдерживается отсутствием физико-химических данных, обеспечивающих повышение эффективности очистки и возможности реализации в различных двухфазных системах. Совершенствование кристаллизационных методов включает модернизацию традиционных кристаллизационных методов, повышение их эффективности, увеличение количества удаляемых примесей, разработку новых методов очистки и расширение круга очищаемых веществ, в том числе и веществ в газовой фазе. Поэтому настоящая работа посвящена получению физико – химических характеристик, позволяющих эффективно управлять кристаллизационными методами для повышения их возможностей в процессе разделения и очистки веществ, расширять номенклатуру очищаемых веществ.
Следовательно, разработка новых эффективных кристаллизационных методов разделения и глубокой очистки газовых смесей, повышение эффективности традиционных кристаллизационных методов, а также расширение круга удаляемых примесей в виде наноразмерных частиц, является актуальным направлением развития современных отраслей науки и техники.
Цель диссертационной работы:
Целью настоящей работы является определение физико – химических характеристик разделения и очистки веществ, направленных на создание новых кристаллизационных методов для разделения и очистки газовых смесей, повышение эффективности традиционных кристаллизационных методов и расширение круга удаляемых примесей, в том числе и наноразмерных частиц. В соответствие с поставленной целью работа включает :
- Теоретическое и экспериментальное определение влияния изменения размеров кристаллов на эффективность очистки веществ в противоточной кристаллизационной колонне в процессе механического воздействия на систему кристалл - расплав.
- Разработку физико-химической модели для расчета распределения примеси по высоте кристаллизационной колонны в зависимости от размера кристаллов.
- Разработку физико-химической модели перехода наноразмерных частиц в кристалл в процессе его роста с учетом их диффузионной подвижности в расплаве.
- Теоретическая оценка и экспериментальное подтверждение скорости перехода частиц в зависимости от условий роста кристаллов в процессе направленной кристаллизации.
- Разработку физико-химической модели для расчета эффективности очистки жидкостей от наноразмерных взвешенных частиц методом противоточной кристаллизации в зависимости от доли перекристаллизовавшегося расплава.
- Установление распределения примесей между газовым гидратом и газовой фазой.
- Метод расчета коэффициентов распределения примесей между твердой и газовой фазами в процессе газогидратной кристаллизации.
- Методику экспериментального определения коэффициентов распределения примесей в процессе газогидратной кристаллизации.
- Физико-химическую модель для расчета зависимости концентрации примеси в газовой смеси от доли закристаллизовавшегося вещества;
- Теоретическое и экспериментальное определение эффективности очистки веществ в процессе газогидратной кристаллизации.
Научная новизна
- Впервые установлено повышение эффективности очистки жидкостей методом противоточной кристаллизации из расплава в результате изменения распределения кристаллов по размерам в процессе механического воздействия на систему кристалл - расплав.
- Определено влияние условий измельчения на распределение кристаллов по размерам и зависимость степени измельчения кристаллов от концентрации примеси в интервале 10-2 - 10-5 % масс. Получено уравнение для расчета изменения размера кристаллов в зависимости от природы вещества.
- Разработана физико – химическая модель перехода наноразмерных частиц из расплава в кристалл. Определено влияние условий роста кристаллов и диффузионной подвижности частиц на скорость их перехода из расплава в кристалл.
- Разработана физико – химическая модель распределения наноразмерных частиц в процессе противоточной кристаллизации из расплава и определено влияние доли перекристаллизовавшейся жидкости на эффективность очистки от примесей.
- Предложена методика расчета коэффициента распределения примесей при образовании газовых гидратов. Изучено влияние параметров гидратообразования на коэффициент распределения.
- Разработана методика экспериментального определения коэффициентов распределения примесей в процессе газогидратной кристаллизации. Показана возможность использования данных о равновесном коэффициенте распределения компонентов газовой смеси в системе газ - газовый гидрат для определения параметров межмолекулярного взаимодействия.
- Разработана математическая модель процесса газогидратной кристаллизации. Получены аналитические выражения, описывающие перераспределение компонентов смеси между газовой и твердой фазами в процессе непрерывной и дискретной газогидратной кристаллизации.
Практическая значимость работы
- Получены уравнения, позволяющие рассчитать эффективность очистки веществ в процессе противоточной кристаллизации в зависимости от доли перекристаллизовавшегося расплава.
- Впервые на основе теоретических и экспериментальных данных показана возможность использования механического измельчения кристаллов в противоточной кристаллизационной колонне при глубокой очистке веществ на примере очистки агрессивных веществ с низкой (до - 40 оС) и высокой (100 - 1500С) температурой плавления. Получены бензол, тетрахлориды титана и углерода, диэтилцинк и сера, удовлетворяющие требованиям, предъявляемым к веществам для микроэлектроники и волоконной оптики.
- Получены уравнения, позволяющие рассчитать коэффициенты распределения наноразмерных частиц между твердой и жидкой фазами в зависимости от условий роста кристалла.
- Впервые на основе теоретических и экспериментальных данных показана высокая эффективность очистки жидкостей от наноразмерных частиц (размером 50 – 350 нм) методом противоточной кристаллизации из расплава.
- Разработана методика расчета условий образования и коэффициентов распределения примесей между твердой и газовой фазами в процессе газогидратной кристаллизации.
- Разработана методика расчета эффективности очистки газов методом газогидратной кристаллизации в зависимости от условий процесса (температура, давление, скорость потоков и доля закристаллизовавшегося вещества).
- Разработана комплексная технологическая схема получения высокочистого гексафторида серы, которая состоит из трех стадий: газогидратная кристаллизация, криофильтрация и низкотемпературная дистилляция. Качество целевого продукта, полученного по предложенной схеме, соответствует требованиям зарубежных и отечественных стандартов для микроэлектроники.
Основные результаты и положения, выносимые на защиту:
- Физико – химические основы механизма изменения распределения кристаллов по размерам в противоточной кристаллизационной колонне при механическом воздействии на систему кристалл – расплав.
- Система уравнений для расчета распределения концентрации примеси по высоте противоточной кристаллизационной колонны при изменении размера кристаллов и доли перекристаллизовавшейся жидкости.
- Физико – химическая модель перехода наноразмерных частиц из расплава в кристалл. Экспериментальные и теоретические данные по распределению наноразмерных частиц в системе расплав – кристалл.
- Система уравнений для расчета поведения наноразмерных частиц в процессе противоточной кристаллизации из расплава. Экспериментальные и теоретические данные о распределении наноразмерных частиц по высоте противоточной кристаллизационной колонны.
- Метод расчета и экспериментального определения коэффициента распределения примесей между газом и газовым гидратом в многокомпонентной газовой смеси.
- Экспериментальные и расчетные данные по фазовому равновесию в системе газ – газовый гидрат для благородных газов, летучих фторидов и гидридов веществ.
- Метод для определения параметров межмолекулярного взаимодействия по данным о равновесном коэффициенте распределения компонентов газовой смеси в системе газ - газовый гидрат.
- Физико – химические модели трех типов процесса газогидратной кристаллизации, позволяющие рассчитать зависимость концентрации примеси в газовой фазе от параметров процесса и доли закристаллизовавшегося вещества.
- Противоточная кристаллизационная колонна с механическим воздействием на кристаллы для очистки химически агрессивных веществ и комплексная технологическая схема производства высокочистого гексафторида серы, включающая три стадии: газогидратную кристаллизацию, низкотемпературную криофильтрацию и низкотемпературную дистилляцию.
Личный вклад автора: обоснование и постановка теоретических и экспериментальных исследований, разработка физико-химических моделей, разработка аппаратуры и методик экспериментальных исследований, участие в получении экспериментального материала, анализе и систематизации расчетных и экспериментальных данных, формулировании выводов и положений, разработке комплексной технологической схемы производства гексафторида серы.
Апробация работы. Результаты работы докладывались и обсуждались на ряде Всесоюзных, Всероссийских и Международных научных конференциях в период с 1985 по 2011 гг.
VIII, IX, X, XI Конференции по химии высокочистых веществ. Горький, 1985 и 1988, Н. Новгород, 1995, 2000
III и IV Всесоюзные конф. по массовой кристаллизации и кристаллизационным методам разделения, Черкассы, 1985 и Иваново, 1990.
Х Международный симпозиум по промышленной. кристаллизации, ЧССР, Бехине, 1987.
VIII Всесозная конференция по росту кристаллов, Харьков, 1992
XI International Conf. On Crystal Grouth, Hague, the Netherland, 1995
2nd International Conf. on Natural Gas Hydrates, Toulouse, 1996
Всерос. науч. конференции «Мембраны-98», Москва, 1998
The 13 International Conference of Crystal Growth in Conjunction with The Eleventh International Conference on Vapor Growth and Epitaxy, 30 July – 4 August 2001. – Kyoto.
Международная научная конференция "Кристаллизация в наносистемах", 2002 г., Иваново
XVII, XIX Менделеевские съезды по общей и прикладной химии. Казань, 2003 г., Волгоград, 2011 г.
14 International Conference of Crystal Growth, Grenoble, 2004
16-th Symposium of Industrial Crystallization, Dresden, Germany, 2005
Ш, IV, VI Международные конференции “Кинетика и механизм кристаллизации”. Иваново, 2004 г., 2006 и 2010 г.
XII, XIV Конференции “Высокочистые вещества и материалы. Получение, анализ, применение.” Н. Новгород, 2004, 2011 г.
Публикации. Основные результаты диссертации опубликованы в 28 статьях в научных журналах и изданиях, из них 26 – в рецензируемых российских журналах, а так же в 30 тезисах докладов на российских и международных конференций. По результатам работы получено 1 авторское свидетельство, опубликована одна монография.
Структура и объем работы. Диссертация состоит из 6 глав, введения, заключения, списка литературы. Содержание диссертации изложено на 350 страницах машинописного текста, включает 60 рисунков и 40 таблиц. Список литературы содержит 300 наименований.
СОДЕРЖАНИЕ ДИССЕРТАЦИИ
Глава 1. Литературный обзор
Кристаллизационные методы, включающие в себя методы направленной кристаллизации, зонной плавки, противоточной кристаллизации, используются для разделения и глубокой очистки веществ и имеют ряд преимуществ, например, перед дистилляционными методами.
В литературном обзоре рассматриваются существующие теории процесса направленной и противоточной кристаллизации из расплава, основанные на различных механизмах массообмена между твердой фазой и расплавом. Показано, что имеется ряд причин, которые сдерживают использование метода противоточной кристаллизации для глубокой очистки веществ на практике. К ним прежде всего следует отнести явление укрупнения кристаллов, движущихся в кристаллизационной колонне. Поэтому представляет большой научный и практический интерес разработка способов уменьшения размера кристаллов и оценка их влияния на эффективность очистки и разделения веществ.
В очищаемых веществах кроме примесей, растворенных в молекулярной форме, присутствуют наноразмерные частицы. Они также могут образовываться и в противоточной кристаллизационной колонне в результате трения ее движущихся частей. Обзор литературных данных показал, что только для микрочастиц ( размером 1 мкм) теоретически и экспериментально изучено их поведение в процессе направленной кристаллизации. Влияние наноразмерных частиц на эффективность очистки веществ методом направленной кристаллизации и противоточной кристаллизации из расплава не исследовалось.
Приведены имеющиеся в литературе сведения об условиях образования газовых гидратов, их структуре, областях применения, математические модели, позволяющие рассчитывать переход газа в газовый гидрат и давление паров воды над его поверхностью. Однако в литературе отсутствуют описания методик экспериментального и теоретического определения коэффициентов распределения примеси между газовой фазой и газовым гидратом, отсутствуют математические модели, позволяющие рассчитывать эффективность очистки газов методами газогидратной кристаллизации с использованием наноразмерной фазы в двухфазных методах разделения и глубокой очистки газов.
Таким образом, для инновационного развития технологий получения высокочистых веществ представляет интерес разработка физико – химических основ глубокой очистки и разделении веществ для создания эффективных кристаллизационных методов, позволяющих расширить круг очищаемых веществ и удаляемых из них примесей.
Глава. 2. Глубокая очистка веществ методом противоточной кристаллизации из расплава с механическим измельчением
кристаллов
Более широкое использование метода противоточной кристаллизации из расплава сдерживается его малой эффективностью, обусловленной укрупнением кристаллов при их движении по колонне. Рассмотрим влияние размеров кристаллов на эффективность разделения и очистки веществ в противоточной кристаллизационной колонне и возможности ее повышения.
В известной диффузионной модели уравнение, описывающее распределение примеси по высоте противоточной кристаллизационной колонны для безотборного режима, имеет вид:
, ( 1 )
где D =DT zк / LTR2 - приведенный коэффициент диффузии, a и o – постоянные коэффициенты, определяемые из граничных условий; LТ - скорость потока твердой фазы, DТ - коэффициент диффузии примеси в твердой фазе, zк - высота колонны.
Из анализа уравнений (1) следует, что распределение примеси по высоте колонны должно быть экспоненциальным, если все параметры, входящие в него, остаются постоянными в процессе работы колонны. Однако в экспериментах на примере очистки бензола от тиофена и стильбена от азобензола было показано, что реальная эффективность очистки ниже рассчитанной по уравнению (1), а распределение примеси по высоте колонны существенно отличается от экспоненциального. При этом средний размер кристаллов увеличивается при их прохождении от кристаллизатора к плавителю.
Из – за укрупнения кристаллов при их движении по колонне, дальнейшее увеличение высоты разделительной секции не приводит к существенному повышению эффективности очистки веществ, как это следует из уравнения (1).
Исследованные в настоящее время методы предотвращения укрупнения кристаллов – малоэффективны и не позволили решить проблему роста кристаллов в колонне, так как они приводят либо к нарушению условий разделения (ультразвук, температурное поле), либо к дополнительному продольному перемешиванию твердой фазы и расплава (механическое измельчение). Нами разработан способ изменения размеров кристаллов без уменьшения доли твердой фазы, нарушения температурного режима в колонне и без дополнительного перемешивания расплава. Наилучшие результаты были достигнуты при механическом измельчении кристаллической фазы, основанном на комбинированном воздействии давления и сдвиговой деформации. Данный способ изменения размеров кристаллов отличается малой энергоемкостью и высокой эффективностью измельчения. В этом способе почти вся подводимая энергия расходуется на образование новых поверхностей. Кроме того, измельчение возможно при малых скоростях вращения, что снижает возможность загрязнения разрушаемого материала и уменьшает перемешивание расплава. После измельчения кристаллической фазы, наблюдается уменьшение среднего размера кристаллов и распределение кристаллов становится более монодисперсным.
В работе для характеристики процесса измельчения кристаллов при глубокой очистке веществ использован параметр К, равный отношению площади поверхности контакта фаз до (S0) и после (S1) измельчения.
Рассмотрим модель для расчета степени измельчения кристаллической фазы. Работа всех сил, необходимых для измельчения кристалла запишется в виде:
, (2)
где k V = Аg - работа упругого деформирования разрушаемого материала, k - коэффициент пропорциональности, равный работе деформирования единицы объема твердого тела, V - изменение объема разрушаемого материала, q S = Ап - работа образования новой поверхности, q - коэффициент пропорциональности, равный работе, затрачиваемой на образование единицы новой поверхности твердого тела, S - вновь образованная поверхность.
Уравнение (2) представляет собой математическую запись обобщенного закона Ребиндера. Первое слагаемое в нем определяет работу упругого деформирования разрушаемого материала и следует из закона Кирпичева-Кика. Второе слагаемое определяет работу, необходимую на образование новой поверхности, и следует из закона Реттингера.
При тонком измельчении, когда размер частиц исходного материала менее 3 – 5 мм, согласно гипотезе Реттингера, можно пренебречь работой деформации объема из-за ее относительной малости по сравнению с работой образования новой поверхности. Тогда, учитывая, что изменение поверхности измельчаемого материала пропорционально его начальной поверхности, после преобразования получим выражение для определения степени измельчения кристаллов в виде:
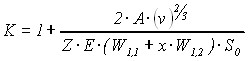, (3)
где Z - координационное число, Е - доля разрываемых связей на один атом, v - объем кристаллов, приходящийся на одну частицу основы,(1/v)- число частиц в 1 см3 кристалла, W1,1 - энергия взаимодействия атомов основного вещества, W1,2 - энергия взаимодействия атомов основного вещества с примесью, W1,i = H1,i / Z Na, Н1,I - энтальпия сублимации, Na – число Авогадро, x - концентрация примеси.
Как видно из уравнения (3) степень измельчения является функцией природы измельчаемого материала, концентрации в нем примеси, исходного дисперсного состава и подводимой на измельчение энергии.
Применительно к глубокой очистке веществ, т. е. в области концентрации примеси 10-2 % об. и ниже, величиной хW1,2 в уравнении (3) можно пренебречь. Тогда, уравнение для определения степени измельчения запишется в виде:
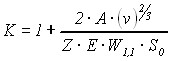. (4)
Экспериментальные исследования зависимости параметра К от концентрации примеси проводились на кристаллизационной колонне, состоящей из двух разделительных секций высотой 400 мм каждая и узла дробления кристаллов высотой 100 мм между ними. Дробитель представлял собой жернов, посаженный на вал шнека колонны и скользящий по неподвижной ступице.
Для исследуемой системы бензол-тиофен получена зависимость степени измельчения от концентрации примеси. В пределах ошибки эксперимента, степень измельчения остается постоянной величиной в интервале концентраций тиофена 10-2 - 10-5 % об. и равна 1,2. Подставляя данные по индивидуальным компонентам в уравнение (4), можно рассчитать значение энергии, необходимой для изменения площади поверхности кристаллов системы бензол – тиофен в 1,2 раза. Эта величина А=1,1.10-7 кдж/см3. Для данного измельчающего аппарата эта энергия является постоянной величиной. Зная значение А, можно рассчитать величину степени измельчения К для различных веществ.
В таблице 1 представлены значения степени измельчения, рассчитанные по уравнению (4) для ряда веществ, использующихся в технологии волоконно – оптических световодов и микроэлектронике.
Таблица 1
Экспериментально полученные и рассчитанные по уравнению (4)
значения степени измельчения.
| Система | Нсуб., кДж/моль | v, 1030 м3 | К рассч. | Кэксп. |
| CCl4 | 37,1 | 149 | 1,22 | 1,3 |
| TiCl4 | 52,7 | 155 | 1,16 | – |
| GeCl4 | 45,9 | 171 | 1,20 | – |
| POCl3 | 47,3 | 155 | 1,18 | – |
| C6H6 | 40,5 | 143 | 1,20 | 1,2 |
| C6H12 | 33,3 | 174 | 1,28 | 1,4 |
| Zn(C2H5)2 | 53,0 | 157 | 1,16 | – |
| Cd(CH3)2 | 43,8 | 117 | 1,16 | – |
Для проверки правильности методики расчета степени измельчения, было проведено ее экспериментальное определение для бензола, циклогексана и четыреххлористого углерода. Получено достаточно хорошее согласие между рассчитанными и экспериментально полученными значениями. Следовательно, уравнение (4) с достаточной точностью описывает процесс измельчения кристаллической фазы в противоточной кристаллизационной колонне. Из таблицы видно, что для различных веществ, степень измельчения изменяется не более чем на 10%. Таким образом, полученные результаты хорошо согласуются с литературными данными о подобии прочностных характеристик молекулярных кристаллов.
Из анализа уравнения (4) видно, что степень измельчения зависит от энергии, подводимой к измельчающему устройству. В предложенной конструкции измельчителя необходимая энергия определяется двумя величинами. Первая – это усилие пружины, которая прижимает активную часть измельчителя – жерновок к пассивной части – ступице. Для данного измельчающего аппарата эта величина является постоянной. Вторая – это скорость вращения жернова, жестко закрепленного на валу шнека колонны. Таким образом, степень измельчения кристаллической фазы будет зависеть от скорости вращения шнека колонны. Полученная экспериментально зависимость степени измельчения кристаллической фазы от скорости вращения шнека позволяет выбрать наиболее оптимальную скорость вращения шнека, при которой происходит максимальное увеличение площади поверхности массообмена. В дальнейшем, при глубокой очистке веществ методом противоточной кристаллизации из расплава, скорость вращения составляла 11 об/мин
Рассмотрим вопрос о распределении примеси по высоте кристаллизационной колонны, с учетом измельчения кристаллов механическим дробителем. Знание этой зависимости позволит рассчитать в какой мере увеличение высоты колонны с введением устройств для измельчения кристаллов будет влиять на ее разделительную способность.
Так как в дробителе имеет место измельчение кристаллов и интенсивное перемешивание твердой и жидкой фаз, то дробитель можно рассматривать как источник кристаллов для нижней секции кристаллизационной колонны. В этом случае, кристаллизационную колонну с измельчающим устройством можно представить, как состоящую из m последовательно соединенных кристаллизационных колонн. Так как фактор разделения каскада F, состоящего из m секций определяется как произведение факторов разделения для каждой секции Fi, то справедливо уравнение:
. (5)
Зависимости концентрации примеси в твердой и жидкой фазах и фактора разделения противоточной кристаллизационной колонны от размера кристаллов определяются уравнениями:
, (6)
, (7)
где Y() = y / yo,, F = Y(1), = Z / Zk, параметр 
,
D = DT Zk / (L Ro2), 1 находится как корень характеристического уравнения:
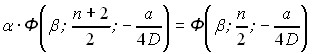, (8)
где n = 3 – для сферических, n = 2 – для цилиндрических и n = 1 – для пластинчатых кристаллов, Ф – вырожденная гипергеометрическая функция.
Подставляя уравнение (6), (7) в (5), получим выражение, описывающее распределение примеси по высоте колонны, состоящей из m секций, разделенных дробителями кристаллов
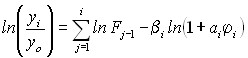, (9)
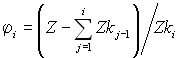, (10)
где i = 1 – m, Fo= 1, Zko= 0. Полученное уравнение (9) описывает распределение примеси по высоте кристаллизационной колонны с учетом механического измельчения кристаллов.
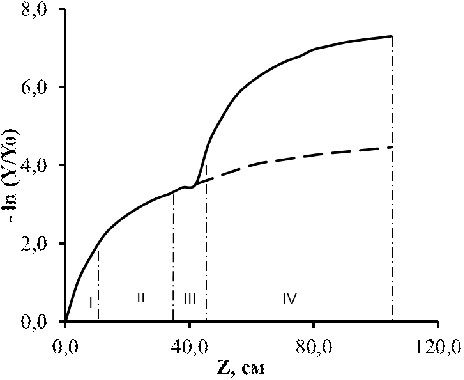
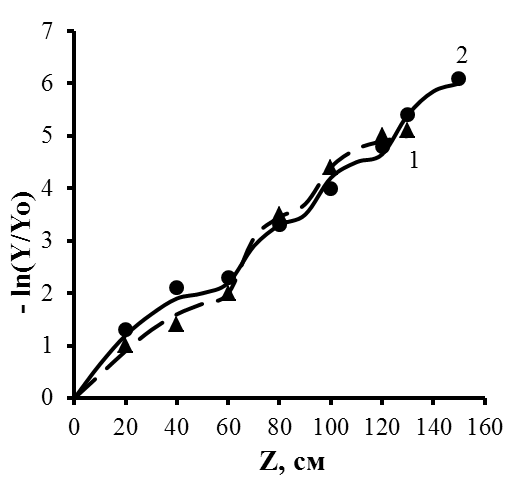
| Рис. 1. Распределение примеси по высоте кристаллизационной колонны. Модельная система бензол – тиофен. Концентрация тиофена 0,25 % об., L = 1,210-2 см/с, = 0,5, = 2,38. 1 – работа колонны с измельчителем; 2 – работа колонны без измельчителя. I – кристаллизатор, II – верхняя разделительная секция, III – дробитель, IV – нижняя разделительная секция. | Рис. 2. Распределение примеси по высоте кристаллизационной колонны с несколькими измельчителями кристаллов. Модельная система бензол – тиофен. Концентрация тиофена 0,25 % об. 1 – два измельчителя; 2 – три измельчителя |
Рассчитанные по уравнению (9) для m = 2 и экспериментально полученные значения концентрации примеси в различных точках по высоте колонны приведены на рис. 1 (кривая 1). Для сравнения, на том же рисунке представлены результаты расчета значения концентрации примеси по высоте колонны без измельчающего устройства (кривая 2). В обоих случаях общая высота кристаллизационной колонны одинакова. Как видно из приведенных результатов, использование механического измельчения кристаллов приводит к существенному повышению глубины очистки веществ в противоточной кристаллизационной колонне. Например, для рассматриваемых параметров концентрация примеси уменьшается более чем на порядок. Для дальнейшего увеличения эффективности очистки веществ в кристаллизационной колонне, целесообразно использовать несколько устройств для измельчения кристаллов.
Как видно из рис. 1 (кривая 1), наиболее эффективно очистка происходит только на начальном участке (15–20 см) разделительной секции колонны. В дальнейшем увеличение высоты разделительной секции не приводит к существенному повышению эффективности очистки веществ из-за увеличения среднего размера кристаллов (рисунок 1, кривая 2).
Для исследования распределения примеси по высоте противоточной кристаллизационной колонны с несколькими узлами дробления использовалась кристаллизационная колонна, состоящая из нескольких разделительных секций длиной 150 мм и узлов дробления длиной 100 мм. Создание унифицированных секций и узлов дробления позволило изменять число измельчающих устройств от одного до трех. Исследования проводились на модельной системе бензол – тиофен.
Расчеты по приведенным уравнениям m = 3 и m = 4 и эксперимен-тальные исследования показали, что увеличение числа измельчающих устройств приводит к существенному повышению глубины очистки веществ методом противоточной кристаллизации из расплава. Так например, экспериментально получено, что при увеличении числа измельчителей распределение примеси по высоте колонны приближается к экспоненциальному виду (рисунок 2).
Таким образом, механическое измельчение кристаллов позволяет существенно повысить эффективность очистки веществ в противоточной кристаллизационной колонне. Так например, для системы бензол – тиофен концентрация примеси дополнительно уменьшается более, чем на порядок при изменении среднего размера кристаллов в 1,25 раз. Распределение примеси по высоте колонны с тремя дробителями приближается к экспоненциальному виду.
Глава. 3. Глубокая очистка веществ от наноразмерных частиц методами кристаллизации из расплава
При очистке веществ кристаллизационными методами в них кроме примесей, растворенных в молекулярной форме, присутствуют наноразмерные частицы, которые в ряде применений лимитируют качество получаемых веществ. Так например, присутствие наноразмерных частиц в высокочистых веществах, используемых в микро-, опто-, наноэлектронике могут вносить существенный вклад в суммарное содержание примесей при получении высокочистых веществ с их содержанием на уровне 10-6 – 10-8 %., оказывать негативное влияние на оптические, электрофизические и другие свойства. Они могут образовываться и в противоточной кристаллизационной колонне в результате трения ее движущихся частей. Не смотря на то, что взвешенные наноразмерные частицы вносят существенный вклад в суммарное содержание примесей при получении высокочистых веществ, поведение их в процессе глубокой очистки жидкостей кристаллизационными методами практически не исследовалось.
Рассмотрим физико-химическую модель для расчета коэффициента распределения наноразмерных частиц между расплавом и кристаллом в процессе его роста с учетом их диффузионной подвижности в расплаве и определим эффективность очистки жидкостей от частиц кристаллизационными методами.
Особенности поведения взвешенных частиц в процессах кристаллизации обусловлены тем, что кристаллы обладают способностью оказывать механическое воздействие на посторонние тела, встречающиеся на пути их роста – развивать, так называемое, расклинивающее давление. Знак расклинивающего давления в зависимости от материала расплава и частиц может быть как положительный, так и отрицательный. Расклинивающее давление считается положительным, когда давление в пленке под частицей меньше, чем в окружающей жидкости. При этом жидкость из объема перетекает в зазор под частицей, и частица отталкивается поверхностью. При отрицательном расклинивающем давлении прослойка под влиянием поверхностных сил уменьшается и частица захватывается поверхностью при всех условиях роста кристалла.
Экспериментально было установлено, что находящиеся в расплаве твердые микрочастицы (размером более 1 мкм) могут захватываться фронтом кристаллизации только в том случае, когда скорость роста кристаллов превосходит некую критическую величину. При построении теории захвата частиц фронтом кристаллизации предполагалось, что пока частица далека от фронта кристаллизации, она не взаимодействует с ним и покоится относительно жидкости. Однако, когда зазор между частицей и поверхностью кристалла уменьшается до величины 10-5 – 10-6 см, оказываются существенными силы молекулярного взаимодействия. Если равнодействующая сил молекулярного взаимодействия отталкивает частицу от фронта кристаллизации, то частица начинает двигаться относительно расплава. В стационарном режиме это будет движение со скоростью роста V. При этом возникает гидродинамическая сила, прижимающая к нему сферическую частицу радиуса Rp. Из равенства этих сил получено выражение для критической скорости и показано, что инородные частицы отталкиваются фронтом кристаллизации, пока скорость роста кристалла не достигает критического значения. При больших скоростях частицы прижимаются к фронту кристаллизации и захватываются им..
Нано размерные частицы, радиусом 10 – 100 нм, уже нельзя считать покоящимися относительно расплава и необходимо учитывать их броуновское движение в расплаве. За счет энергии теплового движения некоторые нано размерные частицы смогут преодолеть потенциальный барьер сил отталкивания на поверхности кристалла и захватываться им.
Для характеристики захвата субмикронных и наноразмерных частиц поверхностью растущего кристалла была введена величина скорости перехода частиц из расплава в кристалл Vn, равная отношению потока частиц на поверхность кристалла к концентрации их в потоке. Для ее определения рассмотрено поведение частиц в пограничном слое толщиной F, в котором существенно влияние сил взаимодействия между частицей и кристаллом (F = 10-5 10-6 см). Рассматривается стационарный случай, когда поток частиц из расплава на поверхность кристалла J = const. Так как в пограничном слое отсутствуют конвективные потоки вдоль поверхности кристалла, а скорость термофоретического движения мала и ей можно пренебречь, то суммарный поток частиц, нормальный к поверхности кристалла, в системе отсчета, связанной с поверхностью фронта кристаллизации будет состоять из трех составляющих:
1. 
- диффузионный поток;
2. 
- поток, обусловленный силами молекулярного взаимодействия;
3. 
- поток, обусловленный движением расплава относительно поверхности твердого тела.
.
Тогда уравнение для суммарного потока частиц на поверхность растущего кристалла записывается в виде:
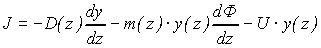, (11)
где y(z) – концентрация частиц (частиц в см3); Ф(z) – потенциал взаимодействия частицы с поверхностью твердого тела ( в работе рассмотрены два вида взаимодействия: сила Ван – дер – Вальса и сила, обусловленная двойным электрическим слоем), D(z) = m(z)kT – коэффициент диффузии частиц в пограничном слое; k – постоянная Больцмана; T – абсолютная температура; m(z) = fБ(z)/(6Rp) – подвижность частиц в пограничном слое; - вязкость расплава; Rp – радиус частицы; fБ(z) – поправочный фактор Бренера, учитывающий отличие подвижности частицы вблизи поверхности от подвижности ее в объеме; U = Vs / l – скорость движения расплава относительно поверхности кристалла; V – линейная скорость роста кристалла; s и l - плотности твердой и жидкой фаз соответственно.
Уравнение (11) решается при условии, что концентрация частиц у поверхности кристалла, вследствие их осаждения на поверхность кристалла, равна нулю. Однако выражение для сил расклинивающего давления и поправочного фактора Бренера справедливы, если пленка между частицей и фронтом кристаллизации содержит хотя бы несколько молекулярных слоев. Поэтому считаем, что частица захватывается поверхностью кристалла, если расстояние между ними менее zm. Переходом частиц с поверхности кристалла в расплав пренебрегаем. Тогда граничное условие запишется;
. (12)
Введя безразмерную переменную 
решение уравнения (11) можно записать в виде:
, (13)
, (14)
где – коэффициент диффузии частиц в объеме расплава,
Q(l) – эффективный потенциал взаимодействия частицы с поверхностью растущего кристалла, Ф(l) – потенциал сил расклинивающего давления в зазоре между фронтом кристаллизации и частицей, 
- безразмерная ширина пограничного слоя на поверхности кристалла.
Первое слагаемое в уравнении (14) определяет энергию взаимодействия частицы с фронтом кристаллизации, она может складываться из энергий молекулярного и электростатического взаимодействия. В работе рассмотрен случай, когда между частицей и поверхностью кристалла существует положительное расклинивающее давление и частицы отталкиваются от фронта кристаллизации. В неполярных средах электрический потенциал поверхностей кристалла и частицы мал и электростатической энергией их взаимодействия можно пренебречь. В этом случае потенциал взаимодействия в системе частица – расплав – кристалл для случая малых расстояний (не учитывая электромагнитное запаздывание) можно записать в виде;
, (15)
где Ео – постоянная, зависящая от диэлектрических свойств материалов.
Электростатическая составляющая расклинивающего давления Р вызвана взаимным отталкиванием диффузионных частей двойных электрических слоев на поверхностях кристалла и частицы, заряженных до потенциалов 1 и 2 соответственно.
Второе слагаемое в уравнении (14) определяет энергию частицы, обусловленную движением расплава относительно фронта кристаллизации. На внешней границе пограничного слоя взаимодействие частицы с поверхностью кристалла пренебрежимо мало, т.е. Ф(l) 0, а энергия частицы, связанная с движением расплава, равна
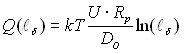. (16)
Знание скорости перехода частиц из расплава в кристалл в процессе его роста позволяет рассчитать коэффициент распределения частиц на границе кристалл – расплав следующим образом. Из равенства потока частиц из расплава на поверхность кристалла JL = Vn yS и их потока в кристалле относительно фронта кристаллизации, вследствие его роста, JS = V xS (в системе отсчета, связанной с фронтом кристаллизации) получим соотношение между концентрациями частиц в кристалле xS и расплаве yS перед фронтом кристаллизации в виде
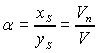. (17)
Результаты расчетов зависимости коэффициента распределения от скорости роста кристалла и размера частиц в процессе кристаллизации неполярных веществ приведены на рис. 3 и 4, а разбавленных растворов электролитов – на рис. 5 и 6. Экстремум на рис. 3 обусловлен разной зависимостью от размера частиц энергии взаимодействия частицы с фроном ( R) и энергии частицы, обусловленной движением расплава относительно фронта кристаллизации ( R2) в уравнении (14).
Проверка предложенной модели захвата наноразмерных частиц фронтом кристаллизации проводилась в экспериментах по направленной кристаллизации следующим образом. Экспериментально определяли коэффициент распределения наноразмерных частиц германия для различных скоростей кристаллизации бензола и циклогексана и по уравнению (17) рассчитывали экспериментальное значение скорости перехода частиц из расплава в кристалл. Концентрацию частиц и их размеры определяли методом лазерной ультрамикроскопии. Для тех же условий по уравнениям (13 – 14) рассчитывали теоретическое значение скорости перехода частиц из расплава в кристалл.
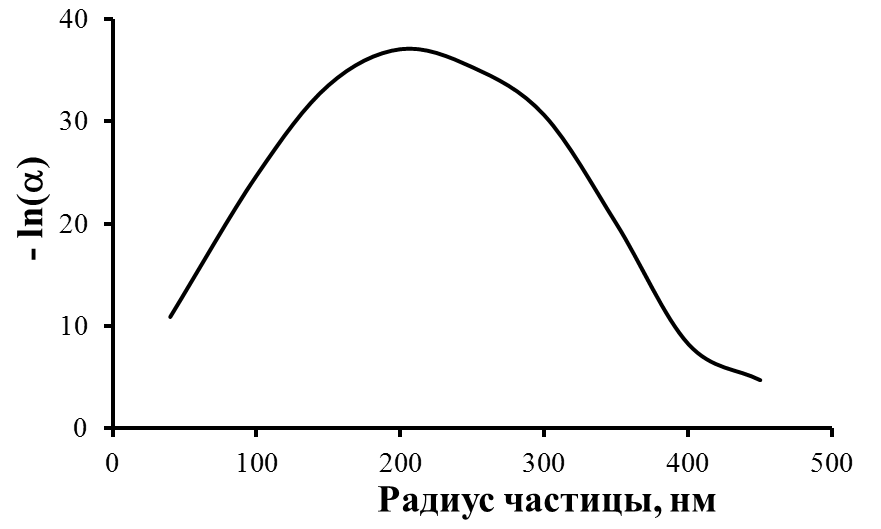
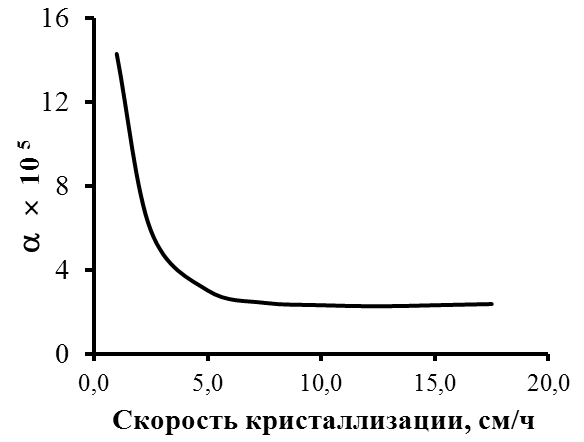
| Рис. 3. Зависимость коэффициента распределения взвешенных частиц между расплавом и кристаллом от их размера при скорости кристаллизации 18 см/час. | Рис. 4. Зависимость коэффициента распределения взвешенных частиц радиусом 40 нм между расплавом и кристаллом от скорости кристаллизации |
Полученные экспериментальные данные хорошо согласуются с результатами расчетов по предложенной модели взаимодействия наноразмерных частиц с фронтом кристаллизации. Значения коэффициентов
распределения наноразмерных частиц перед фронтом кристаллизации (рис. 3) свидетельствуют о том, что кристаллизационные методы очистки веществ могут эффективно удалять из расплава частицы радиусом 40 – 350 нм.
Данное утверждение было проверено на примере очистки бензола, циклогексана и воды от наноразмерных частиц методом направленной кристаллизации.
Используя известное уравнение, учитывающее только диффузионный перенос примеси, можно получить выражение для определения средней концентрации частиц в кристалле толщиной Но
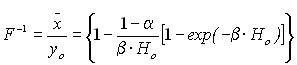, (18)
где = U / Do, yo – концентрация частиц в исходной смеси, F – фактор разделения.
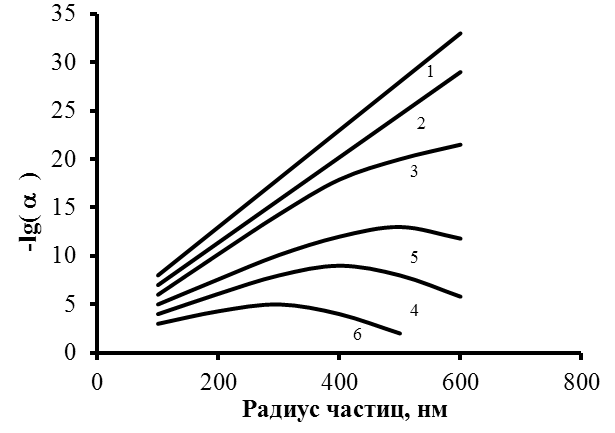
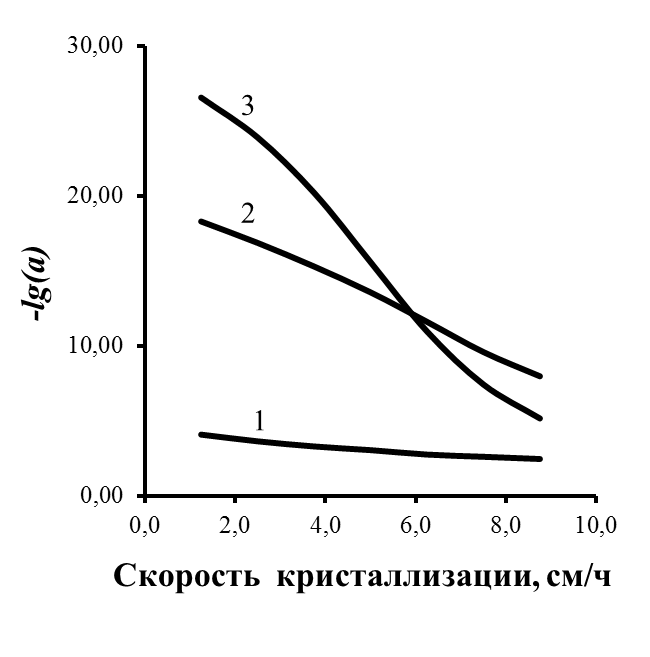
| Рис. 5. Зависимость коэффициента распределения от размера частиц. Потенциалы поверхностей: 1 – 4 – 1= 10,4 мВ; 2 = 52 мВ; 5 – 1 = 10,4 мВ; 2 = 104 мВ; 6 – 1 = 5,2 мВ; 2 = 52 мВ. V = 0,1(1), 1(2), 3 (3), 10 (4 – 6) см/ч. | Рис. 6. Зависимость коэффициента распределения от скорости кристаллизации. Потенциалы поверхностей 1= 10,4 мВ; 2 = 52 мВ. Rр = 50 (1), 300 (2), 500 (3) нм |
Полученные экспериментально и рассчитанные по уравнению (18) значения фактора разделения для различных значений скорости кристаллизации и размера частиц при очистке бензола от частиц германия для толщины слитка Но = 3 см хорошо согласуются. Низкие значения фактора разделения (F < 3 для частиц радиуса R = 40 нм. ) связаны с малой диффузионной подвижностью наноразмерных частиц в расплаве (Do = 5,710-8 см2 / с). Это приводит к возрастанию концентрации частиц перед фронтом кристаллизации более, чем на четыре порядка. Таким образом, лимитирующей стадией очистки веществ от наноразмерных частиц методом направленной кристаллизации является отвод примеси от фронта кристаллизации.
Среди кристаллизационных методов очистки наиболее перспективным является метод противоточной кристаллизации. Рассмотрим поведение взвешенных нано размерных частиц в процессе противоточной кристаллизации из расплава. Массообмен между кристаллами и расплавом в процессе противоточной кристаллизации из расплава может протекать как диффузионным путем, так и в результате перекристаллизации. Для наноразмерных частиц, диффузией которых в твердой фазе можно пренебречь, основной вклад в эффект разделения будет вносить перекристаллизация. В работе предложена математическая модель, позволяющая рассчитать изменение концентрации частиц, обусловленное перекристаллизацией твердой фазы, по высоте колонны.
Для сферических кристаллов концентрация частиц в твердой фазе x(t) определяется уравнением:
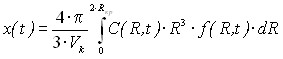, (19)
где C(R,t) - средняя концентрация частиц в кристалле радиусом R в данном сечении колонны, Vk – объем твердой фазы в единичном объеме колонны, численно равный доле твердой фазы. Выражение для функции распределения кристаллов по размерам имеет вид:
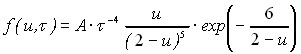, (20)
где u = R / Rкр, R – радиус кристаллов в момент времени t, Rкр – критический радиус кристаллов в это же время, = Rкр / Rкро, Rкро – критический радиус в начальное время t = 0, А – константа, определяемая уравнением:
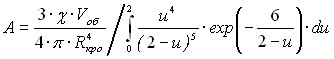. (21)
Пусть R1 – радиус кристаллов, не изменивших свой размер к моменту времени t. Тогда для определения концентрации частиц в кристалле радиусом R можно воспользоваться уравнением:
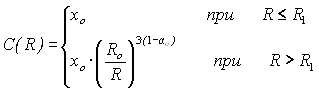, (22)
где хо – начальная концентрация частиц в кристалле. С учетом уравнения (22), уравнение (19) для безразмерного радиуса кристаллов примет вид:
, (23)
,
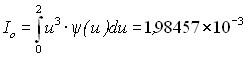где (u) = u exp[ 6/( 2 – u )]/( 2 – u )5 – функция распределения кристаллов по размерам.
Полученные уравнения позволяют рассчитать распределение взвешенных наноразмерных частиц по высоте противоточной кристаллизационной колонны. Результаты расчета для различных значений линейной скорости движения твердой фазы по высоте колонны L приведены на рис. 7.
Так как очистка жидкостей от взвешенных наноразмерных частиц обусловлена перекристаллизацией твердой фазы, то представляет интерес изучение зависимости эффективности очистки от доли перекристаллизовавшейся жидкости. При постоянной доле твердой фазы в кристаллизационной колонне объем расплавившихся кристаллов равен объему закристаллизовавшейся жидкости. В работе получено выражение для расчета объема перекристаллизовавшейся твердой фазы в единичном объеме колонны в процессе ее работы:
. (24)
Если обозначить долю перекристаллизовавшейся твердой фазы через = Vk /, то из уравнения (24) получим:
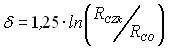. (25)
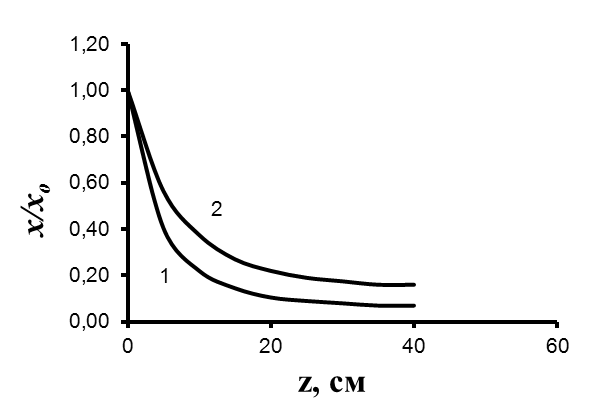
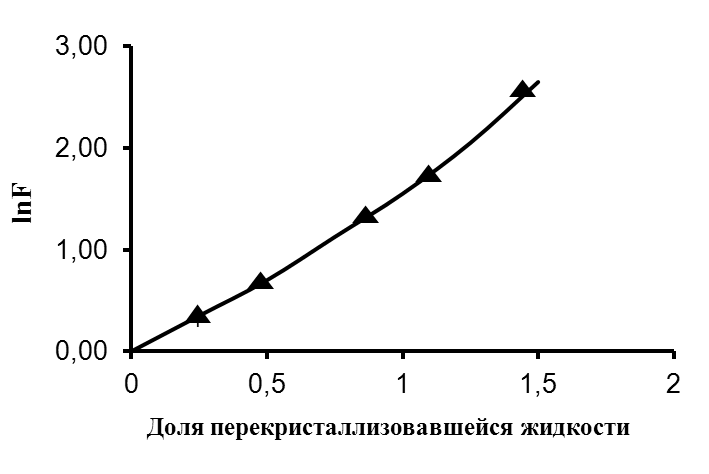
| Рис. 7. Результаты расчета концентрации наноразмерных частиц в различных сечениях кристаллизационной колонны. 1 – L = 1,110-2 см/с, 2 – L = 1,510-2 см/с. | Рис. 8. Зависимость фактора разделения противоточной кристаллизационной колонны от доли перекристаллизовавшейся жидкости. Кривая – расчет по формуле (23), – расчет по формуле (26) |
Сравнивая уравнения (23) и (25), можно сделать вывод о том, что для малых значений эффективного коэффициента разделения или в случае, когда он слабо зависит от скорости роста кристаллов, фактор разделения противоточной кристаллизационной колонны F = xo / xzk однозначно определяется долей перекристаллизовавшейся твердой фазы.
На рисунке 8 представлен график зависимости фактора разделения от доли перекристаллизации твердой фаза . Анализ этой зависимости дает, что при e < 0,1 она может быть описана уравнением:
. (26)
Для сравнения на рисунке 8 приведены результаты расчетов по уравнению (26). Из рисунка видно, что обе формулы дают хорошо совпадающие результаты. Однако уравнение (26) много проще и удобнее для практических расчетов.
Таким образом, предложенные уравнения позволяют рассчитать коэффициенты распределения наноразмерных взвешенных частиц между расплавом и кристаллом, а также оценить эффективность очистки от них кристаллизационными методами. Рассчитанные значения коэффициентов распределения наноразмерных частиц перед фронтом кристаллизации свидетельствуют о том, что кристаллизационные методы очистки веществ могут эффективно удалять из расплава частицы радиусом 40 – 350 нм. Показано, что при очистке веществ от наноразмерных частиц методом противоточной кристаллизации, основной вклад в эффект разделения вносит перекристаллизация.
Глава 4. Распределение примесей в системе газовый гидрат – газ.
Коэффициент распределения
Рассмотрим возможность разделения и очистки газов кристаллизационными методами. До настоящего момента единственным кристаллизационным способом очистки с участием твердой и газовой фаз был метод сублимации, а метод противоточной сублимации в ряде случаев по эффективности не уступает методам противоточной кристаллизации из расплава и ректификации. Однако, систем, которые можно разделять и очищать этим методом, очень мало. Поэтому для разделения и глубокой очистки веществ в газовой фазе предложено использовать кристаллизационный метод, основанный на перераспределении компонентов газовой смеси при образовании газовых гидратов, названный нами методом газогидратной кристаллизации.
При разделении и глубокой очистке многокомпонентных смесей, представляющих собой смесь молекул М1, М2,..., Мi, возможно образование смешанных газовых гидратов при соответствующих значениях давления и температуры. Свойство газовых гидратов изменять состав газовой смеси можно использовать для разделения смесей и глубокой очистки веществ.
Одним из важнейших параметров, характеризующих процесс образования газовых гидратов при заданной температуре, является давление диссоциации Pдис. Давление диссоциации определяет минимальное давление газовой смеси, при котором гидрат термодинамически устойчив. Для определения зависимости давления диссоциации газовых гидратов и давления паров воды над ними от состава газовой смеси можно воспользоваться следующей моделью.
С использованием модели идеальных растворов для случая термодинамического равновесия получено уравнение для расчета давления насыщенного пара воды над поверхностью газового гидрата, образованного смесью газов М1, М2,..., Мi,
, (27)
где Pw - давление насыщенного пара над поверхностью гидрата, Pw0 - давление насыщенного пара над пустой клатратной решеткой (зависит от типа структуры, температуры), n – отношение числа больших и малых полостей в элементарной кристаллической ячейке гидрата, m – число молекул воды, приходящихся на одну полость ( n = 3, m = 5.75 для гидратов, имеющих I тип структуры и n = 2, m = 5.67 для гидратов, имеющих II тип структуры), Q1i и Q2i - доля малых и больших полостей, заполненных газом Мi, соответственно.
Доля полостей типа j, заполненных молекулами Мi, определяется из изотермы Лэнгмюра:
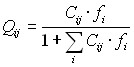, (28)
где f i = i Pi - фугитивность газа Мi, Pi - его давление, i - коэффициент фугитивности, Cij - коэффициенты Лэнгмюра, рассчитанные по сферической ячеечной модели. Заменив средний радиус ячейки, образованной соседними молекулами в жидкости, на средний радиус полости Rj, образованной Zj молекулами воды, получим уравнение для определения коэффициентов Лэнгмюра:
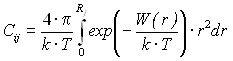, (29)
где W(r) - радиальная потенциальная функция, r - радиальное расстояние внедренной газовой молекулы от центра полости.
Энергия взаимодействия между газом и водой обычно определяется потенциалом Леннарда - Джонса ( 12 - 6 ).
Взаимодействие между молекулами газа в полостях гидрата можно не учитывать из - за его относительной малости по сравнению с взаимодействием газ - вода. Для проверки возможности использовать сферическую ячеечную модель при расчете констант Лэнгмюра, в работе были выполнены расчеты для газовых гидратов аргона, криптона и ксенона. Получено хорошее совпадение результатов расчета с экспериментальными данными, что говорит об адекватности имеющейся теории для описания газовых гидратов.
Так как гидратная решетка, не содержащая молекулы газа – гидратообразователя, не может образовываться непосредственно из жидкой воды или льда, то можно записать:
,
где
- давление насыщенного пара воды над поверхностью жидкости (l) или льда (s). Как следует из уравнения (27), внедрение молекул газа - гидратообразователя в полости гидратной решетки снижает давление паров воды над поверхностью гидрата. Как только оно становится равным или меньше 
, становится возможным образование кристаллической решетки. Таким образом, давление диссоциации определяется из условия
. (30)
Подставляя уравнения (27) и (28) в уравнение (30), получим выражение для расчета давления диссоциации:
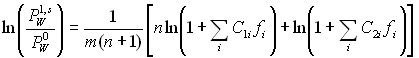. (31)
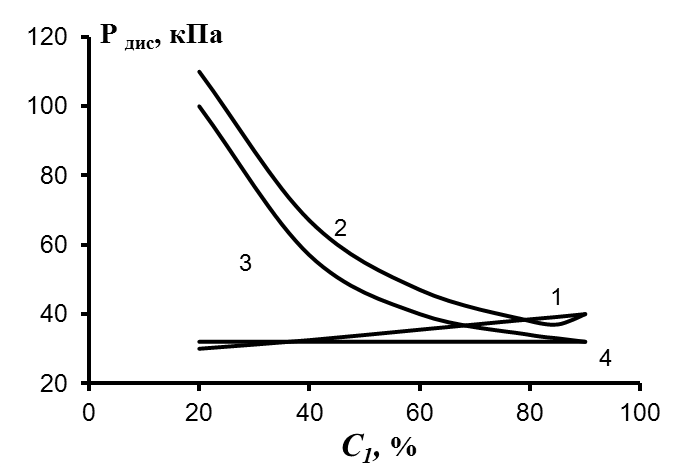
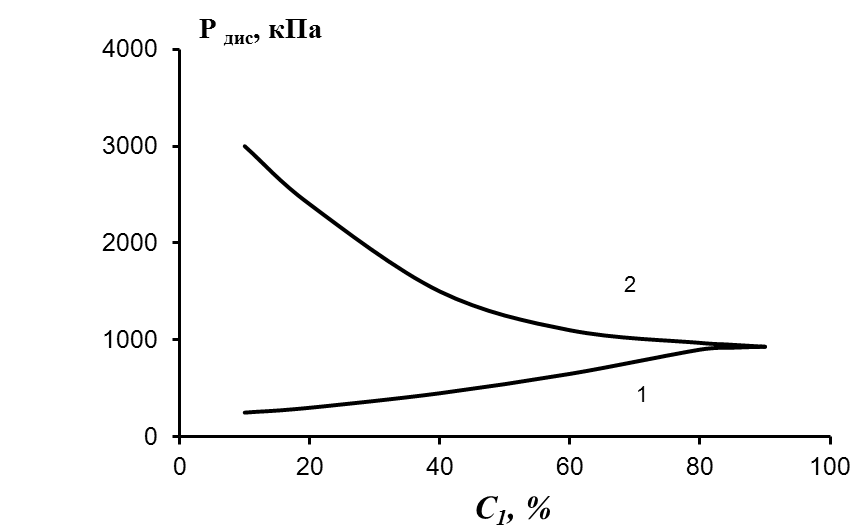
| Рис. 9. Зависимость давления диссоциации газовых гидратов от концентрации основного компонента в газовой смеси для систем: 1 – H2S + H2Se + H2O; 2 – H2S + H2Se + H2O + Kr; 3 – AsH3 + PH3 + H2O + Kr; 4 – AsH3 + PH3 + H2O при температуре 252 K. | Рис. 10. Зависимость давления диссоциации газовых гидратов от концентрации основного компонента в газовой смеси для систем: 1 – H2S + H2Se + H2O; 2 – H2S + H2Se + H2O + Kr при температуре 294 K |
Решение уравнения (31) относительно давления диссоциации было выполнено численными методами для газовых смесей различного состава, содержащих гидриды мышьяка, фосфора, серы, селена, а также криптон при различных температурах процесса гидратообразования. При расчетах по уравнению (31) принимали 
= 2,52 кПа при T = 294 K и 
= 0,092 кПа при T = 252 K. Результаты расчетов представлены на рис. 9 и 10.
Как видно из приведенных рисунков для трехкомпонентной газовой смеси (два гидрида и вода), во всех случаях, когда Рдис отдельных компонентов различны, давление диссоциации существенно зависит от доли основного вещества и температуры процесса гидратообразования. По мере уменьшения доли основного вещества, Рдис монотонно меняется от значения давления диссоциации чистого основного компонента до его значения для чистого примесного компонента.
При расчете систем, содержащих четыре компонента, содержание второго компонента условно принималось равным 10 % от содержания основы и это соотношение поддерживалось постоянным. Доля основного компонента менялась также, как и в случае тройных систем, но за счет изменения доли четвертого компонента. Характер изменения давления диссоциации аналогичен первому случаю. Но в ряде случаев при определенных соотношениях количеств второго и четвертого компонентов (это соотношение для различных систем различно и зависит от температуры и Рдис каждого компонента) возможно образование экстремумов на зависимости давления диссоциации от состава (кривая 2 на рис. 9).
При образовании смешанных гидратов для соответствующих значений давления и температуры будет происходить перераспределение компонентов газовой смеси между газовым гидратом и газовой смесью. Газовый гидрат (или газовая смесь) обогащаются или обедняются по одному или нескольким компонентам за счет различия составов равновесных фаз: газовой и твердой (на безводной основе). Для оценки эффективности очистки необходимо знать состав газовых гидратов, определяемый распределением молекул основного вещества и примесей в его полостях.
Распределение молекул гидратообразователя в полостях газового гидрата можно характеризовать коэффициентом распределения
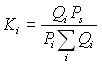, (32)
где Qi - доля полостей гидрата, заполненных молекулами Мi, Qi - суммарная доля полостей, заполненных молекулами гидратообразователя, Pi - парциальное давление молекул Мi в газовой меси, Ps - общее давление газовой смеси. Доля полостей типа j, заполненных молекулами Мi, определяется из изотермы Лэнгмюра (28).
Если nj - доля полостей типа j в газовом гидрате, то
. (33)
Для характеристики перераспределения компонентов газовой смеси при образовании газовых гидратов удобно использовать относительный коэффициент распределения
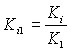, (34)
где компонент смеси с i = 1 условно принимаем за основное (очищаемое) вещество.
Подставляя в (34) уравнение (32) можно получить следующее уравнение:
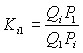. (35)
Относительный коэффициент распределения позволяет оценить, будет ли газовый гидрат обогащен (если Ki1 > 1), или же обеднен (если Ki1 < 1) примесями из очищаемого вещества. Из уравнений (33) и (35) следует, что относительный коэффициент распределения может существенно зависеть от условий гидратообразования и концентрации примеси в газовой смеси.
В работе исследованы зависимости относительного коэффициента распределения от условий образования гидратов и состава газовой смеси на примере смесей, содержащих неорганические гидриды мышьяка, серы, селена, фосфора и сурьмы, а также метан, гексафторид серы, фреоны и азот.
В реальных условиях состав газовой смеси меняется за счет изменения парциальных давлений компонентов смеси.
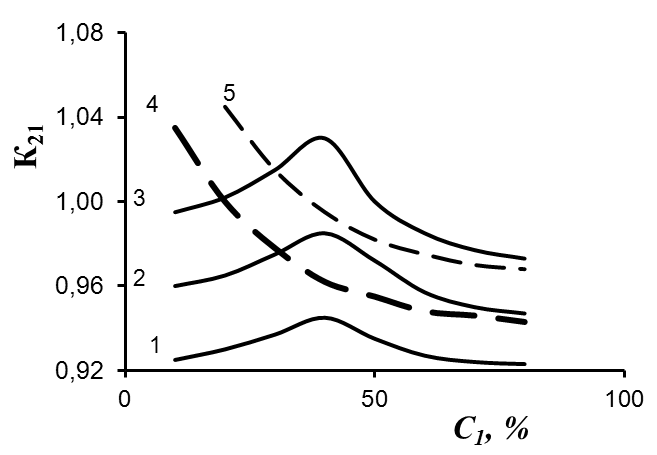
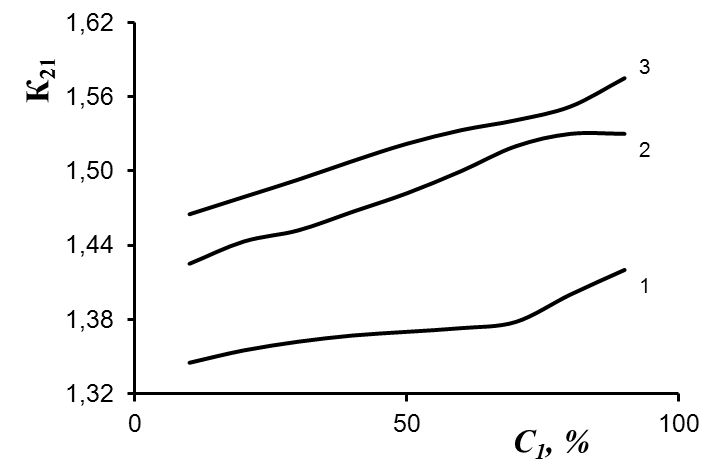
| Рис. 11. Зависимость относительного коэффициента распределения от концентрации основного компонента в газовой смеси для системы AsH3 + PH3 + H3O при температурах 1 - 252 К; 2 - 273 К; 3 - 294 К и для системы AsH3 + PH3 + H2O + N2 при температурах 4 - 273 К; 5 - 294 К. | Рис. 12. Зависимость относительного коэффициента распределения от концентрации основного компонента в газовой смеси для системы H2S + H2Se + H2O при температурах: 1 - 252 К; 2 - 273 К; 3 - 294 К. |
Рассмотрим трехкомпонентную газовую смесь: два гидрида и вода. Давление паров воды в интервале исследованных температур 250 – 290 К мало по сравнению с суммарным давлением газов и им можно пренебречь. Таким образом, суммарное давление газов определяется значениями парциального давления гидридов. Результаты расчета относительного коэффициента распределения по уравнению (35) для этого случая приведены на рисунках 11 и 12. Необходимые для определения по уравнению (28) доли заполненных полостей константы Лэнгмюра рассчитывались с использованием сферической ячеечной модели (уравнение (29)).
Как видно из приведенных рисунков, во всех случаях относительный коэффициент распределения существенно зависит от доли основного вещества. Причем, в зависимости от доли компонентов в смеси, относительный коэффициент распределения второго компонента может быть как больше 1, т.е. в гидратах преимущественно накапливается примесь из очищаемого вещества, так и меньше 1, т.е. в них преимущественно накапливается основное вещество.
Аналогичные результаты получились и при расчете систем, содержащих четыре компонента.
Для оценки возможности глубокой очистки гексафторида серы и фреона – 14 в работе проведен расчет коэффициентов распределения для содержащихся в них примесей. Для гексафторида серы расчеты проводились с использованием потенциала Кихара, параметры которого представлены в таблице 2.
Из полученных результатов расчета относительных коэффициентов распределения следует, что примеси в SF6 можно разделить на три группы.
Таблица 2
Параметры потенциала Кихара
| Вещество | /k, К | , А | a, А | u |
| SF6 | 298,8±0,5 | 2,98±0,03 | 0,360±0,003 | (500±3)·10-5 |
| SO2 | 307,5±0,5 | 3,19±0,02 | 0,320±0,003 | (200±1)·10-4 |
| CO2 | 215,0±0,5 | 3,49±0,02 | 0,320±0,002 | (200±1)·10-4 |
| O2 | 164,0±0,5 | 3,30±0,02 | 0,180±0,001 | (200±1)·10-4 |
| N2 | 112,5±0,5 | 3,45±0,02 | 0,220±0,001 | (200±1)·10-4 |
Примеси первой группы, к ним относятся O2 и N2, имеют значение относительного коэффициента распределения К21<1 и будут концентрироваться в газовой фазе. Во вторую группу примесей входит СО2, значение К21 которого близок к 1. В третью группу примесей входит диоксид серы, для которого К21 > 1 и он будет концентрироваться в газовом гидрате. Коэффициент распределения углекислого газа в зависимости от давления, может принимать значения как меньше 1, (при низких давлениях), так и больше 1. Коэффициенты распределения остальных рассматриваемых примесей значительно отличаются от 1.
В настоящее время во многих производствах в атмосферу выбрасываются большие потоки отходящих газов, содержащих примеси вредных компонентов, таких как диоксид серы, оксид и диоксид углерода, хлорорганические соединения и т.д. "Складирование" их в наноразмерных частицах в воздухе, образованных газовыми гидратами, представляет серьезную опасность для биологических объектов. Расчеты, проведенные по уравнению (5) показали, что газовые гидраты могут образовываться при условиях, характерных для выбросов техногенных примесей в широком интервале температур окружающей среды (средней климатической полосы). При этом в них преимущественно концентрируются типичные техногенные примеси.
Таким образом разработанная физико-химическая модель позволяет рассчитывать относительные коэффициенты распределения примесей между твердой и газовой фазами в процессе газогидратной кристаллизации. По данным об относительных коэффициентах распределения Ki1 можно установить расчетным путем, будет ли газовый гидрат обогащен (если Ki1 > 1), или же обеднен (если Ki1 < 1) примесями из очищаемого вещества.
Глава 5. Газогидратная кристаллизация
Для многих газовых смесей значения относительного коэффициента распределения существенно отличны от единицы и метод газогидратной кристаллизации может быть использован для разделения газовых смесей и очистки веществ. Рассмотрим физико – химическую модель, позволяющую рассчитывать эффективность очистки и разделения газовых смесей методом газогидратной кристаллизации.
Эффективность метода разделения, основанного на явлении перераспределения компонентов смеси между твердой и газовой фазами при образовании газовых гидратов, определяется величиной относительного коэффициента распределения (35).
Основным и по существу единственно надежным источником получения информации о коэффициентах межфазового равновесия является экспериментальный метод. На сегодняшний день в литературе отсутствует какая – либо информация о проведении исследований по непосредственному определению коэффициента распределения в системе газ – газовый гидрат.
В работе предложена методика экспериментального определения коэффициента распределения компонентов газовой смеси при газогидратной кристаллизации, которая не требует знания физико-химических свойств исследуемых газовых гидратов и проводится на несложном лабораторном оборудовании.
Используя уравнение материального баланса получено выражение (36),
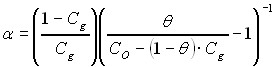, (36)
которое позволяет определить коэффициент распределения в системе газ –газовый гидрат в условиях установившегося равновесия между фазами. При этом для расчета необходимо знать концентрацию исследуемого компонента газовой смеси в начальный СО и конечный момент времени эксперимента Сg и долю вещества, перешедшего в газовый гидрат из газовой фазы.
На основании рассмотренной математической модели процесса газогидратной кристаллизации в работе предложена методика, которая косвенным образом позволяет определить экспериментальное значение коэффициента распределения в системе газ – газовый гидрат. Методика основана на статическом уравновешивании фаз в изотермических условиях. Установление термодинамического равновесия между фазами достигается путем выдерживания при заданной температуре газового гидрата и находящегося над ними в контакте пара в течение некоторого времени. Доказательством установления равновесия является отсутствие зависимости коэффициента разделения, рассчитанного по уравнению (36), от времени проведения эксперимента. Начальная концентрация интересующего компонента в газовой фазе и ее равновесное значение после проведения процесса кристаллизации определяются методом газовой хроматографии.
Проверка предложенной методики определения коэффициента распределения проводилась на системе SF6 – CF2Cl2. Содержание CF2Cl2 в газовой смеси составляло 13,6 об. %. Указанная система выбрана потому, что газовые гидраты SF6 и CCl2F2 хорошо изучены, в литературе имеется подробная информация относительно их давления диссоциации. Получено хорошее совпадение экспериментальных результатов с результатами расчета по уравнению (35), что говорит о правильности применения разработанной модели для расчетов и методики экспериментального определения коэффициента распределения.
Для теоретических расчетов условий гидратообразования необходимо знание параметров потенциала межмолекулярного взаимодействия молекул газа ("гость"), включенных в полости газового гидрата с молекулами воды ("хозяин"), образующими кристаллический каркас. Для определения параметров межмолекулярного взаимодействия типа "гость – гость" методом регрессии в работе предложено использовать экспериментальные данные о коэффициенте распределения исследуемого газа в смеси с хорошо изученным компонентом при газогидратной кристаллизации. В этом случае из экспериментальных данных в рамках теории идеального клатрата рассчитываются параметры межмолекулярного взаимодействия типа "гость – хозяин", откуда можно определить параметры взаимодействия типа "гость – гость".
Суть методики заключается в подборе, в рамках теории идеального твердого клатрата, оптимальных значений параметров потенциала межмолекулярного взаимодействия гость-хозяин.. Нахождение единственно возможной пары параметров, удовлетворяющей одновременно всем экспериментальным значениям коэффициента распределения, проводится графическим способом. Таким образом, определив значения экспериментального коэффициента распределения исследуемого вещества в смеси с хорошо изученным компонентом для различных условий, можно определить параметры как для потенциала взаимодействия гость – хозяин в газовом гидрате, так и для индивидуального компонента гостя, а далее физико-химические характеристики его газового гидрата.
Для иллюстрации предлагаемой методики в работе проведен расчет параметров межмолекулярного взаимодействия для молекул чистого i-го компонента Gi, Gi на примере системы SF6 – CCl2F2. Поскольку молекулы SF6 и CCl2F2 имеют сферическую форму, дихлордифторметан обладает малым дипольным моментом (0,55 D), а молекула гексафторида серы неполярная, то рассматриваемая система с удовлетворительной точностью может быть описана с использованием потенциала взаимодействия Леннарда – Джонса.
В работе рассмотрен случай, когда исследуемым веществом является основной компонент смеси – гексафторид серы. Предварительно необходимые значения параметров потенциала Леннард – Джонса G1, G1 были получены методом регрессии из данных о составе гидрата и давлении диссоциации и оказались равными для SF6 : G1/k = 261,0 K и G1 = 4,28. По предложенной методике были определены параметры Gi и Gi, при которых отклонения значений расчетного коэффициента распределения К1i от экспериментальных будут минимальны для всех рассматриваемых значений температуры. Результатами такого решения являются параметры G1/k = 258,34 K и G1 = 4,28, которые хорошо совпадают с литературными данными. Таким образом, экспериментальные данные по коэффициентам распределения компонентов газовой смеси при газогидратной кристаллизации могут быть использованы для определения параметров межмолекулярного взаимодействия методом регрессии.
Из анализа приведенных в работе коэффициентов распределения следует, что для многих систем они существенно отличны от единицы и метод газогидратной кристаллизации может быть использован для разделения газовых смесей и очистки веществ. Например, в системе CF4 – CF2Cl2 коэффициент распределения равен 7, для системы SF6 – SO2 равен 21.
В работе рассмотрено применение газогидратного кристаллизационного метода для глубокой очистки веществ в динамическом режиме, т.е. в режиме образования газовых гидратов, когда кристаллизация основного компонента происходит медленно, в результате чего выпадают крупные кристаллы, в которых концентрация примеси (распределяющегося вещества) изменяется от центра к периферии. При этом каждый слой кристалла в момент его роста находится в равновесии с газовой фазой.
Рассмотрим смесь газов М1 и М2 в количестве No молей, которая находится в рассматриваемом объеме и имеет давление PО больше, чем давление диссоциации при данной температуре. Давление паров воды Pw (принимается Pw = const) в объеме, равное давлению насыщенного пара, обеспечивает устойчивое образование в нем газовых гидратов.
Эффективность метода разделения характеризуется величиной коэффициента распределения :
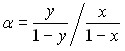, (37)
где x – концентрация примеси в газовой смеси, находящейся в равновесии с газовой смесью в гидрате, мольные доли; y – концентрация примеси в газовой смеси, содержащейся в гидрате, мольные доли.
В работе рассмотрены три варианта организации процесса газогидратной кристаллизации: в первом варианте - газогидратной кристаллизации при постоянном давлении, принималось, что давление газовой смеси и паров воды поддерживается постоянным за счет дополнительного ввода в объём смеси с исходной концентрацией компонентов и необходимого количества воды. При этом часть газовой смеси связывается в гидрат, а оставшаяся смесь отбирается в виде готового продукта по завершении процесса. Решая уравнение материального баланса для примесного компонента, получена зависимость концентрации примеси в газовой фазе от доли отобранного с газовыми гидратами газа, т.е. от доли закристаллизовавшегося вещества:
, (38)
где 
, x0 – начальная концентрация примеси в газовой смеси, мольн. д.; N1 – количество газовой смеси, перешедшей в газовый гидрат при первом варианте организации процесса газогидратной кристаллизации (при постоянном давлении), моль.
Если доля закристаллизовавшегося вещества равна
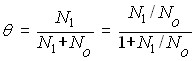, (39)
то совместное решение уравнений (38) и (39) позволяет определить концентрацию примеси в рассматриваемом объеме для данной доли закристаллизовавшегося вещества.
При втором варианте организации процесса – направленной газогидратной кристаллизации, давление газовой смеси в объеме постоянно понижается за счет образования газовых гидратов. Дополнительного ввода газовой смеси не происходит, а отбор готового продукта осуществляется по завершении процесса. При этом концентрация примеси в газе одинакова во всем рассматриваемом объеме и в каждый момент времени связана с концентрацией примеси в газовой смеси, содержащейся в гидрате, уравнением (37). Рассматриваемый вариант по организации процесса аналогичен методу направленной кристаллизации из расплава. Решая уравнение материального баланса для примесного компонента, получена зависимость концентрации примеси в газовой фазе от доли отобранного с газовыми гидратами газа.
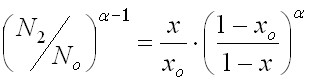. (40)
При этом доля закристаллизовавшегося вещества:
. (41)
Экспериментальную проверку предложенных математических моделей для расчета фактора разделения проводили на системе гексафторид серы с примесью CCl2F2 (коэффициент распределения = 3,0 при Т = 273 К и Р = 250 кПа) для двух вариантов организации процесса газогидратной кристаллизации, рассматриваемых в теоретических моделях. В исходной газовой смеси содержалось 3,5 % молей примеси. Основной узел экспериментальной установки – изготовленная из стекла термостатированная ячейка – кристаллизатор объемом 350 мл на 3/4 заполненная дистиллированной водой. Во внешней рубашке ячейки циркулирует охлаждающая жидкость. При проведении процесса газогидратной кристаллизации с постоянным давлением в ячейке поддерживали давление 245 - 250 кПа. При уменьшении давления в ячейке, по мере связывания газа в газовый гидрат на Р = 5 кПа, в нее добавляли исследуемую смесь, и значение давления вновь принимало исходное значение 250 кПа. Величина доли отбора определялась из уравнения:
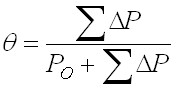. (42)
При втором варианте проведения эксперимента начальное давление в ячейке устанавливали равным РО = 250 кПа. По мере связывания газа в газовый гидрат, давление в ячейке понижалось до значения Рк. Доля отбора в этом случае определялось из уравнения:
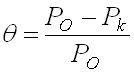. (43)
Полученные экспериментальные данные представлены на рисунках 13 и 14. Как видно из рисунков, с ростом доли отбора происходит увеличение фактора разделения смеси и наблюдается хорошее согласие между экспериментальными и расчетными значениями, полученными по уравнениям (38) – (41). Из приведенных результатов следует, что разработанная математическая модель хорошо описывает экспериментальные данные и может быть использована для практических расчетов фактора разделения газовых смесей газогидратным методом.
| Рис. 13. Зависимость фактора разделения F смеси SF6 - CCl2F2 от степени отбора при постоянном давлении. Концентрация примеси 3,5 % мол. Давление 250 кПа. Температура 273 К. | Рис. 14. Зависимость фактора разделения F смеси SF6 - CCl2F2 от степени отбора при направленной кристаллизации. Концентрация примеси 3,5 % мол. Температура 273 К. Начальное давление 250 кПа. |
Для организации непрерывного разделения и глубокой очистки газовых смесей необходима реализация нового процесса газогидратной кристаллизации – непрерывной газогидратной кристаллизации. В работе приведена математическая модель и результаты экспериментального исследования разделения газов методом непрерывной газогидратной кристаллизации.
При непрерывной газогидратной кристаллизации поток газовой смеси lвх направляется параллельно границе раздела фаз (ось X) и разделяется на два потока: первый поток lотб идет на образование газовых гидратов, а второй поток lвых идет на выход из кристаллизатора. Величина потока lотб определяется скоростью образования газовых гидратов и зависит от температуры и давления в системе, концентрации молекул гидратообразователя, площади поверхности контакта газ – вода.
Решая уравнение материального баланса для примесного компонента, получили зависимость концентрации примеси в газовой фазе от доли отобранного с газовыми гидратами газа:
, (44)
где С0 и Свых – исходная и конечная концентрация примеси соответственно; 
- доля потока вещества связанного в газовые гидраты.
Экспериментальная проверка полученных уравнений, проведенная аналогично двум предыдущим методам, показала хорошее согласие экспериментальных и расчетных значений фактора разделения. Таким образом, метод непрерывной газогидратной кристаллизации позволяет разделять газовые смеси с высокой эффективностью и может быть использован для очистки газов от примесей при несложном аппаратурном исполнении.
Глава 6. Глубокая очистка веществ кристаллизационными методами
Рассмотрим результаты расчетов параметров разделения и очистки газовых смесей ряда веществ, выполненных с использованием предложенных математических моделей.
Высокочистый бензол широко используется в аналитических целях в качестве внутреннего стандарта. Кроме того высокочистый бензол используется как растворитель в микроэлектронике и в волоконной оптике Глубокая очистка бензола методом противоточной кристаллизации из расплава с измельчением кристаллов позволила более чем на три порядка снизить содержание взвешенных наноразмерных частиц в очищаемом бензоле. После проведенной очистки содержание циклогексана, основной примеси в бензоле, уменьшилось в 20 раз и составило 210-4 %. масс. Результаты очистки хорошо согласуются с предварительно проведенными расчетами.
На примере глубокой очистки серы показано, что механическое измельчение кристаллов позволяет существенно повысить эффективность очистки при одной и той же высоте колонны. Концентрация гетерофазных включений в стеклах состава GeS3, полученных с использованием серы, очищенной по предложенной методике, уменьшилась более, чем на порядок, а концентрация примесных групп, таких как CS, SH, Ge-Н, сравнима с их концентрацией в стеклах, полученных после двухкратной дистилляции, то есть более энергоемким процессом. Кроме того, используемый метод очистки не вносит дополнительного загрязнения в очищаемое вещество. Удалось существенно снизить содержание ряда металлов в очищенном продукте.
Используя предложенный ранее алгоритм расчета, получены значения относительных коэффициентов распределения аргона, криптона и ксенона при газогидратной кристаллизации для разных составов исходной смеси и давления. Расчеты проводились как с учетом вспомогательного газа (сероводород или диоксид серы), так и без него. Из полученных результатов следует, что коэффициенты распределения слабо зависят от давления смеси, но существенно зависят от концентрации вспомогательного газа. Показано, что даже без использования вспомогательных газов за две стадии газогидратной кристаллизации можно практически полностью выделить ксенон из смеси. Причем, метод направленной кристаллизации позволяет более полно выделить ксенон, а кристаллизация при постоянном давлении, позволяет получить больший выход очищенного продукта.
Гексафторид серы, являющийся хорошим электроизоляционным газом, в настоящее время все более широко используется в различных приборах - от прерывателей мощных электроустановок до микросхем и лазерных установок. Помимо этого, гексафторид серы применяется в качестве технологической среды при термохимическом травлении и в качестве теплоносителя – диэлектрика в технологиях микроэлектронной техники. Гексафторид серы для всех перечисленных применений должен удовлетворять высоким требованиям к его чистоте.
На основании результатов рассмотрения газогидратного кристаллизационного метода, в работе был предложен способ глубокой очистки гексафторида серы, который включает в себя кроме метода газогидратной кристаллизации две дополнительные стадии очистки. Газогидратная кристаллизация применяется на первой стадии очистки газа. При этом из газовой фазы в твердую переходят примесные компоненты с относительным коэффициентом распределения Кi1 > 1, такие как CO2 и SO2. Для удаления паров воды, которыми насыщается очищаемый газ в процессе газогидратной кристаллизации, на втором этапе очистки предложено использовать криофильтрацию через волокнистые фильтры. На третьем этапе, для удаления оставшихся после двух стадий очистки примесных компонентов с относительным коэффициентом распределения Кi1 < 1, таких как N2 и O2, предлагается использовать низкотемпературную дистилляцию.
Разработанный газогидратный способ очистки гексафторида серы позволяет получить гексафторид серы, удовлетворяющий перспективным требованиям и пригодный для использования в электротехнической промышленности.
Впервые методом противоточной кристаллизации из расплава с механическим воздействием на кристаллы проведена глубокая очистка агрессивных веществ с низкой температурой плавления. Получены тетрахлориды титана и углерода и диэтилцинк, удовлетворяющие предъявляемым к ним требованиям.
Основные выводы
- Развито крупное научное направление, связанное с разработкой новых эффективных кристаллизационных методов разделения и глубокой очистки газовых смесей, повышением эффективности традиционных кристаллизационных методов и расширением круга удаляемых примесей в виде наноразмерных частиц.
- Разработана физико – химическая модель для расчета изменения размера кристаллов в противоточной кристаллизации из расплава в процессе механического воздействия на систему кристалл - расплав. Экспериментально полученные значения степени измельчения кристаллов хорошо согласуются с величинами, рассчитанными по предложенной модели.
- Теоретически и экспериментально показана эффективность очистки веществ в противоточной кристаллизационной колонне при механическом измельчении кристаллов. Установлено, что для системы бензол – тиофен концентрация примеси дополнительно уменьшается более, чем на порядок, а распределение примеси по высоте колонны с тремя дробителями приближается к экспоненциальному виду. Разработана физико-химическая модель расчета распределения примеси по высоте кристаллизационной колонны в зависимости от размера кристаллов и условий процесса. Экспериментально полученное распределение концентрации примеси по высоте колонны хорошо совпадает с результатами расчета.
- Впервые разработана физико-химическая модель перехода наноразмерных частиц из расплава в кристалл в процессе его роста с учетом их диффузионной подвижности. Установлено, что скорость перехода частиц зависит от условий роста кристалла и физико – химических свойств частицы и расплава. Полученные значения коэффициентов распределения наноразмерных частиц перед фронтом кристаллизации являются критерием эффективного удаления из кристаллов частиц радиусом 40 – 350 нм.
- Впервые разработана физико-химическая модель для расчета эффективности очистки жидкостей от наноразмерных взвешенных частиц методом противоточной кристаллизации в зависимости от доли перекристаллизовавшегося расплава. Показано, что при очистке веществ от наноразмерных частиц, основной вклад в разделение вносит перекристаллизация.
- Разработана физико-химическая модель для расчета коэффициентов распределения примесей между твердой и газовой фазами при газогидратной кристаллизации.
- Разработана методика экспериментального определения коэффициентов распределения примесей при газогидратной кристаллизации. Результаты расчета и экспериментально полученные значения коэффициентов распределения примесей хорошо согласуются между собой. Экспериментально определенные значения коэффициентов распределения использованы для расчета параметров межмолекулярного взаимодействия по типу “ гость – гость” и “хозяин – гость.
- Разработаны физико-химические модели для расчета зависимости концентрации примесей в газовой смеси от доли закристаллизовавшегося вещества для трех динамических методов. Экспериментальная проверка полученных уравнений показала хорошее согласие между экспериментально и расчетно полученными значениями фактора разделения.
- На основе разработанных кристаллизационных процессов и математических моделей выполнены расчеты глубокой очистки и разделения газовых смесей и проведена очистка ряда веществ: бензола, тетрахлоридов титана и углерода, диэтилцинка и серы, а также гексафторида серы. Проведен расчет разделения благородных газов методом газогидратной кристаллизации, позволяющий с высоким выходом выделить ксенон из смеси газов.
Основное содержание диссертации опубликовано в научных работах:
Статьи в рецензируемых журналах
- Девятых, Г.Г. Влияние измельчения кристаллов на глубину очистки веществ методом противоточной кристаллизации из расплава / Г.Г. Девятых, В.М. Воротынцев, В.М. Малышев, В.Б. Караксин // Доклады АН СССР. – 1987. - Т.297. №2. - С.396-398.
- Воротынцев, В.М. Влияние измельчения кристаллов на глубину очистки веществ методом противоточной кристаллизации из расплава / В.М. Воротынцев, В.М. Малышев, В.Б. Караксин, А.Р. Фидельман // Высокочистые вещества. – 1988. - №6. - С.47- 51.
- Воротынцев, В.М. Противоточная кристаллизационная колонна для глубокой очистки веществ / В.М. Воротынцев, В.М. Малышев, В.Б. Караксин // Высокочистые вещества. – 1990. - №4. - С.83-86.
- Воротынцев, В.М. О переходе частиц субмикронных размеров из расплава в кристалл в процессе кристаллизации разбавленных растворов электролитов / В.М. Воротынцев, В.М. Малышев // Высокочистые вещества. – 1991. - №1. - С. 92-96.
- Девятых Г.Г. Глубокая очистка веществ в противоточной сублимационной колонне с движением твердой фазы под действием силы тяжести / Г.Г. Девятых, В.М. Воротынцев, В.М. Малышев // Доклады АН СССР. – 1992. -Т.325. № 2. - С.334-336.
- Воротынцев, В.М. Влияние природы очищаемого вещества на степень измельчения кристаллов при глубокой очистке веществ в противоточной кристаллизационной колонне / В.М. Воротынцев, В.М. Малышев, В.Б. Караксин, А.Р. Фидельман // Высокочистые вещества. – 1992. - №4. - С.64- 68.
- Воротынцев, В.М. Противоточная кристаллизационная колонна для глубокой очистки летучих хлоридов и металлоорганических соединений / В.М. Воротынцев, В.М. Малышев, В.Б. Караксин // Высокочистые вещества. -1993. - №2. - С.68-71.
- Воротынцев, В.М. Способ определения коэффициентов разделения при сублимации / В.М. Воротынцев, В.М. Малышев, С.Ю. Кононенко // Высокочистые вещества. – 1993. - №2. - С.44-46.
- Воротынцев, В.М. Оптимизация отборного режима работы противоточной кристаллизационной колонны / В.М. Воротынцев, В.М. Малышев // Высокочистые вещества. – 1993. - №5. - С.37-43.
- Воротынцев, В.М. Газовые гидраты в процессе глубокой очистки газов. 1. Термодинамический анализ их структуры и условий образования с использованием модели идеальных растворов / В.М. Воротынцев, В.М. Малышев // Высокочистые вещества. – 1993. - №6. - С.50-59
- Воротынцев, В.М. Газовые гидраты в процессе глубокой очистки газов. II. Давление паров воды над поверхностью газовых гидратов летучих неорганических гидридов / В.М. Воротынцев, В.М. Малышев // Высокочистые вещества. – 1994. - №2. - С.38-46.
- Воротынцев, В.М. Газовые гидраты в процессе глубокой очистки газов. III. Относительные коэффициенты распределения компонентов смеси между газовой фазой и смешанным гидратом / В.М. Воротынцев, В.М. Малышев // Высокочистые вещества. – 1994. - №2. - С.84-88
- Воротынцев, В.М. Газовые гидраты в процессе глубокой очистки газов. IV Влияние состава газовой смеси на условия образования газовых гидратов и давление пара воды над их поверхностью / В.М. Воротынцев, В.М. Малышев // Высокочистые вещества. – 1994. -№6. - С.89-93
- Воротынцев В.М. Концентрирование техногенных примесей в газовых гидратах атмосферы / В.М. Воротынцев, В.М. Малышев //Доклады РАН. – 1996. - Т.351. №2. - С.256-259.
- Воротынцев, В.М. Газовые гидраты – новый класс примесей в особо чистых газах и газовый смесях / В.М. Воротынцев, В.М. Малышев // Успехи химии. – 1998. - Т.67. №1. - С. 87-99.
- Воротынцев, В.М. Расчет коэффициента распределения примесей между газом и газовыми гидратами / В.М. Воротынцев, В.М. Малышев // Журнал физической химии. – 1999. - Т. 73. №10. - С. 1892-1896.
- Воротынцев, В.М. Разделение газовой смеси методом газогидратной кристаллизации / В.М. Воротынцев, В.М. Малышев // Доклады РАН, 2000, т.372, № 2, С. 192 – 194.
- Воротынцев, В.М. Расчет коэффициентов распределения примесей при образовании газовых гидратов в гексафториде серы / В.М. Воротынцев, В.М. Малышев, П.Г. Тарабуров // Журнал физической химии, 2001, т. 75, №1, С. 129-133.
- Воротынцев, В.М. Разделение газовых смесей методом газогидратной кристаллизации / В.М. Воротынцев, В.М. Малышев, Г.М. Мочалов, П.Г. Тарабуров // Теоретические основы химической технологии, 2001, т.35, №2, С.128-132.
- Воротынцев, В.М. Разделение газовых смесей методом непрерывной газогидратной кристаллизации / В.М. Воротынцев, В.М. Малышев, Г.М. Мочалов, П.Г. Тарабуров // Теоретические основы химической технологии. – 2001. - Т.35. №5. - С.513-516.
- Воротынцев, В.М. Определение параметров межмолекулярного взаимодействия в газовых гидратах SF6 и CCl2F2 / В.М. Воротынцев, В.М. Малышев, П.Г. Тарабуров, И.В. Козырев // Журнал физической химии. – 2004. - Т. 78. №1. - С. 2035-2038.
- Воротынцев, В.М. Экспериментальное определение коэффициента распределения в системе газ – газовый гидрат / В.М. Воротынцев, В.М. Малышев, П.Г. Тарабуров, И.В. Козырев //Изв. ВУЗов. Химия и химическая технология.- 2004. - Т.47. вып. 4. - С.122-125.
- Воротынцев, В.М. Газовые гидраты: наноразмерные фазы в двухфазных методах разделения и очистки веществ / В.М. Воротынцев, В.М. Малышев // Успехи химии. -2011. – Т. 80, №10. – С. 1013 – 1033.
- Воротынцев, В.М. Глубокая очистка бензола от наноразмерных частиц методом противоточной кристаллизации из расплава / В.М. Воротынцев, В.М. Малышев // Вестник ННГУ.Серия Химия – 2011. - №4(1). – С. 118 – 122.
- Воротынцев, В.М. Глубокая очистка серы методом противоточной кристаллизации из расплава с механическим измельчением кристаллов / В.М. Воротынцев, В.М. Малышев // Теоретические основы химической технологии. – 2012. – Т. 46. № 5. – С. 563 – 568.
- Воротынцев, В.М. Расчет коэффициентов распределения и разделение газовой смеси аргона, криптона и ксенона методом газогидратной кристаллизации / В.М. Воротынцев, В.М. Малышев // Журнал Физ. Химии. - 2011. – Т.85. №11. – С. 2131- 2036
Статьи, опубликованные в других изданиях
- Воротынцев, В.М. О переходе частиц субмикронных размеров из расплава в кристалл в процессе кристаллизации / В.М. Воротынцев, В.М. Малышев //Сб. трудов «Техника и технология сыпучих материалов», Иваново, ИХТИ. – 1991. - С.111-116.
- Малышев, В.М. Газогидратный кристаллизациионный метод очистки фторуглеродов и гексафторида серы / В.М. Малышев, П.Г. Тарабуров, И.В. Козырев // Известия АИН РФ. - 2004. -Т. 7. - С. 134 – 141.
Авторские свидетельства и патенты РФ
- Девятых Г.Г., Воротынцев В.М., Малышев В.М., Караксин В.Б. Способ глубокой очистки веществ. // Авторское свидетельство СССР, № 1385343 от 01.12.1987.
Монография
- Воротынцев, В.М. Газогидратная кристаллизация / В.М. Воротынцев, В.М. Малышев. – Н.Новгород, НГТУ, – 2012. – 223 с.
