Адиабатическое замораживание воды холодом гранул льда как задача стефана
На правах рукописи
АЩЕУЛОВА
Алена Сергеевна
АдиабатическОЕ зАМОРАЖИВАНИЕ ВОДЫ ХОЛОДОМ ГРАНУЛ ЛЬДА КАК задачА Стефана
Специальность 02.00.04 «Физическая химия»
АВТОРЕФЕРАТ
диссертации на соискание учёной степени
кандидата физико-математических наук
Кемерово 2007
Работа выполнена в ГОУ ВПО «Кемеровский государственный сельскохозяйственный институт» на кафедре прикладной механики.
Научный руководитель: д.т.н, профессор
Полтавцев
Владимир Иванович
Официальные оппоненты: д. ф.-м. н., профессор
Полыгалов
Юрий Иванович
д.т.н., профессор
Попов
Анатолий Михайлович
Ведущая организация: Кузбасский государственный
технический университет
Защита диссертации состоится «___» ______ 2007 г._____в часов на заседании совета по защите диссертаций Д 212.088.03 в ГОУ ВПО «Кемеровский государственный университет» (650043, г. Кемерово, ул. Красная, 6).
С диссертацией можно ознакомиться в библиотеке ГОУ ВПО «Кемеровский государственный университет».
Автореферат разослан “____” ____________ 200 г.
Учёный секретарь
диссертационного совета Д 212.088.03
доктор химических наук,
профессор Кагакин Е.И.
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность работы. На территории России находится значительное количество рек. Ежегодно с наступлением зимы они уходят под лед, по которому прокладываются зимние дороги и строятся ледовые переправы путем намораживания искусственного льда. Ледовые переправы запускают в эксплуатацию в декабре, а закрывают весной. Стоимость строительства ледовых переправ высока: трасса в Юрге через реку Томь в этом году составили 2,7млн рублей. Экономически выгоден более ранний ввод переправ в эксплуатацию за счет сокращения сроков строительства путем применения искусственного гранулированного льда, получаемого в кипящем слое холодом атмосферного воздуха. Поэтому ускорение строительства переправ является актуальной задачей.
Для ее решения требуется метод расчета намораживания воды на поверхности гранул. Пленка воды на поверхности гранул в кипящем слое замерзает снизу от холода самой гранулы (адиабатический процесс), а сверху – за счет холода конвективного потока ожижающего агента. Движение границы слоя льда в адиабатическом процессе соответствует задаче Стефана, которая характеризуется существенной нелинейностью, исключающей получение аналитического решения. Общих аналитических методов ее решения при произвольной форме области и любом характере изменения температуры на ее границах до сих пор не найдено.
Работа выполнялась в соответствии с планом НИР:
Выполнение научно-исследовательских работ по приоритетным направлениям программы и поисковых исследований фундаментального характера молодыми учеными и преподавателями, проходящими стажировку в крупном (научно-исследовательском) центре - Кемеровском государственном сельскохозяйственном институте
Шифр 2006-РИ-111.0/001/017
Государственный контракт от 24 марта 2006г. №02.444.11.7324
Цель работы. Постановка, исследование и решение модели адиабатического намораживания льда на гранулах в виде задачи Стефана.
В соответствии с поставленной целью необходимо решить следующие задачи:
- Поставить математическую модель адиабатического процесса намораживания воды на поверхности сферической гранулы льда.
- Провести анализ устойчивости модели в заданных границах изменения параметров.
- Разработать метод численного расчета математической модели.
- Экспериментально исследовать процесс намораживания воды на одной и группе гранул в статических условиях.
- Экспериментально проверить кинетику роста льда в динамике на поверхности гранул в условиях кипящего слоя.
Научная новизна работы заключается в следующем:
- Поставлена математическая модель адиабатического намораживания льда на гранулах сферической формы в виде задачи Стефана.
- Создан метод численного расчета задачи Стефана для адиабатического процесса льдообразования.
- Созданы методы экспериментального исследования процесса намораживания воды на сферических гранулах льда в статических и динамических условиях.
- Получены экспериментальные характеристики области самозамораживания ледяных блоков с применением гранулированного льда.
Практическая ценность работы:
- На основе поставленной математической модели предложен метод расчета адиабатического процесса намораживания воды на поверхности гранул.
- Разработана экспериментальная методика определения кинетики роста льда на гранулах в статических и динамических условиях.
- Предложены технические решения использования снежной массы и холода снега для ускорения смерзания ледяных блоков.
Автор защищает:
- Математическую модель адиабатического процесса намораживания льда на гранулах сферической формы.
- Результаты теоретического исследования процесса намораживания льда на сферических гранулах.
- Результаты экспериментального исследования льдообразования на затравке льда.
- Обоснование области самозамораживания водо-снего-ледяных смесей и пределы ее существования.
Личный вклад автора в работы, выполненные в соавторстве и включенные в диссертацию, состоял в общей постановке задачи, активном участии в проведении экспериментальных исследований, анализе и интерпретации полученных данных, написании статей.
Апробация работы: основные положения и результаты исследований, проведенных в работе, докладывались и обсуждались на Всероссийской научно-практической конференции, посвященной 75-летию Чувашской государственной сельскохозяйственной академии (Чувашская государственная с/х академия), Всероссийской научной конференции молодых ученых «Наука. Технологии. Инновации» (Новосибирская с/х академия), на региональных научно - практических конференциях «Тенденции и факторы развития агропромышленного комплекса Сибири» (Кемеровский государственный сельскохозяйственный институт в 2005 и 2006 годах), а так же на международной школе - конференции молодых ученых, аспирантов и студентов «Проблемы рационального природопользования техногенного региона» (Кемеровский государственный сельскохозяйственный институт).
Публикации. Полный список публикаций включает 13 наименований и приведен в конце реферата.
Структура и объем диссертации. Работа состоит из введения, пяти глав, выводов, списка литературы из 138 наименований и 5приложений. Общий объем диссертации составляет 121 страницу основного текста, 43 рисунка, 35 таблиц.
КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ
Во введении обоснована актуальность проблемы, сформулированы цели и задачи исследования, показана научная новизна и практическая ценность работы, изложены основные положения диссертации, выносимые на защиту, приведены сведения об апробации и публикациях основных результатов.
В первой главе проводится обзор современных литературных данных по физической сущности задачи Стефана, физическим основам теории фазового превращения вода-лед, существующих математических моделей задачи Стефана с фазовым переходом, методов численного решения.
Во второй главе рассматривается математическая модель фазового превращения с участием фаз: твёрдое тело - жидкость. Примером таких систем являются процессы затвердевания и плавления. Соответствующие математические модели характеризуются наличием подвижных, заранее неизвестных границ фазового перехода - задач со свободными (неизвестными) границами. Основная предпосылка при моделировании фазовых превращений состоит в том, что фазовый переход происходит при заданной постоянной температуре фазового перехода Т*. Фазовый переход происходит на границе раздела фаз, которую мы обозначаем S=S(t). Эта граница разделяет расчётную область ![]() на две подобласти. Область
на две подобласти. Область ![]() , занята твердой фазой, где температура превышает температуру фазового перехода:
, занята твердой фазой, где температура превышает температуру фазового перехода: ![]() Соответственно, область
Соответственно, область ![]() занята жидкой фазой:
занята жидкой фазой: ![]()
Имеется гранула льда сферической формы радиуса ![]() с температурой
с температурой![]()
![]() . Такую сферу помещаем в воду, температура которой близка к 0С.
. Такую сферу помещаем в воду, температура которой близка к 0С.
Пусть U(r,t) - функция описывающая распределение температуры в грануле в любой момент времени. Таким образом, получаем начальные условия:
![]()
Максимально возможный радиус гранулы в результате ее погружения в воду можно получить из общего баланса тепла, исходя из условия, что весь лёд нагрелся до температуры 0°C, и температура воды не изменилась.
![]()
Уравнение теплового баланса имеет вид:
![]() , (1)
, (1)
где
![]() , c – плотность и теплопроводность льда;
, c – плотность и теплопроводность льда;
![]() – плотность воды;
– плотность воды;
q – энергия фазового перехода, потраченная на единицу массы воды.
С помощью преобразований из (1) выводим максимальный радиус гранулы при использовании ее холода:
![]() (2)
(2)
Рассмотрим процесс намораживания льда за некоторый промежуток времени ![]() :
:
![]()
Всегда должно выполняться уравнение баланса внутри гранулы:
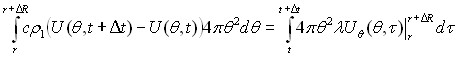 .
.
![]() - поток тепла по закону Фурье.
- поток тепла по закону Фурье.
Сделаем замену:
![]() , тогда
, тогда 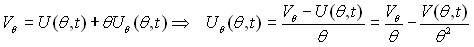 .
.
![]() .
.
Следовательно, подынтегральное выражение равно 0. Таким образом, приходим к следующему уравнению:
![]() . (3)
. (3)
Уравнение (3) описывает закон, по которому меняется температура внутри гранулы льда.
Для завершения построения математической модели процесса намораживания воды на гранулу льда сферической формы необходимо рассмотреть процессы, протекающие на неизвестной (свободной) границе ![]() .
.
Рассмотрим уравнение баланса на границе:
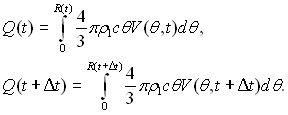
![]() - тепло, которое израсходуется на процесс кристаллизации, то есть:
- тепло, которое израсходуется на процесс кристаллизации, то есть:
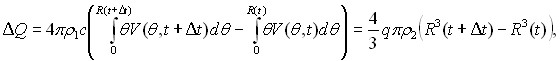
или
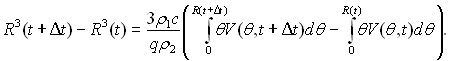
Преобразовав разность интегралов и воспользовавшись уравнением (3), учитывая условие ![]() на разделе границе фаз. Разделим на
на разделе границе фаз. Разделим на ![]() , и
, и ![]() , получим:
, получим:
![]() (4)
(4)
Уравнение (4) связывает скорость движения свободной границы и источник тепла на ней.
Таким образом, мы пришли к следующей краевой задаче:
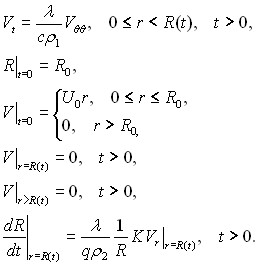 (5)
(5)
Аппроксимируем уравнение
![]() . (6)
. (6)
Для построения разностной схемы надо прежде всего ввести сетку в области изменения независимых переменных и задать шаблон, то есть множество точек сетки, участвующих в аппроксимации дифференциальной задачи (6). Сначала введем пространственную сетку по переменной r с шагом h и временную сетку по переменной t с шагом. Точки ![]() и
и ![]() образуют узлы пространственно – временной сетки:
образуют узлы пространственно – временной сетки:
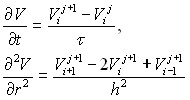
тогда
![]() .
.
В результате получим следующую систему разностных уравнений на (j+1)-ом слое по времени:
![]() (7)
(7)
здесь
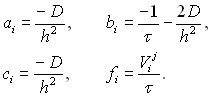
Разностная схема (7) аппроксимирует исходное уравнение (4) с первым порядком точности по t и вторым по r.
Реализацию конечно-разностной схемы проведем методом прогонки. Суть этого метода заключается в том, что решение разностного уравнения второго порядка ищется как решение разностного уравнения первого порядка с неизвестными коэффициентами и правой частью.
Неизвестные величины вычисляются по рекуррентным формулам с помощью одного из условий. После, с помощью другого краевого условия, решается разностное уравнение первого порядка с вычисленными коэффициентами и, таким образом, находится решение исходной задачи.
В соответствии c методом прогонки будем искать решение разностных уравнений (7) в виде:
![]() (8)
(8)
Отсюда найдем
![]()
и подставим в (7):
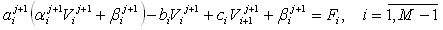 . (9)
. (9)
Сравнивая (8) и (9), получаем
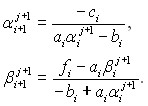
Из граничных условий и условия ![]() находим
находим ![]() и
и ![]() .
.
Радиус в узлах данной сетки вычисляем по следующей формуле:
![]()

В третьей главе изложена методика экспериментальной работы.
Экспериментальное определение скорости движения границы намерзающего слоя льда на поверхности гранул требовало создания сфер изо льда с приемлемыми для опытов размерами в пределах 40-50 мм. Нами были проверены два широко известных способа формования сферических тел, в частности, изо льда:
- Замораживание (отливка) сферических гранул.
- Оплавление колотых частиц льда.
После их детального анализа создан и апробирован следующий способ получения сферических гранул льда в виде шара.
Мы использовали цилиндро-сферические колпачки (рис.2) из-под медицинских бахил.
Колпачок выполнен прозрачным из полистирола и имеет идеальную по сферичности нижнюю часть. Для крепления колпачков использованы отработанные доски лабораторных столов, в которых сверлились отверстия конической формы с конусностью несколько процентов, что было достаточно для надежной установки колпачков в вертикальном положении.
С помощью таких колпачков замораживалась вода в виде полусфер, которые в последствии шлифовались по плоскости и смораживались вместе, образуя идеальную по форме шарообразную частицу льда, пригодную для экспериментов по определению скорости продвижения границы новообразовавшегося льда. На плоской грани одной из полусфер (для потая) при помощи паяльника с заостренным наконечником проплавлялся криволинейный паз, в который, с целью фиксации, укладывался фигурный конец проволоки, повторяющий форму паза; паз накрывался второй полусферой, образуя систему гранула-стержень (рис.3).
С целью удобства проведения и уменьшения погрешности эксперимента, нами сконструирована система подвеса, в которой гранулы с помощью стержней (отрезки медной проволоки) крепились к прямоугольной деревянной рамке – основанию подвеса (рис.3).
Стык полусфер подобной гранулы с проволокой поливался водой, полусферы схватывались первоначально, окунались в воду и на морозе превращались в шары, подвешенные на медных проволочках. Подобные модельные тела были удовлетворительными по всем параметрам: точности шарообразной формы, простоте вспомогательных устройств для изготовления полусфер, малом времени доводки полусфер, небольших затрат труда для укладки медных проволок, малого времени для сборки подвесов.
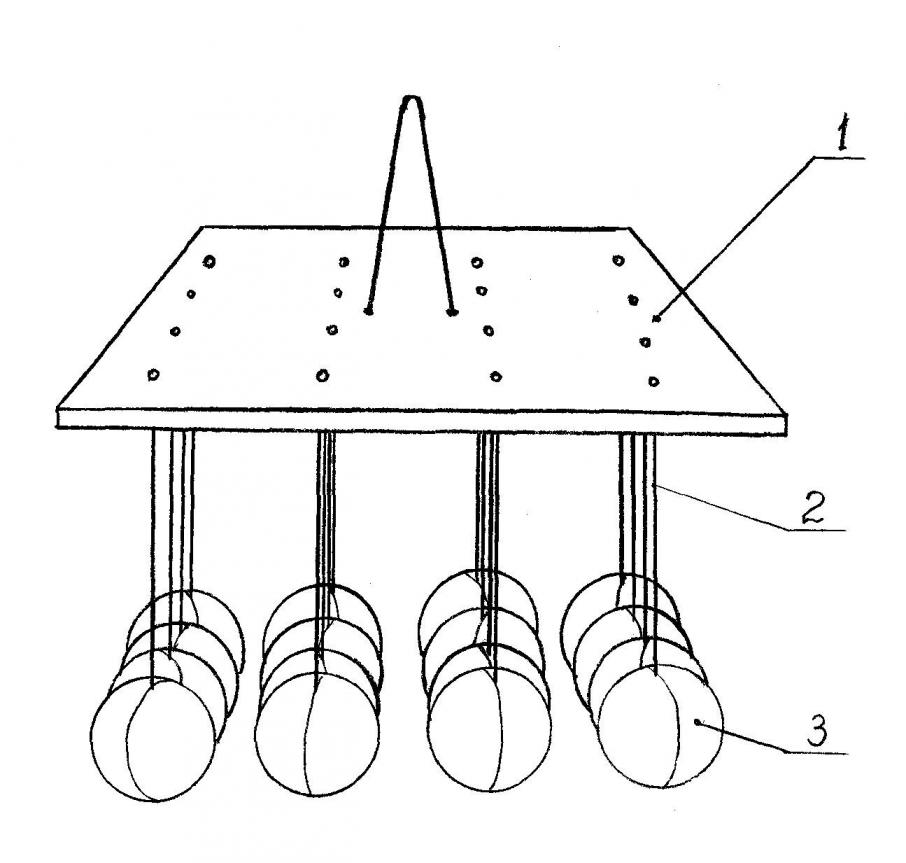
Рис.3. Конструкция подвеса в виде рамки с 16 гранулами:
1-основание; 2 – стержень; 3 – гранула;
2 и 3 образуют систему гранула - стержень.
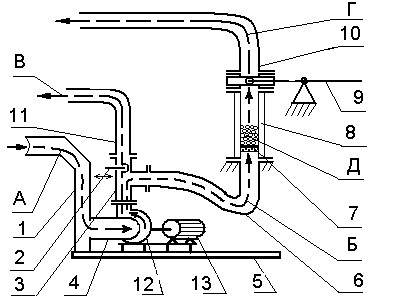
Рис. 4. Модельная установка с кипящим слоем
А-всасываемый поток, Б-нагнетаемый поток, В – регулировочный поток,
Г- выхлоп, Д-затравка; 1- всасывающий трубопровод, 2-регулировочная заслонка,
3- тройник, 4- гибкий рукав, 5- рама, 6-рукав ввода в камеру, 7- распределительная решетка, 8- камера кипящего слоя, 9- рычаг уплотнительного устройства,
10- выпускной трубопровод, 11- перепускной трубопровод, 12- вентилятор высокого давления, 13-электродвигатель.
Основными требованиями, предъявляемыми к льдогенераторам, как и к другим теплообменным устройствам, является простота конструкции, низкая стоимость материалов для их изготовления и высокая интенсивность процессов теплообмена. При определённых условиях эксплуатации этим требованиям в достаточной степени отвечает аппарат, экспериментальная модель которого была разработана и создана для определения режимных параметров процесса льдообразования в кипящем слое. Схема установки показана на рисунке 4.
Экспериментальное устройство относится к аппаратам для контактирования в двухфазных системах твёрдое тело – газ (воздух) и может быть использовано для проведения технологического процесса получения искусственного гранулированного льда, используемого в промышленных целях и для охлаждения пищевых и молочных продуктов.
Работа установки осуществлялась следующим образом: по всасывающему трубопроводу 1 и гибкому рукаву 4 вентилятором 12 засасывался холодный атмосферный воздух. Поток этого воздуха через тройник 3 по патрубку 6 подавался через решетку 7 в камеру кипящего слоя 8. Привод вентилятора осуществлялся электродвигателем 13, причем его крепление, как и крепление вентилятора 12 с патрубком 4, самым жестким образом осуществлено на раме 5.
Загрузка камеры 8 ледяной затравкой осуществлялась через верхний фланец выпускного трубопровода 10 с уплотнительным устройством рычага 9.
С помощью регулировочной заслонки 2 нагнетательный поток воздуха Б регулируется по своей величине: от режима начала кипения - до режима устойчивого псевдоожижения при максимальных размерах гранул льда. Избыток воздуха сбрасывается по патрубку В.
Во время кипения гранул через отверстие в выпускном трубопроводе 10 циклически впрыскивалась вода, размер капель которой можно оценить как 0,4-1,8 мм. Оценка производилась с помощью фотосъемки. Цель экспериментов на установке – определение удельной скорости намораживания воды в интервале слабого мороза с температурой от –5°С до –15°С, что соответствует погодным условиям начала зимы. Можно с уверенностью говорить, что при этих температурах кипящий слой в промышленном варианте может дать удельную производительность порядка 9-11 т льда в час с 1 куб.м рабочего объема кипящего слоя.
Полученные в таких условиях гранулы можно характеризовать следующим образом:
- Температура выходящих из кипящего слоя гранул от –3°С до –6°С, и соответственно они имеют низкую механическую прочность.
- Хранение такого льда в условиях недостаточного холода атмосферного воздуха требует мер против режеляции гранул, например пересыпкой гранулированной массы льда небольшим количеством древесных опилок.
Достоинством установки кипящего слоя, кроме высокой производительности, является низкий уровень энергетических затрат, поскольку гидравлическое сопротивление слоя невелико: 100–120 мм вод.ст.
В четвёртой главе исследована кинетика адиабатического намораживания льда.
Кинетика роста гранул льда исследовалась в статических условиях и условиях кипящего слоя.
Статические условия:
Целью эксперимента являлся сбор данных, характеризующих процесс льдообразования на поверхности гранул за счет их внутреннего холода в статических условиях, а сам эксперимент осуществлялся по следующей схеме:
- Измерение начальных диаметров охлажденных гранул.
- Измерение начальной массы охлажденного набора.
- Опускание гранул в предварительно охлажденную до 00С воду на некоторый промежуток времени.
- Измерение диаметров гранул после опускания в холодную воду.
- Измерение массы набора после опускания в холодную воду.
- Обработка данных, заключающаяся в подсчете изменений диаметров и масс гранул.
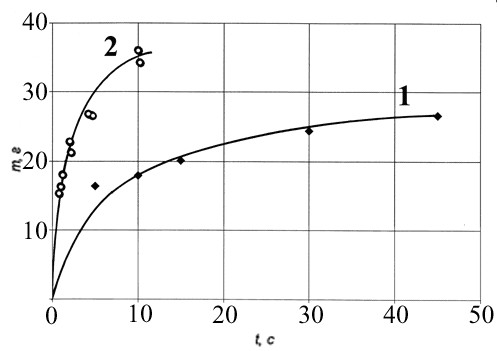
Эксперименты проводились в широком температурном диапазоне от -50С до -420С, при различном времени погружения гранул в воду от одной до 50 сек (результаты всех измерений вносились в рабочий журнал от 27.10.05г).
Результаты эксперимента обобщены в виде графика зависимости прироста массы (m, г) от времени (t, с) опускания льда в воду с температурой 0оС (рис.5).
Условия кипящего слоя
Схема эксперимента в кипящем слое:
- Взвешивание пустой камеры кипящего слоя.
- Охлаждение воды для подачи в камеру кипящего слоя, до 0С и ее взвешивание.
- Охлаждение камеры вместе с установкой (прогонка вхолостую).
- Охлажденные гранулы засыпаются в камеру кипящего слоя и взвешиваются. Получаем чистый вес льда.
- Процесс наморозки.
- Взвешивание камеры вместе с гранулами после намораживания.
- Обработка полученных результатов.


Предложен новый способ получения моноблока льда. Приготовление водно-снеговой суспензии и применение ее для заливки порозного пространства слоя гранул приводит к уменьшению доли жидкости в снежно-гранульном континууме. Подвижность водно-снеговой суспензии всецело зависит от соотношения содержания снега и воды и при некотором его значении суспензия не перемешивается мешалкой и не перекачивается насосом. Рассчитано соотношение - лед: вода: снег (рис.8).
Рис.6. Начальные размер Рис.7. Размер гранул
гранул после эксперимента
В пятой главе предложено практическое использование гранулированного льда
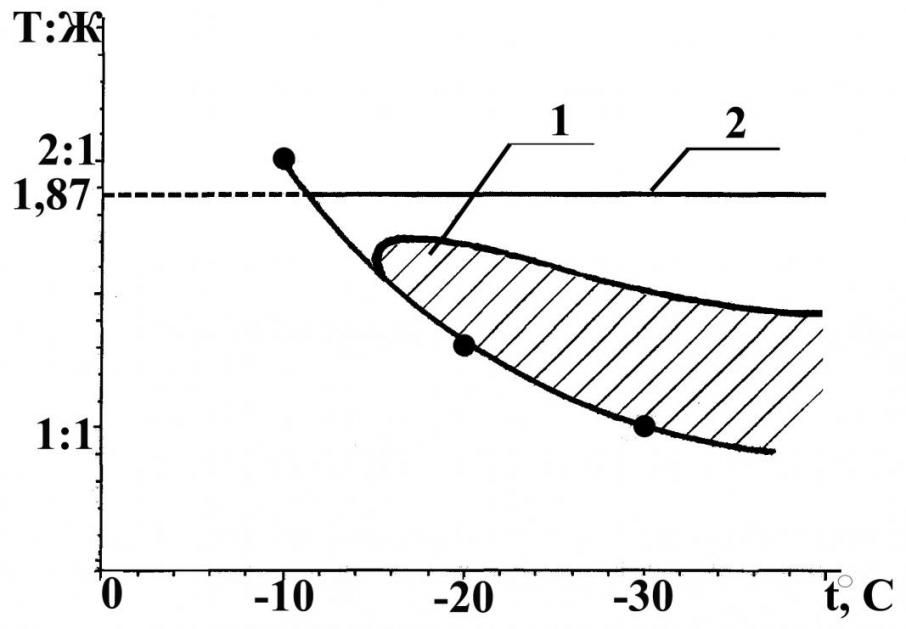
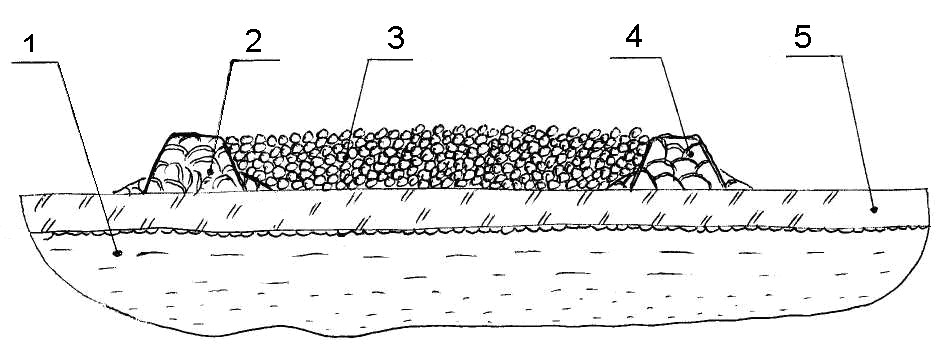
Рис.9. Наращивание ледовой переправы:
1-вода реки, 2, 4 - бурты, 3-гранулированная масса,
5 – ледяное полотно реки
Ледовые переправы, построенные с применением гранулированного льда, могут иметь следующие преимущества:
- повышение несущей способности;
- сокращение сроков строительства;
- применение простейшего оборудования без ледорезной техники;
- усиление монолитности ледяного покрова;
- сокращение сроков и стоимости подготовки переправы;
- увеличение сроков эксплуатации переправы;
- удешевление сооружения.
ВЫВОДЫ
- При помощи математического моделирования поставлена математическая модель адиабатического намораживания воды для сферических частиц, а также найдена функция зависимости максимально возможного радиуса гранулы льда от его начальной температуры. Найден закон изменения температуры внутри гранулы в процессе намораживания льда.
- Предложен и реализован алгоритм численного решения поставленной модели.
- Разработана методика экспериментального измерения кинетики намораживания льда в статике и условиях кипящего слоя. Экспериментально получена кинетика роста льда при различных температурных режимах.
- Показано, что предложенный метод использования гранулированного льда в строительстве ледовых переправ значительно ускоряет процесс.
- Выявлена область самозамораживания ледяных моноблоков при использовании гранулированного льда.
СПИСОК ЦИТИРУЕМОЙ ЛИТЕРАТУРЫ
- Тихонов, А. Н. Уравнения математической физики / А. Н. Тихонов, А. А. Самарский. – М.: Наука, 1977. – 736 с.
- Гольдман, Н. Л. Обратные задачи Стефана. Теория и методы решения / Н. Л. Гольдман. – М.: Изд-во МГУ, 1999.
- Лыков, А. В. Теория теплопроводности / А. В. Лыков. – М.: Высшая школа, 1967. – 599 с.
- Майрманов, А. М. Задача Стефана / А. М. Майрманов. – Новосибирск: Наука, 1986.
ОСНОВНЫЕ РЕЗУЛЬТАТЫ РАБОТЫ ОТРАЖЕНЫ В СЛЕДУЮЩИХ ПУБЛИКАЦИЯХ
- Ащеулова, А. С. Математическая модель намораживания гранул льда для ледовых переправ в виде задачи Стефана / А. С. Ащеулова, А. А. Храпов, В. В. Рагулин, В. И. Полтавцев // Бурение и нефть. – 2007. – №4 –. С.17–19.
- Ащеулова, А. С. Задача Стефана для адиабатического намораживания воды холодом гранул / А. С. Ащеулова, А. А. Храпов, В. В. Рагулин, В. И. Полтавцев // Вестник КрасГАУ. – 2007. – №1. –С.26–30
- Ащеулова, А. С. Моделирование процесса послойного намораживания льда / А. Г. Селедков, В. И. Полтавцев, С. Ю. Гончаров, А. С. Ащеулова // Доклады научно-практической конференции «Тенденции и факторы развития агропромышленного комплекса Сибири». –Кемерово, 2005. –С. 185–187.
- Ащеулова, А. С. Моделирование задачи Стефана при намораживании воды на поверхности гранул льда / А. А. Храпов, А. С. Ащеулова// Материалы VI Региональной научно-практическая конференции студентов, аспирантов и молодых ученых. 10 апреля, 2006 г. – Новокузнецк: НФИ КемГУ, 2006. – С. 10–12.
- Ащеулова, А. С. Задача Стефана как модель адиабатического процесса намораживания воды на гранулах льда / А. А. Храпов, В. И. Полтавцев, А. С. Ащеулова // Вестник Кемеровского государственного сельскохозяйственного института. – №2. – Кемерово: Кузбассвузиздат, 2006. – С. 193–199.
- Ащеулова, А. С. Алгоритм расчета задачи фазового перехода методом сеток / В. В. Рагулин, В. И. Полтавцев, А. С. Ащеулова // Вестник Кемеровского государственного сельскохозяйственного института №2.- Кемерово: Кузбассвузиздат, 2006. –С. 199-202.
- Ащеулова А.С. Гранулированный лед в строительстве ледовых переправ и зимников/ А.А. Храпов, В.И. Полтавцев, А.С. Ащеулова // Вестник Кемеровского государственного сельскохозяйственного института. – №2. – Кемерово: Кузбассвузиздат, 2006. – С.235–242.
- Ащеулова, А. С. Использование холода в адиабатическом процессе получения ледяных гранул / А. А. Храпов, В. И. Полтавцев, А. С. Ащеулова // Доклады научно-практической конференции «Тенденции и факторы развития агропромышленного комплекса Сибири». – Кемерово, 2006. – С. 233–236.
- Ащеулова, А. С. Кондуктор для получения ледяной затравки / А. А. Храпов, В. И. Полтавцев, А. С. Ащеулова // Доклады научно-практической конференции «Тенденции и факторы развития агропромышленного комплекса Сибири». – Кемерово, 2006. – С. 256–258
- Ащеулова, А.С. Моделирование задачи Стефана в адиабатическом процессе намораживания гранул льда / А. С. Ащеулова // Материалы Всероссийской научной конференции молодых учёных «НАУКА. ТЕХНОЛОГИИ. ИННОВАЦИИ».В 7 частях. – Новосибирск: НГТУ, 2006. – Часть.2 – С.259–260
- Ащеулова, А. С. Намораживание льда на поверхности гранул в условиях адиабатического процесса / А. А. Храпов, В. И. Полтавцев, А. С. Ащеулова // Актуальные вопросы совершенствования технологии производства и переработки продукции сельского хозяйства: Мосоловские чтения / Материалы межрегиональной научно-практической конференции. – Йошкар-Ола. – 2006. – Вып. 8. – С.257–259.
- Ащеулова, А. С. Операционный метод решения задачи адиабатического процесса намораживания льда / А. А. Храпов, В. И. Полтавцев, А. С. Ащеулова // «Проблемы рационального природопользования техногенного региона»: сборник научных трудов Международной школы - конференции молодых ученых, аспирантов и студентов. 15-17 декабря, 2005, КГСХИ. – Кемерово: Кемеровский ГСХИ, 2006. – С.261-264.
- Ащеулова, А. С. Ледовые переправы: необходимость, стоимость, опасность / В. И. Полтавцев, Л. А. Полтавцева, А. С. Ащеулова // «Роль науки и образования в инновационных процессах регионов»: материалы Всероссийской научно-практической конференции, посвященной 50-летию образованию кафедры «Общеинженерные дисциплины». – Улан-Удэ: Изд-во БСХА им. В. Р. Филиппова, 2007. – С.153–155.
Принятые обозначения
| начальный радиус | |
| начальная температура | |
| t | время |
| R(t) | радиус в момент времени t |
| U(r,t) | функция описывающая распределение температуры в грануле в любой момент времени |
| плотность льда | |
| c | теплопроводность льда |
| плотность воды | |
| q | энергия фазового перехода, потраченная на единицу массы воды |
| максимальный радиус гранулы при использовании ее холода | |
| изменение радиуса за время |
Подписано к печати 13.04.2007г. Формат 60x84 1/16.
Бумага офсетная №1. Печать офсетная. Усл. печ. л. 1,5.
Тираж 100 экз. Заказ № 37/
____________________________________________
ГОУ ВПО «Кемеровский государственный университет».
650043, г. Кемерово, ул. Красная, 6.
Отпечатано в типографии издательства «Кузбассвузиздат».
650043, г. Кемерово, ул. Ермака, 7.

