Фазовые переходы первого рода в контакте низкоплавких металлов
На правах рукописи
Саввин Владимир Соломонович
ФАЗОВЫЕ ПЕРЕХОДЫ ПЕРВОГО РОДА
В КОНТАКТЕ НИЗКОПЛАВКИХ МЕТАЛЛОВ
01.04.14 – Теплофизика и теоретическая теплотехника
Автореферат
диссертации на соискание ученой степени
доктора физико-математических наук
НАЛЬЧИК 2009
Работа выполнена на кафедре физики ГОУ ВПО
«Уральский государственный технический университет–УПИ
имени первого Президента России Б.Н.Ельцина», г. Екатеринбург
Научный консультант –
доктор физико-математических наук,
профессор Повзнер Александр Александрович
Официальные оппоненты:
доктор физико-математических наук,
профессор Гуфан Юрий Михайлович
доктор физико-математических наук,
профессор Загребин Леонид Дмитриевич
доктор физико-математических наук,
профессор Попель Пётр Станиславович
Ведущая организация –
Институт теплофизики УрО РАН (г. Екатеринбург)
Защита состоится « 17 » июня 2009 г. в 14.00 часов на заседании диссертационного совета Д 212.076.02 при Кабардино-Балкарском госуниверситете им. Х.М. Бербекова по адресу: 360004, КБР, г.Нальчик, ул.Чернышевского, 173.
С диссертацией можно ознакомиться в библиотеке
Кабардино-Балкарского государственного университета.
Автореферат разослан « » февраля 2009 г.
Ученый секретарь
диссертационного совета А.А. Ахкубеков
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы исследования. Процессы зарождения, роста и взаимодействия фаз находятся в центре внимания современной физики конденсированного состояния. В основе научных представлений о равновесии фаз лежит классическая работа Дж.В. Гиббса [1].
Полное описание процессов фазообразования выходит не только за рамки классической термодинамики, но и линейной неравновесной термодинамики. Отсутствие фундаментальной теории образования фаз в условиях, далеких от равновесия, повышает роль экспериментальных исследований.
Существующие взгляды на взаимодействие фаз при фазовых переходах первого рода не перекрывают спектра имеющегося экспериментального материала. Отсутствие в контактной зоне фаз, имеющихся на диаграмме состояния, возникновение метастабильных состояний в нанослоях, примыкающих к межфазным границам, роль поверхностного слоя на границе взаимодействующих фаз, – вот неполный перечень проблем, требующих решения при исследованиях возникновения и роста промежуточных фаз.
Ряд вопросов, связанных с образованием новых фаз, остаются дискуссионными. В частности, в литературе активно обсуждается природа возникновения промежуточной жидкой фазы в контакте разнородных веществ – контактное плавление. Развитие получили диффузионная и адгезионная гипотезы, которые не охватывают имеющиеся экспериментальные результаты.
Таким образом, актуальна разработка модели образования и роста новой фазы в контакте разнородных веществ, которая соответствует экспериментальным фактам. Эта модель строится на основе рассмотрения особенностей состояния вещества в области контакта разнородных фаз. В частности, непосредственно при приведении в контакт разнородных кристаллов, вещество в области контакта находится в экстремальном состоянии. Реакцией системы на экстремальное состояние является контактное плавление или Т-эффект контактного плавления.
Для выяснения природы указанных особенностей необходима разработка экспериментальных методов изучения физических свойств твердого и жидкого состояния в области контакта разнородных веществ, в частности, состава, фазового состояния, а в случае Т-эффекта и температуры вещества на межфазных границах.
Целью работы является выяснение особенностей возникновения, формирования и развития новых фаз на межфазной границе разнородных веществ, в частности металлов, при фазовых переходах первого рода. Для достижения указанной цели решены следующие задачи:
- разработана методика и осуществлена оценка толщины поверхностного слоя на границе жидкий металл–собственный пар и межфазного слоя между твердыми растворами;
- экспериментально исследована кинетика роста жидкой фазы в двухкомпонентных металлических системах простого эвтектического типа и содержащих промежуточные фазы. Контактные пары составляли чистые металлы, твердые растворы, интерметаллиды;
- построена математическая модель роста промежуточных фаз, учитывающая объемные эффекты фазовых переходов первого рода;
- разработана методика измерения температуры контакта разнородных веществ в процессе фазовых переходов первого рода. С помощью разработанной методики исследован Т-эффект контактного плавления в системах с конгруэнтно и инконгруэнтно плавящимися промежуточными фазами;
- на основе результатов исследования возможности Т-эффекта контактного плавления в ртутных системах сформулировано правило знаков тепловых эффектов зарождающихся фаз;
- разработана и применена методика компьютерного эксперимента для исследования роста промежуточных фаз в контакте разнородных металлов.
Научная новизна. В процессе выполнения работы впервые получены следующие научные результаты:
- разработана методика и осуществлена оценка энтропии межфазного слоя, образуемого контактом твердых растворов. Показано, что в отличие от критического фазового перехода, толщина межфазного слоя, образованного эвтектической парой твердых растворов при эвтектической температуре, конечна;
- построена математическая модель диффузионного роста промежуточной жидкой фазы, учитывающая объемные эффекты плавления;
- сформулированы представления о последовательности процессов, происходящих при контактном плавлении, адекватные экспериментальным результатам, согласно которым промежуточные твердые фазы и насыщенные твердые растворы образуются в контактной прослойке в результате распада метастабильных участков жидкой прослойки;
- разработан способ измерения температуры контакта разнородных веществ в процессе фазовых переходов первого рода. Измерена температура контакта пар образцов систем с промежуточными твердыми фазами в процессе Т-эффекта контактного плавления;
- исследована возможность спекания образцов ртутных систем с промежуточными фазами при температурах, ниже эвтектических. На основе полученных результатов сформулировано правило знаков тепловых эффектов зарождающихся фаз;
- разработана методика компьютерного эксперимента, имитирующего контактное плавление в нестационарно–диффузионном режиме. С помощью компьютерного эксперимента исследовано контактное плавление в простых эвтектических системах и в системах с промежуточными твердыми фазами. Подтверждена возможность осуществления последовательности процессов, включающих образование и последующий распад метастабильной жидкости. Полученные результаты адекватны результатам реального эксперимента.
Достоверность полученных результатов обеспечена
- использованием апробированных экспериментальных методов, соответствующих задачам исследования, и корректной оценкой погрешностей измерений;
- единством экспериментальных результатов, их интерпретации и соответствующей этим результатам модели явлений, происходящих при зарождении и росте промежуточных фаз в контакте разнородных металлов;
- непротиворечивостью предложенных решений известным положениям теплофизики и физики конденсированного состояния.
Практическая значимость работы. Методика оценки толщины поверхностного слоя применяется при исследованиях поверхностных и межфазных явлений.
Оценка температурного коэффициента поверхностного натяжения, характеризующего межфазную границу твердых растворов, составляющих эвтектическую пару, может использоваться как в теории межфазного взаимодействия, так и в практических целях, например для оптимизации режимов гомогенизации сплавов.
Разработанная методика косвенного измерения состава жидкости на границе с кристаллами применяется для исследования фазообразования в контактной зоне.
Способ измерения температуры в контакте разнородных образцов применяется для исследования кинетики фазовых превращений и химических реакций, происходящих между твердыми телами.
Разработанные представления о процессах, происходящих при Т-эффекте контактного плавления, позволяют целенаправленно подходить к выбору компонентов для осуществления соединения образцов при температурах, ниже эвтектической.
Методика компьютерного эксперимента, разработанная для исследования контактного плавления в простых двухкомпонентных эвтектических системах и системах с промежуточными фазами, применяется для исследования фазообразования в контакте разнородных веществ.
Сведения о природе состояния вещества на границе разнородных фаз находят применение в металлургии, порошковой металлургии, микроэлектронике, где используются сплавы с диаграммами состояния эвтектического типа. Исследование процессов формирования переходных слоев необходимо для создания конструкционных материалов с заданными свойствами, так как механические и коррозионные свойства конструкционных материалов в конечном итоге определяются фазовым составом и состоянием межфазных границ. Детальный анализ явлений, происходящих на межфазных границах важен при разработке электронных приборов с различными типами электронно-дырочных переходов. Перспективным направлением практического применения результатов исследований фазообразования на межфазных границах является разработка и совершенствование композиционных и наноматериалов.
Изложенные в работе представления о возникновении и росте промежуточных фаз используются в процессе преподавания курса «Строение и теплофизические свойства металлов и сплавов» и в специальном физическом практикуме для студентов специальности "Физика" Уральского государственного технического университета–УПИ. Методика расчета эффективной толщины поверхностного слоя применяется в курсе физики поверхностных явлений, читаемом студентам физического факультета Чеченского государственного университета.
Основные положения, выносимые на защиту:
- роль межфазного слоя, образованного компонентами эвтектической пары, в процессе зарождения жидкой фазы при контактном плавлении;
- методика определения и экспериментальные результаты измерений состава жидкости на границе с исходными твердыми фазами при контактном плавлении в простых эвтектических системах и в системах с промежуточными твердыми фазами;
- способ и результаты измерения температуры контакта при Т-эффекте контактного плавления;
- модель реализациии условий квазиравновесности на межфазных границах путем кристаллизации метастабильной жидкости;
- методика и результаты компьютерного эксперимента по исследованию контактного плавления с возможностью образования метастабильной жидкости.
Личный вклад автора. Диссертация представляет итог самостоятельной работы автора, обобщающий полученные им, а также в соавторстве с сотрудниками результаты. Соавторы участвовали в апробации авторских свидетельств и патента, проведении экспериментов, обработке и обсуждении некоторых результатов, за что автор им благодарен.
Автору принадлежит выбор направления работ, трактовка и обобщение большинства полученных результатов.
Научный консультант, профессор А.А. Повзнер, участвовал в обсуждении отдельных результатов, и постановку некоторых задач, за что автор выражает свою признательность.
Апробация работы. Основные положения и результаты работы докладывались и обсуждались на межвузовской научной конференции по физике межфазных явлений и избранным вопросам математики (Нальчик, 1971 г.), на VIIXI Всесоюзных конференциях по поверхностным явлениям в расплавах и твердых фазах (Грозный, 1976 г., Киржач, Моск. обл., 1980, 1986, Николаев, 1982, Киев, 1991), на III и XIII Чтениях по физике Северо-Кавказского научного центра высшей школы (Ростов-на-Дону, 1975, 1985), на Всесоюзных школах молодых ученых по поверхностным явлениям в расплавах (Нальчик, 1978, Грозный, 1988), на II Всесоюзной конференции по поверхностным явлениям в жидкостях (Ленинград, 1978), на V Всесоюзном семинаре "Магнетизм редкоземельных сплавов" (Грозный, 1988), на Всесоюзном семинаре "Проблемы зонной теории кристаллов" (Грозный, 1990), на II Всесоюзном совещании "Метастабильные фазовые состояния – теплофизические свойства и кинетика релаксации" (Свердловск, 1989), на International Conference "Hight Temperature Capillarity" (Smolenice Castle, Bratislava, Slovakia, 1994), на IXXI Российских конференциях "Строение и свойства металлических и шлаковых расплавов" (Екатеринбург, 1998, 2001, 2004), на VI региональной конференции "Вузовская наука Северо-Кавказскому региону" (Ставрополь, 2002), на X, XI Российских конференциях по теплофизическим свойствам веществ (Казань, 2002, Санкт-Петербург, 2005), на международной конференции "Фазовые переходы и критические явления в конденсированных средах" (Махачкала, 2005), на IIV Всероссийских конференциях "Физические свойства металлов и сплавов" (Екатеринбург, 20012007), на 13 International Conference on Liquid and Amorphous Metals (Ekaterinburg, 2007).
Публикации. Основные результаты, изложенные в диссертации, опубликованы в работах [1-39], список которых приведен на последних страницах автореферата. Отдельные результаты работы защищены четырьмя авторскими свидетельствами и патентом.
Объем и структура и диссертации. Диссертация состоит из введения, шести глав, заключения и списка литературы, включающего 229 названий. Материал изложен на 303 страницах и проиллюстрирован 87 рисунками и 13 таблицами.
ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ
Во введении обосновывается актуальность темы работы, сформулирована цель и задачи работы, указаны основные научные результаты и практическая ценность работы.
В первой главе анализируется роль поверхностного слоя как зародыша новой фазы, рассматриваются изменения, происходящие в поверхностном слое с температурой при равновесии фаз, подчеркивается различие в поведении поверхностного слоя с изменением температуры при критических фазовых переходах и фазовых переходах первого рода.
Обзор работ по контактному плавлению показывает, что для объяснения снижения температуры плавления кристалла под воздействием инородного вещества привлекаются, в основном, две гипотезы, – диффузионная и адсорбционная, каждая из которых находится в противоречии с теми или иными опытными результами.
При обсуждении природы контактного плавления важным параметром является время появления жидкости после приведения кристаллов в соприкосновение. Нами осуществлена экспериментальная оценка верхнего временного предела появления жидкости при контактном плавлении. Для этого пры легкоплавких металлов, образующих как простые эвтектические системы, – висмут–олово, висмут–кадмий, свинец–олово, так и системы с промежуточными твердыми фазами, – висмут–таллий, висмут–свинец, кадмий–олово, приводились в кратковременный контакт при температурах на 0.5–1.0 К превышающих эвтектическую. Наименьшая продолжительность контакта, которую удалось достичь, составляла 0.02 с. На соприкасавшихся поверхностях наблюдались застывшие капли металла, свидетельствующие о произошедшем контактном плавлении. Было показано, что образование жидкости происходит во время соприкосновения образцов. Верхний временной предел, упоминаемый в литературе, достигал 0.5 с.
При рассмотрении природы возникновения и роста промежуточных фаз часто игнорируется роль поверхностного слоя, разделяющего исходные фазы. Поверхностный слой рассматривается нами как зародыш промежуточных фаз. Анализируются и сравниваются поверхностные слои между жидкостью и насыщенным паром и между твердыми растворами, составляющими эвтектическую систему. В первом случае с увеличением температуры происходит критический фазовый переход, во втором – контактное плавление.
В связи с этим в рамках модели поверхностного слоя конечной толщины получена формула, позволяющая оценить толщину поверхностного слоя между однокомпонентной жидкостью и насыщенным паром при температурах, когда плотность пара мала по сравнению с плотностью жидкости:
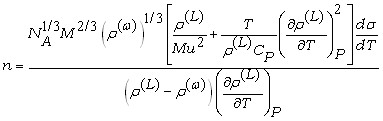1 2
где n – число атомных слоев, составляющих поверхностный слой, NA – постоянная Авогадро, M – молярная масса вещества, Т – температура, Р – давление, (L) и () – плотности вещества в жидкости и в поверхностном слое, – поверхностное натяжение, СР – молярная теплоемкость вещества при постоянном давлении, u – скорость звука в жидкости. Для моделирования поверхностного слоя было выбрано 
.
Измерение плотности и поверхностного натяжения жидких металлов, необходимое для применения формулы (1), производилось с металлами высокой чистоты, отфильтрованными или перегнанными в вакууме, в стеклянной аппаратуре. Поверхностное натяжение жидких металлов измерялось методом максимального давления в капле, плотность – с помощью двухкапиллярного дилатометра. С помощью формулы (1) показано, что толщина поверхностного слоя исследованных металлов, кроме ртути, составляет один-два атомных слоя и практически не изменяется в исследованном интервале температур. Толщина поверхностного слоя ртути быстро растет с температурой, что объясняется сравнительно низкой критической температурой ртути.
Иначе ведет себя поверхностный слой, разделяющий две конденсированные фазы, при приближении к фазовому переходу первого рода. Рассмотрим двухфазную двухкомпонентную конденсированную систему –, находящуюся в термодинамическом равновесии при температуре ниже температуры плавления эвтектики. Из уравнений Гиббса, записанных для двух фаз и разделяющего их поверхностного слоя можно получить известное [2] уравнение
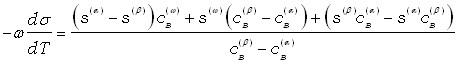3 4
где индексы, и являются идентификаторами фаз и поверхностного слоя, сВ – молярная доля компонента В в соответствующей фазе, s – молярная энтропия вещества соответствующей фазы, – молярная площадь вещества поверхностного слоя.
При эвтектической температуре возможно как трехфазное равновесие –жидкость–, так и двухфазное равновесие –, причем твердые растворы имеют тот же состав, что и при трехфазном равновесии, а поверхностный слой между ними, остается устойчивым. Сопоставление двух перечисленных состояний системы при эвтектической температуре позволяет приписать поверхностному слою, разделяющему твердые растворы и, свойства жидкой фазы в эвтектической точке.
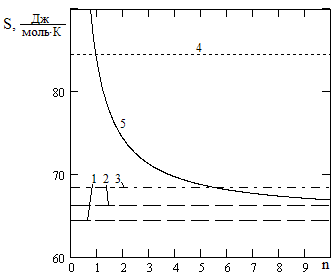
Рис. 1. Молярные энтропии: 1 и 2 – твердых растворов висмута в олове и олова в висмуте, 3 – гипотетического твердого раствора эвтектического состава, 4 – расплава эвтектического состава, 5 – межфазного слоя по (2) в зависимости от толщины межфазного слоя, выраженной числом атомных слоев, при d/dT= 0.3103 Дж/(м2К)
С помощью формулы (2) удается оценить возможную толщину межфазного слоя при эвтектической температуре, связав ее с молярной площадью. Так как эвтектическая точка одновременно принадлежит жидкой и смеси твердых фаз, то логично предположить, что средний состав межфазного слоя – при эвтектической температуре равен составу эвтектики. Из результатов расчетов, показанных на рисунке 1, следует, что при толщине межфазного слоя в 1–2 атомных слоя, энтропия межфазного слоя близка к энтропии жидкой фазы. Такое значение энтропии межфазного слоя отвечает физическим представлениям о природе этого слоя и, в этом смысле, адекватна реальности. Только при температурах, превышающих эвтектическую, межфазный слой – разрастается в жидкую фазу.
Инструментом, позволяющим выяснить состояние вещества в приповерхностных участках образцов в контакте разнородных веществ, в данной работе являются экспериментальные результаты исследования диффузионного роста жидкой прослойки. Поэтому вторая глава посвящена диффузионным аспектам контактного плавления. Рассматривается роль диффузии чужеродных атомов из растущей жидкой фазы в исходные твердые образцы. Подчеркивается зависимость коэффициентов диффузии от системы отсчета. Учитывается смещение жидкой прослойки при контактном плавлении в нестационарно-диффузионном режиме, связанное с объемными эффектами плавления исходных образцов. Показано, что указанное смещение жидкой прослойки не изменяет параболическую закономерность перемещения изоконцентрационных плоскостей со временем. Получено решение второго закона Фика с учетом общего смещения жидкой прослойки. Дано описание разработанной нами методика определения концентрации жидкости на границе с твердой фазой.
Для исследования роста промежуточных фаз требуется учет диффузионного проникновения атомов всех сортов в растущие фазы. Рассмотрена диффузия атомов А из жидкости в твердую фазу в процессе контактного плавления. Для упрощения принято, что растворимость атомов В в твердом образце отсутствует. Предполагается, что концентрация атомов А на межфазной границе со стороны -кристалла соответствует стабильному солидусу. Ввиду оценочного характера расчета пренебрегается конвективным смещением диффузионной зоны и зависимостью коэффициентов диффузии от состава. Тогда решение уравнения диффузии для твердой фазы с учетом соответствующего краевого условия имеет вид
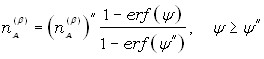5 6
где nA – концентрация атомов А, штриховые индексы (') и (") определяют межфазные границы /жидкость и жидкость/, 
, D – коэффициент диффузии, – кинетический множитель, определяющий координату z изоконцентрационной плоскости, в частности межфазной границы, в момент времени t в соответствии с параболическим законом 
.
Из-за малости коэффициента диффузии в твердой фазе, erf(")1, и непосредственные расчеты по формуле (3) затруднительны. Поэтому, ограничившись двумя первыми членами разложения функции erf() в ряд, получили
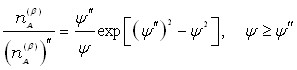.7 8
Введено понятие эффективной глубины проникновения чужеродных атомов из жидкой прослойки в твердый образец zA() как толщины слоя, который образовали бы внедрившиеся в фазу атомы А, локализованные вблизи межфазной границы с концентрацией (nA())". После интегрирования (4), получено
.910
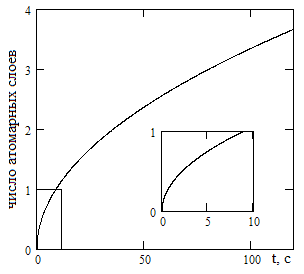
Рис. 2. Рост эффективной глубины диффузионного проникновения атомов висмута в свинец из жидкой фазы в процессе контактного плавления при температуре 200оС
Из результатов расчета, показанных на рисунке 2, следует, что при диффузионном механизме растворения на заполнение только первого атомарного слоя потребовалось бы около десяти секунд, – слишком большое время не только по масштабам теплового движения атомов, но и по сравнению с экспериментально зафиксированным временем появления жидкости при контактном плавлении (см. выше).
Из (4) так же следует, что количество вещества А в твердой -фазе мало по сравнению с количеством вещества А в жидкой фазе:
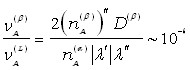11 12
Оценка (6), выполненная для системы Bi–Pb, верна, пока |'|">>D().
Известно (например, [3]), что описание диффузии связано с определенной системой отсчета. Кроме того, в двухкомпонентной жидкостной системе коэффициенты диффузии, характеризующие диффузионной перемещение атомов А и В, связаны между собой. В системе отсчета Фика [3], определяемой условием
, 1314
где vA, vB – парциальные молярные объемы компонентов в расплаве, jA(F), jB(F) – проекции плотностей потоков компонентов на направление диффузии в системе отсчета Фика, парциальные коэффициенты диффузии компонентов равны между собой: DA(F)=DB(F).
При проведении экспериментов применялась известная методика контактного плавления, когда вертикально расположенные в термостате твердые цилиндрические образцы в процессе диффузионного отжига не перемещаются, а растущая между твердыми образцами жидкая прослойка заключена в стеклянную трубку, внутренний диаметр которой равен диаметрам твердых образцов. Для предотвращения гравитационной конвекции сверху помещают менее плотный образец.
Нами разработана и применена модель контактного плавления, в которой учитывается общее смещение жидкой цилиндрической прослойки, возникающее в результате объемного эффекта плавления. Принята независимость парциальных молярных объемов компонентов от состава в жидкой прослойке. Скорость общего смещения жидкости при указанных предположениях равна скорости системы отсчета Фика. В работе показано, что в рамках рассматриваемой модели общее смещение жидкости относительно лабораторной системы, происходит по параболическому закону. Если концентрация жидкости на границе с кристаллами не изменяется в процессе опыта, то положение межфазных границ жидкость–кристалл и протяженность жидкой прослойки так же следуют параболическому закону:
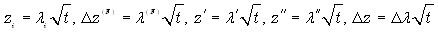, 15 16
где i, (F), ', ", – соответствующие кинетические множители, t – время, отсчитываемое с момента приведения исходных твердых образцов в контакт.
С учетом общего смещения жидкой прослойки второе уравнение Фика принимает вид
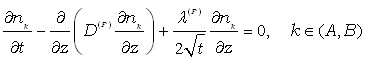, 17 18
где nk – концентрация k-го компонента.
В приближении независимости коэффициента диффузии от концентрации уравнение (9) имеет решение
19 20
где
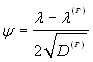. 21 22
Полученные при рассмотрении роста контактной прослойки результаты позволяют составить систему базовых уравнений, используемых в дальнейшем:
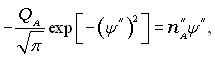. 23 24
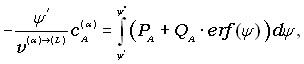
где предполагается, что -фаза может быть не только чистым веществом, но и твердым раствором или интерметаллидом, и v()(L) – молярный объем вещества -фазы при переходе в жидкое состояние, cA() – молярная доля компонента А в -фазе. Первые два уравнения системы (12) представляют собой краевые условия на основе решения (10). Третье уравнение представляет собой применение первого уравнения Фика к межфазной границе жидкость–-фаза с учетом распределения (10). Четвертое уравнение представляет собой утверждение, что количество компонента А, находившееся в расплавившейся части -фазы, перешло в жидкую фазу.
При наличии данных о составах жидкости на межфазных границах, молярных объемах компонентов из (12) могут быть найдены и. Если из опытов по контактному плавлению известен кинетический множитель =”-' из (8), то из (12) определяется коэффициент диффузии
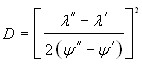. 25 26
При заданных D, и известном составе жидкости на одной из межфазных границ, может быть определен состав на другой межфазной границ, если же, кроме того, определены ' и ", то состав может быть определен на обеих межфазных границах со стороны жидкости.
В третьей главе приводятся результаты экспериментального исследования контактного плавления в системах, имеющих промежуточные твердые фазы, при температурах выше эвтектических. Показано, что квазиравновесность процессов роста промежуточной жидкой фазы достигается путем образования промежуточных твердых фаз кристаллизацией метастабильной жидкости.
При достаточно продолжительном изотермическом формировании диффузионная зона, образованная неистощимыми исходными образцами A–B, содержит все промежуточные фазы, представленные вдоль соответствующей изотермы на равновесной диаграмме состояния. Если какая-либо промежуточная фаза в контактной зоне отсутствует, то соседние с отсутствующей фазы могут находиться в равновесии, только будучи в метастабильном состоянии. Одной из причин отсутствия фаз в диффузионной зоне является малость коэффициентов диффузии, характеризующих рост этих фаз, по сравнению с соседними фазами. Наиболее сильно указанный фактор должен проявляться, если одной из промежуточных фаз является жидкость, то есть при контактном плавлении.
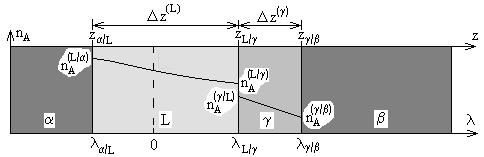
Рис. 3. Гипотетическое сосуществование растущих жидкой (L) и твердой () промежуточных фаз в диффузионной зоне
Рассмотрена возможность существования промежуточной твердой фазы, растущей в диффузионной зоне наряду с конкурирующей жидкой фазой. Соответствующая диффузионная зона изображена на рисунке 3. Пусть L/ – кинетический множитель, характеризующая перемещение границы между жидкой (L) и рассматриваемой твердой () фазами. Тогда ширину жидкой фазы z(L) за время t оценивается как
27 28
где коэффициент "2" в (14) принят из естественного предположения, что ширина прослойки примерно в два раза больше, чем одна из ее частей. Проекция плотности потока частиц А на направление z сквозь плоскость, прилегающую к границе жидкость–-фаза со стороны -фазы без учета смещения контактной зоны равна
2930
где uA(/L) – средняя скорость направленного движения частиц А в рассматриваемых точках. Эта скорость не может быть меньше скорости перемещения соответствующей границы. В противном случае -фаза не могла бы сформироваться из-за недостатка частиц А. Следовательно
3132
Для оценки принято, что распределение компонентов в -фазе, занимающей концентрационный интервал (nA(/), nA(/L)), является линейным. Тогда из первого закона Фика и выражений (15, 16) получено
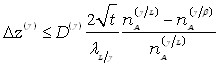33 34
Сравнение протяженностей -фазы и жидкой прослойки приводит, после деления (17) на (14), к
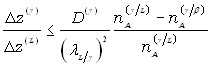3536
Для численной оценки использованы значения, характерные, в частности, для системы индий-висмут: D()~10-15 м2/с [4], (L/InBi)~105 м/с1/2 (результат измерений), nInBi/nInBi~0.01, где nInBi – интервал гомогенности фазы InBi. Пусть за время диффузионного отжига сформировалась жидкая прослойка толщиной 3 мм. Тогда, в соответствии с полученным результатом, формальная толщина интерметаллида должна составлять 3·1010 м, то есть по порядку величины равна атомарному слою. Такой объект не может быть термодинамической фазой, то есть не обладает физическими характеристиками, которые свойственны фазе, состоящей из таких же атомов при тех же внешних условиях. Сделан вывод, что, в условиях конкурентного роста жидкой фазы, промежуточная твердая фаза за достижимое для реального эксперимента время диффузионным путем сформироваться не может.
В результате возникает вопрос о соответствии состава жидкой фазы на границах с твердыми ликвидусным значениям стабильной диаграммы состояния. Объектами экспериментального исследования служили система свинец–висмут, имеющая промежуточную инконгруэнтно плавящуюся фазу (рис. 4), и система висмут–индий, имеющая ряд промежуточных фаз, две из которых плавятся конгруэнтно (рис. 5).
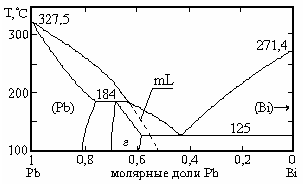
Рис. 4. Схематическое изображение диаграммы состояния свинец–висмут. mL – метастабильный ликвидус
Задача выяснения состава жидкости на межфазной границе со стороны возможного существования промежуточной твердой фазы решалась в два этапа. Сначала изучалась кинетика контактного плавления пар, которые не образуют промежуточных твердых фаз или для которых промежуточные фазы не оказывают сущетвенного влияния на температурный ход стабильного ликвидуса. При этом принудительно обеспечивается соответствие граничных концентраций равновесной диаграмме состояния. Из базовой системы уравнений (12) находили параметры ' и ", после чего, используя полученные при измерениях значения кинетического множителя роста жидкой фазы, по (13) находили коэффициент диффузии:
На втором этапе полученные коэффициенты диффузии и экспериментально найденные кинетические множители использовали для расчета состава жидкости на границе с образцом, к которому, согласно диаграмме состояния, прилегают промежуточные твердые фазы.
Для системы свинец-висмут найдено, что при 150оС, когда между свинцом и жидкой фазой на диаграмме состояния существует -фаза, молярная доля свинца в жидкой прослойке на границе со стороны свинца сPb(L/Pb)=0.52+0.01 при доверительной вероятности 95%. В пределах погрешности измерений полученное значение совпадает с ликвидусным значением равновесной диаграммы состояния, которое равно 52 мол. % Pb.
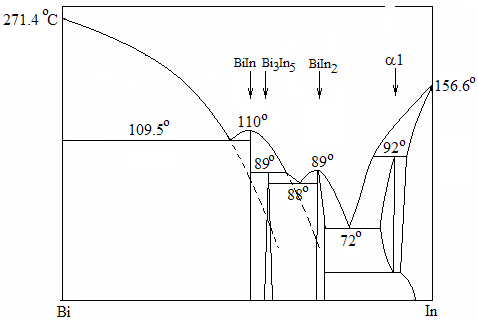
Рис. 5. Схематическое изображение диаграммы состояния системы индий–висмут
Аналогичные результаты получены при исследовании контактного плавления в системе висмут-индий. Как показано выше, в условиях конкуренции с растущей жидкой фазой промежуточные твердые фазы диффузионным путем не могут сформироваться. Наибольшее отклонение от равновесных значений ликвидуса следует ожидать при контактном плавлении пары Bi–In в области температур 72–88оС, когда между легкоплавкой эвтектикой и висмутом существуют три промежуточные твердые фазы. Согласно диаграмме состояния исследуемой системы при температурах выше 110оС диффузионная пара Bi–In может образовать единственную промежуточную фазу – жидкий раствор, область гомогенности которого ограничена линиями ликвидуса. Теми же свойствами обладают диффузионные зоны, образуемые парой BiIn–In в интервале температур 92–110oС и парой BiIn2–In в интервале температур 72-89оС.
Для всех перечисленных контактных пар на основе результатов измерения кинетического множителя роста жидкой фазы найдены коэффициенты диффузии D.
Полученные значения коэффициентов диффузии использованы для расчета состава жидкости на границе жидкости и висмутосодержащего кристалла. Рассматривались коэффициенты диффузии, найденные как для стабильных участков диаграммы состояния, так и для метастабильных, рассчитанные путем экстраполяции в низкотемпературную область. Искомой величиной являлась молярная доля висмута на границе с кристаллом со стороны висмута.
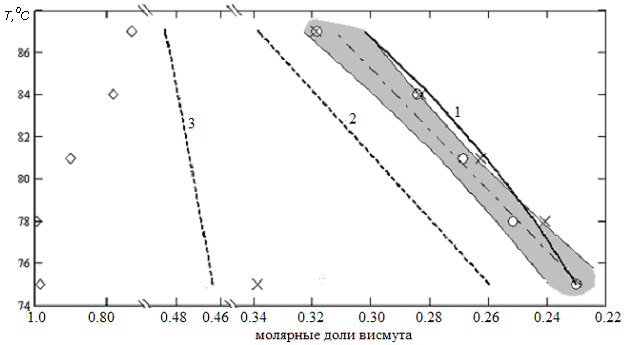
Рис. 6. Молярные доли висмута в жидкой прослойке на границе с кристаллом при контактном плавлении пары Bi–In (72–88оС). 1 – стабильный ликвидус, 2 и 3 – линии метастабильного ликвидуса, полученные экстраполяцией ликвидуса, образованного соединением BiIn и висмутом, соответственно,,, – расчеты на основе эффективных коэффициентов диффузии, полученных по результатам контактного плавления пар BiIn2–In, BiIn–In и Bi–In, соответственно. Затемненная полоса – 95-% доверительная область результатов, обозначенных символом
На рисунке 6 в качестве примера приведены результаты, полученные для каждого из вариантов расчета D, которые сравниваются с равновесным ликвидусом и с соответствующими вариантами метастабильного ликвидуса. Аналогичные результаты получены так же для пары BiIn–In в интервале температур 72–88°С и пары Bi–In в интервале температур 89–109.5оС.
Таким образом, для контактных пар, которые при температурах диффузионного отжига согласно диаграмме состояния, приведенной на рисунке 5, образуют интерметаллиды, обнаружено, что жидкость на границе с образцом, содержащим висмут (Bi, BiIn), имеет состав близкий к стабильному ликвидусу. Для контактных пар In-BiIn при t(72-88oC) и In-Bi при t(72-88oC) по сравнению с равновесным ликвидусом указанный состав обогащен висмутом. Разность между найденными составами и ликвидусом находится в пределах или близка к 95% доверительной области, характеризующей разброс полученных результатов. Для контактной пары In-Bi при t(89-109.5oC) также наблюдается смещение граничной концентрации относительно равновесного ликвидуса в сторону висмута, но в этом случае смещение существенно превышает указанную 95-% доверительную область.
Невозможность образования в контактной зоне промежуточной твердой фазы при наличии растущей жидкой фазы в сочетании с экспериментально обнаруженной близостью концентрационного интервала жидкой прослойки области гомогенности жидкости стабильной диаграммы состояния объяснены следующим образом. Между исходными образцами в начальный момент времени, а в дальнейшем между жидкостью и исходным образцом, к которому по диаграмме состояния прилегают промежуточные твердые фазы, происходит контактное плавление по метастабильной диаграмме состояния без образования промежуточных интерметаллидов. В результате часть жидкой прослойки находится в метастабильном состоянии. Время существования метастабильной жидкости зависит от случайных процессов, ведущих к образованию зародышей интерметаллидов, после чего метастабильная жидкость распадается на стабильные интерметаллиды и стабильную жидкость. Вероятность возникновения зародышей интерметаллида на поверхности кристалла выше, чем в объеме метастабильной жидкости, поэтому рост выпадающей из жидкости промежуточной твердой фазы происходит на поверхности исходного кристалла. Далее происходит контактное плавление интерметаллидов по равновесной диаграмме состояния. После полного расплавления промежуточных интерметаллидов жидкость вновь взаимодействует с первичным образцом, после чего последовательность процессов повторяется. Чем больше продолжительность существования метастабильных состояний жидкости, тем больше отклонение средней по времени концентрации жидкости на границе с исходным образцом от стабильного ликвидуса. При этом разные области межфазной поверхности в один и тот же момент времени находятся на различных стадиях процесса.
Наблюдаемый граничный состав жидкости представляет собой суперпозицию стабильного и метастабильного ликвидусных значений с множителями, пропорциональными временам существования интерметаллидов и метастабильной жидкости. Плавление интерметаллидов лимитируется диффузионным переносом атомов через жидкую прослойку и занимает основную часть периода повторяющегося процесса, меньшую часть которого занимает кристаллизация метастабильной жидкости. Этим объясняется незначительное смещение граничного состава жидкости от равновесного ликвидуса к метастабильному.
Прямым экспериментальным доказательством возникновения метастабильной жидкости при контакте фаз, характеризуемом скачком химических потенциалов компонентов, является Т-эффект, рассмотренный в главе V.
В четвертой главе рассматриваются результаты исследования контактного плавления в простых эвтектических системах галлий-индий, галлий-олово, галлий-цинк и олово-висмут. Помимо роста жидкости между кристаллами рассмотрен случай плавления индия и олова при температурах выше температуры плавления галлия.
На примере системы галлий–индий показана адекватность распределения компонентов в контактной прослойке, рассчитанной в предположении независимости коэффициентов диффузии от состава, найденному экспериментально.
Параболический закон роста жидкой прослойки (8), фиксируемый на опыте, свидетельствует о постоянстве состава на границах с кристаллами. В то же время, диффузионное проникновение чужеродных атомов из жидкости в кристалл приводит к медленному изменению состава прилегающих к жидкости атомных слоев кристалла в процессе опыта (рис. 2), что должно привести к соответствующему изменению граничного состава жидкости и, как следствию, к отклонению от параболического закона. Для выяснения выполнимости условий квазирановесности на межфазных границах была изучена зависимость кинетики перемещения межфазных границ в системе висмут–твердый раствор висмута в олове в зависимости от состава твердого раствора. Состав образцов, содержащих олово, изменялся в пределах 0–10.1 мол.% Bi при 149оС и в пределах 0–5.3 мол.% Bi при 170оС. Установлено, что, как и при контактировании чистых веществ, параболический закон роста жидкой прослойки выполняется и в том случае, когда одним из исходных образцов является твердый раствор (рис. 7). Скорость контактного плавления возрастает по мере увеличения содержания висмута в твердом растворе (Sn+Bi), причем за счет увеличения скорости плавления твердого, скорость плавления образца висмута при это уменьшается.
Измерение кинетического множителя и отношения |'|/" при различных составах твердого раствора позволило с помощью методики, изложенной в главе II, рассчитать состав жидкости на границах с кристаллами. При 95%-й доверительной вероятности получили: при 149оС c'=0.62±0.01 и c"=0.51±0.01, при 170оС c'=0.72±0.01 и c"=0.42±0.01. Соответствующие ликвидусные значения: при 149оС c'=0.61 и c"=0.51, при 170оС c'=0.72 и c"=0.42. Таким образом, концентрационная протяженность жидкой прослойки совпадает со стабильным равновесным интервалом гомогенности при соответствующей температуре.
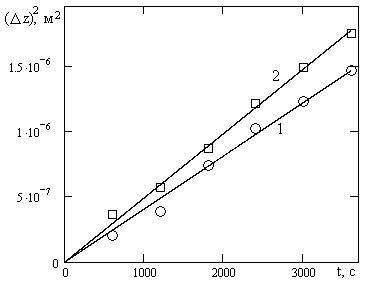
Рис. 7. Кинетика роста жидкой прослойки в контакте Bi–Sn (1) и Bi–(Sn+5.9 мол.% Bi) при 146оС
Противоречие между соответствием концентрационного интервала жидкой прослойки стабильной диаграмме состояния и неравновесностью концентрационного распределения в твердых образцах снимается гипотезой об образовании стабильных твердых растворов в результате кристаллизации метастабильных (пересыщенных) участков жидкой прослойки, то есть в простых эвтектических системах действует тот же механизм взаимодействия фаз, что и в системах с интерметаллидами, рассматриваемый в третьей главе.
Процесс распада метастабильной жидкости происходит быстро по сравнению с характерным временем диффузионных процессов того же пространственного масштаба. Поэтому основная часть времени роста жидкой прослойки приходится на квазиравновесное контактное плавление в соответствии со стабильной диаграммой состояния и периодические локальные отклонения от стабильного равновесия заметно не влияет на общий ход процесса. Образование метастабильной жидкости и выпадение твердого раствора на различных участках межфазной границы происходит некоррелировано.
Прямым доказательством возникновения метастабильной жидкости в экстремальных условиях является Т-эффект контактного плавления, рассматриваемый в пятой главе. Т-эффект контактного плавления представляет собой прочное соединение разнородных кристаллов, образующих системы с промежуточными твердыми фазами, при температурах ниже наименьшей температуры стабильного ликвидуса соответствующей системы. Такое соединение является следствием образования и кристаллизации метастабильной жидкости в контакте разнородных кристаллов (рис. 8).
Рис. 8. Электронография (200) шва висмут–таллий, полученного в результате контакта при 140оС. =0.05 мм
Для объяснения Т-эффекта часто привлекают тепловую гипотезу, согласно которой плавление происходит в результате локального разогрева контакта образцов, происходящее вследствие выделения теплоты при экзотермическом образовании интерметаллидов. В настоящей работе решается соответствующая одномерная тепловая задача для массивных металлических образцов с плоским источником, теплота в котором выделяется при росте интерметаллида. Получено, что разность температур контакта образцов и термостата равна
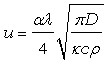, 37 38
где – множитель, принимающий значения 24, – удельная (в расчете на единицу объема) теплота образования промежуточной фазы, –теплопроводность стержня, с – удельная теплоемкость, – плотность вещества стержня, D – коэффициент диффузии, характеризующий рост промежуточной фазы. Ориентируясь на систему таллий–висмут, воспользуемся следующими значениями: =3, =1.4108 Дж/м3, D=1.010-16 м2/с, =25 Вт/(мК), с=130 Дж/(кгК), =1.0104 кг/м3. Подставив эти величины в (19), получим, что повышение температуры зоны реакции составляет 0.3 мК.
Незначительный разогрев контакта образцов приводит к выводу, что тепловая гипотеза не может объяснить наблюдаемые результаты Т-эффекта. Так как рекордно малые разности температур, которые определяются термопарой, имеют порядок 10 мК, то попытки обнаружить разогрев контакта в результате твердофазной экзотермической реакции в массивных образцах (не в порошках) обречены на неудачу.
Т-эффект представляет собой систему фазовых переходов первого рода, и, следовательно, сопровождается тепловыми эффектами. Изучение этих эффектов позволяет получить важную информацию о природе происходящих в контакте разнородных веществ процессов. Поэтому нами разработан специальный метод, защищенный авторским свидетельством. Метод основан на использовании самих спекаемых образцов в качестве термопары. Рабочим спаем термопары являлся контакт образцов. Противоположные концы образцов, имеющие температуру термостата и соединенные с гальванометром, являлись опорным спаем термопары. Погрешность градуировки составляла 1%. Погрешность измерения температуры в контакте образцов оценивается в 10%.
Исследовали тепловой эффект при контактировании висмута с таллием, индием, свинцом и кадмием. Система висмут-кадмий промежуточных твердых фаз не образует и рассматривалась в контрольных целях.
Методика измерений состояла в следующем. Образцы изготавливали в виде цилиндров диаметром 3 мм и длиной 2 см. Их располагали горизонтально в канале специальной кассеты, изготовленной из текстолита (рис. 10). Образцы подпружинивались навстречу друг другу, упираясь при этом в стальную пластину с противоположных сторон. К свободным концам образцов припаивали провода, которые замыкались на зеркальный гальванометр. Торец висмутового образца, предназначенный для контактирования, предварительно шлифовался. Для предотвращения внешних температурных неоднородностей кассету с образцами помещали в латунный бокс, который укреплялся внутри термостата ТС-15. Термостатирующей жидкостью являлся парафин, который заполнял свободное пространство как внутри латунного бокса, так и вне его. Выбор парафина в качестве термостатирующей жидкости обусловлен его диэлектрическими свойствами. В тех случаях, когда опыты велись при комнатной температуре, все операции осуществлялись в воздухе.
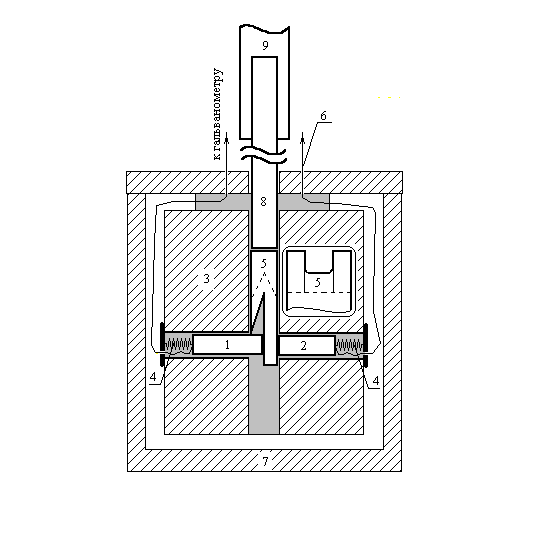
Рис.9. Устройство для исследования теплового эффекта спекания (1 и 2 – исследуемая пара образцов; 3 – кассета из текстолита; 4 – пружины; 5 – стальная пластина-нож; 6 – провода; 7 – бокс; 8 – шток для проталкивания пластины-ножа; 9 – теплоизолирующее продолжение штока).
Система Bi–Me, замкнутая через стальную пластину на гальванометр, образует термопару, с помощью которой контролируется градиент температуры вдоль образцов. Стальная пластина, в которую упираются образцы до контактирования, представляет собой деталь ножа, выполненного в виде ступени. После установления теплового равновесия, о чем судили по отсутствию отклонения светового луча гальванометра от нулевого положения, перемещением ножа срезали покрытую оксидом поверхность образца, предназначенного для контактирования с висмутом. Под действием пружин образцы приходили в контакт. Происходящие в контакте процессы нарушают тепловое равновесие, что и фиксируется гальванометром.
Для проверки с помощью предложенной методики измеряли снижение температуры контакта образцов при обычном контактном плавлении и сравнивали с расчетом по формуле (19). Как эксперимент, так и расчет дают снижение температуры в контакте образцов в начальный момент контактного плавления в 1К.
В системах висмута с таллием, индием и свинцом наблюдалось прочное соединение образцов, сопровождаемое повышением температуры контакта. Разогрев контакта во всех случаях составлял доли кельвина. Характерное время достижения максимальной температуры составляет 1–2 с. Затем происходит сравнительное медленное снижение температуры контакта до температуры термостата. Полное время температурной релаксации системы обычно составляло 20–30 с.
Различие на три порядка с расчетом по формуле (19) свидетельствует о том, что реальный механизм выделения теплоты не связан с экзотермической твердофазной реакцией, происходящей по диффузионному механизму. В то же время отсутствует знакопеременный тепловой эффекта, который свидетельствовал бы о выполнении правила ступеней Оствальда.
Были проведены опыты по контактированию образцов систем ртуть-таллий и ртуть-индий при температурах ниже наименьших температур на линиях ликвидуса. Особенностью системы ртуть-таллий является то, что интерметаллид Hg5Tl2 в этой системе образуется с поглощением теплоты. При приведении в контакт образцов ртути и индия при -54оС, что на 15оС ниже температуры наименьшей температуры на линии ликвидуса, происходит обычное для Т-эффекта прочное соединение образцов, в системе же ртуть–таллий соединения образцов не происходит.
Наблюдаемые на опыте явления могут быть объяснены следующим образом. При приведении в контакт двух разнородных образцов образуется существенно неравновесная система со скачком химических потенциалов компонентов на поверхности контакта. Межфазный слой представляет собой источник зародышей новых фаз, как стабильных, так и метастабильных, снимающих скачок химических потенциалов. В рассматриваемых случаях стабильными промежуточными фазами являются интерметаллиды, метастабильной фазой – жидкость. Зародыши интерметаллидов растут по твердофазному диффузионному механизму, то есть достаточно медленно, и не вносят заметного вклада в процесс быстрого спекания образцов. Возникают также зародыши метастабильной жидкой фазы. Развитие таких зародышей требует подвода теплоты. Если подвод теплоты отсутствует, то такие зародыши, будучи неравновесными, не получают развития и исчезают. Так как жидкая фаза является метастабильной, то ее рост будет происходить только в том случае, если энергия, требуемая на плавление, будет выделяться в виде теплоты практически в тех же точках, где существует зародыш жидкой фазы. Такая ситуация возникает, если зародыш жидкой фазы сопряжен с зародышем интерметаллида.
Таким образом, в некоторых точках межфазный слой в неравновесном контакте образцов распадается на зародыши метастабильной жидкости и стабильного интерметаллида. Зародыш интерметаллида растет, в основном, в результате кристаллизации метастабильной жидкости. Метастабильная жидкая фаза растет в результате контактного плавления по метастабильной диаграмме, при этом необходимая теплота образования этой жидкости обусловлена теплотой, поступающей от кристаллизующегося интерметаллида. Такой механизм роста интерметаллида с помощью жидкой фазы, играющей роль лидера, аналогичен известному механизму роста кристаллических усов, когда на растущем конце кристалла находится капелька жидкости.
В шестой главе приводится методика компьютерной имитации роста промежуточных фаз, основанная на идеологии целлюлярного равновесия и впервые примененная нами при исследовании фазообразования при контактном плавлении. Разработанная методика компьютерного эксперимента применена как к простым эвтектическим системам, так и к системе с промежуточной твердой фазой. Продемонстрирована возможность процессов, происходящих через образование и частичную кристаллизацию метастабильной жидкости.
Целлюлярная модель строилась в виде линейной последовательности ячеек, каждая из которых обладает набором характеристик. Изменение значений характеристик ячейки происходит по заданным правилам и в зависимости от значений соответствующих характеристик соседних ячеек. Каждая ячейка характеризуется молярной долей компонента A – сi, долей жидкости в данной ячейке – fLi, долей fSi стабильного твердого раствора, образовавшегося в результате кристаллизации метастабильной жидкости, состав которого определяется стабильным солидусом. Величина (1- fLi- fSi) представляет собой долю исходного твердого вещества в ячейке с номером i. Первоначально, когда оба контактируемых образца являются твердыми, значение параметра fi каждой ячейки равно нулю. Если рассматривается плавление между чистыми компонентами A и В, то первоначально половине ячеек, представляющих образец А, присваивается значение сi=1, а другой половине ячеек, представляющих образец В, присваивается значение ci=0. Если же моделируется контактное плавление между твердым раствором и чистым кристаллом, то изначально для половины ячеек устанавливается концентрация, соответствующая твердому раствору.
В процессе счета между ячейками происходит обмен веществом. Фазовое состояние ячейки после очередного изменения состава определяется на основе диаграммы состояния с учетом возможного образования метастабильных состояний. В частности, если в ячейке присутствует стабильная твердая фаза или ячейка соприкасается со стабильной твердой фазой, а состав ячейки попадает в двухфазную область диаграммы состояния, то соотношение фаз в ячейке определяется правилом рычага 
, где cS и cL – молярные доли компонента А, соответствующие стабильным солидусу и ликвидусу при данной температуре. В ячейке со смешанным фазовым составом концентрации твердой и жидкой фаз соответствуют солидусу и ликвидусу при температуре ячейки, твердая часть ячейки примыкает к твердой части образца, жидкая – к жидкой прослойке.
Если твердая фаза в ячейке имеет состав исходного образца или жидкая ячейка граничит с исходным твердым образцом, то жидкость может находится в метастабильном состоянии и иметь состав метастабильного ликвидуса. Количество жидкой фазы при этом вновь определяется правилом рычага с применением метастабильного ликвидуса. Устойчивость метастабильного состояния в рассматриваемой модели имитируется с помощью генератора случайных чисел. Предполагается, что чем более пересыщена метастабильная жидкость относительно стабильного ликвидуса, тем больше вероятность ее распада на стабильную жидкость и насыщенный твердый раствор. С помощью генератора случайных чисел на отрезке [0, 1] выбирается случайное число r. С этим числом сравнивается величина
39 40
которая принимает значения в пределах отрезка [0, 1]. Здесь cLm – молярная доля компонента А, соответствующая метастабильным ликвидусу при данной температуре. Чем меньше (), тем устойчивее метастабильное состояние. Если при случайном выборе r выполняется соотношение ()<r, то метастабильная жидкость сохраняется. В противном случае происходит распад метастабильной жидкости в соответствии со стабильной диаграммой состояния. Параметр в (20) позволяет регулировать устойчивость метастабильной фазы.
Имитировалось контактное плавление в простых эвтектических системах галлий-индий и олово-висмут. Получена параболическая зависимость (8) роста жидкой прослойки (рис. 10). Найденные в компьютерном эксперименте зависимости кинетики плавления твердых растворов от их состава и температурный ход кинетических множителей
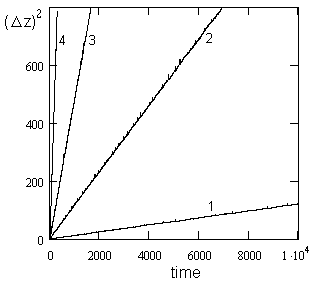
Рис. 10. Зависимость квадрата ширины жидкой прослойки от номера шага в системе, имитирующей пару Bi-Sn. Линии 1, 2, 3, 4 соответствуют температурам 140, 150, 180, 230оС
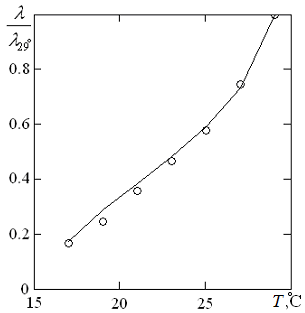
Рис. 11. Сопоставление температурного хода парциального, для индия, кинетического множителя компьютерного (—) и реального (о) экспериментов в системе галлий-индий
соответствует реальному эксперименту. В качестве примера на рисунке 11 сопоставляются кинетические множители для системы галлий-индий.
На рисунке 12 показано значение концентрации жидкости на границе с оловом в течении одного из опытов. В процессе имитации контактного плавления граничная концентрация принимает значения как стабильного, так и метастабильного ликвидусов при заданной температуре. В системе олово-висмут среднее значения относительной концентрации жидкости на границе с кристаллом при =1 составляет 0.620 долей олова при принятом значении стабильного ликвидуса равном 0.617. Таким образом, заключение, сделанное в главе IV, о том, что ликвидусные значения на межфазной границе обеспечиваются малым временем жизни метастабильных состояний, оправдывается в данной модели.
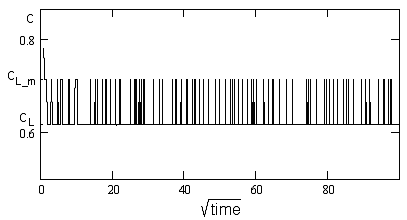
Рис. 12. Временная развертка состава жидкой фазы на границе с кристаллом в модельной системе Sn–Bi при 150оС. с – доля олова. cL и cL_m – доли, соответствующие стабильному и метастабильному ликвидусу
Успешное применение компьютерного моделирования к простым эвтектическим системам позволило построить модель плавления в системе с промежуточной твердой фазой, повторяющей в основных чертах диаграмму состояния системы висмут-индий. При этом учитывалась возможность образования метастабильных жидких растворов. Сохранение или распад метастабильных состояний определялся путем сравнения величины
, 41 42
со случайным числом r [0,1]. В формуле (21) с, сL1, cS – доли компонента А в ячейке, соответствующие стабильному ликвидусу и метастабильному солидусу, – параметр, управляющий устойчивостью метастабильного состояния.
В процессе имитационного контактного плавления при <19 установлено, что на границе с кристаллом, соответствующим висмуту, возникают короткоживущие метастабильные состояния. При этом рост жидкой прослойки происходит по параболическому закону (8) и средний по времени состав на указанной межфазной границе со стороны жидкости практически совпадает с ликвидусным значением стабильной диаграммы состояния (рис. 13).
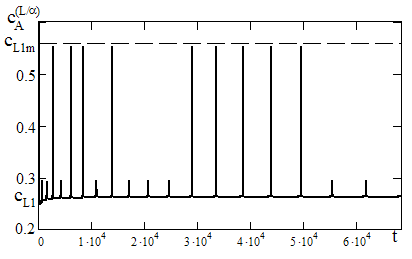
Рис. 13. Временная развертка доли компонента А в жидкости на границе с образцом А при =18. cL1 – стабильный ликвидус, cL1m – метастабильный ликвидус
Таким образом, в результате компьютерной имитации контактного плавления в системе с промежуточной твердой фазой выяснено, что представления об образовании интерметаллидов в результате кристаллизации метастабильной части жидкой прослойки не противоречат выводам, сделанным на основе результатов измерения кинетических множителей в системе индий–висмут. При малой (~1) и большой (~100) устойчивости метастабильных состояний в компьютерном эксперименте выполняется параболический закон роста жидкой прослойки. В промежуточных случаях (например, при =20) наблюдается кусочно-линейная зависимость протяженности жидкой прослойки от корня из времени. При малой устойчивости метастабильных состояний граничные значения концентрации жидкой фазы соответствуют ликвидусу стабильной диаграммы состояния. Если метастабильные состояния достаточно устойчивы, то наблюдаются смещения граничных концентраций в жидкой прослойке в сторону метастабильного ликвидуса.
В заключении сформулированы основные из полученных результатов:
- разработана методика оценки толщины межфазного слоя в контакте разнородных кристаллов. Слой между твердыми растворами при эвтектической температуре сохраняет конечные размеры, а контактирующие фазы сохраняют свою индивидуальность.;
- рассмотрена диффузия чужеродных атомов из жидкой фазы в твердую. Показано, что в условиях перемещения межфазной границы в результате контактного плавления насыщения макроскопического объема в приповерхностном слое кристалла не происходит;
- показана невозможность образования макроскопической промежуточной твердой фазы в процессе конкурентного роста с жидкой фазой;
- исследована кинетика роста жидкой фазы в системах с промежуточными твердыми фазами. Установлено, что концентрационная протяженность жидкой фазы соответствует стабильной диаграмме состояния. Полученные результаты объяснены образованием на границе с кристаллами метастабильных участков жидкости, при кристаллизации которых выделяются стабильные интерметаллиды, обеспечивающие непрерывность химических потенциалов компонентов;
- на примере системы олово–висмут исследована зависимость кинетики роста жидкой фазы от состава твердого раствора, являющегося одним из исходных кристаллов. Найдено, что концентрационный интервал жидкой фазы соответствует стабильной диаграмме состояния. С учетом отсутствия насыщения приповерхностных слоев кристалла такой результат объясняется образованием участков метастабильной жидкости, прилегающей к первичным кристаллам, и дальнейшей кристаллизацией метастабильных участков жидкости с выделением насыщенных твердых растворов, обеспечивающих квазиравновесный процесс роста жидкой фазы;
- разработана оригинальная методика измерения температуры в контакте разнородных кристаллов при Т-эффекте контактного плавления, защищенная авторским свидетельством;
- в системах с конгруэнтно и инконгруэнтно плавящимися промежуточными фазами измерена температура контакта образцов при Т-эффекте. Установлено, что наблюдается разогрев контакта на доли кельвина. Сравнение экспериментальных результатов с расчетами теплового источника позволило сформулировать гипотезу, согласно которой в системах с интерметаллидами при температурах ниже эвтектической в контакте исходных образцов одновременно растут метастабильная жидкая фаза и стабильный интерметаллид. Интерметаллид, в основном, образуется в результате кристаллизации метастабильной жидкости, причем в процессе совместного роста интерметаллид поставляет теплоту, способствующую росту метастабильной жидкой фазы;
- осуществлено приведение в контакт образцов систем ртуть–таллий и ртуть–индий при температурах ниже температур плавления стабильных эвтектик. Наблюдалось прочное соединение кристаллов ртути и индия, что свидетельствует о протекании Т-эффекта. В системе ртуть–таллий Т-эффект не обнаружен. Отсутствие Т-эффекта в этой системе объяснено эндотермической реакцией образования промежуточной твердой фазы, что не создают условий роста метастабильной жидкой фазе;
- разработана методика компьютерного эксперимента, базирующегося на идеологии целлюлярного равновесия – клеточных автоматов. Компьютерная имитация, основанная на работе клеточных автоматов, применена для исследования роста фаз при контактном плавлении. При разработке компьютерной модели учтена возможность возникновения метастабильных состояний в жидкости на границе с кристаллом. Методика апробирована путем сравнения результатов компьютерного и реального экспериментов для простых эвтектических систем;
- проведен компьютерный эксперимент по исследованию процессов, происходящих в системе с промежуточной твердой фазой. Результаты показывают возможность процессов, предложенных для объяснения результатов реального эксперимента в этой системе, включающих образование стабильных промежуточных твердых фаз при распаде меатстабильной жидкости.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
- Гиббс Дж.В. Термодинамика и статистическая механика. М.: Наука, 1982.
- Guggenheim E.A. Thermodynamics. Amsterdam: North-Holland Publishing Co., 1967.
- Хаазе Р. Термодинамика необратимых процессов. М.: Мир, 1967.
- Canegallo S., Agrigento V., Moraitou C., Toussimi A., Bicelli L.P., Serravalle G Indium diffusion inside InBi during and after electrodeposition at various temperatures // J. Alloys Comp. 1996. № 237. P. 211-217.
ОСНОВНОЕ СОДЕРЖАНИЕ ДИССЕРТАЦИИ ПРЕДСТАВЛЕНО В СЛЕДУЮЩИХ ПУБЛИКАЦИЯХ:
- Савинцев П.А., Ахкубеков А.А., Гетажеев К.А., Рогов В.И. Саввин В.С. Определение коэффициентов диффузии и коэффициентов активности в системе галлий-индий методом контактного плавления // Известия вузов. Физика. 1971. № 4. С. 53-57
- Ахкубеков А.А., Саввин В.С., Савинцев П.А., Рогов В.И. Построение линий ликвидуса диаграмм состояния двойных систем методом контактного плавления // Заводская лаборатория. 1972. № 2. С. 208
- Ахкубеков А.А., Рогов В.И., Саввин В.С., Савинцев П.А. Контактное плавление галлиевых систем // Смачиваемость и поверхностные свойства расплавов и твердых тел. Киев: Наукова думка, 1972. С. 121-123.
- Савинцев П.А., Ахкубеков А.А., Рогов В.И., Саввин В.С., Теммукуев И.М., Гаврилов Н.И. Исследование взаимной диффузии в бинарных эвтектических расплавах методом контактного плавления // Уч. записки Кабардино-Балкарского гос. университета. Нальчик: КБГУ, 1972. С. 130-134.
- Нальгиев А.Г.-М., Ибрагимов Х.И., Саввин В.С. Исследование поверхностного натяжения, плотности и работы выхода электрона системы олово-ртуть // Известия Северо-Кавказского научного центра высшей школы. Естественные науки. 1976. № 2. С. 36-38
- Ибрагимов Х.И., Саввин В.С., Дадашев Р.Х.. Прибор для определения плотности жидких металлических растворов // Журнал физической химии. 1976. Т. 50. № 8. С. 2158-2159
- Ибрагимов Х.И., Саввин В.С. Поверхностное натяжение и плотность расплавов ртуть-свинец // Известия вузов. Цветная металлургия. 1976. № 4. С. 148-149
- Саввин В.С., Ибрагимов Х.И. Поверхностное натяжение жидких растворов висмут-свинец-ртуть // Известия Северо-Кавказского научного центра высшей школы. Естественные науки. 1976. № 3. С. 111-112
- Саввин В.С., Ибрагимов Х.И. Исследование поверхностного натяжения и плотности жидких сплавов висмут-свинец-ртуть // Известия АН СССР. Металлы. 1977. № 1. С. 67-69
- Саввин В.С., Ибрагимов Х.И. Поверхностные свойства расплавов висмут–свинец–ртуть // Физика поверхностных явлений. Ч. 1. Материалы VII Всесоюзной конференции по поверхностным явлениям в расплавах. Грозный: ЧИГУ, 1977. С. 172-184.
- Ибрагимов Х.И., Саввин В.С. Приборы для совместного измерения плотности, поверхностного натяжения и работы выхода электрона жидких металлических растворов // Методы исследования и свойства границ раздела контактирующих фаз. Киев: Наукова думка, 1977. С. 40-46.
- Ибрагимов Х.И., Саввин В.С. Расчет параметров поверхностного слоя однокомпонентных металлических расплавов // Физико-химические исследования металлургических процессов. Свердловск: УПИ, 1979. Вып. 7. С. 34-40.
- Ибрагимов Х.И., Саввин В.С. Поверхностное натяжение расплавов системы таллий–ртуть // Физико-химические исследования металлургических процессов. Свердловск: УПИ, 1980. Вып. 8. С. 61-66.
- Ибрагимов Х.И., Саввин В.С. Расчет характеристик поверхностного слоя растворов / / Поверхностные свойства расплавов. Киев: Наукова думка, 1982. С. 22-24.
- Ибрагимов Х.И., Саввин В.С., Вигаев В.П. Поверхностное натяжение расплавов системы ртуть–кадмий / Чечено–Ингушский гос. ун–т им. Л.Н. Толстого. Грозный, 1983. Деп. в ВИНИТИ. № 998-84.
- Айтукаев А.Д., Саввин В.С., Эльсункаева Ш.В. К вопросу о механизме доэвтектического контактного плавления // Известия вузов. Физика. 1983. № 7. С. 60-63
- Саввин В.С., Вигаев В.П., Кислицина Н.Н., Колесникова И.М. Поверхностное натяжение расплавов системы индий-кадмий // Известия АН СССР. Металлы. 1985. № 2. С. 67-69
- Саввин В.С. К расчету капиллярной постоянной по данным эксперимента // Адгезия расплавов и пайка материалов. 1985. Вып. 14. С. 5-7
- Саввин В.С. Определение коэффициентов взаимной диффузии в расплавах по данным о контактном плавлении // Известия вузов. Физика. 1986. № 10. С. 54-58
- Саввин В.С., Магомедова П.Р. Контактное плавление в режиме свободной конвекции / Чечено–Ингушский гос. ун–т им. Л.Н. Толстого. Грозный, 1986. Деп. в ВИНИТИ. № 2661-86
- Саввин В.С., Айтукаев А.Д., Хашиева Ф.Д., Мальсагова Ж.Х. Измерение температуры формирующейся зоны контакта массивных образцов // Чечено–Ингушский гос. ун–т им. Л.Н. Толстого. Грозный, 1988. Деп. в ВИНИТИ. № 1590-В88
- Саввин В.С., Абдуллаев В.А., Рябова Н.И., Ярошевская С.В. Дилатометрическое тестирование гетерогенного строения жидких металлов // Известия АН СССР. Металлы. 1992. № 4. С. 33-35
- Ibragimov Kh.I., Savvin V.S. Surface Effects in Mercury-Based Binary Melts // High Temperature Capillarity. An International Conference. Smolenice Castle, Bratislava, Slovakia. May 8-11, 1994. Abstracts. Bratislava. 1994. P. 13-16.
- Ибрагимов Х.И., Саввин В.С. Поверхностное натяжение амальгам систем амальгам систем Hg-M (M – Cd, In, Sn, Tl, Pb, Bi) // Неорганические материалы. 1996. Т. 32. № 9. С. 1100-1107
- Саввин В.С Волюмометрическое тестирование квазиполикристалличности жидких висмута и галлия // Расплавы. 1999. № 4. С. 26-31
- Саввин В.С., Михалёва О.В., Повзнер А.А. Кинетика контактного плавления в нестационарно-диффузионно режиме // Расплавы. 2001. № 2. С. 42-50
- Саввин В.С., Михалёва О.В., Повзнер А.А. Контактное плавление твердых растворов в нестационарно-диффузионно режиме// Расплавы. 2002. № 2. С. 49-56
- Саввин В.С., Михалёва О.В., Повзнер А.А. Исследование фазового состава диффузионной зоны системы Pb-Bi при контактном плавлении компонентов // Неорганические материалы. 2002. Т. 38. № 7. С. 826-830
- Саввин В.С. Измерение капиллярной постоянной и краевого угла смачивания методом сообщающихся цилиндров // Заводская лаборатория. Диагностика материалов. 2003. № 2. С. 38-39
- Саввин В.С., Айтукаев А.Д. Спекание образцов систем Bi-Tl, Bi-In, Bi-Pb, Hg-In // Неорганические материалы. 2004. Т. 40. № 2. С. 147-151
- Саввин В.С., Азави А.К., Ватолина Н.Д., Повзнер А.А. Моделирование контактного плавления с помощью клеточного автомата // Расплавы. 2004. № 6. С. 86-92.
- Саввин В.С., Азави А.К., Кадочникова А.С., Повзнер А.А. Исследование фазового состава диффузионной зоны системы висмут-индий при контактном плавлении // Физика металлов и металловедение. 2005. Т. 99. № 5. С. 79-85.
- Повзнер А.А., Саввин В.С. Исследование образования и роста промежуточных фаз в контакте разнородных металлов // Вестник ГОУ ВПО УГТУ-УПИ № 13 (65). Екатеринбург. 2005. С. 85–87.
- Саввин В.С., Азави А.К., Ситников П.В., Ватолина Н.Д., Повзнер А.А. Влияние теплового эффекта на кинетику роста промежуточной жидкой фазы // Расплавы. 2005. № 5. С. 55–60.
- Саввин В.С., Михалёва О.В., Зубова Ю.А. Диффузия атомов из жидкой фазы в твердую при контактном плавлении // Письма в журнал технической физики. 2007. Т. 33. № 10. С. 27-32.
- Саввин В.С., Азави А.К., Повзнер А.А. Компьютерное моделирование роста промежуточной жидкой фазы в простой эвтектической системе // Теплофизика высоких температур. 2007. № 3.
- Саввин В.С., Азави А.К., Повзнер А.А. Компьютерная имитация роста промежуточных фаз в сложной металлической системе // Физика металлов и металловедение. 2007. № 8.
- Savvin V S, Kazachkova Yu A and Povzner A A. Phase formation in contact of dissimilar metals // Journal of Physics: Conference Series Volume 98, 2008 052002
- Саввин В.С., Казачкова Ю.А., Повзнер А.А. Оценка температурного коэффициента поверхностного натяжения границы раздела фаз, образующих эвтектику // Теплофизика высоких температур. 2008. Т. 46. № 2. С. 308-309.
ИЗОБРЕТЕНИЯ, ЗАЩИЩЕННЫЕ ПО МАТЕРИАЛАМ ДИССЕРТАЦИИ
- А.с. 371481 СССР. Способ измерения концентрационного распределения в диффузионной зоне / П.А. Савинцев, А.А. Ахкубеков, В.И. Рогов, В.С. Саввин, И.М. Теммукуев. Заявлено 06.07.1970. Опубл. 22.11.1973, бюлл. № 12
- А.с. 1158897 СССР. Устройство для определения плотности металлических расплавов / Х.И. Ибрагимов, В.С. Саввин. Заявлено 20.12.1983. Опубл. 30.05.1985, бюлл. № 12
- А.с. 1276959 СССР. Способ определения капиллярной постоянной металлических расплавов / В.С. Саввин. Заявлено 17.09.1984. Опубл. 15.12.1986, бюлл. № 46
- А.с. 1497539 СССР. Способ исследования кинетики фазовых превращений и химических реакций, происходящими между твердыми металлическими образцами / В.С. Саввин, А.Д. Айтукаев. Заявлено 23.10.1987. Опубл. 30.07.1989, бюлл. № 28
- Патент 2019814 РФ. Способ исследования гетерогенности поликомпонентных жидкостей / В.С. Саввин. Заявлено 15.08.1991. Опубл. 15.09.1994, бюлл. № 17.
