Метод построения асимметричного масштабного уравнения состояния в физических переменных
На правах рукописи
РЫКОВ СЕРГЕЙ ВЛАДИМИРОВИЧ
МЕТОД ПОСТРОЕНИЯ АСИММЕТРИЧНОГО МАСШТАБНОГО УРАВНЕНИЯ СОСТОЯНИЯ В ФИЗИЧЕСКИХ ПЕРЕМЕННЫХ
Специальность 01.04.14 – Теплофизика и
теоретическая теплотехника
Автореферат
диссертации на соискание ученой степени
кандидата технических наук
Санкт-Петербург
2009
Работа выполнена в ГОУ ВПО «Санкт-Петербургский государственный университет низкотемпературных и пищевых технологий»
Научный руководитель: доктор технических наук, профессор
Самолетов Владимир Александрович.
Официальные оппоненты: доктор технических наук, профессор
Васьков Евгений Тихонович,
кандидат технических наук,
научный сотрудник
Лаптев Юрий Александрович.
Ведущая организация: ГОУ ВПО «Санкт-Петербургский государственный университет информационных технологий, механики и оптики»
Защита диссертации состоится “27” мая 2009 г. в 12 час на заседании диссертационного совета Д 212.234.01 при Санкт-Петербургском государственном университете низкотемпературных и пищевых технологий, 191002, Санкт-Петербург, ул. Ломоносова, д. 9, тел/факс 315-30-15.
С диссертацией можно ознакомиться в библиотеке университета.
Автореферат разослан “23” апреля 2009 г.
Ученый секретарь
диссертационного совета,
доктор технических наук,
профессор Л.С. Тимофеевский
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Диссертация посвящена расчетно-теоретическому исследованию поведения индивидуальных веществ в широкой окрестности критической точки системы жидкость-пар. Разработано асимметричное масштабное уравнение состояния в физических переменных, которое апробировано на примере описания равновесных свойств аргона и использовано при построении неаналитических фундаментальных (единых) уравнений состояния аргона и аммиака.
Актуальность темы:
При разработке новой техники и современных технологий важно иметь достоверную и точную информацию о теплофизических свойствах рабочих тел. Таким образом, получение данной информации является важной народнохозяйственной задачей. В настоящее время твердо установлено, что аналитические уравнения состояния даже качественно не передают поведение термодинамической поверхности в широкой окрестности критической точки.
Поэтому значительные усилия исследователей направлены на разработку так называемых неаналитических уравнений состояния в физических переменных. Эти уравнения должны качественно верно, то есть в соответствии с требованиями масштабной теории критических явлений, воспроизводить околокритическую область термодинамической поверхности. Однако до сих пор не удалось разработать в физических переменных уравнение состояния, которое учитывало бы асимметрию реальной жидкости относительно критической изохоры и обладало такими же аналитическими характеристиками, как и асимметричные масштабные уравнения в параметрической форме.
Решение данной задачи требует разработки метода построения в физических переменных нерегулярных составляющих термодинамических функций, воспроизводящих асимметрию реальной жидкости. Так называемая критическая катастрофа наступает в диапазоне параметров состояния ![]() ,
, ![]() . Область применения существующих асимметричных уравнений состояния, как в параметрической форме, так и в физических переменных существенно уже.
. Область применения существующих асимметричных уравнений состояния, как в параметрической форме, так и в физических переменных существенно уже.
Поэтому задача разработки метода построения в физических переменных асимметричного масштабного уравнения состояния в настоящее время является актуальной. Это уравнение должно удовлетворять, по крайней мере, двум требованиям. Во-первых, должно иметь хорошие аппроксимационные характеристики, чтобы его можно было использовать для разработки широкодиапазонных и единых уравнений состояния. Во-вторых, иметь более широкую рабочую область, по размерам близкую к той, в которой имеет место критическая катастрофа аналитических уравнений.
Цель работы:
Разработка метода построения в физических переменных масштабного уравнения состояния, описывающего широкую окрестность критической точки и учитывающего асимметрию системы жидкость-пар относительно критической изохоры в соответствии с требованиями современной теории критических явлений.
Задачи исследования:
В соответствии с поставленной целью решались следующие задачи:
- Разработка метода расчета нерегулярных составляющих термодинамических функций, передающих поведение жидкости и газа в широкой окрестности критической точки.
- Построение и выбор структуры масштабных функций в физических переменных, отвечающих за передачу асимметрии жидкости и газа в окрестности критической точки.
- Апробация разработанных уравнений состояния на примере описания разнородных экспериментальных данных хорошо изученных веществ.
Основные положения, выносимые автором на защиту:
- Метод построения асимметричного масштабного уравнения состояния в физических переменных, включающий в себя метод расчета асимметричных составляющих термодинамических функций, передающих поведение жидкости и газа в широкой окрестности критической точки, и метод построения и выбора структуры масштабных функций в физических переменных, отвечающих за передачу асимметрии жидкости и газа в окрестности критической точки.
- Асимметричное масштабное уравнение состояния аргона, имеющее рабочую область
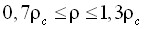 ,
, 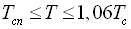 .
. - Метод построения асимметричного уравнение состояния со сглаживающими функциями и модернизированное асимметричное уравнение состояния аргона, имеющее рабочую область
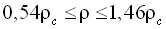 ,
, 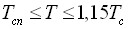 .
. - Асимметричное фундаментальное уравнение состояния аргона, имеющее рабочую область
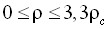 ,
, 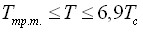 и асимметричное фундаментальное уравнение состояния аммиака, имеющее рабочую область
и асимметричное фундаментальное уравнение состояния аммиака, имеющее рабочую область 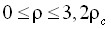 ,
, 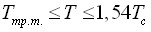 .
.
Практическая значимость работы:
Разработанные асимметричные масштабные уравнения состояния позволяют рассчитывать равновесные свойства индивидуальных веществ практически во всей области термодинамической поверхности, в которой для аналитических уравнений имеет место так называемая “критическая катастрофа”. Предложенный метод расчета составляющих термодинамических функций в физических переменных, воспроизводящих асимметрию системы жидкость-пар в околокритической области, позволяет обоснованно, с точки зрения современной физики критических явлений, выбирать структуру не только масштабных, но и единых и широкодиапазонных уравнений состояния и на их основе рассчитывать равновесные свойства жидкости и газа, как в регулярной части термодинамической поверхности, так и в широкой окрестности критической точки и в области метастабильных состояний.
Внедрение результатов работы:
- Разработан пакет прикладных программ на алоритмическом языке Фортран для нахождения параметров уравнения состояния и расчета термодинамических свойств веществ.
- Результаты работы использованы при разработке таблиц ГСССД аммиака, хладонов R218 и R23.
- Результаты работы использованы в учебном процессе на следующих кафедрах СПбГУНиПТ: «Теоретические основы тепло–хладотехники» и «Информатика и прикладная математика».
Апробация работы:
Содержание диссертации обсуждалось на следующих конференциях и симпозиумах: 1) Международная научно-техническая конференция «Холодильная техника России. Состояние и перспективы накануне XXI века» (Санкт-Петербург, 1998 г.); 2) Всероссийская научно-техническая конференция «Прогрессивные технологии и оборудование пищевых производств» (Санкт-Петербург, 1999 г.); 3) XI Российская конференция по теплофизическим свойствам веществ (Санкт-Петербург, 2005 г.); 4) III Международная научно-техническая конференция «Низкотемпературные и пищевые технологии в XXI веке» (Санкт-Петербург, 2007 г.); 5) XXII Международная конференция «Воздействие интенсивных потоков энергии на вещество» (Эльбрус, 2007 г.); 6) Научно-техническая конференция с международным участием «Безопасный холод» (Санкт-Петербург, 2007г.); 7) Научно-техническая конференция с международным участием «Глобальные проблемы холодильной техники» (Санкт-Петербург, 2007 г.); 8) Научно-техническая конференция с международным участием «Сто лет, которые изменили мир (к юбилею I Международного конгресса по холоду 1908 г.)» (Санкт-Петербург, 2008 г.); 9) Научно-техническая конференция «Криогенная техника и технология на рубеже второго столетия» (Санкт-Петербург, 2009 г.); 10) Научно-техническая конференция с международным участием «Холод и климат Земли. Стратегия победы или выживания» (Санкт-Петербург, 2009 г.); 11) Научно-практических конференциях профессорско-преподавательского состава, сотрудников, аспирантов, докторантов и студентов СПбГУНиПТ (Санкт-Петербург, 2007–2009 г.г.).
Публикации:
Основные результаты диссертации опубликованы в семнадцати печатных работах, из них четыре в издании, рекомендуемом ВАК РФ.
Структура и объем работы:
Диссертация состоит из введения, пяти глав и выводов. Диссертация содержит 137 страниц основного машинописного текста, 73 рисунка, 3 таблицы. Список использованной литературы включает 138 наименований работ, из них 85 отечественных и 73 зарубежных авторов.
СОРЖАНИЕ РАБОТЫ
Согласно современной теории критических явлений поведение равновесных свойств чистых веществ в широкой окрестности критической точки должно удовлетворять следующим законам:
– на критической изотерме:
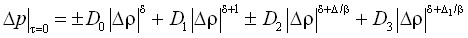 , (1)
, (1)
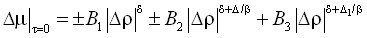 , (2)
, (2)
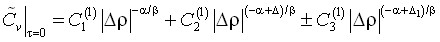 , (3)
, (3)
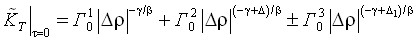 , (4)
, (4)
– на критической изохоре:
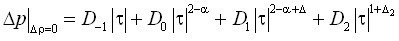 , (5)
, (5)
![]() , (6)
, (6)
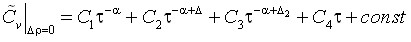 , (7)
, (7)
![]() , (8)
, (8)
– на линии равновесия:
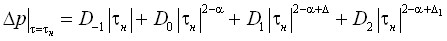 , (9)
, (9)
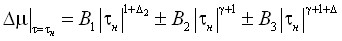 , (10)
, (10)
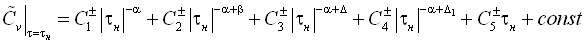 , (11)
, (11)
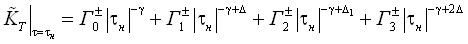 . (12)
. (12)
Проблеме построения масштабных уравнений состояния в физических переменных посвящены многочисленные работы Абдулагатова И.М., Алибекова Б.Г., Лысенкова В.М, Шустрова А.В., Рыкова В.А. и других. Однако до сих пор не удалось решить задачу построения масштабного уравнения состояния, удовлетворяющего всем требованиям (1)–(12).
Для того чтобы решить задачу построения масштабного уравнения состояния, удовлетворяющего всем требованиям (1)–(12), в работе предложен метод построения асимметричных составляющих свободной энергии Гельмгольца, обеспечивающих учет асимметрии реальной системы жидкость-пар относительно критической изохоры, критической изотермы и линии фазового равновесия, в соответствии с требованиями (1)–(12).
Из анализа выражений (1)–(12) следует, что поведение свободной энергии Гельмгольца и ее частных производных на критической изотерме, критической изохоре и линии фазового равновесия описывается следующими степенными законами:
![]() ,
, ![]() ,
, ![]() . (13)
. (13)
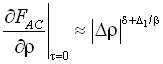 ,
, 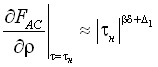 ,
, 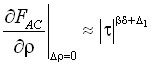 . (14)
. (14)
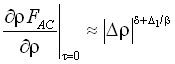 ,
, 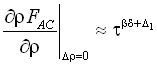 . (15)
. (15)
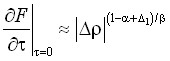 ,
, 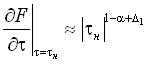 ,
, 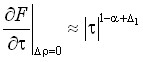 . (16)
. (16)
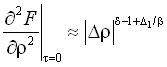 ,
, 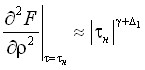 ,
, 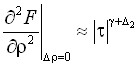 . (17)
. (17)
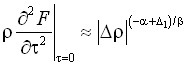 ,
, 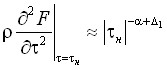 ,
, 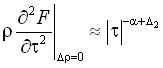 . (18)
. (18)
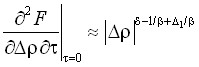 ,
, 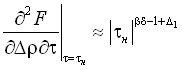 ,
, 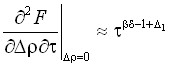 . (19)
. (19)
Метод основан на совместном анализе степенных законов (13)–(19) и степенных функционалов. В работе рассмотрены функционалы следующего типа:
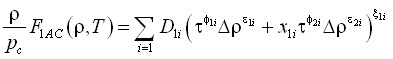 , (20)
, (20)
![]() , (21)
, (21)
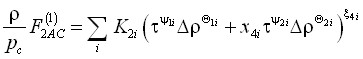 , (22)
, (22)
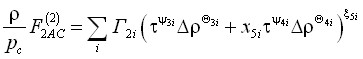 . (23)
. (23)
На основе совместного анализа соотношений (13)–(19) и степенных зависимостей (20)–(23) установлена связь между коэффициентами выражений (20)–(23), а также между показателями степени выражений (20)–(23) и критическими индексами ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Показано, что слагаемое свободной энергии, ”отвечающее” за асимметричный характер поведения термодинамических функций на критической изотерме и линии фазового равновесия, т.е. передающее те соотношения (13)–(19), в которые входит критический индекс
. Показано, что слагаемое свободной энергии, ”отвечающее” за асимметричный характер поведения термодинамических функций на критической изотерме и линии фазового равновесия, т.е. передающее те соотношения (13)–(19), в которые входит критический индекс ![]() , имеет вид:
, имеет вид:
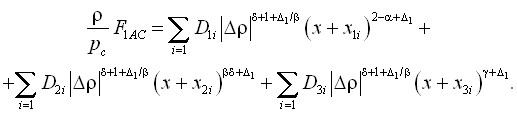 (24)
(24)
А слагаемое свободной энергии, передающее все соотношения (13)–(19), содержащие критический индекс ![]() , описывается выражением:
, описывается выражением:
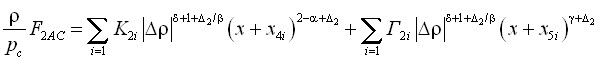 . (25)
. (25)
Показано, что выражения (24) и (25) в полном объеме передают все степенные законы (1)–(12), если вместо масштабной переменной ![]() использовать "обобщенную" масштабную переменную
использовать "обобщенную" масштабную переменную ![]() , где зависимость
, где зависимость ![]() устанавливается из равенства
устанавливается из равенства ![]() .
.
В работе проведен анализ полученных на основе (24), (25) масштабных функций свободной энергии в физических переменных и уточнена их структура. Показано, что разработанное на основе этих масштабных функций асимметричное уравнение состояния в околокритической области передает поведение термодинамических функций в соответствии со степенными законами (1)–(12)
То обстоятельство, что составляющая свободной энергии передает в соответствии с требованиями современной теории критических явлений особенности термодинамической поверхности, еще не означает, что полученное на ее основе асимметричное масштабное уравнение состояния будет количественно верно передавать термодинамическую поверхность. На основе предложенного в работе метода анализа поведения асимметричных масштабных функций в физических переменных на изолиниях, получено следующее выражение для ![]() :
:
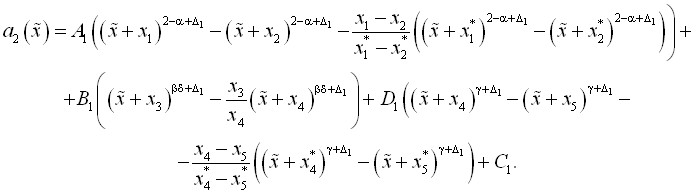 (26)
(26)
Анализ масштабной функции ![]() , такой же, как и для функции
, такой же, как и для функции ![]() , позволил установить ее структуру:
, позволил установить ее структуру:
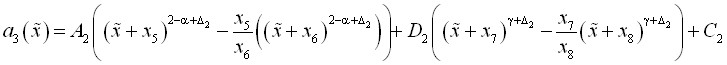 . (27)
. (27)
В работе показано, что (26) и (27) удовлетворяют следующему требованию: если ![]() , то первые четыре частные производные химического потенциала по плотности, рассчитанные на основе (26), (27), являются конечными на термодинамической поверхности, а если
, то первые четыре частные производные химического потенциала по плотности, рассчитанные на основе (26), (27), являются конечными на термодинамической поверхности, а если ![]() то первые три частные производные химического потенциала по плотности, полученные из соотношений (26), (27), принимают конечное значение на термодинамической поверхности.
то первые три частные производные химического потенциала по плотности, полученные из соотношений (26), (27), принимают конечное значение на термодинамической поверхности.
Итак, масштабные функции свободной энергии (26), (27) обеспечивают в соответствии с требованиями масштабной теории описание равновесных свойств жидкости в окрестности критической точки и имеют в этой области такие асимптотики, которые позволяют рассчитывать на правильное не только качественное, но и количественное описание термодинамической поверхности.
С целью уменьшить число подгоночных параметров асимметричного масштабного уравнения состояния разработан метод расчета параметров масштабных функций в физических переменных путем решения системы равенств, связывающих параметры асимметричных уравнений состояния в параметрической форме и уравнений в физических переменных на критической изохоре и критической изотерме.
Предложенное в работе асимметричное масштабное уравнение состояния имеет следующий вид:
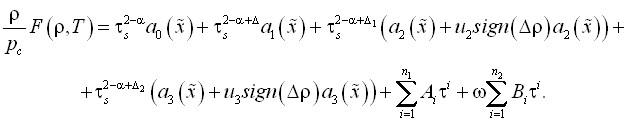 (28)
(28)
Асимметричное масштабное уравнение состояния в физических переменных апробировано на примере описания равновесных свойств хорошо изученных веществ. При выборе образцового вещества обращалось внимание не только на представительность массива экспериментальных данных, полученных в широкой окрестности критической точки, и их точность, но и на то, насколько согласованы разнородные экспериментальные данные между собой. В обзоре, приведенном в диссертации, показано, что этим требованиям в значительной степени отвечает аргон. Значительный вклад в исследование теплофизических свойств аргона в околокритической области внесли Анисимов М.А., Шавандрин А.М., Смирнов В.А. и другие исследователи. Поэтому в первую очередь предложенное масштабное уравнение состояния апробировано на примере описания термической и калорической поверхности аргона.
Рабочая область описания разнородных равновесных свойств аргона на линии фазового равновесия и в однофазной области составила по плотности ![]() и по температуре
и по температуре ![]() .
.
Предложенное асимметричное масштабное уравнение состояния имеет рабочую область, которая практически совпадает с рабочей областью как асимметричных масштабных уравнений состояния в параметрической форме, так и асимметричных масштабных уравнений состояния, полученных путем интегрирования преобразований Покровского. Вместе с тем, уравнение состояния (28), в отличие от уравнений в параметрической форме и полученных путем интегрирования преобразований Покровского, может быть модифицировано путем включения в его структуру функций, зависящих только от температуры.
В общем виде предлагаемое асимметричное масштабное уравнение стояния со сглаживающими функциями имеет следующую структуру:
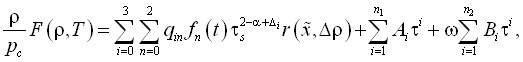 (29)
(29)
где ![]() ,
, ![]() .
.
Результаты расчета по уравнению (29) представлены на рис.1–2.
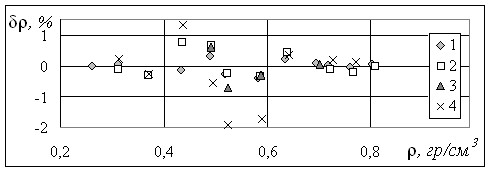
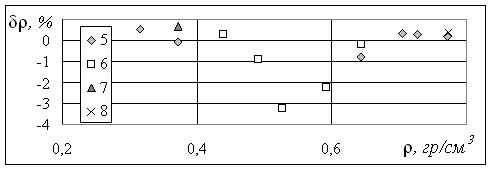
Рис.1. Отклонения значений плотности, рассчитанных по уравнению состояния аргона (29), от экспериментальных данных Michels A. и др. на изотермах:
1 – 173,15 К, 2 – 163,15 К, 3 – 158,15 К, 4 – 153,15 К; 5 – 150,65 K; 6 – 151,65 K;
7 – 150,15 K;, 8 – 148,85 K.
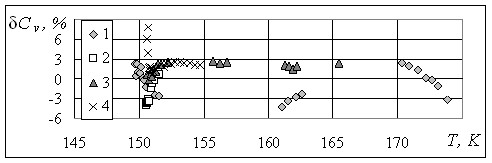
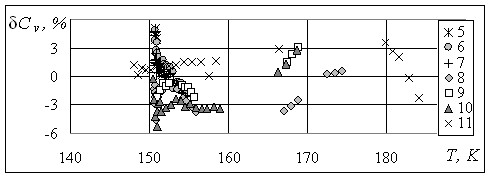
Рис.2. Отклонение значений изохорной теплоемкости, рассчитанных по уравнению (29), от экспериментальных данных Анисимова M.A. и др. на изохорах:
1 – 374,3 кг/м3; 2 – 457,6 кг/м3; 3 – 473,6 кг/м3; 4 – 497,3 кг/м3, 5 – 534,4 кг/м3;
6 – 541,9 кг/м3; 7 – 565,5 кг/м3; 8 – 604,4 кг/м3; 9 – 632,2 кг/м3; 10 – 647,70 кг/м3;
11 – 805,70 кг/м3.
Анализ полученных результатов свидетельствует о том, что в однофазной области уравнение (29) с удовлетворительной точностью описывает имеющиеся термические данные в области параметров состояния ![]() ,
, ![]() .
.
Опытные данные об изохорной теплоемкости описываются уравнением (29) в области ![]() ,
, ![]() с погрешность, практически совпадающей с погрешностью эксперимента. Однако на линии фазового равновесия рабочая область уравнения (29) по плотности всего
с погрешность, практически совпадающей с погрешностью эксперимента. Однако на линии фазового равновесия рабочая область уравнения (29) по плотности всего ![]() .
.
С целью увеличить рабочую область уравнения состояния (29) воспользуемся тем, что линия псевдокритических точек ![]() лежит в области лабильных состояний. Поэтому, не нарушая целостности уравнения (29), положим
лежит в области лабильных состояний. Поэтому, не нарушая целостности уравнения (29), положим ![]() при
при ![]() и
и ![]() при
при ![]() . Значения всех остальных параметров остаются неизменными. Результаты расчета плотности и давления на линии фазового равновесия приведены на рис.3–4. Теперь линия фазового равновесия описывается с погрешностью, практически совпадающей с погрешностью опытных данных в диапазоне
. Значения всех остальных параметров остаются неизменными. Результаты расчета плотности и давления на линии фазового равновесия приведены на рис.3–4. Теперь линия фазового равновесия описывается с погрешностью, практически совпадающей с погрешностью опытных данных в диапазоне ![]() .
.
Таким образом, рабочая область асимметричного масштабного уравнения состояния (29) может быть расширена до следующих границ: по плотности ![]() , по температуре
, по температуре ![]() .
.
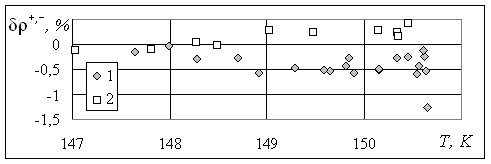
Рис.3. Отклонения значений плотности на линии фазового равновесия, рассчитанных по уравнению (29), от экспериментальных и табличных данных М.А. Анисимова в области: 1 – ![]() , 2 –
, 2 – ![]() .
.
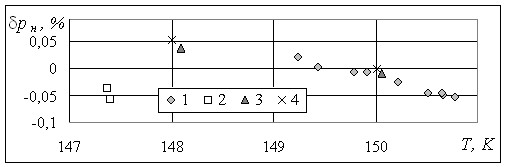
Рис.4. Отклонения значений давления насыщения, рассчитанных по уравнению (29) от значений: 1 – Verbeke O.B.; 2 – Van Itterbeek A.; 3 – Bowman D.H.; 4 – Stewart R.B.
Полученные результаты свидетельствуют о хороших экстраполяционных характеристиках асимметричного масштабного уравнения состояния в физических переменных. Это показано на примере построения единых уравнений состояния аргона и аммиака.
Единое уравнение состояния, которое использовано для апробации предложенных асимметричных масштабных функций, выбрано в виде:
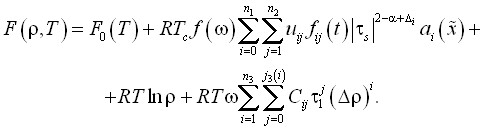 (30)
(30)
Уравнение состояния (30) использовано для описания равновесных свойств аргона. Показано, что использование в уравнении (30) масштабных функций (26), (27) позволяет количественно более точно воспроизвести калорические свойства. Так в околокритической области данные по изохорной теплоемкости Gladun C. описываются со среднеквадратичной погрешностью 1,8 %, в то время как по асимметричному единому уравнению Кудрявцевой И.В. эта погрешность составляет 6 %.
Исследованию равновесных свойств аммиака посвящены работы Клецкого А.В., Рябушевой Т.И., Ершовой Н.С., Циклиса Д.С., Казарновского Я.С. и других.
Рабочая область разработанного асимметричного уравнения состояния аммиака составляет: по плотности ![]() , по температуре
, по температуре ![]() . Результаты расчета по уравнению (30) представлены на рис.5–9.
. Результаты расчета по уравнению (30) представлены на рис.5–9.
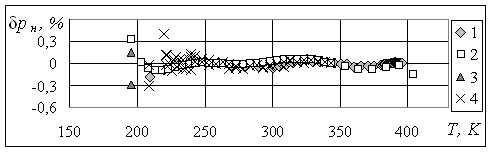
Рис.5. Отклонение значений давления на линии упругости аммиака, рассчитанных по уравнению (30), от данных: 1 – Huber M. и др.; 2 – Клецкий А.В.;
3 – Mc Kelvy E.C. и др.; 4 – Cragoe S.C. и др.
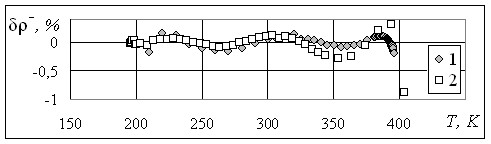
Рис.6. Отклонение значений плотности на паровой ветви линии фазового равновесия аммиака, рассчитанных по уравнению (30), от данных: 1 – Huber M. и др.;
2 – Клецкий А.В.
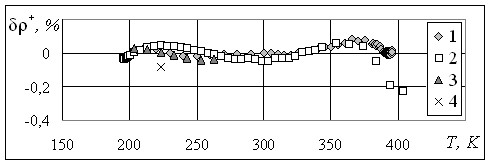
Рис.7. Отклонение значений плотности на жидкостной ветви линии фазового равновесия аммиака, рассчитанных по уравнению (30), от данных: 1 – Huber M. и др.;
2 – Клецкий А.В.; 3 – Timmermans J.; 4 – Манжелий В.Г.
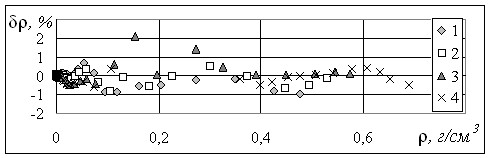
Рис.8. Отклонения значений плотности аммиака, рассчитанных по уравнению (30), от данных Клецкого А.В. на изотермах: 1 – 623,15 К; 2 – 593,15 К; 3 – 513,15 К;
4 – 423,15 К.
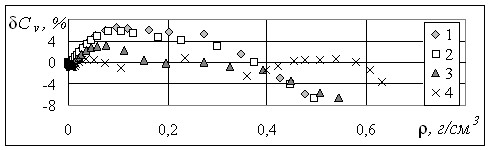
Рис.9. Отклонения значений изохорной теплоемкости аммиака, рассчитанных по уравнению (30), от данных Клецкого А.В. на изотермах: 1 – 623,15 К; 2 – 593,15 К;
3 – 513,15 К; 4 – 423,15 К.
Основные выводы и заключение
- Проведенный анализ асимметричных и кроссоверных параметрических уравнений состояния позволил сделать вывод о том, что они не могут конкурировать с широкодиапазонными неаналитическими уравнениями состояния в физических переменных, разработанными в рамках метода псевдокритических точек, во-первых, по рабочей области. Во-вторых, по точности при передаче разнородных равновесных свойств чистых веществ, находящихся в жидком или газообразном состоянии.
- Разработан метод выбора нерегулярных составляющих термодинамических функций, удовлетворяющих современной теории критических явлений и воспроизводящих асимметрию жидкости относительно критической изохоры. При этом предложенные нерегулярные составляющие термодинамических функций не уступают по своим аналитическим характеристикам составляющим известных асимметричных параметрических уравнений.
- Установлено, что введение в структуру полученных выражений свободной энергии "обобщенной" масштабной переменной позволяет в соответствии с требованиями современной теории критических явлений передать поведение свободной энергии и ее производных на линии фазового равновесия.
- Впервые получено выражение в физических переменных для асимметричной составляющей свободной энергии, передающей поведение химического потенциала в соответствии с подходами, развитыми в работах Лей-Ку и Грина, Анисимова и Киселева, Матезина и Покровского. Показано, что при соответствующем выборе второго критического индекса, могут быть получены асимптотические разложения, вытекающие, соответственно, из преобразований Покровского, или асимметричного уравнения состояния Киселева.
- Разработан метод расчета параметров масштабных функций в физических переменных асимметричных членов термодинамических функций путем решения системы равенств, связывающих параметры асимметричных уравнений состояния в параметрической форме и уравнений в физических переменных на критической изохоре и критической изотерме. Этот метод позволил уменьшить число подгоночных параметров асимметричного масштабного уравнения состояния.
- Асимметричное масштабное уравнение состояния, предложенное в данной работе не только точно передает равенство химических потенциалов на линии фазового равновесия, но и не приводит к возникновению разрывов второго рода в частных производных старших порядков химического потенциала, что выгодно отличает уравнения состояния (28) от известных масштабных и широкодиапазонных уравнений состояния в физических переменных; оно количественно верно, практически в пределах экспериментальной погрешности, передает опытные данные об изохорной теплоемкости, плотности на линии фазового равновесия и давления на линии упругости в следующей области параметров состояния:
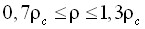 ,
, 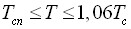 .
. - Предложен метод построения асимметричного масштабного уравнения состояния со сглаживающими функциями. Этот метод апробирован на примере описания разнородных экспериментальных данных о равновесных свойствах аргона. Установлено, что рабочая область асимметричного масштабного уравнения аргона со сглаживающими функциями составила: по плотности
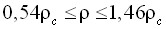 и по температуре
и по температуре 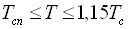 . При этом рабочая область для расчета термических данных по предложенному уравнению состояния составляет по плотности
. При этом рабочая область для расчета термических данных по предложенному уравнению состояния составляет по плотности 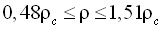 .Следовательно, разработанное здесь асимметричное масштабное уравнение позволяет рассчитывать равновесные свойства жидкости и пара практически во всей области параметров, в которой наблюдается так называемая “критическая катастрофа” аналитических уравнений состояния.
.Следовательно, разработанное здесь асимметричное масштабное уравнение позволяет рассчитывать равновесные свойства жидкости и пара практически во всей области параметров, в которой наблюдается так называемая “критическая катастрофа” аналитических уравнений состояния. - На основе предложенных в работе масштабных функций свободной энергии разработано асимметричное фундаментальное уравнение состояния аргона, имеющее рабочую область
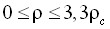 ,
, 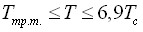 и асимметричное фундаментальное уравнение состояния аммиака, имеющее рабочую область
и асимметричное фундаментальное уравнение состояния аммиака, имеющее рабочую область 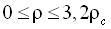 ,
, 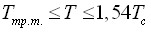 .
.
Таким образом, на основе предложенного метода расчета масштабных функций, учитывающих асимметрию системы жидкость-пар в широкой окрестности критической точки, построено асимметричное уравнение состояния в физических переменных, которое имеет рабочую область, сопоставимую с областью параметров состояния, в которой наблюдается так называемая “критическая катастрофа” аналитических уравнений состояния. Показано, что предложенные масштабные функции и разработанные на их основе составляющие свободной энергии могут быть использованы для обоснованного выбора структуры фундаментальных уравнений состояния в физических переменных, которые в соответствии с требованиями современной теории критических явлений описывают равновесные свойства жидкости и газа в околокритической области термодинамической поверхности.
Список основных работ по теме диссертации
- Рыков С.В. Уравнение линии упругости Ar, R23, R134a и R218. [Текст] / Рыков В.А., Рыков С.В. // Тезисы докладов Международной научно-технической конференции «Холодильная техника России. Состояние и перспективы накануне XXI века» – Санкт-Петербург, – 15–16 декабря 1998 г. – С. 5–6.
- Рыков С.В. Описание линии фазового равновесия аргона и озонобезопасных хладагентов R23, R218 и R134a. [Текст] / Рыков В.А., Лысенков В.В., Рыков С.В. // В кн. тезисы докладов Всероссийской научно-технической конференции «Прогрессивные технологии и оборудование пищевых производств». Санкт-Петербург, – 1999. С. 264.
- Рыков С.В. Единое уравнение состояния хладагента R134a. [Текст] / Рыков В.А., Рыков С.В. // В кн. тезисы докладов Всероссийской научно-технической конференции «Прогрессивные технологии и оборудование пищевых производств». Санкт-Петербург, – 1999. С. 266–267.
- Рыков С.В. Единое уравнение состояния аргона. [Текст] / Кудрявцева И.В., Рыков В.А., Рыков С.В. // В кн. тезисы докладов XI Российской конференции по теплофизическим свойствам веществ. – 2005. – Т. 1. – С. 31.
- Рыков С.В. Описание линии фазового равновесия хладагента R134а. [Текст] / Кудрявцева И.В., Рыков С.В. // В кн. тезисы докладов XI Российской конференции по теплофизическим свойствам веществ. – 2005. Т. 1. – С. 32.
- Рыков С.В. Единое уравнение состояния аммиака. [Текст] / Рыков В.А., Самолетов В.А., Рыков С.В. // В кн. тезисы докладов XI Российской конференции по теплофизическим свойствам веществ. – 2005. Т. 1. – С. 40.
- Рыков С.В. Хладон R-218. Плотность, энтальпия, энтропия, изобарная и изохорная теплоемкости, скорость звука в диапазоне температур 160…470 К и давлений 0,001…70 МПа. [Текст] / Рыков В.А., Устюжанин Е.Е., Попов П.В., Кудрявцева И.В., Рыков С.В. // ГСССД 211-05. Деп. в ФГУП “Стандартинформ” 08.12.2005 г., № 813-05 кк.
- Рыков С.В. Метод построения асимметричных составляющих свободной энергии. [Текст] / Рыков С.В. // Сборник «Проблемы пищевой инженерии», СПбГУНиПТ. СПб. 2006 г., Деп. в ВИНИТИ 23.06.06, № 833-B2006, с. 53–56.
- Рыков С.В. Хладон R23. Плотность, энтальпия, энтропия, изобарная и изохорная теплоемкости, скорость звука в диапазоне температур 235…460 К и давлений 0,01…25 МПа. [Текст] / Рыков В.А., Устюжанин Е.Е., Попов П.В., Кудрявцева И.В., Рыков С.В. // ГСССД 214-06. Деп. в ФГУП “Стандартинформ” 08.06.2006 г., № 816-06 кк.
- Рыков С.В. Единое уравнение состояния R23 для широкого интервала давлений и температур, включая критическую область. [Текст] / Кудрявцева И.В., Рыков С.В. // Доклады III Международной научно-технической конференции «Низкотемпературные и пищевые технологии в XXI веке». – 2007. С. 232–238.
- Рыков С.В. Метод расчета асимметричных составляющих свободной энергии и уравнения состояния. [Текст] / Кудрявцева И.В., Рыков С.В. // Тезисы докладов XXII международной конференции «Воздействие интенсивных потоков энергии на вещество», – 2007, С. 175–176.
- Рыков С.В. Аммиак. Плотность, энтальпия, энтропия, изобарная и изохорная теплоемкости, скорость звука в диапазоне температур 196–606 К и давлений 0,001–100 МПа. ГСССД 227-2008. [Текст] / Рыков В.А., Устюжанин Е.Е., Попов П.В., Кудрявцева И.В., Рыков С.В. // Деп. в ФГУП “Стандартинформ” 15.05.2008 г., № 837-2008 кк.
- Рыков С.В. Асимметричное единое уравнение состояния R134a. [Текст] / Кудрявцева И.В., Рыков В.А., Рыков С.В. // Вестник Международной академии холода. – 2008. – № 2. – С.36–39.
- Рыков С.В. Асимметричное масштабное уравнение состояния. [Текст] / Рыков С.В., Багаутдинова А.Ш., Кудрявцева И.В., Рыков В.А. // Вестник Международной академии холода. – 2008. – № 3. – С. 30–33.
- Рыков С.В. Линия насыщения аммиака. [Текст] / Рыков С.В., Самолетов В.А., Рыков В.А. // Вестник Международной академии холода. – 2008. – № 4. – С. 20–21.
- Рыков С.В. Асимметричное масштабное уравнение состояния аргона в переменных плотность-температура. [Текст] / Рыков С.В., Кудрявцева И.В., Рыков В.А. // Электронный научный журнал СПбГУНиПТ Холодильная техника и кондиционирование. – 2008. № 2.
- Рыков С.В. Выбор структуры асимметричных масштабных функций свободной энергии в физических переменных. [Текст] / Рыков С.В., Кудрявцева И.В. // Вестник Международной академии холода. – 2009. – № 1. – С. 43–45.
Подписано к печати. Формат 60х80 1/16. Бумага писчая.
Печать офсетная. Печ. Л. 1.0. Тираж 80 экз. Заказ №
СПбГУНиПТ. 191002, Санкт–Петербург, ул. Ломоносова, 9.
ИИК СПбГУНиПТ. 191002, Санкт–Петербург, ул. Ломоносова, 9.

