Изэнтропическое сжатие вещества импульсным магнитным полем
На правах рукописи
Прут
Вениамин Вениаминович
Изэнтропическое сжатие вещества
импульсным магнитным полем
Специальность 01.04.17 – химическая физика,
в том числе физика горения и взрыва
Автореферат диссертации на соискание ученой степени
доктора физико-математических наук
Москва 2008
Работа выполнена в Институте ядерного синтеза РНЦ “Курчатовский институт”
Официальные оппоненты:
доктор физико-математических наук, профессор
Демченко Владимир Владимирович
доктор физико-математических наук, профессор
Набиев Шавкат Шарифович
доктор физико-математических наук, профессор
Чарахчьян Александр Агасиевич
Ведущая организация: Институт проблем химической физики РАН
Защита состоится " ___ " ____________ 2009 г. в ______ часов
на заседании диссертационного совета Д 520.009.05
при РНЦ “Курчатовский институт” по адресу: 123182, Москва, пл. Курчатова 1
С диссертацией можно ознакомиться в библиотеке
РНЦ “Курчатовский институт”
Отзывы на автореферат просьба присылать по адресу:
123182, Москва, пл. Курчатова 1, РНЦ “Курчатовский институт”
Автореферат разослан " ____ " ________________ 200 года
Ученый секретарь В.Ф. Серик
диссертационного совета Д 520.009.05
доктор химических наук, профессор
Общая характеристика работы
Актуальность. Исследование веществ при высоких давлениях осуществляется тремя методами: статическим (изотермическим), ударно-волновым и изэнтропическим. Максимальные плотности, которые могут быть получены экспериментально при статическом сжатии в алмазных наковальнях, ограничены прочностью материалов. Достижимое статическое давление 
Мбар, что соответствует предельной «идеальной» величине модуля сдвига. Максимальные температуры в алмазных наковальнях ограничены графитизацией алмаза.
Современные ударно-волновые методы используют легко-газовые пушки, химические и ядерные взрывчатые вещества, электромагнитное ускорение, лазеры, электронные и ионные пучки. С помощью подземных ядерных взрывов достигнуты давления 
Гбар. Особенность ударно-волнового сжатия заключается в существовании предельной величины плотности, после достижения которой давление возрастает, в основном, из-за увеличения температуры. Вырождение снимается, и вещество превращается в «обычную» (идеальную, невырожденную) плазму. При ударном сжатии «мягких» веществ, таких как гелий, водород, молекулярные кристаллы, предельные плотности соответствуют давлениям в сотни кбар. Даже металлизация гелия, которая «должна» происходить при давлении 
Мбар, не достижима ни при статическом, ни при ударно-волновом сжатии.
Поэтому единственная возможность получения очень высоких плотностей есть изэнтропическое сжатие вещества. При изэнтропическом сжатии не существует термодинамических, гидродинамических или конструктивных ограничений на достижение больших плотностей при относительно низких температурах. На изэнтропе конечная температура пропорциональна начальной, так что можно изменять в широких пределах температуру сжатого вещества, варьируя его начальную температуру. Ограничения обусловлены, в основном, выбором и формой импульса источника энергии.
Идея получения высоких плотностей при изэнтропическом сжатии принадлежит Гюгонио и Рэлею, которые рассматривали плоскую центрированную волну Римана. И самые известные способы реализации этой идеи были осуществлены лишь спустя более полувека в неуправляемом инерционном ядерном синтезе, а затем в концептуальном проекте управляемого ядерного синтеза. Однако в задачах термоядерного синтеза необходимо нахождение оптимального соотношения между температурой и плотностью при минимуме вкладываемой энергии для достижения максимального сгорания ядерного топлива. Идеализированные, в частности, автомодельные задачи применяются в качестве начального приближения в двух и трехмерных задачах, учитывающих возможно полную совокупность физических процессов.
Существуют многочисленные физические задачи, представляющие значительный интерес, быть может, больший, нежели задача управляемого термоядерного синтеза. Прежде всего, это измерение уравнения состояния при низких температурах в мегабарном и гигабарном диапазонах и проверка различных теоретических моделей, включающих оболочечные эффекты. При изэнтропическом сжатии могут быть достигнуты все планетарные параметры: Земли и больших планет. По-видимому, a priori не следует исключать возможности достижения звездных параметров: солнечных и звёздных карликов. Для того чтобы получить плотности звёздных карликов в объёме 
мм3, достаточно энергии 
Дж (
кт тротила). Получение высоких плотностей открыло бы возможность исследования в лабораторных условиях пикноядерных реакций, определяемых плотностью – в отличие от «обычных» термоядерных реакций.
Ближайшей задачей на этом пути достижения высоких плотностей есть, безусловно, задача получения металлического водорода, который при давлении несколько мегабар «должен» перейти в металлическое состояние, обладающего гипотетически высокой (
K) температурой перехода в сверхпроводящее состояние. Несмотря на значительные усилия в последние десятилетия, когда было опубликовано несколько работ, зафиксировавших резкое возрастание проводимости водорода и гелия, в настоящее время, по-видимому, нет независимых доказательств их металлизации при низкой температуре.
Паллиативом изэнтропическому сжатию может быть так называемое квазиизэнтропическое сжатие – серия относительно слабых ударных волн, что приводит к снижению температуры по сравнению с однократной ударной волной. Рассматривались различные промежуточные среды для преобразования ударных волн как в изэнтропическую волну сжатия, так и квазиизэнтропическую. В частности, в качестве промежуточной среды использовалось магнитное поле в геометрии 
-пинча. К недостаткам этих экспериментов следует отнести: отсутствие прямого измерения давления, что в значительной степени обусловлено неприемлемо низкой точностью рентгенографического измерения объёма; обычно возникающую неоднородность по длине; невозможность сохранения образца при высоких давлениях.
Эти недостатки в значительной степени можно устранить, используя в качестве динамического пресса металлический 
-пинч, основанный на взаимодействии тока, протекающего через металлическую трубку с собственным магнитным полем. Выбранная схема эксперимента, кроме принципиального преимущества в однородности сжатия, позволяет значительно увеличить точность измерения радиуса сжимающейся трубки от времени: возможна непрерывная оптическая регистрация и рентгеновская съемка со значительно большей точностью.
В диссертационной работе рассматриваются несколько основных направлений исследований, подчиненных главной цели: поиску путей получения изэнтропических давлений мегабарного диапазона при сжатии импульсным магнитным полем.
- Решение автомодельных задач изэнтропического сжатия вещества.
- Автомодельное и численное решение задач нелинейной диффузии магнитного поля.
- Аппроксимация уравнения состояния вещества в широком диапазоне параметров.
- Разработка экспериментальных методов получения высоких давлений и создание соответствующей техники.
- Измерение уравнения состояния вещества в широком диапазоне давлений.
Основные научные результаты и новизна работы
- Решена автомодельная задача изэнтропического сжатия сферическим или цилиндрическим поршнем однородного вещества с реальным уравнением состояния. Особенность данной работы, в отличие от всех известных, заключается в том, что предложенный метод решения применим к любым уравнениям состояния. Установлены асимптотические зависимости. Описаны эволюция профилей и временные зависимости на поршне.
Решена задача релятивистского изэнтропического сжатия плоским поршнем вещества со степенным уравнением состояния построена релятивистская центрированная волна сжатия. Получено численное решение, а также приближенные решения в ультрарелятивистском и нерелятивистском пределах. Рассмотрены особенности, которые вносит релятивизм при переходе к предельным сжатиям. Приведены оценки времени перехода к релятивистскому пределу в цилиндрической и сферической геометрии.
Решена задача сферического сжатия конденсированного вещества оболочкой в приближении несжимаемой среды. Величины на внутренней границе оболочки определяются решением автомодельной задачи. Установлены асимптотические зависимости скорости и кинетической энергии оболочки при вхождении в коллапс.
Полученные результаты показали принципиальную возможность достижения очень высоких плотностей и давлений, ограниченных лишь источником энергии. Выбор начального состояния определяет конечную температуру, соотношение между конечными значениями упругой и тепловой частями давления и энергии. Обсуждается отсутствие физических ограничений при получении плотностей и температур, характерных для физики больших планет и даже звёздных карликов. - Решена автомодельная задача уравнений нелинейной диффузии магнитного поля в полупространство. Задача содержит две нелинейные зависимости: в граничном условии магнитного поля и зависимости сопротивления от энергии. Построено распределение магнитного поля и внутренней энергии на фронте волны. Получена характерная величина ширины фронта волны. Найдено соотношение между внутренней и магнитной энергиями в зависимости от параметров задачи. Предложена физическая модель, описывающая нелинейную диффузию сильного магнитного поля в проводник. Дана аппроксимация электропроводности и теплопроводности во всем диапазоне рассматриваемых параметров, которая интерполировалась между электропроводностями твердого тела (вырожденной плазмы) и идеальной (невырожденной) плазмы. Приведены результаты численного решения этой задачи, в частности, зависимость достижимого давления при токах до 1 ГА. Показано, что токи величиной несколько десятков мегаампер могут приводить к увеличению времени удержания вещества в магнитном поле.
- Предложена аппроксимация уравнения состояния вещества, при которой во всей нерелятивистской области последовательно используется интерполяционный подход, как по плотности, так и по температуре. «Холодная» составляющая определяется при нормальных условиях экспериментальными параметрами. Тепловая ионная составляющая описывает переход от колебаний решетки со свободной энергией Дебая с вводимой характеристической температурой. Это позволяет расширить диапазон ее применения от твердого тела до идеального газа. Приведена интерполяция функции Дебая. Предложена аппроксимация свободной энергии электронов. Тепловая электронная составляющая описывает переход свободных электронов от идеального вырожденного газа к невырожденному состоянию. Получена формула, позволяющая вычислить степень ионизации при произвольных плотностях и температурах. Описаны непрерывные функции, аппроксимирующие потенциалы и энергии ионизации. Для меди вычислены фазовая диаграмма, ударные адиабаты для сплошного и пористого вещества, изэнтропы. В рамках предложенной модели рассматриваются особенности кривой плавления при высоких давлениях. Результаты расчетов иллюстрируются зависимостями от степени сжатия в диапазоне
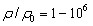. Адекватность модели подтверждается сравнением расчетных и экспериментальных данных. Предложена иная форма аппроксимации уравнения состояния вещества, справедливая не только во всей нерелятивистской области, но и «близкой» релятивистской области (
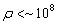г/см3). Для непрерывной энергии ионизации использовалась сплайн-интерполяция, что позволяет унифицировать процесс построения энергии ионизации для большого количества веществ. Проведены расчеты «холодной» и тепловых составляющих энергии и ряда других термодинамических функций, а также ударных адиабат для большинства элементов. - Рассмотрено квазиклассическое уравнение состояния с квантовыми поправками на неоднородность электронного газа к корреляционной энергии. Приводится аппроксимация корреляционной энергии во всем диапазоне плотностей. Рассматривается аппроксимация уравнения состояния, когда в квазиклассическом приближении в обменно-корреляционной и кинетической энергиях учитывается поправка на неоднородность электронного газа. Решена задача нахождения параметров модели, удовлетворяющих «нормальным» условиям. Приведены результаты численного решения уравнений модели при различных степенях сжатия. Найдены значения параметра квазиклассичности, определяющего точность рассматриваемого приближения. Вычислена степень ионизации элементов как функция плотности. Предлагаемая модель построения уравнения состояния позволяет сравнительно просто и с достаточной точностью приблизиться для рассматриваемых функций к экспериментальным величинам. Кроме того, модель предоставляет значительно больший объем самосогласованной информации по сравнению с обычной аппроксимацией.
- Проведены экспериментальные исследования сжимаемости твердого водорода при высоких давлениях в металлическом z-пинче. Разработаны методы измерения уравнения состояния в изэнтропическом процессе: «эталонный» и «вариационный». «Эталонный» метод основан на использовании эталонных веществ с известным уравнением состояния. Давление в исследуемом веществе определяется по сжимаемости эталонного вещества при условии относительного равенства давлений. Проведен анализ погрешности методов. Точность «эталонного» метода определяется степенью однородности давлений, точностью измерения размеров исследуемого и эталонного веществ и точностью уравнения состояния эталонного вещества. «Вариационный» метод основан на численном моделировании процесса и варьировании параметров уравнения состояния. Его точность определяется точностью измерения тока, точностью измерения размеров трубок и точностью уравнения состояния сжимающего вещества. Получено уравнение состояния водорода при давлениях до 150 кбар «эталонным» методом с максимальной погрешностью измерений объема
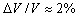, давления 
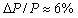. Предложен способ аппроксимации уравнения состояния водорода, основанный на интерполяции свободной энергии по плотности и температуре. Рассмотрен непрерывный переход из твердого состояния в молекулярный газ, а также свободных вращений молекул и внутримолекулярных колебаний в колебания решетки. Для определения параметров уравнения состояния используются экспериментальные результаты. Проведено сравнение с экспериментальными и теоретическими результатами других авторов. Давление перехода молекулярного водорода в металлическое состояние оценивается величиной 5-6 Мбар. - Проведены МГД расчеты сжатия твердого водорода и инертных газов в мегабарном диапазоне давлений в металлическом z-пинче. Определены условия согласования параметров лайнера, генератора тока и исследуемого вещества. Приведена зависимость давления от этих параметров. Показано, что могут быть получены давления перехода для всех этих веществ при параметрах генератора тока, реально осуществимых в настоящее время.
Рассмотрены в качественном приближении (нульмерная модель) процессы динамики и нагрева металлической трубки, применяемой в качестве поршня при сжатии вещества магнитным полем. Проведен численный анализ динамики металлического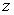
-пинча в приближении несжимаемости вещества лайнера. Получены оптимальные параметры сжатия веществ, определены возможности и ограничения этого метода. - Для исследования реологических характеристик металла при высокоскоростной деформации проведены эксперименты по деформированию медных и алюминиевых трубок магнитным полем Предложена дислокационная модель высокоскоростной деформации изотропной среды. Модель основана на линейной континуальной теории дислокаций и теоретических и экспериментальных результатах по динамике дислокаций. Модель позволила описать наши экспериментальные результаты в пределах погрешности измерений. Определены параметры модели. Дислокационная модель дает значительно более высокую точность, нежели рассматриваемые феноменологические реологические модели.
- Проведены эксперименты, демонстрирующие возможность сохранения вещества, сжатого при сильноточном разряде конденсаторной батареи через металлический лайнер. Проводилось сжатие красного фосфора магнитным давлением
кбар. Переход красного фосфора в черный подтверждался рентгеноструктурным анализом. На основе этих экспериментов предложена схема превращения графита в алмаз в изэнтропическом процессе сжатия в металлическом z–пинче с сохранением алмаза. Построено уравнение состояния графита и алмаза в широком диапазоне плотностей и температур. Приведена система уравнений фазового перехода графита в алмаз. Вычислены ударные адиабаты графита и алмаза. Изложены результаты численного моделирования превращения графита в алмаз в z-пинче. - Созданы четыре экспериментальные установки для исследования сжимаемости веществ при высоких давлениях, в частности, конденсированного водорода, а также для исследования высокоскоростной деформации металла и исследования сжатия плазмы. Установка «Юпитер» состоит из генератора импульсных токов, криогенной техники, рентгеновской и оптической систем регистрации, систем запуска и синхронизации. При рабочем токе до 5 МА установка обеспечивает генерирование мегагауссных магнитных полей и давлений в конденсированном водороде ~ 2 Мбар. Разработана специальная криогенная техника, предназначенная для конденсации водорода в рабочей трубке с контролируемой температурой и плотностью, подвода к трубке мегаамперного тока. Оптические и рентгеновские измерения обеспечивают регистрацию размеров сжимающейся трубки с высоким временным (10 нс) и пространственным (10 мкм) разрешением. По результатам проведенных исследований создана и испытана установка «z-пинч», включающая в себя конденсаторную батарею энергоемкостью 1.2 МДж, генератор импульсов запуска, систему зарядки, схему запуска, вакуумную систему, разрядную камеру. Описываемая установка может быть использована для генерации мегагауссных импульсных магнитных полей и мегабарных давлений, а также исследования возможности получения гигагауссных полей, мощных нейтронных и рентгеновских импульсов излучения.
Практическая ценность работы
- Полученные результаты открыли принципиальную возможность достижения очень высоких плотностей и давлений, ограниченных лишь источником энергии. Возможно получение плотностей и температур, характерных для физики Земли, больших планет и даже звёздных параметров.
- Предложенное уравнение состояния позволяет не только аналитически описать многие известные экспериментальные результаты, но быть надежной основой для предсказания термодинамических свойств веществ с ограниченным набором экспериментальных параметров. Полученное экспериментальное уравнение состояния водорода использовано при проверке теоретических моделей уравнения состояния.
- Предложена и экспериментально подтверждена возможность сохранения образца после снятия давления при сильноточном разряде конденсаторной батареи через металлический лайнер. Рассчитана схема превращения графита в алмаз в изэнтропическом процессе сжатия в металлическом z-пинче с сохранением алмаза. Эти результаты открывают альтернативную существующим методам возможность создания производства алмазов.
- Предложенная физическая модель нелинейной диффузии сильного магнитного поля в проводник позволяет создать основу для получения мегагауссных магнитных полей и давлений мегабарного и гигабарного диапазонов в макроскопических объёмах на технических устройствах, в основном, достижимых в настоящее время.
- Созданный экспериментально-диагностический комплекс аппаратуры может быть использован при конструировании современных и мощных установок для создания больших импульсных токов, магнитных полей и давлений.
Апробация. Основные результаты диссертации докладывались на 3, 4, 5, 6-й Международных конференциях по генерации мегагауссных магнитных полей и родственным экспериментам (Новосибирск, 1983 г.; Санта-Фе (США) 1986 г. Новосибирск, 1989 г.; Альбукерк (США), 1992 г.), на 3-й Международной конференции по плотным z-пинчам (Лондон, 1993 г.), на 3-м Всесоюзном совещании по аномальным свойствам водорода (Москва, 1984 г.), на 1 и 3-й Всесоюзных конференциях по импульсным источникам энергии (Юрмала, 1983 г, Ленинград. 1989 г.), 10 Europe Conf. on Contr. Fusion and Plasma Physics, M.: 1981, на семинаре Института высоких давлений, на Звенигородских конференциях по физике плазмы и УТС, на конференциях и семинарах РНЦ «Курчатовский институт».
Личный вклад автора. Все расчетно-теоретические результаты получены лично автором. Экспериментальные работы выполнены в основном в соавторстве с сотрудниками руководимой автором группы, а также коллегами по ИЯС. Работа [18] выполнена под руководством В.П. Смирнова. Вклад автора состоял в постановке задачи, организации и участии в экспериментальной работе, обработке, интерпретации полученных результатов и подготовке к публикации.
Публикации. Основные результаты диссертации изложены в 18 статьях, опубликованных в журналах, отвечающих требованиям ВАК. Кроме того, по теме диссертации опубликовано 32 другие работы: доклады, препринты, авторское свидетельство.
Структура и объем работы. Диссертация состоит из введения, 7 глав, содержит 314 страницы, включая 112 рисунков, 2 таблицы и список цитируемой литературы из 462 наименований.
Содержание диссертации
Глава 1. Автомодельные задачи изэнтропического сжатия вещества и нелинейной диффузии магнитного поля.
1.1. Автомодельное изэнтропическое сжатие вещества [1]. Решена автомодельная задача изэнтропического сжатия сферическим или цилиндрическим поршнем однородного вещества с реальным уравнением состояния. Особенность данной работы, в отличие от всех известных, заключается в том, что предложенный метод решения применим к любым уравнениям состояния. Описаны эволюция профилей и временные зависимости на поршне. Установлены асимптотические зависимости.
Уравнения сохранения приводятся к виду
, 
,
исходя из автомодельной переменной 
и автомодельных функций: 
, 
. Чтобы избежать ударных волн, интегральные кривые должны лежать в треугольнике 
(рис. 1.1.1), ограниченном критической линией 
и осями 
и 
.
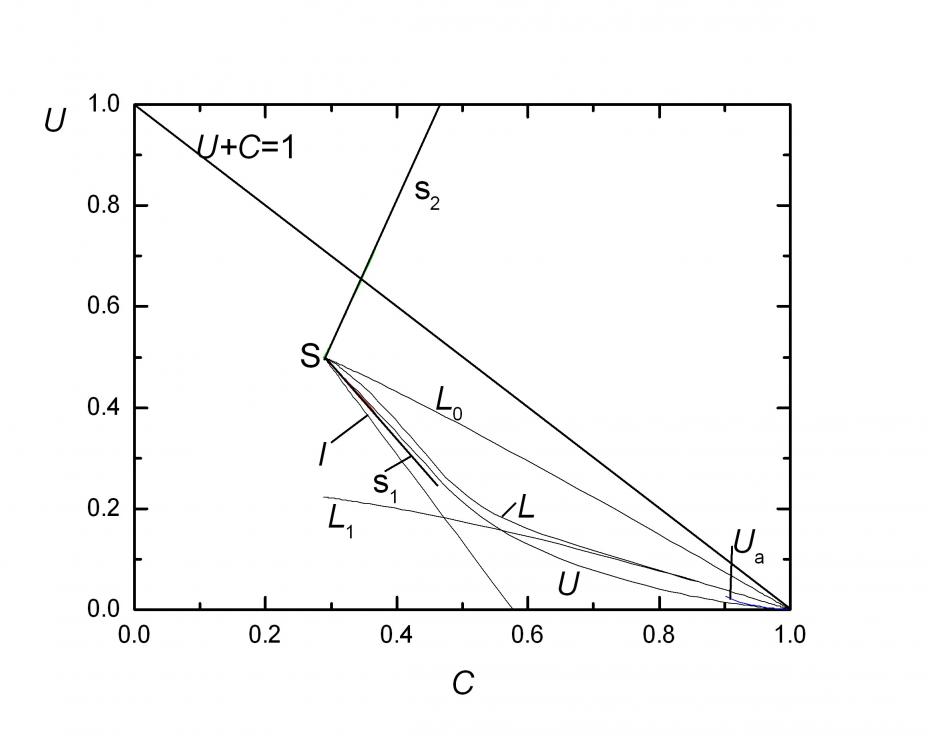
Рис. 1.1.1. Решение 
.
В вершинах 
находятся особые точки:
, 
, 
(все узлы). Координаты и типы O, A, B не зависят от 
. Параметры особой точки 
(седло): 
,
.
Хотя координаты 
зависят от 
, но 
всегда лежит в рассматриваемом треугольнике, а тип 
не зависит от 
. Точка 
соответствует фронту изэнтропической волны сжатия c 
. В отличие от степенного уравнения состояния, когда автомодельные уравнения расщепляются и решение упрощается, для реального уравнения необходимо их совместное решение. Предложенный метод заключается в нахождении интегральной кривой, которая соединяет особые точки 
и 
. Решение соответствующей краевой задачи для обыкновенных дифференциальных уравнений находилось вариационным методом, исходя из 
либо из 
.
Аналитические решения вблизи 
есть 
, где 
; 
. 
определяет характер процесса. При величине 
, определяемой из численного решения, соответствующая интегральная кривая входит в точку 
по сепаратрисе.
Уравнение сепаратрис: 
,
, где
. 
(со знаком минус) определяет сепаратрису, выход вдоль которой из точки 
определяет искомую интегральную кривую. Для выхода из точки 
при малых величинах получена аналитическая зависимость: 
, где
. варьируемый параметр, определяемый из условия выполнения граничного условия в B: =1. Траектория поршня определяется уравнением 
, уравнение характеристик: 
. Вблизи 
и 
решение для поршня есть 
и соответственно 
(время изменяется от 1 до 0). Для характеристик: 
и 
. Зависимость 
, где 
. Здесь приведен не только показатель степени, но и предстепенной множитель для произвольного уравнения состояния, т.е. дается полная асимптотическая зависимость. На рис. 1.1.2 показано решение как функция 
. 
определяет фронт волны сжатия, а 
поршня (см. также рис. 1.1.3)
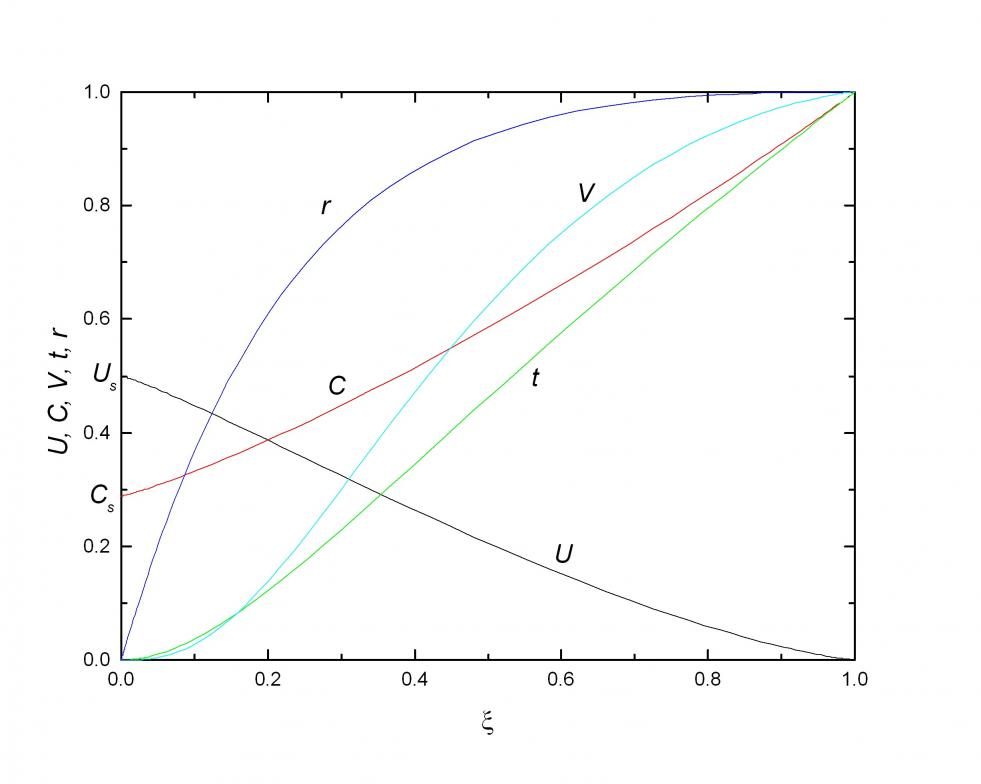
Рис. 1.1.2. Автомодельные зависимости 
, 
, 
, t, 
от.
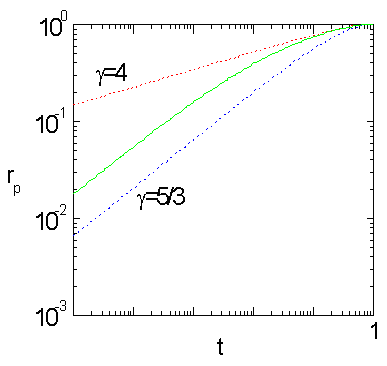
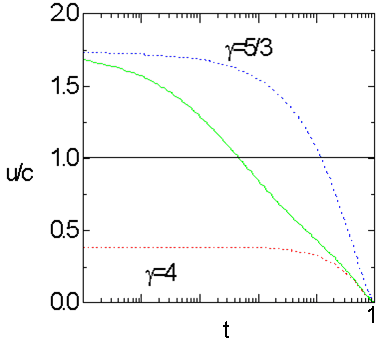
Рис. 1.1.3 
и 
иллюстрируют различие между реальным и степенным уравнением состояния.
1.2. Изэнтропическое сжатие вещества оболочкой. Если вещество сжимается оболочкой, сжимаемость которой значительно меньше сжимаемости основного вещества, можно значительно упростить задачу, полагая оболочку несжимаемой. Тогда уравнение движения оболочки приводится к обыкновенному дифференциальному уравнению. Приводится анализ соотношений, возникающих при различных параметрах вещества. В частности, при приближении к коллапсу кинетическая энергия оболочки может увеличиваться при 
, где 
, уменьшаться или оставаться постоянной. Для физически предельных =5/3<к=2, поэтому реально в коллапсе всегда скорость внешней границы 
, и кинетическая энергия оболочки 
.
1.3. Релятивистская центрированная волна сжатия [2].
Автомодельные задачи о поршне, посвященные предельным сжатиям, имели, по-видимому, всегда нерелятивистский характер. Так что при переходе к предельным плотностям, а в коллапсе достигается бесконечная плотность, скорости вещества и звука превышают скорость света. Поэтому необходимо решение релятивистских уравнений движения и использование релятивистского уравнения состояния. Поэтому целью работы является рассмотрение особенностей, которые может внести релятивизм при переходе к предельным параметрам в задачах изэнтропического сжатия. Задача состоит в определении временной зависимости скорости поршня, ограниченной скоростью света, при которой вся масса вещества, находящегося между стенкой и плоским поршнем, изэнтропически сжимается в плоскость. Т.е. задача состоит в построении релятивистской центрированной волны сжатия. Полученное решение может быть использовано как тест при разработке разностных схем одномерных релятивистских уравнений.
Релятивистские уравнения сохранения массы, импульса и энергии через релятивистские инварианты Римана: 
, где 
, преобразуются к характеристической форме 
, а уравнения релятивистских характеристик к виду 
.
Релятивистская адиабатическая скорость звука выражена в виде 
, где 
есть предельная скорость звука в веществе.
Уравнения приводятся к соотношению 
. Условие инвариантности в простой волне преобразуется к виду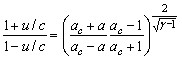 
.
Через автомодельную переменную 
и функции 
и 
уравнения преобразуются к виду 
, 
, 
. Для траектории поршня принято 
. В отличие от нерелятивистского предела, когда аналогичные уравнения линейны, эти уравнения нельзя разрешить относительно 
. Поэтому получено аналитическое приближенное решение в обоих пределах и численное решение.
Приближенное решение в релятивистском пределе: 
, где 
характерное время. Параметры поршня: 
, 
, 
.
Численное решение. При характерной величине 
безразмерная скорость света 
. Численно задача решалась с 
и 
. Решение представлено на рис. 1.3.1.
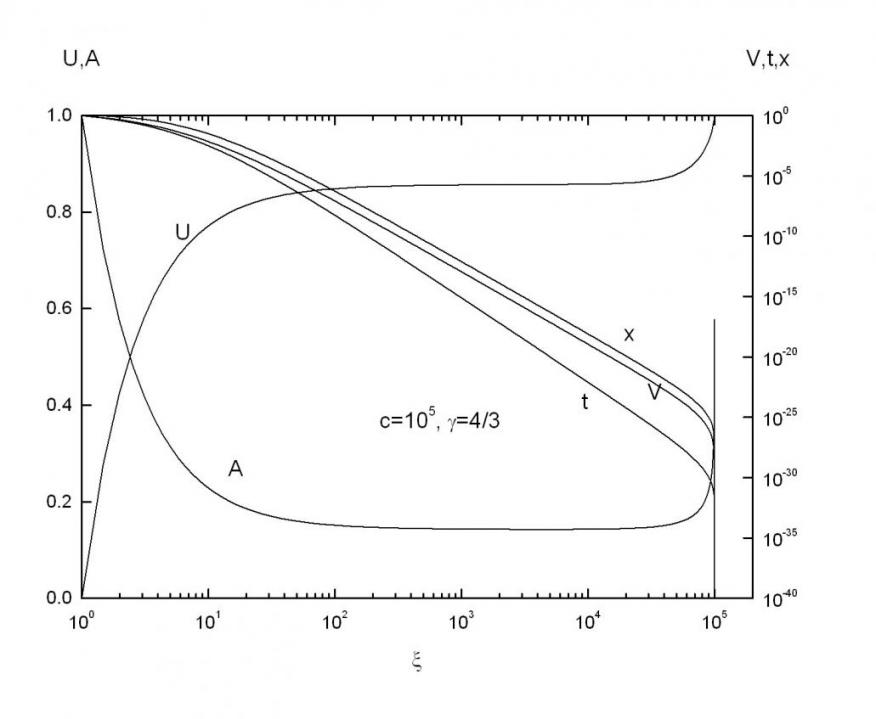
Рис. 1.3.1. Зависимости U, A, V, t, x от при 
и =4/3.
изменяется от 1 до с; при 
всегда находится фронт волны сжатия, а значение на поршне увеличивается от 1 до 
. Поэтому временные зависимости на поршне и пространственные распределения величин в волне определяются в диапазоне [1,] – рис. 1.3.2.
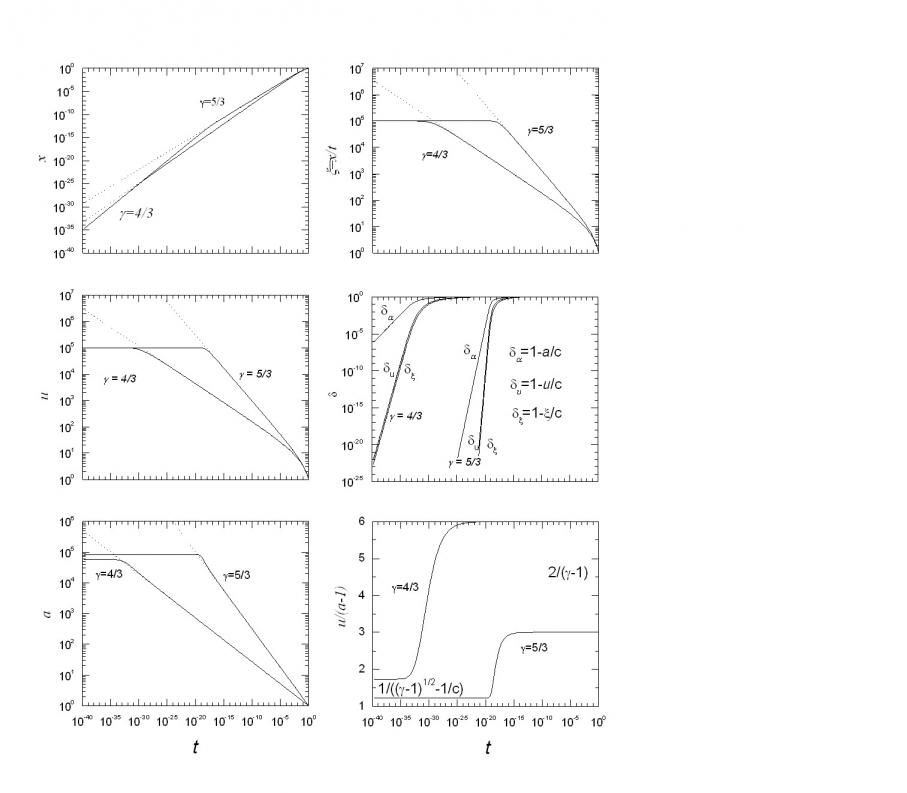
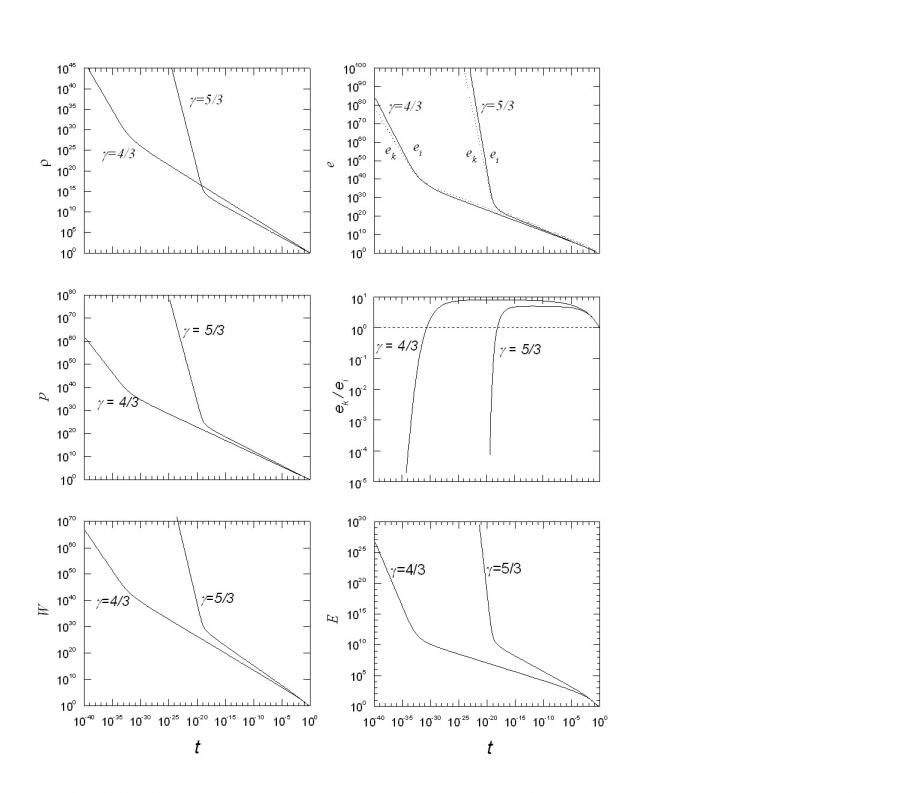
Рис. 1.3.2. Временные зависимости на поршне: при 
и =4/3, 5/3. Сплошные кривые показывают точное решение, а точечные кривые – нерелятивистское решение.
Эти зависимости безальтернативно иллюстрируют различие между нерелятивистским и релятивистским решениями. Нерелятивистское решение резко переходит в релятивистское, особенно при большей скорости звука, поэтому для времени перехода можно воспользоваться нерелятивистским решением. Радиус поршня в релятивистском пределе уменьшается быстрее, нежели в нерелятивистском решении, хотя скорость в релятивистском пределе меньше. Это объясняется тем, что учет релятивизма приводит сначала к увеличению скорости, а затем – к уменьшению. Выход на асимптотический режим в нерелятивистском (
) и релятивистском (
) случаях происходит различным образом. Поэтому нерелятивистские зависимости 
при различных отличаются, а релятивистские сливаются в одну линию. В нерелятивистском пределе 
, здесь большие приводят к большей плотности. В релятивистском пределе 
; при 
, а при 
. Мощность в нерелятивистском пределе: 
,
; в релятивистском пределе: 
, 
.
Степени при 
в релятивистском пределе существенно больше. На рис. 1.3.3 показаны пространственные распределения величин в волне (с=105 ).
Рис. 1.3.3. Пространственные зависимости от 
при 
и =4/3. Индексы у кривых соответствуют: “4”– 
, “3” - 
, “2” - 
, “1” - 
, “0” - 
.
Скорости в волне изменяются почти линейно, однако плотность в релятивистском пределе резко увеличивается у поршня.
Переход к релятивистскому пределу при увеличении индекса симметрии пространства 
происходит значительно раньше. Эта оценка следует из нерелятивистского решения предыдущего раздела. Время перехода 
определяется уравнением 
, где скорость поршня 
. Например, при 
времена перехода: 
, 
и 
. Приведены оценки энергии, необходимые для достижения релятивистского сжатия.
1.4. Автомодельное решение уравнений нелинейной диффузии магнитного поля [3].
Уравнения, граничные и начальные условия, описывающие модель диффузии магнитного поля в полупространство, приняты в виде
, 
,
Магнитное поле 
, 
, 
.
Энергия 
, 
=эрг/см3, 
начальное значение.
Коэффициент диффузии магнитного поля 
, 
Автомодельная переменная 
, где 
, 
Функции 
, 
где 
“автомодельные” магнитное поле, энергия и плотность тока.
Решение показано на рис. 1.4.1-3.
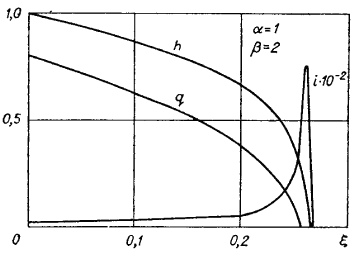
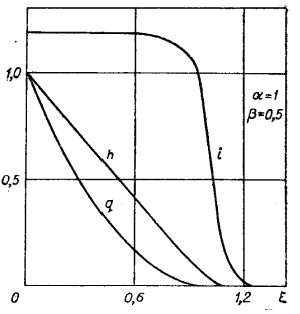
Рис. 1.4.1. Рис. 1.4.2.
Распределение поля и внутренней энергии на фронте получено в виде 
, 
, так что при 
, при 
и при 
. Фронт токовой волны распространяется по закону 
. Автомодельное положение фронта определяется численно: 
. Изменение нелинейного скин-слоя 
по сравнению с линейным (
)
Ширина фронта токовой волны определяется величиной 
, где 
скорость токовой волны: 
.
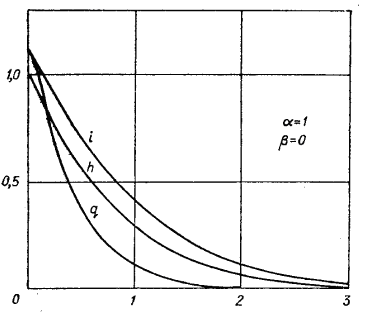
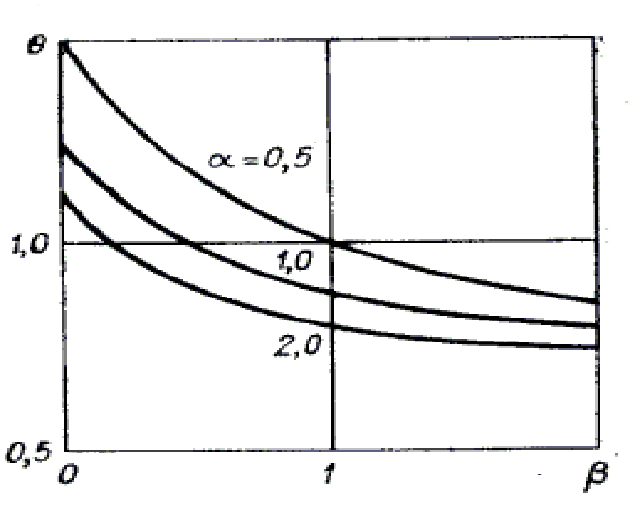
Рис. 1.4.3 Рис. 1.4.4.
Наибольший интерес для практического использования представляет соотношение между внутренней и магнитной энергией. Коэффициент 
, определяемый из 
, в области автомодельности 
. Для некоторых 
зависимости 
показаны на рис. 1.4.4. С увеличением 
, независимо от 
, 
медленно уменьшается, причем при 
. Последний результат естественен, поскольку в задаче отсутствует малый параметр и есть одна переменная с размерностью энергии. При 
, т.е. увеличение крутизны нарастания поля приводит к увеличению 
и соответственно
.
Ограничение “толщины“ полупространства по отношению к фронту 
волны приведет к увеличению 
: 
(
), где 
, и для 
при приближении к асимптоте все проводники взрываются.
Глава 2. Полуэмпирическое уравнение состояния [4].
2.1. Введение. Постановка задачи. Наиболее удобным и надежным способом описания свойств веществ в широком диапазоне плотностей и температур для использования их в расчетах является создание полуэмпирических моделей, в которых, исходя из теоретических асимптотических приближений, задается функциональная аналитическая зависимость, а параметры модели определяются из эксперимента. Цель работы, изложенной в главе 2, создание во всей нерелятивистской области по плотности и температуре уравнения состояния, необходимого либо для непосредственного проведения численных гидродинамических расчетов, либо для генерации соответствующих таблиц. Предлагается способ аппроксимации уравнения состояния вещества, последовательно использующий интерполяционный подход. Выбор функциональных зависимостей весьма нетривиален, именно он определяет успех всей процедуры аппроксимации. Во многом трудность заключается в том, что предъявляются жесткие требования к удобному способу представления всех составляющих свободной энергии предпочтительно аналитический, совпадение со всеми асимптотиками, совпадение с экспериментальными результатами, гладкость, монотонность не менее трех производных энергии. В представленной работе функциональные зависимости свободной энергии выбраны таким образом, чтобы автоматически выполнялись соответствующие асимптотики. Число свободных параметров минимально, но достаточно для сопоставления с экспериментальными данными. Кроме того, предпочтительным является вычисление степени ионизации по какой-либо физической модели, что позволяет повысить надежность построения функциональных зависимостей.
2.2. Уравнение состояния при Т=0. Для давления в главе 2 принята следующая форма во всем диапазоне плотностей:
. Впервые аналогичная зависимость предложена автором для водорода в [37] и для меди в [19]. Здесь 
давление идеального однородного вырожденного нерелятивистского электронного газа. 
давление, обусловленное взаимодействиями и первыми квантовыми поправками вырожденного нерелятивистского электронного газа. 
давление нулевых колебаний, в котором 
температура Дебая, 
параметр Грюнайзена. Параметры 
, входящие в это уравнение, определяются четырьмя экспериментальными величинами при «нормальных» условиях (
, 
): удельным объемом 
, энергией связи 
, модулем объемного сжатия 
и параметром 
. На рис. 2.1.а представлены зависимости давлений 
и 
, вычисленного в приближении TFDW (см. главу 3).
Существенное отклонение 
от 
наблюдается лишь при сжатии 
. Подчеркнем, что такое согласие 
и 
достигнуто без каких-либо подгоночных параметров, только за счет выбора соответствующей функциональной зависимости 
.
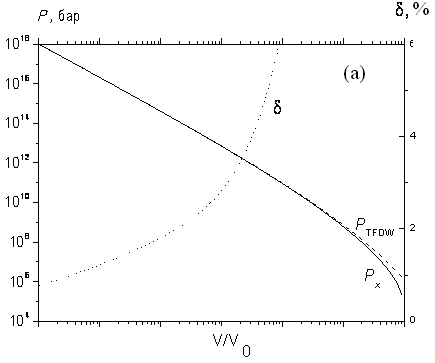
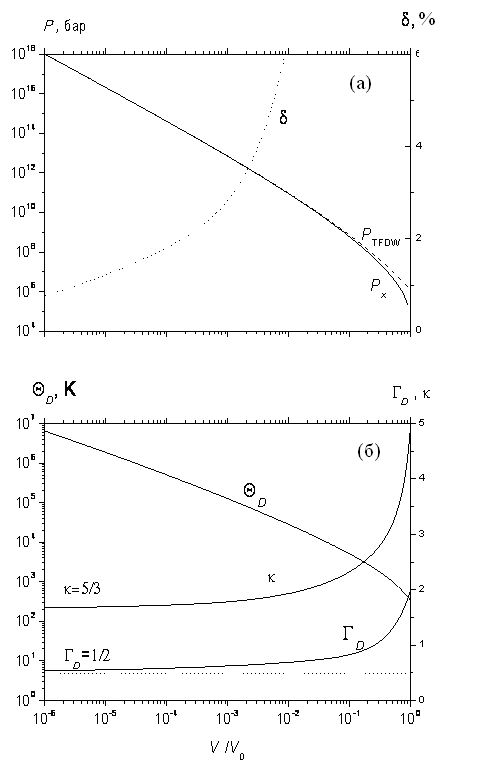
Рис. 2.1(а, б).
2.3. Обобщение дебаевского приближения. Для описания непрерывного перехода от твердого тела к газу полагаем, что свободная энергия Дебая справедлива во всей фазовой области с обобщенной характеристической температурой: 
, где 
, а безразмерная функция 
зависит только от безразмерного аргумента 
. Вводится эффективная температура перехода твердое тело-газ 
. На функцию 
накладываются асимптотические требования при малых и больших 
. При 
(
): 
(
). В этом случае уравнение описывает твердое тело с температурой Дебая. При 
(
): 
. Тогда 
, где 
, т.е. уравнение переходит в уравнение Больцмана.
Во всем диапазоне плотностей аппроксимируем температуру Дебая следующим образом: 
; параметр Грюнайзена 
(рис. 2.1.б). Эти формулы дают правильное асимптотическое поведение при 
. Коэффициент 
определяется в приближении TF, другие коэффициенты определяются из условия равенства 
и 
их значениям при нормальных условиях. Предложена и использовалась аналитическая аппроксимация функции Дебая.
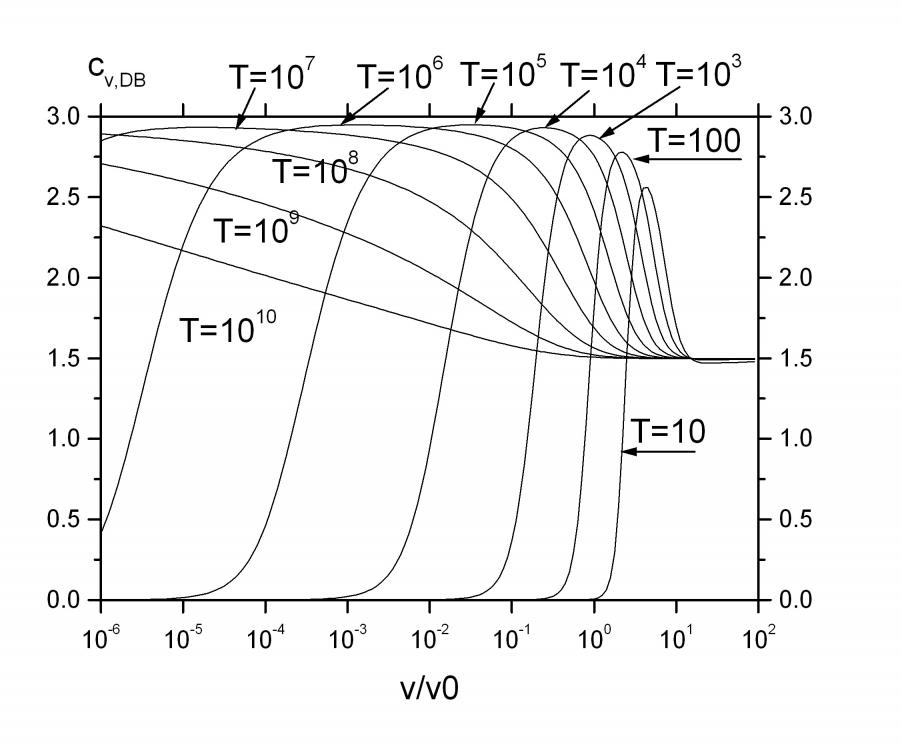
Рис. 2.2. Зависимость ионной теплоемкости от плотности при различных температурах.
2.4. Распределение тепловых электронов. Для свободной энергии свободных электронов рассматривались три приближения. Наиболее точная и достаточно удобная форма тепловой части свободной энергии электронов представлена в виде
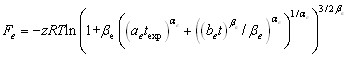. Здесь 
, 
, 
энергия Ферми идеальных электронов, 
экспериментальная энергия Ферми электронов (взаимодействующих с решеткой и между собой), 
константы. Эта формула сконструирована так, чтобы в обоих пределах она совпадала с теоретическими и экспериментальными значениями при низких температурах и высоких температурах. Свободные параметры выбраны вблизи минимума погрешности: 
, 
. Максимальная погрешность вычисления используемых функций не превышает нескольких процентов.
2.5. Ионизационное равновесие. Степень ионизации 
представлена в аддитивном виде 
, где «холодная» степень ионизации 
определяется только плотностью при 
, а другая часть 
температурой и плотностью. Такое представление основано на аддитивном разложении свободной энергии на «холодную» и тепловую составляющие. Первое приближение 
может быть получено на основе квазиклассических расчетов по методу Томаса Ферми [5]. Кроме него могут быть использованы иные формы 
, моделирующие оболочечную структуру. В термодинамическом равновесии при постоянных 
и 
свободная энергия минимальна по отношению к числу частиц. Из свободной энергии исключается часть, связанная с уже определенной зависимостью 
. Тогда уравнения ионизационного равновесия примет вид
.
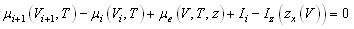В частном случае идеального невырожденного газа из этого уравнения получается уравнение Саха. Для уменьшения времени вычислений при газодинамических расчетах используется так называемый метод среднего иона. Тогда эта система приводится к одному уравнению 
. Решение этого уравнения позволяет определить 
. Для непрерывной энергии ионизации предложена аналитическая зависимость, использующая экспериментальные или вычисленные потенциалы ионизации. Рис. 2.3 и 2.4 иллюстрируют вычисленные зависимости.
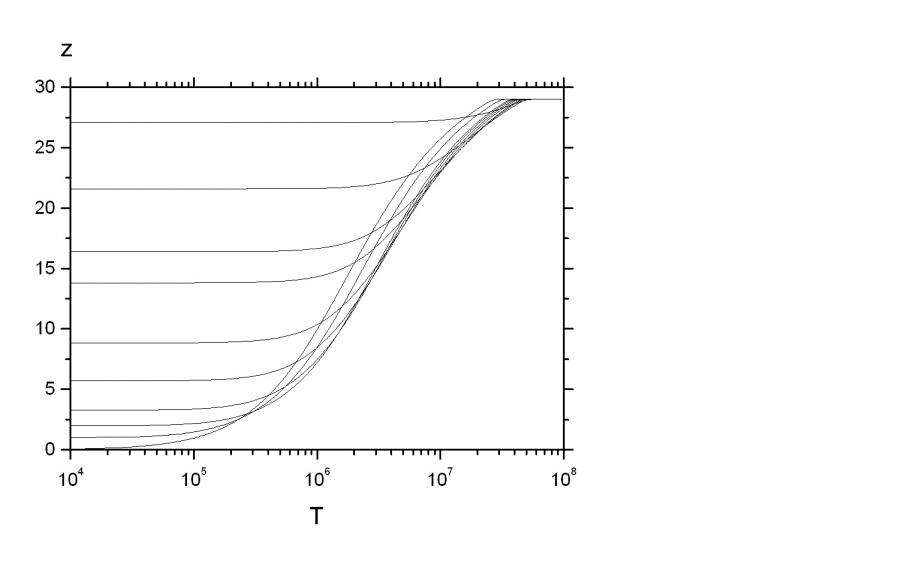
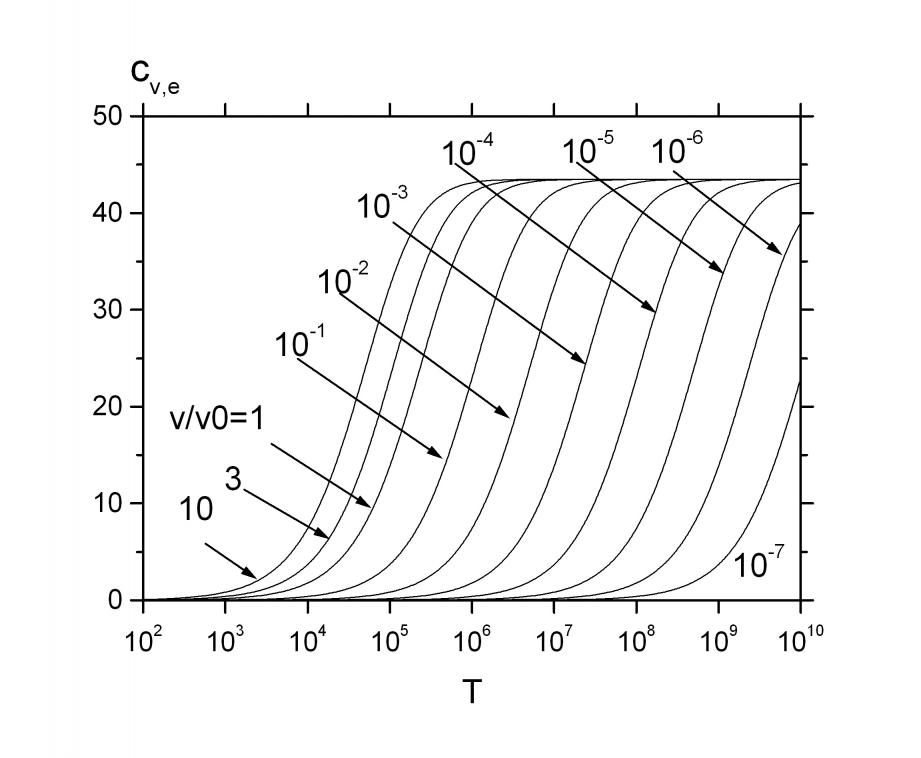
Рис. 2.3. Зависимость степени ионизации от температуры при различных плотностях.
Рис. 2.4 Зависимости электронной теплоемкости от температуры.
2.6. Фазовая диаграмма. Линия сосуществования жидкости и пара (бинодаль) вычислялась по «определению» в результате решения двух нелинейных уравнений 
, 
, где индекс «1» относится к жидкой фазе, а «2» – к пару. Линия, ограничивающая область несуществования одной фазы (спинодаль), рассчитывалась в соответствии с уравнением 
, которое имеет два решения. Критическая точка находилась в результате решения двух уравнений: 
, 
. Фазовая диаграмма, бинодаль и спинодаль, показаны на рис. 2.5 в виде зависимостей 
(без учета плавления). Вычисленные параметры критической точки меди: 
см3/моль, 
г/см3, 
K, 
бар. Но параметры критической точки меди не измерены. Известные оценки и вычисления по некоторым аппроксимациям дают близкие значения.
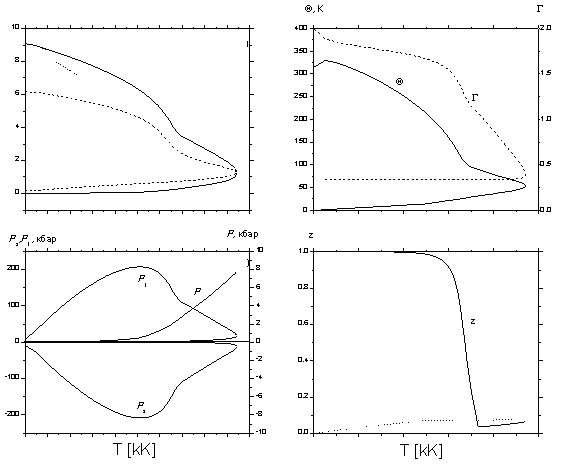
Рис. 2.5. Фазовая диаграмма: бинодаль (сплошная кривая), спинодаль (пунктир) и экспериментальная зависимость 
(точечная кривая).
2.7. Ударные адиабаты сплошного и пористого вещества. На рис. 2.6 показаны вычисленные и экспериментальные зависимости скорости ударной волны 
от массовой скорости 
на ударных адиабатах сплошного вещества и веществ с различной пористостью 
. Точность аппроксимации достаточно высока (
) при 
, а затем падает, и при 
погрешность 
. На том же рис. 2.6 показана скорость звука в сплошном веществе, измеренная с погрешностью 
. Вычисленные и экспериментальные зависимости изэнтропического расширения сплошного и пористого веществ показаны на рис. 2.7.
2.8. Вычисление 
и 
. Измерение 
веществ с различной пористостью позволяет вычислить параметр Грюнайзена 
. Для этого уравнения преобразуются к виду 
, где индексы 1 и 2 соответствуют двум измерениям 
. На рис. 2.8 представлены экспериментальные значения (124 точки) 
при сжатии пористых образцов. В качестве первого измерения всегда использовалась ударная адиабата сплошного вещества. На том же рис. 2.8 показаны наши линейные аппроксимации и часто используемая зависимость 
.
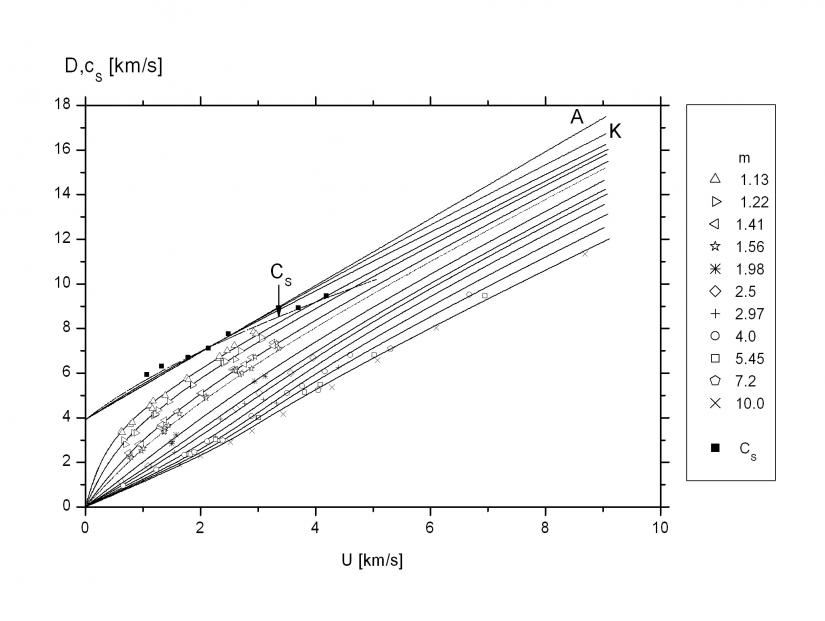
Рис. 2.6. Зависимости 
на ударной адиабате сплошного и пористых веществ. А – линейная аппроксимация. Скорость звука 
: наш расчет (точечная кривая) и эксперимент.
Рис. 2.7. Ударные адиабаты и изэнтропы расширения. Кривые – наш расчет, точки – эксперимент.
Рис. 2.8. Экспериментальные зависимости параметра Грюнайзена 
от плотности и линейные аппроксимации.
2.9. Модель плавления. Принято, что между твердой и жидкой фазами существует граница раздела, а функциональные зависимости «холодной» энергии и дебаевской температуры обеих фаз одинаковы. Однако значения трех параметров в них различны. В формуле для 
коэффициент 
для твердой фазы 
, а для жидкой фазы определяется из величины энтропии плавления 
при нормальных условиях. Вычислены: 
, 
К, 
К. В формуле 
изменяются коэффициенты 
и 
. Для жидкой фазы они определяются при известном значении изменения объема 
из уравнений: 
и 
бар. Вычислены: 
и 
; 
бар/К. Все параметры на кривых плавления получены из уравнений 
, 
. Приведено сравнение с экспериментальными результатами. В численном решении (рис. 2.9) при увеличении температуры 
вычислялись параметры 
, 
и 
. Одновременно проверялось, что это решение единственно.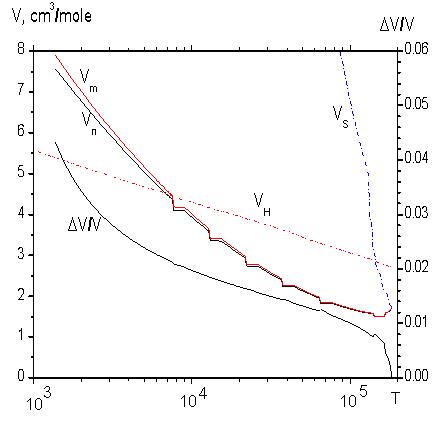 
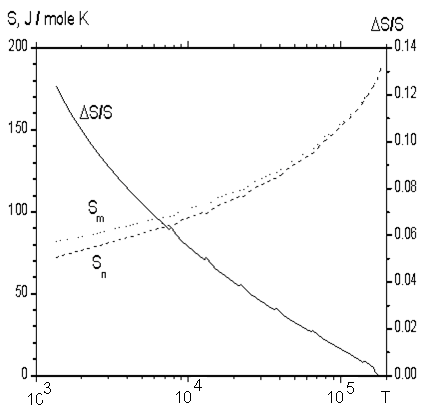
Рис. 2.9. Температурные зависимости молярных объемов твердой и жидкой фаз, относительное изменение объема при плавлении, молярные объемы на адиабате Гюгонио и на изэнтропе; молярные энтропии каждой фазы и ее изменение.
2.10. Сравнение моделей. Обсуждаются достоинства и недостатки представленной модели и других моделей, опубликованных в литературе.
Глава 3. Аппроксимация уравнения состояния элементов.
3.1. Уравнение состояния в квазиклассическом приближении.
Искомый функционал 
принят в виде
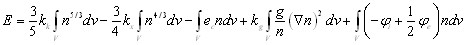. Чтобы ввести в это уравнение корреляционную энергию, она аппроксимировалась, исходя из ее асимптотических выражений, полученных в пределе больших и малых плотностей, а один свободный параметр определялся из сравнения с численными расчетами при промежуточных плотностях: 
(рис. 3.1).
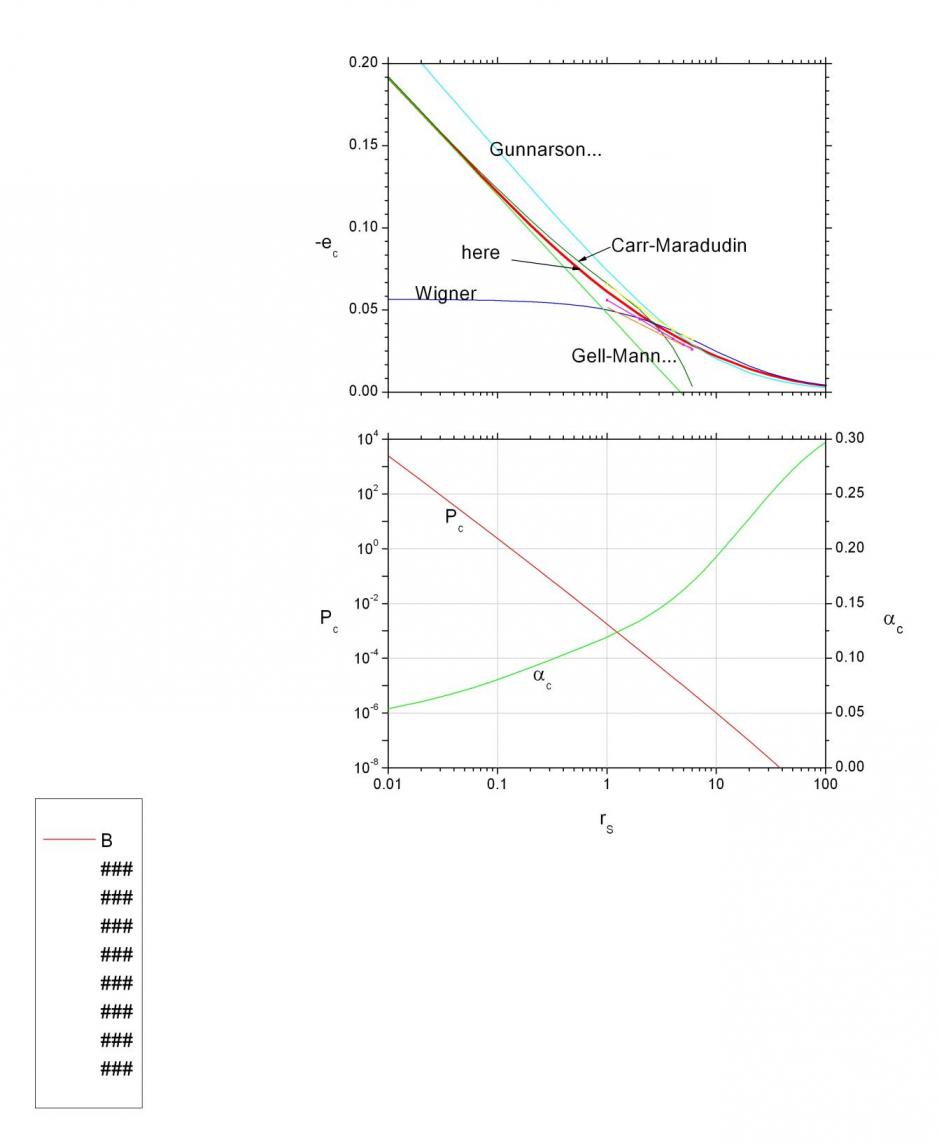
Рис. 3.1 Аппроксимация корреляционной энергии и асимптотические зависимости.
Градиентные члены – при кинетической и обменно-корреляционной энергии приняты в виде 
, где функция 
. Условие сохранения заряда 
, где 
– заряд ядра. Потенциал 
удовлетворяет уравнению Пуассона 
. Левые граничные условия 
и 
, правые: 
и 
. Минимизация функционала относительно плотности 
приводит к уравнению
,
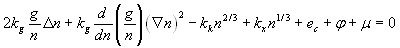где - энергия Ферми. Плотность связанных и свободных электронов определялась условием – полная энергия 
. Плотность связанных электронов 
находилась из решения уравнения
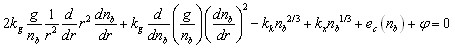
Плотность свободных электронов находилась из уравнения 
. Полное количество свободных электронов – степень ионизации определялась как 
.
3.2. Численный метод решения. Уравнение приводится к виду
.
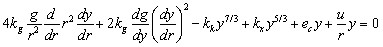Затем оно линеаризовывалось по 
и
. Уравнение и граничные условия аппроксимировались разностными соотношениями со вторым порядком точности. Сходимость проверялась.
3.3. Результаты расчетов. Подробные результаты расчетов приведены для меди. Рис. 3.2 иллюстрирует, прежде всего, возможность выполнения условия 
вследствие вычисления параметров модели 
или
.
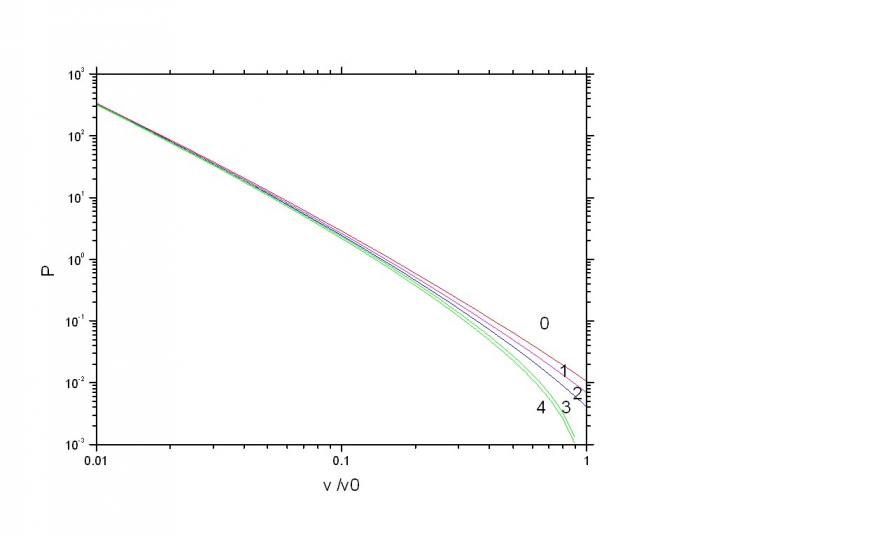
Рис. 3.2. Зависимость давления от удельного объема. Обозначения кривых:
“0” - уравнение TF; “1” TFD; “2” 
, 
; “3” 
, 
; “4” 
, 
.
Давление в модели TF при нормальной плотности 3.16 Мбар, в модели TFD 2.05 Мбар, в модели TFDW 1.2 Мбар. Разность в давлениях разных моделей нивелируется лишь при сжатии в ~10–100 раз, что соответствует давлению >~1-100 Гбар. Представлены составляющие давления для полной плотности, для связанных и свободных электронов. Основную роль играет, естественно, кинетическое давление; обменное примерно на порядок меньше (в показанном диапазоне плотностей), а затем они расходятся в соответствии с 
и
. Корреляционное давление еще меньше на ~ 1.5 порядка, при нормальной плотности оно составляет величину 100 кбар и не может компенсировать недостатки модели. Градиентные давления заметно различаются в модели TFDW и представленной модели, они сходятся лишь при сжатии в ~ 100 раз. Причем градиентное давление при относительном сжатии <~3 даже превышает обменное. Именно это существенное увеличение градиентного давления и позволяет удовлетворить условию
. Это также говорит о том, что приближение локальной плотности в квазиклассическом приближении не может дать приемлемую точность расчетов. Обсуждаются возможные механизмы согласования с экспериментом.
На рис. 3.3 представлены зависимости полного количества свободных электронов 
от удельного объема. При нормальной плотности модель TF дает неприемлемо высокую величину 
, модель TFD 
, модель TFDW 
, модель TFDW с cк = 3.14 (
) 
, уравнение (3.2) дает величину 
. Полное количество свободных электронов сначала резко возрастает при сжатии: при ~10-кратном сжатии (давлении P109 бар) 
, при ~100-кратном сжатии (давлении P1012 бар) 
, но полностью все электроны выдавливаются в непрерывный спектр для меди лишь при 
(давлении P1017 бар). Для некоторых других элементов 
показана на рис. 3.4.
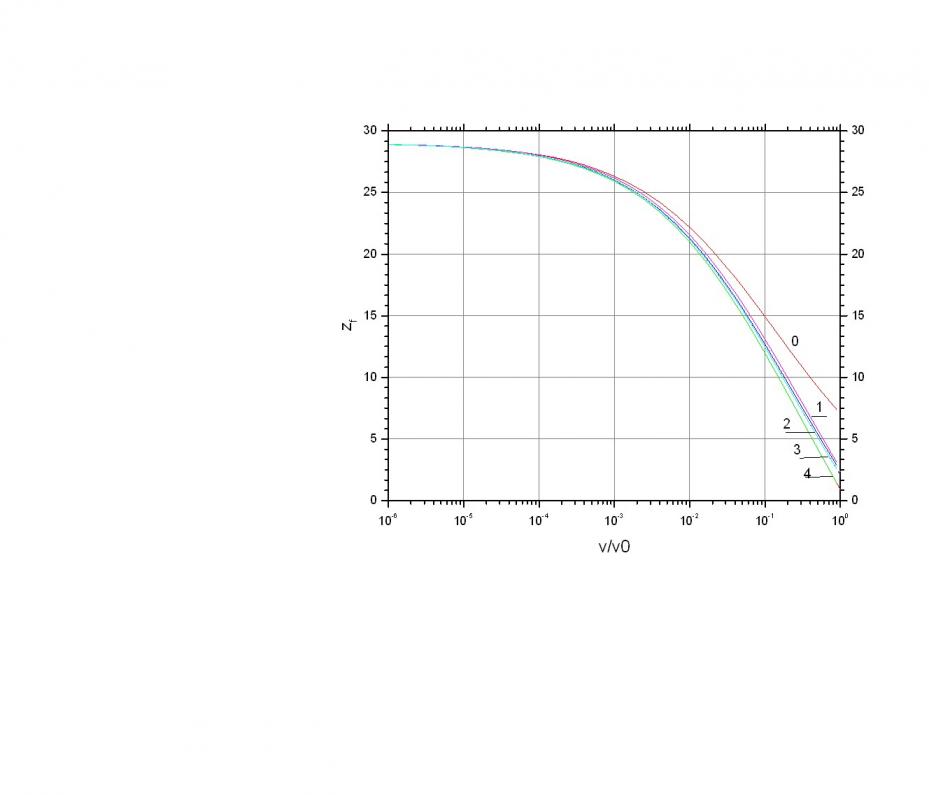
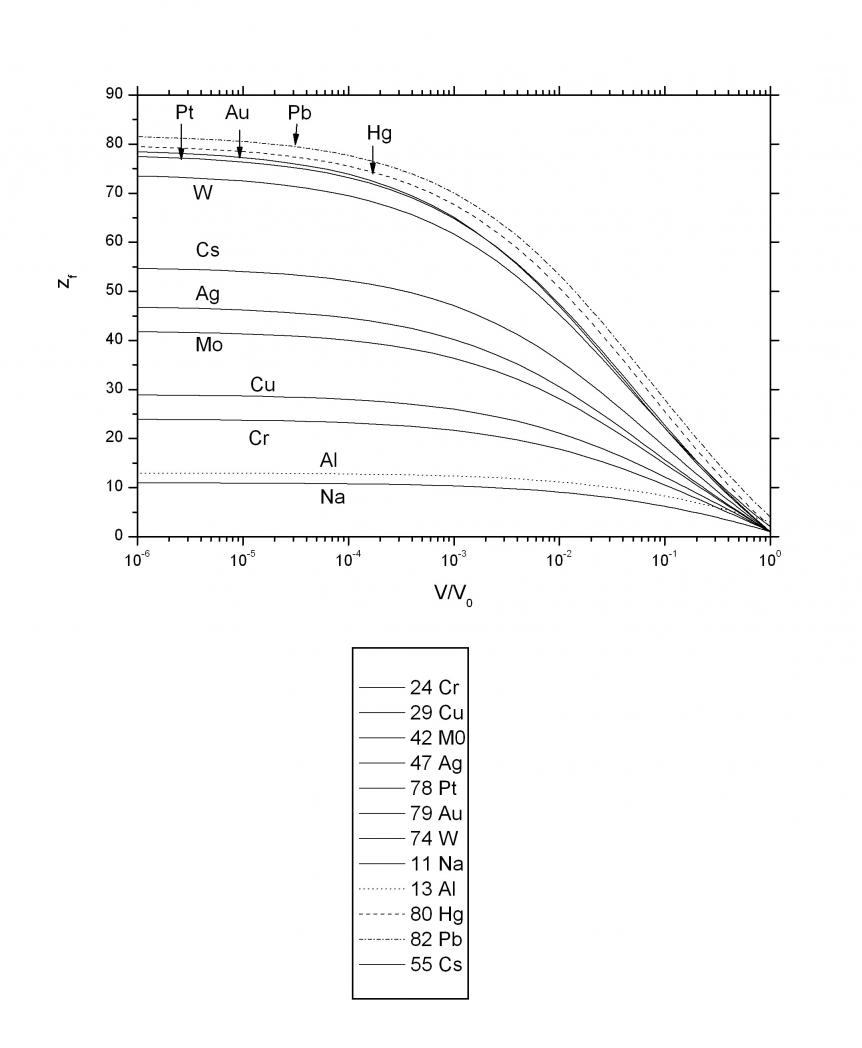
Рис. 3.3. 
для меди Рис. 3.4. 
- Интерполяция «холодной» энергии.
Примем для «холодной» энергии следующие формы во всем диапазоне плотностей: нерелятивистской и релятивистской. При 
(3.4)
где 
, 
. При 
, где 
.
Первый множитель определяет энергию вырожденного идеального нерелятивистского (
) и релятивистского (
) однородного электронного газа. Здесь 
, 
, 
, 
. Второй множитель сконструирован так, чтобы автоматически выполнялись условия: 
и давление
, но следующие производные энергии
. Третий множитель сконструирован так, что модуль сжатия 
определяется автоматически. Однако параметр 
определяется численным решением однопараметрического уравнения 
. При 
энергия 
сконструирована так, что 
, где 
энергия связи, 
, 
, а следующие производные 
. Два параметра отвечают за выполнение условий: 
и 
, который определяется однопараметрическим уравнением относительно 
. Два параметра могут быть выбраны из условия 
, которое обусловливает первую поправку энергии ван-дер-ваальсовского газа. Могут быть учтены другие экспериментальные зависимости.
3.5. Результаты расчетов уравнения состояния элементов.
Проведены расчеты «холодной» составляющей энергии для большинства элементов, для которых доступны необходимые экспериментальные или теоретические данные. Для систематического сравнения были выбраны «холодные» кривые, рассчитанные в квазиклассическом приближении TFDW. Приведены вычисленные зависимости 
при 
в диапазоне 
в виде, представленном на рис. 3.5. Вычисленное давление может приближаться к квазиклассическому давлению как сверху, так и снизу, что во многом определяется соотношением между экспериментальной и квазиклассической начальной плотностью. Представлены также результаты расчетов нерелятивистской ударной волны. Приведены скорости ударной волны 
от массовой скорости при 
км/c, давления 
и 
. Дано сравнение с ударными адиабатами, вычисленными в квазиклассическом приближении (без учета излучения). Верхняя граница 
определяется началом заметного влияния излучения и релятивизма.
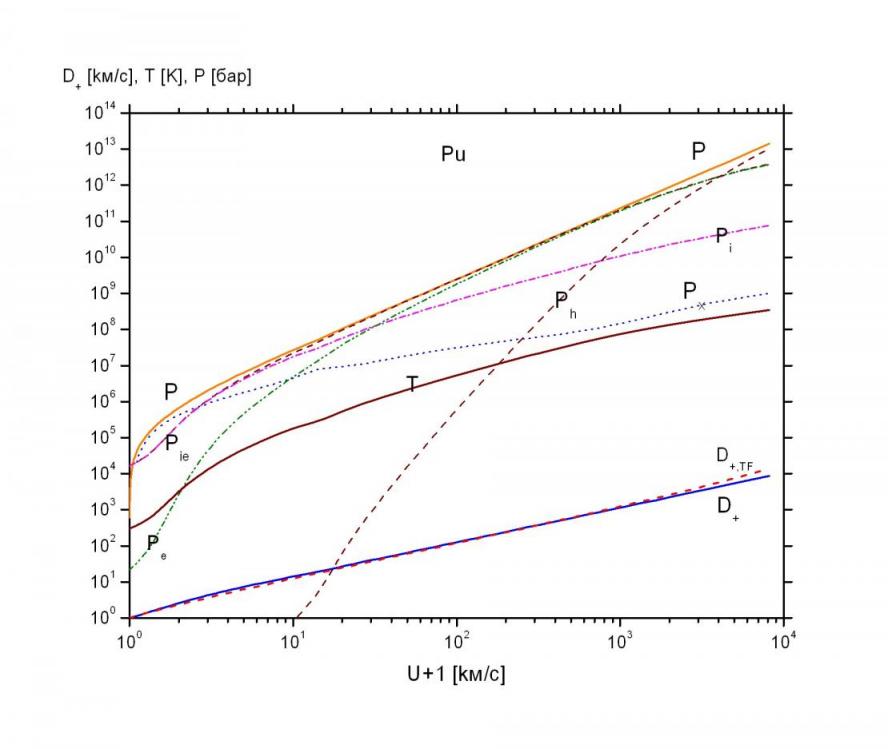
Рис. 3.5. Плутоний Pu Z=94, A=244
Глава 4. Численное моделирование изэнтропического сжатия веществ мегагауссным магнитным полем.
4.1. Магнитогидродинамическая модель z-пинча.
Приведена система магнитогидродинамических уравнений в лагранжевом представлении в цилиндрической симметрии и уравнения цепи, которые использовались для моделирования физических процессов в металлическом z-пинче. Дана аппроксимация электропроводности и теплопроводности во всем диапазоне рассматриваемых параметров, которая интерполировалась между электропроводностями твердого тела (вырожденной плазмы) и идеальной (невырожденной) плазмы. Проводимость 
, где функция 
определяется экспериментальными значениями и учитывает зависимость электрического сопротивления от температуры: 
при низких температурах, 
в области нормальных температур, скачок при плавлении и степенную зависимость от плотности. Приведенная в гл. 2 и 3 модель для определения 
позволила впервые адекватно описать проводимость. Теплопроводность представлена аддитивно 
, где 
электронная теплопроводность и 
лучистая теплопроводность Электронная теплопроводность 
вычислялась, исходя из соотношения Видемана – Франца 
, где 
константа Лоренца. Для твердого тела 
определяется из эксперимента и хорошо согласуется с теоретическим значением в нормальных условиях. Для плазмы 
определяется теоретически.
4.2. Численное моделирование нелинейной диффузии мегагауссного магнитного поля.
Предложена физическая модель, описывающая нелинейную диффузию сильного магнитного поля в проводник. Приведены результаты численного решения этой задачи при токах до 1 ГА. Показано, что токи величиной несколько десятков мегаампер могут приводить к значительному увеличению удержания вещества в магнитном поле. Характерная величина тока 
МА определяет различные картины процесса. При меньших токах в результате нагрева тепловое давление становится больше магнитного и проводник «медленно» расширяется. Плотность проводника в процессе этого расширения неоднородна. Когда внешние части проводника расширятся до характерной плотности, происходит рекомбинация, что проводит к существенному различию в механизмах расширения. При токах 
степень ионизации в основном «холодная», поэтому при расширении степень ионизации становится практически нулевой, резко возрастает электрическое сопротивление, ток вытесняется из внешних слоев, магнитное давление 
резко уменьшается и проводник расширяется с тепловой скоростью. Та часть тока, которая осталась во внешнем слое из-за резкого роста сопротивления, приводит к увеличению джоулевой энергии и возрастанию степени ионизации, увеличению проводимости, однако ток уже не успевает перераспределиться и остановить расширение вещества. При токах 
в степени ионизации наряду с «холодной» составляющей начинает играть значительную роль тепловая составляющая. Поэтому степень ионизации внешних слоев уже не может уменьшиться до нуля, более того, при увеличении тока и, соответственно, температуры проводимость становится плазменной. Проводник в течение длительного времени колеблется около квазиравновесного радиуса, который определяется равенством магнитного и теплового давлений (рис. 4.2.1). С увеличением тока время колебаний увеличивается, а равновесный радиус уменьшается. Значительная часть вводимой энергии увеличивает не температуру, а степень ионизации, теплоемкость резко увеличивается по сравнению со значением 
для твердого тела.
Максимальное магнитное поле, полученное из соотношения 
, для металлов (Ag, Al, Cu, Fe, Ta, W): 
МГс. При учете степени ионизации оно модифицируется на соотношение
, где 
и 
энергии связи и ионизации (на единицу объема), причем
. Например, для меди 
эВ/атом, а полная энергия ионизации 
кэВ/атом. Именно это увеличение внутренней энергии может привести к увеличению магнитного давления и поля на порядки величин. Вычислена зависимость максимально достижимого давления от тока. Предполагается, что давления мегабарного и гигабарного диапазонов могут быть реализованы в макроскопических объёмах на технических устройствах, в основном достижимых в настоящее время.
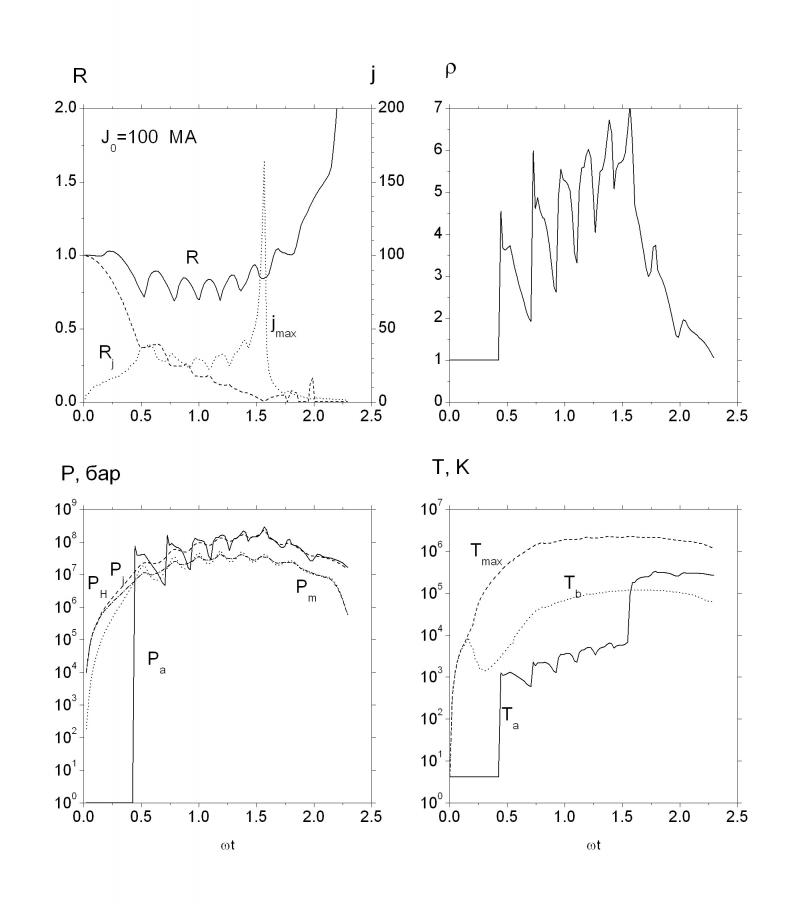
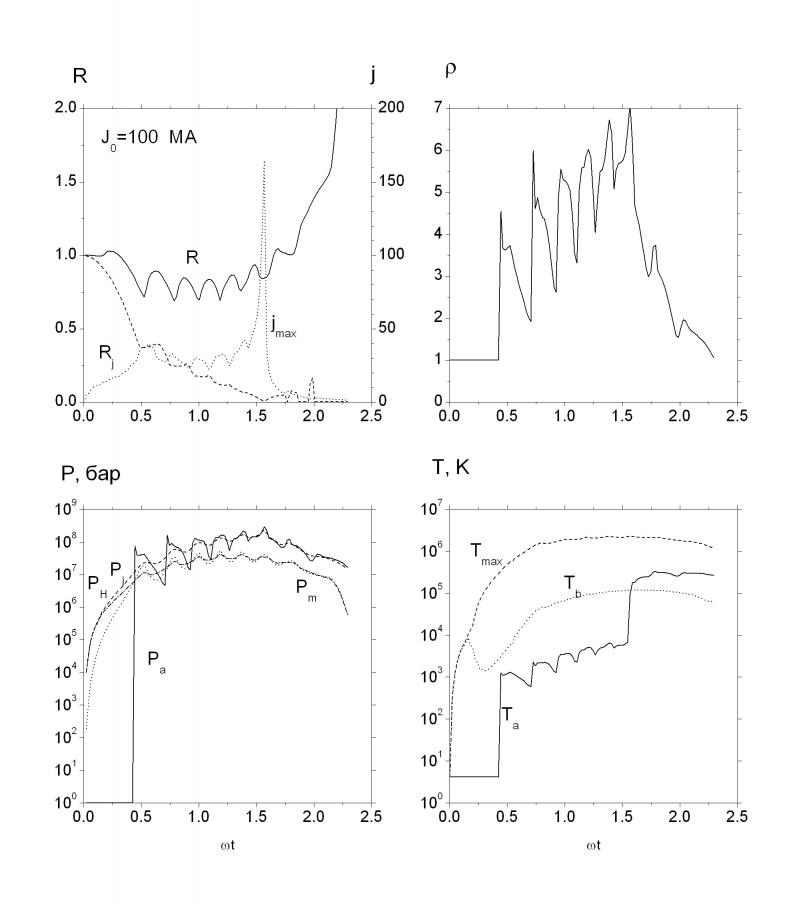
Рис. 4.2.1. Временные зависимости радиусов: трубки и токовой волны, максимальной плотности тока, и давлений: магнитного, среднего и на оси.
4.3. Моделирование перехода графит-алмаз в изэнтропическом процессе. Поскольку ни один из существующих статических и динамических (ударно-волновых) методов превращения графита в алмаз не оптимален, научный и большой практический интерес представляет рассмотрение альтернативных методов. Преимуществом метода металлического z-пинча, по сравнению с взрывными методами изэнтропического сжатия, является возможность сохранения образца. В работе [13] (см. гл. 7) была экспериментально показана возможность сохранения образца – фосфора после полиморфного перехода при давлении 
кбар.
Цель настоящей работы показать возможность перехода графита в алмаз с сохранением алмаза в контейнере при характерном давлении 
кбар. Блок коаксиальных цилиндров состоит из трех веществ. Внутреннего – графита. Внешнего – веществ с хорошей проводимостью: меди или алюминия. По внешнему цилиндру протекает ток конденсаторной батареи величиной 
МА с характерным временем 
мкс, создающий магнитное поле и давление 
Мбар, которое сжимает все вещества. Джоулев нагрев сильно увеличивает температуру внешней трубки, однако, из-за скинирования тока за время процесса, ток не успевает проникнуть во внутреннюю часть трубки и нагреть ни средний цилиндр, ни графит. Если ток достаточно велик, наружная часть токонесущей трубки взрывается, однако средняя трубка служит контейнером, в котором сохраняется углерод. В электрическую цепь вводится переменное электрическое сопротивление – аналог плавкого предохранителя. Его параметры выбираются таким образом, чтобы максимально достижимое давление снижалось несущественно, но после максимально достигнутого давления этот предохранитель резко увеличивал свое сопротивление и диссипировал всю оставшуюся энергию конденсаторной батареи и магнитного поля. Для осуществления этой цели проведено численное моделирование превращения графита в алмаз в изэнтропическом процессе. Построено уравнение состояния графита и алмаза в широком диапазоне плотностей и температур. Предложено математическое описание системы уравнений фазового перехода графит-алмаз. Фазовый переход графит-алмаз описан системой уравнений: 
, 
, 
, 
, где 
, 
, 
концентрации графита и алмаза. Индекс «g» относится к графиту, индекс «d» к алмазу. Однако второе условие фазового равновесия 
, вообще говоря, не выполняется. Рассматривались два способа определения 
. В первом способе определялось кинетическое уравнение. Во втором способе концентрация определялась только как функция удельного объема. Вид функции и значения параметров, её определяющих, вычислялись из сравнения с экспериментальными данными. Проведено сравнение с экспериментальными ударными адиабатами (рис. 4.3.1, 4.3.2).
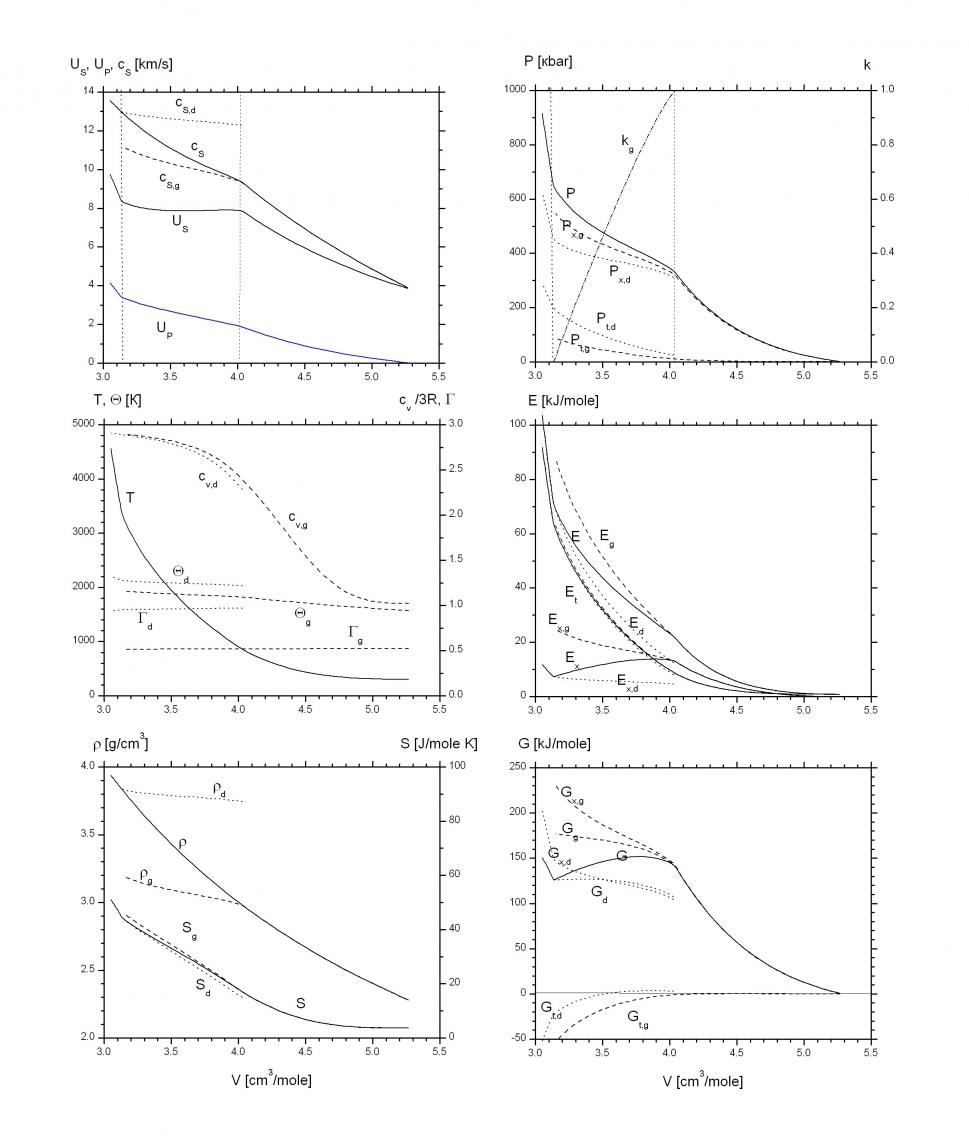
Рис. 4.3.1. Сравнение с экспериментальными результатами для графита и алмаза в зависимости от массовой скорости.
Рис. 4.3.2. Расчеты ударной адиабаты в области перехода графит-алмаз в зависимости от удельного объема.
На рис. 4.3.3 и 4.3.4 представлены временные и радиальные распределения.
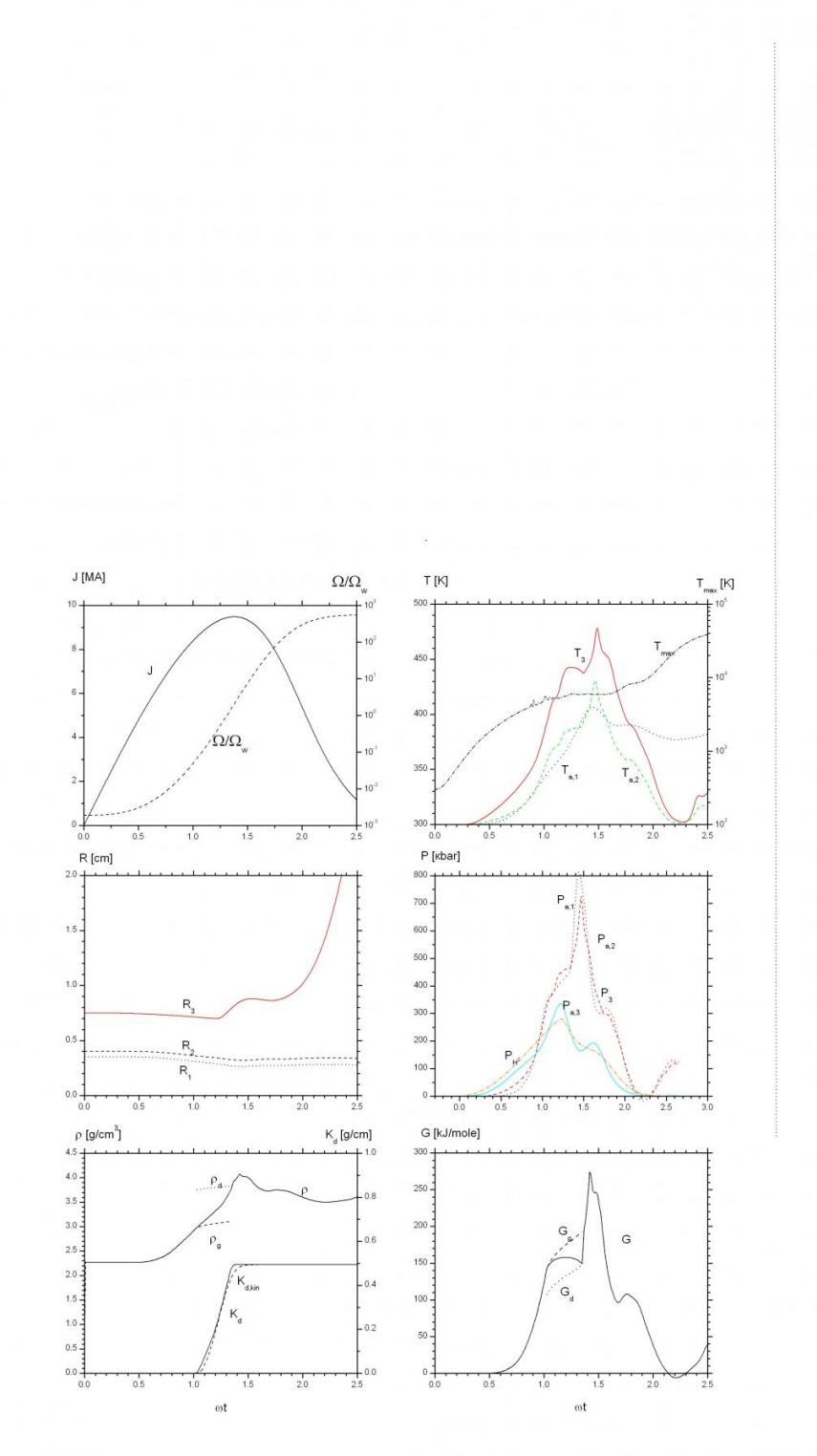
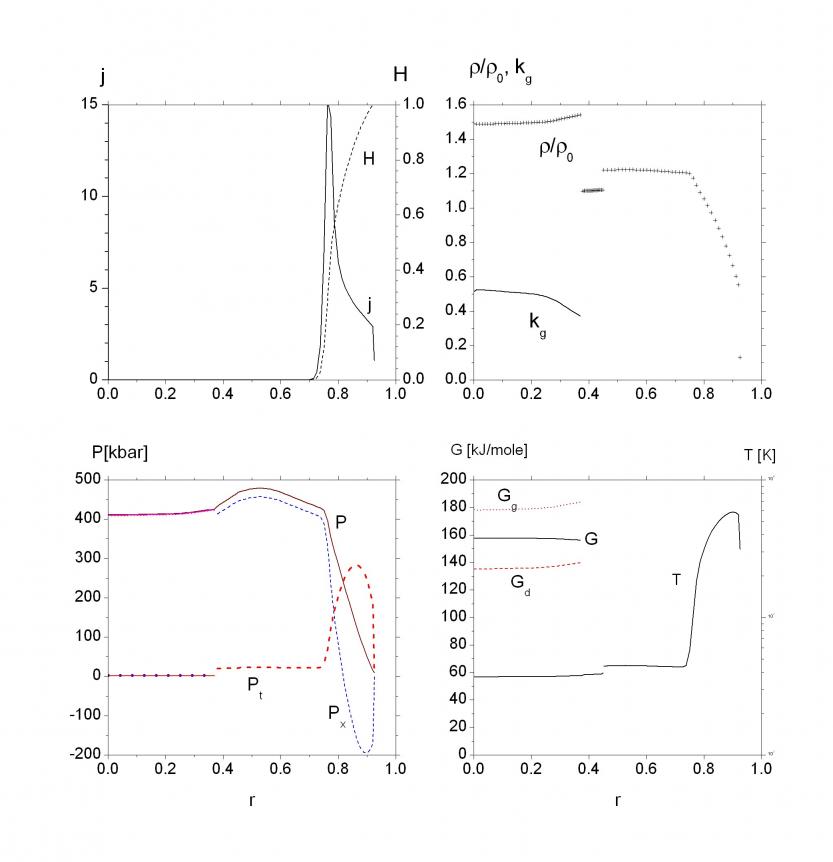
Рис. 4.3.3. Временные распределения плотности и давления.
Рис. 4.3.4. Радиальные распределения в момент времени, когда половина графита превратилась в алмаз.
4.4. Качественный анализ параметров несжимаемой трубки в магнитном поле. Цель настоящего раздела – качественный (аналитический) анализ динамики и нагрева металлической трубки, которая используется как поршень при сжатии вещества. Основные упрощения связаны с предположением о несжимаемости вещества трубки, однородности распределения тока в ней и однородности сжимаемого вещества. Во многих задачах это предположение выполняется удовлетворительно. Приведены безразмерные параметры, определяющие характер процесса сжатия. Показано влияние динамики и джоулева нагрева на искомые параметры.
4.5. Численный анализ динамики металлического z-пинча.
Проведен численный анализ динамики металлического z-пинча во всем возможном диапазоне параметров. Полученная информация позволяет определить область оптимальных параметров сжатия веществ, выяснить в принятом приближении возможности и ограничения этого метода сжатия.
Глава 5. Методы измерения уравнения состояния водорода [9, 12].
5.1. Введение. Приведен краткий обзор современного состояния проблемы. Рассмотрены экспериментальные и теоретические работы.
5.2. Интерполяция уравнения состояния водорода. Уравнение состояния при T = 0 представлено в двух видах. Во-первых,
,
где 
, 
(здесь 
и 
в атомных единицах). При 
, где первый член есть энергия полностью вырожденного однородного электронного газа, а второй член определяет поправки на кулоновское, обменное и квантовое взаимодействия. Такая форма 
обеспечивает правильное асимптотическое представление энергии при малых 
независимо от а, 
(> 1/3), b и 
. При больших 
можно выбором 
обеспечить необходимую степень по 
. Параметры а, 
, b (
=5) определялись, исходя из среднеквадратичной аппроксимации к экспериментальным данным Anderson & Swenson (1974). Другая форма уравнения состояния была принята аналогично уравнению 3.4. Она учитывает данные Hemley, Mao (1994) и Loubeyre et al (1996).
На рис. 5.1 и 5.2 представлены полученные здесь экспериментальные результаты и интерполяционные уравнения состояния, а также экспериментальные уравнения состояния и их интерполяция других авторов.
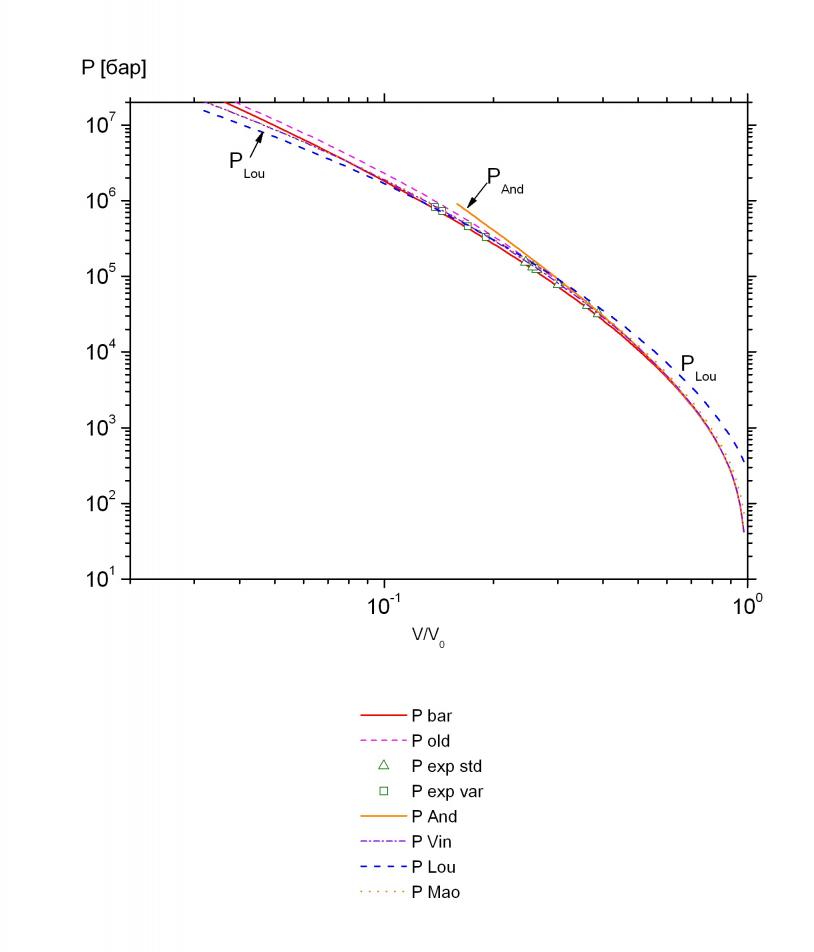
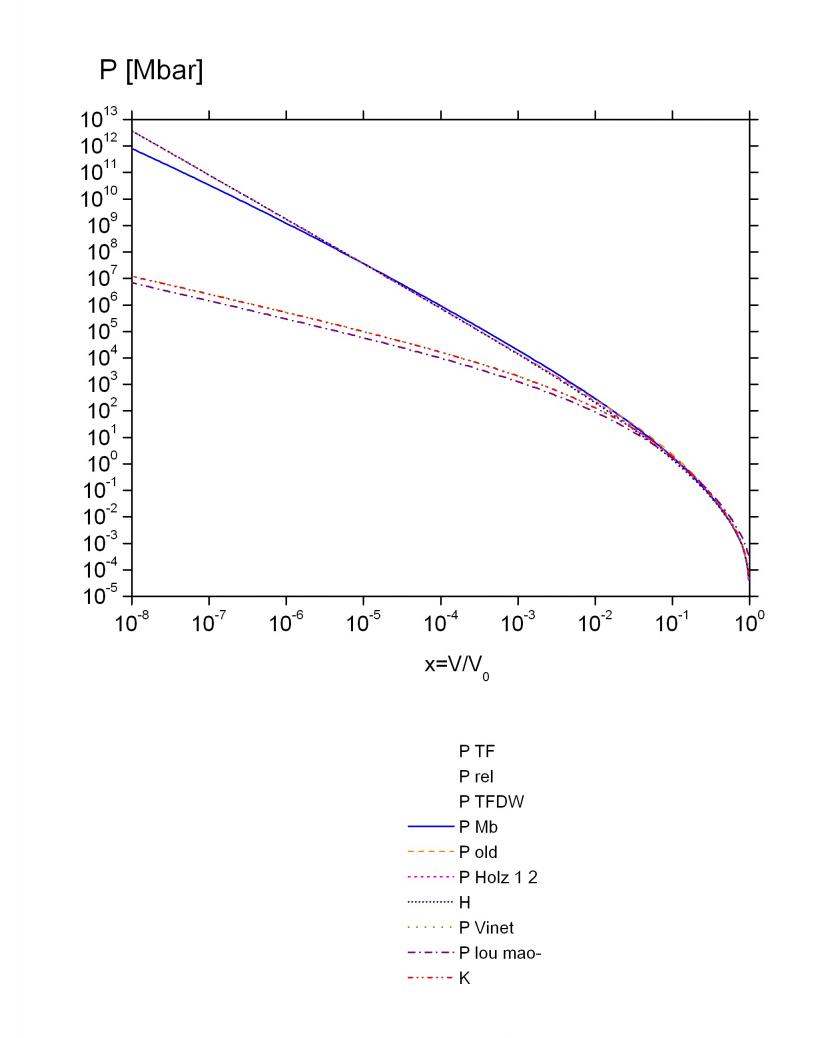
Рис. 5.1. Нулевые изотермы при «низких» давлениях: 
Мбар. Обозначения линий: ур. 3.4.1 – сплошная линия, ур. 5.1.1 – пунктирная линия, интерполяция по Vinet et al – штрих пунктирная линия, результаты и интерполяция Loubeyre et al (1996) – пунктирная линия, результаты и интерполяция Hemley&Mao (1994) – точечная линия, Anderson&Swenson (1974) сплошная линия.
Рис. 5.2. Нулевые изотермы при высоких давлениях: 
Мбар.
Уравнение состояния при 
. Для получения тепловой части уравнения состояния ионов свободная энергия представлена в форме 
, 
свободная энергия решетки, 
свободная энергия вращения молекул водорода, 
свободная энергия внутримолекулярных колебаний. Свободная энергия решетки аппроксимировалась двумя способами. В первом способе свободная энергия решетки аппроксимировалась аналогично [4]. Во втором способе, описанном в [37], свободная энергия рассматривалась в виде 
в соответствии с представлениями статистических сумм при относительно низких температурах (твердое тело) и высоких температурах (молекулярный газ). 
интерполяционная статистическая сумма между статистической суммой решетки 
и статистической суммой поступательного движения молекул газа 
. Функция 
осуществляет переход между твердым и газовым состоянием среды с эффективной температурой перехода 
. 
статистическая сумма, определяемая двумя вращательными степенями свободы, где 
, 
. При больших плотностях свободное вращение переходит во вращательные колебания с эффективной температурой, соответствующей характеристической температуре решетки 
; при не слишком высоких температурах 
, которая соответствует статистической сумме двумерной решетки. В широком диапазоне сравнительно малых плотностей колебания решетки не влияют на внутримолекулярные колебания: 
. Температура сверху ограничена неучетом диссоциации. Вычислены интерполяционные значения обобщенной дебаевской температуры, вращательной и колебательной температуры, их параметров Грюнайзена.
5.3. МГД расчет сжатия водорода и инертных газов.
МГД уравнения, изложенные в гл. 4, с описанным в гл. 3 уравнением состояния, решались в диапазоне параметров: токи 
МА, время нарастания 
нс 50 мкс. В качестве материала проводника использовались медь и алюминий. На рис. 5.3 представлена вычисленная зависимость максимального давления при частоте 
, характерной для быстрых конденсаторных батарей энергоемкостью 
МДж.
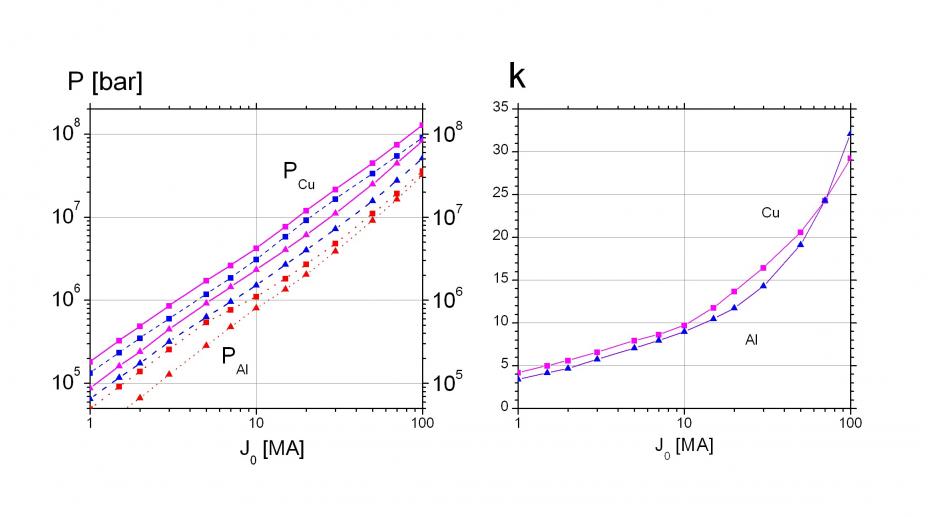
Рис. 5.3. Зависимость максимального давления, его «холодной» (пунктир) и тепловой (точки) составляющих, а также зависимость коэффициента усиления давления по отношению к магнитному давлению 
при сжатии водорода медной трубкой (квадратики) и алюминиевой трубкой (треугольники).
Как видно из рис. 5.3, для того чтобы достигнуть давления 
Мбар предполагаемой верхней границы перехода в металлическое состояние необходимы токи 
МА для меди и 
МА для алюминия.
На рис. 5.4 показано сравнение максимальных давлений и коэффициента усиления для инертных газов. Как видно, для гелия можно получить значительно большее давление из-за его большей начальной сжимаемости. Для достижения давления 
Мбар, когда можно ожидать металлизации гелия, необходимы токи 
МА. Для других инертных газов «холодное» давление металлизации ниже, поэтому необходимые токи значительно ниже.
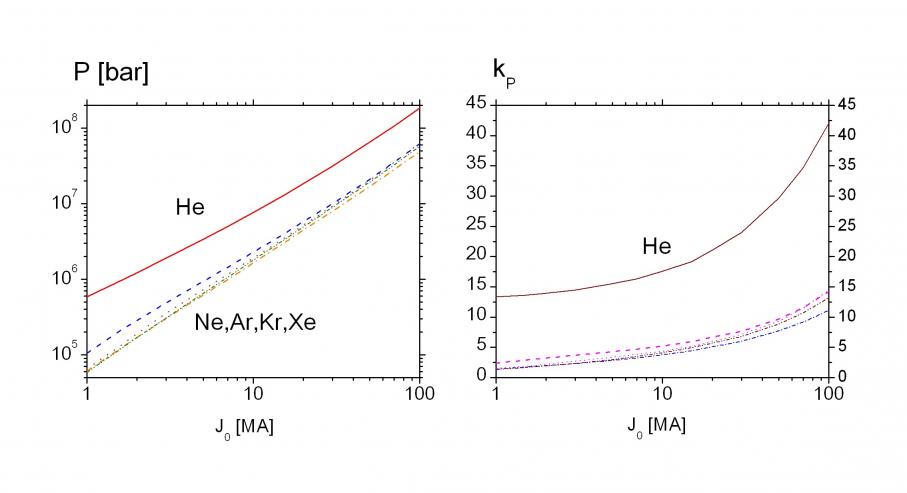
Рис. 5.4. Зависимость максимального давления и коэффициента усиления давления 
.
5.4. Диагностика и точность измерений. При исследовании сжимаемости водорода основной задачей диагностики является измерение объемов водорода, а также эталонного вещества в процессе сжатия. Технические сложности этой задачи обусловлены малыми размерами образцов и малым временем сжатия. Поэтому для достижения точности 
<1% абсолютная погрешность измерений должна быть 
мкм. При характерном времени изменения давления 
нс либо при скорости движения границ ~1 км/с время экспозиции должно быть <10 нc. Разработана метрология импульсных давлений, основанная на использовании эталонных веществ с известным уравнением состояния. Давление в исследуемом веществе определяется по сжимаемости эталонного вещества, помещенного внутрь исследуемого, в предположении равенства давлений. Точность метода определяется степенью однородности давлений, погрешностью измерения размеров исследуемого и эталонного веществ и неопределенностью уравнения состояния эталонного вещества. При измерении до давлений 
Мбар наибольшая точность может быть достигнута при использовании в качестве эталона щелочных металлов. Рассмотрено влияние параметров источника излучения, параметров лайнера и геометрических условий съемки на точность измерений.
5.5. Измерение уравнения состояния водорода.
Рассматривались два метода измерения уравнения состояния: «эталонный» и «вариационный». «Эталонным» методом измерено уравнение состояния твердого водорода до 150 кбар. Плотность определялась по рентгенографическому измерению объёма, а давление по уравнению состояния эталонного вещества. Цилиндрический блок веществ, состоял из трех веществ: внешнего алюминия, среднего водорода и внутреннего эталонного вещества. В качестве эталонных веществ использовались калий и цезий. Для увеличения контрастности все вещества разделены никелевыми 10-мкм трубками.
По рентгеновским снимкам, сделанным в начальный момент и в один из моментов сжатия, определялось относительное сжатие водорода и эталонного вещества, а по уравнению состояния эталонного вещества давление. По относительному равенству давлений водорода и эталонного вещества определялось давление водорода. Начальные параметры нормального водорода: 
K, 
. Длина рабочей части трубок 30 мм; радиусы 
мм. Ток с амплитудой 0.5 – 1.5 МА и временем 
мкс. Технические характеристики экспериментальной аппаратуры описаны в гл. 7.
На рис. 5.5 представлены результаты расчета эксперимента. Одно из основных условий предложенного метода с использованием эталонного вещества – равенство давлений исследуемого и эталонного вещества. Оно выполняется с точностью 
%. Кроме того, для подтверждения радиальной однородности проводился эксперимент, в котором вместо калия намораживался водород. Измеренная степень неоднородности 
. Изэнтропичность процесса подтверждается численными расчетами. Разница между средней расчетной и изэнтропической температурами лежит в пределах погрешности расчетов. Вычисленная температура T < 100 K; поэтому, во-первых, водород еще остается твердым и, во-вторых, тепловое давление 
, так что нулевая изотерма в пределах погрешности измерений совпадает с изэнтропой. Расчеты также показывают, что внутренняя поверхность алюминиевой трубки не нагревается текущим по ней током.
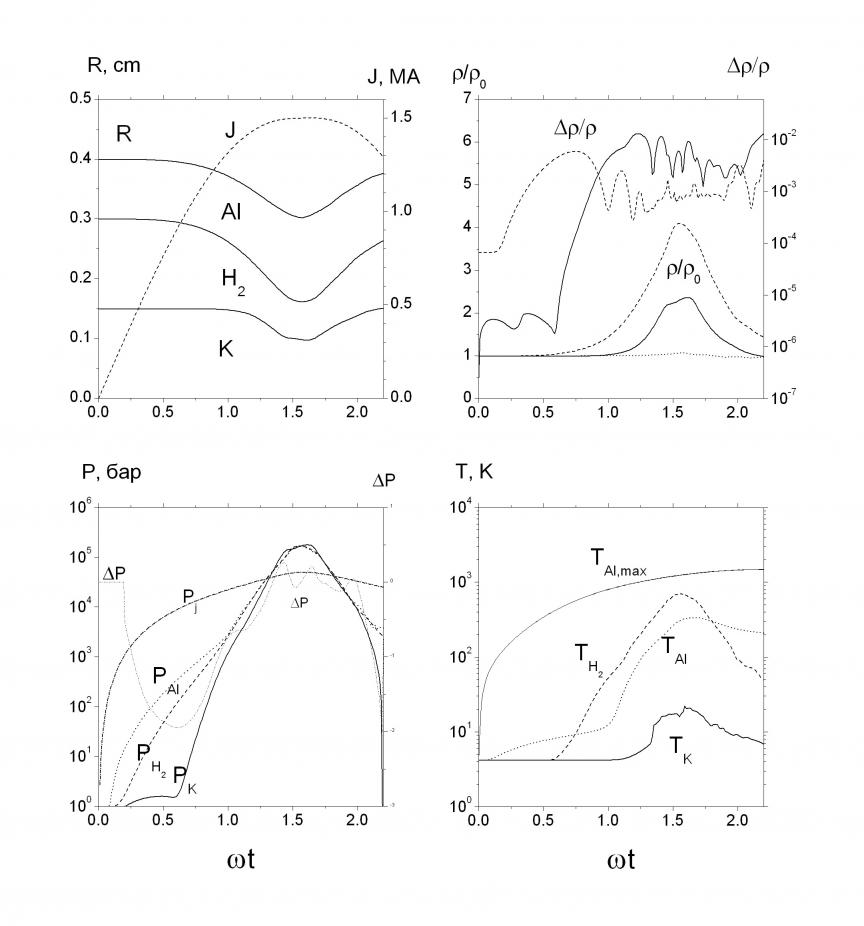
Рис. 5.5. Временные зависимости радиусов трубок, тока, плотности, коэффициента неоднородности плотности 
для калия и водорода, давления, коэффициента «неравенства» давления в калии и водороде, температуры в алюминии: максимальной и на внутренней границе, температуры водорода и калия.
Результаты экспериментов представлены на рис. 5.1, 5.6. Максимальная погрешность 
и 
, определяемая как 
. Сравнение с уравнениями состояния других авторов также дано на рис. 5.1, 5.6, 5.7.
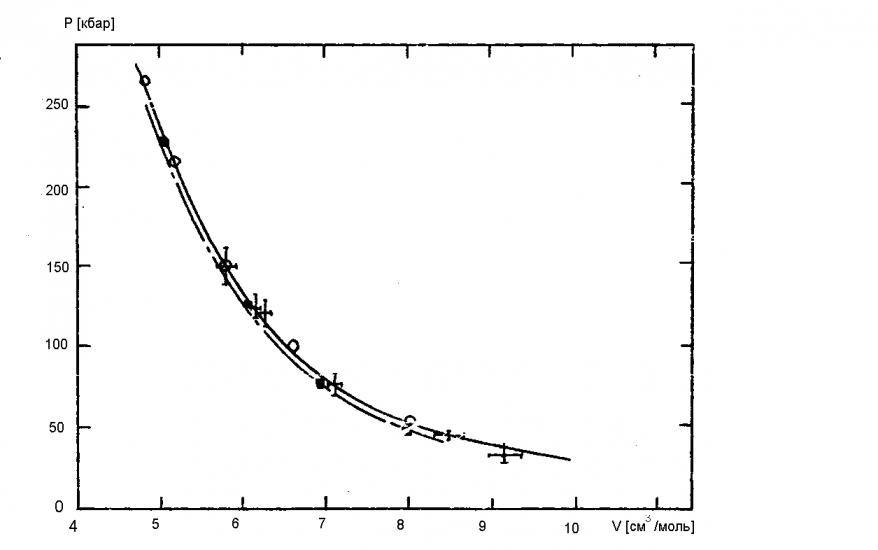
Рис. 5.6. Экспериментальные уравнения состояния. Точки настоящей работы (
). Нулевые изотермы: непрерывная кривая (ур. 5.1), 
изотерма при Т=300 К (Mao, Jephcoat, Hemley1988) и штрих-пунктирная линия – их результаты, приведенные к Т=0; сплошные квадратики – результаты (Van Straaten, Silvera, 1988).
Рис. 5.7. Сравнение относительных отклонений в объёме 
при разных давлениях между результатами работы (Van Straaten, Silvera, 1988) (горизонтальная ось) и других работ, указанных на графике.
«Эталонный» метод применим для данного генератора тока при меньших давлениях, нежели возможные, из-за жесткого условия однородности давлений. При больших давлениях может оказаться предпочтительным «вариационный» метод. Для его использования необходимо измерить ток и радиус (или радиусы) сжимающей трубки, а затем моделировать процесс сжатия с варьированием параметров определяемого уравнения состояния. Можно использовать медную трубку, в которой давление в ~2 раза больше, чем в алюминиевой (рис. 5.3). Однако в медной трубке при выбранных параметрах рентгеновского источника надежно регистрируется только внешний диаметр, а для определения объема сжатого водорода необходим пересчет от внешнего диаметра к внутреннему диаметру, что увеличивает погрешность измерения. При сжатии водорода в алюминиевой трубке появляется возможность более точного измерения объема водорода рентгеновской съемкой. Для определения отклонения принятое в начальном приближении уравнение состояния варьировалось двумя способами. Погрешность измерения давления оценивается величиной 
%, поэтому проведенные эксперименты и соответствующие расчеты следует рассматривать как разработку методики измерения уравнения состояния при высоких давлениях.
Глава 6. Метод измерения реологического уравнения состояния металлов.
6.1. Реологические модели высокоскоростной деформации. При исследовании веществ магнитным полем, динамика деформирования металлической трубки, сжимающей вещество, влияет на величину достигаемого давления и должна учитываться при интерпретации экспериментальных результатов. В этом разделе, служащим введением, приведен краткий обзор методов высокоскоростного деформирования, обсуждаются особенности 
-пинча как метода исследования деформации.
6.2. Дислокационная модель высокоскоростного деформирования изотропной среды. Определяющее соотношение для скорости деформации представлено в виде: 
. Здесь 
скорости упругой и пластической деформации; 
вектор Бюргерса; 
плотность дислокаций; 
девиатор напряжения. Предполагается изотропия поликристаллического тела с дислокациями физически малый объем содержит совокупность кристаллов с изотропным распределением векторов Бюргерса. Скорость движения дислокаций определена в виде: 
, 
сдвиговая скорость звука, 
параметр модели, 
второй инвариант девиатора напряжения. При низких напряжениях это уравнение дает линейную зависимость от напряжения; при высоких приближение к скорости звука.
Существующие теоретические и экспериментальные данные не позволяют сделать однозначный выбор модельного кинетического уравнения для плотности дислокаций. Наши эксперименты в определенной степени свидетельствуют, что в рассматриваемой области напряжений термоактивированные механизмы в первом приближении можно не учитывать. Полагаем, что энергия образования дислокаций пропорциональна энергии, диссипируемой при пластической деформации: 
, здесь 
параметр модели, вероятность «рождения» дислокаций. При учете дислокаций эта энергия учитывалась в уравнении для энтропии. Для металла после плавления принимаем модель вязкой жидкости, описываемую в следующем разделе. Переход между твердым и жидким состоянием осуществлялся линейной интерполяцией в малой области вблизи температуры плавления с учетом теплоты плавления.
6.3. Феноменологические вязкопластические модели. Рассмотрена модель жестко-вязко-пластической среды. Для интегрирования системы уравнений движения и энергии уравнение представлено в виде 
, 
. Условие начала течения 
. В этой модели вещество ведет себя, как вязкая жидкость с коэффициентом вязкости, зависящим от скорости деформации. Рассмотрено несколько способов обобщения модели.
6.4. Интегрирование уравнения движения несжимаемой среды. Несжимаемость среды позволяет свести уравнение сохранения массы и импульса к одному обыкновенному дифференциальному уравнению. Исходя из уравнения 
, 
, 
, получено уравнение 
. Приводится способ численного интегрирования этого уравнения.
6.5. Экспериментальное исследование реологических свойств металлов. Проведены многочисленные эксперименты по деформированию медных (медь М1) и алюминиевых (сплав АД1) трубок магнитным полем в геометрии zпинча. Большинство опытов проведено по сжатию трубок во внешнем коаксиальном токопроводе: часть с расширяющимися трубками.. Сжимающиеся трубки имели начальный внешний диаметр 4-8 мм и толщину стенки от 0.25 до 1 мм; расширяющиеся трубки внешний диаметр 12-16 мм, толщину стенки 1-3 мм. Длина деформируемой части трубки 24-30 мм. Для получения различных режимов деформации (кроме начальных размеров трубок) варьировались частота и амплитуда тока изменением зарядного напряжения ГИТ, индуктивности токопровода и отключением части секций конденсаторной батареи. В экспериментах 
МА, 
мкс, 
кбар. Экспериментальные результаты представляют собой синхронизированные зависимости от времени тока, проходящего по трубке, и диаметра трубки. В каждом опыте производилась непрерывная регистрация внешнего диаметра трубки фоторегистратором и однократная рентгеновская съемка трубки в выбранный момент времени в направлении, перпендикулярном оптической оси фоторегистратора. Для сопоставления с расчетами необходимо обеспечить точную повторяемость результатов и одномерность деформации, поэтому экспериментально проверялось влияние на однородность и повторяемость сжатия различных факторов. Контролировалась однородность сжатия.
На рис. 6.1 представлены результаты измерения тока, внешнего и внутреннего диаметров алюминиевой трубки в зависимости от времени. В каждом опыте регистрировалась осциллограмма тока, фоторазвертка внешнего диаметра и одна точка рентгеновского измерения внешнего и внутреннего диаметров. Для оценки влияния температурных факторов при построении реологической модели были проведены эксперименты по сжатию трубок с различной начальной температурой (
К). Влияние начальной температуры оказалось несущественно; во всех опытах сжатие охлажденной трубки происходило в пределах погрешности измерения так же, как при комнатной температуре.
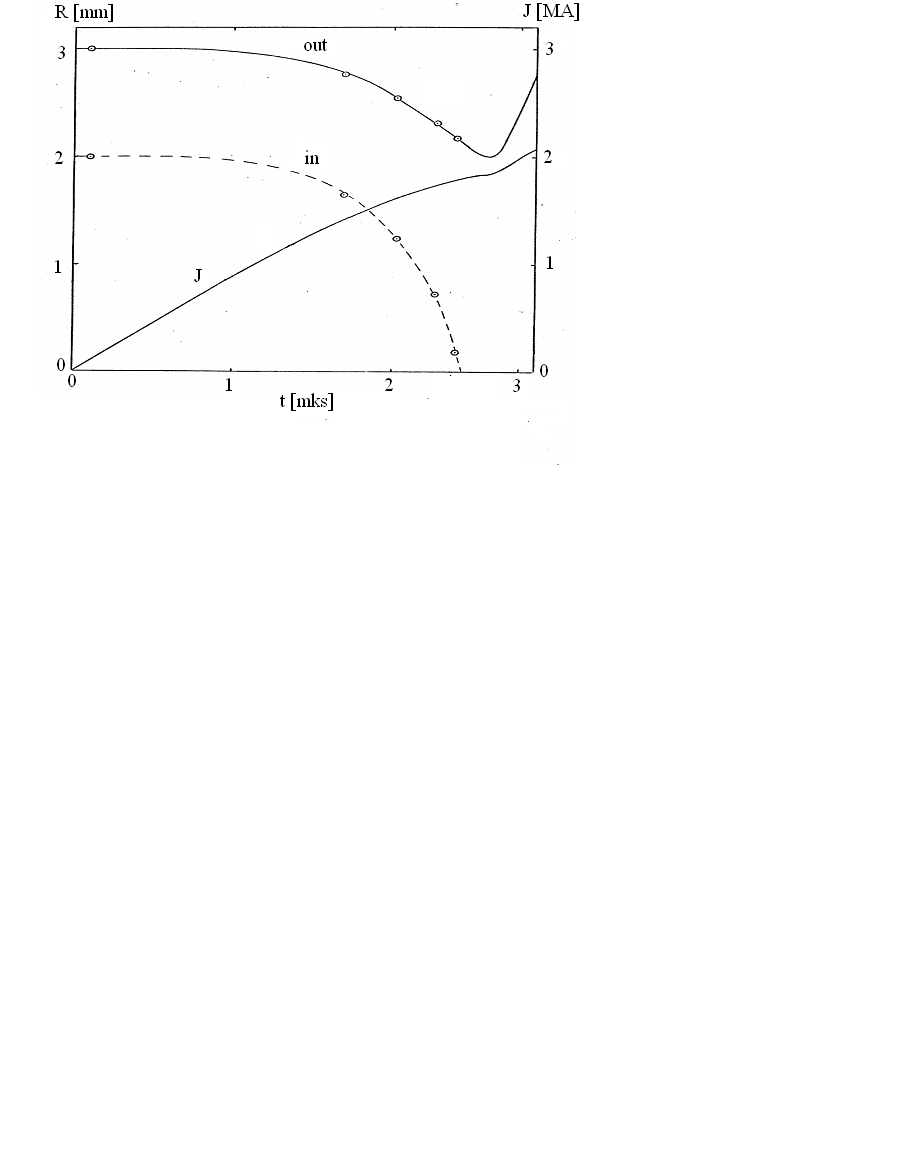
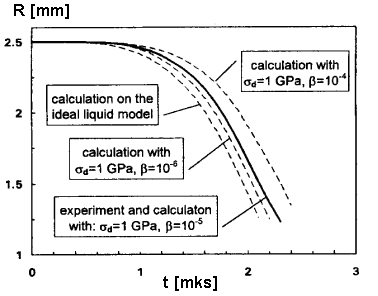
Рис. 6.1. Временные зависимости тока, внешнего и внутреннего радиусов алюминиевой трубки по оптическим (сплошная линия) и рентгеновским (
) измерениям. Рис. 6.2. Экспериментальные и вычисленные зависимости радиуса медной трубки диаметром 5/4 мм. 
МА, 
мкс. Толщина экспериментальной линии есть экспериментальная погрешность.
6.6. Численное моделирование экспериментов по деформации магнитным полем. Для описания деформации трубок в магнитном поле проходящего по ним тока использована система МГД уравнений, приведенная в главе 4, уравнение состояния описаны в главе 2 и 3, интерполяционные формулы для электропроводности и теплопроводности в главе 4, реологические модели приведены выше. Для твердого состояния дислокационная модель раздела 6.2 содержит только два параметра: 
и 
. Начальная плотность дислокаций в расчетах принималась 
см-2, варьирование начальной плотности дислокаций на порядок величины не влияет на результаты. Рис. 6.2 иллюстрирует влияние параметров на расчетные зависимости радиуса трубки от времени и согласование с экспериментальными результатами.
Совокупность наших экспериментальных результатов в пределах погрешности измерений описывается при значении параметров: для меди 
кбар и 
; для алюминия 
кбар и 
. Величины 
хорошо коррелируют с опубликованными данными по скорости дислокаций. Аналогичные расчеты были проведены для вязкопластической модели. Принципиальная разница между расчетами по дислокационной и вязкопластической модели состоит в том, что типичное среднеквадратичное отклонение для дислокационной модели 
, а для вязкопластической 
, т.е. отличаются на порядок.
Эффективный коэффициент вязкости, определяемый в разделе 6.3, уменьшается монотонно от величины 
Пас до 
. Только определяемая представленной моделью зависимость 
позволила согласовать теоретические и экспериментальные результаты. Она не может быть получена в рамках феноменологической модели. Отметим, что дислокационная модель позволяет объяснить основные результаты и трудности сопоставления формальных реологических моделей с экспериментальными результатами. Максимум сдвигового напряжения, определяемый скоростью нагружения и скоростью размножения дислокаций, аналогичен вводимому в ряде работ “динамическому пределу текучести”. Как отмечалось, он значительно превосходит статический предел текучести и зависит от истории нагружения. При увеличении амплитуды давления магнитного поля влияние сдвиговых напряжений на динамику трубки снижается. При давлении ~ 100 кбар деформация практически описывается моделью идеальной жидкости; влияние пластичности сводится к задержке в начале движения трубки.
Глава 7. Экспериментальная техника.
7.1. Схема экспериментальной аппаратуры. Схема экспериментальной установки «Юпитер», предназначенной для исследования сжимаемости веществ и высокоскоростной деформации металла, представлена на рис. 7.1. Установка состоит из генератора импульсных токов, криогенной техники, рентгеновской и оптической систем регистрации, систем запуска и синхронизации. Установка позволяет проводить исследования при гелиевой температуре.
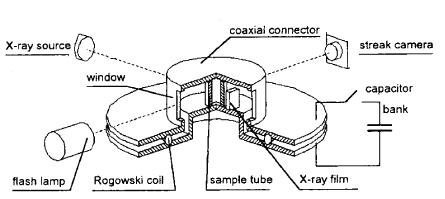
Рис. 7.1. Схема экспериментальной аппаратуры.
7.2. Генератор импульсных токов с энергией 150 кДж. Генератор импульсных токов (ГИТ) предназначен для получения магнитных полей мегагауссного диапазона и импульсных магнитных давлений <1 Мбар. ГИТ представляет собой малоиндуктивную конденсаторную батарею с разрядниками, устройством поджига и зарядки. Характеристики ГИТ: емкость 
мкФ, рабочее напряжение 
кВ, энергия 
кДж, собственная индуктивность 
нГн, максимальный ток 
МА.
7.3. Криогенная техника. При исследовании в области высоких давлений веществ, начальная температура которых по условиям эксперимента должна быть ниже азотной, возникают значительные технические трудности, связанные с созданием таких низких температур на установке. Проблема заключается в том, что требования, предъявляемые к конструкции установки криогенной техникой, во многом противоположны требованиям техники высоких давлений и регистрирующей давление аппаратуры. В отличие от известных видов криостатов к данному устройству предъявляется важное дополнительное требование возможность ввода в криостат импульсного тока 
МА длительностью 
мкс. В этом случае требования на токоввод по сопротивлению и индуктивности во многом трудно совместимы с требованием малого теплопритока при гелиевой температуре. Кроме того, ток должен быть хорошего качества. Эксперимент носит взрывной характер. Следовательно, криогенное оборудование должно быть либо защищено от взрыва, либо быть простым, недорогим и легко заменимым при его однократном использовании. Исследуемое вещество в нагрузке должно иметь однородную структуру, его количество, плотность и температура должны контролироваться. Рассмотрены различные схемы криостатов, удовлетворяющие этим требованиям. При проектировании криостата с необходимостью выбраны компромиссные решения для выполнения тепловых и электротехнических требований. На рис. 7.2 показана схема конструкции, разработанной и использованной в [12] для исследования сжимаемости конденсированного водорода. Процессы конденсации и сжатия водорода были разнесены. Сначала происходит охлаждение трубки в гелиевом криостате и замораживание в ней водорода. Затем трубка с водородом быстро переносится в рабочую камеру, где к ней подключаются токоподводящие шины, и пропускается ток. Время переноса трубки и задержки между подключением трубки к контактам и запуском ГИТ много меньше времени тепловой релаксации. Движение и торможение трубки не влияет на состояние водорода.
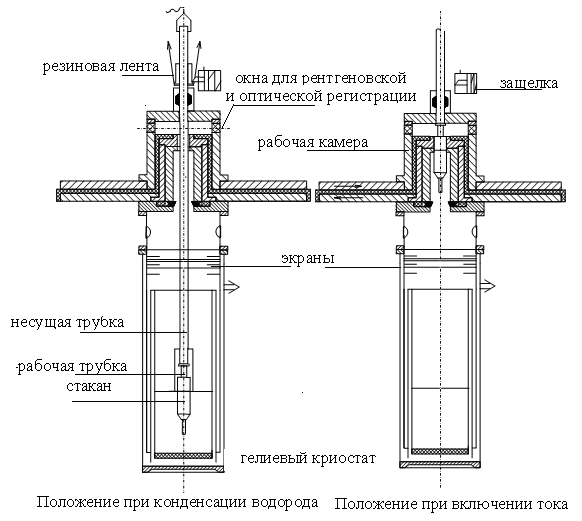
Рис. 7.2. Схема криостата
7.4. Оптические и рентгеновские измерения. Цель оптических и рентгеновских измерений определение с возможно большей точностью зависимостей от времени внешнего и внутреннего диаметров рабочей трубки при ее сжатии. Существенная особенность измерений на нашей установке состоит в необходимости защиты оптической системы, рентгеновского источника и пленки. При сжатии и последующем взрыве трубки в рабочей камере выделяется большая часть энергии ГИТ, что вызывает интенсивную ударную волну и быстрый разлет продуктов взрыва трубки.
Рентгеновский источник. Для рентгенографического измерения с высоким пространственным (
мкм) и временным (
нс) разрешениями размеров металлического лайнера необходимо создание новой рентгеновской аппаратуры. Описывается созданный электронный ускоритель, предназначенный для получения интенсивного тормозного рентгеновского излучения. Параметры ускорителя: ток 35 кА, напряжение на трубке 300 кВ, длительность импульса 10 нс, диаметр сфокусированного пучка на аноде 1 мм, доза на расстоянии 0.5 м составляет 100 мР. На рис. 7.3 приведена рентгенограмма металлического лайнера, используемого для сжатия веществ.
Pис. 7.3. Рентгенограмма металлического лайнера
Приведено описание конструкции защиты рентгеновской пленки. Описана технология изготовления датчика давления. В качестве эталонных веществ использовались щелочные материалы: калий и цезий. Датчик давления представлял собой изготовленную гальваническим способом никелевую трубку толщиной 10 мкм, заполняемую щелочным металлом.
7.5. Сохранение сжимаемого вещества. Преимуществом метода z-пинча, по сравнению с взрывными экспериментами, является возможность сохранения сжимаемого вещества после снятия давления. Сохранить исследуемое вещество можно, выбрав сечение трубки таким образом, чтобы температура её не превосходила температуры плавления, либо при полном разряде конденсаторной батареи, либо к произвольному моменту (в качестве которого естественно выбрать момент первого максимума) с отключением в этот момент тока. Эксперимент (рис. 7.4), демонстрирующий возможность сохранения образца, проводился на установке "Шок" с энергией 30 кДж и током 
МА.
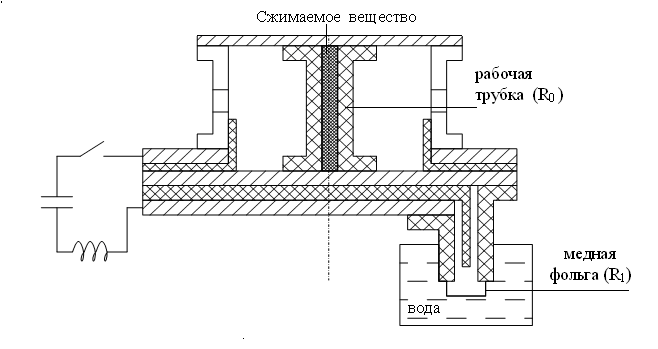
Рис. 7.4.Схема эксперимента с фосфором
В качестве прерывателя использовалась медная фольга. При резком обрыве тока инициируется высокое напряжение, вызывающее вторичный пробой в пространстве, окружающем проводник. Чтобы затруднить шунтирование, фольга помещалась в воду. Трубка заполнялась красным фосфором. Магнитное давление достигало ~70 кбар с характерным временем нарастания 2 мкс. О наличии давления свидетельствовал переход красного фосфора в черный, подтверждаемый рентгеноструктурным анализом.
7.6. Плазменный z-пинч. В плазменном (радиационном) zпинче достигнуто значение 
МГс при 
МА (см. [11]). С увеличением тока следует ожидать ещё больших значений поля. Поэтому одной из целей этих работ – создание такого пинча, когда начальные условия определяются плазмой высокого давления. Описана экспериментальная установка, предназначенная для проведения экспериментов по сжатию z-пинча с импульсным напуском. Отличительная особенность установки возможность одновременной инжекции газовой оболочки и плазменного лайнера, что позволяет получить симметричный начальный пробой и исключить шунтирование тока в момент максимального сжатия плазмы. Описаны устройства для импульсного напуска вещества в разрядный промежуток: электродинамический клапан и инжектор плазмы эрозионного типа. Проведены исследования динамики плазменной оболочки в z-пинче с импульсным напуском газа и плазменной оболочки. Применявшиеся диагностические методики: электротехнические, оптические, нейтронные, рентгеновские. Наилучшей была такая организация разряда, когда основную массу дейтерия напускает клапан, а инжектор по периферии инжектирует «поджигающую» плазму. Это обеспечивает стабильность, повторяемость и симметрию плазменной оболочки. Кроме того, это позволило проводить разряд при большом давлении. Предложенный способ является, по-видимому, практически универсальным, поскольку позволяет не только инжектировать любые газы, но и любые элементы, входящие в состав твердых тел. Приводится сравнение полученных экспериментальных данных с численными расчетами.
7.7. Экспериментальная установка энергоемкостью 1.2 МДж.
Созданная установка предназначена для генерации мегагауссных и, возможно, гигагауссных импульсных магнитных полей, мегабарных давлений, а также исследования возможности получения мощного нейтронного и рентгеновского излучений. Конденсаторная батарея состоит из 60 независимых модулей с энергией модуля 20 кДж. Полная ёмкость батареи 
мФ, рабочее напряжение 
кВ, индуктивность батареи 
нГ, максимальный ток 
МА.
Результаты, выносимые на защиту
- Решение автомодельной задачи изэнтропического сжатия сферическим или цилиндрическим поршнем однородного вещества с реальным уравнением состояния. Решение задачи сферического сжатия вещества оболочкой в приближении несжимаемой среды.
- Решение задачи релятивистского изэнтропического сжатия плоским поршнем вещества со степенным уравнением состояния построение релятивистской центрированной волны сжатия.
- Автомодельное и численное решение уравнений нелинейной диффузии магнитного поля.
- Решение квазиклассического уравнения для плотности электронов с квантовыми поправками на неоднородность электронного газа к корреляционной энергии.
- Полуэмпирическое широкодиапазонное уравнение состояния вещества, включающее аппроксимацию «холодной» и тепловых составляющих.
- Результаты МГД моделирования и оптимизации сжатия твердого водорода и инертных газов в мегабарном диапазоне давлений в металлическом z-пинче.
- Экспериментальные и теоретические результаты, демонстрирующие возможность сохранения вещества, сжатого при сильноточном разряде конденсаторной батареи через металлический лайнер.
- Разработка методики измерения импульсных давлений, основанная на использовании эталонных веществ с известным уравнением состояния. Результаты измерения изэнтропического уравнения состояния твёрдого водорода «эталонным» методом.
- Разработка методики измерения реологических динамических характеристик среды, измерение параметров дислокационной модели высокоскоростной деформации.
Список литературы по теме диссертации
- Прут В.В. Автомодельное изэнтропическое сжатие вещества // Ж. вычисл. матем. и матем. физики. 2001. Т. 41. № 2. С. 327.
- Прут В.В. Релятивистская центрированная волна сжатия // Математическое моделирование. 2007. Т. 19, № 6. С. 43.
- Прут В.В. Автомодельное решение уравнения нелинейной диффузии магнитного поля // ПМТФ. 1982. № 1. С. 16.
- Прут В.В. Полуэмпирическое уравнение состояния конденсированных сред // ТВТ. 2005. Т. 43. В. 5. С. 713.
- Прут В.В. Уравнение состояния в квазиклассическом приближении // ЖТФ. 2004. Т. 74. В. 12. С. 10.
- Прут В.В. Оценка параметров критической точки плавления элементов // ЖТФ. 2008. Т. 78. В. 5. С. 138
- Прут В.В. Моделирование нелинейной диффузии сильного магнитного поля // Прикладная физика. 2008. В. 3. С. 2713
- Прут В.В. Адиабатическое сжатие вещества оболочкой // ЖТФ. 2000. Т. 70. В. 8. С. 133.
- Прут В.В., Храбров В.А., Матвеев В.В., Шибаев С.А. Метод металлического zпинча: изэнтропическое сжатие водорода // Письма в ЖЭТФ. 1979. Т. 29. В. 1. С. 33.
- Prut V.V., Shybaev S.A. High rate deformation of metallic liner and its dislocation description // J. Phys. D: Appl. Phys. 1996. V. 29. P. 3071.
- Вихрев В.В., Иванов В.В., Прут В.В. Динамика z-пинча с учетом потерь энергии на излучение // Физика плазмы. 1986. Т. 12. № 3. С. 328.
- Матвеев В.В., Медведева И.В., Прут В.В., Суслов П.А., Шибаев С.А. Адиабатическое уравнение состояния водорода до 150 кбар // Письма в ЖЭТФ. 1984. Т. 39. № 5. С. 219.
- Матвеев В.В., Прут В.В., Храбров В.А. Переход красного фосфора в черный при квазиизэнтропическом сжатии // Письма в ЖТФ. 1978. Т. 4. № 9. С. 551.
- Мокеев А.Н., Прут В.В. О нейтронном излучении z-пинча // ЖТФ. 1991. Т. 61. № 6. С. 17.
- Мокеев А.Н., Прут В.В. Z-пинч с импульсным напуском газа // ПТЭ. 1986. № 6. С. 17.
- Земсков Л.И., Мокеев А.Н., Прут В.В. Трехэлектродный разрядник под давлением // ПТЭ, 1984, № 1, С. 133.
- Матвеев В.В., Прут В.В., Суслов П.А., Шибаев С.А. Многоканальный генератор высоковольтных наносекундных импульсов // ПТЭ, 1982, № 3, С. 90.
- Знатнов Е.В., Королев В.Д., Матвеев В.В., Прут В.В., Смирнов В.П., Черненко А.С. МИР – мощный рентгеновский источник // ПТЭ, 1985, № 1, С. 183.
- Прут В.В., Шибаев С.А., Медведева И.В. и др. Кумуляция токовой волны. Сверхсильные магнитные поля. Труды 3 межд. конф. по генерации мегагауссных магнитных полей и родственным экспериментам (Новосибирск, 1983). М.: Наука, 1984. С. 378.
- Medvedeva I.V., Prut V.V., Shybaev S.A. Dynamics of liners under the Megagauss magnetic field // In: Megagauss fields and related power systems (Proceedings of 4 Int. Conf. on Megagauss Magnetic Field Generation and Related Topics, Novosibirsk, 1986), New York, Plenum Press, 1986, p. 63.
- Matveev V.V., Medvedeva I.V., Prut V.V., Suslov P.A., Shybaev S.A. Compression of solid hydrogen with a liner under the megagauss magnetic field // In: Megagauss fields and related power systems (Proceedings of 4 Int. Conf. on Megagauss Magnetic Field Generation and Related Topics, Novosibirsk, 1986), New York, Plenum Press, 1986, p. 63.
- Matveev V.V., Mokeev A.N., Prut V.V. Strong magnetic field in metallic and plasma z-pinches // In: Megagauss fields and related power systems (Proceedings of 5 Int. Conf. on Megagauss Magnetic Field Gen. and Related Topics, Novosibirsk, 1989), Nova Science Publishers, New York, 1990, p. 73.
- Mokeev A.N., Prut V.V. 1.2 МJ capacitor bank fоr dense z-pinch investigations // In: Megagauss fields and related power systems (Proceedings of 6 Int. Conf. on Megagauss Magnetic Field Generation and Related Topics, Albuquerque, 1992), Nova Science Publishers, New York, 1993, р. 88.
- Mokeev A.N., Prut V.V. А powerful capacitor bank for dense z-pinch investigations // In: AIP conference proceedings, vol. 299. Dense z-pinches (Proceedings of 3 Int. Conf. on Dense Z-pinches, London, U.K., 1993), AIP Press, New York, 1994, р. 690.
- Zemskov A.I., Matveev V.V., Prut V.V., Udalov A.M. A short z-pinch // 10 Europ. Conf. on Contr. Fusion and Plasma Physics. M.: 1981. V. 1, D-8.
- Прут В.В., Храбров В.А., Матвеев В.В., Удалов А.М., Шибаев С.А. Isentropic compression of substances by a pulsed magnetic field // 7th Inter/ AIRAPT High Pressure Conf, Le Creusot, France, 1979.
- Земсков А.И., Мокеев А.Н., Прут В.В. Сильноточный малогабаритный разрядник // Тезисы докладов 1 Всесоюзной конференции по импульсным источникам энергии для физических и термоядерных исследований, Юрмала, 1983, с. 47.
- Мокеев А.Н., Прут В.В. Емкостной накопитель на 1.2 МДж // Тезисы докладов 3 Всесоюзной конференции по импульсным источникам энергии для физических и термоядерных исследований, Ленинград. 1989,С.54.
- Прут В.В. Полуэмпирическое уравнение состояния вещества // М.: ИАЭ-6264, 2003.
- Прут В.В. Вычисление градиентных поправок в квазиклассическом приближении // М.: ИАЭ-6265, 2003.
- Прут В.В. Моделирование уравнения состояния. М.: ИАЭ-6463, 2007.
- Прут В.В. Модель плавления с критической точкой//М.: ИАЭ-6365, 2005.
- Прут В.В. Численный расчет перехода графит алмаз в металлическом z-пинче // М.: ИАЭ-6462, 2007.
- Прут В.В. Численное моделирование токовой волны // М.: ИАЭ-6465, 2007.
- Прут В.В. К вопросу о центрированной волне сжатия в релятивистском приближении // М.: ИАЭ-6220. 2001.
- К вопросу о параметрах критической точки плавления элементов // М.: ИАЭ-6464, 2007.
- Прут В.В. Программа расчета деформации вязкопластической металлической трубки магнитным полем // М.: ИАЭ-3115. 1979.
- Прут В.В. Об интерполяции уравнения состояния водорода // М.: ИАЭ-3026. 1978.
- Прут В.В. Об измерении адиабатического уравнения состояния // М.: ИАЭ-3255. 1980.
- Прут В.В., Матвеев В.В., Медведева И.В. и др. Качественный анализ динамики металлической трубки в магнитном поле // М.: ИАЭ-2888. 1977.
- Прут В.В., Матвеев В.В., Медведева И.В. и др. Деформация и нагрев вязкопластической металлической трубки магнитным полем // М.: ИАЭ-2802. 1977.
- Прут В.В., Матвеев В.В., Медведева И.В. и др. Адиабатическое сжатие калия алюминиевой трубкой // М.: ИАЭ-2799. 1977.
- Прут В.В., Матвеев В.В., Медведева И.В. и др. Схема и АЛГОЛ-программа для расчета одномерных нестационарных МГД-уравнений с вязкостью // М.: ИАЭ-2766. 1977.
- Мокеев А.Н., Прут В.В. Методы исследования фазовых переходов при высоких давлениях // М.: ИАЭ-3636, M.: 1982.
- Земсков А.И., Мокеев А.Н., Прут В.В. Трехэлектродный разрядник под давлением на 40 кВ, 300 кА // М.: ИАЭ-3746, M. 1983.
- Матвеев В.В., Прут В.В., Суслов П.А., Удалов А.М., Шибаев С.А. Генератор импульсных токов с энергией 150 кДж и током 5 МА // М.: ИАЭ-3533, 1982.
- Земсков А.И., Матвеев В.В., Прут В.В., Удалов А.М. О согласовании параметров плазменной оболочки и электротехнической цепи в z-пинче // М.: ИАЭ-3526. 1982.
- Вихрев В.В., Иванов В.В., Прут В.В. Моделирование радиационного сжатия z-пинча // М.: ИАЭ-3787. 1983.
- Prut V.V. Possibility of producing magnetic fields >100 MG and neutron scaling law of the z-pinch // MG -5 (Novosibirsk, 1989), New York, 1990, p. 73.
- Мокеев А.Н., Поликарпов Н.В.., Прут В.В., Суслов П.А., Шибаев С.А. Криостат с импульсным потребителем тока // Авт. свидетельство 1158816 (СССР) БИ, 1985, № 20.
