Моделирование процесса зарядки пылевой частицы и установления межчастичного расстояния в плазме низк о го давления
ПЕТРОЗАВОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
На правах рукописи
ШЕЛЕСТОВ АЛЕКСАНДР СЕРГЕЕВИЧ
МОДЕЛИРОВАНИЕ ПРОЦЕССА ЗАРЯДКИ ПЫЛЕВОЙ ЧАСТИЦЫ И УСТАНОВЛЕНИЯ МЕЖЧАСТИЧНОГО РАССТОЯНИЯ В ПЛАЗМЕ НИЗКОГО ДАВЛЕНИЯ
Специальность 01.04.04 - физическая электроника
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата физико-математических наук
Петрозаводск
2006
Работа выполнена на кафедре электроники и энергетики
физико-технического факультета
Петрозаводского государственного университета
Научный руководитель: доктор физико-математических наук,
профессор,
Сысун В. И.
Официальные оппоненты:
доктор физико-математических наук Мольков С.И.
кандидат физико-математических наук Филиппов А.В.
Ведущая организация: Институт теплофизики экстремальных состояний Объединенного института высоких температур РАН, Москва
Защита диссертации состоится «___» ___________ г. в ___ часов на заседании диссертационного совета К 212.190.01 при Петрозаводском государственном университете по адресу:
Петрозаводск, пр. Ленина, 33,
отзывы направлять по адресу:
185640, Петрозаводск, пр. Ленина, 33, ПетрГУ, ученому секретарю
диссертационного совета К 212.190.01.
С диссертацией можно ознакомиться в библиотеке
Петрозаводского государственного университета.
Автореферат разослан «___»_______________2006 г.
Ученый секретарь
диссертационного совета К 212.190.01
кандидат физико-математических наук __________________
Алешина Л.А.
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность работы. Физика пылевой плазмы является в настоящее время активно развивающейся областью фундаментальной науки. Это связано, как с попытками понять сущность явлений образования плазменных кристаллов, так и с тем, что пылевые кристаллические образования имеют ряд интересных свойств и эффектов, перспективных для практического применения. Исследование механизмов образования подобного рода структур перспективно с точки зрения фундаментальной науки – оно вносит вклад в изучение многокомпонентной плазмы в целом, позволяет лучше объяснить и промоделировать процессы образования атомарных и молекулярных кристаллов в физике твердого тела, улучшает понимание процессов фазовых переходов, в частности процесса конденсации, а также находит применение при анализе процессов образования упорядоченных плазменно-пылевых облаков во Вселенной. Помимо этого, данного рода исследования актуальны и для прикладных аспектов физики плазмы. Прикладными задачами можно считать проблему удаления пылевых частиц в микроэлектронике при производстве микросхем методами плазменных технологий, очистка реакторов термоядерного синтеза, получение новых наноструктурных материалов, таких, например, как тонкие пленки с заданными свойствами, порошки, пористые компоненты и их модификации.
Наиболее значимым процессом в образовании кристаллической структуры является процесс зарядки пылевой частицы в плазме и установление распределения потенциала вокруг нее. Стоит отметить тот факт, что имеющиеся теории зарядки пылевой частицы в плазме, такие как модель ограниченных орбит (ОО), заимствованная из теории зондов, модель радиального дрейфа (РД) или гидродинамическая модель диффузионного ограничения (ДО), применимы лишь в ряде частных случаев.
Поэтому построение более адекватных математических моделей для процессов, происходящих в пылевой плазме и приводящих к структурному упорядочиванию пылевых частиц, актуальны и несут в себе большой потенциал.
Цель работы заключалась в построении математической модели зарядки пылевой частицы в плазме низкого давления с учетом ионизации в межчастичной области, выработке критерия образования упорядоченных пылевых структур и определении, на основе полученных результатов численного эксперимента, параметров плазменных кристаллов, что являлось бы научно-обоснованной базой для объяснения имеющихся опытных данных.
Научная новизна работы определяется тем, что в ней впервые:
- проведено компьютерное моделирование ионного тока на частицу в плазме низкого давления с учетом ионизации в области возмущения в широком диапазоне изменения параметров плазмы, размеров пылевых частиц и межчастичных расстояний.
- получен критерий установления межчастичного расстояния, основанный на максимуме силы, действующей на единицу поверхности заряженной пылинки со стороны электрического поля.
- на основании результатов численного эксперимента с применением разработанной модели показано, что основополагающим параметром в процессе формирования упорядоченных пылевых структур в плазме низкого давления является отношение размера пылинки к электронному дебаевскому радиусу
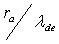 .
. - проведено двумерное моделирование плазменных цепочек, образование которых может являться начальной фазой формирования кристаллической структуры.
Научно-практическая значимость работы определяется тем, что в ней получена новая важная информация, способствующая развитию представлений о механизмах формирования плазменных кристаллов и критерии их образования. Данный критерий позволяет определить параметры плазмы и условия, при которых будет происходить формирование упорядоченной пылевой структуры. Разработаны модели зарядки пылинки в плазме, рассчитаны параметры формирующихся плазменных кристаллов при данных условиях в плазме для различных размеров пылинок.
Основные положения выносимые на защиту приводятся в заключении.
Апробация работы: Основные результаты диссертационной работы были доложены на: заочной электронной конференции «Современные наукоёмкие технологии», проводимой Российской академией естествознания (РАЕ), 20-25 февраля 2005г., заочной электронной конференции «Фундаментальные исследования», проводимой РАЕ, 20-25 февраля 2005г., Второй международной научно-практической конференции «Исследование, разработка и применение высоких технологий в промышленности» 7 – 9 февраля 2006 г., Санкт-Петербург, Россия., конференции «Фундаментальные и прикладные проблемы современной физики», Демидовские чтения, Москва-Екатеринбург-Томск, Россия, 25 февраля – 6 марта 2006 г., Второй всероссийской конференции молодых ученых «Физика и химия высокоэнергетических систем», 4 – 6 мая 2006 г., Томск, Россия., IV конференции «Фундаментальные и прикладные исследования. Образование, экономика и право», Римини, Италия, 9 – 16 сентября 2006 г., заочной электронной конференции «Математическое моделирование», проводимой Российской академией естествознания (РАЕ), 15-20 сентября 2006г.
Основные результаты опубликованы в виде статей и материалов докладов конференций, перечень которых приведен в конце автореферата.
Вклад автора. Исследования проведены в период 2003 – 2006 г. при непосредственном участии автора, которым сформулированы и обоснованы задачи диссертации. Разработка математической модели проведена при содействии Сысун А. В. Результаты раздела 2 были получены при содействии Подопригора А. В. В коллективных работах автору принадлежат изложенные в диссертации защищаемые положения. Все численные расчеты и написание текстов программ проведены автором.
Обьем и структура диссертации. Диссертация состоит из введения, 5 разделов, заключения, списка литературы и трех приложений. Диссертация содержит 138 стр., включая 28 рисунков, 11 таблиц и 55 наименований библиографических ссылок.
ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ
Во Введении обоснована актуальность темы диссертации, сформулированы цель работы, научная новизна, научно-практическая значимость.
Раздел 1 содержит обзор литературных данных по параметрам плазменно-пылевых кристаллов и цепочек и условиям их существования. Рассмотрены существующие модели зарядки пылевой частицы: взятая из теории зондов модель ограниченных орбит, основанная на сохранении энергии и кинетического момента ионов в центральном поле заряда пылинки в предположении их потока из бесконечности, модель радиального дрейфа, предполагающая свободное радиальное движение ионов из бесконечности в поле пылинки и модель диффузионного ограничения, предполагающая также радиальное движение ионов, но с учетом столкновений с атомами при высоких давлениях. Между тем, пылевая компонента плазмы при концентрации пыли 106 см-3 является такой же компонентой плазмы, как ионная и электронная, и играет важную роль из-за рекомбинации на поверхности пылинок. Эта рекомбинация существенно превышает рекомбинацию на стенках и требует такого же существенного увеличения объемной ионизации. Ионный ток на пылевые частицы как раз и формируется ионами, возникающими в результате ионизации в непосредственной близости от пылевой частицы. Учет этого факта требует разработки соответствующей модели.
В литературе рассмотрены следующие механизмы взаимодействия пылевых частиц и условия, при которых они играют существенную роль для устойчивого существования кристаллической структуры.
а) Длинномасштабное взаимодействие пылевых частиц. Поле заряда пылевых частиц не экранируется по обычному закону экспоненциального экранирования, что объясняется наличием потока плазменных частиц на пылинку. Большинство существующих моделей рассматривающих длинномасштабное взаимодействие основаны на подборе выражения для хода потенциала, при котором на некотором расстоянии от частицы возможно притяжение пробного заряда того же знака.
б) Притяжение из-за бомбардировки пылинок ионами. В присутствии других пылинок поток плазмы на пылинку становится асимметричным. Пылинки взаимно экранируют друг друга, чем и объясняется возникновение силы притяжения между ними, но так как ионы образуются непосредственно вблизи пылинки – их поток на каждую частицу в отдельности равномерен. Следовательно, данная сила обусловлена лишь внешним потоком ионов на структуру и способна вызвать коллективные эффекты в пылевой плазме: колебания, волны, неустойчивости, но она не является определяющей в процессе формирования упорядоченной пылевой структуры.
в) Притяжение и отталкивание, связанные с потоком нейтралов. Если температура поверхности пылинки отличается от температуры нейтральной компоненты, то при их взаимодействии также происходит передача импульса. Поэтому сказанное выше для ионов применимо и для нейтральных частиц. Однако данная сила изотропна и однородна – она не зависит от межчастичного расстояния.
По нашему мнению наиболее существенное действие на заряженную поверхность пылинки в плазме, при наличии соседних пылинок на некотором расстоянии, производит сила со стороны полного электрического поля. Следовательно, необходим расчет распределения потенциала вблизи пылинки в зависимости от расстояния между частицами.
В ряде работ для этого предлагается использовать метод молекулярной динамики. В работе [1] PIC-MC моделированием в ячейке вблизи частицы определялся потенциал и заряд пылевой частицы в аргоне с давлением 0,1 тор. И хотя в широком диапазоне изменялась концентрация плазмы и, соответственно, дебаевский радиус, фиксация межчастичного расстояния не позволила обнаружить его влияние на заряд и потенциал частицы и, тем более, определить критерий его установления.
В работе [2] методом молекулярной динамики определялся заряд и потенциал пылевой частицы в плазме неона. Радиус расчетной сферической ячейки был фиксирован и выбирался достаточно большим, чтобы тепловой хаотический поток ионов извне на ячейку существенно превышал уход ионов на пылевую частицу. Ионизация в объеме ячейки не учитывалась, поэтому такое приближение более подходит для одиночной пылевой частицы в плазме.
Помимо этого на настоящий момент предложены общие методы молекулярного моделирования пылевой плазмы, включая сами пылевые частицы. В этом случае межчастичное расстояние установится автоматически в процессе моделирования, но это потребует на несколько порядков больших машинных затрат. Такой метод моделирования рационально использовать для проверки конкретного распределения пылевых частиц и для моделирования коллективных эффектов в пылевой плазме.
Итак, исходя из всего вышеперечисленного, стоит отметить тот факт, что ряд численных экспериментов использовал для определения потенциала и заряда пылевой частицы метод молекулярной динамики, однако при этом не варьировалась величина межчастичного расстояния и в большинстве работ не учитывалась ионизация в области возмущения. Учет ионизации проводился при численном моделировании плазменного кристалла в разряде азота в работе [3].Здесь рассматривался случай высоких давлений, когда применимо гидродинамическое приближение для процессов переноса электронов и ионов плазмы.
Исходя из этих выводов, сформулированы следующие задачи работы.
- Промоделировать процесс зарядки пылевой частицы в сферически симметричной ячейке для одномерного случая, учесть процесс ионизации, то есть образование ионных потоков в межчастичной области при низких давлениях;
- Произвести максвелловское распределение вновь образующихся ионов по скоростям, с температурой равной температуре атомов;
- Статистически разыграть длину свободного пробега ионов до столкновения с атомами, так как даже редкие столкновения нарушают орбитальное движение ионов;
- Получить зависимости заряда, потенциала, полной энергии поля, энергии частицы в поле окружающей ее плазмы, а также силы, действующей на единицу поверхности заряженной частицы, от параметров плазмы и размеров частиц;
- Установить критерий межчастичного расстояния пылевых структур. Найти зависимости этого расстояния от параметров плазмы и размеров частицы и сравнить с имеющимися опытными данными;
- Провести численный эксперимент для двумерной модели процесса зарядки частиц в нитевидных пылевых структурах с целью подтверждения адекватности полученных результатов;
- Моделирование проводить во времени в режиме установления заряда и потенциала частиц, начиная с невозмущенного состояния;
Раздел 2 содержит описание одномерной модели в сферической системе координат и результаты численного моделирования процесса зарядки пылевой частицы в плазме низкого давления путем прямого интегрирования уравнения Пуассона с учетом ионизации в межчастичной области. Расчет производился в ячейке Зейтца-Вигнера, которая представлялась сферической с радиусом rd, определяемым концентрацией частиц rd=(4/3 nd)-1/3. При кубической решетке пылевого кристалла ![]() , где h – межчастичное расстояние. При гранецентрированной решетке, чаще всего наблюдаемой в экспериментах,
, где h – межчастичное расстояние. При гранецентрированной решетке, чаще всего наблюдаемой в экспериментах, ![]() .
.
Уход электронов и ионов на частицу компенсируется ионизацией в объеме. Так как ячейка окружена аналогичными областями соседних частиц, то можно считать, что электронный и ионный поток на частицу создаются в самой ячейке за счет рождения зарядов в непосредственной близости от частицы.
В приближении нулевой температуры ионов в режиме свободного пролета ионов уравнение Пуассона (1), представленное аналогично Ленгмюру в виде уравнения “плазма-слой” [4], решалось численно с частными аналитическими решениями на границе ячейки Зейтца-Вигнера и тонких сеточных слоях в промежутке.
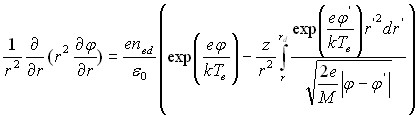 (1)
(1)
На границе ячейки ввиду подобности соседних ячеек положим нулевое значение потенциала и его градиента. Потенциал на поверхности частицы определяется в процессе решения подбором частоты ионизации z, с тем, чтобы ионный ток на частицу (2) сравнивался с электронным, определяемым согласно (3).
![]() (2).
(2).
![]() (3)
(3)
Нормировкой координаты r на дебаевский электронный радиус d и потенциала на электронную температуру Te получен безразмерный вид уравнения (1), что показывает что d и Te, совместно с атомным весом иона являются определяющими параметрами плазмы.
Безразмерные величины:
координата ![]() , потенциал
, потенциал ![]() ,
,
концентрация электронов и ионов ![]() ,
,
где ned - концентрация электронов на границе ячейки Зейтца-Вигнера.
Скорость ионов 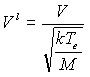 , частота ионизации
, частота ионизации ![]() ,
,
где i – ионная плазменная частота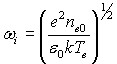 .
.
Тогда уравнение (1) будет иметь вид (1)
![]() , (1)
, (1)
где выражения для концентрации электронов и ионов будут следующими (4):
![]() ,
, 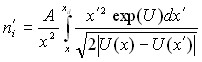 . (4)
. (4)
Численное решение уравнения затруднено из-за неопределенности правой части при близком к нулю значении знаменателя. Часто всю область возмущения разбивают на две подобласти: подобласть квазинейтральной плазмы с нулевой левой частью уравнения и подобласть слоя, где пренебрегается концентрацией электронов и поток ионов считается постоянным. В нашем случае, когда размер слоя сравним с размерами всей ячейки, такое приближение неприменимо.
Для большей устойчивости численного решения использовались параболическая интерполяция потенциала по трём точкам (5):
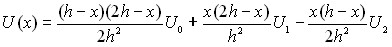 (5)
(5)
где h – шаг дискретизации, x – отсчитывается от точки x0,а также приближённое аналитическое решение для концентрации на каждом шаге (6):
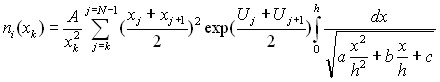 (6),
(6),
где a=Uj-2Uj+1+Uj+2, b=-3 Uj+4 Uj+1- Uj+2, c=2 Uj-2Uk, причём
![]()
Результаты численных расчётов для распределения потенциала в разряде паров Ne для ряда значений rз/d (отношения радиуса зонда-пылинки к электронному дебаевскому радиусу) и rd/d (отношения размера ячейки Зейтца-Вигнера к электронному дебаевскому радиусу) приведены на рисунке 1.
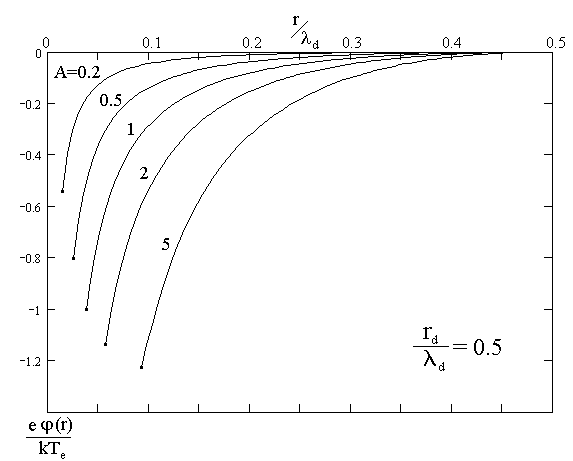
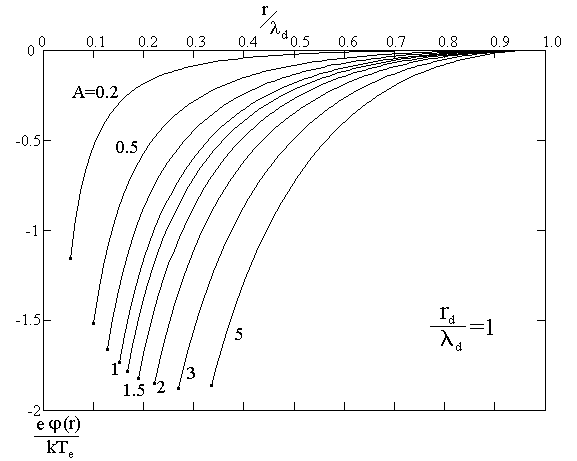
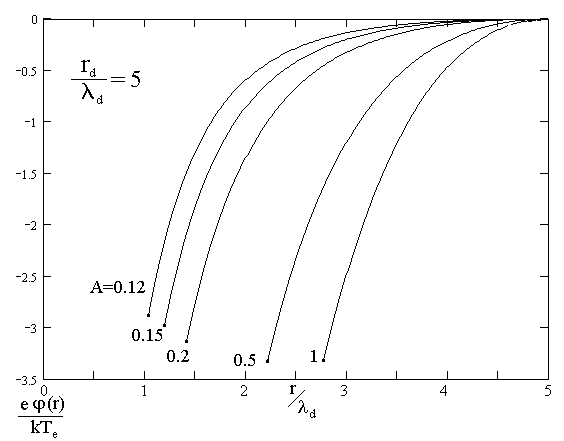
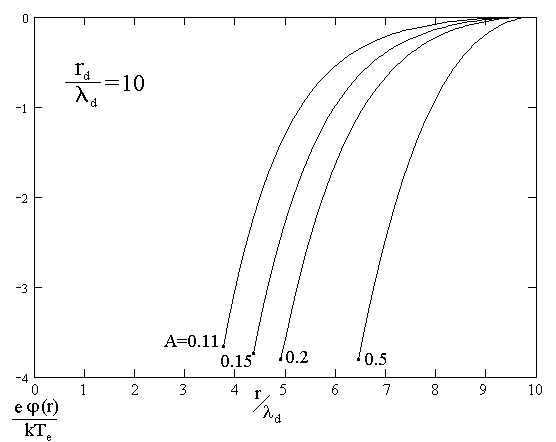
Рис.1
На всех кривых ход потенциала хорошо описывается приближенным аналитическим выражением (7):
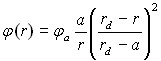 (7)
(7)
,где a- радиус пылинки, a – ее потенциал, а rd – размер ячейки Зейтца-Вигнера.
Одновременно рассчитывались полный заряд электронов (8) в ячейке, приведенный к заряду дебаевской сферы, заряд пылевой частицы (9), определенный по градиенту потенциала на ее поверхности, и общая потенциальная энергия электрического поля в ячейке (10), нормированная на полную тепловую (кинетическую) энергию электронов в дебаевской сфере:
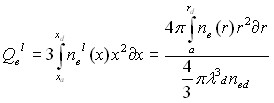 (8)
(8)
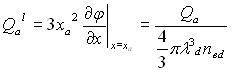 (9)
(9)
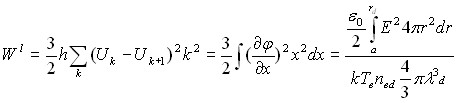 (10)
(10)
Показаны существенные зависимости этих величин от размеров ячейки Зейтца-Вигнера. и радиуса пылинки
Раздел 3 содержит описание моделирования процесса зарядки пылевой частицы методом молекулярной динамики.
Здесь же рассмотрен критерий установления межчастичного расстояния в образующейся упорядоченной пылевой структуре.
Прямое интегрирование уравнения Пуассона (1) возможно не всегда. Помимо условия нулевой температуры ионов ![]() ограничением такого решения являлось появление неустойчивостей при больших отношениях
ограничением такого решения являлось появление неустойчивостей при больших отношениях ![]() , где a – радиус частицы, вследствие неопределенности правой части выражения для концентрации ионов (4) при близком к нулю значении знаменателя.
, где a – радиус частицы, вследствие неопределенности правой части выражения для концентрации ионов (4) при близком к нулю значении знаменателя.
Более устойчивым является метод молекулярной динамики, позволяющей осуществлять моделирование процесса зарядки пылевой частицы в плазме и при отличной от нуля ионной температуре. Однако данный метод требует значительно больших затрат машинного времени.
В методе молекулярной динамики ионный состав плазмы заменяется модельными макроиноами общим числом от одного до несколько миллионов. Начальное состояние макроионов определяется функцией распределения ионов по скоростям, как и элементарных ионов, так как скорости макроионов равны скоростям элементарных ионов. Увеличивается пропорционально заряд и масса модельных частиц, при сохранении их отношения q/m. При этом не изменяются уравнения движения (11) и, соответственно, их решения.
![]() ;
; ![]() . (11)
. (11)
Последнее уравнение является законом сохранения углового момента в центральном поле. Движение макроионов продолжается до столкновения их с пылинкой, которой они поглощаются. Число ушедших макроионов восполняется ионизацией в объеме, которая принималась пропорциональной концентрации электронов в сеточной ячейке. Образованные ионы случайным образом распределялись внутри ячеек сетки, а их скорость разыгрывалась в соответствии с Максвелловским распределением с температурой атомов. На границах области возмущения ![]() установлен режим зеркального отражения макроионов, так как она окружена аналогичными ячейками, и уход ионов компенсируется аналогичным приходом.
установлен режим зеркального отражения макроионов, так как она окружена аналогичными ячейками, и уход ионов компенсируется аналогичным приходом.
В процессе движения некоторые макроионы могут перейти в режим спутника, непрерывно вращаясь вокруг пылевой частицы, и может, следовательно, происходить их накопление. Однако, в реальной плазме даже при низких давлениях существует конечная длина пробега ионов, вследствие столкновения с атомами. При этом ион останавливается (режим перезарядки) и необходимо снова разыгрывать его начальную скорость, в соответствии с температурой атомов Ta. Длина пробега определяется давлением газа, причем распределение длин пробега для разных ионов определяется распределением Пуассона с плотностью вероятности (12)
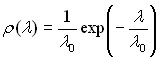 , (12)
, (12)
где ![]() - средняя длина пробега (
- средняя длина пробега (![]() -сечение столкновения,
-сечение столкновения, ![]() -концентрация атомов).
-концентрация атомов).
Концентрация электронов принималась распределенной по Больцману (4). В контрольных численных расчетах использовалось более точное выражения для концентрации электронов (13), [5], учитывающего уход электронов на частицу:
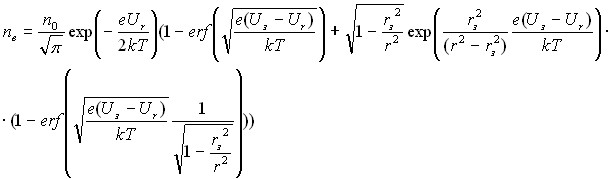 (13)
(13)
Контрольный расчет, с концентрацией электронов (13), проведенный при малых размерах пылевых частиц, когда их установившийся потенциал был малым, ![]() показал на близость Больцмановского распределения даже в этом случае. Таким образом распределение Больцмана достаточно точно описывает концентрацию электронов и его использование допустимо для дальнейших численных расчетов.
показал на близость Больцмановского распределения даже в этом случае. Таким образом распределение Больцмана достаточно точно описывает концентрацию электронов и его использование допустимо для дальнейших численных расчетов.
Электрическое поле определялось на каждом временном шаге решением уравнения Пуассона на сетке, по радиусу состоящей из N=200 – 500 интервалов, в зависимости от радиуса расчетной области При этом компьютерная переменная времени нормировалась на ионную плазменную частоту![]() . Решение начиналось от внешней границы с граничными условиями
. Решение начиналось от внешней границы с граничными условиями ![]() . Потенциал пылевой частицы
. Потенциал пылевой частицы ![]() определялся в конце счета. Заряд частицы находился согласно (9), он оказывался равным разности суммарных зарядов ионов и электронов в расчетной области с небольшими статистическими отклонениями, что указывает на правильность решения уравнения Пуассона.
определялся в конце счета. Заряд частицы находился согласно (9), он оказывался равным разности суммарных зарядов ионов и электронов в расчетной области с небольшими статистическими отклонениями, что указывает на правильность решения уравнения Пуассона.
Процесс счета продолжался до стабильного состояния системы, критерием которого выступало равенство ионного (2) и электронного (3) токов на пылинку.
Стоит отметить, что данный расчет весьма затратен в плане машинного времени, вследствие образования большого числа макроинов (до 107). С учетом оптимального соотношения координатного и временного шагов, выбранного исходя из устойчивости схемы интегрирования, время расчета одного режима составляло десятки часов.
Рассмотрим критерий установления межчастичного расстояния в пылевой плазме. Для системы заряженных частиц в качестве критерия устойчивого состояния используется минимум полной энергии электрического поля (14):
![]() (14)
(14)
С другой стороны, критерием устойчивого положения заряженной частицы qa во внешнем электрическом поле с потенциалом внеш. является минимум потенциальной энергии этого заряда (15):
![]() (15)
(15)
Потенциал внешнего поля (поля плазмы без вносимого заряда) можно определить как разность истинного потенциала заряженной частицы и потенциала на ее поверхности, создаваемого только ее зарядом (16):
![]() (16),
(16),
где ra - радиус частицы.
Оба вышерассмотренных критерия справедливы для изолированной системы зарядов с сохранением значений зарядов и отсутствием поступления энергии извне. Пылевая плазма такой системой не является и не только из – за постоянной рекомбинации электронов и ионов плазмы на пылевых частицах и восполнением их ухода объемной ионизацией с соответствующими затратами энергии. В пылевой плазме при изменении расстояния между частицами изменяется также заряд этих частиц, как и пространственный заряд окружающей их плазмы. Вследствие этого более точным критерием установления стационарного состояния является равенство нулю суммарной силы на частицу от всех окружающих ее зарядов. С другой стороны, сила, действующая на частицу с поверхностным зарядом ![]() , равна (17):
, равна (17):
![]() (17),
(17),
здесь Е – напряженность поля на поверхности частицы, причем ![]() , где En - нормальная составляющая напряженности. Для проводящей частицы E и En совпадают, а, ввиду малой поверхности пылевой частицы (ra~10-6 м.), это условие можно применять и для непроводящей частицы, из – за поверхностного перераспределения элементарных зарядов при возникновении даже малейшей разности потенциалов.
, где En - нормальная составляющая напряженности. Для проводящей частицы E и En совпадают, а, ввиду малой поверхности пылевой частицы (ra~10-6 м.), это условие можно применять и для непроводящей частицы, из – за поверхностного перераспределения элементарных зарядов при возникновении даже малейшей разности потенциалов.
За критерий установления межчастичного расстояния можно принять максимум значения этой поверхностной силы, действующей на частицу со стороны электрического поля. Другая частица будет притягиваться к данной до установления максимума силы. Смещение пылевой частицы в обе стороны приведет к возникновению результирующей силы, возвращающей ее обратно.
Для проверки адекватности этого критерия в процессе моделирования помимо силы, действующей на заряженную пылинку со стороны электрического поля плазмы, рассчитывались полная энергия электрического поля, энергия пылинки в поле окружающей ее плазмы, а также сила от импульса ионов, поглощаемых частицей, которая также зависит от межчастичного расстояния, в отличии от силы, создаваемой импульсом потока нейтралов.
Расчеты производились для безразмерных параметров в диапазоне: ![]() ;
;![]() ;
; ![]() 0, 0.01, 0.1;
0, 0.01, 0.1; ![]() 1, 10, 1000, где
1, 10, 1000, где 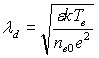 - электронный дебаевский радиус, li – длина пробега иона до столкновения с атомом.
- электронный дебаевский радиус, li – длина пробега иона до столкновения с атомом.
Как и в случае прямого интегрирования уравнения Пуассона, заряд пылевой частицы нормировался на заряд дебаевской сферы невозмущенной плазмы, энергия электрического поля и пылевой частицы в поле плазмы нормировались на полную тепловую энергию электронов в дебаевской сфере, а сила на единицу поверхности пылевой частицы нормировалась на давление электронной компоненты плазмы (18):
![]() (18)
(18)
Значения потенциала и заряда пылинки, полученные по результатам численного эксперимента при нулевой температуре ионов в зависимости от межчастичного расстояния для различных радиусов пылинки, представлены на рисунке 2. Отдельные точки справа на графиках – расчеты, произведенные по радиальной теории, подобно тому, как это было проделано в работе [6]. Также была построена зависимость плавающего потенциала пылинки от ее радиуса в рамках радиальной теории для Ne, аналогично тому, как это было проделано в работе [6] для Ar и H. Как видно из рисунков, радиальная теория является предельным случаем предложенной модели.
Заряд пылинки хорошо описывается выражением (19):
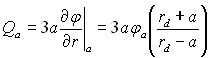 (19)
(19)
Потенциальная энергия пылинки в поле окружающей ее плазмы можно приближенно рассчитать по (20):
![]() , (20)
, (20)
а сила, действующая на пылинку, описывается согласно (21):
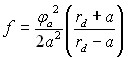 (21)
(21)
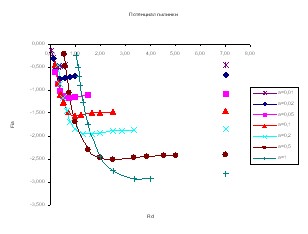
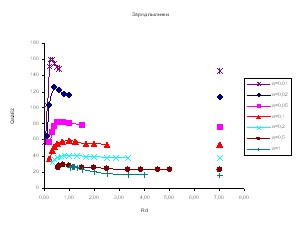
Рис. 2
На рисунке 3 показан график зависимости приведенной силы, действующей на пылинку от размера ячейки. Согласно предложенному критерию, если удаленная пылинка приближается к другой, то сила, действующая на частицу, возрастает до максимума, что и видно на рисунке 3, а далее резко уменьшается, что свидетельствует об устойчивой конфигурации системы пылевых частиц в области максимума этой силы.
Отметим, что поверхностная сила от импульсов поглощаемых ионов оказалась существенно меньшей данной силы, и ею можно было пренебречь вплоть до размеров частиц, больших дебаевского радиуса электрона.
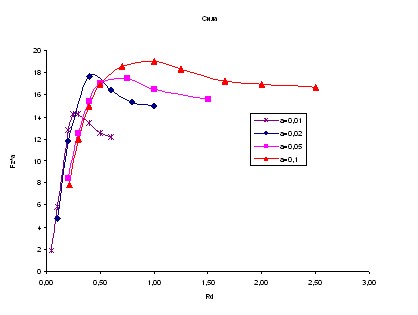
Рис. 3
Подобным образом были получены зависимости потенциала, заряда и силы от размера ячейки, рассчитанные при отличном от нуля отношении ионной и электронной температур ![]() . При близких положениях максимума силы увеличивается потенциал и заряд пылевых частиц.
. При близких положениях максимума силы увеличивается потенциал и заряд пылевых частиц.
Аналогичные зависимости были построены и для случая, где параметром здесь являлась длина свободного пробега макроинов in. При in/ d <<10 уменьшался потенциал пылевых частиц.
Раздел 4 содержит описание математической модели двумерного цилиндрического случая образования упорядоченных пылевых структур.
В плазме с фрактальными частицами (пыль) часто образуются пылевые структуры в виде нитей (цепочек) вытянутых вдоль электрического поля. Часто такие цепочки наблюдаются на окраинах трехмерных плазменных пылевых структур (Рисунок 5).

Рис. 5
При моделировании цепочки будем считать область возмущения такой цепочки в плазме в виде цилиндра, считая, что радиус области возмущения (то есть области, где создаются за счет объемной ионизации электроны и ионы, идущие на частицу) больше межчастичного расстояния. Выделим одну ячейку такой области и рассмотрим условия на ее границах. Для совпадения границ частицы с цилиндрической сеткой, форму частицы будем считать цилиндрической, с равными высотой и диаметром (рисунок 6).

Рис. 6
Потенциал описываем двумерным уравнением Пуассона в цилиндрической системе координат (22):
![]() (22)
(22)
с граничными условиями (23)
[M,N]=0; ![]() ;
; ![]() (23)
(23)
Потенциал определялся методом итераций (100-200) на каждом временном шаге. Ионы движутся в электрическом поле согласно уравнениям движения (24). В цилиндрической системе имеем три компоненты скорости Vr, Vz, V.
![]() ;
; ![]() (24)
(24)
Так как в силу симметрии ![]() , то угловая скорость определяется условием сохранения углового момента.
, то угловая скорость определяется условием сохранения углового момента.
Полное число макроинов в ячейке достигало десятков миллионов. Расчетное время одного режима (одна точка) в двумерном случае составляло несколько суток.
На рисунке 7 приведены зависимости потенциала, заряда и силы, действующей на частицу от размера ячейки, при характерном отношении размера пылинки к дебаевскому радиусу 0.05, рассчитанные при нулевой температуре ионов для двумерного случая.
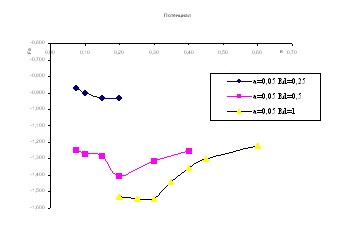
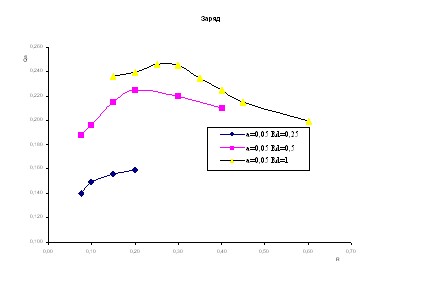
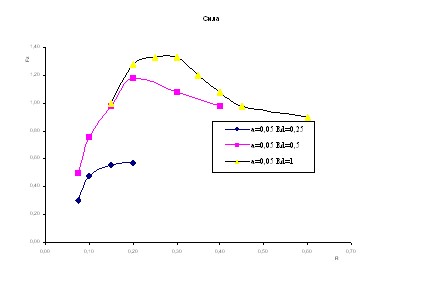
Рис. 7
Результаты численного моделирования, полученные с использованием двумерной модели дают несколько меньшие значения межчастичного расстояния, что связано с азимутальным перераспределением ионов в межчастичной области, с увеличением их концентрации на оси между пылинками. Эти ионы увеличивают силу притяжения между пылинками, что приводит к меньшему межчастичному расстоянию. В целом результаты моделирования двумерной модели согласуются с результатами численного эксперимента для одномерного сферического случая.
Раздел 5 содержит обсуждение результатов расчета, выводы и сравнение рассчитанных данных с результатами эксперимента.
Здесь же приведены итоговые зависимости межчастичного расстояния (Рис. 8), потенциала и заряда пылинки, а также силы, действующей на единицу ее поверхности от размеров пылевой частицы.
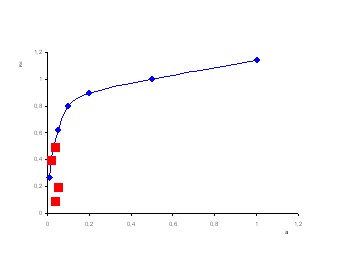
Рис. 8
Отдельными точками на графике зависимости межчастичного расстояния от размеров пылинки показаны экспериментальные данные.
В Заключении перечислены основные результаты и выводы работы.
- Разработана математическая модель процесса зарядки пылевой частицы в плазме низкого давления, учитывающая ионизацию в области возмущения.
- Предложен критерий установления межчастичного расстояния пылевых структур, согласно максимуму силы, действующей на частицу со стороны окружающей ее плазмы.
- . Показано, что при заданных параметрах плазмы и размерах частиц существует установившийся размер ячейки Зейтца-Вигнера.
- Установлено, что определяющим в образовании кристаллических структур в пылевой плазме является отношение размера частиц к электронному дебаевскому радиусу.
- Получены зависимости потенциала, заряда, полной энергии, энергии пылинки в поле плазмы, силы, действующей на пылинку со стороны поля плазмы а также ионного тока в широком диапазоне изменения параметров плазмы, размеров пылевых частиц и межчастичных расстояний, при различных давлениях и температурах.
- Предложено выражение для описания хода потенциала вблизи заряженной пылинки в упорядоченной плазменно-пылевой структуре.
Приложение А содержит текст программы для моделирования одномерного сферического случая зарядки пылевой частицы в плазме.
Приложение Б содержит текст программы для моделирования двумерного цилиндрического случая зарядки пылевой частицы в плазме.
Приложение В содержит текст программы для расчета потенциала и заряда пылевой частицы в плазме по радиальной теории, без учета ионизации в области возмущения, в приближении «холодных ионов».
Основные результаты опубликованы в виде статей и материалов докладов конференций:
- Сысун В.И., Хахаев А.Д., Олещук О.В., Шелестов А.С. Заряд и потенциал пылевой частицы в плазме низкого давления с учётом ионизации в области возмущения // «Физика плазмы» 2005, т.31, №9, с. 834-841.
- V.I. Sysun, A.D. Khakhaev, O.V. Oleshuk and A.S. Shelestov Investigation of the Charge and Potential of a Dust Grain in a Low-Pressure Plasma with Allowance for Ionisation in the Integrain Space // Plasma Physics Reports, Vol. 31, № 9, 2005, pp.772-779.
- Сысун В.И., Хахаев А.Д., Олещук О.В., Шелестов А.С. Формирование ионного потока на пылевую частицу в плазме // «Современные наукоёмкие технологии» 2005, №3, с. 30-34.
- Шелестов А.С., Подопригора А.В. Моделирование ионного потока на пылевую частицу в плазме методом «крупных частиц в ячейке» // «Фундаментальные исследования» 2005, №3, с. 60-62.
- Шелестов А.С., Сысун А.В., Двумерная модель заряда пылевой частицы в плазме низкого давления // сборник трудов «Высокие технологии, фундаментальные и прикладные исследования, образование», изд – во Политехнического университета, том 5 стр. 310-312, материалы Второй международной научно - практической конференции «Исследование, разработка и применение высоких технологий в промышленности» 7 – 9 февраля 2006 г., Санкт-Петербург, Россия.
- Шелестов А.С., Сысун В.И., Численное моделирование параметров низкотемпературной плазмы методом крупных частиц // Материалы конференции «Фундаментальные и прикладные проблемы современной физики», Демидовские чтения, Москва-Екатеринбург-Томск, Россия, 25 февраля – 6 марта 2006 г., стр. 21 – 22.
- Шелестов А.С., Модель расчета параметров кристаллических структур пылевой плазмы низкого давления // Материалы Второй всероссийской конференции молодых ученых «Физика и химия высокоэнергетических систем», 4 – 6 мая 2006 г., Томск, Россия, стр. 338 – 341
- Сысун А.В., Шелестов А.С., Критерий установления межчастичного расстояния в пылевой плазме // Материалы IV конференции «Фундаментальные и прикладные исследования. Образование, экономика и право», Римини, Италия, 9 – 16 сентября 2006 г.
- Sysun A.V., Shelestov A.S., Criterion of intergrain distance establishing in dusty plasma // European Journal of Natural History, 2006, №5, pp.86-88.
- Шелестов А.С., Сысун А.В., Моделирование процесса зарядки пылевой частицы в плазме низкого давления методом молекулярной динамики // Материалы заочной электронной конференции «Математическое моделирование», проводимой Российской академией естествознания (РАЕ), 15-20 сентября 2006г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
[1] J. P. Baeuf, Physical Review A., v.46, №12, p.7910, 1992.
[2] А.В. Зобнин, А.П. Нефедов, В.А. Синельщиков, В.Е. Фортов, ЖТЭФ, 2000, т.118, вып 3(9), стр. 554-559.
47-67.
[3] А.Ф. Паль, Д.В. Сивохин, А.Н. Старостин, А.В. Филиппов, В.Е. Фортов, Физика плазмы, 2002, т.28, №1, стр. 32-44.
[4] Tonks L., Langmnuir I. Phisycal Review. 1929. v.34. p.876-922.
[5] Lam S.H. The Langmuir Probe in a Collisionless Plasma, Physics Fluids, v.8, pp. 73-87, 1965.
[6] Kennedy R.V., Allen J.E. J. Plasma Phisics. V.67. 2002. pp.243-250.
Подписано в печать 16.11.2006
Формат 6084 1/16 Бумага офсетная
Уч-изд. л. 1. Тираж 100 экз. Изд. № 268
Государственное образовательное учреждение
высшего профессионального образования
ПЕТРОЗАВОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Типография Издательства ПетрГУ
185910, г.Петрозаводск, пр.Ленина, 33

