Токи и электромагнитные поля, формируемые при взаимодействии узконаправленного импульса гамма излучения с газовой средой.
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
На правах рукописи
ВАЛИЕВ Фархат Фагимович
ТОКИ И ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ, ФОРМИРУЕМЫЕ ПРИ ВЗАИМОДЕЙСТВИИ УЗКОНАПРАВЛЕННОГО ИМПУЛЬСА ГАММА ИЗЛУЧЕНИЯ С ГАЗОВОЙ СРЕДОЙ.
Специальность 01.04.16 – физика атомного ядра и элементарных частиц
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
доктора физико-математических наук
Санкт-Петербург
2010
Работа выполнена на кафедре ядерной физики Физического факультета Санкт-Петербургского государственного университета
Научный консультант: доктор физико-математических наук,
профессор,
КРАСНОВ Леонид Васильевич
Официальные оппоненты: доктор физико-математических наук,
старший научный сотрудник
БЛЕДНОВ Вадим Алексеевич
доктор физико-математических наук,
ведущий научный сотрудник
КИРИЛЛОВ Виталий Васильевич
доктор физико-математических наук,
профессор
ЛОЩАКОВ Игорь Иванович
Ведущая организация: Федеральный Научно-производственный центр ФГУП НИИ Комплексных испытаний оптико-электронных приборов и систем
Защита состоится «24» февраля 2011 г. в 11 часов на заседании диссертационного совета Д. 212.232.16 по защите докторских и кандидатских диссертаций при Санкт-Петербургском государственном университете по адресу: 199034, Санкт-Петербург, Университетская наб., д. 7/9, циклотронная лаборатория, ауд. 302.
С диссертацией можно ознакомиться в научной библиотеке им. М.Горького при Санкт-Петербургском государственном университете по адресу: 199034, Санкт-Петербург, Университетская наб. д.7/9.
Автореферат разослан «_____»_____________2010 г.
Ученый секретарь диссертационного совета кандидат физико-математических наук Власников А.К.
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Диссертация посвящена теоретическому и экспериментальному изучению электромагнитных процессов, происходящих в результате прохождения импульса ионизирующего излучения через среду.
Актуальность темы исследования обусловлена необходимостью изучения процессов формирования импульсов тока и их полей в ядерной физике и физике элементарных частиц, где вторичные электромагнитные процессы могут быть либо сигналами исследуемых эффектов (явлений), либо фоном.
В литературе широко представлены работы посвященные рассмотрению электромагнитных полей источников, перемещающихся со скоростями большими, равными и меньшими скорости света в вакууме.
Сверхсветовое движение источников в вакууме рассматривалось в [1
], [2
]. Примеры источников, перемещающихся со скоростью большей скорости света в вакууме, приведены в [3
] и в обзоре актуальных проблем в УФН [4
]. Отметим, что в приведенных работах сам источник (импульс тока) электромагнитного излучения, как правило, не рассчитывался. Интерес к созданию сверхсветовых источников в последние годы возрос в связи с обсуждением возможности с их помощью генерировать мощные электромагнитные импульсы [5
]. Волны, формируемые такими источниками, имеют сложную зависимость от временных и пространственных переменных. Методы расчета полей в пространственно-временном представлении изложены в [6
], [7
], [8
]. Расчеты полей сверхсветовых источников в этих работах проведены для конкретных форм импульсов тока (точечный ток, ток, распределенный по нормальному закону). Для выявления особенностей волн, формируемых сверхсветовыми источниками, необходимо рассмотрение задачи в общем виде при произвольных формах тока.
Теоретические и экспериментальные исследования локализованных электромагнитных волн проводятся с конца девятнадцатого века. Эти работы связаны с проблемой возбуждения узконаправленных электромагнитных полей и создания соответствующих излучателей. Известно, что уравнения Максвелла допускают существование электромагнитных волн, сохраняющих неизменной пространственно-временную структуру при распространении в вакууме [9
]. Несмотря на то, что решение известно давно, описываемая им локализация волн не обсуждалась до работы Н.Бриттенгама [10
]. В ней он получил локализованные электромагнитные волны (сфокусированные волновые моды). Позднее, сфокусированные волновые моды были получены как решения системы уравнений Максвелла, удовлетворяющие специальному условию – “гауссову” поперечному распределению волны на плоскости, перемещающейся со скоростью света [11
]. Были найдены Эрмит-Гаусс, и Бессель-Гаусс волновые структуры [12
]. Для возбуждения этих волн предложены простые источники – токи, распределенные на плоскости, перемещающейся со скоростью света: точка [13
], круговой контур [14
], диск [12
]. В работе [13
] импульс макроскопического тока, скорость перемещения которого равна скорости света, предлагалось формировать при поглощении энергии импульса жесткого излучения средой, при этом изучение способа формирования источников локализованных электромагнитных волн не проводилось.
В экспериментах С.И.Вавилова и П.А.Черенкова [15
] был открыт эффект направленного излучения в оптическом диапазоне (ИВЧ), возникающий при воздействии на жидкости гамма квантов и показано, что он отчетливо наблюдается в тех случаях, когда скорость перемещения электрона больше скорости распространения света в среде. Спустя 30 лет на пучке электронов обнаружили слабое оптическое излучение в газовом черенковском счетчике при энергии меньшей пороговой [16
]. Это излучение называемое подпороговым излучением Вавилова – Черенкова изучалось в газовых детекторах [17
]. В [18
] показано, что учёт подпорогового ИВЧ существенно влияет на точность определения состава пучка вторичных частиц в экспериментах на ускорителях. Объяснение эффекта подпорогового излучения предложено в [19
], [20
], [21
]. Рассмотрение приведенных работ показывает, что исследование формирования подпорогового излучения остается актуальной задачей.
Перечисленные задачи объединяет то, что их изучение возможно в рамках единой схемы построения источников и единой методики решения начальной электродинамической задачи в пространственно-временном представлении. Отметим, что при теоретическом изучении токов и полей, формируемых в результате взаимодействия импульсов излучения с веществом, необходимо рассматривать как физические процессы, приводящие к образованию заряженных частиц, так и, что не менее важно, вторичные процессы взаимодействия образующихся частиц с атомами среды.
В экспериментальной ядерной физике и физике высоких энергий имеются задачи, для решения которых необходимы расчет токов и электромагнитных полей, формируемых в детекторах. Поэтому количественное описание токов, появляющихся при взаимодействии излучения с веществом детекторов, имеет большое прикладное значение.
Объекты исследования – токи, возникающие при взаимодействии узконаправленного импульса гамма-излучения с газовой средой, и электромагнитные поля, формируемые этими импульсами тока.
Цель работы - изучение формирования импульсов тока при взаимодействии узконаправленных импульсов гамма излучения с веществом и характерных особенностей вторичных электромагнитных волн.
Сформулированная цель определила направления исследований:
1) разработка метода расчета токов, формируемых при взаимодействии узконаправленных импульсов гамма излучения с веществом.
2) изучение пространственно - временных распределений электронов в газовой среде при различных энергиях падающих гамма-квантов и определение возможности применения модели линейного тока для расчета электромагнитных полей.
3) создание алгоритмов и оптимизация программ расчета пространственно - временных и частотных характеристик электромагнитных полей источников, перемещающихся по отрезку прямой со скоростями равными и большими скорости света в вакууме.
4) применение разработанных алгоритмов для узконаправленных импульсов гамма излучения, распространяющихся в веществе, с учетом геометрических параметров среды и анализ получаемых токов и полей. Подпороговое излучение, сверхсветовые импульсы токов, локализованные волны.
5) оптимизации параметров детекторов на микроканальных пластинах (МКП) с использованием разработанного метода формирования импульса тока.
оптимизации параметров детекторов на микроканальных пластинах (МКП) с использованием разработанного метода формирования импульса тока.
Научная новизна работы .
Предложен метод расчета пространственно-временной структуры тока, формируемого при взаимодействии импульса гамма излучения с веществом. Новизна метода заключается в учете на микроскопическом уровне элементарных актов взаимодействия узконаправленного импульса ионизирующего излучения со средой.
Установлена возможность применения модели линейного тока для описания электромагнитного поля тока, создаваемого узконаправленным импульсом гамма излучения в газовой среде.
Получены в явном виде выражения для расчетов полей импульсов тока произвольной формы, перемещающихся по отрезку прямой со скоростями большими скорости света в пространственно-временном представлении.
Проведен расчет электромагнитных полей для модельных источников, перемещающихся со скоростью большей скорости света в вакууме. Определены условия, при которых излучение сверхсветового источника в вакууме и в среде без дисперсии аналогично излучению Вавилова-Черенкова.
Для импульса тока, перемещающегося со скоростью света, рассчитано электромагнитное поле во временном представлении. Показано, что в этом случае формируются два импульса электромагнитного поля противоположной полярности, сдвинутые по времени прихода в фиксированную точку наблюдения.
Представлены модели возникновения излучения в световом диапазоне в результате прохождения импульса ионизирующего излучения через воздушную среду до порога эффекта Вавилова-Черенкова.
Доказана принципиальная возможность физической реализации электромагнитных волн, локализованных в пространстве и времени.
Рассчитана форма импульса тока на выходе канала микроканальной пластины (МКП) и показано, что она согласуется с экспериментально наблюдаемой. На основе разработанного метода проведена оптимизация конструкций и режимов работы детекторов на МКП.
Смоделированы и разработаны детекторы на базе МКП с различными системами съема информации, позволяющие выполнять прецизионные измерения координат и времени прохождения заряженных частиц через детектор.
Практическая ценность работы .
С использованием метода имитационного моделирования получено описание формы импульса тока на выходе микроканального детектора, согласующееся с формой экспериментально наблюдаемого импульса.
На основе моделирования проведен выбор параметров детекторов на базе МКП. Для проведения экспериментов в ядерной физике и физике высоких энергий предложены и разработаны детекторы на базе МКП с различными системами съема информации.
Результаты моделирования с использованием пакетов GEANT и FLUKA используются в процессе обучения на кафедре ядерной физики физического факультета СПбГУ.
Положения, выносимые на защиту.
1. Метод и результаты расчета пространственно-временных распределений токов, образующихся при взаимодействии узконаправленных импульсов ионизирующего излучения с газовой средой, учитывающие микроскопические перемещения вторичных электронов.
2. Решение в явном виде задачи формирования электромагнитных волн импульсом линейного тока произвольной формы и длительности движущимся со скоростью 
по отрезку прямой.
3. Результаты анализа особенностей электромагнитных полей, формируемых при перемещении импульса тока со сверхсветовой скоростью по отрезку прямой.
4. Разработанные модели, описывающие подпороговое излучение, возникающее при прохождении гамма квантов через газовую среду.
5. Оценки параметров пространственно-временного распределения жесткого излучения, обеспечивающие формирование направленных электромагнитных волн.
6. Результаты численного моделирования конструкций детекторов заряженных частиц, разработанных на базе микроканальных пластин для ядерной физики и физики высоких энергий.
7. Результаты экспериментального тестирования детекторов на микроканальных пластинах с различными системами съема информации.
Апробация работы. Результаты, содержащиеся в диссертации, докладывались и обсуждались:
на ежегодных Международных совещаниях по ядерной спектроскопии и структуре атомного ядра (на 34, 42, 47, 49 - 59 совещаниях.) в 1984, 1992, 1997, 1999-2010 гг.,
на международных семинарах «Дни дифракции», Санкт-Петербург, 2006, 2007, 2009 гг.
на научных семинарах кафедр ядерной физики и радиофизики Санкт-Петербургского государственного университета.
Созданные по теме диссертации программы и результаты компьютерного моделирования докладывались:
на 3-ем совещании по вторичному электронному излучению. Санкт-Петербург, Радиевый инст., 1998 г.
на совещании по компьютерной физике "Workshop on Computational Physics. " Санкт-Петербург, 2003.
Часть результатов, представленных в диссертации, была получена в рамках исследований, поддержанных грантами РФФИ и МНТЦ.
Публикации и личный вклад автора.
Основная часть задач, составляющих содержание работ в приведенном ниже списке публикаций, была поставлена и решена автором. Вклад автора настоящей диссертации в работы с соавторами заключается в участии в постановке задач, создании компьютерных программ, анализе полученных решений, в приложении их к экспериментальным исследованиям и в изготовление и тестирование детекторов.
СОДЕРЖАНИЕ РАБОТЫ
Диссертация состоит из введения, одной обзорной и четырех оригинальных глав, положений выносимых на защиту, а также библиографического списка используемой литературы из 111 наименований. Общий объем диссертации составляет 149 страниц машинописного текста, включая 8 таблиц и 33 рисунка.
В главе 1 приводится обзор физических задач и применяемых для их решения методов расчета импульсов тока и полей, создаваемых ими.
В 1.1 приводится обзор рассматриваемых физических задач:
излучение сверхсветовых линейных источников в вакууме,
источники локализованных волн,
подпороговое излучение в газовой среде.
моделирование и реализации детекторов на МКП.
В 1.2 приведены обзор и обоснование выбора методов расчета токовых распределений и электромагнитных импульсов
Наиболее часто используют три подхода для расчета токов.
Первый подход феноменологический, второй основан на решении кинетических уравнений. В третьем подходе расчет импульса тока проводится на основе анализа элементарных актов взаимодействия с использованием метода Монте-Карло. Ранее использование этого метода осложнялось недостатком компьютерных мощностей. С появлением возможности проведения расчетов на высокоскоростных компьютерах и компьютерных кластерах эта сложность частично снята. Точность метода Монте-Карло достаточно высока и сравнима с экспериментальной и поэтому в данной работе формы импульсов тока получены исходя из рассмотрения микроскопических перемещений отдельных электронов.
При описании электромагнитных полей источников, произвольно зависящих от времени, обычно используют временные и пространственные Фурье преобразования, что связано со значительными вычислительными трудностями. В данной работе использованы запаздывающие потенциалы в пространственно-временном представлении.
В главе 2 рассмотрена методика расчета пространственно-временного распределения электронов в фазовом пространстве, на основе имитационного моделирования.
При взаимодействии импульса гамма излучения с атомами среды образуются электроны и ионы. Скорости ионов малы, и поэтому они не вносят существенный вклад в формирование вектора плотности тока. Свободные электроны движутся со скоростью меньшей скорости света, но при этом перемещение области пространства, где плотность тока отлична от нуля, может быть представлено как движение некоторого эффективного заряда со скоростями равными или большими скорости света.
В данной главе приводится методика расчета пространственно-временного распределения тока, формируемого при взаимодействии узконаправленного импульса жесткого излучения с веществом, на основе имитационного моделирования [1, 2, 3]. Суть методики состоит в учете основных физических процессов взаимодействия фотонов со средой: фотопоглощение, комптоновское рассеяние, образование пар, а также вторичные эффекты взаимодействия электронов со средой, ионизационные процессы, вызванные вторичными электронами. Отметим, что задача расчета электромагнитных полей упрощается, когда допустима модель линейного тока. В главе приведено обоснование возможности применения этой модели.
Вектор плотности тока определялся из векторов плотностей токов отдельных электронов. Это позволило исследовать изменения плотности тока со временем. Полученные в модельных экспериментах энергетические и угловые распределения электронов сравнивались с экспериментальными данными. Тестирование показало, что результаты моделирования согласуются с экспериментальными данными по взаимодействию излучения с веществом.
Раздел 2.1 посвящен рассмотрению формирования импульсов тока, перемещающихся со скоростью света. Импульс тока формируется при облучении среды узконаправленным пучком жесткого гамма-излучения в виде дельта импульса во времени, причем вектор плотности тока определяется скоростями отдельных электронов, образующихся в поглощающей среде, и зависит от их координат. В работе использовано численное моделирование. В программу вводились данные о геометрии и элементном составе поглощающей области, пространственно-временном распределении первичных гамма - квантов и их импульсах.
Технику исследования импульса тока, перемещающегося со скоростью равной скорости света, с помощью имитационного моделирования можно продемонстрировать на следующем примере [1]. Рассмотрим однородную поглощающую среду ограниченную цилиндрической поверхностью и плоскостями, ортогональными оси цилиндра, по которой перемещается импульс первичного излучения.
Схема численного эксперимента представлена на рис.1. Пусть начало координат находится в точке О (
,
,
), принадлежащей одной из указанных плоскостей, а ось z совмещена с осью цилиндра. За начало отсчета времени примем момент прохождения импульсом гамма излучения границы поглощающей области. Рассмотрим результаты численных экспериментов при прохождении гамма квантов с энергией 10 МэВ через воздушную среду при давлении воздуха 10 атмосфер. Облучение 
- квантами проводилось в направлении оси z. Угол вылета электронов 
отсчитывался от направления первичных 
квантов.
На рис.1 показаны траектории электронов (сплошные линии) и гамма - квантов (штриховые линии).
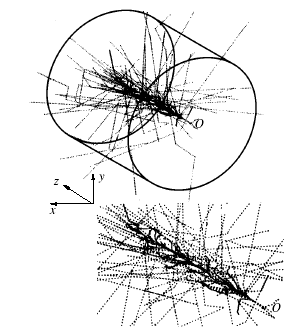
Рис.1. Схема численного эксперимента (внизу представлена увеличенная часть центральной области).
Видно, что электроны сгруппированы вблизи оси 
.
На рис.2 представлены импульсы тока для различных сечений поглощающей области, перпендикулярных ее оси. Длительность импульса 
по уровню 0.1 меньше 2 нс, что соответствует его пространственной протяженности 
, где с - скорость света.
Полученное значение 
представляет собой - оценку пространственной локализации тока вдоль оси 
. Из рисунка также следует, что импульс тока перемещается со скоростью света.
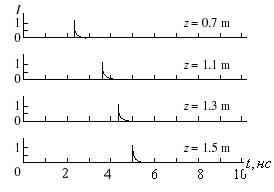
Рис.2. Формы импульсов тока в сечениях цилиндра (z = 0.7 м,
1.1 м, 1.3 м, 1.5 м) при энергии первичных 
квантов 10 МэВ.
Приведенные выше оценки продольной и поперечной локализации позволяют утверждать, что при облучении газовой среды узконаправленным дельта импульсом жесткого излучения в рассматриваемом интервале времени и при выбранных параметрах эксперимента формируется перемещающаяся со скоростью света ограниченная область пространства, где 
.
Таким образом, выполнено необходимое условие применимости модели линейного тока (импульс тока, бегущий по прямой линии) [4].
Форма бегущего импульса тока аппроксимирована функцией
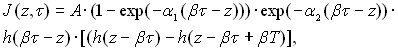(1)
, 
,
где 
- временная переменная, 
- длительность импульса тока в единицах 
, 
- функция Хевисайда, 
,
, 
- постоянные коэффициенты [5].
По рассмотренной методике были проведены и представлены в диссертации расчеты импульсов токов при давлениях воздуха от 0.1 атм. до 10 атм. в интервале энергий падающих гамма квантов от 50 кэВ до 40 МэВ. Полученные значения коэффициентов 
позволяют в дальнейшем не проводить длительных расчетов c использованием метода Монте-Карло.
Пункт 2.2 посвящен изучению формирования импульсов тока, перемещающихся со скоростью большей скорости света. Источники, перемещающиеся со световой скоростью, могут формироваться при поглощении гамма квантов средой. Если фронт гамма излучения направлен по оси цилиндра, заполненного веществом, то импульс тока перемещается по оси области поглощения со скоростью света, для всех остальных направлений движения фронта скорость его перемещения по оси цилиндра больше скорости света в вакууме (
).
В результате расчетов [6] получены формы импульсов тока в поперечных сечениях цилиндра, и установлено, что скорость их перемещения вдоль направления оси цилиндра подчиняется закону 
.
В третьей главе приведен вывод формул для расчета электромагнитных полей импульсов тока, бегущих по отрезку прямой со скоростью 
и рассмотрены особенности полей модельных источников излучения, перемещающихся по отрезку прямой со скоростями равными и большими скорости света [7].
Компоненту вектора плотности тока 
записывают в цилиндрической системе координат 
в виде:
, (2)
Здесь 
- функция Дирака, 
- функция, описывающая полный ток. Для импульса длительности 
, бегущего по отрезку прямой длиной 
,
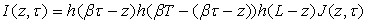где 
- произвольная непрерывная функция, 
- скорость перемещения импульса тока, 
- скорость света, 
- время, 
, 
.
Для аксиально-симметричного тока формула запаздывающего потенциала имеет вид:
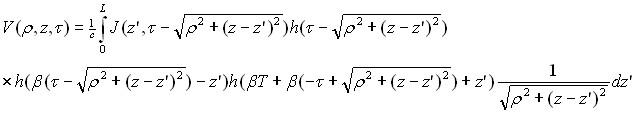
В 3.1 получены формулы в квадратурах для запаздывающих потенциалов для сверхсветовых источников
где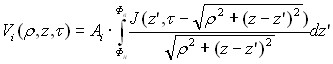 
,
,
зависят от координаты точки наблюдения, времени 
и соотношения параметров 
и 
.
Формулы применены для расчета электромагнитного поля для источников, перемещающихся по отрезку прямой со сверхсветовой скоростью: дельта-импульса, импульсов прямоугольной и гауссовой форм.
В 3.2 рассмотрены особенности поля источника излучения, перемещающегося по отрезку прямой со скоростью света. Для конкретных параметров однородной поглощающей среды и дельта импульса жесткого излучения определена пространственно-временная структура аксиально-симметричного импульса тока и решена электродинамическая задача. Установлено, что с приближением угла наблюдения 
(
-полярный угол сферической системы координат) к 
формы импульса тока и формы запаздывающего потенциала практически совпадают [8]. Эта особенность запаздывающего потенциала наблюдается при работе с токовыми импульсами произвольной формы.
Сравнение форм запаздывающих потенциалов под разными углами наблюдения при перемещении импульсов тока со скоростями большими и меньшими скорости света приводит к следующим выводам:
- с увеличением скорости до 
угол, при котором достигается максимум амплитуды и наиболее короткий фронт запаздывающего потенциала, убывает, в то время как при 
угол, при котором достигается максимум амплитуды и наиболее короткий фронт, возрастает.
- в случае малых отношений 
наблюдается сходство запаздывающего потенциала с формой тока как при скоростях больших, так и меньших скорости света под произвольными углами.
В главе установлена и объяснена близость форм запаздывающего потенциала и формы импульса тока при скорости большей скорости света под углом равным 
и получено аналитическое выражение для функции 
для дельта-импульса тока, перемещающегося со сверхсветовой скоростью по отрезку прямой [8, 9].
В четвертой главе представлены результаты применения в ядерной физике методики расчета векторов плотности тока и импульсов тока и формул для расчета электродинамической задачи из глав 2 и 3.
Рассмотрены
излучение сверхсветовых линейных источников в вакууме,
источники локализованных волн,
модели подпорогового излучения в газовой среде.
В 4.1 рассмотрено излучение сверхсветового источника, возникающее при движении импульса тока со скоростью большей скорости света в вакууме.
На основе полученных в гл.2 форм тока и c использованием формул главы 3, рассчитаны электромагнитные поля сверхсветового источника [10, 11].
Форма тока, возникающего в результате взаимодействия импульса гамма излучения с газом, аппроксимируется выражением (1).
С использованием формулы главы 3 рассчитаны временные зависимости 
при угле падения гамма – квантов 
(
) и углах наблюдения в диапазоне от
до 
, когда 
50 м и 
6 см, и плоскость наблюдения расположена на расстоянии 50 км от точки старта импульса тока.
На рис. 3 представлены нормированные на максимальную амплитуду временные зависимости запаздывающего потенциала 
при разных углах наблюдения 
: 1 – 
, 2 – 
, 3 - 
, 4 – 
, 5 – 
, 6 - 
, 7 – 
.
Из рисунка видно, что с приближением 
к углу 
наблюдается обострение формы запаздывающего потенциала с одновременным ростом его амплитуды. Форма 
близка в этом случае к форме импульса тока.
Для изучения зависимости 
от длины области поглощения были проведены расчеты при 
200 м, 50 м, 5 м и 
6 см, когда плоскость наблюдения расположена на расстоянии 50 км от точки старта импульса тока. В результате было получено, что длительности и амплитуды 
зависят от угла наблюдения 
и сходны с приведенными на рис 3.
Расчеты, проведенные для конкретного примера, были повторены при различных расстояниях от точки старта импульса тока. Временные зависимости 
, наблюдаемые под одними и теми же углами, на разных расстояниях оставались сходными, в то время как амплитуда уменьшалась обратно пропорционально расстоянию.
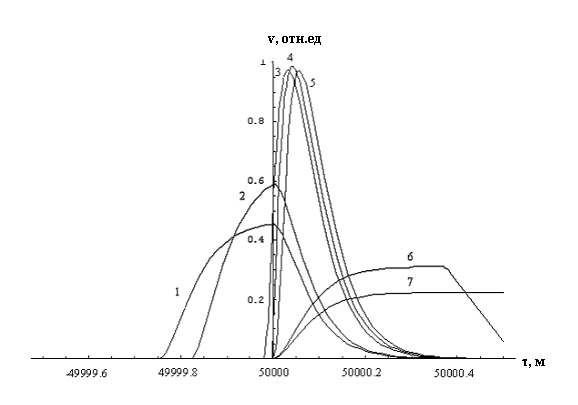
Рис. 3. Нормированные на максимальную амплитуду временные зависимости запаздывающего потенциала 
(
в единицах ct ) при разных углах наблюдения.
- полярный угол сферической системы координат.
1 – 
, 2 – 
, 3 - 
, 4 – 
, 5 – 
, 6 - 
, 7 – 
.
Отметим, что при достаточно большом 
исчезает характерный максимум в распределении 
при 
.
Для определения спектрального распределения плотности энергии электромагнитного поля при угле падении гамма квантов 
был проведен переход от пространственно-временного представления решения задачи к частотному представлению. Разложение 
в интеграл Фурье позволило получить спектральные плотности энергии электромагнитного поля 
под разными углами наблюдения в дальней зоне.
Спектры электромагнитных импульсов под разными углами наблюдения в световом диапазоне частот при 
представлены на рис.5.
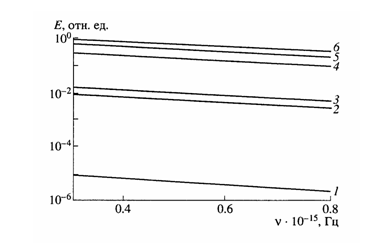
Рис.5. Частотные спектры электромагнитных импульсов (спектральные плотности энергии) под углами наблюдения 1-
,2- 
, 3- 
, 4- 
, 5- 
, 6- 
, в дальней зоне (
) в диапазоне частот (
) Гц при 
Видно, что при небольшом (около одного градуса) отклонении угла наблюдения от угла 
спектральная плотность электромагнитной энергии в дальней зоне 
падает на порядки. Таким образом, под углом 
наиболее вероятна регистрация светового излучения.
Расчеты были проведены при различных соотношениях 
и 
и было выявлено, что с приближением 
к 
угловое распределение интенсивности излучения расплывается.
Отметим, что к аналогичным результатам можно прийти при рассмотрении полей импульсов тока, перемещающихся со скоростями большими скорости света в среде без дисперсии. Все результаты остаются справедливыми с точностью до замены скорости света в вакууме на скорость распространения света в среде.
Рассмотренные нами примеры являются частными случаями решение задачи возбуждения электромагнитных волн импульсом линейного тока, в общем виде рассмотренного в главе 3.
Можно сделать следующие выводы для излучения сверхсветовых источников, получаемых в результате моделирования прохождения гамма излучения через вещество: излучение при 
сосредоточено в кольце; при 
близком к 
излучение сосредоточено внутри кольца; при 
излучение распространяется во все стороны равномерно.
В 4.2 рассмотрены условия, которым должны удовлетворять параметры пространственно-временного распределения гамма излучения, которые необходимы для обеспечения формирования направленных электромагнитных волн.
Несмотря на то, что электродинамические расчеты, в которых рассматриваются локализованные электромагнитные волны, проведены в большом числе работ, вопрос о формировании источников этих волн недостаточно изучен. Для изучения возможности формирования источников направленных электромагнитных волн, было выполнено численное моделирование взаимодействия импульса гамма излучения с газовой средой согласно методу, описанному в главе 2.
В 4.2.1 приведены некоторые результаты численного моделирования источников направленных электромагнитных волн. При взаимодействии узконаправленного гамма излучения с воздухом формируется импульс тока, перемещающийся со скоростью света. Как было установлено в гл.2 при давлениях газа от 0.1 атм. до 10 атм. и энергиях гамма квантов от 50 кэВ до 40 МэВ из-за существенного различия в длинах свободного пробега гамма–квантов и электронов выполняется необходимое условия применимости модели линейного тока. Тем самым выполнено условие существования одного из вариантов источника направленных (локализованных) электромагнитных волн – импульс тока, перемещающийся со скоростью равной скорости света по отрезку прямой.
Отметим важную особенность этого источника. С увеличением давления импульс тока становится короче, так как происходит сжатие пространственного распределения свободных электронов из-за уменьшения их длины свободного пробега, и его можно приближенно рассматривать как точечный источник.
Таким образом, оказывается возможным создавать источники электродинамической задачи, приводящие к направленным волнам (упрощенные источники – токи, распределенные на плоскости, перемещающейся со скоростью света: точка, гауссово распределение, круговой контур, диск), т.к. вектор плотности тока, создаваемый источником жесткого излучения с бесконечно малой длительностью, ограничен в пространстве и времени. Отметим, что использование метода имитационного моделирования позволило получить токовые распределение на плоскости, перемещающейся со скоростью света, которые должны приводить к направленным (локализованным) электромагнитным волнам.
Газовая среда изотропна в пространстве, поэтому разработанный метод получения токовых распределений может быть распространен на широкий интервал значений давлений газовой среды и энергий гамма квантов.
В 4.2.2 рассмотрены особенности поля источника излучения, перемещающегося по отрезку прямой со скоростью света [5].
Проведены расчеты временных зависимостей 
компоненты вектора магнитной индукции, формируемых линейными источниками с использованием коэффициентов аппроксимации формы импульса тока, перемещающегося со скоростью равной скорости света в вакууме из главы 2. Показано, что основные закономерности во временных зависимостях (двуполярность, увеличение длительности при увеличении угла наблюдения.) сохраняются при всех полученных в результате моделирования формах импульсов тока (изменение давления воздуха в пределах от 0.1 атм. до 10 атм. и изменениях энергии гамма квантов от
50 кэВ - до 40 МэВ).
В 4.3 представлены модели, описывающие подпороговое излучение в газовой среде, основанные на предположении возможности формирования импульса с заполнением и без заполнения в результате взаимодействия жесткого излучения с веществом [12, 13, 14].
В первой модели для описания подпорогового излучения предполагается, что поглощение энергии излучения веществом сопровождается возбуждением элементарных осцилляторов, распределенных на линии. Далее процесс вынужденного излучения атомов среды приводит к формированию импульса макроскопического тока (импульса поляризации), возбуждающего когерентное излучение. Задача возбуждения волн сводится к электродинамической задаче, где источник - импульс тока с заполнением, стартующий в фиксированный момент времени и движущийся вдоль прямой линии с постоянной скоростью Множитель распределения полного тока
, где 
, 
- частота колебаний осцилляторов, 
- амплитудный множитель, медленно меняющаяся функция, 
- фаза макроскопического тока.
Исходя из полученных в 4.3 соотношений, рассмотрим распределение интенсивности возбуждаемых волн вне области излучателя 
. Предполагая, что 
(дальняя зона) и 
, находим интенсивность
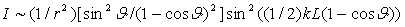
Здесь 
,
- полярный угол сферической системы координат, 
,
- частота колебания осцилляторов.
В полученном соотношении множитель 
стремится к бесконечности, когда угол 
, отсчитываемый от направления перемещения импульса жесткого излучения, стремится к нулю, что определяет направленность возбуждаемых волн вперед.
Множитель 
, зависящий от протяженности излучателя и длины волны колебаний осциллятора, определяет интерференционную картину, и если 
много больше 
то получается многолепестковая структура распределения интенсивности. При 
= 0 интенсивность 
= 0.
Медленно меняющаяся амплитуда возбуждаемых волн зависит от времени жизни осцилляторов и длительности импульса излучения. Отметим, что в обсуждаемой модели направленность волн связана с перемещением импульса жесткого излучения со скоростью света, что приводит к частично согласованному включению осцилляторов.
Во второй модели импульс тока без заполнения формируется электронами, возникающими в результате процессов взаимодействия импульса ионизирующего излучения со средой. Рассмотрение электромагнитных волн в рамках второй модели (импульсом тока без заполнения) проведено в 4.1.2.
Исходя из полученных соотношений получено распределение интенсивности возбуждаемых волн вне области излучателя при 
(дальняя зона):
Таким образом, в главе 4 на основе модели линейного тока:
показано, что в зависимости от параметров среды и параметров излучения наблюдается сходство получаемых пространственно-временных распределений вторичного электромагнитного излучения с распределениями тормозного (при 
) и черенковского излучения (при 
).
доказано, что излучение сверхсветового источника при 
сосредоточено в кольце (конусе), при 
близком к 
оно сосредоточено внутри конуса, а при 
излучение распространяется во все стороны практически изотропно.
предложено описание подпорогового излучения, сопровождающего прохождение гамма квантов в газовой среде.
установлены параметры пространственно-временного распределения гамма излучения, обеспечивающие формирование направленных электромагнитных волн близких к локализованным волнам. Выполнен расчет магнитной составляющей поля для точки наблюдения вблизи излучателя и в дальней зоне. Расчет проведен для гамма квантов с энергиями от 50 кэВ до 40 МэВ в диапазона давлений воздуха от 0.1 атм до 10 атм.
В пятой главе обсуждаются результаты моделирования и экспериментального изучения сконструированных детекторов на МКП для проведения экспериментов в различных областях физики высоких энергий и ядерной физики.
МКП широко используются для детектирования различных сортов частиц благодаря их высокой скорости счета, низкого уровня шума, высокой радиационной стойкости, малого количества вещества на пути частиц, способности работать в магнитных полях, возможности применения в позиционно-чувствительных детекторах. С использованием результатов моделирования, созданы различные детекторы на базе МКП.
Подраздел 5.1 посвящен моделированию импульса тока в канале МКП при прохождении через нее ионизирующей частицы с использованием методики, рассмотренной в главе 2 [15, 16]. Такое моделирование работы канала МКП необходимо для оптимизации временной и амплитудной характеристик детектора. Используемые для этого последовательные алгоритмы требуют больших затрат времени, т.к. необходимо рассчитывать траектории и энергии большого числа частиц. Поэтому работа проведена с использованием параллельного алгоритма моделирования развития электронной лавины.
Пункт 5.2 посвящен рассмотрению свойств созданных детекторов. В 5.2.1 рассмотрен позиционно-чувствительных детектор (ПЧД) на МКП для измерения слабоинтенсивных конверсионных электронов. Было изготовлено несколько детекторов на МКП с различными системами съема информации для призменного магнитного спектрометра [17, 18]. Применение линией задержки в качестве анода ПЧД на МКП позволило уменьшить число электронных блоков. Полученная разрешающая способность по координате равнялась 200 мкм. Разработанные ПЧД на МКП позволяют уменьшать время проведения экспериментов на бета – спектрометрах на порядок.
Пункт 5.2.2 посвящен изучению возможности использования ПЧД на МКП в качестве вершинного и стартового детектора для изучения редких процессов в реакциях с пионами и протонами высоких энергий [19]. Для экспериментальных исследований редких процессов требуются специальные детекторы, работающие в интенсивных пучках и обеспечивающие эффективную регистрацию частиц в широкой области углов и временную отметку о прохождении частицы. При проведении таких исследований был предложен ПЧД, использующий МКП и высокочастотную линию задержки в качестве анода. Детектор способен определять временную и пространственные координаты с высокой точностью [20, 21, 22, 23]. Так как эффективность регистрации пионов и протонов высоких энергий детекторами на МКП была изучена недостаточно, этот вопрос исследован более детально. Полученный индуцированный стартовый сигнал от стрипов, расположенных под линией задержки, позволил измерить вторую координату. Измерения пространственного разрешения вдоль одной из осей сделаны с помощью специальной маски. Получено пространственное разрешение 150 мкм. Созданный детектор позволил определять временную и две пространственные координаты пересечения заряженной частицей фронтальной плоскости МКП
В 5.2.3 рассмотрен низкофоновый детектор на МКП для системы “Ion Guide” [24]. В настоящее время резонансная лазерная ионизация является одним из наиболее чувствительных методов детектирования и изучения одиночных атомов. Таким образом, появляется дополнительная возможность исследования оптическими методами ядер, имеющих малые сечения образования в ядерных реакциях, а также для работы с образцами, содержащими малое число исследуемых атомов. Информация при этом извлекается из сверхтонкой структуры и изотопических сдвигов атомных спектров радионуклидов.
Регистратором ионов являлся низкофоновый детектор на МКП [25]. Тестирование подтвердило возможность использования детекторов с МКП в установке для детектирования низкоэнергетических ионов.
В 5.2.4 рассмотрена система, позволяющая бесконтактно определять положение пучка заряженных частиц, используя остаточный газ внутри ионопровода. Координата определяется с помощью линии задержки, расположенной под сборкой МКП [26].
В 5.2.5 рассмотрен детектор множественности. Интерес к детекторам множественности на основе МКП обусловлен задачами, возникшими в последние годы в физике высоких энергий на ускорителях со встречными пучками [27, 28].
Первый способ определения множественности рождающихся частиц основан на регистрации частиц с помощью линии задержки [29], второй на восстановлении ее из величины зарегистрированного заряда [30]. В 5.2.5 проведена оценка погрешности восстановления множественности при использовании МКП детектора и изучены свойства быстрого детектора множественности. Для съема сигнала с индивидуальных пикселей использован пассивный сумматор.
В результате проведенных исследований была доказана возможность применения МКП детекторов в качестве детектора множественности методами имитационного и физического моделирования и тестированием в экспериментах на пучках [31, 32, 33, 34]. В [35, 36, 37] приведены патентные документы, полученные по результатам работ.
Основные результаты работы
1. Предложен алгоритм, использующий квантовый и классический электродинамические подходы, для расчета токов и электромагнитных полей, формируемых при взаимодействии узконаправленного импульса излучения с веществом. Описание пространственно-временного распределения заряженных частиц выполнено с использованием сечений взаимодействий, рассчитанных в квантово- электродинамическом подходе, а расчет полей, создаваемых этим током, проводился методами классической электродинамики.
2. Для расчета стороннего источника электродинамической задачи разработана методика имитационного моделирования, которая позволила получить пространственно-временные распределения электронов и обосновать применимость модели линейного тока. Исследование распределений заряженных частиц проводилось с использованием выражений для сечений взаимодействий, полученных методами квантовой электродинамики, включенных в пакет имитационного моделирования. Методика использована для расчета форм импульсов тока, возникающих при взаимодействии импульсов гамма излучения (с энергией от 50 кэВ до 40 МэВ) с воздушной средой в диапазоне давлений от 0.1 атм. до 10 атм. Получены функции, аппроксимирующие формы тока.
3. Для расчета полей импульсов тока, перемещающихся по прямой как со скоростями большими скорости света в вакууме, так и со скоростями меньшими скорости света, разработана методика вычисления запаздывающего потенциала, основанная на анализе систем нелинейных неравенств. Найдено в явном виде решение начальной задачи формирования электромагнитных волн импульсом линейного тока произвольной формы и длительности, движущимся со скоростью большей скорости света в вакууме по отрезку прямой. В общем виде решение представляется как сумма двадцати слагаемых. В зависимости от отношений длительности импульса тока к длине отрезка прямой, времени и координат точки наблюдения вклад в потенциал вносят не более трех слагаемых. Установлена и объяснена близость форм запаздывающего потенциала и формы импульса тока при скорости 
большей скорости света 
под углом равным 
.
4. Предложен способ формирования источников, перемещающихся со скоростью больше скорости света, и рассчитаны для них запаздывающие потенциалы. Для прямоугольных и гауссовых форм импульсов тока, а также для форм, рассчитанных в результате моделирования, получены следующие результаты:
при равенстве длительности импульса тока (в единицах ct) и длины отрезка прямой, по которой он перемещается, – распространение излучения почти изотропно;
когда длина отрезка прямой много больше длительности импульса тока, то в дальней зоне формируется кольцевое распределение интенсивности излучения на плоскости, перпендикулярной перемещению тока;
в промежуточном случае наблюдается размытое кольцевое распределение на плоскости, перпендикулярной перемещению тока. Основные особенности поля, формируемого при перемещении заряженной частицы в воздушной среде со скоростью большей скорости света в среде и поля, создаваемого импульсом тока, перемещающимся со сверхсветовой скоростью в вакууме, совпадают.
5. Методом имитационного моделирования взаимодействия импульса жесткого излучения с веществом обоснована принципиальная возможность физической реализации источников локализованных волн. Для этого проведен выбор параметров пространственно-временного распределения первичного пучка гамма квантов, обеспечивающий формирование направленных электромагнитных волн. Волны близкие к локализованным формируются при взаимодействии узконаправленного пучка гамма квантов, одновременно входящих в однородную газовую среду. Выполнен расчет магнитной составляющей поля для точки наблюдения вблизи излучателя и в дальней зоне.
6. Предложено описание подпорогового излучения, возникающего при прохождении ионизирующего излучения через газовую среду. В основе описания лежит модель бегущего по линии импульса с заполнением и без заполнения со скоростью равной или меньшей скорости света. Подпороговое излучения в обоих случаях направлено в сторону перемещения ионизирующего излучения.
7. Методика имитационного моделирования стороннего источника позволила получить пространственно-временные токовые распределения в микроканале детектора с МКП. Последовательно с моделированием взаимодействия первичного ионизирующего излучения с МКП с помощью пакета GEANT использовалось моделирование развития лавины внутри микроканала. Формы и длительности импульсов тока, полученные в результате моделирования, совпали с эксперименально наблюдаемыми, что позволило оптимизировать конструкции детекторов заряженных частиц для проведения экспериментов в ядерной физике и физике высоких энергий. Разработаны и созданы позиционно-чувствительные и стартовые детекторы ионизирующих частиц на МКП. В результате экспериментального тестирования детекторов на микроканальных пластинах с различными системами съема информации показана возможность их применения в позиционо-чувствительных системах. Разработанные ПЧД на МКП позволяют уменьшать время проведения экспериментов на бета – спектрометрах на порядок. В результате физического моделирования и с помощью тестов на пучках минимально-ионизирующих частиц показана возможность применение детекторов на МКП в качестве детектора множественности для экспериментов в физике высоких энергий.
Основные результаты диссертации опубликованы в
следующих работах:
1. Ф.Ф.Валиев. Формирование стороннего источника электродинамической задачи при взаимодействии импульса жесткого излучения со средой // ЖТФ, 2001, т.71, вып.12, 92-94.
2. Ф.Ф.Валиев. О формировании источников направленного электромагнитного излучения, сопровождающего поглощение 
квантов // Изв.Акад.Наук. сер.физ. 2001, том 65, N.5, с. 630-633
3. F.F.Valiev. On the source formation of the directed electromagnetic radiation accompanying the gamma-quanta absorption // Proceedings of the international workshop “Physics of isomers”. 2001. p.17-21.
4. П.А.Болохов, Ф.Ф.Валиев, А.В.Ярмоленко Обоснование модели линейного тока при поглощении узконаправленного гамма-излучения. // Тезисы докладов 48 международного совещания по ядерной спектроскопии и структуре атомного ядра.1998. с.309.
5. В.В.Борисов, Ф.Ф.Валиев. Описание линейного тока в задаче формирования электромагнитных волн, сопровождающих поглощение узконаправленного импульса жесткого излучения // Вопросы Атомной науки и техники, сер. физ. 2002, вып. 1/2 c. 25-29
6. Ф.Ф.Валиев. Об аналоге излучения Вавилова-Черенкова, возникающем при движении макроскопического источника // Письма в ЖТФ. 2004. том 30. вып.6. с.62-66.
7. F.F.Valiev. Application of the retarded potential for the description of the electromagnetic field produced by current’s pulse, running along the line segment // Abstracts of the international conference “Days on diffraction 2009”. p.8
8. F.F.Valiev. On similarity between superluminal current pulse shape and time derivative of Whittaker potential // Proceedings of the international conference “Days on diffraction 2007”. 2007. p.149-150.
9. Ф.Ф.Валиев. Поле дельта импульса тока, перемещающегося со скоростью большей скорости света по отрезку прямой, в пространственно-ременном представлении // Тезисы докладов LIII международного совещания по ядерной спектроскопии и структуре атомного ядра. 2003. с.286.
10. Валиев Ф.Ф. Поле импульса тока, перемещающегося по отрезку прямой со сверхсветовой скоростью, в пространственно-временном и частотном представлениях // Изв.Акад.Наук. сер.физ. 2005, том 69, N.1, с. 156-159.
11. Валиев Ф.Ф. Особенности поля сверхсветового источника излучения, перемещающегося по отрезку прямой // Изв.Акад.Наук. сер.физ. 2005, том 69, N.5, с. 682-685
12. В.В.Борисов, Ф.Ф.Валиев. О возбуждении электромагнитных волн при поглощении узконаправленного жесткого излучения // В сб. : Точные измерения в ядерной спектроскопии. 1996. с.46-48
13. В.В.Борисов, Ф.Ф.Валиев, И.И.Симоненко. Формирование электромагнитных волн узконаправленными 
квантами и частицами высокой энергии // Изв.Акад.Наук. сер.физ. 2000, том 64, N.1, с. 186-189
14. Ф.Ф.Валиев. Допороговое излучение, индуцированное электронами при ионизации газовой среды // Тезисы докладов 59 совещания по ядерной спектроскопии и структуре атомного ядра.2009. Санкт-Петербург. с.317.
15. П.А.Болохов, Ф.Ф.Валиев, О.И.Столяров, А.В.Ярмоленко, С.В.Корж. Модельная форма импульса тока с детектора на МКП // Тезисы докладов 3-го Совещания по вторичному электронному излучению. Санкт-Петербург. Радиевый институт. 1998. с.9.
16. F.F.Valiev, K.V.Zuev, S.A.Nemnugin. Parallel computing in modeling of microchannel plates // Workshop on computing in modeling of microchannel plates. 2003. St.Petersburg. p. 37-38
17. Ф.Ф.Валиев, В.О.Сергеев. Эффективность регистрации электронов микроканальными пластинами в магнитном спектрометре // Тезисы докладов 34 совещания по ядерной спектроскопии и структуре атомного ядра. 1984. Л: Наука. с.516.
18. Ф.Ф.Валиев, и др. Позиционно-чувствительный детектор на микроканальных пластинах с различными системами съема информации // Тезисы докладов 42 совещания по ядерной спектроскопии и структуре атомного ядра. 1992. Л: Наука. с.388.
19. V.A.Krasnov,.., F.F.Valiev et al. Rare pion-nucleon, pion-nuleus, and photonuclear reactions // Programm of physical studies at the AMPIR spectrometer// FUB-HEP//90-21.
20. F.F.Valiev, G.A.Feofilov, A.P.Tsvinev Y.K.Gavrilov, A.A.Baldin, et al. Microchannel plates as a detector for 800 MeV/c charged pions and protons // JINR Rapid Communications. 1991. No 4/50/-91. p.27-36.
21. A.A.Baldin, G.A.Feofilov, Y.K.Gavrilov, A.P.Tsvinev, F.F.Valiev. Proposals for a new type of microchannel-plate-based vertex detector //
Nuclear Instr. And Methods in Phys.Research. A323. 1992. p. 439-444.
22. A.A.Baldin, L.G.Efimov, G.A.Feofilov,S.N.Filippov, V.S.Pantuev, F.F.Valiev. Some results of MCP timing resolution measurements with minimum ionizing particles // Краткие сообщения ОИЯИ. 1994. No.2[65]-94.c.33-39.
23. G.A.Feofilov, O.I.Stolyarov, F.A.Tsimbal, F.F.Valiev, L.I.Vinogradov. Position-sensitive MCP-based detectors with high timing resolution: some results and perspectives // Nuclear Instr. And Methods in Phys.Research A367. 1995. p. 402-407.
24. Ю.П.Гангрский,.., Ф.Ф.Валиев и др. Ion-guide-источник для лазерного спектрометра // Изв. АН СССР сер.физ. т. 60 N 5, с. 182-188.
25. Ю.П.Гангрский,.., Ф.Ф.Валиев и др. Лазерный спектрометр с резонансной ионизацией // Тезисы докладов 46 международного совещания по ядерной спектроскопии и структуре атомного ядра. 1996, Санкт-Петербрг. с.349.
26. Ф.Ф.Валиев и др. Координатно-чувствительный детектор для диагностики пучков // Тезисы докладов 48 международного совещания по ядерной спектроскопии и структуре атомного ядра. 1998. Л: Наука. с.306.
27. N.Antoniou,.., F.F.Valiev et al. Letter of Intent for a large ion collide experiment // CERN/LHCC/93-16. LHCC/14 1993
28. A.E. Antropov,.., F.F.Valiev et al. FMD-MCP forward multiplicity detector based on microchannel plates //Preliminary technical design report. 1999. StPetersburg. p.137.
29. Ф.Ф.Валиев и др. Детектор малой множественности на МКП с линией задержки // Тезисы докладов 48 совещания по ядерной спектроскопии и структуре атомного ядра. 1998. Л: Наука. с.307.
30. T.M.Avdeeva,.., F.F.Valiev at all. Determination of charged particles multiplicity with microchannel plate detector // Тезисы докладов 46 межд. совещ. по физике атомного ядра.1996. Санкт-Петербург. с. 368.
31. A.A.Baldin,.., F.F.Valiev et al. Concept of the MCP-based Forward Multiplicity Detector for Alice at LHC //ALICE/94-12 Internal Note/FMD. 1994
32. A.E Antropov,.., F.F.Valiev at al. Fast microchannel plate detector. //
Nuclear Physics В (Ргос. Suppl.) 1999. 78 p.416-421
33. Ф.Ф.Валиев и др. Физическое моделирование детектора множественности // Тезисы докладов 51 совещания по ядерной спектроскопии и структуре атомного ядра. М: Наука 2001г. с. 238
34. A.E. Antropov,.., F.F.Valiev at al. Sector multipad prototype of the FMD-MCP detector for ALICE // Nucl.Instrum.Meth. 1998. A419. p. 654-659
35. Ф.Ф.Валиев, Г.А.Феофилов. Устройство для регистрации заряженных частиц // Патент РФ N2045078. 1991. кл. GOST 1/28, 19.06.1991.
36. О.И. Столяров, Г.А.Феофилов, Ф.Ф.Валиев и др. Устройство для регистрации заряженных частиц // Патент РФ N2152057. 1999. кл. GOST 1/17, 05.01.1999.
37. О.И. Столяров, Ф.Ф.Валиев, Г.В.Мышинский и др. Детектор 
–излучения (варианты) // Патент РФ N2370789. 2009. кл. GOST 1/28, 20.10.2009
Список цитируемой литературы.
1
. O. Heaviside. Electromagnetic theory. N.Y.Dover Publications, INS, 1950, p.386 (chapter 9)
2
. A.Sommerfeld. Zur Elektronentheorie // Nachr.Akad.Wiss.Goetingen. Math.Phys.K1.99. 1904. p. 99-439
3
. Гинзбург В.Л. Теоретическая физика и астрофизика. М.: Наука, 1981. с. 506.
4
. Б.М.Болотовский, А.В. Серов. Излучение сверхсветовых источников в вакууме // УФН. 2005. Т.175. N9. с. 943-955
5
. Ю.Н. Лазарев, П.В. Петров, Ю.Г. Сырцова. Фотоэмиссионный импульсный источник широкополосного направленного электромагнитного излучения // ЖТФ. 2004. т. 74, вып. 11. с. 92-94
6
. G.S.Smith, Cherenkov radiation from a charge of finite size or charges // Amer.J.Phys. 1993, v. 61(2), p.147-155
7
. V.V.Borisov. On transient waves in dispersive media produced by moving point sources // J.Phys.A:Math.Gen. 2002. v.35 p.5403-5409
8
. G.NAfanasiev, Kh.Beshtoev and Yu.P.Stepanovsky. Vavilov-Cherenkov radiation in a finite region of space // Helv.Phys.Acta, 69, p.11-129
9
. Г.Бейтмен. Математическая теория распространения электромагнитных волн. 1958. М., 180 c.
10
. N.Brittingam. Focus wave modes in homogeneous Maxwell’s equations: transverse electric mode // J. Appl. Phys. 1983. v.54. p. 1179-1189
11
. A. Sezginer. A general formulation of focus wave modes // J.Appl.Phys. 1985. v. 57. p. 678-683
12
. P.L. Overfelt. Bessel-Gauss pulses. Phys.Rev. A. 1991.v. 44(6). p. 3941-3947
13
. V.V. Borisov, A.B. Utkin. Electromagnetic fields produced by the spike pulse of hard radiation // J.Phys.A: Math.Gen. 1993. v.26. p. 4081- 4085.
14
. V.V.Borisov, I.I.Simonenko. Transient waves generated by a source on a circle // J.Phys.A:Math.Gen.1994. v.27. p. 6243-6252
15
. П.А.Черенков. Видимое свечение чистых жидкостей под действием 
- радиации // ДАН СССР. 1934. т.2. N 8. c. 451- 454.
16
. Aitken D.K. et al. Transition Radiation in Cerenkov Detectors // Proc. Phys.Soc., 1963 v.82, p.710-722.
17
. J.Ruzicka, V.P.Zrelov. Optical transition radiation in a transparent medium and its relation to the Vavilov-Cherenkov radiation // Czechosl. J. of Phys., 1993, v.43, p.551-567.
18
. Bodek A. et al. Observation of Light Below Cerenkov Threshold
in a 1.5 Meter Long Integrating Cerenkov Counter // Z. Phys.C-Particles and Fields, 1983, v. 18, p. 289-299.
19
. А.П.Кобзев, И.М.Франк. Некоторые особенности излучения Вавилова-Черенкова, связанные с конечной толщиной // Ядерная физика. 1981, т.34, с.125-133.
20
. V.P. Zrelov, J.Ruzicka. Analysis of Tamm’s problem on charge radiation at its uniform motion over a finite trajectory // Czech.J.Phys. B39. 1989. p. 368-383.
21
. А.А.Тяпкин Микроскопическая природа излучения, лежащего в основе эффекта Вавилова-Черенкова // ФЭЧАЯ 2001. т.2001. т.32. вып.4.
22
. W.J. Karzas, R Latter. Electromagnetic radiation from a nuclear explosion in space // Phys.Rev. 1962. 126 (6). p.1919-1926.
