WWW.DISUS.RU

БЕСПЛАТНАЯ НАУЧНАЯ ЭЛЕКТРОННАЯ БИБЛИОТЕКА
 
<< ГЛАВНАЯ [ АГРОИНЖЕНЕРИЯ ] [ АСТРОНОМИЯ ] [ БЕЗОПАСНОСТЬ ] [ БИОЛОГИЯ ] [ ЗЕМЛЯ ] [ ИНФОРМАТИКА ] [ ИСКУССТВОВЕДЕНИЕ ] [ ИСТОРИЯ ] [ КУЛЬТУРОЛОГИЯ ] [ МАШИНОСТРОЕНИЕ ] [ МЕДИЦИНА ] [ МЕТАЛЛУРГИЯ ] [ МЕХАНИКА ] [ ПЕДАГОГИКА ] [ ПОЛИТИКА ] [ ПРИБОРОСТРОЕНИЕ ] [ ПРОДОВОЛЬСТВИЕ ] [ ПСИХОЛОГИЯ ] [ РАДИОТЕХНИКА ] [ СЕЛЬСКОЕ ХОЗЯЙСТВО ] [ СОЦИОЛОГИЯ ] [ СТРОИТЕЛЬСТВО ] [ ТЕХНИЧЕСКИЕ НАУКИ ] [ ТРАНСПОРТ ] [ ФАРМАЦЕВТИКА ] [ ФИЗИКА ] [ ФИЗИОЛОГИЯ ] [ ФИЛОЛОГИЯ ] [ ФИЛОСОФИЯ ] [ ХИМИЯ ] [ ЭКОНОМИКА ] [ ЭЛЕКТРОТЕХНИКА ] [ ЭНЕРГЕТИКА ] [ ЮРИСПРУДЕНЦИЯ ] [ ЯЗЫКОЗНАНИЕ ] [ РАЗНОЕ ] КОНТАКТЫ
Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.

Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.

Авторефераты диссертаций  >>  Авторефераты по Физике

Генерация ультракоротких импульсов света в резонансных средах и волоконных световодах

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ

На правах рукописи

Козлов Виктор Викторович

Генерация ультракоротких импульсов света в резонансных средах и

волоконных световодах

Специальность 01.04.05 - оптика

АВТОРЕФЕРАТ

диссертации на соискание ученой степени

доктора физико-математических наук

Санкт-Петербург

2008

Работа выполнена на 1 кафедре общей физики Санкт-Петербургского

государственного университета

Научный консультант: доктор физико-математических наук, профессор

Фрадкин Эвальд Евсеевич

Официальные оппоненты: доктор физико-математических наук, профессор

Маймистов Андрей Иванович

доктор физико-математических наук, профессор

Розанов Николай Николаевич

доктор физико-математических наук, профессор

Тулуб Александр Владимирович

Ведущая организация: Санкт-Петербургский государственный технический

университет

Защита состоится «____» _________2009 г. в ___ч _______мин в ауд. ______ на заседании совета Д 212.232.45 по защите докторских и кандидатских диссертаций при Санкт-Петербургском государственном университете по адресу: 199034, Санкт-Петербург, Университетская наб., д. 7/9, СПбГУ

С диссертацией можно ознакомиться в научной библиотеке им. М.Горького СПбГУ

Автореферат разослан «_____» ______________ 2008 г.

Ученый секретарь совета Д 212.232.45

по защите докторских и кандидатских диссертаций

доктор физ.-мат. наук Ионих Ю.З.

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Объект исследования и актуальность темы. Теория электромагнетизма, обобщенная Максвеллом, в совокупности с квантовой теорией строения атомов и молекул определяет прогресс и наше современное понимание оптики и развитие такого важного практического приложения как лазерная физика [1-4]. Квантовые эффекты особенно важны, когда частота электромагнитного поля настроена вблизи резонанса с атомным переходом или вращательным или колебательным переходом в молекуле. Даже в том случае, когда поле отстроено далеко от резонанса, и во многих случаях адекватно представление об атомах или молекулах как о простых классических линейных или нелинейных осцилляторах, тем не менее мы подразумеваем, что в основе этого упрощенного описания лежит микроскопическая теория квантованных уровней. Именно квантовая теория атомов и молекул во многом определила успех развития лазерной физики, и именно она используется в качестве основного инструмента при моделировании процессов генерации когерентных импульсов света в поглощающих и усиливающих резонансных средах [5-8]. С другой стороны, для описания подавляющего большинства экспериментальных ситуаций нет необходимости использовать квантовую теорию света и можно ограничиться классическим пределом электромагнитной волны. Такое сочетание квантового описания среды и классического описания света является каноническим подходом в оптике и лазерной физике и получило название полуклассической теории. Этому походу мы следуем во всех пяти главах настоящей диссертационной работы и докладываем о новых методах генерации оптических импульсов в средах, проявляющих когерентный отклик на приложенное поле.

Практически во всех предлагаемых моделях генерации, кроме модели суперфлюоресценции в когерентной трехуровневой среде и синхронизации мод с трехуровневым поглотителем, используются солитонные эффекты, а именно рассматриваются солитоны самоиндуцированной прозрачности и солитоны нелинейного уравнения Шредингера [4]. Этот предпочтительный выбор обязан роли солитонов в развитии высокоскоростных телекоммуникаций.

Цели и задачи работы. Целью диссертационной работы является разработка новых методов генерации ультракоротких импульсов света с заданными свойствами.

В соответствии с этой целью были поставлены и решены следующие задачи:

  • Разработка аналитических и численных методов описания импульсного комбинационного (рамановского) рассеяния в трехуровневой среде с V-конфигурацией уровней. Применение этих методов для исследования эффективности комбинационного рассеяния при возбуждении среды 2p-солитоном самоиндуцированной прозрачности (СИП), а также солитонами высшего порядка. Исследование эффективности комбинационного усиления слабого пробного импульса в среде с неоднородным уширением уровней и в частности в плазме положительного столба тлеющего разряда в неоне.
  • Разработка аналитических и численных методов описания эффекта суперфлюоресценции (СФ) в трехуровневой среде с V-конфигурацией уровней, накачиваемых сильным когерентным полем на одном из переходов. Применение этих методов к исследованию эффективности генерации импульсов СФ и нахождению зависимости параметров импульса от условий возбуждения.
  • Разработка аналитических и численных методов описания взаимодействия пробного импульса с трехуровневой средой V-конфигурации, накачиваемой сильным когерентным лазерным полем. Применение этих методов к исследованию обнаруженного двухфотонного эффекта СИП и к модели активной синхронизации мод с трехуровневым когерентным усилителем.
  • Разработка аналитических и численных методов описания взаимодействия короткого импульса излучения с двухуровневыми когерентными поглотителем и усилителем. Применение этих методов к созданию модели солитонного лазера на основе эффекта СИП. Исследование устойчивости солитонного режима генерации и переходной динамики к стационарному режиму, стартуя из затравочного импульса малой амплитуды.
  • Разработка аналитических методов описания твердотельного лазера с когерентным неоднородноуширенным поглотителем. Применение этих методов к созданию твердотельного солитонного лазера на основе эффекта СИП и исследование устойчивости солитонного режима генерации.

Научная новизна работы и положения, выносимые на защиту.



  1. Предложена аналитическая и численная модель резонансного комбинационного усиления ультракоротких импульсов света в среде с V-конфигурацией уровней, накачиваемой фундаментальным солитоном СИП или солитонами высшего порядка на смежном переходе. Показано, что возможна 100%-ая конверсия энергии солитона накачки в пробный импульс, который асимптотически преобразуется в солитон СИП. Обнаружен эффект "захвата" пробного импульса, выражающийся в том, что пробный импульс захватывается импульсом накачки, так что оба импульса распространяются с одинаковыми групповыми скоростями.
  2. Продемонстрировано, что двухфотонный эффект Допплера и релаксация фазовой памяти среды делают процесс комбинационного усиления пороговым: ниже порога происходит поглощение пробного поля, выше порога - его усиление. В условиях двухфотонного резонанса и присутствии однофотонного эффекта Допплера захват импульса сопровождается инициированием эффекта солитонно-индуцированной прозрачности. Механизм прозрачности объясняется фазировкой атомных диполей в поле накачки в форме солитона СИП.
  3. Разработаны аналитические и численные методы описания эффекта СФ в трехуровневой среде с V-конфигурацией уровней, накачиваемых сильным квазимонохроматическим когерентным полем на одном из переходов. Показана возможность генерации ультракоротких импульсов СФ в условиях комбинационного усиления. В среднем, то есть после усреднения по периоду Раби осцилляций, процесс характеризуется как СФ без инверсии населенностей.
  4. Разработаны аналитические и численные методы описания взаимодействия пробного импульса с трехуровневой средой V-конфигурации, накачиваемой сильным когерентным лазерным импульсом. Обнаружен двухфотонный эффект СИП.
  5. Развита модель лазера с активной синхронизацией мод с трехуровневым когерентным усилителем. Отличительной особенностью такого лазера является генерация импульсов, характеризующихся спектром шире линии усиления двухуровневого перехода в отсутствии накачки. Продемонстрированы режимы генерации без инверсии, с инверсией и режим рамановской генерации.
  6. Разработаны аналитические и численные методы описания взаимодействия короткого импульса излучения одновременно с двухуровневыми когерентными поглотителем и усилителем. Создана модель солитонного лазера на основе эффекта СИП. Исследована устойчивость солитонного режима генерации и переходная динамика к стационарному солитонному режиму, стартуя из затравочного импульса малой амплитуды. Солитонный режим характеризуется генерацией импульсов шире линии усиления.
  7. Разработаны аналитические методы описания твердотельного лазера с когерентным неоднородно-уширенным поглотителем. Создана модель твердотельного солитонного лазера на основе эффекта СИП и исследована устойчивость солитонного режима генерации. Продемонстрирована неустойчивость солитонов СИП по отношению к фазовой самомодуляции, наведенной эффектом Керра в волоконных световодах. Обнаружено, что выше определенного порога кубичной нелинейности, образование уединенных волн невозможно. Также продемонстрирована неустойчивость внутрирезонаторных солитонов СИП по отношению к возникновению непрерывного режима генерации за счет выжигания спектральных дыр в неоднородно-уширенном контуре поглощения.

Практическая ценность. Полученные в работе результаты могут быть использованы для создания новых лазерных устройств с улучшенными динамическими характеристиками, в частности, новых солитонных лазеров, высокоэффективных комбинационных усилителей и лазеров без инверсии. Эти лазеры оперируют в малоизученных режимах генерации импульсов со спектрами шире полосы усиления, и тем самым открывают новый диапазон в сторону укорочения длительностей. Режимы комбинационного усиления и генерации без инверсии могут применяться в тех областях длин волн, в которых создание инверсии населенностей затруднительно или невозможно.

Апробация работы. Полученные в работе результаты были представлены автором на следующих конференциях и семинарах:

  1. Seventh Rochester Conference on Coherence & Quantum Optics, Rochester, New York, U.S.A., June 07-10, 1995.
  2. IX International Symposium on Ultrashort Processes in Spectroscopy (UPS'95), Trieste, Italy, October 30 - November 3, 1995.
  3. 28th Winter Colloquium on the Physics of Quantum Electronics, Snowbird, Utah, U.S.A., January 4-7, 1998.
  4. International Quantum Electronics Conference (IQEC-98), San Francisco, California, U.S.A., May 3-8, 1998.
  5. XVI Международная Конференция по Когерентной и Нелинейной Оптике (КиНО-98), Москва, Россия, 29 июня - 3 июля, 1998.
  6. 1998 TAMU/ONR Summer Workshop on Quantum Optics, Jackson Hole, Wyoming, U.S.A., August 3-6, 1998.
  7. 2-nd Annual Cross Border Workshop on Laser Science, Ann Arbor, Michigan, May 18-20, 2000.
  8. First International Conference on Laser Optics for Young Scientists (LOYS'2000), St. Petersburg, Russia, June 26-30, 2000.
  9. International Symposium in Laser Physics, Novosibirsk, Russia, July 2-7, 2000.
  10. Kolloquium Schwerpunktprogramm Quanteninformationsverarbeitung, Huenfeld bei Fulda, Germany, January 17-18, 2001.
  11. Deutschen Physikalischen Geselshhschaft Spring Meeting, Berlin, Germany, April 02-06, 2001.
  12. Eighth Rochester Conference on Coherence \& Quantum Optics, Rochester, New York, U.S.A., June 13-16, 2001.
  13. XVII Международная Конференция по Когерентной и Нелинейной Оптике (КиНО-2001), Минск, Беларусь, 26 июня - 1 июля, 2001.
  14. OSA New Laser Scientists Conference (APS), Long Beach, California, U.S.A., October 13, 2001.
  15. OSA Annual Meeting and 17-th Interdisciplinary Laser Science Conference, Long Beach, California, U.S.A., October 14-18, 2001.
  16. Kolloquium des DFG-Schwerpunktprogramms Quanteninformationsverarbeitung, Bad Honnef, Germany, January 28-30, 2002.
  17. Deutschen Physikalischen Geselshhschaft Spring Meeting, Osnabrueck, Germany, March 04-08, 2002.
  18. NATO Advanced Study Institute, Quantum Communication and Information Technologies, Bilkent University, Ankara, Turkey, June 3-14, 2002.
  19. Humboldt Symposium, Moscow, Russia, September 27-29, 2002.
  20. Soliton Quanteninformation Workshop, Veilbronn, Germany, December 11-13, 2002.
  21. Deutschen Physikalischen Geselshhschaft Spring Meeting, Hannover, Germany, March 24-28, 2003.
  22. XIX Международная Конференция по Когерентной и Нелинейной Оптике (КиНО-2005), Санкт-Петербург, Россия, май 11-15, 2005.
  23. Princeton-TAMU BEC Symposium, Princeton, New Jersey, U.S.A., October 14-15, 2005.
  24. 36-th Winter Colloquium on the Physics of Quantum Electronics, Snowbird, Utah, U.S.A., January 2-6, 2006.
  25. Princeton-TAMU Molecular Physics Symposium, Princeton. New Jersey, U.S.A., May 18-19, 2006.
  26. Seminars on Quantum Optics at the Department of Physics of the Texas A&M University.
  27. Seminars on Quantum Optics at the Department of Physics and Astronomy of the University of Rochester, Rochester, U.S.A.
  28. Physics Colloquium at the University of Ulm, Ulm, Germany.
  29. Семинары квантовой оптики Санкт-Петербургского Педагогического государственного университета им. Герцена.

Публикации и личный вклад. По теме диссертации опубликовано 23 научных статей, приведенных в конце автореферата. В диссертацию включены данные самостоятельных исследований автора, из совместных работ - результаты, полученные при его непосредственном участии или под его научным руководством.

Структура и объем диссертации. Диссертация состоит из введения, 5 глав и заключения. Она изложена на 265 страницах, включая 46 рисунков, и список литературы из 167 наименований.

ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ

Во введении обоснована актуальность исследуемой проблемы, сформулирована цель и задачи диссертационной работы, перечислены полученные новые результаты, их практическая ценность, представлены положения, выносимые на защиту и описана структура диссертации.





В главе 1 рассмотрено резонансное комбинационное (рамановское [9-12]) рассеяние света в трехуровневой среде с V-конфигурацией уровней с нижним состоянием |b и возбужденными состояниями |aс и |cс. Переход |bс«|cс накачивается коротким импульсом с Раби частотой W. Пробный импульс с Раби частотой a приложен на переходе |bс«|aс. Полагаем, что несущие частоты импульсов настроены в точный резонанс с соответствующими переходами и импульсы нефазовомодулированы. Пренебрежем неоднородным уширением и предположим, что среда уширена однородно.

Перед приходом импульсов среда находится под действием некогерентной накачки, которая приготовляет требуемое распределение населенностей между уровнями: r0bb, r0aa и r0cc. Все недиагональные элементы матрицы плотности первоначально равны нулю, так что система не приготовлена в когерентном состоянии. Мы рассмотрим случай, когда первоначально в системе отсутствует инверсия населенностей на лазерном переходе: r0aa < r0bb. Если в дополнение присутствует инверсия на двухфотонном переходе (то есть, r0aa > r0cc), будем говорить, что система приготовлена в состоянии с рамановской инверсией. В противном случае, r0aa < r0cc, в системе отсутствует инверсия любого типа.

Для простоты аналитического анализа положим, что импульсы настолько коротки, что все некогерентные члены в уравнениях для матрицы плотности могут быть полностью исключены. Также предположим, что пробный импульс настолько слаб, что он не способен сколь-либо существенно возмутить состояние |aс, и тогда применимо линейное приближение по пробному полю a. В этом пределе пробный импульс не меняет атомных населенностей и его влияние на динамику импульса накачки пренебрежимо мало. Следовательно, динамика импульса накачки сводится к распространению импульса в резонансной двухуровневой среде. Уравнения для rcb, rcc и rbb расцепляются с остальными уравнениями матрицы плотности.

Важные выводы получаются, если вывести закон эволюции энергии Ja(z):

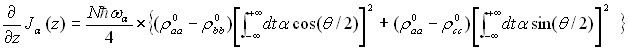(1)

где - частичная площадь импульса накачки.

Уравнение (1) представляет собой ключевой аналитический результат

1-ой главы. Оно описывает эволюцию энергии пробного импульса для импульсов произвольной формы и верен до тех пор, пока работает линейное приближение по a. Первый член в уравнении (1) пропорционален инверсии населенностей (r0aa) и, благодаря начальному предположению об отрицательности этой инверсии, соответствует однофотонному поглощению пробного поля на переходе |aс«|bс. Однако, это поглощение модифицируется присутствием импульса накачки, и может быть полностью скомпенсировано для определенной формы импульсов. Второй член пропорционален рамановской инверсии между двумя верхними cостояниями |aс и |cс,(r0aa -r0cc ), и, если эта инверсия положительна, то она ответственна за двухфотонное усиление пробного поля. Легко убедиться, что при любом z один из двух видов инверсии необходим для получения усиления на пробном переходе. Это рассмотрение доказывает, что в данной системе для ультракоротких импульсов линейное усиление без инверсии (r0aa< r0bb, r0cc) невозможно.

Показано, что если все атомы первоначально приготовлены в нижнем состоянии (r0aa=1) и рамановская инверсия равна нулю, то специальное согласование формы пробного импульса и импульса накачки ведет к полному отсутствию поглощения и искажений пробного импульса. Если такая пара импульсов запущена в среду, то они распространяются без изменения своей формы. Более того, показано, что если условие согласования формы импульсов не выполнено на входе в среду, то они быстро эволюционируют к согласованному состоянию после короткого переходного процесса. Присутствие в среде небольшой рамановской инверсии не приводит к нарушению формы обоих импульсов: временной масштаб переходного процесса значительно быстрее, чем процесс двухфотонного усиления.

С целью получения ясной картины динамики импульсов разделим эффекты

подавления линейного поглощения и двухфотонного рамановского усиления.

Сначала рассмотрим случай невозбужденной среды, (r0aa = r0cc = 0). Напомним, что любой импульс площадью большей p в резонансной двухуровневой среде после переходного процесса распадается на последовательность 2p-импульсов. В пренебрежении релаксацией каждый из 2p-импульсов распространяется через среду без поглощения и изменения формы. Для лучшего понимания динамики пробного импульса в накачиваемой среде выберем импульс накачки в простейшей форме -. в виде стационарного 2p-импульса МкКолла и Хана. Более сложная ситуация, когда начальная форма отличается от 2p-импульса, также рассмотрена, но уже исключительно численными методами.

Пробный импульс предполагается слабым в том смысле, что его площадь много меньше p. Известно, что в резонансной двухуровневой среде такой импульс приобретает осциллирующую форму и быстро «расползается». В трехуровневой системе в присутствии импульса накачки ситуация кардинально меняется. Численный анализ показывает, что импульс накачки, будучи запущенным в среду в виде 2p-импульса, вынуждает пробный импульс принять стационарную колоколообразную форму и при этом оба импульса распространяются с одной и той же групповой скоростью. Эффект «захвата импульса» имеет место независимо от начальной формы пробного импульса. В стационарном режиме эта форма может быть найдена аналитически. В принятом линейном приближении по a находим

a = a0cosh-e(u), (2)

где a0 -амплитуда пробного импульса. Параметр e, определяемый уравнением

e2 = (3)

должен быть действителен, иначе локализованного решения не существует.

Одновременное распространение импульсов оправдывает название «эффект захвата» импульса по отношению к пробному импульсу. Как отмечалось выше, если для пары импульсов импульс накачки имеет форму 2p-импульса, то начальный профиль пробного импульса несущественен: пробный импульс произвольного профиля эволюционирует к стационарной самосогласованной форме (2). Численный расчет демонстрирует, что «эффект захвата» остается в силе и в нелинейном режиме, когда пробный импульс становится мощным.

Теперь рассмотрим случай, когда в среде приготовлена рамановская инверсия: r0aa > r0cc. В соответствии с уравнением (1), энергия пробного импульса будет расти. Если рамановское усиление имеет небольшую величину, r0aa - r0cc † r0bb - r0aa, переходный процесс к самосогласованной форме можно отделить от процесса усиления. (Грубо оценивая временные масштабы, переходный процесс происходит в ((r0bb - r0aa )/( (r0aa - r0cc ) раз быстрее, чем процесс усиления.) Так, на первой стадии распространения пробного импульса, он эволюционирует к самосогласованной форме (2). Затем пробный импульс адиабатически усиливается, сохраняя свою форму.

Чтобы проследить эволюцию импульсов во всей полноте были проведены многочисленные численные расчеты. Их общей чертой оказалась полная 100%-ая конверсия фотонов импульса накачки в фотоны пробного поля. При этом пробное поле трансформируется так, чтобы на конечной (нелинейной) стадии процесса принять форму обычного 2p-импульса СИП.

При анализе физики двухфотонного усиления оказалось, что усиление пробного импульса возникает именно благодаря рамановской инверсии, а не за счет временных «окон инверсии», открываемых сильным импульсом накачки в те времена, когда он полностью опустошает нижний уровень. Достаточно немного отстроиться в сторону от точного резонанса, чтобы окна инверсии исчезли, а усиление, тем не менее, сохранилось.

До сих пор рассматривался случай, когда спектры импульсов намного превосходили ширины неоднородно-уширенных линий соответствующих переходов. Теперь предположим обратное соотношение ширин, то есть когда неоднородное уширение шире спектров импульсов. Напомним, что в отсутствие импульса накачки такая среда за счет расфазировки диполей является поглощающей даже для импульсов пробного поля короче времен всех диссипативных процессов. Контрастируя с этим наблюдением, в присутствии 2p-импульса накачки на смежном переходе возникает эффект прозрачности для пробного поля. Механизм прозрачности объясняется фазировкой атомных диполей в поле 2p-импульса накачки. Такой тип прозрачности назван солитонно-индуцированной прозрачностью (СОИП). Этот эффект демонстрируется для близко лежащих (или вырожденных по частоте) верхних уровней. Возбуждением атомов на верхний лазерный уровень можно перейти от эффекта прозрачности к генерации и получить усиление пробного поля, по аналогии со случаем, когда линия поглощения уширена однородно.

Другой аспект допплеровского уширения появляется при рассмотрении

конверсии вверх и вниз, когда частоты переходов для поля накачки и пробного импульса значительно различаются. При этом допплеровское уширение различно для двух переходов. Продемонстрировано, что двухфотонное допплеровское уширение (разность однофотонных допплеровских уширений) разрушает СОИП и делает комбинационное усиление пороговым эффектом: ниже определенного порога имеет место поглощение пробного поля, выше - усиление. Выше порога двухфотонное доплеровское уширение замедляет процесс конверсии по сравнению со случаем близколежащих уровней, хотя эффективность при этом по-прежнему остается равной 100%, то есть все фотоны накачки обмениваются на фотоны пробного поля, один к одному.

Также рассмотрено комбинационное усиление пробного импульса в реальной системе, отвечающей V-конфигурации уровней 2p6-1s5-2p4 в плазме положительного столба тлеющего разряда в неоне. Параметры импульсов заимствованы из эксперимента, поставленного на кафедре оптики НИИФ СПбГУ. Единственное отличие с экспериментальной ситуацией в том, что исследуется не пассивное совместное распространение импульса накачки и пробного импульса в поглощающей среде, а режим комбинационного усиления в условиях некогерентной накачки верхнего лазерного уровня. Основное внимание уделяется влиянию неидеальности граничных условий и процессов диссипации на эффективность комбинационного рассеяния. Так же как и в случае двухфотонного допплеровского уширения, конкуренция процесса комбинационного усиления и диссипации делает ВКР пороговым эффектом.

В главе 2 рассмотрена суперфлюоресценция (СФ) (сверхизлучение [13-18]) без инверсии в когерентно накачиваемой трехуровневой системе V-типа. Снова переход |bс«|cс когерентно накачивается сильным полем с Раби частотой W, но теперь это поле берется не в виде короткого импульса а, наоборот, в виде длинного импульса, а именно должен быть, по крайней мере, немного длиннее, чем время характерной эволюции импульса СФ. Пробный импульс a возникает на переходе |aс«|bс из затравочной флуктуации поляризации rab. Будем также полагать, что линии переходов уширены преимущественно однородно и неоднородным уширением можно пренебречь.

Предполагается, что NV трехуровневых атомов заключены в объем V,

имеющей форму цилиндра длины L и сечением S (L ‡ ЦS)

Будем рассматривать случай, когда первоначально отсутствует инверсия

населенностей на пробном переходе: r0aa >r0bb. Вместо однофотонной инверсии подготавливается двухфотонная (рамановская) инверсия: (r0aa > r0cc ).

Прежде чем перейти к численным расчетам, при достаточно общих предположениях получим аналитические результаты, находящиеся в хорошем согласии с численными решениями.

Существенное упрощение уравнений становится возможным в приближении a † W. В этом приближении доминирующим процессом становится процесс Раби осцилляций на переходе накачки с частотой 2W и осцилляциями с другими частотами можно пренебречь. Теперь задача становится похожей на выделение быстрой несущей частоты и медленной огибающей как и в методе медленно меняющихся фаз и амплитуд. Удерживая лишь главные гармоники, после ряда достаточно нетривиальных преобразований получим систему в форме уравнений Максвелла-Блоха для двухуровневой среды:

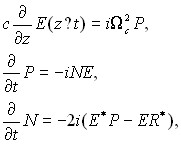(4)

где введены следующие определения инверсии, поляризации и поля:

; ; ,

выраженные в терминах амплитуд соответствующих гармоник в разложениях

(5)

(6)

(7)

[Интересно, что только одна (синусная) компонента поля усиливается, в то время как косинусная компонента поглощается.] В уравнение (4) введена кооперативная частота Wс. Самосогласованная система уравнений (4) - (6) представляет основной аналитический результат этой главы. Отсюда можно сделать вывод, что огибающая импульса СФ эволюционирует в трехуровневой среде, накачиваемой сильным когерентным непрерывным полем, как будто в двухуровневой среде с начальной разностью населенностей N0 = (r0aa - r0cc)/2.

Синусная компонента пробного поля испытывает усиление с инкрементом, пропорциональным рамановской инверсии населенностей, W2cN0, в отличие от двухуровневой системы, для которой инкремент зависит от разности населенностей между нижним и верхним состоянием.

Развитый двухуровневый формализм Максвелла-Блоха поясняет физику эффекта СФ в накачиваемых трехуровневых системах. В пределе сильного поля накачки природа СФ та же, что и в системах двухуровневой конфигурации.

Пользуясь приближением заданного поля на переходе когерентной накачки, система связанных уравнений для шести элементов матрицы плотности была редуцирована к двум уравнениям. Последние описывают взаимодействие поля с эффективной (псевдо) двухуровневой системой. Полученная таким образом двухуровневая система отражает не реальную экспериментальную ситуацию с неким двухуровневым переходом, а появляется как математический результат редукции исходных уравнений. С формальной точки зрения просто найден удобный базис, в котором сложная картина взаимодействия двух полей с двумя связанными оптическими переходами упрощается до взаимодействия одного пробного поля с одним оптическим переходом.

Редукция исходных уравнений для матрицы плотности трехуровневой системы к двухуровневой модели возможна благодаря разделению быстрых осцилляций атомных переменных с Раби частотой поля накачки и медленной эволюции под действием импульса СФ. Действительно, характерный импульс СФ представляется в виде огибающей, заполненной быстрыми синусоидальными осцилляциями.

Исследовалась физика СФ в когерентно накачиваемой трехуровневой системе. Раби осцилляции населенностей на смежном переходе периодически открывают на СФ переходе «окна» инверсии: : raa > rbb. Поляризация : rab на СФ переходе нарастает на временных интервалах, когда инверсия (r0aa - r0bb) достигает максимума, и стремится к нулю в минимуме (r0aa - r0bb). В среднем, то есть в результате интегрирования по периоду Раби осцилляций, населенности распределяются как (raa )av < (rcc )av Ј (rbb)av, то есть на СФ переходе отсутствует как обычная так и рамановская инверсия. Такое распределение населенностей характерно для лазеров без инверсии [19]. Поэтому, по аналогии, можно говорить об исследуемом эффекте как о «суперфлюоресценции без инверсии».

В главе 3 рассмотрена модель синхронизации мод в трехуровневых системах и сопутствующие эффекты, включая эффект двухфотонной СИП. Как и в предыдущих главах наиболее адекватным является формализм, основанный на решении уравнений Масвелла для двух электромагнитных полей совместно с системой уравнений для элементов матрицы плотности для трех атомных состояний. Однако в отличие от уже рассмотренных формализмов в этой главе ключевую роль играют константы распадов и их природа. Предполагается, что распад уровня |с> происходит много быстрее, чем |а>, и в этом приближении выведена эффективная двухуровневая система уравнений Блоха для пробного поля. Для длительностей импульсов в диапазоне gc-1<ta<ga-1 возможна дальнейшая модификация уравнений Блоха. В этом режиме обнаружена когерентная динамика поляризации, которая ведет себя в точности как в эффекте СИП. В заключении рассмотрена модель активной синхронизации мод, демонстрирующая возможность генерации импульсов много короче, чем в соответствующей двухуровневой модели и, более того, позволяющая поддерживать эту генерацию в отсутствии инверсии населенностей.

В диссертации подробно приведен вывод эффективной системы уравнений Максвелла-Блоха.

Строго говоря, предшествующий анализ предполагает пренебрежение членами порядка (gcta)-1 и выше. Здесь ta введена как характерная длительность пробного импульса. Поправка первого приближения по (gcta)-1 изменяет скорость, вызывая задержку (или ускорение) пробного импульса. Получена зависимость скорости от |W|2, что позволяет управлять задержкой пробного импульса посредством изменения интенсивности поля накачки.

Поправка второго порядка по (gcta)-1 приобретает особую важность для коротких импульсов. Она ответственна за меньшее поглощение (усиление) крыльев спектра импульса в поглотителе (усилителе). Этот эффект имеет решающее значение в режиме синхронизации мод, когда ширина линии усиления накладывает существенное ограничение на спектр генерируемого импульса. Здесь снова проявляется свойство, выходящее за рамки обычной двухуровневой системы, а именно возможность управления шириной лазерного перехода изменением интенсивности поля на смежном переходе. На этом пути открывается возможность генерировать импульсы в десятки раз короче обычного предела.

В диссертации подробно рассмотрено усиление короткого пробного импульса в условиях отсутствия инверсии на пробном переходе и рамановской инверсии, то есть в условиях усиления без инверсии. Сравнение численных расчетов на основе полной системы уравнений с одной стороны и аналитически выведенной редуцированной системы с другой стороны демонстрирует адекватность и точность редуцированной модели.

Наибольший интерес представляют когерентные поправки в выражении для поляризации. Действительно, в диссертации приведен пример, когда на переднем фронте пробного импульса поляризация развивает часть цикла, ответственную за поглощение, а на заднем фронте - ответственную за усиление. В целом импульс поглощается, так как поглощательная часть по площади больше. Заметим, что модель скоростных уравнений основана на адиабатическом слежении за пробным импульсом и предсказывает только

некогерентный «горб» поглощения. Дисперсионный вид кривой поляризации имеет когерентную природу, то есть является проявлением фазовой памяти среды. Подобная эволюция поляризации типична для эффекта СИП, с той разницей, что в эффекте СИП поглощательная часть кривой в точности скомпенсирована усилительной частью.

Показано, что пробный импульс возмущает состояние |bс много меньше, чем состояние |сс, то есть в динамике атомов доминирует двухфотонное взаимодействие, приводящее к когерентному обмену населенностей между верхними состояниями |aс и |сс, практически полностью минуя нижнее состояние. Возбуждение и опустошение верхних состояний управляется динамикой пробного импульса, в то время как приближение скоростных уравнений предполагает опустошение только через канал спонтанной эмиссии. Обменная динамика населенностей между верхними состояниями, минуя нижнее состояние, является когерентным эффектом, также характерным для эффекта СИП. По своим основным признакам, обсуждаемый эффект может быть классифицирован как двухфотонная СИП.

Далее рассмотрено действие лазера с синхронизацией мод простейшей конфигурации, когда активная трехуровневая среда и модулятор потерь помещается внутрь кольцевого резонатора. Цель состоит в получении устойчивой генерации последовательности коротких импульсов El(t) на лазерном переходе |aс « |bс. В отсутствии поля накачки Ec на смежном переходе, схема превращается в обычную двухуровневую лазерную конфигурацию, известную как активная синхронизация мод. Как и все применяемые на практике методы генерации ультракоротких импульсов активная синхронизация мод с необходимостью требует инверсии населенностей между лазерными уровнями |aс и |bс и безусловно ограничивает спектральную ширину генерируемого импульса шириной линии Gab лазерного перехода. Центральной темой раздела является отказ от обоих ограничений при «включении» поля накачки Eс. То есть предлагается метод, который не требует доминирующего заселения верхнего лазерного состояния и при этом генерируемые импульсы оказываются много короче установленных пределов.

Эффект Штарка составляет ключевую характеристику модели. Под действием сильного поля накачки нижний уровень расщепляется на две компоненты, отстоящие друг от друга на величину Раби частоты W=mWЕс /2. При этом пробное поле на лазерном переходе воспринимает линию поглощения/усиления как контур сложной формы шириной G’ab (W), где

G’ab =Gab + |W|2 /Gaс вместо обычного лоренциана ширины Gab. Так как именно ширина перехода ограничивает спектр генерируемых импульсов, можно ожидать укорочения предела в G’ab / Gab раз по сравнению с обычными методами синхронизации мод. Действительно, как продемонстрировано приближенным аналитическим решением задачи, а затем точным численным расчетом, длительность импульса может сокращаться в десятки раз по сравнению со стандартным пределом gab-1 как для лазеров с инверсией так и для лазеров без инверсии.

В главе 4 рассмотрена пассивная синхронизация мод с двухуровневым поглотителем и усилителем. Обычно длительность генерируемого импульса ограничивается шириной линии лазерного усиления, но не шире. Это может быть спектральная ширина профиля линии усиления лазерной среды, ширина внутрирезонаторного частотно-зависимого элемента или обратная оптическая частота. (видеоимпульсы рассмотрены в [20]) Однако, в отличие от

пассивных частотно-зависимых элементов, дисперсия усиливающей среды

является нелинейной функцией поля. Это свойство позволяет усиливающей среде поддерживать импульсы длительностью короче стандартного предела. Как только импульс становится короче фазовой памяти среды, взаимодействие принимает когерентный характер. В этой главе свойства когерентной нелинейной среды положены в основу нового метода синхронизации мод, «когерентной синхронизации мод», позволяющего формировать импульсы

короче обратной спектральной ширины профиля усиления. Здесь усилитель действует и как активная среда и как модулятор, формирующий импульс. По мере распространения через усилитель передний фронт импульса нарастает, забирая запасенную в усилителе энергию, в то время как задний фронт затухает, испытывая меньшее усиление. В ходе процесса формообразования импульс в усиливающей среде эволюционирует к p-импульсу, который движется со скоростью света и извлекает всю энергию, запасенную в среде.

Для устойчивости режима синхронизации мод следует обеспечить

отрицательность коэффициента линейного усиления для непрерывного излучения. Это условие можно выполнить, если поместить в резонатор ячейку с пассивной средой - поглотителем. В нашем случае используется та же самая среда для поглотителя, что и для усилителя, но без внешней некогерентной накачки. Эффект самоиндуцированной прозрачности (СИП), обнаруженный МакКолом и Ханом [21-22], оказывается отличительной характеристикой нашей когерентной поглощающей среды. В лазере с когерентным поглотителем СИП служит дополнительным формообразующим механизмом. Конструкция резонатора с шириной пучка в усилителе, в два раза превышающей ширину пучка в поглотителе, дает возможность образоваться 2p-импульсу в поглотителе, который одновременно является p-импульсом для усилителя. Интересно отметить, что обе среды поддерживают образование импульсов одинаковой формы sech. Центральной темой этой главы является разработка основ нового механизма генерации импульсов - синхронизации мод с когерентным поглотителем, в котором используются когерентные свойства как поглощающей, так и усиливающей среды [7,23].

Будем интересоваться стационарным решением, то есть потребуем, чтобы импульс воспроизводил сам себя при каждом обходе резонатора. Получим

a = А sech[(t – z/v)/ta] (8)

Характерной чертой найденного решения является его существование только в области малых длительностей, ограниченной сверху неравенством: t < 1.6T2 (для T2a = T2g = T2). Следовательно, область существования импульсов, полученных путем когерентной синхронизации мод, не перекрывается с областью существования импульсов, генерируемых традиционными методами (ta > T2a, T2g). Этот, чисто когерентный, характер решения показывает, что оно качественно отличается от полученных другими типами синхронизации мод, и необходимым признаком его реализации служит наблюдение спектра импульса шире контура линейного усиления.

В диссертационной работе доказана устойчивость решений в виде p-импульсов в усилителе (и, соответственно, 2p-импульсов в поглотителе), имеющих энергию равную стационарной. Однако, из этого рассмотрения не следует, что форма импульса, обладающая этими свойствами, устойчива. Для доказательства устойчивости формы следует линеаризовать исходные уравнения около стационарного решения. Теорию возмущений первого порядка возможно развить аналитически и получить уравнение Шредингера на собственные значения и собственные функции для движения частицы в потенциальной яме в форме sech2. Такая задача решена в курсе квантовой механики Ландау и Лифшица и ее решением является набор гипергеометрических функций. Найдено, что все, кроме одного, собственные значения задачи отрицательны и принадлежат непрерывному спектру. Единственное неотрицательное собственное значение равно нулю и принадлежит дискретному спектру. Отсутствие положительных собственных значений показывает, что решение устойчиво, но не асимптотически устойчиво, так как существует нулевое собственное значение. Физически это означает, что решения для возмущений, соответствующие этому нулевому собственному значению, не затухают и не нарастают. Этот вывод аналогичен, полученному Лэмбом Дж. для задачи распространения 2p-импульса в поглотителе без потерь.

Были проведены численные расчеты на основе полной модели. Результаты этих расчетов служат двум целям. Во-первых, численное моделирование

воспроизводит практически важную динамику достижения стационарного режима генерации, инициируемую не слишком сильным всплеском электромагнитного излучения. Во-вторых, становится возможным убедиться в том, что достигнутый установившийся режим совпадает со стационарным решением, найденным аналитически. Численные расчеты проведены как для области параметров, где поперечная релаксация важна, так и для режима предельно коротких длительностей. Рассмотрены также режимы генерации (2N+1)p-импульсов, где N - неотрицательное целое число. Показано, что линейные потери в резонаторе препятствуют генерации солитонов порядка выше чем первый и в результате переходной эволюции выживает лишь единственный p-импульс. Этим рассматриваемый солитонный лазер качественно отличается от канонического эффекта СИП.

В качестве замечания о практической реализации метода когерентной

синхронизации мод следует отметить его применимость к целому классу сред

с узкими линиями поглощения/усиления с целью генерации импульсов со спектральной шириной, превышающей ширину линии усиления. Преимущество метода состоит в простоте его воплощения. Он не требует интерферометрической настройки длины резонатора или специального подбора пар усилитель-поглотитель. Одинаковые среды могут служить и в качестве усиливающей, и в качестве поглощающей среды. Единственно, требуется обеспечить различие диаметров поперечных сечений пучка в поглотителе и усилителе. Также, необходимым требованием является подбор достаточно высокодобротного резонатора (l<0.44g, где l – линейные потери и g – коэффициент усиления).

В главе 5 рассмотрена теория твердотельного солитонного лазера с когерентным неоднородно-уширенным двухуровневым поглотителем. В отличие от теории предыдущей главы усилитель в данном случае реагирует на поле некогерентно. Также важным отличием является медленная релаксация населенностей по сравнению со временем обхода импульсом резонатора.

Аналогично с теорией предыдущей главы данный лазер попадает в категорию солитонных лазеров. В отличие от принятой терминологии данный солитонный лазер подразумевает солитонные эффекты, основанные на резонансном эффекте СИП, а не на нерезонансном взаимодействии, описываемом нелинейным уравнением Шредингера [8].

Найдено решение в виде стационарных 2p-импульсов и проведено сравнение с условиями эксперимента Накадзавы с соавторами [24], базирующемся на идее формирования солитонного лазера использующего комбинацию волокна, допированного ионами эрбия, при комнатной температуре в качестве усиливающей среды и аналогичного волокна при температуре 4.2K в поглощающем режиме в качестве среды, формообразующей импульс на основе эффекта СИП. Несмотря на идеальное для СИП соотношение времен: T*† T2 [где (T*)-1 - неоднородная ширина линии, T2 – время релаксации поляризации], длительность генерируемых импульсов оказалась длиннее T2, что означает преобладание в эксперименте эффектов насыщенного поглощения над когерентным процессом формообразования. Авторы эксперимента не предложили объяснения неудавшейся попытке. В этой главе предложено две гипотезы, объясняющие отсутствие когерентного режима генерации неподходящим подбором параметров пары усилитель-поглотитель. Первая гипотеза выдвигает в качестве механизма, разрушающего режим СИП Керровскую нелинейность. Второй механизм неустойчивости связан с выжиганием провала в спектральном контуре поглощения. Дело в том, что на каждом обходе резонатора импульс СИП оставляет в поглотителе часть своей энергии из-за незавершенности цикла возврата населенности на нижний уровень. Таким образом, часть атомов остается на верхнем уровне. Так как населенность релаксирует очень медленно, T1ab » 10 мс, по сравнению с временем обхода резонатора, TR » 660 нс, поглотитель насыщается в среднем T1ab /TR » 15000 импульсами (все параметры взяты из экспериментальной работы Накадзавы и соавторов). Поскольку центральная группа атомов насыщается сильнее, чем частотно-отстроенные атомы, в стационарном режиме Гауссов неоднородный контур оказывается модифицированным - с глубоким провалом в центре.

В середине спектрального провала, выжженного импульсом, фоновое излучение (например, спонтанная эмиссия) испытывает особенно малое поглощение. Если коэффициент поглощения солитона окажется больше, чем коэффициент поглощения слабого фонового излучения, режим СИП станет неустойчивым. Ниже будет показано, что неустойчивость, вызванная процессом выжигания спектральных провалов, проявляется для относительно длинных импульсов СИП. Также рассчитано, что параметры эксперимента Накадзавы и соавторов лежат в области неустойчивости. Чтобы достичь устойчивого режима СИП следует увеличить мощность накачки выше определенного порога.

Проанализируем это неравенство в применении к экспериментам Накадзавы и соавторов. Для TR » 660 нс и T1ab » 10 мс получим ta < 0.042 T2ab, то есть мощность накачки в эксперименте должна быть достаточной, чтобы обеспечить генерацию импульса длительностью в 24 раза короче времени

фазовой релаксации. Для T2ab = 3 нс это означает, что импульсы должны быть короче 120 пс, что соответствует минимальной пиковой внутрирезонаторной мощности ~ 500 Вт. В эксперименте накачка была слабее. Так как режим генерации импульсов мощностью ниже критической неустойчив по отношению с усилению слабого узкополосного излучения, эта неустойчивость может быть причиной, или одной из причин, по которой режим генерации солитонов СИП реализован не был.

Заметим, что в отсутствии насыщения коэффициенты затухания непрерывного излучения и солитона СИП относятся друг к другу с коэффициентом пропорциональности ta / T2ab (меньшим единицы). Поэтому импульсы короче времени фазовой памяти среды всегда имеют безусловное преимущество перед узкополосным излучением. Поскольку для насыщенной линии поглощения условие устойчивости более строгое, это различие указывает на необходимость учета эффектов насыщения при моделировании волоконного солитонного лазера.

Основные результаты работы.

  1. Предложена аналитическая и численная модель рамановского усиления ультракоротких импульсов света в среде с V-конфигурацией уровней, накачиваемой фундаментальным солитоном СИП или солитонами высшего порядка на смежном переходе. Показано, что возможна 100 %-ая конверсия энергии солитона накачки в пробный импульс, который асимптотически преобразуется в солитон СИП. Обнаружен эффект «захвата» пробного импульса, выражающийся в том, что пробный импульс захватывается импульсом накачки, так что оба импульса распространяются с одинаковыми групповой скоростями. Продемонстрировано, что двухфотонный эффект Допплера и релаксация фазовой памяти среды делают процесс усиления пороговым: ниже порога происходит поглощение пробного поля, выше порога - его усиление. В условиях двухфотонного резонанса и присутствии однофотонного эффекта Допплера захват импульса сопровождается инициированием эффекта солитонно-индуцированной прозрачности (СОИП). Механизм прозрачности объясняется фазировкой атомных диполей в поле накачки в форме солитона СИП.
  1. Разработаны аналитические и численные методы описания эффекта суперфлюоресценции (СФ) в трехуровневой среде с V-конфигурацией уровней, накачиваемых сильным квазимонохроматическим когерентным полем на одном из переходов. Показана возможность генерации ультракоротких импульсов СФ в условиях рамановского усиления. В среднем, то есть после усреднения по периоду Раби осцилляций, процесс характеризуется как СФ без инверсии населенностей.
  1. Разработаны аналитические и численные методы описания взаимодействия пробного импульса с трехуровневой средой V-конфигурации, накачиваемой сильным когерентным лазерным импульсом. Обнаружен двухфотонный эффект СИП. Развита модель лазера с активной синхронизацией мод с трехуровневым когерентным усилителем. Отличительной особенностью такого лазера является генерация импульсов, характеризующихся спектром шире линии усиления двухуровневого перехода. Продемонстрированы режимы генерации без инверсии, с инверсией и рамановской генерации.
  1. Разработаны аналитические и численные методы описания взаимодействия короткого импульса излучения одновременно с двухуровневыми когерентными поглотителем и усилителем. Создана модель солитонного лазера на основе эффекта СИП. Исследована устойчивость солитонного режима генерации и переходная динамика к стационарному солитонному режиму, стартуя из затравочного импульса малой амплитуды. Солитонный режим характеризуется генерацией импульсов шире линии усиления.
  1. Разработаны аналитические методы описания твердотельного лазера с когерентным неоднородно-уширенным поглотителем. Создана модель твердотельного солитонного лазера на основе эффекта СИП и исследована устойчивость солитонного режима генерации. Продемонстрирована неустойчивость солитонов СИП по отношению к фазовой самомодуляции, наведенной эффектом Керра в волоконных световодах. Обнаружено, что выше определенного порога кубичной нелинейности, образование уединенных волн невозможно. Также продемонстрирована неустойчивость внутрирезонаторных солитонов СИП по отношению к возникновению непрерывного режима генерации за счет выжигания спектральных провалов в неоднородно-уширенном контуре поглощения.

Основное содержание диссертации изложено в следующих статьях:

  1. Kozlov V. V., Fradkin E'. E. Distortion of self-induced-transparency solitons as a result of self-phase modulation in ion-doped fibers//Optics Letters. - 1995. - Vol. 20, № 21. -- Pp. 2165-2167.
  2. Козлов В.В., Фрадкин Э.Е. Влияние далекой линии поглощения на условия распространения солитона самоиндуцированной прозрачности// Известия вузов «Прикладная нелинейная динамика». - 1995. - т. 3, вып. 6.--- С. 112-119.
  3. Козлов В.В., Фрадкин Э.Е. Механизм формирования импульсов самоиндуцированной прозрачности в присутствии Керровской нелинейности//ЖЭТФ. - 1996. - т. 82. - С. 46-59.
  4. Kozlov V. V. Self-induced transparency soliton laser via coherent mode-locking//Physical Review A - 1997. - Vol. 56. - Pp. 1607-1612.
  5. Kozlov V. V. Transformation of self-induced transparency soliton into nonlinear Schroеdinger soliton in doped fibers and semiconductor waveguides//Journal of Optical Society of America B. - 1997. - Vol. 14. - Pp. 1765-1767.
  6. Kozlov V. V., Fradkin E. E. Coherent effects in ultrashort pulse propagation through an optically thick three-level medium//Письма ЖЭТФ. - 1998. - т. 68, № 5. - C. 359-363.
  7. Денисова Н. В., Егоров В. С., Козлов В. В., Сердобинцев П. Ю., Фрадкин Э. Е. Просветление оптически плотной трехуровневой среды для слабого импульса при распространении 2 p-импульса на смежном переходе (V-схема)//ЖЭТФ.--- 1998.--- т. 113, \no 1.--- C. 71-88.
  8. Kozlov V.V., Polynkin P.G., Scully M.O. Resonant Raman amplification of ultrashort pulses in a V-type medium//Physical Review A. - 1999. - Vol. 59. - Pp. 3060-3070.
  9. Козлов, В.В. Self-induced transparency soliton laser//Письма ЖЭТФ. - 1999. - т. 69, вып. 12. - С. 856-861.
  10. Фрадкин Э.Е., Козлов, В.В., Воронов М.В. Индуцированная прозрачность при нестационарном комбинационном рассеянии//Квантовая электроника. - 1999. - т. 28, вып. 3. - С. 239-244.
  11. Kozlov V. V., Kocharovskaya O., Scully M. O. Effective two-level Maxwell-Bloch formalism and coherent pulse propagation in a driven three-level medium//Physical Review A. - 1999. - Vol. 59, № 5. - Pp. 3986-3997.
  12. Kozlov V., Kocharovskaya O., Rostovtsev Yu., Scully M. Superfluorescence without inversion in coherently driven three-level systems//Physical Review A. - 1999. - Vol. 60. - Pp. 1598-1609.
  13. Kozlov V.V., Eberly J.H. Ultrashort pulses in phaseonium: the interplay between SIT and EIT//Optics Communications. - 2000. - Vol. 179. - Pp. 85-96.
  14. Scully M.O., Agarwal G.S., Kocharovskaya O., Kozlov V.V., Matsko A.B. Mixed electromagnetically and self-induced transparency//Optics Express. - 2000. - Vol. 8, № 2. - Pp. 66-75.
  15. Eberly J.H., Kozlov V.V. Propagation of double resonance and dark area//Acta Physica Polonica A. - 2002. - Vol. 101, № 3. - Pp. 459-462.
  16. Eberly J.H., Kozlov V.V. Wave equation for dark coherence in three-level media//Physical Review Letters. - 2002. - Vol. 88, № 24. - P. 243604.
  17. Eberly J.H., Kozlov V.V. Propagation of short pulses in a coherently prepared Lambda medium//Laser Physics. - 2002. - Vol. 12, № 8. - Pp. 1188-1190.
  18. Kozlov V.V., Scully M.O. Mode-locking in coherently driven laser systems//Journal of Modern Optics. - 2002. - Vol. 49, № 3-4. - Pp. 431-438.
  19. Kozlov V.V., Wallentowitz S., Raghavan S. Ultrahigh reflection from a medium with ultraslow group velocity// Physics Letters A – 2002.- Vol. 296,, № 4-5 - Pp. 210-213.
  20. Козлов В. В., Козлова Е. Б., Фрадкин Э. Е. Теоретическое исследование рамановского усиления ультракоротких импульсов света в плазме положительного столба тлеющего разряда в неоне//Сб. статей «Лазерные исследования в СПбГУ»/Под ред. А. А. Петрова. - СПб.: С.-Петерб. ун-т, 2005. - С. 61-67.
  21. Kozlov V.V., Rostovtsev Yu. and Scully M. O. Inducing quantum coherence via decays and incoherent pumping with application to population trapping, lasing without inversion and quenching of spontaneous emission//Physical Review A – 2006. - Vol. 74, № 6 - 063829, 10 pages.
  1. Merkel W., Mack H., Freyberger M., Kozlov V.V., Schleich W.P., Shore B.W. Coherent transport of single atoms in optical lattices//Physical Review A – 2007. – Vol. 75, № 3 -, 033420, 14 pages.

Цитированная литература.

  1. Ханин Я.И. Основы динамики лазеров. - М.: Физматлит, 1999.
  2. Yariv A. Quantum electronics. 3rd ed. - New York: Wiley, 1989.
  3. Herrman J., Wilhelmi B. Lasers for ultrashort light pulses.--- Berlin: Akademie, 1987.
  4. Maimistov A.I., Basharov A.M. Nonlinear optical waves. - Dordrecht: Kluwer Acad. Publ., 1999.
  5. Haus H.A. Modelocking of lasers//IEEE Journal of Selected Topics in Quantum Electronics. - 2000. - Vol. 6. - Pp. 1173-1185.
  6. Зельдович Б.Я., Кузнецова Т.И. Генерация сверхкоротких импульсов света с помощью лазеров//УФН - 1972. - Vol. 15, № 1. - С. 47-84.
  7. Комаров К.П., Угожаев В.Д. Стационарные 2p-импульсы при пассивной синхронизации лазерных мод//Квант. электрон. - 1984. - т. 11, № 6. - С. 1167-1173.
  8. Mollenauer L.F., Stolen R.H. Soliton laser//Opt. Lett. - 1984. - Vol. 9, № 1. - Pp. 13-15.
  9. Bloembergen N. The stimulated Raman effect//The American Journal of Physics. - 1967. - Vol. 35, № 11. - Pp. 989-1023.
  10. Basov N.G. (Ed.). Stimulated Raman Scattering.- New York: Consultants Bureau, 1982.
  11. Полуэктов И.А., Попов Ю.М., Ройтберг В.С. Когерентное распространение мощных импульсов света через среду в условиях двухквантового взаимодействия//Письма ЖЭТФ. - 1974. - Vol. 20, № 8. – Pp.533-537.
  12. Большов Л.А., Ёлкин Н.Н., Лиханский В.В., Персианцев М.И. К теории когерентного преобразования частоты ультракоротких импульсов света в резонансных средах//ЖЭТФ -1988. - т. 94, вып. 10. - С. 101-109.
  13. Dicke R.H. Coherence in Spontaneous Radiation Processes//Phys. Rev. - 1954. - Vol. 93, № 1. - Pp. 99-110.
  14. MacGillivray J.C., Feld M.S. Theory of superradiance in an extended optically thick medium//Phys. Rev. A. - 1976. - Vol. 14, № 3. Pp. 1169-1189.
  15. Раутиан С.Г., Черноброд Б.М. Кооперативный эффект в комбинационном рассеянии света//ЖЭТФ. - 1977. - т. 72, № 4. - С. 1342-1348.
  16. Трифонов Е.Д., Трошин А.С., Шамров Н.И. Кооперативное комбинационное рассеяние света//Опт. Спектр. - 1980. - т. 48, № 5. - С. 1036-1039.
  17. Андреев А.В., Емельянов В.И., Ильинский Ю.А. Кооперативные явления в оптике. - М.: Наука, 1988.
  18. Габитов И.П., Захаров В.Е., Михайлов А.В. Нелинейная теория суперфлюоресценции//ЖЭТФ - 1984. - т. 86. - С. 1204-1216.
  19. Кочаровская О.А., Ханин Я.И. Когерентное усиление ультракороткого импульса в трехуровневой среде без инверсии населенностей//Письма ЖЭТФ. - 1988. - т. 48, вып.11.- С. 581-584.
  20. Высотина Н.В., Розанов Н.Н., Семенов В.Е. Предельно короткие импульсы усиленной самоиндуцированной прозрачности//Письма ЖЭТФ.- 2006. - т. 83, вып. 7.- С. 337-340.
  21. McCall S.L., Hahn E.L. Self-induced transparency by pulsed coherent light//PRL - 1967. - Vol. 18. - Pp. 908-911.
  22. Аллен Л., Эберли Дж. Оптический резонанс и двухуровневые атомы. - М.: Мир, 1978.
  23. Андреев А.В., Полевой П.В. Динамика усиления и распространения импульсов в двухкомпонентных средах//ЖЭТФ. - 1994. - т. 106, № 5(11). - С. 1343-1359.
  24. Nakazawa M., Suzuki K., Kubota H., Kimura Y. Self-Q-Switching and mode locking in a 1.53-mm fiber ring laser with saturable absorption in erbium-doped fiber at 4.2 K//Optics Letters. - 1993. - Vol. 18, № 8. - Pp. 613-615.


 
Авторефераты диссертаций  >>  Авторефераты по Физике




наверх

<


 
<<  ГЛАВНАЯ   |    КОНТАКТЫ
2013 www.disus.ru - «Бесплатная научная электронная библиотека»

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.