Физические процессы в активных средах лазеров на самоограниченных переходах в парах металлов и их взаимосвязь с параметрами разрядного контура

На правах рукописи

ЮДИН НИКОЛАЙ АЛЕКСАНДРОВИЧ

ФИЗИЧЕСКИЕ ПРОЦЕССЫ В АКТИВНЫХ СРЕДАХ ЛАЗЕРОВ

НА САМООГРАНИЧЕННЫХ ПЕРЕХОДАХ В ПАРАХ МЕТАЛЛОВ И ИХ ВЗАИМОСВЯЗЬ С ПАРАМЕТРАМИ РАЗРЯДНОГО КОНТУРА

специальность: 01.04.21 – лазерная физика

АВТОРЕФЕРАТ

диссертации на соискание ученой степени

доктора физико-математических наук

Томск – 2009

Работа выполнена в Томском государственном университете,

Институте оптики атмосферы СО РАН (г. Томск),

Институте физики полупроводников СО РАН (г. Новосибирск).

Научный консультант: доктор физико-математических наук,

Солдатов Анатолий Николаевич

Официальные доктор физико-математических наук,

оппоненты: Соломонов Владимир Иванович

доктор физико-математических наук,

Сорокин Александр Разумникович

доктор физико-математических наук,

Тарасенко Виктор Федотович

Ведущая организация:

Институт теоретической и прикладной механики им. С.А. Христиановича СО РАН, г. Новосибирск

Защита состоится “8” апреля 2010 г. в 14 час. 30 мин. на заседании диссертационного Совета Д 212.267.04 при Томском государ­ственном университете (634050, г. Томск, пр. Ленина, 36)

С диссертацией можно ознакомиться в Научной библиотеке Томского госу­дарственного университета

Автореферат разослан “___” декабря 2009 г.

Ученый секретарь диссертационного Совета Пойзнер Б.Н.

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Диссертация посвящена исследованию частотно-энер­ге­ти­ческих характери­стик лазеров на самоограниченных переходах атомов металлов, повышению надежности работы лазеров, их срока службы и определению оптимальных условий накачки активной среды при газоразрядном способе возбуждения.

Актуальность темы. Лазеры на самоограниченных переходах атомов металлов (ЛПМ) – лазеры, инверсная заселенность в которых возникает ме­жду резонансными и метастабильными уровнями атомов и ионов металлов в период ионизационной неравновесности плазмы, являются одним из наибо­лее эффективных источников излучения в видимой области спектра среди га­зовых лазеров. Существенный прогресс в развитии ЛПМ, наметился благо­даря реализации саморазогревного способа получения паров за счет диссипа­ции энер­гии импульсно - периодического разряда с высокой частотой следо­вания импульсов (ЧСИ) возбуждения. Простота и надежность высокотемпе­ратур­ной тех­ники, созданной на этом принципе, позволили реализовать практи­ческий КПД ЛПМ ~ 1% и сущест­венно повысить как импульсную, так и среднюю мощности генерации. Однако потреб­ности таких областей науки и техники, как зондиро­вание атмосферы, локация и связь, ла­зерная обработка материалов, лазерная фо­тохи­мия, лазерное разде­ление изотопов и др., по-прежнему стимулируют работы по созданию эффективных лазеров видимого диапа­зона. Саморазогрев­ной режим работы, в его классическом варианте, по­зволил улучшить выходные пара­метры ЛПМ, но не исчерпал их потенциала по повышению эффективности, которая составляет по оценкам ~ 10%, сред­ней мощности ~ 1 Вт/см3 и ЧСИ ге­нерации > 100 кГц [1-4]. Возможность достижения вышеперечисленных параметров в газоразрядных трубках (ГРТ) с малым рабочим объемом экспериментально была показана в работах А.Н. Солдатова и И.И. Климовского.

Для эффективной накачки ЛПМ, как хорошо известно, необходимо фор­мировать импульс возбуждения с крутым фронтом и длительностью им­пульса соизмеримой со временем существования инверсии [1-5]. Реальные условия накачки существенно отличаются от идеальных условий возбужде­ния (прямоугольный импульс возбуждения), что накладывает определенные ограничения на частотно-энергетические характеристики (ЧЭХ) лазеров. Экспериментально наблюдаемые зависимости позволили П.А. Бохану и др. сделать заключение, что одной из основных причин ограничения ЧЭХ рас­сматриваемого класса лазеров при газоразрядном способе возбуждения явля­ется наличие индуктивной составляющей в разрядном контуре лазера. Это не позволяет быстро разогревать предымпульсные электроны (ne0), что приво­дит к заселению метастабильных состояний на фронте импульса возбужде­ния и к перераспределению скоростей заселения лазерных уровней в пользу метастабильных с ростом ne0. В тоже время, исходя также из наблюдаемых экспериментальных зависимостей, Г.Г. Петраш и др. обуславливают ограни­чения ЧЭХ ЛПМ медленной релаксацией метастабильных состояний в меж­импульсный период. Очевидно, что существующая неоднозначность интер­претации экспериментальных результатов не позволяет, с одной стороны, однозначно оценить энергетический потенциал активной среды ЛПМ и воз­можные практические пути его реализации, а с другой стороны, указывает на возможность неоднозначного проявления механизма ограничения ЧЭХ ЛПМ, в зависимости от условий накачки. Последнее предположение обусловлено следующим. Всегда полагалось, что развитие разряда в активных средах с высокой проводимостью плазмы осуществляется без стадии пробоя. Поэтому эквивалентную схему разрядного контура в модельных расчетах представ­ляют в виде активной и индуктивной составляющих импеданса ГРТ, парал­лельно которым подключена обостряющая емкость. Однако данная эквива­лентная схема применима только для анализа процессов в ГРТ с электродами расположенными в горячей зоне разрядного канала. Впервые о наличие про­боя в активных средах с высокой проводимостью плазмы указано в [6]. Про­веденный в [7] анализ показал, что в типичных условиях работы ЛПМ сопро­тивление разряда в его начальной стадии определяется в основном не прово­димостью нагретой активной части ГРТ, где ne0 может быть велико, а процес­сами на электродах и в холодных приэлектродных областях. Это дает осно­вание предположить [7], что в концевых зонах к приходу следующего им­пульса возбуждения плотность электронов мала, сопротивление, соответст­венно, велико, и в этих зонах происходит пробой с образованием катодного слоя с большим падением напряжения и контрагированием разряда. В этом случае должны изменяться как эквивалентная схемы разрядного контура так и, соот­ветственно, кинетика процессов в разрядном контуре и активной среде ЛПМ. Вышесказанное дает основание предположить наличие дуализма кинетики процессов ЛПМ в зависимости от расположения электродов в горячей зоне разрядного канала или холодных буферных зонах ГРТ.

В соответствии с вышесказанным, общей задачей диссертационной ра­боты явля­лось выяснение закономерностей формирования инверсной на­селенности в активной среде лазеров на парах металлов и физиче­ских причин ог­раничения частотно-энерге­тиче­ских характеристик, а также разра­ботка способов эффек­тивной накачки активной среды лазеров на само­ограниченных переходах атомов металлов.

Ее конкретная реализация предполагала решение та­ких самостоятель­ных вопросов, как:

1. Экспериментальное исследование процесса ступенчатой ионизации с верх­них ла­зер­ных уров­ней и его влияния на формирование инверсной населенно­сти.
2. Изучение механизма влияния предымпульсных параметров плазмы на энер­гети­ческие характеристики лазеров.
3. Исследование причин, приводящих к ограничению частоты следова­ния им­пульсов ге­нерации, и на их основе уточнение принципов управления ха­рактеристиками излучения лазе­ров.
4. Определение параметров накачки, оптимальных для эффективного воз­буж­дения ак­тивной среды.

Методы исследований. В качестве методов исследований в работе при­нят физический эксперимент с использованием методов численного расчета изучаемых физических процессов в условиях идеальной накачки (прямо­угольный импульс возбуждения), а процессов в контуре, исходя из анализа экспериментальных данных с привлечением теории нелинейных электриче­ских цепей.

Научные положения, выносимые на защиту:

1. В импульсных лазерах на самоограниченных переходах атома меди из-за высокой скорости процесса ступенчатой ионизации с резонансных уровней и наличия вынужденных переходов наблюдается оптогальванический эффект, проявляю­щийся в уменьшении тока разряда и обратного напряжения на аноде тира­трона при возникновении светового поля в резонаторе. При этом обобщенная константа ступенчатой ионизации с резонансных уровней атома меди оценивается значением <v> ~ (1,93,9)·10-7см3сек-1. Высокая скорость ступенча­той ионизации не только определяет насыщение населенности резонансных уровней в импульсе возбуждения, но и обуславливает снижение эффективно­сти накачки активной среды с ростом предымпульсной концентрации элек­тронов.
2. Накачка активной среды происходит после пробоя промежутка “плазма – анод” в случае расположения электродов в холодных буферных зонах газо­разрядной трубки (ГРТ). Момент начала пробоя определяется прекращением токов смещения зарядов в процессе зарядки от накопительного конденсатора всех емкостных составляющих разрядного контура в условиях, когда импеданс активной среды до момента пробоя проявляет себя как система с сосредоточенными пара­метрами. Скорость нарастания напряжения на плазме определяется вре­менем развития пробоя промежутка “плазма – анод”. Импеданс активной среды с момента пробоя проявляет себя как система с сосредоточенными па­раметрами только в случае, когда время развития пробоя превышает время распространения электромагнитного поля в активной среде. В противопо­ложном случае импеданс активной среды с момента пробоя проявляет себя как система с распределенными параметрами.
3. Величина инверсной населенности определяется энерговкладом от трех па­раллельных контуров возбуждения, образованных собственной емкостью ГРТ, обостряющим и накопительным конденсаторами, при условии, что время развития пробоя промежутка “плазма – анод” превышает время рас­пространения электромагнитного поля в активной среде лазера. При этом:

собственная емкость ГРТ определяет обострение тока на фронте импульса возбуждения и является источником подогрева электронов в меж­импульсный период;

к числу основных факторов, ограничивающих энергию импульса генера­ции, относятся также эмиссионная способность катода электронных ламп и допустимая скорость нарастания тока в тиратроне;

энергозатраты на формирование инверсии в активной среде снижаются в режиме двухимпульсного возбуждения, когда первым импульсом формиру­ется оптическое поле в резонаторе, а вторым его усиление.

4. Время развития пробоя определяется временем прохождения промежутка “плазма – анод” электроном, стартовавшим из плазмы на анод с момента пробоя. В случае перехода электронов в режим убегания, когда граничное значение напряженности поля Ecr для пробоя соответствует условию i(Ecr, NHe)d = 1 (i – таунсендовский коэффициент размножения электронов, d – расстояние между разрядным каналом и анодом ГРТ, NHe – концентрация бу­ферного газа в промежутке “плазма – анод”), величина инверсной населенно­сти в лазере на парах стронция определяется энерговкладом собственной емкости ГРТ с эффективностью генерации ~ 6-8%. При этом форми­руется однородное распределение излучения лазера по сечению разрядного канала, энергосъем растет пропорционально объему активной среды и в парогазовой смеси (Sr + He + Ne) наблюдается одновременная генерация на самоограниченных переходах SrI и SrII, атома гелия (21P1 – 21S0) – = 2058 нм и пе­реходах 2s – 2p атома неона. Средняя мощность генерации на = 2058 нм атома гелия ~ 15-20% от суммарной средней мощности генерации на всех линиях.
5. Критическая населенность метастабильных состояний Nmcr, при которой инверсия в активной среде не возникает, определяется как сумма предым­пульсной плотности метастабильных состояний Nm0 и заселенности метаста­бильных состояний Nmf на фронте импульса возбуждения в течение времени разогрева электронов до критической температуры, при которой скорость за­селения верхних лазерных уровней начинает превышать скорость заселения нижних уровней. Это определяет два предельных случая ограничения час­тотно-энергетических характеристик лазеров, а именно:

Nmf является определяющим фактором ограничения в случае расположения электродов в горячей зоне разрядного канала ГРТ;

Nm0 является определяющим фактором ограничения в случае расположения электродов в холодных буферных зонах ГРТ.

В этих условиях изменение населенности метастабильных состояний через подогрев электронов определяет минимальные энергозатраты на управление характеристиками лазерного излучения. Данный метод управления не эффек­тивен для лазерных переходов с квантовым КПД < 20%.

Достоверность научных положений под­тверждается:

1. Совпадением полученного значения константы скорости ступенчатой иони­зации с резонансного уровня CuI с расчетными значениями [9].
2. Совпадением экспериментальных результатов с расчетными, а также с оцен­ками и экспериментальными данными, полученными другими авторами [6-7, 13].
3. Экспериментально наблюдаемыми зависимостями частотно-энергетиче­ских характеристик лазеров на самоограниченных переходах, полученными другими авторами [1-4], а также прямыми измерениями временного хода на­селенности рабочих уровней [11].
4. Экспериментально наблюдаемыми зависимостями энергетических характе­ристик лазера на парах стронция в условиях накачки, соответствующих кри­терию перевода электронов в режим убегания [12, 16] в промежутке “плазма – анод”.
5. Экспериментально наблюдаемыми зависимостями энергетических характе­ристик лазеров, полученными другими авторами: в случае расположения электродов в горячей зоне разрядного канала [8, 17]; в случае расположения электродов в холодных буферных зонах [1-4, 11].

Новизна защищаемых положений:

1. Обнаружен (1999 г.) оптогальванический эффект в лазере на парах меди. Дано объяснение (2004 г.) снижению эффективности накачки с увеличением предымпульсной концентрации электронов.
2. Установлена зависимость (2007-2008 гг.) изменения эквивалентной схемы ГРТ от расположения электродов. Обнаружен момент начала накачки актив­ной среды в случае расположения электродов в холодных буферных зонах ГРТ. Предложена интерпретация импеданса активной среды как системы с сосредоточенными или распределенными параметрами в зависимости от времени развития пробоя.
3. Выявлена (2008-2009 г.) роль собственной емкости ГРТ в обострении фронта импульса возбуждения и подогреве электронов в межимпульсный пе­риод. Подтверждается полученными патентами РФ (№2242828; №2288536)
4. Обнаружены (2008-2009 гг.) факторы определяющие время развития про­боя, а также величину инверсной населенности.
5. Показаны (1997-2008 гг.) два предельных случая ограничения частотно-энер­гетических характеристик лазеров, которые возникают в зависимости от расположения электродов в ГРТ. Определен фактор, позволяющий управлять характеристиками лазерного излучения с минимальными энергозатратами. Оригинальность технических решений подтверждается полученными авторскими свидетельствами СССР (№1101130; №1253397; №1676410), патентами РФ (№2082263; №2230409; №2237955; №2254651).

Научная значимость защищаемых положений:

1. Дано объяснение снижению эффективности накачки с увеличением предым­пульсной концентрации электронов.
2. Исходя из физических представлений о процессах в разрядном контуре лазе­ров на парах металлов, найден путь преобразования эквивалентной схемы ГРТ в зависимости от расположения электродов. Определен момент начала накачки активной среды в случае расположения электродов в холод­ных буферных зонах ГРТ. Предложена интерпретация импеданса активной среды как системы с сосредоточенными или распределенными параметрами в зависимости от времени развития пробоя.
3. Определен источник подогрева электронов в межимпульсный период, сни­жающий скорость релаксации метастабильных состояний. Определены усло­вия его возникновения и причины, обуславливающие неоднозначность мас­штабирования энергетических характеристик лазерного излучения с измене­нием геометрических размеров и диэлектрических характеристик разрядного канала ГРТ.
4. Показан путь реализации сверхбыстрого пробоя промежутка “плазма – анод” ГРТ, в условиях которого реализуются высокие энергетические пара­метры активной среды лазеров на парах металлов, что значительно изменяет представления о перспективности газоразрядного способа возбуждения.
5. Определены два предельных случая ограничения частотно-энергетических характеристик лазеров, которые возникают в зависимости от расположения электродов в ГРТ.

Практическая значимость заключается в следующем:

1. Физически обоснована техническая возможность повышения эффективно­сти накачки в условиях высокой скорости ступенчатой ионизации с резо­нансных уровней за счет снижения энергозатрат на формирование инверсии.
2. Обоснована необходимость учета в модельных расчетах условия того, что эквивалентная схема ГРТ зависит от расположения электродов, геометриче­ских размеров и диэлектрических характеристик разрядного канала. При этом законы Ома и Кирхгофа применимы только в случае, когда импеданс активной среды проявляет себя как система с сосредоточенными парамет­рами. Показано, что активную среду необходимо рассматривать как длинную линию в случае распределенных параметров ее импеданса.
3. Разработан ряд рекомендаций:

– при оптимизации параметров накачки необходимо учитывать, что собст­венная емкость ГРТ имеет пренебрежимо малую величину при малых диа­метрах разрядного канала. В этих условиях отсутствует источник подогрева электронов в межимпульсный период, а формирование инверсии осуществ­ляется внешними контурами – обостряющей емкостью и накопительным конденсатором. Это обуславливает неоднозначность масштабирования энер­гетических характеристик лазерного излучения с изменением геометриче­ских размеров и диэлектрических характеристик разрядного канала ГРТ;

– в режиме двухимпульсного возбуждения реализуется возможность повы­шения до ~ 80% и более эффективности преобразования излучения лазера в пучок с дифракционной расходимостью и управления энергией импульса ге­нерации без нарушения теплового режима работы лазера;

– срок службы тиратрона соответствует паспортным значениям при величине обратного напряжения < 3 кВ. Снизить величину обратного напряжения на аноде тиратрона в оптимальных условиях накачки можно за счет увеличения давления буферного газа и используя, в качестве контура накачки, систему связанных контуров.

4. Найдены условия, при которых величина инверсной населенности определя­ется энерговкладом собственной емкости ГРТ.
5. Предложена методика и определены условия реализации одновременной генерации на всех компонентах парогазовой смеси активной среды лазера, что определяет принципиальную возможность создания многоволновых ла­зерных источников излучения.
6. Найдены условия, определяющие принципиальную возможность оператив­ного управления параметрами генерации, и установлены границы их приме­нимости.
7. Предложена методика синхронизации работы тиратронов типа ТГИ в систе­мах “задающий генератор – усилитель” с нестабильно­стью ~ 1 нс.
8. Уточнена методика измерения концентрации электронов в ближнем послес­вечении разряда лазеров на парах металлов по штарковскому ушире­нию линии водорода Н.

Внедрение результатов диссертации и предложения по дальнейшему их использованию:

Разработаны:

• Серия малогабаритных лазеров на парах меди со встроенным нагревате­лем в ГРТ “Милан-М”, “Милан-М/2Е”, работающих в широком диапазоне час­тот следования им­пульсов генерации со стабилизацией теплового ре­жима работы и возможностью работы лазера в дежурном режиме. На базе этих лазеров разработаны лазерные створные маяки “Радуга 1” и “Радуга 2” для проводки судов в условиях ограниченной видимости, кото­рые были при­няты для экс­периментальной эксплуатации в составе навигационного обо­рудования Вент­спилским (Латвия) и Клайпедским (Литва) торговыми пор­тами в 1989-1991 гг. (А.с. СССР №1253397; №1676410)

• Лазер на парах меди “Милан – 5/01” со стабилизацией выходных харак­те­ристик ла­зерного излучения. Лазер передан по контракту на лицензион­ной основе в Болгарию для серийного производства в 1983-1986 гг. (А.с. СССР №1101130, получен знак “Изобретатель СССР”).

• Лазеры на парах меди “Малахит” со 100% глубиной управления выход­ными характе­ристиками лазерного излучения (патент РФ №2082263, №2230409).

• Лазерный комплекс – система “задающий генератор - усилитель” на па­рах меди со средней мощностью в дифракционном пучке до 170-200 Вт для за­дач лазерного разде­ления изотопов.

Лазеры неоднократно демонстрировались на Российских и междуна­род­ных вы­ставках. Лазер “Милан-М” награжден золотой медалью ВДНХ СССР в 1982 г. Результаты работы могут быть использованы при разработке лазе­ров на парах металлов, например, ФГУП НПО “ИСТОК” (г. Фрязино); Ин­ститутами оптики атмосферы и физики полупроводников СО РАН; Том­скими государственным и политехническим университетами, Южным феде­ральным университетом и др.

Апробация работы и публикации.

Основные результаты, приведенные в диссертации, обсуждались: на Всесо­юзных симпозиумах по лазерному и акустическому зондирова­нию атмо­сферы в 1982 г., 1984 г. (г. Томск); Все­союзных и Российских семинарах “Ла­зеры на парах металлов и их приме­нение” в 1982 г., 1991-2008 гг. (г. Ростов на Дону); Межотраслевой научно-технической конференции “Импульсные газоразрядные лазеры” в 1986 г. (г. Москва); рабочем совещании “Активные среды плазменных и га­зораз­ряд­ных лазеров” в 1987 г. (г. Гродно); Нацио­нальной конференции “Лазеры и их применение” в 1988 г. (г. Пловдив, Бол­гария); 5-7ой Всерос­сий­ских (меж­дународных) на­учных конференциях “Фи­зико-химические про­цессы при се­лекции атомов и молекул” в 1999-2002 гг. (г. Звенигород); Между­народной конференции “Импульсные лазеры на пере­хо­дах атомов и моле­кул” в 1992-2009 гг. (г. Томск); III Всероссийской кон­ференции “Взаимодействие высококонцентрированных потоков энергии с материалами в перспективных технологиях и медицине” в 2009 г. (г. Новоси­бирск).

Основные результаты работы изложены в 66 печатных работах (из них 13 без соавторов), в том числе в изданиях, рекомендованных ВАК, 28 и 16 ав­торских сви­детельствах СССР и патентах РФ.

Личный вклад автора. В исследованиях, представленных в диссертации, автору принадлежит инициатива проведения исследований, постановка за­дач, анализ и интерпретация полученных результатов. Результаты экспери­ментальных исследований и модельных расчетов получены лично автором либо при его определяющем участии. Под­готовленные на их основе публи­кации сделаны по инициативе и при непосредственном уча­стии автора. На различных этапах исследований в постановке некоторых конкретных задач и обсуждении результатов принимали участие А.Н. Солдатов, П.А. Бохан, Г.С. Евтушенко, Г.Г. Петраш и М.А. Казарян.

Структура и объем диссертации. Диссертация состоит из введения, шести глав, общих выводов, прило­жения и заключе­ния, содержит 248 стра­ниц текста, 133 рисунка, 11 таблиц и список литера­туры из 366 наименова­ний.

СОДЕРЖАНИЕ РАБОТЫ

Во введении обоснована актуальность темы диссертации, формулиру­ется цель ра­боты, постановка задачи, показана научная новизна, приведены наи­более важные практические результаты и основные положения, представ­лен­ные к защите.

Глава I посвящена определению условий накачки ак­тив­ной среды, при которых реализуется высокое значение физического КПД ЛПМ и экспери­ментальному изучению роли ступенчатых процессов ионизации.

КПД импульсных лазеров определяется соотношением

пр = (Еg/Pвып)100%, (1) где Eg – энергия импульса генерации; f – ЧСИ генерации; Egf – средняя мощ­ность ге­не­рации; Рвып – мощность, потребляемая от выпрямителя. По­скольку Рвып определяет общие за­траты энер­гии в лазере, в том числе и по­тери в коммутаторе, в зарядном контуре ла­зера и т.д., то реальный КПД лазера не мо­жет отражать энерге­ти­ческий по­тенциал активной среды. Энергетический потенциал активной среды опре­деляется из соотношения

пр = (Еgf/Еdf)100%, (2) где Ed – энергия импульса возбуждения; Ed f = P – const – мощность, вво­ди­мая в актив­ную среду для поддержания режима саморазогрева. Из­вестно, что с увеличе­нием ЧСИ возбуждения уменьшается Eg и, соответ­ст­венно, КПД ла­зера. В этом случае оп­тимизация ус­ло­вий возбужде­ния является многопа­ра­метрической за­да­чей, из которой очень сложно вычленить параметр или па­раметры, оп­ре­де­ляющие энергети­ческий по­тенциал активной среды. Мето­дологически бо­лее пра­виль­ным яв­ля­ется подход к оценке энергетического потенциала, проводимый в три этапа. На первом этапе следует определить условия, при которых реа­лизу­ется максимальное значение соотноше­ния - Eg/Ed, т.е. оп­ределить фи­зиче­ский КПД активной среды

физ = (Еg/Еd)100%, (3) который определяет максимально возможный уровень энергетических харак­теристик ЛПМ, на втором этапе выяснить причины, ограни­чи­вающие ЧСИ генерации, т.е. практический КПД (2) лазера. И наконец, на третьем этапе рассмотреть при­чины, определяющие реальный практиче­ский КПД лазера (потери в коммута­торе, зарядных цепях и т.д.).

Исследуя зависимости энергетических характеристик Cu-лазера от вели­чины индуктивности разрядного контура в [8] был сделан вы­вод, что эф­фек­тив­ность ЛПМ возрастает с умень­шением вол­нового сопро­тивления разряд­ного контура. Из этого следует, что эффективность ЛПМ должна возрастать относительно энерговклада до окончания импульса генерации с увели­че­нием емкости накопительного конденсатора. Проведен­ные нами исследования подтверждают, что в этом случае действительно наблюдается рост эффек­тивности Cu-лазера относительно энерговклада в активную среду до оконча­ния им­пульса генерации. Осуще­ствляя “отсечку” энерговклада после им­пульса генерации можно реализовать высокий фи­зический КПД. Наибо­лее важный результат, по­лученный нами, сви­детельствует, что режим “отсечки” резко снижает энерговклад в разряд без потери мощности генерации. Физиче­ский КПД Cu-лазера в режиме полного об­рыва энерговклада в ГРТ после импульса генера­ции достигает 9%, что является наглядным подтвер­ждением прогнозируемого энергетического потенциала активной среды Cu-лазера. Визу­альное наблюдение разряда показало, что инте­гральное излу­че­ние в по­следнем случае ос­лаблено, и практически не наблюда­ется даже харак­терное свечение бу­ферного газа в холод­ных зонах ГРТ. Детальный ана­лиз спектра спонтанного излу­чения по­зволил определить, что 90% энергии вводимой в разряд обуславливают ступенчатые процессы возбуждения и иониза­ции рабочей среды после импульса генерации.

Особенностью лазерного перехода в CuI является энергетиче­ская бли­зость резо­нансного уровня к первой границе ионизации. Такое энергети­че­ское положение ре­зонанс­ного уровня способствует его девоз­буждению в со­стояние ионизации либо непо­средст­венно, либо через про­межуточные высо­ковозбужденные состояния. В результате с ростом раз­рядного тока на­селен­ность резонансного состояния насыщается, что огра­ничивает энерге­тические параметры лазерного перехода. В расчетных моделях лазеров ступенчатая ионизация резонансного уровня, как пра­вило, учитывается, и в части прово­димости плазмы и в части удельных энергетиче­ских параметров лазерного излучения, однако, прямых экспериментальных подтвер­ждений не было. С этой целью нами было предпринято экспериментальное наблюдение ступен­чатой ионизации CuI в активной среде Cu-лазера. Для этого исследовалось влияние возмущений населенностей резонансного уровня CuI собственным световым полем на проводимость плазмы разряда. Резонатор лазера моду­ли­ровался введением экрана между зеркалами резонатора и трубкой. В ре­зуль­тате обработки осциллограмм было установлено, что световое поле умень­шает амплитуду разрядного тока на вели­чину 23% (рис.1), а "быстрый" отклик плазмы более значителен и состав­лял 45% для тока. Наиболее за­метно оптогальванический эффект про­являлся в из­мене­нии обратного на­пряжения на тиратроне - с 2,8 кВ при наличии поля до 2,9 кВ при перекрытии резонатора. Анализ полученных ре­зультатов по­зволил оценить константу скорости ионизации резонансного уровня <v> = (1,93,9)10-7 см3 сек-1. Эта вели­чина, по крайней мере, на два порядка превышает константу ско­рости прямой ио­низа­ции из основного со­стояния CuI.

Рис.1. Осциллограммы импульсов тока с полем (1) и без поля (2) в резонаторе ла­зера.

Модуляция светового поля в резона­торе лазера, в условиях более высокой электронной температуры (коммута­тор ГМИ-29А), приводила к более существенной модуляции тока, причем модуляция тока была заметна и на осциллограммах импульсов тока, как в вышерассмотренном случае, и наблюдалась модуляция среднего тока, по­требляемого от выпрямителя.

Это является подтверждением теоретических расчетов констант скоро­стей ступенчатых процессов в ЛПМ [9] и определяет единственно возмож­ный путь повышения эффективности лазера за счет снижения предымпульс­ной концентрации электронов. Не менее важным, из вышесказанного, явля­ется вывод о том, что рост физического КПД лазера возможен не за счет уве­личения энергии в импульсе генерации, а только за счет снижения энергоза­трат на формирование инверсной населенности в активной среде. Это связы­вает, по сути, значения практического КПД и средней мощности генерации с ЧСИ генерации.

Глава II посвящена исследованию механизма влияния предымпульсных параметров плазмы на частотно-энергетические характеристики (ЧЭХ) лазе­ров на самоограниченных переходах атомов ме­таллов.

2.1. Критическая плотность метастабильных состояний.

Рассмотрим идеальный случай, ко­гда осуществляется мгновенный разо­грев электронов до температуры, определяе­мой напряженностью поля на ГРТ, а электронная температура (Те) не меняется в течение всего импульса воз­буждения. Кинетику плотности населенностей лазерных уровней Cu и плотности электро­нов во время импульса возбуждения рассмотрим исходя из модели, учитывающей засе­ление лазерных уровней из основного состояния CuI и ионизацию CuI за счет процессов прямой и ступенчатой ионизации с резонансных уровней:

dNm/dt = Nm0 + (NCu – NiCu)nek0m, (4)

dNr/dt = (NCu – NiCu)nek0r - Nrnekri, (5)

dNiCu/dt = ne0 + (NCu – NiCu)nek0i + 2Nrnekri, (6)

где NCu, Nm, Nr, NiCu – плотности населенностей основного, метастабильного, резонансного уровней CuI и ионов CuII, соответственно; ne = NiCu – плот­ность электронов; ne0 – предымпульсная концентрация электронов; Nm0 – предымпульсная плотность метастабильных состояний; k0m, k0r, k0i, kri – кон­станты скоростей процессов возбуждения метастабильного, резонансного уровней, прямой ионизации из основного состояния, а также ступенчатой ионизации с резонанс­ного уровня, соответственно. Соответствующие кон­станты скоростей процессов возбуж­дения и ионизации взяты из [9], а kri – обобщенная константа, учитывающая девозбужде­ние резонансного уровня.

Моделирование показало, что с увеличением ne0 и Те сокращается время достижения пороговых условий для генерации и время существования ин­версии, возрас­тает скорость энерговклада, но величина инверсной населен­ности возрастает только с увеличением Те. С увеличением ne0 уменьшается не только величина инверсной населен­ности, но и время существования инвер­сии. Существует критическая плотность населенности нижних лазерных уровней Nmkr ~ 3-51013 см-3, при которой инверсия не возникает. Наличие Nmkr с учетом конеч­ной скорости их релаксации в межимпульсный период озна­чает, что с увеличением ЧСИ возбуждения будет возрастать Nm0 и предельная ЧСИ генерации определяется условием

Nm0 = Nmkr. (7)

Вышеприведенное рассмотрение проведено без учета влияния реактив­ных составляющих импеданса. Наличие реактивных составляющих в контуре не позволяет мгновенно разогревать ne0 и, соответственно, в реальном лазере существует определенная скорость разогрева электронов. Поэтому в течение времени разогрева электронов до критической температуры, при которой скорость заселения верхних лазерных уровней начнет превышать скорость заселения нижних уровней, будет дополнительно осуществляться заселение метастабильных состояний на величину Nmf. Поэтому предельно возможная ЧСИ генерации будет определяться суммой

Nm0 + Nmf = Nmkr (8) и соответственно какой из параметров Nm0 или Nmf более быстро достигает значения Nmkr, тот и является определяющим в ограничении ЧСИ генерации. Как известно, кинетика процессов в активной среде определяется констан­тами скоростей этих процессов. Значение этих констант зависит от Те, кото­рая, согласно [3], отслеживает изменение напряжения на активной состав­ляющей импеданса ГРТ. Изменение напряжения на активной составляющей импеданса в контуре, как известно, определяется апериодическим или коле­бательным характером развития процесса. Анализ процессов в разрядном контуре и экспериментальные исследования показали, что нарастание на­пряжения на активной составляющей импеданса ГРТ определяется:

1. Постоянной времени L/R в случае апериодического процесса (для идеаль­ного коммутатора), где L – индуктивность ГРТ, а R - сопротивление плазмы. При этом Nmf ~ L(ne0)2, что обуславливает определяющую роль ne0 в ограничении ЧСИ генерации;
2. Частотой свободных колебаний в случае колебательного процесса в кон­туре, что обуславливает принципиальную возможность устранения эффекта преимущественного заселения метастабильных уровней на фронте импульса возбуждения. Работа на высокой частоте свободных колебаний характеризу­ется рассогласованием источника питания с нагрузкой. Это приводит к пере­заряду накопительного конденсатора до обратного напряжения Uобр, что на­кладывает определенные ограничения на работу тиратрона. При этом до Uобр заряжаются все емкостные составляющие разрядного контура и ГРТ. Дисси­пация этой энергии будет осуществляться в активной среде в межимпульс­ный период. Данный процесс может обуславливать наличие высокой плотно­сти Nm0, если процесс диссипации энергии и, соответственно, подогрев элек­тронной компоненты плазмы осуществляется в течение всего межимпульс­ного периода, поскольку хорошо известно, что метастабильные состояния эффективно тушатся в столкновениях с остывающими электронами в отсут­ствии источника их подогрева.

Продемонстрировать вышесказанное можно следующим примером. Фор­мируя перед каждым импульсом возбуждения дополнительный импульс, по­догревающий электроны, можно осуществлять заселение метастабильных уровней Nmkr. Это приведет к срыву инверсии в импульсе возбуждения. Из­меняя задержку между дополнительным и возбуждающим импульсами можно судить о скорости релаксации метастабильных состояний в межим­пульсный период, исходя из процесса восстановления характеристик генера­ции в импульсе возбуждения. В то время как, энерговклад от дополнитель­ного импульса демонстрирует уровень энергии, которая должна запасаться в реактивных составляющих импеданса разрядного контура, чтобы сущест­венно ограничить процесс релаксации метастабильных уровней в межим­пульсный период. Прове­денные исследования в Cu-лазере (рис.2) пока­зали, что ограничения энергети­ческих характе­ристик, свя­занные с Nm0, необходимо учи­тывать при ЧСИ возбуж­дения > 100 кГц. Однако когда плазма харак­тери­зуется высокой степенью ионизации, необхо­дим пренебрежимо малый вклад энергии в активную среду, чтобы поддер­живать высо­кую на­селенность ниж­них лазер­ных уровней. В этом случае Nm0 в ак­тивной среде будет опреде­ляться не столько про­цессом релакса­ции, сколько “паразитными” вкладами энергии в межим­пульсный период. Из сказанного следует, что Nmkr является абсолютным фак­тором ограничения ЧЭХ генерации лазеров на самоограниченных переходах. А оптимизация параметров накачки активной среды сводится к выяснению источника “паразитного” энерговклада в межимпульсный период, выяснению механизма диссипации этой энергии в активной среде и роли элементов раз­рядного контура (коммутатора, шунтирующей индуктивности и ГРТ) в огра­ничении скорости нарастания напряжения на активной составляющей импе­данса ГРТ.

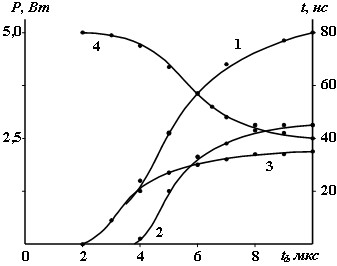
Рис.2.Изменение суммарной средней мощности (1), средней мощности ге­нерации на = 510,6 нм (2) и = 578,2 нм (3), а также времени за­держки генерации от начала им­пульса возбу­ждения (4) в зависимо­сти от времени задержки td между им­пульсами.

2.2. Критическая плотность электронов.

В [10] рассмотрен один из механизмов срыва инверсии в ЛПМ, обуслов­ленный высокой ne0. При рассмотрении причин ограничения использовались простые кинетические модели, непосредственно опирающиеся на экспери­ментальные зависимости временного поведения плотности тока. Это позво­ляет, согласно [10], получить простую оценку критической плотности элек­тронов. В качестве необходимого условия создания инверсии используется известное ограничение Те снизу. Оценка критической плотности электронов в [10] проведена для экспериментальных условий работы [11]. Модельные рас­четы [10] показали, что именно критическая плотность электронов является причиной срыва инверсии в ЛПМ, а не высокая Nm0, как полагалось в [11]. Одной из основополагающих ошибок, как показал анализ, в довольно логич­ном обосновании [10] существования Necr является предположение, что пе­риод квазистационарной ионизации реализуется с момента начала импульса возбуждения. В [10] записана система уравнений, для процесса прямой иони­зации атомов меди и неона, а константы скорости прямой ионизации соот­ветствуют константам скоростей возбуждения резонансных уровней, хотя хорошо известно, что эти константы различаются почти на два порядка. Для определения значение Necr необходимо использовать систему уравнений типа (6), описывающих ионизационный процесс с учетом ступенчатой ионизации с резонансных уровней. Следовательно можно утверждать, что затраты энер­гии на ионизацию в период формирования инверсии в ЛПМ завышены в [10] как минимум на порядок и, в условиях эксперимента [11] не реализуются значения Necr. Тем не менее, если в [10] использовать систему уравнений типа (6), не меняя всей последовательности анализа, то вполне очевидно, что с ростом ne0 в активной среде будут возрастать затраты энергии на разогрев электронов без изменения величины инверсии (если полагать, что по каким то причинам Nm0 пренебрежимо мала). Следовательно, с ростом ne0 должна снижаться эффективность накачки активной среды. Однако энергия им­пульса возбуждения всегда ограничена в реальных условиях работы ЛПМ режимом саморазогрева. В этих условиях возникает определенное ограниче­ние. Оно определяется тем, что для реализации высокой средней мощности генерации необходимо увеличивать ЧСИ возбуждения. С ростом ЧСИ увели­чивается предымпульсная концентрация электронов, а с ростом ne0 необхо­димо увеличивать энергию импульса возбуждения. Это определяет наличие оптимальной ЧСИ генерации, при которой реализуется максимальная сред­няя мощность генерации в саморазогревных ЛПМ, а ne0, следовательно, имеет относительный характер ограничения ЧЭХ генерации лазеров.

Глава III посвящена изучению работы тиратрона в разрядном контуре лазеров. Прове­ден качественный анализ устойчивой работы тиратрона. Пред­ставлены результаты экспериментальных ис­следований, подтверждающие, что тира­троны имеют узкую область устой­чивой работы, определяемую пре­дельными значе­ниями обрат­ного напря­жения на аноде тиратрона. Срок службы тиратрона возрастает с уменьше­нием обратного напряжения (Uобр) на аноде тиратрона и соответствует паспорт­ным значениям при Uобр 3 кВ. Рассматриваются причины: опре­деляющие надежность работы тиратрона, ограничивающие коммутационные характеристики тиратрона, опре­деляю­щие не­стабиль­ность срабатывания тиратронов относительно импульса за­пуска, за­паздывания тока анода и разброса фронта импульса тока анода от импульса к импульсу. Приводятся технические решения, позволяющие уст­ранить вышеперечисленные недос­татки тира­тро­нов. Показано, что низкая допустимая скорость нарастания тока в тиратроне является дополнительным фактором ограничения энергетических характеристик ЛПМ.

Глава IV посвящена изучению влияния шунтирующей индуктивности на энергетические характеристики ЛПМ, а также рассмотрены особенности формирования инверсии в активных средах с квантовым КПД < 20% на при­мере лазера на парах стронция.

Показано, что в реальных условиях работы ЛПМ всегда можно выбрать параметры шунтирующей индуктивности, устраняющие протекание тока за­ряда накопительного конденсатора через ГРТ. При этом в шунтирующей ин­дуктивности запасается энергия во время импульса возбуждения, которая вкладывается в активную среду в ближнем послесвечении разряда ~ 3-5 мкс. Поскольку длительность энерговклада намного меньше межимпульсного пе­риода, то он не должен оказывать существенного влияния на процесс релак­сации метастабильных состояний в межимпульсный период, но обуславли­вает нарастание проводимости плазмы в ближнем послесвечении. Временной ход проводимости плазмы в ближнем послесвечении разряда соответствует временному ходу концентрации электронов в этот период времени, измерен­ному по штарковскому уширению линии водорода H. Проведенный анализ и представленные результаты в данной главе показали, что наблюдаемое на­растание проводимости плазмы в ближнем послесвечении разряда обуслов­лено изменением Те, а не ne. При этом наблюдаемое нарастание ne в измере­ниях по штарковскому уширению линии H не отражает реальный процесс, а связано с погрешностью измерений, точнее с тем, что при обработке резуль­татов не учитывалось влияние возбуждения водорода в ближнем послесвече­нии разряда на интенсивность линии H, которое может осуществляться в процессе тройной рекомбинации.

Показано, что имеется существенное различие в формировании инверсии в лазерах на самоограниченных переходах видимого и ближнего ИК диапа­зонов (Cu, Au, Рb, Bi, SrII и т.д.) и лазерах на самоограниченных переходах щелочноземельных (Sr, Ca) металлов, излучающих на ИК линиях среднего и дальнего диапазона ( 5 мкм). Различие в формировании инверсии определя­ется тем, что в лазерах видимого и ближнего ИК диапазонов (с квантовой эффективностью рабочего перехода условно большей 20%) существует опре­деленное значение Те при которой скорость заселения верхних лазерных уровней начинает превышать скорость заселения нижних лазерных уровней (например, для CuI ~ 1,7 эВ). Следовательно, формирование населенности на рабочих переходах атомов осуществляется группами электронов с разной энергией. В то время как, в лазерах с квантовой эффективностью рабочего перехода (условно) меньше 20%, излучающих на ИК линиях среднего и дальнего диапазона, отсутствуют пороговые условия по накачке. В этом слу­чае в формировании населенности на рабочих переходах участвуют все элек­троны, а величина инверсии определяется отношением сечений возбуждения рабочих лазерных уровней. Поэтому, не смотря на то, что управ­ле­ние характе­ри­стиками излучения лазеров на самоограниченных переходах можно осуществлять через изменение плотности метастабильных состояний подог­ревая электронную компоненту плазмы, данный способ управления не эф­фективен для лазерных переходов с квантовым КПД < 20%. На рис. 3 пред­ставлены зависимости мощностей линий генерации Sr-лазера от напряжения дополнительного импульса для трех разных рабочих емкостей дополнитель­ного канала. В этих экспериментах задержка дополнительного импульса вы­биралась с точки зрения максимального влияния дополнительного импульса при его напряжении 1кВ на выходные параметры трубки. С увеличением энергии (Ср и Uдоп) дополнительного импульса мощность генерации на ~ 3 мкм и ~ 1 мкм постепенно уменьшается и исчезает. Это способствует уве­личению скорости заселения нижних уровней для указанных линий генера­ции атомов и ионов стронция до исчезновения инверсии между лазерными уровнями. В свою очередь мощность генерации на = 6.45 мкм уменьшается при увеличении энергии дополнительного импульса лишь на 30%. Дальней­шее увеличение энергии дополнительного импульса ведет к появлению гене­рации в дополнительном импульсе.

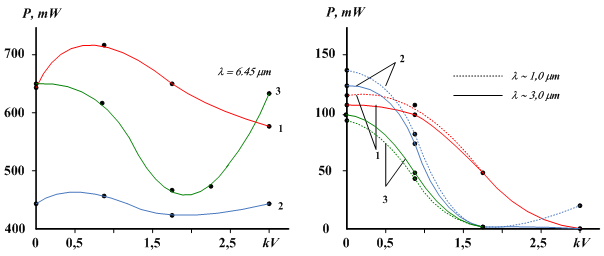
Рис. 4. Зависимости мощности генерации на = 6.45 мкм, ~ 3 мкм, ~ 1 мкм от напряжения дополнительного импульса при рабочей емкости дополнительного ка­нала Ср = 500пФ – 1, Ср = 891пФ – 2, Ср = 1650пФ – 3.

Глава V посвящена изучению влияния конструктивных особенностей ГРТ на ЧЭХ лазеров на самоограниченных переходах атомов металлов. Показано, что существенное влияние на кинетику процессов в активной среде оказы­вает расположение электродов в ГРТ.

Активная среда импульсно-периодических лазеров на парах металлов ха­рактеризуется высокой проводимостью плазмы с ne0 ~ 1013 см-3. Поэтому по­лагалось, что развитие разряда в активной среде осуществляется без стадии пробоя разрядного промежутка. Эквивалентную схему разрядного контура лазера всегда представляют в виде простого колебательного контура в мо­дельных расчетах, а импеданс ГРТ в виде последовательно включенных ак­тивной и индуктивной составляющих, параллельно которым подключена обостряющая емкость. В действительности подобную эквивалентную схему разрядного контура можно использовать только при моделировании процес­сов в ГРТ с электродами, расположенными в горячей зоне разрядного канала. Апериодический процесс в разрядном контуре лазера может наблюдаться только в таких конструкциях ГРТ. Определяющим фактором ограничения ЧЭХ для таких конструкций ГРТ является преимущественное заселение ме­тастабильных состояний на фронте импульса возбуждения и быстрая релак­сация этих состояний в межимпульсный период.

Впервые о наличие пробоя в активных средах с высокой проводимостью плазмы указано в [6]. Проведенный в [7] анализ показал, что в типичных ус­ловиях работы ЛПМ сопротивление разряда в его начальной стадии опреде­ляется в основном не проводимостью нагретой активной части разрядной трубки, где ne0 может быть велико, а процессами на электродах и в холодных приэлектродных областях. Можно предположить [7], что в концевых зонах к приходу следующего импульса возбуждения плотность электронов мала, со­противление, соответственно, велико, и в этих зонах происходит пробой с образованием катодного слоя с большим падением напряжения и контраги­рованием разряда.

Проведенные нами исследования подтверждают наличие пробоя в конце­вых зонах разрядного канала в случае расположения электродов ГРТ в хо­лодных буферных зонах. При этом эквивалентная схема ГРТ существенно отличается (рис.4) от используемой схемы в модельных расчетах. Формиро­вание инверсии осуществляется после пробоя в промежутке “плазма – анод” ГРТ в процессе энерговклада от трех параллельных контуров, образованных собственной емкостью ГРТ, обостряющим и накопительным конденсато­рами, которые определяют ЧЭХ лазера. Наиболее высокая частота свободных колебаний в разрядном контуре и, соответственно, скорость нарастания на­пряжения на активной составляющей импеданса ГРТ определяется первым контуром возбуждения, образованным собственной емкостью ГРТ. Поэтому экспериментально всегда наблюдается повышение КПД лазера с увеличе­нием диаметра разрядного канала ГРТ, т.е. с увеличением собственной емко­сти и снижение оптимальной ЧСИ генерации. Последнее определяется тем, что после импульса возбуждения в собственной емкости ГРТ запасается энергия, которая диссипирует в активной среде в межимпульсный период. Согласно [7], рекомбинационный процесс в концевых зонах разрядного ка­нала происходит намного быстрее, чем в активной среде. Поэтому диссипа­ция энергии, запасаемой в собственной емкости ГРТ, происходит в межим­пульсный период в результате высокочастотных колебаний в контуре с высо­кой добротностью, который образуется из-за наличия составляющих С1 и С3. Моделирование показало, что диссипация этой энергии может наблюдаться (рис.5) в течение всего межимпульсного периода, что поддерживает высокий уровень Nm0. Собственная емкость ГРТ возникает вследствие того, что плазму можно рассматривать как проводник с высокой проводимостью, ко­торая в предымпульсных условиях намного больше проводимости проме­жутка “плазма – анод”. Геометрические размеры плазмы определяются раз­рядным каналом, имеющим определенную диэлектрическую проницаемость. Поэтому плазма и разрядный канал относительно ”земли” или обратного то­копровода лазера образуют конденсатор или длинную линию, в котором плазма является одной из обкладок конденсатора. Заряд обостряющей емко­сти и собственной емкости ГРТ осуществляется в процессе разряда накопи­тельного конденсатора через тиратрон, который ограничивает скорость за­ряда этих емкостей. Поэтому импеданс ГРТ в процессе зарядки можно рас­сматривать как систему с сосредоточенными параметрами, а все точки плазмы будут находиться в течение этого времени под одним потенциалом. В этих условиях электроны в плазме не могут набирать энергию, необходимую для осуществления неупругих соударений.

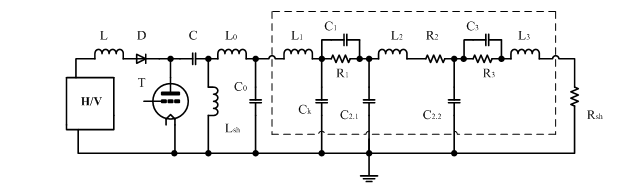
Рис.4. Схема генератора накачки лазера; где пунктирной линией вы­делена эквива­лентная схема ГРТ, H/V – высоковольтный выпрямитель, L – D – зарядные дрос­сель и диод, соответственно, С – накопительный конденсатор, Со – обостряющая емкость, Т – тиратрон, Lsh - шунтирующая индуктивность, Rsh – измерительный шунт (пояс Роговского). Активная, емкостная и индуктивная состав­ляющие импе­данса ГРТ представлены в виде последовательно соединенных R-L-C цепо­чек, где L1 и L3 – индуктивности токовводов ГРТ; R2, L2, C2 – активная, индуктивная и ем­костная составляющие импеданса активной среды ГРТ, соответственно; R1, R3, C1, C3 - активная и емкостная составляющие электродных узлов относительно актив­ной среды, соответственно.

Устранить недостатки и объединить преимущества рассмотренных конструкций ГРТ можно, используя двухимпульсное возбуждение активной среды, когда первым импульсом возбуждения осуществляется формирование (рис.6) собственного поля в резонаторе лазера, а вторым – его усиление. Дан­ный способ накачки позволяет осуществлять управление характеристиками лазерного излучения (рис.7), а так же реализовать систему “генератор-усили­тель” в одном активном элементе с преобразованием ~ 80% энергии генера­ции в излучение с дифракционной расходимостью.

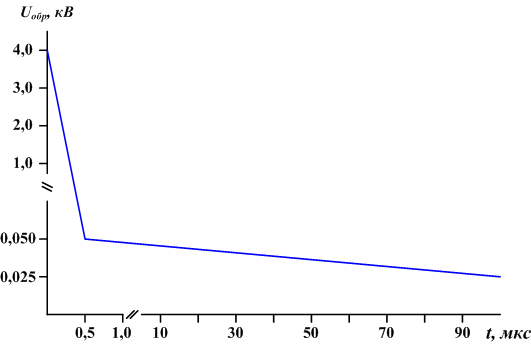
Рис.5. Изменение амплитуды напряжения на ГРТ в межимпульсный период после импульса возбуждения.

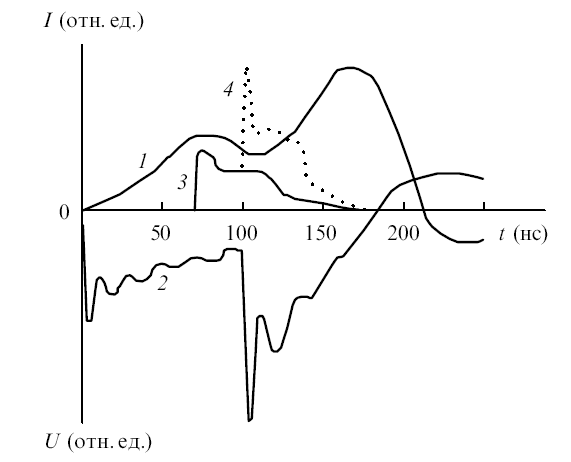
Рис.6. Осциллограммы импульсов тока (1), напряжения (2) на ГРТ и импульса ге­не­рации (3), формируемого в слаботочном импульсе возбуждения. (4) – усиле­ние им­пульса генера­ции (3) сильноточным импульсом возбуждения.

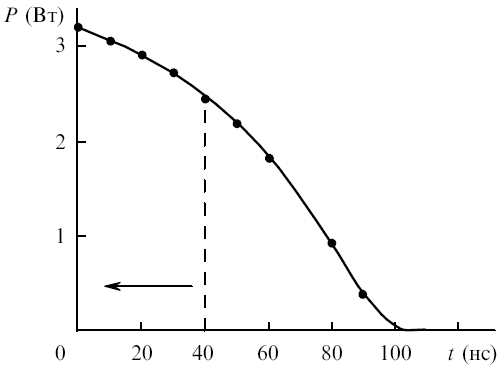
Рис.7. Изменение средней мощности генерации при изменении временного распо­ложения сильноточного импульса возбуждения относительно импульса ге­нерации.

Глава VI посвящена изучению влияния времени развития пробоя в концевых зонах ГРТ на кинетику процессов в активной среде.

В Главе 5 показано, что все точки плазмы находится под одним потенциалом во время зарядки собственной емкости ГРТ от накопительного конденсатора, а разность потенциалов возникает между обкладками собственной емкости ГРТ, т.е. между плазмой и “землей”, имеющей нулевой потенциал. По­скольку анод ГРТ также заземлен, то разность потенциалов возникает между плазмой и анодом. Возникающее напряжение между плазмой и анодом в данном случае можно рассматривать как внешнее поле, которое, как из­вестно, может проникать в плазму на глубину порядка дебаевского радиуса экранирования. Если принять, согласно [6-7], предымпульсные значения Тe ~ 0,25 эВ и среднее предымпульсное значение ne ~ 2,51013 см-3, то глубина проникновения внешнего поля в плазму составляет ~ 1 мкм. Следовательно, только слой плазмы ~ 1 мкм является эмиттером электронов на анод во время зарядки емкостных составляющих ГРТ и разрядного контура лазера. Уход заряда из плазмы на анод должен компенсироваться поступающим зарядом из накопительного конденсатора в этот период времени. Возможность по­добной компенсации обусловлена тем, что в начальный момент (до зарядки емкостных составляющих) разность потенциалов между плазмой и анодом равна нулю. Скорость зарядки емкостных составляющих составляет ~ 4 А/нс (для тиратрона ТГИ1-1000/25), что намного больше скорости нарастания тока в промежутке “плазма – анод” в этот период времени. Из вышесказанного следует, что пробой в промежутке “плазма – анод” может возникнуть только после зарядки емкостных составляющих ГРТ и разрядного контура, т.е. при достижении равенства напряжений на емкостных составляющих и накопи­тельном конденсаторе, что подтверждается экспериментально. На рис. 8. в качестве иллюстрации приведены осциллограммы импульсов тока, проте­кающего через тиратрон, импульса напряжения на ГРТ и тока смещения за­ряда в газоразрядной трубке лазера на парах стронция. Представленные ос­циллограммы наиболее наглядно демонстрируют вышесказанное. Положи­тельная часть осциллограммы (Рис. 8с) отражает скорость и время заряда ем­костных составляющих. Начало процесса заряда совпадает по времени с на­чалом протекания тока через тиратрон и ростом напряжения на ГРТ. Пре­кращение зарядки соответствует максимуму напряжения на ГРТ. Отрица­тельная часть осциллограммы (Рис. 8с) отражает процесс разряда собствен­ной емкости ГРТ. С момента начала разряда наблюдается спад напряжения на ГРТ. Это подтверждает, что пробой промежутка “плазма – анод” в им­пульсно-периодическом режиме работы лазера происходит после заряда ем­костных составляющих ГРТ и разрядного контура, т.е. когда эти емкости за­ряжаются до напряжения сопоставимого с напряжением на накопительном конденсаторе. Поэтому, напряжение “пробоя” промежутка “плазма – анод” не является какой-то определенной величиной, а определяется величиной на­пряжения на накопительном конденсаторе. Следовательно, напряжение про­боя не зависит от расстояния d между разрядным каналом ГРТ и электро­дами. Момент пробоя не означает возникновение разности потенциалов на плазме, а лишь отмечает точку отсчета начала формирования напряжения на плазме. Для возникновения разности потенциалов на плазме электрическая цепь должна быть замкнута, что будет определяться процессом образования электронной лавины, стартовавшей в момент пробоя с поверхности плазмы.

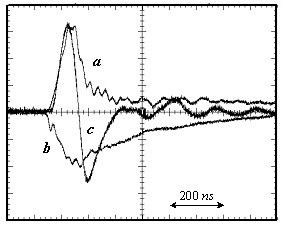
Рис.8. Осциллограммы импульсов тока – а, протекающего через тиратрон, b – на­пряжения на ГРТ и c – тока смещения зарядов. Временной масштаб – 200 нс/на клетку.

В этом случае, время развития про­боя и, соответственно, время нарас­тания напряжения на плазме будет определяться временем прохождения электроном, стартовавшим с поверхности плазмы в момент пробоя, расстоя­ния между плазмой и анодом. Поскольку в процессе ускорения электрона в электрическом поле его энергия на длине свободного пробега может ме­няться от нуля до потенциала ионизации, то средняя скорость движения электрона с поверхности плазмы до анода определяется, как ср = (E/2me)1/2, где Е – энергия электрона, me – масса электрона. Следовательно, время раз­вития пробоя

tфр = d/ср = d/(E/2me)1/2. (9)

Из теории электрических цепей хорошо известно, что главным условием выполнения квазистационарности тока, кроме замкнутости цепи является медленность изменения тока по сравнению со скоростью распространения электромагнитного возмущения по цепи. В этом случае для анализа цепи можно использовать законы Ома и Кирхгофа. Однако часто встречаются длинные цепи передач сигналов или линии не очень длинные, но служащие для передачи сигналов высокой частоты. В этих цепях мгновенные значения тока в различных точках цепи различны, и кроме того, здесь становится су­щественной распределенная емкость отдельных элементов цепи друг к другу. Из вышесказанного следует, что импеданс ГРТ с момента пробоя можно рас­сматривать как систему с сосредоточенными параметрами, если время разви­тия пробоя превышает время распространения электромагнитного поля в ак­тивной среде лазера. В противоположном случае активную среду лазера не­обходимо рассматривать как длинную линию. Если расстояние d выбрать со­измеримое с длиной свободного пробега электрона, то имитируемый элек­трон из плазмы должен набирать энергию равную потенциалу на плазме. Время пробоя будет составлять ~ 0,1 нс при d 2 мм и напряжении на про­межутке “плазма – анод” 10 кВ. В общем случае критерий, определяющий граничное значение напряженности поля Ecr для “быстрого пробоя” можно записать аналогично [12], в виде

i(Ecr, NHe)d = 1, (10) где i - коэффициент Таунсенда, NHe – концентрация буферного газа (гелия) в промежутке “плазма – анод”.

“Быстрый уход электронов” из пограничного слоя плазмы с момента про­боя на анод приводит к нарушению квазинейтральности плазмы на глубину дебаевского радиуса экранирования. Это приводит к поляризации плазмы между пограничными областями и возникновению электрического поля

= 4 = 4eNex, (11)

cтремящемуся восстановить квазинейтральность плазмы в возмущенном слое, где х – толщина разделения пространственного заряда, – поверхностная плотность заряда. Таким образом, поле, возникшее в пограничном с анодом слое плазмы, порождает волну поляризации, которая движется от анода к катоду и достигая катода, восстанавливает квазинейтральность плазмы. При этом, возникающая волна поляризации не меняет потенциал на плазме, что обеспечивает запирание внешних контуров.

На электроны со стороны поля (11) действует также возвращающая сила

F = - e = - (4e2Ne/me)x, (12) которая должна привести к возникновению плазменных колебаний на лен­гмюровской частоте 0. Однако поле заряженной собственной емкости ГРТ может являться фактором, устраняющим действие возвращающей силы. В этом случае вместо плазменных колебаний на ленгмюровской частоте может возникнуть направленное движение ионов к аноду ГРТ вслед за смещением электронов. В процессе резонансной перезарядки формируется пучок быст­рых атомов направленный в сторону анода ГРТ, что должно приводить к осаждению металла в холодной части анода. В результате распространения волны поляризации предымпульсные электроны в плазме набирают энергию направленного движения с фронтом нарастания ~ 0,1 нс и их движение под­держивается полем собственной емкости ГРТ, что должно приводить к воз­никновению диффузного разряда. При этом волна поляризации плазмы должна распространяться от анода к катоду без затухания, что позволяет формировать моноэнергетические электроны в плазме.

Также хорошо известно, что в случае “быстрого замыкания” заряженной линии возникает обратная высокоскоростная волна ионизации [13]. Поэтому в рассматриваемом нами случае мгновенные значения тока в различных точ­ках активной среды различны, здесь нельзя применять законы Ома и Кирх­гофа, нельзя считать распределенные параметры сосредоточенными в одном месте, кроме того, здесь становится существенной и распределенная емкость отдельных элементов цепи друг к другу. В электротехнике быстрых токов прибегают к упрощению. Распределенную линию разбивают на участки dz, меньшие длины волны, и для таких участков применяют теорию квазиста­ционарных токов, т.е. вводят сосредоточенные элементы – R = Rndz; L = Lndz; C = Cndz, где Rn, Ln, Cn  - распределенные параметры на единицу длины, и за­писывают для такого элемента законы Ома и Кирхгофа. Для моделирования процесса формирования высокоскоростной волны ионизации в активной среде мы воспользовались компьютерными программами, применяемыми для моделирования переходных процессов в электротехнических цепях, при этом импеданс активной среды был представлен в виде 10 последовательно включенных цепочек Ln, Cn, Rn – элементов.

Моделирование данного процесса показало, что в плазме протяженно­стью ~ 50 см реализуется бегущая волна с начальной напряженностью у анода ГРТ ~ 1 кВ/см при напряжении на емкостной составляющей активной среды ~ 10 кВ и предымпульсной концентрации электронов ~ 1012 - 1013 см-3. Моделирование проводилось без учета распространения волны поляризации плазмы, что в совокупности представляет весьма сложную задачу. В случае справедливости представленной модели процессов, экспериментально должны реализоваться:

диффузный разряд, и соответственно, равномерное распределение излучения лазера по сечению разрядного канала ГРТ; энергосъем должен возрастать пропорционально объему активной среды; возможность получения генера­ции на всех компонентах парогазовой смеси активной среды; высокая пре­дельная ЧСИ генерации; высокая эффективность накачки активной среды.

В качестве модельной среды в исследованиях использовался лазер на па­рах стронция, для которого характерно наличие генерации, как в случае ио­низационной неравновесности плазмы [1-4], так и рекомбинационной [14].

Исследование Sr-лазера проводилось с ГРТ, разрядный канал которой выполнен из ВеО – керамической трубки внутренним диаметром 2 см и дли­ной 50 см. В спектре излучения наблюдались типичные линии генерации на самоограниченных переходах SrI и SrII при уровне суммарной средней мощ­ности генерации на всех линиях ~ 4 Вт при ЧСИ генерации ~ 20 кГц. Добавка к буферному газу Не ~ 10% Ne, приводила к увеличению средней мощности генерации до ~ 5 Вт. При этом разряд имел диффузный характер, и не на­блюдалось характерной для лазеров на парах металлов привязки разряда к электродам ГРТ в виде катодного и анодного пятен (рис.9с). Анодное и ка­тодное пятна на поверхности электродов наблюдаются только в начальный момент разогрева разрядного канала ГРТ (рис.9a-b). Пленка стронция на аноде ГРТ, нарастающая в процессе работы лазера, отчетливо видна на рис.9.

Измерение вольтамперных характеристик разряда (рис.10) показало, что в начальный момент разрядки накопительного конденсатора парал­лельно заряжаются емкостные составляющие импеданса разрядного контура и ГРТ лазера. Поэтому наблюдается одновременное нарастание напряжения на ГРТ и тока, протекающего через тиратрон. При этом ток, протекающий через ГРТ пренебрежимо мал. После пробоя промежутка “плазма – анод” ГРТ, соответствующий максимуму напряжения на ГРТ, наблюдается нарас­тание тока через ГРТ и возникает генерация. Зная амплитуду напряжения на ГРТ – U, тока – I, протекающего через тиратрон и время заряда емкостных составляющих – t можно оценить их емкость, поскольку С = q/U = It/2U или C = C0 + C2 ~ 300 пФ. Прямые измерения показали, что обостряющая емкость C0 ~ 240-250 пФ, соответственно, собственная емкость ГРТ C2 ~ 50 – 60 пФ. Следовательно, мощность, вводимая в ГРТ от первого контура возбуждения, образованного собственной емкостью ГРТ составляет 60 – 70 Вт при частоте следования импульсов возбуждения ~ 20 кГц. Первый контур должен определять формирование инверсии в активной среде лазера, а остальные, образованные обостряющей емкостью и накопи­тельным конденсатором, обуславливают дополнительный энерговклад, при­водящий к существенному снижению практического КПД лазера. В этом случае физический КПД лазера относительно энерговклада от первого кон­тура должен составлять ~ 6-8%.

Рис.9. Изменение анодного пятна на поверхности электрода по мере разогрева раз­рядного канала ГРТ, а – разряд в гелии, b – расконтракция разряда, c – режим на­чала генерации.

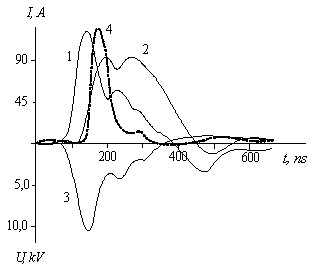
Однако чтобы действительно оценить физи­ческий КПД лазера, необходимо знать – осуществляется в этот период вре­мени или нет подпитка из внешних контуров. Для этого необходимо после­довательно “исключить” из накачки третий и второй контура.

Рис.10. Импульсы тока, протекаю­щего через тиратрон – 1 и через ГРТ – 2, импульс напряжения на ГРТ – 3 и импульс генерации – 4

Только в случае, если не будет на­блюдаться уменьшение средней мощности генерации, можно ут­верждать, что накачка активной среды осуществляется энергией, запасаемой в емкостной состав­ляющей импеданса ГРТ. Для того чтобы “исключить” из накачки третий и второй контур достаточно между обостряющей емкостью и ГРТ ввести ин­дуктивность (использовали индуктивность ~ 20 мкГн). Введение индуктив­ности приводит к резкому снижению частоты свободных колебаний второго и третьего контуров, и исключает их из процесса формирования инверсии. Проведенные нами исследования подтвердили, что в формировании инвер­сии участвует только первый контур возбуждения, а энерговклады от второго и третьего контуров в активную среду не осуществляются в течение этого времени. При этом реализуется режим практически полного согласования ис­точника питания с нагрузкой, что позволяет рассчитывать на существенное увеличение ЧСИ генерации. Накачка активной среды лазера на парах строн­ция цугом сдвоенных импульсов в условиях саморазогревного режима ра­боты лазера показала, что генерация наблюдается во втором импульсе воз­буждения при задержке между импульсами возбуждения вплоть до 1.35 мкс, а предельная ЧСИ генерации, соответственно, может достигать ~ 1 МГц. Экспериментальные исследования также подтвердили, что наблюдается ли­нейный рост средней мощности генерации с увеличением объема активной среды лазера на парах стронция (рис.11). При объеме активной среды лазера 650 см3 суммарная средняя мощность на всех линиях генерации составляла 13,6 Вт. Отклонение от линейного нарастания средней мощности генерации наблюда­лось с уменьшением объема активной среды (< 150-200 см3), что связано с пре­небрежимо малой величиной собственной емкости ГРТ. Исследование рас­

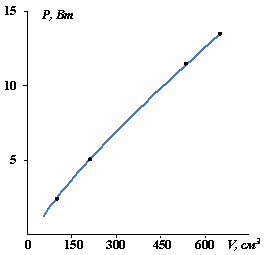
пределения мощности генерации по диаметру разрядного канала проводи­лось с ГРТ, диаметр разрядного канала которой составлял 30 мм, а объем ак­тивной среды 650 см3, соответственно.

Рис.11. Зависимость средней мощности гене­рации лазера на парах стронция от величины активного объема ГРТ [15].

Это распределение представлено на рис.12 при мощностях генерации ~ 4,6 Вт; 7,4 Вт; 9 Вт, которое показывает, что распределение достаточно равномерное. Излучение занимает ~ 70 % от всей рабочей площади или 85% его диаметра по полувысоте амплитуды мощности генерации.

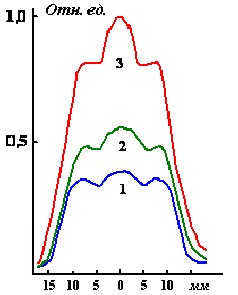
Рис.12. Распределение мощности излучения Sr-лазера по диаметру активного объ­ема. Мощность генерации: 1 – 4,6 Вт; 2 – 7,4 Вт; 3 – 9 Вт, диаметр канала 30 мм [15].

Полученные в [16] результаты расчета условий для кривой убегания в па­рах меди соизмеримы с условиями накачки активной среды лазера на парах стронция в наших экспериментах, что указывает на принципиальную воз­можность перевода предымпульсных электронов в режим убегания. Доказа­тельством осуществления такого режима может являться реализация одно­временной генерации не только на самоограниченных переходах атома и иона стронция, но и на переходах буферных газов, например, на самоограни­ченных переходах атома гелия. Поскольку возможности повышения напря­жения на накопительном конденсаторе ограничены тиратроном, то исследо­валась возможность перевода предымпульсных электронов в режим убегания за счет снижения концентрации атомов стронция в разряде. Полагалось, что необходимые условия для перевода электронов в режим убегания должны возникнуть в результате снижения концентрации атомов стронция за счет выноса металла в холодные буферные зоны в процессе длительной работы лазера. Именно в этих условиях нами была получена генерация на самоогра­ниченных переходах SrI и SrII, атома гелия (21P1 – 21S0) – = 2058 нм и пе­реходах 2s – 2p атома неона.

В ПРИЛОЖЕНИИ рассмотрены возможности увеличения средней мощ­ности ге­нерации ЛПМ за счет увеличения рабочего объема лазера при соот­ветствующем увели­чении коммутируемой энергии в условиях, когда комму­тационные возможности ис­пользуемых для накачки активной среды ком­му­таторов ограничены. Рассмотрены раз­личные способы решения этой про­блемы за счет параллельного и поочередного вклю­чения нескольких комму­таторов, разделения функций возбу­ж­дения и нагрева активной среды - за счет введения омических нагревате­лей в ГРТ, использования сдвоенных им­пульсов на­качки. Приводятся примеры кон­крет­ной реализации полученных резуль­та­тов в виде приборных образцов лазерной тех­ники для различных приме­не­ний.

ЗАКЛЮЧЕНИЕ

Параметрические исследования лазеров на самоограниченных переходах атомов и ионов металлов, проводимые в течение почти 40 лет многими ис­следователями, позволили установить основные закономерности изменения частотно-энергетических характеристик лазерного излучения от параметров накачки. За истекшее время неоднократно проводилось обобщение результа­тов исследований [1-4] с целью объяснить наблюдаемые зависимости с по­зиций лазерной физики, физики газового разряда, физики низкотемператур­ной плазмы. В настоящей работе предпринята попытка объяснить наблюдае­мые зависимости с позиций радиофизики, т.е. исходя из теории нелинейных электрических цепей; рассмотрены процессы в разрядном контуре лазеров на самоограниченных переходах и их влияние на кинетику процессов в актив­ной среде. Совокупность радиофизического и традиционных методов анализа процессов в активной среде и разрядном контуре позволила:

1. Определить – зависимость изменения эквивалентной схемы ГРТ от распо­ложения электродов; момент начала накачки активной среды в случае распо­ложения электродов в холодных буферных зонах ГРТ; роль собственной ем­кости ГРТ в обострении фронта импульса возбуждения и подогреве электро­нов в межимпульсный период; факторы, определяющие время развития про­боя; два предельных случая ограничения частотно - энергетических характе­ристик лазеров.

При этом показано, что развитие пробоя в концевых зонах ГРТ и наличие трех параллельных контуров возбуждения (в случае расположения электро­дов в холодных буферных зонах ГРТ) объясняет экспериментально наблю­даемые зависимости частотно-энергетических характеристик лазеров на са­моограниченных переходах. Поскольку релаксация метастабильных состоя­ний в межимпульсный период связана с процессом диссипации энергии соб­ственной емкости ГРТ, то ограничение ЧСИ генерации, обусловленное про­цессом релаксации метастабильных состояний, следует рассматривать как техническую причину, устраняя которую можно повышать среднюю мощ­ность генерации. Однако затруднительно повысить практический КПД лазера в условиях, когда импеданс активной среды является системой с сосредото­ченными параметрами, что обусловлено неэффективностью использования энергии, запасаемой в накопительном конденсаторе. По этой причине КПД лазеров на самоограниченных переходах до настоящего времени на порядок ниже прогнозируемого.

2. Показать принципиальную возможность и продемонстрировать путь техни­ческой реализации (Патенты РФ №2082263; № 2230409; №2237955) управления населенностью метастабильных состояний в рекомбинирующей плазме. Данный эффект можно применять для повышения эффективности ла­зерного разделения изотопов, поскольку позволяет использовать для селек­тивного возбуждения изотопов непосредственно излучение лазеров на само­ограниченных переходах. По крайней мере, для разделения изотопов тех элементов, на которых получена генерация на самоограниченных переходах.
3. Предсказать – условия “сверхбыстрого пробоя”, когда электроны, имити­руемые из плазмы на анод, с момента пробоя переходят в режим убегания в промежутке “плазма – анод”.

При этом экспериментально показано для лазера на парах стронция, что в условиях “сверхбыстрого пробоя” реализуется равномерное распределение излучения по сечению разрядного канала ГРТ, энергосъем возрастает про­порционально объему активной среды, предельная частота следования им­пульсов генерации может достигать ~ 1 МГц, а эффективность ~ 6-8%. Это позволяет рассчитывать на увеличение оптимальной ЧСИ генерации до ~ 100 кГц в лазерах на парах металлов и оценить достижимый уровень средней мощности генерации в лазере на парах стронция ~ 100 – 200 Вт, а в лазере на парах меди ~ 1,0 – 1,5 кВт с литрового объема активной среды.

Очевидно, что необходимо детальное изучение механизма формирования разряда и инверсной населенности в условиях “сверхбыстрого пробоя” для выяснения энергетического потенциала активной среды, что обуславливает необходимость проведения дальнейших исследований. При этом независимо можно проводить параметрические исследования энергетических характери­стик лазеров на парах металлов, поскольку технический путь реализации “сверхбыстрого пробоя” продемонстрирован, как и его преимущества отно­сительно импульсно-периодического разряда, когда импеданс активной среды проявляет себя как система с сосредоточенными параметрами.

Основные результаты диссертации опубликованы в работах:

1. Воронов В.И., Кирилов А.Е., Солдатов А.Н., Федоров В.Ф., Юдин Н.А. Высокочас­тотная коммутация большой мощности // ПТЭ. – 1982. – №1. – С. 151-152.
2. Воронов В.И., Евтушенко Г.С., Егоров А.Л., Елаев В.Ф., Карманов Г.А., Мальцев А.Н., Мирза С.Ю., Суханов В.Б., Солдатов А.Н., Федоров В.Ф., Филонов А.Г., Юдин Н.А. Лазер на красителях с распределенной обрат­ной связью и накачкой лазером на парах меди со ста­билизацией выход­ных характеристик // Оптика атмосферы. – 1988. – №1. – С.86-91.
3. Гарагатый С.Н., Пеленков В.П., Юдин Н.А. Лазер на парах меди с незави­симым по­догревом “Милан - М/2Е” // Квантовая электроника. – 1988. – Т. 15. – С. 1974-1975.
4. Демкин В.П., Солдатов А.Н., Юдин Н.А. Эффективность лазера на парах меди // Оптика ат­мосферы и океана. – 1993. – Т. 16. – №6. – С. 659-665.
5. Солдатов А.Н., Федоров В.Ф., Юдин Н.А. Эффективность лазера на парах меди с частичным разрядом накопительной емкости // Квантовая элек­троника. – 1994. – Т. 21(8). – С. 733-734.
6. Soldatov A.N. and Yudin N.A. Excitation Efficiency of Working Transitions in Copper-Vapour Lasers // J. of Russian Laser Research. – 1995. – Vol. 16. – №2. – Р. 128-133.
7. Skripnitenko A.S., Soldatov A.N., Yudin N.A. Method of Two-pulse Fre­quency Regulation of Cop­per-Vapour Laser Parameters // J. of Russian Laser Research. – 1995. – Vol. 16. – №2. – Р. 134-137.
8. Солдатов А.Н., Суханов В.Б., Федоров В.Ф., Юдин Н.А. Исследование лазера на па­рах меди с повышенным КПД // Оптика атмосферы и океана. – 1995. – Т. 8. – №11. – С. 1626-1636.
9. Елаев В.Ф., Солдатов А.Н., Юдин Н.А. Исследование поведения проводи­мости плазмы ла­зера на парах меди // Оптика атмосферы и океана. – 1996. – Т. 9. – №2. – С. 169-173.
10. Воронов В.И., Полунин Ю.П., Солдатов А.Н., Кирилов А.Е., Шумейко А.С., Юдин Н.А. Ла­зер на парах бромида меди с воздушным охлажде­нием и средней мощностью генерации 10-15 Вт // Оптика атмосферы и океана. – 1998. – Т. 11. – №2-3. – С. 187-188.
11. Юдин Н.А. Устойчивость работы тиратрона в разрядном контуре лазеров на самоог­рани­ченных переходах // Оптика атмосферы и океана. – 1998. – Т. 11. – №2-3. – С. 213-215.
12. Воронов В.И., Солдатов А.Н., Суханов В.Б., Юдин Н.А. Медицинская уста­новка на базе ла­зера на парах меди для дерматологии // Оптика атмо­сферы и океана. – 1998. – Т.11. – №2-3. – С. 240-242.
13. Юдин Н.А. Энергетические характеристики лазера на парах меди в об­ласти устойчи­вой ра­боты тиратрона // Квантовая электроника. – 1998. – Т. 25. – №9. – С. 795-798.
14. Юдин Н.А., Климкин В.М., Прокопьев В.Е. Оптогальванический эффект в лазере на самоог­раниченных переходах атома меди // Квантовая электро­ника. – 1999. – Т. 28. – №3. – С. 273-276.
15. Юдин Н.А., Климкин В.М., Прокопьев В.Е., Калайда В.Т. Эксперименталь­ные на­блюдения ступенчатой ионизации атома Cu в ак­тивной среде Cu-лазера // Известия вузов. Физика. – 1999. – №9. – С. 128-132.
16. Юдин Н.А. Влияние параметров разрядного контура на частотно - энергети­ческие ха­рактери­стики генерации лазера на самоограниченных переходах атома меди // Квантовая электро­ника. – 2000. – Т. 30. – №7. C. 583-586.
17. Юдин Н.А. Погрешность измерения концентрации электронов в лазере на парах меди по штарковскому профилю линии водорода // Оптика атмо­сферы и океана. – 2001. – Т. 14. – №11. – С. 1022-1026.
18. Юдин Н.А. Оптимальные режимы работы лазера на парах меди в усло­виях эффек­тивной на­качки // Оптика атмосферы и океана. – 2002. – Т. 15. –№3. – С. 228-233.
19. Юдин Н.А. Влияние параметров коммутатора на эксплуатационные харак­теристики лазера на парах меди // Квантовая электроника. – 2002. – Т. 32. – №9. – С. 815-819.
20. Полунин Ю.П., Юдин Н.А. Управление характеристиками излучения ла­зера на па­рах меди // Квантовая электроника. – 2003. – Т. 33, – №9. – С. 833-835.
21. Юдин Н.А. Ограничение эффективности лазера на парах меди и пути его преодоле­ния // Оптика атмосферы и океана. – 2004. – Т. 17. – №2-3. – С. 140-145.
22. Юдин Н.А. Влияние предымпульсных параметров активной среды на харак­тери­стики гене­рации лазера на парах меди // Оптика атмосферы и океана. – 2004. – Т.17. – №8. – С. 689-691.
23. Kazaryan M.A., Lyabin N.A., Yudin N.A. Prospects for further development of self-heated lasers on the self-contained transitions of a copper atom // Journal of Russian laser Re­search. – 2004. – Vol. 25. – №3. – P. 267-297.
24. Kazaryan M.A., Lyabin N.A., Soldatov A.N. and Yudin N.A. Role of the den­sity of lower laser levels in the control of generation parameters of copper va­por laser // Journal of Russian laser Re­search. – 2005. – Vol. 26. – №5. – P. 373-379.
25. Юдин Н.А. Влияние предымпульсных параметров плазмы на частотно-энергетические характеристики лазера на парах меди. //Оптика атмо­сферы и океана. – 2006. – Т.19. – №2-3. – С. 145-150.
26. Бохан П.А., Закревский Д.Э., Ким В.А., Фатеев Н.В., Юдин Н.А. Тушение атомов Pb(6p2 1D2) в столкновениях с молекулами // Химическая физика. – 2007. – Т. 26. – №11. – С. 15-21.
27. Юдин Н.А., Суханов В.Б., Губарев Ф.А., Евтушенко Г.С. О природе фан­томных токов в активной среде лазеров на самоограниченных переходах атомов металлов // Квантовая электроника. – 2008. – Т. 38. – №1. – С. 23-29.
28. Солдатов А.Н., Юдин Н.А., Полунин Ю.П., Реймер И.В., Хохряков И.В. Импульсно-периодический лазер на RM-переходах гелия и стронция // Известия вузов. Физика. – 2008. – №1. – С. 6-9.
29. Солдатов А.Н., Юдин Н.А., Васильева А.В., Полунин Ю.П., Чеботарев Г.Д., Латуш Е.Л., Фесенко А.А. О предельной частоте следования импульсов генерации ионного самоограниченного лазера на парах стронция // Квантовая электроника. – 2008. – Т. 38. – №11. – С. 1009-1015.
30. Солдатов А.Н., Юдин Н.А., Васильева А.В., Полунин Ю.П., Латуш Е.Л.,Чеботарев Г.Д., Фесенко А.А. О предельной частоте следования импульсов генерации самоограниченного He-Sr+ лазера // Оптика атмосферы и океана. – 2008. – Т. 21. – №8. – С. 696-699.
31. Солдатов А.Н., Юдин Н.А., Васильева А.В., Полунин Ю.П. Эффективность накачки лазера на парах стронция в условиях бегущей волны возбуждения // Известия вузов. Физика. – 2008. – №12. – С. 79-87.
32. Полунин Ю.П., Солдатов А.Н., Юдин Н.А. Формирование инверсии в лазерах на самоограниченных переходах атомов металлов в условиях сверхбыстрого пробоя // Оптика атмосферы и океана. – 2009. – Т.22. - №11. С.1051-1056.
33. Солдатов А.Н., Юдин Н.А. Способ возбуждения импульсных лазеров на самоограни­ченных переходах // А.с. СССР №1101130. – 1982.
34. Воронов В.И., Юдин Н.А. Импульсный лазер на парах веществ // А.с. СССР №1253397. – 1984.
35. Пеленков В.П., Прокопьев В.Е., Юдин Н.А. Импульсный лазер на парах веществ // А.с. СССР №1445496. – 1986.
36. Воронов В.И., Юдин Н.А. Импульсный лазер на парах химических элемен­тов // А.с. СССР №1676410. – 1989.
37. Скрипниченко А.С., Солдатов А.Н., Юдин Н.А. Способ возбуждения им­пульсных ла­зеров на самоограниченных переходах // Патент РФ №2082263. – 1997.
38. Воронов В.И., Кирилов А.Е., Солдатов А.Н., Юдин Н.А. Импульсный ла­зер на парах химических элементов // Патент РФ № 2230409. – 2004.
39. Юдин Н.А. Импульсный лазер на парах химических элементов // Патент РФ № 2175158. – 2001.
40. Юдин Н.А. Импульсно-периодический лазер на парах химических элемен­тов с управляе­мыми параметрами генерации // Патент РФ №2237955. – 2004.
41. Юдин Н.А. Способ возбуждения импульсного лазера на самоограничен­ных перехо­дах // Патент РФ №2242828. – 2004.
42. Юдин Н.А. Импульсно-периодический лазер на парах химических элемен­тов // Патент РФ №2254651. – 2005.
43. Воронов В.И., Юдин Н.А. Генератор с умножением напряжения // Патент РФ №2288536. – 2006.

Цитируемая литература.

1. Петраш Г.Г. Импульсные газовые лазеры // УФН. – 1971. – Т.105. – С. 645-676.
2. Солдатов А.Н., Соломонов В.И. Газоразрядные лазеры на самоограни­чен­ных пере­хо­дах в парах металлов / – Новосибирск: Наука. – 1985. – 151 с.
3. Батенин В.М., Бучанов В.В., Казарян М.А., Климовский И.И., Молодых Э.И. Ла­зеры на самоограниченных переходах атомов металлов / – М.: На­учная книга. – 1998. – 544 с.
4. C.E. Litlle. Metal Vapour Lasers. Physics, Engineering and Application / – New York: John Wiley & Sons. – 1999. – 620 p.
5. Вохмин П.А., Климовский И.И. Предельные характеристики лазеров на самоограниченных переходах // Теплофизика высоких температур. – 1878. – Т. 16. – Вып. 5. – С. 1080-1085.
6. Hogan G.P., Webb C.E. Pre-ionization and discharge breakdown in the cop­per va­pour laser: the phantom current // Optics Communications. – 1995. – Vol. 117. – №5. – P. 570-579.
7. Земсков К.И., Исаев А.А., Петраш Г.Г. Развитие разряда в импульсных лазерах на парах металлов // Квантовая электроника. – 1999. – Т. 27. – №2. – С. 183-188.
8. Бохан П.А., Герасимов В.А., Соломонов В.И., Щеглов В.Б. О механизме генерации ла­зера на парах меди // Квантовая электроника. – 1978. – Т. 5. – №10. –С. 2162-2173.
9. Carman R.J., Brown D.J.W., Piper J.A. A self-consistent model for the dis­charge kinetics in a high-repetition-rate copper-vapor laser // IEEE J. Quantum Electronics. – 1994. – Vol. 30. – №8. – P. 1876-1895.
10. Яковленко С.И. Критическая плотность электронов при ограничении час­тоты сле­до­вания импульсов в лазере на парах меди // Квантовая электро­ника. – 2000. – Т. 30. – №6. – С. 501-505.
11. Исаев А.А., Михкельсоо В.Т., Петраш Г.Г. и др. Кинетика возбуждения рабочих уровней лазера на парах меди в режиме сдво­енных импульсов // Квантовая электроника. – 1988. – Т. 15. – №12. – С. 2510-2513.
12. Тарасенко В.Ф., Яковленко С.И. Механизм убегания электронов в плот­ных газах и формирование мощных субнаносекундных электронных пучков // УФН. – 2004. – Т.174. – С. 953-971.
13. Василяк Л.М., Костюченко С.В., Кудрявцев Н.Н., Филюгин И.В. Высоко­скоростные волны ионизации при электрическом пробое // УФН. – 1994. – Т. 164. – С. 263-285.
14. Иванов И.Г., Латуш Е.Л., Сэм М.Ф. Ионные лазеры на парах металлов / – М.: Энергоатомиздат. – 1990. – 256 с.
15. Soldatov A.N., Filonov A.G., Polunin Yu.P., and Sidorov I.V. SrI- and SrII-Vapor Laser Active Volume Scaling // The 8-th International Symposium on Laser Physics and Laser Technologies. Tomsk. – 2006. – P.5-10.
16. Ткачев А.Н., Феденев А.А., Яковленко С.И. Коэффициент Таунсенда и кривая ухода для паров меди // Письма ЖТФ. – 2007. – Т. 33. – вып.2. – С. 68-73.
17. Бохан П.А., Бучанов В.В., Закревский Д.Э., Казарян М.А., Калугин М.М., Прохоров А.М., Фатеев Н.В. Лазерное разделение изотопов в ато­марных парах / – М.: Физматлит. – 2004. – 208 с.