Томография плазменно-пылевых структур
На правах рукописи
УДК 533.9.082.5
Бульба Артём Владимирович
ТОМОГРАФИЯ ПЛАЗМЕННО-ПЫЛЕВЫХ СТРУКТУР
Специальность 01.04.04 – физическая электроника
Автореферат диссертации на соискание учёной степени кандидата физико-математических наук
Петрозаводск
2007
Работа выполнена на кафедре информационно-измерительных систем
и физической электроники физико-технического факультета
Петрозаводского государственного университета.
| Научный руководитель: | доктор физ.-мат. наук, профессор Хахаев Анатолий Диамидович |
| Официальные оппоненты: | доктор физ.-мат. наук, профессор Герасимов Геннадий Николаевич кандидат физ.-мат. наук, доцент Карасёв Виктор Юрьевич |
| Ведущая организация: | Объединённый институт высоких температур РАН |
Защита состоится «2» ноября 2007 г. на заседании диссертационного совета К 212.190.01 при Петрозаводском государственном университете по адресу: г. Петрозаводск, пр. Ленина, д. 33.
Отзывы направлять по адресу:
185910, г. Петрозаводск, пр. Ленина 33, ПетрГУ,
ученому секретарю диссертационного совета К 212.190.01.
С диссертацией можно ознакомиться в библиотеке Петрозаводского государственного университета.
Автореферат разослан «27» сентября 2007 г.
Учёный секретарь диссертационного совета К 212.190.01
![]()
доктор физ.-мат. наук, профессор
Фофанов Анатолий Дмитриевич ___________
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность работы
При определенных условиях в плазме, в частности, в тлеющем разряде постоянного тока в газах из введенных в плазму макрочастиц
размером от нескольких до сотен микрометров возникают самоупоря-
доченные плазменно-пылевые структуры. В случае высокой степени упорядоченности структуры называют “плазменным кристаллом”.
При диагностике пылевых образований особую роль играет выяснение геометрических параметров формируемой в плазме структуры пылевых частиц. Традиционно пространственная диагностика плазменно-пылевых структур сводится к анализу их изображений, полученных в лазерном “ноже”, т. е. в каждый момент времени регистрируется одно горизонтальное или вертикальное изображение структуры, не отражающее распределение частиц в пространстве, если речь не касается исследования монослойных плазменных образований. Достоверность получаемых таким способом результатов зависит от толщины “ножа” и характера структуры; в некоторых случаях возможны значительные ошибки как
в оценке среднего расстояния между частицами, так и в виде парной
корреляционной функции, характеризующей степень упорядоченности структуры. В некоторых экспериментах плазменно-пылевые объекты наблюдались путём горизонтального сканирования вертикальным лазерным “ножом”. При этом осуществлялась запись положения каждой частицы с помощью телекамеры. Полная длительность такого сканирования составляла более десятка секунд, что совершенно неприемлемо в случае осцилляции частиц. Использование же классической стереоскопической системы машинного зрения позволяет осуществлять реконструкцию только приблизительно, поскольку остаётся не решённой задача сопряжения характерных точек изображений.
Поэтому существует необходимость развивать методы оптической томографии применительно к задаче пространственной диагностики пылевых структур, позволяющие получать полную и достоверную информацию о пространственном распределении частиц в плазменно-пылевых образованиях.
Цель работы, задачи
Главная цель данной работы – на основе оптической томографии разработать метод пространственной диагностики пылевых структур, позволяющий получать полную и достоверную информацию о распределении частиц в плазменно-пылевых образованиях.
Для достижения этой цели необходимо решить ряд задач:
- Проанализировать существующие оптические методы пространственной диагностики плазменно-пылевых структур.
- Адаптировать метод оптической томографии применительно
к задаче пространственной диагностики пылевых структур. - Сформулировать ограничения и условия применимости метода.
- Разработать алгоритм реализации метода, учитывая ограничения, накладываемые используемой аппаратурой и условиями проведения эксперимента.
- Разработать необходимое ПО. Проверить работоспособность
и эффективность разработанного алгоритма с использованием модельных и экспериментальных проекционных данных. - Предложить способ подготовки экспериментально полученных изображений структур для дальнейшей обработки разработанным алгоритмом томографии.
- Проиллюстрировать работоспособность предложенного метода
и алгоритма его реализации определением распределения частиц в малых пылевых структурах в тлеющем разряде постоянного тока.
Научная новизна
- Развит метод оптической томографии применительно к задаче пространственной диагностики плазменно-пылевых образований.
- Сформулированы ограничения и условия применимости развитого метода.
- Предложен и реализован новый алгоритм томографии, увеличивающий надёжность и объективность получения информации о пространственном распределении частиц в пылевых образованиях.
- Впервые предложенным методом в тлеющем разряде постоянного тока проведено исследование зависимости межчастичных расстояний трехмерной пылевой структуры от условий разряда.
Научно-практическая значимость работы
Развитая методика, разработанный алгоритм и созданное программное обеспечение позволяют решать целый класс задач, в которых ключевым моментом является выяснение пространственных геометрических параметров формируемой в плазме структуры пылевых микрочастиц: расстояния между частицами и степень упорядоченности структуры.
Так, например, разработанная методика необходима при исследовании переходной области между различными типами кристаллических структур пылевых образований для настоящего 3-х мерного случая,
исследовании микроскопической геометрии структурного перехода, его стабильности и динамики, отклика на различные типы малых колебательных возмущений, изучения дислокации кристаллической решетки и трёхмерный анализ дефектов.
Изучение плазменных кластеров (как двумерных, так и трёхмерных) представляет собой отдельную, очень интересную, развивающуюся область исследований. Здесь поставлено множество вопросов, в решение которых представленная методика может сыграть существенную роль, как инструмент контроля геометрических параметров:
– одной из наиболее интересных проблем является образование центров кристаллизации, переход от “пылевой” молекулы к молекулярному кластеру и, затем, к твердому состоянию.
– проблема непрерывного перехода малых пылевых кластеров
с небольшим количеством пылинок к трёхмерным или двумерным “кристаллам” с многими пылинками.
– исследования кластеров, образованных пылинками одного размера, на однородном фоне пылинок другого размера с целью определения роли коллективного взаимодействия в комплексной плазме.
– исследование двойных смесей (кластеров с пылинками различного размера) и неоднородных кластеров.
Результаты разработки комплекса программных средств могут быть использованы и уже активно используются в научно-образова-
тельном процессе при подготовке специалистов по физической электронике и информационно-измерительной технике в Петрозаводском государственном университете.
На защиту выносятся:
- Метод оптической томографии, адаптированный применительно к задаче пространственной диагностики плазменно-пылевых структур, для которого сформулированы ограничения и условия применимости.
- Разработанный алгоритм томографии, реализованный в приложении к задаче пространственной диагностики пылевых структур, позволяющий итеративно находить оптимальное решение, повышающий объективность и надёжность получения информации.
- Набор программных модулей “Tomography 2”, основанный на предложенном алгоритме, в реализации которых учитывалось влияние используемых оптических систем регистрации и зашумленность проекционных данных
- Зависимости межчастичных расстояний трехмерной пылевой структуры из полидисперсного порошка с диаметром частиц от нескольких единиц до нескольких десятков микрон от токов и давлений
в тлеющем разряде постоянного тока в Ar.
Апробация работы
Содержание работы докладывалось на Международной конференции Оптических Обществ Дании, Финляндии, Норвегии и Швеции «Северная оптика 2003» (г. Эспоо, Финляндия, 16–18 июня 2003 г.), Международной конференции «Образование и обучение в оптике и фотонике (ETOP)» (г. Туссон, USA, штат Аризона, 5–9 октября 2003 г.),
IV международном симпозиуме по теоретической и прикладной плазмохимии ISTAPC-2005 (г. Иваново, Россия, 13–18 мая 2005 г.), V международной конференции «Физика плазмы и плазменные технологии» PPPT-5 (г. Минск, Белоруссия, 18–22 сентября 2006 г.), IV Курчатовской молодежной научной школе (г. Москва, 20–22 ноября 2006 г.), Всероссийской (с международным участием) конференции “Физика низкотемпературной плазмы – 2007” (г. Петрозаводск, 24–28 июня 2007 г.).
Успешно пройдена процедура государственной регистрации в «На-
циональном информационном фонде неопубликованных документов» разработки, предъявленной в отраслевой фонд алгоритмов и программ: программа для определения пространственного расположения набора точечных объектов методом оптической реконструктивной томографии “Tomography 2” (номер государственной регистрации: 50200701083 от 28.05.2007). Отраслевым фондом алгоритмов и программ выдано свидетельство об отраслевой регистрации разработки № 8356.
Федеральной службой по интеллектуальной собственности, патентам и товарным знакам (РОСПАТЕНТ) выдано свидетельство об официальной регистрации программы для ЭВМ “Tomography 2” (объекту регистрации присвоен регистрационный № 2007612629 от 20.06.2007).
Пройдена процедура государственной регистрации в «Национальном информационном фонде неопубликованных документов» раз-
работки, предъявленной в отраслевой фонд алгоритмов и программ: программа для обучения алгоритмам реконструктивной томографии “Tomography” (номер государственной регистрации: 50200700997 от 15.05.2007). Отраслевым фондом алгоритмов и программ выдано свидетельство об отраслевой регистрации разработки №8286.
Федеральной службой по интеллектуальной собственности, патентам и товарным знакам (РОСПАТЕНТ) выдано свидетельство об официальной регистрации программы для ЭВМ “Tomography” (объекту регистрации присвоен регистрационный № 2007611674 от 20.04.2007).
Разработанные программы прошли успешную проверку в ходе экспериментальных исследований на кафедре информационно-изме-
рительных систем и физической электроники Петрозаводского государственного университета и в Научно-образовательном центре по фундаментальным проблемам приложений физики низкотемпературной плазмы, а также в лабораторных практикумах студентов по курсам: “оптические методы диагностики плазмы”, “физические основы получения информации”.
Список работ, опубликованных по результатам диссертации, приведён в конце автореферата.
Структура и объём диссертации
Диссертация состоит из введения, пяти глав, заключения и при-
ложения. Работа содержит 120 страниц, 74 рисунка, 6 таблиц. Список использованной литературы включает 54 наименования.
Благодарности
Работа выполнена, благодаря финансовой поддержке по гранту RUX0-000013-PZ-06 (НОЦ «Плазма») Американского фонда гражданских исследований и развития, а также Министерства образования
и науки РФ и правительства Республики Карелии.
СОДЕРЖАНИЕ РАБОТЫ
Во введении обосновывается выбор темы работы, её актуальность, определена цель диссертационной работы и задачи, которые необходимо решить. Показана научная и практическая значимость работы, описаны основные результаты, полученные в ходе работы и выносимые на защиту положения.
В первой главе кратко рассматривается суть явления плазменно-пылевых образований, и анализируются существующие оптические методы пространственной диагностики плазменно-пылевых структур.
Впервые трёхмерная плазменно-пылевая структура была исследована в [18] с использованием горизонтально и вертикально ориентированных лазерных ножей толщиной 90 мкм. Эксперимент проводился
в ВЧ – разряде в криптоне при давлении 1.4 Тор. В разряд инжектировались почти монодисперсные (9.4±0.3 мкм) сферические полимерные пылинки. Объемная структура наблюдается путём сканирования лазерным “ножом”. При этом осуществлялась запись положения каждой частицы по “x”, “y” и “z” координатам с помощью цифровой телекамеры, а данные представляли собой набор плоских горизонтальных изображений, по которым вычислялось объемное представление. Эта методика применялась при исследовании пылевых структур в [19–24], однако её временное разрешение пока всё ещё недостаточно. Так,
в [23] скорость развертки лазерного пучка и телекамеры была равна 0.3 мм/с, а полная длительность развертки – 18.3 с., что совершенно неприемлемо в случае осцилляции частиц и, например, для трёхмерных наблюдений фазовых переходов.
В работе [25] предлагается использовать стереоскопический подход в решении задачи трёхмерного восстановления плазменного “кристалла”.
Классическое стереозрение включает два процесса: совмещение деталей, наблюдаемых двумя камерами и восстановление их трёхмерного прообраза [26, 27]. Последний процесс относительно прост: прообраз соответствующих точек можно найти как точку пересечения
лучей, проходящих через эти точки и центры соответствующих диафрагм камер [28]. Следовательно, если характерную точку изображения можно наблюдать и однозначно идентифицировать на всех камерах в любой момент времени, стереозрение реализуется просто. В то же время, каждая сцена состоит из сотен тысяч пикселей (или десятков и сотен характерных объектов), так что для определения точных соответствий между точками различных изображений сцены требуются некоторые методы, исключающие ошибочные измерения глубины. Таким образом, центральной проблемой компьютерного стереозрения является поиск сопряженных точек.
Традиционно [28] задача поиска сопряженных точек решается двумя известными способами:
1. учетом эпиполярного условия;
2. корреляционным методом нахождения пиксельных соответствий путем сравнения профилей яркости [27].
В первом случае, применительно к задаче восстановления трехмерной плазменно-пылевой структуры, реконструкция может быть приблизительной, т. к. метод позволяет только несколько сократить размер зоны поиска.
Второй подход в принципе не применим для нашей задачи, поскольку невозможно сравнением профилей яркости найти сопряженные точки, когда искомые объекты на изображениях выглядят прак-
тически одинаково, т. к. приблизительно одного размера и освещены одним источником.
В [29] частицы освещены двумя параллельными световыми лучами лазеров (686 и 656 нм), чьи интенсивности предварительно были промодулированы по глубине кристалла. Рассеянный свет регистрируется двумя камерами, расположенными под углом в 68 относительно друг друга. В этом случае сопряженные точки находятся корреляционным методом.
Однако в диссертации показано присутствие локальных отличий
в яркости сопряженных фрагментов изображений вследствие рассеивающих свойств частиц кристалла и геометрического размытия изображения, что делает корреляционный метод сопряжения не применимым к поставленной задаче.
Таким образом, показана необходимость развивать методы трёхмерной диагностики плазменно-пылевых структур с целью получения полной, объективной и достоверной информации о пространственном распределении частиц. Одним из решений поставленной задачи является применение к пылевым структурам принципов оптической томографии.
Во второй главе рассмотрены принципы и некоторые алгоритмы томографии.
Суть всех типов томографии едина: по интегральной информации (проекциям) полученной от некоторого слоя вещества, нужно определить локальную информацию f(x,y) в том же сечении [30], а затем по сечениям восстановить объем f(x,y,z), где “z” – координата, перпендикулярная слоям.
Современную томографию можно без преувеличения считать всеволновой. В зависимости от характера конкретной задачи восстановление структуры объекта может основываться на регистрации пучков электронов, ионов, нейтронов, фотонов во всем диапазоне электромагнитного спектра, звуковых волн [31, 32]. Исследуемый объект при этом облучается извне или сам является излучателем. В различных типах томографии суммарная информация качественно различна, однако есть тенденция описывать все виды томографии с точки зрения единого подхода, т.к. конечная цель одна [33].
Рассмотрим простейший случай. Пусть двухмерное сечение исследуемого объекта “1” (рис. 1) описывается функцией плотности f(x,y). Вдоль подвижной оси “v” сканируем слой объекта просвечивающим излучением “4”, используя излучатель “3” (рис. 1), и фиксируем ослабление луча детектором “2”, получая проекцию при заданном угле![]() . Следует отметить, что объект может излучать и сам (в этом случае излучатель не потребуется).
. Следует отметить, что объект может излучать и сам (в этом случае излучатель не потребуется).
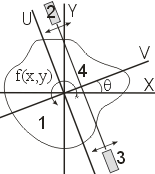 Рис. 1. Схема сканирования слоя. Рис. 1. Схема сканирования слоя. | Проекция представляет со- бой отображение N-мерной функции в (N-1)-мерную функцию, получаемое путем ее интегрирования в заданном направлении. В рассматриваемом двухмерном случае проекция |
Итак, задача восстановления заключается в решении интегрального уравнения (1). Самый естественный и мощный способ дает преобразование Фурье. Воспользовавшись основными свойствами преобразования, а также теоремой о проекциях и сечениях [32] получаем:
![]() , (2)
, (2)
Если в (2) принять ![]() , тогда
, тогда 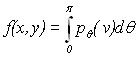 , (3)
, (3)
(3) представляет собой метод “обратного проецирования”, позволя-
ющий оценивать плотность в любой точке сечения посредством сложения лучевых сумм ![]() для всех лучей, проходящих через искомую точку.
для всех лучей, проходящих через искомую точку.
Предположим, в объеме восстановления есть набор светящихся точечных объектов “A”, “B” и пусть известны их двухмерные проекции “P1”, “P2”, “P3” при трёх различных углах (рис. 2).
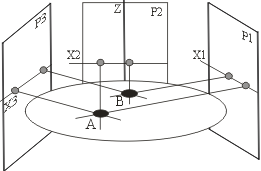 Рис. 2. Схема восстановления. Рис. 2. Схема восстановления. |
Для каждой точки изображения восстановленная плотность является суммой всех трёх лучевых проекций, которые проходят через эту точку, что позволяет определить геометрические координаты точечных объектов “A” и “B”.
Таким образом, показано, что метод оптической томографии и алгоритм “обратного проецирования” потенциально возможно адаптировать применительно к задаче пространственной диагностики плазменно-пылевых структур.
В третьей главе описан и протестирован предлагаемый алгоритм.
Чтобы применить томографические методы к пылевой плазме, мы должны осветить анализируемую область плазмы с рассеивающими частицами (D1, D2, D3) расширенным лазерным пучком, установить фоторегистрирующие системы в горизонтальной плоскости, и зарегистрировать несколько двумерных изображений (проекций P1, P2, P3) этой области под различными углами наблюдения ![]() ,
,![]() (Рис.3).
(Рис.3).
Рис. 3. Схема томографирования. O1, O2, O3 – оптические оси.
При использовании оптической системы с большим увеличением можно применить видоизмененный алгоритм обратной проекции. Трехмерный массив “V”, соответствующий всем элементам области восстановления структуры, первоначально обнуляется. Рассчитываются координаты точек, через которые пройдет прямая, восстановленная из каждой точки плоскости проекции (“P1”, “P2”, “P3”, рис. 3) и проходящая через центр оптической системы, и ко всем элементам массива области восстановления, через которые проходит эта прямая, добавляется “1”. В результате за координаты реальных частиц принимаются
те элементы массива, в которых появилось значение “3” (при трех проекциях). Однако, в реальном эксперименте фоторегистрирующие системы не откалиброваны, главные оптические оси не находятся в одной плоскости (оптические системы сдвинуты в пространстве на неизвестные “Shift_Y”, “Shift_Z” – рис. 3), межугловые расстояния известны приблизительно (в диапазоне Q±Q), а следы частиц на проекциях
являются не точками, а пятнами из-за ограниченной глубины резкости оптической системы.
Остаётся возможность варьировать неизвестные значения в некотором диапазоне и осуществлять проверку точности восстановления, например, вычисляя проекции с восстановленного объекта и накладывая вычисленные проекции на экспериментально полученные. Остановить такой итерационный процесс можно при достижении некоего минимального значения отклонения. Сложность в том, что подобный подход требует значительных временных и аппаратных ресурсов.
Очевидно, для решения поставленной задачи необходимо:
- воспользоваться априорной информацией об исследуемом объекте;
- отказаться от принципа заполнения и анализа трехмерного массива “V”.
Априорной информацией послужит тот факт, что обычно плазменный “кристалл” представляет собой структуру, в которой есть заметная, однозначно определяемая на всех проекциях частица, которая может быть использована для калибровки системы.
Отказаться от заполнения и анализа трехмерного массива “V” возможно, решив задачу аналитически. Лучи, идущие от каждого следа на проекции через объем восстановления, будем задавать пересечением двух плоскостей. При поиске точки пересечения лучей сделаем допуск на возможность некоторого расхождения лучей (будем рассматривать объем, в котором могут пересекаться искомые прямые), поскольку
в реальном эксперименте следы частиц на проекциях являются не точками, а пятнами и треками. Из рисунка 4 видно, что прямая “A1K1”, задаваемая плоскостями “A1A5K1” и “A1A4K1” (где “h” – малое произвольное смещение относительно следа “A1”), проходит через след на проекции “P1” и оптический центр линзы “K1”.
Для более компактного описания алгоритма введём следующие операторы: F{} – итерационный оператор; C{} – оператор априорных ограничений;
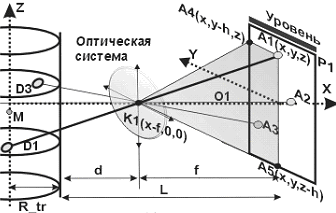 Рис. 4. Принципы задания плоскости и прямой. Рис. 4. Принципы задания плоскости и прямой. |
M{} – оператор вычисления координат объёма пересечения; H{} – оператор вычисления проекций с восстановленного объекта;
Тогда итерационный алгоритм можно представить системой (4,5). Задаём начальные приближения (выбираем начальную точку у стенки газоразрядной трубки на прямой “B1K2”, рис. 3) и осуществляем восстановление на приближении “w” c вычислением проекций (4). Далее проводим проверку точности восстановления (6) и, если отклонение меньше предыдущего (итерация “w-1”), запоминаем параметры (“shift”, “Q” для каждой проекции). С учетом априорных ограничений продолжаем варьировать параметры с целью минимизации отклонения (6) и вычисления координат частиц плазменно-пылевой структуры (5), т. е. будем программно изменять координаты фоторегистрирующих систем “P1”, “P3” (при неизменном расстоянии между трубкой и фотоматрицей “L”) посредством одновременного смещения прямых “A1K1” и “C1K3” вдоль прямой, идущей из следа “B1” частицы “D1”.
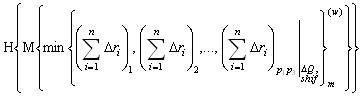 =
=
![]() =
=![]() =
=![]() , (4)
, (4)
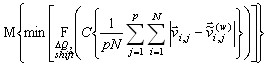 =
=![]() , (5)
, (5)
где ![]() – сумма расстояний между точками множества, образующих объем пересечения, n=6, “p1” – следов на проекции “P1”, “p3” – следов на проекции “P3”, “m” – порядковый номер следа на проекции “P2” и восстановленной частицы,
– сумма расстояний между точками множества, образующих объем пересечения, n=6, “p1” – следов на проекции “P1”, “p3” – следов на проекции “P3”, “m” – порядковый номер следа на проекции “P2” и восстановленной частицы, ![]() ,
, ![]() =
=![]() ,
, ![]() =
=![]() – координаты следа “i” на проекции “j”, “~” – указывает на приближение,
– координаты следа “i” на проекции “j”, “~” – указывает на приближение, ![]() =
=![]() – вычисленная проекция с координат
– вычисленная проекция с координат ![]() при заданных Q и смещении “shift”, “shift” – смещение фоторегистрирующих систем, (w) – w-я итерация.
при заданных Q и смещении “shift”, “shift” – смещение фоторегистрирующих систем, (w) – w-я итерация.
В результате выполнения итерационного процесса будет найдено оптимальное пространственное расположение частиц восстанавлива-
емого объекта с минимальным отклонением “R” (6). Варьирование углов в диапазоне “![]() ” для каждой проекции можно реализовать как дополнительный процесс восстановления с проверкой по уравнению (6) после каждого малого смещения по прямой “B1K2” (рис.3).
” для каждой проекции можно реализовать как дополнительный процесс восстановления с проверкой по уравнению (6) после каждого малого смещения по прямой “B1K2” (рис.3).
![]() , (6)
, (6)
где “p”– число проекций, “N” – количество частиц, ![]() =
=![]() – координаты следа “i” на проекции “j”,
– координаты следа “i” на проекции “j”, ![]() =
=![]() – вычисленная проекция. Фактически “R” показывает среднюю ошибку позиционирования каждой восстановленной частицы.
– вычисленная проекция. Фактически “R” показывает среднюю ошибку позиционирования каждой восстановленной частицы.
Далее в этой главе на математических моделях проиллюстрирована работоспособность и эффективность предложенного алгоритма. Рассмотрены ограничения, накладываемые на метод, вследствие применения оптических систем с большим увеличением.
В четвёртой главе описан процесс предварительной обработки экспериментально полученных изображений структур плазменно-пылевых образований для дальнейшего использования изображений разработанным алгоритмом томографии. Рассмотрены методы фильтрации в частотной области и фильтрации с глобальным порогом, цветовая модель RGB и алгоритм выделения в двоичном изображении множеств смежных объектов (изображений частиц плазменно-пылевых образований).
Главная цель предобработки заключается в такой обработке изображения, чтобы результат оказался более подходящим с точки зрения конкретного применения, удобного для последующей компьютерной обработки. Конкретно, нужно из экспериментально полученных изображений получить бинарные, представляющие собой изображения, яркость элементов которого может принимать только два значения 0
и 1 [34], с целью выделения множеств смежных объектов и координат их центров, необходимых в предложенном алгоритме томографии.
Однако в экспериментах реальный сигнал на выходе прибора содержит кроме полезного сигнала еще и шумы.
Так, в нашем случае шум возникает из-за недостатка освещения
и использования лазера (шум Эрланга), что приводит к появлению
несуществующих деталей или разорванности объектов.
Хотя человеческое зрение без труда ликвидирует образовавшиеся пробелы в разрывах и несуществующие детали, автоматические системы сталкиваются с серьёзными трудностями при распознавании.
Поскольку исследуемый объект освещается лазером (532 нм), из полученных изображений можно сразу отсечь два канала, отвечающих за красный и синий цвета.
Известно, что резкие перепады яркости на изображении (например, связанные с шумом) вносят значительный вклад в высокочастотную часть его Фурье-преобразования. Следовательно, сглаживание достигается в частотной области ослаблением высокочастотных компонент определённого диапазона Фурье-образа данного изображения [34], что позволяет исключить или существенно уменьшить яркость деталей, имеющих размеры меньше интересующих, а также ликвидировать образовавшиеся пробелы в разрывах. В качестве же фильтра в работе применяется гауссов фильтр низких частот, отражающий наши априорные предположения о характере искомого сигнала.
И, наконец, применяется обработка с глобальным порогом, а на выходе мы получаем бинарное изображение, анализируемое описанным алгоритмом выделения множеств смежных объектов благодаря привлечению возможностей математической морфологии.
Описанный подход предобработки экспериментальных данных реализован в виде модуля “Filtration” в составе программы “Tomograpty 2”.
В пятой главе описаны условия эксперимента и результаты применения разработанного алгоритма и программных средств к задаче пространственной диагностики плазменно-пылевых образований методом оптической томографии.
Экспериментальная установка представляет собой вакуумную установку с вертикально установленной газоразрядной трубкой с внутренним диаметром 2.6 см (внешний 3 см). Промежуток между электродами 45 см. Макрочастицы – полидисперсный порошок Al2O3 (1–60 мкм), инжектируются из контейнера, расположенного в верхней части трубки. Исследования проводились в постоянном токе тлеющего разряда
в атмосфере Ar.
В установке использовались три идентичные фотокамеры “Canon EOS 10D” с объективами “Canon EF 100 F2.8 Macro” и удлинительными кольцами. Камеры устанавливались по уровню в штативы на одинаковом расстоянии от трубки. Синхронизация фотокамер осуществлялась, благодаря возможности одновременного электронного управления
несколькими затворами. Структура была освещена расширенным лучом полупроводникового лазера с длиной волны 532 нм и мощностью
51 мВт. При этом луч направлялся не перпендикулярно трубке, а под углом 45, чтобы избежать бликов.
Для обработки результатов эксперимента предложенным алгоритмом использовалась разработанная программа “Tomography 2”. В качестве входных параметров используются: L – расстояние от газоразрядной трубки до светочувствительной матрицы (на корпусе фотоаппа-
ратов Canon EOS 10D есть метка, указывающая на расположение матрицы); R_tr – радиус газоразрядной трубки; физические размеры пикселя светочувствительной матрицы; масштаб проекций; углы поворота фотоаппаратов; диапазон угловой погрешности Q; начальные смещения проекций (задаются нулевыми).

Рис.5. Проекции (a, b, c) и восстановленная структура (d).
В реальном эксперименте восстанавливалась структура, состоящая из нескольких десятков частиц, проекции которой представлены на рис. 5. Газ Ar, P=29 Па, I=0.31 мА, масштаб 105 pix на 250 мкм, время экспозиции 1/500 с., диафрагма 4, L=388 мм, размер пикселя светочувствительной матрицы 7.25 мкм.
Серые размытые пятна (рис. 5) – частицы плазменно-пылевой структуры; чёрные одинаковые кружки – проекции, вычисленные с восстановленной структуры и наложенные поверх изображений частиц плазменно-пылевой структуры для проверки точности восстановления.
Результат обработки можно сразу оценить визуально, т. к. восстановленная структура выводится в 3-х мерном виде (рис. 5d), благодаря использованию разработанного модуля “Result of reconstruction” в составе программы “Tomography 2”.
В качестве начальных приближённых значений в программу были введены следующие углы проекций: 00, -36.030, -160.020 (относительно первой проекции). В результате обработки оптимальными признаны углы: -1.050, -31.630, -158.530. Для смещений оптимальные результаты: shift X=6 pix (вторая проекция), shift Y=29 pix (вторая проекция), shift X=2 pix (третья проекция), shift Y=67 pix (третья проекция).
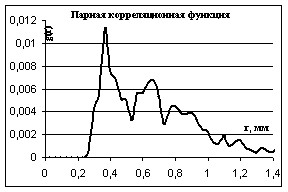 Рис. 6. Парная корреляционная функция. Рис. 6. Парная корреляционная функция. |
Восстановленная структура содержит 40 частиц. Минимальное отклонение “R” составляет 2.83 pix. Среднее межчастичное расстояние 298±7 (мкм). На рис. 6. представлена парная корреляционная функция восстановленной трёхмерной структуры с rgmax=364 мкм.
Предложенным методом исследованы зависимости параметров трехмерной пылевой структуры из полидисперсного порошка Al2O3
с диаметром частиц от нескольких единиц до нескольких десятков микрон от токов (в диапазоне 0.1–1.2 мА, с шагом 0.1 мА) и давлений (27–80 Па, с шагом 13 Па) в тлеющем разряде постоянного тока в Ar.
При заданном давлении делался вброс частиц, регистрация проекций осуществлялась через каждые 15 минут после установки тока разряда.
Применение томографии позволило обнаружить разницу между горизонтальными (rxy) и вертикальными (rz) составляющими межчастичного расстояния (rср). Выявлено, что “rz“ в пределах погрешности
не зависит от токов и давлений. “rxy“ показывало зависимость от токов при всех давлениях: линейную при давлениях 27 Па (рис. 7), 40 Па
и 53 Па; не линейную, которую можно аппроксимировать квадратичной зависимостью, при, например, 67 Па (рис. 8), 80 Па. Зависимость “rср“ от тока проявляется как линейно, при давлении 67 Па, так и не линейно при 80 Па (рис. 9). Зависимость “rср” от давления в пределах погрешности не обнаружена.
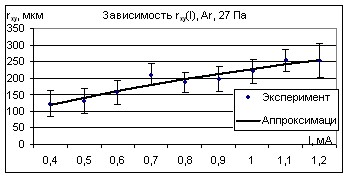
Рис. 7. Зависимость горизонтальной составляющей от тока при P=27 Па.
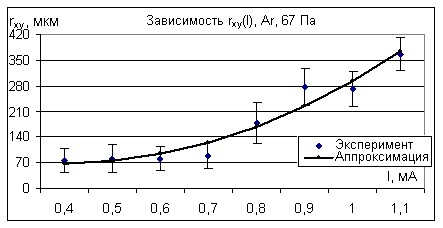
Рис. 8. Зависимость горизонтальной составляющей от тока при P=67 Па.
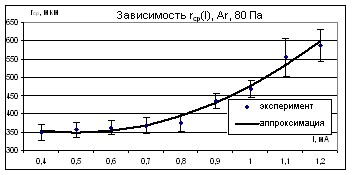
Рис. 9. Зависимость среднего расстояния от тока при P=80 Па.
В заключении сформулированы основные результаты, полученные автором:
- Адаптирован метод оптической томографии применительно к задаче пространственной диагностики плазменно-пылевых образований.
2. Сформулированы ограничения и условия применимости адаптированного метода.
3. Предложен и реализован новый алгоритм томографии, позволяющий итеративно находить оптимальное решение для случая неоткалиброванных камер, увеличивающий надёжность и объективность получения информации о пространственном распределении частиц
в плазменно-пылевых образованиях. Разработанный алгоритм позволяет учитывать влияние используемой оптической системы. При этом поиск объектов идёт напрямую без промежуточного заполнения 2-х (вычисление сечений) или 3-х мерных массивов.
4. Предложенным методом проведено исследование зависимости средних межчастичных расстояний при различных токах (0,1–1,2 мА,
с шагом 0,1 мА) и давлениях (27–80 Па, с шагом 13 Па) в тлеющем разряде постоянного тока в Ar для полидисперсного порошка Al2O3.
В приложении даны описания интерфейсов разработанного программного обеспечения и базовые понятия теории множеств.
Публикации по материалам диссертации
- Bulba A. V., Luizova L. A., Khakhaev A. D. The computer training program on tomography // Education and Training in Optics and Photonics (ETOP) Conference (October 5–9, 2003, Tucson, Arizona). Tucson, 2003. Pp. 89–97.
- Bulba A. V., Luizova L. A., Khakhaev A. D. Dusty plasma tomography // Northern Optics 2003. The joint conference of the Optical Societies of Denmark, Finland, Norway and Sweden (16–18 June 2003, Espoo, Finland). Espoo, 2003. P. 49.
- Luizova L., Khakhaev A., Podryadchikov S., Scherbina A., Bulba A. Investigation of ordered dusty structures in the glow discharge // Proceedings of the 30th EPS Conference on Controlled Fusion and Plasma Physics ( July 7–11, 2003, St. Petersburg, Russia). St. Petersburg, 2003.
- Бульба А. В. Томография плазменного кристалла // Восьмая Санкт-Петербургская ассамблея молодых ученых и специалистов. СПб, изд. СПбГУ, 2003. С. 27.
- Бульба А. В., Луизова Л. А. Компьютерная обучающая програм-
ма по томографии // Технологии Microsoft в теории и практике программирования (Санкт-Петербургский государственный политехнический университет, 4–5 марта 2004 г.). СПб, изд. СПбГПУ, 2004. С. 80. - Bulba A. V., Luizova L. A., Khakhaev A., Podryadchikov S. F., Shty-
kov A. S., Scherbina A. I. The Influence of Physical-Chemical Characteristics of Plasma-Forming Gas and Macroparticle Matter in Complex Plasma on Ordered Structure Self-Organization // New Vistas in Dusty Plasmas. AIP Conference proceeding.V. 799, Melville, New York, 2005, pp. 359–362. - Bulba A. V., Luizova L. A., Khakhaev A. D. Research Possibilities of 3D Dasty Plasma Structures // New Vistas in Dusty Plasmas. AIP Conference proceeding.V. 799, Melville, New York, 2005, pp. 355–358.
- Bulba A. V., Ekimov D. A., Luizova L. A., Khakhaev A. D. Investigation of 3D dusty plasma structures // V International Conference «Plasma Physics and Plasma Technology» (18-22 September 2006, Minsk, Belarus). Contributed papers. Minsk, 2006. V. 1. Pp. 396–399.
- Бульба А. В., Луизова Л. А., Подрядчиков С. Ф., Хахаев А. Д., Щер-
бина А. И. Самоорганизация и рост пылевых структур в тлеющем разряде // Химия высоких энергий. 2006. том 40. № 2. C. 155–160. - Анисимов А. Л., Бульба А. В., Луизова Л. А., Хахаев А. Д., Штыков А. С. Невозмущающие методы оптической диагностики гетерогенной плазмы // Химия высоких энергий. 2006. том 40. № 3. C. 233–237.
- Бульба А. В., Луизова Л. А., Хахаев А. Д. Обучение принципам компьютерной томографии для решения задач диагностики плазмы // Электронный журнал «Исследовано в России». 2006. C. 677–686. http://zhurnal.ape.relarn.ru/articles/2006/ 068.pdf
- Бульба А. В., Екимов Д. А., Луизова Л. А., Хахаев А. Д. Пространственная диагностика плазменно-пылевых структур // IV Курчатовская молодежная научная школа (20–22 ноября 2006 г., Москва, РНЦ Курчатовский Институт). Сборник трудов. Москва, 2006.
- Бульба А. В. Программа для определения пространственного расположения набора точечных объектов методом оптической реконструктивной томографии «Tomography 2». // Компьютерные учебные программы и инновации (Телеграф отраслевого фонда алгоритмов и программ). – 2007, № 5. С. 26.
- Бульба А. В. Программа для обучения алгоритмам реконструктивной томографии «Tomography». // Компьютерные учебные программы и инновации (Телеграф отраслевого фонда алгоритмов
и программ). – 2007, № 5. С. 10. - Бульба А. В. Исследование пространственного распределения точечных масс методом оптической томографии // Вестник ИРГТУ. 2007. № 3. С. 116–125.
- Бульба А. В., Луизова Л. А., Хахаев А. Д. Томография плазменно-пылевых структур // Материалы семинара-школы молодых ученых, студентов и аспирантов “Физика низкотемпературной плазмы 2004”. Изд. Скандинавия, 2005. С. 116–126.
- Бульба A. В., Луизова Л. А., Пискунов А. А., Соловьев А. В. Иссле-
дование структуры плазменно-пылевых образований // Материалы Всероссийской (с международным участием) конференции “Физика низкотемпературной плазмы – 2007” (24–28 июня 2007 г), изд. ПетрГУ, 2007, Т 2, С. 214–218.
Цитированная литература
- Chu J. H., Lin I. Coulomb Lattice in a Weakly Ionized Colloidal Plasma // Physica A. 1994. V. 205. P. 183.
- Thomas H., Morfill G. E., Demmel V., Goree J. Plasma crystal: coulomb crystallization in a dusty plasma // Phys. Rev. Lett. 1994. V. 73. P. 652.
- Нефедов А. П., Петров О. Ф., Фортов В. Е. Кристаллические структуры в плазме с сильным взаимодействием макрочастиц // УФН. 1997. Т. 167. № 11. С. 1215–1226.
- Фортов В. Е., Петров О. Ф., Молотков В. И. Пылевая плазма в условиях микрогравитации: эксперименты на международной космической станции // Электронный научный журнал «ИССЛЕДО-
ВАНО В РОССИИ» http://zhurnal.ape.relarn.ru/articles/2002/204.pdf. C. 2244–2247. - Ваулина О. С., Нефедов А. П., Петров О. Ф., Фортов В. Е. Формирование упорядоченных структур заряженных макрочастиц в фотоэмиссионной ловушке // ЖЭТФ. 2000. Т. 118. С. 351.
- Zuzic M., Ivlev A. V., Goree J., et al Three-Dimensional Strongly Coupled Plasma Crystal under Gravity Conditions // Phys. Rev. Lett. 2000. V. 85, № 19. P. 4064.
- Arp O., Block D., Piel A. Structure and trapping of three-dimensional dust clouds in a capacitively coupled rf-discharge // New Vistas in Dusty Plasmas. AIP Conference proceeding. V. 799, Melville, New York, 2005, pp. 20–21.
- Kading S., Melzer A., Arp O., Block D., Piel A. Stereoscopic Investigations of 3D Coulomb Balls // New Vistas in Dusty Plasmas. AIP Conference proceeding. V. 799, Melville, New York, 2005, pp. 335–338.
- Хорн Б. К. П. Зрение роботов. – М.: Мир, 1989.
- Форсайт Д., Понс Ж. Компьютерное зрение. Современный подход.: Пер. с англ. – М.: Издательский дом “Вильямс”, 2004.
- Абрамов В. В., Киричук В. С. и др. Реконструкция трехмерных поверхностей по двум проекциям при отслеживании камерой заданной точки сцены. // Автометрия, 1998, № 5, с. 3.
- Antipov S. N., Khrustalyov Yu. V., Petrov O. F., Statsenko K. B., Vasiliev M. M., Levchenko V. D. Structure and melting of 3D anisotropic dust crystals in dc glow discharges // 33rd EPS Conference on Plasma Phys. Rome, 19–23 June 2006 ECA Vol. 30I, D-5.028 (2006)
- Сизиков В. С. Математические методы обработки результатов измерений: Учебник для вузов. – СПб: Политехника, 2001.
- Пикалов В. В., Преображенский Н. Г. Вычислительная томография
и физический эксперимент. // УФН. 1983. Т. 143. вып. 3. С. 469–498. - Терновой К. С., Синков М. В. Введение в современную томографию. – Киев: Наукова думка. 1983.
- Тихонов А. Н., Арсенин В. Я., Тимонов А. А. Математические задачи компьютерной томографии. М.: Наука. 1987.
- Гонсалес Р., Вудс Р. Цифровая обработка изображений. – М.: Техносфера. 2006.
Подписано в печать 19.09.07. Формат 60х84 1/16.
1 уч.-изд. л. Тираж 100 экз. Изд. № 220.
Государственное образовательное учреждение
высшего профессионального образования
ПЕТРОЗАВОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Отпечатано в типографии Издательства ПетрГУ.
185910, г. Петрозаводск, пр. Ленина, 33

