Диагностика плазмы с использованием моделирования и обработки оптических и пространственных спектров
На правах рукописи
УДК 533.9.082.5
Соловьев Алексей Владимирович
ДИАГНОСТИКА ПЛАЗМЫ С ИСПОЛЬЗОВАНИЕМ МОДЕЛИРОВАНИЯ И ОБРАБОТКИ ОПТИЧЕСКИХ И ПРОСТРАНСТВЕННЫХ СПЕКТРОВ
Специальность 01.04.04 – физическая электроника
Автореферат диссертации на соискание учёной степени
кандидата физико-математических наук
Петрозаводск 2006
Работа выполнена на кафедре информационно-измерительных систем и физической электроники физико-технического факультета Петрозаводского государственного университета.
Научный руководитель:
доктор физ.-мат. наук, профессор Хахаев Анатолий Диамидович
Официальные оппоненты:
доктор физ.-мат. наук, профессор Фофанов Анатолий Дмитриевич
кандидат физ.-мат. наук, доцент Карасев Виктор Юрьевич
Ведущая организация:
Карельский государственный педагогический университет
Защита состоится 18 декабря 2006 г. на заседании диссертационного совета K 212.190.01 при Петрозаводском государственном университете по адресу: г. Петрозаводск, ул. Университетская, д. 10.
Отзывы направлять по адресу:
185910, Петрозаводск, пр. Ленина 33, ПетрГУ,
ученому секретарю диссертационного совета К 212.190.01.
С диссертацией можно ознакомиться в библиотеке Петрозаводского государственного университета.
Автореферат разослан 17 ноября 2006 г.
Учёный секретарь диссертационного совета К 212.190.01
кандидат физ.-мат. наук, доцент
Алешина Людмила Александровна _________________
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность работы
При решении задач физической электроники часто используются мощные и бесконтактные спектроскопические методы исследования объектов. В частности они широко применяются для исследования, диагностики и контроля различных плазменных образований. При этом извлечение информации из спектра часто сопряжено со сложной математической обработкой, которая сводится к выделению различных факторов, сформировавших регистрируемый сигнал (исключению аппаратных искажений, преобразованию яркости поверхности в коэффициенты излучения с учётом неоднородности объекта, разделению причин, сформировавших контур излучения тонкого слоя), при этом возникает необходимость построения алгоритмов, устойчивых к шумам эксперимента. В некоторых случаях к лучшим результатам приводит имитационное моделирование спектральных распределений с учётом вышеперечисленных факторов и физически обоснованный подбор ряда неизвестных параметров объекта для наилучшего совпадения с экспериментом.
К этому же кругу задач можно отнести специфические проблемы изучения газоразрядной плазмы с конденсированной дисперсной фазой. В этом случае существенную информацию, в том числе и о физической природе явления, можно извлечь непосредственно из обработки изображения пылевых структур в разряде.
Хотя работы в указанных направлениях ведутся давно, актуальной является задача создания инструментов, которые бы позволяли решать широкий круг диагностических задач с использованием всех возможностей современной вычислительной техники и накопленных теоретических знаний в автоматизированных программно-аппаратных исследовательских и контрольно-диагностических комплексах, существенно увеличивающих надёжность и объективность, а также скорость получения необходимой информации.
Цель работы, задачи
Главная цель описываемых исследований – развить методы оптической диагностики пространственно неоднородной и комплексной плазмы, увеличить их эффективность, достоверность и информативность.
Для достижения этой цели необходимо решить ряд задач:
- Исследовать возможности, предоставляемые высокопроизводительными программно-аппаратными комплексами сбора и обработки данных оптико-спектральных измерений характеристик плазмы.
- Проанализировать существующие алгоритмы обработки оптических и пространственных спектров.
- Исследовать возможности применения статистических методов для повышения устойчивости результатов измерений к шумам и исключения аппаратных искажений при извлечении информации о параметрах плазменных объектов из оптических спектров.
- Разработать необходимый программный инструментарий для реализации новой методики решения диагностических задач, легко адаптируемый к различным приложениям, и проиллюстрировать эффективность его применения.
- Исследовать эффективность предлагаемого программного комплекса при обработке данных экспериментов, например, с «пылевой» плазмой, неоднородной плазмой в металлогалоидной лампе и плазмой индукционного разряда, являющихся в настоящее время актуальными объектами исследований и инженерных расчётов.
Научная новизна
- Для решения задач спектроскопической диагностики неоднородной плазмы предложен и реализован новый рациональный алгоритм коллективной обработки экспериментальных данных на основе метода главных компонент, обеспечивающий повышение надёжности и достоверности информации, получаемой в результате эксперимента, снижающий трудоёмкость обработки результатов и влияние шумов.
- Впервые использованы новые алгоритмы обработки данных, получаемых в спектрометре изображения с интерферометром Фабри – Перо.
- Впервые получены пространственные распределения атомной температуры и заселённости метастабильных уровней в индукционно-связанной плазме разряда в неоне.
- Впервые исследованы пространственные спектры упорядоченных пылевых структур цинка и оксида алюминия в комплексной плазме тлеющего разряда в инертных газах. Установлена корреляция характеристик таких спектров с условиями в разряде и типом системы «газ – макрочастица».
- Показано, что пространственный спектр позволяет контролировать строение структуры, определять параметры структуры и отслеживать динамику их изменения.
Научно-практическая значимость работы
Разработанный набор алгоритмов и программных средств позволяет комплексно решать задачи локальной количественной диагностики неоднородной плазмы, в частности, «очищать» регистрируемые спектральные распределения от влияния аппаратных искажений, вносимых регистрирующим прибором, и корректно учитывать характер неоднородности объекта.
Анализ данных, полученных в результате исключения аппаратных искажений при помощи разработанных программных средств, обеспечивает возможность исследовать вклады различных физико-химических процессов, происходящих в неоднородной плазме, что содействует развитию представлений и знаний о плазме в конкретных приложениях и весьма полезно для разнообразных инженерных и конструкторских разработок.
Контроль пространственных спектров плазменно-пылевых образований позволяет гибко и эффективно следить за изменением характера структуры, даёт возможность увеличить надёжность результатов видеорегистрации.
Результаты разработки комплекса программных средств могут быть использованы и уже активно используются в научно-образовательном процессе при подготовке специалистов по физической электронике и информационно-измерительной технике в Петрозаводском государственном университете.
На защиту выносятся:
- Рациональный алгоритм обработки экспериментальных данных на основе метода главных компонент, повышающий надёжность и достоверность информации, получаемой в результате эксперимента, снижающий трудоёмкость обработки результатов и влияние шумов.
- Набор программных модулей, основанный на использовании как современных представлений о физических процессах в низкотемпературной плазме, так и на концепции на новейших информационных технологий, легко адаптируемый к конкретным спектроскопическим исследованиям и применимый для решения как прямых, так и обратных задач спектроскопии плазмы (программный комплекс «Meccano»).
- Пространственные распределения атомной температуры и заселённости метастабильных уровней в индукционно-связанной плазме разряда в неоне.
- Радиальное распределение концентрации электронов в ртутной дуге высокого давления переменного тока с добавкой йодида таллия, совпадающее с рассчитанным по модели локального термодинамического равновесия для центральной области разряда вплоть до половины радиуса и для момента времени, когда ток дуги максимален.
- Метод анализа упорядоченных плазменно-пылевых структур по их пространственным спектрам.
Апробация работы
Содержание работы докладывалось на Международной конференции по инженерному и компьютерному образованию ICECE-2003 (г. Сантус, Бразилия, 16–19 марта 2003 г.), на IV Российском семинаре по современным средствам диагностики плазмы и их применению (г. Москва, 1214 ноября 2003 г.), на конференции «Современные проблемы науки и образования» (г. Умаг, Хорватия, 3–10 июля 2004 г.), на Всероссийском симпозиуме молодых ученых, студентов и аспирантов «Фундаментальные проблемы приложений физики низкотемпературной плазмы» (г. Петрозаводск, 5–11 сентября 2005 г).
Комплекс программных средств прошёл успешную проверку в ходе экспериментальных исследований на кафедре информационно-измерительных систем и физической электроники Петрозаводского государственного университета и в Научно-образовательном центре по фундаментальным проблемам приложений физики низкотемпературной плазмы, а также в лабораторных практикумах студентов по курсам: «оптические методы диагностики плазмы», «физические основы получения информации», «метрология и измерительная техника» и при выполнении студентами курсовых и дипломных работ.
Список работ, опубликованных по результатам диссертации, приведён в конце автореферата.
Структура и объём диссертации
Диссертация состоит из введения, шести глав, заключения и приложений. Работа содержит 98 страниц, 49 рисунков, 4 таблицы. Список использованной литературы включает 46 наименований.
Благодарности
Работа выполнена благодаря финансовой поддержке по гранту RUX0-000013-PZ-06 (НОЦ «Плазма») Американского фонда гражданских исследований и развития, а также Министерства образования и науки РФ и Правительства Республики Карелии.
СОДЕРЖАНИЕ РАБОТЫ
Во введении обосновывается выбор темы работы, её актуальность, формулируется цель работы и задачи, решить которые необходимо для достижения цели, показана научная и практическая значимость работы, описаны основные результаты, полученные в ходе работы, и выносимые на защиту положения.
В первой главе рассматриваются теоретические основы спектроскопических методов диагностики плазмы и анализируются существующие методы извлечения информации из оптических спектров.
В основе оптической диагностики плазмы лежит совокупность теоретически обоснованных методов, позволяющая по оптическим характеристикам, таким как спектральная энергетическая яркость поверхности источника в направлении наблюдения, оптическая толщина плазмы и др. определить локальные и мгновенные значения её основных параметров: концентрации электронов, ионов, атомов в основном и возбуждённом состояниях, а также параметры законов распределения их по энергиям. Надлежащим образом полученные экспериментальные данные позволяют проверить или построить физическую модель плазмообразующей среды и описать происходящие в ней явления. Очевидно, такой путь получения информации относится к категории косвенных измерений, поэтому для получения искомого результата необходимы априорные предположения о свойствах объекта и процессах, протекающих в нём. Такие априорные предположения удобно разбить на блоки, описывающие независимые процессы и процессы, связанные причинно-следственными связями.
В случае оптической диагностики плазмы выделены три основных блока моделей:
- Модель элементарного объёма описывает физические процессы внутри достаточно малого объёма плазмообразующей среды, в котором плазму можно считать однородной и оптически тонкой.
- Модель источника описывает геометрию источника плазмы и взаимодействие элементарных объёмов плазмы между собой.
- Модель экспериментальной установки описывает особенности регистрации данных об оптических характеристик источника плазмы, учёт аппаратных искажений.
Цель оптической диагностики плазмы можно достигнуть, решая одну из двух задач:
- моделируя источник плазмы как совокупность элементарных объёмов и подбирая параметры плазмообразующей среды таким образом, чтобы результат моделирования соответствовал наблюдаемым экспериментально данным («прямая задача»);
- решая аналитически или численно математические системы, описывающие взаимосвязь наблюдаемых параметров с искомыми («обратная задача»).
В экспериментальной установке по оптической диагностике плазмы, как правило, измеряемой физической величиной является спектральная энергетическая яркость поверхности источника в некотором направлении наблюдения (перпендикулярном к поверхности). В общем случае её можно представить как интеграл вдоль оси наблюдения от мощности излучения элементарных объемов в малый телесный угол, отнесённый к величине этого угла, с учётом поглощения. Аксиально-симметричный источник можно представить в виде совокупности тонких однородных слоёв. В пределах одного слоя можно считать параметры постоянными. C учетом суммарного излучения и взаимного поглощения слоёв, находящихся на срезе, можно рассчитать яркость поверхности следующим образом:
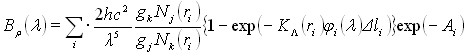 , (1)
, (1)
где h – постоянная Планка, c – скорость света в вакууме, – длина волны излучения, gk/j – статистические веса уровней переходов, Nk/j(ri) – заселённости уровней переходов для i-го слоя, K(ri) – интегральный коэффициент поглощения для i-го слоя, i() – контур спонтанного излучения для i-го слоя (i=n–1, n–2, … ![]() ,
, ![]() , … n–1), который формируется рядом независимых процессов (движение атомов, Штарк-эффект, резонансное уширение, уширение Ван-дер-Ваальса [17, 21]); n – число слоёв (слои нумеруются 0, 1, … n-1), R=R/n – толщина слоя, R – радиус источника, ri=i·R – расстояние i-го слоя от оси источника,
, … n–1), который формируется рядом независимых процессов (движение атомов, Штарк-эффект, резонансное уширение, уширение Ван-дер-Ваальса [17, 21]); n – число слоёв (слои нумеруются 0, 1, … n-1), R=R/n – толщина слоя, R – радиус источника, ri=i·R – расстояние i-го слоя от оси источника, ![]() – толщина i-го слоя по данному срезу. При расчёте поглощения для i-го слоя используется промежуточная величина:
– толщина i-го слоя по данному срезу. При расчёте поглощения для i-го слоя используется промежуточная величина: ![]() , учитывающая поглощение в слоях на пути излучения к поверхности источника.
, учитывающая поглощение в слоях на пути излучения к поверхности источника.
В реальном эксперименте фиксируется не непосредственно яркость (1), а массив отсчетов, связь которых со спектральным распределением яркости поверхности определяется чувствительностью регистрирующей системы (которая может быть и нелинейной) и искажениями из-за конечности спектрального и пространственного разрешения аппаратуры, поэтому необходимо принять во внимание ещё модель аппаратных искажений экспериментальной установки.
Однако однократное моделирование не даёт конечного физического результата, поскольку смоделированные данные должны быть сравнены с экспериментальными, что может потребовать корректировки исходных параметров модели и повторных вычислений. Очевидно, существенный вклад в эффективность решения прямой задачи вносит алгоритм поиска оптимальных параметров модели. При этом решение прямой задачи диагностики плазмы осложняется тем, что количество варьируемых параметров велико, а погрешность экспериментальных данных может оказаться существенной, так что соответствие модельных и экспериментальных данных при варьировании параметров будет обеспечиваться в очень широких пределах и информация, полученная таким образом, может оказаться ненадёжной.
Решение обратной задачи упрощается, если считать плазму оптически тонкой неоднородной с осевой симметрией, что соответствует многим актуальным приложениям. Обратная задача решается в два этапа. Сначала выполняется исключение аппаратных искажений, затем – обратное преобразование Абеля. В результате мы непосредственно получаем значения коэффициентов мощности спонтанного излучения для различных точек источника. Однако и исключение аппаратных искажений, и обратное преобразование Абеля представляют собой некорректные обратные задачи [23], т. к. очень чувствительны к шумам и погрешностям экспериментальных данных. Решение таких задач требует использования различных ресурсоёмких алгоритмов регуляризации [22, 23, 24].
Во второй главе описан предлагаемый алгоритм коллективной обработки данных. Ранее [19, 26] был предложен вариант регуляризации обращения Абеля, основанный на предположении, что значения яркости внутри контура спектральной линии для конкретного источника коррелированны, благодаря чему становится возможной одновременная обработка двумерного массива отсчётов яркости Y. В данной работе метод обобщается на случай, когда требуется выполнить и обратное преобразование Абеля, и исключение аппаратных искажений.
Метод заключается разложении каждого поперечного профиля яркости по собственным векторам информационной матрицы AW-1, где A – ковариационная матрица «объектов»:
![]() , (2)
, (2)
W – вычисляемая аналогичным образом ковариационная матрица погрешностей измерений. Предполагая погрешности отсчётов в разных точках независимыми и оценку их дисперсии Sy2 одинаковой для всех точек, получим:
![]() (3)
(3)
Найдём собственные вектора Up матрицы AW-1 и представим радиальное распределение в следующем виде:
![]() , (4)
, (4)
где Cip – проекция i-й спектральной точки на значимый собственный вектор Up:
![]() (5)
(5)
Проекции Cip подвергаются редукции к идеальному инструменту:
![]() , (6)
, (6)
а результат, с учётом (4) – обратному преобразованию Абеля:
![]() (7)
(7)
Таким способом непосредственно определяется распределение спектральных коэффициентов излучения по объёму источника. Поскольку количество значимых собственных векторов невелико (в реальных экспериментах Q=2-5) количество выполняемых операций существенно уменьшается, по сравнению с индивидуальной обработкой данных, а устойчивость к шумам эксперимента повышается, т. к. обрабатываемые распределения Cip – результат усреднения по большому массиву данных.
В третьей главе описан предлагаемый метод обработки изображений пылевых образований в комплексной плазме.
При диагностике плазмы с конденсированной дисперсной фазой (КДФ) особую роль играет выяснение геометрических параметров формируемой в плазме структуры пылевых микрочастиц (размеры, расстояния между частицами и степень упорядоченности структуры [25]). Если размеры легко определяются по изображению структуры, то для получения других характеристик в настоящее время проводится сложный анализ изображения, в частности, построение гистограммы расстояний между частицами (аналог бинарной корреляционной функции). Представляется возможным извлечение подобной информации из пространственного спектра изображения такой структуры, полученного цифровой видео или фотокамерой.
Проанализировав основные принципы формирования пространственного двумерного изображения пылевой структуры, полученного регистрацией сечения структуры в «лазерном ноже» и состоящего из светлых точек на тёмном фоне, можно сделать следующие выводы:
- центральный максимум (на нулевой частоте) имеет высоту, пропорциональную количеству частиц в исходном изображении;
- в спектре присутствуют пики с периодом, обратно пропорциональным расстоянию между частицами в исходной структуре, причём этот период не зависит от количества частиц и размера их изображений.
По расстоянию характерных пиков от центрального максимума в пространственном спектре точно определяются расстояния между точками в исходных структурах, причём легко определяются такие расстояния по любому направлению. Если в исходной структуре расстояния между точками варьируются, в пространственном спектре количество характерных максимумов изменяется и они становятся более размытыми, однако всё же остаётся возможность определить средние расстояния.
Анализ пространственных спектров смоделированных двумерных структур подтвердил наличие этих особенностей, что обеспечивает также диагностические возможности метода и его применимость для контроля динамики изменения структур.
В четвёртой главе описан использованный в работе комплекс аппаратных и программных средств. В первой части главы кратко описаны использованные программно-аппаратные комплексы для спектроскопической диагностики неоднородной плазмы и проанализированы их возможности.
Получить пространственное распределение спектральной энергетической яркости можно в установке с одноэлементным приёмником излучения. Однако в этом случае потребуется сканирование по всем пространственным координатам (в случае аксиально-симметричного источника – две координаты: вдоль радиуса и вдоль оси источника) и длине волны. Примером такого комплекса является АРМ «Свет». Комплекс позволяет регистрировать обзорные спектры в диапазоне 360–800 нм и контура спектральных линий с шагом по длине волны 0,015 нм в различных пространственных точках и в 8 фазах переменного тока промышленной частоты [7].
Не менее эффективной схемой измерений представляется одновременная регистрация спектра различных точек поверхности источника при помощи фотоприёмных линеек или матриц. Приборы, организованные таким образом, называют спектрометрами изображения. При этом сканирование по спектру может быть заменено считыванием одномерного или двумерного сигнала с изображения объекта в фокальной плоскости спектрометра.
Использование интерферометра Фабри – Перо [16, 18] позволяет получить на фотоприёмной матрице одновременно изображение источника и изображение интерференционных колец. Изменение толщины ИФП (например, путём изменения давления воздуха между зеркалами) позволяет сканировать по длинам волн спектр в различных пространственных областях. Однако при работе с интерферометром можно обойтись и без сканирования по длинам волн, что существенно для нестационарных объектов. Описана автоматизированная установка спектроскопии высокого разрешения для исследования неоднородных источников по контурам спектральных линий на основе интерферометра Фабри – Перо и спектрографа ДФС–8. Регистрация излучения осуществляется ПЗС-линейкой из 3648 регистрирующих элементов, высотой 200 мкм и шириной 8 мкм [15].
Для обработки результатов экспериментов и решения задач диагностики плазмы автором был разработан комплекс программных средств, который описан во второй части этой главы.
При решении обратной задачи спектроскопической диагностики плазмы для выполнения обращения Абеля можно воспользоваться разработанной ранее программой [26]. Для исключения аппаратных искажений была разработана оригинальная программа – «Моделирование и исключение аппаратных искажений» [5], которая в частности используется для исключения аппаратных искажений из проекций (5) при реализации алгоритма, описанного во второй главе.
Для решения прямой задачи спектроскопической диагностики плазмы был создан программный «конструктор» «Meccano» на основе платформы Java. Элементы этого «конструктора» могут быть собраны в различные программные схемы для обработки данных конкретного эксперимента. Описаны программные схемы для моделирования контура спектральной линии и для моделирования интерферограммы в спектрометре изображения на основе интерферометра Фабри – Перо. Вторая программная схема обладает уникальной возможностью быстрого варьирования параметров аппаратной функции (базы интерферометра Фабри – Перо) без пересчёта всего массива спектральной энергетической яркости поверхности.
Для обработки пространственных спектров из конструктора «Meccano» были взяты блоки быстрого преобразования Фурье и интерфейсный блок. Такая программная схема была собрана в приложение «Meccano-2D».
В пятой главе описаны результаты применения разработанных алгоритмов и программных средств к задачам диагностики конкретных плазменных объектов: металлогалоидной лампы и плазмы индукционного разряда, являющих в настоящее время актуальными объектами исследования и инженерных разработок для светотехники и других приложений.
На установке «Свет» были зарегистрированы пространственные и временные распределения яркости для линий ртути 577 нм, 579 нм и линий таллия 552,8 нм, 654,9 нм. По линиям ртути, основным уширением для которых являлось резонансное уширение, были определены концентрации атомов ртути в основном состоянии.
По линиям таллия, основным фактором уширения которых являлся Штарк-эффект, при помощи описанного алгоритма коллективной обработки было получено пространственное распределение концентрации электронов. Полученное распределение было сравнено с теоретически рассчитанным по уравнению Саха. Для фазы, когда ток максимален, в центральной части разряда значения в пределах экспериментальной погрешности совпадают (рис. 1).
Таким образом, было установлено, что для центральной части разряда (r/R<0,4) в максимальной фазе тока выполняется баланс Саха для электронной концентрации и заселённостей верхних возбуждённых уровней, что важно как для теоретических разработок ламп, так и для диагностики.
Интересным объектом для исследования является источник света нового типа (так называемая индукционная лампа) на основе индукционно-связанной плазмы, разработанный в Институте термодинамики СО РАН [27]. Лампа представляет собой тороидальную трубку с внутренним диаметром 35 мм, заполненную неоном при давлении 100 Па. Трубка является «вторичной обмоткой» трансформатора, работающего на частоте 250 кГц. Вкладываемая в разряд мощность может регулироваться напряжением на выходе автотрансформатора, питающего ВЧ-генератор от сети. Лампа исследовалась при напряжении 150В.
Путём моделирования распределения яркости в картине, получаемой в спектрометре изображения с интерферометром Фабри – Перо, в программе «Meccano» и сравнением результата моделирования с экспериментальными данными для нескольких длин волн (585,2 нм, 614,3 нм, 638,3 нм) было получено радиальное распределение атомной температуры (рис. 2), которое в данном случае описывается как
![]() , где 2,5K3,5. (8)
, где 2,5K3,5. (8)
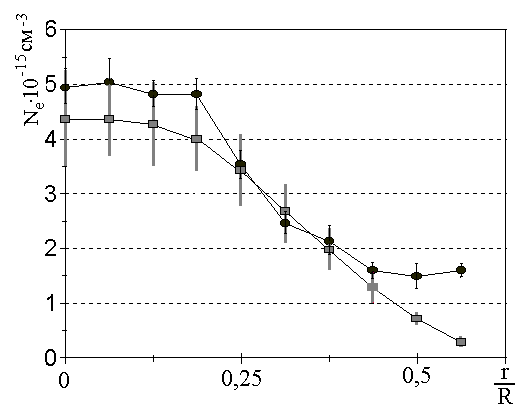
Рисунок 1 – Радиальное распределение концентрации электронов в металлогалоидной лампе (чёрный) и сравнение с рассчитанным по уравнению Саха (серый), R=0,8 см
Погрешность может быть уменьшена путём совершенствования экспериментальной установки или при сканировании спектра, если считать источник стационарным. Эти данные важны для построения теории теплопроводности плазмы индукционных разрядов.
По контурам линии 640,2 нм, измеренным с помощью спектрометра изображения в различных точках диаметра разряда, было получено радиальное распределение заселённости метастабильного уровня 2p53s (2P03/2) в неоне (рис. 3), причём N(0)=(8,4±0,6)1011 см-3.
В шестой главе представлены результаты исследования пылевых образований в комплексной плазме. Описанная методика была применена к изображениям пылевых образований из частиц цинка и оксида алюминия в тлеющем разряде в различных газах (рис. 4), полученным на установке «Пылевой кристалл» [20]. Исследовался тлеющий разряд постоянного тока в инертных газах в вертикально расположенной разрядной трубке. Использовались полидисперсные пылевые частицы размером 3–5 мкм. Обнаружено очевидное различие пространственных спектров для различных условий разряда и сорта газа и пылевых частиц.
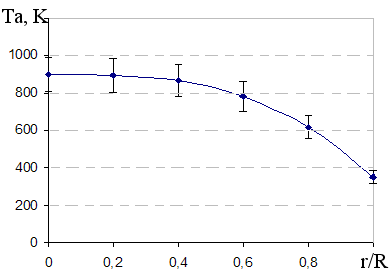
Рисунок 2 – Радиальное распределение атомной температуры в индукционном разряде
Рисунок 3 – Радиальное распределение заселённости метастабильного уровня 2p53s (2P03/2) в неоне
Анализ пространственного спектра показал, что в случае аргона в пылевом образовании имеется два характерных значений расстояния между частицами – в горизонтальном направлении и вертикальном направлении. В спектрах структур после первых вбрасываний характерные пики сильно смазаны, что говорит о больших отклонениях от какой-либо упорядоченности. Расчёт средних расстояний по пространственному спектру показывает, что, во-первых, с увеличением числа вбрасываний (n) и роста объема структуры расстояние между частицами практически не меняется и, во-вторых, с изменением тока меняется расстояние между частицами по вертикали.
 | |||
| а) Al2O3/Ar, I=0,3 мА | б) Al2O3/Ar, I=0,6 мА | в) Zn/Ar, I=0,6 мА | г) Al2O3/He, I=0,3 мА |
Рисунок 4 – Пример изображений пылевых образований из микрочастиц цинка и оксида алюминия в тлеющем разряде в различных газах и их пространственные спектры при давлении p=80 Па
Результаты определения средних расстояний между частицами по двум осям приведены в табл. 1. Было замечено, что в горизонтальном направлении среднее расстояние определяется с большей погрешностью, что говорит о большем разбросе межчастичных расстояний вдоль этого направления. Различие в средних расстояниях между частицами пылевого образования по вертикали и горизонтали может служить показателем условий формирования структуры, в частности, характеристик радиального и продольного электрических полей и кинетики частиц в пределах структуры. Эти результаты в пределах экспериментальной погрешности подтверждают значения межчастичных расстояний, полученных методом прямой обработки видеоизображений [20].
Таблица 1 – Средние расстояния между микрочастицами пылевой структуры по горизонтали (ax) и по вертикали – вдоль оси газоразрядной трубки (ay), давление p=80 Па
| Условия | Zn/Ar, I=0,6 мА | Zn/Ar, I=1,0 мА | Zn/Ne, I=0,5 мА | |
| ax, мм | 0,29±0,03 | 0,27±0,01 | 0,16±0,01 | |
| ay, мм | 0,24±0,01 | 0,20±0,01 | 0,16±0,01 | |
| Условия | Al2O3/Ar, I=0,3 мА | Al2O3/Ar, I=0,6 мА | Al2O3/Ar, I=1,0 мА | Al2O3/Ne, I=0,2 мА |
| ax, мм | 0,32±0,03 | 0,36±0,03 | 0,38±0,03 | 0,24±0,02 |
| ay, мм | 0,296±0,005 | 0,31±0,01 | 0,28±0,01 | 0,24±0,02 |
В заключении кратко сформулированы основные результаты, полученные автором.
В приложениях даны подробные описания интерфейсов и структур разработанных программных модулей.
Публикации по материалам диссертации
- Соловьев А. В. Обучающая программа «Моделирование и исключение аппаратных искажений» // 18 Межд. конф. «Школьная информатика и проблемы устойчивого развития»: Тезисы. СПб, 1999.
- Soloviev A., Luizova L. Computer training program: instrument distortions simulation and elimination // Learning and Teaching Science and Mathematics in Secondary and Higher Education: Proc. of 5th Inter-Karelian Conference. (May 17–19, 2000, Petrozavodsk). Joensuu, 2000. Pp. 158–162.
- Luizova L. A., Soloviev A. V. Computer training program for elimination of instrument distortions // 7th International Conference on Education and Training in Optics and Photonics (Singapore, 2002) / SPIE Proc. 2002. V. 4588. Pp. 440–447.
- Luizova L., Khakhaev A., Ekimov K., Soloviev A. Rational tools for data obtaining and processing in local plasma spectroscopy // 16th International Symposium on Plasma Chemistry (June 22–27, 2003, Taormina, Italy). Taormina, 2003. P. 107.
- Soloviev A., Luizova L. Free accessible web-based programs «Simulation and elimination of instrument distortion» for educational and scientific applications // 3rd International Conference on Engineering and Computer Education (ICECE-2003) (March 16–19, 2003, Santos, Brazil). Sao Paolo, 2003.
- Luizova L., Khakhaev A., Ekimov K., Soloviev A. The setup and software for local plasma spectroscopy // Proceedings of the 30th EPS Conference on Controlled Fusion and Plasma Physics (July 7–11, 2003, St. Petersburg, Russia). St. Petersburg, 2003.
- Екимов К. А., Луизова Л. А., Соловьев А. В., Хахаев А. Д. Автоматизированный комплекс для спектроскопической диагностики неоднородной плазмы // Материалы IV Российского семинара «Современные средства диагностики плазмы и их применение для контроля веществ и окружающей среды» (Москва, 12–14 ноября 2003 г.). Москва, 2003. С. 49–51.
- Екимов К. А., Луизова Л. А., Приходченко Р. В., Соловьев А. В., Хахаев А. Д. Лабораторные работы по спектроскопии с использованием виртуальных инструментов и удаленного доступа. Петрозаводск, 2003. 62 с.
- Соловьев А. В., Луизова Л. А. Учебное моделирование и исключение аппаратных искажений // Фундаментальные исследования. 2004. № 3. С. 84–86.
- Екимов К. А., Луизова Л. А., Соловьев А. В., Хахаев А. Д. Рациональные технологии в локальной спектроскопии неоднородной плазмы // Совр. наукоемкие технологии. 2004. № 2. С. 52–54.
- Khakhaev A., Luizova L., Ekimov K., Soloviev A. Spatial and time-dependent distribution of plasma parameters in the metal-halide arc lamp // 12th International congress of plasma physics (October 25–29, 2004, Nice): Book of abstracts. Nice, 2004. P. 109.
- Научно-образовательный центр по фундаментальным проблемам приложений физики низкотемпературной плазмы (НОЦ «Плазма»): Отчет о НИР / Рук. темы А. Д. Хахаев. Рег. во ВНТИЦ № 01.20.0215108, инв. № 0220.0505263. Петрозаводск, 2004. 337 с.
- Ekimov K., Luizova L., Soloviev A., Khakhaev A. Data array acquisition and joint processing in local plasma spectroscopy // J. of Quantum Spectroscopy & Radiative Transfer. 2005. V. 96. Pp. 513–523.
- Кравченко А. А., Луизова Л. А., Хахаев А. Д., Соловьев А. В. Координатно-чувствительная спектроскопия с использованием интерферометра Фабри – Перо // Материалы Всеросс. симпозиума молодых ученых, студентов и аспирантов «Фундаментальные проблемы приложений физики низкотемпературной плазмы» (Петрозаводск, 5–11 сентября 2005 г). Петрозаводск, 2005. С. 283–288.
- Kravchenko A. A., Luizova L. A., Soloviev A. V. High Resolution Local Spectroscopy of Inhomogeneous Plasma // Proc. of XVIth International Conference on Gas Discharges and Their Applications (September 11–15, 2006, Xian). Xian, 2006.
Цитированная литература
- Балебанов А. В. и др. Спектрометр с пространственным разрешением на основе интерферометра Фабри – Перо // Приборы и техника эксперимента. 1985. № 2. С. 179–180.
- Вайнштейн Л. А., Собельман И. И., Юков Е. А. Возбуждение атомов и уширение спектральных линий. М.: Наука, 1979. 319 с.
- Веклич А. Н., Осидач В. Е. Спектроскопия плазмы свободно горящего дугового разряда между композиционными материалами // Материалы IV Российского семинара «Совр. средства диагностики плазмы и их применение для контроля веществ и окружающей среды» (Москва, 12–14 ноября 2003 г.). Москва, 2003. С. 82–85.
- Луизова Л. А. Физически обоснованный приём регуляризации в задаче радиального преобразования // Оптика и спектроскопия. 1982. Т. 52. Вып. 4. С. 690–695.
- Луизова Л. А., Подрядчиков С. Ф., Хахаев А. Д. Влияние плазменного кристалла на поперечный профиль яркости излучения тлеющего разряда // Материалы Всероссийской научной конференции по физике низкотемпературной плазмы ФНТП–2001. Т. 2. Петрозаводск, 2001. С. 129–132.
- Очкин В. Н. Спектроскопия низкотемпературной плазмы. М.: Физматлит, 2006. 472 с.
- Петров Ю. П., Сизиков В. С. Корректные, некорректные и промежуточные задачи с приложениями. СПб: Политехника, 2003. 264 с.
- Тихонов А. Н., Арсенин В. Я. Методы решения некорректных обратных задач. М.: Наука, 1979. 288 с.
- Buie M. J. et al. Abel's inversion applied to experimental spectroscopic data with off-axis peaks // Journal of Quantitative Spectroscopy & Radiative Transfer. 1996. V. 55. Pp. 231–249.
- Fortov V. E. et al. Complex (dusty) plasmas: current status, open issues, perspectives // Physics Reports. 2005. V. 421. Pp. 1–103.
- Luizova L. A. Abel's inversion applied to array of spectral line profiles // Journal of Quantitative Spectroscopy & Radiative Transfer. 2000. V. 66. Pp. 277–283.
- Ulanov I. M., Kolmakov K. N., Isupov M. V., Litvintsev A. Yu. Study of the transformer-coupled induction toroidal discharge for the development of plasma chemical reactions and new light sources // IV International Conf. «Plasma Physics and Plasma Technology» (Minsk, September 15–19, 2003). Contributed Papers. V. 1. Minsk, 2003. Pp. 3–6.
Подписано в печать 15.11.06.
Формат 60х84 1/16. Бумага офсетная. Печать офсетная.
Уч.-изд. л. 1. Тираж 100 экз. Изд. №264
Петрозаводский государственный университет
Типография Издательства
Петрозаводского государственного университета
185910, Петрозаводск, пр. Ленина, 33

