Поляризационное самовоздействие импульсов предельно коротких длительностей в диэлектрических средах
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ
На правах рукописи
УДК 535.2:621.373.826
Украинский Алексей Оскарович
Поляризационное самовоздействие
импульсов предельно коротких длительностей
в диэлектрических средах
Специальность 01.04.05 - Оптика
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата физико-математических наук
Санкт-Петербург
2003 г.
Работа выполнена на кафедре фотоники и оптоинформатики Санкт-Петербургского государственного университета информационных технологий, механики и оптики.
| Научный руководитель: | Доктор физико-математических наук, профессор Козлов С.А. |
| Официальные оппоненты: | Доктор физико-математических наук, профессор Либенсон М.Н. Кандидат физико-математических наук, доцент Белашенков Н.Р. |
| Ведущая организация: | Федеральное государственное унитарное предприятие “Научно-исследовательский институт лазерной физики” (г. С.-Петербург) |
Защита диссертации состоится 18 ноября 2003 года в 15 часов 30 минут в аудитории 308 на заседании диссертационного совета Д 212.227.02 при Санкт-Петербургском государственном университете информационных технологий, механики и оптики по адресу: 197101, Санкт-Петербург, ул. Саблинская, д. 14.
С диссертацией можно ознакомится в библиотеке института.
Автореферат диссертации разослан 12 октября 2003 г.
Отзывы и замечания по автореферату в двух экземплярах, заверенные печатью, просьба высылать по вышеуказанному адресу на имя ученого секретаря диссертационного совета.
| Ученый секретарь диссертационного совета Д 212.227.02, доктор технических наук, профессор | Новиков А.Ф. |
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы
В настоящее время созданы лазерные системы, способные генерировать импульсы, которые состоят из малого числа колебаний светового поля. Импульсы из числа колебаний порядка и менее десяти уже принято называть предельно короткими импульсами (ПКИ).
ПКИ могут взаимодействовать с веществом без разрушения последнего (по крайней мере, за длительность импульса) обычно при гораздо более высоких интенсивностях излучения, чем у более длинных импульсов. Поэтому в поле ПКИ можно наблюдать нелинейные явления, редко встречающиеся до сих пор даже в поле оптических импульсов пикосекундных длительностей, – например, сильное уширение временного спектра импульса при взаимодействии с нелинейными средами до размеров, сравнимых с центральной частотой излучения (генерация спектрального суперконтинуума (ССК)).
Использование ПКИ с континуумным спектром открывает новые возможности в различных областях науки и техники. Длительность ПКИ определяет новый масштаб измерения временных процессов в видимом и ближнем ИК диапазоне, а широкие спектры – возможность все более точных спектральных измерений. Кроме того, сфазировав ССК, можно получить световые образования, состоящие всего из одного – двух колебаний светового поля, – действительно предельно коротких по числу колебаний импульсов. В настоящее время уже разработаны и используются оптические устройства, позволяющие сжимать фемтосекундные импульсы, как при распространении, так и при их отражении; известны эксперименты по получению световых образований аттосекундного временного диапазона.
Разработка техники получения и управления параметрами фемтосекундных импульсов открывает широкие возможности для создания информационных оптических систем, по характеристикам на порядки превышающих существующие сейчас. Одно из важных ограничений промышленно используемых в настоящее время систем – обработка информации электронными устройствами. Поэтому в настоящее время активно исследуются возможности создания сверхбыстрых оптических переключателей, логических вентилей, мультиплексоров, нелинейных фильтров и т.п. Один из методов создания таких устройств, уже достаточно давно обсуждающийся в литературе, – поляризационное управление параметрами импульсов. К моменту начала работы широко изучалось взаимодействие линейно поляризованных ПКИ с веществом, а публикаций по изучению ПКИ произвольной поляризации было мало. Поэтому работы по исследованию поляризационных эффектов при взаимодействии импульсов предельно коротких длительностей с веществом представляются актуальными.
Цель работы
Выявление основных закономерностей нелинейной динамики поляризации импульсов, состоящих из малого числа колебаний светового поля, при их распространении в прозрачных изотропных оптических средах с нерезонансной нелинейностью, а также при их отражении от таких сред.
Задачи исследования
- Построение уравнений, описывающих самовоздействие ПКИ произвольной поляризации в изотропных диэлектрических средах с нерезонансной электронной нелинейностью и анализ пределов их применимости.
- Выявление основных закономерностей поляризационного самовоздействия ПКИ при их распространении в оптических волноводах.
- Разработка метода анализа отражения ПКИ произвольной поляризации от изотропных диэлектрических сред с нерезонансной электронной нелинейностью.
- Выявление основных закономерностей нелинейного отражения ПКИ с произвольной поляризацией при их падении на границу раздела диэлектрических сред.
Научные положения, выносимые на защиту
- Выведено уравнение, описывающие эволюцию сверхшироких спектров сверхкоротких импульсов с произвольной поляризацией, в том числе состоящих лишь из нескольких колебаний светового поля, в изотропных оптических средах с произвольной дисперсией линейного показателя преломления и нерезонансной электронной нелинейностью. Показано, что в предельном случае среды со слабой дисперсией полученное уравнение сводится к известному векторному модифицированному уравнению Кортевега де Вриза, являясь обобщением последнего на случай сред с произвольной дисперсией.
- Показано, что поляризационное самовоздействие импульсов из малого числа колебаний светового поля в прозрачных изотропных средах с нерезонансной нелинейностью проявляется в неоднородном по импульсу самовращении эллипса поляризации, приводящем к формированию концом вектора напряженности электрического поля в плоскости фронта волны (на фазовом портрете) S-образных аттракторов. Показано, что эллиптичность колебаний, составляющих наиболее интенсивную часть импульса, при этом меняется слабо.
- Показано, что эффективность сверхуширения спектра импульса из малого числа колебаний светового поля в прозрачных изотропных средах с нерезонансной нелинейностью гладко уменьшается при изменении входной поляризации импульса от линейной до циркулярной (при сохранении его входной энергии и длительности). Например, в смоделированном случае распространения импульсов в полом волноводе, заполненном аргоном, при уширении спектра в десять раз (для линейно поляризованного излучения) разница в уширении спектра линейно поляризованного и циркулярно поляризованного импульсов составляла 20%. При этом эффективность генерации колебаний на утроенной частоте падала в 20 раз.
- Выведено уравнение, описывающее временную зависимость параметров отраженного излучения от параметров падающего, при нормальном падении импульсов произвольной поляризации, содержащих малое число колебаний светового поля, на границу раздела прозрачных изотропных сред с дисперсией, одна из которых линейная, а нелинейность другой имеет нерезонансную электронную природу.
- Показано, что укорочение длительности эллиптически поляризованного импульса из малого числа колебаний светового поля при отражении от среды, нелинейность которой имеет нерезонансную электронную природу, может сопровождаться сжатием фазового портрета отраженного импульса без его поворота.
Научная новизна
Все результаты, включенные в положения, выносимые на защиту, являются новыми.
Практическая значимость работы
- Получены новые спектральные уравнения, описывающие эволюцию сверхшироких спектров сверхкоротких импульсов с произвольной поляризацией, в изотропных оптических средах с дисперсией произвольного вида и нерезонансной электронной нелинейностью.
- Разработан программный комплекс для проведения инженерных расчетов, визуализации и анализа поляризационного самовоздействия ПКИ при их распространении в изотропных диэлектрических средах с нерезонансной электронной нелинейностью, а также при нелинейном отражении от таких сред.
- Предложен принцип построения оптического поляризационного умножителя, основанного на анализе генерации третьей гармоники в спектре распространяющегося в нелинейной среде импульса.
- Продемонстрирована возможность управления длительностью отраженного импульса при отражении ПКИ от нелинейной среды в случае, когда линейные показатели преломления граничащих диэлектрических сред выровнены.
Апробации работы
Основные результаты диссертационной работы докладывались на IV и VII Международных Симпозиумах по Фотонному Эхо и Когерентной Спектроскопии (Йошкар-Ола, 1997, Великий Новгород, 2001); III и IV Международных Конференциях по Лазерной Физике и Спектроскопии (Гродно, Беларусь, 1997, 1999); XIV Международной Конференции по Когерентной и Нелинейной Оптике (Москва, 1998); V Конгрессе по Современной Оптике (Будапешт, Венгрия, 1998); I и II Конференциях «Фундаментальные проблемы оптики» в рамках I и II Международных Оптических Конгрессов "Оптика-21 век" (С.-Петербург, 2000 и 2002); Interdisciplinary International Conference on Polarization Effects in Lasers, Spectroscopy and Optoelectronics (Southampton, UK, 2000); X Конференции по Нерезонансному Взаимодействию Лазерного Излучения с Веществом (С.-Петербург, 2000); X Конференции по лазерной оптике (С.-Петербург, 2000); XVII Interdisciplinary Laser Science Conference (Los Angeles, USA, 2001).
Личный вклад
Диссертант принимал участие в постановке и решении задач, обработке и обсуждении полученных результатов. Представленные результаты расчетов выполнены диссертантом. Работы [6,7,10] выполнены автором самостоятельно, в работах [1-5,8,9] вклад автора диссертации был равноценным.
Структура и объем диссертации
Диссертация состоит из введения, трех глав, заключения, и списка литературы, содержащего 149 наименований. Работа изложена на 111 страницах, включая 30 рисунков и 1 таблицу.
КРАТКОЕ СОДЕРЖАНИЕ ДИССЕРТАЦИИ
Во введении обосновывается актуальность работы, сформулированы ее цель, задачи и основные научные результаты, выносимые на защиту.
В первой главе, носящей обзорный характер, рассмотрены экспериментальные результаты по получению спектрального суперконтинуума в изотропных средах. Рассмотрены теоретические и экспериментальные работы по анализу генерации третьей гармоники оптическими импульсами коротких длительностей. Обсуждаются публикации по анализу взаимодействия произвольно поляризованных импульсов с веществом, поляризационному управлению параметрами распространяющихся в среде импульсов и по анализу отражения лазерных импульсов от нелинейных сред. Обсуждаются статьи, посвященные изучению эффектов нового временного порядка в оптике – генерации аттосекундных импульсов.
Во второй главе представлен вывод системы укороченных спектральных уравнений, описывающих эволюцию сверхшироких спектров сверхкоротких импульсов с произвольной поляризацией при однонаправленном распространении в изотропных диэлектрических средах с нерезонансной электронной нелинейностью. В первом параграфе приводится волновое уравнение общего вида, которое может быть получено из системы уравнений Максвелла, описывающее распространение электромагнитного поля в немагнитной среде. Так как в работе изучается распространение оптического излучения с неизменной поперечной структурой, далее волна рассматривается как плоская. Для нахождения решения система дополняется материальными уравнениями, описывающими поляризационный отклик среды. Линейный поляризационный отклик учитывается дисперсией линейного показателя преломления произвольного вида 
, в общем случае, комплексного, а нелинейный вводится в виде нерезонансного электронного отклика 
, где 
– кубическая восприимчивость, а 
– поле плоской волны произвольной поляризации. Далее система волнового и материальных уравнений преобразуется в систему нелинейных интегро-дифференциальных уравнений для временных спектров 
и 
декартовых компонент 
и 
поля импульса произвольной поляризации 
. Для описания однонаправленного распространения излучения в веществе уравнения укорачиваются. Во втором параграфе описана процедура укорочения, которое проводилось в предположении малости нелинейного поляризационного отклика 
относительно линейного отклика среды, что справедливо при распространении импульсов с такими интенсивностями, при которых не происходит формирование плазмы. В результате, полученная система имеет вид
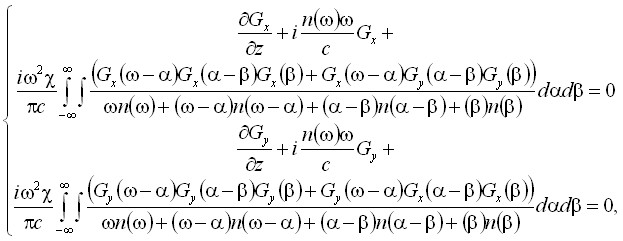(1)
где 
, 
- спектры декартовых компонент 
, 
поля импульса произвольной поляризации, z – направление распространения плоской волны. Эти уравнения описывают, в том числе, и распространение световых образований произвольной поляризации, состоящих лишь из нескольких колебаний светового поля, поскольку при их построении не использовались приближение медленно меняющейся огибающей или медленно меняющегося профиля. В третьем параграфе показано, что в предельном случае среды с нормальной дисперсией, описываемой феноменологическим соотношением 
, причем 
, где N, a – феноменологические дисперсионные параметры среды, полевым аналогом полученного уравнения является известное векторное модифицированное уравнение Кортевега де Вриза (мКдВ), описывающее нерезонансное взаимодействие импульсов фемтосекундных длительностей с диэлектрическими средами
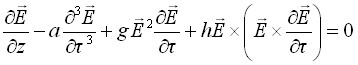, (2)
где 
– время в сопровождающей импульс системе координат, 
, 
– параметры, характеризующие нелинейный поляризационный отклик среды.
Таким образом, полученная в данной работе система спектральных уравнений является обобщением уравнения (2) на случай описания распространения импульсов произвольной поляризации в средах с произвольной дисперсией. Далее показано, что уравнения, описывающие самовоздействие импульсов предельно коротких длительностей в средах со слабой дисперсией, отвечают принципу соответствия и для импульсов, состоящих из большого числа колебаний поля, переходят в уже известное в литературе уравнение для огибающей поля таких импульсов.
В последнем параграфе главы проведена нормировка полученных уравнений для постановки численных экспериментов, описаны понятия дисперсионной длины и нелинейной длины - расстояний, на которых, соответственно, дисперсионные и нелинейные эффекты существенно влияют на эволюцию импульса.
В третьей главе изучается поляризационное самовоздействие ПКИ в изотропных нелинейных средах. В первом параграфе рассмотрено поляризационное самовоздействие ПКИ на расстояниях меньших длины дисперсионного расплывания. Показано, что в этом случае волновое уравнение (2) может быть записано в виде системы для амплитуды 
и фазы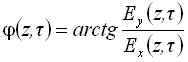 
вектора электрического поля импульса
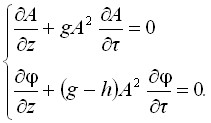(3)
Из системы (3) видно, что при прохождении ПКИ в веществе на расстояниях меньших длины дисперсионного расплывания его поляризационное самовоздействие проявляется в изменении ориентации вектора напряженности электрического поля в направлении распространения ПКИ, пропорциональном квадрату величины поля и скорости поворота вектора напряженности. Далее приведены результаты численного моделирования, соответствующие распространению импульсов длительностью до 10 фс в полых волноводах, заполненных аргоном. Продемонстрирован поворот портрета импульса в плоскости фронта волны, формируемого концом вектора напряженности электрического поля с течением времени (далее фазового портрета), известный для длинных импульсов (состоящих из большого числа колебаний с одинаковой амплитудой) как эффект самовращения эллипса поляризации. При этом характер эволюции поля декартовых компонент импульса соответствует режиму формирования ударных волн. Показано формирование нечетных высокочастотных компонент в спектре ПКИ.
Далее анализируется распространение ПКИ на длинах больших длины дисперсионного расплывания. Показано, что в этом случае при распространении ПКИ, все спектральные компоненты которого находятся в области нормальной дисперсии, происходит генерация новых колебаний, сопровождающаяся сильным уширением спектра. При этом каждое колебание поля импульса вносит в фазовый портрет квазиэллипс (квази -, т.к. с течением времени конец вектора напряженности электрического поля ПКИ на фазовой плоскости замкнутых кривых не описывает), повернутый относительно квазиэллипса поляризации излучения на входе в среду, поэтому на фазовом портрете происходит неоднородное по импульсу вращение эллипса поляризации без существенного изменения его эллиптичности. Результаты расчета динамики декартовых компонент импульса на различных расстояниях в волноводе, соответствующего, например, распространению эллиптически поляризованного ПКИ с центральной длиной волны 
=780 нм, длительностью 10 фс, с интенсивностью I=3·1013 Втсм-2 и эллиптичностью e=0.5, в полом волноводе длиной z=64 см, заполненном аргоном под давлением P=3 атм показаны на Рис.1. Вдоль оси времени для каждого графика изображены
Рис.1. Вращение эллипса поляризации вдоль импульса на различных расстояниях в капилляре, заполненном аргоном.
фрагменты фазового портрета, соответствующие колебаниям данной временной части импульса. Все фазовые портреты колебаний импульса для наглядности смасштабированы.
Далее обсуждаются изменения, происходящие на фазовом портрете уширяющегося и во времени и спектрально импульса. На Рис.2. показаны фазовые портреты импульса, соответствующие расчету, приведенному на Рис.1.
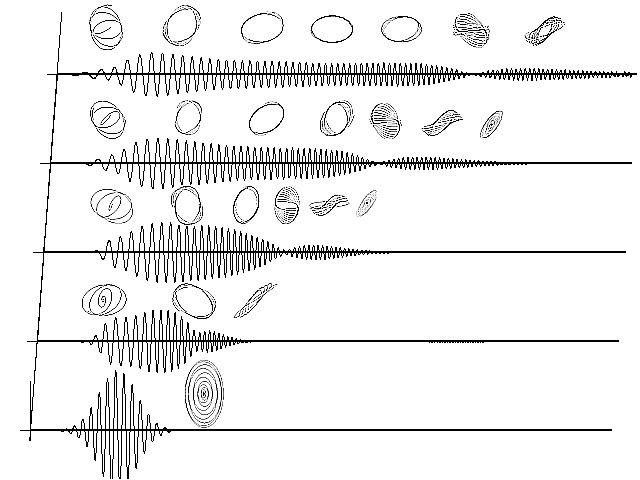
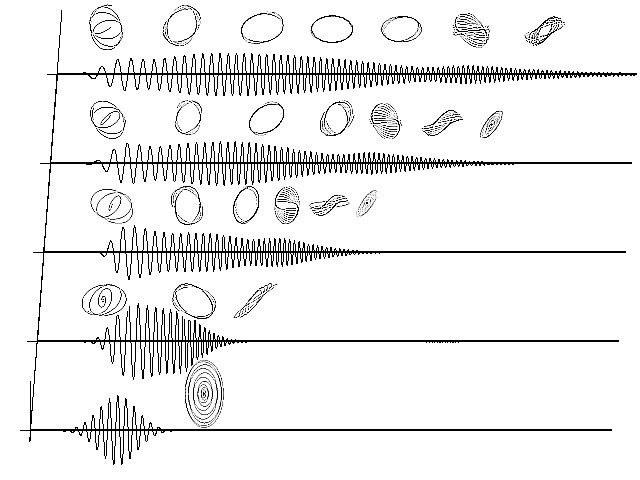
Каждый портрет иллюстрирует временную динамику конца вектора напряженности электрического поля на соответствующем расстоянии в волноводе. Т.к. амплитуды колебаний, составляющих импульс, сильно различаются, на фазовых портретах не формируются замкнутые кривые, характерные для длинных импульсов, состоящих из большого числа колебаний светового поля. Как видно из рисунков, в среде происходит неоднородное по
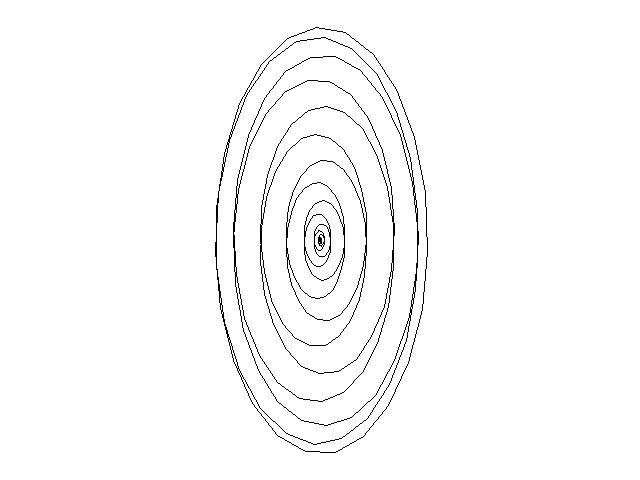
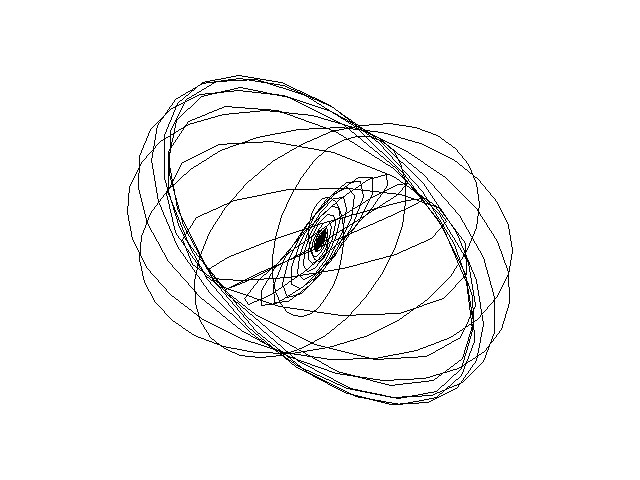
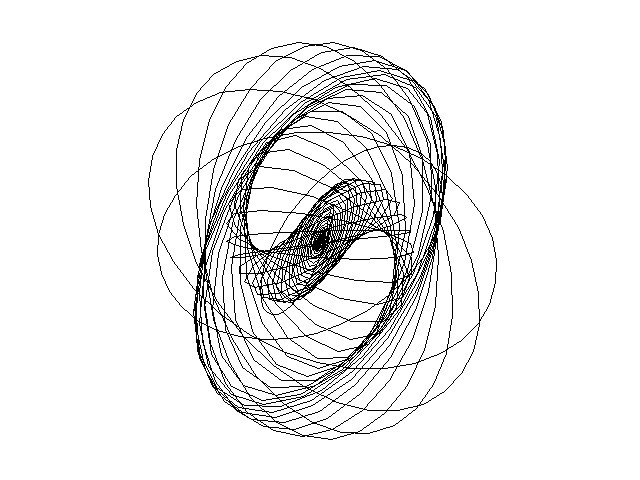
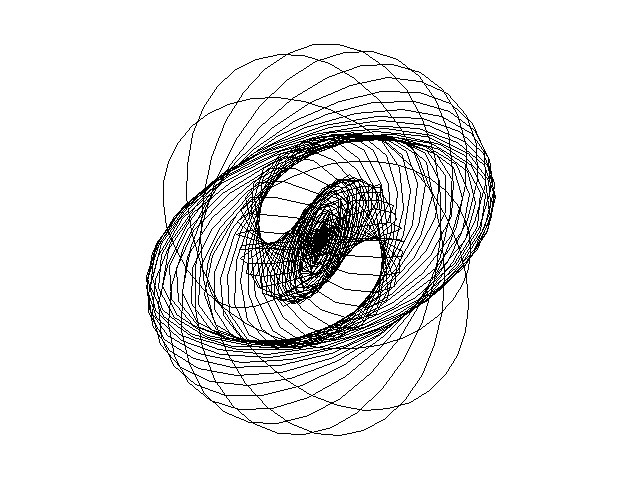
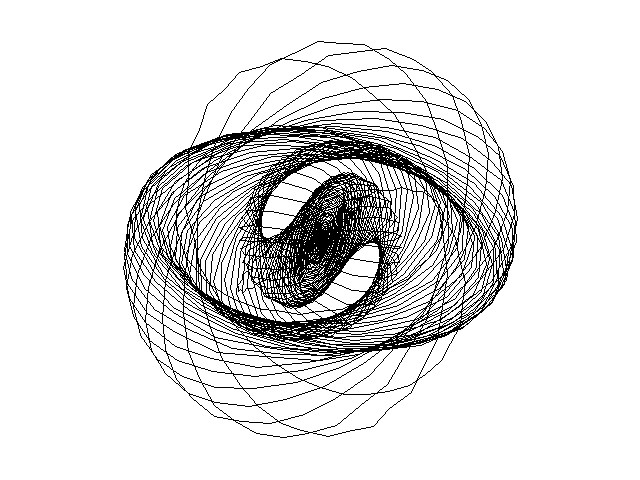
Рис.2. Формирование S-образных областей на фазовом портрете импульса на различных расстояниях в капилляре, заполненном аргоном (рисунки смасштабированы).
импульсу вращение эллипса поляризации, причем эллипсы, соответствующие колебаниям с меньшей интенсивностью вращаются медленнее, чем эллипсы, соответствующие более интенсивной части спектра.
Показано, что при распространении света в среде эллипс поляризации испытывает неоднородное по импульсу вращение, соответственно, из-за многократного наложения эллипсов, сформированных различными периодами импульса, на фазовых портретах отчетливо видны S-образные области, куда вектор электрического поля ПКИ с течением времени попадает чаще всего. Далее проанализирована динамика эллиптичности и вращения колебаний поля, составляющих импульс. Показано, что эллиптичность колебаний наиболее интенсивной части импульса сохраняется, при этом поворот эллипсов может различаться. Например, в приведенном на Рис.1,2 расчете поворот составлял до 270 градусов.
Далее обсуждаются результаты моделирования распространения ПКИ с поляризацией близкой к линейной. Показано, что неоднородное по импульсу перетекание энергии от одной декартовой компоненты к другой, соответствующее эффекту самовращения эллипса поляризации, может приводить к появлению значительных провалов во временной динамике декартовых компонент ПКИ с начальной поляризацией близкой к линейной. Например, при моделировании распространения ПКИ с центральной длиной волны 
=780 нм, длительностью 10 фс, с интенсивностью I=3·1013 Втсм-2 и эллиптичностью e=0.142 в полом волноводе длиной z=48 см, заполненном аргоном под давлением P=3 атм, продемонстрировано формирование последовательности из двух коротких световых образований во временной динамике одной из декартовых компонент импульса.
Третий параграф посвящен анализу зависимости генерации спектрального суперконтинуума от эллиптичности импульса на входе в среду. Показано, что генерация ССК эллиптически поляризованными импульсами качественно не отличается от генерации ССК линейно поляризованными: более сильное уширение происходит в анти-стоксову область спектра, хотя максимум смещается в стоксову область, и на больших расстояниях генерация ССК переходит в линейный режим из-за уменьшения интенсивности вследствие значительного временного расплывания. Однако, из расчета, приведенного на Рис.3. видно, что при самовоздействии эллиптически поляризованных импульсов генерация спектрального суперконтинуума происходит медленнее, чем для линейно поляризованных. В приведенном расчете показано несимметричное относительно центральной частоты входящего импульса уширение спектральной плотности линейно поляризованного импульса в 10 раз и показана зависимость уширения спектра от эллиптичности падающего излучения, понижающая эффективность генерации суперконтинуума на 20% для циркулярно поляризованного импульса. Далее показано, что величина понижения эффективности генерации суперконтинуума от эллиптичности излучения на входе в среду зависит от длительности импульса и существует диапазон длительностей, при которых различия наиболее заметны. Например, для импульсов с центральной длиной волны 
=780 нм, с интенсивностью I=3·1013 Втсм-2 эти различия наиболее заметны в диапазоне 10-20 фс.
Далее изучается зависимость генерации колебаний на утроенной частоте, возникающих в спектре импульса при генерации ССК, от эллиптичности ПКИ на входе в среду. Представлены результаты численного моделирования и показано, что генерация колебаний на утроенной частоте, также как и генерация ССК, происходит слабее в спектре эллиптически поляризованного ПКИ, при этом фазовый портрет колебаний на утроенной частоте формируется из квази-эллипсов, которые могут иметь различную поляризацию.
В заключение главы обсуждается принцип создания оптического поляризационного умножителя, основанного на факте практического отсутствия утроенных частот в спектре циркулярно поляризованного импульса, и наиболее эффективной их генерации в спектре линейно поляризованного импульса. При рассмотрении декартовых компонет поля падающего импульса как входных сигналов устройства, генерация или отсутствие утроенных частот будет соответствовать логической операции исключающего ИЛИ входных сигналов. Показана достоверность построения такого устройства.
В четвертой главе представлен вывод обыкновенных дифференциальных уравнений, описывающих отражение ПКИ на границе раздела прозрачных изотропных сред с дисперсией, одна из которых линейная, а нелинейность другой имеет нерезонансную электронную природу. В первом параграфе обсуждаются граничные условия, вытекающие из уравнений Максвелла и связывающие декартовы компоненты полей падающего, отраженного и преломленного импульсов на границе раздела двух сред. Во втором параграфе на основе описанных во второй главе модифицированных волновых уравнений Кортевега де Вриза вида (2) для поля ПКИ и граничных условий, построенных в первом параграфе, показано, что нормальное отражение произвольно поляризованного ПКИ от нелинейной среды может быть описано системой обыкновенных дифференциальных уравнений, связывающих декартовы компоненты полей падающего и отраженного импульсов на границе раздела двух сред, вида
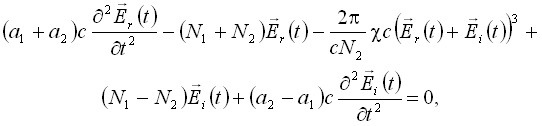(4)
где 
и 
– временные зависимости векторов напряженности электрического поля, соответственно, отраженного и падающего импульсов, 
, 
– законы нормальной дисперсии линейных показателей преломления граничащих сред, 
– кубическая восприимчивость, характеризующая нелинейный отклик отражающей среды. В третьем параграфе с помощью метода последовательных приближений получено решение линеаризованного по полю отраженной волны уравнения вида (4). Показано, что фазовый портрет отраженного импульса, а также колебаний, возникающих в его спектре на утроенной частоте, может деформироваться, при этом не происходит его вращения. Далее проведена нормировка полученных уравнений для постановки численных экспериментов. При численном моделировании использовался метод Розенброка для обыкновенных дифференциальных уравнений, обеспечивающий второй порядок точности по временному шагу.
В пятой главе проведено исследование нормального отражения ПКИ от нелинейной среды на границе раздела сред с выровненными линейными показателями преломления. В первом параграфе проводится постановка задачи нормального отражения ПКИ на границе раздела сред, подобранных так, чтобы 
. Такая модель может быть справедлива при анализе отражении на границе раздела жидкость – твердое тело при определенных условиях. Во втором параграфе рассмотрены различные сценарии отражения декартовых компонент поля ПКИ, соответствующие различной эллиптичности падающего излучения. Например, показано, что при отражении линейно поляризованного ПКИ происходит сужение колебаний декартовых компонент поля отраженного импульса, а при отражении эллиптически поляризованного – характер деформации одной компоненты может сохраняться, а во временной динамике другой компоненты может происходить сглаживание колебаний. Типичные фазовые портреты падающего и отраженного импульса показаны на Рис.4. Показано отсутствие вращения эллипса поляризации и деформация, приводящая к изменению эллиптичности фазового портрета. При этом в спектре отраженного импульса появляются нечетные высокочастотные компоненты. Проведен анализ колебаний различных гармоник в спектре импульса. Показано, что вращения и неоднородной деформации фазовых портретов колебаний на центральной частоте, утроенной и пятикратной частотах не происходит, но может происходить их сжатие. В третьем параграфе получена и изучена зависимость длительности отраженного импульса от
а) б)
Рис.4. Фазовый портрет падающего 5 фс импульса (а) и отраженного (б) от границы раздела сред с выровненными линейными показателями преломления (портреты смасштабированы).
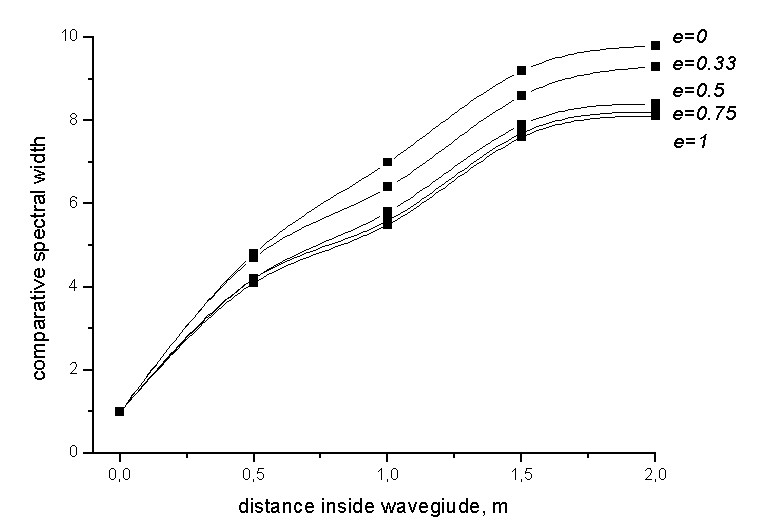
эллиптичности падающего для импульсов различных длительностей. Например, в смоделированном случае различия составляли до 10% длительности для 2 фс импульса и становились менее заметными для более длинных импульсов (2% для 10 фс импульса, Рис.5).
Рис.5. Зависимость длительности компоненты отраженного импульса (относительно длительности падающего импульса) от эллиптичности падающего излучения.
В заключении сформулированы основные результаты, полученные в диссертации:
- Получена система уравнений, которая описывает динамику спектров импульсов произвольной поляризации, состоящих из нескольких колебаний светового поля, при их распространении в изотропных средах с произвольной дисперсией линейного показателя преломления и безынерционной кубичной нелинейностью.
- Разработан алгоритм и программа расчета для численного моделирования распространения ПКИ в изотропных прозрачных средах со слабой дисперсией и безынерционной кубичной нелинейностью.
- Описано формирование S-образных аттракторов на фазовом портрете ПКИ при распространении в капиллярах, заполненных аргоном, вызываемое неоднородным по импульсу вращением эллипса поляризации, без существенного изменения его эллиптичности.
- Показана возможность формирования последовательности из двух световых образований во временной динамике ПКИ с поляризацией близкой к линейной при распространении в капиллярах, заполненных аргоном.
- Показано гладкое снижение эффективности генерации суперконтинуума на 20% (в приведенных результатах моделирования), а также генерации третьей гармоники в спектре распространяющегося импульса, при изменении эллиптичности излучения на входе в среду от линейной до циркулярной. Показан диапазон длительностей падающих импульсов, в котором этот эффект наиболее заметен.
- Разработан принцип построения оптического поляризационного умножителя, производящего вычисление логической операции исключающего ИЛИ сигналов, представляющих собой декартовы компоненты произвольно поляризованного ПКИ, путем анализа генерации третьей гармоники в спектре прошедшего в нелинейной среде импульса.
- Построена система обыкновенных дифференциальных уравнений, описывающих зависимость компонент поля отраженного излучения от компонент поля падающего, при нормальном падении импульсов произвольной поляризации, содержащих малое число колебаний светового поля, на границу раздела прозрачных изотропных сред с дисперсией, одна из которых линейная, а нелинейность другой имеет нерезонансную электронную природу.
- Продемонстрирована деформация эллипса поляризации без его поворота и укорочение отраженного импульса при нормальном отражении импульсов произвольной поляризации от нелинейной среды в случае, когда линейные показатели преломления граничащих диэлектрических сред выровнены.
- Показано увеличение длительности отраженного импульса при изменении эллиптичности падающего импульса на входе в среду от линейной до циркулярной и сохранении остальных его параметров (длительности, энергии). Показано уменьшение данного эффекта при увеличении длительности падающих импульсов.
СПИСОК РАБОТ, ОПУБЛИКОВАННЫХ ПО ТЕМЕ ДИССЕРТАЦИИ
- Kozlov S.A., Oukrainski A.O., Shpolyanskiy Yu.A., Self-induced changes in the polarization of pulses of a few oscillations duration in isotropic dielectric media. - Proc. SPIE, 1997, v.3239, p.169-176.
- Bespalov V. G., Kozlov S. A., Oukrainski A. O., Shpolyanskiy Yu. A., Nonlinear reflection of extremely short light pulses. - Proc. SPIE, 1998, v.3573, p.82-85.
- Bespalov V.G., Kozlov S.A., Sazonov S.V., Oukrainski A.O., Shpolyanskiy Yu.A., Spectrum supercontinuum generation by temporal broadening in isotropic nonlinear media of femtosecond light pulses. - Physics of Vibrations, 1999, v.7, N1, p.19-28.
- Bespalov V.G., Kozlov S.A., Oukrainski A.O., Sazonov S.V., Shpolyanskiy Yu.A., Self-action of continuum spectrum femtosecond pulses. - Proc. SPIE, 1999, v.3735, p.43-54.
- Kozlov S.A., Bespalov V.G., Krylov V.N., Oukrainski A.O., Shpolyanskiy Yu.A., Nonlinear optics problems of one and more cycles light pulses. - Proc. SPIE, 1999, v.3609, p.276-281.
- Украинский А.О. Поляризационные эффекты при нелинейном распространении импульсов из нескольких колебаний светового поля в диэлектрических средах. - Вестник молодых ученых, сер. физические науки, 2000, вып. 1, с. 28-33.
- Украинский А.О. Поляризационные эффекты при распространении предельно коротких импульсов в нелинейных средах. - в кн.: Проблемы когерентной и нелинейной оптики. СПб, 2000, с. 153-160.
- Ukrainsky A.O., Kozlov S.A. Polarization effects in the interaction of extremely short light pulses with nonlinear media. - J. Opt. B: Quantum Semiclass. Opt., 2001, N 3, p. S180–S184.
- Козлов С.А., Украинский А.О. Поляризационные эффекты при взаимодействии предельно коротких импульсов с диэлектрическими средами. - Изв. РАН, сер. физическая, 2001, вып. 4, с. 32-41.
- Украинский А.О. Отражение предельно коротких импульсов от диэлектрических сред. – В кн.: Сборник трудов конференции “Фундаментальные проблемы оптики”, 2002, СПб, с.27-28.
