Теплофизика и теплообмен при формировании защитных покрытий низкотемпературным газодинамическим методом
На правах рукописи
Степаненко Светлана Анатольевна
ТЕПЛОФИЗИКА И ТЕПЛООБМЕН ПРИ ФОРМИРОВАНИИ
ЗАЩИТНЫХ ПОКРЫТИЙ НИЗКОТЕМПЕРАТУРНЫМ
ГАЗОДИНАМИЧЕСКИМ МЕТОДОМ
Специальность: 01.04.14
«Теплофизика и теоретическая теплотехника»
Автореферат
диссертации на соискание ученой степени
кандидата технических наук
Москва – 2009
Работа выполнена на кафедре “Авиационно-космическая теплотехника” Московского авиационного института (государственного технического университета)
Научный руководитель:
доктор технических наук, Заслуженный деятель
науки РФ, профессор Никитин Петр Васильевич
Официальные оппоненты:
доктор технических наук, профессор
Михатулин Дмитрий Сергеевич.
кандидат технических наук, зам. начальника
отделения «РКК «ЭНЕРГИЯ» им. С.П. Королева
Доморацкий Александр Николаевич
Ведущая организация:
«Сибирский государственный аэрокосмический
университет им. академика М.Ф. Решетнёва», г. Красноярск.
Защита состоится « » 2009 г. на заседании диссертационного Совета Д 212.125.08 в Московском авиационном институте (государственном техническом университете), по адресу: 125993, г. Москва, А-80,
ГСП-3,Волоколамское шоссе, д. 4.
С диссертацией можно ознакомиться в библиотеке МАИ.
Отзывы на автореферат в 2-х экземплярах, заверенные печатью, просьба прислать по адресу: 125993, г. Москва, А-80, ГСП-3, Волоколамское шоссе,
д. 4, МАИ.
Автореферат разослан « » 2009 г.
Ученый секретарь
диссертационного Совета Д 212.125.08
доктор технических наук, профессор Ю.В. Зуев
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ.
Актуальность работы. В технике проблема надежности и долговечности машин и механизмов, экономного использования материалов, энергии и трудовых ресурсов имеют особое значение. Решение этой проблемы неразрывно связано с обеспечением эффективной защиты поверхности деталей и конструкций от коррозии и изнашивания. В настоящее время около 30% ежегодной выплавки металлов расходуется на восполнение потерь, вызванных указанными факторами.
Применение разнофункциональных покрытий открывает принципиально новый подход к использованию конструкционных материалов. В настоящее время среди разнообразных технологий нанесения защитных покрытий интенсивное развитие получают газотермические методы: электродуговой, газопламенный, плазменный и детонационный. Они объединены единым принципом формирования покрытий с использованием гетерогенных потоков. Однако указанные выше методы обладают рядом существенных недостатков и прежде всего, использование в качестве газа-носителя высокотемпературной (несколько тысяч градусов) газовой струи. Решение задачи улучшения этих технологий связано с устранением в высокотемпературном газе-носителе плавления и испарения частиц порошка, а также гомогенных и гетерогенных химических реакций.
Логическим совершенствованием газотермических методов является низкотемпературный газодинамический метод нанесения покрытий (НТГДМ). Метод разработан на кафедре “Авиационно-космическая теплотехника” МАИ, патент № 2082823 от 17.06.91 "Способ получения покрытий". Разработанные технологии нанесения покрытий получили наименование НТГДМ-технологий. С использованием НТГДМ-технологии получены высокие механические и теплофизические параметры покрытий. Поэтому исследование механизма формирования разнофункциональных покрытий низкотемпературным газодинамическим методом, является важной, актуальной научной и прикладной задачей.
Цель диссертационной работы – Разработка научных основ механизма формирования защитных покрытий низкотемпературным газодинамическим методом.
Для достижения указанной цели в работе поставлены и решены следующие задачи:
- проведен критический анализ газотермических методов и альтернативного им низкотемпературного газодинамического метода;
- определены методы диагностики как параметров высокоскоростных гетерогенных потоков, так и теплофизических свойств покрытий в условиях эксплуатации, близких к реальным;
- проанализирована общая и разработана инженерная математические модели расчета градиентного течения и межфазного теплообмена неизотермической гетерогенной смеси;
- исследован механизм взаимодействия высокоскоростного гетерогенного потока с поверхностью. Предложена физическая модель динамики удара высокоскоростной частицы о твердую стенку. Разработан алгоритм оценки локальной температуры частицы и подложки в зоне удара;
- проанализировано влияние параметров сверхзвукового гетерогенного потока и других факторов на эффективность технологического процесса формирования покрытий. Разработаны научные основы НТГДМ-технологии.
Научная новизна работы заключается в том, что проведено исследование теплофизических процессов, сопутствующих формированию разнофункциональных покрытий НГДМ - технологией, что позволило установить экспериментально физические основы принципа формирования разнофункциональных покрытий низкотемпературным газодинамическим методом; разработать методы и средства диагностики параметров как сверхзвуковых гетерогенных и гомогенных потоков, так и теплофизических свойств покрытий; - исследовать характер течения гетерогенной смеси в микроканалах (ускорителях) большого удлинения с учетом нарастания пограничного слоя; - разработать упрощенную математическую модель до - и сверхзвуковых течений гетерогенных потоков в микроканалах (ускорителях) большого удлинения с учетом межфазного теплообмена; - исследовать экспериментал гетерогенного потока на преграду; - сформулировать научные основы закономерностей формирования покрытий с учетом процессов тепло - и массообмена в зоне высокоскоростного взаимодействия частиц с подложкой.
Практическая ценность и реализация результатов работы состоит в том, что по результатам исследования: - разработана принципиальная схема, создана и апробирована лабораторная установка для синтеза разнофункциональных покрытий на металлических и неметаллических поверхностях; - разработаны основы НТГДМ - технологии формирования разнофункциональных покрытий;- составлен алгоритм и разработана программа расчета элементов газодинамического тракта и течения сверхзвуковых гетерогенных потоков для целей проектирования промышленного оборудования; - разработаны и апробированы методы и средства диагностики параметров гомогенных и гетерогенных сверхзвуковых потоков и теплофизических свойств покрытий; - результаты работы внедрены в Научно-производственном центре «ДИАРИМ-АБ» Московская обл., в ООО «Промышленный центр», г. Саранск, Республика Мордовия, в учебном процессе МАИ, что подтверждено Актами о внедрении. Результаты были использованы при выполнении грантов РФФИ в 2007 и 2008 г.
Положения, выносимые на защиту: - анализ газотермических методов и альтернативного им НТГДМ; - физическая сущность НТГДМ и способы его реализации; - методы диагностики параметров высокоскоростных гомогенных и гетерогенных потоков и теплофизических свойств покрытий; - общая и инженерная математические модели расчета градиентного течения и межфазного теплообмена неизотермической гетерогенной смеси в каналах (ускорителях) удлиненных форм; - инженерная математическая модель расчета газодинамики и теплообмена при натекании сверхзвукового гетерогенного потока на преграду; - механизм взаимодействия высокоскоростного гетерогенного потока с поверхностью;- алгоритм оценки температур частицы и подложки в зоне удара; - анализ влияния разных факторов на эффективность формирования покрытий.
Достоверность полученных результатов обуславливается большим объемом проведенных экспериментов с использованием современных методов и средств газодинамической и теплотехнической диагностики. Достоверность данных теоретических исследований подтверждается убедительной корреляцией с результатами экспериментов.
Личный вклад автора. Основные экспериментальные и теоретические результаты работы получены в лаборатории кафедры «Авиационно – космической теплотехники». Большинство представленных конструктивных решений, все представленные в работе экспериментальные и расчетно-теоретические исследования, обработка и анализ полученных результатов выполнены лично автором.
Апробация результатов работы. Основные результаты диссертационной работы докладывались на заседании кафедры "Авиационно-космической теплотехники" МАИ, на научном семинаре ведущей организации «Сибирский государственный аэрокосмический университет СибГАУ», г. Красноярск, на 5-ой и 6-ой Международных конференциях «Авиация и космонавтика – 2006 и 2007», г. Москва.
Публикации. Основные результаты работы отражены в пяти статьях, опубликованных в журналах: «Вестник МАИ», "Современные проблемы науки и образования". Изд-во «Российская Академия Естествознания», в тезисах четырех докладов на Международных конференциях «Авиация и космонавтика – 2006 и 2007» и двух научно-технических отчетах по теме диссертации при выполнении грантов РФФИ.
Структура и объем работы. Диссертационная работа состоит из введения, пяти глав и выводов. Объем работы составляет 168 страниц, включая 44 рисункa, 13 таблиц, список используемых литературных источников из 156 наименований.
Содержание работы
В введении обоснована актуальность работы, ее практическая значимость. Проанализированы вопросы защиты конструкций путем нанесения покрытий газотермическими методами. Сформулированы цель и задачи исследования
В первой главе на базе основных положений физической химии проанализированы принципы формирования защитных покрытий. Выполнен сравнительный анализ нанесения покрытий газотермическими методами. Обоснован выбор НТГДМ, как альтернативного традиционным газотермическим методам. Определены его основные характеристики. Приведены технологические преимущества метода.
Во второй главе рассмотрены физические основы НТГДМ. Описан механизм формирования покрытий. Отмечено основное преимущество метода, выражающееся в использовании высокого уровня кинетической энергии частиц, в то время как, температура гетерогенного потока существенно ниже температуры плавления частиц. Представлена блок-схема реализации НТГДМ - технологии. Проведен анализ возможностей НТГДМ - технологии, перечислены межотраслевые области перспективного применения. Дано описание схемы лабораторной установки.
Предложены основы диагностики сверхзвуковых гетерогенных потоков и представлены результаты исследования механических и теплофизических характеристик разнофункциональных покрытий. В качестве примера на рис.1 и 2 приведены схемы используемого в работе оборудования для определения температуры поверхности покрытий и степени их черноты.
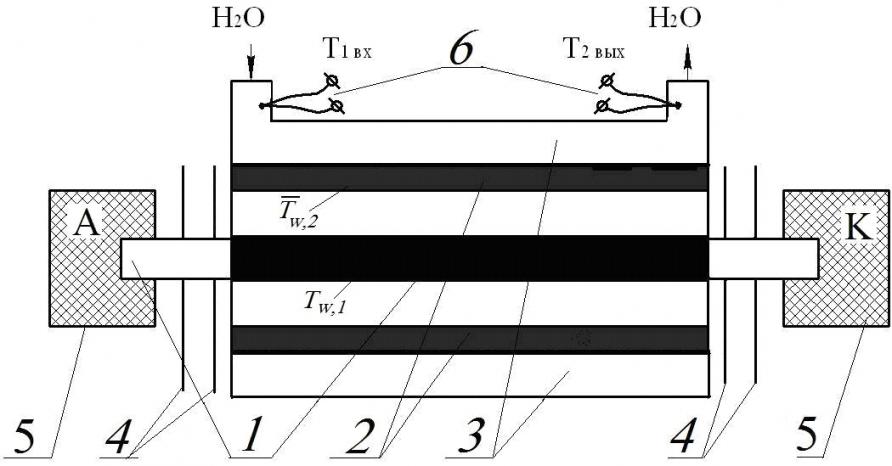
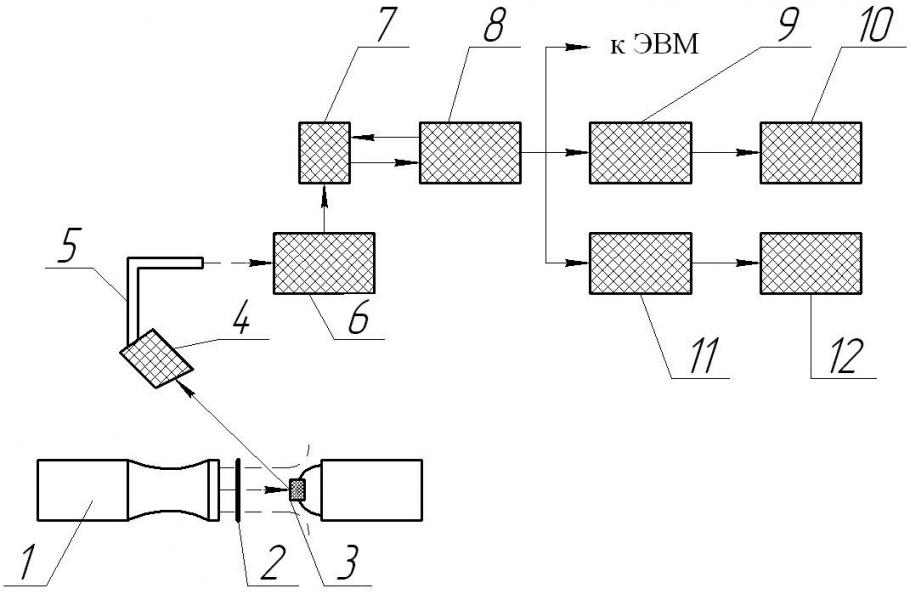
Разработан алгоритм испытания термостойких и жаропрочных покрытий на газодинамических стендах в высокотемпературных сверхзвуковых химически агрессивных потоках. Предложены и апробированы методы и средства диагностики теплофизических параметров покрытий. Схемы газодинамического стенда для испытаний приведены на рис.3
В главе 3 представлены разработанные физическая и математическая модели расчета установившихся гетерогенных течений в профилированном канале газодинамической установки. Приведен алгоритм решения. При математическом описании гетерогенного течения приняты следующие допущения: на входе в газодинамический тракт стенда скорости и температуры фаз одинаковые; течение гетерогенной смеси в тракте стационарно; геометрия тракта обеспечивает применимость квазиодномерного приближения; при описании межфазного теплообмена и трения использовались критериальные зависимости, применяемые в широких диапазонах чисел Маха и Рейнольдса; взаимодействие частиц со стенкой тракта либо отсутствует, либо происходит без обмена массой, энергией и импульсом.
Система уравнений, соответствующая данной физической постановке имеет вид:
уравнение неразрывности 
, (1)
уравнение движения 
, (2)
где для газовой фазы 
, а для твердой фазы 
; 
-сила аэродинамического сопротивления, Саэр- коэффициент аэродинамического сопротивления сферических частиц.
уравнение энергии 
, (3)
где для газовой фазы Qi кон – тепловой поток межфазного конвективного теплообмена в единице объема гетерогенной смеси, представляен уравнением конвективного теплообмена Ньютона. Система уравнений решалась на ЭВМ численным методом для соответствующих граничных условий.
В работе предложен упрощенный алгоритм расчета течения гетерогенной смеси в каналах при наличии межфазного теплообмена, базирующийся на использовании интегральных соотношений второго закона механики Ньютона. В газодинамическом тракте стенда Rаэр не будет оставаться постоянной. Поэтому вся длина газодинамического тракта стенда разбивается на niэлементарных участков длиной Li, на каждом из которых Rаэр.i считается величиной постоянной. Расчет ведется по следующей системе уравнений:
расчет ускорения частицы p,i производится с использованием 2-го закона механики Ньютона: 
, (4)
расчет времени i пролета частицей элементарного участка длиной Li существляется с использованием формулы для равноускоренного движения:
, (5)
расчет скорости Vp,i частицы в конце расчетного участка осуществляется по формуле:
. (6)
- скорость частицы на входе в расчетный участок, i- время пролета частицей расчетного участка, рассчитывается с использованием соотношения (5). Расчет параметров проводится для каждого i-го участка газодинамического тракта, при этом параметры частицы на выходе из участка являются исходными для расчета последующего участка.
Алгоритм расчета межфазного теплообмена в гетерогенном потоке.
Решение задачи межфазного теплообмена в гетерогенном потоке сводится к нахождению закономерности изменения температуры частиц Тр по длине тракта. Алгоритм расчета теплообмена в движущейся неизотермической гетерогенной среде строится на базе постулата первого закона термодинамики, записанного для твердого термодинамического рабочего тела (частицы). При этом учитывалось, что в НТГДМ-технологии частицы при ускорении в канале не претерпевают фазовых переходов. Тогда имеем: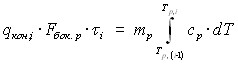 
, (7)
где 
- конвективный тепловой поток, на единицу боковой поверхности частицы 
массой mр за время 
пролета частицей i-го расчетного участка длиной Li. Согласно закону конвективного теплообмена Ньютона 
представляется в виде:
, (8)
где Тгаз.i - температура газа-носителя на длине расчетного i-го участка длиной Li, 
- средняя температура частицы на длине i-го участка, i- коэффициент теплоотдачи на расчетном i-ом участке, ср,i – удельная теплоемкость материала частицы при средней температуре 
.
Уравнение (7) принимает вид: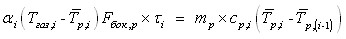 
. (9)
Коэффициент теплоотдачи i между газовой фазой и частицами определяется из критерия Нуссельта, который для частиц микронного диапазона представляется критериальным соотношением типа: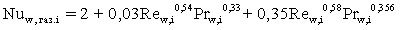
, (10)
где критерий Рейнольдса
, критерий Прандтля 
, dр – диаметр частицы.
Из уравнения (9) следует: 
, (11)
где 
- температура частицы на предыдущем расчетном участке. Поскольку в выражении (11) все параметры зависят от искомой температуры поверхности, то расчет
проводится методом последовательных приближений.
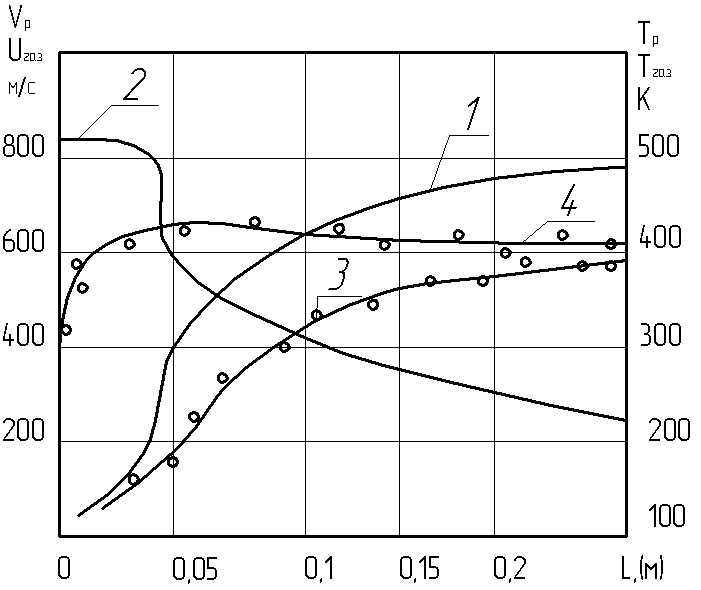
Результаты расчета с использованием общей и предложенной упрощенной математическими моделями изменения скорости газа-носителя uгаз, а также Vр и температуры Tр твердой фазы по длине ускорителя приведены на рис.5. Газовая фаза– воздух, твердая фаза – частицы Al d=40 мкм. Форма ускорителя – коническое сопло Лаваля. Видно удовлетворительное соответствие результатов расчета по общей и приближенной моделям. Из приведенных данных также следует, что максимальный темп нагрева частиц реализуется в докритической части сопла, т.е. в области максимальной температуры и плотности газа-носителя. Кроме того, на интенсивность нагрева частицы в докритической части сопла сильное влияние оказывает то обстоятельство, что частницы находятся в этой области достаточно долго, вследствие малой относительной скорости газовой uгаз и твердой Vр фаз (кр.1 и 3, рис.5).
Течение гетерогенной смеси в микросоплах с большим удлинением
Из задач, которые приходится решать при формировании защитных покрытий НТГДМ – технологией, следует выделить две проблемные, играющие определяющую роль в получении покрытий высокого качества. Таковыми являются:
- формирование течения гетерогенной смеси в микросоплах с большим удлинением;
-взаимодействие высокоскоростной частицы субмикронного диаметра с твердой поверхностью.
Решение первой задачи связано с динамикой ускорения твердых частиц, формирующих покрытие. Скорость частиц определяет важнейшие технико-экономические показатели технологического процесса нанесения покрытий, такие как качество покрытия, производительность, коэффициент использования порошка.
В установках применяются удлиненные ускорители с малыми площадями критических сечений (dкр = 1...5 мм). Относительное удлинение таких каналов может изменяться в широких пределах (L/dкр = 50...200).
Основная особенность течений вязких газов в соплах удлиненных форм заключается в том, что образовавшийся на поверхности стенок канала пограничный слой существенно уменьшает фактическое проходное сечение сопла по сравнению с расчетным, технологическим сечением. Это снижает массовый секундный расход потока, т.е. его скорость. Поэтому появилась необходимость оценки влияния пограничного слоя на динамику течения гетерогенной смеси в каналах удлиненной формы. При проведении такого анализа принимался ряд допущений. Вследствие малости размеров частиц перепад температуры в их объеме не учитывался. Кроме того, считалось, что вязкостные эффекты, которые, зависят от температуры поверхности, в связи с низкими уровнями величин температуры частиц не оказывают существенного влияния на аэродинамическое сопротивление частицы. Это позволило при анализе рассматривать динамическую и тепловую задачи, как две независимые. В такой постановке алгоритм расчета параметров потока вязкого газа был составлен на базе использования классической модели плоского пограничного слоя. При этом динамическая задача представлялась системой интегро-дифференциальных уравнений импульса и толщины вытеснения. Исходными данными для расчета являлись параметры газа в форкамере ускорителя рк, Тк и геометрические размеры сопл. В таблице 1 приведены некоторые результаты расчетов. Для сравнения в таблице последние две строки представляют данные других авторов.
Таблица 1.
| dкр | dсрр | Mср.фак | Reх | Mср.р | dср.ф/dср.р | Mср.эк |
| мм | мм | - | - | - | - | - |
| 3,5 | 12,2 | 3,45 | 6,3х105 | 4,14 | 0,71 | - |
| 4,5 | 9,5 | 2,55 | 4,36х105 | 3,05 | 0,84 | 2,48 |
| 4,5 | 9,5 | 2,67 | 5,19х105 | 3,05 | 0,845 | 2,6 |
| 2,72 | 12,65 | 3,87 | 1,2х105 | 4,8 | 0,67 | - |
| 4,72 | 12,65 | 2,84 | 1,27х105 | 3,58 | 0,71 | - |
Проведенные расчеты показывают, что в коническом сопле с dкp=1 мм пограничный слой смыкается на расстоянии L = 10... 12 мм от критического сечения и далее устанавливается турбулентное течение. При увеличении dкp до 2 мм пограничный слой смыкается уже на расстоянии L = 100...120 мм. Данное обстоятельство существенно усложняет применение микросопл в технологических установках. Их проектирование необходимо осуществлять с учетом нарастания толщины пограничного слоя вдоль стенок ускорителя частиц. На рис. 6 представлены результаты расчетов и измерений относительной скорости частиц алюминия в сопоставлении с результатами данных других авторов. В экспериментах применялись промышленные порошки с дисперсностью dр = 5...50 мкм. Скорость газового потока варьировалась в пределах uгаз = 200...1200 м. Здесь же наложены результаты машинного эксперимента на ЭВМ, проведенного в МАИ по изложенной выше методике.
При Cf =1,0 наблюдается хорошая корреляция результатов, влияние нарастания пограничного слоя на уменьшение uгаз составляет порядка 16% и на Vp до 20%.
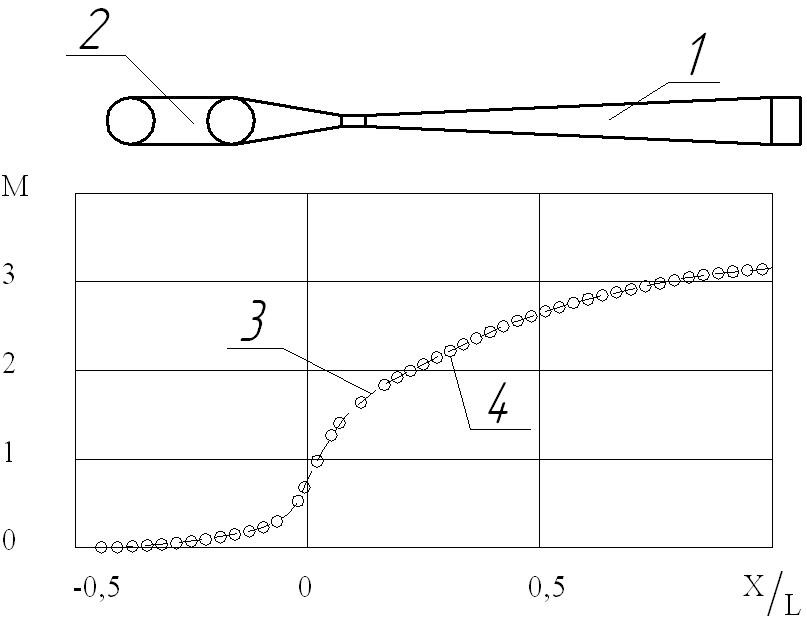
Газодинамика и математическая модель при натекании сверхзвукового гетерогенного потока на плоскую преграду. Газодинамику течения сверхзвукового гетерогенного потока над поверхностью тел разных форм при реализации НТГДМ – технологии можно классифицировать как задачу натекания сверхзвуковой осесимметричной гетерогенной струи конечных размеров на плоскую стенку. Схема течения представлена на рис. 7. В общем случае задача двухмерная, так как при переходе через отошедшую ударную волну и сжатый слой, вектора скоростей газовой и твердой фаз меняют направление. В работе предлагается приближенный подход к решению данной задачи, позволяющий рассчитать параметры частиц непосредственно перед ударом о поверхность, т.е. на начальном участке свободного гетерогенного потока от среза сопла до ударной волны. Этот участок определяется координатой вдоль оси потока Xс = H – h (рис. 7).
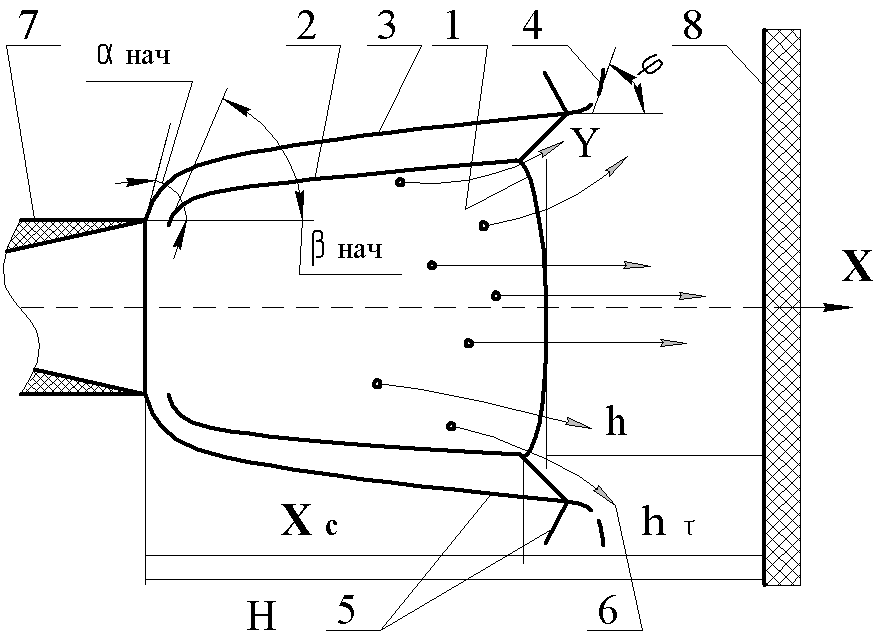
Газодинамика течения гетерогенного потока у поверхности стенки описывается уравнениями Прандтля-Майера. Система уравнений, представленная в работе, позволяет рассчитать угол поворота гетерогенного потока 
в виде:
, (12)
где 
- текущий угол распространения малых возмущений в потоке.
Решение системы осуществляется с использованием параметров гетерогенного потока на срезе сопла, полученных из расчета по алгоритму, изложенному выше. Расчет велся методом итераций от среза сопла до ударной волны (сечение Хс рис.7), которое рассчитывалось с использованием соотношения:
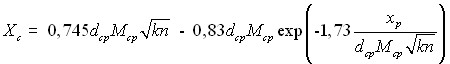, (13)
где dср и Мср - диаметр и число Маха на срезе сопла; n = pср/pн; pн – атмосферное давление.
Параметры газа за прямым скачком уплотнения, вследствие того, что параметры частиц при переходе через ударную волну не претерпевают разрыва, определялись соотношениями Ренкина – Гюгонио. В работе представлен алгоритм расчета параметров частиц (их скорость, температура, а также распределение в сверхзвуковом гетерогенном потоке). Он включает несколько последовательных этапов:- расчет распределения скорости uгаз(х) и давления р(х) газовой фазы по длине канала; - из соотношения (13) определялась координата ХС отошедшей ударной волны; - решалась система уравнений Ренкина – Гюгонио и определялись параметры газовой фазы за ударной волной. Результаты расчета скоростей газовой и твердой фаз перед ударной волной приведены на рис. 8.
Модель расчета инерционного движения частиц сверхзвукового гетерогенного потока через ударную волну и сжатый слой
Задача решалась при допущениях, сформулированных Стерниным Л.Е.: отошедшая ударная волна плоская; плотность газа, его температура и градиенты скорости в сжатом слое постоянны; коэффициенты релаксации скорости и температуры частиц постоянны и равны значениям, вычисленным по параметрам газа и частиц после прохождения ударной волны и сжатого слоя.
Из уравнения неразрывности получим выражение для поля скоростей газовой фазы за плоской ударной волной: 
, (14)
где x и y – текущие координаты, h – см. рис.7, 
для плоского и 
для осесимметричных случаев. При этом у = уmax = Rст – радиус потока перед ударной волной.
Уравнения движения и энергии для частиц:
уравнения движения , (15)
, (16)
начальные условия:
при =0, 
, 
при =0 -, при =0, 
при =0
уравнение энергии 
(17)
при следующих начальных условиях: Tp=Tpнач, при =0. Система координат для сформулированной задачи приведена на рис.9.
Решения дифференциальных уравнений (15) и (16)имеют вид:
по направлению Х
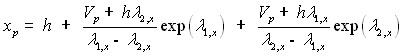, где
(18)
по направлению Y
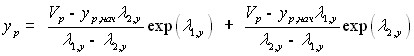,где 
(19)
температура частицы: 
(20)
Коэффициенты Vp и Tp в уравнениях (18…20) зависят от режима обтекания частицы потоком газа-носителя и определяются соответствующими соотношениями.
Из анализа соотношений (18), (19) и (20) следует, что в общем случае возможны несколько режимов, которые могут реализоваться при нанесении покрытий, а температура частиц Тр монотонно стремится к температуре газа в сжатом слое. На этом факте строятся научные основы НТГДМ-технологии формирования покрытий.
Подробный анализ выявления условий, при которых возможна реализация тех или иных режимов проводится в соответствующих разделах работы. Здесь же следует отметить: расчетами установлено, что частицы, например, из Al диаметром d < 2 мкм после прохождения ударной волны откланяются от первоначальной траектории, т. е. не достигают поверхности и не участвуют в формировании покрытий. Частицы 2 <d< 5 мкм достигают поверхности, но не формируют покрытие вследствие потери кинетической энергии в результате сильного торможения при прохождении ударной волны и сжатого слоя.
В главе 4 представлена физическая модель взаимодействия сверхзвукового гетерогенного потока с твердой поверхностью. Этот механизм интегрирует комплекс физико-химических процессов, включая пластическую деформацию частиц и подложки, их нагрев, а также возможные химические и фазовые переходы материалов частиц и подложки. Из комплекса указанных процессов необходимо особо выделить два определяющих - проникновение высокоскоростной частицы в подложку, сопровождающееся их пластической деформацией, нагревом, а также возможным локальным изменением агрегатного состояния материалов частицы и подложки (механическое взаимодействие), а также сильное контактное взаимодействие, проявляющееся в образовании прочных связей.
В процессе удара высокоскоростной частицы о твердую поверхность, уравнение баланса энергии в момент удара представляется в виде:
Екин.р=Едеф.р+Едеф.под+Енаг.р+Енаг.под (21)
В первом приближении для оценки величины потребного для формирования покрытия уровня кинетической энергии частицы, используем гипотезу, считая, что не вся кинетическая энергия, приобретенная частицей при ускорении, затрачивается на ее нагрев с фазовыми переходами.
В этом случае имеем: 
, (22)
где kак — коэффициент аккомодации, учитывающий долю кинетической энергии частицы, перешедшей в тепловую, остальные параметры общепринятые.
Проведенный в работе анализ уравнения (22) позволил установить две предельные скорости, при которых процесс формирования покрытий не возможен. Первая из них реализуется при упругом ударе частицы о поверхность и названа первой критической скоростью 
. Вторая критическая скорость 
представляет скорость частицы, при которой твердая поверхность начинает разрушаться (процесс механической эрозии) при бомбардировке частицами ее поверхности. При формировании покрытий НТГДМ-технологией, практический интерес представляет оценка скорости удара частицы в диапазоне 
. С этой целью в работе проведен анализ и составлен алгоритм расчета скорости одиночной сферической частицы, ускоряющейся в потоке газа-носителя. Показано, что уровень скорости 
частицы зависит от ее формы, термо-газодинамических параметров газа-носителя в ускорителе, рода материалов частиц и положки, их теплофизических свойств и др.
Кинетика взаимодействия частиц с подложкой. Механизм взаимодействия частиц с основой и между собой условно разделен на три последовательные стадии:- удар твердой частицы о подложку(образование физического контакта); -активизация контактных поверхностей и химическое взаимодействие материалов с образованием связей на границе; - объемные процессы динамические и тепловые в зоне контакта (теплопроводность, динамическая диффузия и др.).
Известно, что адгезионные свойства металлических покрытий возрастают линейно вплоть до скорости частиц 600 м/с. При дальнейшем увеличении скорости частиц их кинетическая энергия становится столь значительной, что сильно изменяет механизм контактного взаимодействия частицы с подложкой. Адгезия покрытия возрастает уже по более сильной, нелинейной зависимости.. Это объясняется увеличением напорного динамического давления
, которое играет важнейшую роль в активировании процесса взаимодействия частицы и подложки. Экспериментально установлено, что увеличение динамического давления от 1МПа до 7МПа, понижает энергию активации материала на 20...30%, что значительно улучшает качество покрытия. Это можно объяснить активацией поверхностей материалов в зоне контакта при ударе. Известно, что все атомы приповерхностных кристаллических решеток, охваченные полем упругих искажений (полем дислокаций), энергия которых достигла или превысила некий потенциальный барьер, проявляют высокую активность. Это является главной причиной их химического взаимодействия с атомами других даже разнородных металлов. Такие соединения образуется в локальных местах выхода дислокаций на поверхность, где возникают центры очагов химического соединения, в нашем случае, наносимого покрытия и основы.
Динамика удара твердой частицы о поверхность. При скоростях частиц, достигающих значений Vp=600..1200м/с, динамическое давление в зоне контакта может достигать максимальных уровней, порядка ~104МПа, что значительно превосходит предельные значения механических свойств большинства металлов.
Механическое дробление частиц при ударе При нанесении покрытий НТГДМ-технологией соударение высокоскоростных частиц с подложкой приводит к их взаимной сдвиговой деформации, активизации сопряженных поверхностей (включая очистку поверхности от окисных и других пленок), физическому взаимодействию за счет высокого напорного давления. Теплофизические и акустические процессы вызывают деформацию и дробление исходных частиц при ударе, т.е. повышают степень дисперсности порошка в покрытии. На рис.10 представлен факт дробления частиц при ударе о подложку. Образование мелкодисперсных частиц при ударе способствует уменьшению пористости покрытия, улучшая их качество.
Изменение механических свойств материала частиц при ударе Уровни динамического давления при соударении частиц из разного рода металлов с подложкой (сплав Д16) приведены в таблице 2. Скорость частиц в момент удара Vр = 600 м/с
Таблица 2
Давление в пятне контакта при соударении частиц с подложкой
| Материал частицы | Fe | Co | Al | Zn | Cu | Ni |
| Давление, ГПа | 13,81 | 12,76 | 5,11 | 7,93 | 10,0 | 12,7 |
Все приведенные в таблице2 значения давлений превышают величину предела текучести Гюгонио для указанных материалов. Уровни динамических давлений при соударении столь высоки, что в процессе удара осуществляется деформационное упрочнение материала частицы (см.таб. 3). Обнаруженное повышение микротвердости покрытия, синтезируемого НТГДМ-технологией, сохранялось после их продолжительного отжига при температурах, превышающих температуру рекристаллизации.
Таблица 3
Значения микротвердости исходных материалов порошков и покрытий
| Материал порошка | Микротвердость материала порошка, МПа | Микротвердость покрытия, МПа | Отношение микротвердостей, % |
| Zn | 400 | 650 | 163 |
| Al | 300 | 550 | 183 |
| Cи | 600 | 1000 | 167 |
| Cr | 1150 | 2900 | 252 |
Обнаруженная стабильность, по-видимому, обусловлена не сверхбыстрым охлаждением частиц в момент формирования покрытия, а характером ударно-волновых воздействий. В покрытиях, созданных НТГДМ-технологией, эффект упрочнения обнаружен не только на материале покрытия, но и на материале подложки. Это подтверждается результатами механических испытаний стандартных медных образцов без покрытия и с покрытием из карбида ниобия NbC толщиной 40мкм при температуре жидкого водорода (20К) и нормальной температуре (300К). Результаты испытаний представлены в таблице 4.
Отмеченное положительное влияние тонких покрытий на статические характеристики, определяются динамикой удара, являющегося неотъемлемой составляющей процесса формирования покрытий НТГДМ-технологией.
Таблица 4
Результаты испытаний на статическую прочность стандартных медных образцов
без покрытия и с покрытием из NbC
| Род образца | Температура испытаний | Предел прочности | Предел текучести | Модуль упругости | Относительное удлинение |
| - | К | МПа | МПа | ГПа | % |
| без покрытия | 20 300 | 376 288 | 127 86 | 100 98 | 80 85 |
| с покрытием | 20 300 | 448 440 | 328 317 | 157 154 | 47 49 |
Уравнение баланса энергии в зоне удара частицы с подложкой. В символах уравнение баланса энергии в зоне удара представлено в форме (21)
В работе раскрыта физическая сущность и представлено математическое описание каждого из членов этого уравнения.
Кинетическая энергия частицы в момент удара: 
. (23)
Энергия деформации частицы. Процесс деформации частицы сопровождается сжатием частицы и ее растеканием по поверхности подложки. Такой подход позволил вывести зависимость для оценки Едеф.р в виде:
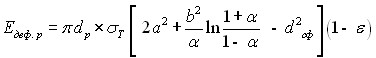, (24)
где
степень деформации частицы при ударе, 2а и 2b – большая и малая оси сфероида, соответственно.
Энергия деформации подложки. Величина этой энергии определяется двумя факторами: глубиной проникновения частицы в тело подложки hсегм и силой сопротивления сжатию материала подложки 
. 
. (25)
Для оценки величины hсегм использовался метод определения твердости материалов по Бринеллю со сферическим ударником. Такой подход позволил получить зависимость для расчета Eдеф.под в виде: 
. (26)
Энергия нагрева частицы и подложки. Доли энергии, затраченные на нагревание частицы Енаг.р и подложки Енаг.под, можно представить в следующем виде:
для частицы 
, (27)
где mp- -доля прогретой массы частицы за время удара, 
- среднемассовая температура прогретого участка частицы, ср – удельная теплоемкость материала частицы при 
, 
- температура частицы до удара;
для подложки 
, (28)
где mподл- доля прогретой массы подложки за время удара, 
- среднемассовая температура прогретого участка подложки, спод – удельная теплоемкость материала подложки при температуре 
, Tнач.подл.- температура подложки перед ударом.
В работе с использованием теории нестационарной теплопроводности твердых тел получены зависимости для оценки прогретых масс как частицы, так и подложки, где время контакта: 
(29)
где 
- предел текучести твердой частицы, 
поверхностного натяжения расплавленной частицы, 
- радиус частицы,V0,р - скорости частицы в момент удара, 
- степени деформации частицы (определяется экспериментально).
В этом случае, соотношения для расчета доли масс частицы и подложки прогретых за время удара, в окончательном варианте принимают вид:
для частицы 
(30)
для подложки 
(31)
Уравнение баланса энергии в окончательном видe
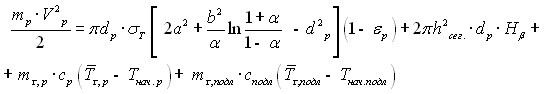(32)
Уравнение (32) позволяет рассчитать температуры частиц и подложки зоне контакта при ударе. При этом должны быть известны: дисперсность порошка, род материалов порошка и подложки, их теплофизика и механические свойства, скорости частиц в момент удара о подложку Vр, степень деформации частиц порошка 
. Локальные средние значения температур частицы 
и подложки 
не равны друг другу, однако различие между ними незначительно в связи с тем, что время удара мало - уд = 10-6...10-7с. Поэтому в инженерных расчетах следует принимать 
.
Результаты оценки по уравнению (32) изменения температуры частицы из алюминия диаметром dp и подложки из меди сведены в таблицу 5. При расчете, скорости частиц и степень их деформации брались из эксперимента.
Таблица 5.
Значение параметров взаимодействующей пары: частица Al, подложка Cu
для разных уровней скоростей частицы.
| Диаметр частицы dp | Скорость частиц Vp | Степень деформ. p | Мех. свойства т,p | Время удара уд | Теплоемкость частицы сp | Теплоемкость подложки сподл | Твердость подложки по Брюнеллю Н | Изменение температуры в зоне удара  |
| м | м/с | - | Па | с | Дж/кгК | Дж/кгК | МПа | град |
| 5·10-5 | 410 | 0,701 | 6,37·107 | 1,49·10-7 | 929 | 400 | 400 | 230 |
| 5·10-5 | 508 | 0,598 | 6,37·107 | 1,27·10-7 | 929 | 400 | 400 | 323 |
| 5·10-5 | 615 | 0,503 | 6,37·107 | 1,1·10-7 | 929 | 400 | 400 | 470 |
| 5·10-5 | 1000 | 0,6 | 6,37·107 | 1·10-6 | 999 | 400 | 400 | 1770 |
Таким образом, определение значений указанных выше температур сводится к решению задачи газовой динамики и теплообмена при течении в канале с большой скоростью неизотермической гетерогенной смеси.
В главе 5 проведен анализ влияния параметров сверхзвукового гетерогенного потока на эффективность процесса формирования покрытий. В качестве критерия эффективности выбран коэффициент использования порошка 
представляющий собой отношение массового расхода порошка, сформировавшего покрытие, к массовому расходу порошка, выданного дозатором.
Влияние температуры и давления гетерогенной смеси в форкамере ускорителя. На первом этапе расчет скорости газа-носителя по длине ускорителя для сопла Лаваля с геометрией dкр/dср = 0,25 и L/dср = 70, проводился с применением общей и приближенной математических моделей для случая изоэнтропического течения. Параметры газа-носителя в форкамере составляли: температура газа 700К, давление газа 2,8 МПа. Результаты расчета представлены на рис11. Видна удовлетворительная корреляция результатов расчета по общей и приближенной математическим моделям. Результаты расчета изменения на сверхзвуковом участке сопла скорости и температуры частиц из алюминия dp =40 мкм в зависимости от давления в форкамере pк при фиксированном уровне температуры Тк приведены на рис 12.
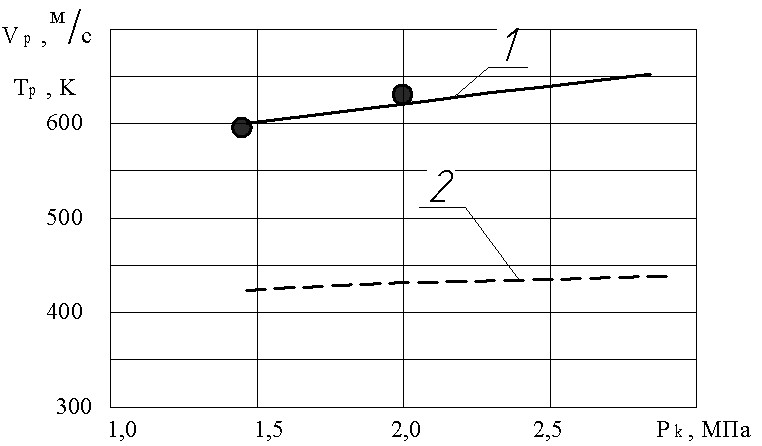
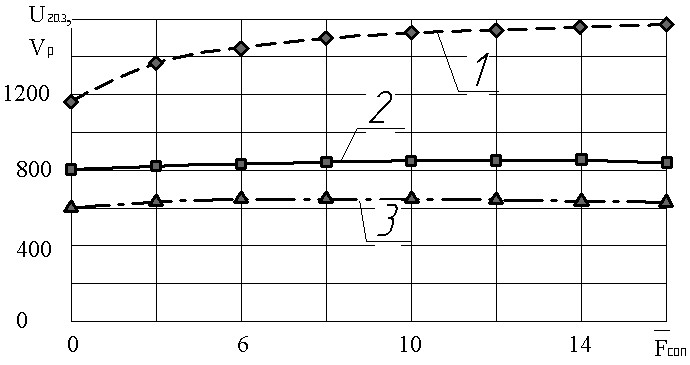
Из приведенных данных следует, что для рассматриваемого случая увеличение рк слабо влияет на изменение скорости частиц Vp (кр.1 рис12) и практически не вызывает заметного повышения температуры частицы (кр.2 рис12). При этом экспериментальные данные удовлетворительно (с погрешностью 5...7%) коррелируются с расчетными.
На рис. 13 представлены расчетные и экспериментальные данные изменения VP и TP частиц в зависимости от роста температуры в форкамере Тк при фиксированном уровне давления рк. Видно, что вариация температуры смеси оказывает заметное влияние как на изменение скорости частицы, так и на увеличение ее температуры. Например, увеличение температуры смеси в форкамере на 36% вызывает рост скорости частицы на 17,5%. Аналогичное влияние оказывает изменение температуры смеси в форкамере на рост температуры частицы. Например, увеличение Тк на 36% вызывает рост температуры частицы на 22% на длине сверхзвукового участка сопла.
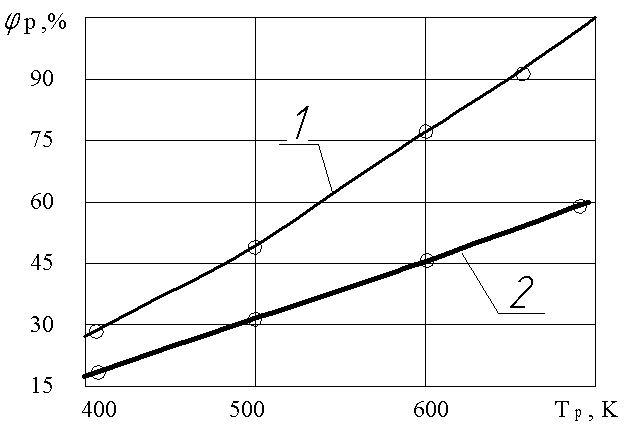
Влияние температуры в форкамере на коэффициент использования порошка
Влияние температуры в форкамере Тк на коэффициент р исследовалось экспериментально. Покрытия наносились двумя типами алюминиевых порошков с дисперсностью 5...20 мкм и 40...70 мкм. При этом превалирующая доля 70% в первом порошке составляла фракция 10мкм.
Во втором порошке с долей 65% составляла фракция 40мкм. Использовалось коническое сопло: dкр/dср = 0,25 и L/dср = 70. Давление в форкамере РК = 2,8 МПа. Температура ТК варьировалась от 400К до 700К. На рисунке 16 приведены экспериментальные данные влияния температуры в форкамере Тк на коэффициент р. Коэффициенты р определялись экспериментально. Из представленных на рис.16 данных следует, что на величину коэффициента р сильно влияет как уровень температуры смеси в форкамере Тк, так и его дисперсность (см. кривые 1 и 2).
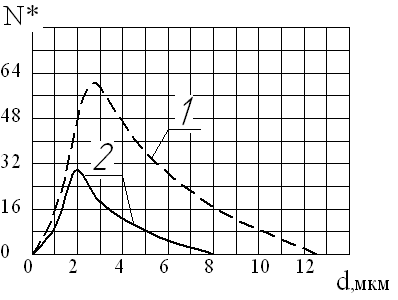
Влияние дисперсности гетерогенной смеси на коэффициент р На рис.15 представлены экспериментальные данные по исследованию влияния дисперсности на коэффициент р. Параметры гетерогенной смеси в форкамере выдерживались постоянными и равными: давление рк = 2,8МПа, температура Тк = 700К.
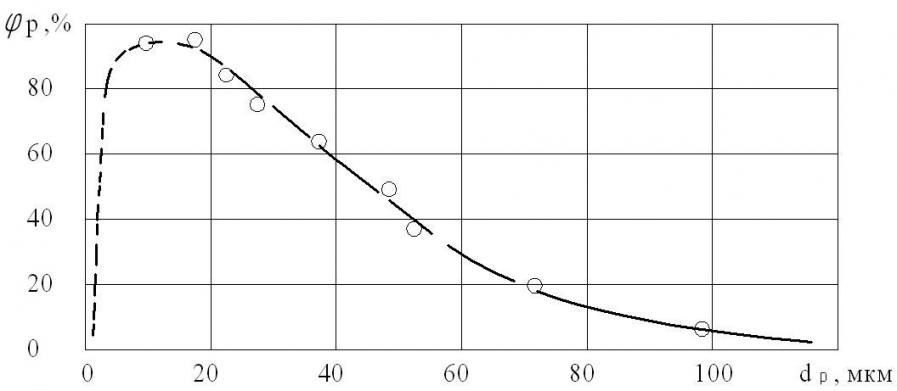
В эксперименте применялись порошки из алюминия с превалирующими фракциями ~ 10 мкм, ~15 мкм, ~ 20 мкм, ~ 25 мкм, ~ 30 мкм, ~ 35 мкм, ~ 50 мкм, ~ 70 мкм и ~ 100 мкм. Анализ полученных данных показал, что коэффициент р для порошка из алюминия имеет оптимум. Его величина может достигать уровня ~ 100% при указанных выше параметрах гетерогенной смеси в форкамере. Очевидно, различие р для разных порошков объясняется тем, что частицы порошка меньшей дисперсностью, ускоряется в сопле до более высоких скоростей, чем частицы с большей дисперсностью. Например, для условий эксперимента частицы диаметром 10 мкм имели скорость на срезе сопла Vp = 900 м/с, в то время как частицы с dp = 40 мкм всего 650 м/с. С такими скоростями частицы достигают ударной волны и сжатого слоя, преодолевая которые, частицы малых размеров меньше тормозятся в отличие от частиц больших размеров. Кроме того, в момент удара о подложку, частицы малых размеров имеют большую удельную энергию (энергия на ед. площади контакта), чем частицы больших диаметров. Поэтому эффективность (коэффициент р) и качество покрытий при их формировании частицами малых размеров значительно выше, чем для порошков высокой дисперсности.
Влияние профилей сопл Лаваля на эффективность формирования сверхзвуковых гетерогенных потоков. В качестве критерия оценки влияния профилей сопл на эффективность формирования сверхзвуковых гетерогенных потоков был выбран комплекс параметров 
, где газа,i плотность газа-носителя, Vгаза,i - скорость газа-носителя, Fi – площадь сечения сопла. Выбор такого критерия обусловлен тем, что физический смысл комплекса рсопл представляет некоторую силу, которая пропорциональна газодинамической силе, действующей в ускорителе на частицу. Задача решалась численным методом. Анализировался случай, когда в эксперименте использовались два конических ускорителя с разными критическими сечениями, но одинаковыми диаметрами их срезов. Так диаметр критического сечения одного из них составлял d1, кр = 2 мм, другого - d2, кр = 3 мм. В обоих расчетных вариантах параметры гетерогенной смеси в форкамерах сопл равнялись: давление рк = 2,0 МПа, температура Тк = 700К.
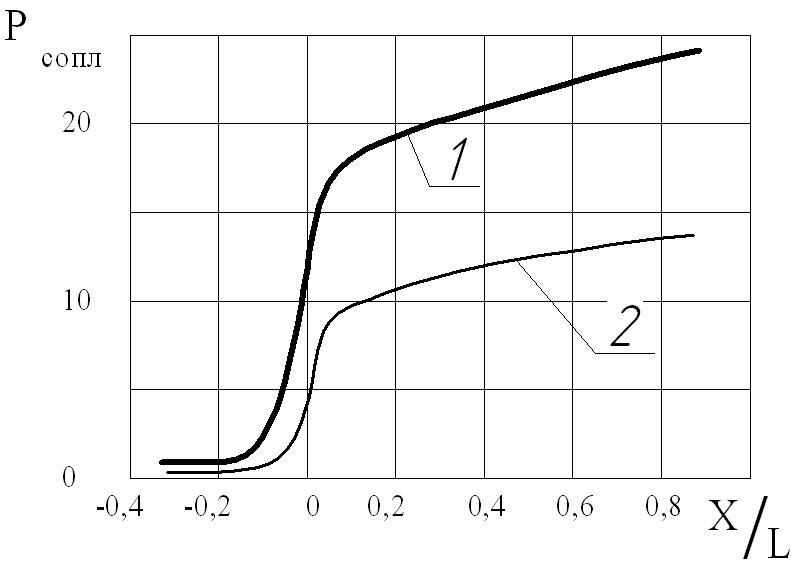
Из приведенных на рис.16 данных следует, что при прочих равных условиях, потенциал ускорения частиц в соплах с малым критическим сечением значительно выше, чем аналогичный параметр для сопл с большим критическим сечением.
Таким образом, при формировании сверхзвуковых гетерогенных потоков с целью получения более высокой скорости частиц, формирующих покрытие, необходимо площадь критического сечения сопла выбирать как можно меньшей.
Влияние расстояния от среза сопла до подложки на процесс формирования покрытий Расстояние от среза сопла до поверхности подложки в работе названо «дистанцией» нанесения покрытия hраб. «Дистанция» hраб является важным параметром, определяющим не только эффективность технологии, но и свойства покрытий. На «дистанции» реализуется процесс натекания сверхзвукового гетерогенного потока на преграду, который определяет скорость частиц в момент удара о подложку. Поэтому предметом данного исследования являлись две задачи: расчет скорости частиц разных диаметров по длине конического сопла Лаваля и на участке «дистанции» hраб, экспериментальное исследования зависимости р = f(h раб).
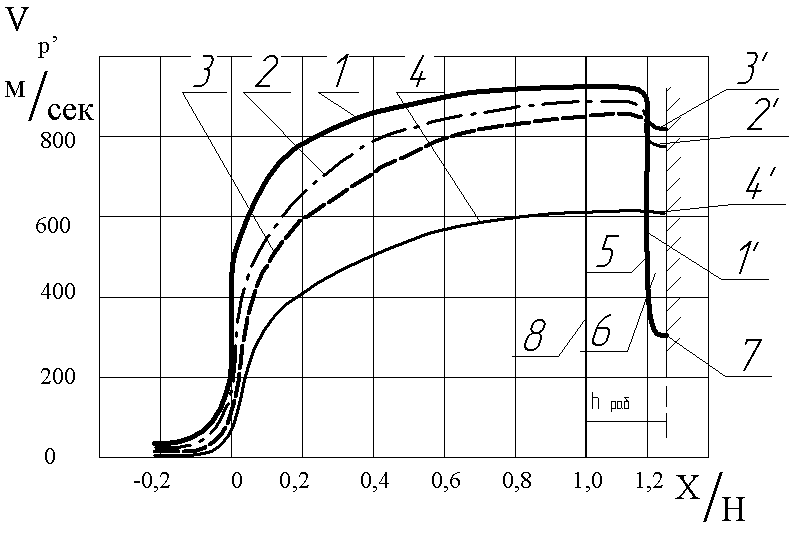
Решение первой задачи проводилось с использованием математической модели, представленной в главе 3. Решение второй задачи проводилось экспериментально с использованием методики, изложенной в главе 4. Результат решения первой задачи приведен на рис.17 в виде зависимости Vр= f(X/Н). Численный эксперимент проводился использованием частиц из алюминия разных диаметров при вариации h раб и следующих параметрах в форкамере: Рк = 2,8МПа, Тк = 700К.Геометрические размеры сопла приведены ранее.
Анализ результатов численного эксперимента показал, что частицы субмикронного диапазона dр < 2 мкм из-за резкого торможения в ударной волне и сжатом слое практически не достигают поверхности подложки, т.е. не участвуют в процессе формирования покрытия (см. рис. 17, кр.1). При использовании в технологическом процессе частиц с размерами 2 < dр < 10...15 мкм изменении скорости заметное, но достаточное, чтобы сформировать покрытие (см. рис. 17, кр. 2 и 3). Наконец, частицы с dр > 15 мкм незначительно теряют свою скорость.
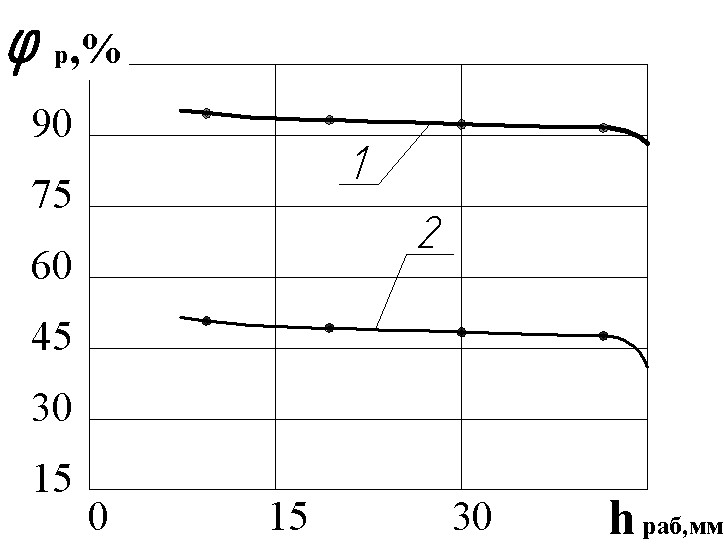
Результаты экспериментального исследования второй задачи приведены на рис. 18. Видно, что увеличение «дистанции» в пределах 10 h раб 40 мм слабо влияет на изменение коэффициента использования порошка р., но дисперсность порошка сильно влияет на коэффициент р. Установлено, что эффективность НТГДМ–технологии при формировании покрытий из алюминия и его сплавов оптимальна, если дисперсность порошков будет изменяться в пределах 3< dр< 20 мкм, а рабочая «дистанция» в пределах 10 hраб 40 мм. Предложенный в работе алгоритм позволяет оценить эффективность технологии для порошка любого рода.
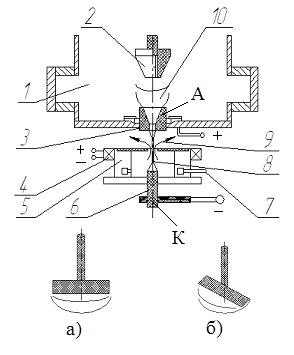
Влияние шероховатости рабочих поверхностей сопла на качество наносимых покрытий. Анализ выполнен с использованием как экспериментальных, так и теоретических данных. Экспериментальная часть работы представляет собой демонстрацию факта влияния шероховатости рабочих поверхностей сопла на качество наносимого покрытия. Эксперимент проведен с использованием плоского сопла, выходное сечение которого показано на рис.19, позиции а) и б)
Качество медного покрытия при использовании в эксперименте сопл с гладкими и шероховатыми поверхностями несравнимо отличается. Физическая интерпретация выявленной особенности дана в работе с привлечением результатов исследований газодинамики течения и теплообмена, при обтекании газовым потоком гладкой и шероховатой поверхностей. Она выражается искусственной турбулизацией гетерогенного потока шероховатой поверхностью, что ухудшает эффективность процесса формирования покрытий. Разработана математическая модель и проведен численный эксперимент для оценки влияния шероховатости стенок на динамику течения гетерогенной смеси в ускорителе Анализ полученных данных показал, что высота шероховатостей до 10мкм практически не влияет режим течения гетерогенной смеси по длине сопла. Если высота шероховатостей превышает 10 мкм, то режим течения меняется, что следует учитывать при формировании покрытий.
Основные выводы по работе
1. Проведен анализ физической сущности НТГДМ. На базе результатов анализа спроектирована и смонтирована установка лабораторного типа с широким диапазоном изменения параметров. Отработаны научные основы НТГДМ - технологий нанесения разнофункциональных покрытий на поверхности разных форм.
2. Предложены и апробированы методы и средства диагностики сверхзвуковых гомогенных и гетерогенных потоков, а также теплофизических характеристик покрытий. Надежность методов подтверждена экспериментально и в сопоставлении с данными других исследователей.
3. Разработана общая математическая модель и программа расчета течения гетерогенной смеси в до- и сверхзвуковых ускорителях при наличии межфазного теплообмена. Проведены оценочные расчеты параметров сверхзвукового течения в укорителях разных профилей (осесимметричные конические, осесимметричные поворотные, плоские и др.). Сопоставление расчетных данных с результатами экспериментальных исследований, полученных с использованием ЛДИС, показало удовлетворительное соответствие результатов.
4. На базе анализа общей математической модели течения, разработана упрощенная (инженерная) математическая модель газодинамики течения и межфазного теплообмена гетерогенной смеси в ускорителях. Сопоставление параметров течения, полученных по общей и упрощенной моделям, показало удовлетворительную корреляцию.
5. Проведен анализ течения гетерогенной смеси в ускорителях (микросоплах) с большим удлинением с учетом нарастания пограничного слоя вдоль стенок канала. Отмечено, что смыкание пограничного слоя внутри канала является отрицательным фактором, оказывающим сильное влияние на термо–газодинамические параметры гетерогенного потока. Определены пути устранения этого фактора.
6. Проведен анализ газодинамики течения и межфазного теплообмена при натекании сверхзвукового гетерогенного потока на плоскую преграду (стенку). Разработана математическая модель, описывающая движение частиц при преодолении ударной волны и сжатого слоя, образующихся у обрабатываемой поверхности. Получены соотношения для оценки влияния этих участков на изменение скорости частиц перед процессом формирования покрытия.
7. Разработана математическая модель процесса взаимодействия высокоскоростных частиц с твердой поверхностью. Получено соотношение для оценки длительности удара. Составлен алгоритм расчета параметров в зоне удара частицы о подложку. Проведена оценка уровня динамического давления, реализуемого при ударе, а также величины локальных температур частиц и подложки в зоне удара.
8. С целью разработки научных основ НТГДМ-технологии проведен анализ влияния различных факторов на эффективность формирования покрытий и их качество.
Основные публикации по теме диссертации
1. Степаненко С.А., Никитин П.В. Низкотемпературный газодинамический метод формирования многофункциональных покрытий на поверхностях конструкций. Доклад на 5-ой международной конференции «Авиация и космонавтика – 2006». Москва. 23-26 октября 2006г. Тезисы доклада. М.:, изд. МАИ, C. 46.
2. П.В. Никитин, С.М. Пророков, Степаненко С.А. Особенности газодинамики и теплообмена при сверхзвуковом течении гетерогенной среды в микросоплах с большим удлинением. Доклад на 5-ой международной конференции «Авиация и космонавтика – 2006». Москва. 23-26 октября 2006г. Тезисы доклада. М.:, изд. МАИ, С. 26.
3. П.В. Никитин, А.Г. Смолин, Степаненко С.А. Тепло-массообмен при формировании разнофункциональных покрытий сверхзвуковым гетерогенным потоком. Доклад на 5-ой международной конференции «Авиация и космонавтика – 2006». Москва. 23-26 октября 2006г. Тезисы доклада. М.:, изд. МАИ, С. 32.
4. Никитин П.В., Степаненко С.А. Упрощенный алгоритм расчета межфазного теплообмена в условиях градиентного течения гетерогенной смеси. Доклад на 6-ой международной конференции «Авиация и космонавтика – 2007». Москва. 23-26 октября 2007г. Тезисы доклада. М.:,С. 12.
5. П.В. Никитин, А.А. Низовитин, С.А. Степаненко Термооптический зонд для измерения температуры гомогенных и гетерогенных потоков. //Современные проблемы науки и образования. № 6, часть 1, 2007 С. 127-130.
НТЦ “ИНФОРМРЕГИСТР”- № 0420700037/0144
6. Никитин П.В., Степаненко С.А.,Пророков С.М., Смолин А.Г. Газодинамика и тепломассообмен при формировании разнофункциональных покрытий низкотемпературным гетерогенным сверхзвуковым потоком. //Современные проблемы науки и образования. № 6, часть 2, 2007, С. 95-102. НТЦ “ИНФОРМРЕГИСТР”- № 0420700037/0169.
7. Никитин П.В., Пророков С.М., Степаненко С.А. Формирование сверхзвуковых гетерогенных потоков в микросоплах с большим удлинением. //Современные проблемы науки и образования. № 6, часть 2, 2007 С. 89-94. “ИНФОРМРЕГИСТР”- № 0420700037/0168.
8. Степаненко С.А. Газодинамика и межфазный теплообмен при натекании сверхзвукового гетерогенного потока на преграду. //Вестник Московского авиационного института, Т 15, №5, 2008, С. 34-39
9. Степаненко С.А., Никитин П.В. Метод определения степени черноты термостойких покрытий. //Вестник Московского авиационного института, Т 15, №5, 2008, С. 58-61
