WWW.DISUS.RU

БЕСПЛАТНАЯ НАУЧНАЯ ЭЛЕКТРОННАЯ БИБЛИОТЕКА
 
<< ГЛАВНАЯ [ АГРОИНЖЕНЕРИЯ ] [ АСТРОНОМИЯ ] [ БЕЗОПАСНОСТЬ ] [ БИОЛОГИЯ ] [ ЗЕМЛЯ ] [ ИНФОРМАТИКА ] [ ИСКУССТВОВЕДЕНИЕ ] [ ИСТОРИЯ ] [ КУЛЬТУРОЛОГИЯ ] [ МАШИНОСТРОЕНИЕ ] [ МЕДИЦИНА ] [ МЕТАЛЛУРГИЯ ] [ МЕХАНИКА ] [ ПЕДАГОГИКА ] [ ПОЛИТИКА ] [ ПРИБОРОСТРОЕНИЕ ] [ ПРОДОВОЛЬСТВИЕ ] [ ПСИХОЛОГИЯ ] [ РАДИОТЕХНИКА ] [ СЕЛЬСКОЕ ХОЗЯЙСТВО ] [ СОЦИОЛОГИЯ ] [ СТРОИТЕЛЬСТВО ] [ ТЕХНИЧЕСКИЕ НАУКИ ] [ ТРАНСПОРТ ] [ ФАРМАЦЕВТИКА ] [ ФИЗИКА ] [ ФИЗИОЛОГИЯ ] [ ФИЛОЛОГИЯ ] [ ФИЛОСОФИЯ ] [ ХИМИЯ ] [ ЭКОНОМИКА ] [ ЭЛЕКТРОТЕХНИКА ] [ ЭНЕРГЕТИКА ] [ ЮРИСПРУДЕНЦИЯ ] [ ЯЗЫКОЗНАНИЕ ] [ РАЗНОЕ ] КОНТАКТЫ
Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.

Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.

Авторефераты диссертаций  >>  Авторефераты по Физике

Метаоптика одномерных фотонных и магнитофотонных кристаллов

На правах рукописи

Дорофеенко Александр Викторович

Метаоптика одномерных фотонных

и магнитофотонных кристаллов

01.04.13 – электрофизика, электрофизические установки

Автореферат

диссертации на соискание ученой степени

кандидата физико-математических наук

Москва – 2008

Работа выполнена в Институте теоретической и прикладной электродинамики РАН.

Научный руководитель: доктор физико-математических наук, гл. н. с. Виноградов А.П.

Официальные оппоненты: доктор физико-математических наук, профессор Шевченко В.В.;

кандидат физико-математических наук, ст. преп. Федянин А.А.

Ведущая организация: Институт спектроскопии РАН.

Защита состоится " " 2008 г. в ч. мин. на заседании Диссертационного совета ДМ 002.262.01 при Институте теоретической и прикладной электродинамики РАН при участии Объединенного института высоких температур РАН по адресу: г. Москва, ул. Ижорская, 13, экспозал ОИВТ РАН.

С диссертацией можно ознакомиться в библиотеке Объединенного института высоких температур РАН.


Автореферат разослан " " 2008 г.

Ученый секретарь Диссертационного совета

кандидат физико-математических наук А.Т. Кунавин

© Институт теоретической и прикладной электродинамики РАН, 2008

Общая характеристика работы

Актуальность темы

Работа посвящена актуальным задачам электродинамики неоднородных сред. Рассмотрены сложные системы, в которых взаимодействие электромагнитного поля с образующими эти системы элементами (включениями в матрице, ячейками фотонного кристалла, молекулами и т.д.) носит непотенциальный характер и не может быть описано, как это традиционно делалось, в рамках только квазистатического приближения. Новые эффекты, обусловленные запаздыванием и соленоидальностью полей, приводят к существенному отличию макроскопических свойств таких сред от свойств традиционных материалов (киральность, искусственный магнетизм, запрещенные зоны и т.д.), что и дало основание выделить такие системы в отдельный класс – класс метаматериалов. Обычно такой композитный материал представляет собой матрицу из вещества с диэлектрической проницаемостью порядка единицы, в которой находятся включения, имеющие резонансный отклик.

Использование металлов или сред с большой диэлектрической проницаемостью как материала для включений позволяет получить включение-резонатор размером много меньше длины волны. В этом случае дипольный отклик резонансного включения приводит к экстремальным значениям эффективной диэлектрической проницаемости , а возбуждение включения-резонатора в магнито-дипольной моде приводит к отличной от единицы (возможно и к отрицательной) эффективной магнитной проницаемости , даже если были использованы только немагнитные материалы [1-4].

Согласно предложенной классификации, к метаматериалам можно отнести также фотонные кристаллы (ФК), т. е. среды с периодической пространственной зависимостью диэлектрической проницаемости. Их период имеет порядок длины волны, и, таким образом, их описание как однородной среды с эффективными параметрами невозможно. Роль упомянутого выше резонанса в этом случае играет брэгговское отражение, которое приводит к возникновению запрещенных зон для распространения электромагнитных волн. Формирование запрещенной зоны лежит в основе разнообразных применений фотонных кристаллов [5].

В узком смысле под метаматериалами понимают среды с отрицательными значениями эффективных и . Применение таких сред теоретически позволяет повысить разрешающую способность оптических приборов, преодолев дифракционный предел. Используя материалы с (и, по возможности, ), можно за счет плазмонного резонанса усилить ближние (неоднородные) волны, ответственные за перенос информации о деталях с размером много меньше длины волны. Идеальной для этой цели является среда Веселаго, имеющая . Среды с одновременно отрицательными и [6] обладают интересными с точки зрения теории и полезными для практики свойствами (распространение обратных электромагнитных волн, отрицательное преломление, создание действительного изображения плоской пластинкой). Однако только в конце 90-ых годов среда Веселаго была смоделирована с помощью метаматериалов [7-9]. Также были получены киральные среды [10], среды с искусственным магнитным и квадрупольным откликом [1-4], среды с сильной пространственной дисперсией [11], с помощью которых пытаются создать приборы с разрешением выше дифракционного предела [12]. В последнее время теме метаматериалов уделяется огромное внимание [13-17].

Цели работы

  1. Исследование зонной структуры одномерных фотонных кристаллов, содержащих метаматериалы (слои с отрицательной диэлектрической или магнитной проницаемостью).
  2. Определение физических пределов разрешения многослойной металинзы, состоящей из слоев с положительной и отрицательной диэлектрической проницаемостью.
  3. Объяснение эксперимента по аномальному нерезонансному прохождению ИК излучения через неупорядоченную систему отверстий в металлической пленке.
  4. Объяснение эксперимента по достижению сверхразрешения в СВЧ диапазоне при помощи проволочной линзы, имитирующей сверхлинзу Пендри.
  5. Исследование возможности усиления магнитооптических эффектов устройствами на основе метаматериалов и фотонных кристаллов.
  6. Разработка алгоритмов, дающих физически правильный ответ при использовании теорий Гарнетта, Бруггемана и симметризованного подхода Гарнетта для расчета эффективных параметров композитных материалов, включающих ингредиенты с диэлектрическими проницаемостями разных знаков.

Научная новизна



    1. Предложен и изучен новый тип одномерных фотонных кристаллов с отрицательной контрастностью диэлектрической проницаемости, в которых зоны прозрачности возникают как результат резонансного возбуждения поверхностных плазмонов.
    2. Найден механизм, определяющий влияние потерь на качество изображения, создаваемого линзой Пендри, включая потери, возникающие при детектировании изображения.
    3. Предсказано усиление магнитооптических эффектов в системах, содержащих поверхностные (таммовские) состояния на границе двух фотонных кристаллов. На основании разработанной теории и проведенных расчетов в Технологическом университете Тояхаши (Япония) был поставлен эксперимент, в котором впервые было экспериментально продемонстрировано существование таммовского состояния и возможность усиления магнитооптики при помощи этого состояния.
    4. Предложен механизм (фильтрация ближних и дальних волн), объясняющий эксперимент по улучшению разрешения металинзы на основе проволок (ИТПЭ РАН, Г. А. Федоров и др.) и эксперимент по нерезонансному аномальному прохождению света через металлическую пленку с неупорядоченной системой субволновых отверстий (ИТПЭ РАН, И.В. Быков и др.)
    5. Развито описание металинз с помощью зонной теории фотонных кристаллов, что позволило впервые выявить физический смысл ограничений разрешающей способности этих устройств.
    6. Показано, что известные схемы усиления магнитооптических эффектов плазмонным резонансом неэффективны из-за слабого взаимодействия плазмона с падающей волной. Предложена модификация, не имеющая этого недостатка.
    7. Предложен алгоритм расчета эффективных параметров композитов, содержащих метаматериалы. Указан способ выбора ветви квадратного корня, при котором формула Бруггемана и симметризованная формула Гарнетта всегда дают физически осмысленный ответ.

Достоверность результатов

Результаты расчетов подтверждены в экспериментах, обнаруживших сверхразрешение в проволочной металинзе, аномальное прохождение света через систему субволновых отверстий, таммовское состояние на границе двух фотонных кристаллов и усиление магнитооптического эффекта Фарадея этим состоянием.

Научная и практическая ценность

Результаты исследования возможности усиления магнитооптических эффектов могут быть использованы для уменьшения размера магнитооптических устройств и для перехода к использованию существенно более дешевых компонент, что может иметь большое практическое значение.

Исследование одномерных фотонных кристаллов отрицательной контрастности имеет фундаментальное значение. Для таких кристаллов предсказан новый тип блоховских волн – блоховских волн ближнего поля, представляющих собой систему поверхностных плазмонов. Показано, что данные волны играют ключевую роль в работе многослойных металинз, предложенных Дж. Пендри [18], а также А. Алю и Н. Энгетой [19]. Показано, что в последних имеются запрещенные зоны нулевой ширины (точки Дирака), которые обеспечивают безотражательное прохождение света через линзу Энгеты. Показано, что блоховская волна в фотонном кристалле может переносить энергию, имея нулевое волновое число.

Так как рассматриваемые в работе металинзы предполагается использовать для улучшения разрешения в фотолитографии, то в работе было проведено исследование устойчивости этих линз к наличию диссипации и случайному отклонению параметров (диэлектрической проницаемости, толщины слоев), которое всегда имеет место при практической реализации.

Основные положения, выносимые на защиту

  1. Предсказан новый тип волн, распространяющихся по фотонному кристаллу. В пределе сильной связи такая волна представляется как комбинация поверхностных плазмонов.
  2. Исследована работа сверхлинзы на основе проволочной среды, имитирующей материал с отрицательной диэлектрической проницаемостью. Показано, что за счет отражения распространяющихся волн и пропускания ТЕ-поляризованных неоднородных волн линза Пендри и ее реализация в виде проволочной среды увеличивают разрешение для ТЕ-поляризованных волн. Ранее предполагалось, что линза Пендри может работать только с ТМ-поляризованными волнами, а повышение разрешения происходит за счет усиления неоднородных ТМ-волн. Необходимо отметить, что в рассмотренной проволочной линзе последний механизм вообще не реализуется.
  3. Показано, что тот же механизм фильтрации волн приводит к аномальному прохождению света через неупорядоченную систему субволновых отверстий в металлической пленке.
  4. Показано, что наличие процесса измерения приводит к частичному разрушению изображения в линзе Пендри, причем механизм ухудшения разрешения такой же, как при наличии диссипации внутри линзы. А именно, возникает расфазировка плоских волн пространственного спектра.
  5. Показано, что диапазон пространственных частот, воспроизводимый многослойной линзой Пендри, ограничивается резонансами. Эти резонансы соответствуют собственным состояниям, для которых линза является резонатором.
  6. Выявлен механизм усиления магнитооптических эффектов в многослойных системах. Показано, что в общем случае усиление эффекта Фарадея связано с резонансной прозрачностью таких систем. При этом угол фарадеевского вращения имеет масштаб разности фаз по разные стороны от резонанса, т.е. 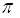. Ранее выдвигались различные гипотезы о механизме усиления: относительное увеличение поля за счет локализации в магнитооптических слоях [20], многократное прохождение резонатора волной [21], уменьшение групповой скорости и, как следствие, увеличение времени взаимодействия волны и вещества [22]. В диссертации показано, что данные механизмы не являются достаточными для усиления магнитооптики, хотя они могут вносить вклад в усиление (эффект Боррмана). В частности, показано, что наличие любого из указанных явлений не обеспечивает усиление.
  7. Исследован оптический аналог эффекта Боррмана. Теоретически предсказано усиление эффекта Фарадея вблизи одного края запрещенной зоны и ослабление вблизи другого края, что связано с отличием в распределении энергии. На основании наших расчетов этот результат подтвержден экспериментально коллегами из Технологического университета Тойохаши (Япония).
  8. Предложен алгоритм, который обеспечивает правильный выбор ветвей квадратного корня, входящего в формулы смешения для расчета свойств композитных материалов, в случае, когда включения могут иметь отрицательную диэлектрическую проницаемость. Отмечено, что в случае метаматериалов различные формулы смешения дают качественно отличающиеся результаты.

Апробация результатов





Результаты докладывались на следующих международных и российских конференциях:

  1. XLVII Научная конференция МФТИ, 26 – 27 ноября 2004, Москва.
  2. Workshop on Metamaterials for Microwave and Optical Technologies, July 18 – 20, 2005, San Sebastian, Spain.
  3. ICMAT 2005, 3 – 8 July 2005, Singapore.
  4. XLVIII Научная конференция МФТИ, 27 – 29 ноября 2005, Москва.
  5. Седьмая ежегодная научная конференция ИТПЭ ОИВТ РАН, 17 – 20 апреля 2006, Москва.
  6. Международная конференция Days of Diffraction 2006, May 30 – June 2, 2006, Saint Petersburg.
  7. Юбилейная XX Международная школа-семинар “Новые магнитные материалы микроэлектроники”, 12 – 16 июня 2006, Москва.
  8. MORIS 2006 Workshop, June 6 – 8 2006, Chiba, Japan.
  9. ETOPIM 7, July 9 – 13 2006, Sydney, Australia.
  10. BIANISOTROPICS 2006, September 23 – 28 2006, Samarkand, Uzbekistan.
  11. Восьмая ежегодная научная конференция ИТПЭ РАН, 9 – 12 апреля 2007, Москва.
  12. VIII научная школа молодых ученых ИБРАЭ РАН, 27 апреля 2007 г., Москва.
  13. Международная конференция DAYS ON DIFFRACTION’2007, May 29 – June 1, 2007, Saint Petersburg.
  14. PIERS 2007, August 27 – 30, 2007, Prague, Czech Republic.
  15. The Fourth International Conference on Materials for Advanced Technologies (ICMAT 2007) Simposium R, Electromagnetic materials, Singapore 2007.
  16. International Conference “Functional Materials” ICFM-2007, Ukraine, Crimea, Partenit October 1 – 6, 2007.
  17. First International Congress on Advanced Electromagnetic Materials, Rome, Italy, October 22 – 26, 2007.
  18. XLX Научная конференция МФТИ, 23 – 27 ноября 2007, Москва.
  19. PIERS 2008, March 24-28, Hangzhou, China.
  20. MISM 2008, June 20-25, Moscow.

Публикации

По теме диссертации опубликовано 40 работ, в том числе 13 статей в реферируемых изданиях и 27 публикаций в сборниках трудов и тезисов докладов на конференциях

Структура и объем диссертации

Диссертация состоит из введения, шести глав, заключения и списка литературы из 137 наименований. Общий объем 190 страниц, в том числе 87 рисунков и 4 таблицы.

Краткое содержание работы

Во введении обсуждается актуальность темы работы, научная новизна, указаны цели, а также положения, выносимые на защиту.

В первой главе дан обзор литературы, относящейся к теме работы.

Прежде всего, определено понятие ближних (неоднородных) полей, экспоненциально убывающих в пространстве, и указано, что эти поля возникают: 1) при полном внутреннем отражении, 2) в средах с (металлах), 3) при рассеянии на объекте произвольной формы, причем в последнем случае спектр ближних полей определяется деталями предмета размером меньше длины волны.

В отличие от плоских волн, одна неоднородная волна не может переносить энергию в направлении своего затухания. Но система из двух перекрывающихся волн, затухающих в противоположных направлениях, в результате интерференции может переносить энергию, при условии наличия разности фаз между этими волнами [23]. Для дальних полей интерференционный член не вносит вклада. Данное явление оказалось важным для понимания работы сверхлинз.

На границе металла и диэлектрика ближние волны могут сформировать решение в виде поверхностной волны (поверхностного плазмона), экспоненциально затухающей в направлениях от границы раздела сред. Такая волна бежит вдоль поверхности. Для возбуждения плазмона распространяющейся волной (плазмонный резонанс) требуется призма или дифракционная решетка. Плазмонный резонанс играет определяющую роль в формировании сверхразрешения многослойными линзами.

Эти системы могут рассматриваться как одномерные фотонные кристаллы, т.е. системы с периодической зависимостью диэлектрической проницаемости от одной координаты . Для них применима теорема Флоке-Блоха, в соответствии с которой решение имеет вид блоховской функции , где функция периодическая с периодом кристалла, – блоховское волновое число. Зависимость частоты от называется дисперсионным уравнением. В некоторых диапазонах частот оказывается комплексным, что соответствует запрещенным зонам. Для расчета дисперсионной зависимости в одномерном случае можно использовать метод Т-матриц. В силу линейности системы амплитуды волн на входе и выходе системы связаны линейным преобразованием, диагонализация которого дает собственное решение, т.е. блоховскую волну.

Прообразом упомянутых металинз является слой среды Веселаго (, ). В такой среде векторы , , образуют левую тройку (поэтому такие среды также называют левыми), а фазовая скорость и вектор Пойнтинга противонаправлены. На границе обычного диэлектрика и среды Веселаго происходит отрицательное преломление света. Это явление дает возможность фокусировать расходящийся луч в точку с помощью плоской пластинки из левого вещества с (линза Веселаго). Из законов геометрической оптики следует, что пластинка должна создавать действительное изображение предмета. Кроме того, как показал Пендри, такая линза усиливает волны ближнего поля за счет поверхностного плазмонного резонанса. В результате изображение предмета будет включать детали размером меньше длины волны, т.е. будет превзойден рэлеевский предел. Получение отрицательного в оптическом диапазоне проблематично, поэтому Пендри предложил использовать пластинку металла с , (линза Пендри), которая создает субволновое изображение лишь для p-поляризованной части спектра. В литературе предлагаются различные модификации линз Веселаго и Пендри: 1) асимметричная линза: изображение формируется в диэлектрике с большим , что увеличивает устойчивость к потерям в металле; 2) многослойная линза: состоит из чередующихся слоев металл/диэлектрик и имеет разрешение лучше, чем однослойная линза той же суммарной толщины; 3) линза Энгеты: отрицательные значения и находятся в разных слоях, что решает проблему взаимодействия включений в метаматериале.

Во второй главе показывается, что перенос энергии ближними полями ограничивает разрешение линзы Пендри. В частности, рассматривается влияние диссипации в материале линзы и в материале детектора. В идеальном случае (без диссипации и детектора) неоднородные волны, отвечающие за субволновые детали изображения, не переносят энергии. Наличие детектора означает появление потока энергии, для создания которого неоднородные волны должны поменять фазу. Возникающая расфазировка портит изображение. Имеет место также и уменьшение амплитуды волн, но этот эффект второго порядка по тангенсу потерь, тогда как изменение фазы линейно.

В третьей главе исследуются свойства одномерных фотонных кристаллов отрицательной контрастности (т.е. включающих слои с ) и их применение для получения сверхразрешения. Если период кристалла состоит из двух однородных слоев – диэлектрика () и металла (), – то в определенных полосах частот в нем существуют распространяющиеся блоховские волны, даже если волна является неоднородной в обоих слоях (в диэлектрике – из-за условия полного внутреннего отражения, в металле – из-за отрицательного ), см. рис. 1. Другими словами, для таких волн существуют разрешенные зоны. В обычных ФК с зонная структура возникает из-за того, что в окрестности условий резонансного брэгговского отражения возникают запрещенные зоны. Теперь же резонанс плазмонный, и он создает разрешенные зоны. Последнее утверждение обосновывается тем, что в предельном случае большой толщины одного из двух слоев периода условие, определяющее центр разрешенной зоны, совпадает с дисперсионным уравнением плазмона. Этот случай соответствует приближению сильной связи, и волна в разрешенной зоне представляет собой цепочку слабо взаимодействующих плазмонов, фазово-модулированных блоховской экспонентой. Они передают энергию друг другу за счет перекрывания неоднородных волн, имеющих разные фазы. Разность фаз образуется за счет блоховского множителя.

На основании развитых представлений исследуется многослойная линза, предложенная Пендри, которая представляет собой чередующиеся слои металла и вакуума. Из литературы известно, что поскольку линза является неидеальной (), то диапазон

пространственных частот, воспроизводимых в изображении, ограничен. В диссертации показано, что данное ограничение связано с возникновением запрещенной зоны соответствующего фотонного кристалла. Но основным ограничением является наличие собственных состояний, существующих в линзе, как в резонаторе блоховских волн. По линзе они распространяются в силу существования разрешенной зоны плазмонного типа (см. третью главу), а из линзы они выйти не могут из-за условия полного внутреннего отражения. Показано, что похожим образом обстоит дело и в случае асимметричной линзы, граничащей с одной из сторон с диэлектриком .

Рассмотрена также реализация металинзы, предложенная в работе Н. Энгеты [19]. Данная металинза представляет собой ФК с периодом из двух слоев (один с , а другой с ). При условиях, найденных Энгетой, любая волна проходит через эту линзу без изменения. Наш анализ, основанный на теории фотонных кристаллов, показал, что в этом случае блоховское волновое число равно нулю, и волна соответствует «запрещенной зоне нулевой ширины», или точке Дирака. Запрещенная зона на границе зоны Бриллюэна не открывается из-за постоянства импеданса в структуре. Хотя волновое число равно нулю, поток энергии создается предэкспонентой блоховской волны.

Четвертая глава посвящена явлению фильтрации, когда падающая по нормали волна почти полностью отражается, а неоднородная волна свободно проходит через объект. Это явление не связано с плазмонным резонансом, т.к. оно наблюдается для s-поляризации и не является резонансным. В данной работе решены две задачи, в которых такая фильтрация является основным механизмом: получение субволнового разрешения и аномальное прохождения света через металлическую пленку с субволновыми отверстиями. В первой из этих задач эксперимент, проведенный в ИТПЭ РАН и моделирующий линзу Пендри в СВЧ-диапазоне системой параллельных металлических проволочек, показал наличие субволнового разрешения. Однако падающая волна была в основном s-поляризована, что исключает плазмонное усиление ближних полей. Выяснилось, что s-поляризованные неоднородные волны проходят через слой металла, практически его не замечая, поскольку для них импеданс и волновое число не зависят от . При этом распространяющиеся однородные волны испытывают сильное отражение от слоя с . Таким образом, мелкие детали предмета передаются линзой, тогда как крупные (больше длины волны) искажаются.

Во второй задаче наличие неупорядоченной системы субволновых отверстий в металлической пленке приводило к улучшению прохождения на несколько процентов в широком диапазоне частот. Анализ показал, что это аномальное прохождение обусловлено не плазмонным резонансом, как в случаях, описанных в литературе, а указанной выше фильтрацией.

В пятой главе изучаются свойства поверхностных состояний, существующих на границе фотонного кристалла в запрещенной зоне, и усиление магнитооптического эффекта Фарадея в системах, поддерживающих эти состояния. Блоховской волне в запрещенной зоне соответствует комплексное волновое число, и она в среднем экспоненциально затухает от границы кристалла. Такие волны могут формировать решения типа поверхностных волн на границе кристалла. Если кристалл граничит с диэлектриком, поверхностная волна всегда имеет ненулевое тангенциальное волновое число, т.е. бежит вдоль поверхности. Это свойство является общим с поверхностным плазмоном. Но в отличие от него, рассматриваемая волна может иметь не только p-, но и s-поляризацию. В первом случае ФК заменяет среду с , во втором – среду с . Если ФК граничит с металлом (), существует частный случай поверхностной волны в виде поверхностного состояния, которое никуда не движется, в том числе вдоль поверхности. Оно аналогично известному для электронных кристаллов таммовскому поверхностному состоянию. На границе двух ФК неподвижное состояние может существовать и без использования металла (рис. 2), что позволяет снизить потери в реальной системе. На основе наших расчетов японскими коллегами был проведен эксперимент, который подтвердил наличие таммовского состояния по пику коэффициента прохождения в запрещенной зоне обоих ФК.

Таммовское состояние, наряду с другими резонансами типа Фабри-Перо, может использоваться для усиления магнитооптического эффекта Фарадея, который заключается в повороте поляризации волны, прошедшей через вещество, при наличии внешнего статического магнитного поля. Обычно рассматривается падение волны на слоистую систему по нормали, и в этом случае решениями являются волны круговых поляризаций. Они имеют различные фазовые скорости, поэтому резонанс расщепляется на два, для правой и левой круговых поляризаций (рис. 3). Такой резонанс может создаваться дефект-модой. В данной работе для этого предлагается использовать таммовское поверхностное состояние на границе двух ФК. Проведенный анализ показал, что угол поворота по

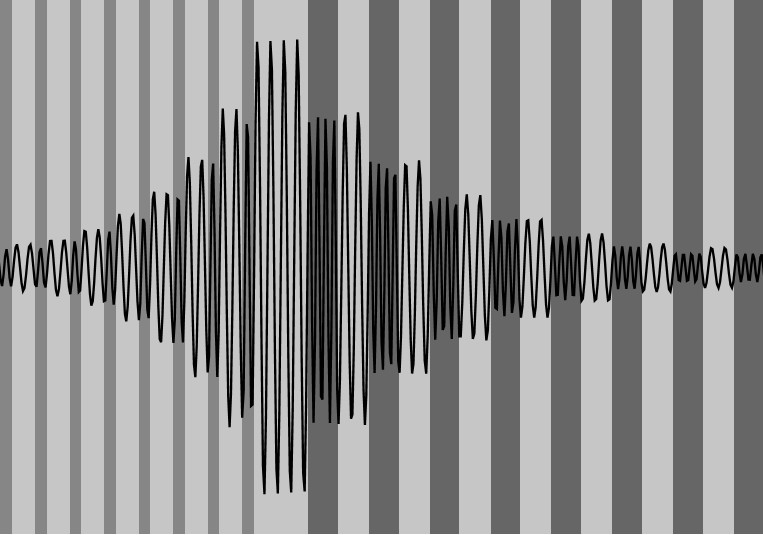
ляризации определяется выражением , где – добротность резонатора, – магнитооптический параметр, пропорциональный внешнему полю (точнее, намагниченности вещества), – доля энергии резонатора, находящейся в магнитооптических слоях. Изменением обусловлено проявление оптического аналога эффекта Боррмана, который заключается в концентра

ции поля в слоях с большой диэлектрической проницаемостью на частотах вблизи низкочастотной границы запрещенной зоны и в слоях с малой диэлектрической проницаемостью – вблизи высокочастотной границы. В случае наличия магнитооптических слоев это означает изменение , что приводит к усилению эффекта Фарадея с одной стороны от запрещенной зоны и ослаблению – с другой. Данный результат получил экспериментальное подтверждение. Кроме того, поскольку усиление эффекта Фарадея носит интерференционный характер, было произведено обобщение метода переотражений Эйри для произвольной неоднородной резонансной структуры.

Усиление фарадеевского вращения также возможно резонансами типа плазмонного, которые усиливают только одну поляризацию. Для исследования соответствующих систем в данной работе был развит метод расчета магнитооптических эффектов, учитывающий появление поляризации, перпендикулярной к падающей (кросс-поляризации), как возмущение. Сначала была рассмотрена известная схема, в которой кросс-поляризация усиливается плазмонным резонансом. В то же время для поляризации падающей волны резонанса нет, и она практически полностью отражается. В результате прошедшая волна имеет поляризацию, перпендикулярную падающей, и угол Фарадея составляет примерно 90, но интенсивность мала. Оказалось, что интенсивность кросс-поляризации на выходе определяется логарифмом добротности плазмонного резонанса. В результате проведенного анализа была предложена модификация этой схемы, когда интенсивность кросс-поляризации линейно зависит от добротности.

В шестой главе обсуждается способ расчета эффективной проницаемости по формулам смешения для композитного материала, в состав которого входят вещества с разных знаков. Например, в оптическом диапазоне это система металлических включений в диэлектрической матрице. Отрицательные значения материальных параметров, о которых шла речь в предыдущих главах, могут моделироваться метаматериалами, представляющими собой композитные среды. Правомерность применения формул смешения и введения эффективных параметров при этом не обсуждается. Формулы смешения (Гарнетта, Бруггемана, симметризованная формула Гарнетта) имеют эмпирический характер и получаются при помощи некоторых правдоподобных рассуждений. В случае различных знаков у компонент композита формула Бруггемана требует определенного выбора ветви многозначной аналитической функции многих переменных (квадратного корня), чтобы получить физически осмысленный результат. В работе указывается, как сделать этот выбор, и проводится анализ эффективной диэлектрической проницаемости, получаемой из формул смешения при вычислении указанным способом.

Основные результаты работы

  1. Показано, что в одномерных фотонных кристаллах (ФК), включающих металлические слои, существуют разрешенные зоны для волны, для которой кристалл является всюду запредельным. В приближении сильной связи показано, что разрешенная зона возникает при условии плазмонного резонанса.
  2. Исследованы поверхностные состояния и волны на границе ФК и однородного вещества (диэлектрика или металла), а также на границе двух ФК. Показано, что последняя схема может быть использована для усиления магнитооптического эффекта Фарадея. Проведен расчет, по которому японскими коллегами поставлен эксперимент, подтвердивший существование таммовского состояния по наличию пика прохождения в запрещенной зоне двух ФК, а также усиление эффекта Фарадея вблизи этого пика.
  3. Объяснены результаты эксперимента (Г.А. Федоров, ИТПЭ РАН), в котором линза Пендри моделировалась слоем параллельных проволочек и наблюдалось сверхразрешение для s-поляризации. Этот эффект оказался обусловленным не плазмонным усилением ближних волн, а фильтрацией, когда ближние s-поляризованные волны «не замечают» слой металла, а дальние волны от него отражаются.
  4. Это же явление фильтрации позволило объяснить аномальное прохождение света через неупорядоченную систему субволновых отверстий в серебряной пленке, обнаруженное в эксперименте (И.В. Быков, ИТПЭ РАН). Получено согласие с экспериментом (спектры прохождения через сплошные пленки), теоретически объяснен спектр прохождения через пленку с отверстиями.
  5. Показано, что попытка детектирования изображения, созданного линзой Пендри, приводит к частичному разрушению изображения, что связано с расфазировкой неоднородных плоских волн, создающих это изображение.
  6. Исследованы пределы разрешения многослойной линзы Пендри. Показано, что область частот, воспроизводимых в изображении, ограничена собственными состояниями линзы. Они являются стоячими блоховскими волнами, которые имеют плазмонную разрешенную зону внутри линзы и не могут выйти наружу.
  7. Исследована линза Энгеты. Показано, что она функционирует на границе зоны Бриллюэна, причем запрещенная зона не может открыться из-за постоянства импеданса в кристалле («запрещенная зона нулевой ширины», или точка Дирака). Хотя блоховское волновое число при этом равно нулю, энергия переносится за счет фазы предэкспоненты блоховской волны.
  8. Показано, что усиление угла Фарадея резонансами типа дефект-моды или таммовского состояния пропорционально добротности резонатора, а в схеме, усиливающей эффект Фарадея плазмонным резонансом, интенсивность кросс-поляризации зависит от добротности логарифмически.
  9. Теоретически предсказано проявление эффекта Бормана в магнитооптике, когда на одной границе запрещенной зоны эффект Фарадея усиливается, а на другой – ослабляется. Результат проверен экспериментально сотрудниками лаборатории М. Инуе (Университет Тойохаши, Япония).
  10. Если композитный материал включает материалы с диэлектрическими проницаемостями разных знаков (металлические включения в диэлектрической матрице), то для применения формул смешения Бруггемана и симметризованной формулы Гарнетта нужно правильно выбрать ветвь квадратного корня. Предложен способ этого выбора.

Список публикаций

Основные результаты диссертации, опубликованные в реферируемых изданиях:

  1. Виноградов А.П., Дорофеенко А.В. Блоховские волны ближнего поля в фотонных кристаллах. // Радиотехника и электроника. 2005. Т. 50. № 10. С. 1246-1251.
  2. Vinogradov A.P., Dorofeenko A.V. Destruction of the image of the Pendry lens during detection // Optics Communications 2005. V. 256. P. 333-336.
  3. Fedorov G., Maslovski S.I., Dorofeenko A.V., Vinogradov A.P., Ryzhikov I.A., Tretyakov S.A. Sub-wavelength imaging: Resolution enhancement using metal wire gratings // Physical Review B. 2006. V. 73 N. 035409.
  4. Федоров Г.А., Виноградов А.П., Дорофеенко А.В., Рыжиков И.А., Масловский С.И., Третьяков С.А. Формирование изображения системой параллельных проводящих проволочек, имитирующей метаматериал. // Радиотехника и электроника. 2006. Т. 51. № 7. С. 831 – 838.
  5. Dorofeenko A.V., Lisyansky A.A., Merzlikin A.M., and Vinogradov A.P. Full-wave analysis of imaging by the Pendry-Ramakrishna stackable lens. // Physical Review B. 2006. V. 73. N. 235126.
  6. Vinogradov A.P., Dorofeenko A.V., Erokhin S.G., Inoue M., Lisyansky A.A., Merzlikin A.M., and Granovsky A.B. Surface State Peculiarities at One-Dimensional Photonic Crystal Interfaces // Physical Review B. 2006. V. 74. N. 045128.
  7. Merzlikin А.M., Inoue M., Vinogradov A.P., Dorofeenko A.V., Granovsky A.B. and Lisyansky A.A. Tamm State in One-Dimensional Photonic Crystals // Journal of the Magnetics Society of Japan. 2006. V. 30, N. 11.
  8. Zouhdi S., Dorofeenko A.V., Merzlikin A.M., and Vinogradov A.P. Theory of zero-width band gap effect in photonic crystals made of metamaterials. // Physical Review B. 2007. V. 75. N. 035125.
  9. Merzlikin A.M., Vinogradov A.P., Dorofeenko A.V., Inoue M., Levy M. and Granovsky A.B. Controllable Tamm states in magnetophotonic crystal // Physica B. 2007. V. 394. N. 2. P. 277-280.
  10. Дорофеенко А.В. Асимметричная многослойная линза Пендри // Радиотехника и электроника. 2007. Т. 52. №9. С. 1116-1121.
  11. Виноградов А.П., Дорофеенко А.В., Мерзликин А.М., Зухди С., Клерк Ж.П. Роль потерь при создании изображений с субволновым разрешением. // Радиотехника и электроника. 2007. Т. 52. № 9. С. 1108-1115.
  12. Виноградов А.П., Дорофеенко А.В., Зухди С. К вопросу об эффективных параметрах метаматериалов // УФН. 2008. Т. 178. № 5. С. 511-518.
  13. Dorofeenko A.V., Merzlikin A.M., Vinogradov A.P., Lisyansky A.A., Granovsky A.B., Inoue M. Enhancement of Faraday effect in open resonators // In: Selected papers of the International Conference Days on Diffraction 2007, May 29-June 1, St.-Petersburg ed. By L.V. Andronov, V. M. Babich, V. E. Grikurov, A. P. Kiselev, M. A. Lyalinov, M. V. Perel., P. 45-49.

Статьи, принятые к публикации:

  1. Быков И.В., Виноградов А.П., Дорофеенко А.В., Мерзликин А.М., Рыжиков И.А., Седова М.В., Ильин А.С. Аномальное прохождение света через систему неупорядоченных отверстий в металлической пленке // Радиотехника и электроника. 2008.
  2. Bykov I.V., Dorofeenko A.V., Ilyin A.S., Ryzhikov I.A., Sedova M.V., Vinogradov A.P. Extraordinary Optical Transmission through a Random Array of Subwavelength Holes. // Physical Review B. 2008. V. 78.

Тезисы конференций:

  1. Дорофеенко А.В., Виноградов А.П. Блоховские волны ближнего поля в фотонных кристаллах. XLVII Научная конференция МФТИ (Труды конференции, часть VIII, стр. 54-55, 26 – 27 ноября 2004, Москва).
  2. Fedorov G., Dorofeenko A.V., Vinogradov A.P., Ryzhikov I.A., Maslovski S.I., Tretyakov S.A. Wire grids as Resolution-Enhancement Elements in Near-Field Imaging. Workshop on Metamaterials for Microwave and Optical Technologies (Book of Abstracts, P. 42, July 18 – 20, 2005, San Sebastian, Spain).
  3. Vinogradov A.P., Dorofeenko A.V. The Role of Phase Shift at Energy Transport by Evanescent Waves. ICMAT 2005 (Proceedings of the Symposium R, Electromagnetic materials, P. 41-43, 3 – 8 July 2005, Singapore).
  4. Дорофеенко А.В., Виноградов А.П. Формирование изображения проволочной средой. XLVIII Научная конференция МФТИ (Труды конференции, часть VIII, C. 67-68, 27 – 29 ноября 2005, Москва).
  5. Дорофеенко А.В., Виноградов А.П., Мерзликин А.М. Электродинамический анализ работы линзы Дж. Пендри. Седьмая ежегодная научная конференция ИТПЭ ОИВТ РАН. (Сборник тезисов докладов, С. 14-15, 17 – 20 апреля 2006, Москва).
  6. Vinogradov A.P., Merzlikin A.M., Dorofeenko A.V. Full Wave Analysis of Imaging by the Pendry-Ramakrishna single-layer and stackable lenses. Days of Diffraction 2006 (Book of Abstracts, P. 77, May 30 – June 2 2006, Saint Petersburg).
  7. Дорофеенко А.В., Виноградов А.П., Мерзликин А.М. Запрещенная зона нулевой ширины в магнитофотонных кристаллах. Юбилейная XX Международная школа-семинар “Новые магнитные материалы микроэлектроники” (Сборник трудов, C. 284, 12 – 16 июня 2006, Москва).
  8. Merzlikin A.M., Dorofeenko A.V., Erokhin S.G., Inoue M., Lisyansky A.A., Vinogradov A.P., Granovsky A.B. Enhancement of Magnetooptic Response by Surface State (Tamm) Resonance in 1D Magneto Photonic Crystal. MORIS 2006 Workshop (Technical Digest, P. 84-85, June 6 – 8 2006, Chiba, Japan).
  9. Vinogradov A.P., Dorofeenko A.V., Merzlikin A.M., Inoue M., Granovsky A.B., Erokhin S.G., Lisyansky A.A. Influence of defect and Tamm states on magneto-optical properties of 1D magneto-photonic crystals. ETOPIM 7 (Proceedings of the conference, July 9 – 13 2006, Sydney, Australia).
  10. Vinogradov A.P., Merzlikin A.M., Dorofeenko A.V., M. Inoue, Khanikaev A.B., Granovsky A.B., Lisyansky A.A. Magneto-optical properties of 2D photonic crystals. ETOPIM 7 (Proceedings of the conference, July 9 – 13 2006, Sydney, Australia).
  11. Vinogradov A.P., Dorofeenko A.V., Merzlikin A.M., Zouhdi S., Clerc J.P. Energy transfer by evanescent waves and related phenomena. ETOPIM 7 (Proceedings of the conference, July 9 – 13 2006, Sydney, Australia).
  12. Vinogradov A.P., Zouhdi S., Dorofeenko A.V., Merzlikin A.M., Clerc J.-P. Revisiting the role of losses in subwavelength imaging. BIANISOTROPICS 2006 (Proceedings of the conference, P. 65-66, September 23 – 28 2006, Samarkand, Uzbekistan).
  13. Виноградов А.П., Дорофеенко А.В., Мерзликин А.М. Усиление магнитооптических эффектов на таммовских состояниях. Восьмая ежегодная научная конференция ИТПЭ РАН. (Сборник тезисов докладов, C. 20, 9 – 12 апреля 2007, Москва).
  14. Дорофеенко А.В., Виноградов А.П. Усиление магнитооптических эффектов в резонансных структурах. VIII научная школа молодых ученых ИБРАЭ РАН (сборник трудов, C. 32, 27 апреля 2007 г., Москва).
  15. Vinogradov A.P., Merzlikin A.M., Dorofeenko A.V. Enhancement of magneto-optic effects with resonant structures. DAYS ON DIFFRACTION’2007 (Abstracts, P. 91, Saint Petersburg, May 29 – June 1, 2007).
  16. Merzlikin A.M., Dorofeenko A.V., Vinogradov A.P. Distinct feature of magneto-photonic-crystals on formation of the Yeh band gap. DAYS ON DIFFRACTION’2007 (Abstracts, P. 91-92, Saint Petersburg, May 29 – June 1, 2007).
  17. Vinogradov A.P., Dorofeenko A.V., Merzlikin A.M. A Comparative analysis of mixing formula for SNG and DNG media. DAYS ON DIFFRACTION’2007 (Abstracts, P. 92, Saint Petersburg, May 29 – June 1, 2007).
  18. Vinogradov A.P., Merzlikin A.M., Dorofeenko A.V., Lisyansky A.A., Inoue M. Role of resonances in amplification of Faraday effect. in: Proc. of PIERS 2007, August 27 – 30, 2007, Prague, Czech Republic, p.300.
  19. Vinogradov A.P., Merzlikin A.M., Dorofeenko A.V., Granovsky A.B., Lisyansky A.A. Distinctive feature of 1D anisotropic and gyrotropic photonic crystals Proceedings of the Fourth International Conference on Materials for Advanced Technologies (ICMAT 2007) Simposium R, Electromagnetic materials, ed. By Lim Hock, S. Matitsine, and Gan Yeow Beng, P. 41-43, Word Scientific, Singapore 2007.
  20. Vinogradov A.P., Merzlikin A.M., Dorofeenko A.V. (invite) Metaoptics. Subwave imaging by metamaterials. Book of abstracts International Conference “Functional Materials” ICFM-2007, Ukraine, Crimea, Partenit October 1-6, 2007, P. 291.
  21. Vinogradov A.P., Merzlikin A.M., Dorofeenko A.V., Inoue M., Lisyansky A.A. Peculiar feature of photonic crystals containing anisotropic and gyrotropic ingredients Proc. of the First International Congress on Advanced Electromagnetic Materials, 200726, Rome, Italy, October 22-26, 2007.
  22. Виноградов А.П., Дорофеенко А.В. Использование формул смешения для нахождения эффективных параметров метаматериалов. XLX Научная конференция МФТИ (Труды конференции, часть VIII, 23 – 27 ноября 2007, Москва), С. 71.
  23. Vinogradov A.P., Merzlikin A.M., Dorofeenko A.V., Granovsky A.B., Lisyansky A.A., Inoue M. Magnetooptics of 1D Magnetophotonic Crystal. PIERS 2008, March 24-28, Hangzhou, China.
  24. Vinogradov A.P., Merzlikin A.M., Dorofeenko A.V., Lisyansky A.A., Zouhdi S., Clerc J.P. Application of Band Theory to the Imaging Problem in Stackable Lenses. PIERS 2008, March 24-28, Hangzhou, China.
  25. Goto T., Dorofeenko A.V., Merzlikin A.M., Baryshev A.V., Vinogradov A.P., Inoue M., Lisyansky A.A., Granovsky A.B. MISM 2008, June 20-25, Moscow, Abstracts, P. 82-83.
  26. Dorofeenko A.V., Vinogradov A.P., Merzlikin A.M., Granovsky A.B., Lisyansky A.A. MISM 2008, June 20-25, Moscow, Abstracts, P. 241-242.
  27. Bykov I.V., Dorofeenko A.V., Ilyin A.S., Ryzhikov I.A., Sedova M.V., Vinogradov A.P. MISM 2008, June 20-25, Moscow, Abstracts, P. 567-568.

Список цитируемых работ

  1. Kostin M.V., Shevchenko V.V. Proc. of CHIRAL’94, ed. by F. Mariotte, J.-P. Parneix, P. 49-56.
  2. Vinogradov A.P., Lagarkov A.N., Romanenko E.V. // Electromagnetics. 1997. V. 17. P. 213.
  3. Pendry J.B., Holden A.J., Robbins D.J., Stewart W.J. // IEEE Trans. Micr. Theory and Techniques. 1999. V. 47. P. 2075-2084.
  4. Щелкунов C.А., Фриис Х.Т. Теория антенн. М.: Гос. изд. технико-теор. лит, 1959.
  5. Sakoda K. Optical Properties of Photonic Crystals. Berlin: Springer, 2001
  6. Веселаго В.Г. // УФН. 1967. Т. 92. С. 517-526.
  7. Smith D.R., Padilla W.J., Vier D.C., Nemat-Nasser S.C., Schultz S. // Phys. Rev. Lett. 2000. V. 84. P. 4184-4187.
  8. Shelby R., Smith D.R., Schultz S. // Science. 2001. V. 292. P. 77-79.
  9. Lagarkov A.N., Kissel V.N. // Phys. Rev. Lett. 2004. V. 92. N. 077401.
  10. Lindell I.V., Sihvola A.H., Tretyakov S.A., Viitanen A.J. Electromagnetic waves in Chiral and Bi-Isotropic Media. London: Artech House, 1994.
  11. Belov P.A., Marques R., Maslovski S.I., Nefedov I.S., Silverinha M., Simovski C.R., Tretyakov S.A. // Phys. Rev. B. 2003. V. 67. N. 113103
  12. Belov P.A., Simovski C.R., Ikonen P. // Phys. Rev. B. 2005. V. 71. N. 193105.
  13. Optical Properties of Random Nanostructures. Ed. V.M. Shalaev. Berlin: Springer Verlag, 2002.
  14. Tretyakov S. Analytical Modeling in Applied Electromagnetics. Northwood, MA: Artech House, 2003.
  15. Sakoda K. Optical Properties of Photonic Crystals. Berlin: Springer, 2001.
  16. Shalaev V.M. // Nature Photonics. 2006. V. 1. P. 41-48.
  17. Garca de Abajo F.J. // Rev. Mod. Phys. 2007. V. 79. P. 1267-1290.
  18. Pendry J.B. // Phys. Rev. Lett. 2000. V. 85. N. 18. P. 3966-3969.
  19. Al A., Engheta N. // IEEE Tr. AP. 2003. V. 51. P. 2558-2571.
  20. Inoue M., Arai K., Fujii T., Abe M. // Journ. of Appl. Phys. 1998. V. 83. N. 11. P. 6768-6770.
  21. Kato H., Matsushita T., Takayama A., Egawa M., Nishimura K., Inoue M. // Journ. of Appl. Phys. 2003. V. 93. N. 7. P. 3906-3911.
  22. Belotelov V.I., Doskolovich L.L., Zvezdin A.K. // Phys. Rev. Lett. 2007. V. 98 N. 077401.
  23. Колоколов А.А., Скроцкий Г.В. // УФН. 1992. Т. 162. №12. С. 165-174.

ДОРОФЕЕНКО Александр Викторович

МЕТАОПТИКА ОДНОМЕРНЫХ ФОТОННЫХ

И МАГНИТОФОТОННЫХ КРИСТАЛЛОВ

Автореферат

Подписано в печать 18.07.08 Формат 60x84/16

Печать офсетная Уч.-изд.л. 1,25 Усл.-печ.л. 1,16

Тираж 100 экз. Заказ N 115 Бесплатно

ОИВТ РАН. 125412, Москва, Ижорская ул., 13, стр. 2



 
Авторефераты диссертаций  >>  Авторефераты по Физике




наверх

<


 
<<  ГЛАВНАЯ   |    КОНТАКТЫ
2013 www.disus.ru - «Бесплатная научная электронная библиотека»

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.