Загоризонтное позиционирование с использованием многочастотного наклонн о го зондирования ионосферных ради о линий
На правах рукописи
Катков Евгений Вениаминович
Загоризонтное позиционирование
с использованием многочастотного
наклонного Зондирования ионосферных
радиолиний
Специальность 01.04.03. - Радиофизика
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата физико-математических наук
Казань – 2007
Диссертация выполнена на кафедре высшей математики ГОУ ВПО «Марийский государственный технический университет»
| Научный руководитель: | доктор физико-математических наук, профессор Иванов Владимир Алексеевич |
| Официальные оппоненты: | доктор технических наук, профессор Песошин Валерий Андреевич |
| доктор физико-математических наук, доцент Шерстюков Олег Николаевич |
| Ведущая организация: | Нижегородский государственный университет им. Н.И. Лобачевского |
Защита диссертации состоится «17» мая 2007г. в 14 часов 30 минут на заседании диссертационного совета Д 212.081.18 при ГОУ ВПО «Казанский государственный университет им. В.И. Ульянова-Ленина» по адресу: 420008, г. Казань, ул. Кремлевская, 18, физический факультет, ауд. 210.
С диссертацией можно ознакомиться в Научной библиотеке им. Н.И. Лобачевского Казанского государственного университета.
Автореферат разослан «12» апреля 2007 г.
 Ученый секретарь диссертационного совета Д 212.081.18 доктор физ.-мат. наук, профессор | Карпов А.В. |
Общая характеристика работы
Актуальность темы. Радиотехнические системы дальней радиосвязи, радионавигации, использующие радиоволны декаметрового (ДКМ) диапазона, стали рассматриваться в последнее время в качестве резервных. В то же время широкое распространение получил метод радиолокации коротковолновыми радиосигналами объектов (самолетов, ракет, кораблей), находящихся далеко за линией горизонта, а также загоризонтной радиолокации морской поверхности, верхней атмосферы, ионосферы и магнитосферы (например, проект SUPER DARN). Поэтому актуальной остается проблема повышения точности местоопределения с использованием сигналов декаметрового диапазона.
В системах коротковолновой радиолокации, дальней радионавигации подвижных объектов (кораблей, самолетов) сложность обеспечения высокой точности определения местоположения по времени распространения сигнала обусловлена частотной зависимостью скорости распространения сигнала, отличием ее от скорости света, а также неоднородностью и пространственно-временной изменчивостью среды распространения. Совершенствование теоретических подходов в решении данной проблемы требует проверки их адекватности в условиях эксперимента. В то же время возможность экспериментальных исследований этой актуальной проблемы долгое время была ограничена недостаточной эффективностью средств наклонного зондирования (НЗ) ионосферы и недостаточной точностью синхронизации разнесенных на тысячи километров передающих и приемных станций ионозондов, что необходимо для измерения с высокой точностью времени распространения сигнала от передатчика к приемнику. Вместе с этим, применение одночастотного зондирования также не позволяло существенно продвинуться в решении указанной проблемы. В этой связи была высказана гипотеза о возможности существенного увеличения точности позиционирования с применением многочастотного зондирования радиолиний сложными декаметровыми сигналами.
В настоящее время существуют все возможности для комплексного (теоретического и экспериментального) исследования данной гипотезы: созданы ионозонды, использующие сложные сигналы с линейной частотной модуляцией (ЛЧМ), обладающие высокой разрешающей способностью по времени распространения сигнала; спутниковые системы точного мирового времени, заменяющие атомные стандарты времени; статистические модели ионосферы (например, модель IRI), позволяющие проводить вычислительные эксперименты, имитируя условия распространения радиоволн, близкие к реальным. В рамках данных исследований возможно решение еще одной актуальной задачи: дистанционного определения основных параметров F слоя ионосферы над трудно доступными регионами Земного шара.
Цель диссертационной работы состоит в создании и исследовании эффективных радиофизических методик определения дальности до объекта по земной поверхности, координат объекта на Земле, а также в развитии методики определения параметров профиля электронной концентрации (N(h) –профиля) в F - слое ионосферы над средней точкой трассы, основанных на использовании данных многочастотного НЗ ионосферных радиолиний с помощью ЛЧМ ионозонда.
Задачами данной работы являются:
- Теоретическое обоснование радиофизических методик определения дальности до объекта по земной поверхности, местоположения (МП) объекта на Земле, а также методики оценки параметров профиля электронной концентрации в F - слое ионосферы над средней точкой трассы, основанных на использовании многочастотного НЗ ионосферы непрерывными ЛЧМ сигналами.
- Разработка математических моделей и алгоритмов, реализующих методики определения дальности до объекта по Земле, координат объекта на Земле и основных параметров F слоя с использованием данных многочастотного НЗ радиолиний.
- Разработка методики фильтрации экспериментальных ионограмм для получения устойчивых решений задачи определения дальности до объекта и основных параметров F – слоя.
- Разработка вычислительного эксперимента для исследования влияния ионосферы, протяженности и географического положения трасс на точность определения дальности, координат объекта и основных параметров слоя F.
- Проведение исследований точности определения дальности, координат объекта и основных параметров слоя F с помощью разработанных методик.
- Разработка методики проведения натурных экспериментов с использованием ЛЧМ ионозонда. Экспериментальная апробация разработанных методик и алгоритмов, получение их точностных характеристик.
Методы исследования. Сформулированные в диссертации научные положения и выводы обоснованы теоретическими решениями поставленных задач, которые базируются на методах теории поля для приближения геометрической оптики, методах математического моделирования с использованием современной технологии вычислительного эксперимента, методах вариационного исчисления и математической статистики, т.е. методах с хорошо изученными границами применимости. Численные эксперименты проводились с использованием международной модели ионосферы (IRI). Натурные эксперименты проведены с применением метода НЗ ионосферы с использованием ЛЧМ ионозондов, передатчики которых расположены в Западной Европе, что позволило реализовать декаметровые радиолинии различной географической ориентации и провести исследования для различных геофизических условий в ионосфере. При обработке экспериментальных данных использовались спектральные и статистические методы анализа данных.
Достоверность и обоснованность результатов и выводов диссертационного исследования определяются использованием адекватного математического аппарата, статистически достаточным набором экспериментальных данных, хорошим согласием натурных экспериментальных данных с результатами математического моделирования, повторяемостью результатов, а также проверкой на соответствие выводам других авторов.
Положения, выносимые на защиту:
- Теоретическое обоснование радиофизических методик определения дальности до объекта по Земле, координат объекта на Земле, а также основных параметров профиля электронной концентрации в F слое ионосферы над средней точкой трассы, основанных на данных многочастотного НЗ ионосферы непрерывными ЛЧМ сигналами.
- Разработанные модели и алгоритмы расчета дальности до объекта по Земле, координат объекта на Земле и параметров N(h) –профиля в F слое ионосферы над средней точкой трассы с использованием экспериментальных ионограмм.
- Методика фильтрации ионограмм для получения устойчивых решений задачи определения дальности до объекта по земной поверхности и основных параметров F слоя.
- Методика численного синтеза ионограмм наклонного зондирования с использованием международной модели ионосферы IRI.
- Полученные экспериментальные характеристики точности предложенных методик, обосновывающие справедливость выдвинутой в работе гипотезы о повышении точности местоопределения объекта на Земле с использованием данных многочастотного НЗ ионосферных радиолиний с помощью ЛЧМ ионозонда.
Научная новизна работы
- Теоретически обоснованы радиофизические методики определения дальности до объекта по Земле, координат объекта на Земле и основных параметров ионосферного слоя F, основанные на использовании данных НЗ ионосферы непрерывным ЛЧМ сигналом при поэлементной его обработке, реализующей принцип многочастотного зондирования.
- Развиты модели, разработаны методики и алгоритмы расчета дальности до объекта по Земле, координат объекта на Земле и основных параметров слоя F для средних точек радиолиний, учитывающие частотные зависимости времени группового запаздывания и не требующие информации о состоянии ионосферы из дополнительных источников.
- Разработана методика фильтрации экспериментальных частотных зависимостей задержек сигнала для получения устойчивых решений задачи определения дальности до объекта по земной поверхности и основных параметров F слоя над средней точкой трассы.
- Впервые в натурных экспериментах (с помощью ЛЧМ ионозонда) получены точностные характеристики разработанных новых методик. Доказана научная гипотеза о том, что метод многочастотного НЗ в сочетании с разработанными методиками обработки экспериментальных данных позволяют увеличить точность определения дальности до объекта по Земле и его координат на поверхности Земли.
Научная и практическая ценность работы заключается в разработке нового радиофизического подхода в решении задачи определения дальности до объекта по земной поверхности, МП объекта на Земле, а также основных параметров F слоя ионосферы над средней точкой трассы, основанных на использовании данных многочастотного наклонного зондирования ионосферных радиолиний сложными декаметровыми сигналами. Разработанные математические модели, алгоритмы и пакеты прикладных программ (ППП) могут быть использованы при разработке перспективных систем дальней радионавигации, загоризонтной радиолокации, использующих ионосферные радиолинии. Научная ценность работы подтверждается поддержкой РФФИ.
Реализация и внедрение результатов исследований. Результаты исследований использовались при выполнении грантов РФФИ: 99-02-17309, 02-02-16318, 04-05-65120, 05-07-90313; МНТП: «Критические технологии, основанные на распространении и взаимодействии потоков энергии»; ФЦП «Исследование и разработки по приоритетным направлениям развития науки и техники», а также в учебном процессе МарГТУ. Они используются в ЛЧМ ионозондах МарГТУ, входящих в экспериментальную Российскую сеть мониторинга ионосферы методами вертикального зондирования (ВЗ) и НЗ.
Личный вклад автора. Теоретические исследования аналитическими и численными методами выполнены лично автором. Им разработаны: методика вычислительного эксперимента; математические модели и алгоритмы определения траекторных характеристик луча, МП объекта и основных параметров ионосферного слоя F; ППП для их реализации. Автором проанализированы полученные результаты и сформулированы основные научные выводы и положения. Учитывая, что экспериментальные исследования со значительным объемом получаемых данных невозможно провести единолично, роль диссертанта в них заключалась в формулировании задач, участии в составлении программы эксперимента, а также в его проведении. По этой же причине некоторые публикации диссертанта имеют соавторство, однако результаты по указанным направлениям принадлежат автору диссертации.
Апробация результатов и публикации. Основные результаты диссертационного исследования докладывались и были представлены: в научно-техническом журнале «Вестник КГТУ им. А.Н. Туполева» (Казань, 2006); «Изв. вуз. Радиофизика» – 1984; на Всероссийских научных конференциях «Сверхширокополосные сигналы в радиолокации, связи и акустике» (Муром, 2003, 2006); на LVI Научной сессии им. А.С. Попова (Москва, 2003); на IX, X Международных научно - технических конференциях «Радиолокация, навигация и связь - RLNC» (Воронеж, 2003, 2004); на Международной Байкальской молодежной научной школе по фундаментальной физике «Взаимодействие полей и излучения с веществом» (Иркутск, 2004); на молодежной научно-практической конференции «Актуальные проблемы науки в 21 веке», посвященной 200-летию Казанского государственного университета (Зеленодольск, 2004); на XXI Всероссийской научной конференции «Распространение радиоволн» (Йошкар-Ола, 2005); на региональной XI конференции Северо-Западного региона России «Распространение радиоволн» (Санкт-Петербург, 2005); а также на научных конференциях МарГТУ «Итоги научно-исследовательских работ», секция «Радиофизика, техника, локация и связь» (Йошкар-Ола, 2003 - 2007); две статьи депонированы в ВИНИТИ.
Всего автором по теме диссертации опубликовано 16 работ, из них две в изданиях, рекомендованных ВАК РФ («Изв. вуз. Радиофизика», «Вестник КГТУ им. А.Н. Туполева»).
Структура и объем диссертации. Диссертация состоит из введения, четырех глав и заключения. Она содержит 206 страниц основного текста, 66 иллюстраций, 48 таблиц, библиографию из 190 наименований.
Основное содержание диссертации
Во введении обоснована актуальность темы диссертации, определены цели и задачи исследования, сформулированы научная новизна и практическая значимость результатов работы, приведена структура диссертации.
В первой главе дается анализ современного состояния решения задачи загоризонтного позиционирования с использованием сигналов ДКМ диапазона. Рассматриваются особенности местоопределения объектов в ДКМ диапазоне.
В сферической системе координат, с использованием позиционных методов определения МП объектов, получены аналитические соотношения для расчета географических координат объекта на Земле. Показано, что точность местоопределения загоризонтного объекта, как и надгоризонтного, зависит от точности измерения величин, характеризующих место объекта в пространстве или на поверхности Земли, и от геометрического фактора. Такими величинами для определения МП загоризонтного объекта могут быть следующие траекторные характеристики сигнала: групповой путь (или абсолютное время распространения сигнала по данной траектории), угол входа и угол выхода луча в вертикальной плоскости, угол прихода луча в горизонтальной плоскости, дальность скачка луча вдоль земной поверхности. В связи с этим рассматриваются радиофизические аспекты определения МП объекта с использованием радиоволн ДКМ диапазона. Показано: поскольку частоты коротких волн (КВ) близки к плазменным частотам ионосферы, то основным радиофизическим фактором, влияющим на МП объекта, является существенное влияние физических свойств ионосферы на характеристики распространяющихся в ней КВ радиоволн. Для этого решалось волновое уравнение в приближении геометрической оптики. Метод геометрической оптики позволяет получить представление КВ поля в ионосфере, если известен способ решения лучевых уравнений. Так, набег фазы волны, прошедшей по траектории L, составит:
(1)
где =2 f, f - частота волны, с - скорость света в вакууме, n - комплексный показатель преломления, 
- радиус - вектор точки наблюдения.
Известно, что первая производная от фазы по частоте связана с групповым запаздыванием «пакета волн» (), каковым является сигнал в ионосфере, следующими формулами:
. (2)
Функция 
является групповой скоростью сигнала. Таким образом, групповая скорость сигнала равна:
. (3)
Поскольку в ионосфере показатель преломления n<1, то групповая скорость распространения в ней несколько меньше, чем скорость света в вакууме. Понятие группового пути связано с гипотезой о том, что в ионосфере сигнал распространяется со скоростью света. Поэтому равенство:
P=c() (4)
определяет кажущееся расстояние, проходимое сигналом вдоль луча. Видно, что групповой путь и время распространения сигнала зависят как от частоты, так и от характеристик среды распространения.
При местоопределении объектов на основе дальнометрии необходимо знать расстояние до объекта по земной поверхности, т.е. длину скачка луча, поэтому рассматриваются методы определения дальности по Земле. Обычно методы расчета дальности основываются на задании модели регулярной ионосферы и модели распространения радиоволн. При этом модель распространения строится в лучевом приближении для решения волнового уравнения. Показано, что при распространении радиоволн за счет однократного отражения от ионосферного слоя F расчет дальности по Земле с использованием времени распространения сигнала связан с решением одноточечной траекторной задачи. Поэтому для ее однозначного решения необходимо знать угол выхода луча (начальные условия) и параметры модели ионосферы. Так как на самом деле параметры ионосферы неизвестны, то при расчете дальности по Земле в одночастотном режиме допускаются погрешности из-за принятых простых моделей траектории распространения, когда считается, что углы приема равны углам излучения. Обычно расстояние по Земле между пунктами приема и излучения сигнала рассчитывается по измеренным величинам вертикального угла выхода (прихода) луча или действующей высоты отражения и абсолютного времени запаздывания.
Рассматривается также ряд других методов расчета дальности по Земле, показаны их недостатки. В частности, для наземных, а в некоторых случаях и приземных объектов значения дальности по земной поверхности могут быть получены из специальных графиков – кривых для пересчета дальности по лучу в дальность по Земле при заданной высоте слоя ионосферы. Рассмотрен метод расчета дальности, основанный на использовании коэффициента удлинения трассы.
Проанализированы факторы, ограничивающие возможности повышения точности определения дальности и, соответственно, МП объекта на Земле. Главными из них являются пространственно-временная изменчивость и неоднородность среды распространения сигналов – ионосферной плазмы. Показано, что изменчивость и неоднородность ионосферы обусловлены как регулярными, так и случайными процессами, поэтому ионосфера вносит ошибки в радиолокационные, радионавигационные измерения координат объекта. Расчет дальности и МП объекта неизбежно связан с процедурой определенного пересчета первично измеряемых траекторных характеристик сигнала в параметры самих обнаруживаемых объектов в географических или других координатах.
Анализируются результаты измерений и расчетов траекторных характеристик ДКМ радиоволн для моделей регулярной ионосферы. Из-за искажающего влияния ионосферы результаты модельных исследований и экспериментальные данные обнаруживают существенные отличия. Поэтому методы расчета дальности с применением одночастотного режима даже в системах с очень высокой инструментальной точностью не позволяют существенно продвинуться в решение проблемы повышения точности определения дальности по Земле и, соответственно, МП объекта на Земле.
Показано, что задача определения основных параметров N(h)-профиля ионосферы важна не только для повышения точности МП объекта, но она актуальна также для исследования ионосферы над трудно доступными регионами Земного шара.
Рассмотрены причины, препятствовавшие проведению исследований местоопределения объектов на Земле на основе данных многочастотного наклонного зондирования ионосферы. Показано, что в последнее время появились технические возможности для осуществления таких исследований.
Таким образом, проведенный анализ современного состояния проблемы загоризонтного позиционирования на основе дальнометрии с использованием сигналов декаметрового диапазона выявил существующие противоречия. Это позволило сформулировать цель и определить задачи настоящего диссертационного исследования.
Вторая глава посвящена научному обоснованию радиофизического подхода в решении задачи позиционирования с использованием многочастотного НЗ ионосферы ЛЧМ сигналами.
Рассматриваются принципы радиофизического метода измерений абсолютных задержек элементов непрерывного сигнала, относящихся к разным рабочим частотам. Для синхронизации передатчиков мировой сети ЛЧМ ионозондов используется система GPS, в которой применяется шкала единого мирового времени, а для синхронизации ЛЧМ ионозондов за начало работы принято время, названное «chirp time». Требования к точности синхронизации были получены из анализа вопроса распространения зондирующего сигнала на ионосферной линии связи. Рассмотрена методика формирования ионограмм НЗ ионосферы.
Сверхширокополосный зондирующий ЛЧМ сигнал с полосой 2-30МГц распространяется на радиолинии по M различным лучам и поступает на вход приемника вместе с комплексом помех. В приемнике он сжимается в частотной области. В результате на его выходе имеем последовательность спектров сигнала разностной частоты F, отнесенных к разным рабочим частотам из диапазона зондирования, заданным на сетке с шагом 100кГц. В работе показано, что произвольный k – й амплитудный спектр сигнала разностной частоты (F) можно представить в виде:
, (5)
где fk - текущее значение зондирующей частоты, соответствующей данному спектру, i - время группового запаздывания на данной частоте, 
, 
- скорость изменения частоты, 
, TЭ - длительность элемента сигнала разностной частоты, fэ - соответствующая ему полоса частот, - точность синхронизации.
Для оценки допустимой точности синхронизации получено условие, при котором ~1,3/f. При f=100кГц значение 10мкс.
Показано, что сжатие сигнала в частотной области приводит к тому, что спектральная плотность мощности сигнала на выходе согласованного приемника возрастает в Вэ = fэTЭ раз по сравнению с плотностью на входе. Это приводит к росту отношения сигнал/шум примерно в 105 раз. Поэтому методика измерения, реализованная с использованием сверхширокополосного зондирующего сигнала, обладает повышенной помехоустойчивостью, что позволяет повысить надежность измерений задержки сигнала. Спектр разностного сигнала, полученный с помощью метода БПФ, представляет собой последовательность отсчетов, а ионограмма - матрицу.
На основе математических моделей регулярной ионосферы и приближения геометрической оптики развиты новые методики определения дальности по Земле и основных параметров F слоя ионосферы над средней точкой трассы на основе многочастотного НЗ ионосферных радиолиний. При этом предполагалось, что абсолютная задержка k на различных рабочих частотах fk; максимально применимая частота (МПЧ) - fМПЧ; наименьшая применимая частота (НПЧ) являются известными величинами и определяются из ионограмм НЗ ионосферы ЛЧМ – ионозондом; радиоволна от передатчика к приемнику распространяется одним скачком.
В рамках плоскослоистой ионосферы и параболического ионосферного слоя F с параметрами: ho - высота нижней границы отражающего слоя от Земли; ym - полутолщина слоя; hm= ho+ ym - высота максимума слоя от Земли; fo - критическая частота - с учетом кривизны Земли, для определения неизвестных параметров слоя ho, ym, fo и дальности по Земле D получена система:
, (6)
где х=Rsin(D/2R)/0,5c, 0< х <1, 
, k - номер рабочей частоты, 
N (натуральное) - число рабочих частот, с – скорость света, МПЧ - время группового запаздывания МПЧ, R – радиус Земли.
В рамках квазипараболической (КП) модели ионосферы с учетом сферичности Земли и ионосферы получена система вида:
, (7)
где k, МПЧ - углы излучения, соответствующие частотам fk и fМПЧ; ro=ho+R; Dз - дальность по Земле и Pл - групповой путь описываются известными уравнениями Крофта Т.А и Хугасьяна Г.
В этой системе ro, ym, fo, k, МПЧ, и D являются неизвестными.
Соотношение: 
(8)
выражает одно из краевых условий.
В диссертации для всестороннего исследования поставленных задач был применен вычислительный эксперимент. Описана методика эксперимента, который включал для заданных пунктов излучения и приема моделирование лучевых траекторий для численного синтеза ионограмм НЗ в международной модели ионосферы IRI. Для эффективного использования результатов моделирования численные эксперименты проводились при различных геофизических условиях (сезоны, время суток, параметры солнечной и магнитной активности, направления трасс и их протяженность), максимально приближенных к реальным условиям. Выбор направлений трасс определялся условием оптимальности эксперимента и наличием в данных направлениях постоянно действующих ЛЧМ передатчиков, что позволяет сопоставить результаты численного и натурного экспериментов.
Поскольку экспериментальные значения k содержат случайную компоненту («зашумлены» случайными погрешностями), значения k численного эксперимента также содержат случайную компоненту, обусловленную точностью вычислительного эксперимента, ошибки которого моделируют влияние случайных неоднородностей ионосферы, то значения k необходимо сглаживать, так как основанные на приближении геометрической оптики, построенные математические модели (6), (7) не учитывают их.
Разработана методика фильтрации ионограммы для получения устойчивых решений систем (6), (7). Сглаживающая функция t(f) выбиралась из множества непрерывно дифференцируемых на интервале (НПЧ, МПЧ) функций частоты f, имеющих стационарную точку с координатами (fМПЧ, b), вида:
(9)
где 
, m – целое положительное число.
В задаче выбора оптимальных параметров фильтрации при фиксированном значении m коэффициенты a и b были найдены из условий:
(10)
где 
, 
, n – соответственно точки и количество точек дискретной модели ионограммы.
Другое условие при построении сглаживающей функции заключалось в подборе целой степени m с тем, чтобы минимизировать среднеквадратическую ошибку (СКО) D в определении дальности предложенными методиками. Алгоритм фильтрации ионограммы определялся системой уравнений (10) для фильтруемой последовательности точек дискретной модели ионограммы и минимизации D.
Проведенные в данной главе аналитическими методами исследования создали теоретическую основу для решения поставленных задач.
В третьей главе исследован вопрос о существовании, устойчивости и однозначности решений предложенных методик определения дальности до объекта по Земле и параметров слоя F, основанных на данных многочастотного НЗ радиолиний; разработаны алгоритмы, реализующие методики. Проведены исследования точности определения дальности, координат объекта и ключевых параметров F слоя с помощью разработанных методик.
Задача решения систем (6), (7) относится к классу некорректных, и в общем случае такие задачи не дают однозначного решения. Решение осложняется еще тем обстоятельством, что связи между определяемыми параметрами и данными являются нелинейными. Чтобы разрешить указанные проблемы был предложен следующий метод определения D. Исключив неизвестные параметры ho, ym, fo, систему (6) можно свести к одному уравнению с одним параметром (неизвестным) x:
(11)
где индексы k1, k2, k3, k4 - номера частот: k1=1n-1, k2=2n, k3=1n-1, k4=2n, k1<k2, k3<k4, (k1, k2)(k3, k4).
Для составления системы (6) необходимо задать три частоты, fМПЧ и соответствующие времена запаздывания. Однако, чтобы уменьшить влияние случайных ошибок в исходных данных k на ошибку результата, нужно брать число уравнений больше, чем число неизвестных. Число уравнений (s) вида (11) определяется количеством используемых рабочих частот и числом их допустимых комбинаций. Поскольку исходные данные содержат случайные погрешности, то решения уравнений будут отличаться друг от друга, то есть не существует такого значения неизвестного x, которое бы удовлетворяло одновременно всем уравнениям. Подстановка любых значений x в уравнения даст некоторые значения 0 (невязки), где 1 s, – номер уравнения. Рассмотрены два способа построения оптимального значения D.
Алгоритм 1. В этом случае алгоритм определения оптимального решения основан на минимизации функции от абсолютных величин невязок. Следует отметить, что минимальное значение обеспечивается для параметра x, который определяет дальность D; параметр x имеет размерность, совпадающую с размерностью исходных данных и по величине соизмеримо с ними. При этом для определения одного параметра x будем иметь одно нормальное уравнение. Такая задача является определенной. Это также позволило однозначно определить параметры hm и fo.
Алгоритм 2. Исследования показали: каждое из уравнений (11) имеет единственное решение, практически не зависящее от выбора начального значения неизвестного x, то есть является устойчивым. Рассматривая каждое уравнение по отдельности, получим s решений, которые можно считать выборкой из множества возможных решений системы (6) для D. Исключив максимальное и минимальное значения D как недостоверные, получим случайный интервал (D, D), который с вероятностью, близкой к 1, покроет искомый параметр D. Установлено, что в качестве оптимального значения дальности нужно взять среднее арифметическое значений D из интервала (D, D).
Проблема фильтрации регулярной составляющей ионограммы потребовала изучения зависимости D от параметров сглаживающей функции для предложенных алгоритмов расчета дальности. Результаты исследования зависимости D от параметра m сглаживающей функции для трасс меридиональной ориентации различных расстояний для алгоритма 1 представлены на рис.1. Аналогичные зависимости имеют место и для алгоритма 2. Исследования показали, что для трасс протяженностью 1000–3200км, как меридиональной, так и широтной ориентации, оптимальным параметром фильтрации для обоих алгоритмов является степень m=3.
Для определения влияния параметров уравнений (11) на неопределенность решения варьировались следующие параметры: диапазон частот, используемый для решения уравнения; шаг (плотность), с которой частоты заполняют диапазон рабочих частот. Установлено, что диапазон частот существенно влияет на неопределенность решения задачи; для уменьшения области неопределенности решения нужно использовать весь диапазон рабочих частот – (НПЧ, МПЧ); оптимальным является равномерное их распределение на интервале, при этом важно привлечь данные измерений в окрестностях МПЧ и НПЧ. При этих условиях число частот fk не влияет заметным образом на расчет дальности. С практической точки зрения, это позволяет в качестве fk выбрать всего 4-5 частот (больше, чем число неизвестных), расположенных приблизительно равномерно на краях и в середине диапазона прозрачности радиолинии, и составить из них комбинации так, чтобы число уравнений было значительно больше, чем число неизвестных.
Пример расчета дальности с использованием алгоритма 1 (s=15) для трассы численного эксперимента Кипр – Йошкар-Ола протяженностью 2552км в 00:00 по местному времени (LT) 27.03.2002г представлен на рис.2. Минимальное значение суммы квадратов невязок достигается при D, равном 2549,5км, абсолютная ошибка расчета дальности составляет 2,5км.
Представлен пример расчета дальности с использованием алгоритма 2 для этого же случая. В результате решений уравнений (11) была получена серия значений D, которые можно записать в виде следующего вариационного ряда: 2484,5; 2485; 2485; 2531; 2531; 2531; 2554; 2561; 2575; 2575; 2575; 2587; 2587; 2587; 2632 (км). Исключив минимальное и максимальное значения решений, как недостоверные, получим интервал (D, D), равный (2485; 2587), который покрывает истинное значение дальности D=2552км. Длина интервала 102км, среднее арифметическое оставшихся значений D=2551,3км, абсолютная ошибка расчета D в данном эксперименте составляет 0,7км.
Показано, что в рассматриваемых задачах погрешность расчета (измерения) можно рассматривать как случайную величину. Поэтому оцениваются, как правило, усредненные значения ошибок за определенный промежуток времени. Анализу подвергались средние значения ошибок за суточный интервал. Погрешности методик определения дальности, координат объекта и основных параметров в слое F оценивались на основе статистических данных, полученных при помощи специально проведенных для этой цели численных экспериментов, и методов математического моделирования. Поскольку истинные значения измеряемых величин (W) на данном этапе исследования известны, то находились: среднесуточные значения измеряемой величины - W, абсолютных - |W| и относительных - W ошибок; максимальные относительные - max W и систематические ошибки, а также вероятностно-статистические оценки точности предложенных методик.
Для анализа предложенных методик были использованы данные численного синтеза около 800 ионограмм НЗ, когда ионосфера задавалась моделью IRI. Для расчета координат объекта были использованы соотношения для дальномерного метода местоопределения. Исследования проводились для пар радиотрасс протяженностью 1000 1000; 1500 1500; 2000 2000; 2552 2500; 3000 3156 (км), первая из которых имела меридиональную, а вторая широтную ориентацию, неизвестным являлось МП пункта приема, который совпадал с координатами Йошкар–Олы (56,6о N, 47,9о E).
Представлены результаты исследований точности определения дальности по Земле и МП объекта на Земле с помощью методики, разработанной с использованием плоскослоистой ионосферы и параболического слоя F.
Таблица 1
| Дальность, км | 1000 | 1500 | 2000 | 2500 | 2552 | 3000 | 3156 |
| D, км | 999,5 | 1499,6 | 1999,5 | 2500,5 | 2553,0 | 3001,0 | 3156,5 |
| |D|, км | 19,3 | 15,6 | 15,5 | 15,0 | 15,1 | 15,4 | 15,2 |
| D, (%) | 1,9 | 1,1 | 0,8 | 0,65 | 0,6 | 0,5 | 0,45 |
| max D, (%) | 4,5 | 3,0 | 2,1 | 1,7 | 1,7 | 1,4 | 1,3 |
| D, км | 22,4 | 19,0 | 19,0 | 17,8 | 18,0 | 18,2 | 18,0 |
Обнаружено, что ошибки расчета дальности существенно зависят от протяженности трассы. В табл. 1 представлены обобщенные результаты исследования сезонно-суточных точностных характеристик предложенной методики определения дальности в зависимости от длины трассы. Установлено, что систематическая ошибка метода составляет ~ +0,2км, потенциальная точность метода Dmin ~ 12км. Наилучшая оценка имеет место для трасс протяженностью ~ 2500км, для которых D ~18км. Для 2000км D 3200км относительные ошибки в определении дальности не превышают 1%.
Рис. 3
На рис. 3, а, б, в соответственно приведены гистограммы распределений ошибок, в определении широты, долготы и ошибки места r объекта для всех рассматриваемых пар трасс. Исследования показали, что систематические ошибки метода в определении широты составляют ~+0,15мин; долготы ~ -0,4мин; потенциальная точность в определении широты составляет ~ 6мин, а долготы ~ 12мин. Выявлено, что различие ошибок в определении и связано, во-первых, с тем, что соотношение между линейными и градусными мерами и различно; во-вторых, с наличием горизонтального градиента электронной концентрации, возникающего при движении терминатора, который оказывает большее влияние на результаты определения долготы. Установлено, что ошибки зависят от геометрии и протяженности трасс.
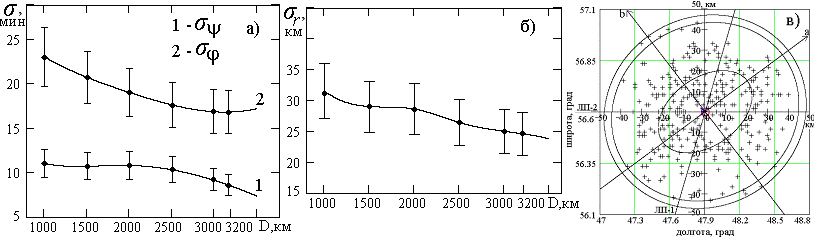
Рис. 4
На рис. 4, а, б соответственно показаны зависимости СКО широты (), долготы () и СКО места (r) от длины трассы, где точками обозначены оценки, и r, а отрезками вертикальных прямых указаны доверительные интервалы для них с доверительной вероятностью 0,99; сплошная линия – интерполяция по расчетным данным. На рис. 4, в приведены эллипсы ошибок, в которые с заданной вероятностью (0,5; 0,95; 0,99) попадают точки МП объекта, рассчитанные для всех пар трасс численного эксперимента.
Одним из существенных факторов, влияющих на точность решения задачи позиционирования, являются вариации параметров hm и fo слоя F2, которые необходимо задавать для расчетов. В рамках предложенной методики представлены результаты исследования точности расчета указанных параметров слоя в модели IRI для средней точки трассы. Обнаружена корреляция ошибки hm в определении параметра hm с тем, что рассматриваемый метод не учитывает слои, лежащие ниже слоя F2, и изменение горизонтальных градиентов электронной концентрации по трассе, которые оценивались по разности углов входа и выхода лучей. Коэффициент корреляции между hm и в зависимости от трасс, сезонов и времени суток принимает значения ~ 0,3 - 0,9.
Исследования вариаций суточных ходов ошибок hm позволили выделить “восходно-заходные” эффекты, которые выражаются в увеличении ошибки в периоды восхода и захода Солнца по местному времени, здесь абсолютные ошибки могут составлять 20-40км, достигает 0,9. Средние относительные ошибки и СКО в определении hm для всех рассматриваемых трасс и сезонов не превосходят соответственно 5%, 17км.
Анализ ошибок в определении критической частоты выявил систематические ошибки, зависящие от длины трассы. Для их устранения (коррекции) предлагается ввести поправочный коэффициент k(D) вида:
, (12)
где 1000км D 3500км.
Установлено, что применение коррекции повышает точность расчета fo в ~ 2–3 раза и относительные ошибки fo не превышают 5%.
В рамках квазипараболической модели ионосферы для решения системы (7) предложен алгоритм выбора начального решения параметров ho, ym и fo, лежащих в окрестности истинных значений, полученных в результате решения системы (6). Поскольку при расчетах с использованием плоскослоистой модели указанные параметры определяются с некоторой погрешностью, то сначала рассматривалась задача о влиянии этих погрешностей на ошибки в определении дальности по Земле. Из соотношения (8) следует, что fo выражается через параметры hо и ym. Поэтому в результате исследований получены выражения для оценки потенциальной точности определения дальности в зависимости от вариаций параметров hо и ym.
Принимая вариации в определении параметров ho, и ym соответственно равными h и y, для нахождения вариации в определении дальности D(h,y) на основе системы (7) получены аналитические соотношения. Результаты моделирования обнаруживают почти линейную зависимость D от h и y. На рис.6 приведены такие зависимости для радиотрассы протяженностью 2500км меридиональной ориентации при 
, равном 0,5; 0,75; 0,85.
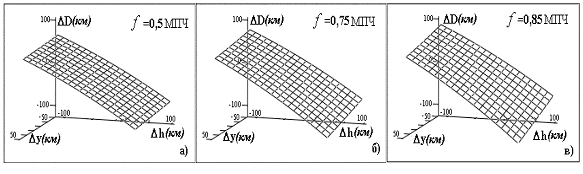
Рис. 5
Аналитически зависимость D(h,y) приближенно можно представить в виде:
D = ah+by, (13)
где a и b - некоторые коэффициенты.
Получены следующие многочлены для коэффициентов 
и 
:
(14)
(15)
где D
[1000км;3500км], fн 
[0,5;0,9].
Если ошибки в определении ho и ym имеют нормальное распределение с нулевым средним и СКО h и y, то среднее значение абсолютной погрешности в определении дальности M(|D|) имеет вид:
. (16)
Практически значимые диапазоны вариаций h
[-100км;+100км], y
[-50км;+50км]. На основании правила «трех сигм» определяем h и y как 100/3км и 50/3км соответственно. В этом случае для трасс протяженностью более 1000км M(|D|) не превосходит 5%, для D>2200км M(|D|) не превосходит 1% длины трассы. Показано, что влияние вариаций ym на ошибки определения дальности меньше по сравнению с вариациями ho. Установлено, что ошибки в определении дальности увеличиваются с ростом рабочей частоты и уменьшаются с увеличением протяженности трассы. Показано, что точность методики определения дальности в рамках КП модели ионосферы, включающей предложенный алгоритм задания начального приближения неизвестных параметров ho, ym и fo, улучшается в сравнении с методом определения дальности с использованием плоскослоистой модели.
В четвертой главе описана экспериментальная установка МарГТУ, основу которой составляет ЛЧМ ионозонд, имеющий следующие характеристики: диапазон рабочих частот 3-30МГц; скорость изменения частоты 100кГц/с; диапазон наблюдаемых задержек сигнала 5мс; излучаемая мощность 100Вт. Была обеспечена точность синхронизации в ± 5мкс, что в расстояниях составляет ±1,5км. В ней приведены результаты исследования реальных точностных характеристик предложенных методик определения дальности, параметров слоя F и МП объекта с использованием данных многочастотного НЗ ионосферных радиолиний широтного, меридионального и приполярного направлений, представленных в табл. 2. Представлена интерпретация результатов натурного эксперимента путем сопоставления их с данными проведенных в работе теоретических исследований. Натурные исследования охватывали различные времена года. Всего было проанализировано и обработано около 820 ионограмм.
Таблица 2
| Номер трассы | Пункты передачи-приема | Протяженность, км |
| 2-1 | Кипр – Йошкар-Ола | 2552 |
| 3-1 | Инскип (Англия) - Йошкар-Ола | 3156 |
| 4-1 | Свалбард (Шпицберген) – Йошкар-Ола | 2715 |
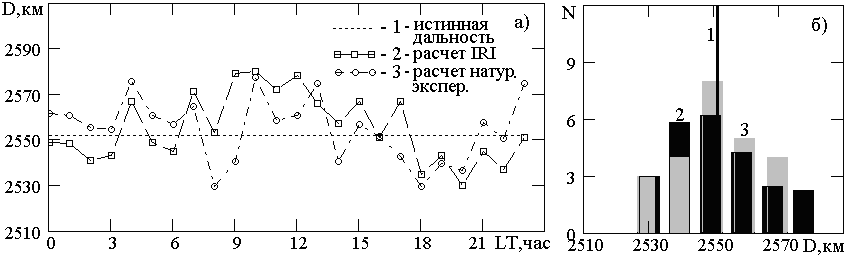
Рис. 6
На рис. 6, а, б приведены примеры суточных ходов измеренной дальности по Земле с использованием алгоритма 1 и гистограммы распределения дальности для трассы Кипр - Йошкар-Ола, полученные в численном и натурном экспериментах 27.03.2002 г. Цифрами 1, 2, 3 отмечены линии, соответствующие истинному значению D и рассчитанным. Видно хорошее соответствие результатов расчета дальности в численном и натурном экспериментах. На рис. 7-9, а также в табл. 3, 4 представлены результаты натурных исследований реальной точности определения дальности до объекта по Земле и его МП на Земле с помощью методики, разработанной с использованием плоскослоистой модели ионосферы. На рис. 7 точками обозначены оценки D для трасс 2-1, 3-1 и 4-1, на рис. 8 точками обозначены оценки, и r для трех пар трасс: первая - 2-1 и 3-1; вторая - 2-1 и 4-1; третья - 3-1 и 4-1, а отрезками вертикальных прямых указаны доверительные интервалы для них с доверительной вероятностью 0,999. Непрерывные кривые получены с помощью интерполяции методом кубического сплайна данных, полученных в результате исследований. Видно, что их точки находятся в доверительных интервалах и тем самым подтверждается достоверность предложенной методики определения дальности до объекта по земной поверхности и координат объекта на Земле.
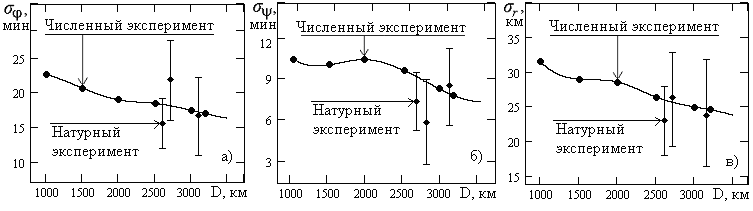
Рис. 8
На рис. 9 для трех пар трасс показаны эллипсы ошибок, в которые с заданной вероятностью (0,68; 0,95; 0,997) попадают точки МП объекта.
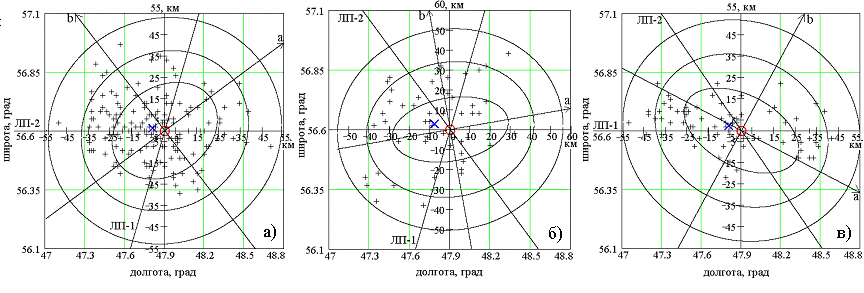
Рис. 9
Итак, результаты проведенных исследований свидетельствуют, что методика, разработанная с использованием модели плоскослоистой ионосферы и параболического слоя F на основе данных многочастотного НЗ радиолиний, в натурных экспериментах обеспечивает точность определения дальности по Земле и МП объекта на Земле, соответствующую результатам теоретических исследований. Отклонения между экспериментальными и теоретическими оценками точности метода не превышают 15%, причем оценки в натурном эксперименте несколько лучше оценок, полученных в результате исследований. Это объясняется тем, что в результате исследований получены оценки точности методики “сверху”.
Представлены результаты исследования точности определения параметров fo и hm слоя F путем сравнения с данными, полученными с помощью ВЗ ионосферы. На рис. 10, а, б, в соответственно приведены вариации параметров fo и hm слоя F в зависимости от времени суток и примеры N(h) - профилей слоя для средней точки трассы, рассчитанные по разработанной методике и полученные из данных ВЗ ионосферы приблизительно в середине трассы Кипр - Йошкар-Ола. В данном эксперименте относительные ошибки в определении hm и fo по предложенной методике не превосходят соответственно 4% и 5%.
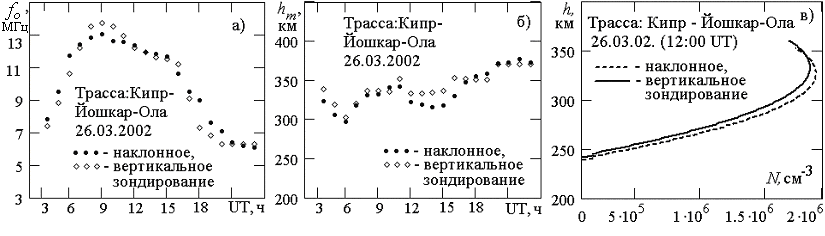
Рис. 10
Для модели зеркального отражения радиоволн от ионосферы получены формулы, позволяющие оценить потенциальную точность расчета дальности. Принимая вариации действующей высоты отражения h радиоволны в средней точке трассы и времени запаздывания равными соответственно h и, для приращения расстояния D получена следующая оценка:
. (17)
Результаты модельных исследований показали, что с увеличением протяженности трассы зависимость D=D(D, h, ) для практически значимых диапазонов вариаций переменных h
[-100км;+100км] и 
[-100мкс;+100мкс] близка линейной и для трасс, протяженностью 1500 – 3500км, аналитически она может быть представлена формулой:
. (18)
Видно, что вариации h оказывают большее влияние на |D|, чем вариации. В случае, когда вариации h и - случайные величины, имеющие нормальные законы распределения с нулевыми математическими ожиданиями, СКО h, и коэффициентом корреляции h, то оценку дисперсии дальности можно представить в виде формулы:
(19)
Здесь h, D и D выражаются в километрах, а - в микросекундах.
На основании формулы (19) показано, что потенциальная точность расчета дальности, ограниченная не прогнозируемыми флуктуациями электронной концентрации в области отражения, составляет ~ 3-6км.
Установлено, что случайная составляющая погрешности метода расчета дальности будет определяться, в основном,, а систематическая составляющая погрешности, в основном, точностью задания высоты отражения.
Анализ суточных ходов показал, что СКО минимальных задержек в 1,5 - 2 раза меньше СКО максимальных задержек. Поэтому при расчетах дальности с использованием зеркальной модели на ионограммах НЗ нужно выделять те горизонтальные участки нижнего луча моды 1F2, для которых изменение от частоты времени группового запаздывания наименьшее.
Представлен анализ реальной точности определения дальности по Земле и МП объекта с помощью методик, разработанных с использованием зеркальной и квазипараболической моделей. Установлено, что методики в натурных экспериментах обеспечивают точность, полностью соответствующую результатам теоретических исследований.
Таблица 3
| Трасса | Измеряемые параметры/Модель | D, км | D, км | D, (%) | max, (%) | D, км |
| Кипр–Йошкар-Ола 2552км | Зеркальная | 2555,0 | 13,0 | 0,6 | 1,9 | 15,8 |
| Плоскослоистая | 2552,4 | 11,4 | 0,5 | 1,8 | 14,7 | |
| Квазипараболическая | 2551,8 | 11,0 | 0,5 | 1,5 | 13,7 | |
| Свалбард –Йошкар-Ола 2715км | Зеркальная | 2717,0 | 13,0 | 0,6 | 1,5 | 15,5 |
| Плоскослоистая | 2714,5 | 12,6 | 0,5 | 1,3 | 15,0 | |
| Квазипараболическая | 2714,8 | 12,0 | 0,5 | 1,3 | 14,3 | |
| Инскип –Йошкар-Ола 3156км | Зеркальная | 3154,8 | 13,5 | 0,5 | 1,5 | 16,2 |
| Плоскослоистая | 3155,4 | 13,2 | 0,45 | 1,2 | 15,6 | |
| Квазипараболическая | 3155,6 | 12,2 | 0,4 | 1,2 | 14,7 |
Таблица 4
| Пара трасс | Измеряемые параметры/Модель | , мин | , мин | , мин | , мин | r, км | r, км | ||||||||
| 1 | Зеркальная | 6,6 | 13,5 | 7,8 | 16,0 | 20,0 | 24,0 | ||||||||
| Плоскослоистая | 5,8 | 13,0 | 7,3 | 15,6 | 19,0 | 22,7 | |||||||||
| Квазипараболическая | 6,0 | 12,0 | 7,2 | 14,5 | 18,5 | 21,4 | |||||||||
| 2 | Зеркальная | 4,6 | 24,0 | 5,5 | 26,8 | 26,3 | 27,5 | ||||||||
| Плоскослоистая | 4,5 | 18,0 | 5,2 | 22,0 | 21,5 | 26,0 | |||||||||
| Квазипараболическая | 4,0 | 21,3 | 4,5 | 26,0 | 23,5 | 25,4 | |||||||||
| 3 | Зеркальная | 7,8 | 13,6 | 9,2 | 16,8 | 21,0 | 25,0 | ||||||||
| Плоскослоистая | 7,4 | 14,0 | 9.0 | 16,7 | 21,5 | 24,1 | |||||||||
| Квазипараболическая | 7,0 | 12,0 | 8,2 | 15,2 | 19,5 | 23,0 | |||||||||
В табл. 3 и 4 соответственно представлены обобщенные за все время натурных экспериментов результаты исследования среднесуточной точности определения дальности по Земле и МП объекта на Земле с помощью разработанных методик (с использованием одних и тех же исходных данных). Видно, что для всех трех предложенных методик ошибки в определении дальности до объекта по Земле для рассмотренных трасс не превышают: средние относительные 1%, а максимальные - 2%, СКО - 17км. При этом систематическая составляющая погрешностей методик стремится к нулю, что является подтверждением корректности моделей.
Ошибки места зависят от геометрии трассы, однако средние и максимальные значения ошибки места не превышают соответственно 1% и 2% длины наименьшей из трасс в паре.
Анализ эффективности методик показал, что, с точки зрения затрат машинного времени, трудоемкости и точности, наиболее эффективной является методика, разработанная с использованием модели плоскослоистой ионосферы и параболического слоя F.
В заключении сформулированы основные результаты диссертации:
- Предложены и теоретически обоснованы радиофизические методики определения дальности до объекта по земной поверхности, МП объекта на Земле и основных параметров профиля электронной концентрации в F–слое ионосферы над средней точкой трассы, основанные на использовании данных многочастотного НЗ ионосферных радиолиний непрерывными ЛЧМ сигналами.
- Построен алгоритм оптимального решения задачи определения дальности, приводящий многопараметрическую задачу к однопараметрической и позволяющий для условий полной априорной неопределенности информации о состоянии ионосферы однозначно определить дальность до объекта по Земле и основные параметры слоя F на основе многочастотного НЗ радиолиний.
- Разработана методика фильтрации экспериментальных частотных зависимостей задержек элементов непрерывного сигнала, приводящая к устойчивым решениям задачи определения дальности до объекта по Земле и основных параметров F слоя. Определен вид сглаживающей функции и получены ее оптимальные параметры для радиолиний протяженностью 1000 - 3200км.
- Разработана методика численного синтеза ионограмм наклонного зондирования ионосферы, использующая моделирование лучевых траекторий в среде IRI и учитывающая координаты пунктов излучения и приема сигнала, горизонтальную неоднородность среды распространения и географическую ориентацию трассы.
- Теоретически и экспериментально с помощью ЛЧМ ионозонда получены среднесуточные характеристики точности разработанных методик определения: дальности до объекта по земной поверхности; координат объекта на Земле и ключевых параметров F слоя. Показано, что ошибки определения дальности для трасс протяженностью 2000 – 3200км не превышают 1%; ошибка места не превышает 1% длины наименьшей из трасс в паре; относительные ошибки определения критической частоты и высоты максимума F слоя не превышают 5%. Характеристики точности в “восходно-заходные” часы ухудшаются в среднем на 30 - 50%.
Основные публикации по теме диссертации
- Катков, Е.В. Восстановление профиля электронной концентрации по ионограммам наклонного зондирования ионосферы в задачах позиционирования. / В.А. Иванов, Е.В. Катков // Вестник КГТУ им. А.Н.Туполева. – Казань, 2006. - №2 (42). - С. 24 - 29.
- Катков, Е.В. Некоторые результаты исследования воздействия мощного КВ излучения на распространение радиоволн на трассе Киев – Йошкар-Ола / Н.М. Богута, В.А. Иванов, Е.В. Катков и др. // Изв. вузов. Радиофизика. – 1984. Т. XXVII. - С. 1477 – 1479.
- Катков, Е.В. Исследование точности определения длины радиолинии по данным ЛЧМ ионозонда / Е.В. Катков, А.А. Колчев // Сборник трудов VII Международной Байкальской молодежной научной школы по фундаментальной физике «Взаимодействие полей и излучения с веществом». – Иркутск, 2004. - С. 122 - 124.
- Катков, Е.В. Реализация различных методов местоопределения с помощью ЛЧМ ионозонда / В.А. Иванов, Е.В. Катков, А.А. Колчев // Труды IX Международной научно-технической конференции “Радиолокация, навигация, связь” RLNC'2003г. – Воронеж: Воронежский НИИ связи, 2003. – Т.2. - С. 977 - 986.
- Катков, Е.В. Реализация метода определения длины радиотрассы с помощью ЛЧМ-ионозонда в модели квазипараболического ионосферного слоя / Е.В. Катков, А.А. Колчев // Труды X Международной научно-технической конференции «Радиолокация, навигация, связь» RLNC’2004г. – Воронеж: Воронежский НИИ связи, 2004. – Т.2. - С. 1080 - 1086.
- Катков, Е.В. Определение местоположения с помощью широкополосных ЛЧМ сигналов / В.А. Иванов, Е.В. Катков, А.А. Колчев // Всероссийская науч. конф. «Сверхширокополосные сигналы в радиолокации, связи и акустике». – Муром, 2003. – С. 271 - 275.
- Катков, Е.В. Реализация метода определения МП объекта по данным многочастотного НЗИ с использованием сверхширокополосных сигналов с линейной частотной модуляцией / В.А. Иванов, Е.В. Катков // Всерос. науч. конф. «Сверхширокополосные сигналы в радиолокации, связи и акустике». – Муром, 2006. – С. 193 – 198.
- Катков, Е.В. Результаты местоопределения объектов с помощью ЛЧМ ионозонда / В.А. Иванов, Е.В. Катков, А.А. Колчев // LVI Научная сессия, посвященная Дню радио. Труды РНТО РЭС им. А.С. Попова. – М., 2003. - Т.2. - С. 265 - 267.
- Катков, Е.В. Местоопределение объекта с помощью многочастотного зондирования ионосферных радиолиний / В.А. Иванов, Е.В. Катков // Тезисы докладов региональной XI конференции по распространению радиоволн. – СПб.: ВВМ, 2005. – С. 32 – 34.
- Катков, Е.В. Результаты измерения длины радиолинии с помощью ЛЧМ ионозонда / Е.В. Катков, А.А. Колчев // Сборник докладов молодежной научно-практической конференции «Актуальные проблемы науки в 21 веке», посвященной 200-летию Казанского государственного университета: Зеленодольский филиал КГУ.- 24 апреля 2004 года. - Зеленодольск, 2004. - С. 26 - 27.
- Катков, Е.В. Исследование коэффициента удлинения коротковолновых радиотрасс / В.А. Иванов, Е.В. Катков // Распространение радиоволн: сборник докладов XXI Всероссийской научной конференции. Йошкар-Ола, 25-27 мая 2005г. - Йошкар-Ола: МарГТУ, 2005. - Т.2. - С. 78 - 82.
- Катков, Е.В. Оценка точности определения дальности по Земле с помощью ЛЧМ-ионозонда в модели параболического ионосферного слоя / Е.В. Катков, А.А. Колчев. // Сб. статей студентов, аспирантов и докторантов по итогам научно-технических конференций МарГТУ в 2003г. - Йошкар-Ола, 2004. - С. 155 - 162.
- Катков, Е.В. Расчет дальности по Земле по данным ЛЧМ-ионозонда в модели квазипараболического ионосферного слоя / Е.В.Катков, А.А. Колчев // Сборник тезисов докладов студентов, аспирантов, докторантов по итогам научно-технической конференции МарГТУ в 2004г. - Йошкар-Ола, 2004. - С. 103 - 104.
- Катков, Е.В. Реализация метода определения дальности декаметровых радиолиний по данным ЛЧМ ионозонда / Е.В. Катков // Наука в условиях современности: Сборник статей. - Йошкар-Ола: МарГТУ, 2006. - С. 140 - 148.
- Катков, Е.В. Точностные характеристики позиционирования с использованием декаметровых радиоволн на различных частотах /В.А.Иванов, Е.В. Катков. – Марийск. госуд. техн. ун-т. – Йошкар-Ола, 2006. – 20 с.: ил. – 17. – Библиогр.: 5 назв. – Рус. – Деп. в ВИНИТИ 24. 01. 2006, № 55 – В 2006.
- Катков, Е.В. Исследование дальности декаметровых радиолиний по ионограммам наклонного зондирования / Е.В. Катков. – Марийск. госуд. техн. ун-т. – Йошкар-Ола, 2006. – 34 с.: ил. – 17. – Библиогр.: 5 назв. – Рус. – Деп. в ВИНИТИ 24. 01. 2006, № 54 – В 2006.
