Реконструкция уравнений колебательных систем при наличии скрытых переменных и внешних воздействий
На правах рукописи
СЫСОЕВ Илья Вячеславович
РЕКОНСТРУКЦИЯ УРАВНЕНИЙ
КОЛЕБАТЕЛЬНЫХ СИСТЕМ
ПРИ НАЛИЧИИ СКРЫТЫХ ПЕРЕМЕННЫХ
И ВНЕШНИХ ВОЗДЕЙСТВИЙ
Специальность 01.04.03 — радиофизика
Автореферат
диссертации на соискание учёной степени
кандидата физико-математических наук
Саратов 2007
Работа выполнена на кафедре динамического моделирования
и биомедицинской инженерии и кафедре электроники, колебаний и волн
Саратовского государственного университета им. Н.Г. Чернышевского,
а также в Саратовском филиале Института радиотехники и электроники РАН
Научный руководитель: доктор физико-математических наук,
профессор Безручко Борис Петрович
Официальные оппоненты: доктор физико-математических наук,
профессор Бутковский Олег Ярославович
кандидат физико-математических наук,
доцент Павлов Алексей Николаевич
Ведущая организация: Саратовский государственный
технический университет
Защита состоится 26 апреля 2007 года в 15 30 часов на заседании диссертационного совета Д 212.243.01 при Саратовском государственном университете им. Н.Г. Чернышевского (410023 Саратов, Астраханская, 83, корп. VIII, ауд. 73).
С диссертацией можно ознакомиться в Зональной научной библиотеке им. В.А. Артисевич Саратовского государственного университета им. Н.Г. Чернышевского.
Автореферат разослан « 19 » марта 2007 года.
Учёный секретарь
диссертационного совета,
доктор физико-математических наук В.М. Аникин
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы. Развитие концепции динамического хаоса продемонстрировало возможность описания сложных, в том числе хаотических, движений с помощью достаточно простых нелинейных уравнений, чем усилило интерес к реконструкции [1] моделей по дискретным последовательностям экспериментальных данных — временным рядам. Вид временного ряда имеют сигналы на выходе аналого-цифровых преобразователей (АЦП) измерительных приборов, бытовых цифровых устройств и компьютерных плат, данные метеорологических наблюдений и т. п. Построенные по рядам эмпирические модели, кроме традиционного использования для прогноза дальнейшего поведения или оценки адекватности представлений, предоставляют исследователю дополнительные возможности, в частности, выявления связей между элементами подсистем только по записям их колебаний, измерения в недоступных приборам точках объекта, кластеризации и т. д. Они служат средством решения значительного числа практически важных задач, среди которых: контроль или управление объектом, диагностика патологий, разбраковка устройств, конфиденциальная передача информации, измерение характеристик нелинейных элементов в режимах их эксплуатации (в частности, больших амплитуд и хаоса). Восстановленные по временным рядам модели используются в настоящее время в радиофизике, лазерной физике, биофизике и биологии (в частности, при изучении структуры и механизмов функционирования клетки), метеорологии, сейсмографии, экономике, медицине и физиологии, астрофизике и т. д.
Долгое время развитие алгоритмов реконструкции шло по пути создания универсальных методик, рассчитанных на широкий класс объектов [2]. Однако при их практическом применении возникают многочисленные и трудноразрешимые проблемы, главная причина которых — «проклятие размерности». Более успешными для решения конкретных практически важных задач являются специализированные алгоритмы, ориентированные на некоторый достаточно узкий класс систем или определённую ситуацию и опирающиеся на априорную или дополнительную информацию об объекте. В диссертационной работе рассматриваются две таких ситуации — наличие внешнего воздействия на объект и присутствие в модели скрытых переменных. Они часто встречаются при решении и фундаментальных и практически важных задач, что и определяет актуальность и важность темы диссертации.
Скрытыми называются те из общего числа 
переменных модели, временные ряды которых, необходимые при подгонке коэффициентов в процедуре реконструкции, отсутствуют, т.к. не могут быть измерены в принципе или не могут быть получены из рядов наблюдаемых величин из-за высокой зашумлённости. Популярным алгоритмом работы со скрытыми переменными является метод Бока (множественной стрельбы) [3], однако его применение для хаотических временных рядов затруднительно из-за чувствительности траектории на больших временах к малым изменениям начальных условий.
Известно несколько подходов и к реконструкции систем, находящихся под внешним воздействием, — неавтономных. Один из них предполагает возможность измерения рядов той же системы в автономном режиме, на основе которых восстанавливаются параметры модели, а затем уже по неавтономным реализациям реконструируется само воздействие [4]. Однако доступность рядов автономной системы — существенное и трудновыполнимое на практике требование, с одной стороны. С другой стороны, разработан подход, позволяющий учесть гармоническое воздействие, хотя и при произвольном способе его внесения [5]. Подход основан на введении в уравнения явной зависимости от времени и требуется его расширение на случай произвольного регулярного (периодического и квазипериодического) воздействия. Поскольку информация о виде воздействия имеется не всегда, а хаотическое или шумовое воздействие не может быть аппроксимировано в явном виде, требуется разрабатывать новые подходы к реконструкции произвольного внешнего воздействия и оценке параметров модели, когда её структура известна.
Целью диссертационной работы является исследование эффективности существующих алгоритмов реконструкции динамических систем по временным рядам сложных, в том числе и хаотических, колебаний при наличии скрытых переменных и внешнего воздействия, их модернизация и применение для решения практически важных задач.
Достоверность полученных результатов и выводов подтверждается их воспроизводимостью в численном, радиофизическом и биофизическом эксперименте и тем, что они опираются на теоретические результаты, полученные в самой работе, и базовые результаты нелинейной динамики и радиофизики.
Научная новизна работы состоит в следующем:
- Способ реконструкции неавтономных систем, использующий введение явной зависимости от времени в структуру уравнений, распространён на случай произвольного регулярного способа воздействия. На примере эталонной динамической системы — неавтономного осциллятора Тоды под воздействием сигналов различных форм и спектра — показано, что в типичном случае использование данного метода может привести к успеху, в то время как применение универсальных методик неэффективно.
- С помощью введённого количественного критерия сформулированы рекомендации по использованию методов множественной стрельбы реконструкции динамических систем при наличии скрытых переменных: условия на оптимальный выбор длины тренировочного ряда, способ его деления на сегменты и подсегменты, способ построения стартовых догадок для скрытых переменных.
- Проведено сравнение работоспособности различных реализаций метода множественной стрельбы. На численных примерах систем Лоренца и Рёсслера показано, что исходный алгоритм Бока уступает его модификации, заключающейся в допуске разрывов траектории модели при сохранении единых значений параметров.
- Предложен принципиально новый подход к реконструкции нелинейных систем под произвольным (в том числе хаотическим и шумовым) воздействием в случае, когда структура уравнений системы хорошо известна. Подход основывается на представлении внешнего воздействия в виде дополнительной скрытой переменной, написании для этой переменной собственного эволюционного уравнения и реконструкции полученной модифицированной системы методами работы со скрытыми переменными.
- На основе методов реконструкции неавтономных систем предложен способ измерения характеристик нелинейных устройств, отличающийся от уже существующих тем, что позволяет находить такие характеристики в произвольном режиме эксплуатации, в том числе и в сложных нелинейных режимах. Кроме того, способ позволяет получать характеристики, недоступные прямому измерению.
Теоретическая и практическая значимость результатов
- Предложена и апробирована на эталонных моделях нелинейной динамики модификация метода множественной стрельбы реконструкции при наличии скрытых переменных более эффективная, чем оригинальный алгоритм Бока. Метод позволяет использовать сколь угодно длинные временные ряды, что улучшает статистические свойства полученных оценок параметров, и задавать менее точные стартовые догадки для неизвестных параметров, что повышает шансы на успех моделирования.
- Возможности известного метода реконструкции неавтономных систем, основанного на введении в структуру модельных уравнений явной зависимости от времени, расширены на случай произвольного регулярного воздействия.
- Предложен новый метод восстановления внешнего воздействия, основанный на его представлении в виде дополнительной скрытой переменной. Метод применим в случае произвольного, в том числе хаотического и шумового, воздействия. Он может быть использован для решения различных прикладных задач, таких как: косвенное измерение, определение наличия связи или воздействия, а также для скрытой передачи и кодирования информации.
- Предложен новый метод измерения нелинейных характеристик радиотехнических устройств, основанный на их реконструкции по экспериментальным рядам токов и напряжений. Его преимущество перед существующими подходами состоит в том, что искомые характеристики могут измеряться в реальном эксплуатационном режиме. Также он может быть использован для кластеризации устройств по выбранной нелинейной характеристике.
Апробация результатов. Основные результаты диссертации были доложены на следующих конференциях: International Symposium «Topical problems of nonlinear wave physics» (Nizhny Novgorod, 2003), «The second international conference on circuits and systems for communication» (Moscow, 2004), «6th International School on Chaotic Oscillations and Pattern Formation» (Saratov, 2001), VII Международной школе-конференции «Хаотические автоколебания и образование структур» (Саратов, 2004), XII и XIII Всероссийских школах-конференциях «Нелинейные волны — 2004» и «Нелинейные волны — 2006» (Нижний Новгород), Международной научно-технической конференции «Радиотехника и связь» (Саратов, 2005), VII Всероссийской научной конференции «Нелинейные колебания механических систем» (Нижний Новгород, 2005), VI научной конференции «Нелинейные колебания механических систем» (Нижний Новгород, 2002), межвузовской конференции «Современные проблемы электроники и радиофизики СВЧ» (Саратов, 2001), научных школах-конференциях «Нелинейные дни в Саратове для молодых» (Саратов, 2000—2005).
Личный вклад автора. Основные результаты диссертации получены лично автором. В большинстве совместных работ автором выполнены все компьютерные расчёты, включая обработку экспериментальных данных, а в работах [3, 20, 23] расчёты, относящиеся к разделам, посвящённым реконструкции неавтономных систем и реконструкции при наличии скрытых переменных. Постановка задач, разработка методов их решения, выбор объектов, объяснение и интерпретация результатов были осуществлены совместно с руководителем и другими соавторами.
Структура и объём диссертации. Диссертация состоит из введения, четырёх глав, приложения, заключения и списка литературы из 110 наименований. Общий объём диссертации составляет 150 страниц, включая 51 рисунок.
Положения и результаты, выносимые на защиту.
- Модифицированный метод множественной стрельбы имеет больший радиус сходимости, чем оригинальный алгоритм Бока, если при его использовании делить тренировочный временной ряд на сегменты длиною порядка величины, обратной старшему ляпуновскому показателю.
- Метод реконструкции дифференциальных уравнений неавтономных систем по скалярным хаотическим временным рядам, основанный на введении явной зависимости оператора эволюции от времени, работоспособен и при произвольных периодическом и квазипериодическом воздействиях.
- Предложенный подход к восстановлению внешнего воздействия путём его перевода в разряд скрытых переменных не требует дополнительных измерений рядов автономной системы и предположений о характере воздействия, что открывает новые прикладные возможности.
- Разработан и запатентован способ измерения характеристик нелинейных устройств, основанный на использовании методов реконструкции неавтономных систем и позволяющий проводить измерения в произвольном эксплуатационном режиме.
КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ
Во введении даётся общая характеристика работы, обосновывается её актуальность, новизна и место диссертации в ряду работ по данной тематике, сформулированы положения, выносимые на защиту.
В первой главе рассматривается задача реконструкции по временным рядам в случае, когда структура модели может быть получена из общих принципов, но часть переменных модели не может быть измерена или сильно зашумлена. Такие переменные называют скрытыми. Их наличие сильно усложняет задачу, требуя использования специальных подходов, основанных на переносе тяжести задачи на этап подбора (оценки) параметров: в число оптимизируемых величин кроме искомых параметров вводят начальные условия.
Одним из наиболее перспективных в настоящее время является метод множественной стрельбы (алгоритм Бока). Его идея — снизить чувствительность к точности задания начальных условий 
на промежуточных этапах минимизации целевой функции путем разбиения исходного ряда на 
более коротких сегментов по 
точек (
). Далее задача сводится к минимизации целевой функции:
. (1).
Дополнительно накладывается условие непрерывности траектории модели:
. (2).
Хотя условие (2) полезно, т.к. уменьшает общее количество свободных параметров, оно ведёт к ограничению на максимальную длину ряда при реконструкции по хаотическим рядам, поскольку чувствительность к начальным условиям затрудняет поиск глобального минимума (1).
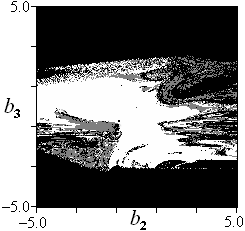
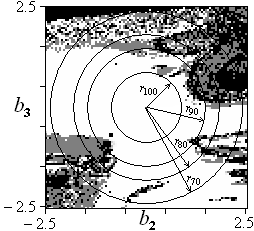
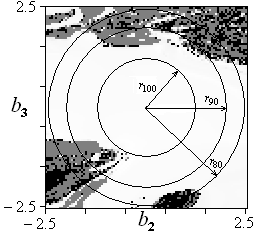
(а) (б) (в)
Рис. 1. Плоскость нормированных стартовых догадок для параметров системы Лоренца (сечение 
). Белым обозначены точки, откуда достигается глобальный минимум, оттенками серого — локальные минимумы, чёрным — алгоритм минимизации расходится: (a), (б) алгоритм Бока при 
, (в) модифицированный метод с 
.
Чтобы избежать этого, в данной работе предлагается отказаться от условия (2) в некоторые 
моментов времени. Такой подход назван модифицированным методом множественной стрельбы.
Для оценки эффективности методов был введён количественный критерий: в пространстве нормированных параметров 
строится круг (шар, гипершар) и в качестве меры 
берётся величина, равная радиусу круга, при котором вероятность сходимости в глобальный минимум (1) составляет 
(см. рис. 1).
С помощью этой меры на примере реконструкции эталонных систем нелинейной динамики показано, что модифицированный метод имеет ряд преимуществ по сравнению с алгоритмом Бока, поскольку он свободен от ограничений, связанных с высокой чувствительностью к начальным условиям: накапливающиеся вдоль фазовой траектории невязки отбрасываются в разрешенных этим подходом разрывах. Во-первых, он позволяет использовать ряды большой длины, что даёт возможность уточнить оценки параметров за счёт введения в рассмотрение дополнительного объёма данных, причём такие оценки статистически предпочтительнее, чем получаемые с помощью кусочного метода множественной стрельбы (когда параметры подгоняются независимо по нескольким рядам малой длины и затем усредняются). Во-вторых, при использовании рядов фиксированной длины он в большинстве случаев предъявляет меньшие требования к стартовым догадкам для искомых параметров (ср. рис. 1б и 1в), а иногда позволяет получить достаточно точные оценки, когда с помощью алгоритма Бока это невозможно сделать ни при каких стартовых догадках, даже равных истинным значениям.
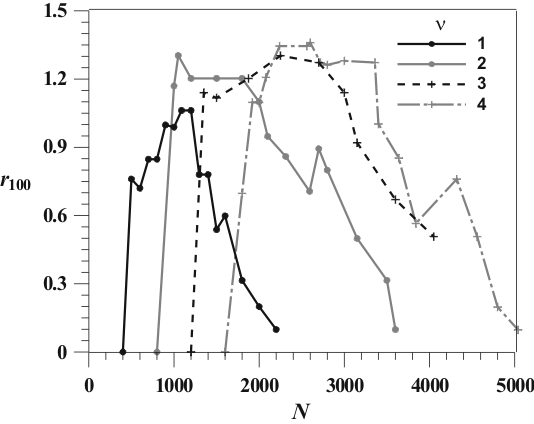
(а) (б)
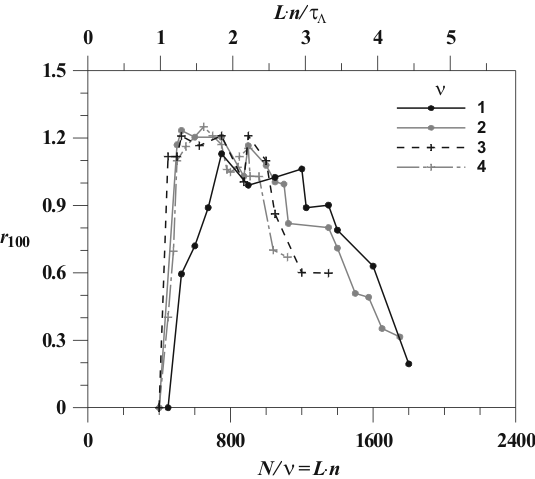
Рис. 2. Зависимость радиуса стопроцентной сходимости 
для системы Лоренца (а) — от общей длины используемого ряда 
при различном числе разрывов 
; (б) — от длины сегмента непрерывности 
.
Исследована степень влияния на результат оценивания параметров длины используемого ряда, количества его сегментов, выбора наблюдаемой и способа задания стартовых догадок для скрытых переменных. Показано, что шансы на успех оценки значений параметров возрастают с увеличением длины ряда, если одновременно увеличивается число допустимых разрывов траектории модели. При этом длина сегмента, на котором соблюдается требование непрерывности траектории, должна быть тем меньше и ближе к ляпуновскому времени, чем больше количество разрывов (рис. 2б).
Продемонстрировано, что стартовые догадки для скрытых переменных необходимо выбирать, основываясь на свойствах объекта, учитывая наиболее общие характеристики аттрактора. Игнорирование свойств объекта может привести к полному провалу, когда метод расходится даже для идеальных стартовых догадок для параметров.
Показано, что влияние шума (вплоть до 0.2 от уровня сигнала) на процесс моделирования несущественно для обеих методик. Следует сказать, что точность оценки параметров при условии попадания в глобальный минимум целевой функции и для выбранной длины ряда наибольшая для алгоритма Бока, предъявляющего самые жёсткие требования при подгонке, меньше для модифицированного метода, и ещё меньше для кусочного метода множественной стрельбы. Если же учесть, что попасть в глобальный минимум гораздо проще при использовании модифицированного метода, то он в итоге имеет практические преимущества даже в смысле точности оценок. Но следует учитывать и то, что, так как модифицированный метод предъявляет меньшие требования к адекватности используемой модели, существует опасность при слишком малом размере сегментов успешно подогнать под наблюдаемый ряд «чужую» модель.
Во второй главе рассматривается задача реконструкции неавтономных систем при регулярном воздействии. В случае, когда измерению доступна лишь одна наблюдаемая величина 
, стандартной структурой обычно является система дифференциальных уравнений (ОДУ):
(3),
где в качестве 
берется сама скалярная наблюдаемая 
, а функция 
представляется в виде степенного полинома порядка 
. Претензии таких моделей на общность теоретически обоснованы, однако случаи успешного применения стандартного подхода на практике единичны. Работоспособность стандартного подхода можно повысить за счет частичного отказа от универсальности и разработки методик (технологий), ориентированных на сравнительно узкий класс объектов, в данном случае — систем, находящихся под регулярным (имеющим дискретный спектр) внешним воздействием.
Модификация структуры (3) заключается во введении в неё явной зависимости от времени:
, (4),
где функция g(t), представляющая внешнее воздействие задаётся в виде тригонометрического полинома в периодическом случае и суммы тригонометрических полиномов в квазипериодическом. Для нахождения коэффициентов полинома 
и функции 
используем метод наименьших квадратов (МНК), минимизируя средний квадрат ошибки аппроксимации:
. (5).
Для апробирования методики были проведены реконструкции модельных ОДУ в стандартном и специальном видах по хаотическим временным рядам, полученным интегрированием неавтономного уравнения осциллятора Тоды:
, (6).
Рассматривались различные виды воздействия: периодическое гладкими импульсами, периодическое треугольными импульсами, периодическое с субгармониками основной частоты и квазипериодическое. Величины 
, 
и 
подбирались оптимальным образом. Критериями качества моделей выступали погрешности аппроксимации 
, дальность прогноза 
и сходство фазовых портретов модели и объекта.
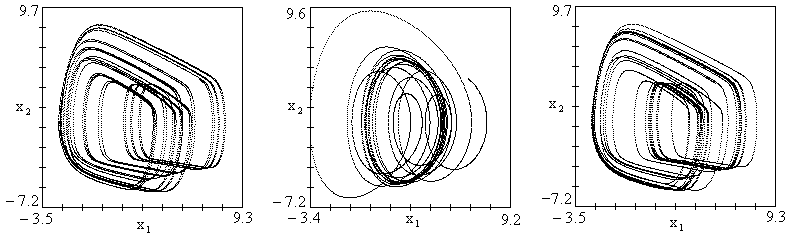
Стандартный алгоритм (3) не дает удовлетворительных результатов ни при одном из приведенных видах воздействия даже в отсутствие шумов (рис. 3б), тогда как модернизированная структура (3, 4) при достаточном количестве учтённых гармоник обеспечивает хорошее качество реконструкции (рис. 3в), в том числе и при наличии шумов, хотя получение оптимальной модели в этом случае требует значительно большей длины тренировочного ряда.
(а) (б) (в)
Рис. 3. Фазовые портреты: (а) — объекта (6) и реконструированных по ряду переменной 
моделей (б) — стандартным методом, (в) — модифицированным методом.
Усложнение формы воздействия заставляет увеличивать число членов тригонометрического полинома, но это остается без негативных последствий, тогда как глобальная неустойчивость стандартных моделей с алгебраическими полиномами высоких порядков была главной причиной неудач стандартного подхода. Так, воздействие в виде треугольных импульсов потребовало учесть весьма большое, порядка 80––90, число членов ряда. Проводились успешные эксперименты с использованием даже 300––500 гармоник.
Присутствие субгармоник во внешнем воздействии не представляет никаких новых трудностей, если в качестве базовой частоты принять наименьшую из частот субгармоник. Чтобы найти эту частоту, необходимо перебирать стартовые догадки для периода воздействия, в качестве которых следует в первую очередь брать величины, кратные периоду, соответствующему основному пику в спектре наблюдаемой.
При квазипериодическом воздействии неавтономная модель продемонстрирует очень хорошее соответствие объекту — фазовые траектории объекта и модели визуально неотличимы. Основная сложность работы с несколькими тригонометрическими полиномами состоит в том, что периоды двух высоких гармоник из разных полиномов на некотором этапе итерационной процедуры могут оказаться столь близкими, что это приведёт к вырожденной или очень плохо обусловленной матрице при решении задачи оценки линейно входящих параметров. Поэтому приходится уменьшать числа членов ряда и очень точно задавать начальные догадки.
В третьей главе предложена и апробирована новая методика реконструкции внешнего воздействия и оценки параметров неавтономных систем. Она заключается в представлении воздействия в виде дополнительной скрытой переменной и преобразования структуры модели к такому виду, что в модифицированной неавтономной системе члены, соответствующие воздействию, могут быть найдены из наблюдаемых величин (не являются скрытыми). Искомая временная реализация восстанавливается вместе с подгонкой коэффициентов в процессе реконструкции получившейся модифицированной системы. Это приводит к увеличению размерности искомой модели, но освобождает от необходимости знания временного ряда автономной системы.
В достаточно общем виде неавтономная модельная система имеет вид:
(7),
где yi — динамические переменные, компоненты вектора 
, ряды которых получают из рядов наблюдаемых, 
— вектор параметров, fi — заданные функции, 
— искомое внешнее воздействие. Пусть 
-тое уравнение, в которое входит воздействие, однозначно разрешено относительно него:
(8).
Представим 
новой 
-й переменной 
, которая, т.к. воздействие не известно, является скрытой. Дополнительное уравнение для 
получается дифференцированием (8) по времени. Наиболее просто это реализуется в случае аддитивного воздействия, когда (8) принимает вид
(9),
а (7) сводится к:
(10).
Несмотря на то, что последнее уравнение системы (10) имеет первый порядок, оно может иметь сложное решение, поскольку является неавтономным, а роль внешнего воздействия играет 
. Для подгонки параметров ряд 
получается численный дифференцированием ряда 
, также, поскольку все функции 
задавались при выборе структуры, функция 
находится аналитически, а её временной ряд — подсчитывается с использованием рядов нескрытых переменных.
(а) (б)
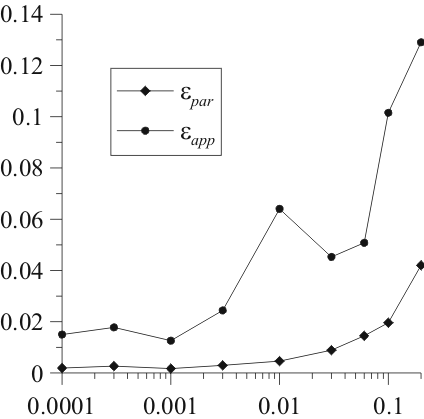
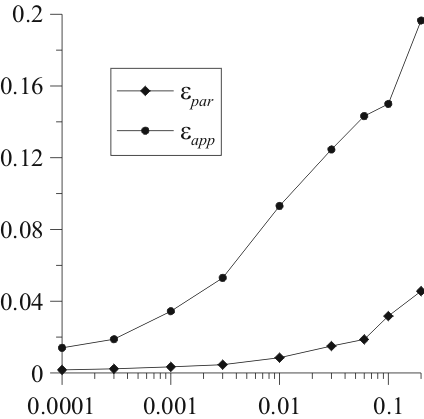
Рис. 4. Зависимости ошибки аппроксимации 
и ошибки в оценке параметров 
при различных автономных режимах воздействуемой системы: (а) периодическом, (б) хаотическом.
Работоспособность предложенного подхода продемонстрирована на примерах реконструкции эталонных систем в различных ситуациях. Показано, что метод успешно работает при различной собственной динамике изучаемой системы: при периодической и хаотической, а также при различных видах воздействия: хаотическом (сигнал детерминированной системы) и шумовом (реализация случайного процесса) (см. рис. 4). Хотя при использовании метода необходимо численно рассчитывать по ряду вторую производную, что приводит к увеличению влияния шумов, этот негативный эффект удаётся значительно снизить, если применять к исходному ряду фильтрацию, проводить дифференцирование с использованием сглаживающего полинома, а восстановленное воздействие дополнительно фильтровать. Такой подход позволяет получать соответствие между восстановленным и исходным сигналом воздействия даже при 10%-ном шуме (см. рис. 5).
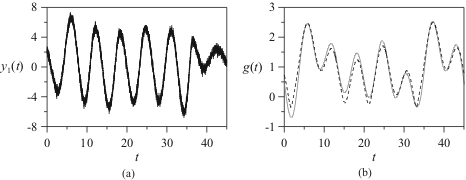
Рис. 5. Графики (a) — исходного сигнала 
и (b) — внешнего воздействия исходного (чёрный пунктир) и восстановленного (серая сплошная линия) при уровне шума 10%.
Дополнительно показано, что предложенный подход может работать и в ситуации, когда не все переменные исследуемой системы доступны измерению, хотя, конечно, шансы на успех в таком случае снижаются.
Обсуждается возможность применения предложенного метода для решения ряда задач, таких как: косвенное измерение величин, недоступных прямому измерению, определение наличия связи между системами или внешнего воздействия на изучаемую систему, скрытая передача или кодирование информации либо приём сигнала в системах связи на хаотической несущей. Последнее приложение демонстрируется на эталонном примере.
В четвёртой главе представлены экспериментальные результаты приложения методов реконструкции по временным рядам неавтономных систем к измерению характеристик и разбраковке полупроводниковых устройств, а также для проверки адекватности моделей биологических объектов: голосовых связок человека и системы регуляции давления в нефроне (функциональная единица почки).
Суть предложенного способа заключается в следующем. Составляется эквивалентное представление исследуемого устройства таким образом, чтобы в него непосредственно вошла искомая характеристика. Например, для диодов с p-n переходом это может быть схема из параллельно и последовательно соединённых нелинейных и линейных элементов: ёмкостей, сопротивлений, индуктивностей, источников тока или напряжения и т. п. Затем для составленного эквивалентного представления на основе законов Кирхгофа необходимо записать уравнения. Эти уравнения представляют собою модель. Одновременно на исследуемое устройство подаётся воздействие, в точности совпадающее с воздействием в его реальном режиме функционирования. Далее снимаются и оцифровываются ряды протекающих через него токов и напряжений на нём — они выступают в роли экспериментальных временных рядов (наблюдаемых). С помощью методов реконструкции уравнения модели восстанавливаются по этим рядам.
Способ обладает двумя преимуществами перед ранее известными: он позволяет измерять искомые характеристики непосредственно в режиме эксплуатации, а также получать величины, недоступные прямому измерению.
Подход был апробирован на примере измерения вольтфарадных характеристик кремниевых выпрямительных диодов типа КД202Р. Для проверки адекватности предложенного метода в режимах малых амплитуд использовались приборы Е7-8 и Е7-12, работающие на частотах 1кГц и 1МГц соответственно.
Продемонстрирована возможность приложения способа для кластеризации устройств на основании интересующей нелинейной характеристики, для чего восстанавливаются искомые характеристики всех устройств и затем подсчитывается интегральная мера сходства в заданном диапазоне. Результаты удобно представить в графическом (рис. 6), где по осям отложены номера устройств, так что каждая клетка соответствует паре образцов, а интенсивностью серого показана степень совпадения характеристик: чем темнее клетка, тем они ближе (диагональ соответствует сравнению образца с самим собою и потому всегда чёрная). В представленном на рис. 6 примере легко можно определить самую близкую пару: это диоды №27 и №43.
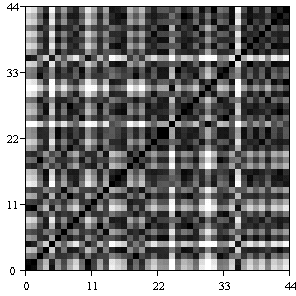
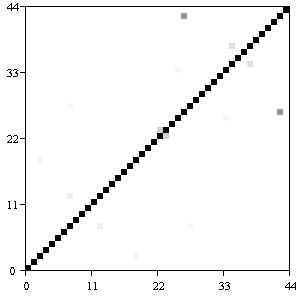
Рис. 6. Результаты кластеризации диодов типа КД202Р, где различными оттенками серого показана величина, характеризующая степень совпадения вольтфарадных характеристик.
Второй рассмотренный пример экспериментального приложения — к оценке адекватности моделей голосовых связок человека по экспериментальным рядам. Несмотря на их сложность: большое количество переменных, параметров и сложный тип нелинейностей, — их реконструкция по временным рядам возможна даже в случае, когда часть переменных являются скрытыми. Однако при этом нужно существенно ограничить число неизвестных параметров тремя-четырьмя наиболее важными, зафиксировав остальные из физиологических соображений, а также специально подобрать стартовые догадки для скрытых переменных, что требует дополнительного изучения реконструируемой системы.
В третьем примере решается задача реконструкции модели нефрона (функциональной единицы почки) по временным рядам. С помощью метода множественной стрельбы оказалось в принципе возможно оценить параметры модели, если зафиксировать большинство из них равными типичным значениям. Модель успешно восстановлена по регулярному ряду и демонстрировала периодический аттрактор. Однако несовершенство модели и недостаток экспериментальных данных препятствуют успешному решению этой задачи в целом: не удаётся реконструкция по хаотическим рядам, а при по регулярным рядам возможно оценить только небольшое количество параметров модели (1, реже 2).
В заключении сформулированы основные результаты и выводы работы.
ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ
- На основании введённого количественного критерия проведено сравнение работоспособности различных реализаций метода множественной стрельбы. Показано, что исходный алгоритм Бока уступает модифицированному методу, допускающему разрывы модельной траектории, поскольку последний позволяет работать с более длинными рядами и имеет больший радиус сходимости. Показано, что шансы на успех оценки значений параметров возрастают с увеличением длины ряда, если одновременно увеличивается число допустимых разрывов траектории модели таким образом, чтобы длина одного сегмента составляла порядка величины, обратной старшему ляпуновскому показателю. Влияние шума (вплоть до 0.2 от уровня сигнала) на процесс моделирования несущественно, особенно для модифицированного метода.
- Стандартный алгоритм реконструкции не позволяет построить адекватную модель ни при каком из рассмотренных видов воздействия даже в отсутствие шумов, тогда как модернизированная структура, где воздействие учитывается введением в уравнения явной функции времени в виде тригонометрического полинома, при достаточном количестве учтённых гармоник обеспечивает хорошее качество реконструкции. При наличии измерительных шумов получение оптимальной модели требует увеличения длины тренировочного ряда. Наличие субгармоник во внешнем воздействии не представляет никаких новых трудностей, если в качестве базовой частоты принять наименьшую из их частот. При квазипериодическом воздействии модифицированная структура сохраняет работоспособность, если использовать несколько тригонометрических полиномов по числу несоизмеримых частот в спектре воздействия.
- В третьей главе предложен новый подход к восстановлению произвольного гладкого, в том числе хаотического и шумового воздействия на динамическую систему. Он позволяет оценить параметры системы и получить сигнал внешнего воздействия, если известна структура объекта моделирования и наблюдаются некоторые (не обязательно все) переменные. В последнем случае восстанавливаются также ряды недостающих переменных. Подход апробирован на примерах реконструкции эталонных систем моделей при различной собственной динамике: как периодической, так и хаотической, а также различных видах воздействия: хаотическом (сигнал детерминированной системы) и шумовом (реализация случайного процесса). Показано, что подход устойчив к аддитивному шуму амплитудою до 10%, если при дифференцировании использовать сглаживающий полином, а полученное воздействие дополнительно фильтровать.
- Предложен новый способ измерения нелинейных характеристик полупроводниковых устройств, основанный на реконструкции уравнений Кирхгофа по экспериментальным реализациям тока и напряжения и позволяющий проводить измерения в условиях последующей эксплуатации. Он апробирован на задаче измерения вольтфарадных и вольтамперных характеристик полупроводникового диода с p-n переходом. Рассмотрены различные способы аппроксимации искомых характеристик и показано, что оптимальный выбор аппроксимирующих функций зависит от конкретной задачи. Продемонстрирована возможность приложения способа для кластеризации устройств по интересующей нелинейной характеристике.
СПИСОК РАБОТ ПО ТЕМЕ ДИССЕРТАЦИИ
- Безручко Б.П., Смирнов Д.А., Сысоев И.В. Реконструкция при наличии скрытых переменных: модифицированный алгоритм Бока // Изв. вузов, «ПНД». — 2004. Т. 12. № 6. — С. 93—104.
- Безручко Б.П., Смирнов Д.А., Сысоев И.В. Реконструкция уравнений регулярно возбуждаемых динамических систем по временному ряду // Тезисы доклада «Нелинейные колебания механических систем: VI научная конференция». — Н. Новгород, 2002. — С. 22—23.
- Некоторые проблемы реконструкции модельных уравнений по временным рядам и пути их решения / Б.П. Безручко, М.Б. Бодров, Т.В. Диканев, А.С. Караваев, В.И. Пономаренко, М.Д. Прохоров, Е.П. Селезнев, И.В. Сысоев, Д.А. Смирнов // Нелинейные волны 2004 / Под. ред. А.В. Гапонова-Грехова, В.И. Некоркина. — Н. Новгород: ИПФ РАН, 2005. — С. 381—397.
- Оценка эквивалентных параметров полупроводниковых элементов в режиме больших амплитуд и хаоса / И.В. Сысоев, Д.А. Смирнов, Е.П. Селезнёв, Б.П. Безручко // Сборник материалов XII Всероссийской школы-конференции «Нелинейные волны — 2004». — Н. Новгород, 2004. — С. 112—113.
- Патент на изобретение №2004115469/28(016733). Способ определения характеристик нелинейных устройств / Б.П. Безручко, Е.П. Селезнёв, Д.А. Смирнов, И.В. Сысоев. МПК 7 G 01 R 27/08, 31/27.
- Реконструкция моделей голосовых связок / И.В. Сысоев, А.С. Ульянов, О.В. Мареев, Б.П. Безручко // Сборник материалов XIII Всероссийской школы-конференции «Нелинейные волны — 2006». — Н. Новгород, 2006. — С. 151—152.
- Реконструкция нелинейных характеристик и эквивалентных параметров по экспериментальным временным рядам / И.В. Сысоев, Д.А. Смирнов, Е.П. Селезнёв, Б.П. Безручко // Сборник трудов Международной научно-технической конференции «Радиотехника и связь». — Саратов, 2005. — С. 114—117.
- Реконструкция эквивалентных характеристик нелинейных полупроводниковых устройств по временным рядам / И.В. Сысоев, Е.П. Селезнёв, Д.А. Смирнов, Б.П. Безручко // Сборник материалов VII Международной школы-конференции «Хаотические автоколебания и образование структур». — Саратов, 2004. — С. 114—116.
- Смирнов Д.А., Сысоев И.В., Селезнёв Е.П., Безручко Б.П. Реконструкция моделей неавтономных систем с дискретным спектром воздействия // Письма в ЖТФ. — 2003. Т. 29. Вып. 19. — С. 69—76.
- Сысоев И.В. Виды модельных отображений и их описательные возможности // Сборник материалов научной школы-конференции «Нелинейные дни в Саратове для молодых — 2000». — Саратов: Изд-во ГосУНЦ «Колледж», 2000. — С. 127—130.
- Сысоев И.В. Захаревич А.М. Эквивалентные представления полупроводникового диода и оценка характеристик этих эквивалентных представлений методами реконструкции по временным рядам // Сборник материалов научной школы-конференции «Нелинейные дни в Саратове для молодых — 2003». — Саратов: Изд-во ГосУНЦ «Колледж», 2003. — С. 258—261.
- Сысоев И.В. Изучение эффективности алгоритма Бока и его модификации для реконструкции по хаотическим временным рядам // Сборник материалов научной школы-конференции «Нелинейные дни в Саратове для молодых — 2004». — Саратов: Изд-во ГосУНЦ «Колледж», 2004. — С. 74—77.
- Сысоев И.В. Моделирование неавтономных систем по временному ряду // Сборник материалов научной школы-конференции «Нелинейные дни в Саратове для молодых — 2001». — Саратов: Изд-во ГосУНЦ «Колледж», 2001. — С. 98—101.
- Сысоев И.В. Применение алгоритма множественной стрельбы для эмпирического моделирования динамики нефрона // Сборник материалов научной школы-конференции «Нелинейные дни в Саратове для молодых — 2002». — Саратов: Изд-во ГосУНЦ «Колледж», 2002. — С. 46—49.
- Сысоев И.В. Реконструкция модельных отображений по хаотическим временным рядам // Материалы межвузовской конференции «Современные проблемы электроники и радиофизики СВЧ». — Саратов, 2001. — С. 150—151.
- Сысоев И.В., Смирнов Д.А., Безручко Б.П. Реконструкция моделей хаотических систем при наличии скрытых переменных по временным рядам // Сборник материалов VII Международной школы-конференции «Хаотические автоколебания и образование структур». — Саратов, 2004 — С. 113—114.
- Сысоев И.В., Смирнов Д.А., Безручко Б.П. Реконструкция при наличии скрытых переменных (модифицированный алгоритм Бока) // Труды VII Всероссийской научной конференции «Нелинейные колебания механических систем». — Н. Новгород, 2005. — С. 204—206.
- Bezruchko B.P., Mosekilde E., Smirnov D.A., Sysoev I.V. Reconstruction of multidimensional multiparametric model equations from time series using Bock’s algorithm (applications to single nephron model and physiological nephron data) // Proceedings of International Symposium «Topical problems of nonlinear wave physics». — Nizhny Novgorod, Russia, 2003. — P. 42—43.
- Bezruchko B.P., Smirnov D.A., and Sysoev I.V. Reconstruction of model equations of nonautonomous systems under regular driving // Abstracts of the «6th International School on Chaotic Oscillations and Pattern Formation». — Saratov, Russia, 2001. — P. 17—18.
- Construction of dynamical model equations for nonautonomous systems from time series (peculiarities and special approaches) / Boris Bezruchko, Dmitry Smirnov, Taras Dikanev, and Ilya Sysoev // Chaos and its Reconstruction / Edited by G. Gouesbet and S. Meunier-Guttin-Cluzel. — Nova Science Publishers, 2003. — P. 215—243.
- Identification of chaotic systems with hidden variables (modified Bock’s algorithm) / Boris P. Bezruchko, Dmitry A. Smirnov and Ilya V. Sysoev // Chaos, Solitons & Fractals Vol. 29 (2006). P. 82—90.
- Reconstruction of nonlinear characteristics and equivalent parameters from experimental time series / Ilya V. Sysoev, Dmitry A. Smirnov, Yeugeny P. Seleznev, and Boris P. Bezruchko // Proceedings of «The second international conference on circuits and systems for communication». –– Moscow, Russia, 2004. –– 3 p.
- Special Approaches to Global Reconstruction of Equations from Time Series / B.P. Bezruchko, Ye.P. Seleznev, V.I. Ponomarenko, M.D. Prokhorov, D.A. Smirnov, T.V. Dikanev, I.V. Sysoev, A.S. Karavaev // Izv. VUZ. «AND». — 2002. Vol. 10. № 3. — P. 137—158.
Научное издание
Сысоев Илья Вячеславович
РЕКОНСТРУКЦИЯ УРАВНЕНИЙ
КОЛЕБАТЕЛЬНЫХ СИСТЕМ
ПРИ НАЛИЧИИ СКРЫТЫХ ПЕРЕМЕННЫХ
И ВНЕШНИХ ВОЗДЕЙСТВИЙ
Автореферат
В авторской редакции
Подписано в печать 12.03.2007. Формат 60Ч84 1/16.
Бумага офсетная. Гарнитура Times New Roman.
Печать офсетная. Усл. печ. л. 1,16. Уч.-изд. л. 1,31.
Тираж 100 экз. Заказ № С
Отпечатано с готового оригинал-макета
Типография Поволжского межрегионального учебного центра
410033, Саратов, ул. Международная, 34
[1] Так называют построение модели по экспериментальным данным в нелинейной динамике, в статистике используется термин «идентификация систем».
[2] Gouesbet G. and Letellier C. Global vector-field approximation by using a multivariate polynomial approximation on nets. Phys. Rev. E. 1994. Vol. 49. P. 4955––4972.
[3] Baake E., Baake M., Bock H.G., and Briggs K.M. Fitting ordinary differential equations to chaotic data // Phys. Rev. A. 1992. Vol. 45. № 8. P. 5524––5529.
[4] Грибков Д.А., Грибкова В.В., Кравцов Ю.А. и др. Б. н. // Радиотехника и электроника. 1994. 39. № 2. С. 231.
[5] Bezruchko B.P. and Smirnov D.A. Constructing of nonautonomous differential equations from experimental time series, Phys. Rev. E. 2000. Vol. 63. 016207.
