Электрон-фононное взаимодействие в смешанной электронной конфигурации редкоземельных ионов в диэлектрических кристаллах
111На правах рукописи
Соловьев Олег Валерьевич
ЭЛЕКТРОН-ФОНОННОЕ ВЗАИМОДЕЙСТВИЕ В СМЕШАННОЙ ЭЛЕКТРОННОЙ КОНФИГУРАЦИИ ![]() РЕДКОЗЕМЕЛЬНЫХ ИОНОВ В ДИЭЛЕКТРИЧЕСКИХ КРИСТАЛЛАХ
РЕДКОЗЕМЕЛЬНЫХ ИОНОВ В ДИЭЛЕКТРИЧЕСКИХ КРИСТАЛЛАХ
01.04.02 – Теоретическая физика
Автореферат
диссертации на соискание ученой степени
кандидата физико-математических наук
Казань – 2009
Работа выполнена на кафедре теоретической физики Казанского государственного университета им. В.И. Ульянова-Ленина.
Научный руководитель: доктор физико-математических наук,
профессор Малкин Борис Залманович
Официальные оппоненты: доктор физико-математических наук,
профессор Никифоров Анатолий Елиферьевич
(Уральский госуниверситет им. А.М. Горького)
доктор физико-математических наук,
профессор Садыков Эдгар Камилович
Ведущая организация: Казанский физико-технический институт им. Е.К. Завойского КазНЦ РАН
Защита состоится 24 декабря 2009 г. в 14:30 на заседании диссертационного совета Д.212.081.15 при Казанском государственном университете по адресу: 420008, г. Казань, ул. Кремлевская, 18.
С диссертацией можно ознакомиться в научной библиотеке имени Н.И. Лобачевского Казанского государственного университета.
Автореферат разослан 20 ноября 2009 г.
Ученый секретарь
диссертационного совета
д. ф.-м. н., профессор Еремин М. В.
Общая характеристика работы
Актуальность темы исследования. Спектроскопия смешанных электронных конфигураций ![]() начала складываться в середине XX-го века, что явилось естественным этапом в развитии спектроскопии кристаллов, активированных редкоземельными (РЗ) ионами. Большая часть термов смешанных
начала складываться в середине XX-го века, что явилось естественным этапом в развитии спектроскопии кристаллов, активированных редкоземельными (РЗ) ионами. Большая часть термов смешанных ![]() конфигураций может наблюдаться лишь в ультрафиолетовой (УФ) и вакуумной ультрафиолетовой (ВУФ) областях спектра, где число прозрачных основ ограничено, что обусловливает экспериментальные трудности изучения смешанных конфигураций. Интерпретация оптических
конфигураций может наблюдаться лишь в ультрафиолетовой (УФ) и вакуумной ультрафиолетовой (ВУФ) областях спектра, где число прозрачных основ ограничено, что обусловливает экспериментальные трудности изучения смешанных конфигураций. Интерпретация оптических ![]() спектров осложняется тем, что большая часть интенсивности приходится на электронно-колебательные полосы, как следствие взаимодействия
спектров осложняется тем, что большая часть интенсивности приходится на электронно-колебательные полосы, как следствие взаимодействия ![]() электрона с колебаниями решетки.
электрона с колебаниями решетки.
В настоящее время проявляется значительный интерес к твердотельным материалам с оптической активностью в УФ и ВУФ областях спектра, связанный с тремя важными применениями, ставшими особенно актуальными в последние годы: лазеры УФ и ВУФ диапазона, быстрые сцинтилляторы, люминофоры. Получены экспериментальные данные по ![]() спектрам поглощения и люминесценции для большинства РЗ ионов в различных кристаллических решетках (см., например, [1]). Предложен метод расчета, позволяющий успешно воспроизводить энергии и интенсивности
спектрам поглощения и люминесценции для большинства РЗ ионов в различных кристаллических решетках (см., например, [1]). Предложен метод расчета, позволяющий успешно воспроизводить энергии и интенсивности ![]() переходов в примесных двух- и трехвалентных РЗ ионах [2,3].
переходов в примесных двух- и трехвалентных РЗ ионах [2,3].
Моделирование электронно-колебательных полос в ![]() спектрах в литературе по существу не проводилось, полосы аппроксимировались гауссовыми кривыми с произвольно варьируемыми характеристиками [1,3]. В настоящем исследовании была поставлена задача восполнить указанный пробел.
спектрах в литературе по существу не проводилось, полосы аппроксимировались гауссовыми кривыми с произвольно варьируемыми характеристиками [1,3]. В настоящем исследовании была поставлена задача восполнить указанный пробел.
Сравнение результатов вычислений ![]() спектров РЗ ионов с данными измерений стимулировало постановку еще одной задачи: получить формулы, позволяющие вычислять электронно-колебательные полосы в спектрах поглощения и люминесценции примесных центров в кристаллах при нарушении «кондоновского» приближения.
спектров РЗ ионов с данными измерений стимулировало постановку еще одной задачи: получить формулы, позволяющие вычислять электронно-колебательные полосы в спектрах поглощения и люминесценции примесных центров в кристаллах при нарушении «кондоновского» приближения.
Цели работы:
- получить аналитические выражения для формы электронно-колебательных полос в оптических спектрах примесных центров в кристаллах при низких температурах в случае нарушения «кондоновского» приближения;
- разработать методику вычисления электронно-колебательных полос в оптических спектрах межконфигурационных
 переходов в примесных РЗ ионах, внедренных в диэлектрический кристалл;
переходов в примесных РЗ ионах, внедренных в диэлектрический кристалл; - выполнить расчеты электронно-колебательных
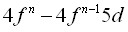 спектров кристаллов LiYF4:Ce3+, LiYF4:Lu3+, CaF2:Tm2+ и выяснить основные механизмы формирования этих спектров из сопоставления результатов вычислений с данными измерений.
спектров кристаллов LiYF4:Ce3+, LiYF4:Lu3+, CaF2:Tm2+ и выяснить основные механизмы формирования этих спектров из сопоставления результатов вычислений с данными измерений.
Научная новизна и положения, выносимые на защиту:
- В работе впервые получены аналитические выражения для форм-функций поглощения и люминесценции оптических центров в кристаллах при нулевой температуре в случае нарушения «кондоновского» приближения.
- Доказано свойство: если оптический переход запрещен в «кондоновском» приближении по симметрии, то «некондоновские» форм-функции поглощения и люминесценции зеркально симметричны, и в них отсутствуют бесфононные линии.
- Разработана методика вычисления электронно-колебательных полос в оптических спектрах межконфигурационных
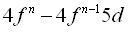 переходов в примесных РЗ ионах, основанная на использовании реального спектра колебаний кристаллической решетки и модели обменных зарядов.
переходов в примесных РЗ ионах, основанная на использовании реального спектра колебаний кристаллической решетки и модели обменных зарядов. - Впервые выполнен расчет тонкой структуры спектров поглощения (возбуждения) и люминесценции, обусловленных
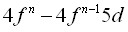 переходами ионов Ce3+ и Lu3+ в кристалле LiYF4, иона Tm2+ в кристалле CaF2. Получено объяснение того, что в спектре поглощения кристалла LiYF4:Ce3+ бесфононная линия наблюдается только в полосе, отвечающей переходу на основной
переходами ионов Ce3+ и Lu3+ в кристалле LiYF4, иона Tm2+ в кристалле CaF2. Получено объяснение того, что в спектре поглощения кристалла LiYF4:Ce3+ бесфононная линия наблюдается только в полосе, отвечающей переходу на основной 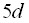 уровень: этот переход имеет наименьший параметр Хуана-Рис среди всех
уровень: этот переход имеет наименьший параметр Хуана-Рис среди всех 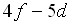 переходов в ионе Ce3+. Получено объяснение того, что в измеренных спектрах возбуждения и люминесценции кристалла LiYF4:Lu3+ на переходах с участием нижних состояний возбужденной конфигурации иона Lu3+ отсутствуют бесфононные линии: показано, что эти переходы запрещены по симметрии, так что бесфононные линии в спектрах отсутствуют в согласии с положением 2.
переходов в ионе Ce3+. Получено объяснение того, что в измеренных спектрах возбуждения и люминесценции кристалла LiYF4:Lu3+ на переходах с участием нижних состояний возбужденной конфигурации иона Lu3+ отсутствуют бесфононные линии: показано, что эти переходы запрещены по симметрии, так что бесфононные линии в спектрах отсутствуют в согласии с положением 2.
Научная и практическая значимость работы. Построенная теория электронно-колебательных оптических спектров примесных центров при нарушении «кондоновского» приближения и разработанная методика расчета электронно-колебательных полос в оптических спектрах межконфигурационных ![]() переходов в примесных РЗ ионах открывают возможность корректной интерпретации
переходов в примесных РЗ ионах открывают возможность корректной интерпретации ![]() спектров РЗ ионов, необходимой для прогнозирования характеристик перспективных лазеров и сцинтилляторов в ВУФ области спектра электромагнитного излучения. Основные результаты работы были получены при выполнении проектов РНП 2.1.1.7348 и 2.1.1/2985 Министерства образования и науки Российской Федерации и 09-02-00930 РФФИ.
спектров РЗ ионов, необходимой для прогнозирования характеристик перспективных лазеров и сцинтилляторов в ВУФ области спектра электромагнитного излучения. Основные результаты работы были получены при выполнении проектов РНП 2.1.1.7348 и 2.1.1/2985 Министерства образования и науки Российской Федерации и 09-02-00930 РФФИ.
Личный вклад автора. Автору принадлежит вывод аналитических выражений для производящих функций и форм-функций поглощения и люминесценции оптических центров в кристаллах при нулевой температуре в случае нарушения «кондоновского» приближения, а также их теоретико-групповой анализ, включая формулировку условий наблюдения в спектре бесфононной линии. Автору принадлежат все результаты расчетов, изложенные в диссертации, за следующими исключениями: расчет полного закона дисперсии фононов и функций Грина кристаллической решетки LiYF4 проведен Сайкиным С.К.; расчет уровней энергии и волновых функций иона Tm2+ проведен автором с использованием компьютерной программы, написанной Малышевым А.Ю.
Апробация работы. Результаты работы были представлены в докладах на международной конференции «Фундаментальные проблемы физики», Казань, 2005; международной конференции «Symposium on the Jahn-Teller effect», Триест, Италия, 28-31.08.2006; итоговых конференциях по научно-исследовательской деятельности Казанского государственного университета за 2006 и 2007 гг.
Публикации. Основное содержание работы опубликовано в 5 статьях (в том числе в журналах Physical Review B, Journal of Luminescence, Journal of Molecular Structure) и 2 тезисах конференций.
Структура диссертации. Диссертация состоит из введения, пяти глав, заключения, приложений А и Б, списка работ автора по теме диссертации, списка цитируемой литературы, включающего 56 наименований. Работа изложена на 134 страницах, содержит 32 рисунка и 7 таблиц.
Основное содержание диссертации
Во введении обосновываются актуальность диссертационной работы, ее научная и практическая значимость, формулируются цели исследования и положения, выносимые на защиту.
В обзорной первой главе описывается принятая в диссертации модель примесно-колебательной системы, излагаются основы теории электронно-колебательных оптических спектров примесных центров [4].
Рассматриваемый гамильтониан примесно-колебательной системы представляет собой сумму трех слагаемых: гамильтониана ![]() оптических электронов примесного парамагнитного центра, включающего энергию взаимодействия электронов со статическим кристаллическим полем; гамильтониана
оптических электронов примесного парамагнитного центра, включающего энергию взаимодействия электронов со статическим кристаллическим полем; гамильтониана ![]() колебательной подсистемы в гармоническом приближении (совокупность нормальных координат будем обозначать
колебательной подсистемы в гармоническом приближении (совокупность нормальных координат будем обозначать ![]() ); гамильтониана
); гамильтониана ![]() электронно-колебательного взаимодействия, линейного по нормальным координатам колебательной подсистемы. Собственные значения
электронно-колебательного взаимодействия, линейного по нормальным координатам колебательной подсистемы. Собственные значения ![]() и собственные функции
и собственные функции ![]() гамильтониана
гамильтониана ![]() считаются известными. Используется адиабатическое приближение; для вырожденных электронных состояний учитывается взаимодействие только с колебаниями, операторы взаимодействия с которыми имеют на этих состояниях нулевые матрицы либо матрицы, пропорциональные единичной. Частотный эффект не учитывается.
считаются известными. Используется адиабатическое приближение; для вырожденных электронных состояний учитывается взаимодействие только с колебаниями, операторы взаимодействия с которыми имеют на этих состояниях нулевые матрицы либо матрицы, пропорциональные единичной. Частотный эффект не учитывается.
Рассматривается поглощение и излучение света примесно-колебательной системой на переходе между электронными состояниями ![]() . С точностью до множителей, медленно меняющихся с частотой света
. С точностью до множителей, медленно меняющихся с частотой света ![]() , зависимость интенсивности поглощения (люминесценции) от
, зависимость интенсивности поглощения (люминесценции) от ![]() определяется форм-функцией [4], представляющей собой линейную комбинацию сил линий переходов между состояниями примесно-колебательной системы. Электронно-колебательным взаимодействием в нижнем по энергии состоянии а пренебрегается (это приближение с хорошей точностью выполняется в случае межконфигурационных переходов
определяется форм-функцией [4], представляющей собой линейную комбинацию сил линий переходов между состояниями примесно-колебательной системы. Электронно-колебательным взаимодействием в нижнем по энергии состоянии а пренебрегается (это приближение с хорошей точностью выполняется в случае межконфигурационных переходов ![]() ). Уравнение для электронной подсистемы решается в первом порядке по возмущению – гамильтониану
). Уравнение для электронной подсистемы решается в первом порядке по возмущению – гамильтониану ![]() . Динамическое возмущение
. Динамическое возмущение ![]() энергии электронного состояния b обозначим
энергии электронного состояния b обозначим ![]() . В «кондоновском» приближении рассматривается статическая электронная волновая функция состояния b, например,
. В «кондоновском» приближении рассматривается статическая электронная волновая функция состояния b, например, ![]() . Тогда «кондоновская» производящая функция оптического перехода [4], представляющая собой преобразование Фурье форм-функции, может быть записана в виде
. Тогда «кондоновская» производящая функция оптического перехода [4], представляющая собой преобразование Фурье форм-функции, может быть записана в виде
![]() , (1)
, (1)
где ![]() – проекция электрического дипольного момента примесного центра на направление поляризации фотона (приводимые ниже выражения можно легко обобщить на случай мультипольного излучения),
– проекция электрического дипольного момента примесного центра на направление поляризации фотона (приводимые ниже выражения можно легко обобщить на случай мультипольного излучения), ![]() , и нормированная «кондоновская» производящая функция
, и нормированная «кондоновская» производящая функция ![]() есть
есть
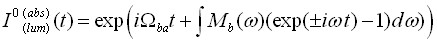 , (2)
, (2)
![]() . (3)
. (3)
Величина ![]() есть частота бесфононного перехода. Здесь и далее верхние знаки берутся для поглощения, нижние – для люминесценции. Интегралы от распределений частоты берутся в пределах от нуля до
есть частота бесфононного перехода. Здесь и далее верхние знаки берутся для поглощения, нижние – для люминесценции. Интегралы от распределений частоты берутся в пределах от нуля до ![]() (при необходимости можно расширить области определения подынтегральных распределений частоты, продолжая их нулевой функцией), знак мнимой части следует относить к опережающей функции Грина для операторов нормальных координат колебательной подсистемы, матричные элементы электронных операторов выносятся за знак мнимой части.
(при необходимости можно расширить области определения подынтегральных распределений частоты, продолжая их нулевой функцией), знак мнимой части следует относить к опережающей функции Грина для операторов нормальных координат колебательной подсистемы, матричные элементы электронных операторов выносятся за знак мнимой части.
Для записи форм-функций в диссертации используется формализм операторов свертки. Для функции ![]() , определенной при положительных значениях аргумента, введем операторы
, определенной при положительных значениях аргумента, введем операторы ![]() и
и ![]() , которые при действии на произвольную функцию
, которые при действии на произвольную функцию ![]() дают ее свертки с
дают ее свертки с ![]() :
: 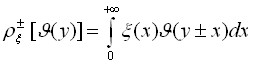 . По определению будем считать, что
. По определению будем считать, что ![]() . Тогда можно записать формулу для нормированных «кондоновских» форм-функций поглощения и люминесценции [4] в следующем виде
. Тогда можно записать формулу для нормированных «кондоновских» форм-функций поглощения и люминесценции [4] в следующем виде
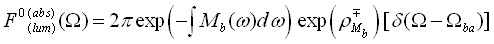 . (4)
. (4)
Величина ![]() есть параметр Хуана-Рис перехода. В «кондоновском» приближении форм-функции поглощения и люминесценции зеркально симметричны относительно частоты бесфононного перехода
есть параметр Хуана-Рис перехода. В «кондоновском» приближении форм-функции поглощения и люминесценции зеркально симметричны относительно частоты бесфононного перехода ![]() .
.
Если интенсивность перехода ![]() в «кондоновском» приближении мала (
в «кондоновском» приближении мала (![]() ), то «кондоновское» приближение неприменимо, и необходимо рассматривать динамическую волновую функцию электронного состояния b. Введем динамическое возмущение волновой функции состояния
), то «кондоновское» приближение неприменимо, и необходимо рассматривать динамическую волновую функцию электронного состояния b. Введем динамическое возмущение волновой функции состояния ![]()
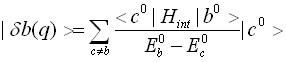 . (5)
. (5)
Производящие функции и форм-функции для этого случая маркируем индексом 1. В работе [4] приведены 0-й и 1-й моменты ![]() и
и ![]() ; показано, что нарушается зеркальная симметрии полос поглощения и люминесценции.
; показано, что нарушается зеркальная симметрии полос поглощения и люминесценции.
Во второй главе строится теория электронно-колебательных оптических спектров примесных центров при нарушении «кондоновского» приближения и предлагается методика полуфеноменологического микроскопического расчета электронно-колебательных полос в оптических спектрах межконфигурационных ![]() переходов в примесных РЗ ионах, внедренных в диэлектрический кристалл.
переходов в примесных РЗ ионах, внедренных в диэлектрический кристалл.
Обозначим ![]() . Введем распределения
. Введем распределения
![]() ,
, ![]() . (6)
. (6)
Полученные в диссертации выражения для «некондоновских» производящих функций поглощения ![]() и люминесценции
и люминесценции ![]() могут быть записаны в виде
могут быть записаны в виде
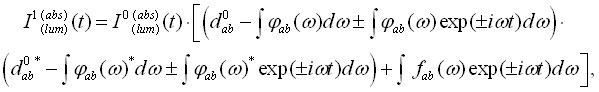 (7)
(7)
а выражения для соответствующих форм-функций – в виде
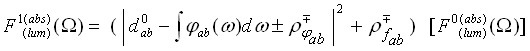 . (8)
. (8)
Асимметрия поглощения и люминесценции заключается в смене знака перед оператором ![]() . Форма «некондоновской» полосы оказывается зависящей от основного электронного состояния
. Форма «некондоновской» полосы оказывается зависящей от основного электронного состояния ![]() , несмотря на то, что взаимодействие с колебаниями в состоянии
, несмотря на то, что взаимодействие с колебаниями в состоянии ![]() не учитывается. «Кондоновская» форм-функция перехода входит в (8) с весом
не учитывается. «Кондоновская» форм-функция перехода входит в (8) с весом ![]() . Это единственное слагаемое (8), в котором сохраняется бесфононная линия. В прочих слагаемых бесфононная линия сворачивается со спектральными распределениями
. Это единственное слагаемое (8), в котором сохраняется бесфононная линия. В прочих слагаемых бесфононная линия сворачивается со спектральными распределениями ![]() и
и ![]() (от свертки с бесфононной линией в основном появляется колебательная структура, отличающая форму этих слагаемых от гауссовой). Единственное слагаемое в (8), содержащее распределение
(от свертки с бесфононной линией в основном появляется колебательная структура, отличающая форму этих слагаемых от гауссовой). Единственное слагаемое в (8), содержащее распределение ![]() , симметрично входит в спектры поглощения и люминесценции.
, симметрично входит в спектры поглощения и люминесценции.
Выделим симметризованные смещения атомов кристаллической решетки, преобразующиеся по неприводимым представлениям точечной группы симметрии гамильтониана ![]() . Рассмотрим распределение
. Рассмотрим распределение ![]() (6). Ввиду адиабатического приближения, оператор
(6). Ввиду адиабатического приближения, оператор ![]() содержит только полносимметричные смещения решетки. В силу диагональности мнимых частей кристаллических функций Грина по индексам неприводимых представлений оператор
содержит только полносимметричные смещения решетки. В силу диагональности мнимых частей кристаллических функций Грина по индексам неприводимых представлений оператор ![]() также содержит только полносимметричные смещения решетки. Следовательно, сумма по состояниям с в (5) ограничена состояниями той же симметрии, что и состояние
также содержит только полносимметричные смещения решетки. Следовательно, сумма по состояниям с в (5) ограничена состояниями той же симметрии, что и состояние ![]() . Для перехода
. Для перехода ![]() , запрещенного в «кондоновском» приближении по симметрии, получим
, запрещенного в «кондоновском» приближении по симметрии, получим ![]() ,
, ![]() , так что (8) сведется к
, так что (8) сведется к ![]() . Отсюда следует, что «некондоновские» форм-функции поглощения и люминесценции запрещенного по симметрии перехода зеркально симметричны, и в них отсутствуют бесфононные линии (это свойство может служить качественным критерием для интерпретации экспериментальных данных). Разрешается такой переход взаимодействием с неполносимметричными адиабатическими колебаниями решетки.
. Отсюда следует, что «некондоновские» форм-функции поглощения и люминесценции запрещенного по симметрии перехода зеркально симметричны, и в них отсутствуют бесфононные линии (это свойство может служить качественным критерием для интерпретации экспериментальных данных). Разрешается такой переход взаимодействием с неполносимметричными адиабатическими колебаниями решетки.
Перечислим основные этапы предлагаемой методики расчета ![]() спектров примесных РЗ ионов, внедренных в диэлектрический кристалл. Энергетический спектр конфигураций
спектров примесных РЗ ионов, внедренных в диэлектрический кристалл. Энергетический спектр конфигураций ![]() и
и ![]() – совокупность величин
– совокупность величин ![]() и
и ![]() – вычисляется с использованием численной диагонализации матрицы эффективного параметризованного гамильтониана примесного иона
– вычисляется с использованием численной диагонализации матрицы эффективного параметризованного гамильтониана примесного иона ![]() , включающего электростатическое взаимодействие между электронами, спин-орбитальное взаимодействие и взаимодействие электронов с кристаллическим полем решетки. Параметры
, включающего электростатическое взаимодействие между электронами, спин-орбитальное взаимодействие и взаимодействие электронов с кристаллическим полем решетки. Параметры ![]() варьируются с целью согласования с экспериментальными данными, либо используются значения, приведенные в литературе. Параметры кристаллического поля и параметры электронно-колебательного взаимодействия для
варьируются с целью согласования с экспериментальными данными, либо используются значения, приведенные в литературе. Параметры кристаллического поля и параметры электронно-колебательного взаимодействия для ![]() электрона вычисляются согласованно с использованием модели обменных зарядов [5]. Используется «кластерное» приближение, учитывается только модуляция действующего на
электрона вычисляются согласованно с использованием модели обменных зарядов [5]. Используется «кластерное» приближение, учитывается только модуляция действующего на ![]() электрон кристаллического поля колебаниями ближайших соседей примесного центра. Вычисляются полный закон дисперсии возбуждений невозмущенной кристаллической решетки и мнимые части решеточных функций Грина. Вычисляемые по формулам (4) и (8) огибающие оптических спектров сворачиваются с распределениями Лоренца и Гаусса для учета, соответственно, однородного и неоднородного уширения.
электрон кристаллического поля колебаниями ближайших соседей примесного центра. Вычисляются полный закон дисперсии возбуждений невозмущенной кристаллической решетки и мнимые части решеточных функций Грина. Вычисляемые по формулам (4) и (8) огибающие оптических спектров сворачиваются с распределениями Лоренца и Гаусса для учета, соответственно, однородного и неоднородного уширения.
В третьей главе проводится расчет оптических ![]() спектров кристалла LiYF4:Ce3+. Примесные трехвалентные РЗ ионы замещают в кристалле LiYF4 ионы Y3+ в узлах с симметрией
спектров кристалла LiYF4:Ce3+. Примесные трехвалентные РЗ ионы замещают в кристалле LiYF4 ионы Y3+ в узлах с симметрией ![]() . Возбужденная электронная конфигурация иона Ce3+
. Возбужденная электронная конфигурация иона Ce3+ ![]() в кристаллическом поле с симметрией
в кристаллическом поле с симметрией ![]() расщепляется на пять крамерсовых дублетов, переходам на которые из основного
расщепляется на пять крамерсовых дублетов, переходам на которые из основного ![]() уровня отвечают пять полос в спектре
уровня отвечают пять полос в спектре ![]() поглощения кристалла LiYF4:Ce3+ [3]. Вычислены следующие значения параметров Хуана-Рис для этих переходов: 2.92, 17.4, 5.98, 5.97 и 16.44, в порядке возрастания энергии. Таким образом, в диссертации получено объяснение экспериментально наблюдаемого факта – только в спектре перехода на основной
поглощения кристалла LiYF4:Ce3+ [3]. Вычислены следующие значения параметров Хуана-Рис для этих переходов: 2.92, 17.4, 5.98, 5.97 и 16.44, в порядке возрастания энергии. Таким образом, в диссертации получено объяснение экспериментально наблюдаемого факта – только в спектре перехода на основной ![]() уровень с относительно слабым электрон-фононным взаимодействием наблюдается тонкая структура [3]. На рис. 1 сравниваются результаты расчета спектра этого перехода и соответствующая полоса измеренного в работе [6] спектра
уровень с относительно слабым электрон-фононным взаимодействием наблюдается тонкая структура [3]. На рис. 1 сравниваются результаты расчета спектра этого перехода и соответствующая полоса измеренного в работе [6] спектра ![]() возбуждения кристалла LiGdF4:Ce3+ (0.05%), обладающего той же структурой, что и кристалл LiYF4:Ce3+. Для основного
возбуждения кристалла LiGdF4:Ce3+ (0.05%), обладающего той же структурой, что и кристалл LiYF4:Ce3+. Для основного ![]() уровня иона Ce3+ адиабатическое приближение выполняется с высокой точностью, и результаты вычислений хорошо согласуются с экспериментом. На рис. 2 сравниваются вычисленный в диссертации и измеренный в работе [7] спектры
уровня иона Ce3+ адиабатическое приближение выполняется с высокой точностью, и результаты вычислений хорошо согласуются с экспериментом. На рис. 2 сравниваются вычисленный в диссертации и измеренный в работе [7] спектры ![]() люминесценции кристалла LiYF4:Ce3+. На рисунке обозначены идентифицированные пики эксперимен-
люминесценции кристалла LiYF4:Ce3+. На рисунке обозначены идентифицированные пики эксперимен-
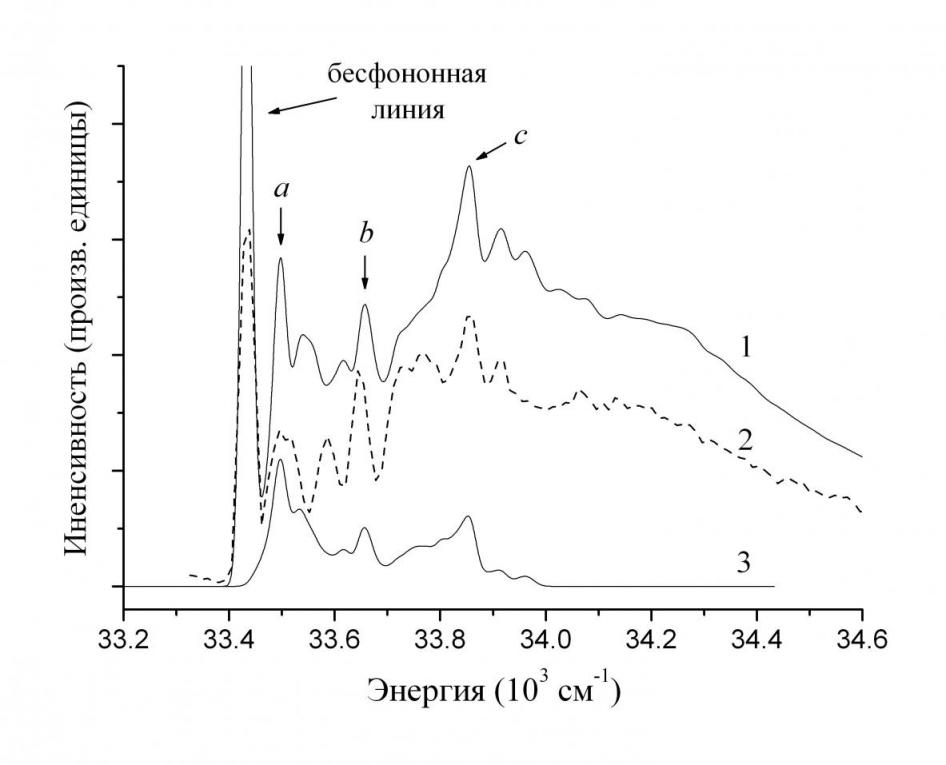
Рис. 1. Вычисленный спектр ![]() поглощения кристалла LiYF4:Ce3+, отвечающий переходу на основной
поглощения кристалла LiYF4:Ce3+, отвечающий переходу на основной ![]() уровень иона Ce3+, при нулевой температуре (1). Однофононная составляющая вычисленного спектра с уменьшенной в 2.5 раза интенсивностью (3). Спектр
уровень иона Ce3+, при нулевой температуре (1). Однофононная составляющая вычисленного спектра с уменьшенной в 2.5 раза интенсивностью (3). Спектр ![]() возбуждения кристалла LiGdF4:Ce3+ (0.05%) при температуре 10 К [6] (2, сдвинут по оси абсцисс). Cтрелками показаны три наиболее интенсивных максимума в колебательной структуре полосы.
возбуждения кристалла LiGdF4:Ce3+ (0.05%) при температуре 10 К [6] (2, сдвинут по оси абсцисс). Cтрелками показаны три наиболее интенсивных максимума в колебательной структуре полосы.
тального спектра люминесценции. Символами «a, b, c» на рис. 2 отмечены максимумы колебательной структуры полос (ср. рис. 1). Три интенсивных пика экспериментального спектра не объясняются колебательной структурой полос и, следовательно, обусловлены бесфононными переходами на подуровни конфигурации ![]() . Бесфононные линии на рис. 2 обозначены «ZPL i», где i – номер
. Бесфононные линии на рис. 2 обозначены «ZPL i», где i – номер ![]() уровня в порядке возрастания энергии. Таким образом, в диссертации определены энергии трех возбужденных уровней локализованного на ионе Ce3+
уровня в порядке возрастания энергии. Таким образом, в диссертации определены энергии трех возбужденных уровней локализованного на ионе Ce3+ ![]() электрона (514, 2222 и 2320 см-1), которые уточняют значения, приведенные в [7].
электрона (514, 2222 и 2320 см-1), которые уточняют значения, приведенные в [7].
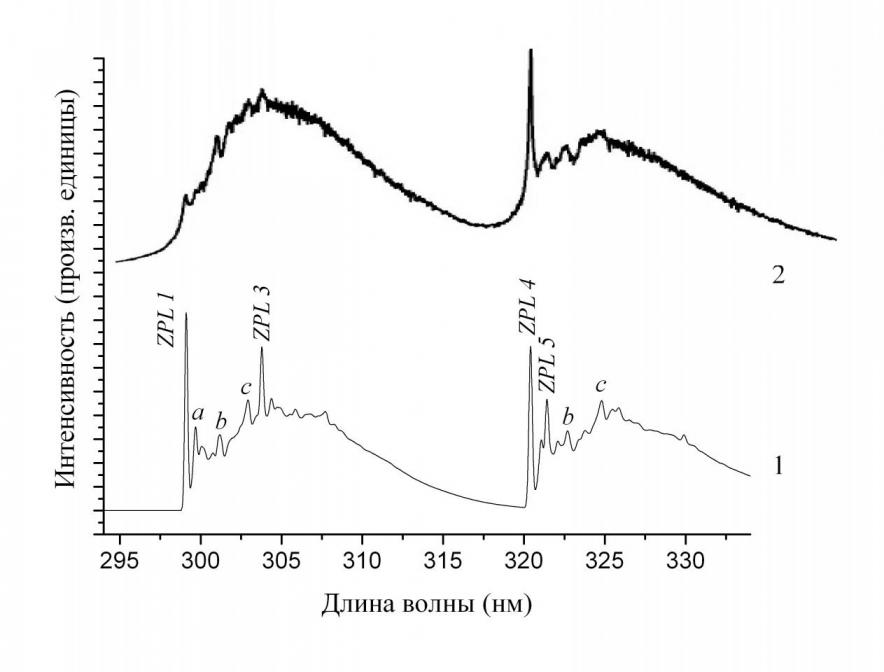
Рис. 2. Вычисленный при нулевой температуре (1) и измеренный при температуре 10 К [7] (2) спектры ![]() люминесценции кристалла LiYF4:Ce3+ (1%).
люминесценции кристалла LiYF4:Ce3+ (1%).
В четвертой главе проводится расчет оптических ![]() спектров кристалла LiYF4:Lu3+. В диссертации дается объяснение отсутствию бесфононных линий в измеренных спектрах возбуждения и люминесценции кристалла LiYF4:Lu3+ [6], обусловленных переходами между основным электронным состоянием
спектров кристалла LiYF4:Lu3+. В диссертации дается объяснение отсутствию бесфононных линий в измеренных спектрах возбуждения и люминесценции кристалла LiYF4:Lu3+ [6], обусловленных переходами между основным электронным состоянием ![]() иона Lu3+ и нижними состояниями возбужденной конфигурации
иона Lu3+ и нижними состояниями возбужденной конфигурации ![]() (вычисленные в диссертации и измеренные [6] спектры сравниваются на рис. 3). Как следует из проведенных вычислений, эти переходы запрещены по симметрии, так что в соответствующих электронно-колебательных спектрах бесфононные линии должны отсутствовать по доказанному во второй главе свойству. Из развитой во второй главе теории также следует, что спектры поглощения и люминесценции в данном случае должны быть симметричными. Измеренные в работе [6] спектры возбуждения и люминесценции не являются симметричными. Следует, однако, отметить, что спектры поглощения и возбуждения могут различаться.
(вычисленные в диссертации и измеренные [6] спектры сравниваются на рис. 3). Как следует из проведенных вычислений, эти переходы запрещены по симметрии, так что в соответствующих электронно-колебательных спектрах бесфононные линии должны отсутствовать по доказанному во второй главе свойству. Из развитой во второй главе теории также следует, что спектры поглощения и люминесценции в данном случае должны быть симметричными. Измеренные в работе [6] спектры возбуждения и люминесценции не являются симметричными. Следует, однако, отметить, что спектры поглощения и возбуждения могут различаться.
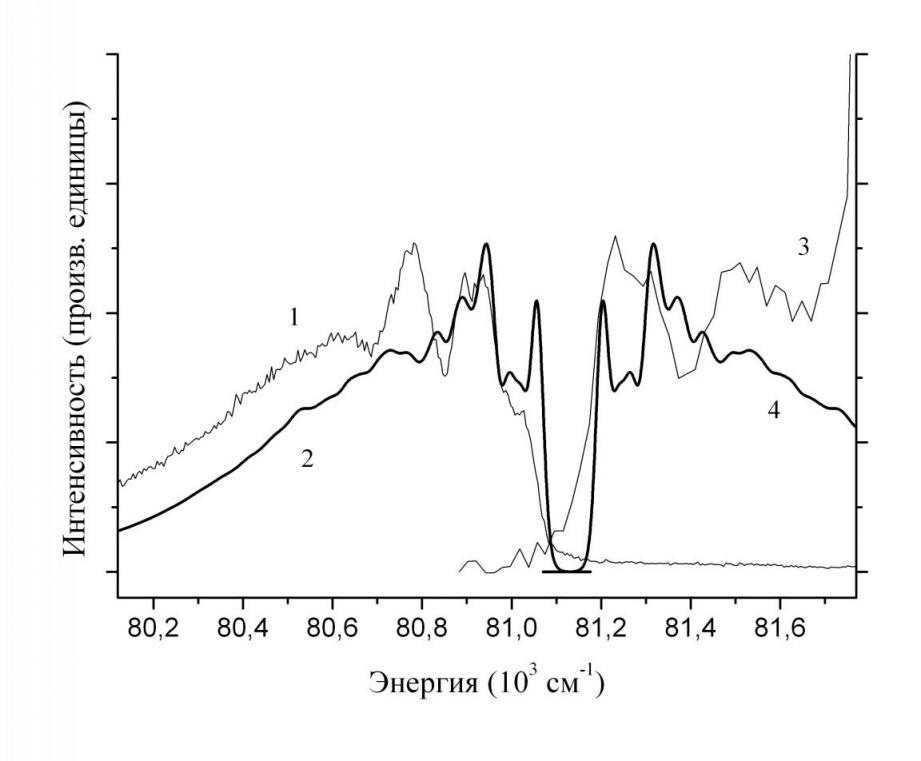
Рис. 3. 1 и 2 – измеренный при температуре 8 К [6] и вычисленный при нулевой температуре спектры ![]() люминесценции кристалла LiYF4:Lu3+. 3 и 4 – фрагменты измеренного при температуре 12 К [6] и вычисленного при нулевой температуре спектров
люминесценции кристалла LiYF4:Lu3+. 3 и 4 – фрагменты измеренного при температуре 12 К [6] и вычисленного при нулевой температуре спектров ![]() возбуждения кристалла LiYF4:Lu3+, отвечающие запрещенным переходам.
возбуждения кристалла LiYF4:Lu3+, отвечающие запрещенным переходам.
В пятой главе проводится расчет оптических ![]() спектров кристалла CaF2:Tm2+. Ионы Tm2+ замещают в кристалле CaF2 ионы Ca2+ в узлах с симметрией
спектров кристалла CaF2:Tm2+. Ионы Tm2+ замещают в кристалле CaF2 ионы Ca2+ в узлах с симметрией ![]() . Показано, что измеренный в диапазоне 14000 – 34000 cм-1 спектр поглощения кристалла CaF2:Tm2+ [8] обусловлен переходами на
. Показано, что измеренный в диапазоне 14000 – 34000 cм-1 спектр поглощения кристалла CaF2:Tm2+ [8] обусловлен переходами на ![]() состояния, происходящие в основном от
состояния, происходящие в основном от ![]() терма
терма ![]() электрона; параметры Хуана-Рис этих переходов принимают значения порядка 1.
электрона; параметры Хуана-Рис этих переходов принимают значения порядка 1.
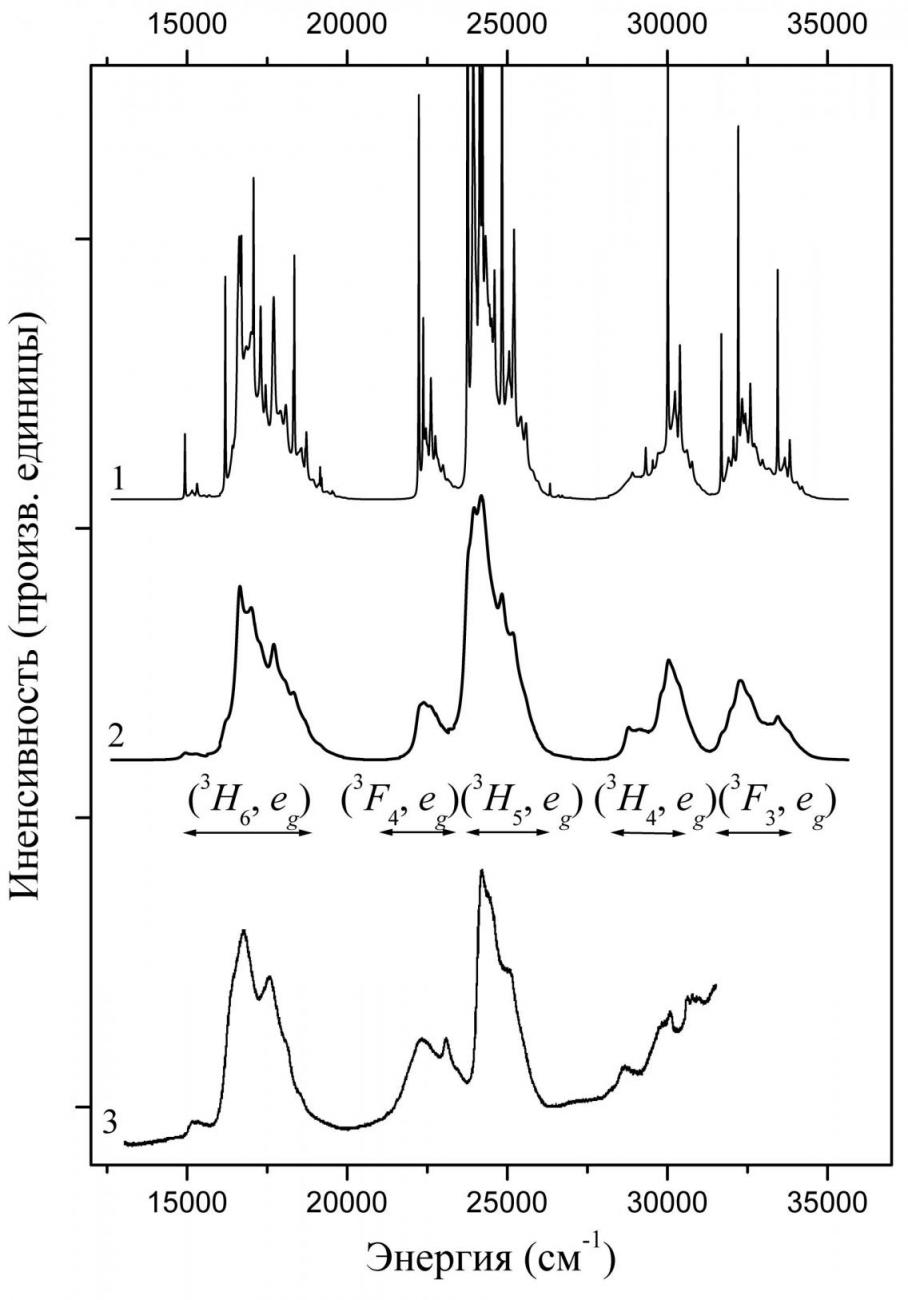
Рис. 4. Спектры ![]() поглощения кристалла CaF2:Tm2+: вычисленные при нулевой температуре (1 – вычисленные релаксационные ширины, 2 – релаксационная ширина положена равной 250 см-1) и измеренный (3) при температуре 10 К [8].
поглощения кристалла CaF2:Tm2+: вычисленные при нулевой температуре (1 – вычисленные релаксационные ширины, 2 – релаксационная ширина положена равной 250 см-1) и измеренный (3) при температуре 10 К [8].
Для согласования вычисленного в диссертации и измеренного в работе [8] спектров ![]() поглощения кристалла CaF2:Tm2+ требуется свернуть вычисленную огибающую полосы поглощения с распределением Лоренца шириной порядка 250 см-1 – см. рис. 4. Вычисленные в диссертации значения релаксационных ширин, пропорциональные вероятностям однофононных безызлучательных переходов [5] из состояний возбужденной конфигурации на нижележащие уровни, оказались в среднем значительно меньше 250 см-1, что указывает на необходимость учета многофононной релаксации и взаимодействия с неадиабатическими колебаниями для согласования с данными измерений. Полосам в измеренном спектре поглощения поставлены в соответствие термы (
поглощения кристалла CaF2:Tm2+ требуется свернуть вычисленную огибающую полосы поглощения с распределением Лоренца шириной порядка 250 см-1 – см. рис. 4. Вычисленные в диссертации значения релаксационных ширин, пропорциональные вероятностям однофононных безызлучательных переходов [5] из состояний возбужденной конфигурации на нижележащие уровни, оказались в среднем значительно меньше 250 см-1, что указывает на необходимость учета многофононной релаксации и взаимодействия с неадиабатическими колебаниями для согласования с данными измерений. Полосам в измеренном спектре поглощения поставлены в соответствие термы (![]() ,
, ![]() ), где
), где ![]() – термы конфигурации
– термы конфигурации ![]() (см. рис. 4).
(см. рис. 4).
Переходы между основным уровнем конфигурации ![]() иона Tm2+ и нижними уровнями конфигурации
иона Tm2+ и нижними уровнями конфигурации ![]() запрещены по спину и имеют малую интенсивность. Вычисленная по формуле (8) огибающая оптического спектра на этих переходах имеет форму, близкую к «кондоновской». На рис. 5 сравниваются измеренный в [8] и вычисленный в диссертации спектры
запрещены по спину и имеют малую интенсивность. Вычисленная по формуле (8) огибающая оптического спектра на этих переходах имеет форму, близкую к «кондоновской». На рис. 5 сравниваются измеренный в [8] и вычисленный в диссертации спектры ![]() люминесценции кристалла CaF2:Tm2+. Наблюдаемая в спектре люминесценции [8] колебательная полоса отвечает переходу с рождением одного фонона.
люминесценции кристалла CaF2:Tm2+. Наблюдаемая в спектре люминесценции [8] колебательная полоса отвечает переходу с рождением одного фонона.
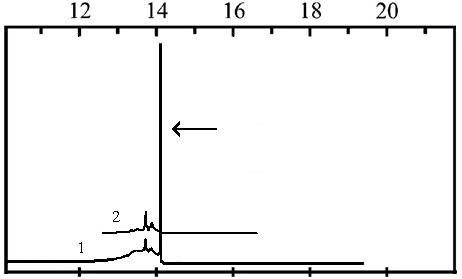
Энергия (103 см-1)
Рис. 5. Спектры ![]() люминесценции кристалла CaF2:Tm2+, измеренный (1) при температуре 10 К [8] и вычисленный (2) при нулевой температуре. Спектры разнесены по оси ординат. Стрелкой указан уровень вычисленной бесфононной линии.
люминесценции кристалла CaF2:Tm2+, измеренный (1) при температуре 10 К [8] и вычисленный (2) при нулевой температуре. Спектры разнесены по оси ординат. Стрелкой указан уровень вычисленной бесфононной линии.
Основные результаты работы
- Получены аналитические выражения для форм-функций поглощения и люминесценции оптических центров в кристаллах при нулевой температуре в случае нарушения «кондоновского» приближения.
- Доказано свойство: если оптический переход запрещен в «кондоновском» приближении по симметрии, то «некондоновские» форм-функции поглощения и люминесценции зеркально симметричны, и в них отсутствуют бесфононные линии.
- Разработана методика вычисления электронно-колебательных полос в оптических спектрах межконфигурационных
 переходов в примесных РЗ ионах. Впервые проведен микроскопический расчет электронно-колебательных оптических спектров
переходов в примесных РЗ ионах. Впервые проведен микроскопический расчет электронно-колебательных оптических спектров  переходов на примере кристаллов LiYF4:Ce3+, LiYF4:Lu3+, CaF2:Tm2+. Результаты выполненных расчетов оптических спектров хорошо согласуются с данными измерений. Полученные из сравнения с экспериментом значения феноменологических параметров модели обменных зарядов различаются для трех исследованных кристаллов лишь незначительно.
переходов на примере кристаллов LiYF4:Ce3+, LiYF4:Lu3+, CaF2:Tm2+. Результаты выполненных расчетов оптических спектров хорошо согласуются с данными измерений. Полученные из сравнения с экспериментом значения феноменологических параметров модели обменных зарядов различаются для трех исследованных кристаллов лишь незначительно. - Получено объяснение того, что в спектре поглощения кристалла LiYF4:Ce3+ бесфононная линия наблюдается только в полосе, отвечающей переходу на основной
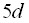 уровень. Вычислениями воспроизведены колебательные максимумы указанной полосы. На основе интерпретации тонкой структуры спектра люминесценции кристалла LiYF4:Ce3+ определены энергии трех возбужденных уровней локализованного на ионе Ce3+
уровень. Вычислениями воспроизведены колебательные максимумы указанной полосы. На основе интерпретации тонкой структуры спектра люминесценции кристалла LiYF4:Ce3+ определены энергии трех возбужденных уровней локализованного на ионе Ce3+ 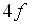 электрона.
электрона. - Получено объяснение того, что в измеренных спектрах возбуждения и люминесценции кристалла LiYF4:Lu3+ на переходах с участием нижних состояний возбужденной конфигурации иона Lu3+ отсутствуют бесфононные линии.
- Идентифицированы полосы в измеренном спектре поглощения кристалла CaF2:Tm2+. Показано, что форма полосы люминесценции кристалла CaF2:Tm2+ при низких температурах близка к «кондоновской», вычислениями воспроизведена тонкая структура полосы.
Список работ автора по теме диссертации
- Solovyev, O.V. Electron-phonon interaction in the 4f125d electronic configuration of the Tm2+ ion in CaF2 / O.V. Solovyev // Magn. Resonance in Solids. EJ. – 2009. – Vol. 11. – P. 14–19.
- Vacuum-ultraviolet 5d-4f luminescence of Gd3+ and Lu3+ ions in fluoride matrices / M. Kirm, G. Stryganyuk, S. Vielhauer, G. Zimmerer, V.N. Makhov, B.Z. Malkin, O.V. Solovyev, R.Yu. Abdulsabirov, S.L. Korableva // Phys. Rev. B. – 2007. – Vol. 75. – P. 075111(1-13).
- Theoretical studies of electron-vibrational 4fn-4fn-15d spectra in LiYF4:RE3+ crystals / B.Z. Malkin, O.V. Solovyev, A.Yu. Malishev, S.K. Saikin // J. Lumin. – 2007. – Vol. 125. – P. 175–183.
- Solovyev, O.V. Modeling of electron-vibrational 4fn-4fn-15d spectra in LiYF4: RE3+ crystals / O.V. Solovyev, B.Z. Malkin // J. Mol. Struct. – 2007. – Vol. 838. – P. 176–181.
- Соловьев, О.В. Электронно-колебательные полосы в 4fn-4fn-15d спектрах / О.В. Соловьев // Сборник статей итоговой научно-образовательной конференции студентов КГУ за 2005 год. – Казань, 2005. – C. 46–48.
- Соловьев, О.В. Моделирование электронно-колебательных полос спектра 4fn-4fn-15d в кристалле LiYF4:Re3+ / О.В. Соловьев, Б.З. Малкин // Сборник материалов Итоговой конференции по НИР КГУ за 2006 г. Образование и наука, ч.1. Естественные науки. – Казань, 2007. – С. 6.
- Электронно-колебательные межконфигурационные спектры поглощения и излучения редкоземельных ионов в кристалле LiYF4 / Б.З. Малкин, О.В. Соловьев, А.Ю. Малышев, С.К. Сайкин // Тезисы докладов международной конференции «Фундаментальные проблемы физики», Казань, 2005. – КГУ, 2005. – C. 31.
Цитируемая литература
- 4fn4fn-15d transitions of the light lanthanides: Experiment and theory / L. van Pieterson, M.F. Reid, R.T. Wegh, S. Soverna, A. Meijerink // Phys. Rev. B. – 2002. – Vol. 65. – P. 045113(1-16).
- Eремин, М.В. 4fn-15d-конфигурации ионов в кристаллах: II Спектр 4f14-4f135d иона Yb2+ / M.В. Еремин // Оптика и спектроскопия. – 1970. – Т. 29. – С. 100–108.
- Spectroscopy and calculations for 4fn4fn-15d transitions of lanthanide ions in LiYF4 / M.F. Reid, L. van Pieterson, R.T. Wegh, A. Meijerink // Phys. Rev. B. – 2000. – Vol. 62, № 22. – P. 14744–14749.
- Перлин, Ю.Е. Эффекты электронно-колебательного взаимодействия в оптических спектрах примесных парамагнитных ионов / Ю.Е. Перлин, Б.С. Цукерблат. – Кишинев: Штиинца, 1974. – 368 c.
- Malkin, B.Z. Crystal field and electron-phonon interaction in rare-earth ionic paramagnets / B.Z. Malkin // Spectroscopy of Solids Containing Rare-Earth Ions / Eds. A.A. Kaplyanskii, R.M. Macfarlane. – Amsterdam: North-Holland, 1987. – P. 13–49.
- Vacuum-ultraviolet 5d-4f luminescence of Gd3+ and Lu3+ ions in fluoride matrices / M. Kirm, G. Stryganyuk, S. Vielhauer, G. Zimmerer, V.N. Makhov, B.Z. Malkin, O.V. Solovyev, R.Yu. Abdulsabirov, S.L. Korableva // Phys. Rev. B. – 2007. – Vol. 75. – P. 075111(1-13).
- 4fn-15d–4fn emission of Ce3+, Pr3+, Nd3+, Er3+ and Tm3+ in LiYF4 and YPO4 / P.S. Peijzel, P. Vergeer, A. Meijerink, M.F. Reid, L.A. Boatner, G.W. Burdick // Phys. Rev. B. – 2005. – Vol. 71. – P. 045116(1-9).
- 4f-4f and 4f-5d excited states and luminescence properties of Tm2+-doped CaF2, CaCl2, SrCl2 and BaCl2 / J. Grimm, O.S. Wenger, K.W. Kramer, H.U. Gudel // J. Lumin. – 2006. – Vol. 126. – P. 590–596.

