«Математика в древних цивилизациях: Китай»

Вступление

Математика - наука о количественные соотношения и пространственные формы действительного мира. Возникла в древности из практических потребностей человека: "Чистая математика имеет своим объектом пространственные формы и количественные отношения действительного мира, следовательно - очень реальный материал"Это определение наиболее удачное, поскольку учитывает ее содержание и характер, которые со временем изменялись. До того, как стать абстрактивною наукой, математика прошла длинный путь развития. Однако абстрактность математики не означает ее отрыва от материальной действительности. В неразрывной связи с запросами техники и естествознания запас количественных отношений и пространственных форм, которые изучает математика, непрерывно расширяется. Математические результаты получают исключительно на базе логических соображений.

Цель: узнать об использовании математики в Китае, и о китайских ученых.

Задачи: 1. Обработать используемую литературу;

2. Исследовать этапы развития математики в древней цивилизации;

3. Узнать о математических теориях.

Актуальность: как будущие учителя, мы должны знать больше о математике в разных странах.

Объект: целенаправленный процесс формирования знаний у каждого из нас.

Содержание:

Вступление..……………………………………………………………………….3

Раздел 1. Этапы развития китайской математики………………………………4

1. Эпоха раннего Чжоу……………………………………………………5
2. Ханьская эпоха…………………………………………………………6
3. Ранний период династии Ли…………………………………………..6
4. Поздний период династии Ли…………………………………………8

Раздел 2. Великие математики Китая……………………………………………9

2.1 Когурё………………………………………………………………….11

2.2 Пэкче…………………………………………………………………...12

2.3 Корё…………………………………………………………………….13

Раздел 3. Математические теории…………………………………………...…17

3.1 Теорема Пифагора…………………………………………………….17

3.2 Дроби…………………………………………………………………..19

3.3 Вычисление площадей и корней……………………………………..20

3.4 Значение числа «пи»………………………………………………….21

3.5 Треугольник Паскаля…………………………………………………22

3.6 Решение систем уравнений…………………………………………..24

3.7 Система счисления……………………………………………………26

3.8 Магические квадраты…………………………………………………28

Вывод……………………………………………………………………………..33

Список литературы………………………………………………………………34

Часто говорят, что цифры управляют миром; по крайней мере нет сомнения в том, что цифры показывают, как он управляется.

И. Гёте

Раздел 1. Этапы развития китайской математики

Древний Китай обогатил мировую науку и культуру значительными достижениями: он является родиной такого изобретений, как компас (III век до н.э.), спидометр (III век до н.э.), сейсмограф (II век до н нашей эры), порох (X ст.н. э), книгопечатания (VI-VIII века), фарфор (III - V в.). В области математики был открыт метод решения уравнений первой степеня с двумя и тремя неизвестными, вычислено отношение длины окружности к ее диаметру - число л. В области астрономии китайцы знали, как высчитывать дату затмения солнца.

Начальные понятия математики зародились в Древнем Китае, послужили развитию матеатической культуры соседних народов, которые занимали территорию современной Кореи Индокитая и с особенности Японии. В Китае рано начали накапливаться сведения математического характера и появилась запись чисел. При этом китайские иероглифические цифры были по записи еще сложнее египетских. Но, помимо этих иероглифических цифр, в Китае имели распространение и более простые цифровые знаки, которые употреблялись в торговых операциях. Выглядели они следующим образом: | = 1; | | = 2; | | | = 3; ||||= 4; |||||= 5; | = 6; | | = 7; | | | = 8; ||||= 9; 0 = 0. Запись чисел проводилась столбцами сверху вниз. Большим преимуществом китайской записи чисел было введение в употребление нуля для выражения отсутствующих разрядов. Предполагают, что ноль заимствован из Индии в XII в..

По древним преданиям, основам счета китайцев научил мифический первопредок Фуси. Его часто изображают держащим в руках угольник (цзюй). На изображениях рядом с ним находится его жена Нюйва, держащая в руке циркуль (гуй). Как показывают надписи на гадательных костях, уже в эпоху Шан циркуль использовался для вычерчивания круга, а угольник - прямых углов, в частности, углов квадрата. Со временем круг и квадрат стали символами принципов ян и инь. То же самое можно сказать о циркуле и угольнике.

1.1 Эпоха раннего Чжоу

В эпоху раннего Чжоу искусство счета уже входило в программу обучения школьников. В эпоху «Борющихся царств» создаётся сочинение “Чжоу би суань цзин” (“Канон расчета чжоуского гномона”), в котором были даны элементарные математические знания, пригодные для астрономических расчетов.

В пещерах Дуньхуана в провинции Ганьсу были найдены датируемые 1 в. до н.э. бамбуковые дощечки со списками примеров умножения всех чисел от 1 до 9. Числа в них были записаны иероглифами. Запись примеров умножения не списком, а в виде таблицы, в которой перемножаемые числа расположены в двух координатах, появляются в Китае после VIII в.

Первая чисто математическая книга появляется в эпоху раннего Хань - “Искусство счета в девяти разделах” (“Цзю чжан суань шу”). В этой книге было собрано и систематизировано математическое наследие предшествующих периодов. Она состоит из 246 задач, для которых дается числовой ответ и процедура решения. Эта книга сыграла важную роль в развитии математики в Китае. Все китайские математики ссылаются на нее, пишут свои комментарии, добавляя объяснения и доказательства, переписывая процедуры и предлагая новые формулы. Наиболее важный из сохранившихся комментариев приписывается математику Лю Хуэю, жившему в 3 в. Он содержит самый богатый набор доказательств в пределах данной традиции.

1.2 Ханьская эпоха

В Ханьскую эпоху математика достигает относительного расцвета и выделяется в самостоятельную дисциплину. В имперском Китае социальная роль математики определялась бюрократической правительственной системой. В официальной математике ставились задачи, которые должны были решать должностные лица. Ремесленники, применявшие в своей работе некоторые математические знания, и чиновноки-математики были совершенно разделенными группами. В III-IV вв. математик Сунь-цзы представил правила работы со счетной доской, изложил способ решения в целых числах неопределенных уравнений 1-й степени. В его сочинении “Классическая арифметика Сунь-цзы” (“Сунь-цзы суань цзин”) приводятся сведения о геометрической прогрессии. Там имеется задача о ткачихе, которая удваивает продукцию предыдущего дня и производит 5 мер ткани каждые пять дней. Спрашивается, сколько ткани производится в первый и последующий дни?

1.3 Ранний период династии Ли

В соседнем Китае математика вступила в период застоя и была низведена до уровня начетничества, забавы и головоломок. С конца XVI в. в Китай начали проникать открытия европейских ученых в области тригонометрии и алгебры, а затем -логарифмы, методы разложения и бесконечные ряды. Но еще долго уровень оригинальных исследований в Китае оставался более низким, чем в Европе. Крупный китайский математик Сюй Гуанци в 1603 г. выпустил «Основы геометрии» («Цзихэ юань-бянь») — краткий перевод на китайский язык «Геометрии» Эвкли-да и первый перевод европейской книги на китайский язык. В Корее математики пользовались «Азбукой арифметики» («Суань-сюе цимэн»), которая в самом Китае считалось утраченной и была перепечатана там с корейского экземпляра в 1660 г. Это было руководство по счетоводству и коммерческой математике. Оно было составлено в период правления династии Юань не без влияния арабской математики. Круг вопросов, излагаемых в этой книге, является вершиной математической мысли дворцовой науки Кореи. Китайский математический труд «Всеобщее изложение искусства счета» («Суаньфа тунцзуань»), написанный в 1592 г. Чэн Давэем, пользовался в Корее и Японии большой популярностью из-за легкости изложения, позволявшей пользоваться книгой без преподавателя. Математика эпохи Ли отнюдь не носила теоретического характера, это была сугубо прикладная наука, применяемая при землемерных работах, в торговле и государственном аппарате. Под государственным надзором было создано несколько измерительных приборов. В начале XV в. были отлиты бронзовые футы (чхок) и разосланы по уездам и городам. В 1474 г., после того как многие медные футы погибли, были изготовлены железные футы. Линейная метрическая система была десятичной, и в основе ее лежал фут, который делился на 10 чхон, на 100 пун, на 1000 ли. Десять футов составляли один чан. Тогда же была составлена таблица перевода старых футов на новые, причем чжоуский фут приравняли к 6 чхон 6 ли, строительный фут — к 8 чхон 9 ли, фут церемониальной утвари — к 8 чхон 3 пун 3 ли, фут для измерения тканей -к 3 чхон 4 пун 8 ли. В основу весовой системы был положен ту, равный 10 сын, 100 хап, 1000 чак, 15 ту составляли малый сок, 20 ту — большой сок. Большой сок использовался в селах для измерения сыпучих тел. В основе весовой системы лежал лян, равный 10 чхон, 100 пун, 1000 ли. \6лянов равнялись 1 кыну. Кроме того, были еще меры веса: большой чхин — 100 кын, средний чхин -30 кын, малый чхин — 3 кын. Таким образом, меры линейные были основаны на десятиричном принципе, а меры сыпучих тел и веса — на смешанном принципе. Эта система официально продержалась до 1902 г., но сохранила своё влияние и после этой даты.

1.4 Поздний период династии Ли

Прикладная математика нашла себе опору среди купечества Сондо и других го- родов. Именно в их среде опытным путем были выработаны правила коммерческого счетоводства и своеобразной двойной бухгалтерии. Но всеобщего распространения математика как самостоятельная наука при династии Ли не получила. Теоретическая математика в XVIII в. получила в Корее некоторое развитие благодаря изучению западноевропейской математики деятелями сирхакпха. В это же время корейские ученые ознакомились с математикой Эвклида, переведенной на китайский язык. Особого внимания заслуживает сочинение Хон Дэёна «Истолкование и использование цифр» («Чжухви суён»). Оно состоит из трех томов, каждый из которых посвящен самостоятельному разделу математики. Общая часть включала правила арифметических действий, пропорции, прогрессии, правила измерения площадей и геометрические понятия, астрономическую математику. Метрическая система, математическое измерение музыкальных тонов составляли другие разделы книги. Книга содействовала дальнейшему развитию корейской математики, алгебры, геометрии, метрологии, геодезии, астрономических вычислений. Последователь Хон Дэёна — Хон Гилчжу — оставил «Новую теорию геометрии» («Гиха синсол»), в которой на основе новых приборов обосновал возможность ее применения при измерениях в небесной сфере и при топографических съемках. В 1855 г. Ли Санхёк написал книгу «Мой взгляд на математику» («Сансыл квангён»), в которой впервые в стране дал анализ взаимозависимости дуги и хорды на основе европейской геометрии. Последний труд содержал серию тригонометрических функций. Новые математические идеи проникли в страну лишь в конце династии Ли, и Нам Сангил в «Сущности математики» сконцентрировал свое внимание на изучении пропорций и уравнений, а Ли Мёнчжил в «Общедоступной математике» популяризировал арифметику.

Вот, например, какие меры массы существовали в Китае в X веке: 1 лан = 10 цянь = 102 фэнь = 103 ли = 104 хао = 105 сы = 106 хо.

Если вначале десятичные дроби выступали в качестве метрологических, конкретных дробей, десятых, сотых и т.д. частей более крупных мер, то позже они по существу стали все более приобретать характер отвлеченных десятичных дробей.

Целую часть от дробной стали отделять особым иероглифом «дянь» (точка). Однако в Китае, как и в древние, так и в средние века десятичные дроби не имели полной самостоятельности, оставаясь в той или иной мере связанными с метрологией.

Раздел 2. Великие математики Китая

К 5-6 в. относится творчество Цзу Чунчжи и его сына Цзу Гэнчжи, которые вычислили число “пи” с точностью до седьмого знака. Цзу Чунчжи открыл способ вычисления объема шара. Одна из примененных им теорем через тысячу лет была доказана итальянским математиком Бонавентурой Кавальери (1598-1647) и получила название «принципа Кавальери».

В VII в. Математик Ван Сяотун разработал методы решений кубических уравнений и сформулировал правило определения объемов тел сложной формы путем разбиения их на призмы и пирамиды. “Канон расчета чжоуского гномона”, “Искусство счета в девяти разделах” и некоторые из книг, написанные впоследствии, были собраны в сборник и прокомментированы в 7 в. группой математиков под руководством Ли Чуньфэна. Этот сборник служил руководством для должностных лиц, обучаемых в тогдашнем недавно установленном ведомстве математики. Хотя некоторое количество чиновников таким образом официально было обучено математике, никаких крупных достижений не появляется в Китае вплоть до 11 в., когда в 1084 г. указанный сборник был отредактирован и издан под названием “Десять канонов по математике” (“Суань цзин ши шу”). Последующие два с половиной столетия знаменуются крупными достижениям китайской традиционной математики. В этот период работают такие известные китайские ученые, как отшельник Ли Е (12-13 вв.), чиновники Цинь Цзюшао (13 в.) и Ян Хуэй (13 в.), странствующий учитель Чжу Шицзе (13-14 вв.). Ими были исследованы методы решений систем уравнений высших степеней, приемы построения прогрессий, магических квадратов, треугольника Паскаля и др. После этого периода в Китае не было написано ни одной важной работы по традиционной математике.

Абак - устройство вычисления, широко используемое в Китае с древнейших времен и до наших дней. Китайская геометрия была в достаточной степени алгебраична, и это привело к тому, что математики Китая первыми стали выражать геометрические формы алгебраическими уравнениями. Правда, в начале они не использовали специальных алгебраических символов, а довольствовались иероглифической записью.

Матричная форма записи алгебраических уравнений. Знаки “0” обозначают ноль, а перечеркнутые знаки - отрицательные числа. Страница из книги по алгебре Чу Шицзе “Драгоценное зеркало четырех элементов”, изданной в 1303 г. Когда иезуиты в конце 16 в. Прибыли в Китай, они нашли людей, живо интересовавшихся наукой, но не знающих традиционных китайских достижений в математике. Ставя целью проповедь религиозных идей, иезуиты быстро осознали, что данное предприятие будет осуществлено успешнее на фоне передачи китайцам достижений европейской науки. Началась эра переводов на китайский язык западных научных работ. В 1607 г. иезуитами и китайцами были переведены шесть первых книг “Элементов” Евклида. Изучение западных работ стимулировало китайских ученых к восстановлению собственной математической традиции, которая была синтезирована с западной математикой. В начале 17 в. математика Китая прекращает самостоятельное развитие.

2.1 КОГУРЁ

О теоретических работах по математике е Когурё ничего не известно. Но когурёсцы, несомненно, были знакомы с основными математическими законами, открытыми к тому времени в Китае, и умели применять их на практике. Были известны Циркуль и угломер, используемые в строительстве и землемерном Деле, и китайские способы построения с их помощью окружности и квадрата, вычисления длины гипотенузы прямоугольного треугольника. В математическом каноне о чжоу-би, т. е. «О шесте солнечных часов» («Чжоу-би суаньцзин») дается приблизительное значение числа пи. Все эти познания применялись в измерении площадей, сыпучих тел и жидкостей, времени, а главное — в строительстве. Изучение погребальных камер в курганах, остатков храмов и пагод обнаруживает несомненное умение когурёсцев вычислять площадь и объем сооружения, пользоваться простейшими измерительными инструментами. Основной линейной мерой яв-[ялся ханьский фут (чи), а при закладке фундаментов широко применялось соотношение 3:4:5, основанное на знании теоремы Пифагора. Применение этого китайского правила можно было наблюдать еще на памятниках Лолана. Ряд сохранившихся у Пхеньяна фундаментов дворцов и павильонов имеют восьмиугольную форму и сложены, как и потолки в погребальных камерах колодезного типа, по способу двух наложенных друг на друга квадратов.

2.2 Пэкче

В V—VI вв. в Китае прославились математики Цзу Чун и его сын Цзу Хэн. и строительство Цзу Чун вычислил отношение длины окружности к ее диаметру (число пи), которое получило приближение 3,1415927... В Европе к этому пришли лишь в 1573 г. Значение данного вычисления было высоко оценено математиками Дальнего Востока. В Японии число пи получило наименование «числа цзу». Цзу осуществил подробное исследование и комментарий китайской «Математики в девяти книгах» (Цзючжан суаньму»), разработку китайского календаря. Обмеры развалин дворцов и храмов Пэкче показывают, что в строительстве широко применялся принцип масштабности, пропорциональности. Так, при обмере строений горной крепости в Оксо ширина нижней части квадрата платформы составила 40 футов (т. е. чи государств Восточная Вэй и Коре), а верхней квадратной платформы — 36 футов, таким образом, деревянная надстройка занимает 3/5 нижней платформы, т. е. 24 фута. Расстояние между столбами тоже составляет 8 футов. Верхняя часть платформы как бы делится на 20 частей. При постройке этой платформы в основу была положена ее нижняя часть, и в дальнейшем строители руководствовались простой пропорциональностью. Излюбленной формой при постройке платформ был квадрат или прямоугольник, одна из сторон которого была вдвое больше другой. Этот строительный прием уходит корнями в ханьскую архитектуру. Для выполнения ответственных строительных работ был создан при дворе инженерный отдел, в который входили мастера по возведению храмов, каменотесы-гранильщики, мастера по изготовлению черепицы, декораторы. Строители Пэкче славились своим мастерством, они помогали Силла возводить 9-этажную пагоду монастыря Хванёнса, в 577, 588 гг. они ездили в Японию с аналогичной целью. У себя в стране они воздвигали сложные дворцовые ансамбли.

2.3 Корё

Развитие теоретической математики по прежнему значительно отставало от успе- хов прикладной математики и счетоводства. Рост государственного, чиновничьего аппарата открывал широкое поле для практического приложения математических знаний. Почти в каждом отделе и учреждении имелись «счетоводы». Курс прикладной математики считался основным в государственных и частных школах, на государственных экзаменах. Важнейшими математическими пособиями служили древние китайские книги: комментарии к «Математике в девяти главах», старинный труд «Чжоуби суаньцзин» — полуастрономического, полу математического характера. «Математика в девяти главах» известна с Силла, теперь идеи этой книги нашли в Коре широкое распространение. Основные ее главы (измерение площадей, дроби, бесконечно большие числа, проценты, пропорции, измерение объемов, коммерческие счеты) трактовали математические вопросы применительно к хозяйству, быту. Около 1261 г. Ян Хуэй составил «Подробное объяснение метода счета в девяти главах» («Сянцзецзючжан суаньфа»). Правила решения многочисленных уравнений излагались в знаменитой книге «Суань сюе чимын» Цзинь Ши-цзяна (1299). Эта книга попала в Корею, впоследствии снова в Китай, где была утеряна, а в XVI в. в Японии она стала основным пособием японских математиков. Складывалась корейская метрическая система со сложными переводами мер и весов многих стран и народов, торговавших с Коре. Летопись пестрит упоминаниями об измерении площадей, сыпучих и жидких тел, о взвешивании металлов и отмеривании тканей, о ценах на те или иные товары. Интересно при этом отметить, что не существовало единых линейных мер длины, объема, веса, площадей, пригодных для любой группы однородных измеряемых объектов. Для измерения полей употреблялась одна линейная мера, для тканей — другая, для измерения сыпучих тел — несколько (особые для риса, бобовых, проса), для взвешивания — две меры. Для надзора за правильностью применения этих мер была учреждена особая палата мер и весов. В этот период в Коре проник способ счета на бирках. Тем временем на дальнем востоке Евразии другие математики и астрономы пытались постичь те же тайны природы на своём научном языке. В Элладе этот язык состоял, в основном, из чертежей - а в Китае из иероглифов. В сущности, иероглиф - это тоже чертеж особого рода, составленный из простых значков: каждый значок изображает одно простое понятие. Например, знак Шу означает "число", а знак Сюэ - "учение". Однако их сочетание - Шу Сюэ - обозначает не только учение о числах (то есть, арифметику), но и всю математическую науку. Как в таком случае назвать геометрию" Очень просто: Цзи Хэ Сюэ - "учение о том, сколько чего". То есть, геометрию китайцы воспринимали как науку, рассчитывающую свойства фигур – и только! С этой точкой зрения наверняка согласился бы ученый из древнего Вавилона; но Пифагор или Платон ни за что не признали бы правоту китайцев. Если геометры займутся одними только расчетами – кто будет выяснять сущность природных тел или научных понятий" Ученый китаец отвечал на такой вопрос кратко и просто: ничего не нужно выяснять! Вся суть природы и науки уже выражена в иероглифах. Небо даровало их нашим предкам 20 веков назад - и ничего тут ни убавить, ни прибавить. Можно комбинировать известные иероглифы в новом порядке; но изменять их смысл нельзя - это противоречит законам природы и воле Неба! В математике выдающимся китайским достижением было использование десятичных дробей и пустой позиции для обозначения 0, вычисление числа "Пи", открытие метода решения уравнений с двумя и тремя неизвестными. Древние китайцы были образованными астрономами, составили одну из первых в мире звездных карт. Поскольку древнекитайское общество было аграрным, централизованная бюрократия должна была решать сложные технические вопросы, связанные в первую очередь с использованием и охраной водных ресурсов, поэтому высокого развития в Древнем Китае достигли астрономия, знание календарных расчетов и астрологических прогнозов, математика, физика и гидротехника в их инженерном использовании.

При изучении древнекитайской математики значительным препятствием является отсутствие переводов, хотя мы благодаря книгам Миками и Нидхема хорошо осведомлены о положении математики в Древнем Китае. Тем, кто знает русский язык, доступен значительно больший материал, имеется даже русский перевод классического математического произведения «Девять книг (разделов) о математическом искусстве» (Цзю чжан суань шу). Как эта книга, так и «Чжоу-би» в своем нынешнем виде дошли до нас от периода династии Хань (206 г. до н.э. – 220 г. н.э.), но в них, конечно, может содержаться материал значительно более раннего происхождения. Книга Чжоу-би только частично посвящена математике, но интересно, что в ней рассматривается теорема Пифагора. Напротив, «Девять книг (разделов)» – чисто математическое произведение, которое вполне характерно для древнекитайской математики следующего тысячелетия, да и более поздней. Очень стары также некоторые диаграммы из книг периода династии Хань, например из «Книги перемен» (И цзинь, VIII—VII вв. до н.э.). В числе их следующий, связанный со многими легендами, магический квадрат (ло шу):

.

Чжень Шен-Шень (Chern Shiing-Shen), выдающийся китайский

математик, родился в 1911 г. в Китае. В 1930 году он окончил университет в Тяньцзине. В 1934 году Чжень получил стипендию для обучения на Западе, где написал под руководством Бляшке диссертацию (1936). В 1937-1943 годах он профессор математики университета Синьхуа в Пекине. Затем в течение двух лет по приглашению Веблена работает в институте Высших Исследований в Принстоне, где получает обобщение формулы Гаусса-Бонне для произвольных римановых многообразий. Позже это доказательство привело Чженя к открытию характеристических классов для комплексных векторных расслоений (классы Чженя).
       После второй мировой войны Чжень возвращается в Китай, где участвует в организации Института математики Китайской Академии Наук. В 1949 году Чжень является профессором математики в Чикагском университете, а в 1960 году переезжает в Калифорнийский университет в Беркли, где организует Математический научно-исследовательский Институт и является его первым директором.
       С 1981 года Чжень активно помогает восстанавливать математическую жизнь в Китае, нарушенную в ходе культурной революции. Он организует Нанкайский математический институт в Тяньцзине и до недавнего времени был его директором. Сейчас он Почетный директор этого института.
       Чжень написал более 200 научных работ. Кроме работ по алгебраической топологии следует отметить также его исследования по финслеровой геометрии, геометрии тканей.
       Чжень является лауреатом ряда международных наград, Почетным академиком АН Китая, Почетным членом Индийского математического общества, Королевского научного общества Великобритании, Лондонского математического общества и др. В 1992 году в связи с его 80-летием состоялся международный конгресс "Черн - великий математик 20 века". В 2002 году Казанский государственный университет наградил его медалью имени Лобачевского.

Раздел 3.Математические теории

3.1 Теорема Пифагора

Китайцы с ранних времен знали теорему Пифагора, а в последствии представили собственное ее доказательство. Согласно легенде, Чжоу-гун, младший сын Вэнь-вана, имел беседу с математиком Шан Гао, в которой упоминаются закономерности, вытекающие из теоремы Пифагора: если надломить линейку-чи под прямым углом на расстоянии 4 и 3 от концов, то кратчайшее расстояние между ними будет равно 5. Частная формулировка теоремы Пифагора рассматривается в “Счетном каноне о чжоуском гномоне” (“Чжоу би суань цзин”), появившемся в эпоху “Борющихся царств”. Ее доказательство проводится в комментариях к указанному трактату, написанных в 3 в. н.э. Чжао Шуаном (Чжао Цзюньцин). Комментатор приложил чертеж и словесно выразил отношения между гипотенузой и двумя катетами. Доказательство значительно отличается от евклидовского.

Задача “сломанного бамбука”, образующего прямоугольный треугольник. Из книги известного математика Яна Хуэя “Подробное объяснение метода счета в девяти разделах” (“Сян цзе цзю чжан суань фа”), изданной в 1261 г.

3.2 Дроби

В “Искусстве счета в девяти разделах” дроби рассматриваются как естественная часть результата деления, остаток от деления, который принимается как числитель дроби, знаменателем которой является делитель. Например, при делении 22 на 5, получается 4 и остаток 2. Это даёт дробь 2/5. Дробь, таким образом, всегда меньше единицы. Чтобы получить сумму дробей, надо следовать инструкции:

“Перемножте числители и знаменатели слагаемых дробей. Сложите произведения, и получите делимое. Перемножте знаменатели, и получите делитель. Исполните разделение. Если имеется остаток, свяжите его с делителем”.

Сумма набора дробей, таким образом, есть результат деления, состоящий из целого числа плюс дробь. То, что десятичная система использовалась с самых начал развития математики в Китае, дало китайцам существенное преимущество, полагая основание для многих достижений, которые они позже сделали. Десятичный способ записи дробей был достаточно удобен и естественным образом вытекал из десятичной системы мер и весов. Десятичными дробями оперировал в 3 в. математик Лю Хуэй при решении уравнений и при записи измеряемых величин. В это время они не получили широкого распространения, поскольку китайцы были так искусны в использовании обычных дробей, что многие из них просто не чувствовали потребность в переходе к десятичным дробям. Однако они все чаще начинают появляться в литературе. Так, например, в официальной хронике династии Суй в 635 г. приводится число “пи” в виде десятичной дроби 3,1415927, записанной не числовыми знаками, а иероглифами. Полноценное систематическое применение десятичных дробей во всех арифметических действий встречается в трудах математиков 13 в. Ян Хуэя и Цинь Цзюшао. Первое свидетельство использования десятичных дробей в Европе найдено в испанской рукописи 976 г., то есть приблизительно на тысячу лет позже, чем самое раннее китайское упоминание. Первый специальный трактат, посвященный десятичным дробям, был написан Симоном Стевиным в 1585 г.

3.3 Вычисление площадей и корней

В “Искусстве счета в девяти разделах” (“Цзю чжан суань шу”) даются алгоритмические предписания для вычисления площадей прямоугольника, круга, доли круга и сферы. Например, для вычисления площади круга дается следующий алгоритм: “Умножите диаметр на самого себя. Утройте полученное. Делите его на четыре”. В этом алгоритме “пи” принимается равным 3. В дальнейшем комментаторы применяли улучшенные значения для «пи». Нахождение корня мыслилось как обратный процесс возведения в квадратную степень,а с геометрических позиций предполагалось, что корень числа – это сторона квадрата, площадь которого равна этому числу. Сам метод вычисления корня имел алгебраическо-геометрический подход.

В “Искусстве счета в девяти разделах” (“Цзю чжан суань шу”) приводится задача найти кубический корень из числа 1860867 (ответ - 123), при решении которой используется метод, подобный в Европе “методу Горнера”, развитому Вильямом Джорджем Горнером в 1819 г. Это метод оценки корня многократной аппроксимацией, каждый раз более точной, чем на предшествующем шаге. Горнер осуществлял аппроксимацию, увеличивая десятичные дроби. Ранее, в 1767 г., Лагранж сделал это цепными дробями. “Лагранжев метод” использования дробей был развит в Китае к 1 в. до н.э. (за 19 столетий до Лагранжа) и был улучшен в 3 в. н.э. Лю Хуэем (за 15 столетий прежде Горнера). В своих комментариях к трактату “Цзю чжан суань шу” Лю Хуэй дал обоснование метода извлечения корней в терминах десятичных дробей.

3.4 Значение числа “пи”

Число “пи” необходимо было древним математикам для вычисления площади круга и объема сферы. Оно, как известно, выражает отношение окружности круга к его диаметру. Это отношение является иррациональным, т.е. не может быть выражено в виде дроби с целыми числами. У китайцев не было понятия иррационального числа, и они не испытывали никаких трудностей при записи иррациональных чисел, подобных корню из двух или числу “пи”. Если в самом раннем китайском математическом сочинении “Чжоу би суань цзин” (“Счетный канон о чжоуском гномоне”) число “пи” принимается равным 3, то в дальнейшем заботой математиков Китая было получить как можно более точное его значение.

В 3 в. Математик Лю Хуэй методом исчерпывания вычислил “пи” как 3,1416. Около 480 г. н.э. Цзу Чунчжи (429-500), вписывая в окружность 12288- и 24576-угольник, получил значение “пи”, находящееся в пределах 3,1415926 и 3,1415927. Он также дал приближенное значение “пи”, равное 22/7 и 355/113. Последнее приближение в Европе было найдено в 1573 г. (современная величина “пи” - 3,1415926536...).

Диаграмма, объясняющая метод исчерпывания для подсчета значения "пи", разработанный Лю Хуэем в 1264 г.

3.5 Треугольник Паскаля

В эпоху Сун, по крайней мере к началу 12 в., китайцы были знакомы с треугольником для вычисления биноминальных коэффициентов, получившим в Европе название “треугольник Паскаля” - правило, которое дает коэффициенты “биноминального” выражения типа (x + 1), возводимого в различные степени. Треугольник коэффициентов позволяет легко составить уравнение любой степени.

Способ построения “треугольника Паскаля” несложен. Средние числа в каждой строке, начиная с третьей, образуются за счет сложения двух чисел, стоящих над получаемым числом строкой выше. Так, в четвертой строке: 4 = 1 + 3; 6 = 3 + 3; в пятой строке: 5 = 1 + 4; 10 = 4 + 6, и т.д. Такое простое правило позволяет легко найти коэффициенты биноминального уравнения типа (1 + х)n (в общем виде - (a + b)n), получить которые другим способом было бы весьма затруднительно.

Живший в 13 в. Математик Ян Хуэй в книге “Подробное объяснение метода счета в девяти разделах” (“Сян цзе цзю чжан суань фа”) приводит рисунок подобного треугольника для разложения степеней бинома вплоть до шестой. На рисунке треугольника числа изображены таким образом, что можно предположить, что основа треугольника первоначально стояла вертикально слева. Таким образом, степени неизвестных стояли бы по горизонтали.

Этот треугольник интересен для арифмосемиотики тем, что он задает структуру набора гексаграмм “Книги перемен”. Полное их количество равно числу 26. При замене прерывистой и сплошной черт буквами a и b получится “уравнение”, выражающее посредством коэффициентов количество гексаграмм, которые имеют соответствующее степени количество указанных черт.

(a + b)6 = a6 + 6a5b + 15a4b2 + 20a3b3 + 15a2b4 + 6ab5 + b6

Метод расчета биноминальных коэффициентов был открыт в Европе в 1527 г. Блез Паскаль описал его в 1654 г. в “Трактате об арифметическом треугольнике”, приблизительно 500 годами позже его применения в Китае. Однако первыми, возможно, данный метод разработали индусы.

Диаграмма из изданной в 1303 г. книги Чу Шицзе “Драгоценное зеркало четырех элементов”, которая иллюстрирует “табулированную систему для вскрытия биноминальных коэффициентов”, известную в Европе как “треугольник Паскаля” и представляющую собой “старый метод” математика Цзя Сяня, разработанный им в 1100 г.

3.6 Решение систем уравнений

В книге “Искусство счета в девяти разделах” (“Цзю чжан суань шу”) приводятся решения систем уравнений 1-й и 2-й степени.

Первые фактические решения кубических уравнений в Китае были произведены Ван Сяотуном в 7 в., а в Европе - Леонардо Фибоначчи в 13 в., который, как полагают, находился под влиянием китайских источников. В книге Цинь Цзюшао “Девять отделов математики” (“Шу шу цзю чжан”), изданной в 1247 г., был дан метод вычисления действительный корней алгебраических уравнений любой степени с численными коэффициентами. Этот метод близок “методу Горнера”, открытому в 1819 г. Для обозначения неизвестных в системах уравнений китайцы применяли иероглифы “тянь” (“небо”), “жэнь” (“человек”) и “ди” (“земля”). Арифметические действия обозначались фиксированными иероглифами и, по сути, заменяли знаки арифметических действий. При записи отрицательных чисел они перечеркивались косой линией. При счете с помощью счетной доски для обозначения чисел разных знаков использовались палочки красного (положительные числа) и черного (отрицательные числа) цветов или треугольного и квадратного сечений. Кроме того, счетная доска была размечена на позиции, которые связывались с определенными компонентами арифметических действий. Были специальные позиции для неизвестных, степеней и т.д.

В период Сунн такая разметка счетных досок привела к появлению матричного способа вычислений. Ячейки матрицы выполняли функцию компонентов уравнения. Однако общей теории уравнений китайцы не выработали.

В книге “Искусстве счета в девяти разделах” (“Цзю чжан суань шу”), написанной в эпоху раннего Хань, ряд задач сводится к системам линейных уравнений. Например, задача о трех сортах зерна сводится к решению следующей системы уравнений, которая записывается в виде матрицы коэффициентов.

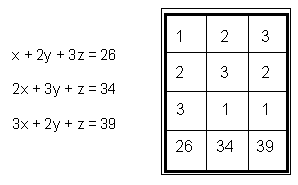
Здесь коэффициенты первого уравнения помещены в левую колонку, а коэффициенты второго и третьего уравнений - в среднюю и правую. При этом в верхнем ряду размещаются коэффициенты первого неизвестного (x), в среднем - второго (y), а в нижнем - третьего (z). Решение производилось сокращением коэффициентов в колонках. Например, для начала коэффициенты средней колонки умножаются на 3 - коэффициент в первой позиции в правой колонке, а затем из средней колонки вычитается правая колонка такое количество раз, какое необходимо, чтобы получить 0 в первой позиции средней колонки, и т.д.

При продолжении процедуры могут получиться отрицательные коэффициенты. В книге даются детальные методы вычисления с положительными и отрицательными коэффициентами в количестве от 2 до 7, что является первым использованием отрицательных чисел в истории математики. Отрицательные числа применяются в Индии с 6 в., а в Европе - с 16 в.

3.7 Система счисления

Система счисления у китайцев всегда была десятичной, и уже во втором тысячелетии до нашей эры мы встречаемся с числами, записанными с помощью девяти символов в позиционной системе. Такой способ записи получил права гражданства в период династии Хань или еще раньше. Девять знаков изображались с помощью бамбуковых палочек, по-разному размещенных; например,  обозначало число 6729, которое именно таким образом и записывалось. Арифметические действия выполнялись с помощью счетных досок; пропуски, т. е. пустые места, обозначали нуль (специальный знак для нуля появляется только в тринадцатом столетии н.э., хотя он, возможно, и старше). При календарных расчетах применялось нечто вроде шестидесятичной системы, что можно сопоставить с сочетанием двух связанных друг с другом зубчаток, из которых одна имеет двенадцать зубьев, а другая – десять. Так число шестьдесят стало единицей высшего разряда, «периодом» («Катэйский период» в одном из стихотворений Тенниорна).

Математика «Девяти книг» состоит в основном из задач и общих указаний, как их решать. Эти задачи возникают из практических применений арифметики и сводятся к алгебраическим уравнениям с числовыми коэффициентами. Вычисляются и квадратные, и кубические корни, например число  определяется как корень квадратный из. При вычислениях с окружностью принимается. Ряд задач сводится к системам линейных уравнений, например к системе

которая записывается «матрицей» своих коэффициентов. Решение этой системы приводится в таком виде, которое мы теперь назвали бы «матричным преобразованием». Эти матрицы содержат и отрицательные числа, здесь впервые появляющиеся в истории математики.

Китайская математика занимает особое положение – практически до последних лет мы видим в ней непрерывность традиции, так что мы можем выяснить, каково ее место в обществе, более полно, чем в случае египетской и вавилонской математики, принадлежащих исчезнувшим цивилизациям.

Например, мы знаем, что кандидаты, подвергавшиеся экзамену, должны были знать «Десять классиков» в точно определенном объеме и что успех на экзамене определяется в основном умением точно цитировать тексты на память. Таким образом, традиционное учение передавалось из поколения в поколение с обременительной тщательностью. В такой застойной культурной атмосфере новые открытия стали чрезвычайно редким явлением, а это опять-таки обеспечивало неизменность математической традиции. Такая традиция могла передаваться в течение тысячелетий и могла пострадать только иногда, при больших исторических потрясениях.

3.8 Магические квадраты

Магический квадрат - это квадратная матрица чисел, располагающихся таким образом, что их суммы по диагоналям или в любом ряду по горизонтали и вертикали всегда составляют одно и тоже число. В китайской науке среди подобных матриц наиболее значимой является числовая схема Ло шу - магический квадрат третьего порядка, в котором сумма трех чисел в любом направлении равна 15.

Упоминания о Ло шу (“Писание [из реки] Ло”) встречаются в литературе эпохи “Борющихся царств”. Изображения этой схемы, относящиеся к данному времени, до нас не дошли. Конкретных описаний также не имеется. В “Си цы чжуани” (I, 11) говорится только, что данную схему “совершенномудрые берут за образец” [1]. В “Чжуан-цзы” (4-3 вв. до н.э.) Ло шу рассматривается как некая девятеричная схема, благодаря которой “осуществляются жизненные свойства вещи” [2]. В раннеханьское время появляется легенда, согласно которой Фуси увидел начертания Ло шу на панцире огромной черепахи из реки Лошуй. Схема Ло шу, составленная из связанных кружков, как они известна в настоящее время, представлена в трактате сунского мыслителя Чжу Си (12 в.) “Чжоу и бэнь и” (“Основной смысл чжоуских перемен”).

Китаевед А.И. Кобзев обнаружил во входящем в “Дао цзан” (“Сокровищница дао”, № 1166 по К.М. Шипперу) сочинении “Фа хай и чжу” (“Жемчуг, оставленный морем законов-дхарм”) полумагический квадрат третьей степени, не описанный ранее в западной синологии и представляющий собой числовую матрицу, в которой суммы чисел в правом столбце и нижней строке равны 9, а по всем остальным направлениям - 18. По А.И. Кобзеву, данный квадрат образуется из Ло шу посредством перемещения чисел по отмеченной на схеме траектории.

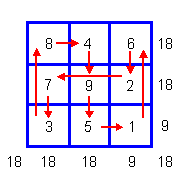
Другой способ преобразования Ло шу для получения данного полумагического квадрата, состоит из двух последовательных процедур: прибавление ко всем числам Ло шу числа 4 и суммирование разрядов в получившихся при этом четырех двухразрядных числах. В общем случае, подобные полумагические квадраты можно строить, прибавляя к девятиклеточному магическому квадрату числа, равные 1 + 3n (где n = 0; 1; 2...)

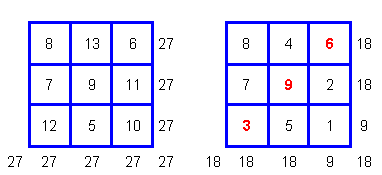
В получившемся квадрате по одной из диагоналей располагаются число 3 и кратные ему числа 6 и 9. При развороте данного квадрата на один шаг против часовой стрелки эти числа выстроятся по вертикали, выполняя как бы функцию некоей организационной оси. Представленный в таком виде полумагический квадрат может рассматриваться в качестве инструмента по преобразованию порядка “взаимопорождения” триграмм (и стихий) в “современный”. Если на круговую схему с порядком “взаимопорождения”, ориентированным в соответствии с реконструированными традиционными китайскими представлениями, наложить этот квадрат, то между его числами и “младшими” триграммами установятся достаточно определенные связи: число 4 будут находиться вблизи триграммы Ли, число 8 - Сюнь, число 7 - Чжэнь, число 5 - Кань, число 1 - Дуй, число 2 - Гэнь.

Структура порядка “взаимопорождения” допускает вставку “старшей” триграммы Кунь только рядом с коррелирующей с ней триграммой Чжэнь. Это означает, что ее можно связать с числом 3. Триграмму Цянь можно поместить только в соседстве с коррелирующей с ней Сюнь, для которой ближайшим из тройки 3, 6 и 9 будет число 9. Число 6 остается не связанным со “старшими” триграммами и будет обозначать точку баланса всей схемы, делимой выделенной диагональю полумагического квадрата на две половины, начала которых связываются с кульминационными периодами годичного и суточного циклов - полуночным и полуденным временем суток, днями зимнего и летнего солнцестояния.

Отталкиваясь от указанной корреляции триграмм и чисел, последние можно перенести на базис-схему с обратным “современным” порядком триграмм. В этом случае числа из полумагического квадрата, коррелирующие с “младшими” триграммами, выстроятся в порядке перечисления с 1 по 8. Числа 3, 6 и 9, не имеющие корреляций с “младшими” триграммами, надо просто поместить в подходящие для них промежуточные места. При этом “старшие” триграммы Цянь и Кунь примут положения, соответствующие их традиционной корреляции в “современном” порядке - с Дуй и Гэнь.

Аналогичным образом можно показать еще ряд преобразований магического квадрата третьего порядка в разного рода полумагические квадраты, которые также служат связью между порядками триграмм и математически определяют структуру построенных на их основе арифмосемиотических схем. Поскольку данные схемы, как показывает реконструкция, имеют достаточно древнее происхождение, относящееся, возможно, к эпохе Западного Чжоу, то и магический квадрат Ло шу следует датировать этим же временем.

В 13 в. математик Ян Хуэй занялся проблемой методов построения магических квадратов. Его исследования были потом продолжены другими китайскими математиками. Ян Хуэй рассматривал магические квадраты не только третьего, но и больших порядков. Некоторые из его квадратов были достаточно сложны, однако он всегда давал правила для их построения.

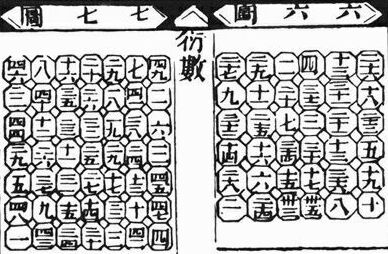
Два магических квадрата, построенных Ян Хуэем и позднее опубликованных в “Суань фа тун цзуне” (1593 г.).

Вывод

В ходе работы я нашла интересную информацию по истории математики в древней цивилизации Китай, а также узнала учёных Китая таких как Лю Хуэю, Ли Е, Ян Хуэй, Ли Чуньфена, Ван Сяотун, Цинь Цзюшао, Чи Шинцзе, Чу Шинцзе и другие, а также их вклад в математику.

Древний Китай обогатил мировую науку и культуру значительными достижениями: он является родиной такого изобретений, как компас (III век до н.э.), спидометр (III век до н.э.), сейсмограф (II век до н нашей эры), порох (X ст.н. э), книгопечатания (VI-VIII века), фарфор (III - V в.). В области математики был открыт метод решения уравнений первой степеня с двумя и тремя неизвестными, вычислено отношение длины окружности к ее диаметру - число л. В области астрономии китайцы знали, как высчитывать дату затмения солнца.

Список литературы:

1. Бурбаки Н. Очерки по истории математики. - М., 1963.

2. Болгарский, Б.В. Очерки по истории математики [Текст] / Б.В. Болгарский. – М.: Вышейш. шк.,1974. – 287 с.

3. Депман, И. Я. История арифметики [Текст]: пособие для учителей / И. Я. Депман. – М.: Просвещение, 1965. – 415 с.

4.http://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0_%D0%B2_%D0%B4%D1%80%D0%B5%D0%B2%D0%BD%D0%B5%D0%BC_%D0%9A%D0%B8%D1%82%D0%B0%D0%

5. http://kosilova.textdriven.com/narod/studia3/math/translatio/3.htm

6. http://matem.uspu.ru/i/inst/dekanat/050201_mathematics/DPP/DPP07.pdf