На правах рукописи
БЫЧКОВ Евгений Дмитриевич
УДК 621. 398:621.317:519.5
МОДЕЛИ УПРАВЛЕНИЯ И МОНИТОРИНГА СОСТОЯНИЯМИ ТЕЛЕКОММУНИКАЦИОННОЙ СЕТИ С ИСПОЛЬЗОВАНИЕМ
ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ
Специальность: 05.12.13 – Системы, сети и устройства телекоммуникаций
А В Т О Р Е Ф Е Р А Т
диссертации на соискание ученой степени доктора технических наук
ОМСК-2010
Работа выполнена на кафедре «Радиотехнических устройств и систем диагностики» ГОУ ВПО Омского государственного технического университета
Научный консультант: доктор технических наук, профессор,
академик МАН ВШ
Вешкурцев Юрий Михайлович
Официальные
Оппоненты:
Ведущая организация:
Защита состоится « ___» __________20__г., в ____ час. на заседании
диссертационного совета ________
Ваш отзыв в 2-х экземплярах, заверенной гербовой печатью, просим направить по адресу:
С диссертацией можно ознакомиться в библиотеке университета
Автореферат разослан «____» 20___ г.
Ученый секретарь
Диссертационного совета _____
Актуальность. За последнее десятилетие технология электросвязи или телекоммуникаций значительно видоизменилась, она стала интеллектуальной и проникла во все сферы деятельности общества, стала неотъемлемой его частью. Появились и продолжают возникать все новые виды услуг, предлагаемые обществу. В связи с бурным развитием IP-технологии, связанной с возможностью передачей и обработкой различных услуг связи по одним и тем же транспортным сетям, возникла необходимость пересмотреть концепции построения самих транспортных сетей связи и управления ими.
Составной частью современных сложных телекоммуникационных сетей являются распределенные системы управления и мониторинга (РСУиМ), к которым должны предъявляться очень высокие требования по качеству функционирования, с целью поддержания высокого уровня работоспособности элементов телекоммуникационной сети и качественного обеспечения как доставки услуг сети до потребителя, так и внедрения новых услуг. Поэтому задачи управления сетями связи являются актуальными.
Проблемам управления пакетными сетями связи, связанным с разработкой методов динамического управления и моделированием алгоритмов маршрутизации посвящены работы В.Г. Лазарева, Г.П. Захарова,
М.Н. Арипова и их учеников. Современные задачи управления мультисервисными сетями телекоммуникаций (поддержание их состояния и услуг) отражены в работах Я.С. Дымарского, Н.П. Крутяковой и Г.Г. Яновского, докторских диссертационных работых А.А. Костина, В.П. Мочалова, кандидатских работах В.В.Лохтина, Е.С. Коротокова, С.В. Яковлева, в которых основой алгоритмов анализа и определения состояний сложных элементов сети при управлении и мониторинге являются аппараты статистических решений, теории телетрафика, очередей, СМО. Успешное использование данных математических методов возможно в том случае, если априорная информация исходных данных статистически устойчивая, т.е. полная.
При управлении и мониторинге сложных процессов и сетевых элементов (СЭ) телекоммуникационной сети в реальном масштабе времени вышеприведенный аппарат может быть и неэффективным, т.к. возможны случаи, когда исходная информация является статистически неустойчивой либо неполной, либо вовсе отсутствует.
Из-за возрастающей сложности решаемых задач СЭ в системе телекоммуникаций усложняются и сами задачи управления и мониторинга. Следует отметить, что современные системы управления и мониторинга (СУиМ) являются человеко-машинными системами и с возрастающей сложностью объектов управления (ОУ/СЭ) возникает так называемый "человеческий фактор" при поиске критических состояний ОУ и сетевой ситуации. Этим самым вводится субъективный фактор в решение сложных задач мониторинга и распознавания качественными методами, что плохо поддается формализации классическими методами принятия решений.
Таким образом, возможная неустойчивость и неполнота статистической информации или её отсутствие, сложность ОУ и субъективный фактор в мониторинге и распознавании состояния распределенных ОУ приводит к методам принятия решений, основанным на концепциях теории нечетких (F) множеств.
Цель диссертационной работы заключается в развитии теории и разработке методов управления и мониторинга состояниями сетевых элементов NE и процессов телекоммуникационной сети в условиях неполной информации с использованием теории нечетких множеств (ТНМ).
Для достижения цели исследования была поставлена и решена следующая совокупность научно-технических задач:
- Адаптирована теория нечетких множеств к анализу систем связи.
- Разработана структурная схема иерархического управления на основе F-множеств.
3. Разработана и исследована F- модель объекта управления (ОУ).
4. Разработаны и исследованы F-модели транспортных каналов сети
управления.
5. Разработаны модели и методики принятия решения, распознавания и
прогнозирования состояния ОУ на основе F- множеств.
6. Разработана модель и алгоритм управления канальным ресурсом транспортной сети на основе F-методов.
7. Разработана F- модель и алгоритм маршрутизации данных в транспортной сети.
Методы исследования. В настоящей работе использованы методы теории вероятностей, теории алгебры логики, теории конечных автоматов, теории нечетких множеств, теории матричного анализа, теории систем массового обслуживания.
Научная новизна. В диссертационной работе на основе методов теории нечетких множеств разработан новый подход к задачам управления и мониторинга элементов телекоммуникационной сети, который может быть использован на этапах проектирования и эксплуатации РСУиМ, а также адаптированы основные теоретические положения и операции F- множеств для анализа систем связи. В связи с этим были получены новые научные результаты.
1. Показана область использования ТНМ в системах связи и разработана иерархическая модель управления сетью связи.
2. Рассмотрены и доказаны теоретические положения нечеткой меры и интеграла при анализе процессов систем связи.
3. Доказана теорема о взаимосвязи степени нечеткой связанности и степени нечеткости Ягера. Введены понятия степени нечеткой концентрации устойчивости нечетких множеств.
4. Разработаны F-модель цифрового объекта управления и две
методики определения состояния объекта управления на основе F-интеграла.
5. Разработаны методики принятия решения о состоянии цифрового объекта управления на основе метрического расстояния, меры включения, нечеткой меры пресечения, апостериорной нечеткой вероятности, на основе F-интеграла. Доказано выражение Байеса в нечеткой форме для функций с различной модальностью.
6. Разработана модель и методика прогнозирования состояния объекта управления на основе полинома Ньютона с использованием F-информации.
7. Построена теория, описывающая как механизм принятия решения о состоянии цифрового когерентного канала связи и регистрации единичного элемента на основе априорных F-шкал, так и формирование нечеткого кодового слова с использованием теории возможностей, а также процедура принятия решения о состоянии ОУ с учетом влияния каналов управления и реакции. Предложена теоретическая основа и F-модели цифровой фильтрации сигналов.
8. Разработан алгоритм цифрового приема сигналов на основе нечеткой логики в программной среде MATLAB.
9. Разработаны F-модель управления канальным ресурсом, алгоритм и
реализация F- управления канальным ресурсом.
10. Разработаны функциональные схемы F-вывода для различных
приоритетов очередей при управлении канальным ресурсом, модель СеМО системы управления «Менеджер- Агент».
11. Разработаны модель и алгоритм F- маршрутизации пакетов в сети
управления.
Основные положения, выносимые на защиту.
1. Иерархическая модель распределенной сети управления и
мониторинга сетью связи.
2. Теоретические положения нечеткой меры и интеграла при анализе процессов систем связи, теорема о взаимосвязи степени нечеткой связанности и степени нечеткости Ягера, степени нечеткой концентрации устойчивости нечетких множеств.
3. F-модель цифрового объекта управления и методика определения состояния ОУ на основе F-интеграла. Методика принятия решения о состоянии цифрового объекта управления с использованием метрического расстояния, меры включения, нечеткой меры пресечения, апостериорной нечеткой вероятности и нечеткого интеграла. Выражение Байеса в нечеткой форме для функций с различной модальностью.
4. Методика прогнозирования состояния объекта управления на основе полинома Ньютона с использованием F-информации.
5. F-модели дискретного канала со стиранием двоичного когерентного приемника, решающего устройства и методики формирования F-кодового слова на основе теории возможностей, а также модель и методика принятия решения о состоянии объекта управления с учетом состояния каналов связи.
6. Алгоритм цифрового приема сигналов на основе нечеткой логики в программной среде MATLAB.
7. F-модель управления канальным ресурсом, алгоритм и реализация F- управления канальным ресурсом.
8. Функциональные схемы F-вывода для различных приоритетов очередей при управлении канальным ресурсом, модель СеМО системы управления «Менеджер-Агент».
9. Модель и алгоритм F- маршрутизации пакетов в сети управления.
Практическая ценность работы заключается в создании теоретико-прикладных основ анализа и проектирования модулей распределенных систем управления различного назначения в условиях неполноты информации и включает следующее:
- расширение диапазона идентификации повреждений цифрового устройства (ЦУ) с использованием методики распознавания их состояний на основе модифицированного критерия Байеса в нечеткой форме и методики распознавания на основе n-кратного нечеткого интеграла;
-расширение функциональных возможностей системы прогнозирования АСУ состояний ЦУ за счет использования прогнозирующих полиномов на основе метода нечеткого обобщенного параметра. Данный метод прогнозирования позволяет в зависимости от полноты текущей информации также использовать опыт технического персонала;
-увеличение разрешающей способности приемника на основе методики регистрации единичного элемента с использованием композиционной априорной нечеткой шкалы и правила принятия решения на основе нечеткой логики. Исследование данной методики показало, что она достаточно эффективно работает в области помех малой и средней интенсивности;
- аналитические соотношения позволяющие оценивать состояния транспортных каналов в системе мониторинга;
- способ управления канальным ресурсом на основе прямых нечетких продукционных правил вывода modus ponens для нечеткой СМО;
- использование формализованного опыта операторов (технический персонал) и разработчиков, который является иногда единственным источником наиболее достоверной информации в периоды эксплуатации и разработки АСУ.
Реализация работы осуществлена в виде участия в хоздоговорных научно-исследовательских работах, проводимых Омским ИРСиД.
Результаты работы использованы в учебных процессах проводимых кафедрами РТУ и СД, ССИБ ОмГТУ, СПИ ОмГУПС, «Электросвязь» ИРСиД в рамках дисциплин «Сетевые информационные технологии», «Основы построения телекоммуникационных сетей и систем», «Сети и системы коммутации», «Теория электрической связи».
В рамках диссертационной работы автор осуществлял руководство студенческой работой, которая была отмечена серебряной медалью «За лучшую научную работу» по итогам открытого конкурса 2003 года на лучшую работу студентов в ВУЗах РФ Министерством образования РФ.
Апробация работы. Материалы и основные положения диссертации обсуждались на 3-х научных сессиях ВНТО РЭС им. А.С. Попова, 20-ти международных, всероссийских конференциях, симпозиумах, конгрессах (г. Новосибирск, г. Омск, г. Воронеж, г. Саратов, Н-Новгород, г. Кисловодск, г. Казань, г. Хабаровск), 6-ти региональных конференциях (г. Ташкент, г. Томск, г. Омск).
Результаты работы докладывались и получили одобрение на расширенных семинарах кафедры РТУ и СД и Радиотехнического факультета ОмГТУ, семинарах кафедры «Системы передачи информации» и на заседаниях постоянно-действующего НТ семинара ОмГУПС.
Публикации. По результатам диссертации опубликовано 64 работы, из них 33 материалы и тезисы докладов на различных международных симпозиумах и научно-технических конференциях, 14 статей в научных изданиях, в которых разрешается публиковать научные результаты докторских диссертаций, 12 статей в межвузовских и международных сборниках научных трудов, 2 учебных пособия электро- и радиотехнических специальностей, 1 монография, 1 комплект программ в Госфонде алгоритмов и программ, 1 авторское свидетельство на изобретение.
Структура и объём работы. Диссертация состоит из введения, шести глав, заключения, списка литературы ( 306 наименований) и ___ приложений, Общий объём работы составляет 356 страниц.
СОДЕРЖАНИЕ РАБОТЫ
Во введении дана краткая характеристика состояния проблемы, обоснована актуальность темы, определены цель и задача работы, сформулированы полученные результаты и научные положения, выносимые на защиту.
Первая глава посвящена анализу проблемы управления телекоммуникационными сетями связи. Рассмотрены общие принципы, задачи и архитектуры системы управления в основе которых лежит идеология TMN. Приведен анализ системы OSS (Система поддержки функционирования предприятий связи) применительно к телекоммуникационным сетям. Рассмотрены математические модели иерархической системы TMN на основе теории СМО и модели управления сетью связи на основе теорий нейронной сети и тензорного анализа. Приведен пример реализации системы иерархического управления телекоммуникационной сетью ЕСМА (Единая система мониторинга и администрирования) ОАО «РЖД».
Согласно рекомендациям МСЭ модель системы управления сетью строится иерархически и имеет следующие уровни (снизу вверх): сетевых элементов; управления элементами; управления сетью; управление услугами; административного управления. Все функции, связанные с управлением, разбиваются на две части: общие и прикладные. Общие функции обеспечивают поддержку прикладных и включают, например, перемещение информации между элементами сети связи и системы управления, хранение информации, ее отображение, сортировку, поиск и т.п. Прикладные функции в соответствии с классификацией Международной организации стандартизации (ИСО) разделяются на пять категорий: управление конфигурацией – Configuration Management (CM); управление рабочими характеристиками (качеством работы) – Performance Management (PM); управление устранением неисправностей – Fault Management (FM); управление расчетами – Accounting Management (AM); управление безопасностью – Security Management (SM).
Архитектура системы автоматического управления (АСУ) сетями связи представляется в виде физической и информационной. Информационная архитектура представляется схемой «менеджер – агент». Под «агентом» понимается посредник (устройство, программа) между управляемым ресурсом и основной управляющей программой-менеджером. Чтобы один и тот же «менеджер» мог управлять различными реальными ресурсами, создается некоторая модель управляемого ресурса. Эта модель отражает только те характеристики ресурса, которые нужны для его контроля и управления. На основе этой схемы могут быть построены системы практически любой сложности с большим количеством агентов и менеджеров разного типа.
Схема «менеджер – агент» позволяет строить достаточно сложные в структурном отношении распределенные системы управления (РСУ). Чаще всего используются два подхода к их построению – одноранговое и иерархическое. Однако более гибким является иерархическое построение связей между менеджерами.
Распределенная система управления телекоммуникационной сетью TMN представляет собой отдельную инфраструктуру, которая должна обеспечивать согласованное взаимодействие между различными типами систем управления и оборудованием систем сети электросвязи, основой которой является сеть передачи данных (СПД). При этом область задач управления телекоммуникациями достаточно многообразная, сложная и в некоторой степени может быть противоречивой. В этой связи при управлении СПД TMN должна обеспечивать справедливое распределение ресурсов передачи сети для управляющих потоков информации до соответствующих служб.
Концепция BSS (Business support Systems) для разработчиков систем управления сетей связи дала новую идею – объединить задачи управления бизнесом и задачи управления сетью. Так на стыке двух задач родилась концепция OSS (Системы поддержки функционирования предприятий связи), которая, с одной стороны, содержала все наработки TMN, с другой – обеспечивала жесткую экономическую связку BSS/OSS, с третьей – включала новые тенденции, опыт и некоторые качественные дополнения, которые всегда сопутствуют синтезу двух независимых идей. Однако телекоммуникационная сеть является сложной распределенной структурой и внедрение OSS, в отличие от внедрения BSS, затрагивает саму основу работы сети связи – аппаратные и программные средства. Сбой в BSS чреват финансовыми потерями, сбой в OSS – потерями сегментов сети. Таким образом, при всей привлекательности OSS, ошибка при ее внедрении может иметь самые тяжелые последствия. Поэтому OSS необходимо рассматривать всего лишь как возможный вариант реализации некоторых задач эксплуатации систем связи, и у нее должны существовать альтернативы в других подсистемах эксплуатации.
В целом на «вживление» системы OSS с учетом требований потенциальных потребителей (процесс кастомизации) уходит от 3 до 10 лет, в зависимости от сложности сети. Если в течение этого срока оператор меняет свою техническую политику, сам факт построения системы OSS становится спорным. Поэтому более перспективным считается эволюционное внедрение новой технологи эксплуатации. На первом этапе создается система мониторинга, на втором этапе рассматриваются задачи для активной компоненты. Однако при внедрении очень часто системы мониторинга и управления импортного производства не могут применяться в России без существенной доработки. Это связано с разницей менталитетов, особенно в области инженерных подходов. В результате рано или поздно возникает вопрос о доработке любых программных продуктов.
Согласно отечественным исследователям (Захаров Г. П., Лазарев В.Г., Лазарев Ю.В., Арипов М.Н., Богуславский Л.Б.) процессы управления в сети связи подразделяются на функции динамического управления потоками информации и функции организационно-технического управления сетью. В соответствие с идеологией TMN все функции, связанные с управлением, можно разбить на две части: общие и прикладные. Общие функции обеспечивают поддержку прикладных процессов (FM, PM, CM, SM, AM). Таким образом, и математические модели традиционно подразделяются на два вышерассмотренных класса управления.
Формальная сторона построения моделей управления потоком (общие функции) заключается в следующем. При построении моделей сетей массового обслуживания (СеМО), позволяющих исследовать критерии эффективности глобального управления, рассматриваются пропускная способность сети передачи данных и среднее время доставки пакетов адресату (время задержки). При этом рассматриваемое СеМО должно удовлетворять уравнению глобального баланса (УГБ) согласно условиям теоремы ВСМР (Baskett, Chandy, Muntz, Palacios).
Первой работой в построении и разработке математической модели TMN на основе известных аналитических методов является докторская диссертация Костина А.А. «Модели и методы проектирования систем управления телекоммуникационными сетями» (2003г.). Здесь математическая модель TMN представляется в виде системы иерархических моделей СМО. Дальнейшее развитие направления Костина А.А. получило в работе его ученика Лохтина В.В. В данной работе предложена модель Интегрированной Системы Управления Телекоммуникациями (ИСУТ) для мультисервисной сети также на основе СМО.
Помимо вышерассмотренных работ, проблеме управления телекоммуникационной сетью на основе идеологии TMN посвящена кандидатская диссертационная работа Коротокова Е.С. В данной работе также на основе теорий очередей и СМО разработаны и исследованы модели прикладных функций TMN: модели TMN для категорий управления неисправностями; модели TMN для категорий управления рабочими характеристиками и конфигурацией. В этих моделях использованы типы СМО М/M/1 и M/G/1. В частности разработана и проанализирована многофазная модель контроля изменения конфигурации TMN.
Значительный вклад в разработку теории управления телекоммуникационными сетями внес Мочалов В.П. докторской диссертационной работой «Разработка распределенных систем управления телекоммуникационными сетями и услугами» (2006 г.). В частности, в этой работе разработаны: комплекс математических моделей оптимизации и исследования характеристик распределенной системы управления (РСУ) на уровнях административного управления, управления услугами, управления сетью, управления сетевыми элементами; информационная платформа анализа вероятностно-временных характеристик (ВВХ) РСУ телекоммуникационными сетями и услугами; методы анализа ВВХ распределенных систем управления телекоммуникационными сетями и услугами на основе аналитических, имитационных, графических и автоматных моделей.
Дальнейшее развитие направления Мочалова В.П. в области разработок управления телекоммуникационной сетью соответственно с идеологией TMN получило в кандидатской диссертационной работе Яковлева С.В. (2007 г.). Здесь на уровне управления услугами предложена модель системы управления услугами (СУУ), в которой в качестве метода многокритериальной оптимизации процесса управления телекоммуникационными услугами использован метод последовательных уступок. В качестве аналитической модели процесса управления конфигурированием системы управления услугами в этой работе выбрана двухфазная СМО.
Модели управления на основе нейронных сетей применительно к беспроводным телекоммуникационным сетям рассмотрены в работах Комашинского В.И., Смирнова Д.А. (2002 г.) и др. Здесь в качестве управляемого параметра потоков пакетов, поступающих в радиоканал, используется вероятность первичной и повторной передачи пакетов. Управление вероятностью передачи и выбор ее оптимального значения позволяют поддерживать коэффициент использования пропускной способности канала c множественным доступом (МД). Управление значением оптимальной вероятности передачи осуществляется на основе анализа пространства состояний радиоканала. Для оценки пространства состояний, складывающегося в МД, и нахождения требуемого значения управляемого параметра используются нейросетевые модели.
Математическим аппаратом, позволяющим оперировать обобщенными n-мерными пространствами и объектами в них, является т е н з о р н ы й анализ. Приложение тензорного анализа значительно упрощает решение задач сетей массового обслуживания при моделировании информационных систем, а также задач из многих других областей, что рассмотрено в работах Пасечникова И.И (2004 г.), Петрова М.Н. и др.(2008 г.), Петрова А.Е. (2009 г.).
Примером реализации иерархической системы управления является Единая система мониторинга и администрирования (ECMA), созданная для управления хозяйством связи ОАО «РЖД». ЕСМА базируется на системе ERP (Система планирования ресурсов предприятия), которая позволяет комплексно реализовать процессный подход к управлению качеством работы технологической сети связи ОАО «РЖД». Архитектура ЕСМА соответствует функциональной иерархической структуре TMN. Однако ЕСМА имеет трехуровневую иерархическую структуру, состоящую из уровня управления элементом сети, уровня управления элементами сети и уровня управления сетью, т.е. не охватывает уровень бизнес-процессов.
Во второй главе рассмотрены задачи мониторинга и управления на основе теории нечетких множеств: математический аппарат и источники F-ситуаций в процессах управления объектами связи; обобщенная модель иерархического управления сетью связи; обобщенная модель управления сетевым элементом; обобщенная поллинговая модель управления подмножеством сетевых элементов; транспортные функции в системе «менеджер – агент»; сформулированы цель и основные задачи диссертации.
Сеть электросвязи является сложной распределенной структурой. Модель управления можно представить в виде схемы, приведенной на рис.1. Обобщенная математическая модель иерархического управления имеет вид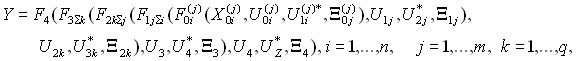 
где X0i – множество входных воздействий на объект управления; 
- оператор сетевого элемента NEi подсети j ; 
- оператор агрегирования по i первого уровня управления в подсети j ; 
- оператор агрегирования по j второго уровня управления сети k ; 
- оператор агрегирования по q третьего уровня управления; F4 - оператор четвертого уровня управления (управления бизнесом); n- количество сетевых элементов NE в подсети j ; m – количество подсетей NE в сети k ; q – количество сетей, обслуживаемых региональной TMN; i - неизвестный вектор воздействий на каждом уровне управления; Uij- управление соответствующего уровня; 
- корректирующее управление с вышестоящего уровня.
На основе результатов контроля и диагностики или мониторинга решаются задачи управления. При этом основными факторами всякого управления являются: цель управления (Z*); информация о состоянии объекта и природы (In), In = < XК, YК, >, где XК, YК, - множество входных, выходных и неизвестных воздействий на объект управления соответственно, определенных по результату мониторинга; целенаправленное воздействие на объект, т.е. собственно управление (U), U=(In,Z*);
алгоритм управления (), : In Z* U. Однако чаще всего в реальных условиях осуществление задач управления объектом эффективно в полном объеме не достигается из-за его сложности, неполноты информации об окружающей среде и состоянии объекта, неточно сформулированной цели управления, ограниченности ресурсов, дефицита времени принятия решения и других факторов. В этой связи в модели управления его составляющие могут формулироваться в концепциях теории нечетких (fuzzy) множеств. Тогда в зависимости от конкретной ситуации возможны различные варианты моделей управления:
МУП = < T, X, Y, 
, 
, 
, L, F,, G, 
, A, B >,
где Т = {t} – множество моментов управления; X = {x} – множество входных воздействий на объект управления (ОУ); Y= {y} – множество выходных откликов ОУ; 
- нечеткое множество управлений, (u) – нечеткая функция принадлежности, (u) [ 0, 1 ] ; 
- нечеткое множество состояний; Z = {z} – множество целей; L, F – операторы перехода состояний и выходов соответственно L: T X Q Q, F: T X Q Y; - оператор алгоритма управления; G{g(q)} – множество нечетких мер, g(q)[0, 1]; C = {c(u)} – множество цен управления; А = {(u)}, B = {(u)} – множества ошибок управления первого и второго рода соответственно.
Иерархическую модель распределённого управления с нечеткими составляющими, с учетом вышеизложенного, можно представить в виде:
Y = F4 (F3 (F2 (F1 (X1, 
1, 1), 
2, 2), 
3, 3), 
4, 4).
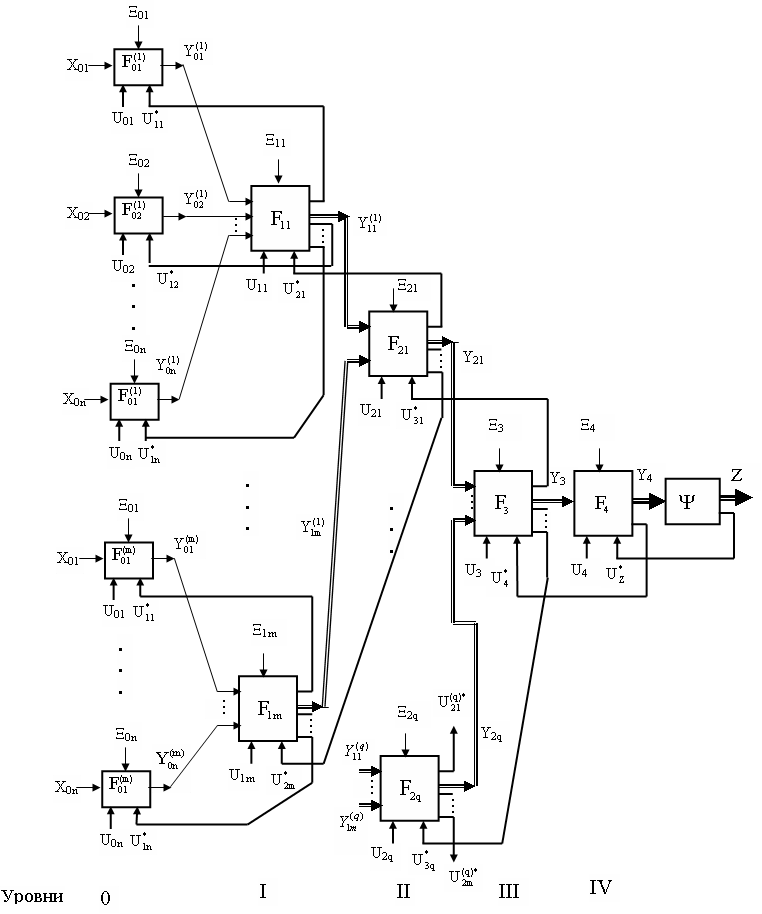
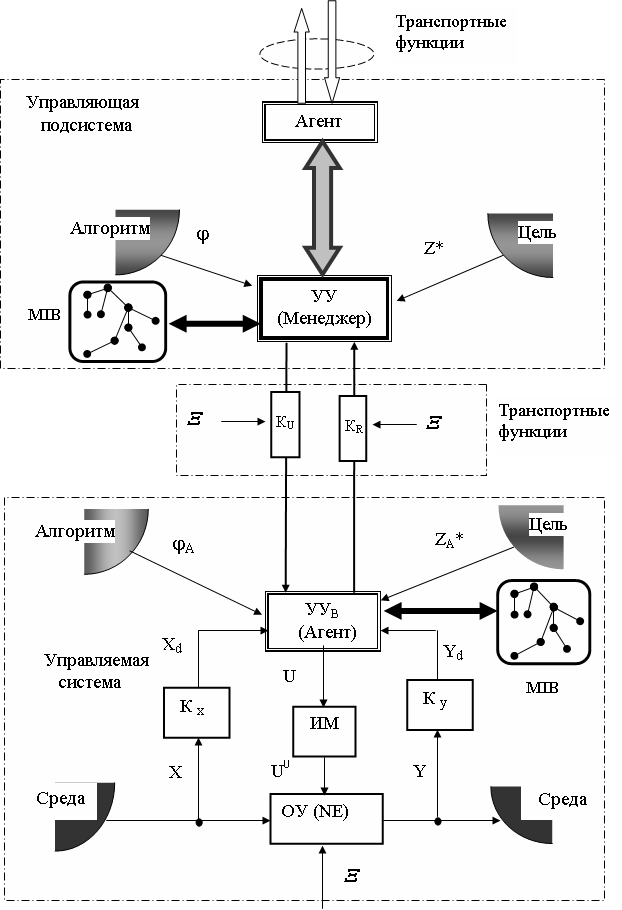
От качественного функционирования сетевых элементов NE существенно зависит и функционирование всей сети связи в целом. Поэтому целью управления сетевым элементом является поддержание его состояния в заданном фазовом пространстве средствами контроля и диагностики (мониторинга), которое достигается своевременной доставкой контролирующей информации до устройства управления (УУ) и управляющей информации до объекта управления. Сетевые элементы NE по своей структуре и назначению в телекоммуникационной сети неоднородны. С точки зрения объектов управления их можно классифицировать как пассивные и активные. К пассивным NE можно отнести оборудование, являющееся относительно несложным и не обладающее самоорганизующими свойствами. К активным NE можно отнести узлы коммутации, Switch-коммутаторы, маршрутизаторы, некоторые сетевые шлюзы и базы данных. Приведенные NE обладают уже некоторым техническим интеллектом. Обобщенная модель управления активным сетевым элементом имеет вид, приведенный на рис. 2.
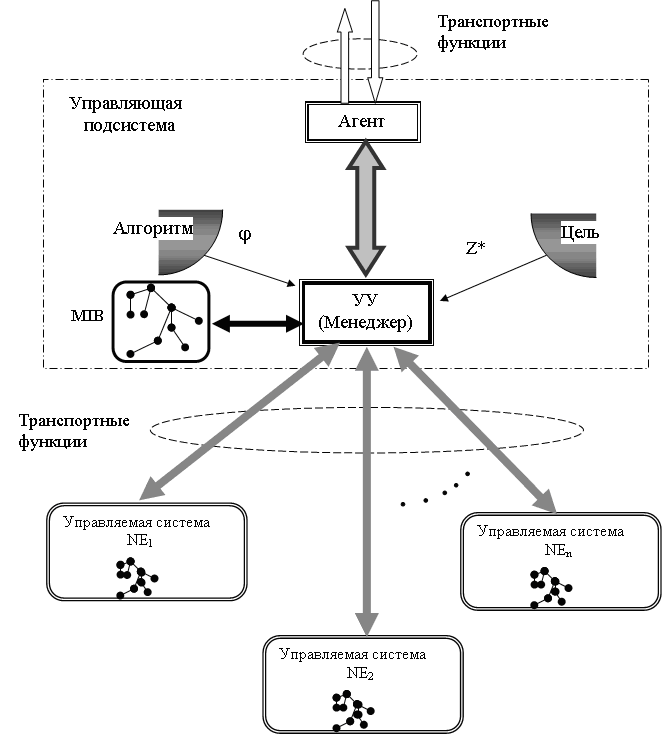
Обобщенная модель управления подмножеством сетевых элементов. В сети связи или в современных мультисервисных телекоммуникационных сетях множество сетевых элементов NE неоднородно. При этом вышестоящий менеджер (или УУ) по уровню иерархии TMN управляет определенным подмножеством NE. Модель такого управления приведена на рис. 3. В данной модели (см. рис. 3) подмножество NE имеет разный характер. Исполнение алгоритмов управления здесь может быть следующим: 1) алгоритм управления только пассивного подмножества NE; 2) алгоритм управления только активного подмножества NE; 3) алгоритм управления комбинированного подмножества. Взаимодействие менеджера в этой модели (см. рис.3) с каждым элементом NE происходит в форме определенного упорядоченного опроса, которая называется поллинговой системой (ПС). Данная система считается разновидностью СМО с несколькими очередями и с одним общим обслуживающим устройством (сервером, здесь в качестве него – менеджер) или несколькими устройствами Математические модели систем поллинга достаточно полно рассмотрены Вишневским В.М., Семеновым О.В. (2007 г.).
Транспортная сеть состоит из каналов и трактов, качественное функционирование которых существенно определяет надежность доставки услуг связи по сети передачи данных (СПД) до потенциального потребителя. Математические модели каналов некоторых СПД достаточно хорошо изучены как отечественными, так и зарубежными учеными с точки зрения доставки услуг связи до потребителя, где допускается сравнительно высокая избыточность информации. Однако для специальных транспортных сетей (например, TMN), где передается некоммерческая информация, каналы связи мало изучены (рис. 2). Особенно это относится к каналам связи для передачи приема контрольно-диагностической информации о состоянии сетевых элементов NE, т.к. на основании этой информации в конечном итоге формируется стратегия обслуживания телекоммуникационной сети.
Задачи, связанные с описанием моделей функционирования трактов и каналов СПД РСУ рассмотрены в диссертационной работе Мочалова В. П. Данные задачи являются многомерными и решаются на основе теории СМО и Марковского процесса. Решения этих задач приближенные, даже при условии ряда оговорок (условий) и наличия исходной статистической информации. Поэтому представляет интерес разработки и исследований моделей каналов связи с использованием аппарата теории нечетких множеств и их влияния на процессы принятия решения о состоянии сетевых элементов NE.
В третьей главе изложены теоретические основы нечетких (F-fuzzy) методов в задачах управления сетями связи: основные теоретические положения и операции F-множеств; нечеткие меры, интеграл и алгоритмы их определения; степени нечеткой связанности и нечеткости F- множеств состояний цифровых устройств (ЦУ); нечеткая логика в задачах связи.
В данной главе впервые разработано тридцать девять специальных примеров, иллюстрирующих операции над нечеткими множествами, применительно к проблемам электросвязи. Подробно рассмотрены нечеткие -мера и интеграл для непересекающихся и пересекающихся нечетких множеств состояний технических систем электросвязи с иллюстрацией на примерах. Важной характеристикой для таких множеств является степень нечеткого пересечения, определяемого выражением
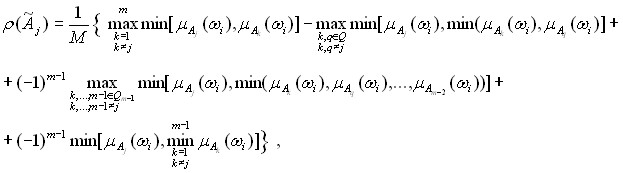
где М- нормирующий множитель, в частности, мощность нечеткого множества Aj. Здесь следует отметить, что предлагаемое определение степени нечеткого пересечения 
отличается от степени нечеткости, введенного в Ягером (Yager R.R.) и др. исследователями, где степень нечеткости рассматривается как нечеткая энтропия, нормализованное расстояние, степенью детального описания или степенью близости между нечетким множеством и его дополнением, т.е. как собственная характеристика множества. Физически степень нечеткого пересечения множества Аj в нашем случае интерпретируется как степень нечеткой связанности (размытости или расплывчатости) в системе технических состояний A, когда носители нечетких множеств пересекаются, Аj Am № Ж. В связи с этим рассматривается связь между степенью нечеткости J(Аj), введенное Ягером, и степенью нечеткой связанности. Для этого доказывается теорема.
ТЕОРЕМА. Если носители нечетких множеств Аj и Ak в системе A пересекаются, Supp Аj Supp Ak № Ж, то максимальное значение степени связанности (Аj Ak) достигается при степенях нечеткости множеств Аj и Ak, когда J( Аj) = J ( Ak) = 0, и минимума – при J ( Аj) ® 1, J ( Ak) ® 1.
Показано, что максимальное значение степени нечеткости по мере Ягера для унимодального и нормированного нечеткого дискретного множества составит
для многомодального дискретного множества
где m- число мод, n – мощность нечеткого множества, p – параметр, принимающий значения 1, 2,. Следовательно, степень нечеткости 
есть функция от мощности множества М(А) (здесь она равна n ) и при М(А)
Согласно условию пересечение носителей нечетких множеств не является пустым, SuppАj SuppAk № Ж, следовательно, и пресечение нечетких множеств непустое, 
. Множество пересечения S является нечетким и определение её степени нечеткости также подчиняется правилу Ягера. Таким образом, теорема доказана.
Рассмотрены теоретические положения F-логики в задачах связи. Разработаны примеры на основе модус поненс и композиционного правил
вывода для оценки состояния канала связи и выбора услуги связи для использования в мультисервисной сети.
Четвертая глава посвящена теоретическим основам методов принятия решений и прогнозирования состояний цифровых систем связи.
Предлагается методика распознавания состояния цифрового устройства (ЦУ) на основе системы минимальных конечных автоматов. Такая система описывает ЦУ как объект управления с множеством упорядоченных (кортежём) переходных элементарных состояний +1 SЭ, определенных в результате шагов управляющих воздействий. Класс SЭ таких состояний представляет множество возможных состояний, присущих некоторым макросостояниям (повреждениям, дефектам, отказам, предотказам и т.д.). Неопределенность состояний на каждом шаге возникает из-за минимизации элементарных состояний автоматов системы. Возможное ожидаемое состояние перехода на каждом шаге определяется через нечеткий интеграл
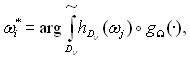(1)
где 
знак нечеткого интегрирования; 
знак композиции; D – возможная область нечетких состояний на шаге, где D ={i}, i ; hD(i) - убывающая функция принадлежности нечеткого множества D ; g() - нечеткая мера множества Fi =(1, 2,….. i) определяется по мере Сугено через априорную нечеткую плотность состояний g(i). В результате процедуры (1) формируется нечеткое множество кортеж
(2)
с соответствующими степенями принадлежности [0, 1]. Здесь следует заметить, что соблюдаются связи состояний, а это очень важно при дальнейшем распознавании макросостояния ЦУ, т.к. сохраняется структура выявленного множества.
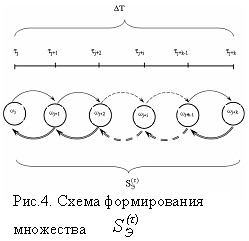
Современные ЦУ и системы связи являются сложными. Они, как правило, содержат в себе встроенные подсистемы контроля, диагностики и управления, что позволяет организовать сбор информации о состоянии объекта управления за некоторый интервал времени. Пусть, за время T в ЦУ через интервалы времени i запоминаются состояния j SB (Здесь SB вырожденный класс состояний в результате минимизации автомата). При этом предполагается, что размер множества 
зависит от количества интервалов i T и ограничивается временем T (см. рис. 4).
Двойная стрелка на рис.4. означает путь формирования нечеткого множества 
от конца временного интервала j+k T. На этапах регистрации состояния j SB в моменты времени j+i, i = 0, 1,..., k, могут быть и вырожденными. Методика снятия вырождения, т.е. определения наиболее возможного состояния *j в моментах регистрации j+i аналогична ранее рассмотренному выражению (1).
Методика определения нечеткого множества 
является менее оптимальной по отношению к методике по определению множества 
. Это связано с тем, что в методике с интервальным окном T нет жесткой причинно-следственной связи между состояниями *j SB, определенными в моменты их регистрации j+i. Здесь регистрируются состояния *j ЦУ в реальном масштабе времени. При этом мощность множества 
является функцией времени
Однако данная методика обладает тем преимуществом по отношению к методике формирования нечеткого множества 
тем, что здесь нет необходимости планирования тестового эксперимента, а это достаточно сложная задача. Тем не менее, возникает необходимость в оптимизации окна T, т.к. T случайная величина.
В основе методики принятия решения о типе макросостояния ЦУ лежит множество SЭ или 
. Для реализации методики можно использовать подходы: 1) минимума метрического расстояния между SЭ и всеми Аj; 2) максимума мер включения SЭ Аj ; 3) максимума нечеткой меры пересечения g (Vj), где Vj = SЭ Аj, Vj={i}V; 4) максимума апостериорной вероятности p(dj / SЭ) проявления дефекта dj по условию SЭ, что определяется формулой Байеса в нечеткой форме; 5) распознавание состояния на основе F-интеграла.
При распознавании на основе апостериорной нечеткой вероятности решение о макросостоянии dj ЦУ принимается по максимуму апостериорной условной вероятности 
, где 
нечеткое множество (в дальнейшем изложении материала значок “~“ над множеством будет убираться). В этом случае предполагается, что априорно известны вероятности р(dj) и условные вероятности 
, i. Как ранее было установлено, что для dj соответствуют множества Aj ={ i }j. Априорно также устанавливается, что для данных dj существуют нечеткие классы множеств Sk ={i}d при соответствующих воздействиях x X и реакциях rУ, Sk(p,q) Aj A. Доказывается следующая теорема.
ТЕОРЕМА. Если нечеткое множество 
нормальное и унимодальное то условная вероятность 
принимает вид
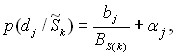(3)
где 
классическое отношение Байесовской вероятности, j – нечеткая часть. Если функция принадлежности нечеткого множества является трапециидальной или имеет более чем одной моды, то формула Байеса в нечеткой форме имеет вид
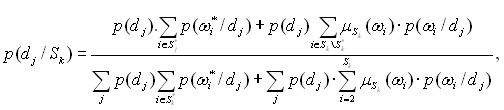(4)
где i* элементарное состояние ЦУ, имеющее степень принадлежности 
Выражение (4) также сворачивается в соотношение (3). Из (3) и (4) вытекают некоторые утверждения, связанные со степенью нечеткости по Ягеру.
УТВЕЖДЕНИЕ 1. Если нечеткое множество 
нормальное, унимодальное или многомодальное и степень нечеткости по Ягеру стремиться к единице, 
, то выражения (3) и (4) принимают вид
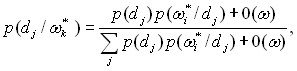(5)
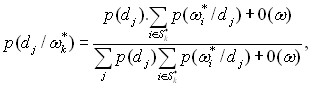(6)
где 0() – бесконечно малые величины высокого порядка. Здесь нечеткое множество 
вырождается в сингильтон, т.е. в единичное множество 
УТВЕЖДЕНИЕ 2. Если нечеткое множество 
нормальное, унимодальное или многомодальное и степень нечеткости по Ягеру равен нулю, 
, то выражения (3) и (4) принимают вид
(7)
где 
кардинальность или мощность множества 
.
УТВЕЖДЕНИЕ 3. Если нечеткое множество 
унимодальное или многомодальное, но ненормальное, то выражения (3) и (4) принимают вид
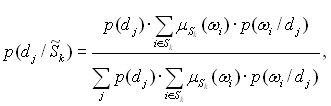(8)
УТВЕЖДЕНИЕ 4. Если нечеткое множество 
унимодальное или многомодальное, но ненормальное и степень нечеткости по Ягеру стремиться к единице, 
, то выражения (3) и (4) принимают вид
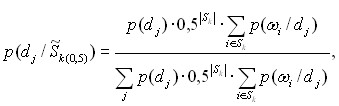(9)
где 
- нечеткое множество уровня 0,5. Решение о типе макросостояния d* системы состоит из двух этапов: 1)определяется нечеткое множество пересечения 
2) определяется наиболее возможное макросостояние d* на основе (3) 
Распознавание ожидаемого типа макросостояния в ЦУ по результату тестового эксперимента или пассивного наблюдения можно осуществить с помощью нечеткого интеграла. Здесь могут быть два варианта.
Как известно, ранее была уже определена методика формирования апостериорного нечеткого множества 
, с помощью которого определяется пресечение 
с каждыми априорным нечетким классом 
, 
Следовательно можно определить нечеткую меру множества 
через F-интеграл, тогда макросостояние d* вычисляется выражением
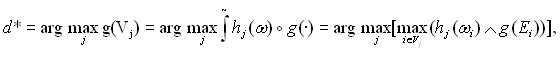(10)
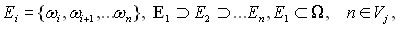
где hj() – упорядоченная функция по убыванию от 
; g(En) – нечеткая мера, определяемая по алгоритмам Сугено или Тсукэмото.
2. Ранее было определено, что для djD установлено соответствие dj Аj, АjA, Аj={i}. Следовательно, определяются априорные меры множеств g(Аj) g(dj), которые можем принять как нечеткие плотности. Далее предполагается, что в процессе эксперимента (активного или пассивного) определяется функция принадлежности 
наиболее возможной нечеткой области макросостояний 
, 
. Тогда наиболее ожидаемое макросостояние определяется выражением
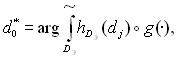(11)
где 
- упорядоченная по убывающим степеням функция от функции принадлежности 
; g() нечеткая мера множества Fi=<dj1, dj2,…, dji>, известно, что dj Aj и если AjAm, то данная мера множества g(Aj). Решение (11) можно представить графически (см. рис. 5).
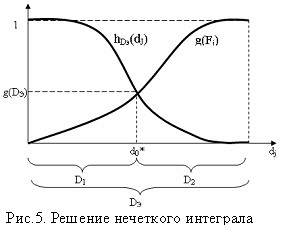
Как видно из рис. 5 решение нечеткого интеграла дает следующие результаты: 1) определяется нечеткая ожидаемая мера множества DЭ ; 2) показывается наиболее возможнее макросостояние d* в области DЭ с нечеткой оценкой этого состояния; 3) макросостояние d* является границей раздела области DЭ на две подобласти D1 и D2, что дает возможность для дальнейшего анализа в уточнении наиболее возможной причины появления макросостояния (например, нарушения, повреждения или дефекта) как ЦУ, так и других сложных систем. Таким образом, применение процедуры нечеткого интегрирования при анализе сложных систем дает возможность классификации их состояний по принципу половинного разбиения. Для дальнейшего анализа ожидаемого дефекта логично выбрать подмножество D1. В противном случае необходимо вычислить нечеткие меры D1 и D2, затем выполнить предпочтение по максимуму их мер. При этом предполагается произвести коррекции их функций принадлежности дефектов и нечетких плотностей. Пусть здесь выбрана подобласть D1. Здесь с помощью дополнительной экспертизы производится коррекция функции принадлежности 
и нечетких плотностей g(dj Aj). С учетом того, что AjAm, в качестве нечеткой плотности можно использовать степень концентрации (Aj), тогда наиболее ожидаемое макросотояние в области D1 определяется выражением
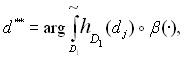(12)
где D1 Dэ ; () нечеткая мера множества Fj*=<A1…..,Aj>, вычисляется как дополнения степени связанности 
. Интеграл, взятый по степени концентрации состояний (Аj), характеризует в нечеткой области связанных дефектов D1 наиболее возможно устойчивый (несвязный) тип макросостояния, с учетом характера функции принадлежности множества D1.
Прогнозирование состояния ОУ на основе F-информации. Анализ математических моделей методов вероятностного прогнозирования показал, что для приемлемого принятия решения о состоянии сложного объекта в будущем необходим достаточно большой объем априорной информации, т.е. информации о точных вероятностных характеристиках параметров функционирования объекта управления, а также вероятностных характеристиках их совместного распределения. Кроме того, при достижении высокой точности прогноза вероятностные модели становятся сложными, мало управляемыми. При статистических методах прогнозирования необходим большой объем выборки об ОУ, в противном случае прогноз будет статистически неустойчивым. Все это требует длительного времени сбора и обработки информации.
Сети связи и потоки информации, циркулирующие в них, функционируют в реальном скоротечном масштабе времени и ситуационная обстановка в сети также может измениться быстро. В этой связи наиболее привлекательными моделями прогнозирования становятся аналитические. Аналитические модели в качестве прогнозирующих функционалов в неявной форме используются и в вероятностных моделях. Преимущество аналитических моделей заключается в том, что в них можно оперативно управлять полиномальными коэффициентами. В качестве базовой модели прогнозирования остановимся на интерполяционном полиноме Ньютона с использованием метода обобщенного параметра, который позволяет вводить информацию нечислового характера при обработке параметров ОУ.
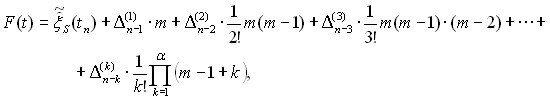(13)
где m – число шагов прогнозирования; количество этапов контроля;
k порядок полинома; 
Здесь 
агрегированный нечеткий параметр. Поскольку в полиноме неизвестным является число шагов прогнозирования m, необходимо воспользоваться способом обратного прогнозирования, т.е. понимая, что система будет не работоспособна через m шагов 
и 
Тогда прогнозирующее уравнение на основе полинома Ньютона имеет вид
В пятой главе разработаны теоретические основы приема дискретных сигналов мониторинга и диагностики на основе теории нечетких множеств: канал связи в системе мониторинга цифровой сети; распознавание состояний объекта управления с учетом прямого и обратного каналов связи; цифровая F-фильтрация сигналов; алгоритм цифрового приема сигналов на основе нечеткой логики.
Поиски аппаратных средств повышения верности передачи дискретной информации привели к интенсивному поиску эффективных методов регистрации единичных элементов (ЕЭ). В связи с этим предлагается производить регистрацию ЕЭ до порогового устройства ПУ, используя метод сканирования длительности 0 ЕЭ и дальнейшего анализа отсчетов u(i ) в дискретные моменты времени i. Однако решение данной задачи усложняется ввиду отсутствия априорной вероятностной и статистической информации о состоянии ЕЭ за время 0 на приеме. Поэтому в дальнейшем для решения задачи регистрации ЕЭ будет использоваться математический аппарат теории нечетких (fuzzy) множеств.
Рассматривается когерентный канал связи со стиранием. Принятый сигнал u(t) анализируется в интервале длительности единичного элемента 0, через дискретные момента времени i, i = 0, 1, 2, 3, …, n. Здесь n количество отсчетов на интервале 0 ЕЭ. Отсчеты u(k ), k= 1, 2, 3, …, n-1, соотносятся с априорной оценочной шкалой G, которая является множеством нечетких F- подмножеств 
- терм множеств, G={
}, q= 1, 2,..., m (рис. 6). Терм множество характеризуется F-функцией, т.е. функцией принадлежности (ф.п.) 
. Кроме того, априорно задается шкала нечеткой плотности распределения (НПР) моментов времени (м.в.) отсчетов g(i) 
.
Далее даётся оценка качества принятого единичного элемента ei за интервал его длительности 0, для принятия решение о приеме двоичной единицы «1» либо «0». Этапы решения задачи следующие: 1) дискретизация сигнала u(k ) = u(t)( k ); 2) процедуры формирования F- множеств отсчетов множества значений нечеткой плотности моментов отсчетов за интервал 0: по шкале G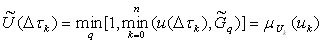 
, 
, 
G; по шкале 
; 3) процедура формирования F-меры множества 
через вычисление нечеткого интеграла, т.е. выполнение процедуры свертки 
4) принятие решения об наиболее возможном двоичном числе еi принимается по правилу
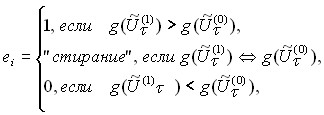(14)
где 
знак эквивалентности.
Доказывается теорема о существовании шкалы на рис. 6.
ТЕОРЕМА. Если ф.п. двух нечетких множеств 
и 
унимодальные на противоположных границах («нижней» и «верхней») ограниченного и упорядоченного базового множества A’ A и их максимальное пересечение (
) 0,5, то всегда можно построить хотя бы одну обобщенную унимодальную ф.п. без разрывов.
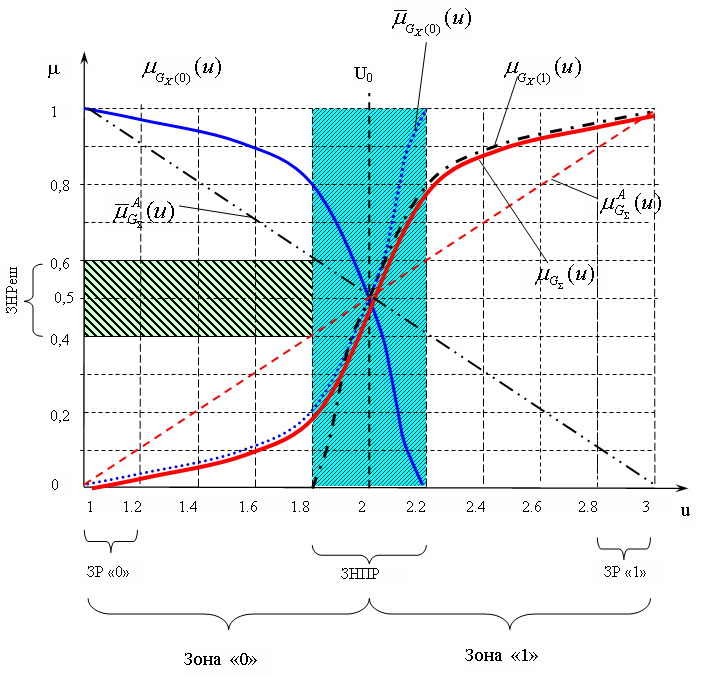
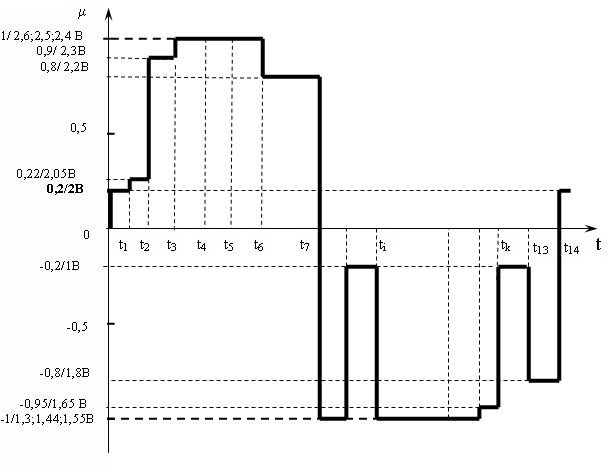
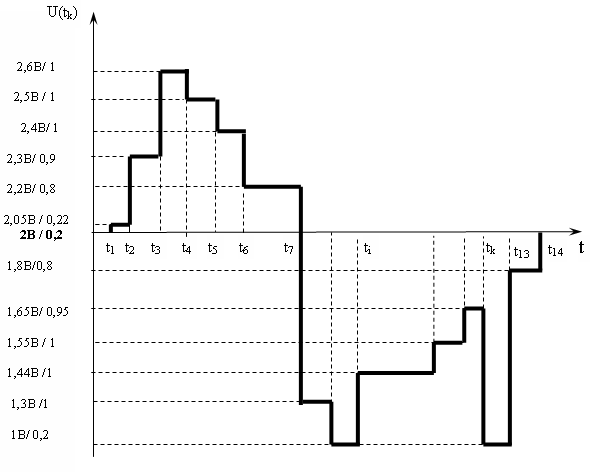
Текущее состояние будет определять качественную сторону КС, которую предлагается описывать математически лингвистическими термами: <ОЧЕНЬ ХОРОШЕЕ>, <НЕХОРОШЕЕ И НЕПЛОХОЕ>, <ОЧЕНЬ ПЛОХОЕ>. С учетом шкалы (см.рис. 6), в результате регистрации единичного элемента за интервал его длительности величины степени принадлежности ui изменяются во времени, т.е. происходит F-процесс. В качестве примера данный процесс можно проиллюстрировать двумя графиками (рис. 7 и 8). Выбор интервала дискретизации ti для оценки КС определяется длительностью e единичного элемента e и требуемой точности оценки 
за время, т.е. отношением 
.
Далее определяются меры нечетких апостериорных кодовых комбинаций yj =(e1, e2, e3,…, ej), которые вычисляются через меры возможностей 
, принимая во внимание факт, что источник порождения кодовых комбинаций один, т.е. четкая кодовая комбинация 
(переданная в канал связи).
Учитывая оценку состояния КС, нечеткие вероятности нечетких кодовых комбинаций можно записать в виде
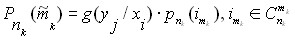
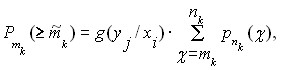(15)
Здесь 
мера хорошего приема по условию xi
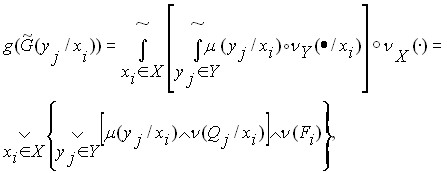(16)
где Qj, Fi – множества: Qj= <y1,…,yj>, Fi= <x1,…,xi>; 
<ХОРОШИЙ ПРИЕМ (yj/xi)>; 
и 
нечеткие меры.
Далее с учетом вышеизложенного рассматривается методика распознавания макросостояния ОУ учетом состояний каналов связи (КU, КR ) и использованием операции нечеткого интегрирования.
Модели (15) и (16) оценивают кодовую комбинацию yj, которая затем преобразуется в отсчет. Далее по n принятым отсчетам через интегратор формируется сигнал реакции от ОУ. Как известно в процессе передачи по КС кодовая комбинация подвергается помехам и от их интенсивности может происходить трансформация единичных элементов ei в ней, что приводит к искажению отсчетов в виде ложных импульсов и как следствие искажается форма сигнала реакции. В связи с этим необходимо производить фильтрацию откликов (сигнала реакции) от ОУ.
Ранее отмечалось, что отсчет xn-k это есть кодовая комбинация, принятая из канала связи с мерой качества (16), тогда выходной отсчет и, следовательно, F-фильтрация будет определяться выражением
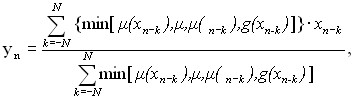(17)
где g(xn-k) мера качества отсчета xn-k (кодовой комбинации) принятого из реального канала связи, которая определяется по выражению (16). Дальнейшие исследования процессов F-фильтрации привели к определению высоко информационных показателей сигнала, определяющих их формы. Это так называемые показатели «выпуклости / вогнутости» (в/в) фронтов видеоимпульсов. На основе (17) и показателя в/в сигналов разработаны алгоритмы низкочастотной фильтрации. Действие цифрового полосового фильтра описывается выражением
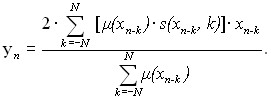(19)
Здесь весовые коэффициенты 
определяют ширину, а 
– центральную частоту фильтра.
Разработанный алгоритм цифрового приема сигналов на основе правила (14) показал, что при соотношении сигнал/шум от 8 до 17 дБ компьютерная модель радиоприёмного устройства (РПУ) в программной среде Matlab на основе нечеткой логики обеспечивает снижение количества ошибок на 20 %, по отношению к модели РПУ с интегральной регистрацией сигнала. При соотношении сигнал/шум около 3 дБ количество ошибок для обеих моделей становится одинаковым. В случае малого уровня шумов на входе обе модели также выдают одинаковое количество ошибок.
В главе 6 изложены основы теории распределения сигналов управления в сети управления на основе F-логики: модель системы управления «Агент- сетевой элемент»; F-модель управления канальным ресурсом; модель взаимодействия менеджера с агентами.
В современной теории СеМО возникает задача эффективного использования и управления канальным ресурсом. Это связано с тем, что в сетях связи интенсивно внедряется технология пакетной обработки и передача данных, позволяющая обрабатывать одновременно различные виды информации (речь, данные, видео) на одном и том же оборудовании, а следовательно, и эффективно его использовать. Однако возникающие огромные потоки разнородных данных являются дополнительной нагрузкой на каналы. Кроме того разнородность потоков в сети создает эффект спонтанного увеличения нагрузки в узлах распределения информации за счет явления с а м о п о д о б и я нагрузки, что может привести к блокировке узла. Построение оперативного управления канальными ресурсами в этих условиях становится иногда проблематичным на основе классической теории СМО. В этой связи предлагается использовать теорию F-множеств для управления канальным ресурсом.
Функциональная схема управления канальным ресурсом приведена на рис. 9. Здесь необходимо в зависимости от текущего состоянии канального ресурса, интенсивности поступающих потоков U,K,D (управления, контроля, диагностики соответственно), состояния очередей r и интенсивности обслуживания K контроллера К определить минимальный канальный ресурс k на шаге k необходимый для минимальной задержки составляющих входных потоков i, i= 1, 2, 3,
(20)
где - общая интенсивность потоков заявок; k – необходимый общий ресурс, равный 
.
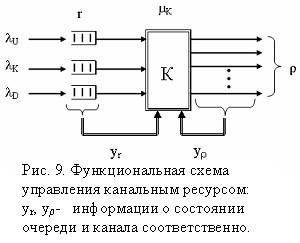
Функциональная схема (рис. 9) соответствует модели СМО вида 
.
Модель управления ресурсом канала построена на основе прямых нечетких продукционных правил вывода modus ponens. Рассмотрим более подробно конструкцию и типы этих правил.
Простейший вариант нечеткого вывода решения канального ресурса * СМО при воздействии потока заявок на обслуживание можно представить в следующей схемой:
ПРАВИЛО (Знание, априорное наблюдение): «Если x есть 
, то y есть 
»
ФАКТ (Наблюдение, измерение): «х есть 
»
ВЫВОДЫ (Решение): «y есть 
», (21)
где 
,
, 
,
-нечеткие множества, описываемые функциями принадлежности (ф.п.) А (х), А’ (х), 
,
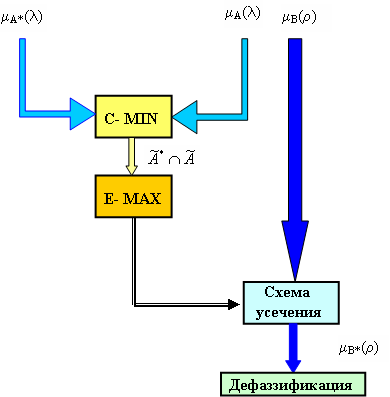
соответственно. Нечеткое управление может быть реализовано специальными нечеткими контроллерами, в основе которых лежит так называемая машина нечетких выводов Т. Тэрано, К. Асаи, М. Сугено (1993), структура которой показана на рис.10. Эта машина реализует нечеткий вывод типа «Если А, то В». Блок, реализующий функцию C-MIN, осуществляет пересечение множеств А и А’. Блок, реализующий функцию E-MAX, выделяет из множества А А’ элемент с максимальным значением, который осуществляет усечение множества В, превращая его во множество В’. Схема нечеткого вывода рис. 10 может быть использована при управлении канальным ресурсом в СМО с бесприоритетными очередями типов 
v = 1, …, N. Для управления СМО со многими приоритетами предлагается многовходовая схема нечеткого вывода рис. 11.
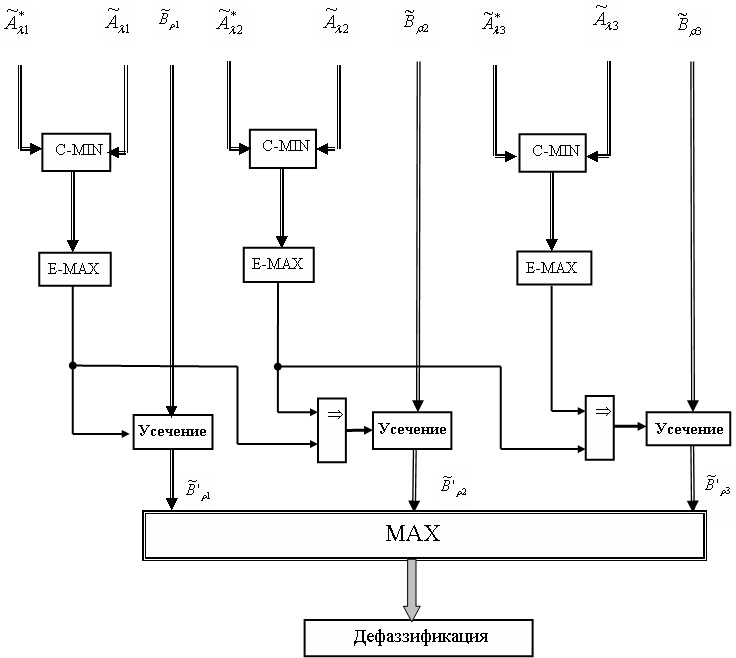
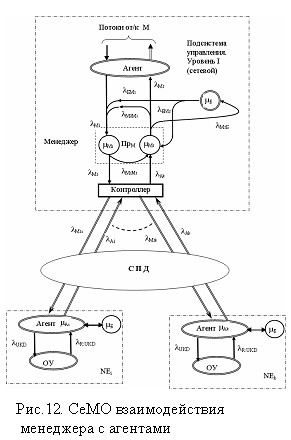
Взаимодействие менеджера в модели (см. рис. 3) с каждым элементом NE происходит в форме определенного упорядоченного опроса, которая называется поллинговой системой (ПС). Данная система является разновидностью СМО с несколькими очередями и с одним общим обслуживающим устройством (сервером, здесь в качестве него – менеджер) или несколькими устройствами. Очереди формируются управляемыми устройствами – агентами. Процесс взаимодействия «Менеджера» с «Агентами» можно представить в виде сети массового обслуживания (СеМО), приведенной на рис. 12. Здесь система имеет один сервер и N (N >2) очередей с неограниченным числом мест для ожидания. Будем полагать, что система «Менеджер-Агент» функционирует (производит мониторинг) циклически с исчерпывающим обслуживанием очередей, тогда основным показателем обслуживания является с р е д н е е время TAi затрачиваемое на обработку агента. Основным составляющим среднего времени TAi является процедура маршрутизации важный элемент в системе «М-А», с точки зрения достоверной и своевременной доставки пакетов до адресатов (агентов). В связи с этим рассматривается алгоритм маршрутизации в структуре системы управления «Менеджер-Агент» телекоммуникационной сетью, в которой сигналы управления распределяются в сети в соответствии с маршрутной матрицей, построенной на основе нечётких матриц предпочтений. Для определения наиболее возможного маршрута 
при k-й ситуации в телекоммуникационной сети можно применить двойное нечёткое интегрирование по функции 
:
где 
уточнённый оптимальный маршрут по результату двойного нечёткого интегрирования; 
функция принадлежности по условию вектора параметров ; 
нечёткая - мера, плотность которой 
а 
Здесь 
упорядоченное нечёткое множество по убывающим степеням функции принадлежности маршрутов 
; 
уточнённая подобласть состояний по результатам первого нечёткого интегрирования, 
; 
нечёткая мера, плотность которой определяется по нечёткой матрице возможностей. Данная матрица строится на основе экспертных оценок с учётом ситуации в сети ck Cц и времени её восстановления 
.
З а к л ю ч е н и е
В соответствие с поставленной целью, в диссертационной работе получены следующие теоретические и практические результаты.
1.Рассмотрены задачи мониторинга и управления на основе теории нечетких (fuzzy) множеств: разработана модель иерархического управления сетью связи с учетом целевой функции; разработаны модель управления сетевым элементом и поллинговая модель управления подмножеством сетевых элементов для активного и пассивного агента с учетом целевой функции.
2. Адаптированы и обоснованы теоретические основы нечетких методов в задачах управления сетями связи: основные теоретические положения и операции F-множеств; нечеткие меры, интеграл и алгоритмы их определения, нечеткая логика в задачах связи. Это поясняется специально разработанными практическими примерами из области связи (39 примеров).
3. Разработана модель, определяющая степень нечеткой связанности состояний технических систем и доказана теорема о взаимосвязанности её со степенью нечеткости F- множеств, введенной Ягером.
4. Разработаны теоретические основы нечетких методов принятия решений и прогнозирования состояний цифровых устройств (ЦУ) связи: две методики распознавания множества состояний ЦУ на основе системы минимальных конечных автоматов, с использованием тестового и пассивного экспериментов; методика принятия решения о макросостоянии ЦУ на основе n-кратного нечеткого интеграла, позволяющего локализировать повреждение в зависимости от требуемой точности и полноты апостериорной информации; методика принятия решения о макросостоянии цифровой системы по максимуму апостериорной вероятности нечеткого события как для унимодальной нечеткой априорной функции принадлежности (ф.п.), так и для многомодальной ф.п., с учетом её степени нечеткости; методика прогнозирования состояния цифрового устройства (системы) с использованием полинома Ньютона на основе метода нечеткого обобщенного параметра. Данный метод прогнозирования позволяет в зависимости от полноты текущей информации также использовать опыт технического персонала.
5. Разработаны теоретические основы приема и обработки дискретных сигналов мониторинга и диагностики на основе теории нечетких множеств: F-модель канала связи в системе мониторинга цифровой сети; методика регистрации единичного элемента с использованием композиционной априорной нечеткой шкалы и правила принятия решения на основе нечеткой логики. Исследование данной методики показало, что она достаточно эффективно работает в областях помех малой и средней интенсивности; разработаны функциональные схемы приема дискретных сигналов на нечеткой логике; исследован F-процесс на примере регистрации единичного элемента, разработаны модель и алгоритм формирования нечеткой кодовой комбинации на приеме; разработана методика распознавания состояния ЦУ с учетом состояния канала связи; с учетом состояния отсчетов (кодовой комбинации) разработаны и исследованы алгоритмы цифровой F-фильтрации сигналов на основе нечеткой логики, в частности, низкочастотного и полосового фильтров.
6. Изложены основы теории распределения сигналов управления в сети управления на основе F-логики: разработана модель системы управления «Агент-сетевой элемент» с использованием теории СеМО для трех потоков данных управления (U), контроля (К) и диагностики (D); F-модель управления канальным ресурсом на основе прямых нечетких продукционных правил вывода modus ponens для нечеткой СМО типов 
, где рассмотрена схема нечеткого вывода для очередей бесприоритетными и со многими приоритетами; предложена модель и алгоритм маршрутизации в поллинговой СеМО на основе нечетких матриц предпочтения с окончательным решением выбора маршрута с использованием нечеткого интеграла.
7. Перспектива использования научных и практичных результатов диссертационной работы связана: с изучением характеристик сложных систем мониторинга, технического контроля и диагностики в иерархии управления сетей связи; проведением научных исследований процессов каналов связи в системе распределенного мониторинга состояний объектов управления как технических, так социальных и биологических; проектированием интеллектуальных средств поддержки принятия решений на всех уровнях иерархии управления, с учетом целевой функции.
По материалам диссертации опубликованы следующие основные работы:
