«Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Нижегородский государственный архитектурно-строительный университет» ...»
где h — высота, 
— длина волны, 
– коэффициент зависимости от длины волны, NR = 8км — толщина атмосферы с однородной плотностью.
Для расчета цвета необходимо вычислить, какая часть изначального пучка света от Солнца рассеялась, а какая осталась и попала на сетчатку глаза. Это определяется уравнением рассеяния. В это уравнение входит громоздкий интеграл, который аналитически не берется, а численное интегрирование довольно сложное. В 1993 году Нишита предложил алгоритм расчета интеграла, который, однако, занимал много времени [74].
Проведение этих расчётов в реальном времени долго было недостижимой задачей. В начале 2000-х годов с появлением графических процессоров и возможности их программирования с помощью языков шейдеров начались разработки по расчёту цвета атмосферы в реальном времени. В 2005 году О’Нил упростил алгоритм Нишиты и адаптировал его для расчета на GPU [75]. Алгоритм подходит для бесшовного рендеринга атмосферы для любого положения камеры от поверхности до дальнего космоса и любого вектора направления на Солнце. Многие авторы в дальнейшем занимались усовершенствованием этого алгоритма [40, 76].
Несмотря на сильное упрощение, алгоритм обеспечивает правдоподобный результат. Из-за его простоты и высокого быстродействия он сейчас используется во многих графических приложениях.
Для сравнения в работе [40] дополнительно используются текстуры с предрассчитанными значениями. В работе [76] дополнительно производится учет множественного рассеяния и учет неровностей рельефа.
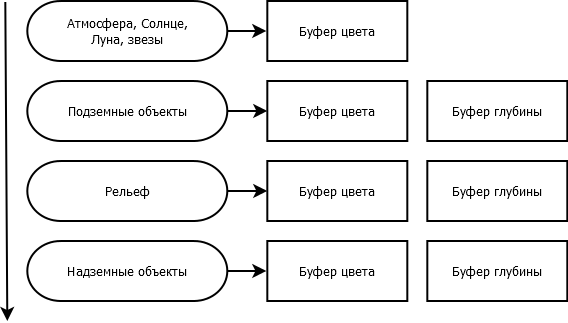
Технически алгоритм распадается на две составные части: вычисление цвета неба и модификация цвета рельефа.
Для рендеринга неба используется сфера с радиусом на 2,5% больше полярного радиуса Земли с включенным отбрасыванием лицевых граней полигонов, чтобы наблюдатель видел только изнанку сферу. Большая часть сферы закрывается земным эллипсоидом. Через каждый пиксель неба пускается луч, и определяются точки входа и выхода из атмосферы. Для полученного отрезка вычисляется интеграл рассеяния методом численного интегрирования. Отрезок разбивается на несколько точек, для которых вычисляется доля рассеянного света (рис. 2.5). Интеграл считается для 3-х компонент света и для 2-х случаев рассеяния. Результат суммируется.
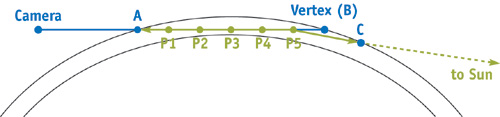
Рис. 2.20. Атмосферное рассеяние
Аналогичный алгоритм можно применить и для рельефа. Отраженный от рельефа луч свет также претерпевает рассеяния в атмосфере. Чем дальше находится точка рельефа, тем сильнее свет рассеивается. Поэтому дальние участки рельефа у горизонта кажутся находящимися в голубоватой дымке. Цвет неба плавно переходи в цвет поверхности (рис. 2.6).
Рис. 2.21. Атмосфера
Эту же идею можно применить к рендерингу объектов на рельефе, например, удаленных деревьев и домов, которые также скрываются в голубоватой дымке.
2.2. Полупрозрачная поверхность глобуса
Была поставлена задача: разработать способ визуализации глобуса с полупрозрачной поверхностью с возможностью как надземного, так и подземного просмотра.
Традиционно при визуализации объектов под поверхностью рельефа не используется виртуальный глобус. Показывается изолированный участок рельефа, его можно «облететь» со всех сторон, можно посмотреть сбоку или сделать сечение (рис. 2.7).
Поэтому визуализация объектов под поверхностью глобуса — новая задача, и здесь необходимо разработать новый подход. Очевидная идея — сделать поверхность рельефа полупрозрачной. Однако при простом включении прозрачности возникает ряд графических артефактов (рис. 2.8, 2.9, 2.10).
2.2.1. Анализ проблемы
Рассмотрим в деталях традиционный подход к рендерингу трехмерной сцены с виртуальным глобусом с включеной полупрозрачностью, основанный на спецификации OpenGL [71]. Вначале рендерятся непрозрачные подземные объекты. Далее рендерится рельеф. Для каждого фрагмента рельефа вычисляется цвет RGB на основе текстуры и с учетом освещения и задается значение прозрачности А (альфа-канал). Если фрагмент прошел тест глубины, то его цвет смешивается с цветом пикселя в буфере цвета, который принадлежит подземному объекту.
Спецификация OpenGL определяет несколько формул для смешивания. Наиболее часто используется следующая:
  , | (2.7) |
где 
— цвет входящего фрагмента, 
— цвет пикселя в буфере цвета, 
— значение прозрачности входящего фрагмента. Итоговый цвет 
записывается в буфер цвета.
 |
| Рис. 2.22. Объект под рельефом |
В случае виртуального глобуса это приводит к следующим эффектам.
Если подземные объекты не локализованы в одной точке, а распределены по всему глобусу, то объекты у дальней поверхности глобуса становятся видны наравне с объектами у ближней поверхности глобуса (рис. 2.8). Это приводит к визуальной «каше» и путанице.
 |
| Рис. 2.23. Просвечивают дальние объекты |
Если используется атмосфера, то она обычно рендерится до глобуса. Поэтому при включении прозрачности атмосфера также начинает просвечивать сквозь рельеф. В зависимости от алгоритма визуальный эффект может быть разным. Например, как на рис. 2.9.
 |
| Рис. 2.24. Просвечивает атмосфера |
 |
| Рис. 2.25. Просвечивают горы |
«Юбки» тайлов также начинают просвечивать. Изображение на экране становится чувствительном к порядку отрисовки тайлов и к повороту камеры относительно тайла: при определенных углах поворота камеры сквозь гористые участки рельефа начинают просвечивать другие части рельефа (рис. 2.10).
Часть этих эффектов может быть сравнительно легко устранена, но при этом могут возникнуть новые графические артефакты. Например, «юбки» тайлов можно вообще отключить. Но тогда станут видны щели между тайлами. Или атмосферу можно рендерить после глобуса, а не до. Но тогда придется сильно разносить ближнюю и дальнюю плоскости отсечения объема видимости. Это приведет к падению точности буфера глубины, а следовательно к эффекту мерцания (z-fighting).
Существуют универстальные алгоритмы корректного учета прозрачности, основанные рендеринге в несколько проходов, такие как depth peeling [82] или depth partition. Однако они устраняют не все графические артефакты.
В целом традиционный подход можно изобразить на рисунке 2.11.
 |
| Рис. 2.26. Традиционный порядок рендеринга |
Поэтому необходим новый способ качественного рендеринга полупрозрачного рельефа виртуального глобуса. Этот способ должен удовлетворять следующим условиям:
- не должны просвечивать объекты с дальней стороны глобуса;
- одни элементы рельефа не должны просвечивать сквозь другие;
- способ не должен влиять на рендеринг самих подземных объектов (не должен требовать изменения алгоритма рендеринга подземных объектов);
- атмосфера, а также другие космические объекты (Солнце, Луна, звезды) не должны просвечивать через глобус;
- рендеринг атмосферы не должен приводить к большому разбросу ближней и дальней плоскостей отсечения.
Кратко поясним последний пункт. Глубина пикселя вычисляется на основе ближней и дальней плоскостей отсечения объема видимости и приводится к диапазону [-1; 1]. В OpenGL используется следующая формула [69, 83]:
 | (2.8) |
где 
— расстояние от камеры до ближней плоскости отсечения, 
— расстояние до дальней плоскости отсечения z — расстояние до искомого пикселя. График зависимости глубины от расстояния изображен на рисунке 2.12.
Видно, что разрешение буфера глубины падает с удалением от камеры. Половина диапазона значений буфера приходится на область вблизи ближней плоскости отсечения.
Это приводит к тому, что для двух далеких полигонов становится невозможным корректное сравнение глубин. Возникает мерцание, которое называется z-fighting: на одном кадре может быть виден пиксель одного полигона, а на следующем кадре — пиксель другого полигона.
 |
| Рис. 2.27. Зависимость глубины от расстояния до камеры |
Это проблема возникает в любых приложениях с 3D графикой [84].
Чтобы избежать такой «борьбы», рекомендуется разброс f-n делать как можно меньше. При просмотре глобуса с атмосферой из космоса значения f и n будут определятся самим глобусом. Но при приближении камеры к поверхности на значение f будет оказывать сильное влияние атмосфера.
2.2.2. Предлагаемый способ
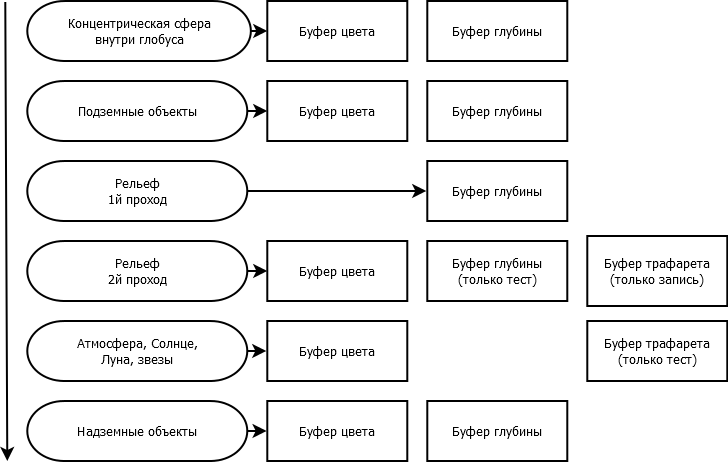
Предлагается способ визуализации глобуса, который устраняет графические артефакты с помощью двухпроходного рендеринга:
1. Вначале рендерится концентрическая сфера внутри глобуса с радиусом R и цветом C. Использование сферы позволяет скрыть подземные объекты с дальней стороны глобуса. Цвет сферы можно выбрать под цвет фона, например, черный. Радиус выбирается в зависимости от подземных объектов, которые нужно показать или скрыть. Для большинства задач подходит 
км, где 
— экваториальный радиус Земли. 1000км выбрано, потому что самые глубокие землетрясения были зарегистрированы на глубние 700км.
Для разных подземных объектов можно придумать собственные алгоритмы для контроля видимости. Можно скрывать объекты по расстоянию от камеры. Можно скрывать объекты с учетом горизонта [85]. Но концентрическая сфера внутри глобуса — один из самых простых и универсальных способов.
2. Далее рендерятся сами подземные объекты обычным способом. Объекты с противоположной стороны глобуса не проходят тест глубины и отбрасываются.
3. Далее в 2 прохода рендерится рельеф. При первом проходе отключается запись в буфер цвета, и происходит заполнение буфера глубины. Значение в буфере глубины для каждого пикселя соответствует ближайшему к камере фрагменту рельефа.
4. При втором проходе происходит запись в буфер цвета при условии совпадения глубины фрагмента со значением в буфере глубины. Это гарантирует, что в буфер цвета попадут только ближайшие к камере фрагменты рельефа. Перед записью в буфер цвета происходит смешивание цветов с уже имеющимися там значениями, которые относятся к подземным объектам.
5. Далее необходимо рендерить звезды, Солнце, Луну и атмосферу. Если включить тест глубины для проверки перекрытия с глобусом, то сильно увеличится разброс между дальней и ближней плоскостями отсечения. Поэтому необходимо использовать буфер трафарета (stencil buffer) [71]. Буфер трафарета позволяет записывать туда значения при наступлении определенных условий, а также выполнять тест трафарета перед записью цвета в буфер цвета.
Буфер трафарета позволяет сформировать маску рельефа во время второго прохода рендеринга рельефа. Для этого в буфер производится запись значения 1. Тест трафарета для рельефа не производится.
Далее рендерятся звезды, Солнце, Луна и атмосфера. Они рендерятся по очереди в указанном порядке, но общая логика рендеринга одинакова. Тест глубины отключается. Вместо этого включется тест трафарета. Цвет фрагмента атмосферы записывается в буфер цвета только при условии, что значение в буфере трафарета не равно 1. Значение в буфере не изменяется.
6. Наконец, последними рендерятся надземные объекты. Здесь существенно, что это происходит после атмосферы, т.к цвет полупрозрачных поверхностей (деревья, частицы) должен смешиваться с цветом атмосферы.
Вся последовательность шагов изображена на рисунке 2.13.
При использовании черезстрочного стерео для создания стереоэффекта также используется буфер трафарета. Необходимо это учесть при реализации алгоритма, чтобы не было конфликтов между ними.
Отдельно встает задача выбора формулы смешивания цвета подземных объектов и цвета рельефа. Использование формулы (2.5) приводит к следующему:
- при выставлении значения альфа-канала в 1 (непрозрачность) подземные объекты становятся не видны;
- при выставлении значения альфа-канала в 0 (полная прозрачность) рельеф становится не виден. Это затрудняет управление виртуальной камерой;
- при выставлении промежуточных значений блекнут цвета и рельефа, и подземных объектов. Яркость цветов подземных объектов уменьшается. Это ухудшает визуальное восприятие.
 |
| Рис. 2.28. Порядок рендеринга для полупрозрачного рельефа |
Предлагается использовать немного другую формулу:
  , | (2.9) |
При этом цвет подземного объекта складывается с цветом рельефа, уменьшенным с помощью значения альфа-канала. Цвета становятся более яркими, но в некоторых случаях возможна «засветка». Необходимо дать пользователю возможно через интерфейс пользователя регулировать значение прозрачности для настройки удобных для восприятия цветов.
Рассмотрим плюсы и минусы предложенного алгоритма. Минусы: необходимость рендерить рельеф 2 раза и необходимость выделения памяти для буфера трафарета. Это приводит снижению производительности приложения. Плюсы: отсутствуют графические артефакты, упомянутые в начале параграфа.
Существует также альтернативный способ обхода проблемы с атмосферой, основанный на логарифмическом буфере глубины [69]. Идея следующая: вместо формулы (2.6) использовать логарифм для вычисления глубины в зависимости от расстояния до камеры:
  , | (2.10) |
где C — калибровочный параметр.
Это полностью решает проблему точности буфера глубины и устраняет мерцание (z-fighting), что позволяет спокойно рендерить атмосферу в общем пространстве с глобусом с включенным тестом глубины без применения буфера трафарета.
Однако у такого подхода есть недостатки. Реализация формулы (2.8) возможна только на уровне шейдеров, а значит пропадает возможность использования фиксированного графического конвейера для отдельных объектов. Более того: вычисление логарифмической глубины необходимо внести в шейдеры для всех объектов трехмерной сцены, что противоречит одному из требований сформулированных выше. Также это повышает вычислительную нагрузку на видеокарту, что приводит к дальнейшему уменьшению производительности.
2.2.3. Вариант с камерой под поверхностью
Рассмотрим режим, когда камера находится под поверхностью земли. Этот режим нужен, чтобы иметь возможность рассмотреть подземный объект со всех сторон, а не только сверху, и без искажений цветов, которые создает полупрозрачная поверхность рельефа.
Существующие алгоритмы рендеринга рельефа рассчитаны, что просмотр будет осуществляться сверху. Поэтому под рельеф убирают вспомогательную геометрию — «юбки» тайлов, отключают рендеринг обратных граней полигонов. Алгоритм определения видимости тайлов зависит от положения камеры над поверхностью. Пример получающихся графических артефактов изображен на рисунке 2.14.
 |
| Рис. 2.29. Графические артефакты при спуске под поверхность рельефа |
Поэтому при спуске камеры под землю необходимо изменить параметры визуализации базового алгоритма, а именно: переключение режима отбрасывания граней с обратных на лицевые, отключение рендеринга юбок тайлов и атмосферы. Это обеспечивает минимально приемлемый подземный вид (рис. 2.15). Для примера на рисунке изображен подземный объект — 3D-модель канала гейзера.
Традиционный подход к рендерингу рельефа предполагает отбрасывание тайлов, когда они выходят за линию горизонта [86]. Базовая идея алгоритма основана на формуле:
 | (2.11) |
где 
— усредненная нормаль тайла, 
— центр тайла, 
— положение камеры. Если 
, то тайл находится за линией горизонта. Для гористых районов эта формула напрямую не подходит, т.к. вершины гор могут быть видны из-за горизонта. Поэтому применяют более сложные вариации этой формулы.
Однако при спуске под землю такая проверка приводит к тому, что виден лишь небольшой участок рельефа вблизи камеры (рис. 2.15). При отключении проверки на выход тайлов за горизонт становится видна изнанка глобуса (рис. 2.16). Но при этом возникает другая проблема: мерцание отдаленных тайлов (z-fighting) из-за большого разброса значений ближней и дальней плоскостей отсечения. По мере спуска дальше под землю ближняя плоскость отсечения отодвигается и эффект мерцания пропадает.
 |
| Рис. 2.30. Вид из под земли |
Выбор между двумя вариантами не является очевидным и зависит от конкретной задачи. Если под землей нужно рассмотреть отдельный объект, то дальние тайлы просто не нужны, и проверку на выход за горизонт можно оставить. Если же рассматривается протяженный объект или множество объектов (например, каталог землетрясений), то проверку на выход за горизонт нужно отключить, а с мерцанием бороться разными способами (например, с помощью логарифмического буфера глубины, который упоминался выше).
Следующий спорный момент — это прозрачность поверхности. Здесь возможны три альтернативы:
- сделать рельеф полностью непрозрачным. Тогда будут видны только подземные объекты;
- сделать рельеф прозрачным для всех объектов. Можно будет из-под земли видеть надземные объекты: дома, машины, деревья;
- сделать рельеф прозрачным только для некоторых объектов: например, которые частично находятся под землей, частично над землей.
Первый вариант - это традиционный рендеринг в один проход с учетом модификаций, описанных в начале этого параграфа. Второй и третий вариант требуют 2х-проходного рендеринга, аналогичного описанному в предыдущем параграфе. При этом необходимо только изменить порядок рендеринга: сначала надземные объекты, потом подземные объекты, затем рельеф. Пример со зданиями показан на рисунке 2.17.
 |
| Рис. 2.31. Вид из-под земли с отключенной проверкой на выход тайлов за горизонт |
 |
| Рис. 2.32. Вид из под земли на надземные объекты |
Выбор конкретного варианта должен осуществляться в каждом проекте индивидуально и зависит от поставленных задач.
2.3. Применимость для подземных объектов
Подземные объекты могут иметь разную природу и визуализироваться с разными целями. Рассмотрим, какие бывают типы подземных объектов, и применимость к ним предложенного способа визуализации глобуса.
1. Облака точек. Это могут быть очаги землетрясений или результаты точечных бурений для изучения свойств земли. Точки хорошо сочетаются с предложенным способом. Они практически не оказывают влияния друг на друга (не «загораживают» другие точки). Облако целиком можно рассмотреть с разных ракурсов или путем перемещения камеры внутри облака. Подробнее визуализация облаков точек рассмотрена в параграфе 3.1.
2. Отдельные объекты: искусственные (шахты, скважины, тоннели) или природные (пещеры, разломы). Они могут быть заданы в виде своих ограничивающих поверхностей и визуализироваться как самые обычные полигональные поверхности (рис. 2.15). Для подчеркивания формы объекта необходимо применять освещение. Но поскольку солнечное освещение под землей не действует, то рекомендуется совместить источник света с виртуальной камерой.
3. Объемные данные — трехмерная матрица значений. Они могут быть получены методом сейсмотомографии или интерполяцией других данных. В параграфе 3.2 предложен алгоритм рендеринга таких данных на глобусе, основанный на прямом объемном рендеринге. При этом доступны все возможности прямого объемного рендеринга: выделение изоповерхностей, назначение прозрачности и цвета в зависимости от значения параметра в ячейке.
4. Слоистые протяженные данные — геологические слои, водоносные горизонты, почвы. Для таких объектов предложенный способ с полупрозрачной поверхностью глобус применим плохо. Под полупрозрачной поверхностью будет располагаться другая поверхность, скрывающая всё остальное.
Возможные варианты решения для слоистых данных:
- регулировка коэффициента полупрозрачности для каждого слоя в отдельности;
- «вырез» участка данных и участка рельефа для просмотра среза слоев. Здесь необходимо разработать алгоритм динамического перемещения выреза глобуса и динамического контроля его размеров, чтобы обеспечить удобную работу с данными.
Также полезна возможность залететь под землю и просмотр подземных объектов вблизи. В случае слоистых данных перед виртуальной камерой может быть фиксирована плоскость среза, которая движется вместе с камерой.
2.4. Выводы по 2 главе
В главе рассмотрены основные способы и варианты визуализации глобуса, предложен новый способ визуализации глобуса, сделаны следующие выводы:
1. В зависимости от потребностей отрасли науки, в которой используется виртуальный глобус, рельеф можно отображать на экране по-разному: модифицировать саму геометрию (растяжение по высоте), раскрашивать с помощью палитры цветов (по высоте, по крутизне склона рельефа и т.д.), смешивать несколько текстур, модифицировать цвет текстуры (учитывать освещение, атмосферное рассеяние).
В геофизике и геологии существует необходимость просмотра подземных объектов и 3D-данных. Визуализация таких данных на глобусе — является новой задачей. Если включить полупрозрачность для поверхности глобуса, то при традиционном подходе возникает ряд графических артефактов.
2. Предлагается способ визуализации полупрозрачной поверхности глобуса, при котором эти артефакты отсутствуют. В предложенном способе рельеф отрисовывается в два прохода. При рендеринге атмосферы используется маска в буфере трафарета.
Дополнительно рассматривается случай, когда виртуальная камера находится под поверхностью рельефа. В этом случае предложенный способ также работает, но с рядом модификаций.
3. Разработанный способ визуализации позволяет просматривать и визуально анализировать подземные 3D-данные: очаги землетрясений, подземные структуры, скважины, слои и т.д. Способ позволяет просматривать данные как сверху, сквозь поверхность рельефа, так и из-под земли.
- Визуализация данных на виртуальном глобусе
3.1. Облака точек
3.1.1. Обзор современного состояния дел
Облака точек — один из самых простых типов данных. Необходимость визуализации таких данных на виртуальном глобусе возникает в разных областях, однако при этом возникает ряд технических сложностей.
Один из примеров точек на глобусе — это гипоцентры землетрясений, которые хранятся в виде каталогов. Гипоцентр — это центральная точка очага землетрясения, которая находится в глубине земли. Проекция гипоцентра на поверхность Земли называется эпицентром. Каталоги гипоцентров свободно доступны на специализированных сайтах, например, на сайте Геологической службы США (USGS) [87], на сайте Камчатского филиала Геофизической службы РАН [88], и др. Каталог землетрясений для всей Земли с 1900 года включает около 1 млн. событий.
Точки из каталогов могут покрывать большие территории, возможно даже всю поверхность глобуса, и могут иметь разные высоты и глубины. Такие точки изначально хранятся в географической системе координат, и перед визуализацией их необходимо переводиться в мировую декартову систему координат.
Другой пример источника облаков точек — лазерное сканирование. Лазерное сканирование — это современный способ для быстрого создания высокоточных 3D-моделей зданий и любых объектов в виде облаков точек [89]. Точность может достигать 1 мм. Сначала производится сканирование объекта с разных позицией, затем — обработка полученых исходных облаков точек. Процесс обработки состоит из 2х этапов: сначала все облака для одного объекта сшиваются в единое облако точек (рис. 3.1), затем по этому облаку точек восстанавливается полигональная 3D-модель. Первый этап проходит быстро и может быть автоматизирован. Однаков второй этап довольно трудоёмкий, требует ручной работы и может затянуться на месяцы.
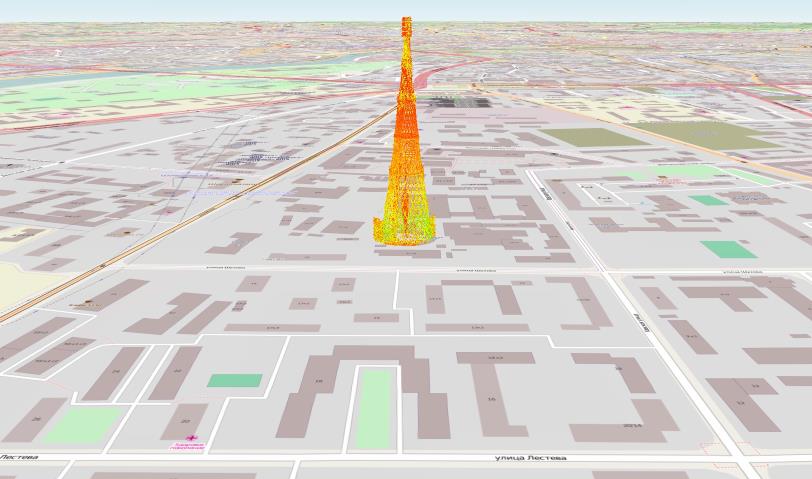
Рис. 3.33. Облако точек Шуховской башни
Поэтому вместо того, чтобы создавать полигональную 3D-модель объекта, можно работать с точечной 3D-моделью. Облако точек для одного здания может содержать 50-100 миллионов точек и занимать в памяти несколько гигабайт. Это делает невозможным интерактивный рендеринг полного облака точек. Необходимо использовать уровни детализации.
Исследования в области обработки и визуализации облаков точек ведутся много лет. Значительные усилия тратятся на развитие методов и разработку библиотек для реконструкции полигональных поверхностей по облакам точек [90].
Кроме того, существуют методы визуализации непосредственно самих облаков точек. Обзор таких методов дан в статье [91]. Они различаются как разбиением облака точек на уровни детализации, так и способами рендеринга самих точек. Существуют три основных способа:
- визуализация облаков точек в виде простого точечного примитива OpenGL (GL_POINT). Они изображаются на экране в виде либо квадрата, либо окружности заданного размера. В вершинном шейдере можно задавать размер индивидуально для каждой вершины;
- визуализация облаков точек в виде спрайта — четырехугольника, который всегда повернут к камере. Это более медленный, но более гибкий вариант, т.к. позволяет использовать текстуру с прозрачностью;
- визуализация в виде одного или нескольких треугольников фиксировано расположенных в пространстве, перпендикулярно вектору нормали. Они называются splats («нашлепки»). Это самый медленный, но наиболее гибкий вариант, который обеспечивает лучшее визуальное качество.
Спрайты и треугольники — это попытка скрыть промежутки между точками, чтобы 3D-модель визуально выглядела целостной, без дыр [92, 93]. Есть и другие подходы к этой проблеме, основанные на постпроцессинге [94].
Поскольку размеры облаков точек растут, то появляются методы по их сжатому хранению и распаковке на видеокарте [95, 96].
Для более качественно рендеринга с освещением необходимо знать нормаль в каждой точке. Если нормали изначально не заданы, то их можно вычислить. Существуют методы для этого [97].
В работе [46] предлагается отказаться от построения полигональных моделей зданий и использовать облака точек для создания 3D-моделей целых городов.
В моно-режиме облака точек сложно воспринимать на экране из-за отсутствия ощущения глубины точек. Все точки кажутся расположенными на одном расстоянии и сливаются в «кашу», особенно если используются не реальные, а условные цвета. Но ситуация меняется в случае использования стереоскопической визуализации. Визуально можно легко отделить точки, расположенные ближе, от точек, расположенных дальше. Это превращает стереовизуализацию в мощный инструмент для визуального анализа научных данных. Именно поэтому в данной работе делается акцент на точечных данных.
Точки удобны тем, что они рендерятся очень быстро, т.к. это базовый геометрический примитив. Современные видеокарты позволяют рендерить около 10 миллионов точек каждый кадр с интерактивной частотой кадров. Поэтому нет необходимости проверять индивидуальные точки на попадание в объем видимости.
На вызов каждой операции отрисовки тратится небольшой время (накладные расходы). Чтобы минимизировать суммарное время, рекомендуется объединять точки из разных облаков в единый массив, для отрисовки одной командой.
С другой стороны, если точки распределны по большой территории, то имеет смысл разбить все точки на несколько частей по пространственному признаку и проверять каждый кусок на попадание в область видимости.
Необходимо динамически определять, какие точки показывать в зависимости от положения виртуальной камеры. При приближении камеры необходимо показывать дополнительные точки в той части модели, которая попадает в область видимости камеры. А при отдалении снова скрывать их.
3.1.2. Алгоритм визуализации облаков точек
Была поставлена задача разработать алгоритм для интерактивного рендеринга больших облаков точек (размером больше 100 млн. точек) на виртуальном глобусе и динамической фильтрации их по заданным параметрам.
Можно заметить, что при разрешении 1920х1080 максимальное число видимых точек на экране составляет около 2 млн. Поэтому при просмотре облака с большого расстояния нет необходимости отображать все 100 млн. точек целиком.
В основе предложенного алгоритма лежит подход с дискретными уровнями детализации, при котором облако разбивается на фрагменты — мини-облака. Когда камера находится далеко, то показывается один фрагмент, который содержит точки случайным образом выбранные из полного облака точек. По мере приближения камеры должны показываться фрагменты более высоких уровней детализации. Все фрагменты должны содержать примерно одинаковое количество точек, но на более высоких уровнях детализации пространственный размер фрагмента должен быть меньше и фрагментов должно быть больше.
Идеологически эта схема напоминает подход с тайлами рельефа, описанный в параграфе 1.3.4. Однако природа точечных данных позволяет сделать одно существенное усовершенствование. В случае рельефа при приближении тайлы более высоких уровней детализации заменяют тайлы низких уровней детализации. Но точечные данные разных уровней детализации могут не мешать друг другу. Точки нескольких уровней детализации можно показывать одновременно. При приближении камеры фрагменты низкого уровня детализации не должны скрываться, а фрагменты более высоких уровней детализации должны добавляться к существующим.
Такой подход позволяет не дублировать точки между уровнями детализации. В памяти облако точек, разбитое на уровни детализации, будет заниматься столько же места, сколько и целое.
Генерация дерева фрагментов
В начале необходимо сгенерировать дерево фрагментов: разбить всё облако точек на фрагменты и расчитать расстояние видимости для каждого фрагмента.
Алгоритм основан на рекурсивном разбиении пространства и хранении данных в древовидной структуре данных. Древовидная структура данных включает квадро- и октодеревья. В случае квадродерева вся область рекурсивно разбивается на 4 ячейки. В случае октодерева — на 8 ячеек (рис. 3.2).
 |
| Рис. 3.34. Схема октодерева |
Далее перечислены шаги алгоритма.
0. Предварительный этап. Если облаков точек несколько, то их всех необходимо объединить в единое облако, и преобразовать координаты из локальных систем координат в географическую систему координат.
1. Построение корневого ограничивающего бокса. На этом шаге перебираются все точки полного облака точек для определения минимальных и максимальных значений координат по 3м осям. Далее вычисляются координаты вершин ограничивающего бокса, который плотно содержит в себе полное облако точек.
2. Начальное построение дерева. Каждый узел дерева имеет следующие атрибуты: соответствующий этому узлу ограничивающий бокс, массив вершин этого узла, массив цветов (и возможно массивы интенсивностей и других вершинных атрибутов) и ссылки на дочерние узлы.
Построенный на первом шаге бокс используется для создания корневого узла дерева.
На этом шаге происходит последовательное чтение точек (из файла или другого источника данных для облака точек) и помещение их в корневой узел дерева с помощью метода добавитьТочку() (рис. 3.3).
В методе добавитьТочку() происходит помещение точки в локальный массив вершин этого узла до тех пор, пока их количество не превысит значение параметра 
.
Если количество точек превысило 
то происходит разбиение ограничивающего бокса и построение соответствующих дочерних подузлов. Все имеющиеся в данном узле точки распределяются по дочерним узлам, вызывая метод добавитьТочку() у каждого из дочерних подузлов.
При последующих вызовах добавитьТочку() происходит рекурсивный вызов добавитьТочку() у дочерних узлов. Когда количество точек в некотором узле достигнет значения 
, то процедура разбиения повторяется.
Вначале разбиение прозводится на 4 подбокса путем разрезания исходного по середине по долготе и широте. Далее квадродерево переходит в октодерево — дополнительно производится разрезание по средней высоте.
В конце этого этапа, когда все точки из полного облака будут обработаны, получится древовидная структура. Точки будут распределены по листовым узлам этого дерева.
 |
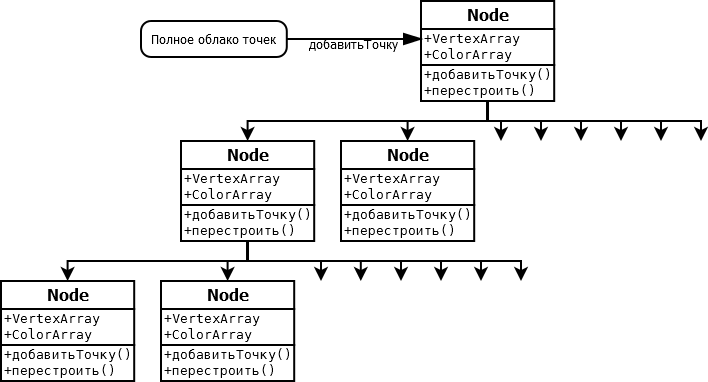| Рис. 3.35. Распределение вершин по узлам |
3. Перераспределение точек в дереве. В начале этого этапа все точки распределены по узлам максимального уровня детализации M. Теперь нужно заполнить точками другие уровни детализации. При этом точки не должны дублироваться, т.е. точки будут браться из дочерних узлов и подниматься вверх в иерархии.
Рекурсивно для всех промежуточных узлов, начиная с узлов уровня детализации М-1 и вверх по дереву должна быть выполнена следующая операция. Случайным образом из всех дочерних узлов нужно отобрать 
точек и поместить в массив вершин данного узла. 
, поэтому эта операция всегда возможна. Далее перебираются все дочерние узлы. Если в каком-то из них осталось меньше 
точек, то они все переходят в массив вершин данного узла.
В результате этого этапа корневой узел будет содержать 
точек, каждый промежуточный узел будет содержать не меньше 
и не больше 
точек, а листовые узлы не меньше 
и не больше 
.
4. Генерация геометрии. На основе каждого узла дерева создается объект, который будет отвечать за визуализацию данного фрагмента облака точек.
При визуализации глобального облака точек возможна следующая ситуация: при попытке приблизиться к точке или к группе рядом стоящих точек возникает дрожание (jittering). Как упоминалось в параграфе 1.3.4, это связано с использованием типа данных с одинарной точностью (float). Числа с плавающей точкой имеют фиксированную относительную точность, но изменяющуюся абсолютную точность. Точность обратно пропорциональная расстоянию от начала координат (центра глобуса). На поверхности глобуса абсолютная точность составляет около 1м. Чем выше от поверхности, тем ниже точность.
Поэтому координаты всех точек узла преобразуются из географической в локальную декартову систему координат данного узла.
Разработка приложения велась на основе фреймворка OpenSceneGraph, поэтому удобно представить результирующую структуру данных с использованием классов OpenSceneGraph наподобие схемы для тайлов рельефа на рисунке 1.15.
Конечная геометрия хранится в объектах класса Geode. Класс Group отвечает за группировку элементов графа сцены, а класс PagedLOD за переключение видимости в зависимости от расстояния и за подгрузку объектов с диска.
На рисунке 3.4 представлена часть графа сцены, которая относится к одному фрагменту облака точек и хранится в одном файле. Этот файл прикреплен к экземпляру класса PagedLOD. Когда камера приблизится к заданному расстоянию, то файл будет подгружен с диска в память. На экране отобразится геометрия данного фрагмента (Geode) и будут задействованы еще 8 экземпляров PagedLOD, который в нужный момент подгрузят дочерние узлы следующего уровня детализации.
Алгоритм имеет несколько степеней свободы: значение параметров 
, 
, 
и расстояние, с которого нужно подгружать данный фрагмент.
 |
| Рис. 3.36. Граф сцены |
Если параметры 
, 
, 
будут слишком маленькие, то возрастут затраты времени на накладные расходы видеокарты и на проверку видимости каждого фрагмента. Если эти параметры будут слишком большие, то новые фрагменты будут долго подгружаться с диска или интернета, и станут заметны скачки частоты кадров. Предлагается использоваться следующие значения: 
, 
, 
.
5. Вычисление расстояний видимости фрагментов
Необходимо также настроить переключение видимости фрагментов. Расстояние, с которого нужно подгружать фрагмент, должно определяться, исходя из визуальной плотности точек на экране в момент подгрузки.
Угловой размер каждого пикселя экрана определяется по следующей формуле:
 | (3.12) |
где sd — расстояние до экрана, sh — высота экрана, 
— количество пикселей экрана по высоте.
Для каждого фрагмента строится своя ограничивающая сфера радиуса R. Со стороны наблюдателя сфера будет казаться диском радиусом R. Если считать, что все точки распределены по диску равномерно, то угловой размер расстояния между точками будет равен:
 | (3.13) |
где M — число точек во фрагменте, d— расстояние до центра фрагмента, которое и нужно найти.
Если теперь положить, чтобы угловое расстояние между точками равнялось угловому расстоянию между пикселями, мы получим нужное расстояние до центра фрагмента:
 | (3.14) |
В зависимости от производительности видеокарты и желаемой частоты кадров можно ввести коэффициент пропорциональности, чтобы уменьшить визуальную плотность точек.
Вышеописанный алгоритм для работы загружает все облако точек в память. Однако на 32х-битных системах существует ограничение по памяти в 2Гб. Поэтому если размер облака точек превосходит 2Гб, то необходимо предварительно разбить всё облако на несколько частей и применить алгоритм к каждой части по отдельности.
Визуализация и фильтрация точечных данных
Обычно точки имеют не только координаты, но и визуальные атрибуты (размер и цвет) и множество дополнительных атрибутов. Например, в случае лазерного сканирования это может быть интенсивность отраженного луча лазера. В случае гипоцентров землетрясений — магнитуда, время события, регион принадлежности события [11].
Визуальные атрибуты могут быть заданы изначально, а могут вычисляться на основе дополнительных атрибутов. Например, если атрибут x изменяется от 0 до 1, то цвет можно вычислить по формуле спектра [98]:
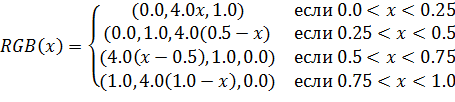 | (3.15) |
При этом цвет плавно изменяется от синего до красного (рис. 3.5).
 |
| Рис. 3.37. Непрерывная палитра цветов |
Для размера точек еще проще:
 | (3.16) |
Также часто необходимо осуществлять фильтрацию облака точек по заданным параметрам. Например, показывать только точки, атрибуты которых попадают в заданный диапазон.
Вычисление визуальных атрибутов и фильтрацию можно делать на центральном процессоре. Однако этот процесс занимает время, т.к. выполняется или последовательно, или в лучшем случае распараллеливается на нескольких ядрах ЦП. При попытке выполнять такие вычисления в реальном времени для больших объемов точек произойдет серьезное падение производительности.
Однако современные видеокарты позволяют визуализировать миллионы точек с интерактивной частотой кадров и производить вычисления в вершинном шейдере прямо во время рендеринга. Можно динамически изменять цвета точек, их размер, и производить фильтрацию на основе значений вершинных атрибутов.
У разных облаков точек могут быть разные атрибуты. Даже в рамках одного облака может быть необходимо изменять параметры фильтрации и вычисления визуальных атрибутов. Для каждого случая нужно иметь свою версию вершинного шейдера. Чтобы не писать каждый раз шейдер вручную, лучше его генерировать автоматически.
Рассмотрим весь процесс подробнее.
1. Задание вершинных атрибутов. Спецификация OpenGL позволяет загружать на видеокарту вершинные атрибуты, которые далее можно использовать в вершинном шейдере. Каждый атрибут — это 4х-мерный вектор со значениями типа float [99]. Однако сырые данные могут быть в других форматах: целочисленный, дробный, булевский, дата-время. Их нужно перевести в тип с плавающей точкой. Целые числа и булевские переводятся однозначно. Приведение даты-времени зависит от требуемой точности: дни, секунды или доли секунды. Например, если все даты относятся к периоду после 1970 года, то можно использовать Unix-time представление: число секунд, прошедшее с 1го января 1970 года. Если нужно охватить больший период времени, или нужна большая точность, то дату-время можно превратить в 2 числа с плавающей точкой: одно описывает номер дня, начиная с заданного момента в прошлом, другое — время в рамках одного дня.
4 разных атрибута точки можно передать на видеокарту как компоненты 4-вектора вершинного атрибута.
2. Создание uniform-переменных. Для каждого атрибута создаются несколько uniform-переменных. 2 переменные задают минимальное и максимальное значение атрибута. Во время исполнения шейдера проверяется попадание значения атрибута в выбранный диапазон. Если он не попадает, то вершина отбрасывается. 2 булевские переменные задают условия: нужно вычислять цвет точки или размер точки на основе этого атрибута.
3. Генерация тела шейдера. В цикле по всем атрибутам к шапке и к телу вершинного шейдера добавляются вставки.
Пример, шапки для одного атрибута:
attribute vec4 attr1;
uniform float attr1xMin;
uniform float attr1xMax;
uniform bool attr1xColor;
uniform bool attr1xSize;
Пример, тела шейдера для одного атрибута:
if (attr1.x < attr1xMin || attr1.x > attr1xMax)
{
discardPoint = true;
}
else if (attr1xColor)
{
float ratio = (attr1.x - attr1xMin) /
(attr1xMax - attr1xMin);
gl_FrontColor = getColorFromPalette(ratio);
}
else if (attr1xSize)
{
float ratio = (attr1.x - attr1xMin) /
(attr1xMax - attr1xMin);
gl_PointSize = minSize + ratio * (maxSize - minSize);
}
Здесь переменная discardPoint задается один раз на весь шейдер. Также отдельно определена функция getColorFromPalette на основе формулы (3.4).
Выше приведен пример проверки на попадание значения атрибута в заданный диапазон. Но могут быть и более сложные виды фильтрации. Например, проверка на принадлежность точки некоторому региону. Все облако точек делится на N областей-регионов. Каждый регион имеет свой идентификатор — число от 0 до N-1. Номер региона, к которому принадлежит точка передается в шейдер через вершинный атрибут.
Далее пользователь может выбрать какие регионы показывать. Например: 3, 5 и 10. Могут выбраны одновременно несколько регионов. Поэтому uniform-переменные attr1xMin и attr1xMax здесь уже не применимы. Вместо этого в шейдер передается массив булевских uniform-переменных, которые определяют видимость каждого региона:
uniform bool attr1xRegion[100];
if (attr1xRegion[int(attr1.x)] == false)
{
discardPoint = true;
}
Примеры применения.
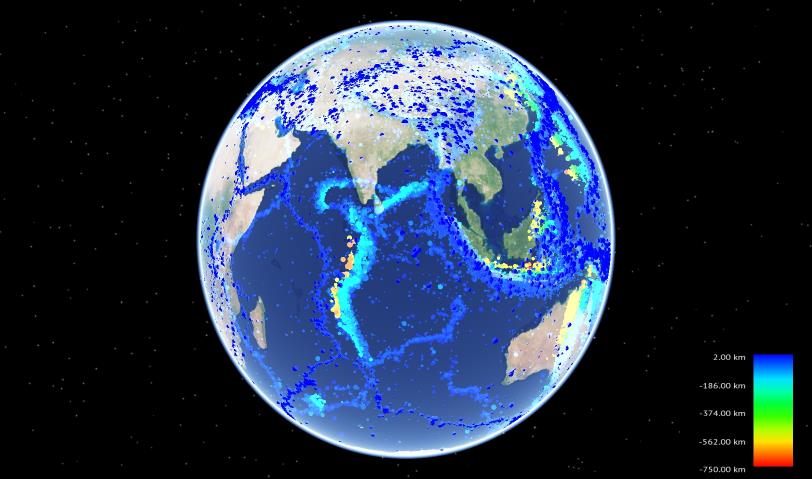
Предложенный подход использовался для визуализации и фильтрации каталога гипоцентров землетрясений (рис. 3.6, 3.7).
 |
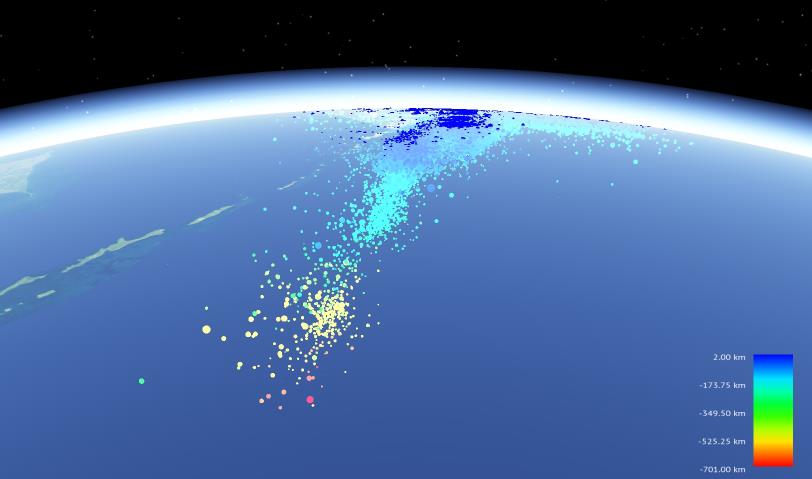| Рис. 3.38. Региональный каталог сейсмических событий в районе Курило-Камчатской дуги, по данным КФ ГС РАН [88] |
 |
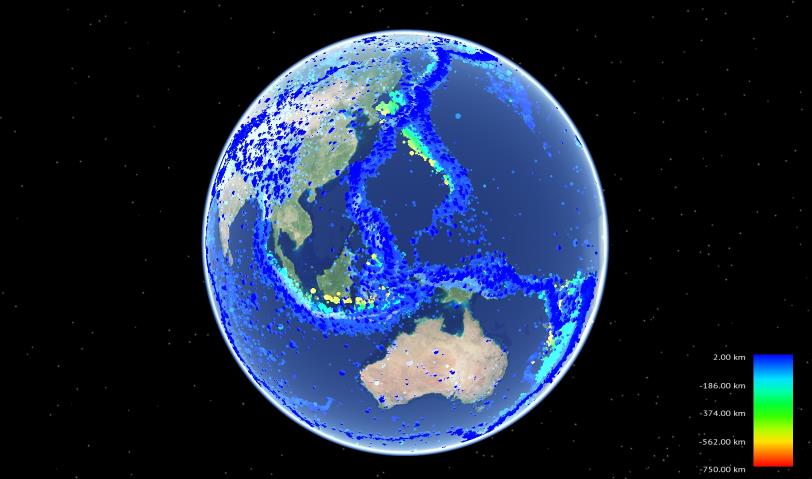| Рис. 3.39. Мировой каталог сейсмических событий USGS за 1900-2011 гг, по данным USGS [100], в редакции А. В. Ландера (МИТП РАН) |
Каждый гипоцентр имеет атрибуты: широта, долгота, глубина, дата, время (час, мин, сек), магнитуда, регион.
Глубина задается своим реальным значением (от 5км до -700км) с типом float и используется для вычисления цвета гипоцентра. Цветовое кодирование позволяет лучше определить глубину гипоцентра при обычном (не-стереоскопическом) просмотре, а также является традиционным обозначением в геофизике. Цвет берется из линейной палитры от синего на малых глубинах до красного на больших глубинах.
Магнитуда также задается реальным значением от 0 (если не определена) до 9.5 с типом float. Значения магнитуды от минимального до максимального отображаются на диапазон размеров точек от 1го до 6ти пикселей.
Также происходит фильтрация гипоцентров по регионам. Для каждого гипоцентра хранится идентификатор региона, к которому относится гипоцентр. При выборе алгоритма фильтрации учитывались следующие условия: (1) регионы не пересекаются и (2) одновременно можно выбирать несколько регионов. Тестировался набор из 10 регионов для Курило-Камчатской дуги.
3.2. Объемные данные
Объемные данные — это данные, заданные в виде трехмерной матрицы значений. Традиционно эти данные получаются в медицине с помощью методов магнитно-резонансной томографии или рентгеновской компьютерной томографии. Однако природа этих данных может быть любая. Возможны геопривязанные объемные данные — когда ячейки объема расположены через равные интервалы по долготе, широте и глубине.
Такие данные могут возникать в результате бурения в узлах периодической решетки и измерения каких-либо параметров почвы, например, температуры. Также объемные данные получаются с помощью метода сейсмотомографии, который сейчас активно развивается [101, 102]. По аналогии с медицинской томографией сейсмотомография позволяет получить распределение некоторых пространственных характеристик земной коры путем анализа данных с сети сейсмостанций, регистрирующих сейсмические волны от землетрясений.
Землетрясения создают продольные и поперечные волны, которые обозначают буквами P и S соответственно. Скорости распространения сейсмических волн различны и зависят от модуля упругости и плотности среды. Это позволяет идентифицировать некоторые характеристики земной коры на пути следования сейсмических волн. Результатом обработки множества данных является трехмерная матрица (воксельный массив), в ячейках которой записано значение отношения скоростей P-волн и S-волн в данной точке. Каждая ячейка матрицы (воксель) имеет координаты: долгота, широта, глубина.
3.2.1. Прямой объемный рендеринг
Существует 2 основных метода для рендеринга объемных данных: генерация полигональной сетки по объемным данным (алгоритм marching cubes [103]) и прямой объемный рендеринг [104].
Для визуализации объемных данных на виртуальном глобусе был предложен алгоритм на основе прямого объемного рендеринга.
Рассмотрим сначала, как работает прямой объемный рендеринг на основе обзорной работы [105].
Для хранения объемных данных на видеокарте используется 3D-текстура. В ней содержится не цвет, а скалярное значение (плотность
). В случае сейсмотомографии — это значение параметра Vp/Vs, приведенное к интервалу [0; 255]. Отдельно задается передаточная функция (transfer function), которая ставит в соответствие плотности цвет (RGB) и прозрачность (A) и хранится на видеокарте в виде 1D-текстуры.
Считается, что каждая ячейка объема испускает свет и поглощает свет. Чтобы определить цвет пикселя итогового изображения пускается луч из камеры через центр пикселя, и интегрируются оптические свойства объема вдоль хода луча. Интеграл берется численно следующим образом.
Через равные интервалы берется значение из 3D-текстуры с учетом трилинейной фильтрации. На основе этого значения с помощью передаточной функции вычисляется цвет (RGB) и прозрачность (A). Цвета последовательно смешиваются от задних к передним или наоборот (рис. 3.8). Формула смешивания от задних к передним:
 | (3.17) |
Суммирование ведется от 
до 0. 
и 
— цвет и прозрачность в точке объема i. 
— накопленный цвет.
 |
| Рис. 3.40. Бросание лучей |
3D-текстура привязывается к полигональной модели прямоугольного параллелепипеда, и интеграл считается для каждого пикселя параллелепипеда. Параллелепипед погружается в трехмерную сцену, где могут находиться и другие объекты.
Существуют также разновидности прямого объемного рендеринга:
- проекция максимума интенсивности: цвета не смешиваются вдоль луча, а берется цвет точки с максимальной плотностью;
- освещение: в каждой точки вычисляется нормаль по градиенту, и цвет считается с учетом освещения (косинус угла между нормалью и источником света);
- изоповерхность: берутся только точки, значение плотности которых равно заданному.
Существуют модификации базового алгоритма для увеличения быстродействия [106], для улучшения качества визуализации [107], устранения визуальных артефактов [108], для мультиобъемного рендеринга [109].
3.2.2. Алгоритм визуализации объемных данных на глобусе
Была поставлена задача разработать алгоритм для визуализации объемных данных на виртуальном глобусе.
Будем рассматривать частный случай, когда объем ограничен двумя параллелями, двумя меридианами и двумя уровнями высоты.
Для небольших объемов (с площадью крышки несколько десятков квадратных километров) можно считать Землю локально плоской и выводить объем традиционным способом в виде прямоугольного параллелепипеда (рис. 3.9). Сначала рендерятся подземные объемные данные, а затем трехмерный рельеф в режиме прозрачности с помощью алгоритма, описанного в параграфе 2.2.
 |
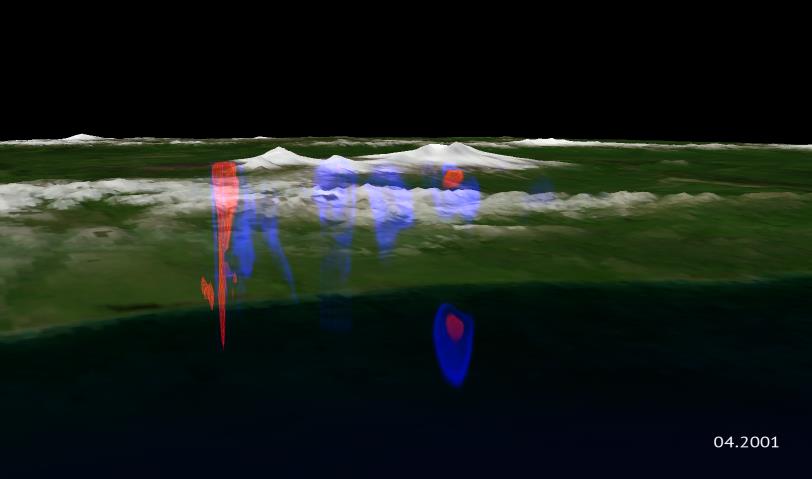| Рис. 3.41. Визуализация результатов сейсмической томографии в районе Ключевской группы вулканов на Камчатке за 2004 год, по данным И. Ю. Кулакова (ИНГГ СО РАН) |
Для больших объемов уже необходимо учитывать форму Земли. В географических координатах (долгота, широта, высота) данные имеют прямоугольный вид: координаты ячеек объема расположены в узлах равномерной сетки. Но эти объемные данные необходимо вписать в часть объема глобуса, ограниченную параллелями, меридианами и высотами (рис. 3.10).
Предлагается модификация алгоритма прямого объемного рендеринга для рендеринга объемных данных на глобусе.
 |
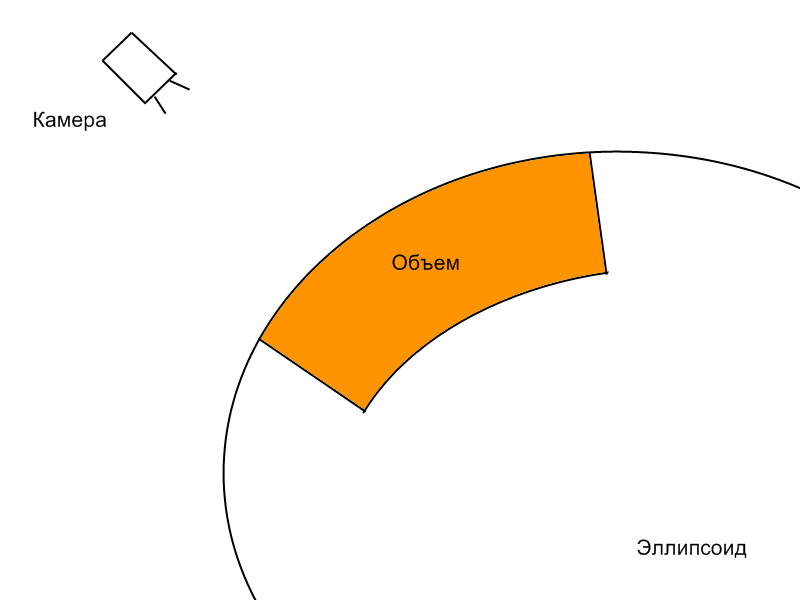| Рис. 3.42. Форма объема |
1. Сначала генерируется полигональная поверхность объёма с заданным уровнем приближения к поверхности эллипсоида. Далее эта поверхность рендерится в 2 прохода.
2. Во время первого прохода происходит рендеринг в текстуру задней части поверхности. Текстура имеет формат RGB и содержит числа с плавающей точкой. В текстуру записываются декартовы координаты фрагментов задней части поверхности (рис. 3.11).
 |
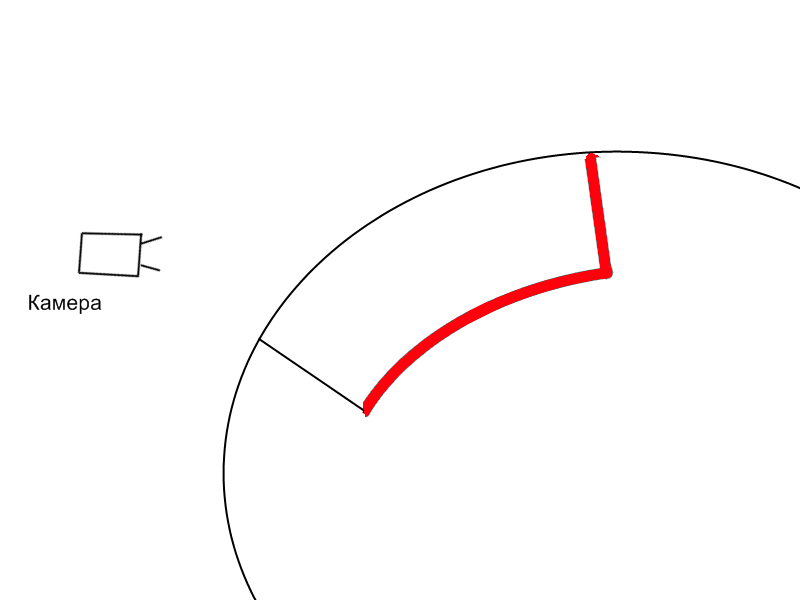| Рис. 3.43. Проход 1: рендеринг задней поверхности объема в текстуру |
3. Во время второго прохода рендерится уже передняя часть поверхности объёма. Вычисляются декартовы координаты фрагмента, которые являются координатами точки входа луча в объем. Также во фрагментный шейдер передается текстура, полученная во время первого прохода. Из нее берутся декартовы координаты точки выхода луча из объема.
4. Зная координаты точки входа луча и точки выхода луча, можно с заданным шагом пройтись вдоль луча и получить декартовы координаты промежуточных точек (рис. 3.12).
 |
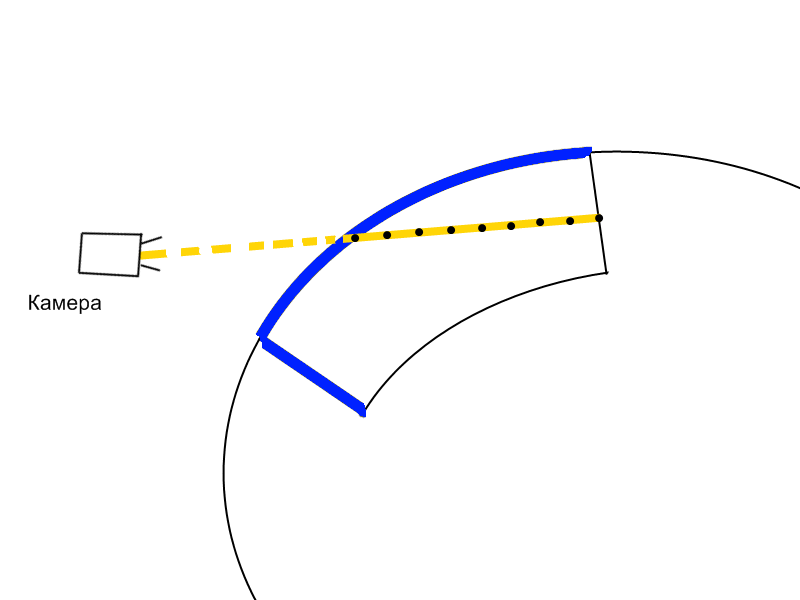| Рис. 3.44. Проход 2: рендеринг объемных данных |
5. Декартовы координаты каждой из промежуточных точек можно преобразовать в географические координаты на основе формул из статьи [110], которые обеспечивают точность в 1см для высот меньше 1000км:
  , | (3.18) |
  , | (3.19) |
  , | (3.20) |
  , | (3.21) |
  , | (3.22) |
  , | (3.23) |
  , | (3.24) |
  , | (3.25) |
  , | (3.26) |
где (x; y; z) – декартовы координаты точки, 
и 
– экваториальный и полярный радиусы Земли, 
– вспомогательные переменные, lat – широта, lon – долгота, h – высота.
6. Пользуясь начальным условием, что наш объём ориентирован вдоль параллелей и меридианов, из географических координат точки можно получить текстурные координаты в 3D-текстуре. Тем самым задача сводится к оригинальному прямому объемному рендерингу: происходит чтение плотности из текстуры, вычисление цвета с помощью передаточной функции и смешивание цветов от дальних точек к ближним по формуле (3.6).
Результат применения алгоритма представлен на рисунке 3.13 на примере восточной части Евразии. Использовался объем размером матрицы 241х241х24. Шаг по долготе и широте 0.25
, шаг по глубине 25 км. Для наглядности была использована передаточная функция с двумя пиками красного и синего цвета для показа двух изоповерхностей.
 |
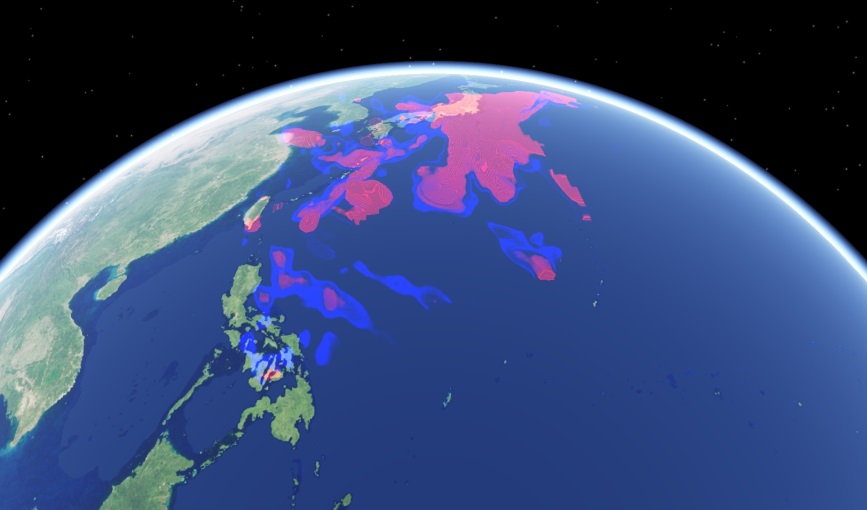| Рис. 3.45. Визуализация результатов сейсмической томографии в восточной части Евразии, по данным д.г.-м.н. И.Ю. Кулакова (ИНГГ СО РАН) |
