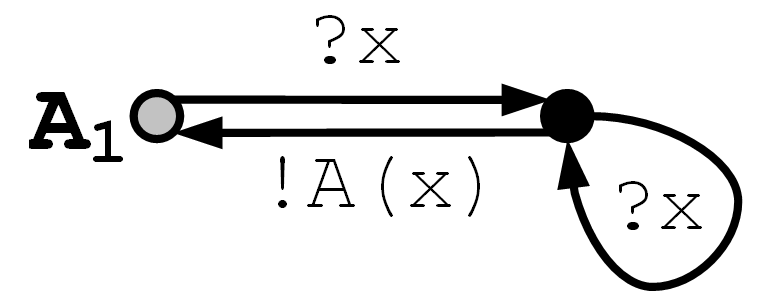Институт Системного Программирования
Российской Академии Наук
На правах рукописи
БУРДОНОВ Игорь Борисович
Теория конформности для функционального
тестирования программных систем
на основе формальных моделей
специальность 05.13.11 –
математическое и программное обеспечение вычислительных машин, комплексов и компьютерных сетей
ДИССЕРТАЦИЯ
на соискание учёной степени
доктора физико-математических наук
Москва - 2008
Оглавление
Введение 6
Глава 1. Используемые понятия и обозначения 40
1.1. Классы, множества, числа и соответствия 40
1.2. Последовательности 43
1.3. Деревья последовательностей 45
1.4. Порождающий граф 47
Глава 2. Формализация тестового эксперимента 49
2.1. Спецификационная и реализационная модели. Конформность 49
2.2. Тестирование конформности 52
2.3. Реализационная модель 57
2.4. Управление и наблюдение 63
2.5. Остановка машины и наблюдение отказов 69
2.6. Взаимодействие теста и реализации. Безопасное тестирование 74
2.7. Гипотеза о безопасности и безопасная конформность 81
2.8. Пополнение спецификаций 83
2.9. Монотонность конформности 86
2.10. Разрушение 87
2.11. Дивергенция 91
2.12. Примеры тестовых семантик и конформностей 94
2.13. Проблема выбора семантики тестового взаимодействия 101
2.13.1. Блокировка стимулов 102
2.13.2. Стимулы «на выбор» 107
2.13.3. Реакции «на выбор» 109
2.13.4. «Торможение» реакций 111
2.14. Трассы готовности 122
2.15. Репликация и симуляции 128
2.16. Глобальное тестирование 130
2.17. Бесконечные и отрицательные наблюдения 133
2.18. Приоритеты 135
2.19. Выводы 135
Глава 3. Модель наблюдаемых трасс 138
3.1. Определение модели 140
3.1.1. Внешнее действие, разрушение и дивергенция 140
3.1.2. Отказы, R/Q-семантика и R-трассы 141
3.1.3. Свойства трасс и деревьев трасс 142
3.1.4. Определение R-модели 145
3.2. Полная модель (F-модель) 150
3.2.1. F-модель и её R-проекция 151
3.2.2. Расширение R-модели до F-модели 152
3.3. Объединение и пересечение моделей 154
3.3.1. Объединение моделей 154
3.3.2. Пересечение моделей 155
3.4. Машина тестирования и трассовая модель 155
3.5. Разложение трассовой модели на поддеревья 156
3.5.1. Стабильные и контрстабильные деревья и квази-модели 158
3.5.2. Вспомогательные утверждения 159
3.5.3. Утверждение о разложении трассовой модели 161
3.6. Безопасность и конформность 162
3.6.1. Безопасность в реализации 163
3.6.2. Безопасность в спецификации 164
3.6.3. Гипотеза о безопасности 166
3.6.4. Безопасная конформность 167
3.7. Генерация тестов 169
3.7.1. Тестовые трассы 170
3.7.2. Вердикт 173
3.7.3. Конечность времени выполнения теста 174
3.7.4. Управляемые тесты 177
3.7.5. Определение теста и тестового набора 180
3.7.6. Значимые, исчерпывающие и полные наборы тестов 180
3.7.7. Строгие тесты 181
3.7.8. Полный набор примитивных тестов 183
3.7.9. Оптимизация 185
3.7.10. Алгоритмизация 188
3.8. Выводы 192
Глава 4. Система помеченных переходов (LTS-модель) 195
4.1. Определение LTS-модели 196
4.2. R-трассы и F-трассы LTS-модели 202
4.2.1. Преобразование LTS-модели в трассовую модель 203
4.2.2. Распространение LTS-обозначений на R-трассы 205
4.2.3. R-маршруты 206
4.3. Объединение множества LTS-моделей 207
4.4. Машина тестирования и LTS-модель 209
4.5. Эквивалентность трассовой и LTS-моделей 210
4.5.1. Преобразование трассовой модели в LTS-модель 211
4.5.2. «Компактное» преобразование 213
4.5.3. Утверждение об эквивалентности 215
4.6. Безопасность и конформность 215
4.7. Композиция LTS и тесты 217
4.7.1. Параллельная композиция LTS 218
4.7.2. LTS-тесты 222
4.7.3. Классификация LTS по ветвимости 227
4.7.4. Алгоритмизация 230
4.8. Выводы 233
Глава 5. Пополнение спецификаций 235
5.1. -семантика и отношение ioco 237
5.2. Допущения полноты в -семантике 242
5.2.1. Виды пополнения состояний 243
5.2.2. Несохранение ioco при пополнении состояний 245
5.2.3. Демоническое и гамма-пополнения состояний и трасс 248
5.3. Рефлексивность и транзитивность конформности 251
5.4. Существование пополнения 255
5.5. Проблема сохранения безопасности 260
5.5.1. Расширение класса безопасных реализаций 260
5.5.2. Сужение класса безопасных реализаций 262
5.5.3. Причины сужения класса безопасных реализаций 264
5.6. Пополнение с не-отказами 269
5.6.1. Основные идеи пополнения с не-отказами 270
5.6.2. Формальное определение пополнения с не-отказами 273
5.6.3. Теорема о пополнении с не-отказами 278
5.6.4. Алгоритмизация 280
5.6.5. Частные случаи -, - и -семантик 281
5.7. Выводы 282
Глава 6. Верификация композиции 285
6.1. Общая теория монотонности 294
6.1.1. Корректная спецификация, косая композиция и монотонность 294
6.1.2. Восемь достаточных условий монотонности 299
6.2. R-мажорирование и конформность 303
6.2.1. R-мажорирование 303
6.2.2. Эквивалентность конформности R-мажорированию 304
6.3. -трассы и -модель 305
6.3.1. Определение -символов и -трасс 305
6.3.2. -трассы и -маршруты LTS 306
6.3.3. Нормальные -трассы и каноническая LTS 313
6.3.4. -модель 317
6.3.5. Эквивалентность LTS- и -моделей 321
6.3.6. -оператор и генеративность -трасс 324
6.3.7. Композиция -трасс и аддитивность 327
6.4. Объединение -трасс конформных реализаций 332
6.4.1. Мажорирование -трасс как равенство 333
6.4.2. Конформность и мажорантность объединения 334
6.4.3. Существование преобразования 334
6.5. Мажорирование -трасс 335
6.5.1. Определение мажорирования -трасс 336
6.5.2. Рефлексивность и транзитивность -мажорирования 338
6.5.3. Генеративность -мажорирования 338
6.5.4. Композиционность -мажорирования 339
6.6. Монотонные модели 340
6.6.1. Финальность 343
6.6.2. Однородность 346
6.6.3. Сингулярность 349
6.7. Спецификации с ограниченной ветвимостью 365
6.7.1. Конформно-конечно-ветвящиеся спецификации 366
6.7.2. LTS-модели с ограниченной ветвимостью 367
6.7.3. Минимальные -символы 368
6.7.4. Power-LTS 374
6.7.5. Доминанты и конечная сингуляризация 378
6.8. Монотонное преобразование 382
6.8.1. Определение монотонного преобразования 383
6.8.2. Оптимизация 385
6.8.3. Преобразование при многократной композиции 387
6.8.4. Алгоритмизация 390
6.9. Композиция 394
6.9.1. Ветвимость результата композиции 395
6.9.2. Ограничения на преобразованные LTS 396
6.9.3. Ограничения на исходные LTS 400
6.9.4. Алгоритмизация 401
6.9.5. Проблема сохранения безопасности при композиции 403
6.10. Выводы 406
Заключение 412
Литература 419
Приложение: Доказательства утверждений 435
(84 Леммы и 49 Теорем)
Введение
Структура введения:
- Актуальность исследования
- Общая характеристика работы
- Область исследования
- Проблематика
- Цели и задачи исследования
- Методологическая и теоретическая основа исследования
- Научная новизна исследования
- Практическая значимость работы
- Апробация результатов исследования
- Публикации
- Структура и объём работы
Актуальность исследования
История информационных технологий – это, прежде всего, история их проникновения во все сферы деятельности человека: экономику, военную область, науку, образование, культуру и т.д. Они становятся всё более неотъемлемой частью инфраструктуры современной жизни. Этот процесс, естественно, вызывает интенсивное развитие самих этих технологий: создаются всё более мощные компьютеры и компьютерные системы, всё более сложные программы и программные комплексы.
Однако, чем шире распространяется использование компьютеров, чем более важные и ответственные задачи возлагаются на их «плечи», тем выше становится цена ошибок в программно-аппаратных средствах. Только в США потери от этих ошибок составляют от 20 до 60 млрд. долларов ежегодно, причём около 60% убытков терпят конечные пользователи. Складывается ситуация, когда производители выпускают, а потребители вынуждены оплачивать заведомо бракованный товар. Но дело не только в материальном ущербе: некорректное поведение компьютерных систем способно вызвать дезорганизацию управления государством, привести к техногенным и экологическим катастрофам, поставить под угрозу жизнь и здоровье людей.
Как показывает практика, чаще всего источником ошибок в компьютерных системах оказывается программное обеспечение (ПО), которое модифицируется гораздо чаще, чем аппаратура. Поэтому проблема повышения качества ПО становится всё более важной и актуальной. Программистские компании вынуждены тратить дорогостоящее время и не менее дорогие усилия разработчиков не только на то, чтобы создать нечто новое, но и гарантировать, что оно действительно решает нужные задачи, делает это правильно, надёжно и безопасно.
Ключевой частью решения этой проблемы является тестирование программ [124], часто требующее времени и ресурсов больше, чем создание этих программ [39-44,62,68]. Из второстепенной и как бы «побочной» деятельности тестирование выходит на первый план, интегрируется с самим процессом разработки ПО и существенно изменяет представления о том, как надо создавать сложные программные комплексы. Тестирование становится жёсткой «обратной связью», замыкает «жизненный цикл» разработки ПО и перестраивает пространственно-временную структуру процесса разработки и организацию коллектива разработчиков.
Противоречивая задача повышения качества программ и снижения затрат на тестирование диктует необходимость поиска путей автоматизации тестирования. Одним из важнейших методов решения этой задачи является тестирование на основе формальных (математических) моделей, целью которого является проверка того, что реализационная модель (модель тестируемой системы) соответствует (конформна) спецификации (модель требований). Конформность понимается как отношение «похожести» реализации на спецификацию. Если спецификационная модель и конформность определены строго формально, то становится возможным по спецификации автоматически генерировать тесты, проверяющие эту конформность.
В то же время внедрение в практику соответствующих методов тестирования сталкивается сегодня с двумя серьёзными препятствиями. Первое – это большое разнообразие типов моделей и, что ещё важнее, видов конформностей. Для многих конформностей в последние годы были созданы соответствующие математические теории, на основе которых разработаны методы генерации тестов и построены практически используемые тестовые системы. И этот процесс далёк от завершения: продолжает расти количество предлагаемых конформностей и основанных на них методов и инструментов тестирования. В результате тестировщик оказывается перед серьёзной проблемой выбора того, что ему подходит.
Причина такого экстенсивного роста не только, и не столько, во внутренней логике развития теории тестирования, сколько в потребностях практики: «спрос превышает предложение». Поэтому каждый раз, когда практическое тестирование сталкивается с проблемой, которая «не вписывается» в уже существующие теоретические подходы, поиск путей её решения приводит к новому пониманию «похожести» реализации на спецификацию, «изобретению» новой конформности и созданию основанных на ней теории, методов и инструментов тестирования. При этом каждый автор, предлагающий свою конформность, формально начинает теорию «с нуля», и больше внимания уделяет тому, чтобы показать адекватность своей теории той практической проблеме, которая послужила стимулом к её созданию, чем поиску идей и методов, общих с другими теориями конформности.
Вместе с тем сегодня уже становится ясно, что такие общие идеи и методы «витают в воздухе», поскольку в математических формализмах различных конформностей и методах тестирования на их основе много общего. Поэтому задача выявления этих общих идей и методов, задача создания обобщающей теории конформности, покрывающей широкий класс практически используемых или требуемых конформностей, стала чрезвычайно актуальной как для теории, так и для практики, и впервые наметились пути её решения.
Среди всех видов тестирования наиболее важным для практики является функциональное тестирование. Это тестирование методом «чёрного ящика», когда внутреннее устройство реализации, её внутренние работа и состояния не наблюдаемы, и о правильности или ошибочности реализации судят по её внешнему поведению в ответ на внешние тестовые воздействия. Именно набор этих тестовых воздействий и возможных наблюдений над ответным поведением реализации может быть различным в различных практических случаях. Этот набор определяет ту или иную семантику тестового взаимодействия, которая, в свою очередь, определяет ту или иную конформность. Для программных систем чаще всего используется отношение редукции – «сводимости» реализации к спецификации, когда спецификация предоставляет на выбор несколько вариантов правильного поведения, а правильная программа демонстрирует лишь некоторые из них.
Второе серьёзное препятствие, с которым сталкивается тестирование на основе формальных моделей, – это неразвитость теории тестирования сложных, иерархически построенных систем, состоящих из многих компонентов. Помимо ошибок в реализациях компонентов, здесь появляется новый вид архитектурных ошибок, вызванных тем, что требования к системе некорректно декомпозированы в требования к её компонентам. Такие ошибки не только труднее обнаруживать, но они имеют более печальные последствия: изменение архитектуры системы и переделка всех или части её компонентов. В существующей теории тестирования проблема верификации декомпозиции системных требований не имеет общего решения. Предлагаются лишь частичные решения этой проблемы для некоторых конформностей.
Таким образом, актуальной задачей является создание теории конформности («сводимости» реализации к спецификации при функциональном тестировании), которая предлагала бы как методы автоматической генерации тестов по спецификации, так и методы автоматической верификации декомпозиции системных требований для сложных систем, состоящих из многих компонентов.
Решению этой задачи посвящена данная диссертация.
Общая характеристика работы
В работе рассматривается класс конформностей типа редукции, основанных на наблюдаемом поведении и параметризуемых семантикой тестового взаимодействия при функциональном тестировании. Такая семантика определяется набором допустимых тестовых воздействий и возможных ответных наблюдений над поведением системы. Такие наблюдения бывают двух типов: наблюдение внешнего действия, выполняемого реализацией, и, в некоторых случаях, наблюдение отказа – отсутствия действий. В начестве основной модели в диссертации выбрана система помеченных переходов (Labelled Transition System – LTS).
Для того, чтобы каждое тестовое воздействие завершалось наблюдением, не должно возникать ненаблюдаемых отказов и дивергенции («зацикливание») – бесконечной внутренней работы системы без взаимодействия с тестом. Кроме этого, в диссертации впервые вводится понятие разрушения, моделирующего поведение, которого не должно быть при тестировании по тем или иным причинам. Предлагается новая концепция безопасного тестирования, которое избегает ненаблюдаемых отказов, дивергенции и разрушения. Вводится гипотеза о безопасности, определяющая класс безопасно-тестируемых реализаций, и основанная на ней безопасная конформность. Для этой конформности предлагается метод генерации безопасных тестов по спецификации, параметризуемый семантикой тестового взаимодействия. Этот метод является обобщением методов генерации тестов для частных случаев, известных в теории и применяемых на практике. Для этих частных случаев он даёт те же результаты, но область его применения гораздо шире.
Также в диссертации рассматривается асинхронное тестирование (тестирование в контексте), когда взаимодействие теста и реализации происходит не напрямую, а через ту или иную промежуточную среду взаимодействия. Проблема несохранения конформности заключается в том, что асинхронные тесты могут ловить ложные ошибки, то есть те, которые не обнаруживаются при синхронном тестировании, когда тест и реализация взаимодействуют непосредственно друг с другом без какой-либо буферизации в среде. Это является особым случаем общей проблемы композиции, когда составная система, собранная из реализаций компонентов, конформных своим спецификациям, оказывается неконформной композиции этих спецификаций. Тесты, сгенерированные по такой композиции спецификаций, также могут ловить ложные ошибки.
В диссертации предлагается общее решение проблемы несохранения конформности при композиции, в том числе, при асинхронном тестировании с различными средами взаимодействия. Решение основано на специальном алгоритмическом преобразовании спецификаций. Преобразованная спецификация эквивалентна исходной спецификации в том смысле, что определяет тот же класс конформных реализаций и не суженный класс безопасно-тестируемых реализаций. Для преобразованных спецификаций конформность уже сохраняется при композиции и при асинхронном тестировании.
Решение проблемы композиции впервые даёт полное решение проблемы верификации декомпозиции системных требований в рассматриваемой области. Спецификация составной системы оказывается согласованной со спецификациями компонентов тогда и только тогда, когда ей конформна композиция преобразованных спецификаций. Это можно проверить после преобразования спецификаций компонентов и их алгоритмической композиции с помощью методов, основанных на генерации тестов по заданной спецификации системы.
В практическом плане результаты диссертационной работы сводятся к предлагаемым методам генерации тестов и преобразования спецификаций. Это даёт, во-первых, возможность создавать тестовые системы для самых разных семантик тестового взаимодействия на базе единого подхода с использованием общего метода генерации тестов. Во-вторых, в сочетании с преобразованием спецификации метод применим для асинхронного тестирования с самыми разными средами взаимодействия. В-третьих, заложена основа для построения инструментов автоматической верификации декомпозиции системных требований, причём спецификации компонентов и системы в целом могут пониматься в самых разных семантиках тестового взаимодействия.
Область исследования
Тестирование на основе формальных моделей
Тестирование на основе формальных моделей – это новая дисциплина, сложившаяся последние десятилетия на стыке теории и практики информационных технологий. Это актуальное направление во многом опирается на работы различных исследователей, выполненные в 80-х и в 90-х годах прошлого века и посвященные проблемам тестирования телекоммуникационных протоколов. Самые первые же статьи, которые с полным правом можно отнести к этой области, появились еще в конце 60-х – начале 70-х годов [30,78,97,123]. Тем не менее, серьезный практический и массовый интерес к результатам в этой области возник только на рубеже веков, в связи с востребованностью эффективных методов контроля и обеспечения качества сложных программных и программно-аппаратных систем в индустрии. Тестирование на основе моделей начинает применяться в промышленных компаниях. Первые же успехи (и, в не меньшей степени, первые неудачи) сделали разработку формальных методов тестирования чрезвычайно актуальными на сегодняшний день [49,50,65,72,75-77,79,80,83,85,87,92,94,106,108,110,114,116,129,135,145,147,151].
Основная идея тестирования на основе моделей вполне прозрачна: поскольку сложная система не поддается проверке «в лоб», создайте сначала более простую ее модель, описав в ней только то, что для вас важно на данном этапе, а затем стройте тесты только на основании полученной модели. Такой подход хорошо работает на практике, если саму модель и набор тестов удаётся строить по частям (инкрементально), постепенно отражая в модели набор свойств реальной системы и, соответственно, расширяя охват тестами различных аспектов работы системы. Как возможность такой инкрементальной разработки моделей и тестов, так и конкретные техники, используемые при этом, существенно зависят от самого вида применяемых моделей, и от того, какие имеются возможности по управлению тестируемой системой и наблюдению ее поведения.
Модели должны быть одновременно достаточно просты, чтобы поддаваться строгому анализу, и достаточно универсальны, чтобы описывать большой класс практически важных систем. Возможность строгого анализа свойств модели становится актуальной, если необходимы определенные гарантии того, что все важные аспекты поведения системы покрываются построенными тестами. Такие модели должны быть формальны, то есть описаны на языке математики. Само же тестирование строится на некоторой математической теории, предписывающей определенные способы построения тестов, которые обеспечат им нужные свойства полноты, а тестированию придадут необходимую глубину и надежность.
Тестирование на основе моделей проверяет соответствие тестируемой системы требованиям. Предполагается, что требования к системе выражены в терминах её взаимодействия с внешним миром (окружением), что как раз и даёт возможность проверять их выполнение в тестовом эксперименте. На формальном уровне соответствие системы требованиям означает, что модель тестируемой системы и модель требований связаны заданным математическим соответствием (бинарным отношением) (Рис.1) [141].
|
В диссертационной работе модель тестируемой системы называется реализационной моделью или (для краткости) реализацией, модель требований – спецификацией, а их соответствие – (модельной) конформностью[1] [132,141-143,148]. При тестировании (в отличие от аналитической верификации) предполагается, что реализационная модель не задана или слишком сложна для анализа. Поэтому основной задачей является генерация по заданной спецификации модельных тестов, назначение которых – проверить конформность любой реализационной модели из рассматриваемого класса. Эта проверка основана на модели взаимодействия реальной системы с её окружением. Такую модель, как сказано выше, называют семантикой взаимодействия. Вводится модельное отношение «реализация проходит тест». Набор тестов принято называть полным, если реализация проходит каждый тест из набора тогда и только тогда, когда она конформна спецификации. После того, как тесты созданы, они транслируются в реальные тестовые программы, которые, взаимодействуя с реальной системой, устанавливают её соответствие или несоответствие исходным требованиям. Эта схема работы основана на следующих предположениях: во-первых, адекватны модели объектов (реализация и спецификация) и отношений (конформность и семантика взаимодействия), во-вторых, правильно выполняются преобразования (генерация модельных тестов и их трансляция в реальные тестовые программы).
Спецификация неоднозначно определяет реализацию, оставляя разработчику значительную свободу в рамках специфицированных требований. Как именно нужно понимать эти требования, в чём разработчик свободен, а в чём «скован» требованиями, как раз и описывается конформностью. Оно определяется предполагаемыми правилами взаимодействия системы с окружением, которые должны быть адекватно отражены на уровне моделей. Спецификация не требует от реализации правильного поведения при взаимодействии с любым её окружением, а только с таким, которое само ведёт себя правильно. Например, в терминах пред- и постусловий [119] тесты должны проверять выполнение постусловия (программа работает правильно) только при таком взаимодействии, которое не нарушает предусловий (к программе правильно обратились). При тестировании правила взаимодействия как раз и определяют те тестовые возможности по управлению и наблюдению за тестируемой системой, которые необходимы и достаточны для проверки конформности.
Выбор модели
По поводу вида моделей, которые нужно использовать для описания сложных систем, большинство исследователей сегодня еще не пришли к общему мнению [24]. Можно выделить три вида моделей в порядке их усложнения.
Самая простая модель – математическая функция как абстракция реентерабельной процедуры. Основная проблема здесь – большое количество значений аргумента, которые нужно проверить для того, чтобы убедиться, что результат всегда правильный. Особенно, когда аргумент – это большие данные со сложной структурой как, например, для компиляторов.
Вторая модель – это автомат (finite automata, finite state machines), взаимодействие с которым сводится к той же простой схеме «стимул-реакция», что и для функции. В отличие от функции результат зависит не только от аргумента, но и от состояния автомата, которое является абстракцией таких объектов как глобальные переменные или поля данных объектов классов. Здесь добавляется проблема перебора состояний. Сложность в том, что состояние может быть не наблюдаемо при тестировании.
Третья модель – это система помеченных переходов – LTS (Labelled Transition System). Для таких систем характерно сложное взаимодействие. Например, в ответ на стимул может быть несколько реакций или ни одной. Можно подавать несколько стимулов подряд или получать реакции без стимулов. Кроме того, система может выполнять внутренние действия, не наблюдаемые извне. В этих случаях, когда взаимодействие с системой сводится к обмену сообщениями: стимулами и реакциями, такая система называется реактивной [76,117,136,149]. В общем случае говорят просто о внешних действиях, наблюдаемых при взаимодействии.
Для LTS характерны такие явления как недетерминизм, отказы, когда нет никаких действий, а также дивергенция – зацикливание, когда система выполняет только внутреннюю работу и не взаимодействует с тестом. В данной работе внимание концентрируется, прежде всего, на этом.
Для систем последнего типа применяются и другие модели: сети Петри, алгебраические спецификации, в частности ASM (Abstract State Machine), а также контрактные спецификации, построенные на пред- и постусловиях.
Можно назвать три причины, по которым в данной работе выбрана модель LTS:
- Распространённость этой модели.
- Удобство генерации тестов по LTS.
- На LTS определена композиция, моделирующая взаимодействие компонентов составной системы.
Взаимодействие между LTS-моделямиS понимается как синхронное: передатчик передаёт сообщение, а приёмник принимает его без какой-либо буферизации. Это моделируется оператором параллельной композиции той или иной алгебры процессов. В диссертации выбрана композиция є№ в духе алгебры процессов CCS (Calculus of Communicating Systems), предложенной Милнером [120,122]. Выдача сообщения x обозначается как !x, а приём – как ?x; внутренние действия обозначаются символом.
Функциональное тестирование и конформность типа редукции
Что касается конформности, которую следует выбирать для построения тестов, то на этот счёт имеются десятки различных точек зрения. В 1990-93 г.г. Ван Глаббек [89,90] сумел классифицировать для LTS многие из конформностей, описав 155 семантик тестового взаимодействия, на которых они основаны. При этом он не учитывал семантики, специфические для реактивных систем, когда принципиально различаются передача стимулов и передача реакций.
В диссертационной работе исследуется тестирование, которое основано только на наблюдаемом поведении системы. Такое тестирование называют тестированием «чёрного ящика»: тест может только извне взаимодействовать с системой, осуществляя тестовые воздействия и наблюдая внешнее поведение системы, но «не знает и не видит» её внутреннего устройства, отражаемого в понятии состояния, и её внутреннего поведения, не наблюдаемого извне. Такое тестирование называют также функциональным, акцентируя внимание на том, что оно проверяет только те свойства системы, которые отражаются в её внешней функциональности и наблюдаемы при её внешнем функционировании. Понятно, что такое тестирование имеет важное практическое значение, поскольку во многих реальных случаях внутренние действия и состояния реализации не наблюдаемы из теста (например, при удалённом взаимодействии). Но более важно то, что учёт состояний и внутреннего поведения может оказаться «переспецификацией», требуя от реализации того, что никак не проявляется при взаимодействии с ней.
При тестировании методом «чёрного ящика» мы можем наблюдать только такое поведение реализации, которое, во-первых, «спровоцировано» тестом (управление) и, во-вторых, наблюдаемо во внешнем взаимодействии. Такое взаимодействие моделируется с помощью, так называемой, машины тестирования (Милнер [121] и Ван Глаббек [89,90]). Она представляет собой «чёрный ящик», внутри которого находится реализация. Управление сводится к тому, что оператор машины, выполняя тест, нажимает кнопки, «приказывая» или «разрешая» реализации выполнять те или иные действия, которые могут им наблюдаться. Наблюдения (на «дисплее» машины) бывают двух типов: наблюдение некоторого внешнего действия, разрешённого оператором и выполняемого реализацией, и наблюдение отказа как отсутствия каких бы то ни было действий из числа тех, что разрешены нажатыми кнопками. Важно отметить, что отказ принципиально не сводится к какому-либо внешнему действию, вроде реакции «нет действий», поскольку, в отличие от действия, гарантированно не меняет состояния реализации.
Результатом тестового эксперимента является трасса (последовательность) наблюдений: действий и отказов. В соответствующих конформностях, тем самым, не учитываются состояния. Поэтому в диссертации не рассматриваются конформности типа симуляций, которые основаны на соответствии состояний реализации и спецификации.
Также не рассматриваются конформности типа эквивалентностей, когда внешнее поведение реализации и спецификации совпадают. В диссертационной работе внимание сосредоточено на конформностях типа редукции (сводимости) реализации к спецификации [71]. Суть такой конформности в том, что конформная реализация не должна демонстрировать внешнее поведение, которое так или иначе запрещено спецификаций, но спецификация может предоставлять на выбор несколько вариантов правильного поведения, и конформная реализация может демонстрировать лишь некоторые из них. Разумеется, речь идёт о поведении в реализации и спецификации в одной и той же ситуации, то есть после одной и той же трассы наблюдений.
К рассматриваемому классу семантик и конформностей относятся: трассовая семантика (trace semantics) и трассовый предпорядок (tr – trace preorder); семантика завершённых трасс (completed trace semantics) и предпорядок завершённых трасс (ct – completed trace preorder); семантика трасс с отказами (failure trace semantics или refusal semantics) и предпорядок трасс с отказами (failure trace preorder или rf – refusal preorder); семантика для реактивных систем без блокировки стимулов, но с возможностью наблюдения отсутствия реакций, и конформности ior (input-output refusal relation или repetitive quiescence relation) и ioco (input-output conformance); семантика для реактивных систем с блокировками стимулов и конформность ioco (модификация конформности ioco, учитывающая блокировку стимулов); семантика для систем с мультиканалами стимулов и реакций (MIOTS – Multi Input-Output Transition Systems) и конформность mioco (модификация конформности ioco для таких систем) и др.
Как дальнейшее развитие теории тестирования, так и её практическое применение сталкиваются с рядом проблем, решению которых посвящена диссертационная работа.
Проблематика
Выбор семантики взаимодействия и генерация тестов
Прежде всего, на практике приходится сталкиваться с разнообразием семантик тестового взаимодействия, которое строится на пересечении того, что мы можем, и того, что нам нужно. Речь идёт о тестовых возможностей: какие есть тестовые воздействия и какие есть наблюдения. То, что мы можем или не можем, – это ограничение тестовых возможностей «сверху». То, что нам требуется для проверки конформности, – это ограничение «снизу».
Отношение ioco (Input-Output Conformance), предложенное Яном Тритмансом [148,149], является одной из наиболее распространённых, хорошо проработанных в теории и зарекомендовавших себя на практике конформностей типа редукции для реактивных систем. Тестовые воздействия двух типов: можно либо послать в реализацию один выбранный стимул, либо принять из реализации одну, но любую из выдаваемых ею реакций. Если тест принимает реакции, он всегда что-нибудь наблюдает: либо реакцию, либо отсутствие реакций (например, по тайм-ауту). Отсутствие реакций называется стационарностью (quiescence). Если тест посылает стимул, он может наблюдать только приём стимула реализацией. Соответствующий отказ, когда реализация отвергает стимул, называется блокировкой стимула (input refusal) и считается ненаблюдаемым. Это ограничение «сверху» на наши тестовые возможности.
Для ioco создано несколько инструментов для генерации тестов, в том числе: TGV (Test Generation with Verification technology) интегрированный в CADP (Construction and Analysis of Distributed Processes Software Tools for Designing Reliable Protocols and Systems), TestGen (входной язык LOTOS, генерирует тест для верификации hardware design и компонентов), TorX (генерация тестов, выполнение их и анализ результатов тестирования on-fly).
В то же время существует целый ряд практических системы, для тестирования которых ioco-семантики недостаточно. Приведём ряд примеров.
Блокировка стимулов обычно (в частности, для ioco) считается ненаблюдаемой (ограничение «сверху»). Но в последние годы появляется всё больше и больше работ, в которых наблюдаемые блокировки допускаются или допускаются частично [21-23,25-27,95,96,115]. Более важно то, что наблюдение блокировок требуется (ограничение «снизу»), например, для тестирования сред взамодействия ограниченной ёмкости, в частности, очередей ограниченной длины. Здесь стимул – это помещение в очередь, а реакция – выборка из очереди. Когда среда полностью заполнена, стимул должен блокироваться и это нужно уметь проверять.
Другим примером наблюдения блокировок могут служить системы с графическим интерфейсом. Широко распространена ситуация, когда в окне высвечивается меню, в котором некоторые кнопки «бледные», то есть соответствующие стимулы блокируются. Это существенно отличается от приёма стимула с последующей выдачей соответствующей реакции, когда кнопка не «бледная», а в ответ на её нажатие всплывает окошко с надписью «операция не может быть выполнена». Ещё один пример – автомат по продаже «чего-нибудь», который блокирует приём монет, когда это «чего-нибудь» кончается. Это также отличается от автомата, в котором монета в любом случае принимается, но потом возвращается в окошке для сдачи.
Обычно (в частности, для ioco) тест посылает в реализацию стимулы по одному. Необходимость (ограничение «снизу») в передаче сразу нескольких стимулов, из которых реализация сама выбирает один стимул для приёма, требуется для тестирования систем с несколькими входными портами, когда спецификация разрешает любой порядок приёма из портов (система F на Рис.2).
|
После передачи одного стимула, тест предлагает реализации оставшиеся стимулы и так далее до тех пор, пока не будут переданы стимулы на все входные порты реализации. Этот пример представляет класс пороговых систем, которые сначала принимают в любом порядке несколько стимулов на разные входные порты, а потом выдают реакцию.
Такая система-приёмник может получать стимулы от другой системы-передатчика, в которой, наоборот, имеется несколько выходных портов и для которой передаваемые стимулы являются реакциями (система T на Рис.2). Чтобы обеспечить передачу всех сообщений при любом порядке их приёма, мы вынуждены (ограничение «снизу») потребовать от передатчика того же, что требуем от теста приёмника: начинать с выдачи сразу всех сообщений. Выдача двух реакций последовательно: сначала по первому порту, а потом по второму, или наоборот, является ошибкой. Если тест, как это чаще всего бывает (в частности, для ioco), принимает любую реакцию, то по какому бы порту ни пришла реакция, это приходится считать правильным, и ошибка не обнаруживается. Чтобы обнаружить ошибку, нам нужно уметь в тесте принимать не все реакции, а только из одного порта: один тест обнаружит ошибку как отсутствие реакций по первому порту, а другой – по второму. Та же самая тестовая возможность требуется для тестирования широковещания: для каждого выходного порта нужно проверить, что тест, принимающий реакции из этого порта, не обнаружит их отсутствие. Отношение mioco [95,96] является как раз такой модификацией отношения ioco, в которой реакции принимаются по отдельным выходным портам системы с возможностью наблюдения частичной стационарности
Совмещение передачи стимулов с приёмом реакций, обычно являющееся излишним (не увеличивающим мощность тестирования), необходимо (ограничение «снизу») для тестирования систем с откатами (Рис.3).
|
В такой системе два типа стимулов: «начать транзакцию» и «откатить транзакцию», и, соответственно, два типа реакций: «транзакция завершена» и «откат выполнен». После начала транзакции реализация часто выполняет её в два этапа так, что откат возможен только на первом этапе, а на втором этапе стимул «откатить» отвергается, то есть блокируется. Если блокировки ненаблюдаемы (ограничение «сверху»), мы не можем давать команду «откатить» и, тем самым, не можем тестировать интересующие нас реализации. Однако мы можем обойти это ограничение «сверху», если одновременно с посылкой стимула «откатить» будем принимать реакции. Отказа не будет, так как всегда либо будет принят откат, либо выдана реакция «транзакция завершена».
Поведение, не наблюдаемое при тестировании
Кроме наблюдаемого поведения (действия и отказы) реализация может иметь поведение, которого следует избегать при тестировании по тем или иным причинам. Можно выделить три типа такого поведения.
Первый тип – это ненаблюдаемый отказ. Его возникновение плохо тем, что мы не получим никакого наблюдения в ответ на тестовое воздействие: действий нет, а отказ не наблюдаем. Обычно предполагается, что в тестируемой реализации вообще нет ненаблюдаемых отказов. Для отношения ioco реализация должна принимать стимулы в каждом своём состоянии (input-enabled). В то же время такое требование слишком сильное.
Например, на Рис.4 приведена системы A, взаимодействие с которой происходит по «автоматному» правилу «стимул-реакция». Спецификация – LTS A0. Формально, она не может служить своей собственной тестируемой реализацией, так как в ней есть блокировка стимула. В то же время тесты, построенные для ioco, не только не вызовут блокировку стимула (после наблюдения трассы стимул не посылается, если его нет в спецификации после этой трассы), но и не обнаружат никаких ошибок. Эти тесты вообще не отличат LTS A0 от тестируемой и конформной LTS A1.
| ||||||
Второй тип – это дивергенция – бесконечная последовательность внутренних действий системы, «зацикливание». При дивергенции мы также можем не получить в ответ на тестовое воздействие никакого наблюдения просто потому, что всё время будут выполняться внутренние действия. Проблеме дивергенции посвящено довольно много теоретических работ. Однако в теориях, имеющих выход в практику, то есть развитых до алгоритмов генерации тестов, обычно просто предполагается, что в реализации не должно быть дивергенции.
В то же время проблема дивергенции не в том, что она может возникнуть в реализации, а в том, что она не должна возникать при том или ином взаимодействии. К такому взаимодействию, в частности, относится взаимодействие реализации как компонента сложной, составной системы с другими, заданными компонентами. Эти другие компоненты взаимодействуют с реализацией не произвольным, а вполне определённым образом, из-за чего имеющаяся в реализации дивергенция может стать недостижимой. Есть и обратная проблема: даже при отсутствии дивергенции в компонентах она может возникнуть в их композиции как бесконечное взаимодействие этих компонентов между собой. При иерархическом построении системы такая дивергенция может, в свою очередь, оказаться промежуточной, то есть исчезающей при дальнейших композициях. Поэтому, запрещая дивергенцию на всех уровнях, мы выбрасываем из рассмотрения целый класс работоспособных систем.
Таким образом, представляется важным и полезным допустить наличие дивергенции в реализации, но при тестировании избегать тестовых воздействий в ситуации, когда возможна дивергенция.
Третий тип – это поведение, которое прямо запрещено при тестировании по тем или иным причинам. Этой теме посвящено очень мало работ. Лишь в редких случаях вводятся запрещённые состояния, в которые реализация не должна попадать. Между тем, это довольно частое явление. Например, запрещённым можно считать поведение программы при нарушении предусловия обращения к ней. Тестирование такого поведения не только бессмысленно, но может быть и опасным, если тестируемая система имеет высокий уровень доступа к привилегированным программам и данным. В частности, эта тема весьма актуальна в теории и практике информационной безопасности, где система считается безопасной, если в ней нет недекларированного поведения, которое можно понимать как запрещённое. В то же время, такая система может быть построена из компонентов, которые сами по себе не являются безопасными, но запрещённое поведение недостижимо при работе системы в целом за счёт того, что каждый компонент взаимодействует не с произвольным окружением, а с заданными компонентами системы.
В целом, является актуальной задача расмотрения в теории конформности всех трёх указанных типов ненаблюдаемого поведения. Спецификация должна позволять описывать случаи, когда в реализации допустимы (не влияют на конформность) ненаблюдаемые отказы, дивергенция и запрещённое поведение. В то же время при тестировании их следует избегать, что требует определённой модификации самой конформности. Особое внимание должно быть уделено дивергенции и запрещённому поведению в случае сложной системы, собранной из отдельных компонентов.
Асинхронное тестирование
Ещё одной проблемой является степень доступа теста к реализации. На практике чаще приходится иметь дело не с синхронным, а с асинхронным взаимодействием теста и реализации. В стандарте ISO [141] асинхронное тестирование определяется как тестирование реализации, помещённой в тестовый контекст. Чаще всего такой контекст понимают как пару неограниченных очередей, буферизующих стимулы и реакции. Чтобы правильно оценивать результаты тестирования, мы должны понимать, что в реализации проходится не обязательно та трасса, которую мы наблюдаем, как это имело место при синхронном тестировании. Наблюдаемой трассе соответствует, вообще говоря, множество синхронных трасс, которые могла бы пройти реализация при таком наблюдении. Ошибка фиксируется, если ни одной из этих трасс нет в спецификации. Этот процесс называется сериализацией. Кроме того, ослабляются требования к допустимым тестовым воздействиям, поскольку теперь никаких блокировок нет: входная очередь всегда принимает посылаемый стимул. Дивергенцию и разрушение в реализации мы, по-прежнему, должны учитывать.
В общем случае тестовый контекст можно понимать как среду взаимодействия, которая моделируется подходящей LTS и компонуется с LTS-реализацией. Это может быть несколько входных и выходных очередей, очереди с приоритетами, стеки, порядок передачи может нарушаться, стимулы и реакции могут пропадать или генерироваться лишние и так далее. Для каждой такой среды определение допустимых тестовых воздействий и сериализацию нужно делать по своим правилам. Составление правил такого тестирования – это интеллектуальный труд, далеко не всегда простой.
Решением является общий метод, когда тесты генерируются не по исходной спецификации с учётом этих правил, а по композиции спецификации со средой, и по ней же проверяются наблюдения. Однако здесь возникает, так называемая, проблема несохранения конформности. Дело в том, что асинхронные тесты могут ловить ложные ошибки, то есть ошибки, не обнаруживаемые при более полном синхронном тестировании. Продемонстрируем эту проблему на двух примерах.
Первый пример – это система на Рис.4, рассматриваемая в ioco-семантике (семантике с ненаблюдаемыми блокировками). При асинхронном тестировании через неограниченную входную очередь всегда можно послать два стимула x подряд: очередь их примет, а реализация потом будет выбирать стимулы из очереди. Если после этого принимать реакции, то, согласно спецификации A0, должны быть последовательно приняты две реакции A(x). В то же время, хотя реализация A1 конформна, при асинхронном тестировании в ней будет обнаружена ошибка, поскольку второй реакции может не быть (стационарность в начальном состоянии).
| |||||||||
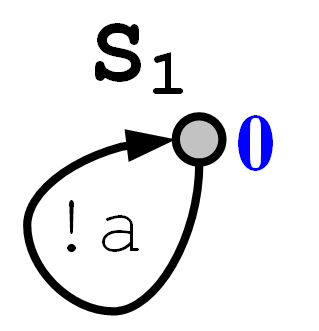
Второй пример – асинхронное тестирование системы S с помощью среды взаимодействия Q (Рис.5). Среда – это одна ограниченная выходная очередь (на рисунке длины 1) с дополнительной командой «обнуления» (b). Спецификация S0 рассматривается в семантике с наблюдаемыми блокировками (ненаблюдаемых отказов нет). Она описывает следующие требования к системе: сначала стимул блокируется, но можно выдавать цепочку реакций a, потом можно обнулить очередь (b), принять стимул x и закончить в терминальном состоянии. Реализация S1 конформна: она не обнуляет очередь и, соответственно, не принимает стимул. Когда с очередью Q компонуется спецификация, первый посылаемый стимул не блокируется. Однако при композиции реализации S1 такая блокировка появляется, что при асинхронном тестировании будет квалифицировано как ошибка (показано стрелками).
Верификация декомпозиции системных требований
Последние годы большое внимание уделяется тестированию составных систем, которые компонуются инкрементально и иерархически из компонентов разных уровней. Основная проблема композиции – это проблема соотношения спецификации системы и спецификаций её компонентов. Это соотношение корректно, если композиция компонентов, конформных своим спецификациям, всегда конформна спецификации системы. К сожалению, это не всегда так. Проверку правильности такого соотношения называют верификацией декомпозиции системных требований.
Конечно, если спецификация системы никак не связана со спецификациями компонентов, то трудно ожидать их правильного соотношения. Казалось бы, спецификацию системы можно получить как композицию спецификаций компонентов, выполняя её по тем же правилам, по которым сама система компонуется из реализаций компонентов. Но оказывается, что полученная таким способом спецификация системы может быть некорректной. Эта проблема называется проблемой сохранения конформности при композиции [66] или проблемой монотонности [105]. В диссертации проблема несохранения конформности при асинхронном тестировании рассматривается как особый случай общей проблемы монотонности [66].
Примером может служить система, составленная из двух компонентов: передатчика и приёмника на Рис.2. При несогласованности спецификаций компонентов может возникнуть тупик во взаимодействии: передатчик начинает с передачи сообщения через один порт, а приёмник начинает приём через другой порт (Рис.6). Если спецификация системы в целом не предусматривает такого тупика, то это означает, что спецификации компонентов с ней не согласованы.
| 1 | 2 | ||||
 |  | ||||
| F | |||||
| T | |||||
| 1 |  | ||||
| 2 |  | 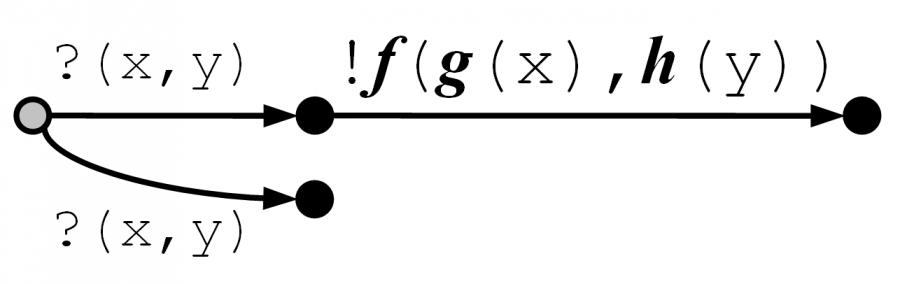 | |||