Влияние сварочных процессов на пространственную устойчивость усиливаемых под нагрузкой элементов стержневых конструкций
На правах рукописи
Михаськин Владимир Владимирович
ВЛИЯНИЕ СВАРОЧНЫХ ПРОЦЕССОВ НА ПРОСТРАНСТВЕННУЮ УСТОЙЧИВОСТЬ УСИЛИВАЕМЫХ ПОД НАГРУЗКОЙ ЭЛЕМЕНТОВ СТЕРЖНЕВЫХ КОНСТРУКЦИЙ
Специальность 05.23.01 – Строительные конструкции, здания и сооружения
Автореферат
диссертации на соискание учёной степени
кандидата технических наук
Санкт-Петербург
2010
Диссертационная работа выполнена на кафедре металлических конструкций и испытаний сооружений ГОУ ВПО «Санкт-Петербургский государственный архитектурно-строительный университет»
Научный руководитель: доктор технических наук, профессор
Белый Григорий Иванович
(СПбГАСУ)
Официальные оппоненты: доктор технических наук, профессор
Егоров Владимир Викторович
(ПГУПС)
кандидат технических наук, доцент
Любаров Борис Исаевич
(ООО «Стройреконструкция»)
Ведущая организация: ЗАО ПИ «Ленпроектстальконструкция»
г. Санкт-Петербург
Защита диссертации состоится 17 июня 2010 г в 16.00 на заседании диссертационного совета по защите докторских и кандидатских диссертаций Д 212.223.03 при ГОУ ВПО «Санкт-Петербургский государственный архитектурно-строительный университет» по адресу: 190005, г. Санкт-Петербург, 2-я Красноармейская ул., д. 4, зал заседаний.
Эл. почта: [email protected]
Факс: (812) 316-58-72
С диссертацией можно ознакомиться в фундаментальной библиотеке ГОУ ВПО «Санкт-Петербургский государственный архитектурно-строительный университет»
Автореферат разослан мая 2010 г.
Учёный секретарь
диссертационного совета
доктор технических наук Л.Н. Кондратьева
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы. В последнее время наряду с созданием новых современных промышленных предприятий зачастую экономически целесообразно реконструировать существующие. В связи с этим часто возникает необходимость усиления отдельных элементов конструкций по причине увеличения эксплуатационных нагрузок или наличия дефектов и повреждений. При этом присоединение дополнительных элементов в большинстве случаев выполняется при помощи сварки. Последняя сопровождается развитием специфических деформаций и напряжений, зачастую являющихся причиной снижения несущей способности. Исчерпывающей оценки термического влияния на пространственную работу и устойчивость усиливаемых элементов до настоящего времени ещё не дано. Поэтому исследование данного вопроса, имеющего особенно важное значение при усилении элементов конструкций под нагрузкой, представляется весьма актуальным.
Целью работы являются теоретические и экспериментальные исследования влияния термических напряжений и деформаций на напряжённо-деформированное состояние, пространственные деформации и устойчивость усиленных методом увеличения сечения стержневых элементов открытого профиля.
Научную новизну работы составляют:
- алгоритмы расчёта на прочность и пространственную устойчивость стержневых элементов открытого профиля с размещением элементов усиления в наиболее напряжённой зоне с учётом термических деформаций;
- результаты численного исследования теплового влияния сварки на пространственные деформации и устойчивость внецентренно-сжатых усиленных стержней;
- результаты экспериментальных исследований устойчивости несимметрично усиленных стержней двутаврового профиля с учётом термических напряжений.
Достоверность результатов проведённых исследований базируется на использовании хорошо апробированных теоретических основ и методов расчёта стержневых элементов металлических конструкций, удовлетворительном согласовании теоретических и экспериментальных результатов, а также на результатах проверочных расчётов, выполненных методом конечных элементов.
Практическая ценность работы заключается в разработке алгоритмов, программы на ЭВМ и практических рекомендаций по расчёту на пространственную устойчивость усиленных стержневых элементов. Инженерная методика, разработанная на примере двутаврового профиля, представлена в удобной форме, используемой в нормах проектирования, с введением факторов, характеризующих некоторые параметры усиления: технологические параметры сварки, эксцентриситеты приложенной нагрузки, гибкости усиливаемых элементов, уровень начального нагружения, место расположения элемента усиления относительно центра тяжести основного сечения, его длина, а также площадь.
Внедрение результатов. Результаты диссертационной работы, представленные инженерной методикой расчёта на пространственную устойчивость двутавровых стержней, усиленных методом увеличения сечения при помощи сварки, приняты к внедрению ЗАО ПИ «Ленпроектстальконструкция», ОАО «СПбЗНИиПИ».
Апробация диссертации. Основные положения диссертационной работы доложены и одобрены на 58, 59, 61, 62 международных научно-технических конференциях молодых учёных, проходивших в СПбГАСУ (СПб., 2005, 2006, 2008, 2009), а также на 62, 63, 64, 66, 67 научных конференциях профессоров, преподавателей, научных работников, инженеров и аспирантов СПбГАСУ (СПб., 2005, 2006, 2007, 2009, 2010).
Публикации. По теме диссертации опубликовано шесть работ, в том числе одна – в рецензируемом издании, включённом в список ВАК РФ.
Структура и объём работы. Диссертация состоит из введения, пяти глав, основных выводов, списка литературы и приложений. Общий объём работы составляет 201 страницу, 70 рисунков и 17 таблиц. Список литературы содержит 181 наименование, из них 172 на русском языке.
Основные положения, выносимые на защиту:
- Методика учёта тепловых деформаций при определении напряжённо-деформированного и предельного состояний в сечениях усиливаемых элементов (обобщённый алгоритм «Сечение»).
- Алгоритм расчёта на пространственную устойчивость усиленных стержней, учитывающий термическое влияние сварки.
- Инженерная методика проверки пространственной устойчивости усиленных при помощи сварки стержней.
- Экспериментальные исследования внецентренно-сжатых двутавровых стержней, усиленных под нагрузкой.
ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ
Во введении обосновывается актуальность темы, формулируются основные цели и задачи исследования, изложены сведения о научной новизне и практической ценности работы.
В первой главе приводится обзор работ по вопросам проектирования усиления металлических конструкций, при этом основное внимание уделяется методу увеличения сечения; рассмотрен ряд работ по исследованию сварочных напряжений и деформаций, отражающих влияние последних на несущую способность усиленных элементов; проанализированы работы, посвящённые расчёту тонкостенных стержней по пространственно-деформированной схеме, в том числе за пределом упругости; характеризуется современный уровень исследований несущей способности стержней, усиленных под нагрузкой методом увеличения сечения, в том числе с использованием сварки.
Прежде всего, упомянем, что исторически сложились и в настоящее время существует три основных метода усиления:
- увеличение площади поперечного сечения отдельных элементов конструкций,
- изменение конструктивной схемы всего сооружения или отдельных его элементов (иначе говоря, изменение расчётной схемы),
- регулирование напряжений.
Наиболее распространённым из перечисленных является первый метод, которому и посвящена данная работа.
Накопленный опыт в области усиления металлических конструкций впервые в отечественной практике был обобщён в монографии М.Н.Лащенко. Дальнейшее развитие этого вопроса связано с разработкой новых, более эффективных методов и приёмов усиления, изложенных в работах Г.А. Шапиро, Б.И. Беляева и В.С. Корниенко, М.М Сахновского и А.М. Титова, А.В. Сильвестрова, М.Р. Бельского и А.М. Лебедева и других учёных.
Одним из первых предложений по расчёту прочности усиленных под нагрузкой элементов было сделанное в 1939 г Б.Г. Шварцбургом и Я.Л. Куцёнком. Экспериментальные исследования работы сжатых и растянутых элементов, усиливаемых до загружения и под нагрузкой, были проведены М.Н. Неминским и В.П. Кушневым. Теоретическое и экспериментальное исследование упругопластической работы балок, усиливаемых под нагрузкой увеличением сечений, было выполнено Е.И. Беленя и продолжено И.Я. Донником и М.Я. Шепельским. Устойчивость сжатых стержней, усиливаемых в напряжённом состоянии, рассматривалась В.М. Колесниковым.
Исследование работы сжатых элементов, усиленных под нагрузкой, было продолжено И.С. Ребровым и его учениками А.В. Столбовым и А.П. Коноваловым. Предложенные И.С. Ребровым рекомендации по усилению балок и внецентренно-сжатых стоек включены в соответствующие разделы пособия по проектированию усиления стальных конструкций к СНиП II23–81*.
Что касается термических напряжений, то здесь прежде всего необходимо отметить монографию Н.О. Окерблома «Сварочные напряжения и деформации», в которой впервые наиболее полно отражён механизм их образования, а также предложены методы, способствующие уменьшению сварочных деформаций и напряжений. Идеи Н.О. Окерблома были развиты в работах его ученика И.П.Байковой.
Общая теория температурных процессов при сварке была разработана Н.Н. Рыкалиным и отражена в монографии «Тепловые процессы при сварке».
Особенностям учёта сварочных напряжений применительно к судовым конструкциям посвящены работы Г.А. Бельчука, К.М. Гатовского, В.П. Вологдина, С.А. Кузьминова.
Большое количество исследований отражает влияние остаточных напряжений на работу сварных элементов, среди них можно отметить работы Л.П. Шелестенко, Я. Августына, Д.И. Навроцкого, В.И. Махненко, В.П. Вершинина, В.С. Игнатьевой.
С внедрением в расчётную практику ЭВМ всё большую популярность приобретали численные методы. Н.Н.Прохоровым предложен численный метод расчёта деформаций, возникающих при наплавке валика на кромку пластины. По сути это одна из первых попыток решить задачу Н.О.Окерблома численным методом. Сюда следует также отнести исследования В.А. Винокурова и А.Г. Григорьянца.
Влияние сварки на работу элементов, находящихся под нагрузкой, отражено в работах И.К. Родионова, Б.И. Десятова, Р. Кизингера, И.С. Реброва.
И.С. Ребров в своих исследованиях вводит существенную предпосылку об отсутствии перемещений из плоскости элемента и об отсутствии кручения. С целью исключения изгибно-крутильных деформаций предлагается использовать технологию усиления, которая будет способствовать обеспечению симметрии температурного поля относительно силовой плоскости, – последовательную сварку небольшими участками парных симметричных швов. Представляется достаточно трудновыполнимым соблюдение указанного выше допущения, поскольку параллельное наложение сварных швов в условиях существующих конструкций весьма сложно осуществить с точки зрения технологии производства работ. Кроме того, симметричное расположение элемента усиления в случае сжатых стержней может быть неэффективным и приведёт лишь к незначительному увеличению несущей способности, так как ослабление сечения вследствие действия сварки увеличится.
П.А. Пяткиным теоретически и экспериментально были исследованы вопросы прочности и пространственной устойчивости стержневых элементов, несимметрично усиленных при помощи болтовых соединений. Разработана инженерная методика расчёта по форме, принятой в СНиП II-23-81* с введением новых коэффициентов, характеризующих влияние элементов усиления. Однако, предполагаемое усиление при помощи болтов не дало возможности оценить влияние сварки.
Резюмируя сказанное, отметим, что при решении задач подобного рода необходимо использовать теорию расчёта тонкостенных стержней по пространственно-деформированной схеме.
Основы теории устойчивости стержней были заложены в работах Л. Эйлера, Ф. Энгессера, Ф.С. Ясинского, Т. Кармана, Ф. Шенли. Распространение на случай неупругих деформаций эта теория получила в работах К. Ежека, Н.С. Стрелецкого, А.Р. Ржаницина, С.Д. Лейтеса, А.А. Пиковского, А.В. Геммерлинга, Г.Е. Бельского и многих других учёных.
Изучению устойчивости тонкостенных стержней, подверженных действию сжимающей силы с двухосными эксцентриситетами, посвящены работы П.Я. Ларичева, Ю.Д. Копейкина, В.В. Пинаджана, А.З. Зарифьяна, Г.М. Чувикина, Р.А. Скрипниковой и некоторых других. Все исследования базируются на технической теории В.З. Власова и уравнениях равновесия для пространственно-деформированной схемы, полученных В.З. Власовым, Б.М. Броуде, Л.Н. Воробьёвым, С.П. Вязьменским, впоследствии обобщённых Е.А. Бейлиным. Данные уравнения являются весьма громоздкими и практически не допускают решения в замкнутом виде даже при упругой стадии работы материала.
Г.И. Белым предложен приближённый аналитически-численный метод расчёта тонкостенных стержней по деформированной схеме. Решение основано на аппроксимации пространственных форм деформирования в виде линейной комбинации частных форм: форм, полученных расчётом по недеформированной схеме, и форм потери устойчивости, вытекающих из решения бифуркационных задач устойчивости. Физическая нелинейность учитывается введением дополнительных пространственных перемещений сечений стержня.
Этот метод использовался в работах Н.Г. Сотникова, Н.Н. Родикова, П.А. Пяткина, И.В. Астахова, многих других исследователей, а также в данной работе.
В заключение главы определена цель настоящей диссертации – теоретическое и экспериментальное исследование прочности, пространственных деформаций и устойчивости стержневых элементов открытого профиля, усиленных под нагрузкой методом увеличения сечения при помощи сварки, а также разработка практических методов их расчёта на пространственную устойчивость, свободных от указанных недостатков.
Во второй главе описываются некоторые известные физические и механические явления, влияющие на образование деформаций и напряжений при сварке: дилатометрический эффект, структурные и фазовые превращения, упрочнение металла околошовной зоны, а также природа усадочной силы. Приводится решение дифференциального уравнения теплопроводности. Изложен метод теоретического определения сварочных деформаций и напряжений Н.О. Окерблома.
Определение температурного поля при сварке сводится к решению двумерного дифференциального уравнения теплопроводности (1) для каждого из элементов (пластин), входящих в состав стержня:
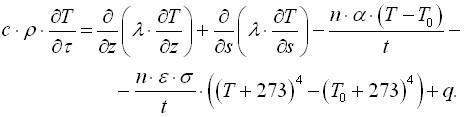(1)
При помощи метода конечных разностей (МКР) в форме локально-одномерной схемы, разработанной А.Н.Тихоновым и А.А.Самарским, выражение (1) сводится к системе линейных алгебраических уравнений. Решение последней осуществляется с использованием метода прогонки. Результатом вычислений являются температуры в узлах сетки МКР в момент времени 
.
Далее в главе на основе решения (1) продемонстрированы некоторые результаты численного исследования и проиллюстрировано влияние некоторых известных факторов, таких как, скорость охлаждения, мощность дуги и скорость её передвижения, на распределение температур.
Показано образование сварочных напряжений и деформаций в соответствии с методом Н.О.Окерблома на примере неравномерного нагрева полосы, на кромку которой осуществляется наплавка валика (рисунок 1). Упругопластические деформации в данном случае представляют собой разность свободных температурных 
и соответствующих гипотезе плоских сечений 
. Заштрихованная на рисунке 1 эпюра упругих деформаций определяет «сварочные» напряжения каждого волокна. При 
значения механических характеристик стали падают практически до нуля, поэтому область в районе сварного шва характеризуется наличием чисто пластических деформаций.
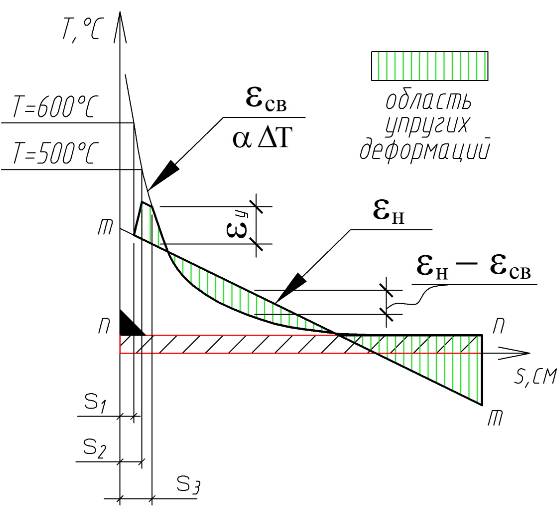
Рис. 1. Распределение упругопластических деформаций по сечению
В третьей главе исследуются напряжённо-деформированные и предельные состояния в сечениях усиленных под нагрузкой стержневых элементов открытого профиля при помощи сварки. Описывается метод определения деформаций и напряжений В.П. Коломийца, обобщённый Г.И. Белым на общий случай загружения при произвольном размещении дополнительных элементов усиления. Упомянутый метод, получивший название алгоритм «Сечение», обобщён нами на случай учёта тепловых деформаций.
В решении задачи приняты следующие ограничения по форме и условиям симметрии сечения:
- Усиленное сечение должно быть открытого профиля.
- Сечение может быть моно-, бисимметричным, а также не иметь ни одной оси симметрии.
При оценке напряжённо-деформированного состояния усиленных элементов будем исходить из общепринятых положений, установленных в технической теории тонкостенных стержней открытого профиля В.З. Власова.
В качестве критерия, определяющего предельное состояние по прочности, в соответствии со СниП II-23-81*, будем использовать предельную деформацию 
.
Для удобства исследования поведения стержневых элементов в процессе сварки и роста нагрузки решение будем вести в приращениях. Считая справедливой гипотезу плоских сечений в сочетании с законом секториальных площадей, запишем выражение для приращения относительной деформации волокна в виде:
. (2)
Влиянием касательных напряжений на развитие пластических деформаций в задачах устойчивости, как это было показано С.Н. Сергеевым, можно пренебречь. Поэтому в сечении рассматривается комплекс силовых факторов 
, при котором будем иметь, следуя В.П. Коломийцу, выражения для приращений усилий с учётом дополнительных членов, введённых Г.И. Белым, которые учитывают стеснённое кручение:
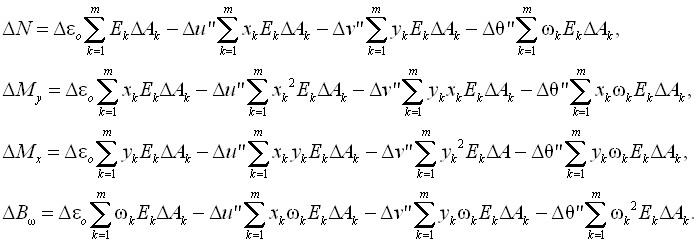(3)
В случае термического воздействия для ненагруженного сечения будем иметь нулевые усилия [левые части (3)], так как в данном случае напряжения являются самоуравновешенными. В таком случае для получения ненулевых перемещений по (3) необходимо задаться некоторыми фиктивными усилиями, вытекающими из решения температурной задачи:
(4)
Упругопластические деформации при тепловом воздействии будут определяться разностью относительных деформаций и свободных температурных:
. (5)
Порядок определения напряжённо-деформированного состояния несимметрично усиленного стержня в момент времени 
показан на рисунке 2.
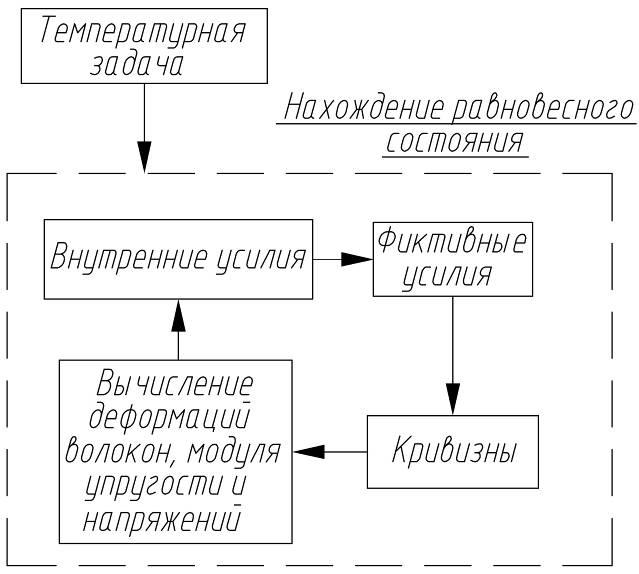
Рис. 2. Схема определения НДС от теплового действия сварки
Как было показано Г.И. Белым и П.А. Пяткиным, наиболее эффективным является размещение элемента усиления в наиболее напряжённой зоне. Для этого она предварительно определяется расчётом по пространственно-деформированной схеме, или, в упрощённом варианте, расчётом по прочности.
Сечение разбивается на ряд малых площадок (рисунок 3). В центре тяжести каждой из них будем определять температуры, деформации и напряжения.
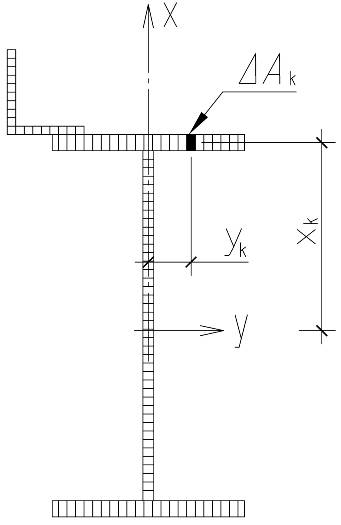
Рис. 3. Сечение усиленного стержня
Методика определения напряжённо-деформированного состояния в сечении представляет собой алгоритм «Сечение», разработанный Г.И. Белым, который следует обобщить на случай учёта тепловых деформаций.
Имея значения температур волокон, вычисляем приращения усилий по (4). Затем, решая систему уравнений (3), определяем приращения компонент деформаций 
. Далее вычисляем приращения относительных деформаций волокон по (2). Суммируя полученное приращение с деформацией к данному моменту времени, получаем полную деформацию волокна 
. Затем определяем упругопластические деформации по (5).
По 
и температуре волокна находим модуль упругости по известной диаграмма 
. Далее определяем напряжения:
. (6)
На этом заканчивается первая итерация. Вторую итерацию начинаем с вычисления внутренних усилий по найденным напряжениям во втором приближении:
(7)
Эти усилия не должны превышать наперёд заданного малого числа. Если они его превышают, продолжаем итерационный процесс, принимая в качестве исходных данных эти усилия.
На основе обобщённого алгоритма «Сечение» разработана программа на языке 
. Данная программа позволяет численно исследовать напряжённо-деформированные и предельные состояния элементов в сечении открытого профиля, загруженных комплексом усилий, вызывающих нормальные напряжения, с учётом физической нелинейности и тепловых деформаций. Ниже приведены некоторые результаты расчётов.
На примере внецентренно-растянутого широкополочного двутавра 
, усиливаемого уголком 
в наиболее напряжённой зоне при уровне начального нагружения 
(
), продемонстрированы характерные эпюры напряжений и деформаций (рисунок 4). Красным цветом показаны эпюры линейных деформаций 
, зелёным – эпюры упругопластических деформаций 
. Эпюра остаточных напряжений (рисунок 4б) характеризует их распределение после полного охлаждения обоих швов; эпюра, соответствующая предельному состоянию усиленного на сварке сечения, показана на рисунке 4в. Видно, что напряжения распределяются по сечению крайне неравномерно, достигая после охлаждения значений близких к пределу текучести в зоне шва. Важно отметить, что элемент усиления в предельном состоянии полностью находится в пластическом состоянии.
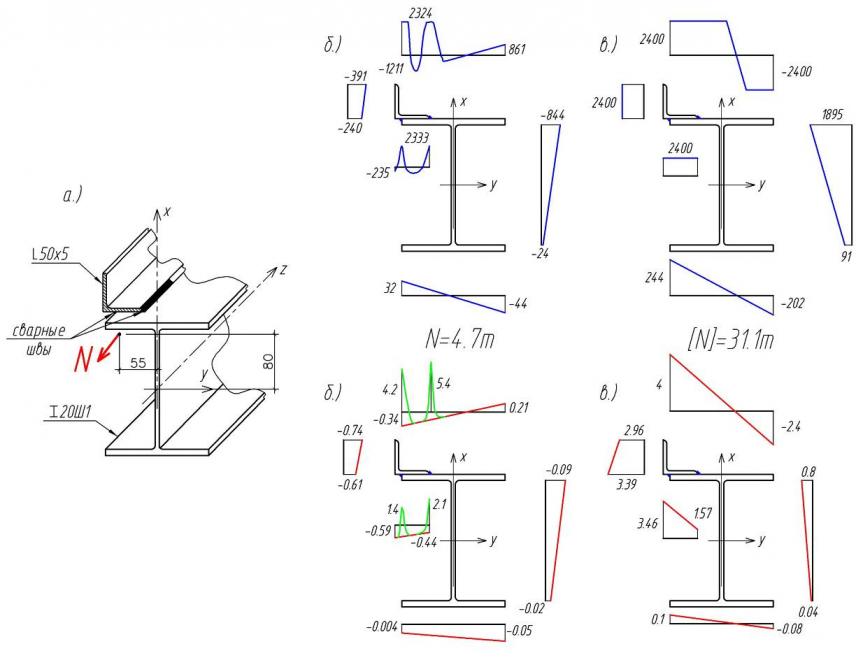
Рис. 4. Напряжённо-деформированное б и предельное в состояния в сечении усиленного стержня а при =0.4
С целью выявления температурного влияния на прочность усиленных элементов был выполнен сравнительный расчёт усиления на болтах и на сварке для трёх случаев начального нагружения при 
(рисунок 5). Из графиков видно, что способ усиления (механический или термический) и начальное нагружение не оказывают существенного влияния на предельную силу при любом значении эксцентриситета, что подтверждает в том числе известное положение об отсутствии влияния начальных напряжений на прочность при условии критерия ограниченных пластических деформаций.
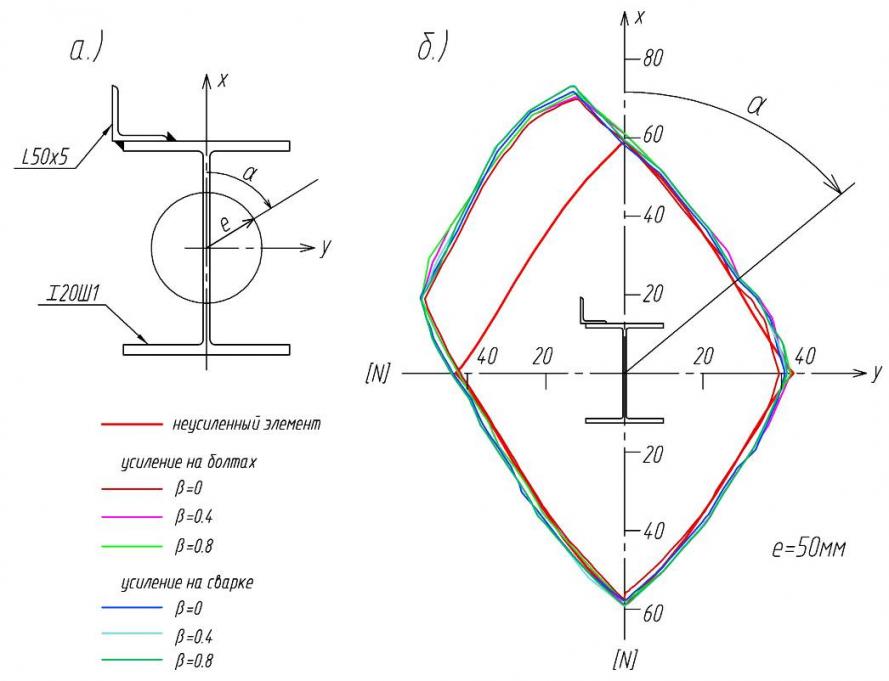
Рис. 5. Предельные состояния в сечении элемента, усиленного при разных уровнях начального нагружения для двух случаев: на сварке и на болтах
В отличие от остаточных, временные напряжения (существующие во время нагрева и охлаждения) существенно влияют на прочность нагреваемых элементов в процессе усиления. На рисунке 6 показано изменение величины касательного модуля, являющегося в данном случае функцией температуры, в момент максимального нагрева волокон верхней полки. Из рисунка видно, что упругие свойства (зелёная линия) резко снижаются при приближении к зоне высоких температур и в районе сварного шва уменьшаются до нуля (красная линия). Для стенки и нижней полки искомая зависимость не показана, поскольку в них отсутствуют пластические деформации.
Как показали расчёты, возникающее ослабление сечения в среднем составляет до 
от площади неусиленного элемента для данного стержня. Из этого следует, что исчерпание несущей способности при высоких уровнях начального нагружения 
возможно уже в процессе усиления.
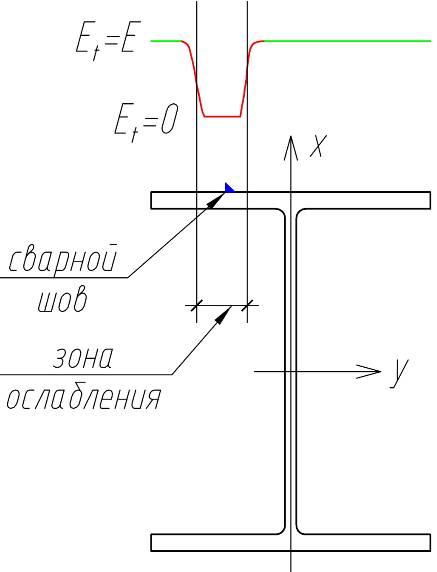
Рис. 6. К вопросу влияния временных напряжений на прочность
В четвёртой главе исследуется пространственная устойчивость усиленных под нагрузкой с использованием сварки стержневых элементов конструкций открытого профиля; даётся оценка обоснованности применения плоской схемы потери устойчивости по сравнению с пространственной; приводится сравнительный анализ расчётов, выполненных по алгоритму «Стержень» и методу конечных элементов; предложена инженерная методика расчёта усиленных стержней.
В качестве объекта рассматривается стержневой элемент, загруженный продольной сжимающей силой 
с двухосным эксцентриситетом 
(рисунок 7.а). Закрепление на опорах принято шарнирным в двух плоскостях, а закручивание концевых сечений отсутствует (вилочные опоры).
Работу элемента усиления, находящегося в наиболее напряжённой зоне, будем рассматривать как действие растягивающей силы 
с эксцентриситетами относительно главных осей 
неусиленного элемента 
(рисунок 7.б).
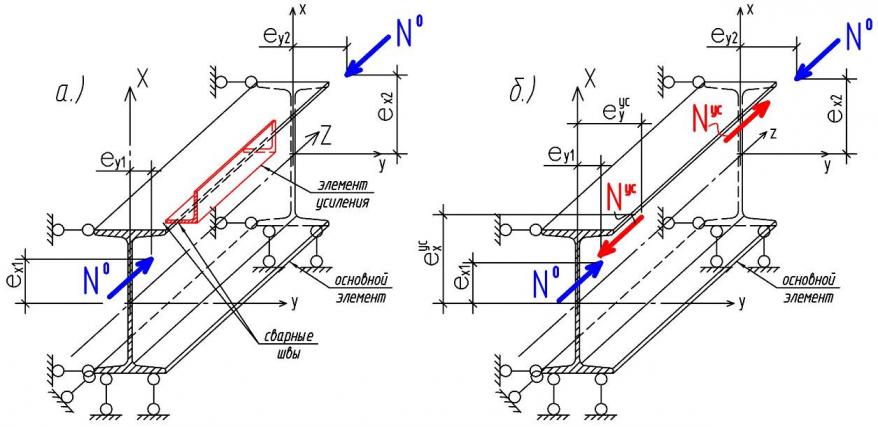
Рис. 7. Расчётная схема несимметрично усиленного стержня
Для решения задачи устойчивости по пространственно-деформированной схеме воспользуемся деформационной теорией расчёта упругих стержней В.З. Власова, обобщённой Б.М. Броуде и Е.А. Бейлиным. Тогда система дифференциальных уравнений применительно к неусиленному элементу, но с дополнительным действием 
, после предварительного интегрирования первых двух уравнений примет вид:
(8)
где 
– главные оси сечения; 
– главные осевые моменты инерции; 
– секториальный момент инерции; 
– момент инерции при чистом кручении; 
– модули линейной и сдвиговой деформации; 
– полярный радиус инерции; 
– продольная сила; 
– крутящий момент; 
– функции перемещений сечений вдоль осей 
соответственно; 
– угол закручивания сечений; 
; 
– длина стержня; 
– изгибающие моменты, полученные расчетом по недеформированной схеме. Напомним, что все геометрические характеристики в (8) относятся к неусиленному, симметричному сечению.
Считаются справедливыми те же кинематические и статические гипотезы и допущения, что и перечисленные в третьей главе.
Для решения (8) используем аналитически-численный метод Г.И. Белого, в соответствии с которым общие пространственные деформации усиленного стержня ищутся в виде линейной комбинации частных решений:
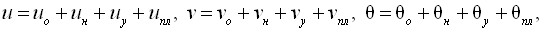(9)
где 
– начальные перемещения и начальный угол закручивания сечений; 
– перемещения и угол закручивания сечений, определяемые расчётом по недеформированной схеме; 
– функции, вытекающие из решения бифуркационной задачи устойчивости, которые решаются с точностью до констант 
, имеющих соответствующие перемещениям размерности, 
; 
– перемещения и угол закручивания, учитывающие развитие пластических деформаций и температурное влияние сварки, которые аппроксимируем в виде тригонометрических полиномов, удовлетворяющих граничным кинематическим условиям задачи (получены Н.Н. Родиковым):
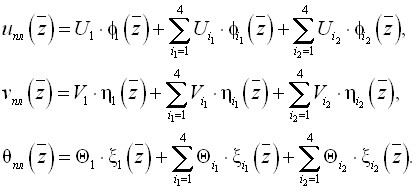(10)
Подставив (9) в (8), имеем:
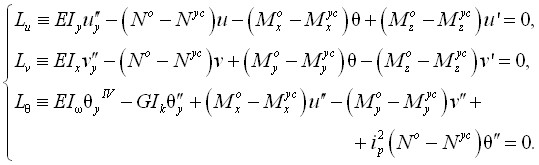(11)
Применив метод Бубнова–Галёркина для решения (11):
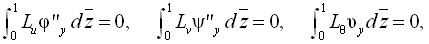(12)
получим систему трёх алгебраических уравнений относительно неизвестных констант функций потери устойчивости 
, решив которую будем иметь все компоненты полных перемещений (9). Зная их, можно определить деформационные усилия:
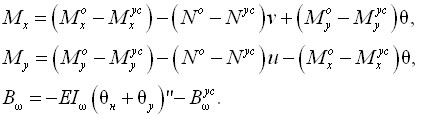(13)
Описанный алгоритм носит название «Стержень».
Ниже на рисунке 8 показан порядок решения деформационной задачи.
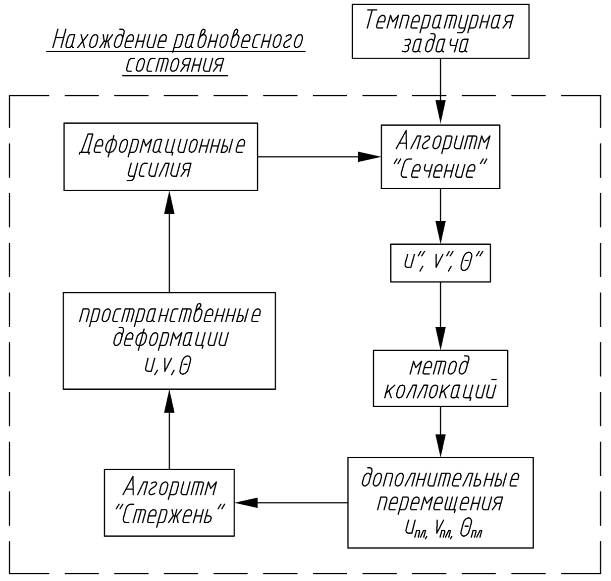
Рис. 8. Схема определения пространственных деформаций и устойчивости усиленного элемента
Работу усиливаемого элемента разделим на три этапа.
До усиления. Пошаговое увеличение силы 
продолжаем до некоторого значения 
и соответствующего ему коэффициента начального нагружения 
, где 
– напряжение в наиболее нагруженном волокне неусиленного стержня. При этом дополнительные усилия 
равны нулю.
Во время усиления. Приварка элемента усиления при постоянной силе 
. Определение сварочных перемещений, возникающих вследствие ослабления сечения (уменьшения модуля упругости) и появления температурных деформаций, производим с помощью алгоритма «Сечение».
После усиления. Дальнейшее ступенчатое увеличение продольной силы 
до момента потери устойчивости (расходимости итерационного процесса).
В первом приближении на этапе 
пространственные деформации (9) принимаем с предыдущего шага нагружения 
. Задаём продольной силе очередное приращение 
. Вычисляем деформационные усилия (13) при нулевых значениях 
и устанавливаем их приращения:
(14)
Попутно заметим, что на втором этапе передаём в алгоритм «Сечение» вместо (14) приращения фиктивных усилий (4), предварительно решив температурную задачу. Обращаясь к алгоритму «Сечение», определяем приращения кривизн и второй производной угла закручивания для усиленного сечения. Далее, используя метод коллокаций и принятые аппроксимирующие функции (10), определяем перемещения и угол закручивания, учитывающие развитие пластических деформаций (
), а также тепловое влияние сварки на втором этапе.
Вычисляем усилия 
по напряжениям волокон элемента усиления, полученным в алгоритме «Сечение»:
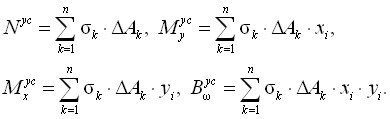(15)
Решив систему (11), определим константы 
, а, следовательно, перемещения 
.
Определяем во втором приближении пространственные деформации (9) и деформационные усилия (13).
На этом заканчивается первая итерация алгоритма «Стержень». Итерационный процесс продолжаем до тех пор, пока разность между усилиями на двух соседних итерациях не будет находиться в пределах заданной точности.
С ростом нагрузок сходимость процесса ухудшается, и на определённом этапе он становится расходящимся. Это соответствует нарушению устойчивости процесса деформирования, тогда приращение продольной силы 
принимаем меньшего значения. Таким образом, с требуемой точностью определяем величину нагрузок, при которых процесс ещё сходится. При этом достаточно малое приращение нагрузки приводит к расходимости процесса. Эти нагрузки считаем предельными.
На основе алгоритма «Стержень» разработана программа на языке 
, которая позволяет численно исследовать пространственные деформации и устойчивость внецентренно-сжатых двутавровых стержней, несимметрично усиленных с помощью сварки.
В качестве примера на рисунке 9 показаны кривые повышения устойчивости для болтового и сварного соединения (в скобках указан уровень начального нагружения 
). Площадь элемента усиления составляет: 
. Из графиков хорошо видно, что в случае применения болтов указанная зависимость практически линейная даже для больших значений 
. Для сварки же даже для изначально усиленного элемента она имеет ярко выраженную нелинейность. Кроме того, для больших гибкостей в результате появления значительных остаточных деформаций от термического влияния эффект усиления резко падает.
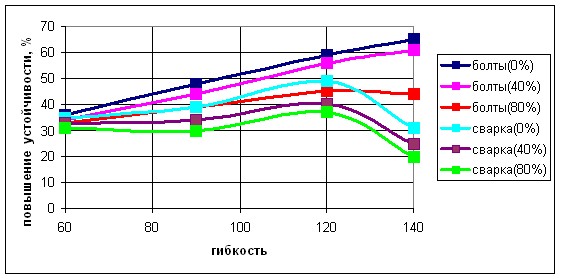
Рис. 9. Влияние гибкости, уровня начального нагружения, а также способа усиления на повышение устойчивости
На рисунке 10 показаны графики зависимости предельной силы от направления двухосного эксцентриситета 
(
,
) и уровня начального нагружения 
для стержня гибкостью 
. Кривые построены в полярных координатах. Анализ результатов позволяет сделать вывод о том, что наиболее эффективным усиление будет в случае расположения дополнительного элемента в наиболее напряжённой зоне (левый верхний квадрант). При других направлениях возрастание устойчивости незначительно.
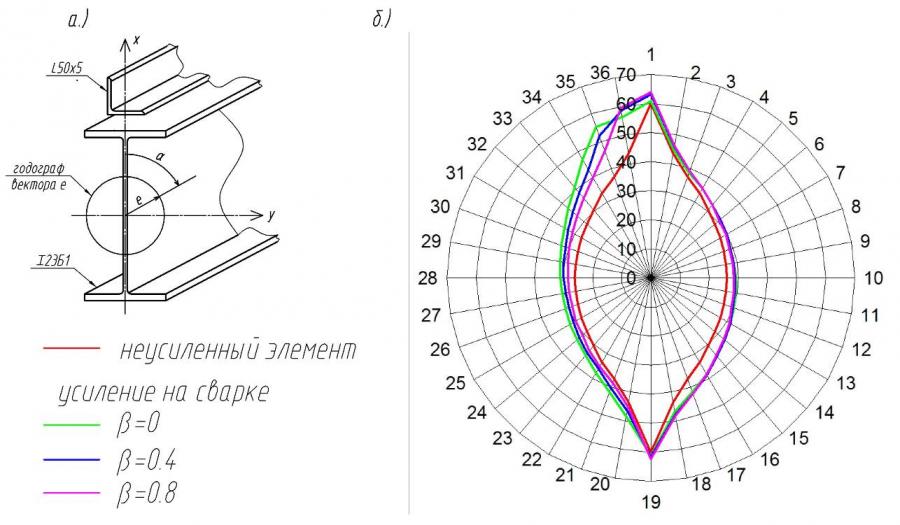
Рис. 10. Влияние направления эксцентриситета e на величину предельной силы при усилении на сварке
Для оценки действительной работы усиленного элемента выполним сравнительный расчёт симметрично усиленного профиля по пространственно-деформированной и плоской схемах. На рисунке 11 показана схема сечения усиливаемого элемента. Усиление предполагается в виде стальной полосы 
, располагаемой на верхней полке двутавра симметрично относительно вертикальной оси. Прикрепление осуществляется при помощи сварки. Постоянный эксцентриситет в плоскости меньшей жёсткости принят в виде случайного 
. В плоскости большей жёсткости величина эксцентриситета переменная.
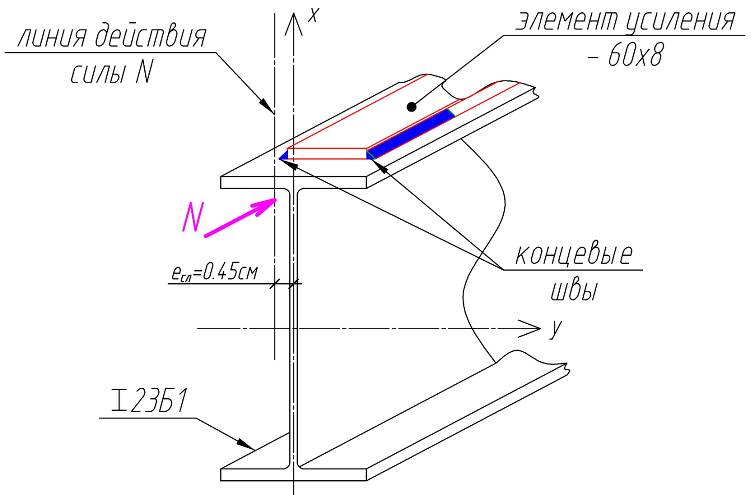
Рис. 11. Симметричное усиление верхней полки двутавра
На рисунке 12 показаны графики предельных сил в зависимости от относительного эксцентриситета в плоскости большей жёсткости и расчётной схемы (плоской и пространственно-деформированной). Установлено, что использование плоской схемы, не учитывающей изгибно-крутильные деформации, приводит к существенному завышению устойчивости на 
.
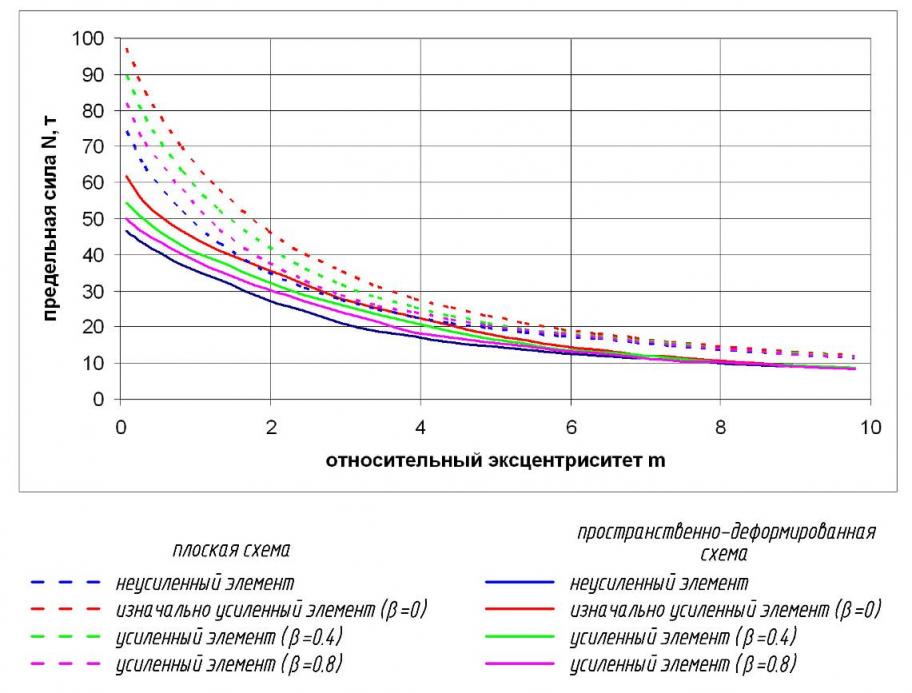
Рис. 12. Графики предельных сил в зависимости от относительного эксцентриситета
С целью проверки достоверности теоретических расчётов по разработанному алгоритму было проведено решение аналогичных задач с использованием метода конечных элементов при помощи программного комплекса ANSYS. Сравнивая полученные результаты, можно отметить, что значения предельных нагрузок и дополнительных сварочных прогибов (горизонтальных участков) удовлетворительно согласуются. Разница значений не превышает 
. В целом можно сказать, что создание точной модели, адекватно описывающей процесс усиления при помощи сварки, даже в таком универсальном программном продукте как ANSYS, является весьма трудоёмким, поскольку в процессе расчёта изменяется геометрия поперечного сечения, причём это происходит постепенно по мере заварки швов. Немаловажное значение имеет и время расчёта, которое на два порядка больше, чем при использовании алгоритмов «Сечение» и «Стержень».
В заключение главы предложена инженерная методика проверки пространственной устойчивости усиленных с помощью сварки стержней, представленная в форме СНиП II-23-81*:
, (16)
где 
– площадь сечения и расчётное сопротивление металла неусиленного стержня; 
– коэффициент снижения расчётного сопротивления при внецентренном сжатии, учитывающий пространственную работу неусиленного стержня, введён Н.Н. Родиковым; 
– коэффициент усиления, учитывающий не только присутствие дополнительного элемента, но и влияние сварки.
Коэффициент 
зависит от двухосных относительных эксцентриситетов 
; условной гибкости в плоскости меньшей жёсткости 
; соотношений радиусов инерции 
; площади элемента усиления 
; координат центра тяжести элемента усиления 
; уровня начального нагружения 
.
На рисунке 13в представлены некоторые значения коэффициентов 
для зоны, указанной на рисунке 13а. Для сравнения приведены значения для усиления на болтах (сплошной линией) и на сварке (штриховой линией). В результате анализа графиков выделена наиболее эффективная зона 
, заштрихованная на рисунке 13б.
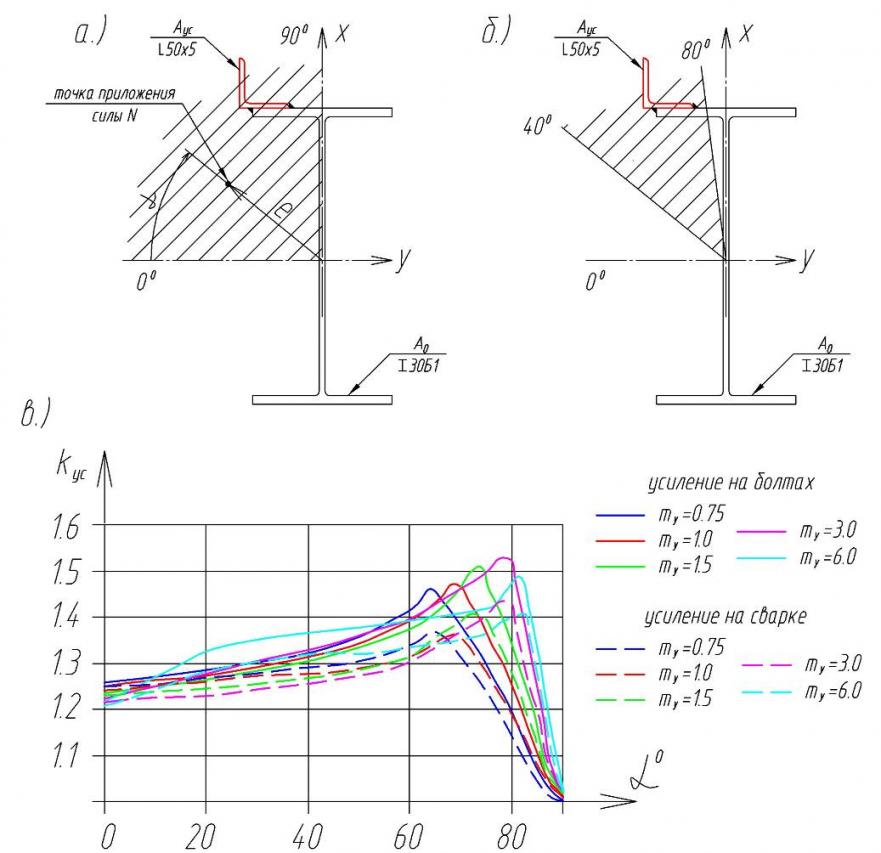
Рис. 13. Графики коэффициентов усиления 
(гибкость 120, =0.4) в зависимости от относительных эксцентриситетов
В пятой главе описаны постановка, порядок проведения и результаты экспериментального исследования пространственных деформаций и устойчивости внецентренно-сжатых двутавровых стоек, усиленных под нагрузкой с помощью сварки.
Экспериментальные исследования проводились с целью подтверждения теоретических расчётов и осуществлены в механической лаборатории СПбГАСУ.
Всего испытано двадцать восемь стальных стержней, разбитых на четыре гибкости 
. Сечение основного элемента – двутавр 
, сечение элемента усиления – уголок 
. Площадь сечения элементов усиления составила 
от площади сечения стержней, длина – 
длины образцов.
Соединение основного элемента и элемента усиления осуществлялось с помощью двух фланговых шпоночных швов. Длины концевых участков сварных швов принимались в соответствии с предварительным расчётом. Размеры промежуточных шпонок, назначены конструктивно.
Установка для испытания моделей колонн на внецентренное сжатие была сконструирована на базе 500-тонного пресса фирмы «Амслер». Нагрузка на модели передавалась с помощью специального опорного приспособления, которое имитировало одновременно шаровой шарнир и вилочную опору.
Перед испытанием у образцов замерялись начальные искривления оси в двух плоскостях и углы закручивания сечений, которые были учтены при определении теоретических значений предельных сил и пространственных деформаций.
Линейные деформации измерялись тензорезисторами КФ5. Перемещения регистрировались прогибомерами ПАО-6 с ценой деления 0,01мм. Перемещения замерялись в среднем и опорных сечениях.
Значения относительных эксцентриситетов принимались следующими: 
, 
.
Основные результаты испытаний представлены в виде таблиц и графиков зависимости перемещений и углов закручивания сечений от гибкости и уровня начального нагружения.
В качестве одного из примеров на рисунке 14 показаны графики в координатах «нагрузка-перемещение» для гибкости 120, отражающие все три компонента пространственных перемещений среднего сечения стержня 
, 
и 
. Приведены кривые, соответствующие теоретическому расчёту, а также полученные в результате эксперимента, что дало возможность их сравнить и оценить возможные расхождения. В целом можно сказать, что теоретические кривые подобны экспериментальным и характер деформирования идентичен, а полученные результаты достаточно удовлетворительно согласуются между собой. Это свидетельствует о том, что разработанный алгоритм расчёта достаточно адекватно описывает действительную пространственную работу двутавровых стержней, усиленных под нагрузкой при помощи сварки.
Несущая способность по результатам эксперимента увеличивается на 
в зависимости от уровня начального нагружения и гибкости. Повышение эффективности наблюдается с увеличением гибкости, за исключением 
, и уменьшается с увеличением начальной нагрузки. Расхождение между соответствующими значениями предельных сил, полученными из эксперимента и теории, укладывается до 
.
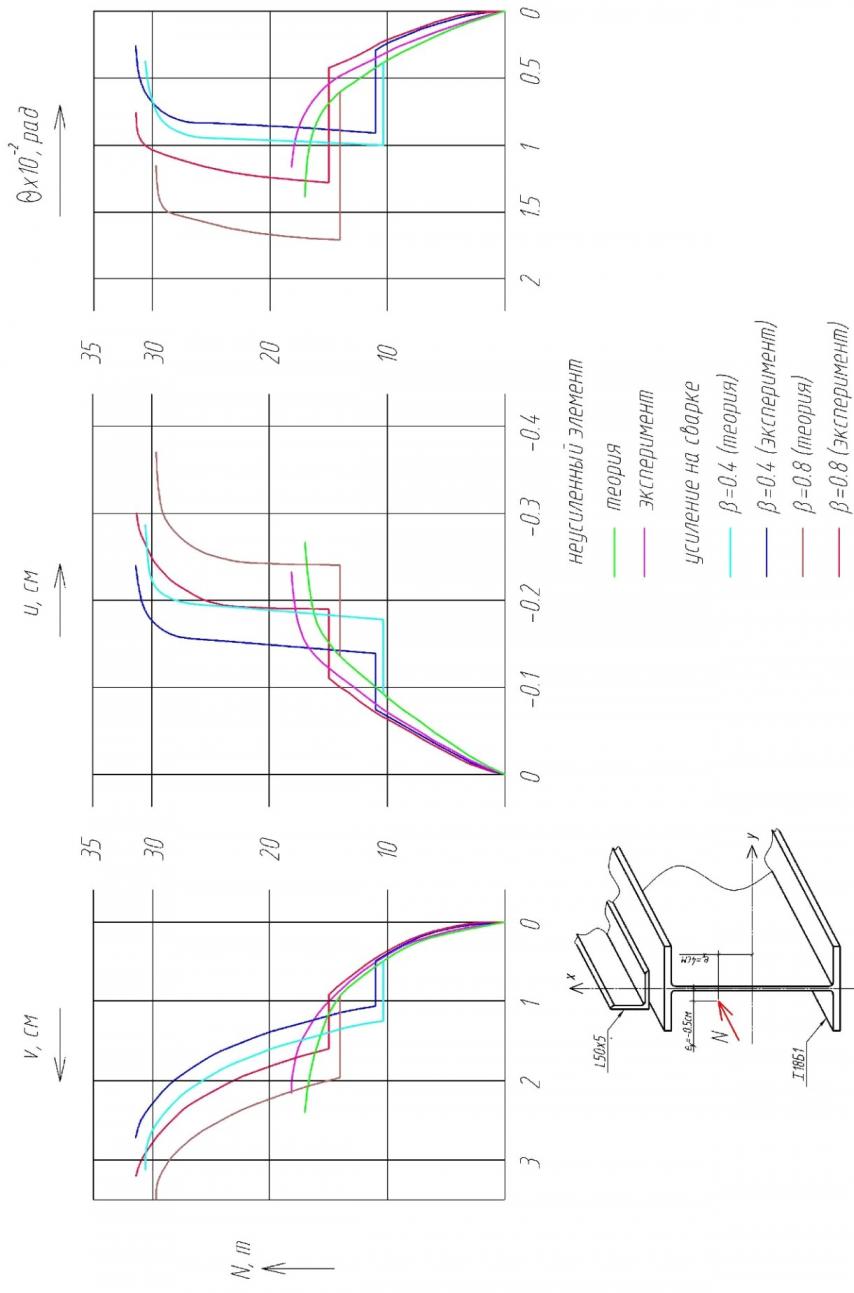  | Рис. 14. Графики зависимости пространственных деформаций для стержня гибкостью 120 |
Основные результаты и выводы
- Разработаны алгоритмы и программа расчёта на прочность и пространственную устойчивость усиленных под нагрузкой при помощи сварки методом увеличения сечения стержневых элементов открытого профиля при общем случае размещения элементов усиления. За основу приняты хорошо апробированные алгоритмы «Стержень» и «Сечение», разработанные Г.И.Белым, которые были обобщены на случай учёта тепловых деформаций.
- Установлено снижение эффективности усиления сжато-изогнутого элемента в результате сварочных процессов в пределах
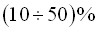в зависимости от различных факторов, таких как: гибкости, величины и направления двухосных концевых эксцентриситетов продольной силы, места постановки элемента усиления, остаточных сварочных напряжений, а также уровня начального нагружения. - Подтверждено, что рациональным является место размещения дополнительного элемента в зоне наибольших напряжений неусиленного элемента. При этом повышение несущей способности относительно введённой площади усиления возрастает в несколько раз. Так, например, при увеличении площади на
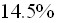устойчивость повышается в пределах 
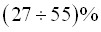в зависимости от гибкости.
- Показано, что использование плоской схемы при расчёте устойчивости двутавровых стержней, загруженных в плоскости большей жёсткости и с учётом случайного эксцентриситета из этой плоскости, приводит к существенному и необоснованному завышению устойчивости в зависимости от гибкости и величины эксцентриситетов по сравнению с расчётом по пространственно-деформированной схеме. Так, например, для двутавра
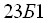искомое расхождение составляет 
.
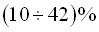- Выполнен сравнительный анализ расчётов двутаврового элемента по разработанным алгоритмам и методом конечных элементов, который показал удовлетворительную сходимость результатов. Установлено, что принятые гипотезы и предпосылки в разработанных алгоритмах являются обоснованными. Разработанный алгоритм и программа позволяют получать результаты расчёта на несколько порядков быстрее, чем при использовании МКЭ.
- Разработана инженерная методика расчёта на пространственную устойчивость с введением коэффициентов
, характеризующих влияние элементов усиления и сварки. Использование этих коэффициентов позволяет обеспечить внедрение результатов по форме, принятой в СниП II-23-81*. - Экспериментально исследована устойчивость усиленных под нагрузкой при помощи сварки двутавровых стержней, сжатых с двухосными эксцентриситетами. Характер деформирования свидетельствует о пространственных деформациях, которые проявляются с самого начала нагружения. Это подтверждает необходимость использования пространственно-деформированной схемы в расчётах на общую устойчивость. Результаты теоретических исследований удовлетворительно согласуются с данными эксперимента.
Основное содержание диссертации изложено в следующих работах:
- Михаськин, В.В. Влияние сварочных процессов на пространственные деформации и устойчивость усиливаемых под нагрузкой стержневых элементов / Г.И. Белый, В.В. Михаськин // Изв. высш. учеб. заведений. Стр-во. – Новосибирск, 2009. – №11/12. – С. 3-11 (из списка ВАК).
- Михаськин, В.В. К вопросу о влиянии сварочных деформаций на напряжённо-деформированное состояние усиленных сжатых элементов / В.В. Михаськин, П.А. Пяткин // 64-я науч. конф. проф., преподавателей, науч. работников, инженеров и аспирантов ун-та: сб. докл. / С.-Петерб. гос. архитектур.-строит. ун-т. – СПб., 2007. – Ч.1. – С. 53-58.
- Михаськин, В.В. Методика определения деформированного состояния стальных стержней при сварочном нагреве / В.В. Михаськин // Актуальные проблемы соврем. стр-ва: 59-я междунар. науч.-техн. конф. молодых учёных: сб. докл. / С.-Петерб. гос. архитектур.-строит. ун-т. – СПб., 2006. – Ч.1. – С. 18-24.
- Михаськин, В.В. Некоторые подходы к решению задачи по определению температурных полей при усилении стальных конструкций с использованием сварки / В.В. Михаськин // Актуальные проблемы соврем. стр-ва: 58-я междунар. науч.-техн. конф. молодых учёных: сб. докл. / С.-Петерб. гос. архитектур.-строит. ун-т. – СПб., 2005. – Ч.1. – С. 24-29.
- Михаськин, В.В. Особенности использования тепловидения в натурных исследованиях сварочных температурных полей / В.В. Михаськин, П.А. Пяткин // 63-я науч. конф. проф., преподавателей, науч. работников, инженеров и аспирантов ун-та: сб. докл. / С.-Петерб. гос. архитектур.-строит. ун-т. – СПб., 2006. – Ч.1. – С. 63-68.
- Михаськин, В.В. Учёт сварочных деформаций при усилении сжатых стержневых элементов / В.В. Михаськин, П.А. Пяткин // 62-я науч. конф. проф., преподавателей, науч. работников, инженеров и аспирантов ун-та: сб. докл. / С.-Петерб. гос. архитектур.-строит. ун-т. – СПб., 2005. – Ч.1. – С. 60-62.
