Расчет и рациональное проектирование многоэтажных железобетонных зданий с оболочечными перекрытиями
На правах рукописи
Данг Хань Ан
РАСЧЕТ И РАЦИОНАЛЬНОЕ ПРОЕКТИРОВАНИЕ
МНОГОЭТАЖНЫХ ЖЕЛЕЗОБЕТОННЫХ ЗДАНИЙ
С ОБОЛОЧЕЧНЫМИ ПЕРЕКРЫТИЯМИ
Специальность 05.23.01 – Строительные конструкции,
здания и сооружения
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата технических наук
Санкт-Петербург
2010
Работа выполнена на кафедре Строительной механики ГОУ ВПО «Санкт-Петербургский государственный архитектурно-строительный университет»
Научный руководитель: доктор технических наук, профессор
Плетнев Валентин Иванович
(Санкт-Петербургский государственный
архитектурно-строительный университет)
Официальные оппоненты: доктор технических наук, профессор
Веселов Анатолий Александрович
(Санкт-Петербургский государственный
архитектурно-строительный университет)
кандидат технических наук
Дмитровская Любовь Николаевна
(Петербургский государственный
университет путей сообщения)
Ведущее предприятие: ЗАО “НИИ ПетербургКомплексПроект”
Защита состоится « 17 » июня 2010 года в 14 час 30 мин на заседании совета по защите докторских и кандидатских диссертаций Д 212.223.03 ГОУ ВПО “Санкт-Петербургский государственный архитекурно-строительный университет” по адресу: 190005 г. Санкт-Петербург, 2-я Красноармейская ул., д. 4, зал заседаний.
Факс: (812) 316–58–72
С диссертацией можно ознакомиться в фундаментальной библиотеке при ГОУ ВПО “Санкт-Петербургский государственный архитекурно-строительный университет”
Автореферат разослан « ___» мая 2010 года
Ученый секретарь
диссертационного совета
доктор технических наук Л.Н. Кондратьева
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы. Увеличение шага колонн в многоэтажных зданиях до 9 – 12 и более метров желательно в общественных, торговых и деловых центрах. В то же время пакет перекрытий большого пролета создает возможность прогрессирующего обрушения типа падения одного перекрытия и лавинообразного разрушения нижележащих перекрытий. Обе эти проблемы могут быть решены путем использования оболочек в качестве основной несущей конструкции междуэтажных перекрытий.
При этом необходима выравнивающая конструкция, на которую опирается плоскость пола. Выполненная в виде ребер оболочки, она может быть эффективно включена в работу каркаса на горизонтальную нагрузку.
Диссертационная работа посвящена решению расчетных и конструктивных проблем, связанных с внедрениям оболочечных перекрытий многоэтажных зданий.
Цель работы:
– обосновать достоинства оболочечного перекрытия многоэтажных зданий;
– найти формы оболочек наиболее рациональные по прочностным и функциональным критериям;
– определить рациональные типы выравнивающих конструкций, на которые опирается плоскость пола;
– оценить влияние таких перекрытий на горизонтальную жесткость каркаса здания;
– исследовать возможность использования ребристых оболочек в качестве связей-платформ между башнями зданий сложной макроструктуры(ЗСМ), определить рациональный способ сопряжения платформ с башнями ЗСМ;
– оценить возможность снижения кренов и усилий в ЗСМ от неравномерной осадки башен с помощью деформационных швов в связях-платформах;
– оценить сейсмостойкость ЗСМ с оболочечными платформами;
– оценить возможность снижения усилий в ЗСМ от сейсмической нагрузки с помощью деформационных швов в связях-платформах.
Научную новизну составляют и выносятся на защиту:
– результаты численных экспериментов над оболочками различного вида и с различными типами выравнивающих конструкций под действием вертикальных нагрузок;
– рациональная форма междуэтажного перекрытия в виде крестовой оболочки с контурными и диагональными выравнивающими ребрами;
– сравнение перекрытия в виде крестовой оболочки с плоским в виде кессонной плиты;
– результаты анализа горизонтальной жесткости зданий с оболочечными перекрытиям различной этажности;
– конструкция связей-платформ между башнями ЗСМ и способы их сопряжения с башнями;
– использование сдвиговых деформационных швов в платформах ЗСМ для снижения кренов и усилий от неравномерных осадок башен и снижения усилий от сейсмической нагрузки.
Внедрение результатов работы. Результаты диссертационной работы приняты к использования в проектировании монолитных железо- бетонных зданий повышенной этажности в OOО “Ремарк” (Санкт-Петербург).
Достоверность результатов работы основывается на использовании строгих упругих КЭ-моделей конструкций и сооружений, а также сертифицированного ПК ING+.
Практическое значение работы состоит в расчетно-конструктивном обеспечении внедрения в строительную практику зданий с оболочечными междуэтажными перекрытиям и платформами.
Это позволяет значительно увеличить шаг колонн каркаса и высотность зданий с одновременными увеличением их надежности, безопасности и комфортности.
Апробация работы. Основные положения диссертационных исследований представлены и одобрены на 61-й, 62-й, 63-й международных научно-технических конференциях молодых ученых (аспирантов, докторантов) и студентов (СПбГАСУ 2008 г., 2009 г., 2010 г.), на 66-й научной конференции профессоров, преподавателей, научных работников, инженеров и аспирантов университета(СПбГАСУ 2009 г.), на 23-й международной конференции математического моделирования в механике деформируемых тел и конструкций. Методы граничных и конечных элементов Санкт-Петербург, Россия 30 сентября 2009 года. На семинаре «Расчет и рациональное проектирование высотных зданий сложной макроструктуры(ЗСМ). Современные программные средства для расчета и проектирование высотных зданий», 10-11 марта 2010 года в СПбГАСУ.
Публикации. По теме диссертации опубликовано 5 печатных работ, в том числе 2 работы в журналах, входящих в перечень ВАК.
Структура и объем работы. Диссертация состоит из введения, пяти глав, заключения, списка литературы, приложения. Общий объем работы 132 страниц, в том числе 77 рисунков, 56 таблиц и список литературы, включающий 124 наименований.
КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ
Во введении обосновывается актуальность темы диссертации, формулируются цели и задачи исследований, приводятся основные положения диссертации, которые выносятся на защиту, обосновывается их научная новизна.
В первой главе диссертационной работы выполнен обзор литературы, посвященной проблемам исследования многоэтажных зданий.
Дана классификация многоэтажных зданий по этажности, по соотношению размеров в трех измерениях, по характеру расположения одномерных и плоских силовых элементов, по конструктивной схеме, по материалу, по технологии возведения.
Рассматриваются основные элементы конструкции, которые часто используются в многоэтажных зданиях. Плоские перекрытия (ребристые с балочными плитами; ребристые с плитами, опертыми по контуру; безбалочные; часторебристые перекрытия; перекрытие по фермам) и оболочечные перекрытия. Вертикальные несущие конструкции много- этажных зданий (колонны; стены и диафрагмы; тонкостенные колонны; ядра жесткости). Рассматриваются фундаменты многоэтажных зданий в зависимости от инженерно-геологических условий и экономики. Существуют 2 типа фундамента: открытый котлован (отдельные фундаменты; ленточные фундаменты под колонны; ленточные фундаменты под стены; сплошные фундаменты ) и закрытый котлован (свайный фундамент).
Наиболее распространен каркасно-стеновой тип несущих систем высотных зданий повышенной этажности (чисто-каркасные здания; каркасно-стеновые конструкции; стоечно-стеновые конструкции; перекрестно-стеновые конструкции; конструкции с тонкостенными колоннами).
Из приведенного обзора видно, что рассмотренные плоские перекрытия достигают пролетов только 9м, перекрытие по фермам применимо лишь с построением технического этажа. Оболочечное перекрытие обладает многими достоинствами: увеличение пролета до12 и более метров, увеличение прочности и надежности здания, активная работа при горизонтальных нагрузках в составе каркаса.
Во второй главе излагаются результаты исследования трех вариантов оболочек ( крестовая, сферическая и трансляционная) с различными подкрепляющими (и одновременно выравнивающими верхнюю поверхность перекрытия) конструкциями. Рассмотрены следующие варианты: 1.Чистая оболочка;2.Оболочка с контурными фермами; 3.Оболочка с контурными и диагональными фермами; 4.Оболочка с контурными, центральными и диагональными фермами; 5.Оболочка с контурными фермами и центральными ребрами сплошного сечения; 6.Оболочка с контурными фермами и сплошными диагональными ребрами; 7.Оболочка с контурными фермами и сплошными центральными и диагональными ребрами; 8.Оболочка со сплошными ребрами по контуру; 9.Оболочка со сплошными центральными и контурными ребрами; 10.Оболочка со сплошными контурными и диагональными ребрами; 11. Оболочка со сплошными контурными, диагональными и центральными ребрами.
Рассматривается наиболее неблагоприятный случай угловой оболочки, не взаимодействующий по бокам с другими оболочками. Работа же в составе многоэтажного каркаса учитывается введением в расчетную схему выше и ниже оболочки четырех колонн длиною hэт/2 с шарнирно неподвижными опорами по концам. (рис. 2)
Расчет производится с помощью ПК ING+, реализующий метод конечных элементов.Скорлупа оболочки и ребра моделируется с использованием плоских оболочечных элементов, составляемых из элементов „балка-стенка” и „плита”(первый имеет в каждом узле 3 степени свободы - две поступательных и одна вращательная, элемент „плита”-2 вращательных и одна поступательная):
[ r ] = [ r(a) ]+ [ r(b) ] (1)
(18x18) (9x9) (9x9)
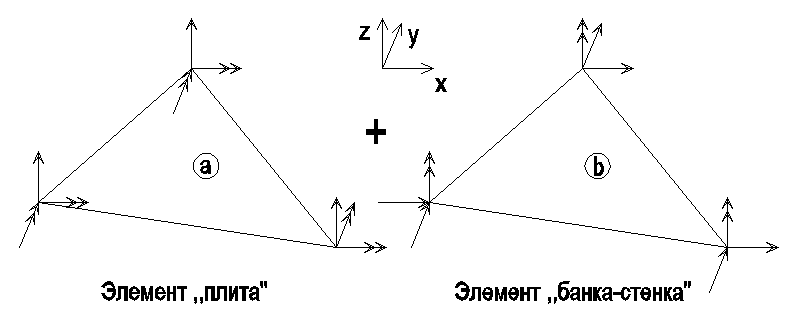
Рис. 1. Элемент
КЭ модель приведена на рис.2:
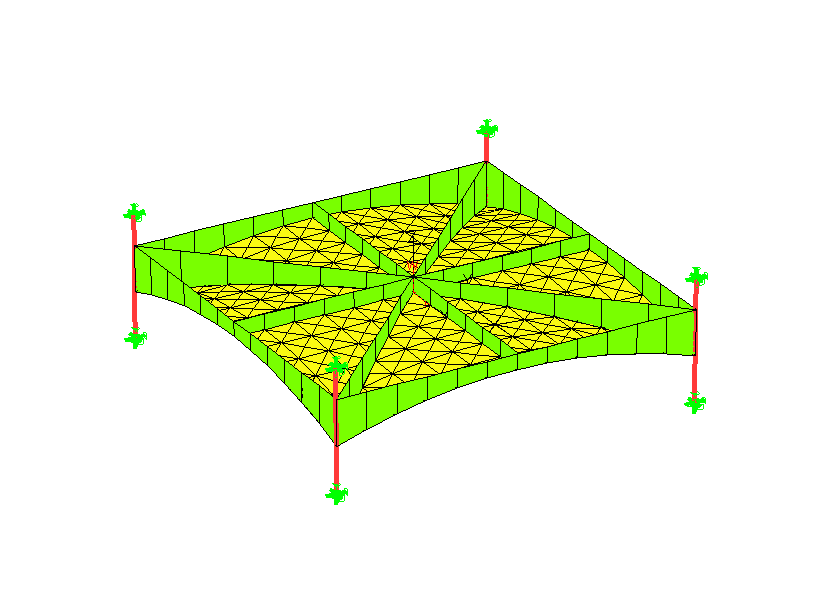
Рис. 2. КЭ-модель
Глобальная система имеет вид:
[K].{Z}={P} (2)
где [K]-матрица жесткости размера[1200x1200], {Z}- матрица перемещений размера[1200x1],{P}- матрица узловых нагрузок размера[1200x1].
Рассматривались крестовые оболочки пролетом 12м при двух значениях стрелы подъема: f=1м (R=18.5м) и f=1.5м (R=12.75м). Затем сферические оболочки и оболочки переноса того же пролета и радиусом 18.5м. Нагрузки : постоянная q=5.54 Кн/м2 и временная p=10.40 Кн/м2.
Результат исследования приведены в таблицах 1,2.
Таблица 1: Перемещения Uz(мм)
| Крестовые оболочки R=18,5м | Крестовые оболочки R=12,75м | Сферические оболочки R=18,5м | Трансляционные оболочки R=18,5м | |
| 1 | -44.63 | -27.05 | -18.9 | -20.7 |
| 2 | -41.03 | -25.2 | -8.19 | -9.85 |
| 3 | -24.72 | -18.06 | -8.54 | -8.53 |
| 4 | -27.54 | -16.07 | -8.46 | -8.45 |
| 5 | -25.39 | -16.85 | -8.47 | -10.1 |
| 6 | -14.42 | -9.3 | -6.62 | -8.32 |
| 7 | -14.14 | -9.28 | -6.99 | -8.69 |
| 8 | -35.31 | -20.37 | -4.42 | -5.31 |
| 9 | -21.59 | -13.82 | -4.57 | -5.41 |
| 10 | -12.97 | -8.37 | -4.20 | -4.96 |
| 11 | -12.5 | -8.32 | -4.33 | -5.01 |
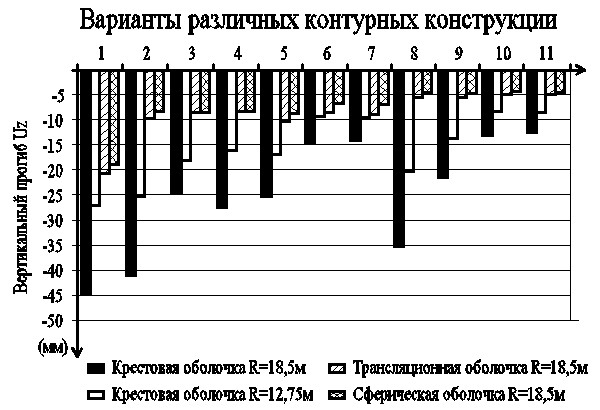
Рис. 3. График сравнения
перемещения Uz различных оболочечных вариантов
Таблица 2 : Напряжение в оболочках, вариант подкрепления 11 (кН/м2)
| Крестовые оболочки R=18.5м | Крестовые оболочки R=12.75м | Сферические оболочки R=18.5м | Трансляционные оболочки R=18.5м | |
| Sr(-) | -5798.5 | -3703.4 | -2051.2 | -2119.9 |
| Sr(+) | +1132.2 | +679.0 | +3760.8 | +4623.1 |
| Ss(-) | -8447.6 | -5622.8 | -7320.9 | -7531.1 |
| Ss(+) | +3340.0 | +2257.8 | +380.5 | +477.8 |
Sr – широтное напряжение, Ss – меридианальное напряжение.
Для большой наглядности перемещения представлены в виде диаграмм (рис. 3)
Из полученных результатов можно сделать следующие выводы :
- Уменьшение стрелы подъема конечно ухудшает НДС крестовой оболочки, но не слишком и ввиду архитектурных преимуществ может быть принята к реализации оболочка f=1.0м.
- Из рис. 3 видно что по жесткости оболочки располагаются так: сферическая оболочка, трансляционная оболочка, крестовая оболочка.
- Для чистой оболочки характерен большой прогиб и большие усилия в колоннах вследствие большого распора.
- Контурные фермы повышает жесткость оболочки, но не уменьшают усилия в оболочках.
- Контурные конструкция в виде ребер сплошного сечения воспринимают распор и уменьшается усилия в оболочках лучше чем контурные фермы.
- В сферических и трансляционных оболочках растягивающие усилия Sr много больше чем в крестовых оболочках, но сжимающие усилия Sr меньше чем в крестовых оболочках.
- Вариант 11 самый лучший из всех вариантов выравнивающих конструкцией.
В целом же видно, что наиболее эффективная в архитектурном отношении крестовая оболочка не на много уступает по прочностным качествам сферической и трансляционной.
Сравнивается работа этой оболочки с кессонным перекрытием(рис.4) с пролетом 12м. Сравнивается НДС каждого перекрытия и расход материалов.Нагрузки оболочечного перекрытия : постоянная q=5.54 Кн/м2 и временная p=4.80 Кн/м2. Нагрузки кессонного перекрытия : постоянная q=2.66 Кн/м2 и временная p=4.80 Кн/м2.
Конструкция кессонного перекрытия (рис.4)
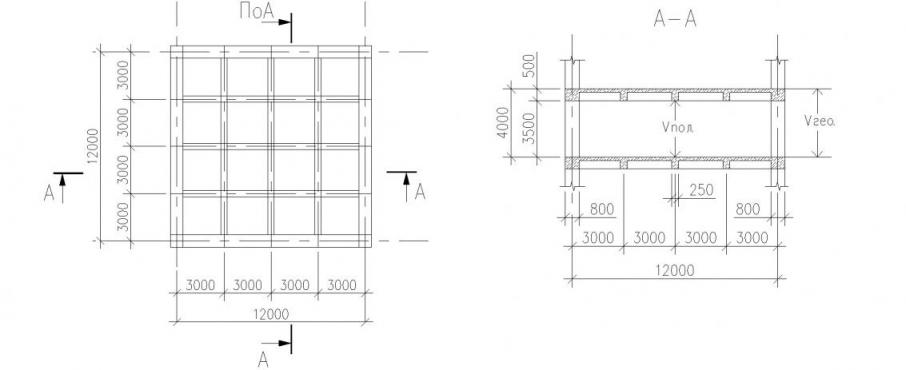Рис. 4. План кессонного перекрытия, разрез А-А
Конструкция крестового оболочечного перекрытия (рис.5)
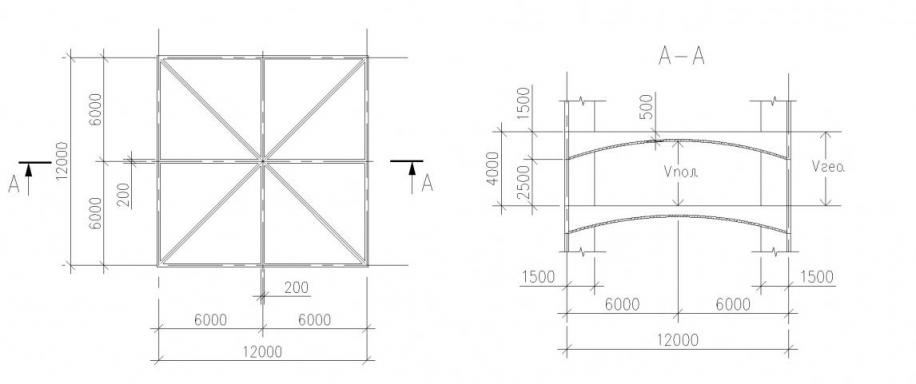Рис. 5. План оболочечного перекрытия, разрез А-А
Таблица 3 : Сравнение напряжений в двух перекрытиях (кН/м2)
| Крестовое оболочечное перекрытие | Кессонное перекрытие | |
Sr(кН/ м2) | -3638.8/+473.8 | -7038.7/+12391.8 |
| Ss(кН/ м2) | -5456.5/+1345.3 | -7038.7/+12391.8 |
| Srs(кН/ м2) | -2252.2/+2251.9 | -4359.5/+4359.5 |
Таблица 4 : Сравнение жесткости и расхода материалов в двух перекрытиях
| Вариант перекрытия | Крестовое оболочечное перекрытие | Кессонное перекрытие |
| Вертикальный прогиб Uz (мм) | 8.37 | 39.3 |
| Объем бетона каждого перекрытия(м3) V(м3) | 30.83 | 38.94 |
| Расход арматуры в скорлупе(кг) | 1370 | 2130 |
| Расход арматуры в ребрах(кг) | 1440 | 3960 |
| Суммарный расход арматуры (кг) (скорлупа+ребро) | 2810 | 6090 |
Из полученных результатов можно сделать следующие выводы:
Жесткость оболочечного перекрытия в 5 раз больше чем жесткость кессонного перекрытия.
Объем бетона оболочечного перекрытия незначительно меньше чем объем бетона кессонного перекрытия. По расходу же арматуры оболочечное перекрытие значительно эффективнее. Можно ожидать значительное превосходство его и по несущей способности.
Следует отметить, что кессонное перекрытие несколько превосходит оболочечное по проценту полезного использования объема здания (Vпол./Vгеом.)*100%. В первом случае он равен 87.5%, во втором – 79.2%.
В третьей главе рассмотрена крестовая оболочка со сплошными контурными, диагональными и центральными ребрами, применёная в одной новой форме многоэтажного здания с оболочечными перекрытиями (рис.6) и исследована его горизонтальная жесткость. Место строительства: Санкт-Петербург, климатический район: по весу снегового покрова (III), по ветровому давлению (II).
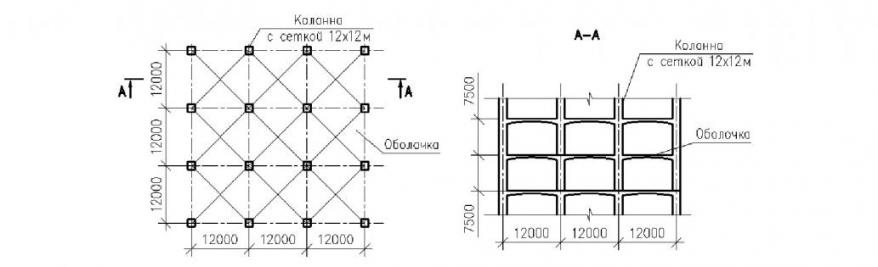
Рис. 6. План и разрез A-A здания
Конструкция колонн : 1-ый вид. (4 колонны находятся в глубине здания ) ; 2-ой вид. (8 колонн находятся на краю здания ); 3-ий вид. (4 колонны находятся на углу здания ) (рис.7). По нормам максимальное горизонтальное смещение верха здания (Uy) должно быть меньше 1/500 высоты здания (H).
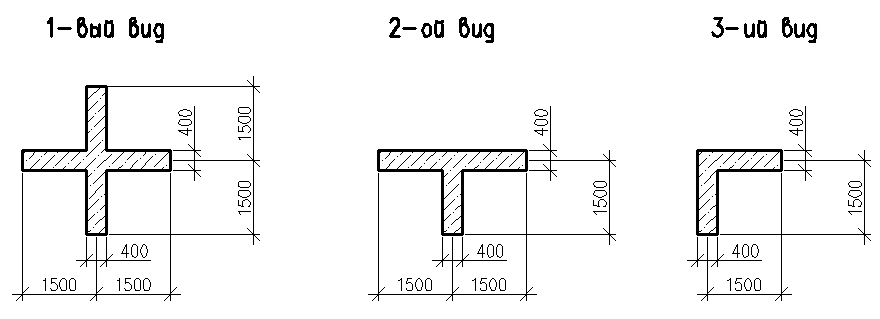
Рис. 7. Конструкция колонн
Определение собственных частот и форм собственных колебаний.Данный этап является наиболее трудоемкой частью расчёта. Матрицы частот и форм собственных колебаний определяются из обобщенной проблемы собственных значений:
(К- 2М). = 0; (3)
det(К- 2М)=0.
где К – матрица жесткости, М – матрица масс
Критерием точности вычисления коэффициентов форм собственных колебаний является удовлетворение их условиям ортогональности, имеющим вид:
i.К. j = 0;(ij); (4)
i.M. j = 0;(ij).
Периоды рассмотриваемых зданий находятся в промежутке T=4 10с.
Рис. 8. Расчетная схема
Таблица 5 : Перемещения верха здания от ветровой нагрузки Uy(мм) и
ускорение верха здания при ветровой пульсации апуль (м/с2)
| Варианты зданий | Uy(мм) | апуль (м/с2) | |
| 1(Н=75м; 10 эт.) | 61 | 0.041 | |
| 2 (H=112.5м; 15 эт.) | 184 | 0.077 | |
| 3(H=150.0м; 20 эт.) | 177 | 0.035 | |
| 4(H=187.5м; 25 эт.) | 362 | 0.076 | |
| 5(H=225м; 30 эт.) | 409 | 0.076 | |
| 6(H=262.5м; 35 эт.) | 651 | 0.09 | |
Результаты вычислений показывают, что до 15 этажей – проходит чисто рамный каркас, до 25 этажей – с центральным ядром, до 30 этажей – с центральным ядром и с диафрагмами по внешнему контуру здания, до 35 этажей – здание не проходит по жесткости даже с раскосами по внешнему контуру здания.
В четвертой главе рассматривается возможность использования ребристых оболочек в качестве связей-платформ между башнями зданий сложной макроструктуры(ЗСМ). Выполнены расчеты двухбашенного ЗСМ на вертикальные и ветровые нагрузки. Конструкция башни: толщина стены 200мм, толщина перекрытия 160мм.
Сравниваются 2 варианта здания:
а) ЗСМ с двумя башнями, которые соединяются друг с другом коробчатой системой с ребрами переменной высоты с верхней пластиной и нижней обшивкой в виде цилиндрической оболочки.(толщина ребер – 200мм, толщина пластины – 160мм, толщина цилиндрической оболочки – 160мм).
б) Только одна башня.
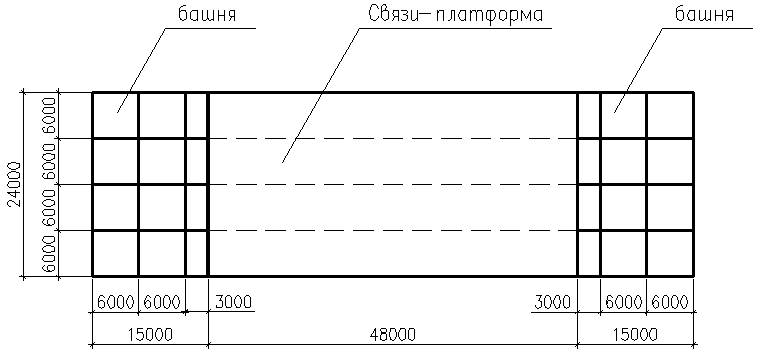
Рис. 9. План здания
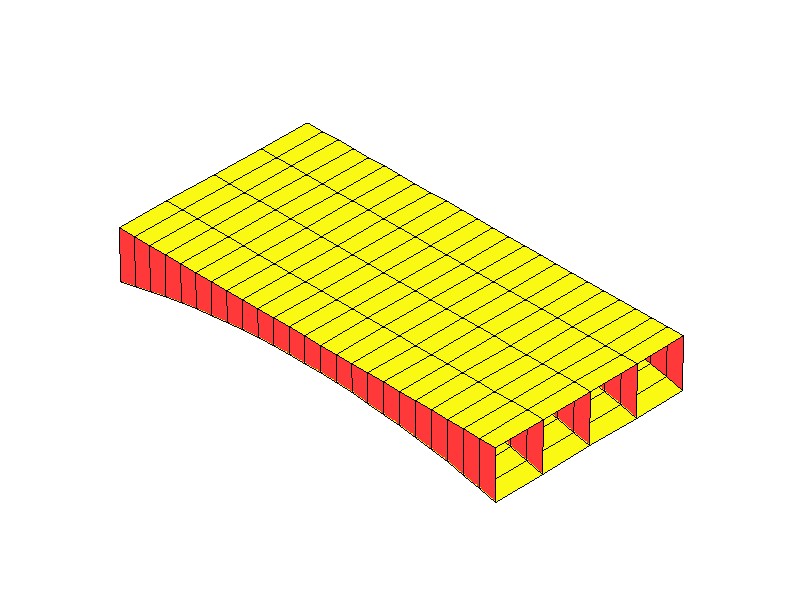
Рис. 10. Конструкция платформы и расположение связи-платформы.
Таблица 6 : Сравнение деформации и усилия в ЗСМ и отдельной башне
| Деформация | Усилия в башнях | Усилия в связи – платформы | ||||
| Варианты | Uу(мм) | Ux(мм) | Sr(кН/м2) | Ss(кН/м2) | Sr(кН/м2) | Ss(кН/м2) |
| ЗСМ | 35.0 | 12.2 | -3360.72/ 4696.35 | -12298.1/ 1016.4 | -3804.25/ 3811.04 | -4396.31/ 2880.4 |
| Одна башня | 35.0 | 56.36 | -2544.07/ 21.75 | -12169.3/ 24.97 | - | - |
Таблица 7 : Сравнение собственных колебаний двух схем конструкций
| N формы | ЗСМ | Одна башня |
| 1 | 2.51 | 3.31 |
| 2 | 2.49 | 2.28 |
| 3 | 1.34 | 0.58 |
Из полученных результатов можно сделать следующие выводы:
ЗСМ по направлению пермычки имеет жесткость больше чем башня в 5 раз и уменьшает период колебания.
Усилия от вертикальной нагрузки в башнях и платформах ЗСМ вполне допустимы.
Большая жесткость может отрицательно сказатья при неравномерной осадке башен. Она может вызвать дополнительные усилия в патформе и крен ЗСМ. Проблему можно решить введением сдвигового деформационного шва в середине платформы. Он будет представлять собой штрабу, с арматурой, герметизированной эластичным материалом или бетоном низкой марки. Ширина штрабы lш зависит от ожидаемых сдвигов и от площади арматурных стержней в сечении. При большой lш штраба может заполняться чередующимися слоями резины и перфорированными металлическими пластинками.
Упругая жесткость вертикального сдвига такого деформационного шва определяется по формуле:
, (5)
где 
- жесткость изгиба отдельного арматурного стержня. Она должна быть достаточно малой, чтобы давать эффект снижения усилий от неравномерной осадки башен.
lш - ширина штрабы.
Таблица 8: Упругая жесткость вертикального сдвига отдельного арматурного стержня с различными длинами арматуры.
| Z(Кн) | ||||
| L= 0.3м | L= 0.5м | L= 0.7м | L= 1.0м | |
| Ф=12мм | 485.0 | 100.0 | 36.5 | 12.5 |
| Ф=16мм | 1530.0 | 316.0 | 115.0 | 39.5 |
| Ф=20мм | 3742.0 | 770.0 | 281.6 | 96.5 |
Выполнен расчет ЗСМ при осадке одной башни Uz =0.1м, при разных длинах деформационного шва: 1.ЗСМ без деформационного шва; 2. ЗСМ с шириной деформационного шва lш =0.3м; 3. lш =0.5м; 4. lш =0.7м; 5. lш =1.0м.
Таблица 9: Сравнение усилия в связи-платформе ЗСМ и кренов при осадке одной башни Uz=0.1м
| Усилия Варианты | Sr(кН/м2) | Ss(кН/м2) | Uxвверх(мм) |
| ЗСМ без шва | -4539.4 /4514.9 | -3046.0/3033.0 | 111.0 |
| ЗСМ с деформационным швом при ширине швы lш =0,3м | -3691.6/3670.5 | -2593.3 /2690.8 | 96.3 |
| ЗСМ с деформационным швом при ширине швы lш =0,5м | -2344.8/2330.3 | -2013.6 /2089.0 | 67.6 |
| ЗСМ с деформационным швом при ширине швы lш =0,7м | -1328.7 /1331.6 | -1303.2 /1341.2 | 42.1 |
| ЗСМ с деформационным швом при ширине швы lш =1м | -623.6/603.7 | -610.5 /633.3 | 18.7 |
Показана возможность снижения кренов и усилий в ЗСМ от неравномерной осадки башен с помощью деформационных швов в связях-платформах. При lш =0.7м усилия снижаются в 3.5 раза, а крен в 2.5 раз. При lш =1.0м усилия снижаются в 7.5 раза, а крен в 6 раз.
Далее сделаны расчеты четырехбашенных ЗСМ, которые соединяются друг с другом оболочечными связями-платформами
Рассмотрим расчеты на горизонтальную (ветровую) нагрузку и вертикальные нагрузки для двух вариантов а), б) расположения платформ (рис.12) и в) Одна башня.
Конструкция оболочечного перекрытия (рис.11). Пролет (размеры в плане) 2a x 2a(a=15.0м); Стрела подъема f (2.0метра, 1/15 пролета); Радиус кривизны оболочек R=57.25м
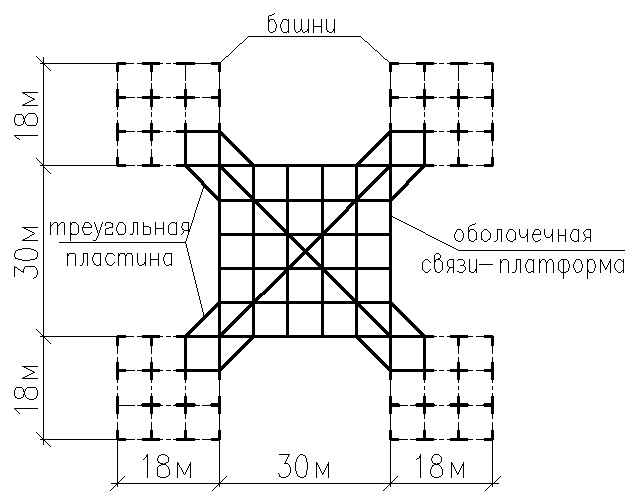
Рис. 11. План здания сложной макроструктуры с оболочечным связями-платформами и конструкция оболочечной связи-платформы
Таблица 10 : Сравнение деформации и усилия в ЗСМ двух схем конструкций
| Деформация | Усилия в ЗСМ | Усилия в оболочках | |||
| Варианты ЗСМ | Ux(мм) | Sr (кН/м2) | Ss кН/м2) | Sr (кН/м2) | Ss кН/м2) |
| ЗСМ с 9 платформами | 118 | -19769.3/ 22738.6 | -29510.1/ 8009.2 | -11871.3/ 5042.1 | -12236.5/ 5030.5 |
| ЗСМ с 4 платформами | 151 | -20165.2 /25464.4 | -25414.0 /6204.1 | -12321.9 /6269.1 | -8505.3 /6180.8 |
| Одна башня | 226 | -3550.5/ 712.7 | -23661.2/ 1334.5 | - | - |
Рис. 12. Два варианта расположения оболочечных связей-платформ.
Из полученных результатов можно сделать следующие выводы:
Как видно, горизонтальная жесткость обеспечивается при 2-х платформах.
Как видно, НДС крестовой оболочки от вертикальной нагрузки вполне приемлемое. Возможно уменьшение высоты опорного сечения ребра до 0.2м, толщина верхней и нижней оболочки (пластины) до 0.1м.
Имеет место концентрация усилий в углах примыкания платформ и это требует усиления участков стен, примыкающих этому углу (t=0.3м).
Исследуем 2 варианта сопряжения оболочечных связей-платформ с башнями ЗСМ.
Вариант 1: Сопряжения оболочечных связей-платформ с башней ЗСМ в одной точке (пересечение ребер оболочки и стен башни, добавив еще усиленную стену с толщиной 0.3м). Для варианта 1, мы рассмотрим 2 варианта оболочки:
1а. Крестовая оболочка: пролет (размеры в плане) 2a x 2a(a=15.0м); Стрела подъема f (2.0метра, 1/15 пролета); Радиус кривизны оболочек R=57.25м.
1б. Сферическая оболочка: пролет (размеры в плане) 2a x 2a(a=15.0м); Стрелы подъема на сторонах контура f1=1м; f2=1м; Радиус
кривизны оболочек R=113.0м.
1) 2)
Рис. 13. Вариант 1 и Вариант 2
Вариант 2: Сопряжения оболочечных связей-платформ с башней ЗСМ в трех точках. Для варианта 2, рассмотрим 2 варианта оболочки:
2а. Крестовая оболочка: пролет (размеры в плане) 2a x 2a(a=21.0м); Стрела подъема f (2.0метра, 1/15 пролета); Радиус кривизны оболочек R=111.25м.
2б. Сферическая оболочка: пролет (размеры в плане) 2a x 2a(a=21.0м); Стрелы подъема на сторонах контура f1=1.5м; f2=1.5м; Радиус кривизны оболочек R=147.75м.
Таблица 11 : Сравнение деформации вариантов ЗСМ
| Форма Варианты | Ux(мм) Горизонтальный прогиб | Uz(мм) Вертикальный прогиб |
| 1а | 151.1 | 105.3 |
| 2а | 118.7 | 86.3 |
| 1б | 117.6 | 95.9 |
| 2б | 147 | 118.5 |
Таблица 12 : Сравнение усилий в оболочке ЗСМ
| Усилия Варианты | Sr(кН/м2) | Ss(кН/м2) |
| 1а | -12321.9 /6269.1 | -8505.3 /6180.8 |
| 2а | -5902.4 /3365.8 | -7177.7 /3340.0 |
| 1б | -10933.0/12595.4 | -34989.2 /1598.8 |
| 2б | -5810.7/8135.7 | -16553,3/1078,9 |
Таблица 13 : Сравнение усилия в ЗСМ
| Усилия Варианты | Sr(кН/м2) | Ss(кН/м2) |
| 1а | -20165.2 /25464.4 | -25414.0 /6204.1 |
| 2а | -15052.5 /21921.9 | -27332.7 /6771.4 |
| 1б | -20581.1 /21052 | -28989.2 /3605.9 |
| 2б | -22529.8 /30829.2 | -33711.6 /11801.8 |
Из таблиц 11; 12; 13 получены несколько выводов
-Если добавить пластину в месте сопряжения оболочки и башни (при 2a=30м) можно повысить горизонтальный жесткость здания и понизить усилия в здании.
-Вариант 2а: ЗСМ с крестовыми оболочечными связями-платформами 2a=42м представляет самый жесткий вариант с наименьшими усилиями.
Выполним расчет ЗСМ при осадке двух башен Uz =0.1м. Ширина деформационного шва влияет на его эффект.
Таблица 14: Сравнение усилия в оболочке и кренов ЗСМ при неравномерной осадке 2х башен в Uz =0.1м
| Усилия Варианты | Sr(кН/м2) | Ss(кН/м2) | Uxвверх(мм) |
| ЗСМ без шва | -3227.3 /3275.3 | -5369.7/5334.0 | 150 |
| ЗСМ с деформационным швом при ширине швы lш =0.5м | -2116.4 /2051.0 | -2930.1 / 2926.1 | 100 |
| ЗСМ с деформационным швом при ширине швы lш =0.7м | -1202.8 /1198.9 | -1438.3 / 1429.8 | 60 |
| ЗСМ с деформационным швом при ширине швы lш =1м | -648.7 /682.5 | -755.6 /750.9 | 34 |
Показана возможность снижения кренов и усилий в ЗСМ от неравномерной осадки башен с помощью деформационных швов в связях-платформах. При lш =0.7м усилия снижаются в 3.0 раза, а крен в 2.5 раза. При lш =1.0м усилия снижаются в 4.5 раза, а крен в 4.5 раза.
В пятой главе выполнен анализ сейсмостойкости зданий сложной макроструктуры (ЗСМ) рассмотренных в главе IV со сдвиговыми деформационными швами посредине платформы и без шва.
 |  |  |  |
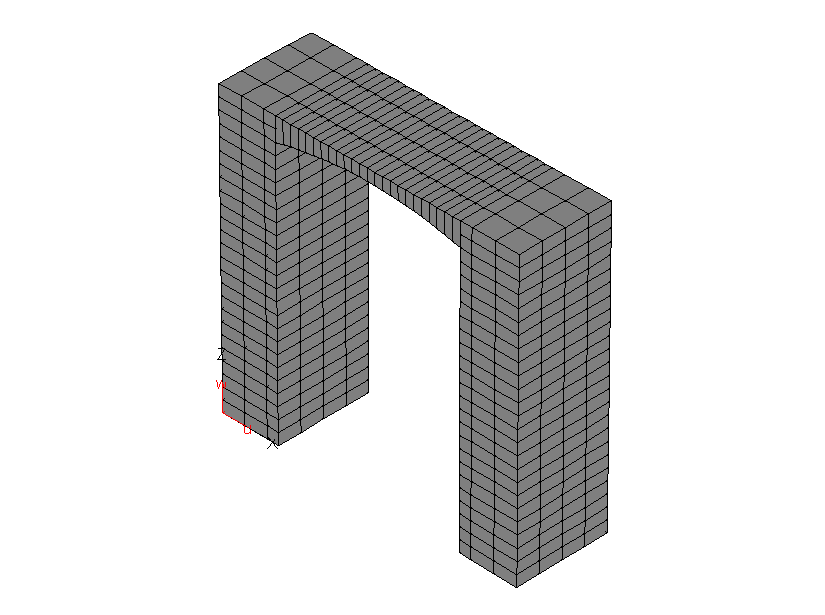| H=75м | H=150м | H=75м | H=150м |
Рис. 14. Расчетная схема здания
Расчётная сейсмичность площадки строительства - 9 баллов; Категория грунта по сейсмическим свойствам - II; Учитывается поступательное сейсмическое воздействие вдоль осей х, у и вращательное воздействие вокруг оси z. Расчёт ведётся по линейно-спектральной теории (методика СНиП II-7-81* строительство в сейсмических районах) при абсолютном жёстком основании.
2ух башенное здание (H=75м)
Таблица 15: Сравнение периодов T (с) колебаний ЗСМ с различными длинами шва
| N формы | Без шва | lш = 0,5м | lш = 1,0м |
| 1 | 0.91 | 1.00 | 1.06 |
| 2 | 0.75 | 0.75 | 0.76 |
| 3 | 0.55 | 0.65 | 0.73 |
Таблица 16: Сравнение напряжений в ЗСМ с различными длинами шва (Поступательная сейсмика).
| Напряжения в башне | Напряжения в перемычке | |||
| Варианты ЗСМ | Sr(кН/м2) | Ss(кН/м2) | Sr(кН/м2) | Ss(кН/м2) |
| Без шва | ±3837.3 | ±10266.9 | ±4078.1 | ±3333.9 |
| lш = 0,5м | ±2083.2 | ±10616.7 | ±1740.9 | ±1487.6 |
| lш = 1,0м | ±1983.78 | ±9924.56 | ±568.9 | ±539.1 |
Таблица 17: Сравнение напряжений в ЗСМ с различными длинами шва (Вращательная сейсмика).
| Напряжения в башне | Напряжения в перемычке | |||
| Варианты ЗСМ | Sr(кН/м2) | Ss(кН/м2) | Sr(кН/м2) | Ss(кН/м2) |
| Без шва | ±949.83 | ±4318.95 | ±949.83 | ±996.22 |
| lш = 0,5м | ±831.6 | ±4082.9 | ±319.66 | ±297.2 |
| lш = 1,0м | ±749.1 | ±3746.7 | ±118.0 | ±101.6 |
В таблицах 16 и 17 приведены напряжения от сейсмического воздействия. Как видно вращательная сейсмика в здании даже без сдвигового шва дает добавку всего в 25 30%. Сдвиговые швы снижают сейсмические напряжения, особенно в перемычках(почти на порядок).
2ух башенное здание (H=150м)
Таблица 18: Сравнение периодов T (с) колебаний ЗСМ с различными длинами шва
| N формы | Без шва | lш = 0,5м | lш = 1,0м |
| 1 | 2.51 | 3.00 | 3.48 |
| 2 | 2.49 | 2.51 | 2.51 |
| 3 | 1.34 | 1.59 | 2.11 |
Таблица 19: Сравнение напряжений в ЗСМ с различными длинами шва (Поступательная сейсмика).
| Напряжения в башне | Напряжения в перемычке | |||
| Варианты ЗСМ | Sr(кН/м2) | Ss(кН/м2) | Sr(кН/м2) | Ss(кН/м2) |
| Без шва | ±12120.9 | ±15737.5 | ±10253.7 | ±10117.5 |
| lш = 0,5м | ±6743.76 | ±15683.4 | ±5490.83 | ±5760.1 |
| lш = 1,0м | ±2966.45 | ±15733.8 | ±1429.67 | ±2182.7 |
Таблица 20: Сравнение напряжений в ЗСМ с различными длинами шва (Вращательная сейсмика).
| Напряжения в башне | Напряжения в перемычке | |||
| Варианты ЗСМ | Sr(кН/м2) | Ss(кН/м2) | Sr(кН/м2) | Ss(кН/м2) |
| Без шва | ±2388.1 | ±4179.7 | ±2495.5 | ±2740.8 |
| lш = 0,5м | ±1423.7 | ±3922.6 | ±1420.7 | ±1540.3 |
| lш = 1,0м | ±818.6 | ±4148.2 | ±355.2 | ±671.3 |
В таблицах 19 и 20 приведены напряжения от сейсмического воздействия. Как видно вклад вращательная сейсмика для более высоких зданий снижается. Также уменьшается эффект сдвигового шва.
4ех башенное здание (H=75м)
Таблица 21: Сравнение периодов T (с) колебаний ЗСМ с различными длинами шва
| N формы | Без шва | lш = 0,5м | lш = 1,0м |
| 1,2 | 2.38 | 2.58 | 2.72 |
| 3 | 2.31 | 2.43 | 2.54 |
Таблица 22: Сравнение напряжений в различных элементах ЗСМ. (Поступательная сейсмика).
| Напряжения в башнях | Напряжения в перемычке | |||
| Варианты ЗСМ | Sr(кН/м2) | Ss(кН/м2) | Sr(кН/м2) | Ss(кН/м2) |
| Без шва | ±4456.2 | ±28078.4 | ±27434.8 | ±10903.9 |
| lш = 0,5м | ±4324.5 | ±30849.1 | ±13971.9 | ±3652.2 |
| lш = 1,0м | ±4088.2 | ±29413.4 | ±4998.7 | ±1063.7 |
Таблица 23: Сравнение напряжений в ЗСМ с различными длинами шва (Вращательная сейсмика).
| Напряжения в башне | Напряжения в перемычке | |||
| Варианты ЗСМ | Sr(кН/м2) | Ss(кН/м2) | Sr(кН/м2) | Ss(кН/м2) |
| Без шва | ±976.7 | ±7447.0 | ±6093.0 | ±2137.8 |
| lш = 0,5м | ±921.4 | ±7051.9 | ±2254.5 | ±1096.9 |
| lш = 1,0м | ±991.8 | ±7643.4 | ±800.7 | ±453.5 |
4ех башенное здание (H=150м)
Таблица 24: Сравнение периодов T (с) колебаний ЗСМ с различными длинами шва.
| N формы | Без шва | lш = 0,5м | lш = 1,0м |
| 1,2 | 5.87 | 6.66 | 7.22 |
| 3 | 5.47 | 5.78 | 6.09 |
Таблица 25: Сравнение напряжений в ЗСМ (Поступательная сейсмика).
| Напряжения в башне | Напряжения в перемычке | |||
| Варианты ЗСМ | Sr(кН/м2) | Ss(кН/м2) | Sr(кН/м2) | Ss(кН/м2) |
| Без шва | ±4772.33 | ±25605.4 | ±34009.9 | ±13960.5 |
| lш = 0,5м | ±3644.99 | ±24595.7 | ±15751.1 | ±4586.22 |
| lш = 1,0м | ±3371.39 | ±22769.6 | ±5623.83 | ±2468.5 |
Таблица 26: Сравнение напряжений в ЗСМ (Вращательная сейсмика).
| Напряжения в башне | Напряжения в перемычке | |||
| Варианты ЗСМ | Sr(кН/м2) | Ss(кН/м2) | Sr(кН/м2) | Ss(кН/м2) |
| Без шва | ±956.4 | ±7372.7 | ±8359.3 | ±2700.6 |
| lш = 0,5м | ±865.6 | ±6686.7 | ±3022.2 | ±1039.3 |
| lш = 1,0м | ±806.2 | ±6245.5 | ±1274.3 | ±667.8 |
Как видно, для четырехбашенных ЗСМ справедливы те же выводы, что и для двухбашенных:
Сравнительный анализ форм и периодов собственных колебаний показывает, что при введении податливого шва в горизонтальном элементе происходит снижение общей жёсткости здания. Вместе с тем изменяются формы собственных колебаний здания.
Развитость ЗСМ в плане требует учета вращательной компоненты сейсмического воздействия. Однако она дает небольшую добавку к сейсмическим напряжениям от поступательных воздействий. Для ЗСМ высотою 75м порядка 25%. С увеличением высоты эта дабавка снижается.
Сдвиговые деформационные швы существенно снижают напряжения от сейсмического воздействия. В башнях напряжения снижаются в 1.52 раза, в перемычках- почти на порядок.
Основные результаты данной работы состоят в следующем:
- Предложены различные конструкции оболочечных перекрытий (крестовые, сферические, трансляционные) для междуэтажных перекрытий зданий.
- Произведено сравнение различных форм оболочечного перекрытия
с пролетом 12м и выбран рациональный по совокупности свойств вариант крестового оболочечного перекрытия (оболочка со сплошными контурными, диагональными и центральными ребрами с стрелой подъема f=1.0м; радиус кривизны оболочек R=18.5м).
- Исследована горизонтальная жесткость конструкций многоэтаж- ного здания с использованием оболочечного перекрытия (габаритные размеры здания в осях 36х36м, высота этажа составляет 7.50м). Найдена максимальная высота здания – в рамном варианте (15 этажей при высоте Н= 112.5м) и в рамно-связевом варианте (30 этажей при высоте Н= 225м).
- Рассмотрен дальнейший способ увеличения горизонтальной жесткости зданий – использование некоторых новых схем зданий сложной макроструктуры (ЗСМ). Достигнуто снижение кренов и усилий в ЗСМ от неравномерной осадки башен с помощью деформационных швов в связях-платформах. Для двух-башенных зданий: при lш=0.7м усилия снижаются в 3.5 раза, а крен в 2.5 раз; при lш=1.0м усилия снижаются в 7.5 раза, а крен в 6 раз. Для четырех-башенных зданий: при lш=0.7м усилия снижаются в 3.0 раза, а крен в 2.5 раза; при lш=1.0м усилия снижаются в 4.5 раза, а крен в 4.5 раза.
- Показана достаточная сейсмостойкость 2х и 4х башенных ЗСМ при 9ти бальном воздействии. Вращательная сейсмика дает вклад в усилия не более 25%. Возможно снижение сейсмических усилий введением сдвиговых деформационных швов. В башнях напряжения снижаются в 1.52 раза, в перемычках- почти на порядок.
Основные положения диссертации опубликованы в следующих работах:
- Данг Хань Ан. Анализ горизонтальной жесткости многоэтажных зданий с оболочечными перекрытиями при сетке колонн 12x12 метров / Данг Хань Ан // Актуальные проблемы современного строительства: сб. материалов 61-й Междунар. науч.-техн. конф. молодых ученых / С.-Петерб. гос. архитур.-строит. ун-т. – СПб., 2008. – Ч. 1. – С. 93-98.
- Данг Хань Ан. Анализ работы оболочек различного вида в составе междуэтажного перекрытия здания / Данг Хань Ан // Докл. 66-й науч. конф. проф., предподавателей, науч. работников, инженеров и аспирантов ун-та / С.-Петерб. гос. архитект.-строит. ун-т. – СПб., 2009. – В 5 ч., Ч. 1. – С. 46-51.
- Данг Хань Ан. Анализ работы междуэтажного оболочечного перекрытия и его влияния на горизонтальную жесткость здания / Данг Хань Ан // Промышленное и гражданское строительство. – 2009. – № 4. – С. 51-52. ( публикация в издании, рекомендованном ВАК ).
- Данг Хань Ан. Сравнение железобетонного междуэтажного перекрытия в виде крестовой оболочки с кессонным перекрытием с опиранием на сетку колонн 12x12м / Данг Хань Ан // Актуальные проблемы современного строительства: сб. материалов 62-й Междунар. науч.-техн. конф. молодых ученых / С.-Петерб. гос. архитектур.-строит. ун-т. – СПб., 2009. – Ч. 1. – С. 194-197.
- Голых О. В., Нгуиен К.Т., Данг Х. А. Упруго-пластические вставки в зданиях сложной макро-структуры, их жесткостные характеристики и влияние на напряженно-деформированное состояние зданий при неравномерной осадке / О. В. Голых, К. Т. Нгуиен, Х. А. Данг // Вестник гражданских инженеров. – 2010. – № 1. – С. 51-55. ( публикация в издании, рекомендованном ВАК ).
