Фильтрационно-температурный режим системы плотина-основание
На правах рукописи
АНИСКИН
Николай Алексеевич
ФИЛЬТРАЦИОННО-ТЕМПЕРАТУРНЫЙ РЕЖИМ
СИСТЕМЫ «ПЛОТИНА-ОСНОВАНИЕ»
Специальность 05.23.07 – Гидротехническое строительство
Автореферат
диссертации на соискание ученой степени
доктора технических наук
Москва 2009
Работа выполнена в Государственном образовательном учреждении высшего профессионального образования Московском государственном строительном университете (ГОУ ВПО МГСУ)
Официальные оппоненты: доктор технических наук
Беликов Виталий Васильевич
доктор технических наук, профессор
Анахаев Кошкинбай Назирович
доктор технических наук
Покровский Геннадий Иванович
Ведущая организация - ОАО «Институт Гидропроект»
Защита диссертации состоится « 29 » сентября 2009 года в 15 час. 30 мин.
на заседании диссертационного совета Д 212.138.03 при ГОУ ВПО Московском государственном строительном университете по адресу:
г. Москва, ул. Спартаковская, д.2/1, ауд. 212.
С диссертацией можно ознакомиться в библиотеке ГОУ ВПО Московского государственного строительного университета.
Автореферат разослан «_____» ________________ 2009 года
Ученый секретарь
диссертационного совета Орехов Г.В.
Общая характеристика работы.
Актуальность темы. В настоящее время планами развития гидроэнергетики и других отраслей водного хозяйства России предусматривается строительство ряда гидроузлов, включающих в свой состав водоподпорные сооружения или плотины различных конструкций. Такие конструкции практически всегда являются весьма ответственными с экономической, социальной и экологической точек зрения. Методы оценки надежности и безопасности гидротехнических сооружений во многом зависят от правильного определения действующих нагрузок и воздействий.
Как правило, каждая плотина является по-своему уникальным сооружением, включающим в свой состав различные конструктивные элементы (например противофильтрационные экраны, ядра из глинистых грунтов, противофильтрационные элементы из негрунтовых материалов –экраны и диафрагмы из бетона, железобетона, асфальтобетона, дренажи, переходные зоны и т.д.). Часто плотина возводится в сложных инженерно-геологических условиях, и ее основания и борта представляют собой весьма разнородную по фильтрационным свойствам структуру, часто с явно выраженной анизотропией свойств, с присутствием в ней трещин, разломов, зон повышенной проницаемости и т.д.. Топография створа строительства, посадка в нем сооружения, система противофильтрационных мероприятий в основании и бортах сооружения часто вызывают сложный пространственный характер фильтрационного потока.
Помимо воздействия фильтрационного потока, гидротехническое сооружение и его основание подвержены температурным воздействиям. В строительный период основным фактором, влияющим на формирование температурного режима бетонных сооружений является экзотермия цемента. Формирование температурного режима бетонного сооружения представляет собой очень сложный, постоянно изменяющийся во времени процесс. Он начинается с момента укладки первого блока или слоя, на которые разбита массивная конструкция и продолжается в эксплуатационный период. Непрерывное изменение температуры бетонного сооружения вызывает изменение его напряженного и деформированного состояния. Трещинообразование в бетоне является наиболее опасным последствием температурных воздействий, которое может вызвать аварийную ситуацию. Даже для плотин из укатанного бетона, несмотря на существенное снижение расхода цемента, проблема температурного трещинообразования стоит достаточно остро. Все это говорит о необходимости расчетного прогноза поведения конструкции на температурное воздействие.
Весьма важной является задача прогнозирования фильтрационно-температурного режима системы «грунтовая плотина – основание» применительно к сооружениям, возводимым в условиях вечной мерзлоты. Вопросы обеспечения устойчивости и надежности таких сооружений невозможно решать без четкого представления о фильтрационном и температурном режимах плотин и их оснований. Отепляющее воздействие фильтрационного потока может вызвать нежелательное чрезмерное оттаивание грунтов, что в свою очередь вызовет увеличение проницаемости плотины и основания и утечкам воды из водохранилища, появление зон локальной усиленной фильтрации, увеличение пористости и осадок сооружения. Примером такого проявления может служить ситуация на плотине Курейской ГЭС, хотя ее первопричиной являются скорее всего технологические факторы. Очевидно, что прогноз фильтрационно-температурного режима должен постоянно вписываться в процесс проектирования, так как при принятии проектных решений необходимо учитывать результаты таких расчетов и при необходимости вносить коррективы в проект.
Все вышесказанное говорит о необходимости проведения тщательных исследований фильтрационного, температурного и, в необходимых случаях, совместного фильтрационно-температурного режимов плотин с основанием.
Целью диссертационной работы явились:
- разработка методики решения фильтрационных, температурных и температурно-фильтрационных задач применительно к системе «плотина-основание» с учетом пространственности, неоднородности и нелинейности свойств материалов плотины и основания, возможной анизотропии и нестационарности процесса;
- создание численных фильтрационных и температурно-фильтрационных моделей гидротехнических сооружений и их оснований;
- анализ влияния отдельных факторов на формирование фильтрационного и температурного режимов плотин и их оснований.
Основные задачи исследований:
- разработка методики, алгоритмов и вычислительных программ расчета на ПЭВМ фильтрационного, температурного и температурно-фильтрационного состояния плотин и оснований с учетом факторов пространственности, нелинейности свойств и нестационарности процесса;
- тестирование разработанной методики и программ расчета на основе сравнения результатов расчета с результатами имеющихся аналитических решений, решений по уже апробированным методикам, результатами экспериментальных исследований и натурных наблюдений;
- создание численных моделей фильтрационного, температурного и температурно-фильтрационного состояний плотин совместно с их основаниями с целью прогноза и дальнейшего анализа влияния отдельных факторов на формирование и изменения состояний сооружений.
Научная новизна работы состоит:
- в разработке методики численного решения пространственных фильтрационных, температурных и совместных фильтрационно-температурных задач для сложных расчетных областей, включающих плотину с основанием и бортовыми примыканиями с учетом нелинейности свойств и нестационарности процесса;
- в полученных результатах численных исследований систем «плотина-основание» применительно к реальным гидротехническим объектам с выводами о работе сооружения и рекомендациями по его конструктивным элементам.
Достоверность научных результатов подтверждена:
- результатами решения ряда тестовых задач, имеющих точное аналитическое решение;
- сравнением результатов, полученных по разработанной методике с результатами других ранее апробированных методов;
- сравнением результатов численных исследований Юмагузинского, Сангтудинского, Курейского гидроузлов с данными натурных наблюдений.
Практическое значение работы и полученных результатов заключается:
- в разработке и внедрении метода расчета фильтрационных, температурных и совместных температурно-фильтрационных задач и на его основе создание пространственных математических моделей системы «плотина-основание», учитывающих природные и инженерно-геологические условия, конструктивные особенности сооружений и технологию их возведения;
- в разработке комплексов вычислительных программ «FILTR» и «TERMIC» на базе метода конечных элементов для решения фильтрационных, температурных и совместных задач;
- в создании численных моделей фильтрационных режимов плотин совместно с основаниями применительно к следующим гидроузлам: Бурейскому, Камбаратинскому, Юмагузинскому, Сангтудинскому, Загорской ГАЭС-2, температурно-фильтрационной модели и прогнозу работы для плотины Курейской ГЭС, в решении задач по прогнозу нестационарных фильтрационных режимов ограждающих дамб Северной и Мезенской ПЭС;
- в использовании результатов численных исследований фильтрационных и температурных режимов гидроузлов в практике проектирования и строительства.
Апробация работы Основные положения методики и результаты исследований докладывались на научно-технических конференциях:
- на научно-технических конференциях МИСИ-МГСУ;
- на Всесоюзном координационном совещании «Прочность и температурная трещиностойкость бетонных гидротехнических сооружений при температурных воздействиях, г. Нарва, 1989;
- на второй, третьей и четвертой научно-технических конференциях «Гидроэнергетика, новые разработки и технологии» в 2006, 2007 и 2008 годах в г. Санкт-Петербурге.
Личный вклад автора Диссертантом непосредственно разработана методика решения фильтрационных, температурных и совместных задач в плоской и пространственной постановках, методика реализована в программных вычислительных комплексах. Проведены численные исследования по Бурейскому, Камбаратинскому, Юмагузинскому, Сангтудинскому, Загорской ГАЭС-2, Курейской ГЭС, решены задачи по прогнозу нестационарных фильтрационных режимов ограждающих дамб Северной и Мезенской ПЭС. Сделан анализ влияния технологических факторов на температурный разогрев бетонного массива при его возведении. Проведены численные расчеты температурных режимов гравитационных плотин из укатанного бетона плотин Хлонг Та Дат (Тайвань) и Шон Ла (Вьетнам) в строительный и эксплуатационный периоды, позволившие дать оценку эффективности принятых параметров возведения.
Публикации. Основные положения диссертации опубликованы в 16 научных работах, в том числе 9 работ в ведущих рецензируемых научных журналах и изданиях, рекомендованных ВАК: в журнале «Гидротехническое строительство» -6, сборнике «Вестник МГСУ» -2, в журнале «Строительные материалы, оборудование, технологии XXI века» -1. Основные положения методики и некоторые результаты исследований помещены в учебник «Гидротехнические сооружения» (издательство АСВ, 2008 год).
На защиту выносятся:
- методика численного решения пространственных фильтрационных, температурных и температурно-фильтрационных задач с учетом множества действующих факторов;
- разработанные алгоритм и комплекс вычислительных программ по решению фильтрационных, температурных и совместных температурно-фильтрационных задач с учетом неоднородности, анизотропии и нелинейности свойств, пространственного характера и нестационарности процессов;
- численные математические модели фильтрации и на их основе анализ работы сооружений и противофильтрационных элементов, выполненные для Бурейского, Камбаратинского, Юмагузинского, Сангтудинского гидроулов, Загорской ГАЭС-2, температурно-фильтрационная модель и прогноз работы на перспективу плотины Курейской ГЭС, результаты решения задач по прогнозу нестационарных фильтрационных режимов ограждающих дамб Северной и Мезенской ПЭС.
Структура и объем диссертации. Работа состоит из введения, пяти глав, заключения и списка литературы. Объем диссертации составляет 415 страниц, из них 244 страницы текста, список литературы состоит из 272 наименований.
Основное содержание работы.
В первой главе дается краткое описание развития теории фильтрации и теплопроводности, методов решения фильтрационных и температурных задач и современного уровня расчетных исследований в этой области.
Теория фильтрации, началом которой можно считать открытие в 1856 году французским инженером Г.Дарси (Darcy, 1856) закона движения фильтрационного потока, нашла свое развитие в работах Буссинеска (1904 )Дюпюи Ж. (1857)Жуковского Н.Е. (1889), Павловского Н.Н.(1922, 1956), Маскета М. (Muskаt 1937, 1949), Лейбензона Л.С.(1947, 1953), Форхгеймера Ф. (1901), Щелкачева В.Н. и Лапука Б.Б.(1949), Полубариновой-Кочиной П.Я. (1952), Шейдеггера А.Э.(1960), Чарного И.А. и т.д.
Огромные масштабы гидроэнергетического и гидромелиоративного строительства в СССР в период с 1920 до 1980 годы потребовали от ученых решения многих задач напорной и безнапорной фильтрации. В начале этого периода внимание исследователей было сконцентрировано на решениях так называемой плоской задачи теории установившейся фильтрации. Решений фильтрационных задач в пространственной постановке в те времена практически не существовало, и в тех случаях, когда фильтрация носила пространственный характер, решение сводилось к плоской задаче с использованием разумной схематизации и упрощений задачи.
К числу точных теоретических методов относится гидромеханика, основанная на математических методах: конформных отображений; функции комплексной скорости; метод, основанный на использовании аналитической теории обыкновенных линейных дифференциальных уравнений; метод, основанный на приведении плоской задачи теории установившейся фильтрации к смешанной задаче теории аналитических функций; обратный метод и др.
Во всех вышеперечисленных работах пористая среда рассматривалась как однородная и изотропная. Однако в природе достаточно часто встречаются грунты с анизотропными свойствами. В работах Дахлера Р. (1933), Шаффернака Ф.(1933), Ризенкампфа Б.К. (1938), а затем Аравина В.И. (1937) и др. рассматривались задачи фильтрации в анизотропной пористой среде, решение которых сводится к решению в фиктивной изотропной пористой среде с последующим возвращением в исходную область. Задачи безнапорной фильтрации в анизотропной однородной пористой среде рассмотрены в работах Полубариновой-Кочиной П.Я.(1940), а затем Михайлова Г.К. (1951).
Множество работ с использованием аналитических методов было посвящено изучению влияния неоднородности среды на фильтрацию. Наибольший практический интерес представляли так называемые слоистые среды, состоящие из конечного числа однородных слоев произвольной конфигурации.
Лишь частные результаты были получены теоретическими методами при решении задач нелинейной фильтрации, когда скорость фильтрации и градиент напора связаны нелинейной зависимостью (например, по зависимости Смрекера). Такие задачи могут быть решены методом последовательных приближений линейных задач, или, по предложению Христиановича С.А.(1940) методом ЭГДА.
Точные решения задач фильтрации получены для достаточно ограниченного круга задач. Все это, а также потребность в более доступных инженерных методах расчета различных фильтрационных задач вызвало развитие приближенных теоретических методов их решения.
Одним из таких методов является метод фрагментов, основные положения которого были разработаны Павловским Н.Н.(1931) для расчета установившейся фильтрации в земляных плотинах различной конструкции на горизонтальном водоупоре. Второй областью применения метода фрагментов является изучение напорной и полунапорной фильтрации в основаниях бетонных плотин. Этому вопросу посвящены работы Павловского Н.Н.(1936), Давидовича В.И.(1937), Аравина В.И. и Нумерова С.Н. (1947,1955), Недриги В.П.(1956) и др.
Метод фрагментов подготовил почву для разработки широко применяемого и сегодня для приближенных оценок фильтрации метода фильтрационных сопротивлений, который был впервые сформулирован в 1951 году Нумеровым С.Н. и, почти одновременно с ним Борисовым Ю.П. (1951). Метод фильтрационных сопротивлений использован для решения задач фильтрации в работах Нумерова С.Н.(1953,1954), Аравина В.И.. Нумерова С.Н. (1953,1955), Павловской Л.Н. (1964), Шестакова В.М. (1964), Чугаева Р.Р. (1955) и др.
Однако, несмотря на множество перечисленных выше теоретических методов, их использование не позволяло считать окончательно решенной задачу фильтрации в грунтовых плотинах и основаниях гидросооружений ввиду многообразия и сложности их конструкций, инженерно-геологических и гидрогеологических условий и т.д.
Поэтому помимо теоретических методов, параллельно шло развитие экспериментальных или модельных исследований. Одно из направлений экспериментальных исследований фильтрации – моделирование процесса путем пропускания вязкой жидкости в щели между двумя параллельными пластинками (так называемые щелевые лотки). Эта методика была использована в работах Аравина В.И., Замарина Е.А., Каранфилова Т.С. Следует отметить, что моделирование фильтрации с помощью вязкостной аналогии достаточно широко использовалось не только в СССР, но и в других странах: США, ГДР, Румынии и др.
Получили очень широкое развитие аналоговые методы. Наиболее широкое применение нашел метод электро-гидродинамических аналогий (метод ЭГДА), основанный на математической аналогии течения электрического тока в электропроводном материале и фильтрации жидкости в пористой среде.
С развитием вычислительной техники начинается эффективное использование численных методов решения фильтрационных задач, которые позволяют получить эффективные решения многих задач теории фильтрации, в том числе и в деформируемых средах. Большинство работ, выполненных до 1967 года, относятся к задачам плановой неустановившейся и нелинейной фильтрации.
Использование одного из численных методов – метода конечных разностей (МКР) при фильтрационных расчетах было впервые предложено в 1924 году Николаи Е.Л. (задолго до появления ЭВМ). Большинство последовавших за этим работ с использованием МКР были посвящены численному решению уравнения Буссинеска.
Метод математического моделирования получил в последние десятилетия широкое распространение, что связано с развитием численных методов и вычислительной техники. Если на первых этапах развития и применения численных методов превалировал МКР, то позднее наибольшее распространение получил метод конечных элементов (МКЭ). Преимущество последнего метода над МКР объясняется его вариационной сущностью, большими возможностями при моделировании областей сложной геометрии и неоднородностью свойств материалов, возможностью использовать элементы различных типов. Основной недостаток МКЭ – большой порядок разрешающей системы уравнений, что вызывало определенные сложности при расчетах сложных систем в 70-80 –х годах прошлого столетия. В связи с этим появился метод «локальнных вариаций» (Черноусько Ф.Л., Банничук Н.В.), нашедший применение при решении статических и сейсмических задач для бетонных и грунтовых плотин.
Дальнейшим развитием численных методов стало появление метода суперэлементов (МСЭ), в котором расчетная область разбивается на отдельные подструктуры, каждая в свою очередь разделяется на отдельные части и т.д., пока не образуются достаточно малые и простые по форме «базисные элементы». Другой вариант совершенствования численных методов, также уменьшающий порядок разрешающей системы – метод «граничных элементов» (МГЭ).
В настоящее время появилось множество комплексов, позволяющих решать набор задач (статических, динамических, фильтрационных, температурных и т.д.) в плоской и пространственной постановках. В качестве примеров использования таких комплексов можно назвать комплекс «DRENA» (ВНИИГ им. Б.Е.Веденеева), «CRISP-PATH FEM» (Чехия, д-р М.Долежалова), расчетный комплекс «ANSYS». Достаточно широкое применение нашел программный комплекс «Visual MODFLOW», разработанный канадской фирмой Waterloo Yelrogeologic, использующийся для создания пространственных геофильтрационных моделей, комплекс вычислительных программ «Земля» (институт «Гидропроект») и др..
Тем не менее, решение пространственных фильтрационных задач для системы «плотина-основание», имеющей, как правило, сложную геометрию, с учетом множества факторов (неоднородность, анизотропность свойств материалов, нелинейность и нестационарность процесса, наличие в системе трещин, разломов, зон повышенной проницаемости и т.д.) является весьма трудоемкой задачей.
Аналогичное развитие претерпела современная теория теплопроводности и методы решения температурных задач. Эволюция методов решения температурных задач аналогична развитию фильтрационных методов. В первой половине XX века широко используются аналитические и графо-аналитические методы. С середины века интенсивное развитие гидротехники и необходимость решения практических задач в СССР вызывает «бум» модельных исследований и аналоговых методов. Появление вычислительной техники и ее развитие во 2-ой половине XX столетия вызывают разработку численныых методов применительно к решению температурных задач.
Вопросы, связанные с определением температурного режима бетонных конструкций с применением различных методов рассматриваются в работах Александровского С.В., БеловаА.В., Васильева П.И., Гутмана С.Г., Дзюбы К.И., Ламкина М.С., Маслова Г.Н., Орехова В.Г., Фрадкиной Н.И., Фрида С.А., Чилингаришвили Г.И., Цыбина А.М., Fanelli M. и Giuseppetti G. и многих других авторов.
Промышленное освоение районов с суровыми климатическими условиями начиная с первой половины ХХ века вызвало интенсивное строительство грунтовых плотин и дамб, использующихся на объектах энергетики, водоснабжения, горнодобывающей промышленности и т.д. Особый интерес и внимание исследователей-гидротехников в этот период занимала совместная фильтрационно-температурная задача Вопросам формирования температурных режимов грунтовых плотин и их оснований в таких условиях посвящены работы П.А.Богословского, Е.С.Гоголева, Е.Н.Горохова, В.В.Знаменского, И.С.Клейна, Н.А.Мухетдинова, С.В.Соболя, А.П.Ставровского, А.М.Цыбина, Р.Т.Шугаевой, В.И.Белана, Г.Л.Шульца, Февралева А.В., Янченко А.В. и др.
Приведенный обзор исследований по изучению фильтрационных, температурных и «совместных» режимов гидротехнических сооружений свидетельствует об огромном интересе к этой проблеме со стороны ученых, проектировщиков, инженеров-практиков. Разработаны и использованы в исследованиях разнообразные методики решения задач. В последние десятилетия наиболее широкое применение нашли численные методы (особенно, метод конечных элементов -МКЭ). Несмотря на обилие методов, и программ расчета, необходимо и в дальнейшем развивать методы и программы расчета для более полного решения множества практически значимых задач и проверки многих теоретических предположений.
Во второй главе излагаются методика и алгоритмы решения фильтрационно-температурных задач. Математические уравнения, описывающие движение фильтрационного потока в пористой среде и распространение тепла, относятся к так называемым уравнениям математической физики. В математической литературе часто встречаются такие их определения, как уравнения теории поля или дифференциальные уравнения с частными производными 2-го порядка
Основное дифференциальное уравнение в частных производных неустановившейся фильтрации в пространственной постановке записывается в виде (уравнение Пуассона):
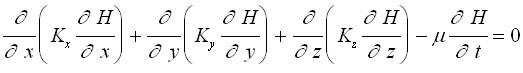 , (1)
, (1)
где Н=f(x,y,z,t) – искомая напорная функция в расчетной области, изменяющаяся во времени t; Кх, Ку, Кz - коэффициенты фильтрации по направлениям координатных осей X, Y, Z; - коэффициент водоотдачи грунта.
Прямое численное решение уравнения (1) является весьма трудоемкой задачей. В настоящей работе отыскание напорной функции происходит в ходе минимизации некоторого, специальным образом подобранного функционала Ф, для чего и создан специальный расчетный аппарат, основанный на синтезе МКЭ и МЛВ (метод локальных вариаций).
В основе метода локальных вариаций лежит принцип: минимум функционала Ф всей системы последовательно отыскивается среди минимумов локальных областей, образующихся вокруг рассматриваемых узлов. Решение осуществляется методом последовательных приближений.
На основании теоремы Эйлера функционал Ф (для случая трёхмерной задачи) имеет вид:
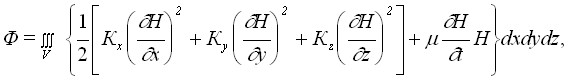 (2)
(2)
Решение фильтрационной задачи сводится к отысканию напорной функции Н(x, y, z, t), которая была бы непрерывной внутри замкнутой области V, удовлетворяла бы начальным и граничным условиям, и доставляла бы минимум функционалу Ф (2).
В случае использования граничного условия 2-го рода (на границе области задан удельный фильтрационный расход q) и учета фильтрации в трещинах скального основания минимизируемый функционал включает дополнительные члены:
Ф = 
+ ![]() +
+ 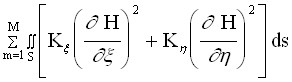 , (3)
, (3)
где где - поверхность расчетной области, на которой выполняется граничное условие 2-го рода, ![]() - коэффициенты проницаемости трещиноватого элемента по направлению осей локальной системы координат.
- коэффициенты проницаемости трещиноватого элемента по направлению осей локальной системы координат.
Предлагаемая методика позволяет достаточно просто решать нелинейные фильтрационные задачи. В этом случае согласно предложению Смрекера связь между скоростью фильтрации и градиентом записывается в виде:
V = - КфJ n, (4)
где n - показатель степени, определяемый по экспериментальным данным (изменяется в интервале от 1,0 до 0,5); при n = 1,0 выполняется закон Дарси; при n = 0,5 имеем турбулентный закон фильтрации; если 1,0< n< 0,5 имеет место переходный режим от ламинарного к турбулентному.
В общем случае составляющие скорости фильтрации по координатным осям i=x, y, z могут быть представлены в следующем виде (формула Смрекера): Vi = - Ki Ji n = - Ki Jin-1 Ji = - Kiн Ji (5)
где Kiн - нелинейные коэффициенты фильтрации по осям координат i=x, y, z.
Задача в нелинейной постановке решается методом последовательных приближений. Первоначально решается линейная фильтрационная задача, из которой определяются величины градиентов. Затем, в соответствии с зависимостью (5) определяются нелинейные коэффициенты фильтрации Kiн= Ki Jin-1 и процесс минимизации возобновляется. Итерационный процесс заканчивается в случае неизменности величин Kiн на текущем и предыдущем шагах (с заданной точностью).
Решение температурной задачи базируется на решении аналогичного уравнению (1) основного дифференциального уравнения теории теплопроводности, которое с учетом наличия внутренних источников тепла (экзотермии цемента) записывается в виде:
 , (6)
, (6)
где t = t (x, y, z,) - искомая температурная функция; ax, ay, az - температуропроводность материала по направлению координатных осей X,Y,Z; - время; c - удельная теплоемкость бетона; - плотность бетона; Э – удельное тепловыделение цемента; Ц - расход цемента в 1 м3 бетона.
Решение дифференциального уравнения (6) аналогично решению основного дифференциального уравнения теории фильтрации (1) сводится к минимизации следующего объемного интеграла при заданных начальных и граничных условиях:
Ф = 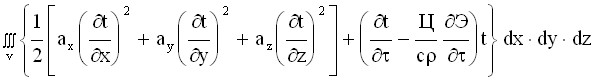 +
+
+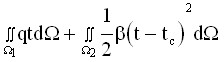 , (7)
, (7)
где 1, 2 - поверхности расчетной области, на которой выполняются соответственно граничные условия 2 (задание на поверхности удельного теплового потока q) и 3 (теплообмен с окружающей средой, имеющей температуру tc) родов.
Решение совместной фильтрационно-температурной задачи при равенстве температуры твердого скелета грунта и температуры фильтрующей жидкости в любой точке области фильтрации сводится к решению известного уравнения Фурье-Кирхгофа:
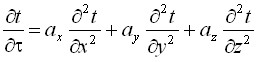 -
- ![]()
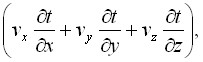 (8)
(8)
t(x,y,z,) – температура твердого тела (материала плотины или основания); – время; ах, ау, z – коэффициенты температуропроводности твердого тела, насыщенного водой, по осям х, у, z; vx, vy, vz – компоненты скорости фильтрации по осям х,у,z; Св, Ст – удельная объемная теплоемкость воды и твердого тела; в, т – плотности воды и твердого тела.
Решение дифференциального уравнения (8) равносильно минимизации функционала:
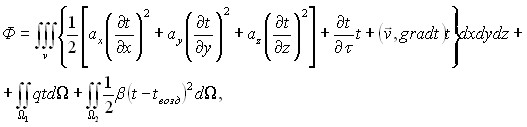 (9)
(9)
где  - скалярное произведение векторов фильтрационной скорости и температурного градиента;
- скалярное произведение векторов фильтрационной скорости и температурного градиента; ![]() - поверхности расчетной области, на которой выполняются соответственно граничные условия 2-го и 3-го рода.
- поверхности расчетной области, на которой выполняются соответственно граничные условия 2-го и 3-го рода.
Для всех типов рассмотренных задач (фильтрационных, температурных и совместных) минимизация соответствующих функционалов в расчетных областях производится методом конечных элементов в локально-вариационной постановке.
В качестве основной элементной базы используются объемный 8-узловой и плоский 4-узловой элементы произвольной формы, позволяющий достаточно точно аппроксимировать исследуемую область. Для моделирования трещин используются 4-узловой элемент произвольной формы (пространственная задача) и 2-х узловой линейный элемент (плоская задача).
На основе изложенной методики были составлены программные комплексы для ПЭВМ расчета фильтрации "FILTR" и расчета температурного режима «ТЕRМIC». В состав программных комплексов входят несколько подпрограмм: подпрограмма подготовки исходной информации; подпрограмма проверки исходной информации; подпрограмма минимизации функционала в расчетной области; подпрограмма обработки к печати полученных результатов; подпрограмма визуализации полученных результатов.
Сетки разбивки на конечные элементы при современном уровне развития вычислительной техники могут включать до 800000 узлов для объемных задач и до 100000 узлов для плоских задач (при необходимости количество узлов может быть увеличено.
В третьей главе приводятся результаты численных исследований фильтрационного режима системы «плотина-основание», которые проводились на примере реальных гидротехничеких объектов и позволили сделать ряд важных обобщений.
Грунтовая плотина Юмагузинского гидроузла- с центральным ядром из суглинка и боковыми призмами из гравийно-галечникового грунта имеет максимальную высоту 70 метров. Плотина возведена в сложных с точки зрения фильтрации инженерно-геологических условиях. Основание плотины в русловой части и, особенно, на правобережной пойме характеризуется крайней неоднородностью фильтрационных свойств: коэффициенты фильтрации различных слоев грунта изменяются от 0,3 до 90 м/сут. Аллювиальные отложения в пределах правобережной поймы представляют собой напластование грунтов с различными фильтрационными характеристиками суммарной глубиной до 40 метров. Целью проведенных исследований было сопоставление плоских и пространственных решений, проведение анализа влияния таких факторов, как фильтрационная неоднородность, размеры противофильтрационных элементов. Исследование фильтрационного режима плотины и основания Юмагузинского гидроузла проводились в несколько этапов с 1999 по 2006 год.
Первый этап фильтрационных исследований (1999-2000 год) проходил в период начальной стадии проектирования грунтовой плотины Юмагузинского гидроузла и начала ее строительства. Для оценки эффективности принятых в проектном варианте противофильтрационных элементов (ПФЭ) и их необходимости были проведены расчеты в плоской и пространственной постановках для двух конструктивных вариантов: с устройством ПФЭ в основании и без них. Проектом предусматривалось устройство 2-х рядной инъекционной противофильтрационной завесы под плотиной и в бортовых примыканиях, дополнительной 5-ти рядной завесы в основании ядра в русловой части створа и «стены в грунте» на участке залегания аллювиальных отложений на правобережной пойме.
На рис.1, а представлено плановое сечение расчетной области фильтрации в основании под плотиной со следами эквипотенциальных поверхностей по результатам решения пространственной задачи. Видно, что фильтрационный поток имеет пространственный характер движения за исключением русловой части створа. На береговых склонах и в бортовых примыканиях движение потока направлено в обход противофильтрационных элементов и к руслу реки в нижнем бьефе. В результате расчетов на первом этапе была определена необходимость устройства глубинной цемзавесы ориентировочно до отметки ~120,0. Выявлено возможное положение депрессионной поверхности и дана оценка фильтрационному расходу. На рис.1, б дана картина пространственной фильтрации в левобережном примыкании и основании плотины Юмагузинского гидроузла для варианта с ПФЭ.
Для определения возможных интервалов изменения параметров фильтрационного режима (расхода, градиентов, положения депрессионной кривой) была сделана попытка создания математической модели с учетом возможного интервала изменения коэффициентов фильтрации грунтов основания и уровня верхнего бьефа. При этом использовалась методика факторного анализа.
Была составлена упрощенная модель основания плотины (с объединением слоев грунта с близкими значениями коэффициента фильтрации). Выделено шесть слоев грунтов, для каждого из которых на основании инженерно-геологических данных определялись максимальные, минимальные и средние коэффициенты фильтрации. Так, для галечника эти значения соответственно равны 100, 10 и 55 м/сут, для суглинков и глин – 0,4, 0,01 и 0,205 м/сут.
В плоской постановке задача решалась для пяти характерных сечений. В каждом из рассматриваемых сечений в качестве варьируемых факторов рассматривались коэффициенты фильтрации грунтов основания, количество которых принималось в соответствии с конкретными инженерно-геологическими условиями. В качестве откликов рассматривался удельный фильтрационный расход в основании и максимальный градиент напора по оси цементационной завесы или стены в грунте.
Для каждого расчетного сечения была построена матрица планирования, описывающая варианты расчетов с соответствующими сочетаниями уровней факторов. Для каждого варианта были получены функции откликов. На основе полученных функций откликов были построены номограммы, удобные для анализа результатов натурных наблюдений и прогноза параметров фильтрационного потока. Также они могут быть использованы при решении прямых задач.
На основе полученных зависимостей удельных фильтрационных расходов от факторов по сечениям была получена зависимость для суммарного фильтрационного расхода, проходящего через створ гидроузла (в пределах выделенной области фильтрации), которая после сокращения маловлияющих членов имеет вид:
Q = 1,5 + 0,051Х1+0,164 Х2 + 0,61Х5 + 0,052 Х2Х5 (10)

При этом величина суммарного расхода изменяется от Q =0,72 м3/сек (при минимальных коэффициентах фильтрации) до Q =2,5 м3/сек (при максимальных коэффициентах фильтрации). Как видно из уравнения (10), наибольшее влияние на величину суммарного расхода оказывает фактор Х5 (коэффициент фильтрации известняка в пределах Кф = 5,030,0 м/сут) и фактор Х2 (коэффициент фильтрации суглинков и глин в пределах Кф = 0,010,4 м/сут).
В связи со значительным количеством слоев основания с изменяющимися в широком диапазоне коэффициентами фильтрации и трудоемкостью расчетов в пространственной постановке, принято условие, что все материалы одновременно рассматриваются или с максимальными или с минимальными коэффициентами фильтрации. Рассматривались следующие факторы: Х1 – уровень воды в верхнем бьефе (Х1 =-1 соответствуют отметке НПУ 260,0; Х1 =+1 – отметке ФПУ 270,0); Х2 – значения коэффициентов фильтрации грунтов, залегающих в основании плотины (Х2 =-1 – все значения коэффициентов фильтрации; Х2 =+1 – все значения коэффициентов максимальны). Уровень нижнего бьефа принимался равным отметке 210,0. В качестве откликов, как и в предыдущих исследованиях, рассматривались величины фильтрационного расхода и максимального градиента напора по оси противофильтрационного устройства. Были получены следующие функции откликов:
- для расхода: Q = 1,87 + 0,2Х1 + 1,125Х2 + 0,115 Х1 Х2 (11)
- для градиента: Jx = 18,375 + 1,625Х1 + 9,125Х2 + 0,875 Х1 Х2 (12)
Можно отметить следующие различия в результатах решения задач в плоской и пространственной постановках: величина суммарного фильтрационного расхода, полученного из пространственной задачи несколько выше величины, полученной из плоского решения. При максимальных значениях коэффициентов фильтрации грунтов основания величина суммарного расхода в объемной задаче составляет 3,31 м3/сек, в плоской – 2,5 м3/сек. При минимальных значениях коэффициентов фильтрации эти значения соответственно равны 0,83 м3/сек и 0,72 м3/сек. Увеличение суммарного расхода в пространственной задаче получено за счет обходной фильтрации в бортовых примыканиях.
Использование методики факторного анализа позволило оценить величины параметров фильтрационного потока при любых возможных значениях коэффициентов фильтрации грунтов основания (в принятом интервале между минимальными и максимальными значениями). Полученные функции откликов и построенные на их основе номограммы могут быть использованы при мониторинге за работой гидросооружения и основания, что дает возможность оценить действительные средние значения коэффициентов фильтрации по слоям. Построение подобного типа номограмм позволят более обоснованно проектировать сооружения, а при наличии статистических данных по коэффициентам фильтрации грунтов возможна вероятностная оценка фильтрационных параметров.
Последующие исследования (2001 –2006 г.г.) были вызваны уточнением данных по инженерно-геологическому строению основания, свойствам грунтов тела плотины и конструкции противофильтрационных элементов в основании и бортах сооружения. Была предпринята попытка создания более совершенной и достоверной численной фильтрационной модели, учитывающей уточненные инженерно-геологические условия, реальные параметры и конструкции как самой плотины и других сооружений, входящих в состав гидроузла (эксплуатационного водосброса, ГЭС) и противофильтрационных устройств в основании. Совершенствование программных и вычислительных возможностей также позволило значительно увеличить частоту аппроксимационной сетки метода конечных элементов (в 2001 году сетка МКЭ пространственной задачи состояла всего из 9729 узлов и 8398 элементов. Количество узлов и элементов новой сетки МКЭ в каждом поперечном оси плотины сечении равно соответственно 2721 и 2595. Общее количество узлов и элементов аппроксимационной сетки составило соответственно 179586 и 168675.
Результаты решения фильтрационной задачи сравнивались с натурными данными. Это сравнение показало, что математическая геофильтрационная модель достаточно адекватно отражает реальную ситуацию: величины напоров, полученные в результате пьезометрических измерений достаточно близки (за небольшими исключениями) к расчетным в большинстве пьезометров: в 10 из 15 относительная разница не превышает 6,8%, в 6 пъезометрах относительная разница находится в пределах 5%.
Проведенные исследования фильтрационного режима плотины и основания Юмагузинского гидроузла позволили сделать следующие вывод: учет пространственности фильтрационного потока оказывает большое влияние на общую картину фильтрации и величины ее параметров. Это говорит о необходимости решения фильтрационных задач в пространственной постановке (даже для таких относительно широких створов, как у Юмагузинской плотины).
Фильтрационные исследования Сангтудинского гидроузла велись параллельно активному проектированию и строительству гидроузла. Необходимо было дать прогноз возможного фильтрационного режима и оценку принятым противофильтрационным мероприятиям. Сведения об инженерно-геологической ситуации и фильтрационных свойствах пород основания на этом этапе были неполными и часто ориентировочными.
Согласно рассмотренному первоначальному варианту в русловой части створа и на левом берегу в месте расположения современных аллювиальных пород (галечник с включением валунов с гравийно-песчаным заполнителем) с большим коэффициентом фильтрации-Кф=85 м/с предусмотрено устройство «стены в грунте». Помимо этого по всему створу устраивается площадная цементация под ядром и глубинная противофильтрационная завеса.
Некоторые результаты решения пространственной задачи в виде распределения линий равных напоров в поперечном и горизонтальном сечениях представлены на рис. 2. Можно отметить, что в горизонтальном сечении (рис.2,в), проходящем по отметке 500,0 эффект пространственности фильтрационного потока сказывается на локальных участках основания в бортовых примыканиях, причем на правом берегу этот эффект значительнее, что вызвано особенностями рельефа и геологическим строением. В бортах непосредственно примыкающих к современному и старому руслам движение фильтрационного потока имеет ярко выраженное направление к русловой части створа. На более низких отметках пространственный характер потока более выражен. На всем пространстве под плотиной его движение направлено к руслу реки.
На основании проведенных на первом этапе численных исследований были сделаны следующие выводы. «Стена в грунте» в русловой части плотины (рис. 2,а) и левобережном примыкании в рассмотренном варианте работает неэффективно. Также малоэффективна глубинная цемзавеса в правобережном примыкании. Был сделан вывод о целесообразности изменения конструкций противофильтрационных элементов в русловой части и бортовых примыканиях Фильтрационный расход через выделенную область в основании грунтовой плотины и ее береговые примыкания составляет примерно 5.7 м3/сек.
На момент исследований в 2008 году были произведены некоторые уточнения в части фильтрационных характеристик грунтов основания, несколько изменена конструкция противофильтрационных элементов в
плотине и ее основании. Проведены тщательные натурные наблюдения за фильтрационным режимом, на основании чего создана база данных (показания пьезометров, величины фильтрационных расходов), позволяющая
анализировать фильтрационные процессы в конструкции и основании.
По результатам натурных наблюдений при уровне верхнего бьефа 554,6 фильтрационный расход на 05.05.08 составлял 4,2 м3/с, а на 30.06.08 – 4,0 м3/с, что несколько выше расхода, полученного по численной геофильтрационной модели «Института Гидропроект». Данная модель дала соответственно 3,4 м3/с и 3,45 м3/с, причем на долю обходной фильтрации в бортах приходится 1,13 м3/с и 1,03 м3/с.
На основании модели МГСУ 2006 года при уровне верхнего бьефа 554,6 величина расхода и его распределение по створу может быть оценена следующим образом: суммарный фильтрационный расход составляет примерно 4,39 м3/с из них на долю обходной фильтрации приходится ~ 1,0 м3/с. Как видно, прогнозные значения по фильтрационным расходам, полученные в МГСУ в 2006 году несмотря на ограниченный объем информации и произошедшие изменения в конструкции и оценке фильтрационных свойств грунтов плотины и основания, достаточно хорошо корреспондируются с величинами натурных и модельных исследований «Института Гидропроект». На основании исследований, проведенных на участке создания «стены в грунте» (бурение скважин с отбором керна, сейсмическое просвечивание между скважинами, поверхностного сейсмопрофилирование и резистивиметрия на выборочных участках) был установлен факт отсутствия сплошности в противофильтрационном элементе. Были установлены «окна» в едином фронте противофильтрационного элемента на русловом участке. Для имитации реальных условий была составлена численная модель руслового фрагмента с учетом имеющихся данных по качеству противофильтрационных элементов. Моделируемая часть руслового фрагмента рассматривалась от сечения ПК 2+10 до сечения ПК 4+05. Была составлена сетка разбивки расчетной фильтрационной области на конечные элементы. При этом моделировалась зона повышенной проницаемости или зона разрыва между скважинами струйной и глубокой цементации (см. рис. 4).
Были проведены фильтрационные расчеты для выделенного фрагмента при различных значениях коэффициента фильтрации «окна» в «стене в грунте». По результатам численных исследований, было сделано предположение, что проницаемость окна «стены в грунте» близка к
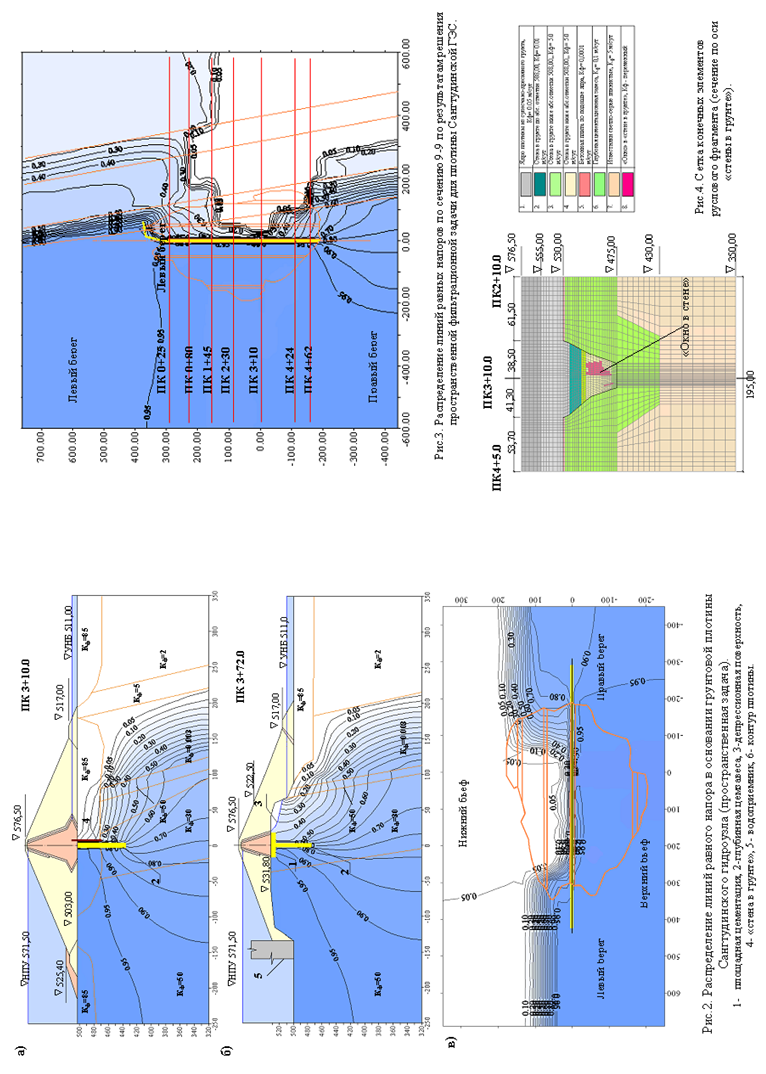
проницаемости галечникового грунта в основании. Возможно, и сам галечник обладает большей проницаемостью, заложенной в фильтрационные модели МГСУ и «Института Гидропроект», что может быть вызвано и процессами фильтрационных деформаций, произошедших в подземном контуре сооружения.
Учитывая, что к моменту исследований фильтрационный расход упал до ~ 2 м3/с вероятно, был сделан вывод, что грунт «в окне» имеет коэффициент фильтрации ориентировочно 1020 м/сут, так как обходную фильтрацию можно оценить в 1 м3/с.
Дальнейшие фильтрационные исследования были проведены с целью создания более совершенной пространственной геофильтрационной модели системы «плотина- основание». Пространственная модель включала в себя численную модель руслового фрагмента (см. выше), в правобережном примыкании моделировалось устройство противофильтрационной глубокой завесы в соответствии с проектом, более детально воспроизведен рельеф в нижнем бьефе с учетом устройства отводящик каналов ГЭС и водосбросов. Была существенно сгущена сетка МКЭ: количество узлов и элементов сетки было увеличено соответственно до 451584 и 433675. Расчеты проводились для двух уровней верхнего бьефа: отметки 554,6 и отметки НПУ 571,5.
Увеличение расчетной области, введение дополнительных пачек грунтов основания, некоторые изменения фильтрационных свойств и более детальное воспроизведение топографии несколько изменили фильтрационную картину. Фильтрационный поток имеет сложный пространственный характер. Получена значительная разница между плоскими решениями в сечениях и пространственной задачей.
На рис.3 дана картина изменения фильтрационного напора в горизонтальном сечении расчетной области на отметке 500,0. Как видно, под плотиной основное падение напора происходит на протифильтрационной завесе. В берегах основным сопротивление является пласт глинистого грунта (Кф=0,003 м3/с).
Полученные на численной модели результаты сравнивались с результатами натурных данных (показания установленных пьезометров) и численной модели института «Гидропроект». Сравнение показало в целом удовлетворительное совпадение с натурными данными по состоянию на 30.06.2008 и данными модели «Гидропроекта». В большинстве пьезометров (в 13 из 16) расхождения с натурой при величине действующего напора 46 м находятся в пределах от 0,03 м (пьезометр 117) до 4,3 м (пьезометр ПО 1-3.7). Несколько больше расхождения в пьезометрах ПО 1-4.10 (5,16 метров) и 123 (7,1 метра). Самое большое расхождение в 22,2 м, как и в модели института «Гидропроект» (23,5 м), получено в пьезометре НП 2.2, расположенном в русловом аллювии в основании ядра плотины. Высокие значения уровня в пьезометре НП 2.2 могут быть вызваны заниженной водопроницаемостью руслового аллювия или завышенной проницаемостью инъекционной завесы. Возможно, это связано с возникновением в аллювиальном слое закольматированной зоны с меньшими значениями коэффициента фильтрации.
Параллельно исследованиям в 2009 году проводились работы по снижению фильтрационного расхода в русловой части створа. Были продолжены работы по устройству скважин трехрядной противофильтрационной завесы со стороны верхнего бьефа от «стены в грунте». Кроме того, было проведено «запесочивание» проницаемого слоя, располагающегося в русловой части под ядром плотины. В результате этих работ величина фильтрационного расхода к апрелю 2009 года была снижена с 4 м3/с до 1,2 м3/с, причем по оценкам ~0,8 м3/с приходится на русловую часть и ~0,4 м3/с – на оставшуюся часть створа. Таким образом, можно утверждать, что в проведенных численных исследованиях была завышена проницаемость «бухарских» известняков (пачка № 23-25 с коэффициентом фильтрации Кф= 50 м/сут выше отметки 460,0 и Кф= 5 м/сут ниже этой отметки по всему створу) и, возможно, глубокой противофильтрационной завесы. Была проведена очередная калибровка численной модели и проведены расчеты при значении коэффициента фильтрации «бухарских» известняков Кф= 15 м/сут выше отметки 460,0. Это привело к снижению фильтрационного расхода до ~1,2 м3/с, что соответствует наблюдаемому. Дальнейшее совершенствование численной модели может быть связано с локальными уточнениями характеристик пород на основании натурных данных. Конечно, только численные исследования могли позволить провести настолько подробные исследования в столь сложных геологических условиях.
Часто негативные последствия фильтрации сказываются на устойчивости грунтовых склонов. В частности, весьма остро стоит вопрос об устойчивости склонов, на которых располагаются водоводы ГАЭС. Исследование фильтрационного режима склона и ограждающей дамбы ГАЭС проведено на примере сооружений Загорской ГАЭС-2. Пристальное внимание к фильтрационному режиму склона вызвано проблемами, возникшими при строительстве Загорской ГАЭС-1.
Грунты, складывающие верхнюю часть склона характеризуются достаточно низкими коэффициентами фильтрации (порядка 10-2 м/сут и ниже). Влияние колебаний уровней бассейнов, происходящие за достаточно короткие промежутки времени, будет сказываться незначительно и только вблизи бассейнов, не сказываясь на общем фильтрационном режиме всего склона. Вследствие этого решалась задача установившейся фильтрации для наихудшего случая: в верхнем бассейне максимальный уровень НПУ 266,5 метров, в нижнем бассейне УМО 152,5 метра (величина расчетного фильтрационного напора составляет 114,0 м).
По результатам фильтрационных расчетов склона водоводов можно отметить: движение фильтрационного потока из верхнего аккумулирующего бассейна имеет ярко выраженный пространственный характер. Это положительно сказывается на фильтрационном режиме склона, что приводит к значительному снижению депрессионной поверхности по сравнению с результатами плоской фильтрационной задачи. Четко просматривается влияние оврага №2 и других понижений рельефа, играющих роль естественного дренажа. Учет пространственности также значительно снизил фильтрационное давление на водоприемник ГАЭС.
Помимо склона водоводов несомненный интерес предтавляет фильтрационный режим грунтовой дамбы верхового бассейна. Были проведены исследования фильтрационного режима дамбы верхнего аккумулирующего бассейна Загорской ГАЭС-2 в плоской постановке с учетом возможной отсыпки боковых призм дамбы слоями различной проницаемости, что вызвано стремлением к всепогодной технологии укладки грунта. При этом рассматривалось влияние таких факторов, как толщины отсыпаемых слоев, их протяженность, расположение водосборного коллектора в низовой призме дамбы. Решалась задача установившейся фильтрации при уровне воды в верхнем бассейне ГАЭС на уровне НПУ 266,5 метров для 2-х сечений дамбы: ПК 26+00 и ПК+11.00. Следует отметить, что рассматривался наихудший с точки зрения фильтрации случай: уровень воды верхнего бассейна ГАЭС рассматривался на отметке НПУ.
Конструкция дамбы в сечении ПК 26+00 представляет собой следующее. Вдоль верхового откоса дамбы выполнен экран из суглинистого грунта толщиной 5,0 метров с коэффициентом фильтрации Кф=0,005 м/сут. По оси дамбы устроен вертикальный дренаж толщиной 2,0 м из грунта с коэффициентом фильтрации Кф=1,0 м/сут. Вдоль основания под низовой призмой и частично под верховой уложен горизонтальный дренаж толщиной 2,0 м из грунта с коэффициентом фильтрации Кф=1,0 м/сут. Горизонтальный дренаж сопрягается с вертикальным и заканчивается водосборным коллектором. В проведенных расчетах варьировалось удаленность коллектора от оси дамбы. Верховая и низовая призмы дамбы представляют собой слоистую конструкцию, уложенную чередующимися слоями одинаковой толщины, выполненными из грунтов с различной проницаемостью: с коэффициентами фильтрации Кф=0,5 м/сут (укладываемый в любых погодных условиях) и Кф=0,01 м/сут. Варьировалась толщина укладываемых слоев (1 и 2м).
Аналогичные исследования были проведены для сечения дамбы в ПК 11+00, имеющей аналогичную конструкцию. Исследования фильтрационного режима дамбы ВАБ ГАЭС позволили сделать вывод о возможности послойной укладки грунта различной проницаемости при заданных характеристиках грунтов и нормальной работе противофильтрационных элементов.
Конструкциями, для которых особый интерес представляет решение фильтрационной задачи в нелинейной постановке, являются взрывонабросные плотины. Грунтовые плотины, возводимые методом направленного взрыва, при некоторых условиях могут дать существенную экономию по сравнению с другими конструкциями водоподпорных сооружений. При этом существенно снижается объем дорогостоящих подготовительных работ (отпадает необходимость в устройстве сети дорог, карьерного хозяйства) и количество землеройной и транспортной техники.
Вместе с тем, недостатком таких конструкций является повышенная проницаемость, что может привести к большим фильтрационным потерям.
Особенностями фильтрационной задачи взывонабросной плотины является нелинейная зависимость между скоростью фильтрационного потока и градиентом фильтрационного напора. Еще одной особенностью взрывонабросной плотины является неравномерность распределения геотехнических свойств грунта (в том числе и коэффициента фильтрации) как по высоте конструкции, так и от борта к борту, что обусловлено неравномерным уплотнением в результате навала грунта от действия направленного взрыва. Исследования влияния этих особенностей на фильтрационный режим взрывонабросной плотины, а также оценка эффекта «пространственности» проводились на примере плотины Камбаратинского гидроузла-2. Кроме того, было необходимо оценить фильтрационные потери через эту конструкцию и возможность ее эксплуатации (хотя бы временной) без устройства противофильтрационного элемента.
Камбаратинская плотина возводится направленным взрывом в сложных топографических условиях. Каньон плотины имеет сложную форму – в борту правого берега имеется естественная выемка, в пределах которой длина плотины по гребню достигает 400 метров. Затем по течению реки каньон сужается до 200 метров (на отметке НПУ) и после сужения наблюдается вновь плавное расширение каньона в сторону нижнего бьефа (рис. 7, а). На основании прогноза изменения геотехнических свойств грунта по высоте в рассмотренной плотине было выделено пять зон с различными коэффициентами фильтрации и показателями степени от Кф = 2.5 см/сек ( = 0.6 ) в верхних слоях и в бортовых примыканиях до Кф = 0.3 см/сек ( = 0.95 ) в нижней части плотины. Некоторы результаты пространственного расчета фильтрации в теле плотины даны на рис.7. На рис. 7,а показаны в плане следы поверхностей равных напоров и поверхностей тока на депрессионной поверхности и низовом откосе плотины. Линии равных напоров (эквипотенциали) проведены с шагом 0.1 в долях относительной величины статического напора. Следы поверхностей тока построены по касательным к проекциям вектора скорости на плоскость чертежа. Можно отметить четко выраженный пространственный характер движения фильтрационного
потока с отклонением линий тока к правому борту каньона. К нижнему бьефу линии тока концентрируются к русловой части створа. Направление движения потока на депрессионной поверхности иллюстрируется на рис. 7, б, где по продольным сечениям построены эпюры составляющей скорости Vx. Как видно из данного рисунка, со стороны верхнего бьефа поток в плане направлен в сторону выемки в правобережном борту, где максимальная составляющая скорости Vx достигает величины 0.48 см/сек. Затем, в сечении В-В на выходе из выемки, поток меняет направление на противоположное, а по мере приближения к нижнему бьефу вновь изменяет направление, повторяя изгибы правого борта каньона. В результате, на выходе фильтрационного потока в нижний бьеф ниже кривой высачивания депрессионной поверхности на низовой откос образуются два встречных потока, смыкающихся в районе продольного сечения VI-VI. Максимальная выходная скорость здесь равна 1.87 см/сек.
Положение депрессионной поверхности, следы поверхностей равных напоров и тока показаны также в продольном сечении V-V (рис. 7. в). Следует отметить, что поверхности тока имеют угол наклона к напорной грани несколько меньше, чем 90 градусов, что обусловлено использованием нелинейного закона фильтрации. В верховом клине сечения V-V

наблюдаются изломы следов поверхностей тока и небольшие искривления эквипотенциалей на границах зон с различными коэффициентами фильтрации.
Для поперечного сечения А-А, параллельного плоскости XOZ, построены положение депрессионной поверхности, следы поверхностей тока и направления проекций векторов скорости фильтрации на плоскость XOZ (рис. 7, г). Можно отметить достаточно плавный характер следов поверхностей тока в верховом сечении А-А, отклонение фильтрационного потока в сторону правобережной выемки. По мере продвижения потока в сторону нижнего бьефа и, особенно, в низовом сечении С-С, наблюдается интенсивная циркуляция воды в вертикальном направлении, которая образуется в результате взаимодействия встречных потоков.
Сформировавшаяся в плотине депрессионная поверхность имеет сложную пространственную форму. Как видно из рис. 7, г, положение депрессионной поверхности изменяется от борта к борту: ее средний уклон в направлении от верхнего к нижнему бьефу уменьшается от правого борта к левому борту, и в продольном сечении IX-IX она становиться горизонтальной. Одновременно наблюдается понижение уровня депрессионной поверхности от центра потока к бортам (сечения А-А, В-В, С-С). Высота выклинивания на низовой откос также непостоянна – в русловом сечении V-V она достигает максимальной отметки 21.0 м, уменьшаясь к бортам каньона.
Величина фильтрационного расхода для контроля определялась по двум сечениям – входному (вдоль верхового откоса) и выходному (вдоль низового откоса). Невязка по величинам расхода составила 5% при его средней величине 17 м3/сек. При этом получено неравномерное распределение расхода по высоте плотины. Основная часть потока фильтрует через две верхние зоны с максимальными коэффициентами фильтрации, а в нижних зонах значения скорости резко уменьшаются. В связи с этим была дана рекомендация о возможном снижении проницаемости верхних слоев за счет их замыва мелкозернистым грунтом или формирования более высокой плотины, что позволит исключить высокопроницаемый материал из фильтрационной области. При условии снижения проницаемости верхних слоев до уровня нижних слоев следует ожидать снижение фильтрационного расхода в 2.5 – 3.0 раза.
Нелинейность закона фильтрации значительно сказывается на проницаемости материала в теле плотины, которая в зонах, близких к верхнему бьефу, оказывается в 30-50 раз выше, чем со стороны нижнего бьефа. Это приводит к «запиранию» фильтрационного потока со стороны нижнего бьефа и подъему депрессионной поверхности по сравнению с режимом линейной фильтрации, где величина коэффициента фильтрации не зависит от градиента.
Для сравнения результатов этим же методом была решена плоская задача фильтрации через русловое сечение плотины. Определена величина удельного фильтрационного расхода – 0.085 м3/сек. При пересчете на объемную задачу в самом узком сечении (В-В) получен полный расход порядка 15 м3/сек. При этом в плоской задаче точка высачивания получена на 14 метров ниже, чем в русловом сечении V-V пространственной задачи (рис. 7, в). Это объясняется сильным сжатием фильтрационного потока в узкой части каньона.
Получены также другие отличия результатов пространственной и плоской задач. Так, в плоской задаче получено более равномерное распределение компоненты скорости Vy по глубине потока, что объясняется перераспределением плановых скоростей в пространственной задаче. Максимальные скорости на выходе фильтрационного потока в нижний бьеф в плоской задаче оказались в 1.2 раза ниже, чем в пространственной.
Как видно из сопоставления результатов, учет пространственности при расчетах фильтрации для взрывонабросных плотин необходим, что обусловлено особенности формирования тела плотины в результате навала грунта. Для рассмотренной конструкции это еще необходимо и из-за сложной формы каньона. Следует отметить, что решение задачи при условии нелинейных фильтрационных свойств вызывает «наведенную» анизотропию.
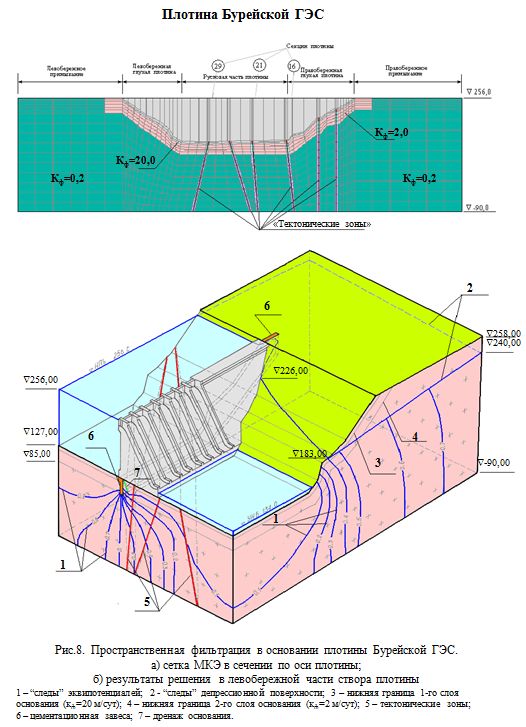
Исследования о влиянии трещин и разломов на фильтрационный режим скального основания плотины в плоской и пространственной постановках были выполнены на примере плотины Бурейского гидроузла. Скальное основание рассматривалось как дискретная среда, состоящая из цельных пористых блоков с различной водопроницаемостью и системы трещин определенной проницаемостью. Согласно использованной геофильтрационной модели ЦСГНЭО ОАО "Институт Гидропроект" каждая "тектоническая зона" представляет собой трехслойное образование: в центре располагается так называемая «зона сместителя» (зона дробления), заполненная материалами с определенной водопроницаемостью. По бокам от «зоны сместителя» располагаются «зоны влияния», представляющие собой области повышенной трещиноватости и водопроницаемости. В конечно-элементной аппроксимации в плоской и в пространственной постановках «зоны сместителей» моделировались трещинными элементами, а «зоны влияния» – обычными конечными элементами с толщинами, равными толщинам зон.
Фильтрационная задача в плоской постановке решалась для 3-х сечений по осям секций №№ 16, 21 и 29 бетонной плотины. Учет «тектонических зон» изменил распределение линий равных напоров и увеличил удельные расходы на 1019 % под секциями № 16, 21 и на 50% в основании секции № 29. Общий фильтрационный расход с учетом "тектонических зон" в русловой части, полученный из решения плоских задач, ориентировочно равен примерно 0,16 м3/с.
Для описания геометрии массива основания бетонной плотины Бурейского гидроузла для пространственной фильтрационной задачи был выделен массив основания. Сетка МКЭ выделенной расчетной области фильтрации в продольном разрезе по оси плотины представлена на рис 8,а. В основании также выделены шесть наиболее крупных тектонических зон. В проведенных расчетах принимались максимальные пределы изменения коэффициентов фильтрации и значения толщин «зон влияния». Под напорной гранью бетонной плотины моделировалась цементационная завеса, доходящая в русловой части до отметки 85.0. За цементационной завесой воспроизводился глубинный дренаж основания.
На рис. 8,б дана картина пространственной фильтрации в левобережной части створа. Положение депрессионной поверхности фильтрационного потока показано в виде ее следов на поверхностях, образующих поверхность основания и границы расчетной области. Также показаны "следы" поверхностей равных напоров.
Без учета «тектонических зон» величина фильтрационного расхода через расчетную область составляет величину ~0,313 м3/сек, большая часть которого приходится на основание под русловой частью створа (~0,160 м3/сек). Учет "тектонических зон" с большой водопроницаемостью значительно увеличил значения расходов под русловой часть и под правобережной глухой частью плотины, где сосредоточены эти нарушения. Расход под русловой частью плотины увеличился с 0,160 м3/сек до 0,709 м3/сек, под правобережной глухой частью плотины с 0,059 до 0,501 м3/сек. Величина суммарного расхода в створе увеличилась с 0,313 до 1,365 м3/сек. Полученная величина фильтрационного расхода Qф 1,4 м3/сек при учете "тектонических нарушений" с максимальной водопроницаемостью, по видимому, является близкой к верхнему пределу, так как в расчеты вводились максимальные значения коэффициентов фильтрации и толщины
зон с повышенной водопроницаемостью. Эта величина может быть использована при выборе контрольного параметра при натурных измерениях фильтрационного расхода. Проницаемость «тектонических зон» значительно влияет на величину фильтрационного расхода. Так, при уменьшении величин коэффициентов фильтрации «зон влияния» в 10 раз по сравнению с максимальными принятыми, расход снижается до 0,607 м3/с (из них 0,215 м3/с – под русловой частью).
В целом по проведенным исследованиям фильтрационного режима основания плотины Бурейской ГЭС можно сделать следующие выводы. Решение пространственной фильтрационной задачи позволило получить картину распределения фильтрационного потока с учетом расположения «тектонических зон» в объеме расчетной области. Основная часть фильтрационного расхода проходит в основании русловой части и правобережной глухой плотины, где и сосредоточены крупные трещины. Приведенное исследование позволило рассмотреть в новой постановке движение фильтрационного потока в скальном основании. Движение воды рассмотрено с использованием закона Дарси для цельных пористых блоков и гидравлических решений Г.М.Ломизе при движении потока по крупным трещинам, которые в то же время могут играть роль дренажа. Такой прием привел к увеличению фильтрационного расхода. Учет трещиноватости повысил фильтрационный расход до 1,4 м3/с.
Нестационарный фильтрационный режим грунтовых плотин, создающих бассейны приливных электростанций (ПЭС), или так называемых «отсечных» дамб вызывает особое внимание при проектировании. Особенности такой конструкции в фильтрационном смысле заключаются в следующем. Дамба работает в двустороннем нестационарном режиме: уровень воды больше то со стороны моря, то со стороны бассейна. При этом период колебания достаточно короткий (для Северной ПЭС он составляет 12
часов). Водонепроницаемость дамбы должна обеспечивать фильтрационный расход через ее створ несоизмеримо меньший по сравнению с полезным объемом бассейна. В противном случае возможно снижение напора на агрегаты ПЭС и, как следствие, снижение выработки электроэнергии. В качестве основного материала для ограждающих бассейн дамб чаще всего используются крупнозернистые грунты (горная масса), имеющие значительную проницаемость. Поэтому приходится решать задачу по устройству противофильтрационного элемента дамбы, что удорожает конструкцию.
Исследования фильтрационного режима дамбы Северной ПЭС в губе Долгая проводились с целью оптимизации ее возможной конструкции. Дамба имеет максимальную высоту 42,55 метра (отметка гребня 13,55, нижняя отметка поверхности основания со стороны бассейна –29,0, со стороны моря -21,0). В основании залегают слои различной мощности и проницаемости.
Графики изменения во времени уровней моря и бассейна в случае малофильтрующей дамбы (когда фильтрационные потери через ограждающую дамбу незначительны и практически не сказываются на уровне воды в бассейне ПЭС) приведены на рис.9, а. Рассматривалось четыре варианта конструкции грунтовой ограждающей дамбы: однородная дамба из горной массы, каменно-набросная дамба с толстым трапецеидальным ядром толщиной 10 м по верху и 60 м по основанию, каменно-набросная дамба с прямоугольным ядром толщиной 20 м и каменно-набросная дамба с трапецеидальным ядром толщиной по верху 5 м и по низу 20 м.
Решалась нестационарная фильтрационная задача с колебаниями уровней со стороны моря и бассейна с заданным графиком изменения уровней (см. рис.9). Временной интервал разбивался на шаги по времени, равные 1 часу.
При решении фильтрационной задачи учитывалось, что в горной массе имеет место турбулентная фильтрация, и использовалась известная формула (6) зависимости скорости фильтрации и фильтрационного градиента. Для гравийно-галечниковых и песчано-гравийных грунтов рассматривалась линейный закон фильтрации, и использовался, соответственно, закон Дарси.
Для первого вариантта дамбы при коэффициенте фильтрации горной массы Кф= 65000 м/сут или 75 см/с фильтрационные потери настолько велики, что пришлось параллельно с решением фильтрационной задачи также определять ориентировочные положения уровней воды в бассейне. Для этого на каждом временном шаге определялся удельный фильтрационный расход. В том случае, если движение фильтрационного потока было направлено из бассейна в море, оценивался полный фильтрационный расход в течение часа через всю дамбу (примерная длина эквивалентной дамбы с ее высотой 42,55 м в рассматриваемом сечении была принята 500 м). Полученные фильтрационные потери вычитались из объема бассейна. По батиграфической характеристике бассейна уточнялся уровень воды в бассейне, закладываемый в расчет на следующем временном шаге. Аналогично корректировался уровень бассейна и в случаях, когда фильтрационный расход направлен из моря в бассейн. В результате был получен график изменения уровней в бассейне с учетом фильтрационных потерь, представленный на рис. 9, б.
Из сравнения графиков на рис. 9 видно, что в случае с сильнофильтрующей дамбой из горной массы значительно снижается перепад между уровнями воды в бассейне и море. Если для варианта с малофильтрующей дамбой (рис. 9, а) этот перепад достигает почти 2 метров (момент времени 9-10 часов с начала суток), то для рассмотренного варианта ограждающей дамбы этот перепад снижается до 0,8-1,0 метра (момент времени 14 часов на рис.9, б).
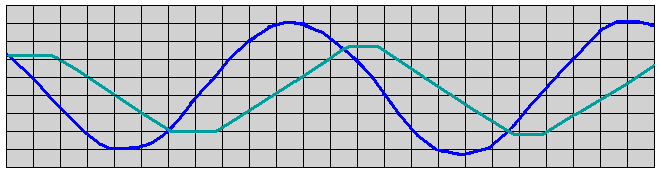
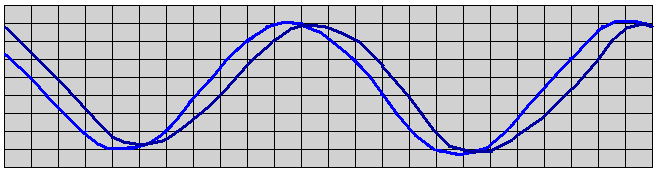
Рис. 9. Графики колебания уровней моря и бассейна и фильтрационных напоров в ядре дамбы во времени ( в течении суток).
а – для малофильтрующей ограждающей дамбы (с ядром или с замывом горной массы песком).
б – для случая однородной ограждающей дамбы из горной массы ( Кф = 65000 м/сут);
в –для малофильтрующей ограждающей дамбы с трапецеидальным ядром.
Условные обозначения: ![]() уровень моря;
уровень моря;
![]() уровни бассейна;
уровни бассейна;
![]()
![]()
![]() фильтрационные напоры в ядре дамбы (по оси ядра соответственно на отметках 23,0; -10,0; -24,5)
фильтрационные напоры в ядре дамбы (по оси ядра соответственно на отметках 23,0; -10,0; -24,5)
Остальные рассмотренные варианты с противофильтрационными ядрами различной конструкции также допустимы с точки зрения фильтрационных расходов и могут рекомендоваться к возведению при экономическом обосновании. Вариант однородной дамбы из горной массы возможен только за счет увеличения мелких фракций в материале наброски с d<5 мм.
Таким образом, в 3-ей главе представлены результаты нескольких практически значимых фильтрационных задач, которые позволили выявить целый ряд особенностей в работе системы «плотина-основание» и отдельных
конструкций при воздействии фильтрационного потока.
В четвертой главе приводятся результаты численных исследований температурного режима бетонных и грунтовых плотин. Основным фактором, влияющим формирование температурного режима бетонных плотин в период строительства является экзотермия цемента, практически всегда вызывающая трещинообразование. Степень температурного разогрева зависит от состава бетона и ряда технологичеких факторов. На сегодняшний день существуют некоторые рекомендации по выбору состава бетонов и режиму возведения сооружений, однако в каждом конкретном случае необходим тщательный анализ возможного температурного разогрева массива бетона при его возведении. Исследования влияния отдельных факторов на температурный режим возводимых гравитационных плотин проводились ранее, например, для плотины Бурейской ГЭС. Однако этот пример иллюстрирует конкретные условия возведения. В данной работе предпринята попытка создания математической прогнозной модели температурного режима послойно укладываемого бетонного массива в зависимости от основных действующих факторов, изменяющихся в широком диапазоне. Использование такой модели позволит принимать рациональные решения по составу бетонов (расхода цемента и его тепловыделения) и технологической схемы возведения бетонных гравитационных плотин в различных условиях.
Рассматривалось послойное возведение бетонного столба на массиве основания. Расчеты проведены для трех случаев температурного воздействия среды: температура воздуха принималась постоянной и равной 30°С, 20°С (летний период) и 5 °С (зимний период). Температура укладываемой бетонной смеси принималась постоянной и равной tб.с.= 16 oC.
Для анализа влияния факторов и создания имитационной модели использовалась методика факторного анализа. Рассматривался полно факторный эксперимент, для которого функция откликов принимает следующий вид:
Yi = bo + b1X1 + b2X2 + b3X3 + b4X4 + b12 X1 X2 + b13 X1 X3 + b14 X1 X4 +
b23 X2 X3 + b24 X2 X4 + b34 X3 X4 + b1234 X1 X2 X3 X4 (13)
В качестве факторов в проведенных исследованиях рассматривались следующие величины. Х1 – расход цемента (принято, что Х1= -1 - нижний уровень фактора, соответствующий минимальному значению расход цемента - 50 кг/м3, Х1= +1 - верхний уровень фактора, соответствующий максимальному значению расход цемента -170 кг/м3); Х2 – толщина укладываемого слоя бетона ( в первом интервалеот 0.3м до 1,0 м, во втором интервале от 1,0 до 5,0 м); Х3 – интенсивность (скорость) бетонирования массива по высоте (рассмотрено два интервала изменения этого фактора: первый интервал - от 0,15 до 0,6 м/сут, второй интервал – от 0,6 до 2,0 м/сут); Х4 – полное тепловыделение цемента (от 120 КДж/кг до 350 КДж/кг). В качестве откликов рассматривались следующие величины: максимальная температура tmax, возникающая в возводимом массиве или максимальное приращение температуры tmax по отношению к начальной температуре бетонной смеси (разница между максимальной температурой и температурой укладки бетонной смеси). Были получены функции откликов в виде полиномов для определения максимальных температур внутри возводимого бетонного массива при интенсивности бетонирования в пределах от 0,15 до 0,6 м/сут и толщинах слоев от 0,3 до 1,0 метра (после исключения малозначимых членов):
- при температуре наружного воздуха 20°С
tmax = 24,65+3,21Х1- 0,02Х2+1,77Х3+2,55Х4+ 1,43Х1Х3+1,88Х1Х4 +
0,32Х2Х3+0,93Х3Х4+0,74Х1Х3Х4; (14)
- при температуре наружного воздуха 5°С
tmax=16,15+3,32Х1+1,01Х2+3,08Х3+3,10Х4+1,14Х1Х3+1,91Х1Х4+
0,34Х2Х3+0,94Х3Х4+0,43Х1Х3Х4. (15)
Полученные зависимости удовлетворяют условию адекватности.
В рассмотренных примерах интенсивность бетонирования задавалась в интервале от 0,15 до 0,6 м/сут, что, в основном, и имеет место при современных методах возведения плотин из укатанного бетона. Однако, в некоторых случаях возможно возведение и при более высоких темпах возведения. Например, при бетонировании на высоких отметках, когда объемы бетонирования снижаются ввиду уменьшения ширины бетонируемого профиля, а производительность бетонного хозяйства достаточно высока. Кроме того, постоянное совершенствование технологии не исключает в недалеком будущем повышения интенсивности бетонных работ. Поэтому исследования были расширены и рассматривались примеры с бетонированием бетонного массива при интенсивности бетонирования в интервале от 0,6 до 2,0 м/сут и толщинах слоев от 0,3 до 1,0 метра. Были получены функции откликов аналогичные выражениям (14, 15)
Для получения математической модели при возведении сооружения из вибрированного бетона были проведены исследования также с применением факторного анализа. Рассматривались те же факторы, что и в предыдущих исследованиях, но с другими интервалами изменения: Х1 – расход цемента от 170 до 400 кг/м3; Х2 – толщина укладываемого слоя бетона от 1,0 до 5,0 м; Х3 – интенсивность возведения массива по высоте для первого факторного пространства от 0,15 до 0,6 м/сут, для второго факторного пространства от 0,6 до 2,0 м/сут; полное тепловыделение цемента от 120 до 350 КДж/кг. В качестве откликов также рассматривались максимальная температура или максимальный разогрев внутри бетонного массива. Были получены зависимости, аналогичные уравнениям (14-15).
Для удобства использования полученных зависимостей в практических расчетах были построены номограммы, позволяющие по значениям факторов определять величину максимальной температуры, а также решать обратную задачу: по значению допустимой температуры определять состав бетона
Номограмма для определения максимальной температуры бетона после укладки (tвоз=5oС, расход цемента 50-170 кг/м3, толщина слоя 0.3-1.0 м, Эmax 120 – 350 КДж/кг, интенсивность бетонирования 0.6- 2.0 м/сут)
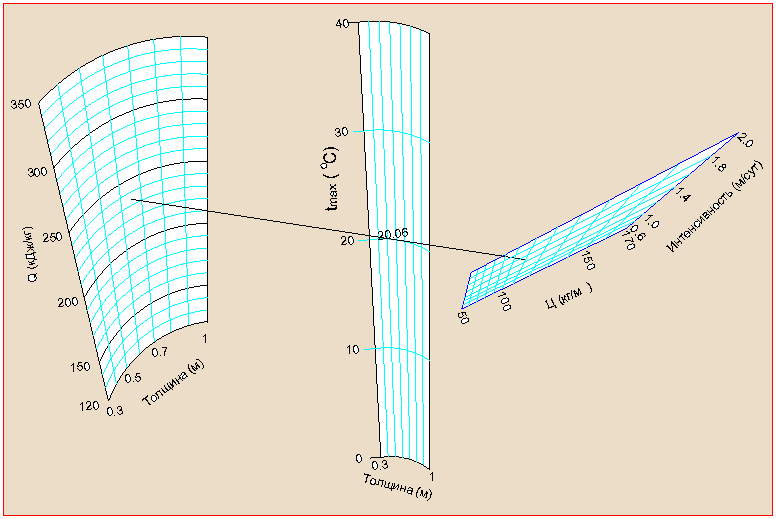
Номограмма для определения максимальной температуры бетона после укладки (tвоз=20oС, расход цемента 50-170 кг/м3, толщина слоя 0.3-1.0 м, Эmax 120 – 350 КДж/кг, интенсивность бетонирования 0.6- 2.0 м/сут)
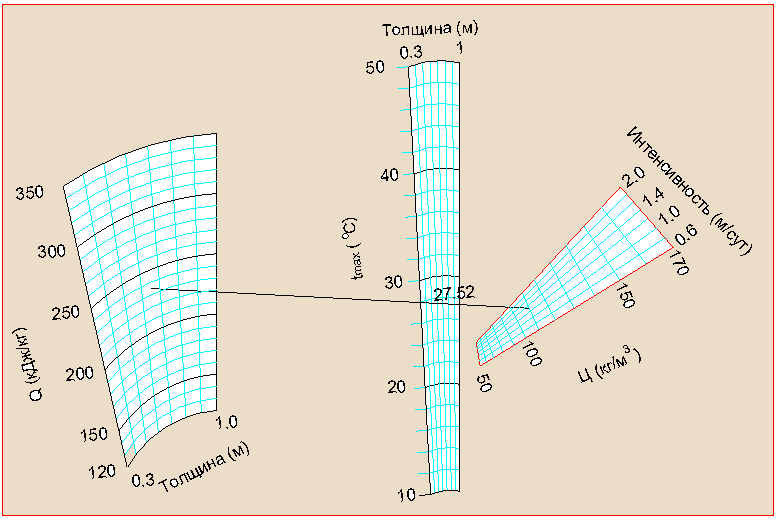
Рис. 10. Номограммы для определения максимальной температуры в
бетонном массиве.
(расход цемента и его тепловыделение) и технологию его укладки (толщину слоев и интенсивность возведения). Пример номограмм для двух расчетных случаев представлен на рис.10.
Полученная имитационная модель сравнивалась с аналогичной моделью возведения бетонного столба плотины Бурейской ГЭС, полученной во ВНИИГе им Б.Е.Веденеева. Значения температурного разогрева вследствии экзотермии, полученные по двум разным математическим моделям, практически равны, что подтверждает достоверность полученной модели.
По разработанной методике были исследованы температурные режимы гравитационных плотин из укатанного бетона: Хлонг Та Дат (Тайвань) и Шон Ла (Вьетнам). Получены температурные поля для различных моментов времени периодов строительства и эксплуатации, необходимые для дальнейшего решения задачи термонапряженного состояния.
Исследования термического режима грунтовой плотины Богучанской ГЭС проводились для определения температурного состояния асфальтобетонной диафрагмы. Прогноз температурного режима
асфальтобетонной диафрагмы необходим как для определения временных шагов технологического процесса укладки асфальтобетона и грунта, так и для определения свойств асфальтобетона, влияющих на напряженно-деформированное состояние системы «плотина-диафрагма»
Рассматривался процесс остывания асфальто-бетонной диафрагмы при ее послойной укладке при различных температурах воздуха: зимний вариант –24,1С и летний вариант +20,0С. Возведение диафрагмы производится слоями по 0,6 метра, каждый из которых, в свою очередь, укладывается в триприема по 0,2 метра с интервалом укладки ~ 6 часов. Толщина асфальтобетонной диафрагмы –1,2 метра. Укладка и остывание асфальтобетона от температуры укладки 160С до 40С происходит в теплоизолирующей опалубке (фенолпласт толщиной 6 см) со стороны боковых поверхностей. В резульате численного решения получены минимально допустимое время охлаждения асфальтобетона: в зимнее время ~48 часов и в летнее время ~72 часа, что хорошо корреспондируется с результатами физического эксперимента опытного фрагмента в г.Братске (ВНИИГ, 1984 г.)
Для прогноза температурного режима конструкции в строительный и эксплуатационный периоды решалась 2-х мерная нестационарная задача теории теплопроводности. В расчетную схему вошли грунтовая плотина с диафрагмой и прилегающим основанием. Выделены области с разными теплофизическими характеристиками. Разбивка на конечные элементы делалась с учетом поэтапности возведения сооружения и наполнения водохранилища. Была выделена часть плотины уже возведенная к началу данных исследований. Некоторые результаты исследований в виде изохром температуры на различные моменты времени представлены на рис.11. Можно отметить, что температурное поле плотины и диафрагмы в период строительства достаточно неоднородно и представляет собой чередование зон с отрицательными и положительными температурами. Процесс выравнивания температур происходит достаточно медленно. Подъем уровня воды в верхнем бьефе привел к достаточно быстрому прогреву диафрагмы по высоте. Учитывая то, что прочностные свойства асфальтобетона в значительной степени зависят от температуры, полученные на различные моменты возведения и эксплуатации температурные поля использовались на следующих этапах исследований в расчетах напряженно-деформированного состояния конструкции.
Такие решения температурных задач необходимы при проектировании сооружений разного типа. Построение номограмм позволяет постоянно контролировать отклонения от принятых технических условий бетонирования, которые достаточно часто имеют место.
Глава 5 посвящена совместной фильтрационно-температурной задаче, решение которой необходимо для сооружениий, возводимых в условиях вечной мерзлоты. Вопросы обеспечения устойчивости и надежности таких сооружений невозможно решать без четкого представления о фильтрационном и температурном режимах плотин и их оснований. Исследования, связанные с совместным решением фильтрационно-температурной задачи, были проведены на примере плотины Курейской ГЭС.
Рассматривался участок грунтовой плотины во втором правобережном понижении. Данный участок плотины представляет собой интерес в связи с
поведением этой конструкции в период эксплуатации. В 1989 году в пределах данного участка (у ПК 10) произошла аварийная ситуация,
связанная с выходом фильтрационного потока на низовой откос грунтовой плотины. Осадки гребня плотины за 10-летний период эксплуатации (с 1990 по 2000 гг.) достигли 64 см и продолжали постепенно увеличиваться. Дальнейшее продолжение роста осадок могло вызвать понижение гребня противофильтрационного элемента плотины до отметки ниже уровня водохранилища и необходимость его снижения.
Расчеты температурного режима грунтовой плотины проведены в соответствии со схемой поэтапного возведения и наполнения водохранилища. К моменту возведения плотины до ее полного профиля (конец 1987 года), все ее поперечное сечение за исключением ядра выше отметки 90,0 м находилось в промороженном состоянии. К моменту наполнения водохранилища это состояние сохранялось. В средней части профиля отрицательные температуры составляли величины - 0,4 -0,6 0С.
На начальных этапах наполнения водохранилища воздействие фильтрационного потока не ощущалось. В дальнейшем тепломассоперенос за счет фильтрационного потока начинает сказываться интенсивнее и к декабрю 1989 года тепловой поток проникает через каменную наброску и температура на верховой грани экрана достигала положительных температур ~120С.
Температурное поле грунтовой плотины в сечении ПК 12+50 в 1993 году (рис.12) характеризовалось следующим. В талом состоянии находится довольно значительная часть экрана. По подошве экрана положительная температура достигла низовой грани экрана. Низовая призма плотины – в
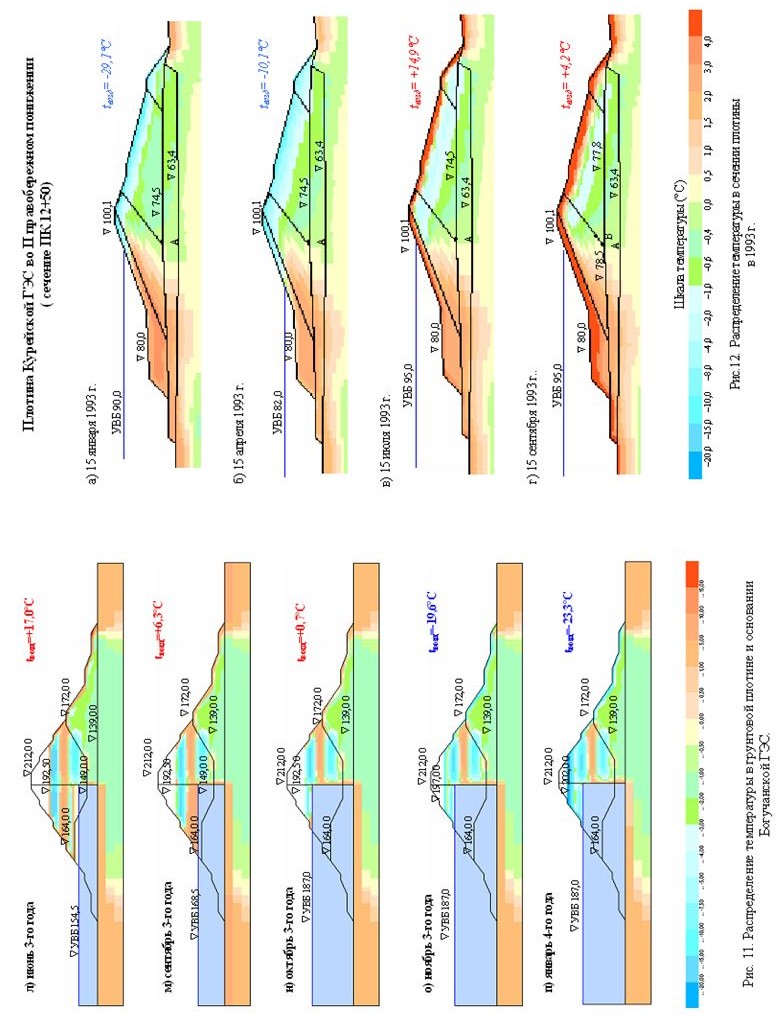
мерзлом состоянии. В средней ее части температура в пределах -0,2 -1,00С. Продолжается тепломассоперенос на границе экрана и цокольной части плотины. Показательна динамика изменения температуры в точке пересечения низовой грани экрана с поверхностью цокольной части (точка А, рис. 12): - 0,092 0С в январе, - 0,008 0С в июле и + 0,05 0С в сентябре месяце.
К 2002 году процесс проникновения тепла фильтрационным потоком продолжался. В январе 2002 года по сравнению с январем 1993 года граница оттаявшего грунта сместилась еще дальше в сторону нижнего бьефа. По контакту плотины с цокольной частью оттаял грунт экрана и незначительная часть грунта низовой призмы. В течение 2002 года наблюдалось увеличение положительных температур в области фильтрации (область талых грунтов). Для сравнения с 1993 годом в точке А значения температуры в течение 2002 года изменяются следующим образом: январь - +0,74°C, апрель - +0,76°C, июль - +0,78°C, сентябрь - +0,81°C.
К 2015 году тенденция проникновения теплового потока по контакту экрана и цокольной части плотины сохранялась, хотя скорость этого процесса достаточно низка. Значения температуры в точке А в 2015 году следующие: в январе +1,14°С, в апреле +1,15°С, в июле +1,16°С и в сентябре +1,18°С. Расстояние от точки А до границы талого и мерзлого грунтов по горизонтали в сторону нижнего бьефа в сентябре 2015 года составляет примерно 17,0 м. Для сравнения в сентябре 1993 года это расстояние равнялось 0, а в сентябре 2002 года – 12,3 м. Таким образом, средняя горизонтальная скорость продвижения нулевой изотермы в сторону нижнего бьефа составляет 1,4 м/год за период 1993 2002 годы и 0,36 м/год за период 20022015 годы. Если судить по данным расчёта, то будет иметь место некоторая стабилизация температурного режима плотины к 2015 году.
Расчеты в пространственной постановке подтвердили качественную картину фильтрационно-температурного режима, полученную из решения плоской задачи. Несколько меньшее проникновение нулевой изотермы внутрь конструкции получено у бортов плотины. Были примерно оценены скорости продвижения нулевой изотермы в нижней части экрана и цоколя. Продвижение границы мерзлых и талых грунтов за период 19932002 годов характеризовалось средней скоростью по горизонтали 0,9 м/год. В вертикальном направлении средняя скорость продвижения нулевой изотермы составляла примерно 0,5 м/год. За период 20022015 гг. эти величины соответственно равны 0,3 м/год по горизонтали и 0,1 м/год в вертикальном направлении. Таким образом, скорость продвижения тепловой волны в пространственной задаче меньше, чем в плоской. Сохраняется тенденция ее уменьшения со временем.
Результаты, полученные при решении пространственной задачи, сравнивались с имеющимися натурными данными. Сопоставление с натурными данными показало, что результаты решения пространственной задачи лучше соответствуют натурным данным, чем результаты решения в плоской постановке. Изменения температуры по глубине конструкции натуры и полученного численного решения практически аналогичны. Некоторые расхождения с натурными данными получены на поверхности грунтовой плотины, что, возможно, вызвано отклонениями принятых значений климатического воздействия (температуры воздуха и воды, толщины снежного покрова) от реальных величин. Сравнивая решения, полученные для плоской и пространственной задач можно отметить, что решение в пространственной постановке дает более благоприятную картину, чем в плоской. Область талых грунтов в центральных сечениях плотины, полученная из пространственного решения несколько меньше, чем в плоской задаче. Пространственная задача позволила учесть влияние бортовых примыканий на фильтрационный и температурный процессы. Общие качественные выводы о температурно-фильтрационном режиме плотины в пространственных условиях совпадают с выводами по плоской задаче. Можно ожидать, что к 2015 году стабилизация температурного режима плотины завершится.
Общие выводы.
- На основе метода конечных элементов в локально-вариационной постановке разработана методика расчетов фильтрационных, температурных и совместных фильтрационно-температурных задач в плоской и пространственной постановках, позволяющая решать задачи с достаточно полным учетом влияющих на исследуемые процессы факторов. Разработанная методика реализована в алгоритмах и программных комплесах FILTR и TERMIC. Достоверность получаемых с использованием методики и программ расчета подтверждена решением ряда тестовых задач и сравнением результатов численных исследований с апробированными методами и натурными данными.
2. Были проведены сопоставления результатов плоских и пространственных задач в различных условиях: при линейных и нелинейных законах фильтрации, в стационарной и нестационарной постановках, для нескальных оснований и скальных грунтов с трещинами, при различной густоте сеток МКЭ, при двусторонних и односторонних колебаниях уровня воды, при одновременном действии фильтрационного и температурного потоков. Эти сопоставления показали, что практически во всех случаях надо стремиться к решению пространственных задач. Даже в относительно «простом» створе плотины Юмагузинского гидроузла с коэффициентом створа порядка 10 фильтрационный поток имеет ярко выраженный пространственный характер.
3. Создание математической фильтрационной, температурной или совместной модели является в современных условиях процессом поэтапным, развивающимся параллельно с проектированием, строительством и мониторингом сооружения. На начальном этапе исследований дается общая оценку фильтрационного режима плотины и основания. Делаются выводы о необходимости проектирования противофильтрационных элементов в основании под плотиной и оценка фильтрационного расхода. Сопоставляются результатов плоских и пространственных задач.
На следующем этапе уточняются инженерно-геологические условия в основании и бортах створа, и корректируется пространственная модель. Даются рекомендации по совершенствованию и оптимизации противофильтрационных элементов. Возможно использование методики факторного анализа, что позволяет связать математическую модель с возможными комбинациями характеристик грунтов, входящих в расчетную область.
Создание математической модели, в конечном счете, приводит к методике непрерывных в контакте с проектировщиками уточняющих исследований. Такая откалиброванная математическая модель позволяет осуществить прогноз поведения конструкции, что необходимо для мониторинга и декларации безопасности сооружения.
4. Решения нестационарных и нелинейных фильтрационных задач всегда вызывали достаточно большие сложности. Сейчас получена возможность решения таких задач в плоской и пространственной постановках. Решение задач применительно к взрывонабросным плотинам снова приобретет большое значение, когда мы вплотную приблизимся к освоению таких створов как Камбаратинский №1(р. Нурек) и Достимжумский (р. Пяндж). К этому уже надо быть готовыми.
5. Фильтрационно-температурный класс задач очень важен для освоения Севера. Решения этих задач диктовались проблемами строительства в условиях крайнего Севера. И Курейская ГЭС тому пример. Успешное решение задач тепломассопереноса позволило прогнозировать движение нулевой изотермы в плотине в пространстве и времени. Полученное в результате расчетов распределение температуры в плотине достаточно приемлемо корреспондируется с данными натурных наблюдений.
- XX век был веком решения фильтрационных и температурных задач аналитическими методами, в основном, плоских, в стационарной и линейной постановках. Во второй половине века появились численные методы, но возможности вычислителной техники были еще весьма ограничены. К концу XX столетия, с появлением мощных быстродействующих ЭВМ происходит «бум» численных решений. Это был, в определенном смысле, прорыв. XXI век будет, вероятно, веком решения нестационарных нелинейных задач в пространственной постановке. Современная вычислительная техника уже сейчас позволяет решать эти задачи, но она быстро совершенствуется, и ее возможности будут необъятны.
- Большинство из приведенных в данной работе исследований базировались на достаточно скудных исходных данных (по крайней мере, на начальных этапах). При решении фильтрационных задач главное – иметь достаточно полную и точную исходную информацию, но получить ее современными методами, которые практически себя исчерпали, невозможно. Нужны новые, видимо, геофизические методы изысканий. И, в первую очередь, это относится к скальным трещиноватым основаниям плотин. Методы эти должны быть не только качественными, но и количественными, что особенно важно.
Основные положения диссертации изложены в следующих работах:
| 1. | Анискин Н.А. Расчет температурного режима и напряженно-деформированного состояния арочной плотины в «объемной» постановке. Труды Всесоюзного координациооного совещания «Прочность и температурная трещиностойкость бетонных гидротехнических сооружений при температурных воздействиях, -Л.,Энергоиздат, 1989. | ||
| 2. | Анискин Н.А., То Ван Тхань. Прогноз фильтрационного режима грунтовой плотины Юмагузинского гидроузла и ее основания. «Гидротехническое строительство», 2005, № 6, М., Энергопрогресс. | ||
| 3. | Анискин Н.А. Температурный режим гравитационной плотины из укатанного бетона. «Гидротехническое строительство», 2005, № 12, М., Энергопрогресс. | ||
| 4. | Анискин Н.А. Фильтрация в основании и бортах бетонной гравитационной плотины Бурейского гидроузла. «Вестник МГСУ», 2006, №2. | ||
| 5. | Анискин Н.А. Температурно-фильтрационный режим основания и плотины Курейской ГЭС во втором правобережном понижении. «Вестник МГСУ», 2006, №2. | ||
| 6. | Анискин Н.А. Исследования фильтрационного и температурно-фильтрационного режимов плотин и оснований. Материалы Второй научно-технической конференции «Гидроэнергетика. Новые разработки и технологии», ВНИИГ им. Б.Е.Веденеева, г. Санкт-Петербург, 2006 г. | ||
| 7. | Анискин Н.А.,Нгуен Данг Жанг. Численное моделирование температурного режима гравитационной плотины из укатанного бетона. Строительные материалы, оборудование, технологии XXI века, 2006, №10, МГСУ, Москва. | ||
| 8. | Анискин Н.А. Численное моделирование фильтрации в трещиноватых скальных основаниях плотин. «Инженерные изыскания», декабрь 2007 года. | ||
| 9. | Анискин Н.А. Неустановившаяся фильтрация в грунтовых плотинах и основаниях. Сборник «Вестник МГСУ», 2009, №2. | ||
| 10. | Анискин Н.А., Нгуен Данг Жанг Прогноз температурного режима бетонных гравитационных плотин из укатанного бетона. «Гидротехническое строительство», 2007, № 12, М., Энергопрогресс. | ||
| 11. | Рассказов Л.Н., Анискин Н.А. и др. Фильтрация в грунтовых плотинах в плоской и пространственной постановке. «Гидротехническое строительство», 1989, №11. | ||
| 12. | Рассказов Л.Н., Анискин Н.А. Фильтрационные расчеты гидросооружений и оснований. «Гидротехническое строительство», 2000, №11. | ||
| 13. | Рассказов Л.Н., Анискин Н.А. и др. Сангтудинский гидроузел: напряженно-деформированное состояние и фильтрация в основании плотины и в обход гидроузла. «Гидротехническое строительство», 2008, №5. | ||
| 14. | Рассказов Л.Н., Орехов В.Г., Анискин Н.А. и др. Гидротехнические сооружения. Учебник для ВУЗов, АСВ, М., 2008. | ||
| 15. | Рассказов Л.Н., Анискин Н.А. и др. Конструктивные решения морских грунтовых плотин при строительстве ПЭС, «Гидротехническое строительство», 2009, №7. | ||

