Анализ напряженно-деформированно го состояни я сетчатых пластин и стержневых плит на основе континуальной и дискретной расчетных модел ей с уч е том деформации поперечного сдвига

На правах рукописи

Кондрашов Владимир Владимирович

АНАЛИЗ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ

СЕТЧАТЫХ ПЛАСТИН И СТЕРЖНЕВЫХ ПЛИТ НА ОСНОВЕ

КОНТИНУАЛЬНОЙ И ДИСКРЕТНОЙ РАСЧЕТНЫХ МОДЕЛЕЙ

С УЧЕТОМ ДЕФОРМАЦИИ ПОПЕРЕЧНОГО СДВИГА

Специальность 05.23.17 - Строительная механика

А в т о р е ф е р а т

диссертации на соискание ученой

степени кандидата технических наук

Волгоград 2011

Работа выполнена в Государственном образовательном учреждении высшего профессионального образования «Волгоградский государственный архитектурно-строительный университет»

Научный руководитель: доктор технических наук,

доцент Беликов Георгий Иванович

Официальные оппоненты: доктор технических наук,

доцент Ким Алексей Юрьевич

ФГОУ ВПО «Саратовский государственный аграрный университет имени Н.И. Вавилова»

доктор технических наук,

профессор Клочков Юрий Васильевич

ФГОУ ВПО «Волгоградская государственная сельскохозяйственная академия»;

Ведущая организация: ГОУ ВПО «Саратовский государственный

технический университет»

Защита состоится 17 марта 2011 г. в 10 часов на заседании диссертационного совета Д 212.026.01 при ГОУ ВПО «Волгоградский государственный архитектурно-строительный университет» по адресу: 400074, г. Волгоград, ул. Академическая, д.1, ауд. Б-203.

С диссертацией можно ознакомиться в библиотеке Волгоградского государственного архитектурно-строительного университета.

Автореферат разослан 10 февраля 2011г.

Ученый секретарь диссертационного совета

Пшеничкина В.А.

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность темы. Сетчатые пластины и оболочки широко используются в различных областях техники и особенно в строительстве. Сетчатые системы применяются не только как самостоятельные конструкции, но и как подкрепляющие элементы. Конструктивно сетчатые системы являются регулярными или циклически регулярными стержневыми системами с унифицированными узловыми соединениями. При этом сами стержни могут быть в свою очередь сложными конструкциями (ферменный или рамный составной стержень, многоветвевой составной стержень, многослойный стержень из композиционных материалов с пониженной сдвиговой жесткостью и т.д.). С внедрением в инженерную практику сетчатых систем возникла необходимость разработки теории и методов их расчета.

Все исследования по решению этой проблемы можно отнести к одному из двух основных направлений: исследования, основанные на дискретной расчетной модели, и исследования, основанные на континуальной расчетной модели.

Расчеты по дискретной модели осуществляются методами строительной механики, в том числе и по МКЭ. При большом числе узлов и стержней возникают существенные трудности численной реализации этой модели.

Это обстоятельство привело к разработке других подходов, позволяющих существенно понизить порядок разрешающей системы уравнений (метод суперэлементов, конденсационные методы, метод обобщенных неизвестных, метод дискретных конечных элементов). Наиболее полно это направление представлено работами В.А. Игнатьева и его учеников.

Сущность континуальной модели заключается в том, что область с густой сеткой узлов может быть заменена некоторой эквивалентной пластиной или оболочкой. Наибольший вклад в это направление внесен работами Г.И. Пшеничнова, Г.И. Беликова, В.И. Волченко, В.В. Кузнецова, В.В. Пономарева, И.Г. Тагиева, Л.В. Лозы и др.

Каждое из этих двух расчетных моделей имеет свои преимущества и недостатки. Исследования, основанные на этих моделях успешно развиваются и совершенствуются, взаимно дополняя и обогащая друг друга.

Одним из путей совершенствования этих моделей является их уточнение, связанное со специфическим поведением стержней имеющих низкую сдвиговую жесткость.

Теориям и методам расчета сплошных пластинок и оболочек посвящено большое количество статей и монографий. Однако для сетчатых систем уточнение классической теории на базе сдвиговой модели по-прежнему является актуальной задачей и представляет несомненный практический интерес.

Целью диссертационной работы является разработка усовершенствованных методов анализа напряженно-деформированного состояния сетчатых пластин и стержневых плит по континуальным и дискретным расчетным схемам с учетом деформации поперечного сдвига.

Для достижения цели поставлены следующие задачи:

-построить более совершенные расчетные модели, уточняющие теорию упругих сетчатых пластин, стержневых плит и составных стержней;

- разработать теоретические основы методов и алгоритмы исследования напряженно-деформированного состояния сетчатых пластин и стержневых плит с учетом деформации поперечного сдвига для решения задач статики, динамики и устойчивости;

- построить матрицы жесткости, масс и потенциала нагрузки конечного элемента – стержня с учетом деформации поперечного сдвига; - провести решение задач статики, динамики и устойчивости составных стержней и сетчатых пластин с различными типами сеток и характеристиками материала на базе усовершенствованных континуальной и дискретной расчетных схем;

- дать оценку влияния податливости материала, топологии сетчатых пластин и составных стержней на напряженно-деформированное состояние, частоты свободных колебаний и критические нагрузки.

Научную новизну диссертационной работы составляют:

- уточненная модель упругих сетчатых пластин на базе континуальной расчетной схемы повышающая точность расчетов;

- матрицы жесткости, матрицы масс и матрицы потенциала нагрузки конечных элементов – составных стержней и стержней из композиционных материалов, позволяющие на основе МКЭ исследовать степень влияния деформации поперечного сдвига на напряженно-деформированное состояние сетчатых конструкций (стержневых плит и пластинок);

0. уравнения состояния расчётной модели и зависимости, позво­ляющие осуществлять обратный переход к усилиям в стержнях;

- основные уравнения теории упругих сетчатых пластин и составных стержней на базе континуальной и дискретной модели с учетом деформации сдвига;

- методика и алгоритм расчёта сетчатых пластин, образованных сплошными и составными стержнями на основе дискретной и континуальной расчётных схем в задачах статики, динамики и устойчивости;

1. решение задач статики, динамики и устойчивости составных стержней и сетчатых пластин, с различными типами сетки и характеристиками материала;
2. оценка влияния податливости материала, топологии сетчатых пластин и составных стержней на напряжённо-деформированное состояние, частоты свободных колебаний и критические нагрузки.

Достоверность результатов работы подтверждается сравнением результатов расчета по различным расчетным схемам, с данными результатами других ученых.

Достоверность базируется на корректной математической постановке задач, использовании апробированных исходных положений и соотношений теории сетчатых пластин, анализе всех этапов решения.

Хорошее совпадение сравниваемых результатов, дает основание считать их достоверными.

Практическая ценность работы состоит в разработке методик и алгоритмов определения напряженно-деформированного состояния сетчатых пластин и составных стержней в задачах статики, динамики и устойчивости с учетом поперечного сдвига.

Произведено численное исследование сетчатых пластин и стержневых плит с оценкой влияния учета деформации поперечного сдвига и топологии сетчатых пластин и составных стрежней.

Данные методики могут найти применение в практике проектирования и исследования сетчатых пластин и стержневых плит.

Внедрение результатов. Материалы диссертационной работы получили внедрение в учебном процессе Волгоградского государственного архитектурно-строительного университета.

Апробация работы. Основные положения и результаты работы докла­дывались и обсуждались:

- IV Международной научно-технической конференции «Надёжность и долговечность строительных материалов, конструкций и оснований и фундаментов» (Волгоград, май 2005 г.);

- Всероссийской научно-технической конференции «Социально-экономические и технологические проблемы развития строительного комплекса и жилищно-коммунального хозяйства региона» (Волгоград, ноябрь 2006 г.);

- VIII Международной научно-технической конференции «Информационно-вычислительные технологии и их приложения» (Пенза, июнь 2008 г.);

- IV Международной научно-технической конференции «Наука, техника и технология XXI века» (Нальчик, октябрь 2009);

- ежегодных конференциях профессорско-преподавательского состава Волгоградского государственного архитектурно-строительного университета.

Публикации. Основные результаты выполненных исследований опубли­кованы в 9 научных статьях, в том числе 3 статьи в изданиях из перечня, определенного Высшей аттестационной комиссией Министерства образования и науки Российской Федерации.

Структура и объем работы. Диссертационная работа состоит из введе­ния, четырех глав, заключения, списка литературы из 260 наименований, содержит 44 рисунков и 14 таблиц. Основное содержание работы изложено на 129 страницах машинописного текста.

Соискатель выражает благодарность д.т.н., профессору, заведующему кафедрой Строительная механика ВолгГАСУ Игнатьеву Владимиру Александровичу за оказанную помощь и консультации в ходе выполнения диссертационной работы.

СОДЕРЖАНИЕ РАБОТЫ

Во введении показана актуальность темы, сформулированы цели и задачи диссертации.

В первой главе работы дан обзор теории и методов расчета сетчатых систем на статику, динамику и устойчивость.

Наиболее широкое применение стержневые пластинки типа сис­тем перекрестных балок получили сначала в судостроении. Поэто­му первые фундаментальные исследования по их расчету были вы­полнены учеными-кораблестроителями И. Г. Бубновым, А. Н. Кры­ловым и позднее П. Ф. Папковичем, А. А. Курдюмовым, А. И. Сегалем и др.

Обстоятельные обзоры истории развития методов расчета регулярных и квазирегулярных стержневых систем и систем перекрестных балок в частности даны в работах С.В. Симеонова и В.А. Игнатьева.

Большую роль в развитии методов расчета стержневых пластинок и плит сыграли также работы С.П. Тимошенко, Воровича И. И., Устинова Ю. А., Кадомцева И. Г., С.В. Симеонова, М.Ш. Минцковского, М. Рожи, В.И. Трофимова, Л.Н. Лубо, В. А. Игнатьева и его учеников.

Исторически, развитие теории стержневых (и сквозных в общем случае) конструкций связано с развитием и последовательным уточнением двух расчетных моделей: континуальной, в которой непрерывная среда наделяется специфическими свойствами, лишь в некотором интегральном смысле сопоставимыми с упруго-механическими свойствами исходной конструкции, и дискретной, более точно учитывающей индивидуальные особенности каждого элемента конструкции.

Следует отметить, что решения, основанные на классических методах в матричной форме, наряду с высокой точностью имеют один существенный недостаток: все они численные и поэтому даже для регулярных перекрестных систем не дают аналитических зави­симостей между силовыми и деформационными параметрами, что особенно необходимо при предварительном проектировании. Кро­ме того, использование методов сил и перемещений в классической форме при большом числе узлов системы ведет к большим затра­там машинного времени.

В этом отношении в расчетах регулярных стержневых систем метод обобщенных неизвестных В.А. Игнатьева имеет несомненные преимущест­ва: решения имеют аналитическую форму и охватывают широкий класс задач, кроме того, функциональные неизвестные, лежащие в его основе, значительно улучшают обусловленность матриц систем разрешающих уравнений в расчетах квазирегулярных систем.

Теория тонких упругих сетчатых оболочек и пластинок, разработанная Г.И. Пшеничновым, построена на основе континуальной расчетной схеме и развита в работах Г.И. Беликова, В.И. Волченко, В.В. Кузнецова, В.В. Пономарева, И.Г. Тагиева, Л.В. Лозы. Теории сетчатых пластин, построенные на основании гипотезы недеформируемых нормалей, не отражают явлений, связанных с учетом поперечных деформаций и напряжений, и дают существенные погрешности даже при рассмотрении сетчатых пластин из традиционных анизотропных материалов, еще большая погрешность появляется в случаях, когда стержни пластинок выполнены в виде составных стержней или из композиционных материалов.

Анализ существующих разработок и программных средств позволяет сделать вывод о необходимости дальнейшего исследования по расчету сетчатых пластин из композиционных материалов и составных стержней на базе теории деформации поперечного сдвига, как по континуальной, так и по дискретной модели.

Во второй главе обсуждены подходы к моделированию упругих сетчатых пластин и стержневых плит.

Один подход основан на континуальной расчетной модели Г.И. Пшеничнова с учетом деформации поперечного сдвига по С.П. Тимошенко. Разработана континуальная модель, в основу которой ставится более строгий учет трех факторов: поперечной деформации, деформации сдвига и депланации сечения. Учет этих факторов важен при исследовании сетчатых систем, выполненных из композиционных материалов.

Другой подход основан на дискретной расчетной модели по методу обобщенных неизвестных В.А. Игнатьева и методу конечных элементов.

Для описания напряженно-деформированного состояния сетчатых пластин и составных стержней, на базе принятых моделей получены полные системы уравнений по континуальной и дискретным расчетным схемам.

По дискретной модели для описания напряженно-деформированного состояния рассмотрен стержневой конечный элемент сетчатой пластины и составные стержни плиты.

Построена матрица жесткости для конечного элемента – балки с учетом деформации поперечного сдвига.

(1)

где - безразмерный параметр, учитывающий влияние сдвига; - длина балки.

Когда стержни сетчатой пластинки являются составными стержнями, используется уточненная В.А. Игнатьевым методика учета деформаций сдвига в решениях Энгессера-Тимошенко.

Физическая сущность расчета по Энгессеру-Тимошенко заключается в том, что решетчатый или планочный составной стержень заменяется стержнем сплошного сечения, эквивалентным ему по единичным углам сдвига.

При этом не принимается во внимание то обстоятельство, что при сравнимой с шириной длине элемента взаимное смещение концов элемента происходит и за счет изгибающих моментов, создаваемого поперечной нагрузкой. В учете этого влияния заключается уточнение методики Энгессера-Тимошенко, предложенное В.А. Игнатьевым.

Наиболее наглядно это можно проиллюстрировать на примере расчета симметричных решетчатых (ферменного и рамного) составного стержня.

Получены уточненные значения углов сдвига для ферменного и рамного составных стержней.

(2)

(3)

По Тимошенко угол сдвига для рамного стержня:

(4)

Использование уточненных значений позволяет в ряде случаев получить решения, совпадающие с точными, а в других – близкие к точным, полученным по методу конечных элементов с учетом продольных деформаций ветвей (поясов) составного стержня, когда за элемент принимается стержень между узлами фермы или рамы.

Простота и высокая точность решений, получаемых на основе изложенной выше теории составных стержней позволяет использовать их и при выводе формул метода перемещений для решетчатых и рамных составных стержней, т.е. для построения матрицы жесткости конечного элемента в виде изгибаемого составного стержня. В данном случае матрица жесткости будет иметь вид (1), а величина . Значение принимается по (2) или (3) в зависимости от типа составного стержня. Оно используется как при расчете сетчатых пластин по дискретной расчетной схеме, так и по континуальной.

По дискретной расчетной модели построено решение по методу обобщенных неизвестных.

За основную принимаем систему, получаемую из заданной по­сле замены соединительных связей во всех узлах усилиями, возни­кающими в них.

Система канонических уравнений метода обобщенных неизвестных разделяется на отдельные блоки уравнений относительно обобщенных неизвестных с индексом kr:

(5)

По найденным значениям найдены перемещения узлов регулярной системы перекрестных балок, а также усилия в балках и реакции на контуре.

В частном случае, когда приложена только узловая нагрузка

(6)

где

(7)

При предельном переходе из (6) получается решение для ортотропной пластинки, у которой коэффициенты Пуассона

(8)

В качестве примера определено напряженно-деформированное состояние прямоугольной сетчатой пластины, шарнирно опертой по контуру, от действия поперечной распределенной нагрузки. Численная реализация задач производилась с помощью программ написанных на языке FORTRAN для ПЭВМ.

При расчете сетчатых пластин по континуальной модели рассматриваются три группы уравнений. Уравнения равновесия и геометрические уравнения изгиба пластинок совпадают с соответствующими уравнениями теории сплошных пластин.

Уравнения состояния (уравнения упругости) получены на ос­нове теории сетчатых пластин и оболочек Г.И. Пшеничнова, с использованием кинематической гипотезы С.П. Тимошенко.

Исследуются сетчатые пластины, сетка которых образованна четырьмя семействами стержней (рис. 1).

Считаем что, материал стержней одинаков, а также одинаковы характеристики стержней первого и второго семейств. Геометрия сетки характеризуется следующими соотношениями:

1 = 2 =, 3 = /2, 4 = 0, a1 = a2 = a, а3 = а /2sin, а4 = а/2cos (9)

Закон изменений перемещений пластины с учетом принятой гипотезы не деформированных нормалей принимает вид:

, , (10)

,

где и - углы поворота отрезка нормали к срединной плоскости пластинки в плоскостях и ; и - соответствующие углы поперечного сдвига расчетной модели сетчатой пластины, зависящие от вида стержней сетчатой пластины (композитные, составные и т.д.).

Усилия и моменты в стержнях сетчатой пластины с учетом поперечного сдвига определяются через компоненты деформации по формулам:

, (11)

,

,

Уравнения состояния сетчатой пластинки образованной четырьмя семействами стержней имеют вид:

M1= –[(D11+K11)1+(D12 – K12)2+(D16 –K16)2 ],

M2= –[(D21 – K21)1+(D22+ K22)2+(D26 +K26)2 ], (12)

H1=(D61–K)1+(D62+K)2+(D66+K)2,

H2=(D61+K)1+(D62 –K)2+(D66 –K)2,

Здесь , , - параметры, учитывающие геометрические и физические характеристики сетки пластины.

Получены формулы, позволяющие осуществить переход от континуальной модели к усилиям и моментам в стержнях сетчатой пластины.

Расчет сетчатых пластин по уточненной модели построен на основе более строгой теории деформации стержней пластин по сравнению с классической теорией и теорией Тимошенко на базе континуальной расчетной схемы Г.И. Пшеничнова.

В основу уточненной теории ставится более точный учет поперечной деформации, деформации сдвига и депланация сечения.

Принимая закон Гука для плоского напряженного состояния, получены формулы для определения продольных и поперечных перемещений и нормального напряжения в прямолинейном стержне:

(13)

где U (х), W(x) – осевые и поперечные перемещения стержня (z = 0); w(x,z) – перемещение в направлении нормали к срединной поверхности.

Поправки, вносимые в классическую теорию и теорию Тимошенко, могут влиять на результаты значительно.

Уравнения равновесия и геометрические уравнения совпадают с соответствующими уравнениями теории сплошных пластин.

Усилия и моменты в стержнях сетчатой пластины определяются по уточненной теории следующим образом:

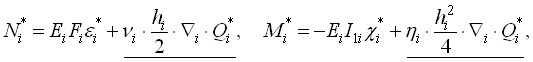(14)

где 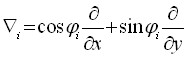; - коэффициент Пуассона; ; - высота сечения стержня.

Выражения для компонентов деформации оси стержня i-го семейства сетчатой пластины имеют вид:

(15)

Уравнения состояния сетчатой пластинки по уточненной теории принимают вид:

N1=С111+С122+С16 + ,

N 2=С211+С222+С26+,

S1=C611+C622+C66+, (16)

S2=C611+C622+C66+,

M1= – [(D11+K11)1+(D12 – K12)2+(D16 – K16)2 + ],

M2= – [(D21 – K21)1+(D22+ K22)2+(D26 + K26)2 + ],

H1=(D61– K)1+(D62+K)2+(D66 + K)2­­­­ – ,

H2=(D61+ K)1+(D62 – K)2+(D66 – K)2 – .

Имеем полную систему уравнений уточненной теории сетчатых пластин как континуальной системы.

Сформулирован общий подход к записи граничных условий. Приведены наиболее распространенные однородные и неоднородные граничные условия на контуре сетчатой пластины.

Рассмотрены задачи изгиба прямоугольных сетчатых пластин с различными типами сеток, нагруженных поперечной нагрузкой, с учетом и без учета деформации поперечного сдвига по континуальной расчетной модели (КРМ) и дискретной расчетной модели с использованием метода обобщенных неизвестных (МОН) и метода конечных элементов (МКЭ).

Результаты вычислений перемещений W и изгибающих моментов M в безразмерных параметрах для точки сетчатой квадратной пластины с координатами , представлены на рис. 2 и 3. Сетка пластины представлена семействами стержней 3 и 4 с углом 3=90 (рис. 1).

Анализ результатов показывает, что влияние сдвига существенно зависит от соотношений сторон пластин l/b и E/G. Учет деформаций сдвига приводит к повышению усилий и моментов до 40%, поперечного перемещения до 60%.

Следует отметить, что поправки вносимые в классическую теорию и теорию Тимошенко по уточненной теории (13), (14) влияют на результаты значительно. Более строгая теория дает увеличение нормального поперечного перемещения по сравнению с классической теорией до 40% и увеличению нормальных напряжений до 7%.

Сравнение расчетов сетчатых пластин по дискретной и континуальной моделям с учетом поперечного сдвига и уточненной модели, показывает, что погрешность по максимальному прогибу сетчатой пластины не превышает 5% уже при сетке узлов 55 и уменьшается с увеличением густоты сетки.

Третья глава посвящена проблеме устойчивости сетчатых пластин с учетом и без учета деформации поперечного сдвига на базе дискретной и континуальной расчетных схем.

При расчете по дискретной расчетной схеме получена матрица потенциала нагрузки стержневого конечного элемента с учетом деформации поперечного сдвига.

Проведен анализ точности решения задач устойчивости решетчатых составных стержней на основе уточненной континуальной модели.

При замене многопанельных регулярных ферм и рам эквивалентным составным стержнем с приведенной изгибной жесткостью EIпр и единичным углом сдвига за условие эквивалентности принято совпадение их перемещений только в узловых точках (границах панелей).

Это допущение соответствует действительности в случае решетчатого составного стержня (фермы). Для рамного составного стержня такая форма упругой линии между узлами ближе к действительности, чем упругая линия сплошного заменяющего стержня.

Выполненные рачеты показали, что использование уточненной теории составного стержня, обеспечивает получение практически точных результатов не только в задачах изгиба, но и в задачах устойчивости составных стержней.

При расчете сетчатых пластин на базе континуальной расчетной модели Г.И. Пшеничнова с учетом поперечных сдвиговых деформаций, получены основные уравнения устойчивости сетчатых пластин.

Исходное напряженное состояние до потери устойчивости принято безмоментным. Величина фиктивной поперечной нагрузки, входящей в уравнения равна:

Z = –(Nx01 + Ny02 +2S0) (17)

где Nx0, Ny0, S0 – внутренние тангенциальные силы начального безмоментного состояния пластинки;

Компоненты изгибной деформации определяются по формулам:

(18)

Получены основные уравнения теории сетчатых пластинок с учетом поперечного сдвига. При аналитическом решении исходная система уравнений сведена к системе дифференциальных уравнений относительно перемещений.

Принимая компоненты вектора перемещений в виде тригонометрических рядов Фурье, приходим к системе линейных однородных алгебраических уравнений относительно , , . Равенство нулю определителя системы приводит к собственным значениям нагрузки.

Рассмотрены задачи устойчивости шарнирно опертых прямоугольных сетчатых пластин с различной конфигурацией сетки, сжатых в своей плоскости по двум главным направлениям x и y, которые параллельны ее краям.

Принято, что отношение сжимающих усилий постоянно (-некоторая постоянная).

Значения критической нагрузки определялось по формуле:

Минимизируя это выражение по и , можно найти значения критической нагрузки.

Рассмотрена устойчивость из своей плоскости прямоугольной пластины с различными типами сеток при действии сжимающих сил в двух направлениях.

Построено решение задач устойчивости сетчатой пластины, образованной тремя семействами (1, 2 и 4, рис. 1) и двумя семействами (3 и 4, рис. 1) стержней одинаковых поперечных сечений с учетом поперечного сдвига.

Исследовалось влияние на величину критической силы параметров - отношения сторон пластины, - деформации поперечного сдвига в стержнях пластины, - угла между стержнями 1-го и 2-го семейств и - коэффициента, учитывающего отношение сжимающих усилий.

Результаты вычисления безразмерных значений критических сил приведены в таблице 1 и на рис. 4 и 5. В таблице и на рисунках, значению параметра соответствует , а соответствует .

Таблица 1.

	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09	0,10
ркр при
30	3.105	2.41	1.971	1.668	1.446	1.277	1.143	1.035	0.945	0.87
60	3.977	3.081	2.518	2.13	1.846	1.63	1.459	1.321	1.207	1.111
ркр при
30	1.301	1.148	1.028	0.931	0.851	0.784	0.726	0.677	0.634	0.596
60	1.916	1.679	1.494	1.346	1.225	1.124	1.038	0.965	0.901	0.845

Расхождение в результатах расчета сетчатых платин по континуальной и дискретной расчетных схемах, составляет не более 5%.

При фиксированном значении отношения с увеличением значение критической силы уменьшается, при до 13%, а при до 50%. Увеличение отношения сторон пластины и угла между стержнями приводит к увеличению критической силы.

Рассмотрена устойчивость бесконечно длинной сетчатой пластины сжатой по короткой стороне и устойчивость прямоугольной сетчатой пластины сжатой в одном направлении. Получены формулы для определения критических сил для сетчатой пластины, образованной равносторонними треугольниками, с использованием континуальной расчетной схемы на базе теории Г.И. Пшеничнова и теории сплошных пластин. Результаты расчетов практически совпали, расхождение составило до 1%. Формулы позволяют при исследовании пластин с указанной сеткой использовать теорию изотропных пластин и решения многочисленных задач на ее основе.

В четвертой главе рассмотрены свободные колебания составных стержней, сетчатых пластин с учетом деформации поперечного сдвига.

При рассмотрении составных стержней по дискретно-континуальной расчетной схеме используется уточненная теория. Получена матрица масс балочного конечного элемента – составного стержня, моделирующего ферму или раму.

Рассмотрены свободные колебания продольно сжатого составного стержня шарнирно опертого по концам и загруженного регулярно расположенными приведенными к узлам точечными массами (рис. 6 а).

а)

б)

Рис. 6.

На основе принципа возможных перемещений получено аналитическое решение для частот свободных колебаний:

, где , (19)

Рис. 7.

Для составного стержня, эквивалентного регулярной ферме, изображенной на рис. 6, величина определяется выражением (2), а для составного стержня, эквивалентного регулярной раме (рис. 7) – выражением (3).

Получено частотное уравнение в замкнутом виде позволяющее определять частоту свободных колебаний.

, где (25)

Это решение совпадает с точным.

Показано, что использование теории составных стержней на базе континуально-дискретной расчетной схемы обеспечивает получение результатов, практически совпадающих с точными в задачах колебаний.

Исследованы свободные поперечные колебания сетчатых пластин с учетом поперечного сдвига на базе континуальной расчетной схемы.

Построена система разрешающих дифференциальных уравнений свободных колебаний сетчатых пластин с учетом поперечной инерционной силой и инерцией вращения.

Первые две группы уравнений совпадают с соответствующими уравнениями теории сплошных пластин за исключением того, что в уравнениях движения иначе подсчитываются значения массы в инерционных членах.

Для принятой континуальной модели сетчатой пластины приведенная толщина и приведенный момент инерции имеют вид:

где Fi, Ii — площадь и момент инерции поперечного сечения i-го стержня; аi — расстояние между стержнями.

Геометрические уравнения совпадают с теорией сплошных пластин с учетом поперечного сдвига. Уравнения состояния получены при исследовании вопросов статики сетчатых пластин.

Рассмотрены свободные колебания прямоугольной сетчатой пластины, образованной четырьмя семействами стержней, шарнирно опертой по контуру.

Принимая компоненты вектора перемещений в виде тригонометрических рядов получим алгебраическую систему линейных однородных уравнений , , . Приравнивая нулю определитель системы уравнений найдем частотное уравнение, с учетом сил инерции и инерции вращения:

(26)

Если ограничится определением технических частот, то значение низшей частоты может быть найдено по приближенной формуле:

, (27)

Определены безразмерные значения частоты свободных поперечных колебаний сетчатой пластины с ромбической сеткой при учете деформации поперечного сдвига при различных параметрах , и угла сетки .

Результаты вычислений представлены в таблице 2 и на рис. 8 и 9. В таблице и на рисунках, значению параметра соответствует , а соответствует .

Таблица 2

°	0,50	1,00	0,50	1,00
	Собственная частота основного тона колебаний
10	95.902	108.804	113.67	174.949
20	91.129	137.656	106.47	181.614
30	82.569	170.466	95.152	189.193
45	62.403	194.818	72.937	194.818
60	36.909	170.466	49.491	189.193
70	21.156	137.617	36.501	181.605
80	10.088	108.804	27.857	174.949

Анализ результатов, показывает, что частоты собственных колебаний при учете поперечных сдвигов заметно отличаются от соответствующих частот, найденных по классической теории. Расхождение увеличивается с увеличением отношения . Так, например, при =30 и частота собственных колебаний снижается до 40%.

В диссертации показано, что если сетка пластины образованна равносторонними треугольниками с одинаковыми геометрическими и физическими параметрами стержней, для исследования свободных колебаний можно использовать теорию сплошных пластин и полученные на ее основе решения многих задач.

Исследованы свободные колебания прямоугольной сетчатой пластины с указанной сеткой, шарнирно опертой по контуру. Получены формулы для определения частот свободных колебаний сетчатой пластины на базе континуальной расчетной схемы Г.И. Пшеничнова и теории сплошных пластин. Собственные частоты пластин с указанной сеткой найдены по двум формулам практически совпали.

ОСНОВНЫЕ ВЫВОДЫ

1. Разработанная методика моделирования сетчатых пластин, позволяет построить единую континуальную расчетную модель с учетом поперечного сдвига для всех типов стержней, из которых может состоять сетчатая пластина (стержни из композитных материалов, составные стержни в виде ферм и рам и т.д.).
2. На базе континуальной расчетной схемы построены системы дифференциальных уравнений статики, свободных колебаний и устойчивости сетчатых пластин с учетом поперечного сдвига. Получены уравнения состояния и зависимости позволяющие осуществить переход от усилий и моментов в континуальной модели к усилиям и моментам в элементах сетчатой пластины.
3. Разработана методика решения задач по расчету сетчатой пластины на базе уточненной теории и континуальной расчетной схемы. Более точно берется в расчет поперечная деформация, деформация с учетом сдвига и депланация сечения по сравнению с классической теорией и теорией Тимошенко. Сравнения показывают, что более строгая теория дает увеличение деформаций до 40%.
4. Полученные на основе дискретных расчетных схем решения задач статики, динамики и устойчивости, с использованием уточненной В.А. Игнатьевым теории составных стержней С.П. Тимошенко, имеют более высокую степень точности (для рамных составных стержней), а в ряде случаев и совпадают с точными (для ферменных составных стержней).
5. Полученные на основе предложенного алгоритма матрицы жесткости, масс и потенциала нагрузки конечных элементов – составных стержней сетчатой пластинки с учетом деформаций поперечного сдвига в стержнях позволяют выполнить расчет сетчатых пластин и стержневых плит на основе МКЭ.
6. Численными экспериментами установлено существенное влияние деформации поперечного сдвига в стержнях на напряженно-деформированное состояние сетчатых пластин, частоты свободных колебаний и величину критической нагрузки. Дана оценка применимости континуальной расчетной схемы для сетчатых пластин сравнением с расчетами по дискретной расчетной схеме.
7. Показана возможность использования теории сплошных пластин и решений на ее основе для исследования сетчатых пластин, образованных сеткой из равносторонних треугольников с одинаковыми характеристиками стержней.

Основные положения диссертации опубликованы

в следующих работах:

Статьи в ведущих рецензируемых научных журналах и изданиях, определенных Высшей Аттестационной Комиссией России

1. Кондрашов В. В. Анализ точности теории упругих сетчатых пластин на основе дискретной и континуальной расчетных моделях при различной густоте сетки // Вестн. ВолгГАСУ. Сер.: Стр.-во и архитектура. Волгоград : ВолгГАСУ, 2007. Вып. 7 (26). С. 78-82. Библиогр.: с. 82 (4 назв.).
2. Кондрашов В. В. Исследование прогибов балки при учете различных эффектов уточненной теории изгиба и ее прикладное значение // Вестн. ВолгГАСУ. Сер.: Стр.-во и архитектура. Волгоград : ВолгГАСУ, 2007. Вып. 8 (27). С. 55-57. Библиогр.: с. 57 (4 назв.).

3. Кондрашов В. В. Решение задач динамики сетчатых пластин с учетом деформации поперечного сдвига в постановке метода конечных элементов // Вестн. ВолгГАСУ. Сер.: Стр.-во и архитектура. Волгоград : ВолгГАСУ, 2008. Вып. 12 (31). С. 25-28.

Публикации в других изданиях

4. Кондрашов В. В., Беликов Г. И. Композиционные материалы и конструкции из них / Волгогр. гос. архит.-строит. ун-т [и др.] // Надежность и долговечность строительных материалов, конструкций и оснований фундаментов : материалы IV Междунар. науч.-техн. конф. (12-14 мая 2005 г.) : [в 4 ч.]. Волгоград : Изд-во ВолгГАСУ, 2005. Ч. II. С. 22-25. Библиогр.: с. 25 (7 назв.).
5. Кондрашов В. В., Беликов Г. И. Обзор развития теорий и методов расчета сетчатых оболочек из композиционных материалов. Волгоград, 2005. 47 с. Библиогр. 256 назв. Деп. в ВИНИТИ 17.02.2005 № 235-В 2005.
6. Кондрашов В. В., Беликов Г. И., Тарасов А. А. Основы нелинейной теории упругих сетчатых оболочек из композиционных материалов / Волгогр. гос. архит.-строит. ун-т [и др.] // Надежность и долговечность строительных материалов, конструкций и оснований фундаментов : материалы IV Междунар. науч.-техн. конф. (12-14 мая 2005 г.) : [в 4 ч.]. Волгоград : Изд-во ВолгГАСУ, 2005. Ч. II. С. 17-21. Библиогр.: с. 21 (5 назв.).
7. Кондрашов В. В., Беликов Г. И., Тарасов А. А. Регулярные стержневые системы из композиционных материалов (неклассическая теория) / Волгогр. гос. архит.-строит. ун-т [и др.] // Социально-экономические и технологические проблемы развития строительного комплекса и жилищно-коммунального хозяйства региона : материалы Всерос. науч.-техн. конф. г. Волгоград - г. Михайловка, 24-25 ноября 2006 г. : [в 3 ч.]. Волгоград : Изд-во ВолгГАСУ, 2006. Ч. 1. С. 95-99. Библиогр.: с. 99 (7 назв.).
8.  Кондрашов В. В. Учет плоского напряженного состояния и деформации поперечного сдвига стержней в теории сетчатых пластин на базе континуальной расчетной модели с использованием математического пакета MATHCAD // Информационно-вычислительные технологии и их приложения : сб. ст. VIII Междунар. науч.-техн. конф., июнь 2008 г. Пенза : ПГСХА, 2008. С. 228-231. Библиогр.: с. 231 (4 назв.).
9. Кондрашов В. В. Исследование влияния уточнений, вносимых различными гипотезами, на результаты расчета сетчатых пластин на базе континуальной расчетной модели // Проблемы и тенденции устойчивого развития аграрной сферы : материалы Междунар. науч.-практ. конф., посвящ. 65-лет. Победы в Сталингр. битве, 4-7 февр. 2008 г. Волгоград : ВГСХА, 2008. Т. 2. С. 186-189. Библиогр.: с. 189 (6 назв.).

Кондрашов Владимир Владимирович

АНАЛИЗ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ

СЕТЧАТЫХ ПЛАСТИН И СТЕРЖНЕВЫХ ПЛИТ НА ОСНОВЕ

КОНТИНУАЛЬНОЙ И ДИСКРЕТНОЙ РАСЧЕТНЫХ МОДЕЛЕЙ

С УЧЕТОМ ДЕФОРМАЦИИ ПОПЕРЕЧНОГО СДВИГА

Автореферат

на соискание ученой степени кандидата технических наук

Подписано в печать 26.01.2011 г. Формат .

Гарнитура «Times New Roman». Бумага офсетная. Печать трафаретная.

Усл. Печ. Л. 1,0. Тираж 100 экз. Заказ № 35.

Волгоградский государственный архитектурно-строительный университет

Центр оперативной полиграфии ЦИТ,

400074, г. Волгоград, ул. Академическая, д. 1